Алгоритм вычисления LU-разложения матрицы
Стр 1 из 5Следующая ⇒LU-разложение и LUP-разложение матрицы
LU — разложение(LU-декомпозиция) — представление данной матрицы A в виде произведения
A=LU,
где матрица L является нижне-треугольной с единицами на главной диагонали, U — верхне-треугольная общего вида,
Процесс построения LU-разложения называется методом исключения Гаусса. Сначала удаляется первая переменная из всех уравнений, кроме первого, путем вычитания из этих уравнений первого, умноженного на соответствующий коэффициент. Затем такая же операция выполняется со вторым уравнением, чтобы в третьем и последующих уравнениях отсутствовали первая и вторая переменные. Процесс продолжается до тех пор, по не получим верхне-треугольную матрицу – это и будет искомая матрица U.
Алгоритм вычисления LU-разложения матрицы
Пусть матрица C = A. На каждом i-м шаге в качестве опорного (ведущего) элемента берётся элемент Cii. После этого все элементы текущего i-го столбца, находящиеся ниже i-й строки, делятся на опорный. Далее из всех элементов , находящихся ниже i-й строки и правее i-го столбца (то есть таких что j>i и k>i) вычитается произведение . После этого счётчик iувеличивается на единицу и процесс повторяется пока i<n где n — размерность исходной матрицы. После того как все шаги будут выполнены матрица C будет представлять собой следующую сумму: C=L+U-E, где E —единичная матрица.
LU_Decomposition(A,C)
n=rows(A)
C=A
for i=1 to n
do
for j=i+1 to n
do
Cji=Cji/Cii
for k=i+1 to n
do
Cjk=Cjk-CjiCik
В алгоритме используется три вложенных линейных цикла, так что общую сложность алгоритма можно оценить как O(n³).
Необходимо отметить, что LU-разложение работает корректно не для всех невырожденных матриц. Данный метод не работает корректно, если опорный элемент равен 0, так при этом должно быть выполнено деление на ноль.
Важным классом матриц, для которых LU-разложение всегда работает корректно, является класс симметричных положительно определенных матриц.
Задача: Найти LU-разложение матрицы:
Решение:
а) б)
в) г)
Выбираем в 1-ом столбце матрицы С опорный элемент C11=2. На рис.б) он помечен серым цветом. Делим все элементы первого столбца, начиная со второй строки (С21, С31, C41) на значение опорного элемента. А все элементы, находящиеся ниже первой строки и правее первого столбца вычисляем по формуле (j, k>1) (рис.б). Далее в качестве опорного элемента берём С22=4. Делим элементы второго столбца, начиная с 3-й строки на опорный, а затем вычисляем значение элементов Cjk=Cjk—Cj2*C2j (j,k>2) (рис.в). Выбираем в качестве опорного элемента C 33=1. Делим элементы третьего столбца, начиная с 4-й строки (это один элемент С43 ) на опорный, а затем вычисляем значение элемента C44=C44—C43*C34 (рис.г).
На рис.б) он помечен серым цветом. Делим все элементы первого столбца, начиная со второй строки (С21, С31, C41) на значение опорного элемента. А все элементы, находящиеся ниже первой строки и правее первого столбца вычисляем по формуле (j, k>1) (рис.б). Далее в качестве опорного элемента берём С22=4. Делим элементы второго столбца, начиная с 3-й строки на опорный, а затем вычисляем значение элементов Cjk=Cjk—Cj2*C2j (j,k>2) (рис.в). Выбираем в качестве опорного элемента C 33=1. Делим элементы третьего столбца, начиная с 4-й строки (это один элемент С43 ) на опорный, а затем вычисляем значение элемента C44=C44—C43*C34 (рис.г).
Получили LU-разложение матрицы A:
A L U
Поиск по сайту:
Метод Гаусса и LU — разложение
Метод Гаусса упорядоченного исключения переменных используется для приведения СЛАУ к верхней треугольной форме с последующим решением методом обратной подстановки. Оценка общего числа необходимых операций равна (2/3)п3, где п — число уравнений.
Метод Гаусса основан на разложении
L1c L2
где U — верхняя треугольная матрица; Lkc— нижние столбцовые элементарные матрицы, поддиагональные элементы k-го столбца которых находятся на k-м шаге факторизации следующим образом:
Обращение таких матриц осуществляется заменой знаков внедиа-гональных ненулевых элементов. Умножение матрицы А слева на обращает в ноль поддиагональные элементы k-го столбца матрицы А. Приведенное выше разложение может быть получено умножением матрицы А и получающихся из нее матриц на пары . Тогда
,
где .
Таким образом, исходную СЛАУ АХ = В привели к виду
далее, последовательно умножив левую и правую части на затем на и т.
.
Решение осуществляется по следующему алгоритму:
1) Положить А(°) = А и выполнить шаги факторизации для k = 1,2,…, п — 1 в coответствии со следующими пунктами:
а)для каждого шага определить элементы матрицы Lkc, которые записывают на место обращаемых в ноль элементов матрицы
б)выполнить вычисление значений элементов преобразованной матрицы путем умножения на матрицу, обратную к Lkc:
| i=k+1, k+2,…, n; j=k+1, k+2,…, n. |
в) выполнить вычисление вектора правых частей В(k)путем
умножения на матрицу, обратную к Lkc:
| , i=k+1, k+2,…, n. |
2) Полученную систему решить методом обратной подстановки, учитывая, что .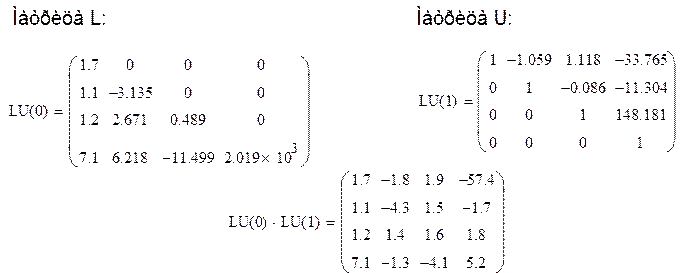
3) Конец алгоритма.
С целью повышения численной устойчивости реализуют алгоритм метода Гаусса с выбором главного элемента по столбцу. Для этого перед выполнением пункта 1а алгоритма необходимо найти т такое, что и переставить местами строки с номерами т и k.
Данный пункт в матричной форме соответствует использованию матриц перестановок Ртk — Тогда факторизация принимает вид
.
Поскольку элементы матриц Lkcв данном алгоритме записывают на место обращенных в ноль элементов матрицы А, то можно решать много СЛАУ с различными правыми частями, не выполняя повторную. Учитывая свойства элементарных нижних столбцовых матриц можно, заметить, что на месте матрицы А получено ее разложение в виде произведения нижней и верхней треугольных матриц:
LU = А,
где , называемого LU — разложением.
Следует иметь в виду, что в результате применения алгоритма на главной диагонали матрицы А и над ней будут записаны элементы матрицы U, под диагональю — элементы матрицы L, но в силу того, что диагональные элементы заняты U, то для диагональных элементов L места нет. Однако в силу свойств нижних столбцовых элементарных матриц, на диагонали L должны находиться только единицы, для их хранения отводить место не обязательно, достаточно просто иметь в виду, что они существуют и не забывать в расчетах.
Для получения
LUX = В
и может быть решена на основе типовых подходов. Обозначим Y = — UX, решим методом прямой подстановки систему LU = В, а затем методом обратной подстановки систему UX = Y. Получим искомый вектор X.
К недостаткам метода Гаусса можно отнести повышенную чувствительность к особенностям матрицы А, невозможность его использования для решения переопределенных систем, в которых число уравнений больше числа неизвестных. 5:
5:
cond(A2)
ans =
1.9000e+05
[pic 3]
Вектор правых частей b2:
[pic 4]
- LU-разложение матрицы.
Теорема. Пусть все ведущие подматрицы [pic 5] , [pic 6] , матрицы [pic 7] являются невырожденными. Тогда [pic 8] единственным образом представима в виде:
[pic 9]
где [pic 10] — нижняя треугольная матрица с единицами на главной диагонали, [pic 11] — верхняя треугольная матрица.
[pic 12]
Элементы матриц [pic 13] могут быть найдены по следующим формулам:
[pic 14]
- Решение СЛАУ с помощью LU разложения.
Пусть решается СЛАУ, при этом имеется LU-разложением матрицы системы. Тогда метод решения СЛАУ, основанный на LU-разложении заключается в следующем. Исходная система [pic 15] представляется в эквивалентном виде:
[pic 16]
Обозначим произведение матрицы [pic 17] на вектор неизвестных [pic 18] через вектор новых неизвестных [pic 19] :
[pic 20]
тогда система примет вид:
[pic 21]
Таким образом, чтобы решить исходную систему общего вида в методе, основанном на LU-разложении, надо решить последовательно две системы, но с треугольными матрицами.
СЛАУ – система с нижней треугольной матрицей с единицами на главной диагонали:
[pic 22]
Ее решение происходит сверху вниз путем последовательной подстановки уже найденных значений [pic 23] . После того, как [pic 24] найден, решается СЛАУ:
[pic 25]
- Анализ результатов, полученных после реализации решения СЛАУ в программе MATLAB.
- Погрешность хорошо обусловленной матрицы (А1)
X—~X=
1.0e-13 *
0.0377
0.2842
0.0888
-0.3197
0.1421
-0.2576
-0.1421
0.0266
-0.0711
0.0178
- Невязка хорошо обусловленной матрицы
A1*~X—b1=
1.0e-12 *
-0.0568
0.0142
0.0853
-0.0284
0.0284
0
-0.0568
-0.0142
-0.1705
0.1137
- Погрешность плохо обусловленной матрицы (А2)
X—~X=
1. 0e-10 *
0e-10 *
0.0105
-0.0961
-0.1269
0.0085
-0.1559
0.0784
-0.1204
-0.0467
-0.0293
0.1993
- Невязка плохо обусловленной матрицы
A2*~X—b2=
1.0e-09 *
-0.0582
-0.2328
0
0.3492
0.2328
0
0.3492
0
0
0.0582
- Исследование на устойчивость к погрешностям исходных данных.
- Возмущение вектора правой части для:
- Хорошо обусловленной матрицы (А1)
~b1=(1+δ)*b1
||δX|| = ||X — ~X|| — норма разности решений, где ~X — решение уравнения A1*X=~b1, полученное после возмущения вектора b1
Возмущение δ | ||δX|| |
0.1 | 6.5276 |
0.01 | 0.6528 |
0.001 | 0.0653 |
0. | 0.0065 |
0.00001 | 0.0007 |
Разность решений X — ~X в зависимости от возмущения:
δ = 0.1 | δ = 0.01 | δ = 0.001 | δ = 0.0001 | δ = 0.00001 | |
X — ~X = | 0.1000 | 0.0100 | 0.0010 | 0.0001 | 0.00001 |
-5.6000 | -0.5600 | -0.0560 | -0.0056 | -0.00056 | |
-0.7000 | -0.0700 | -0.0070 | -0.0007 | -0.00007 | |
-2.4000 | -0.2400 | -0.0240 | -0.0024 | -0.00024 | |
0.5000 | 0.0500 | 0.0050 | 0.0005 | 0.00005 | |
-0. | -0.0600 | -0.0060 | -0.0006 | -0.00006 | |
-1.7000 | -0.1700 | -0.0170 | -0.0017 | -0.00017 | |
0.2000 | 0.0200 | 0.0020 | 0.0002 | 0.00002 | |
0.9000 | 0.0900 | 0.0090 | 0.0009 | 0.00009 | |
-0.8000 | -0.0800 | -0.0080 | -0.0008 | -0.00008 |
- Плохо обусловленной матрицы (А2)
~b2=(1+δ)*b2
||δX|| = ||X — ~X|| — норма разности решений, где ~X — решение уравнения A2*X=~b2, полученное после возмущения вектора b2
Возмущение δ | ||δX|| |
0.1 | 6.5276 |
0.01 | 0.6528 |
0. | 0.0653 |
0.0001 | 0.0065 |
0.00001 | 0.0007 |
Разность решений X — ~X в зависимости от возмущения:
δ = 0.1 | δ = 0.01 | δ = 0.001 | δ = 0.0001 | δ = 0.00001 | |
X — ~X = | 0.1000 | 0.0100 | 0.0010 | 0.0001 | 0.00001 |
-5.6000 | -0.5600 | -0.0560 | -0.0056 | -0.00056 | |
-0.7000 | -0.0700 | -0.0070 | -0.0007 | -0.00007 | |
-2.4000 | -0.2400 | -0.0240 | -0.0024 | -0.00024 | |
0.5000 | 0.0500 | 0.0050 | 0.0005 | 0. | |
-0.6000 | -0.0600 | -0.0060 | -0.0006 | -0.00006 | |
-1.7000 | -0.1700 | -0.0170 | -0.0017 | -0.00017 | |
0.2000 | 0.0200 | 0.0020 | 0.0002 | 0.00002 | |
0.9000 | 0.0900 | 0.0090 | 0.0009 | 0.00009 | |
-0.8000 | -0.0800 | -0.0080 | -0.0008 | -0.00008 |
— как реализовать разложение LU с частичным поворотом в Python?
Переполнение стека- Около
- Продукты
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
- Реклама Обратитесь к разработчикам и технологам со всего мира
- О компании
LU — math-linux. com
com
Пусть $ A $ представляет собой матрицу $ n \ times n $. Факторизация $ LU $ — это процедура разложения $ A $ на произведение нижней треугольной матрицы $ L $ (диагональные элементы L равны единице) и верхней треугольная матрица $ U $, например $ A = LU $ с
$$
L =
[ \слева(
\ begin {array} {c c c c}
1 \\
l_ {21} & 1 \\
\ vdots & \ vdots & \ ddots \\
l_ {n1} & l_ {n2} & \ cdots & 1
\ end {array} \ right)
]
$$
и
$$ U = [ \слева( \ begin {array} {c c c c} u_ {11} & u_ {12} & \ cdots & u_ {1n} \\ & u_ {22} & \ cdots & u_ {2n} \\ & & \ ddots & u_ {n-1, n} \\ & & & u_ {nn} \ end {array} \ right) ] $$
Решение линейной системы
Для разрешения линейной системы: $ Ax = b $, система принимает вид
$$ LUx = b \ Leftrightarrow \ left \ {\ begin {array} {cc} Ly = b & (1), \\ Ux = y & (2).{n} u_ {ij} x_j) & \ forall i = n-1, n-2, \ ldots, 1. \ end {array} \ right. $$
Теоремы
– если факторизация LU существует, то она уникальна.
— Обратимая матрица $ A $ допускает LU-факторизацию тогда и только тогда, когда все ее главные миноры отличны от нуля (главный минор порядка $ k $ является определителем матрицы $ (A) _ {1 \ leq i , j \ leq k} $).
— Если $ A $ только обратимо, тогда $ A $ можно записать как $ A = PLU, $, где $ P $ — матрица перестановок.{(n)} _ {ij}) _ {1 \ leq i, j \ leq n} & L = (l_ {ij}) _ {1 \ leq i, j \ leq n} &
\ end {массив}
$$
Расчет определителя матрицы
LU-разложение также позволяет вычислить определитель $ A $, который равен произведению диагональных элементов матрицы $ U $, если $ A $ допускает LU-факторизацию, поскольку
$$ det (A ) = det (L) \ times det (U) = 1 \ times det (U) = det (U) $$
Разложение матрицы CUR
Выбор столбца (атрибута) и выбор строки — это заключительный этап разложения матрицы CUR.
Выбор атрибута: выбирает атрибуты с высоким уровнем воздействия и сообщает их имена, баллы (как важность) и ранги (по важности).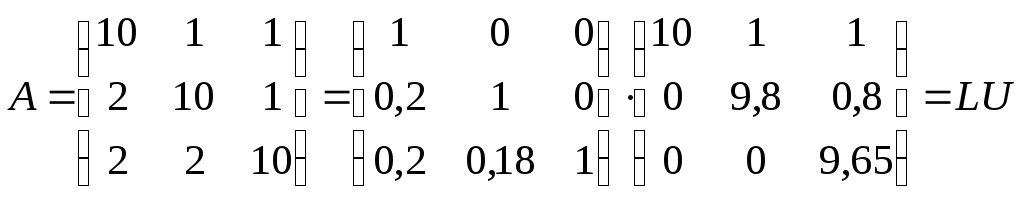
Выбор строки: выбирает строки с высокими показателями кредитного плеча и сообщает их имена, оценки (по важности) и ранги (по важности).
- При разложении матрицы
CUR сначала выбирается j -й столбец (или атрибут) A с вероятностью
p j = min {1, cπ j }для всехj ε {1 ,..., n} Если пользователи разрешают выбор строки, выберите i -ю строку A с вероятностью
pˊ i = min {1, rπˊ i }для всехi ε {1, ..., m}Сообщите имя (или идентификатор) и оценку (как важность) для всех выбранных атрибутов (если важность строки отключена) или для всех выбранных атрибутов и строк (если важность строки включена).

c — это приблизительное (или ожидаемое) количество столбцов, которые пользователи хотят выбрать, а r — это приблизительное (или ожидаемое) количество строк, которые пользователи хотят выбрать.
Чтобы реализовать выбор столбца и строки, необходимо рассчитать вероятность выбора каждого столбца и строки.
Рассчитайте вероятность для каждого столбца следующим образом:
p j = min {1, cπ j }
Рассчитайте вероятность для каждой строки следующим образом:
pˊ i = min {1, cπˊ i } .
Столбец или строка выбираются, если вероятность больше некоторого порога.
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследование
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
определение разложения lu и синонимы разложения lu (английский)
В линейной алгебре, разложение LU (также называемое разложением LU ) факторизует матрицу как произведение нижней треугольной матрицы и верхней треугольной матрицы. Иногда продукт также включает в себя матрицу перестановок. LU-декомпозиция является ключевым этапом в нескольких фундаментальных численных алгоритмах линейной алгебры, таких как решение системы линейных уравнений, обращение матрицы или вычисление определителя матрицы. Его можно рассматривать как матричную форму исключения Гаусса. LU-разложение было введено математиком Аланом Тьюрингом [1] .
Иногда продукт также включает в себя матрицу перестановок. LU-декомпозиция является ключевым этапом в нескольких фундаментальных численных алгоритмах линейной алгебры, таких как решение системы линейных уравнений, обращение матрицы или вычисление определителя матрицы. Его можно рассматривать как матричную форму исключения Гаусса. LU-разложение было введено математиком Аланом Тьюрингом [1] .
Определения
Пусть A будет квадратной матрицей. Разложение LU — это разложение формы
, где L — нижняя треугольная матрица, а U — верхняя треугольная матрица.Это означает, что L имеет только нули над диагональю, а U имеет только нули под диагональю. Например, для матрицы 3 на 3 A ее LU-разложение выглядит следующим образом:
Однако не все матрицы с «хорошим поведением» можно разложить на множители в этой форме. Например, легко проверить (развернув матричное умножение), что. Следовательно, если, то хотя бы одно из и должно быть равно нулю. Однако в любом случае произведение LU становится единичным, в то время как A не обязательно является единичным.Это означает, что такие матрицы не могут быть разложены на LU. Чтобы преодолеть это ограничение, обычно используется LUP-декомпозиция.
Следовательно, если, то хотя бы одно из и должно быть равно нулю. Однако в любом случае произведение LU становится единичным, в то время как A не обязательно является единичным.Это означает, что такие матрицы не могут быть разложены на LU. Чтобы преодолеть это ограничение, обычно используется LUP-декомпозиция.
Разложение LUP (также называемое разложением LU с частичным поворотом ) — это разложение формы
, где L и U снова представляют собой нижнюю и верхнюю треугольные матрицы, а P представляет собой матрицу перестановки, которая при умножении слева на A меняет порядок строк A .Оказывается, все квадратные матрицы могут быть разложены на множители в этой форме [ цитата необходима ] , и факторизация численно стабильна [ цитата необходима ] . Это делает разложение LUP полезным методом на практике.
Разложение LU с полным поворотом (Trefethen и Bau) принимает форму
, где L , U и P определены так же, как и раньше, а Q — это матрица перестановок, которая переупорядочивает столбцы A .
Декомпозиция LDU — это декомпозиция формы
, где D — диагональная матрица, а L и U — треугольные матрицы единиц , что означает, что все элементы на диагоналях L и U едины.
Выше мы требовали, чтобы A была квадратной матрицей, но все эти разложения можно обобщить и на прямоугольные матрицы. В этом случае L и P представляют собой квадратные матрицы, каждая из которых имеет такое же количество строк, что и A , а U имеет точно такую же форму, что и A . Верхний треугольник следует интерпретировать как имеющий только ноль входов ниже главной диагонали, которая начинается в верхнем левом углу.
Пример
Факторизуем следующую матрицу 2 на 2:
Один из способов найти LU-разложение этой простой матрицы — просто решить линейные уравнения путем проверки. Расширение матричного умножения дает
Эта система уравнений недоопределена. В этом случае любые два ненулевых элемента матриц L и U являются параметрами решения и могут быть установлены произвольно на любое ненулевое значение. Следовательно, чтобы найти уникальное разложение LU, необходимо наложить некоторые ограничения на матрицы L и U . Например, мы можем удобно потребовать, чтобы нижняя треугольная матрица L была единичной (т.е. установила все элементы ее главной диагонали в единицы). Тогда система уравнений имеет следующее решение:
В этом случае любые два ненулевых элемента матриц L и U являются параметрами решения и могут быть установлены произвольно на любое ненулевое значение. Следовательно, чтобы найти уникальное разложение LU, необходимо наложить некоторые ограничения на матрицы L и U . Например, мы можем удобно потребовать, чтобы нижняя треугольная матрица L была единичной (т.е. установила все элементы ее главной диагонали в единицы). Тогда система уравнений имеет следующее решение:
Подстановка этих значений в разложение LU выше дает
Существование и уникальность
Квадратные матрицы
Если квадратная матрица A обратима, то
- всегда допускает факторизацию LUP .
- A допускает факторизацию LU (или LDU) тогда и только тогда, когда все его ведущие главные миноры не равны нулю.
- Факторизация LU или LDU уникальна, если мы требуем, чтобы диагональ L (или U ) состояла из единиц.
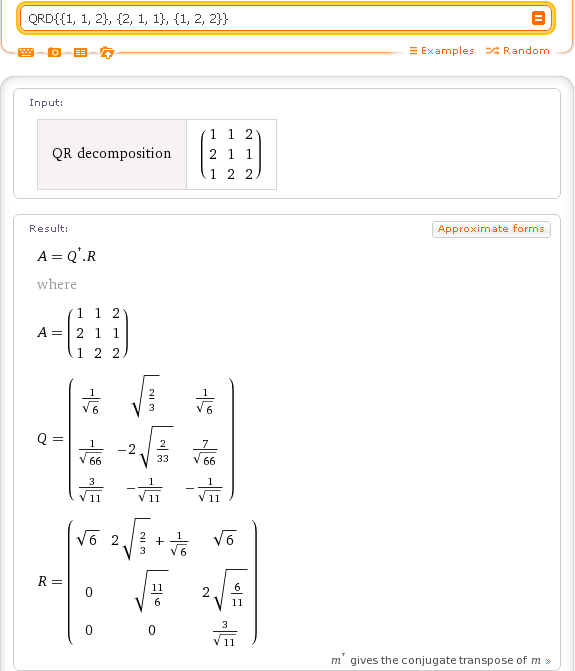
Если квадратная матрица A сингулярна (т.е. не обратима), то
- Может существовать факторизация LU . Фактически, квадратная матрица с рангом k имеет факторизацию LU , если первые k ведущих миноров не равны нулю, хотя обратное неверно.
Симметричные положительно определенные матрицы
Если A является симметричной (или эрмитовой, если A комплексной) положительно определенной матрицей, мы можем расположить материи так, чтобы U было сопряженным транспонированием L . То есть мы можем записать A как
Это разложение называется разложением Холецкого. Разложение Холецкого всегда существует и уникально. Кроме того, вычисление разложения Холецкого более эффективно и численно более стабильно, чем вычисление некоторых других LU-разложений.
Общие матрицы
Для (не обязательно обратимой) матрицы над любым полем известны точные необходимые и достаточные условия, при которых она имеет LU-факторизацию. Условия выражаются в виде рангов определенных подматриц. Алгоритм исключения Гаусса для получения LU-разложения также был расширен на этот наиболее общий случай (Okunev & Johnson 1997).
Условия выражаются в виде рангов определенных подматриц. Алгоритм исключения Гаусса для получения LU-разложения также был расширен на этот наиболее общий случай (Okunev & Johnson 1997).
Алгоритмы
LU-разложение — это в основном модифицированная форма исключения Гаусса.Мы преобразуем матрицу A в верхнюю треугольную матрицу U , удаляя элементы ниже главной диагонали. Алгоритм Дулитла выполняет исключение столбец за столбцом, начиная слева, путем умножения A слева на атомарные нижнетреугольные матрицы. В результате получается нижняя треугольная матрица единиц и верхняя треугольная матрица. Алгоритм Краута немного отличается и строит нижнюю треугольную матрицу и верхнюю треугольную матрицу единиц .
Для вычисления декомпозиции LU с использованием любого из этих алгоритмов требуется 2 n 3 /3 операций с плавающей запятой, игнорируя члены более низкого порядка. Частичное вращение добавляет только квадратичный член; это не относится к полному повороту.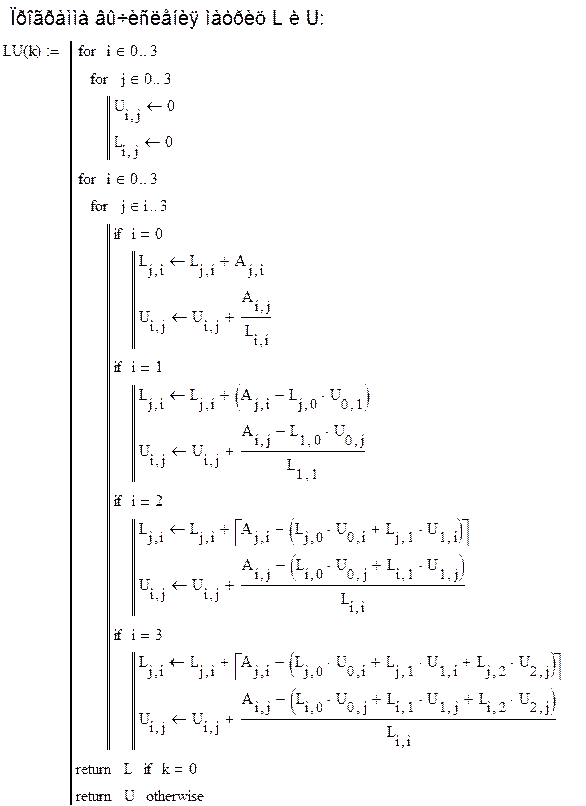 [2]
[2]
Замкнутая формула
Когда LDU-факторизация существует и уникальна, существует замкнутая (явная) формула для элементов L, D и U в терминах отношений определителей определенных подматриц исходной матрицы A (Householder 1975).В частности, и для, — это отношение главной подматрицы к главной подматрице.
Алгоритм Дулиттла
Для матрицы N × N
определяем
, а затем мы выполняем итерацию n = 1, …, N-1 следующим образом.
Мы исключаем элементы матрицы ниже главной диагонали в n -м столбце A ( n-1 ) , добавляя к i -й строке этой матрицы n -й строка умноженная на
для.Это можно сделать, умножив A ( n-1 ) слева на нижнюю треугольную матрицу
.Устанавливаем
После N-1 шагов мы удалили все элементы матрицы ниже главной диагонали, так что мы получили верхнюю треугольную матрицу A ( N-1 ) . Находим разложение
Находим разложение
Обозначим верхнюю треугольную матрицу A ( N-1 ) на U , а.Поскольку матрица, обратная нижней треугольной матрице L n , снова является нижней треугольной матрицей, а умножение двух нижних треугольных матриц снова является нижней треугольной матрицей, следует, что L является нижней треугольной матрицей. Кроме того, видно, что
Получаем.
Понятно, что для того, чтобы этот алгоритм работал, нужно иметь на каждом шаге (см. Определение). Если это предположение в какой-то момент не сработает, необходимо перед продолжением заменить n -ю строкой другой строкой под ней.Вот почему в целом LU-разложение выглядит так.
Реализация алгоритма Дулиттла на C ++
шаблон <класс T> МатрицаМатрица :: lower (void) const { если (строки! = столбцы) { LOG («Неверная квадратная матрица для вычисления нижней треугольной матрицы»); вернуть * это; } Матрица l (столбцы, строки, T (0)); Матрица u (столбцы, строки, T (0)); для (size_t k = 1; k <= строк; k ++) { l. set_entry (k, k, 1); for (int j = k; j <= rows; j ++) { длинная двойная сумма = 0; for (int s = 1; s <= k-1; s ++) { сумма + = l.get_entry (k, s) * u.get_entry (s, j); } u.set_entry (k, j, get_entry (k, j) -sum); } for (int i = k + 1; i <= rows; i ++) { длинная двойная сумма = 0; for (int s = 1; s <= k-1; s ++) { сумма + = l.get_entry (i, s) * u.get_entry (s, k); } l.set_entry (i, k, (get_entry (i, k) -sum) /u.get_entry (k, k)); } } return l; } шаблон <класс T> Матрица
Матрица :: upper (void) const { если (строки! = столбцы) { LOG («Неверная квадратная матрица для вычисления верхней треугольной матрицы»); вернуть * это; } Матрица l (столбцы, строки, T (0)); Матрица u (столбцы, строки, T (0)); для (size_t k = 1; k <= строк; k ++) { л.set_entry (к, к, 1); for (int j = k; j <= rows; j ++) { двойная сумма = 0; for (int s = 1; s <= k-1; s ++) { T lower_entry = l. get_entry (k, s); T upper_entry = u.get_entry (s, j); сумма + = нижняя_запись * верхняя_запись; } T this_entry; this_entry = get_entry (k, j) -сумма; u.set_entry (k, j, this_entry); } for (int i = k + 1; i <= rows; i ++) { двойная сумма = 0; for (int s = 1; s <= k-1; s ++) { T lower_entry = l.get_entry (я, с); T upper_entry = u.get_entry (s, k); сумма + = нижняя_запись * верхняя_запись; } l.set_entry (i, k, (get_entry (i, k) -sum) /u.get_entry (k, k)); } } вернуть u; }
Алгоритмы Crout и LUP
Алгоритм разложения LUP Кормена и др. обобщает разложение матриц Краута. Это можно описать следующим образом.
- Если в первой строке есть ненулевой элемент, то возьмите такую матрицу перестановки, в верхнем левом углу которой есть ненулевой элемент.В противном случае примем за единичную матрицу.
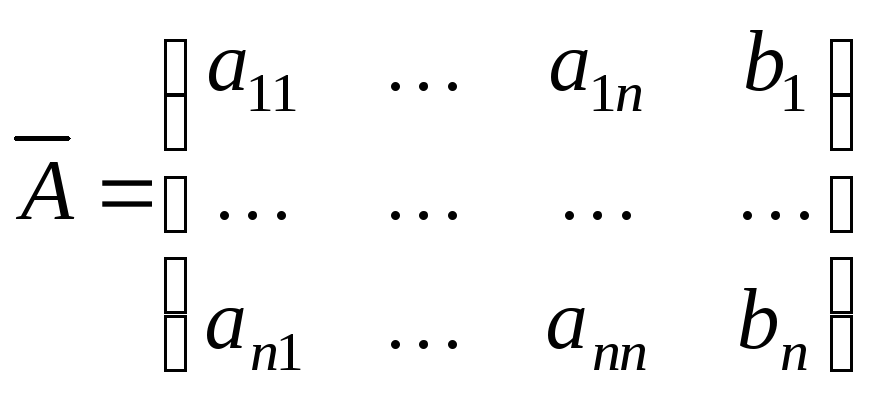 Позволять .
Позволять . - Позвольте быть матрица, из которой получается, удаляя как первую строку, так и первый столбец. Рекурсивно декомпозируйте. Сделайте из, сначала добавив нулевую строку выше, а затем добавив первый столбец слева.
- Сделайте из, сначала добавив нулевую строку вверху и нулевой столбец слева, а затем заменив верхний левый элемент (который в этой точке равен 0) на 1. Сделайте из аналогичным образом и определите. Позвольте быть обратным.
- Здесь то же самое, за исключением (возможно) первой строки. Если первая строка равна нулю, то, поскольку обе имеют нулевую первую строку, и следует, по желанию. В противном случае и имеют такую же ненулевую запись в верхнем левом углу и для некоторой верхней треугольной квадратной матрицы с единицами на диагонали (удаляет записи и добавляет записи через верхний левый угол). Теперь разложение желаемого вида.
Теоретическая сложность
Если две матрицы порядка n могут быть умножены во времени M ( n ), где M ( n ) ≥ n a для некоторого a > 2, то LU-разложение может быть вычислено за время O ( M ( n )).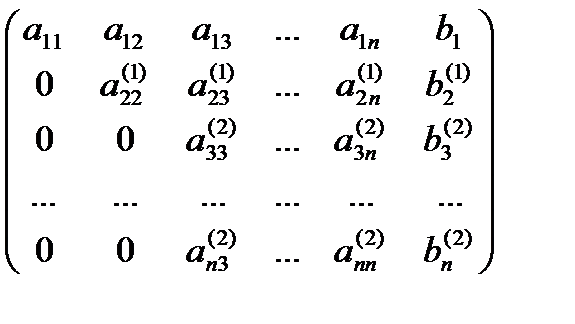 [3] Это означает, например, что существует алгоритм O ( n 2,376 ), основанный на алгоритме Копперсмита – Винограда.
[3] Это означает, например, что существует алгоритм O ( n 2,376 ), основанный на алгоритме Копперсмита – Винограда.
Разложение разреженной матрицы
Разработаны специальные алгоритмы факторизации больших разреженных матриц. Эти алгоритмы пытаются найти разреженные факторы L и U . В идеале стоимость вычислений определяется количеством ненулевых элементов, а не размером матрицы.
Эти алгоритмы используют свободу обмена строками и столбцами для минимизации заполнения (записи, которые изменяются с начального нуля на ненулевое значение во время выполнения алгоритма).
Общая обработка упорядочений, минимизирующих заполнение, может быть решена с помощью теории графов.
Приложения
Решение линейных уравнений
Дана система линейных уравнений в матричной форме
, мы хотим решить уравнение для x с учетом A и b . Предположим, мы уже получили LUP-разложение A , такое, что (или LU-композицию, если она существует, в этом случае) мы можем переписать уравнение эквивалентно как
В этом случае решение выполняется в два логических шага:
- Сначала решаем уравнение относительно y ;
- Во-вторых, мы решаем уравнение для x .

Обратите внимание, что в обоих случаях мы имеем дело с треугольными матрицами ( L и U ), которые могут быть решены напрямую путем прямой и обратной подстановки без использования процесса исключения Гаусса (однако нам действительно нужен этот процесс или его эквивалент для вычисления LU собственно разложение).
Вышеупомянутую процедуру можно многократно применять для решения уравнения несколько раз для разных b . В этом случае быстрее (и удобнее) выполнить LU-разложение матрицы A один раз, а затем решить треугольные матрицы для разных b , вместо того, чтобы каждый раз использовать исключение Гаусса.Можно подумать, что матрицы L и U «закодировали» процесс исключения Гаусса.
Инвертирование матрицы
При решении систем уравнений b обычно рассматривается как вектор, длина которого равна высоте матрицы A . Вместо вектора b у нас есть матрица B , где B - это матрица n на p , поэтому мы пытаемся найти матрицу X (также n - по- п матрица):
Мы можем использовать тот же алгоритм, представленный ранее, чтобы решить для каждого столбца матрицы X . Теперь предположим, что B - это единичная матрица размером n . Из этого следует, что результат X должен быть обратным A . [4]
Вычисление определителя
Учитывая LU-разложение квадратной матрицы A , определитель A может быть вычислен напрямую как
Второе уравнение следует из того факта, что определитель треугольной матрицы - это просто произведение ее диагональных элементов, и что определитель матрицы перестановок равен (-1) S , где S - количество замен строк в разложении. Матричные вычисления . 3-е издание, 1996 г. стр. 121.
- Бау III, Давид; Трефетен, Ллойд Н. (1997), Числовая линейная алгебра , Филадельфия: Общество промышленной и прикладной математики, ISBN 978-0-89871-361-9
- Cormen, Thomas H .; Leiserson, Charles E .; Ривест, Рональд Л .; Стейн, Клиффорд (2001), Введение в алгоритмы , MIT Press и McGraw-Hill, ISBN 978-0-262-03293-3
- Хорн, Роджер А .
 ; Джонсон, Чарльз Р.(1985), Матричный анализ , Cambridge University Press, ISBN 0-521-38632-2. См. Раздел 3.5.
; Джонсон, Чарльз Р.(1985), Матричный анализ , Cambridge University Press, ISBN 0-521-38632-2. См. Раздел 3.5. - Хаусхолдер, Олстон (1975), Теория матриц в численном анализе .
- Окунев Павел; Джонсон, Чарльз (1997), Необходимые и достаточные условия для существования LU-факторизации произвольной матрицы , arXiv: math.NA/0506382.
- Пресс, WH; Теукольский С.А.; Феттерлинг, штат Вашингтон; Фланнери, Б.П. (2007), «Раздел 2.3», Числовые рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8, http://apps.nrbook.com/empanel/index.html?pg=48
Внешние ссылки
Ссылки
Компьютерный код
Интернет-ресурсы
Применение разложения матриц LU для разработки схемы двусторонней аутентификации удаленного пользователя для анонимности
Мы применяем разложение матриц LU для представления схемы двусторонней анонимной аутентификации. Этот документ направлен на повышение безопасности и обеспечение более высокой производительности схемы аутентификации удаленного пользователя. Предлагаемая схема может обеспечивать двустороннюю аутентификацию и согласование сеансового ключа, может быстро проверять действительность введенного пароля и действительно может защитить анонимность пользователя. Безопасность предлагаемой схемы основана на проблеме дискретного логарифмирования (DLP), проблеме Диффи-Хеллмана (DHP) и односторонней хеш-функции. Он может противостоять различным атакам, таким как инсайдерская атака, атака имитации, атака с подменой сервера и атака с украденной смарт-картой.Более того, представленная схема вычислительно эффективна для реальной реализации.
Этот документ направлен на повышение безопасности и обеспечение более высокой производительности схемы аутентификации удаленного пользователя. Предлагаемая схема может обеспечивать двустороннюю аутентификацию и согласование сеансового ключа, может быстро проверять действительность введенного пароля и действительно может защитить анонимность пользователя. Безопасность предлагаемой схемы основана на проблеме дискретного логарифмирования (DLP), проблеме Диффи-Хеллмана (DHP) и односторонней хеш-функции. Он может противостоять различным атакам, таким как инсайдерская атака, атака имитации, атака с подменой сервера и атака с украденной смарт-картой.Более того, представленная схема вычислительно эффективна для реальной реализации.
1. Введение
Схема аутентификации удаленного пользователя позволяет пользователю и удаленному серверу взаимно аутентифицировать друг друга в общедоступных сетевых средах, а затем авторизованный пользователь может получить доступ к службам и ресурсам, которые предоставляются удаленным сервером. Как правило, схема аутентификации на основе пароля обеспечивает эффективный и безопасный способ взаимной аутентификации и позволяет пользователю и серверу устанавливать общий сеансовый ключ для будущей секретной связи после процесса взаимной аутентификации.В 1981 году Лэмпорт [1] впервые предложил схему аутентификации удаленного пользователя на основе пароля для незащищенной связи. С тех пор исследователи предложили множество схем аутентификации удаленных пользователей на основе паролей [2–7] для обеспечения безопасного обмена данными через общедоступную сеть, а также было представлено множество исследований [8–18] для повышения безопасности или улучшения вычислений. и затраты на связь схемы аутентификации удаленного пользователя.
Как правило, схема аутентификации на основе пароля обеспечивает эффективный и безопасный способ взаимной аутентификации и позволяет пользователю и серверу устанавливать общий сеансовый ключ для будущей секретной связи после процесса взаимной аутентификации.В 1981 году Лэмпорт [1] впервые предложил схему аутентификации удаленного пользователя на основе пароля для незащищенной связи. С тех пор исследователи предложили множество схем аутентификации удаленных пользователей на основе паролей [2–7] для обеспечения безопасного обмена данными через общедоступную сеть, а также было представлено множество исследований [8–18] для повышения безопасности или улучшения вычислений. и затраты на связь схемы аутентификации удаленного пользователя.
В общедоступных сетевых средах важно обеспечить анонимность пользователя, чтобы настоящая личность пользователя могла быть раскрыта только авторизованными объектами.В 2000 году Ли и Чанг [19] предложили схему идентификации пользователя с распределением ключей, сохраняющую анонимность пользователя для распределенной компьютерной сети. Однако Ву и Хсу [20] указали, что схема Ли и Чанга не может защитить анонимность пользователя, как они утверждали, и предложили усовершенствованную схему. Позже Ян и др. [21] показали, что схема Ву и Сюй не может противостоять атакам с подделкой личности, и предложили улучшенную схему, которая является более безопасной и эффективной. К сожалению, Mangipudi и Katti [22] представили, что Yang et al.Протокол уязвим для атаки типа «отказ в обслуживании» (DoS) и предлагает безопасную идентификацию и протокол согласования ключей с анонимностью пользователя. Недавно Wang et al. [23] представили безопасный и эффективный протокол идентификации и согласования ключей с анонимностью пользователя, основанный на сложности вычисления эллиптической кривой Диффи-Хеллмана. Стоимость вычислений их схемы ниже и подходит для приложений в вычислительных средах с низким энергопотреблением.
Однако Ву и Хсу [20] указали, что схема Ли и Чанга не может защитить анонимность пользователя, как они утверждали, и предложили усовершенствованную схему. Позже Ян и др. [21] показали, что схема Ву и Сюй не может противостоять атакам с подделкой личности, и предложили улучшенную схему, которая является более безопасной и эффективной. К сожалению, Mangipudi и Katti [22] представили, что Yang et al.Протокол уязвим для атаки типа «отказ в обслуживании» (DoS) и предлагает безопасную идентификацию и протокол согласования ключей с анонимностью пользователя. Недавно Wang et al. [23] представили безопасный и эффективный протокол идентификации и согласования ключей с анонимностью пользователя, основанный на сложности вычисления эллиптической кривой Диффи-Хеллмана. Стоимость вычислений их схемы ниже и подходит для приложений в вычислительных средах с низким энергопотреблением.
В 2004 году Чой и Юн [24] предложили новый подход к шифрованию и распределению данных с использованием LU-разложения матриц.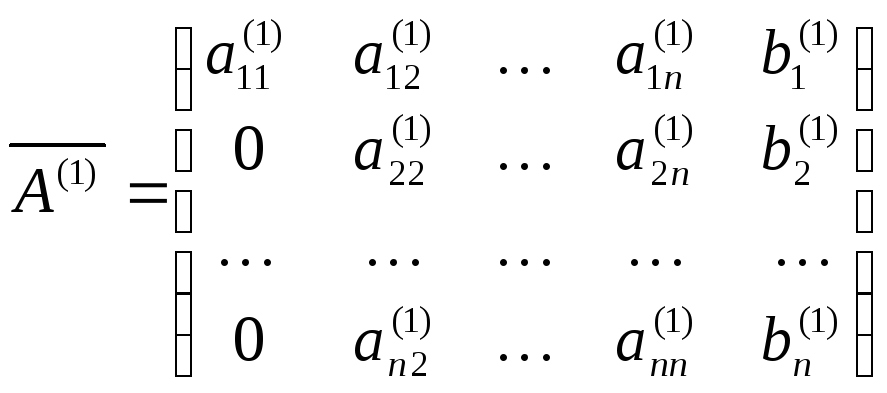 Затем Патан и др. [25, 26] предложили две эффективные схемы двусторонней аутентификации удаленного пользователя, основанные на LU-разложении матриц. Тем не менее, у этих схем есть несколько слабых мест, например, они не могут противостоять атакам повторного воспроизведения, они не могут сохранить анонимность пользователя, сервер и пользователи не могут договориться о сеансовом ключе и так далее. Для решения этих проблем Tseng et al. [27] предложили схему аутентификации пользователя, основанную на LU-разложении матриц. Они утверждали, что их схема может противостоять атакам повторного воспроизведения, атакам с подделкой и инсайдерским атакам и обеспечивать анонимность пользователей.Принимая во внимание, что после тщательного анализа мы обнаруживаем, что схема Ценг и др. По-прежнему уязвима для инсайдерских атак, атак с украденными смарт-картами, неэффективна из-за неправильного пароля для входа в систему и не обеспечивает анонимности пользователя. Чтобы преодолеть эти существующие недостатки схемы Ценг и др.
Затем Патан и др. [25, 26] предложили две эффективные схемы двусторонней аутентификации удаленного пользователя, основанные на LU-разложении матриц. Тем не менее, у этих схем есть несколько слабых мест, например, они не могут противостоять атакам повторного воспроизведения, они не могут сохранить анонимность пользователя, сервер и пользователи не могут договориться о сеансовом ключе и так далее. Для решения этих проблем Tseng et al. [27] предложили схему аутентификации пользователя, основанную на LU-разложении матриц. Они утверждали, что их схема может противостоять атакам повторного воспроизведения, атакам с подделкой и инсайдерским атакам и обеспечивать анонимность пользователей.Принимая во внимание, что после тщательного анализа мы обнаруживаем, что схема Ценг и др. По-прежнему уязвима для инсайдерских атак, атак с украденными смарт-картами, неэффективна из-за неправильного пароля для входа в систему и не обеспечивает анонимности пользователя. Чтобы преодолеть эти существующие недостатки схемы Ценг и др.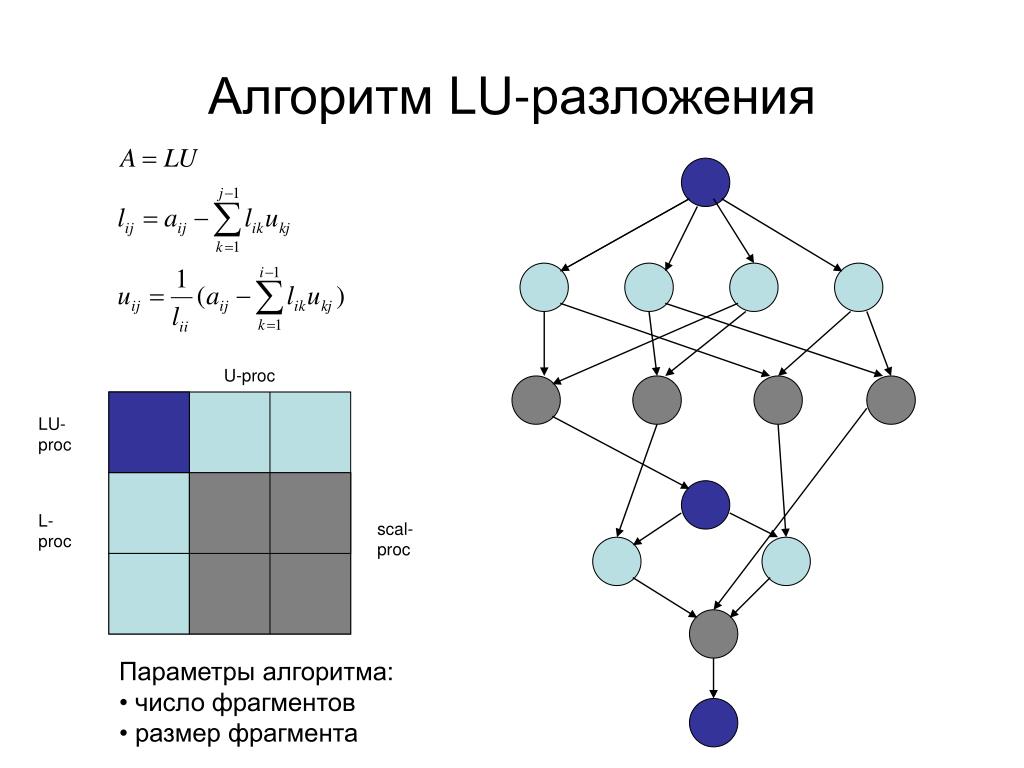 , Мы предлагаем новую схему двусторонней аутентификации с анонимностью пользователя с использованием LU-разложения матриц. Анализ показывает, что наша схема не только обеспечивает лучшие свойства безопасности, но и более эффективна, чем другие схемы аутентификации.
, Мы предлагаем новую схему двусторонней аутентификации с анонимностью пользователя с использованием LU-разложения матриц. Анализ показывает, что наша схема не только обеспечивает лучшие свойства безопасности, но и более эффективна, чем другие схемы аутентификации.
Остальная часть этого документа организована следующим образом: Раздел 2 вводит необходимые предварительные сведения к этой статье. Краткий обзор схемы Ценга и др. Представлен в разделе 3. Раздел 4 описывает криптоанализ схемы Ценга и др. Предлагаемая схема и соответствующий анализ представлены в разделах 5 и 6 соответственно. Наконец, мы завершаем эту статью в разделе 7.
2. Предварительные сведения
В этом разделе мы вводим некоторую базовую информацию о LU-разложении матриц и проблеме дискретного логарифмирования, и они являются математической основой предлагаемой нами двусторонней аутентификации удаленного пользователя. протокол с анонимностью пользователя.
2.1. LU-разложение матриц
Исходя из теории матриц, LU-разложение факторизует матрицу как произведение нижней треугольной матрицы и верхней треугольной матрицы.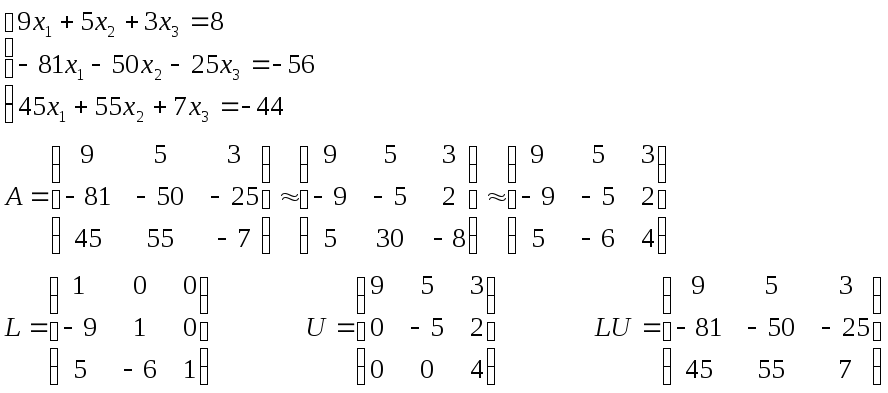 Позвольте быть квадратной матрицей; LU-разложение матрицы - это форма, где - нижняя треугольная матрица, а - верхняя треугольная матрица. Это означает, что над диагональю только нули, а под диагональю только нули. Например, для матрицы ее LU-разложение выглядит как
Позвольте быть квадратной матрицей; LU-разложение матрицы - это форма, где - нижняя треугольная матрица, а - верхняя треугольная матрица. Это означает, что над диагональю только нули, а под диагональю только нули. Например, для матрицы ее LU-разложение выглядит как
Если - сингулярная матрица ранга, она допускает LU-разложение, если все главные миноры -начальные отличны от нуля.
В системе аутентификации личности мы предполагаем, что это количество пользователей, которое система может поддерживать. Мы можем ввести декомпозицию LU в систему аутентификации пользователей, чтобы обеспечить безопасность системы. На этапе инициализации системы удаленный сервер генерирует симметричную матрицу в качестве своего главного секретного ключа. С помощью разложения LU сервер может разделить матрицу симметричного ключа на произведение нижней треугольной матрицы и верхней треугольной матрицы, то есть, и сохранить эти матрицы на других серверах.
Так как это симметричная матрица, у нас есть, что для и, а произведение -й строки матрицы и -ого столбца матрицы равно произведению -й строки матрицы и -й столбец матрицы.
 0001
0001 6000
6000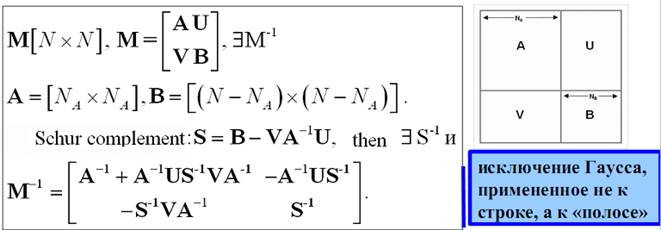 001
001 00005
00005