Разное

Логарифм в маткаде десятичный: Как ввести десятичный логарифм в маткаде

что такое в математике, вычисление, как правильно решать LG, примеры

Содержание:

  • Десятичный логарифм числа – что это такое в математике
  • Определение и формулы десятичного логарифма
  • График десятичного логарифма
  • Как правильно решать задачи на десятичных логарифмах, примеры

Содержание

  • Десятичный логарифм числа – что это такое в математике
  • Определение и формулы десятичного логарифма
  • График десятичного логарифма
  • Как правильно решать задачи на десятичных логарифмах, примеры

Десятичные логарифмы широко применялись в вычислениях до появления компактных калькуляторов. m\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Логарифм будет иметь смысл только при соблюдении ряда условий:

\(k>0,\;\;k\neq1,\;\;n>0\)

Примечание

Если за основание логарифма взята цифра 10, то такой логарифм называется десятичным. Его принято обозначать знаком lg и не указывать основание, равное 10. Например, правильно записывать lg 20, а не log10 20.

Десятичные логарифмы обладают теми же особенностями, что и любые другие логарифмы при основании больше, чем 1.  Например, большему из нескольких положительных чисел будет соответствовать и больший десятичный логарифм. Десятичный логарифм числа, которое больше 0, но меньше 1, будет отрицательным, а больше единицы – положительным.

Десятичные логарифмы обладают рядом характерных признаков:

  1. Десятичный логарифм положительного целого числа, представленного единицей и следующими за ней нулями, представляет собой целое неотрицательное число, которое будет равно количеству нулей в записи выбранного числа: lg 10=1, lg 10000=4.
  2. Десятичный логарифм десятичной неотрицательной дроби, записанной как единица с предыдущими нулями, будет равен (-m). В этом случае m – количество нулей, предшествующих единице, в том числе с учетом и нулевой целой части: lg 0,1=-1, lg 0,0001=-4.
  3. Если умножить число на 10m, то десятичный логарифм увеличится на число m. Это можно записать формулой: lg (a10m) = lg a + lg 10m = lg a + m.
  4. Если разделить число на 10k, то его десятичный логарифм станет меньше на k.

Определение и формулы десятичного логарифма

Определение

Десятичным логарифмом числа k является решение уравнения: 10n=k

В алгебре свойства десятичных логарифмов описываются целым рядом формул. Их использование позволяет значительно проще решать сложные задачи, снижает вероятность ошибок.

Основными формулами десятичных логарифмов являются:

\(1. m\right)\;=\;mlg\;(x)\\6.\;lg\;\sqrt[p]x\;=\;\frac{lg\;(x)}p\)

До изобретения калькуляторов вышеописанные формулы использовались очень широко. Например, они позволяют с легкостью выполнить умножение многозначных чисел. Для этого необходимо воспользоваться простым алгоритмом:

  • найти по таблице логарифмы заданных чисел;
  • в соответствии с третьим свойством сложить их и получить логарифм произведения;
  • по полученному логарифму используя таблицу найти и само произведение чисел.

Аналогичным образом можно выполнить и деление многозначных чисел. Только в данном случае логарифмы следует не складывать, а вычитать.

Использование десятичных логарифмов дает возможность даже без калькулятора выполнить извлечение из корня или возведение в степень.

В настоящее время десятичные логарифмы практически полностью вытеснены натуральными. Они сохраняются только в исторически укоренившихся областях математики, например, в построении логарифмической шкалы.

 

Отрицательные десятичные логарифмы представляют в искусственной форме. В ней они имеют отрицательную характеристику и положительную мантиссу.

Рассмотрим пример:

\(lg\;(0.005)\;=\;\overset-3.69897\\\)

Иначе эту запись можно представить так:

\(lg\;(0.005)\;=\;\overset-3.69897=\;-3\;=\;0.69897=\;-2.30103\\\)

Для перевода десятичного отрицательного логарифма в искусственную форму необходимо увеличить на единицу абсолютную величину характеристики. Над полученным числом поставить знак «минус». Вычесть из девяти все цифры мантиссы кроме последней, не равной нулю.

Ее следует вычесть из десяти. Полученные в ходе вычитания разности записать на тех же местах мантиссы, где находились вычитаемые числа. Нули на конце остаются без изменений.

График десятичного логарифма

При рассмотрении логарифмируемого числа в качестве переменной получаем функцию:

\(y\;=\;lg\;(x)\\\)

Она будет определена при всех значениях

x больше нуля. Область значений функции лежит в пределе:

\(E_{(y)}=(-\infty;\;+\infty)\\\)

График десятичного логарифма представляет кривую линию, называемую логарифмикой.

Всюду, где функция определена, она дифференцируема, непрерывна и монотонно возрастает. Ее производную можно задать формулой:

\(\frac d{d_x}=lg\;x\;=\frac{lg\;e}x\\\)

Ось ординат рассматриваемой функции является вертикальной асимптотой, так как

\(\underset{x\rightarrow0+0}{\lim\;lg\;x}=\;-\infty\\\)

Как правильно решать задачи на десятичных логарифмах, примеры

Рассмотрим примеры решения задач с использованием десятичных логарифмов.

Задача 1. Вычислить значение выражения

\(lg\;\left(400\right)\;+\;lg\;\frac1{40}\)

Для решения данного примера воспользуемся формулой суммы:

\(lg\;\left(400\right)\;+\;lg\;\frac1{40}\;=\;lg\;\left(\frac{400\times1}{40}\right)=\;lg\;10\;=\;1\)

Задача 2. Упростите выражение:

\(lg\;\frac18\;-\;3\;lg\;4\)

В данном случае необходимо воспользоваться формулой степени:

\(lg\;\frac18\;-\;3\;lg\;4\;=\;lg\;2^{-3}\;-\;3\;lg\;2^2\;=\;-3lg\;-\;3\times2\;lg\;2\;=\;-9\;lg\;2\)

Задача 3. 3\;=\;3\times2\;lg\frac3{10}\;-\;2\times3\;lg\;3\;=\;6\;lg\;\frac3{10}\;-\;6\;lg\;3\)

Теперь применим свойство частного, откроем скобки и приведем подобные слагаемые:

\(6\;lg\;\frac3{10}\;-\;6\;lg\;3\;=\;6\;(lg\;3\;-\;lg\;10)\;-\;6\;lg3\;=\;6\;lg\;3\;-\;6\;lg\;10\;-\;6\;lg\;3=\;-\;6\;lg\;10=\;-6\times1\;=\;-6\)

Насколько полезной была для вас статья?

Рейтинг: 1.75 (Голосов: 4)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

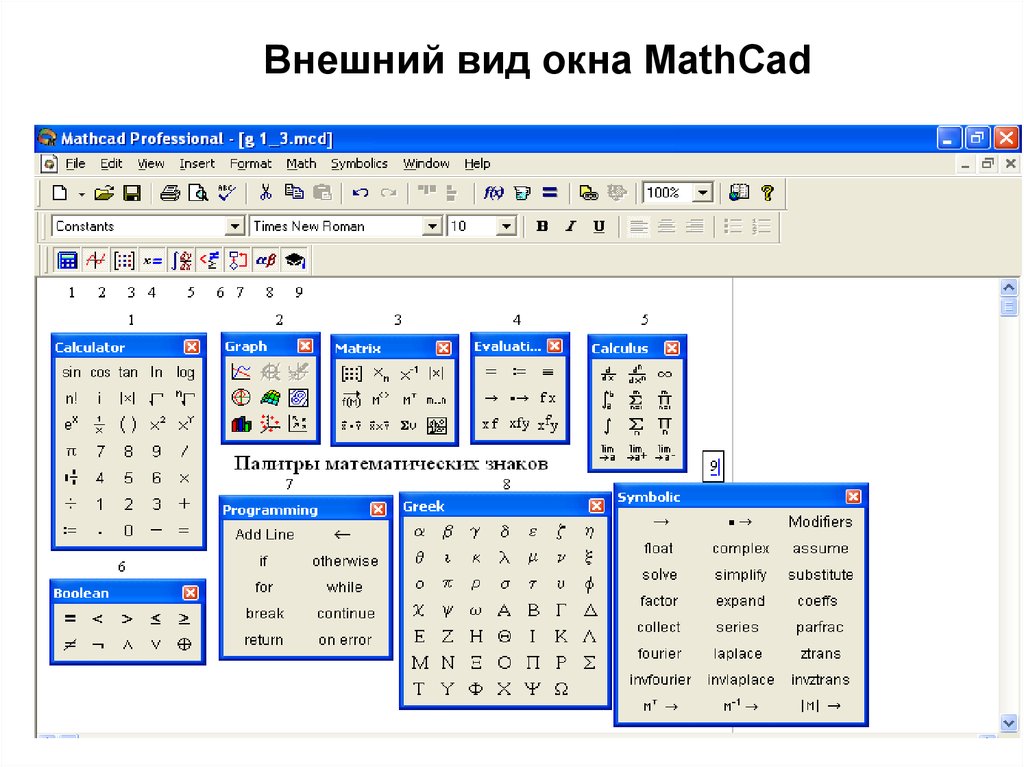
П2.3. Панель Calculator (Калькулятор) MathCAD 12

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

  • Главная
    • /
  • База знаний
    • /
  • CAD / CAM
    • /
  • MathCAD 12
  • Команды меню
  • Панель Math
  • Панель Calculator
  • Панель Graph
  • Панель Matrix
  • Панель Evaluation
  • Панель Calculus
  • Панель Boolean
  • Панель Controls

Таблица П2.3. Панель Calculator (Калькулятор)


Оператор
Перевод
Горячие клавиши

Sin
Синус
  

Cos
Косинус
  

Tan
Тангенс
  

Ln
Натуральный логарифм
  

Log
Десятичный логарифм
  

n!
Факториал
<!>

1
Ввод мнимой единицы
<1>, <i>

|x|
Модуль
<Shift>+<\>

√
Квадратный корень
<\>

√n
Корень n-й степени
<Ctrl>+<\>

ex
Экспонента
  

1/x
Обратная величина
  

()
Скобки
<‘>

x2
Возведение в квадрат
  

xy
Возведение в степень у
<^>

π
Ввод числа n
<Ctrl>+<Shift>+<P>

/
Деление
</>

. /
Смешанное число
<Ctrl>+<Shift>+<+>

X
Умножение
<*>

+
Деление в одну строку
<Ctrl>+</>

+
‘ Сложение
<+>

:=
Присваивание
<:>

.
Десятичная точка
<.>

0,1,2 ….. 9
Числа 0…9
<0>,<1>, <2> ….. <9>

—
Вычитание («минус»)
<->

:=
Вычислить численно («равно»)
<=>

Теги MathCAD САПР

Сюжеты MathCAD

Глава 1 Основы работы с системой Mathcad 11

9906 0

Глава 10 Работа с информационными ресурсами Mathcad 11

6933 0

Глава 2 Работа с файлами Mathcad 11

12361 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2361 s

Матлаб Раунд | Синтаксис и примеры Matlab Round

«Округление» выполняется в математике для ограничения количества значащих цифр. Например, значение «пи» равно 3,14159265358979323, и использование всего этого значения каждый раз в вычислениях может стать громоздким и ненужным. Чтобы этого избежать, округляем значения до необходимого количества знаков после запятой. По этой причине мы в основном видим значение числа пи как 3,14 (округляя значение до 2 знаков после запятой).

В MATLAB мы используем функцию округления для округления числовых значений.

Синтаксис:

R = округление (A)

R = округление (A, N)

Описание: округление

ближайшее целое число. В случае массива все элементы «А» округляются до ближайшего целого числа.

  • R = округление (A, N) округляет «A» до «N» цифр. Если N < 0, округление производится слева от десятичной точки 9.0026

    Примеры округления в Matlab

    Давайте теперь разберемся с кодом функции округления в MATLAB на различных примерах:

    Пример #1

    В этом примере мы возьмем матрицу 3 x 3. Для нашего первого примера мы выполним следующие шаги:

    1. Инициализация входной матрицы 3 x 3
    2. Передать матрицу в качестве входных данных функции округления

    Код:

    А = [3,11  4,015  11,092; -3,45 10,8 3,001; 4.981 2,012 4,1];

    [Объявление входной матрицы 3 x 3]

    R = круглый (А)

    [Передача входной матрицы в функцию округления] [Математически, если мы округлим все элементы в приведенной выше матрице, мы получим следующие значения:

    3     4      11

    -3    11     3

    5     2      4]

    Ввод:

    A = [3,11  4,015  11,092; -3,45 10,8 3,001; 4,981 2,012 4,1];
    R = круглый (А)

    Вывод:

    Как видно из вывода, мы получили округленные значения всех элементов матрицы.

    Пример #2

    В этом примере мы возьмем матрицу 2 x 2. Для этого примера мы выполним следующие шаги:

    1. Инициализация входной матрицы 2 x 2
    2. Передать матрицу в качестве входных данных функции округления

    Код:

    А = [1,11  0,01; -4,45  12,803];

    [Объявление входной матрицы 2 x 2]

    R = круглый (А)

    [Передача входной матрицы в функцию округления] [Математически, если мы округлим все элементы в приведенной выше матрице, мы получим следующие значения:

    1     0

    -4    13]

    Ввод:

    A = [1,11  0,01; -4,45 12,803];
    R = round(A)

    Вывод:

    Как видно из вывода, мы получили округленные значения всех элементов матрицы. В приведенных выше 2 примерах мы видели, что все значения были округлены до ближайших целых чисел.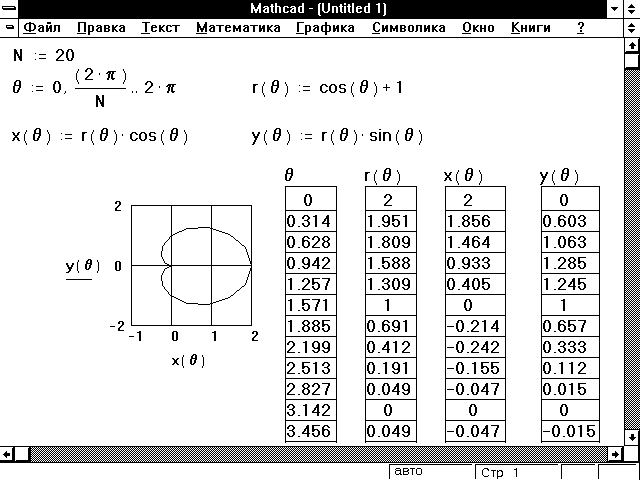 Далее мы научимся округлять значения до необходимого количества знаков после запятой.

    Пример #3

    В этом примере мы возьмем матрицу 2 x 2 и округлим каждый элемент до 1 знака после запятой. i.there будет одна цифра после десятичной точки на выходе. Для этого примера мы выполним следующие шаги:

    1. Инициализация входной матрицы 2 x 2
    2. Передать матрицу в качестве первого аргумента функции округления
    3. Передать «1» в качестве второго аргумента функции округления

    Код:

    А = [1,1134  0,09341; 4,43415 1,8103];

    [Объявление входной матрицы 2 x 2]

    R = круглый(A, 1)

    [Передача входной матрицы в функцию округления. Второй аргумент, «1», передается, чтобы указать количество цифр, которые нам нужны после десятичной точки] [Математически, если мы округлим все элементы в приведенной выше матрице до 1 st знаков после запятой, мы получим следующие значения:

    1,1   0,1

    4,4    1,8]

    Ввод:

    А = [1,1134  0,09341; 4,43415 1,8103];
    R = round(A,1)

    Вывод:

    Как видно из вывода, все элементы в матрице округлены до первого десятичного знака]. Далее мы узнаем, как округлять цифры справа от десятичной точки

    Пример №4

    В этом примере мы возьмем матрицу 2 x 2 и округлим ее до одной точки справа от десятичной запятой. место. т. е. все цифры справа от «десятки» станут равными нулю или будут округлены. Для этого примера мы выполним следующие шаги:

    1. Инициализация входной матрицы 2 x 2
    2. Передать матрицу в качестве первого аргумента функции округления
    3. Передать «-1» в качестве второго аргумента функции округления

    Код:

    А = [321,1134  20,09341; 34.43415 14.8103];

    [Объявление входной матрицы 2 x 2]

    R = круглый (A, -1)

    [Передача входной матрицы в функцию округления. Второй аргумент, «-1», будет округлять все цифры до разряда десятков] [Математически, если мы округлим все элементы в приведенной выше матрице до десятков, мы получим следующие значения:

    320    20

    30    10]

    Ввод:

    A = [321,1134  20,09341; 34. 43415 14.8103];
    R = round(A, -1)

    Вывод:

    Как видно из вывода, все элементы в матрице округлены, а цифры до десятков стали равны нулю]

    Заключение

    • Функция округления используется в MATLAB для округления числовых значений.
    • «округление» по умолчанию округляет значения до ближайшего целого числа. Аргумент может быть передан, если нам нужно округлить значения до какого-то другого места.

    Рекомендуемые статьи

    Это руководство по Matlab Round. Здесь мы также обсудим введение и синтаксис раунда Matlab, а также различные примеры и его реализацию в коде. Вы также можете ознакомиться со следующими статьями, чтобы узнать больше —

    1. Cell to String MATLAB
    2. Данные импорта Matlab
    3. Матлаб Фопен
    4. Матлаб Фопен

    Начало работы

    Начало работы
    Начало работы с MATLAB Служба поддержки

    Выражения

    Как и большинство других языков программирования, MATLAB предоставляет математические выражения , но, в отличие от большинства языков программирования, эти выражения включают в себя целые матрицы. Строительные блоки выражений
    • Переменные
    • номеров
    • Операторы
    • Функции

    Переменные

    MATLAB не требует никаких объявлений типов или выражений размеров. Когда MATLAB встречает новое имя переменной, он автоматически создает переменную и выделяет соответствующий объем памяти. Если переменная уже существует, MATLAB изменяет ее содержимое и при необходимости выделяет новую память. Например
       число_студентов = 25
      создает матрицу 1 на 1 с именем num_students и сохраняет значение 25 в ее единственном элементе. Имена переменных состоят из буквы, за которой следует любое количество букв, цифр или знаков подчеркивания. MATLAB использует только первые 31 символ имени переменной. MATLAB чувствителен к регистру; он различает прописные и строчные буквы. A и a являются , а не одной и той же переменной. Чтобы просмотреть матрицу, назначенную любой переменной, просто введите имя переменной.

      Номера

      MATLAB использует обычную десятичную запись с дополнительной десятичной точкой и начальным знаком плюс или минус для чисел. В научной нотации используется буква e для указания коэффициента масштабирования в десятой степени. Воображаемые числа использует либо i , либо j в качестве суффикса. Некоторые примеры допустимых номеров:
         3 -99 0,0001
9.6397238 1.60210e-20 6.02252e23
1и -3,14159j 3e5i
        Все числа хранятся внутри с использованием формата long , определенного стандартом IEEE для операций с плавающей запятой. Числа с плавающей запятой имеют конечную точность примерно из 16 значащих десятичных цифр и конечный диапазон примерно от 10 -308 до 10 +308 . (Компьютер VAX использует другой формат с плавающей запятой, но его точность и диапазон почти такие же.)

        Операторы

        В выражениях используются знакомые арифметические операторы и правила приоритета. 9       мощность '       комплексно-сопряженное транспонирование ( )    указать порядок оценки

        Функции

        MATLAB предоставляет большое количество стандартных элементарных математических функций, включая abs , sqrt , exp и sin . Извлечение квадратного корня или логарифма отрицательного числа не является ошибкой; соответствующий комплексный результат выдается автоматически. MATLAB также предоставляет множество дополнительных математических функций, включая функции Бесселя и гамма-функции. Большинство этих функций принимают сложные аргументы. Чтобы получить список элементарных математических функций, введите
           помогите эльфу
          Чтобы получить список более сложных математических и матричных функций, введите
             помощь
помогите элмату
            Некоторые функции, такие как sqrt и sin , являются встроенными . Они являются частью ядра MATLAB, поэтому они очень эффективны, но вычислительные детали недоступны. Другие функции, такие как gamma и sinh , реализованы в М-файлах. Вы можете увидеть код и даже изменить его, если хотите. Несколько специальных функций предоставляют значения полезных констант.
            pi      3.14159265
            i      imaginary unit, -1
            j      same as i
            eps      floating-point relative точность, 2 -52
            realmin     наименьшее число с плавающей запятой, 2 -1022
            realmax     largest floating-point number, (2-)2 1023
            inf infinity
            nan Not-a-number

            Бесконечность генерируется делением ненулевого значения на ноль или вычислением хорошо определенных математических выражений, которые переполняют , т.

    • Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *