Линейное представление нод: Линейное представление нод многочленов | stud-baza.bitballoon.com

§1.1.2 Наибольший общий делитель. Алгоритм Евклида

Если dделитаиdделитb, тоd — общий делительчиселаиb. Так как делителей чиселаиbконечное число, то и общих делителей чиселаиbконечное число. Среди любого конечного числа целых чисел существует наибольшее. Наибольший из общих делителей называетсянаибольшим общим делителем чиселаиbи обозначается НОДили простоАналогично вводится наибольший делитель нескольких целых чиселЕсли наибольший общий делитель чиселравен 1, то эти числа называютсявзаимно простыми. Числа попарно взаимно простые являются и взаимно простыми, но числа взаимно простые не обязательно попарно взаимно простые. Например, числа 10, 12, 27 взаимно простые, но пары 10 и 12, 12 и 27 имеют общие множители.

Алгоритм Евклиданахождения наибольшего общего делителя двух целых чисел. Пустьаиb– положительные целые числа иПрименим теорему о делении с остатком несколько раз:

. .. … … …

Процесс деления предыдущего остатка на следующий конечен, так как в последовательности:

может быть только конечное число чисел ( не более, чемbчисел).

Пусть х– общий делитель чиселаиb. Тогда двигаясь от равенства к следующему, начиная с первого, получимделится нах,делится нахи т.д.,делится нах. Двигаясь же от последнего равенства к первому, заметим, чтоделится наделится наи т.д.,bделится на,аделится на. Таким образом,- общий делитель чиселаиb, делящийся на любой другой общий делитель этих чисел, т.е.Таким образом, последний ненулевой остаток в алгоритме Евклида – наибольший общий делитель.

Пример.Найти НОД(1173, 323).

Решение:

Ответ:17.

Упражнения и задачи

1. Найти наибольший общий делитель систем чисел:

а) 546 и 231; б) 1001 и 6253; в) 1517 и 2257;

г) 2737, 9163 и 9639; д) 1411, 4641 и 5253.

2. Доказать, что если то

3. Доказать, что если аделится наb, то

4. Для любого целого положительного числа тдоказать равенство:

5. Если тоДоказать.

6. Доказать, что

7. Доказать, что для любых натуральных аиbимеет место равенство:

8. Если тоДоказать.

§1.1.3 Теорема о линейном представлении наибольшего общего делителя

Теорема.Еслито существуют целые числаииv, для которых

Доказательство:Рассмотрим множество всех целых чисел видагдехиу— любые целые числа

Это множество не пусто, в частности, ему принадлежат числа аиb. Ведьаможно представить в видеаb— в видеДля любых двух целых чисел из этого множества частное от деления одного на другое также принадлежит множествуМ. Действительно, еслито

Пусть — наименьшее положительное число в множествеМ. Тогда любое число изМделится на числобез остатка. Действительно, остаток должен принадлежать множествуМи должен быть меньше, а этому условию удовлетворяют лишь остатки, равные нулю.

Таким образом, и а, иbделятся набез остатка, т.е.– их общий делитель. Очевидно, чтоделится на любой другой их общий делитель, а это означает, что■

Пример.Найти линейное представление наибольшего общего делителя чисел 1173 и 323.

Решение:Из примера, приведенного в предыдущем параграфе, известно, что НОД(1173, 323) = 17. Будем подниматься по равенствам алгоритма Евклида вверх:

Ответ:НОД

Теорема Евклида.Еслиасделится наb,сиbвзаимно просты, тоаделится наb.

Доказательство:Так както по теореме о линейном представлении НОД существуют числаииv, для которых

Тогда

Из условия следует, что слагаемое асиделится наb, слагаемоеabтакже делится наb. Отсюда,аделится наb. Что и требовалось доказать. ■

Калькулятор НОД и НОК по алгоритму Евклида

Наибольший общий делитель (НОД) чисел a и b — это наибольшее число, на которое делятся без остатка числа a и b.

Среди всех способов нахождения наибольшего общего делителя для двух чисел алгоритм Евклида наиболее удобный и простой.

---

Нахождения НОД и НОК по алгоритму Евклида методом деления

Как известно, деление с остатком целых чисел a

— делимое и b — делитель, где b ≠ 0, подразумевает нахождение таких целых чисел q и r, что выполняется равенство:
a = b ∙ q + r, где
q — называется неполным частным,
r — остаток от деления, который не может быть отрицательным числом и по модулю не может быть больше делителя.

Суть метода состоит в том, что сначала выбираем наибольшее из двух чисел, для которых требуется найти НОД и делим большее число на меньшее. Если остаток от деления не равен нулю, делим делитель на остаток от деления, так продолжаем до тех пор, пока остаток от деления не будет равен нулю.

Пример 1

Найдем НОД (36; 30), для этого сначала найдем остаток от деления 36 на 30
36 : 30 = 1 (остаток 6), так как 36 = 30 ∙ 1 + 6, остаток от деления не равен нулю, поэтому продолжаем деление, разделим 30 на 6
30 : 6 = 5 (остаток 0) так как 30 = 6 ∙ 5 + 0, остаток от деления равен нулю, значит НОД равен предыдущему остатку от деление 6

Ответ: НОД (36; 30) = 6
Чтобы найти наименьшее общее кратное НОК чисел a и b необходимо произведение a и b разделить на НОД (a; b)
НОК (36; 30) = (36 ∙ 30) : 6 = 180

---

Пример 2

Найдем НОД (176; 36), для этого сначала найдем остаток от деления 176 на 36
176 : 36 = 4 (остаток 32) так как 176 = 36 ∙ 4 + 32, остаток от деления не равен нулю, поэтому продолжаем деление, разделим 36 на 32
36 : 32 = 1 (остаток 4) так как 36 = 32 ∙ 1 + 4, остаток от деления не равен нулю, поэтому продолжаем деление, разделим 32 на 4
32 : 4 = 8 (остаток 0) так как 32 = 4 ∙ 8 + 0, остаток от деления равен нулю, значит НОД равен предыдущему остатку от деление 4
Ответ: НОД (176; 36) = 4
Чтобы найти наименьшее общее кратное НОК чисел a и b необходимо произведение a и b разделить на НОД (a; b)

НОК (176; 36) = (176 ∙ 36) : 4 = 1584

---

Нахождения НОД и НОК по алгоритму Евклида методом вычитания

Суть метода вычитания состоит в том, что необходимо из большего числа вычитать меньшее, если результат вычитания не равен нулю, тогда уменьшаемое заменяем на получившуюся разность, если разность равна нулю, то НОД равен предыдущему значению разности.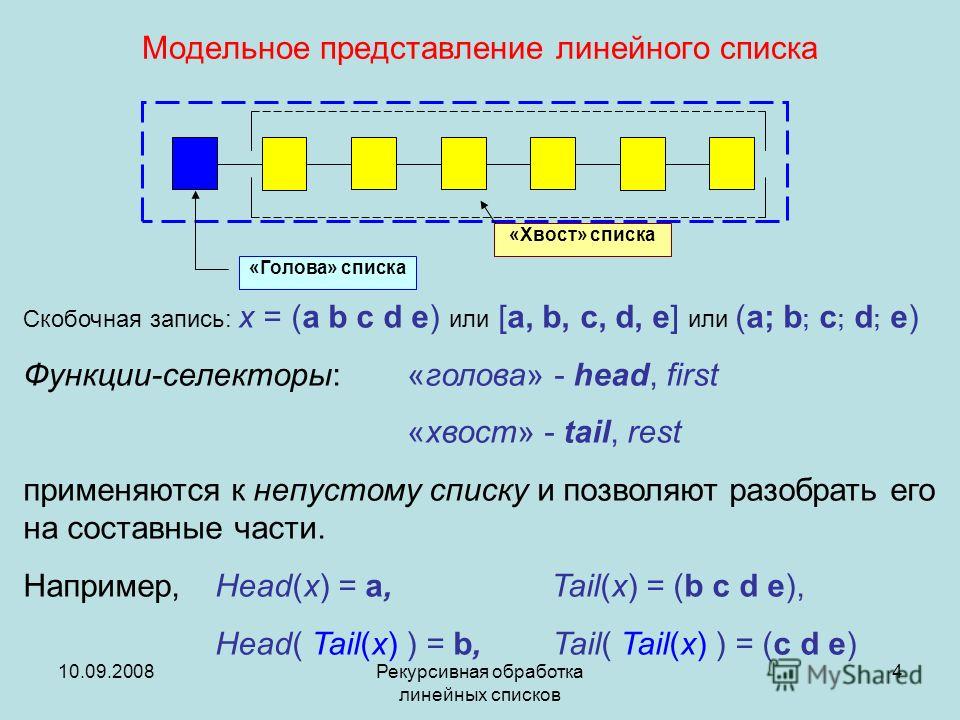

Приведем примеры:

Пример 1

Найдем НОД (36; 30)
36 — 30 = 6
30 — 6 = 24
24 — 6 = 18
18 — 6 = 12
12 — 6 = 6
6 — 6 = 0
Ответ: НОД (36; 30) = 6
Чтобы найти наименьшее общее кратное НОК чисел a и b необходимо произведение a и b разделить на НОД (a; b)
НОК (36; 30) = (36 ∙ 30) : 6 = 180

---

Пример 2

Найдем НОД (176; 36)
176 — 36 = 140
140 — 36 = 104
104 — 36 = 68
68 — 36 = 32
36 — 32 = 4

32 — 4 = 28
28 — 4 = 24
24 — 4 = 20
20 — 4 = 16
16 — 4 = 12
12 — 4 = 8
8 — 4 = 4
4 — 4 = 0
Ответ: НОД (176; 36) = 4
Чтобы найти наименьшее общее кратное НОК чисел a и b необходимо произведение a и b разделить на НОД (a; b)
НОК (176; 36) = (176 ∙ 36) : 4 = 1584

нейронных сетей. Графическое представление линейной… | by Amit Swain

Нейронные сети

Рассмотрим следующий график:

Рисунок 1: Отдельный нейрон

Приведенный выше график просто представляет линейное уравнение: x 2 + w 3 * x 3 + b (1)

Где w1, w2, w3 называются весами, а b — член пересечения, называемый смещением. Таким образом, приведенный выше график является просто графическим представлением простого линейного уравнения. Уравнение также может быть векторизовано следующим образом:

y = W.X + b (2)

Где X = [x1, x2, x3] и W = [w1, w2, w3].T. .T означает транспонирование . Это потому, что мы хотим, чтобы скалярное произведение дало нам желаемый результат, то есть w1 * x1 + w2 * x2 + w3 * x3. Это дает нам векторизованную версию нашего линейного уравнения.

С помощью машинного обучения мы, по сути, пытаемся выяснить, что если нам дано большое количество данных (пары X и соответствующие y), можем ли мы написать алгоритм для определения оптимальных значений W и б? Нам нужно найти способ для нашей модели найти оптимальные значения для W и b, а не абсолютные значения. Абсолютных значений, вероятно, даже не существует, учитывая ограничения нашей математической модели, поскольку мы предполагаем линейную функцию для задачи, которая в действительности может быть гораздо более сложной, и мы не знаем, что это за функция.

Взяв наблюдаемые данные и предложенную модель, мы хотим написать алгоритм для получения значений W и b, которые лучше всего соответствуют данным, и, в конечном счете, таким образом мы узнаем приблизительную функцию, которая отображает входные данные в выходные данные наши данные. Этот тип алгоритма называется алгоритм оптимизации , и существует несколько различных алгоритмов оптимизации, которые обычно используются при обучении нейронных сетей.

Допустим, у нас есть набор данных с примерами формы (60000, 28, 28). Первое измерение — это просто количество примеров, которые у нас есть, поэтому каждый пример имеет форму (28, 28). Если мы развернем этот массив 28 на 28 в одно измерение, он станет 28 * 28 = 784-мерным вектором. Теперь его, вероятно, можно смоделировать как линейное уравнение, верно? Учитывая функции от x1 до x784, мы получаем выход y. Это можно представить так:

Рисунок 2: Один нейрон с функциями 784

Это может действительно работать для действительно простых задач, но в большинстве случаев эта модель окажется недостаточной. Здесь нейронные сети могут быть более эффективными.

Оказывается, мы можем выучить гораздо более сложные функции, просто каскадируя линейных функций одну за другой — и это единственная дополнительная вещь, которую делает узел в нейронной сети (в отличие от узла в линейном уравнении, показанном выше). ), заключается в том, что функция активации применяется к каждому линейному выходу. Функция активации предназначена для того, чтобы помочь нейронной сети найти нелинейные шаблоны в данных, потому что, если мы просто каскадируем узлы, подобные тем, которые описаны выше в примере с линейным уравнением, даже со многими слоями каскадных линейных функций, результат будет по-прежнему быть линейной функцией; это означает, что после обучения модели она изучит линейную функцию, которая лучше всего соответствует данным. Это проблема, потому что во многих, если не в большинстве случаев, карта ввода-вывода будет намного сложнее, чем линейная функция. Таким образом, активация придает модели большую гибкость и позволяет ей изучать нелинейные паттерны.

Теперь, вместо того, чтобы устанавливать y как взвешенную сумму наших входных признаков, мы можем получить несколько скрытых выходных данных, которые представляют собой взвешенные суммы наших входных признаков, прошедших через функцию активации, а затем получить взвешенные суммы этих скрытых выходных данных и так далее. . Мы делаем это несколько раз, а затем получаем наш выход y. Этот тип модели дает нашему алгоритму гораздо больше шансов изучить сложную функцию.

Рисунок 3: Нейронная сеть с двумя скрытыми слоями

В приведенной выше сети у нас есть два скрытых слоев . Первый слой со всеми функциями X называется входным слоем, а выходной слой y называется выходным слоем. В этом примере на выходе есть только один узел . Скрытый слой может иметь много узлов или очень мало узлов в зависимости от того, насколько сложной может быть проблема. Здесь оба скрытых слоя имеют по 2 узла. Каждый узел дает выходные данные линейной функции после того, как линейные выходные данные проходят через функцию активации, и принимает входные данные от каждого узла предыдущего слоя. Все W и все b, связанные со всеми этими функциями, должны быть «выучены» нашим алгоритмом, поскольку он пытается оптимизировать эти значения, чтобы наилучшим образом соответствовать заданным данным. Обратите внимание, что общее количество обучаемых параметров на любом уровне зависит от количества узлов в этом слое, а также от количества узлов в предыдущем слое. Например, обучаемые параметры для скрытый слой 1 можно рассчитать как (количество узлов слоя) * (количество узлов предыдущего слоя) + (количество узлов слоя). Почему? Первая часть очевидна: если каждый узел слоя соединен с каждым узлом предыдущего слоя, мы можем просто перемножить количество узлов этих двух слоев, чтобы получить общее количество весовых параметров. Кроме того, смещение из предыдущего уровня также будет связано с каждым узлом в слое — это дает нам второй член. Итак, за скрытый

слой 1 , получаем: 2 * 2 + 2 = 6 обучаемых параметров.

В задаче классификации рукописных цифр у нас будет 128 узлов для двух скрытых слоев, у нас будет 10 узлов для выходного слоя, где каждый узел соответствует одному выходному классу, и, конечно, мы уже знаем, что вход 784-мерный вектор.

Мы говорили о том, что каждый узел имеет взвешенную сумму входов предыдущего уровня. И прежде чем эта сумма будет передана узлам следующего уровня, она проходит через другую функцию, называемую функцией активации. Итак, каждый узел на самом деле делает две вещи. Первый шаг — это взвешенная сумма, назовем ее Z:9.0003

Z = W.X + b (3)

Вторым шагом в узле является вывод функции активации, назовем его A:

A = ( 8

8) 4)

В нейронных сетях используются различные типы функций активации. Одним из наиболее распространенных является выпрямленный линейный блок функции ReLU. Это довольно простая функция: это линейная функция для всех положительных значений и просто устанавливается на 0 для всех отрицательных значений. Что-то вроде этого:

Рисунок 4: Линейная сумма и функция активации

Другой функцией активации, обычно используемой в задачах классификации, является softmax . Эта функция дает нам оценки вероятности для различных узлов, в данном случае 10 узлов выходного слоя, которые в сумме дают 1. Эта активация дает нам вероятности для различных классов с учетом входных данных. Класс с наибольшей вероятностью дает нам наш прогноз.

Из проекта: Базовая классификация изображений с TensorFlow от Амита Суэйна

Понимание строительных блоков графовых нейронных сетей (введение) | by Giuseppe Futia

Intuitions (с работающим кодом) о нейронной структуре для анализа и обучения на основе данных графа

Этот пост представляет собой введение в серию статей о Graph Neural Networks (GNN). Цель этой серии состоит в том, чтобы предоставить подробное описание с интуицией и примерами строительных блоков GNN.

В этой серии я также поделюсь работающим кодом с использованием Numpy, Pytorch и наиболее известных библиотек, принятых в этой области, таких как Deep Graph Library (DGL) и Pytorch Geometric. В конце этой серии вы сможете комбинировать эти строительные блоки и создавать нейронную архитектуру для выполнения задач анализа и обучения графических данных.

В этой серии будут проанализированы основные компоненты для настройки GNN, включая (i) входной слой, (ii) слой (слои) GNN и (iii) слой (слои) прогнозирования многослойного персептрона (MLP).

Структура для анализа и декомпозиции стандартных архитектур GNN основана на недавней статье под названием «Сравнение графовых нейронных сетей», метаданные которой доступны ниже:

, Ю., и Брессон, X. (2020). Сравнительный анализ графовых нейронных сетей. Препринт arXiv arXiv:2003.00982 .
Источник: https://arxiv.org/abs/2003.00982

Этот пост не охватывает основы теории графов и нейронных сетей. В качестве введения в эту тему я предлагаю следующую статью:

Ноу-хау по теории графов и глубокому обучению

Обучение графам и геометрическое глубокое обучение — часть 0 Основные компоненты

Входной слой определяет начальное представление графических данных, которые становятся входными данными для слоя (слоев) GNN. По сути, идея состоит в том, чтобы присвоить представление признаков узлам и ребрам графа.

Уровень GNN кодирует информацию о структуре графа. Затем он использует эту информацию для обновления исходного представления узлов и ребер.

Слой предсказания MLP выполняет определенную задачу обучения, включая классификация узлов или предсказание канала с использованием представления закодированного графа, полученного в качестве выходных данных от уровня(ей) GNN.

Этот пост представляет входной слой и основные принципы, лежащие в основе слоя GNN. В следующих статьях будут описаны различные типы слоев GNN, объяснены связанные функции и показаны основные различия между ними. Параллельно я представлю обзор традиционных слоев прогнозирования MLP для выполнения конкретных задач с данными графа.

Этот анимированный gif описывает функции узла, обновленные посредством распространения сети GNN. Исходное изображение взято с домашней страницы веб-сайта GraphSAGE. данные графа, назначая признаки узлам и ребрам. Для простоты в настоящее время я рассматриваю только функции узла.

Самый простой способ представить узлы на графе — использовать one-hot векторов. Это представление обычно используется для различения разных слов в словаре для задач НЛП. В нашем случае он используется для представления разных узлов графа. Длина вектора, представляющего каждый узел, равна количеству узлов, и для каждого вектора элемент в другом положении устанавливается равным 1, а другие элементы устанавливаются равными 0.

Чтобы прояснить это представление, следующий скрипт создает график с 5 узлами, представленный с помощью однократных векторов.

 импортировать numpy как npX = np.eye(5, 5) 
 n = X.shape[0] 
 np.random.shuffle(X)print(X) -- вывод:[[0. 0. 1. 0. 0.] # Узел 1 
 [0. 0. 0. 1. 0.] # Узел 2 
 [1. 0. 0. 0. 0.] # .. 
 [0. 0. 0. 0. 1.] # .. 
 [0. 1. 0. 0. 0.]] # Узел 5 

Каждая строка этой матрицы представляет узел графа. Чтобы присвоить начальные функции каждому из этих узлов, входной слой применяет линейное преобразование (также называемое проекцией ) к горячим векторам, которые кодируют представления узлов. Кратко описывая линейное преобразование, определение выглядит следующим образом:

 Y = WX + b 

Как сообщает Dwivedi et al., значение смещения b не используется для линейного преобразования в случае однократных векторов. Таким образом, следующие сценарии выполняют линейное преобразование:

 # Размер элементов узла (встраивание) 
 emb = 3# Матрица весов (инициализирована согласно Glorot & Bengio (2010)) W = np.random.uniform(-np. sqrt(1. / emb), np.sqrt(1. / emb), (n, emb))print(W) -- вывод: 
 [[-0.34857891 -0.5419972   0.43603217] 
 [ 0.26261991  0.04720523 -0.42555547] 
 [-0.09968833  0.3218483   0.09688095] 
 [-0.36646565  0.37652735 -0.45564272] 
 [-0.24990413 -0.50164433 -0.51217414]] 
 --# Linear projection 
 L_0 = X. dot(W) print(L_0)-- output:[[-0.09968833  0.3218483   0.09688095] 
 [-0.36646565  0.37652735 -0.45564272] 
 [-0.34857891 -0.5419972   0.43603217] 
 [-0.24990413 -0.50164433 -0.51217414] 
 [ 0.26261991  0.04720523 -0.42555547]] 

Шаг проекции назначает d -мерное векторное представление каждого узла в графе. В этом примере однократные векторы длиной 5, представляющие узлы, отображаются (или проецируются) в плотные вектора признаков длиной 3.

Перефразируя Dwivedi et al.:

Целью входного слоя является встраивание входных признаков узлов (и ребер) в d-мерный вектор скрытых признаков. Это новое представление получается с помощью простого линейного преобразования (также известного как проекция).

Чтобы прояснить этот аспект, вы можете проанализировать следующий блок:

 # X: Горячие векторы, представляющие узлы 
 [  [0. 0. 1. 0. 0.]   # Узел 1 - 1 элемент в  3-й позиции   
 [0.  0. 0. 1. 0.]  0 в остальных позициях  
 [1. 0. 0. 0. 0.] 
 [0. 0. 0. 0. 1.] 
 [0. 1. 0. 0. 0.]] # W: Матрица весов 
 [[-0,34857891 -0,5419972 0,43603217] 
 [ 0,26261991 0,04720523 -0,42555547] 
  [-0.09968833  0.3218483   0.09688095] # Emphasis to the   3rd   row   
 [-0.36646565  0.37652735 -0.45564272] 
 [-0.24990413 -0.50164433 -0.51217414]]# L_0 (projection) = X.dot(W) 
 [[  -0.09968833  0.3218483   0.09688095  ] #   Features of Node 1,   [-0.36646565  0.37652735 -0.45564272]      represented by the   3rd   row   
 [-0.34857891 -0.5419972   0.43603217]     of the weight matrix   
 [-0.24990413 -0.50164433 -0,51217414] 
 [ 0.26261991 0.04720523 -0.42555547]] 

Текущие функции были сгенерированы случайным образом. Как следствие, эти функции фактически не передают никакой информации об узлах. Однако эти первоначальные характеристики узлов будут обновляться посредством двух разных шагов:

• Агрегирование характеристик соседних узлов с помощью уровня (слоев) GNN.
• Обучение нейронной архитектуры для определенной цели с помощью уровня (слоев) MLP.

В конце этого двойного процесса мы сможем получить встраивание представления узлов, которое будет характеризоваться особенностями, передающими конкретную информацию. Другими словами, векторное представление узлов будет выражать значимую информацию, которую мы, люди, должны быть в состоянии распознать, наблюдая за графом. В простейшем случае аналогичные встроенные функции будут назначены аналогичным узлам графа.

Уровень 9 GNN0110

Целью слоя GNN является обновление d -мерного представления узлов, полученного из входного слоя. Эта цель достигается вычислением, как это определено Dwivedi et. al, «рекурсивное распространение по окрестностям» через так называемую «инфраструктуру передачи сообщений». Основная идея этой структуры заключается в том, что каждая функция узла обновляется функциями своих соседей. Соседние функции передаются целевому узлу в виде сообщений через ребра. Как следствие, новое представление узла кодирует и представляет локальную структуру графа. Для выполнения этого шага нам нужна структура, описывающая отношения (ребра) между узлами в графе. В этом нам помогает матрица смежности, описывающая отношения между узлами в графе.

Рассмотрим следующий скрипт, который инициализирует случайную матрицу смежности в графе из 5 узлов:

 # Случайно сгенерированная матрица смежности 
 A = np.random.randint(2, size=(n, n)) 
 np.fill_diagonal (A, 1) # Включить цикл # Следующие строки являются тривиальным подтверждением для создания симметричной 
 # матрицы Adj, которая определяет ребра неориентированного 
 # графа из 5 узлов 
 A = (A + A.T) 
 A[ A > 1] = 1print(A) -- output:[  [1 1 1 0 1]  # Подключения к узлу 1 
 [1 1 1 1 1] 
 [1 1 1 1 0] 
 [0 1 1 1 0] 
 [1 1 0 0 1]] 

Каждая строка матрицы смежности представляет соединения, идентифицируемые элементом 1 , к узлу. Например, первая строка указывает, что узел 1 соединен сам с собой, узлом 2, узлом 3 и узлом 5. С другой стороны, узел 1 не соединен с узлом 4, поскольку значение в позиции (1, 4) равно 0.

Давайте посмотрим, что произойдет, если мы умножим матрицу смежности на выходные данные входного слоя, который применил проекцию:

 # A: Матрица смежности 
 [  [1 1 1 0 1]   # Подключения к узлу 1  
 [1 1 1 1 1] 
 [1 1 1 1 0] 
 [0 1 1 1 0] 
 [1 1 0 0 1]]# L_0: Output from the input layer 
 [  [-0.09968833  0.3218483   0.09688095] # Features of Node 1   
 [-0.36646565  0.37652735 -0.45564272] 
 [-0.34857891 -0.5419972   0.43603217] 
 [- 0,24990413 -0,50164433 -0,51217414] 
 [ 0,26261991 0,04720523 -0,42555547]]# L_1 = A.dot(L_0) 
 [  [-0,55211298 0.20358368 -0.34828506] # Что это?   
 [-0.8020171  -0.29806065 -0.86045919] 
 [-1.06463701 -0.34526588 -0.434
] 
 [-0.96494868 -0.66711419 -0.53178468] 
 [-0.20353407  0.74558089 -0.78431723]] 

To better understand what is happened to the node representations, рассмотрим следующий скрипт, который суммирует d -мерное представление Узла 1 с d-мерным представлением самого себя, Узла 2, Узла 3 и Узла 5.

 print(L_0[0, :] + L_0[ 1, :] + L_0[2, :] + L_0[4, :]) -- выход: 
   [-0.55211298  0.20358368 -0.34828506]i  # L_1 = A.dot(L_0) 
 [  [-0.55211298  0.20358368 -0.34828506] # Features of Node 1,   
 [-0.8020171  -0.29806065 -0.86045919]     obtained summing the   
 [-1.06463701 -0.34526588 -0.434
]     features of local neighbors   
 [-0.96494868 -0.66711419 -0.53178468] 
 [-0.20353407  0.74558089 -0.78431723]] 

As you can see, the updated vector representation of Node 1 corresponds to агрегация (в данном случае операция суммирования) признаков соседей. Другими словами, это представление кодирует локальную структуру графа.

Одна из ключевых идей этого представления заключается в том, что при суммировании L слоев в нейронной архитектуре результирующее представление целевого узла агрегирует признаки узлов, расстояние которых равно L от целевого узла. Такое поведение является результатом «рекурсивной диффузии окрестностей».

Как подчеркивают Двиведи и др.:

«Наложение L GNN слоев позволяет сети создавать представления узлов из L-hop окрестностей каждого узла».

Основные различия между различными уровнями GNN состоят в типе агрегации, которая выполняется за счет использования структуры локального графа. В простейшей формулировке GNN, такой как сверточные сети Vanilla Graph (GCN), агрегация/обновление представляет собой 9 операций.0007 изотропная операция. Это означает, что характеристики соседних узлов учитываются одинаково. Более продвинутые нейронные архитектуры, такие как Graph Attention Network (GAT), вводят анизотропных операций, в которых вклад каждого соседнего узла в агрегацию взвешивается в соответствии с его важностью.

Что дальше?

Нейронные сети графов для мультиреляционных данных

От GCN к R-GCN: кодирование структуры графов знаний с помощью нейронных архитектур (примеры в коде NumPy)

вычисляется слоем GAT, предлагаю прочитать следующую статью, в которой дается подробное объяснение «от математики до NumPy».