Линейная математика: Линейная алгебра: пробный заезд / Хабр

темы, основы, методы, применение, примеры

Линейная алгебра – это раздел математики, в рамках которого изучаются самые разнообразные объекты линейной природы. В числу таких объектов относят линейные уравнения и пространства, отображения и т.д.

Основным объектом линейной алгебры является линейное пространство — понятие, обобщающее:

• множество V₃ векторов в пространстве и
• множество M_mn(R) матриц одного типа с линейными операциями, заданными на этих множествах.

Элементы линейного пространства называют векторами, обобщая термин из векторной алгебры. Само линейное пространство часто называют векторным.

Линейные пространства — один из самых распространенных математических объектов, и применение линейной алгебры далеко не исчерпывает векторной и матричной алгебрами.

В линейном пространстве действуют две операции:

• сложение векторов и
• умножение вектора на число, которые подчиняются аксиомам линейного пространства.

Однако могут вводиться и другие операции и соответственно дополнительные аксиомы. Эти операции задают дополнительные отношения в линейном пространстве, которые тоже изучаются в линейной алгебре и часто используются в различных приложениях.

Среди базовых инструментов линейной алгебры можно назвать матрицы и  определители, а также сопряжение. В разделе «Линейная алгебра» на нашем сайте можно найти основные определения, кроме того, примеры с подробным решением, а также видеоуроки. Если не нашли нужную тему, или есть трудности с решением каких-то типовых задач — пишите об этом в комментариях.

Перечень тем курса линейной алгебры

Линейная алгебра

Рангом матрицы А называется наибольший из порядков ее миноров, не равных нулю. Обозначается ранг матрицы: r(A) или rang(A). Методы нахождения ранга матрицы Суще…

Линейная алгебра

Общая формула вычисления определителя матрицы 3 на 3 довольно громоздка. Поэтому для вычисления определителя 3 порядка существует метод под названием — пр. ..

Линейная алгебра

Этот метод заключается в следующем: расширенную матрицу системы путем элементарных преобразований нужно привести к ступенчатому виду. К элементарным преобразова…

Линейная алгебра

Решение методом Крамера

Линейная алгебра

Запишем систему линейных алгебраический уравнений (СЛАУ) в матричном виде: AX = B где А — матрица системы, составленная из коэффициентов, стоящих перед не…

Линейная алгебра

Как находить обратную матрицу? Рассмотрим несколько примеров по нахождению обратной матрицы.     Видеоурок на тему — обратная матрица

Линейная алгебра

Определитель 4 порядка на видео

Линейная алгебра

Сформулируем основные свойства определителей матрицы. Величина определителя не изменится от замены строк столбцами. Величина определителя от перестановки двух л…

Линейная алгебра

Видеоурок на тему: определитель 3 порядка

Линейная алгебра

Определение: Алгебраическое дополнение Aij элемента aij называется число: Aij=(-1)i+jMij, где Mij — минор элемента aij Как найти алгебраическое дополнение. ..

Как линейная алгебра используется в машинном обучении?

В предыдущей статье речь шла о математическом анализе. Продолжая серию публикаций к запуску авторского «Онлайн-курса по математике в Data Science Lite», поговорим о применении линейной алгебры в машинном обучении (завершит цикл статья о теории вероятностей и статистике – прим. ред.). За примерами далеко ходить не нужно: напротив, очень трудно найти такую сферу машинного обучения, в которой не используется линейная алгебра. Причем не только ее основные методы, вроде операций с векторами и матрицами, но и продвинутые вроде сингулярного разложения матрицы (Singular Value Decomposition, SVD), метода главных компонент (Principal Component Analysis, PCA) и метода опорных векторов (Support Vector Machines, SVM). Последний – один из основных алгоритмов машинного обучения.

Далеко не каждый курс линейной алгебры, даже на математических факультетах, рассматривает все ее приложения в машинном обучении. (То же самое можно сказать и о статистике, которая также является одной из основ Data Science и машинного обучения). Это обусловливает необходимость специальных курсов математики для Data Science.

Основы

Линейная алгебра работает с векторами и матрицами – а точнее, с их линейными комбинациями, также являющимися векторами и матрицами. Математически вектор можно представить набором действительных чисел:

Такой набор может представлять очень разные сущности: например, геометрический вектор в некоторой системе координат (при этом числа a_i умножаются на векторы базиса), полином (числа a_i умножаются на xⁱ) и вообще любую линейную комбинацию каких-либо элементов. Матрица – это такой же набор действительных чисел, но организованный в виде прямоугольника. Матрицу тоже можно представить в виде длинного вектора, если поставить ее столбцы друг на друга.

Что в машинном обучении можно представить в виде векторов и матриц? Практически всё! Например, одна строка из набора данных – это вектор, каждый элемент которого представляет значение некоторого признака. Весь тренировочный набор данных (или, в случае нейронной сети, один batch из этого набора) – это матрица. Изображение, которое будет распознавать сверточная нейронная сеть – тоже матрица чисел, соответствующих отдельным пикселям. Градиент функции потерь – это вектор, и так далее.

Произведение векторов, умножение матрицы на вектор и произведение матриц – все это используется в машинном обучении. Например, модель линейной регрессии с вектором весов w и вектором признаков x можно записать в виде произведения векторов, если добавить в вектор признаков x[0] = 1:

Поскольку результат линейной регрессии – произведение векторов, произведение матрицы тренировочного набора данных на вектор весов дает вектор предсказаний модели. Если вычесть из него вектор истинных значений, получится вектор ошибок, который можно передать в функцию потерь.

В качестве примера перемножения матриц представим, что у нас есть набор изображений для обучения сверточной нейронной сети, и мы хотим дополнить этот набор поворотами этих изображений, чтобы сеть могла распознавать изображения независимо от их наклона. Поворот изображения – это частный случай умножения матрицы векторов координат на матрицу трансформации, которую также изучает линейная алгебра. Матрица трансформации для поворота координат на угол theta выглядит так:

Поворот исходного изображения (Original) на 112.5 градусов

Измерения

Норма вектора – это термин линейной алгебры, определяющий длину вектора и расстояние между векторами (как длину разности между ними). Существуют нормы различных порядков, но обычно используются только первые два:

Геометрическое место точек, у которых норма равна единице: L₁ (слева) и L₂ (справа)

Норма L₂(x-y) – это расстояние между векторами x и y. Обе нормы используются в машинном обучении для регуляризации функции потерь: лассо-регуляризация использует L₁, регуляризация Тихонова – L₂, а эластичная сеть – и ту, и другую.

Косинус угла между двумя векторами x и y линейная алгебра определяет так:

Эта формула – самый популярный метод оценки сходства двух векторов. Если косинус угла близок к единице, то угол между векторами минимален, то есть векторы направлены почти одинаково. Если он близок к минус единице, векторы направлены почти противоположно. Наконец, если косинус близок к нулю, то векторы перпендикулярны (ортогональны), то есть, совершенно не зависят друг от друга.

Измерение меры сходства используется в машинном обучении очень широко – например, рекомендательные системы часто измеряют сходство векторов пользователей по их предпочтениям, и на основании этого сходства принимается решение, что похожим пользователям можно рекомендовать продукты, которые уже понравились одному из них.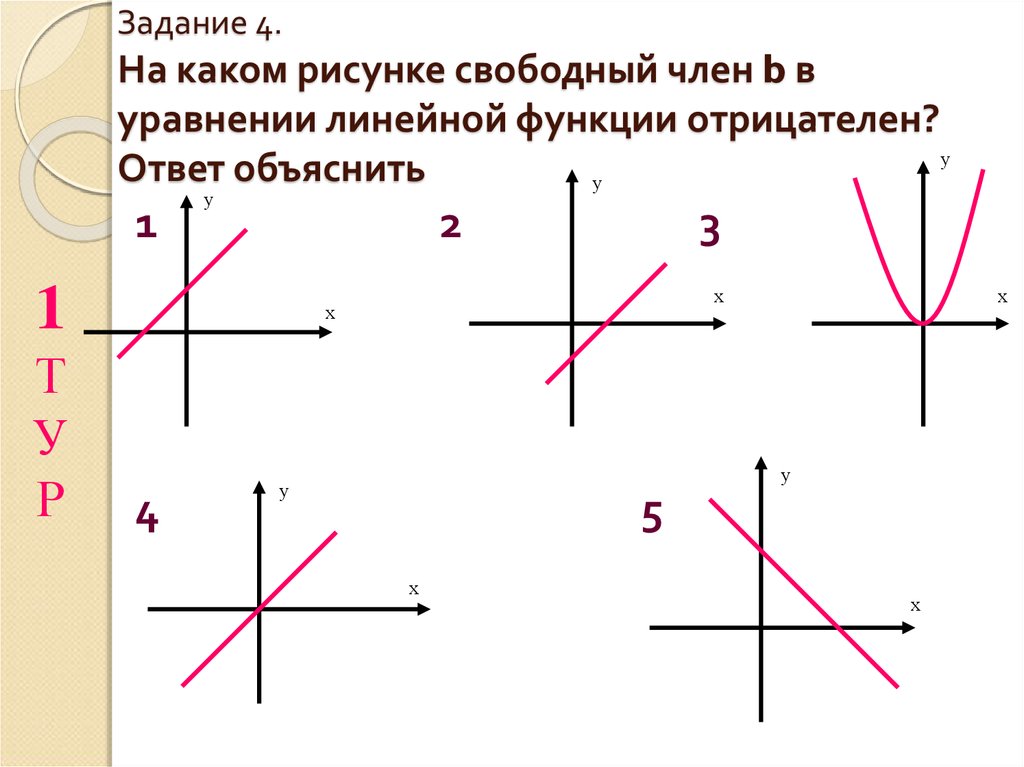

Разумеется, оценка сходства широко применяется и в моделях кластеризации – например, метод k-Nearest Neighbors размечает кластеры именно по степени сходства элементов друг с другом.

Сингулярное разложение матриц (SVD)

Квадратная матрица называется ортогональной, если все ее столбцы ортонормальны – норма каждого из них равна единице, и все они попарно ортогональны, то есть образуют ортонормальный базис. Ортогональные матрицы обладают следующими свойствами:

Сингулярное разложение матрицы вводится следующей теоремой линейной алгебры: любую невырожденную прямоугольную матрицу A^m*n можно представить в виде произведения трех матриц U^m*m, E^m*n и V^n*n, где U и V – ортогональные матрицы, а E – прямоугольная матрица, в которой все элементы, кроме диагональных, равны нулю.

Сингулярное разложение широко используется в рекомендательных системах. Оно позволяет найти базисы пространства строк и пространства столбцов, то есть элементарные признаки обоих пространств. Например, если строки матрицы соответствуют читателям, столбцы – книгам, а сама матрица содержит оценки, которые пользователи поставили книгам, то сингулярное разложение матрицы выделит «типичных читателей» и «типичные книги». Каждого реального читателя и каждую реальную книгу можно представить линейной комбинацией «типичных», после чего будет достаточно легко рассчитать ожидаемую оценку любой книги любым читателем.

Методов, позволяющих современным компьютерам обрабатывать огромные разреженные матрицы пользовательских оценок за приемлемое время, очень мало, так что сингулярное разложение матриц применяется очень широко.

Метод главных компонент (PCA)

Метод главных компонент – один из основных методов сокращения размерности данных, используемых в машинном обучении. Сокращение размерности применяется как при анализе данных, чтобы найти наиболее важные переменные и сконструировать новые признаки на их основе, так и при моделировании, если количество признаков очень велико, и большинство из них слабо влияют на результат. Метод главных компонент находит такую проекцию данных на пространство меньшей размерности, которая максимально сохраняет дисперсию данных.

PCA находит проекцию данных (синие точки) на пространство меньшей размерности (линию)

Продемонстрируем работу метода главных компонент на примере двухмерного набора данных, который мы будем проецировать на одномерное подпространство (линию). Метод состоит из нескольких шагов:

1. Вычитаем среднее значение, чтобы набор данных имел среднее значение 0. Это сокращает риск возникновения числовых проблем.
2. Стандартизируем. Делим элементы данных на стандартное отклонение sigma_d по каждому измерению d. Теперь данные не имеют единиц измерения, а их дисперсия по каждой оси равна 1, что отмечено на рис. в) голубыми стрелками.
3. Выполняем спектральное разложение матрицы ковариации. Вычисляем матрицу ковариации данных, ее собственные векторы и собственные значения. На рис. г) собственные векторы масштабированы соответствующими собственными значениями (голубые стрелки), и более длинный вектор соответствует подпространству главных компонент. Матрица ковариации данных изображена в виде эллипса.
4. Проецируем данные в подпространство. Рисунок е) показывает итоговую проекцию, перенесенную в исходное пространство данных.
   

Из описания метода главных компонент видно, что в нем используются понятия не только линейной алгебры, но и статистики (среднее значение, дисперсия, отклонение, матрица ковариации). Тем не менее, основные операции выполняются методами линейной алгебры, ведь именно она описывает проекции из одного пространства в другое, собственные векторы и собственные значения, а также спектральное разложение матриц.

Метод опорных векторов (SVM)

Один из основных методов построения моделей машинного обучения – это метод опорных векторов (Support Vector Machine). Этот метод основан на построении гиперплоскости, максимально разделяющей объекты разных классов – то есть, обеспечивающей максимальное расстояние между граничными точками. Мы не будем вдаваться в детали его реализации, поскольку они достаточно сложны и выходят за рамки нашей статьи. Метод очень подробно, с примерами кода и анимацией, описан в статье на Хабре, откуда взята следующая иллюстрация:

Иллюстрация метода опорных векторов (опорные векторы отмечены красным цветом)

Метод опорных векторов широко используется для задач бинарной классификации, а также сегментации изображений и многих других задач. Существует множество различных вариаций этого метода, причем он позволяет задать спрямляющее ядро, при правильном выборе которого результирующая модель зачастую оказывается более точной, чем модели на основе нейронных сетей – однако это ядро невозможно подобрать автоматически, так что его выбор представляет собой искусство Data Scientist’а. Метод хорошо работает с данными небольшого объема и с данными, имеющими большое количество признаков.

Для нас главное – то, что векторы и гиперплоскости относятся к линейной алгебре, как и весь метод в целом, и для его успешного применения, а также для правильной интерпретации его результатов, хорошее знание линейной алгебры просто необходимо.

Заключение

Мы рассмотрели только самые важные и очевидные приложения линейной алгебры в машинном обучении, но из приведенных примеров понятно, насколько широко она применяется, и насколько глубоко требуется ее знать для уверенного понимания хотя бы основных методов. Разумеется, для реальной работы в области машинного обучения придется изучить намного больше, чем описано в этой статье (предыдущая публикация была посвящена приложениям математического анализа, а в следующей речь пойдет о теории вероятностей и статистике – прим. ред.).

Надеюсь, что вы по-настоящему любите математику, или, по крайней мере, она вас не пугает.

***

Если вы хотите наработать необходимую для изучения Data Science математическую базу и подготовиться к углубленным занятиям в «Школе обработки данных» или Computer Science Center, обратите внимание на онлайн-курс «Библиотеки программиста». С помощью опытных преподавателей из ведущих вузов страны сделать это будет намного проще, чем самостоятельно по книгам.

Интересно, хочу попробовать

Нежное введение в линейную алгебру

Джейсон Браунли on 26 января 2018 г.

Последнее обновление: 9 августа 2019 г.

Что такое линейная алгебра?

Линейная алгебра — это область математики, которая, по общему мнению, является необходимым условием для более глубокого понимания машинного обучения.

Несмотря на то, что линейная алгебра — обширная область со множеством эзотерических теорий и открытий, базовые инструменты и обозначения, взятые из этой области, полезны для специалистов-практиков в области машинного обучения.

Имея прочную основу того, что такое линейная алгебра, можно сосредоточиться только на хороших или важных частях.

В этом руководстве вы узнаете, что такое линейная алгебра с точки зрения машинного обучения.

После прохождения этого урока вы будете знать:

• Линейная алгебра — это математика данных.
• Линейная алгебра оказала заметное влияние на область статистики.
• Линейная алгебра лежит в основе многих практических математических инструментов, таких как ряды Фурье и компьютерная графика.

Начните свой проект с моей новой книги «Линейная алгебра для машинного обучения», включающей

пошаговые руководства и файлы исходного кода Python для всех примеров.

Начнем.

Нежное введение в линейную алгебру
Фотография Стива Кори, некоторые права защищены.

Обзор учебника

Этот туториал разделен на 4 части; они:

1. Линейная алгебра
2. Числовая линейная алгебра
3. Линейная алгебра и статистика
4. Приложения линейной алгебры

Нужна помощь с линейной алгеброй для машинного обучения?

Пройдите мой бесплатный 7-дневный экспресс-курс по электронной почте прямо сейчас (с образцом кода).

Нажмите, чтобы зарегистрироваться, а также получить бесплатную электронную версию курса в формате PDF.

Линейная алгебра

Линейная алгебра — это раздел математики, но правда в том, что линейная алгебра — это математика данных. Матрицы и векторы — это язык данных.

Линейная алгебра касается линейных комбинаций. То есть, используя арифметические действия над столбцами чисел, называемыми векторами, и массивами чисел, называемыми матрицами, для создания новых столбцов и массивов чисел. Линейная алгебра — это изучение прямых и плоскостей, векторных пространств и отображений, необходимых для линейных преобразований.

Это относительно молодая область исследований, которая первоначально была формализована в 1800-х годах для поиска неизвестных в системах линейных уравнений. Линейное уравнение — это просто набор терминов и математических операций, где некоторые термины неизвестны; например:

у = 4 * х + 1

у = 4 * х + 1

Подобные уравнения являются линейными в том смысле, что они описывают линию на двумерном графике. Линия возникает из-за подстановки различных значений в неизвестный x, чтобы выяснить, что уравнение или модель делает со значением y.

Мы можем составить систему уравнений одинаковой формы с двумя или более неизвестными; например:

у = 0,1 * х1 + 0,4 * х2 у = 0,3 * х1 + 0,9 * х2 у = 0,2 * х1 + 0,3 * х2 …

y = 0,1 * x1 + 0,4 * x2 y = 0,3 * x1 + 0,9 * x2 y = 0,2 * x1 + 0,3 * x2 …

Столбец значений y может быть взят как вектор-столбец выходных данных уравнения. Два столбца значений с плавающей запятой являются столбцами данных, скажем, a1 и a2, и могут быть взяты как матрица A. Два неизвестных значения x1 и x2 могут быть взяты как коэффициенты уравнения и вместе образуют вектор неизвестных б решить. Мы можем записать это компактно, используя обозначения линейной алгебры, как:

у = А . б

у = А . б

Задачи этой формы обычно сложны для решения, потому что неизвестных больше (здесь у нас 2), чем уравнений для решения (здесь у нас 3). Кроме того, часто не существует единой линии, которая безошибочно удовлетворяла бы всем уравнениям. Системы, описывающие часто интересующие нас проблемы (например, линейная регрессия), могут иметь бесконечное количество решений.

Это дает небольшое представление о самой сути линейной алгебры, которая интересует нас как специалистов по машинному обучению. Большая часть остальных операций направлена ​​на облегчение понимания и решения этой и подобных проблем.

Числовая линейная алгебра

Применение линейной алгебры в компьютерах часто называют числовой линейной алгеброй.

«Числовая» линейная алгебра — это действительно прикладная линейная алгебра.

— Страница ix, Численная линейная алгебра, 1997.

Это больше, чем просто реализация операций линейной алгебры в библиотеках кода; это также включает в себя тщательное решение проблем прикладной математики, таких как работа с ограниченной точностью цифровых компьютеров с плавающей запятой.

Компьютеры хорошо выполняют вычисления линейной алгебры, и большая часть зависимости от графических процессоров (GPU) современных методов машинного обучения, таких как глубокое обучение, связана с их способностью быстро выполнять операции линейной алгебры.

Эффективные реализации векторных и матричных операций были первоначально реализованы на языке программирования FORTRAN в 1970-х и 1980-х годах, и большое количество кода или кода, перенесенного из этих реализаций, лежит в основе большей части линейной алгебры, выполняемой с использованием современных языков программирования, таких как Python.

Три популярные библиотеки числовой линейной алгебры с открытым исходным кодом, которые реализуют эти функции:

• Пакет линейной алгебры или LAPACK.
• Подпрограммы базовой линейной алгебры, или BLAS (стандарт для библиотек линейной алгебры).
• Программное обеспечение для автоматической настройки линейной алгебры или ATLAS.

Часто, когда вы вычисляете операции линейной алгебры прямо или косвенно с помощью алгоритмов более высокого порядка, ваш код, скорее всего, будет использовать одну из этих или подобных библиотек линейной алгебры.

Название одной или нескольких из этих базовых библиотек может быть вам знакомо, если вы установили или скомпилировали любую из числовых библиотек Python, таких как SciPy и NumPy.

Линейная алгебра и статистика

Линейная алгебра является ценным инструментом в других разделах математики, особенно в статистике.

Обычно ожидается, что студенты, изучающие статистику, хотя бы один семестр изучали линейную алгебру (или прикладную алгебру) на уровне бакалавриата.

— Страница xv, Линейная алгебра и матричный анализ для статистики, 2014.

Важно учитывать влияние линейной алгебры, учитывая фундаментальную связь обеих областей с областью прикладного машинного обучения.

Некоторые четкие отпечатки линейной алгебры в статистике и статистических методах включают:

• Использование векторной и матричной записи, особенно с многомерной статистикой.
• Решения метода наименьших квадратов и взвешенного метода наименьших квадратов, например, для линейной регрессии.
• Оценки среднего и дисперсии матриц данных.
• Ковариационная матрица, играющая ключевую роль в полиномиальных распределениях Гаусса.
• Анализ главных компонентов для сокращения данных, объединяющий многие из этих элементов.

Как видите, современная статистика и анализ данных, по крайней мере, в том, что касается интересов специалиста по машинному обучению, зависят от понимания и инструментов линейной алгебры.

Приложения линейной алгебры

Поскольку линейная алгебра — это математика данных, инструменты линейной алгебры используются во многих областях.

В своей классической книге на тему «Введение в линейную алгебру» Гилберт Стрэнг предлагает главу, посвященную приложениям линейной алгебры. В нем он демонстрирует конкретные математические инструменты, основанные на линейной алгебре. Кратко:

• Матрицы в машиностроении, такие как ряд пружин.
• Графики и сети, такие как анализ сетей.
• Марковские матрицы, население и экономика, такие как рост населения.
• Линейное программирование, метод симплексной оптимизации.
• Ряд Фурье: линейная алгебра для функций, широко используемых в обработке сигналов.
• Линейная алгебра для статистики и вероятности, например метод наименьших квадратов для регрессии.
• Компьютерная графика, например различные переводы, масштабирование и поворот изображений.

Другим интересным применением линейной алгебры является то, что это тип математики, используемый Альбертом Эйнштейном в некоторых частях его теории относительности. В частности, тензоры и тензорное исчисление. Он также ввел в физику новый тип нотации линейной алгебры, названный нотацией Эйнштейна или соглашением о суммировании Эйнштейна.

Учебники по линейной алгебре

Если вам нужна помощь, чтобы начать работу с линейной алгеброй, взгляните на некоторые из этих руководств:

• Линейная алгебра для машинного обучения (7-дневный мини-курс)
• Памятка по линейной алгебре для машинного обучения
• Основы математической записи для машинного обучения

Удлинители

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.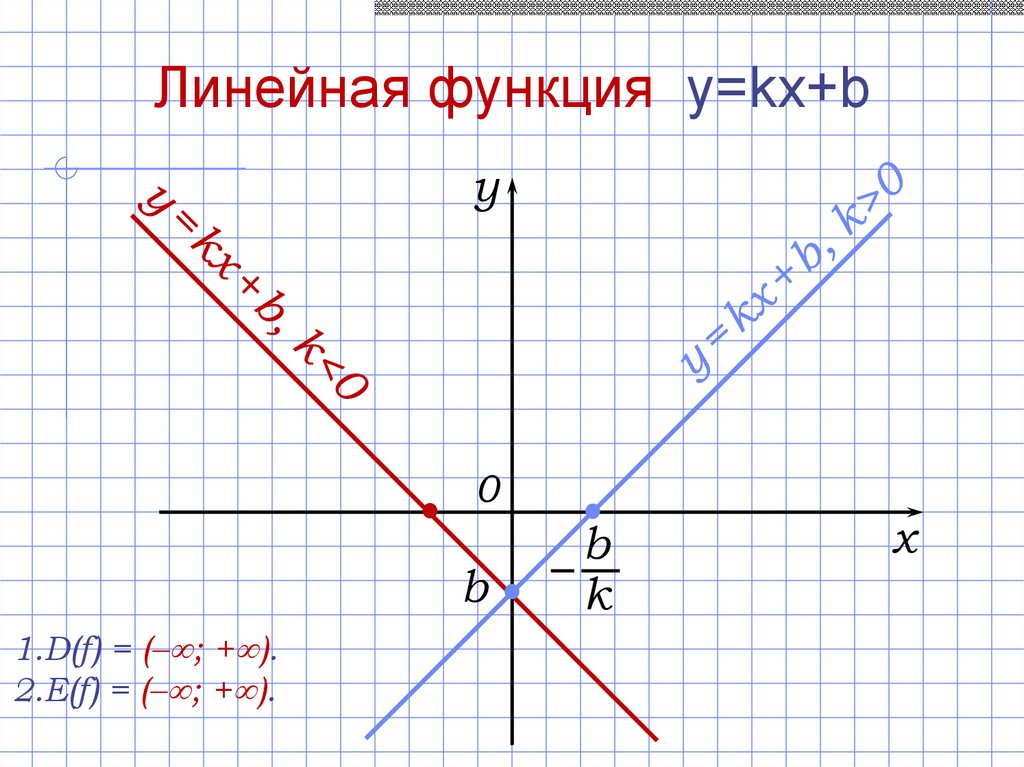

• Найдите в книгах и Интернете 5 цитат, определяющих область линейной алгебры.
• Исследуйте и перечислите еще 5 приложений или применений линейной алгебры в области вероятностей и статистики.
• Перечислите и напишите краткие определения для 10 терминов, используемых при описании линейной алгебры.

Если вы изучите какое-либо из этих расширений, я хотел бы знать.

Дополнительное чтение

В этом разделе содержится больше ресурсов по теме, если вы хотите углубиться.

Книги

• Введение в линейную алгебру, 2016.
• Численная линейная алгебра, 1997.
• Линейная алгебра и матричный анализ для статистики, 2014.

Артикул

• Линейная алгебра в Википедии
• Категория линейной алгебры в Википедии
• Линейная алгебра Список тем в Википедии
• ЛАПАК в Википедии
• Основные подпрограммы линейной алгебры в Википедии
• Автоматически настраиваемое программное обеспечение для линейной алгебры в Википедии
• Обозначение Эйнштейна в Википедии
• Математика общей теории относительности в Википедии

Похожие сообщения

• Линейная алгебра для машинного обучения

Резюме

В этом уроке вы нашли небольшое введение в линейную алгебру с точки зрения машинного обучения.

В частности, вы узнали:

• Линейная алгебра — это математика данных.
• Линейная алгебра оказала заметное влияние на область статистики.
• Линейная алгебра лежит в основе многих практических математических инструментов, таких как ряды Фурье и компьютерная графика.

Есть вопросы?
Задавайте свои вопросы в комментариях ниже, и я постараюсь ответить.

Освойте линейную алгебру для машинного обучения!

Развивайте практическое понимание линейной алгебры

…путем написания строк кода на Python

Узнайте, как это сделать, в моей новой электронной книге:
Линейная алгебра для машинного обучения

В ней содержится учебных пособий для самостоятельного изучения по таким темам, как:
Векторные нормы, умножение матриц, тензоры, собственное разложение, SVD, PCA и многое другое…

Наконец-то поймите математику данных

Пропустите учебу. Просто Результаты.

Посмотреть, что внутри

О Джейсоне Браунли

Джейсон Браунли, доктор философии, специалист по машинному обучению, который обучает разработчиков тому, как получать результаты с помощью современных методов машинного обучения с помощью практических руководств.

Просмотреть все сообщения Джейсона Браунли →

Почему алгоритмы машинного обучения работают с новыми данными?

5 причин изучать линейную алгебру для машинного обучения

Линейная алгебра — Викиучебники, открытые книги для открытого мира

Из Викиучебников, открытые книги для открытого мира

(Перенаправлено из линейной алгебры)

Последняя проверенная версия проверена 14 сентября 2022 . Есть изменения шаблона/файла, ожидающие проверки.

Перейти к навигацииПерейти к поиску

Линейная алгебра

Введение в математический дискурс

В этой книге линейная алгебра обсуждается на основе доказательств. Книга была разработана специально для студентов, которые ранее не знакомились с математикой с точки зрения математиков. То есть как предмет, целью которого является строгое доказательство теорем, исходя из четких непротиворечивых определений. Эта книга пытается помочь учащимся подняться с уровня, когда математика является просто инструментом, обеспечивающим полезные вычисления, до такой степени, что учащиеся понимают ясную и точную природу математики. Для более мягкого введения в линейную алгебру, которое не слишком на основе доказательств , см. викибук Introductory Linear Algebra. Более подробное обсуждение предпосылок и целей этой книги дано во введении.

Эта книга является частью серии по Алгебра:

Базовая алгебра
Алгебра
Промежуточная алгебра
Векторы
Введение в линейную алгебру
Линейная алгебра
Абстрактная алгебра
Введение в кольца и алгебры
Алгебра ассоциативных композиций

• Крышка
• Обозначение
• Введение

Линейные системы

1. Решение линейных систем  (13 июля 2009 г. )
   1. Метод Гаусса  (13 июля 2009 г.)
   2. Описание набора решений  (13 июля 2009 г.)
   3. Общее = Частное + Однородное (13 июля 2009 г.)
   4. Сравнение описаний наборов  (13 июля 2009 г.)
   5. Автоматика  (13 июля 2009 г.)
2. Линейная геометрия n — Космос (13 июля 2009 г.)
   1. Векторы в космосе  (13 июля 2009 г.)
   2. Меры длины и угла  (13 июля 2009 г.)
3. Сокращенная эшелонированная форма  (13 июля 2009 г.)
   1. Сокращение Гаусса-Жордана  (13 июля 2009 г.)
   2. Эквивалентность строк  (13 июля 2009 г.)
4. Тема: Системы компьютерной алгебры  (13 июля 2009 г.)
5. Тема: Анализ затрат-выпуска  (13 июля 2009 г.)
6. M-файл анализа ввода-вывода (24 марта 2008 г. )
7. Тема: Точность вычислений  (13 июля 2009 г.)
8. Тема: Анализ сетей  (13 июля 2009 г.)
9. Тема: Скорость метода Гаусса  (24 марта 2008 г.)

Векторные пространства

 (17 апреля 2009 г.)

1. Определение векторного пространства  (17 апреля 2009 г.)
   1. Определение и примеры  (18 июня 2009 г.)
   2. Подпространства и остовные наборы  (18 июня 2009 г.)
2. Линейная независимость  (17 апреля 2009 г.)
   1. Определение и примеры  (17 апреля 2009 г.)
3. Базис и измерение  (17 апреля 2009 г.)
   1. База (18 июня 2009 г.)
   2. Измерение  (17 апреля 2009 г.)
   3. Векторные пространства и линейные системы  (17 апреля 2009 г.)
   4. Объединение подпространств  (17 апреля 2009 г. )
4. Тема: Поля  (17 апреля 2009 г.)
5. Тема: Кристаллы  (17 апреля 2009 г.)
6. Тема: Парадоксы голосования  (17 апреля 2009 г.)
7. Тема: Анализ измерений  (17 апреля 2009 г.)

Карты между пространствами

1. Изоморфизмы  (21 июня 2009 г.)
   1. Определение и примеры  (19 июля, 2009)
   2. Измерение характеризует изоморфизм  (21 июня 2009 г.)
2. Гомоморфизмы  (21 июня 2009 г.)
   1. Определение гомоморфизма  (21 июня 2009 г.)
   2. Rangespace и Nullspace  (21 июня 2009 г.)
3. Вычисление линейных карт  (21 июня 2009 г.)
   1. Представление линейных карт с помощью матриц  (21 июня 2009 г.)
   2. Любая матрица представляет собой линейную карту  (21 июня 2009 г. )
4. Операции с матрицами  (21 июня 2009 г.)
   1. Суммы и скалярные произведения  (21 июня 2009 г.)
   2. Умножение матриц  (21 июня 2009 г.)
   3. Механика матричного умножения  (21 июня 2009 г.)
   4. Инверсия  (21 июня 2009 г.)
5. Изменение основы  (21 июня 2009 г.)
   1. Изменение представления векторов  (21 июня 2009 г.)
   2. Изменение представлений карты  (21 июня 2009 г.)
6. Проекция  (21 июня 2009 г.)
   1. Ортогональная проекция на прямую (21 июня 2009 г.)
   2. Ортогонализация Грама-Шмидта (21 июня 2009 г.)
   3. Проекция на подпространство  (21 июня 2009 г.)
7. Тема: Линия наилучшего соответствия  (21 июня 2009 г.)
8. Тема: Геометрия линейных карт  (21 июня 2009 г. )
9. Тема: Цепи Маркова  (21 июня 2009 г.)
10. Тема: Ортонормированные матрицы  (21 июня 2009 г.)

Детерминанты

 (21 июня 2009 г.)

1. Определение  (21 июня 2009 г.)
   1. Разведка  (21 июня 2009 г.)
   2. Свойства определителей  (21 июня 2009 г.)
   3. Расширение Permutation  (21 июня 2009 г.)
   4. Существуют детерминанты (21 июня 2009 г.)
2. Геометрия определителей  (21 июня 2009 г.)
   1. Детерминанты как функции размера  (21 июня 2009 г.)
3. Другие формулы для определителей  (21 июня 2009 г.)
   1. Расширение Лапласа  (21 июня 2009 г.)
4. Тема: Правило Крамера  (21 июня 2009 г.)
5. Тема: Скорость вычисления определителей  (21 июня 2009 г. )
6. Тема: Проективная геометрия  (21 июня 2009 г.)

Сходство

 (24 июня 2009 г.)

1. Комплексные векторные пространства  (24 июня 2009 г.)
   1. Факторинг и комплексные числа: обзор  (24 июня 2009 г.)
   2. Комплексные представления  (24 июня 2009 г.)
2. Сходство
   1. Определение и примеры  (24 июня 2009 г.)
   2. Диагональность  (24 июня 2009 г.)
   3. Собственные значения и собственные векторы  (24 июня 2009 г.)
3. Nilpotence  (24 июня 2009 г.)
   1. Самостоятельное составление  (24 июня 2009 г.)
   2. Strings  (24 июня 2009 г.)
4. Jordan Form  (24 июня 2009 г.)
   1. Полиномы карт и матриц  (24 июня 2009 г.)
   2. Jordan Canonical Form (24 июня 2009 г.