Линейная экстраполяция онлайн: Линейная интерполяция Онлайн

Калькулятор Интерполяции

Калькулятор онлайн вычисляет линейную экстраполяцию по двум точкам, выводит формулу с подробным решением и графиком

Содержание

Формула линейной экстраполяции

расчет линейной экстраполяции по двум точкам

Помощь на развитие проекта premierdevelopment.ru

Send mail и мы будем знать, что движемся в правильном направлении.

Спасибо, что не прошели мимо!

I. Порядок действий при расчете линейной экстраполяции онлайн калькулятором:

1. Для проведения экстраполяции требуется ввести значения координат 2 точек ([X1, Y1]; [X2, Y2]) и абсциссу (Х) той точки, значение которой необходимо вычислить.
2. График справа позволяет визуализировать полученный линейной экстраполяцией результат.

II. Для справки:

интерполяция — способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.линейная интерполяция — нахождение промежуточного значения функции по двум точкам (условно проведя прямую между ними). квадратичная интерполяция — нахождение промежуточного значения функции по трем точкам (интерполирующая функция многочлен второго порядка – парабола).экстраполяция — способ нахождения значений функции по уже известным нескольким ее значениям.

ФорумСпециалистыО нас

Ссылка для цитирования в списке литературы: CAE-CUBE: [Электронный ресурс]. URL: https://premierdevelopment.ru/ (дата обращения )

premierdevelopment.ru, все права защищены, 2015&nbsp-&nbsp2021 e-mail: Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.

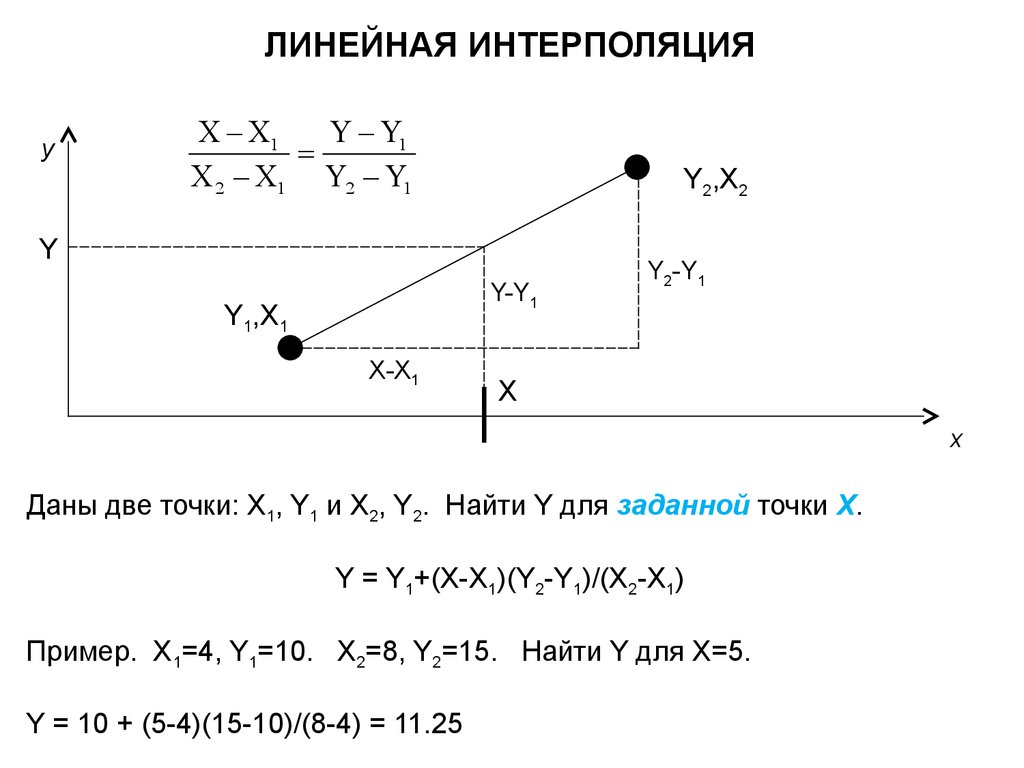
Линейная интерполяция

Простейшим случаем интерполяции является “линейная”, то есть нахождение величины по двум заданным точкам. Данный процесс вычисления можно рассмотреть как линейную функцию, тем самым делая расчёт более наглядным.

Нанесение функции на систему координат называют аппроксимацией. Для этого на оси координат необходимо провести прямую через известные точки. Логично, что искомое значение, находящееся между первыми двумя точками, можно найти графически, зная абсциссу X. Если координата X искомой величины лежит за пределами известных значений (X1, X2), то процесс вычисления называется экстраполяция.

Калькулятор позволяет определить значение ординаты Y искомого значения, зная координаты X и Y двух других функций, а также её абсциссу. Для вычисления необходимо ввести значения заданных двух точек Х1, Y1 и X2,Y2, а также указать координату X искомой точки, а сервис автоматически определит метод расчёта и произведёт его.

Такие науки, как статистика и математика, используют в своей методологии инструмент «Интерполяция». Он используется инженерии и архитектурном проектировании.

Интерполяция применима в следующих случаях:

• Явление было изучено со всесторонне, а не одним путем определенного исчисления.
• Применение данного инструмента возможно только в случаях, когда допускается изменение погрешности, между проверенными точками, которое также подчиняется конкретному закону.
• Применение может быть оправдано не во всех случаях, так как при эмпирических функциях может возникнуть ряд других нюансов.

Так или иначе, применяя метод линейной интерполяции, допущение ошибок при расчетах недопустимо. Для того, чтобы обезопасить специалистов от возникновения ошибок по причине допущения просчета, мы разработали калькулятор линейной интерполяции онлайн. Благодаря этому инструменту теперь есть возможность избежать допущения каких-либо ошибок, поскольку калькулятор имеет предельную точность в расчетах.

Линейная интерполяция онлайн:

• Обезопасить себя от допущения ошибок, которые в случаях со строительством жилых зданий могут приводить к ужасным последствиям.
• Избавить себя от необходимости самостоятельного расчета формулы и просто ввести необходимые значения в соответствующие поля и получить готовый ответ.
• Метод линейной интерполяции покажется очень простым, благодаря интерфейсу нашего калькулятора.

Наш калькулятор, осуществляя расчет методом линейной интерполяции, использует следующую формулу:

Y = y1+(x-x1)/(x2-x1)*(y2-y1),

где y – показатель линейной интерполяции,

y1, y2, x, x1, x2 – известные значения, которые необходимо вставить в поля калькулятора.

Таким образом, используя наш онлайн калькулятор, Вы получите точный ответ, легко разберетесь в функционале калькулятора, благодаря простому интерфейсу, и никогда не допустите ошибки по причине человеческого фактора.

Использование экстраполяции

В отличие от интерполяции, задачей которой является нахождения значения функции между двумя известными аргументами, экстраполяция подразумевает поиск решения за пределами известной области. Именно поэтому данный метод столь востребован для прогнозирования.

В Экселе можно применять экстраполяцию, как для табличных значений, так и для графиков.

Способ 1: экстраполяция для табличных данных

Прежде всего, применим метод экстраполяции к содержимому табличного диапазона. Для примера возьмем таблицу, в которой имеется ряд аргументов (X) от 5 до 50 и ряд соответствующих им значений функции (f(x)). Нам нужно найти значение функции для аргумента 55, который находится за пределом указанного массива данных. Для этих целей используем функцию ПРЕДСКАЗ.

1. Выделяем ячейку, в которой будет отображаться результат проведенных вычислений. Кликаем по значку «Вставить функцию», который размещен у строки формул.

Запускается окно Мастера функций. Выполняем переход в категорию «Статистические» или «Полный алфавитный перечень». В открывшемся списке производим поиск наименования «ПРЕДСКАЗ». Найдя его, выделяем, а затем щелкаем по кнопке «OK» в нижней части окна.

Мы перемещаемся к окну аргументов вышеуказанной функции. Она имеет всего три аргумента и соответствующее количество полей для их внесения.

В поле «X» следует указать значение аргумента, функцию от которого нам следует вычислить. Можно просто вбить с клавиатуры нужное число, а можно указать координаты ячейки, если аргумент записан на листе. Второй вариант даже предпочтительнее. Если мы произведем внесение именно таким способом, то для того, чтобы просмотреть значение функции для другого аргумента нам не придется менять формулу, а достаточно будет изменить вводную в соответствующей ячейке. Для того, чтобы указать координаты этой ячейки, если был выбран все-таки второй вариант, достаточно установить курсор в соответствующее поле и выделить эту ячейку. Её адрес тут же отобразится в окне аргументов.

В поле «Известные значения y» следует указать весь имеющийся у нас диапазон значений функции. Он отображается в колонке «f(x)». Следовательно, устанавливаем курсор в соответствующее поле и выделяем всю эту колонку без её наименования.

В поле «Известные значения x» следует указать все значения аргумента, которым соответствуют внесенные нами выше значения функции.

Эти данные находятся в столбце «x». Точно так же, как и в предыдущий раз выделяем нужную нам колонку, предварительно установив курсор в поле окна аргументов.

После того, как все данные внесены, жмем на кнопку «OK».

После этих действий результат вычисления путем экстраполяции будет выведен в ячейку, которая была выделена в первом пункте данной инструкции перед запуском Мастера функций. В данном случае значение функции для аргумента 55 равно 338.

Если все-таки был выбран вариант с добавлением ссылки на ячейку, в которой содержится искомый аргумент, то мы легко сможем его поменять и просмотреть значение функции для любого другого числа. Например, искомое значение для аргумента 85 буде равно 518.

Урок: Мастер функций в Excel

Способ 2: экстраполяция для графика

Выполнить процедуру экстраполяции для графика можно путем построения линии тренда.

1. Прежде всего, строим сам график. Для этого курсором при зажатой левой кнопке мыши выделяем всю область таблицы, включая аргументы и соответствующие значения функции. Затем, переместившись во вкладку «Вставка», кликаем по кнопке «График». Этот значок расположен в блоке «Диаграммы» на ленте инструментов. Появляется перечень доступных вариантов графиков. Выбираем наиболее подходящий из них на свое усмотрение.

После того, как график построен, удаляем из него дополнительную линию аргумента, выделив её и нажав на кнопку Delete на клавиатуре компьютера.

Далее нам нужно поменять деления горизонтальной шкалы, так как в ней отображаются не значения аргументов, как нам того нужно. Для этого, кликаем правой кнопкой мыши по диаграмме и в появившемся списке останавливаемся на значении «Выбрать данные».

В запустившемся окне выбора источника данных кликаем по кнопке «Изменить» в блоке редактирования подписи горизонтальной оси.

Открывается окно установки подписи оси. Ставим курсор в поле данного окна, а затем выделяем все данные столбца «X» без его наименования. Затем жмем на кнопку «OK».

После возврата к окну выбора источника данных повторяем ту же процедуру, то есть, жмем на кнопку «OK».

Теперь наш график подготовлен и можно, непосредственно, приступать к построению линии тренда. Кликаем по графику, после чего на ленте активируется дополнительный набор вкладок – «Работа с диаграммами». Перемещаемся во вкладку «Макет» и жмем на кнопку «Линия тренда» в блоке «Анализ». Кликаем по пункту «Линейное приближение» или «Экспоненциальное приближение».

Линия тренда добавлена, но она полностью находится под линией самого графика, так как мы не указали значение аргумента, к которому она должна стремиться. Чтобы это сделать опять последовательно кликаем по кнопке «Линия тренда», но теперь выбираем пункт «Дополнительные параметры линии тренда».

Запускается окно формата линии тренда. В разделе «Параметры линии тренда» есть блок настроек «Прогноз». Как и в предыдущем способе, давайте для экстраполяции возьмем аргумент 55. Как видим, пока что график имеет длину до аргумента 50 включительно. Получается, нам нужно будет его продлить ещё на 5 единиц. На горизонтальной оси видно, что 5 единиц равно одному делению. Значит это один период. В поле «Вперед на» вписываем значение «1». Жмем на кнопку «Закрыть» в нижнем правом углу окна.

Как видим, график был продлен на указанную длину с помощью линии тренда.

Урок: Как построить линию тренда в Excel

Итак, мы рассмотрели простейшие примеры экстраполяции для таблиц и для графиков. В первом случае используется функция ПРЕДСКАЗ, а во втором – линия тренда. Но на основе этих примеров можно решать и гораздо более сложные задачи прогнозирования.

Мы рады, что смогли помочь Вам в решении проблемы.

Опишите, что у вас не получилось.

Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

Поделиться статьей в социальных сетях:

Еще статьи по данной теме:

Линейная регрессия

Уравнение регрессии:

Коэффициент a:

Коэффициент b:

Коэффициент линейной парной корреляции:

Коэффициент детерминации:

Средняя ошибка аппроксимации:

Что такое линейная интерполяция в математике?

интерполяция калькулятор – это метод создания новых точек данных в уже известном дискретном наборе точек данных. В этой математической процедуре некоторые исходные точки данных могут быть интерполированы для создания простой и новой функции, которая будет близка к исходным данным. Эта интеграция нового значения называется интерполяцией. Другими словами, мы также можем сказать, что линейный интерполянт – это прямая линия, которая существует между двумя распознанными координатными точками (x0, y0) и (x1, y1). Вы можете легко найти значение интерполяции между двумя координатами на прямой с помощью калькулятор интерполяции.

Формула линейной интерполяции:

Формула линейной интерполяции:

$$ y = y1 + ((x – x1) / (x2 – x1)) * (y2 – y1) $$

В этом уравнении интерполяции:

• X = известное значение,
• y = неизвестное значение,
• x1 и y1 = координаты, которые ниже известного значения x
• x2 и y2 = координаты выше значения x.

Кроме того, интерполяция онлайн калькулятор уклона помогает найти точки уклона или уклона A (x1, y1) и B (y1, y2) в декартовой координатной плоскости.

Пример1:

Если заданными точками данных являются (2, 4) и (6, 8), как вы рассчитаете значение y, когда x = 2.

На первом этапе мы извлечем координаты заданных точек данных.

$$ x1 = 2 $$

$$ y1 = 4 $$

$$ x2 = 6 $$

$$ y2 = 8 $$

На втором этапе мы возьмем следующие уравнения, чтобы получить значения m, а затем y

• (m = y2 – y1 / x2 − x1 ) = уравнение 1
• (y = y1 + m * (x – x1) ) = уравнение 2
• Чтобы вычислить значение m, поместите значения в уравнение 1, (= m = 8−4 / 6−2 = 1 )
• Теперь у нас есть значение m, поэтому мы воспользуемся уравнением 2, чтобы найти значение y.
• (у = 4 + 1 * (2–2) = 4 )

Между тем, x находится в интервале ([x1, x2] ), поэтому мы выполнили расчет линейной интерполяции, чтобы найти значение y.

Однако интерполяция онлайн калькулятор поможет вам найти центр тяжести треугольника (ABC), N-точек и N-стороннего многоугольника для заданных координат.

Пример 2:

Найдите значение (y ^ 2 ) в заданной строке, пока заданные данные

«$$ x1 = 4, y1 = 6, x2 = 8, x3 = 12, y3 = 14 $$».

Решение:

Поскольку у нас есть линейное интерполяционное уравнение:

$$ y_2 = (x_2 – x_1) x (y_3- y_1) / (x_3 – x_1) + y_1 $$

Пошаговое решение для нахождения y2 будет таким, как если бы вышеприведенное уравнение было следующим:

$$ y_2 = (x_3 − x_2) x (y_3 − y_1) / (x_3 − x_2) + y_3 $$

$$ y_2 = (12−8) x (14−6) / (12−8) + 14 $$

$$ y_2 = (4) x (8) / (4) + 14 $$

$$ y_2 = (32) / (4) + 14 $$

$$ y_2 = 8 + 14 $$

$$ y_2 = 22 $$

Формула линейной интерполяции

Для вычисления используется следующая формула:

Часто задаваемые вопросы (FAQ):

Какой метод можно использовать в любом вопросе интерполяции?

Обычно мы используем метод интерполяции калькулятор полиномов. Причины использования полиномов:

• Их легко оценить
• Дифференциация и интеграция просты.

Это называется полиномиальной интерполяцией.

Когда следует использовать интерполяцию?

Как мы уже знаем, с помощью интерполяции мы можем найти неизвестные точки, поэтому ее можно использовать всякий раз, когда нам нужно предсказать неизвестные значения для любых данных географических точек. Это полезно для прогнозирования осадков, полученных в результате концентраций химических веществ, оценки уровней шума и т. Д.

Какой метод интерполяции лучший?

Интерполяция с обратным взвешиванием по расстоянию (IDW) считается одним из лучших методов для достижения лучших результатов, чем любой другой метод интерполяции калькулятор.

Кригинг – это точная интерполяция?

Методика интерполяция калькулятор обычно связана с точной интерполяцией. Все предсказания Кригинга могут постепенно меняться в космосе. Они будут меняться после того, как попадут в место, где были собраны данные. В этот момент происходит «скачок» прогноза к наиболее точному значению, которое было измерено первым. Однако для быстрых и точных прогнозов можно использовать интерполятор.

Пример расчёта

Дано: координаты двух точек А(3;1.5) и B(6;5).
Найти: ординату точки С с абсциссой 4.5.

Для удобства рекомендуется построить график: нанести точки на систему координат и провести прямую.

После этого подставляем значения в указанную формулу:

Y = 5 + (1.5 – 5) / (3 – 6) · (4.5 – 6) = 5 + (-3.5) / (-3) · (-1.5) = 3.25.

интерполяция онлайн калькулятор момент:

Благодаря калькулятор интерполяции линейной для поиска неизвестной точки данных для заданных координат и построения точки на графиках. Кроме того, этот инструмент показывает формулу, которая используется для выполнения требований, с пошаговыми расчетами для облегчения конечных пользователей в кратчайшие сроки. Он обеспечивает бесплатную поддержку в учебных и образовательных целях. Поэтому давайте интерполяция калькулятор найти ответ, поместив известную точку данных в этот интерполятор!

Other Languages: Linear Interpolation Calculator, Kalkulator Interpolasi, Interpolacja Kalkulator, Interpolation Rechner, Interpolasyon Hesaplama, 補間計算, Calculadora De Interpolação, Calcul Interpolation Linéaire, Interpolar Calculadora, Calcolo Interpolazione Lineare, Lineární Interpolace Výpočet, حاسبة الاستيفاء, Interpolointi Laskin.

Онлайн калькулятор: Аппроксимация функции одной переменной

Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.

Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.

Аппроксимация функции одной переменной

83 71 64 69 69 64 68 59 81 91 57 65 58 62

Значения x, через пробел

183 168 171 178 176 172 165 158 183 182 163 175 164 175

Значения y, через пробел

Линейная аппроксимация

Квадратичная аппроксимация

Кубическая аппроксимация

Аппроксимация степенной функцией

Показательная аппроксимация

Логарифмическая аппроксимация

Гиперболическая аппроксимация

Экспоненциальная аппроксимация

Точность вычисления

Знаков после запятой: 4

Линейная регрессия

 

Коэффициент линейной парной корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Квадратичная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Кубическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Степенная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Показательная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Логарифмическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Гиперболическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Экспоненциальная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Результат

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.

Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.

Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.

Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:

Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.

Используя формулу производной сложной функции, получим следующую систему уравнений:

Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.

Как экстраполировать график

Онлайн калькулятор расчета линейной экстраполяции по 2 точкам с выводом формулы решения и графика.

Калькулятор линейной экстраполяции позволяет вычислить значение линейной функции если абсцисса (Х) искомой точки лежит за пределами отрезка интерполяции [X₁, X₂].

Формула линейной экстраполяции

расчет линейной экстраполяции по двум точкам

Помощь на развитие проекта premierdevelopment.ru

Send mail и мы будем знать, что движемся в правильном направлении.

Спасибо, что не прошели мимо!

I. Порядок действий при расчете линейной экстраполяции онлайн калькулятором:

1. Для проведения экстраполяции требуется ввести значения координат 2 точек ([X₁, Y₁]; [X₂, Y₂]) и абсциссу (Х) той точки, значение которой необходимо вычислить.
2. График справа позволяет визуализировать полученный линейной экстраполяцией результат.

интерполяция — способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. линейная интерполяция — нахождение промежуточного значения функции по двум точкам (условно проведя прямую между ними). квадратичная интерполяция — нахождение промежуточного значения функции по трем точкам (интерполирующая функция многочлен второго порядка — парабола). экстраполяция — способ нахождения значений функции по уже известным нескольким ее значениям.

Линейная экстраполяция

Линейная экстраполяция с помощью онлайн-калькулятора по двум точкам — рассчитайте значения линейной функции вне диапазона онлайн или вручную по формулам.

• Расчёт
• Скачать

Экстраполяция используется в научной практике для математического прогнозирования и выявления закономерностей различных ситуаций за границами экспериментального диапазона. Онлайн-калькулятор линейной экстраполяции помогает оценить значение координаты точки за пределами отрезка интерполяции по известным значениям остальных точек. Для выполнения корректных вычислений должны соблюдаться условия: X₁>X>X₂ , Y₁>Y>Y₂ . Теоретическое обоснование расчета и инструкция представлены ниже.

Сущность и методы экстраполяции

Сложное слово «экстраполяция» составлено из двух простых. Первое на латыни звучит extra и означает «вне», «за», «снаружи». Второе на той же латыни звучит polire и означает «изменять», «выправлять», «приглаживать». В целом экстраполяция может быть определена как значение вне двух заданных точек. Она считается оценкой того, что извлечено из известных фактов, которые расширяют данные в неизвестной области, чтобы прийти к предполагаемому результату. Эта концепция также может быть отнесена к предсказанию образа будущего, предполагающего истинность настоящих и прошлых тенденций.

Метод экстраполяции предполагает, что данные или наблюдения в будущем будут по-прежнему похожи. Таким образом, будущие результаты могут быть предсказаны. Ее можно рассматривать как математическую гипотезу. При экстраполяции используются данные и факты определенной ситуации и приводятся прогнозы о том, что может произойти в конечном итоге.

История процесса экстраполяции

Этот метод часто называют экстраполяцией Ричардсона или методом Ромберга. Но это не совсем правильно, поскольку на протяжении веков уже существовали похожие численные методы решения подобных задач. Поэтому знаменитая h3 Ричардсона (экстраполяция для численного решения) не является первой. Подобный метод был применим в вычислениях Гюйгенса еще в 1654 году. Сам термин «экстраполяция» был впервые введен Томасом Д. Кларесоном в 1959 году в книге о науке и художественной литературе.

Методы экстраполяции могут пониматься как расширение данных или процессов, предполагающих, что аналогичный процесс будет применяться и за их пределами. Экстраполяция — важная концепция, используемая не только в математике, но и в других областях, таких как социология, психология, прогнозирование. Например, водитель обычно экстраполирует дорожные условия за пределами своего видения. Экстраполяция может быть отнесена к способу, в котором значения данных рассматриваются как точки x1, x2 . xn, а затем значение приближается к пределу заданного диапазона точек.

1. Простой метод прогнозирования.
2. Не так много данных требуется.
3. Быстрая и дешевая аналитика.

Метод существует в статистических данных. Если какие-то значения периодически убираются, ответ приближается к следующей точке данных. Примером методом экстраполяции является прогноз погоды, в котором рассматривается предыстория данных и экстраполируется прогнозируемая модель будущего. Еще более простой пример, если есть информация о воскресеньях, понедельниках и вторниках, можно экстраполировать среду или четверг.

Недостатки использования экстраполяции:

1. Ненадежность, если имеются значительные колебания в исторических данных.
2. Предположение, что прошлая тенденция будет продолжаться и в будущем, вряд ли возможно во многих конкурентных бизнес-средах.
3. Игнорирует качественные факторы, например изменения вкусов и моды.

Ускорение последовательности

Методы экстраполяции заключается в создании касательной линии в конце известных данных и расширении ее за пределы этой области. Подобно интерполяции, экстраполяция использует множество методов, требующих предварительного знания процесса, который создает существующие точки данных. Метод включает в себя экстраполяцию линейную и полиномиальную, экстраполяцию коники и французской кривой.

Как правило, качество конкретного метода ограничено предположениями о функции. В численном анализе экстраполяция Ричардсона представляет собой метод ускорения последовательности, используемый для улучшения скорости ее сходимости. Он назван в честь Льюиса Фрая Ричардсона. Он представил технику расчета в начале XX века, полезность которой для практических вычислений вряд ли можно переоценить.

Практические применения экстраполяции Ричардсона включают интеграцию Ромберга, которая применяет ее к правилу трапеции и алгоритму Булирша — Стоера для решения обыкновенных дифференциальных уравнений.

Линейный метод

Метод линейной экстраполяции полезен, когда задана линейная функция. Это делается путем рисования касательной линии в конечной точке заданного графика и расширения ее за пределы. Этот метод экстраполяции в прогнозировании дает хорошие результаты, когда точка, которая должна быть предсказана, не слишком далека от данных. Линейная интерполяция полезна при поиске значения между заданными точками. Его можно рассматривать как «заполнение пробелов» таблицы данных.

Стратегия линейной интерполяции заключается в использовании прямой линии для соединения известных точек значений по обе стороны от неизвестной. Линейная интерполяция неточна для нелинейных параметров. Если точки в наборе данных меняются на большую величину, линейная интерполяция может дать неправильную оценку.

Линейная экстраполяция может помочь оценить значения, которые выше или ниже значений в наборе данных. Стратегия ее заключается в использовании подмножества данных вместо всего набора. Для этого типа значений полезно применять в прогнозировании метод экстраполяции, используя последние две или три точки, чтобы оценить значение, превышающее диапазон данных.

Полиномиальная и коническая экстраполяции

Известно, что три точки дают уникальный многочлен. Полиномиальная кривая может быть продолжена после окончания таких данных. Она обычно выполняется методом Ньютона с конечной разностью или с использованием интерполяционной формулы Лагранжа. Полином высшего порядка должен быть экстраполирован с должным вниманием, потому что при полиномиальной экстраполяции есть справедливые шансы на ошибку. Если это произойдет, оценка ошибки будет экспоненциально возрастать вместе со степенью полинома.

В математике минимальная полиномиальная экстраполяция представляет собой преобразование последовательности, используемое для ускорения сходимости. Хотя метод Айткена является самым известным, он часто терпит неудачу, особенно для векторных последовательностей. При этом выполняется итерация, которая строит матрицу. Ее столбцы являются отличиями.

К примеру, методом экстраполяции для конического разреза может быть произведен с помощью 5 точек, указанных ближе к концу данных. В случае, если коническая секция представляет собой круг или эллипс, то она будет образовывать петли назад и воссоединиться с собой. Парабола или гипербола никогда не пересекутся. Но они могут быть изогнуты назад относительно оси X. Экстраполяция конуса может быть выполнена на бумаге с конической секцией или с помощью компьютера.

Математический метод оценки

В этом методе экстраполяции прогнозируется значение за базовый период. Действия, описанные ниже, автоматически выполняются системой и не видны пользователю. Описание предназначено для уточнения алгоритма, который выводит ожидаемые значения из количества, хранящегося в системе, и прогнозирует результат измерения счетчика.

Экстраполяция при использовании определения количества процедуры выполняется с помощью функции: Yt = f (yi, t, aj).

В качестве основы для экстраполяции добавляются округленные данные типичного базового периода, хранящегося в результатах считывания. Система определяет вес Yt данных временного ряда в t (время прогнозируемого периода) для получения правильного решения методом экстраполяции. Где в точке отсчета взяты yi – уровень ряда и aj – параметр уравнения тренда.

Прогнозирование функциональных возможностей

Метод фиксации статистической кривой применим к прогнозированию функциональных возможностей. Статистические процедуры соответствуют прошлым данным одной или нескольких математических функций, таких как линейные, логарифмические, Фурье или экспоненциальные. Наилучшие выбираются статистическим тестом. Тогда этот прогноз экстраполируется из этой математической связи методом математической экстраполяции. Одним из самых простых способов получения приблизительных оценок будущих (или прошлых) условий является экстраполяция данных, которые изменяются со временем.

Например, если нужно провести грубую оценку будущих уровней загрязняющих веществ в питьевых водах на 20 лет вперед, можно экстраполировать эту тенденцию с последних 20 лет. То же наблюдается, если нужно оценить распространенность курения или рак легких в фоновом режиме в будущем. Прогноз можно составить путем расчета тенденции за последние годы. Экстраполяции этого типа можно сделать с использованием менее сложных методов. Во многих случаях (особенно в областях маркетинга и управления бизнесом) традиционно используется метод экстраполяции, например путем просмотра последних данных и интуитивной оценки того, что подразумевается в будущем.

Методы, основанные на правилах, также могут быть использованы путем применения набора предопределенных принципов или ожиданий на основе предварительного понимания системы и учета последних данных для интерпретации будущих событий.

При любом методе в экстраполяции важна осторожность из-за наличия многочисленных неопределенностей. Любая процедура экстраполяции основана на предположении, что в прошлых данных и знаниях имеется достоверная информация. Следовательно, будущее обусловлено теми же факторами, которые действовали ранее.

Ошибки прогнозирования

Ошибочность экстраполяции (точнее, ошибочность неоправданной экстраполяции) возникает, когда явление, ответственное за ряд тривиальных локальных эффектов, считывается в качестве великих глобальных явлений. Еще одна причина ошибки заключается в том, что иногда обобщенные правила выводятся на основе слишком немногочисленных фактов. Так, теория Дарвина об эволюции является фантастическим примером применения метода экстраполяции, в которой механизмы случайных изменений и естественного отбора объявляются для учета развития таких сложных структур, как зрение млекопитающих или иммунная система живых организмов.

При попытке интерпретации результатов исследований ученый должен избегать экстраполяции вне диапазона данных и осознавать лежащие в основе предположения, чтобы избежать принятия недействительных выводов. В общем, экстраполяция является законным научным инструментом. Есть два аспекта, которые помогают различать действительную и ошибочную экстраполяцию. Вероятность ошибочной экстраполяции выше, когда для ее построения были получены точки на недостаточных данных.

Статистические инструменты Excel

Чтобы найти корреляцию между годами и результатами (например, в бизнесе), можно воспользоваться Excel.

Для этих задач используют статистические инструменты для моделирования методом экстраполяции, встроенные во все версии Excel, начиная с 97. Порядок действия:

1. Ввести известные значения, например общие продажи за 2016-2017 годы, если нужно определить их за 2018 и 2020 годы.
2. Установить утилиту Analysis, функцию, требующую использования надстройки.
3. Чтобы установить ее, извлечь из меню «Инструменты», «Дополнения».
4. Проверить окно утилиты анализа и подтвердить с помощью «ОК».
5. Измерить корреляции между двумя сериями.
6. Экстраполяция, которую нужно сделать, имеет смысл только в том случае, если между двумя наборами чисел (годы и продажи) складывается четкая тенденция (корреляция) по методу экстраполяции тенденций.
7. Чтобы измерить эту корреляцию, используют меню «Инструменты», «Утилиты анализа».
8. В списке «Инструменты анализа» выбирают «Анализ корреляции» и нажимают «ОК».
9. В поле Input Range вводят анализируемый диапазон, например A6: B18, Excel добавит символ «$».
10. В области «Параметры вывода» проверяют выходной диапазон и вводят в соседнее поле.
11. Подтверждают с помощью OK.
12. Excel создает массив из двух строк по двум столбцам. Находят расчетное значение (например, 0.981). Поскольку это значение близко к 1, это означает, что существует сильная корреляция между годами и цифрами продаж. Если пользователь получит значение, близкое к нулю, это будет означать, что тенденция не возникает. В этом случае экстраполяция не имеет смысла.
13. Запускается оценка будущих значений.
14. Выбирают необходимый диапазон и нажимают кнопку «Мастер диаграмм».
15. Выбирают диаграмму (например, облака точек) и нажимают «Готово».

Применение скользящих средних

Эти два метода экстраполяции предполагают широкое использование данных по продажам для прогнозирования будущего. Скользящее среднее значение принимает серию данных и «сглаживает» флуктуации в них. Цель состоит в том, чтобы извлекать экстремумы данных из периода в период. Скользящие средние часто вычисляются ежеквартально или еженедельно. Для прогнозирования будущих значений экстраполяция предполагает использование трендов, установленных историческими данными. Основное предположение экстраполяции заключается в том, что образец будет продолжаться и в будущем, если фактические данные не указывают на иное. Чтобы подробнее разобраться в этих методах, можно рассмотреть диаграмму, показывающую продажи гаджетов для крупного бизнеса с 2012 по 2015 годы.

Этот метод экстраполяции расчета показывает фактическую цифру продаж. Как можно увидеть, общая сумма продаж колеблется от года к году, хотя можно догадаться (глядя на данные), что общая тенденция для роста продаж имеется. Черная линия показывает скользящую среднюю. Это рассчитывается путем добавления последних лет продаж (например, Q1 + Q2 + Q3 + Q4), а затем деления на четыре.

Этот метод сглаживает годовые изменения и дает хорошее представление об общей тенденции в годовых продажах. Скользящее среднее помогает указать тенденцию роста, выраженную в процентных значениях. Именно это экстраполяция будет использовать сначала, чтобы предсказать путь будущих продаж. Это можно сделать математически, используя электронную таблицу. В качестве альтернативы экстраполированный тренд можно просто нарисовать на диаграмме в качестве приблизительной оценки.

Корреляция трендов

Всегда одна технология является предшественником другой. Это случается, когда достижения, достигнутые в технологии прекурсоров, могут быть приняты технологией последователей. Когда такие отношения существуют, знание изменений в технологии предшественников может быть использовано для прогнозирования хода технологии последователей в будущем. Кроме того, экстраполяция предшественника позволяет прогнозировать продолжение следования за пределами времени запаздывания.

В этом случае используют метод экстраполяции трендов, в котором сравниваются, например, тенденции скорости боевых и транспортных самолетов.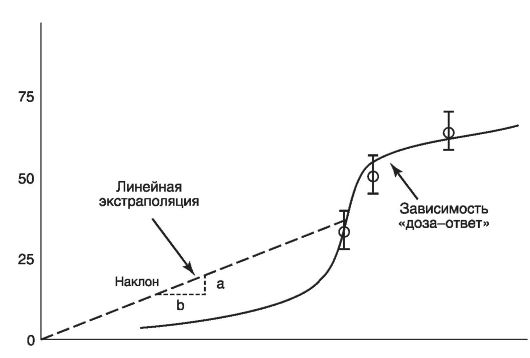 Другим примером прогноза корреляции трендов является прогнозирование размера и мощности будущих компьютеров, основанное на достижениях в области микроэлектронной технологии. Иногда технология последователей зависит от нескольких технологий прекурсоров, а не от одного предшественника.

Фиксированные комбинации предшественников могут влиять на изменение в последовательности, но чаще комбинации не фиксируются, а входы предшественников различаются как по комбинации, так и по силе. Например, увеличение скорости воздушных судов может происходить за счет улучшения двигателей, материалов, элементов управления, топлива, аэродинамики и различных комбинаций этих факторов.

Пример прогноза корреляции, полученной методом экстраполяции трендов: общие пассажирские мили, общие географические мили и средняя посадочная мощность. Экстраполяция статистически определенных тенденций позволяет объективно подходить к прогнозированию. Однако этот подход имеет серьезные ограничения и ловушки. Любые ошибки или неправильный выбор, сделанный при определении исторических данных, будут отражены в прогнозе, что снижает его ценность.

Приложения, атрибуты и лимиты

Метод экстраполяции относится к сфере прогнозирования. Он предполагает, что шаблоны, которые существовали в прошлом, будут продолжаться и в будущем, а также то, что эти шаблоны являются регулярными и могут быть измерены. Другими словами, прошлое является хорошим индикатором будущего. Приложения полезны для разработки базовых данных.

Атрибуты и лимиты — это простые и дешевые инструменты вычислений, как и сложные теоретические модели.

1. Данные процесса — графика и наблюдения.
2. Ключ — наличие хорошей базы данных и понимание структуры внутри нее.
3. Техника — наилучшая подгонка, соотношение и так далее.

Временные стандартные статистические процедуры не приводят к аккуратным подборам тенденций, которые прогнозист может экстраполировать с комфортом, выполняя прогноз методом экстраполяции. В таких случаях прогнозист может «скорректировать» статистические результаты, применяя суждение. Также он может полностью игнорировать статистику и экстраполировать тренд целиком на основе суждения.

Прогнозы, генерируемые таким образом, менее точны, чем статистические, но не обязательно неудовлетворительные. Одним из примеров такой экстраполяции качественного тренда является прогнозирование сложности воздушного судна. Попытки количественной оценки этой тенденции не были успешными. Но процент подвижных или регулируемых частей самолета был экстраполирован с частотой, с которой такие элементы были введены в прошлом. Эти прогнозы были достаточно точными.

Специфические технические изменения не могут быть предсказаны таким образом, но степень изменения может. Это дает полезные материалы для планирования, указывая тенденцию прошлого поведения.

Калькулятор Линейной Интерполяции | Примеры И Формулы

Математические Калькуляторы

Этот бесплатный онлайн-калькулятор рассчитывает линейную интерполяцию и линейную экстраполяцию. Он также обеспечивает наклон линейного уравнения.

Калькулятор линейной интерполяции

Склон = m

Оглавление

◦Что такое интерполяция?

◦Что такое линейная интерполяция?

◦Что такое формула линейной интерполяции?

◦Что такое формула линейной экстраполяции?

◦Как пользоваться калькулятором линейной интерполяции?

◦Как произвести экстраполяцию с помощью этого калькулятора?

Экстраполяция данных с использованием предыдущих данных называется интерполяцией. Например, на фондовом рынке вы можете заявить, что цена выросла на 10% за последний год, поэтому вы экстраполируете, что акции вырастут на 10% и в следующем году. На самом деле это может быть не так, но это пример интерполяции на основе предыдущих данных.

Что такое интерполяция?

Интерполяция — это процесс, позволяющий экстраполировать данные из ряда точек. Его можно использовать для создания кривой или карты или для оценки значения недостающих данных. Интерполяция полезна для различных целей, включая демографические исследования, бизнес-прогнозирование и научный анализ. В этом сообщении блога мы обсудим некоторые распространенные типы интерполяции и то, как они работают. Так что читайте дальше, чтобы узнать больше!

Что такое линейная интерполяция?

Линейную интерполяцию легко понять на примере. Представьте, что вы печете и хотите узнать, сколько печенья вы получите на определенное количество муки. В первый раз вы использовали 400 граммов муки, и у вас получилось 20 печенек. Во второй раз вы использовали 200 граммов муки и получили 10 печенья. На третий раз у вас есть 250 граммов муки, но вы хотите узнать заранее, сколько печенья вы можете получить. Если соотношение между количеством муки и количеством печенья линейное, вы можете узнать результат с помощью линейной интерполяции!

Если вы пытаетесь найти значение, которого нет в тестируемой области, это называется линейной экстраполяцией. В данном случае это может быть один килограмм муки.

Узнать больше о линейной интерполяции

Что такое формула линейной интерполяции?

Если вы хотите найти «y», формула линейной интерполяции будет следующей:

y = (x — x₁) * (y₂ — y₁) / (x₂ — x₁) + y₁

В этом уравнении:

(x₁, y₁) = coordinates of the first data point

(x₂, y₂) = coordinates of the first data point

(x, y) = coordinates of the result point

Что такое формула линейной экстраполяции?

Уравнение линейной экстраполяции идентично формуле линейной интерполяции.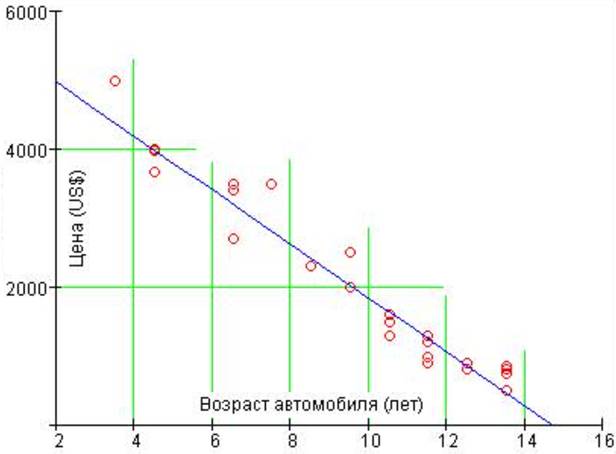 Единственное, что нужно иметь в виду, это то, что при использовании линейной экстраполяции очень часто результаты не подтверждаются экспериментальными данными. Вот почему вы должны быть уверены, что отношения между вашими точками данных являются линейными, прежде чем использовать линейную экстраполяцию.

Пример линейной интерполяции

Как пользоваться калькулятором линейной интерполяции?

Мы можем использовать наш пример cookie для значений в калькуляторе. Итак, мы выясняем, сколько печенья можно испечь из 150 граммов муки?

x₁ = 400

y₁ = 20

x₂ = 200

y₂ = 10

x = 250

Введите эти значения в калькулятор. Вы должны увидеть результат:

y = 12.5

Калькулятор линейной интерполяции также рассчитает наклон линейного уравнения.

Как произвести экстраполяцию с помощью этого калькулятора?

Вы можете использовать этот калькулятор линейной интерполяции также для линейной экстраполяции! Просто введите все значения, как в противном случае, и вы получите результат линейной экстраполяции.

---

Автор статьи

John Cruz

Джон — аспирант, увлеченный математикой и образованием. В свободное время Джон любит ходить в походы и кататься на велосипеде.

---

Калькулятор Линейной Интерполяции русский

Опубликовано: Wed Sep 29 2021

Последнее обновление: Fri Aug 12 2022

В категории Математические калькуляторы

Добавьте Калькулятор Линейной Интерполяции на свой сайт

---

Калькулятор Линейной Интерполяции на других языках

حاسبة الاستيفاء الخطيCalculateur D’interpolation LinéaireLinearer Interpolationsrechner線形補間計算機रैखिक प्रक्षेप कैलकुलेटरDoğrusal Enterpolasyon HesaplayıcısıKalkulator Interpolasi LinierCalculator De Interpolare LiniarăКалькулятар Лінейнай ІнтэрпаляцыіKalkulačka Lineárnej Interpolácie

Как добавить Калькулятор Линейной Интерполяции на мой сайт?

Вы можете легко добавить Калькулятор Линейной Интерполяции на свой веб-сайт с помощью нашего кода. Вставьте код на свой веб-сайт, и калькулятор автоматически появится на этом месте!

Как добавить виджет Калькулятор Линейной Интерполяции на сайт WordPress?

Добавить Калькулятор Линейной Интерполяции на ваш сайт Wordpres быстро и легко! Найдите страницу, на которую вы хотите добавить калькулятор, перейдите в режим редактирования, нажмите «Текст» и вставьте туда код.

Как добавить HTML-виджет на страницу WordPress с помощью нового редактора кодаКак добавить HTML-виджет на страницу WordPress с помощью старого редактора кода

Другие математические калькуляторы

Калькулятор Векторного Произведения

Калькулятор Треугольников 30 60 90

Калькулятор Ожидаемой Стоимости

Математический Онлайн Калькулятор

Калькулятор Стандартного Отклонения

Калькулятор Процентов

Калькулятор Дробей

Конвертер Фунтов В Чашки: Мука, Сахар, Молоко..

Калькулятор Окружности

Калькулятор Формулы Двойного Угла

Вычисление Корня

Калькулятор Площади Треугольника

Калькулятор Котерминального Угла

Калькулятор Скалярного Произведения

Калькулятор Средней Точки

Конвертер Значащих Цифр (калькулятор Sig Figs)

Калькулятор Длины Дуги Для Круга

Калькулятор Балльной Оценки

Калькулятор Процентного Увеличения

Калькулятор Процентной Разницы

Калькулятор QR-разложения

Калькулятор Транспонирования Матрицы

Калькулятор Гипотенузы Треугольника

Калькулятор Тригонометрии

Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника)

45 45 90 Калькулятор Треугольника (калькулятор Прямоугольного Треугольника)

Калькулятор Умножения Матриц

Калькулятор Среднего

Генератор Случайных Чисел

Калькулятор Погрешности

Калькулятор Угла Между Двумя Векторами

LCM Calculator — Калькулятор Наименьшего Общего Кратного

Калькулятор Площади В Квадратных Футах

Калькулятор Экспоненты (калькулятор Мощности)

Калькулятор Математического Остатка

Правило Трех Калькуляторов — Прямая Пропорция

Калькулятор Квадратичных Формул

Калькулятор Суммы

Калькулятор Периметра

Калькулятор Z-счета (значение Z)

Калькулятор Фибоначчи

Калькулятор Объема Капсулы

Калькулятор Объема Пирамиды

Калькулятор Объема Треугольной Призмы

Калькулятор Объема Прямоугольника

Калькулятор Объема Конуса

Калькулятор Объема Куба

Калькулятор Объема Цилиндра

Калькулятор Масштабного Коэффициента Расширения

Калькулятор Индекса Разнообразия Шеннона

Калькулятор Теоремы Байеса

Калькулятор Антилогарифмов

Eˣ Калькулятор

Калькулятор Простых Чисел

Калькулятор Экспоненциального Роста

Калькулятор Размера Выборки

Калькулятор Обратного Логарифма (логарифма)

Калькулятор Распределения Пуассона

Мультипликативный Обратный Калькулятор

Калькулятор Процента Оценок

Калькулятор Отношения

Калькулятор Эмпирических Правил

Калькулятор P-значения

Калькулятор Объема Шара

Калькулятор Чистой Приведенной Стоимости

Что такое интерполяция цифрового изображения

Интерполяция изображений происходит во всех цифровых фотографиях на определённом этапе, будь то дематризация или масштабирование. Она происходит всякий раз, когда вы изменяете размер или развёртку изображения из одной сетки пикселей в другую. Изменение размера изображения необходимо,когда вам нужно увеличить или уменьшить число пикселей, тогда как изменение положения может происходить в самых различных случаях: исправление искажений объектива, смена перспективы или поворот изображения.

Исходное изображение		После интерполяции

Даже если изменению размера или развёртки подвергается одно и то же изображение, результаты могут значительно отличаться в зависимости от алгоритма интерполяции. Поскольку любая интерполяция является всего лишь приближением, изображение будет несколько терять в качестве всякий раз, когда подвергается интерполяции. Данная глава призвана обеспечить лучшее понимание того, что оказывает влияние на результат, — и тем самым помочь вам минимизировать любые потери качества изображения, вызванные интерполяцией.

Концепция

Суть интерполяции заключается в использовании имеющихся данных для получения ожидаемых значений в неизвестных точках. Например, если вам захотелось знать, какова была температура в полдень, но измеряли её в 11 и в час, можно предположить её значение, применив линейную интерполяцию:

Если бы у вас имелось дополнительное измерение в половине двенадцатого, вы могли бы заметить, что до полудня температура росла быстрее, и использовать это дополнительное измерение для квадратической интерполяции:

Чем больше измерений температуры вы будете иметь около полудня,тем более комплексным (и ожидаемо более точным) может быть ваш алгоритм интерполяции.

Пример изменения размера изображения

Интерполяция изображений работает в двух измерениях и пытается достичь наилучшего приближения в цвете и яркости пикселя, основываясь на значениях окружающих пикселей. Следующий пример иллюстрирует работу масштабирования:

	плоскостная интерполяция
Оригинал		до	после	без интерполяции

В отличие от колебаний температуры воздуха и вышеприведенного идеального градиента, значения пикселей могут меняться намного более резко от точки к точке.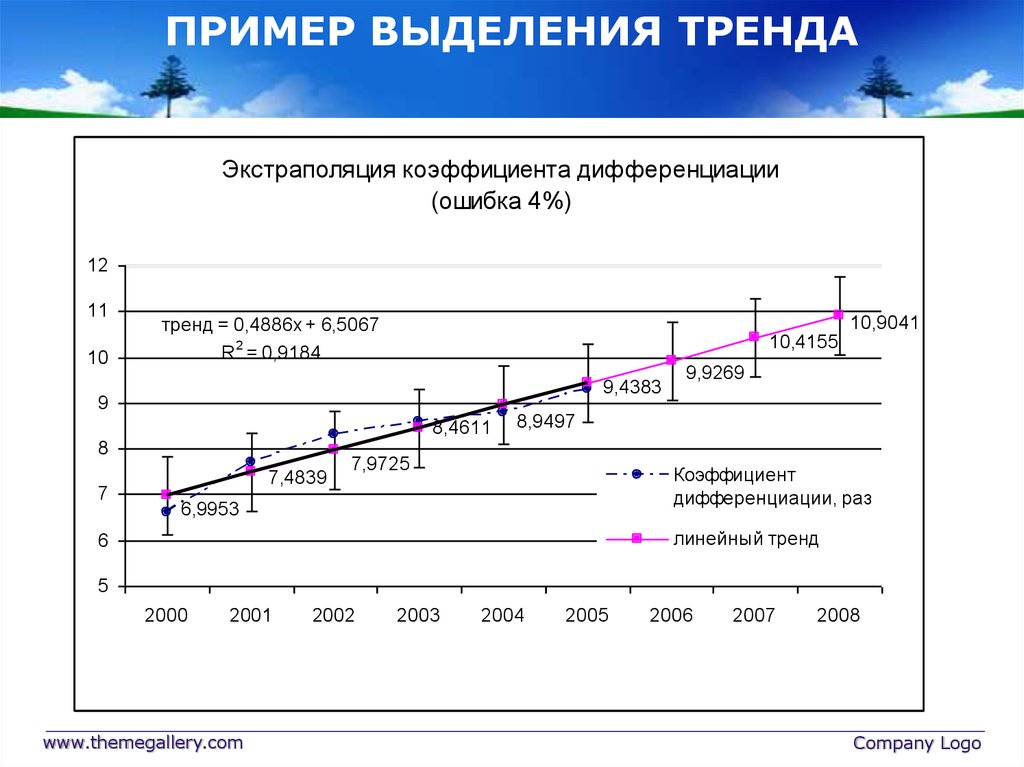 Как и в примере с температурой, чем больше вы знаете об окружающих пикселях, тем лучше сработает интерполяция. Вот почему результаты быстро ухудшаются по мере растягивания изображения, а кроме того, интерполяция никогда не сможет добавить изображению детальности, которой в нём нет.

Пример вращения изображения

Интерполяция происходит также каждый раз, когда вы поворачиваете или изменяете перспективу изображения. Предыдущий пример был обманчив, поскольку это частный случай, в котором интерполяторы обычно работают неплохо. Следующий пример показывает, как быстро может быть потеряна детальность изображения:

			Деградация изображения
Оригинал		поворот на 45°	поворот на 90° (без потерь)	2 поворота на 45°	6 поворотов на 15°

Поворот на 90° не вносит потерь, поскольку ни один пиксель не требуется поместить на границу между двумя (и как следствие разделить).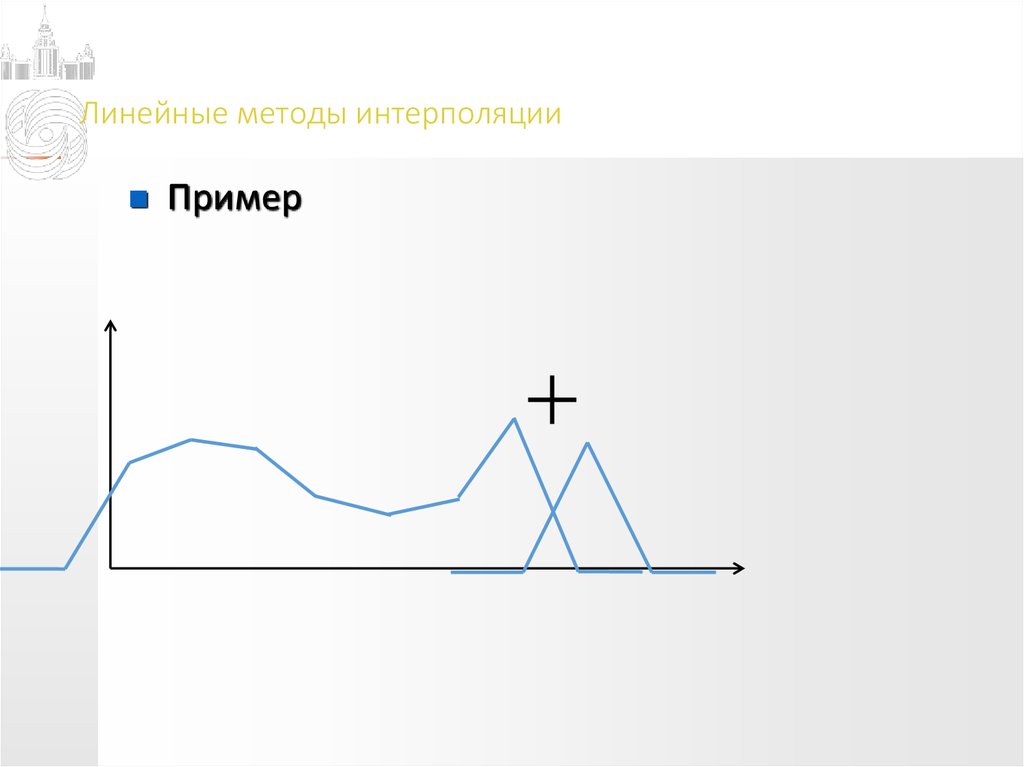 Заметьте, как большая часть деталей теряется при первом же повороте, и как качество продолжает падать при последующих. Это означает, что следует избегать вращений, насколько возможно; если неровно выставленный кадр требует поворота, не следует вращать его более одного раза.

Вышеприведенные результаты используют так называемый «бикубический» алгоритм и показывают существенное ухудшение качества. Обратите внимание, как снижается общий контраст в связи со снижением интенсивности цвета, как вокруг светло-синего возникают тёмные гало. Результаты могут быть значительно лучше в зависимости от алгоритма интерполяции и изображаемого предмета.

Типы алгоритмов интерполяции

Общепринятые алгоритмы интерполяции можно поделить на две категории: адаптивные и неадаптивные. Адаптивные методы изменяются в зависимости от предмета интерполяции (резкие границы, гладкая текстура), тогда как неадаптивные методы обрабатывают все пиксели одинаково.

Неадаптивные алгоритмы включают: метод ближайшего соседа, билинейный, бикубический, сплайны, функция кардинального синуса (sinc), метод Ла́нцоша и другие. В зависимости от сложности, они используют от 0 до 256 (или более) смежных пикселей для интерполяции. Чем более смежных пикселей они включают, тем более точными могут оказаться, но это достигается за счёт значительного прироста времени обработки. Эти алгоритмы могут использоваться как для развёртки, так и для масштабирования изображения.

Оригинал

Адаптивные алгоритмы включают в себя многие коммерческие алгоритмы в лицензированных программах, таких как Qimage, PhotoZoom Pro, Genuine Fractals и другие. Многие из них применяют различные версии своих алгоритмов (на основе попиксельного анализа), когда обнаруживают наличие границы — с целью минимизировать неприглядные дефекты интерполяции в местах, где они наиболее видны. Эти алгоритмы в первую очередь разработаны для максимизации бездефектной детальности увеличенных изображений, так что некоторые из них для вращения или изменения перспективы изображения непригодны.

Метод ближайшего соседа

Это наиболее базовый из всех алгоритмов интерполяции, который требует наименьшего времени обработки, поскольку учитывает только один пиксель — ближайший к точке интерполяции. В результате каждый пиксель просто становится больше.

Билинейная интерполяция

Билинейная интерполяция рассматривает квадрат 2×2 известных пикселя, окружающих неизвестный. В качестве интерполированного значения используется взвешенное усреднение этих четырёх пикселей. В результате изображения выглядят значительно более гладко, чем результат работы метода ближайшего соседа.

Диаграмма слева относится к случаю, когда все известные пиксели равны, так что интерполированное значение просто является их суммой, поделенной на 4.

Бикубическая интерполяция

Бикубическая интерполяция идёт на один шаг дальше билинейной, рассматривая массив из 4×4 окружающих пикселей — всего 16. Поскольку они находятся на разных расстояниях от неизвестногопикселя, ближайшие пиксели получают при расчёте больший вес.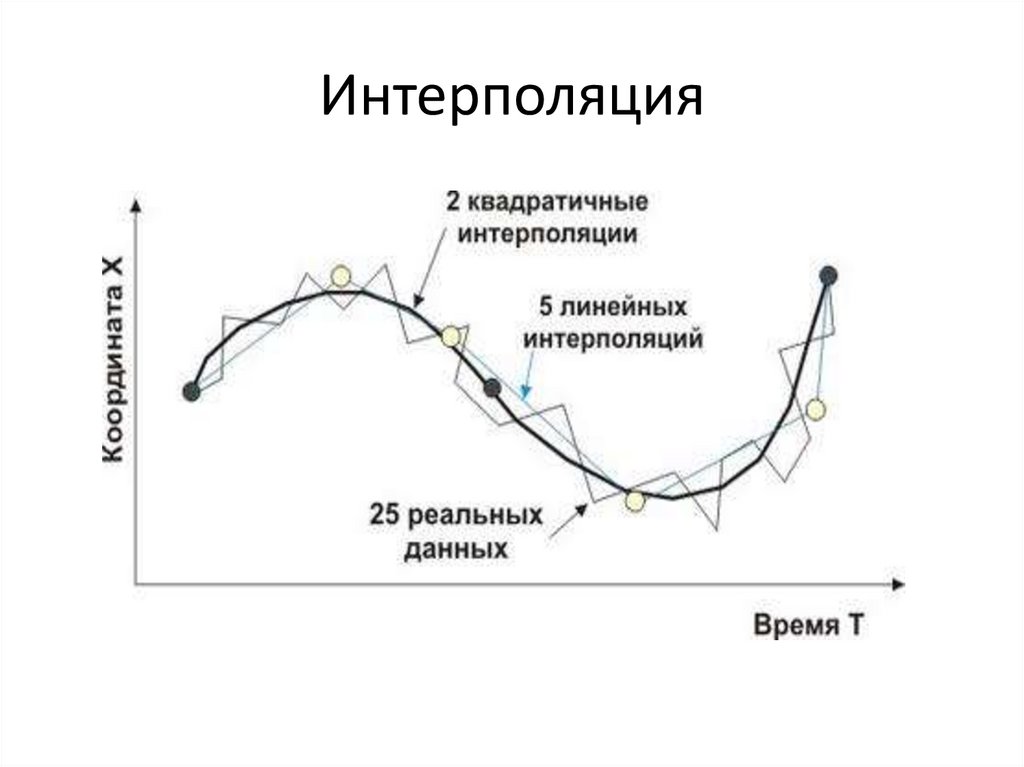 Бикубическая интерполяция производит значительно более резкие изображения, чем предыдущие два метода, и возможно, является оптимальной по соотношению времени обработки и качества на выходе. По этой причине она стала стандартной для многих программ редактирования изображений (включая Adobe Photoshop), драйверов принтеров и встроенной интерполяции камер.

Интерполяция высшего порядка: сплайны и sinc

Есть много других интерполяторов, которые принимают во внимание больше окружающих пикселей и таким образом требуют более интенсивных вычислений. Эти алгоритмы включают в себя сплайны и кардинальный синус (sinc), и они сохраняют большинство информации об изображении после интерполяции. Как следствие, они являются исключительно полезными, когда изображение требует нескольких поворотов или изменений перспективы за отдельные шаги. Однако, для однократных увеличений или поворотов такие алгоритмы высшего порядка дают незначительное визуальное улучшение при существенном увеличении времени обработки. Более того, в некоторых случаях алгоритм кардинального синуса на гладком участке отрабатывает хуже, чем бикубическая интерполяция.

Наблюдаемые дефекты интерполяции

Все неадаптивные интерполяторы пытаются подобрать оптимальный баланс между тремя нежелательными дефектами: граничными гало, размытием и ступенчатостью.

Оригинал
		ступенчатость	размытие	гало

Даже наиболее развитые неадаптивные интерполяторы всегда вынуждены увеличивать или уменьшать один из вышеприведенных дефектов за счёт двух других — как следствие, как минимум один из них будет заметен. Заметьте, насколько граничное гало похоже на дефект, порождаемый повышением резкости с помощью нерезкой маски, и как оно повышает кажущуюся резкость посредством усиления чёткости.

Адаптивные интерполяторы могут создавать или не создавать вышеописанные дефекты, но они тоже могут породить несвойственные исходному изображению текстуры или одиночные пиксели на крупных масштабах:

Оригинал с малоразмерной текстурой		Участок при увеличении 220%

С другой стороны, некоторые «дефекты» адаптивных интерполяторов тоже могут рассматриваться как преимущества. Поскольку глаз ожидает увидеть в областях с мелкой текстурой, таких как листва, детали вплоть до мельчайших подробностей, подобные рисунки могут обмануть глаз на расстоянии (для определённых видов материала).

Сглаживание

Сглаживание или анти-алиасинг является процессом, который пытается минимизировать появление ступенчатых или зубчатых диагональных границ, которые придают тексту или изображениям грубый цифровой вид:

Сглаживание удаляет эти ступеньки и создаёт впечатление более мягких границ и высокого разрешения. Оно принимает во внимание, насколько идеальная граница перекрывает смежные пиксели. Ступенчатая граница просто округлена вверх или вниз без промежуточного значения, тогда как сглаженная граница выдаёт значение, пропорциональное тому, насколько много от границы попало в каждый пиксель:

Идеальная граница в мелком масштабе		Выберите:	ступенчатая	сглаженная

Важным соображением при увеличении изображений является предотвращение чрезмерной ступенчатости в результате интерполяции. Многие адаптивные интерполяторы определяют наличие границ и корректируются с целью минимизировать ступенчатость, сохранив при этом резкость границы. Поскольку сглаженная граница содержит информацию о своём положении при более высоком разрешении, вполне возможно, мощный адаптивный (определяющий границы) интерполятор сможет хотя бы частично реконструировать границу при увеличении.

Оптический и цифровой зум

Многие компактные цифровые камеры могут осуществлять как оптическое, так и цифровое увеличение (зум). Оптический зум осуществляется движением вариобъектива, так чтобы свет усиливался до попадания на цифровой сенсор. На контрасте, цифровой зум понижает качество, поскольку осуществляет простую интерполяцию изображения — уже после получения его сенсором.

оптический зум (10x)		цифровой зум (10x)

Даже несмотря на то, что фото с использованием цифрового зума содержит то же число пикселей, его детальность отчётливо меньше, чем при использовании оптического зума. Цифровой зум следует практически полностью исключить, за вычетом случаев, когда он помогает отобразить удалённый объект на ЖК-экране вашей камеры. С другой стороны, если вы обычно снимаете в JPEG и хотите впоследствии обрезать и увеличить снимок, цифровой зум имеет преимущество в том, что его интерполяция осуществляется до внесения дефектов компрессии. Если вы обнаруживаете, что цифровой зум вам нужен слишком часто, купите телеконвертор, а ещё лучше объектив с большим фокусным расстоянием.

За дополнительной информацией обратитесь к тематическим статьям:
Увеличение цифровых фотографий
Изменение размера изображений для Web и Email

https www bl2 ru matematic interpolation html

Serwis interpolacji online (interpolacja liniowa) pomoże wyliczyć przybliżoną wartość funkcji zmiennej pośredniczącej, mając dostępną wartość funkcji przy zmiennej mniejszej i większej koniecznej.

Interpolacja — (z łacińskiego interpolatio — zmiana, adaptacja), w matematyce i statyce to sposób wyliczenia pośredniej wartości funkcji mając jako dane kilka wartości tej funkcji. Przykład: Dla funkcji f(x) , są znane wartości funkcji f(x) w punktach x₀ i x₂ , inerpolacja pomoże znależć wartość f(x₁) pod warunkiem, że x₁ zawiera się w przedziale x₀ — x₂ . Jeżeli x₁ leży poza przedziałem ( x₀ , x₂ ), interpolacja nie pomoże, należy w takim przypadku posłużyć się «ekstrapolacją», Aby otrzymać wynik dla funkcji z dwiema zmiennymi należy posłużyć się «podwójną interpolacją».

6000	15.5	przykład obliczenia interpolacji
6378	?
8000	19.2

Tą metodę często nazywają «interpolacja liniowa«, dzięki niej można otrzymać 100% dokładny wynik dla równania prostej.

Сервис интерполяции и экстраполяции онлайн (линейная интерполяция/экстраполяция) поможет вам вычислить значение линейной функции, имея в распоряжении f(x) в двух различных точках, а также рассчитает уравнение прямой. Данный сервис автоматически определит нужный способ расчета — вам лишь надо ввести значения в двух произвольных точках, и указать необходимую точку, в которой нужно рассчитать значение. Если установить «галку» внутри кнопки «Рассчитать», калькулятор будет рассчитывать значение автоматически при любом изменении входных данных. Пример расчета интерполяции

Интерполяция — (от латинского interpolatio изменение, переделка), в математике и статике это способ вычислить промежуточное значение функции по нескольким уже известным ее значениям. Например.: Имеется функция f(x) , известны результаты значения f(x) в точке x₀ и точке x₂ , интерполяця помогает найти значение f(x₁) при условии что x₁ принадлежит интервалу от x₀ до x₂ . Если x₁ лежит вне интервала ( x₀ , x₂ ), интерполяция не поможет, для этого нужно использовать «экстраполяцию». Этот метод часто называют «линейная интерполяция«, он дает 100% верный результат для уравнения прямой. Для вычесления резултата функций с двумя переменными существует «Билинейная интерполяция (Двойная интерполяция)». Также для рассчета интерполяции можно воспользоваться сервисом Интерполяция — полином Ньютона и Интерполяция — полином Лагранжа

Экстраполяция — в математике и статике это способ вычислить значение функции по нескольким уже известным ее значениям. Например.: Имеется функция f(x) , известны результаты значения f(x) в точке x₁ и точке x₂ , экстраполяция помогает найти значение f(x₀) либо f(x₃) при условии что x₀ либо x₃ меньше либо больше интервала x₁ до x₂ . Если x_n лежит в интервале ( x₁ , x₂ ), экстраполяция не поможет, для того вам нужно использовать «интерполяцию» — для функций с одной переменной, и «двойная интерполяция» — для функций с двумя переменными.

Этот метод часто называют «линейная экстраполяция«, он дает 100% верный результат для уравнения прямой.

Как для интерполяции так и для экстраполяции в основе их рассчета лежит пропорция (y1 — y0)/(y2 — y0) = (x1 — x0)/(x2 — x0), прирощение значения в первой точке к прирощению значения во второй точке относится также как прирощение переменной в первой точке к прирощению переменной во второй точке (все относительно нулевой точки отсчета), из этой пропорции легко получить формулу рассчета любого значения

Online Programm zur linearen Interpolation (Interpolation online) hielft Ihnen, die Wert der Funktion der Zwischenvariable zu berechnen, mit Werten der Funktion veniger und größer als nötig.

Die Interpolation — (von lateinisch “interpolatio” — Veränderung, Umformung), in der Mathematik und Statik ist ein Weg, die Zwischenwert der Funktion zu berechnen, wenn einige von ihren Verten schon bekannt sind. zB: Es gibt eine Funktion f(x) , von der die Werte in Punkten x₀ und x₂ bekannt sind, Interpolation hilft den Wert f(x₁) zu finden, vorausgesetzt, daß x₁ im Intervall von x₀ bis x₂ liegt. Wenn x₁ außerhalb des Intervalls ( x₀ , x₂ ) liegt, kann Interpolation nicht helfen. In diesem Fall müssen Sie die «Extrapolierung» verwenden, Um das Ergebnis für Funktionen mit zwei Variablen zu berechnen, fervendet man «Doppel-Interpolation».

6000	15.5	Beispiel der Berechnung der Interpolation
6378	?
8000	19.2

Dieses Verfahren wird häufig als «lineare Interpolation«, bezeichnet, weil es 100% richtiges Ergebnis für die Gleichung einer Gerade gibt.

Linear Interpolation Calculator

• login
• register
• Home
• Math
• Finance
• Engineering

y ₂   =  4.8

GENERATE WORK

report this ad

GENERATE WORK

Линейная интерполяция — работа с шагами

Калькулятор линейной интерполяции использует координаты двух точек $A(x_A, y_A)$ и $B(x_B, y_B)$ и $x$-координату интерполируемой точки $C $ в двумерной декартовой координатной плоскости и найти $y$-координату интерполируемой точки $C$. Это онлайн-инструмент геометрии, требующий координаты 2 точек и $x$-координату интерполируемой точки в двумерной декартовой плоскости координат.

Необходимо выполнить следующие шаги:

1. Ввести координаты $(x_A, y_A), (x_B, y_B)$ двух точек $A$ и $B$ и $x$-координату интерполируемой точки $ C$ в коробке. Эти значения должны быть действительными числами или параметрами;
2. Нажмите кнопку » GENERATE WORK «, чтобы произвести вычисления;
3. Калькулятор линейной интерполяции выдаст координату $y$ интерполируемой точки $C$. Эта точка принадлежит прямой, проходящей через точки $A$ и $B$.

Ввод: Две упорядоченные пары действительных чисел или переменных и одно действительное число или переменная. Обратите внимание, что первые координаты в упорядоченных парах должны быть разными.
Вывод: Вещественное число или переменная.

Linear Interpolant Formula:

Прямая, проходящая через две точки $A$ и $B$ в двумерной декартовой координатной плоскости, задается уравнением $$y=\frac{y_B-y_A}{x_B-x_A}(x-x_A)+y_A ,$$ где $(x_A,y_A)$ и $(x_B,y_B)$ — координаты точек $A$ и $B$ соответственно.

$y$-координата интерполируемой точки: $y$-координата точки $C$ на линейной интерполянте $AB$ определяется следующим уравнением $$\begin{align} y_C&=\frac{y_B(x_C-x_A)+y_A(x_B-x_C)}{x_B-x_A}\end{align}$$ где $x_C$ — координата точки $C$, $(x_A,y_A)$ и $(x_B,y_B)$ — координаты точки $A$ и $B$ соответственно.

Что такое линейная интерполяция?

Информация, особенно числовая, появляется во всех областях жизни и науки. Мы можем найти уравнение линии наилучшего соответствия, известного как линия регрессии, и использовать его для минимизации расстояния точек, представляющих набор данных, до линии регрессии. Линия регрессии является хорошим методом, если связь между зависимой и независимой переменными является линейной.
Существуют и другие методы, такие как линейная интерполяция и линейная экстраполяция. Интерполяция — это метод нахождения точки между двумя точками на линии или кривой. Точнее,

• Если мы хотим найти координаты точки между двумя заданными точками, то используем линейную интерполяцию
• Если мы хотим найти координаты точки, не лежащей между двумя заданными точками, то используем линейную интерполяцию экстраполяция.

Другими словами, линейная интерполяция используется для заполнения пробелов в наборе точек. Процедура линейной интерполяции состоит в том, чтобы найти прямую, проходящую через заданных точек, затем найти координаты точки между данными точками. Например, даны две точки $A(x_A,y_A)$ и $B(x_B,y_B)$, как показано на рисунке ниже. Сначала найдем прямую, содержащую точки $A$ и $B$. Для значения $x$ в интервале $(x_1,x_2)$ значение $y$ вдоль невертикальной прямой, проходящей через $A$ и $B$, определяется по наклонам $$\frac{y-y_A}{x-x_A}=\frac{y_B-y_A}{x_B-x_A}$$ Решая предыдущее уравнение относительно $y$, получаем $$\begin{align} y&=\frac{y_B-y_A}{x_B-x_A}(x-x_A)+y_A\\ &=\frac{y_B(x-x_A)+y_A(x_B-x)}{x_B-x_A} \end{align}$$ Эта линия называется линейной интерполянтой между этими точками. Поскольку точка $C$ принадлежит этой прямой, ее координаты $(x,y)$ могут быть найдены с помощью линейной интерполяции.

При нелинейном сборе данных линейная интерполяция часто бывает неточной.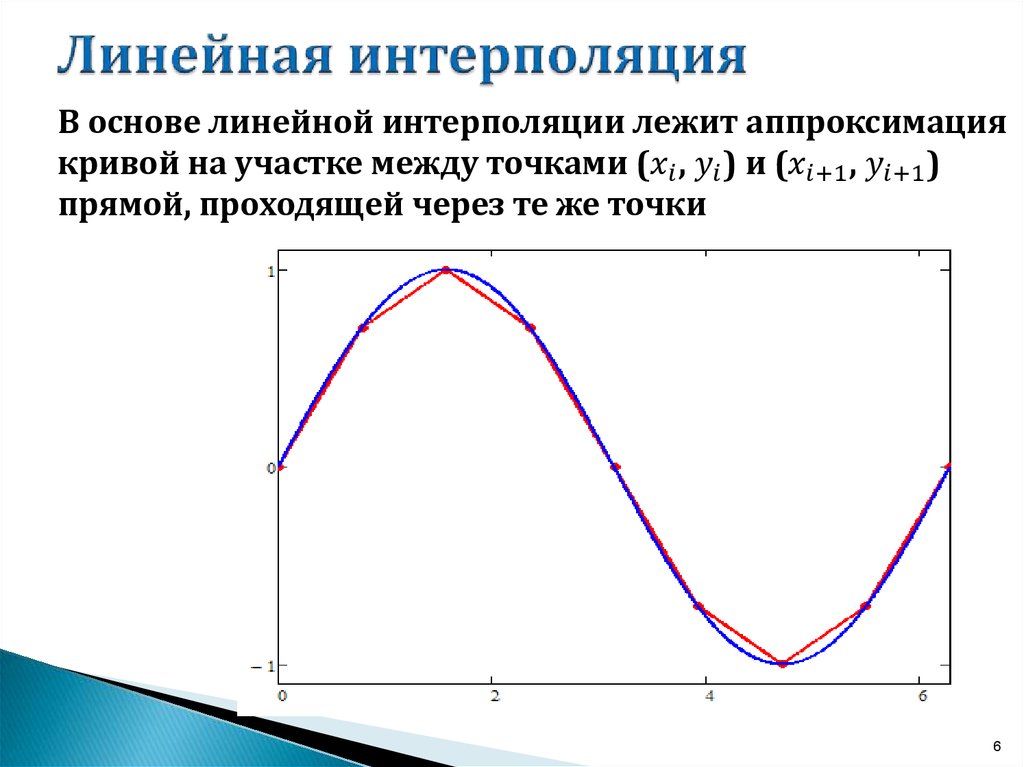 Если точки в наборе данных изменяются на большую величину в интервале, то мы используем кривую вместо линии для оценки значений между точками. Этот метод известен как полиномиальная интерполяция.

Как найти линейную интерполяцию линии?

Если мы подставим координаты точек $A$ и $B$, $(x_A,y_A)$ и $(x_B,y_B)$ в уравнение $$y=\frac{y_B-y_A}{x_B-x_A}(x-x_A)+y_A $$ получаем уравнение линейного интерполянта. Подставив координату $x_C$ точки $C$ в уравнение линейного интерполянта, получим недостающую координату точки $C$. Поэтому недостающая $y$-координата точки $C$ определяется следующим уравнением $$\begin{align} y_C&=\frac{y_B-y_A}{x_B-x_A}(x_C-x_A)+y_A\\ &=\frac{y_B(x_C-x_A)+y_A(x_B-x_C)}{x_B-x_A}\end{align}$$ Линейная интерполяция с шагами показывает полный пошаговый расчет для нахождения значения $y$-координаты интерполируемой точки со значением x-координаты $3$ на прямой через точки с координатами $(2, 4)$ и $(7, 8)$. Для любой другой комбинации координат просто укажите координаты 2-х точек и первую координату требуемой интерполируемой точки и нажмите кнопку «Создать работу».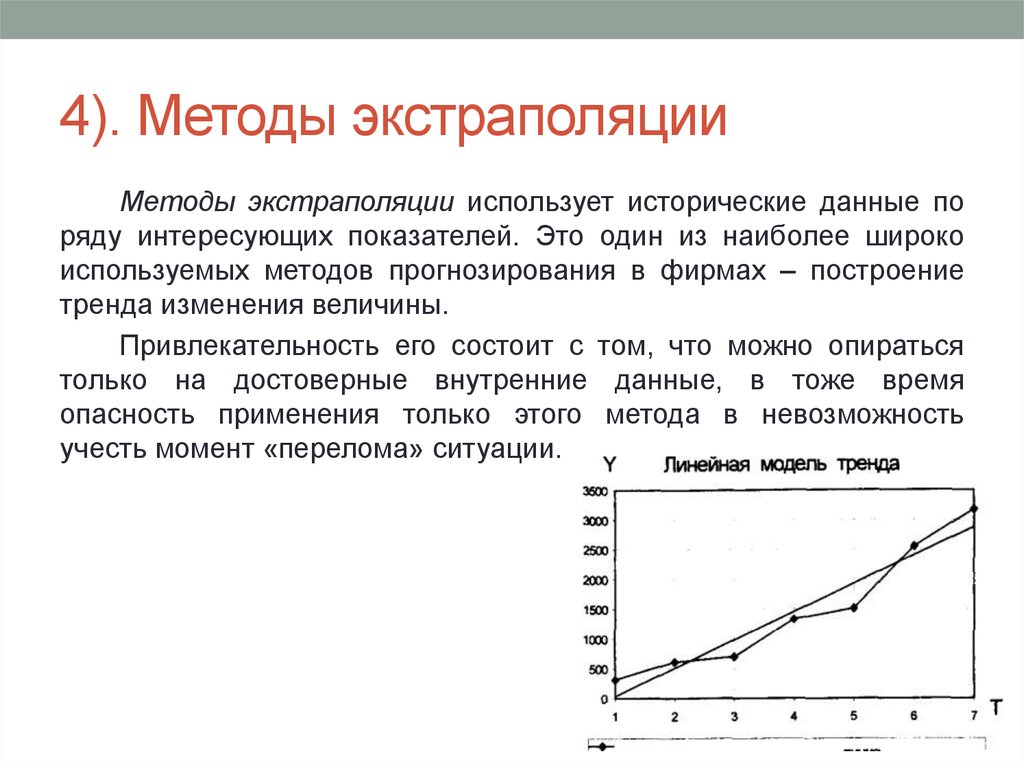 Учащиеся начальной школы могут использовать этот калькулятор линейной интерполяции для создания работы, проверки результатов или эффективного решения домашних заданий.

Применение или использование линейной интерполяции

Интерполяция оценивает значение функции между двумя известными значениями. Уравнение линейной интерполяции может быть реализовано в каком-либо математическом пакете, например в Microsoft Excel или MATLAB, при условии, что табличные значения монотонны по $x$ и нет равных значений $x$. Итак, если нам нужно предсказать значения между двумя существующими точками данных, мы используем метод линейной интерполяции.
Линейная интерполяция широко используется в компьютерной графике. Например, алгоритм Брезенхема постепенно интерполирует точки между двумя конечными точками линии (Брезенхэм, Дж. Э., 9).0034 Алгоритм компьютерного управления цифровым плоттером, IBM Systems Journal, том 4, № 1, (1965), стр. 2530.) Билинейная интерполяция является обобщением линейной интерполяции для интерполирующих функций двух переменных $f(x,y)$. Сначала выполняем линейную интерполяцию в одном направлении, а затем в другом.

Практические задачи линейной интерполяции

Практическая задача 1 : Согласно статистике за 2011$ и 2015$, 20$ процентов и 35$ процентов населения мира курят, соответственно. С помощью линейной интерполяции оцените процент курильщиков в $2012$.

Практическая задача 2 : Найдите значение $y$ при $x=6$, если заданы две точки $(1, 4)$ и $(5, 8).$

Калькулятор линейной интерполяции , формула, пример расчета (работа с шагами), реальные задачи и практические задачи были бы очень полезны для учащихся начальной школы (образование K-12), чтобы научиться находить интерполированные координаты точки на отрезке прямой. Этот метод очень полезен в математике и реальных задачах для прогнозирования значений между двумя заданными точками данных.

• Midpoint of a Line Segment Calculator
• Distance between Two Points Calculator
• Slope Calculator
• Point Slope Form of a Line Calculator
• Slope Intercept Form Calculator
• Perpendicular Distance Calculator

• Perpendicular Bisector Calculator
• Centroid Калькулятор треугольника
• Калькулятор площади треугольника в плоскости XY
• Калькулятор площади и периметра квадрата
• Калькулятор площади и периметра прямоугольника
• Калькулятор площади и периметра круга

Аппроксимация функции с помощью регрессионного анализа

Проблема аппроксимации функции заключается в том, как выбрать функцию из четко определенного класса, которая точно соответствует («аппроксимирует» ) целевая неизвестная функция.

Этот калькулятор использует предоставленные данные таблицы целевых функций в виде точек {x, f(x)} для построения нескольких моделей регрессии, а именно: линейной регрессии, квадратичной регрессии, кубической регрессии, степенной регрессии, логарифмической регрессии, гиперболической регрессии, ab -экспоненциальная регрессия и экспоненциальная регрессия. Результаты можно сравнивать по коэффициенту корреляции, коэффициенту детерминации, средней относительной ошибке (стандартной ошибке регрессии) и визуально, на графике. Теория и формулы, как обычно, даны под калькулятором.

Function approximation with regression analysis

83 71 64 69 69 64 68 59 81 91 57 65 58 62

X values, separated by space

183 168 171 178 176 172 165 158 183 182 163 175 164 175

Значения Y, разделенные пробелом

Линейная регрессия

Квадратичная регрессия

Кубическая регрессия

Степенная регрессия

Аб-экспоненциальная регрессия

Логарифмическая регрессия

Гиперболическая регрессия

Exponential regression

Calculation precision

Digits after the decimal point: 4

Linear regression

 

Linear correlation coefficient

 

Coefficient of determination

 

Average relative error, %

 

Quadratic regression

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя относительная ошибка, %

 

Cubic regression

 

Correlation coefficient

 

Coefficient of determination

 

Average relative error, %

 

Power regression

 

Correlation coefficient

 

Coefficient of determination

 

Средняя относительная ошибка, %

 

ab-Экспоненциальная регрессия

 

Коэффициент корреляции

 

Coefficient of determination

 

Average relative error, %

 

Logarithmic regression

 

Correlation coefficient

 

Coefficient of determination

 

Average relative error, %

 

Hyperbolic regression

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя относительная ошибка, %

Экспоненциальная регрессия

Коэффициент корреляции

Коэффициент определения

Средняя ошибка, %

Результат

3.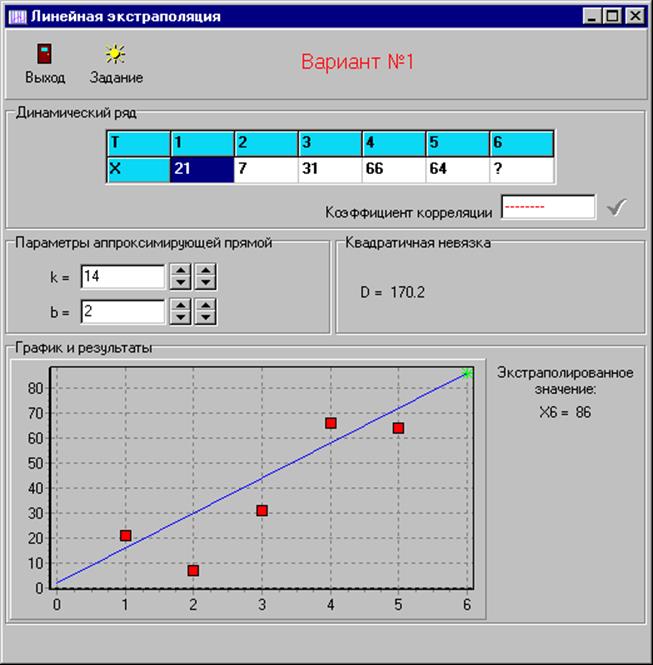 Во время загрузки и создания может происходить замедление работы браузера.

Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же формулы, что и в случае квадратичной регрессии.

Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же формулы, что и выше.

Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – то же.

Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии — те же, что и выше.

Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же, что и выше.

Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же, что и выше.

Начнем с задачи:
Имеем неизвестную функцию y=f(x), заданную в виде табличных данных (например, таких, как полученные из экспериментов).
Требуется найти функцию с известным типом (линейная, квадратичная и т.д.) y=F(x), значения которых должны быть максимально приближены к табличным значениям в тех же точках. На практике тип функции определяют путем визуального сравнения точек таблицы с графиками известных функций.

В результате мы должны получить формулу y=F(x), называемую эмпирической формулой (уравнение регрессии, функция аппроксимации), которая позволяет вычислить y для x, не представленных в таблице. Таким образом, эмпирическая формула «сглаживает» значения y.

Мы используем метод наименьших квадратов , чтобы получить параметры F для наилучшего соответствия. Наилучшее соответствие по методу наименьших квадратов минимизирует сумму квадратов невязок, причем невязка представляет собой разницу между наблюдаемым значением и подобранным значением, предоставленным моделью.

Таким образом, когда нам нужно найти функцию F, такую ​​как сумма квадратов невязок, S будет минимальным

Опишем решение этой задачи на примере линейной регрессии F=ax+b.
Нам нужно найти наилучшее соответствие для коэффициентов a и b, таким образом, S является функцией a и b. Для нахождения минимума найдем точки экстремума, в которых частные производные равны нулю.

Используя формулу для производной комплексной функции, получим следующие уравнения:

Разложив первые формулы с частными производными, получим следующие уравнения:

Из этих уравнений можно получить формулы для a и b , что будет соответствовать приведенным выше формулам.

Калькулятор и формула линейной интерполяции — [100% бесплатно]

Используйте этот калькулятор линейной интерполяции для поиска точек на заданной линии. Вы можете определить значение либо с помощью формы пересечения уклона, либо с помощью двух координат. В этой статье вы узнаете, как использовать калькулятор и другую информацию о линейной интерполяции. Читайте дальше, чтобы узнать больше.

Загрузка калькулятора…

Содержание

Как пользоваться калькулятором линейной интерполяции?

Этот очень простой калькулятор интерполяции служит удобным инструментом, когда вам нужно найти нужные значения.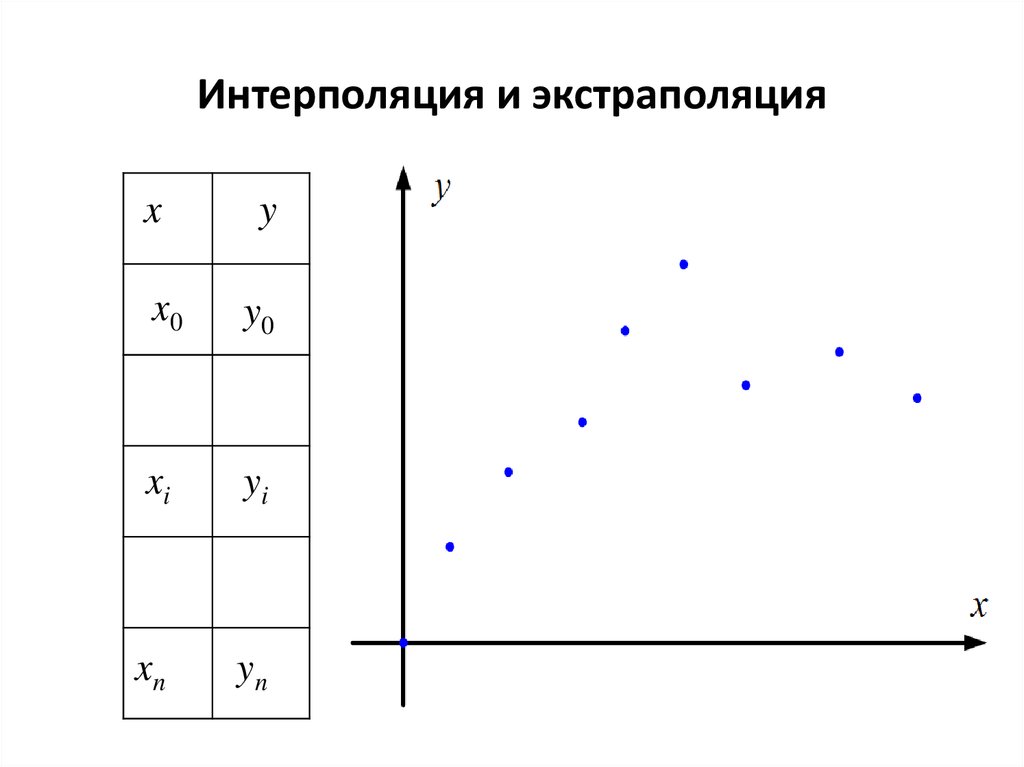 Вместо того, чтобы решать вручную, используя формулу линейной интерполяции, этот калькулятор намного проще и мгновенно предоставляет вам результаты. Вот шаги, которые необходимо выполнить для этого онлайн-инструмента:

• Сначала введите значения x1 и y1 .
• Затем введите значения x2 и y2 .
• Наконец, введите значения x3 и y3 .
• После ввода всех необходимых значений калькулятор линейной интерполяции автоматически генерирует для вас значения m и b с учетом формы пересечения наклона формулы:

y = mx + b.

• Под этими значениями вы также можете увидеть всю формулу с уже подставленными в нее значениями. Это дает вам хорошую ссылку на то, как вы можете записать формулу вместе с требуемыми значениями.

Что такое метод интерполяции?

Метод интерполяции относится к статистическому методу, с помощью которого вы используете связанные известные значения для получения оценки неизвестной потенциальной доходности или цены данной ценной бумаги.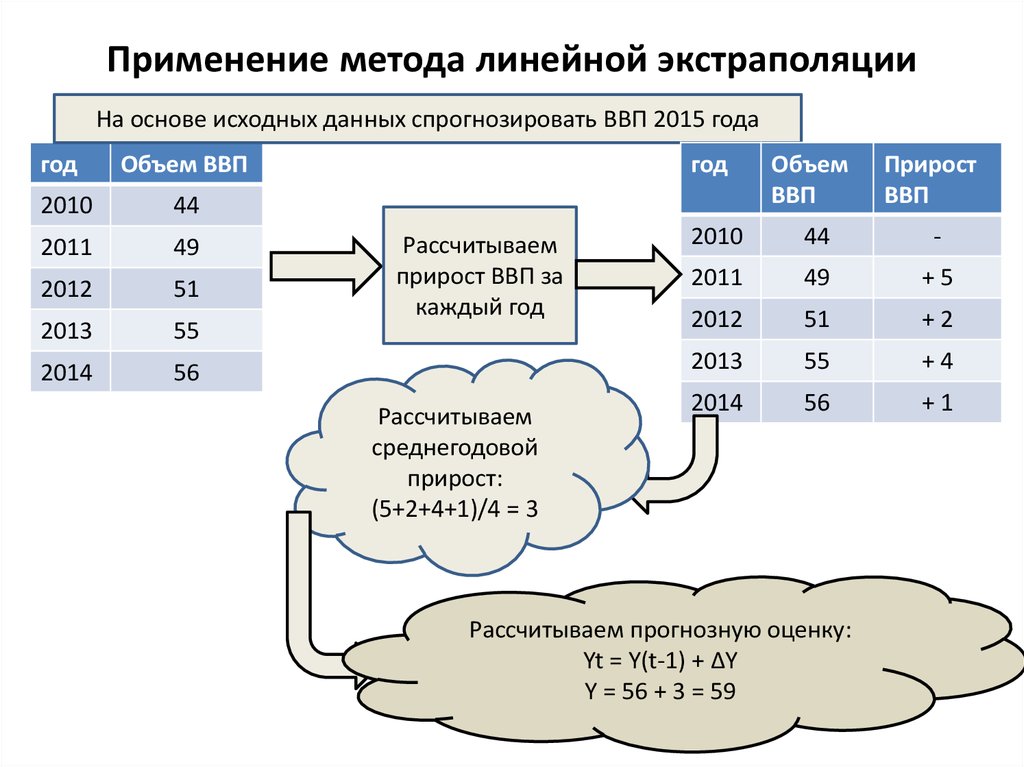 Вы можете достичь этого метода, используя другие известные значения, связанные с ним и которые идут последовательно с неизвестными значениями.

По сути, интерполяция — это простое понятие в математике. Если вы заметили тенденцию в наборе точек данных, которая в целом согласуется, вы можете дать разумную оценку значения набора данных даже в точках, которые вы еще не рассчитали. Конечно, это только оценка в лучшем случае. Проблема с интерполяторами заключается в том, что вы никогда не можете быть полностью уверены в их оценках.

Существуют различные виды интерполяции, с которыми вы можете работать. К ним относятся полиномиальная интерполяция, кусочно-постоянная интерполяция и линейная интерполяция. Среди всех этих методов наиболее распространенным и простым является линейная интерполяция. Для этого метода вы можете использовать уравнение линейной интерполяции или калькулятор линейной интерполяции, что намного удобнее.

Это очень полезно, когда вы пытаетесь оценить стоимость процентной ставки или ценной бумаги для определенного момента, когда нет доступных данных. Не следует путать интерполяцию с экстраполяцией. Последнее относится к методу, с помощью которого вы можете получить оценку для точки данных за пределами известного диапазона данных.

Часто графики, отображающие историю акций, широко интерполируются. Они используют линейную регрессию для создания кривых, которые представляют приблизительное изменение цены ценной бумаги. Даже если диаграмма, которая измеряет акции в течение года, включает точки данных за каждый день, невозможно с полной уверенностью сказать, где акции были бы оценены в данный момент времени.

Хотя это определение на первый взгляд кажется запутанным, фактическая концепция интерполяции относительно проста. Человеческие цивилизации использовали интерполяцию на протяжении веков, особенно ранние месопотамские астрономы, а также астрономы из Малой Азии, когда они пытались заполнить пробелы.

Хотя на движение планетарных тел влияет несколько факторов, они все же лучше подходят для интерполяции с недостаточной точностью по сравнению с колебаниями запасов, которые крайне непредсказуемы. Тем не менее, при огромном количестве данных, задействованных в анализе ценных бумаг, довольно сложно избежать интерполяций с точки зрения движения цен.

Что такое формула линейной интерполяции?

Хотя использование этого калькулятора линейной интерполяции проще, вы все же можете выполнить расчет вручную, используя уравнение линейной интерполяции. Для этого попробуйте представить, что вам нужно измерить зависимость между тем, сколько вам нужно муки, и тем, сколько печенья вы хотите испечь.

В первый раз, когда вы испекли партию печенья, вы использовали 200 граммов муки и в итоге у вас получилось 15 печений. Во второй раз, когда вы испекли партию печенья, вы использовали 300 граммов муки и в итоге у вас получилось 20 печений. Теперь вы хотели бы узнать, сколько печенья получится, если вы используете 250 граммов муки.

Предположим, что эта ситуация имеет линейную зависимость, поэтому вы можете найти решение для линейной интерполяции. Если вам нужно найти значение, выходящее за пределы диапазона, который вы уже протестировали, это относится к экстраполяции.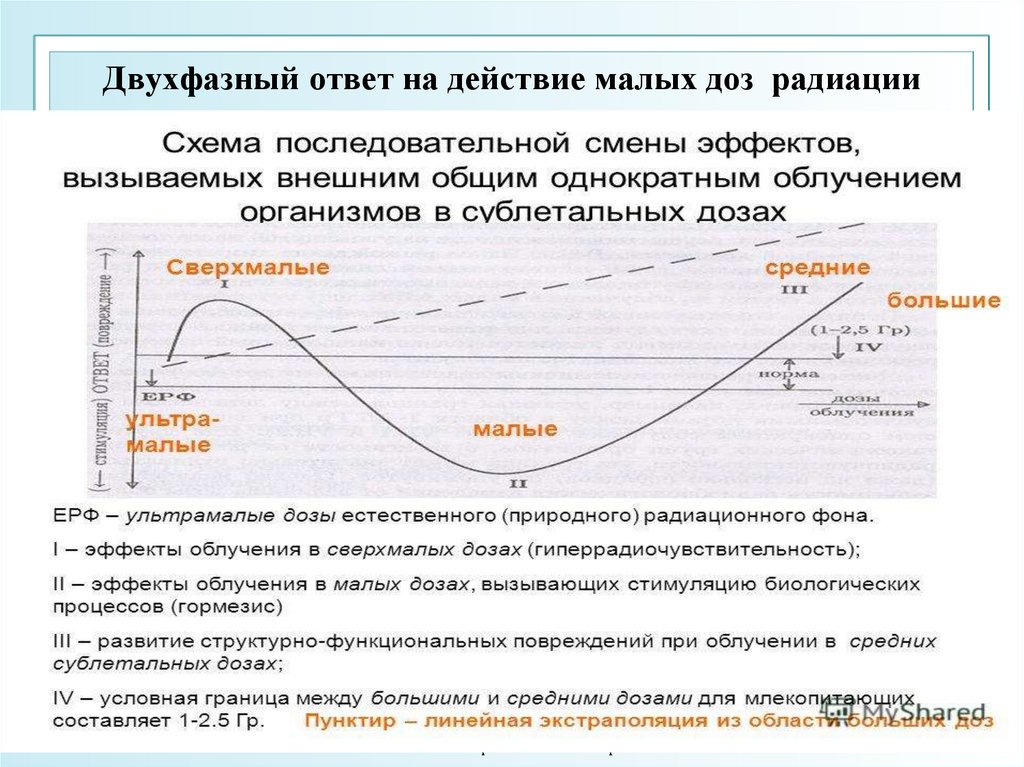 Но если вы хотите получить линейную интерполяцию, используйте формулу линейной интерполяции:

y = (x – x₁) * (y₂ – y₁) / (x₂ – x₁) + y₁

0 0 где:
(x₁, y₁) относятся к координатам 1-й известной точки данных
(x₂, y₂) относятся к координатам 2-й первой известной точки данных
(x, y) относятся к координатам 2-й первой известной точки данных координаты точки, которую вы решаете для

Эта формула точно такая же, как и формула экстраполяции. Имейте в виду, что экстраполяция часто дает вам результат, не подтвержденный никакими экспериментальными данными. Поэтому рекомендуется использовать интерполяцию.

Что такое квадратичная интерполяция?

Квадратичную интерполяцию лучше всего определить с помощью формулы. Если бы у вас была таблица значений

yi=f(xi),0≤i≤2n

На каждом из интервалов [x2j,x2j+2],0≤j≤n−1 , вы бы использовали квадратичный интерполирующий полином на интервале для интерполяции данных.

Как выполнить линейную интерполяцию в Excel?

Интерполяция — это метод, который можно использовать для определения фактора будущей или текущей стоимости, когда точное значение не отображается в таблице значений. Интерполяция предполагает, что любое изменение между двумя заданными значениями является линейным с незначительной погрешностью.

Помимо использования калькулятора интерполяции, вы также можете выполнять линейную интерполяцию в Excel. Для этого вам необходимо ввести конкретную формулу, которая выполняет метод линейной интерполяции, находя значение шага интерполяции. Формула Excel для использования:

=(конец-начало)/(СТРОКА(конец)-СТРОКА(начало))

где:
конец относится к адресу большего ячейка числа
начало относится к адресу ячейки меньшего числа

Формула экстраполяции | Как прогнозировать?

Формула экстраполяции относится к формуле, которая используется для оценки значения зависимой переменной по отношению к независимой переменной, которая должна лежать в диапазоне, выходящем за пределы заданного набора данных, который точно известен, и для расчета линейное исследование с использованием двух конечных точек (x1, y1) и (x2, y2) на линейном графике, когда значение точки, которое необходимо экстраполировать, равно «x», формула, которую можно использовать, представлена ​​​​как y1+ [(x− х ₁ ) / (x ₂ −x ₁ )] *(y ₂ −y ₁ ).

СОДЕРЖАНИЕ

• Определение экстраполяционной формулы
  • Расчет линейной экстраполяции (шаг за шагом)
  • Примеры
    • Пример № 1
    • Пример № 2
    • Пример № 3
  • Администрация № 2
  • #3
• .
• Рекомендуемые артикулы

Y(x) = Y(1)+ (x- x(1)/x(2)-x(1)) * (Y(2) – Y(1))

Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Формула экстраполяции (wallstreetmojo.com)

Примеры

Вы можете скачать этот шаблон формулы экстраполяции Excel здесь – Шаблон формулы экстраполяции Excel

Пример № 1

Предположим, что значение определенных переменных приведено ниже в виде (X, Y):

• (4, 5)
• (5, 6)

Основываясь на приведенной выше информации, вам необходимо найти значение Y(6), используя метод экстраполяции.

Раствор

Для расчета используйте приведенные ниже данные.

• X1: 4,00
• Y2: 6,00
• Y1: 5,00
• X2: 5,00

Вычисление Y(6) с использованием формулы экстраполяции выглядит следующим образом,

23 ( x) – (x1) / (x2) – (x1) x {Y(2) – Y(1)}

Y(6) = 5 + 6 – 4 /   5 – 4 x (6 – 5)

Ответ будет –

• Y3 =  7

Следовательно, значение Y, когда значение X равно 6, будет равно 7.

Пример #2 M и г-н N учатся по стандарту 5 ^th и в настоящее время анализируют данные, предоставленные им учителем математики. Учитель попросил их вычислить вес учеников, чей рост будет 5,9.0 и сообщил, что приведенный ниже набор данных следует линейной экстраполяции.

X	Height	Y	Weight
X1	5.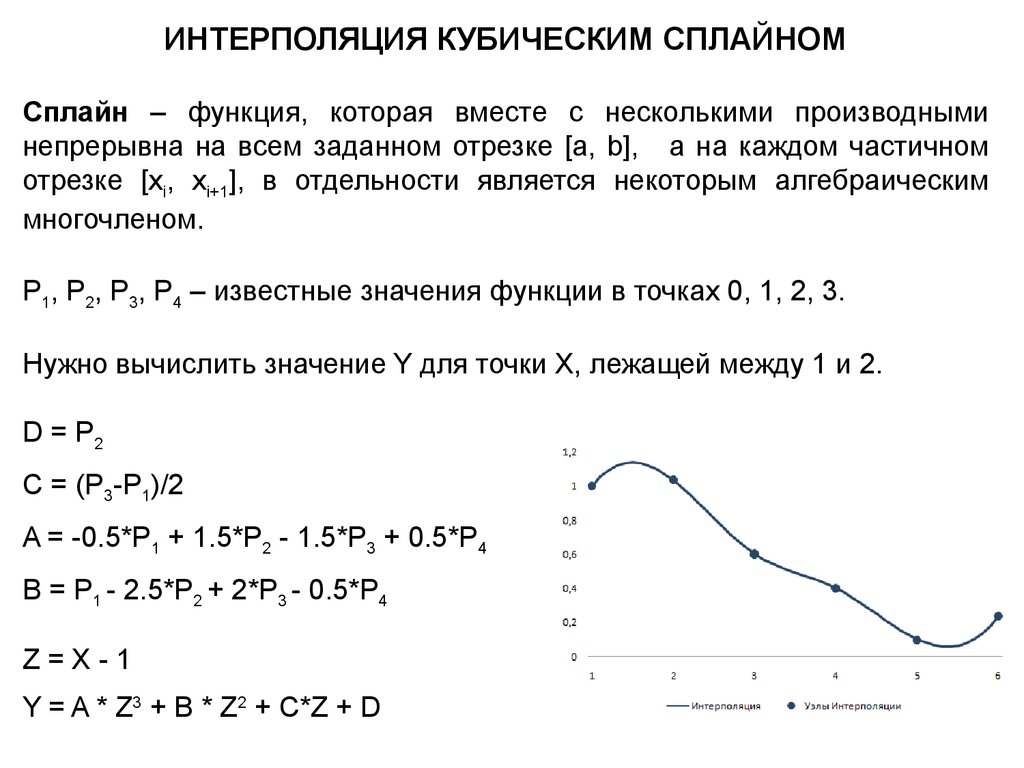 00	Y1	50
X2	5.10	Y2	52
X3	5,20	Y3	53
X4	5.30	Y4	55
X5	5.40	Y5	56
X6	5.50	Y6	57
X7	5.60	Y7	58
X8	5. 70	Y8	59
X9	5.80	Y9	62

Assuming that this data follows a linear series, you are required to рассчитать вес, который будет зависимой переменной Y в этом примере, когда независимая переменная x (рост) равна 5,90.

Решение

В этом примере нам теперь нужно узнать значение, или, другими словами, нам нужно спрогнозировать значение учащихся, чей рост равен 5,90, на основе тенденции, указанной в примере. Мы можем использовать приведенную ниже формулу экстраполяции в Excel для расчета веса, который является зависимой переменной для данного роста, которая является независимой переменной

Расчет Y (5,90) выглядит следующим образом:

• Экстраполяция Y (5,90) = Y (8) + (х) – (х8) /(х9) – (х8)   х [Y(9) — Y (8)]
• Y (5,90) = 59 + 5,90 — 5,70 / 5,80 — 5,70 х (62 — 59)

Ответ будет —

• = 65

. , значение Y, когда значение X равно 5,90, будет равно 65.

Пример #3

Г-н W является исполнительным директором компании ABC. Он был обеспокоен тем, что продажи компании следуют нисходящей тенденции. Он попросил свой исследовательский отдел произвести новый продукт, который будет соответствовать возрастающему спросу по мере увеличения производства. Через 2 года они разрабатывают продукт, который пользуется растущим спросом.

Ниже приведены подробности последних нескольких месяцев:

18 9. 9. .

x (Производство)	Производится (единицы)	Y (Demond)	y (Demond)	9139. 18 918 918918 9. 9036 18 9. 9036198 9.	9. 9036
X1	10.0	Y1	20.00
X2	20.00	Y2	30.00
X3	30.00	Y3	40.00
X4	40.00	Y4	50.00
X5	50.00	Y5	60.00
X6	60.00	Y6	70. 00
X7	70.00	Y7	80.00
X8	80.00	Y8	90.00
X9	90.00	Y9	100,00

Они заметили, что, поскольку это был новый и дешевый продукт и, следовательно, изначально, спрос на него будет линейным до определенного момента.

Следовательно, продвигаясь вперед, они сначала прогнозируют спрос, а затем сравнивают его с фактическим и производят соответственно, поскольку это потребовало от них огромных затрат.

Менеджер по маркетингу хочет знать, какой спрос будет на единицы, если они произведут 100 единиц. Основываясь на приведенной выше информации, вам необходимо рассчитать спрос в единицах, когда они производят 100 единиц.

Решение

Мы можем использовать приведенную ниже формулу для расчета потребности в единицах, которая является зависимой переменной для данных единиц продукции, которая является независимой переменной.

Расчет Y(100) следующий:

• Экстраполяция Y(100) = Y(8) + (x)- (x8) / (x9) – (x8) x [ Y(9) – Y( 8)]
• Y(100)   =  90 + 100 – 80 / 90 – 80 x (100 – 90)

0036

  Следовательно, значение Y, когда значение X равно 100, будет равно 110. В этом случае предполагается, что тенденция будет продолжаться для заданных данных и даже за пределами этого диапазона, что не всегда будет иметь место, и, следовательно, экстраполяцию следует использовать очень осторожно, и вместо этого есть лучший метод сделать то же самое. это использование интерполяцииИнтерполяцияИнтерполяция это математическая процедура, применяемая для получения значения между двумя точками, имеющими заданное значение. Он аппроксимирует значение данной функции в заданном наборе дискретных точек. Его можно применять при оценке различных концепций стоимости, математики, статистики. Подробнее.

Рекомендуемые статьи

Эта статья представляет собой руководство по формуле экстраполяции. Здесь мы обсуждаем формулу для расчета значения зависимой переменной для независимой переменной, а также практические примеры и загружаемый шаблон Excel. Вы можете узнать больше об экономике из следующих статей:

• Скорость роста доходов. свободны от каких-либо сезонных или посторонних эффектов, а рыночные условия останутся постоянными.Подробнее
• Формула скорости обращения денег
• Линия тренда ExcelЛиния тренда ExcelЛиния тренда, часто называемая линией наилучшего соответствия, отображает тренд данных. Он показывает общую тенденцию, закономерность или направление на основе доступных точек данных.Подробнее
• Формула множественной регрессииФормула множественной регрессииФормула множественной регрессии используется при анализе взаимосвязи между зависимыми и многочисленными независимыми переменными. Формула = y = mx1 + mx2+ mx3+ хлеб больше
• Эффективная годовая ставкаЭффективная годовая ставкаЭффективная годовая ставка (EAR) — это ставка, фактически полученная от инвестиций или выплаченная по кредиту после начисления сложных процентов за определенный период времени, и используется для сравнения финансовых продуктов с различные периоды начисления процентов, т. е. еженедельно, ежемесячно, ежегодно и т. д. По мере увеличения периодов начисления процентов EAR увеличивается. Эффективная годовая ставка = (1 + i/n)n – 1Подробнее

Калькулятор линейной интерполяции — графические точки линии!

Калькулятор линейной интерполяции — графические точки линии!

Бесплатные математические калькуляторы, предназначенные для математиков. Этот линейный интерполяционный калькулятор:

• занимает две точки, а x координата
• дает вам отсутствующую координату Y
• Все три точки на линии

Использование линейного интерполяционного расчеты

2020202 вам рассчитать значение точки вдоль линии, если известны две другие точки на этой линии. Введите первую точку данных (First X, First Y) и вторую точку данных (второй X, второй Y), чтобы установить общее направление линии. Затем введите значение X третий пункт. Нажмите «Вычислить» — калькулятор линейной интерполяции сгенерирует интерполированное значение (неизвестную точку) и нанесет неизвестное значение на график вместе с известными координатами.

Этот интерполяционный калькулятор применяет формулу линейной интерполяции для получения зависимого (y) значения третьей точки. Это предполагает, что три точки находятся на прямой линии и что нет естественных отклонений или ошибок в измерении. Функция линейной интерполяции неплохо работает для простых моделей. Это базовая функция прогноза, но она работает относительно хорошо, если заданные координаты (с известным значением y) взяты из аналогичного набора данных. Новая точка данных будет совмещена с существующей тенденцией.

Для удобства ввода вы можете скопировать и вставить свои данные в поле ввода из Excel. Вы можете сохранить свои данные для использования с калькулятор интерполяции и другие калькуляторы на этом сайте. Просто нажмите кнопка «сохранить данные». Это сохранит данные в вашем браузере (не на нашем сервере, он остается закрытым). Сохраненные наборы данных будут отображаются в списке сохраненных наборов данных под панелью ввода данных. Чтобы получить его, нажмите кнопку «Загрузить данные» рядом с ним.

Калькулятор линейной интерполяции

Решение — Y Значение 3-го X:

3,00000

Наблюдения

Первый X

Первый Y

Второй X

Второй Y

Третий X

Обмен результатами калькулятора линейной интерполяции

Нужно передать ответ другу? Легко связать и поделиться результаты калькулятора линейной интерполяции. Нажмите «Рассчитать», а затем просто вырежьте и вставьте URL-адрес после нажатия «Рассчитать» — он сохранит введенные вами значения, чтобы вы могли поделиться ими по электронной почте или в социальных сетях.

Интерпретация результатов инструмента интерполяции

Обзор инструмента: Калькулятор интерполяции

Мы разместили наш онлайн-калькулятор интерполяции в качестве инструмента, который поможет студентам и случайным деловым пользователям упростить свою работу. Этот инструмент берет две точки плюс координату X третьей точки и использует уравнение линейной интерполяции для получить отсутствующее значение Y. Это хорошо работает, если вы пытаетесь интерполировать точки для проблемы, которая может быть аппроксимируется линейной функцией. Это используется в таких областях, как исследование операций, калькуляция затрат и планирование логистики. Линейный тренд почти повсеместно используется для общедоступных статистических и аналитических объяснений.

Вы можете легко адаптировать этот инструмент к онлайн-калькулятору линейной экстраполяции — отрегулируйте значение X для третьей точки. Инструмент экстраполирует отношение, наблюдаемое между двумя известными точками, чтобы получить значение y для 3-й точки.

Когда следует предполагать линейную зависимость?

Главным преимуществом использования линейной зависимости для объяснения связи между значением x и значением y заданного набора данных является простота. Большинство бизнес-аудиторий могут быстро понять линейное уравнение основных факторов; учитывая известную точку данных, вы используете вычисление линейной интерполяции, чтобы найти третью точку данных.

Недостатки? Многие проблемы реального мира не связаны с линейной зависимостью. Маржинальная экономика особенно важна во многих областях бизнеса, где дополнительная прибыль от продажи другой единицы (или потери единицы продаж) увеличивается быстрее, чем ваша текущая средняя норма маржи. Некоторые бизнес-процессы работают с полиномиальными отношениями, что требует более глубокого понимания методов полиномиальной интерполяции. Если мы ошибаемся в отношениях, интерполированная точка не имеет значения.

Mathematics & Science Workbench

Химия: калькулятор процентного выхода Калькулятор теоретической доходности, Калькулятор молярной массы

Анализ: интерполяция Коэффициент вариации, Квадратичная формула

Алгебра: Калькулятор НОД, LCM Калькулятор, Факторный калькулятор, Фактор Целое число, Perfect Numbers

Другое: Калькулятор взвешенных оценок, Калькулятор средневзвешенного значения, Калькулятор модуля, арифметическая последовательность, Геометрическая последовательность, Последовательность Фибоначчи Калькулятор Z-счета,

содержание: интерполяционный калькулятор . Неизвестное значение в точке находится по этой формуле. Если речь идет о формуле линейной интерполяции, ее следует использовать для нахождения нового значения из двух заданных точек. По сравнению с интерполяционной формулой Лагранжа должен быть доступен набор чисел «n», и для нахождения нового значения следует использовать метод Лагранжа.

Читайте также: 5 советов по прохождению онлайн-тестов по математике

Интерполяция — это процесс нахождения значения между двумя точками на линии или кривой. Чтобы помочь нам вспомнить, что это значит, мы должны думать о первой части слова «inter» как о значении «входить», что напоминает нам о том, что нужно заглянуть «внутрь» данных, которые у нас были изначально. Этот инструмент, интерполяция, полезен не только в статистике, но и в науке, бизнесе или в любом случае, когда необходимо предсказать значения, попадающие в две существующие точки данных.

Формула линейной интерполяции

Формула линейной интерполяции

Если две известные точки заданы координатами {\displaystyle (x_{0},y_{0})} и {\displaystyle (x_{1},y_{1}) }, линейный интерполянт   – это прямая линия между этими точками. Для значения x в интервале {\displaystyle (x_{0},x_{1})} значение y вдоль прямой определяется из уравнения наклонов

{\displaystyle {\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}},}

, который можно получить геометрически из рисунка справа. Это частный случай полиномиальной интерполяции с n = 1.

Решение этого уравнения для y , которое является неизвестным значением при x-x_ {0}) {\ frac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}}} = {\ frac {y_ {0} (x_ {1} -x) +y_{1}(x-x_{0})}{x_{1}-x_{0}}},}

, что является формулой для линейной интерполяции в интервале {\ displaystyle (x_ {0}, x_ {1})}. Вне этого интервала формула идентична линейной экстраполяции.

Эту формулу также можно понимать как средневзвешенную. Веса обратно пропорциональны расстоянию от конечных точек до неизвестной точки; ближняя точка имеет большее влияние, чем дальняя. Таким образом, веса равны {\textstyle {\frac {x-x_{0}}{x_{1}-x_{0}}}} и {\textstyle {\frac {x_{1}-x}{x_{ 1}-x_{0}}}} — нормированные расстояния между неизвестной точкой и каждой из конечных точек. Поскольку их сумма равна 1,

{\ displaystyle y = y_ {0} \ left (1 — {\ frac {xx_ {0}} {x_ {1} -x_ {0}}} \ right) + y_ {1} \ left (1 — {\ frac {x_ {1} -x} {x_ {1} -x_ {0}}} \ right) = y_ {0} \ left (1 — {\ frac {x -x_{0}}{x_{1}-x_{0}}}\right)+y_{1}\left({\frac {x-x_{0}}{x_{1}-x_{0} }}\справа),}

Калькулятор формулы интерполяции

Решенные примеры

Вопрос 1: Используя формулу интерполяции, найдите значение y при x = 8 при заданном наборе значений (2, 6), (5, 9) ?
Решение:

Известные значения: x0=8,x1=2,x2=5,y1=6,y2=9y=y1+(x−x1)(x2−x1)×(y2−y1)

y=6+((8−2)(5−2)×(9−6)

y = 6 + 6

y = 12

Что такое метод линейной интерполяции?

Линейная интерполяция  является простейшим методом получения значений в позициях между точками данных. Точки просто соединяются отрезками прямой линии.

Как найти интерполяцию между двумя числами?

Знайте формулу для процесса линейной интерполяции . Формула  есть y = y1 + ((x – x1) / (x2 – x1)) * (y2 – y1), где x – известное значение, y – неизвестное значение, x1 и y1 – координаты, которые ниже известного значения x, а x2 и y2 — координаты выше значения x.

Какой метод интерполяции?

В математической области численного анализа интерполяция  – это метод построения новых точек данных в диапазоне дискретного набора известных точек данных. … Несколько точек данных из исходной функции могут быть интерполированы для получения более простой функции, которая все еще достаточно близка к оригиналу.

Формула интерполяции Excel

Формула интерполяции Excel

Вот пример, иллюстрирующий концепцию интерполяции. Садовник посадил растение томата, и через день она измеряла и отслеживала его рост. Этот садовник любопытный человек, и она хотела бы оценить, какой высоты было ее растение на четвертый день.

Читайте также: Средняя и мгновенная скорость изменения

Ее таблица наблюдений выглядела так:

Судя по диаграмме, нетрудно понять, что на четвертый день растение было, вероятно, 6 мм в высоту. Это потому, что это дисциплинированное растение помидоров росло по линейной схеме; наблюдалась линейная зависимость между количеством измеренных дней и ростом растения в высоту. Линейный узор  означает, что точки образуют прямую линию. Мы могли бы даже оценить, нанеся данные на график.

Но что, если растение росло не по удобной линейной схеме? Что, если бы его рост выглядел примерно так?

Что сделал бы садовник, чтобы сделать оценку на основе приведенной выше кривой? Вот тут-то и пригодилась бы интерполяционная формула.

Формула интерполяции Thermo

Линейная интерполяция использовалась с древних времен для заполнения пробелов в таблицах. Предположим, что у вас есть таблица, в которой указано население какой-либо страны в 1970, 1980, 1990 и 2000 годах, и вы хотите оценить численность населения в 1994 году. Линейная интерполяция — это простой способ сделать это. Считалось, что метод использования линейной интерполяции для составления таблиц использовался вавилонскими астрономами и математиками в Месопотамии Селевкидов (последние три века до нашей эры) и греческим астрономом и математиком Гиппархом (II век до нашей эры). Описание линейной интерполяции можно найти в Альмагест  (2 век н.э.) Птолемея.

Основная операция линейной интерполяции между двумя значениями обычно используется в компьютерной графике. На жаргоне этой области его иногда называют lerp . Термин может использоваться как глагол или существительное для операции. например «Алгоритм Брезенхема пошагово перемещается между двумя конечными точками линии».

Операции Lerp встроены в аппаратную часть всех современных процессоров компьютерной графики. Их часто используют в качестве строительных блоков для более сложных операций: например, билинейную интерполяцию можно выполнить за три лерпа. Поскольку эта операция дешева, это также хороший способ реализовать точные таблицы поиска с быстрым поиском гладких функций без слишком большого количества записей в таблице.

Читайте также: Что такое буквенно-цифровые символы?

Формула интерполяции

Допустим, у нас есть две известные точки x1,y1x1,y1 и x2,y2x2,y2.

Теперь мы хотим оценить, какое значение yy мы получим для некоторого значения xx, находящегося между x1x1 и x2x2. Назовите это оценкой значения yy — интерполированным значением .

На ум приходят два простых способа выбора yy. Во-первых, посмотреть, ближе ли xx к x1x1 или к x2x2. Если xx ближе к x1x1, то мы используем y1y1 в качестве оценки, в противном случае мы используем y2y2. это называется ближайшего соседа интерполяции.