Квазитреугольная матрица: Блочно-диагональная матрица | это… Что такое Блочно-диагональная матрица?

Блочные матрицы. Сложение и умножение блочных матриц. Теорема об определителе квазитреугольной матрицы.

Прямоугольную матрицу А можно вертикальными и горизонтальными линиями разбить на прямоугольные клетки(блоки). В частности матрица может быть разбита только горизонтальными или только вертикальными линиями. (А_α,β)_s,t– блочная матрица. Рассмотрим две матрицы А и В одинаковой размерности и с одинаковым разбиением на блоки. Соответствующие блоки А_α,β и В_α,β имеют одинаковую размерность m_α x n _β , α=1..s, β=1..t. Тогда в соответствии с правилом сложения матриц операция сложения блочных матриц одинаковых размеров с одинаковым разбиением на блоки, производится точно также как если бы вместо блоков стояли числовые элементы.

Чтобы распространить правило умножения матриц на блочные матрицы необходимо чтобы все горизонтальные размеры блоков первой матрицы совпали с соответствующими размерами второго сомножителя.

Число столбцов блока А_α,β равно числу строк блока В_β,с .

b изменяется от 1 до t, с изменяется от 1 до u. Таким образом возможно умножение матриц А и В формально также как если бы вместо блоков стояли числовые элементы.

Определение: Квадратная матрица у которой все элементы расположенные под(над) главной диагональю равны 0 называется верхней(нижней) треугольной матрицей. Аналогичные понятия вводятся и для блочных матриц.

Определение: Блочная матрица А называется верхней(нижней) квазитреугольной матрицей если все диагональные блоки и сама матрица А квадратные матрицы, и все не диагональные блоки расположенные под(над) диагональными блоками нулевые матрицы.

Определение: Блочная матрица А называется квазидиагональной если все диагональные блоки и сама матрица А квадратные матрицы, а все недиагональные блоки – нулевые матрицы.

Теорема: Определитель квазитреугольной матрицы связан с определителем диагональных матриц следующим соотношением:

(♀) где П – произведение.

Доказательство: Рассмотрим сначала квазитреугольную матрицу где А₁₂=0, , ,

По определению

Т.к. А₁₂=0 то из всех произведений могут быть ≠0 только те в которых индексы . Вследствие этого остальные индексы могут принимать значения только из множества . В этих условиях число инверсий в перестановке равно:

т.е.

№7-продолжение———————————————————

Учитывая это находим, что

Отсюда следует что

Рассматривая в общем случае квазитреугольную матрицу

Как матрицу где согласно (*) будем иметь . Матрица снова квазитреугольная. Проделав над ней туже операцию, получим . После (р-1) таких шагов придем к (♀).

Аналогично доказывается равенство (♀) применительно к верхней квазитреугольной матрице.(ч.т.д.)

№8—————————————————————————-Теорема об определителе произведения матриц.

Теорема:

Доказательство: Пусть заданы квадратные матрицы порядка n. и . На основании теоремы об определителе квазитреугольной матрицы () имеем: порядок данной матрицы 2n. Не изменяя определителя, над матрицей порядка 2n выполним последовательно следующие преобразования: к первой строке прибавим . В результате такого преобразования на первых n позициях первой строки будут все 0, а на вторых(во втором блоке) – будет стоять сумма произведений первой строки матрицы А на первый столбец матрицы В. Проделав те же самые преобразования с 2 … n строками получим следующее равенство:

Чтобы привести правый определитель к квазитреугольному виду поменяем в нем местами 1 и 1+ n столбцы, 2 и 2+ n … n и 2 n столбцы. В результате получим равенство:

Замечание: Ясно что теорема справедлива для любого конечного числа матриц. В частности .

№9—————————————————————————-

Теория матриц

Теория матриц

Гантмахер Ф.Р. Теория матриц. – М.: Наука, 1968. — 576 с. Оглавление Предисловие автора к первому изданию Предисловие автора ко второму изданию ЧАСТЬ I. ОСНОВЫ ТЕОРИИ Глава I. Матрицы и действия над ними § 1. Матрицы. Основные обозначения § 2. Сложение и умножение прямоугольных матриц § 3. Квадратные матрицы § 4. Ассоциированные матрицы. Миноры обратной матрицы § 5. Обращение прямоугольных матриц. Псевдообратная матрица Глава II. Алгоритм Гаусса и некоторые его применения § 1. Метод исключения Гаусса § 2. Механическая интерпретация алгоритма Гаусса § 3. Детерминантное тождество Сильвестра § 4. Разложение квадратной матрицы на треугольные множители § 5. Разбиение матрицы на блоки. Техника оперирования с блочными матрицами. Обобщенный алгоритм Гаусса Глава III. Лииейиые операторы в n-мерном векторном пространстве § 1. Векторное пространство § 2. Линейный оператор, отображающий n-мерное пространство в m-мерное § 3. Сложение и умножение линейных операторов § 4. Преобразование координат § 5. Эквивалентные матрицы. Ранг оператора. Неравенства Сильвестра § 6. Линейные операторы, отображающие n-мерное пространство само в себя § 7. Характеристические числа и собственные векторы линейного оператора § 8. Линейные операторы простой структуры Глава IV. Характеристический и минимальный многочлены матрицы § 1. Сложение и умножение матричных многочленов § 2. Правое и левое деление матричных многочленов. Обобщенная теорема Безу § 3. Характеристический многочлен матрицы. Присоединенная матрица § 4. Метод Д. К. Фаддеева одновременного вычисления коэффициентов характеристического многочлена и присоединенной матрицы § 5. Минимальный многочлен матрицы Глава V. Функции от матрицы § 1. Определение функции от матрицы § 2. Интерполяционный многочлен Лагранжа–Сильвестра § 3. Другие формы определения f(A). Компоненты матрицы A § 4. Представление функций от матриц рядами § 5. Некоторые свойства функций от матриц § 6. Применение функций от матрицы к интегрированию системы линейных дифференциальных уравнений с постоянными коэффициентами § 7. Устойчивость движения в случае линейной системы Глава VI. Эквивалентные преобразования многочленных матриц. Аналитическая теория элементарных делителей § 1. Элементарные преобразования многочленной матрицы § 2. Канонический вид матрицы § 3. Инвариантные многочлены и элементарные делители многочленной матрицы § 4. Эквивалентность линейных двучленов § 5. Критерий подобия матриц § 6. Нормальные формы матрицы § 7. Элементарные делители матрицы f(A) § 8. Общий метод построения преобразующей матрицы § 9. Второй метод построения преобразующей матрицы Глава VII. Структура линейного оператора в n-мерном пространстве (геометрическая теория элементарных делителей) § 1. Минимальный многочлен вектора, пространства (относительно заданного линейного оператора) § 2. Расщепление на инвариантные подпространства с взаимно простыми минимальными многочленами § 3. Сравнения. Надпространство § 4. Расщепление пространства на циклические инвариантные подпространства § 5. Нормальная форма матрицы § 6. Инвариантные многочлены. Элементарные делители § 7. Нормальная жорданова форма матрицы § 8. Метод акад. А. Н. Крылова преобразования векового уравнения Глава VIII. Матричные уравнения § 1. Уравнение AX=XB § 2. Частный случай: A=B. Перестановочные матрицы § 3. Уравнение AX-XB=C § 4. Скалярное уравнение f(X)=0 § 5. Матричное многочленное уравнение § 6. Извлечение корня m-й степени из неособенной матрицы § 7. Извлечение корня m-й степени из особенной матрицы § 8. Логарифм матрицы Глава IX. Линейные операторы в унитарном пространстве § 1. Общие соображения § 2. Метризация пространства § 3. Критерий Грама линейной зависимости векторов § 4. Ортогональное проектирование § 5. Геометрический смысл определителя Грама и некоторые неравенства § 6. Ортогонализация ряда векторов § 7. Ортонормированный базис § 8. Сопряженный оператор § 9. Нормальные операторы в унитарном пространстве § 10. Спектр нормальных, эрмитовых, унитарных операторов § 11. Неотрицательные и положительно определенные эрмитовы операторы § 12. Полярное разложение линейного оператора в унитарном пространстве. Формулы Кэли § 13. Линейные операторы в евклидовом пространстве § 14. Полярное разложение оператора и формулы Кэли в евклидовом пространстве § 15. Коммутирующие нормальные операторы § 16. Псевдообратный оператор Глава X. Квадратичные и эрмитовы формы § 1. Преобразование переменных в квадратичной форме § 2. Приведение квадратичной формы к сумме квадратов. Закон инерции § 3. Метод Лагранжа приведения квадратичной формы к сумме квадратов. Формула Якоби § 4. Положительные квадратичные формы § 5. Приведение квадратичной формы к главным осям § 6. Пучок квадратичных форм § 7. Экстремальные свойства характеристических чисел регулярного пучка форм § 8. Малые колебания системы с n степенями свободы § 9. Эрмитовы формы § 10. Ганкелевы формы ЧАСТЬ II. СПЕЦИАЛЬНЫЕ ВОПРОСЫ И ПРИЛОЖЕНИЯ Глава XI. Комплексные симметричные, кососимметрические и ортогональные матрицы § 1. Некоторые формулы для комплексных ортогональных и унитарных матриц § 2. Полярное разложение комплексной матрицы § 3. Нормальная форма комплексной симметрической матрицы § 4. Нормальная форма комплексной кососимметрической матрицы § 5. Нормальная форма комплексной ортогональной матрицы ГЛАВА XII. СИНГУЛЯРНЫЕ ПУЧКИ МАТРИЦ § 1. Введение § 2. Регулярный пучок матриц § 3. Сингулярные пучки. Теорема о приведении § 4. Каноническая форма сингулярного пучка матриц § 5. Минимальные индексы пучка § 6. Сингулярные пучки квадратичных форм § 7. Приложения к дифференциальным уравнениям ГЛАВА XIII. МАТРИЦЫ С НЕОТРИЦАТЕЛЬНЫМИ ЭЛЕМЕНТАМИ § 1. Общие свойства § 2. Спектральные свойства неразложимых неотрицательных матриц § 3. Разложимые матрицы § 4. Нормальная форма разложимой матрицы § 5. Примитивные и импримитивные матрицы § 6. Стохастические матрицы § 7. Предельные вероятности для однородной цепи Маркова с конечным числом состояний § 8. Вполне неотрицательные матрицы § 9. Осцилляционные матрицы Глава XIV. Различные критерии регулярности и локализации собственных значений § 1. Критерий регулярности Адамара и его обобщения § 2. Норма матрицы § 3. Распространение критерия Адамара на блочные матрицы § 4. Критерий регулярности Фидлера § 5. Круги Гершгорина и другие области локализации Глава XV. Приложения теории матриц к исследованию систем линейных дифференциальных уравнений § 1. Системы линейных дифференциальных уравнений с переменными коэффициентами. Общие понятия § 2. Преобразование Ляпунова § 3. Приводимые системы § 4. Каноническая форма приводимой системы. Теорема Еругина § 5. Матрицант § 6. Мультипликативный интеграл. Инфинитезимальное исчисление Вольтерра § 7. Дифференциальные системы в комплексной области. Общие свойства § 8. Мультипликативный интеграл в комплексной области § 9. Изолированная особая точка § 10. Регулярная особая точка § 11. Приводимые аналитические системы § 12. Аналитические функции от многих матриц и их применение к исследованию дифференциальных систем. Работы И. A. Лaппo-Данилевского ГЛАВА XVI. ПРОБЛЕМА РАУСА-ГУРВИЦА И СМЕЖНЫЕ ВОПРОСЫ § 1. Введение § 2. Индексы Коши § 3. Алгоритм Рауса § 4. Особые случаи. Примеры § 5. Теорема Ляпунова § 6. Теорема Рауса-Гурвица § 7. Формула Орландо § 8. Особые случаи в теореме Рауса — Гурвица § 9. Метод квадратичных форм. Определение числа различных вещественных корней многочлена § 10. Бесконечные ганкелевы матрицы конечного ранга § 11. Определение индекса произвольной рациональной дроби через коэффициенты числителя и знаменателя § 12. Второе доказательство теоремы Рауса—Гурвица § 13. Некоторые дополнения к теореме Рауса—Гурвица. Критерий устойчивости Льенара и Шипара § 14. Некоторые свойства многочлена Гурвица. Теорема Стильтьеса. Представление многочленов Гурвица при помощи непрерывных дробей § 15. Область устойчивости. Параметры Маркова § 16. Связь с проблемой моментов § 17. Связь между определителями Гурвица и определителями Маркова § 18. Теоремы Маркова и Чебышева § 19. Обобщенная задача Рауса-Гурвица ДОБАВЛЕНИЕ. НЕРАВЕНСТВА ДЛЯ СОБСТВЕННЫХ И СИНГУЛЯРНЫХ ЧИСЕЛ § 1. Мажорирующие последовательности § 2. Неравенства Неймана-Хорна § 3. Неравенства Вейля § 4. Максимально-минимальные свойства сумм и произведений собственных чисел эрмитовых операторов § 5. Неравенства для собственных и сингулярных чисел сумм и произведений операторов § 6. Другая постановка задачи о спектре суммы и произведения эрмитовых операторов ЛИТЕРАТУРА

T$, $A$ и $Q$ ортогональны. Тогда $T$ ортогонален. Мы хотим доказать, что если $T$ квазитреугольна, то она квазидиагональна. Это следует из следующей теоремы.

Теорема

Предположим $$T=\begin{bmatrix} B_{1,1} & B_{1,2} & \dots & B_{1,m} \\ & B_{2,2} & \dots & \vdots \\ & & \ddots & \vdots \\ & & & B_{м,м} \end{bmatrix}$$ — вещественная ортогональная или комплексная унитарная блочная матрица, где каждая $B_{i,i}$ — это матрица $1 \times 1$ или $2 \times 2$. *$ дает нам $B_{k+1,j}=0$. КЭД

QZVAL

Назначение

            Третий шаг алгоритма QZ для обобщенного
            собственные проблемы. Принимает пару действительных матриц, одну в
            квазитреугольной формы, а другой в верхнетреугольной
            форме и вычисляет собственные значения ассоциированного
            собственная проблема. Обычно предшествует QZHES, QZIT и
            затем QZVEC.
 

Категория GAMS

D4C2C
 

Автор(ы)

           Smith, B.T., et al.
 

Описание

     Эта подпрограмма является третьим шагом алгоритма QZ.
     для решения обобщенных матричных задач на собственные значения,
     СИАМ J. НОМЕР. АНАЛЬНЫЙ. 10, 241-256 (1973) МОЛЕРА и СТЮАРТА.

     Эта подпрограмма принимает пару РЕАЛЬНЫХ матриц, одна из них
     в квазитреугольной форме, а другой в верхнетреугольной форме.
     Это еще больше уменьшает квазитреугольную матрицу, так что любой
     оставшиеся блоки размером 2 на 2 соответствуют парам сложных
     собственные значения и возвращает количества, отношения которых дают
     обобщенные собственные значения.  Обычно ему предшествует QZHES
     и QZIT, за которым может следовать QZVEC.

     При вводе

        NM должен быть установлен равным размеру строки двумерного
          параметры массива, A, B и Z, как объявлено в вызове
          заявление об измерении программы. NM — переменная типа INTEGER.

        N — порядок матриц A и B. N — INTEGER.
          переменная. N должно быть меньше или равно NM.

        A содержит вещественную верхнюю квазитреугольную матрицу. А - это два-
          размерный массив REAL с размером A(NM,N).

        B содержит вещественную верхнюю треугольную матрицу. Кроме того,
          ячейка B(N,1) содержит величину допуска (EPSB)
          вычисляются и сохраняются в QZIT. B является двумерным REAL
          массив размером B(NM,N).

        MATZ должен быть установлен в .TRUE. если правые преобразования
          должны накапливаться для последующего использования в вычислениях
          собственные векторы и .FALSE. в противном случае.  MATZ – это ЛОГИЧЕСКИЙ
          переменная.

        Z содержит, если для MATZ установлено значение .TRUE., преобразование
          матрица производится в редукциях по QZHES и QZIT, если
          выполняется, или же единичная матрица. Если установлен MATZ
          на .FALSE., Z не упоминается. Z является двумерным REAL
          массив размером Z(NM,N).

     На выходе

        Далее А была сведена к квазитреугольной матрице в
          в котором все ненулевые поддиагональные элементы соответствуют парам
          комплексных собственных значений.

        B по-прежнему имеет верхнетреугольную форму, хотя его элементы
          были изменены. B(N,1) не изменяется.

        ALFR и ALFI содержат действительную и мнимую части
          диагональные элементы треугольной матрицы, которые были бы
          получается, если A полностью привести к треугольному виду
          унитарными преобразованиями. Встречаются ненулевые значения ALFI
          в парах, первый член положительный, а второй отрицательный. 
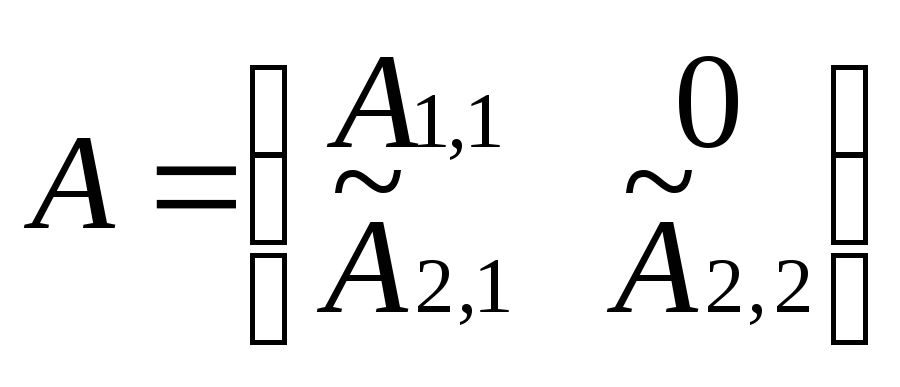          ALFR и ALFI — одномерные массивы REAL, размерами
          АЛЬФР(Н) и АЛЬФИ(Н).

        BETA содержит диагональные элементы соответствующего B,
          нормализуется, чтобы быть вещественным и неотрицательным. Обобщенный
          тогда собственные значения являются отношениями ((ALFR+I*ALFI)/BETA).
          БЕТА представляет собой одномерный массив REAL с размерностью БЕТА(N).

        Z содержит произведение правых преобразований
          (для всех трех шагов), если для MATZ установлено значение .TRUE.

     Вопросы и комментарии следует направлять Б. С. Гарбоу,
     ОТДЕЛ ПРИКЛАДНОЙ МАТЕМАТИИ, АРГОННСКАЯ НАЦИОНАЛЬНАЯ ЛАБОРАТОРИЯ
     -------------------------------------------------- ----------------

 

Каталожные номера

 Б. Т. Смит, Дж. М. Бойл, Дж. Дж. Донгарра, Б. С. Гарбоу,
 Ю. Икебе, В. К. Клема, К. Б. Молер, Matrix Eigen-
 системные процедуры - Руководство EISPACK, Springer-Verlag,
 1976 год.