Линии — геометрия и искусство
Кандинский систематизировал свои взгляды на живопись в книге «Точка и линия на плоскости» (1926). Изучая геометрические формы, художник нашёл, что с их помощью можно усиливать или ослаблять свойства цвета. Для этой картины он использовал приглушённую палитру, смещённую к цветам, расположенным в одной части спектра.
Цитаты из книги:
ЛИНИЯ
Геометрическая линия – это невидимый объект. Она – след перемещающейся точки, то есть ее произведение. Она возникла из движения – а именно вследствие уничтожения высшего, замкнутого в себе покоя точки. Здесь произошел скачок из статики в динамику.
Таким образом, линия – величайшая противоположность живописного первоэлемента – точки. И она с предельной точностью может быть обозначена как вторичный элемент.
ВОЗНИКНОВЕНИЕ
Силы, приходящие извне, преобразовавшие точку в линию, могут быть различными. Разнообразие линий зависит от числа этих сил и их комбинаций.
В конце концов [происхождение] всех форм линий можно свести к двум случаям:
1. приложение одной силы и
2. приложение двух сил:
а) одно- или многократное поочередное воздействие обеих сил,
б) одновременное воздействие обеих сил.
ПРЯМАЯ
Если одна приходящая извне сила перемещает точку в каком-либо направлении, то возникает первый тип линии, причем выбранное направление остается неизменным, и сама линия стремится двигаться по прямому пути бесконечно.
Это – прямая, представляющая в своем напряжении самую сжатую форму бесконечной возможности движения.
…
Среди прямых мы выделяем три типа, по отношению к которым все прочие прямые – лишь отклонения.
1. Простейшая форма прямой – это горизонталь. В человеческом представлении она соответствует линии или поверхности, на которой человек стоит или передвигается. Итак, горизонталь – это холодная несущая основа, которая может быть продолжена на плоскости в различных направлениях. Холод и плоскостность – это основные звучания данной линии, она может быть определена как кратчайшая форма неограниченной холодной возможности движения.

2. Полностью противоположна этой линии и внешне, и внутренне стоящая к ней под прямым углом вертикаль, в которой плоскостность заменяется высотой, то есть холод – теплом. Таким образом, вертикаль является кратчайшей формой неограниченной теплой возможности движения.
3. Третий типичный вид прямой – это диагональ, которая схематичным образом под равным углом отклоняется от обеих вышеназванных и тем самым имеет к обеим равное тяготение, что и определяет ее внутреннее звучание, равномерное соединение холода и тепла. Итак: кратчайшая форма неограниченной тепло-холодной возможности движения…
Замкнутые самопересекающиеся ломаные
Александр Блинков, Александр Грибалко
«Квантик» №11, 2019
В этой статье пойдёт речь о ломаных линиях на плоскости. Для того чтобы изобразить ломаную, достаточно выбрать несколько точек (не меньше трёх), занумеровать их в каком-нибудь порядке, после чего последовательно соединить отрезками точки с соседними номерами. Выбранные точки называются вершинами ломаной, а отрезки — её звеньями (на рисунке 1 — трёхзвенная ломаная с четырьмя вершинами).
Выбранные точки называются вершинами ломаной, а отрезки — её звеньями (на рисунке 1 — трёхзвенная ломаная с четырьмя вершинами).
Если хотя бы два звена ломаной пересекаются (в своих внутренних точках), её называют самопересекающейся (на рисунке 2 — четырёхзвенная самопересекающаяся ломаная).
И наконец, если первая и последняя вершины ломаной совпадают, её называют замкнутой. В такой ломаной количество вершин совпадает с количеством звеньев (на рисунке 3 изображена пятизвенная замкнутая ломаная).
Нас будут интересовать замкнутые самопересекающиеся ломаные.
Начнём с задачи, предложенной А. Пешниным (её частные случаи были использованы на XXV турнире математических боёв имени А. П. Савина).
Очевидно, что трёхзвенная замкнутая ломаная не может быть самопересекающейся. Замкнутая ломаная с четырьмя вершинами также не удовлетворяет условию задачи, так как соседние звенья пересечься не могут, а для каждого звена есть только одно не соседнее.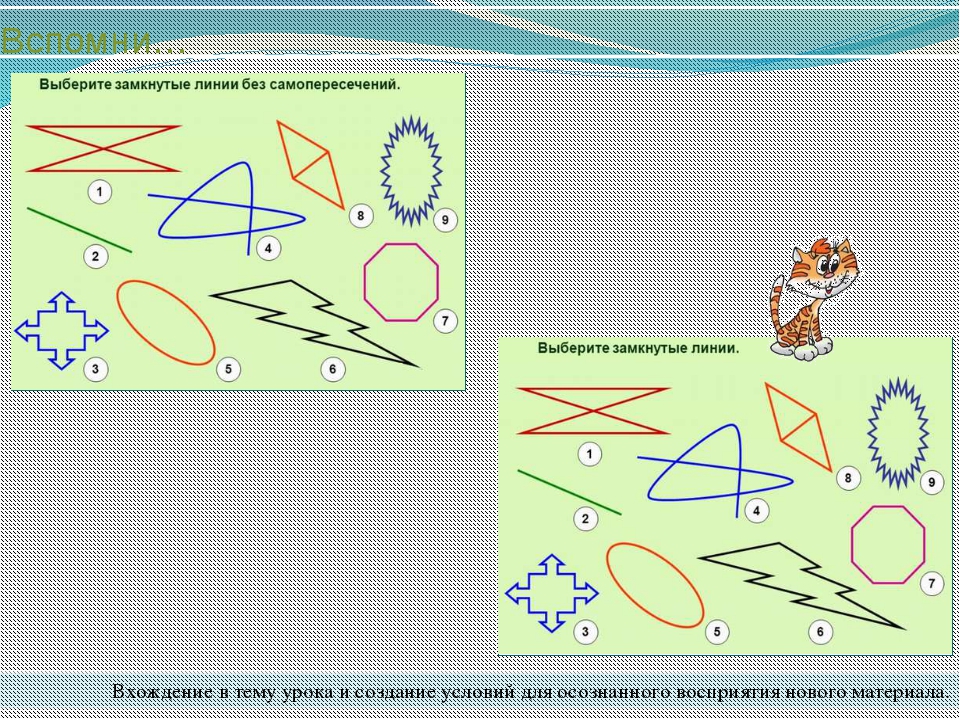 Пример пятизвенной ломаной хорошо известен — это пятиконечная звезда (см. рис. 4, а, где вершины ломаной делят окружность на пять равных частей). Идея использовать окружность тут не обязательна, но удобна и пригодится в дальнейшем.
Пример пятизвенной ломаной хорошо известен — это пятиконечная звезда (см. рис. 4, а, где вершины ломаной делят окружность на пять равных частей). Идея использовать окружность тут не обязательна, но удобна и пригодится в дальнейшем.
Этот пример подсказывает, что аналогичным образом можно построить любую ломаную, удовлетворяющую условию, с нечётным количеством звеньев, большим трёх. Достаточно поставить на окружности требуемое количество вершин и последовательно соединить их через одну. Например, на рисунке 4,
Осталось разобраться с ломаными, у которых чётное количество звеньев, начиная с шести.
Искомой шестизвенной ломаной не существует, но доказывать это мы умеем только перебором всех случаев, который не очень интересен.
Для восьми звеньев существует красивый пример (рис. 5, а). Аналогично можно построить ломаную, удовлетворяющую условию, с любым чётным количеством звеньев, большим восьми. Как это делается, понятно из примеров для десяти и двенадцати звеньев, показанных на рисунках 5, б и 5, в. Сначала мы отмечаем на окружности точки, которых на две меньше, чем нужно, и соединяем их через одну. Так как точек чётное количество, получатся две замкнутые ломаные, все звенья которых пересекаются с другой ломаной в двух точках. После этого удаляем по одному звену в каждой ломаной и соединяем ломаные в одну, используя ещё две вершины, расположенные внутри окружности.
Как это делается, понятно из примеров для десяти и двенадцати звеньев, показанных на рисунках 5, б и 5, в. Сначала мы отмечаем на окружности точки, которых на две меньше, чем нужно, и соединяем их через одну. Так как точек чётное количество, получатся две замкнутые ломаные, все звенья которых пересекаются с другой ломаной в двух точках. После этого удаляем по одному звену в каждой ломаной и соединяем ломаные в одну, используя ещё две вершины, расположенные внутри окружности.
Есть и более простой способ. Воспользуемся тем, что любое чётное число, большее восьми, можно представить в виде суммы двух нечётных слагаемых, каждое из которых не меньше пяти.
Покажем, например, как построить двенадцатизвенную ломаную, удовлетворяющую условию. Изобразим две окружности, которые касаются друг друга внешним образом в некоторой точке. В одной из окружностей построим уже указанным способом пятизвенную ломаную, а в другой — семизвенную, причём точка касания должна быть их общей вершиной. А теперь эту точку «раздвоим» (рис. 6, результат раздвоения — вершины с номерами 1 и 6).
А теперь эту точку «раздвоим» (рис. 6, результат раздвоения — вершины с номерами 1 и 6).
Аналогично строятся все искомые ломаные, у которых количество звеньев чётное и больше восьми.
Возникает вопрос: почему мы начали с двух точек пересечения звеньев, а не с одной, что, казалось бы, более естественно?
Дело в том, что такой порядок более логичен, так как решение следующей задачи будет во многом опираться на решение рассмотренной.
Сразу заметим, что в этом случае звенья ломаной должны разбиваться на непересекающиеся пары, поэтому у искомых ломаных — чётное количество звеньев. Легко проверить, что замкнутая ломаная из четырёх звеньев условию не удовлетворяет.
Пример искомой ломаной из шести звеньев можно построить, исходя из следующих соображений: помимо того, что не могут пересекаться соседние звенья, не могут пересекаться и звенья, стоящие через одно. Действительно, в этом случае образуется треугольник (рис. 7, а), в который можно будет только «войти», если пересечь среднее звено, но нельзя будет «выйти». Поэтому надо пересекать первое звено с четвёртым, второе — с пятым, а третье — с шестым (рис. 7, б).
Поэтому надо пересекать первое звено с четвёртым, второе — с пятым, а третье — с шестым (рис. 7, б).
Пример искомой ломаной из восьми звеньев читателю предлагается построить самостоятельно (см. задачи в конце статьи). А вот пример десятизвенной ломаной можно получить, обратившись к задаче 1. Действительно, рассмотрим пример замкнутой пятизвенной ломаной, которая каждое своё звено пересекает два раза (рис. 4). «Сломаем» каждое звено между двумя точками пересечения и получим искомый пример (рис. 8). Аналогично, рассмотрев семизвенную ломаную из задачи 1, можно получить решение для ломаной с четырнадцатью звеньями; пример восьмизвенной ломаной из задачи 1 помогает получить решение для ломаной из шестнадцати звеньев, и т. д.
Этот приём не годится только для построения двенадцатизвенной ломаной, так как нет шестизвенной ломаной, которая каждое своё звено пересекает два раза. Но в этом случае можно использовать другую идею решения задачи 1: «раздвоение».
Надеемся, что идеи и приёмы, описанные выше, помогут при решении других задач.
Художник Мария Усеинова
Конспект занятия для дошкольников «Замкнутые и незамкнутые линии»
Занятие 10.
Тема: «Замкнутые и незамкнутые линии».
Цель: — познакомить с понятием «замкнутая и незамкнутая линии»;
— закрепить знания детей по теме: «Точка. Прямая и кривая линии»
— развивать память, речь, внимание, мышление;
— воспитывать интерес к занятиям, через разные виды работ.
Оборудование: кубики, картинки с разными линиями.
Ход занятия:
I. Организационный момент.
II. Сообщение темы занятия.
Сегодня мы продолжим путешествие по королевству и узнаем, что линии бывают не только прямые и кривые.
III. Закрепление пройденного материала.
1. Посмотрите на кубики и скажите, какие геометрические фигуры на нем нанесены?
— На каком кубике точек меньше, чем на остальных?
— На каком – больше, чем на остальных?
2. Поставьте у себя в тетради точку и проведите через нее несколько прямых и кривых линий.
3. Поставьте у себя в тетради две точки и проведите через нее прямую и несколько кривых линий.
— Какой вывод вы можете сделать? ( через одну точку можно провести несколько кривых и прямых линий, а через две точки только одну прямую и несколько кривых линий)
IV.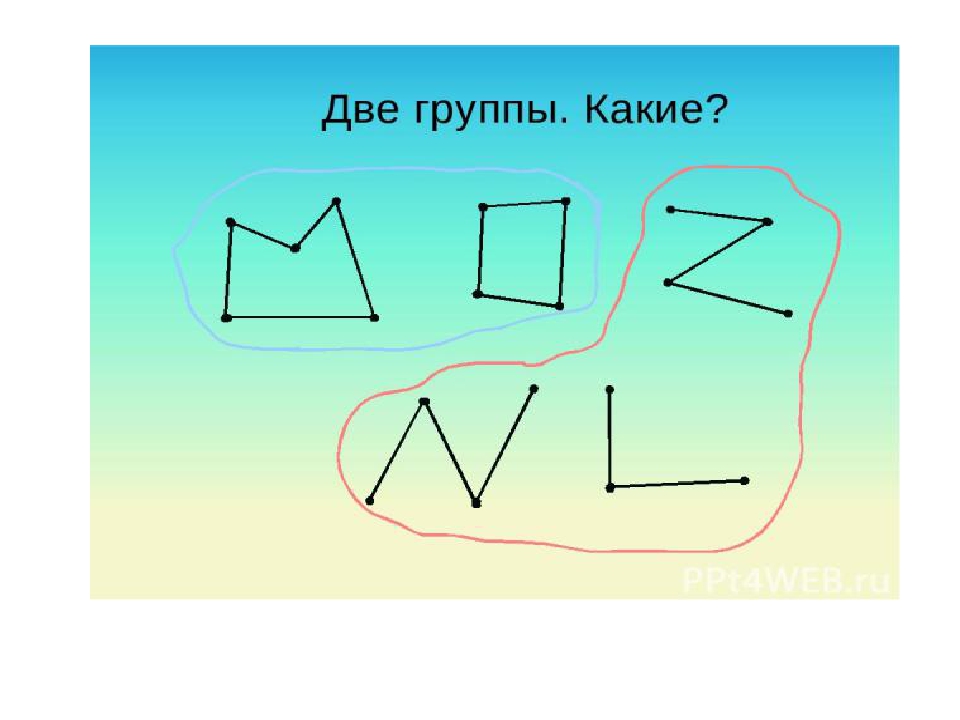 Знакомство с новым
материалом.
Знакомство с новым
материалом.
1. На доске начерчены разные линии.
— Какие линии вы видите на рисунке? (прямые и кривые)
— Покажите прямые линии.
— Покажите кривые линии.
— А еще линии бывают замкнутые и незамкнутые. Как вы думаете, где здесь замкнутые линии, а где незамкнутые?
2. Практическая часть.
А) В своих тетрадях попробуйте начертить незамкнутые линии.
Б) Начертите замкнутые линии.
В) Где в жизни вы видели незамкнутые линии и замкнутые?
(рассуждения детей, примеры замкнутых и незамкнутых линий можно нарисовать в тетради)
V. Подведение итогов.
— Что сегодня мы научились различать?
— С какими новыми словами познакомились?
Королева — Математика вас
благодарит за работу, и она подготовила вам новый рисунок бордюра.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VI. Оценивание работы детей.
Оценивание работы детей.
Рисование кривой или окружности — Служба поддержки Office
Рисование кривой
-
На вкладке Вставка в группе Иллюстрации нажмите кнопку Фигуры.
-
В разделе линиищелкните Кривая .
-
Щелкните место, где необходимо начать кривую, перетащите указатель для рисования кривой, а затем щелкните в место, где необходимо добавить кривую.
-
Чтобы завершить рисование фигуры, выполните одно из следующих действий:
-
Чтобы оставить фигуру незамкнутой, дважды щелкните в любой момент рисования.

-
Чтобы замкнуть фигуру, щелкните вблизи ее начальной точки.
Примечание: К замкнутой фигуре по умолчанию применяется заливка. Чтобы она не скрывала находящиеся под ней ячейки, выберите фигуру, а затем в разделе Средства рисования на вкладке Формат в группе Стили фигур щелкните Заливка фигуры и выберите значение Нет заливки.
-
К началу страницы
Добавление овала или круга
-
На вкладке Вставка в группе элементов Иллюстрации нажмите кнопку Фигуры.
-
В разделе основные фигурыщелкните овал .

-
Щелкните в том месте, откуда следует начать круг. Чтобы получить круг, удерживайте нажатой клавишу SHIFT при перетаскивании указателя.
Примечания:
-
Вы можете изменить внешний вид круга или кривой, добавив заливку или эффект либо настроив границы.
-
Если вы хотите получить более сложную схему, например перекрывающиеся круги, организационную диаграмму или блок-схему, можно создать графический элемент SmartArt, а не рисовать каждую фигуру вручную.
-
К кругу или овалу по умолчанию применяется заливка. Чтобы она не скрывала находящиеся под ней ячейки, выберите фигуру, а затем в разделе Средства рисования на вкладке Формат в группе Стили фигур щелкните Заливка фигуры и выберите значение Нет заливки.

-
К началу страницы
5. Контуры
Контуры это кривые (известны как кривые Безье). Обращению с контурами в GIMP легко научится. За подробной информацией о понятиях и механизмах обращайтесь к главе глоссария Кривые Безье или Википедии [WKPD-BEZIER]. Инструмент «Контуры» очень мощный и позволяет создавать очень сложные контуры. Чтобы использовать этот инструмент в GIMP, нужно сначала создать контур, а затем его обвести.
В GIMP термин «Обводка контура» означает применение специального стиля к контуру (цвет, ширину, шаблон…).
5.1. Создание контуров
Начните с создания обводки контура; её можно изменить позже (см. инструмент Контуры). Для начала активируйте инструмент Контуры одним их этих методов:
Вызовите команду → из меню изображения.

Нажмите на пиктограмму на панели инструментов.
Нажмите клавишу быстрого доступа B.
Когда инструмент контура выбран, указатель мышки меняется на стрелку с кривой. Нажатие левой кнопкой на изображении создаёт первую точку контура. Передвиньте мышку на новое место и нажмите левой кнопкой: обе точки соединятся. И хотя вы можете создать много точек, достачно двух, чтобы понять работу контуров. При добавлении точек у указателя мышки есть маленький знак «+» в близости от кривой; это означает, что при нажатии добавится ещё одна точка. Когда указатель мышки близок к отрезку прямой, знак «+» меняется на крест со стрелками, означающий инструмент перемещения.
Передвиньте указатель мышки близко к отрезку прямой. Нажмите левой кнопкой и передвиньте сегмент. Произойдут две вещи.
Сегмент искривляется по мере перещения.

У каждого сенмента есть начальная и конечная точки, которые ясно обозначены. «Линия направления» теперь начинается у каждой точки каждого передвинутого сегмента.
Сегмент кривой оставляет конечную точку в том же направлении, что и «линия направления». Длина «direction line» определяет, как далеко сегмент кривой следует вдоль «линии направления» до поворота к другой точке. У каждой «линии направления» есть пустой квадрат (называемый обработчик) на конце. Нажмите и передвиньте обработчик, чтобы изменить направление и длину «линии направления».
Рисунок 7.11. Вид контура во время обработки
Контур состоит из двух компонентов с прямыми и кривыми сегментами. Чёрные квадраты являются управляющими точками, открытая окружность — это выбранная точка, два открытых квадрата — её направляющие рычаги.
Сколько кривых можно провести через 1 точку
ТочкаПрямая линияПрямая линия не имеет ни начала, ни конца.
Прямую линию можно продолжить. Она бесконечна.
Через 2 точки можно провести только одну прямую.
Через 1 точку можно провести много прямых линий.
Расстояние между двумя точкамиПоставим две точки на одинаковом расстоянии друг от друга и проведём между ними ломаную линию и прямую линию. Посчитаем расстояние между точками по количеству клеточек.
Вывод: Самое короткое расстояние между двумя точками – это прямая.
КриваяЧерез 1 точку можно провести много кривых линий.
Поделись с друзьями в социальных сетях:
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы узнаем, что называют точкой и линией. Научимся отличать прямую и кривую линию. Выясним, сколько прямых и кривых линий можно провести через одну точку, а сколько – через две точки. Выполним множество интересных заданий.
Научимся отличать прямую и кривую линию. Выясним, сколько прямых и кривых линий можно провести через одну точку, а сколько – через две точки. Выполним множество интересных заданий.
Точка
К нам на урок пришел веселый карандаш. Он очень любит рисовать.
Давайте посмотрим, что у него получилось.
Карандаш коснулся бумаги и оставил точку (рис. 1).
Сколько точек нарисовал карандаш? Пять (рис. 2).
Рис. 2. Пять точек
В математике принято обозначать точки буквами: А, Б, В, Г, Д… (рис. 3).
Рис. 3. Обозначение точек
Посмотрите на рисунок: какая точка самая верхняя? Точка Б. Какая точка самая нижняя? Точка Д. Какая точка стоит между точками А и Г? Точка В. Какая точка находится слева от точки В? Точка А. Какая точка находится под точкой В? Точка Д.
Прямая линия
Посмотрите на рисунок: что теперь нарисовал карандаш (рис. 4)?
Рис. 4. Прямая линия
Без конца и края
Линия прямая.
Хоть сто лет по ней иди,
Не найдёшь конца пути.
О каком свойстве линии идет речь в этом стихотворении?
У линий нет начала и нет конца. Мы можем продолжить линию в одну и в другую сторону. Как получить прямую линию? Мы возьмем лист бумаги и сложим его (рис. 5).
Рис. 5. Складывание листа бумаги
Линия сгиба – это прямая линия (рис. 6).
Рис. 6. Линия сгиба
Есть и другой способ провести прямую линию – с помощью линейки. Поставим точку А и проведем через нее прямую линию (рис. 7, 8).
Рис. 8. Прямая, проходящая через точку А
Сколько прямых линий можно провести через одну точку? На этот вопрос нам поможет ответить карандаш. Понаблюдаем за ним: он провел через точку А множество линий (рис. 9).
Рис. 9. Множество прямых линий, проходящих через точку А
Как вы думаете, сколько прямых линий можно провести через 2 точки?
Рассмотри пример: у нас есть две точки (А и Б) (рис. 10).
Рис. 10. Точки А и Б
С помощью линейки проведем прямую линию (рис. 11).
11).
Рис. 11. Прямая, проходящая через точки А и Б
Теперь попытаемся провести через эти точки еще одну прямую линию. Что мы заметили?
Невозможно сделать это.
Делаем вывод: через две точки можно провести только одну прямую линию.
Кривая линия
Посмотрим, что нарисовал карандаш. Можно ли назвать эту линию прямой (рис. 12)?
Рис. 12. Кривая линия
Нет. В математике такая линия называется кривой.
Чтобы нарисовать ее, линейка не нужна. Посмотрите, какие бывают кривые линии (рис. 13).
Рис. 13. Виды кривых линий
Выясним, сколько линий можно провести через одну точку (рис. 14).
Понаблюдаем за карандашом (рис. 15).
Рис. 15. Кривые, проведенные через точку А
Что мы заметили? Через одну точку можно провести множество кривых линий.
Теперь попробуем провести кривые линии через две точки (рис. 16).
Рис. 16. Кривые, проведенные через две точки
Что мы видим? В отличие от прямой линии, через две точки можно провести множество кривых линий.
Выполнение задания
Карандаш нарисовал картинку (рис. 17).
Рис. 17. Картинка
Посмотрите, где спрятались кривые линии. Кривые линии – это волны на море и чайки (рис. 18).
Рис. 18. Волны и чайки – примеры кривых линий
А паруса, кораблик и лучи солнца – прямые линии (рис. 19).
Рис. 19. Паруса, кораблик и лучи солнца – примеры прямых линий
А вы любите рисовать? Попробуйте нарисовать картинку, используя прямые и кривые линии.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика. 1 класс. – М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. – М.: Русское слово, 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Социальная сеть работников образования Nsportal.ru (Источник).
- Фестиваль педагогических идей “Открытый урок” (Источник).
- Uchmet.ru (Источник).
Домашнее задание
- О каких линиях мы узнали на этом уроке?
- При помощи нитки сложите разные линии.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Данная презентация может быть использована в качестве иллюстративного материала на уроке математики в 1 классе по теме «Прямая и кривая линии» (учебник Н.Б. Истоминой). Смена слайдов происходит по щелчку. Кроме информации по теме, презентация содержит слайды с заданиями, а также слайды «Проверь себя» для организации промежуточного контроля.
Скачать:
| Вложение | Размер |
|---|---|
| matematika_1_kl._pryamaya_i_krivaya_liniit.ppt | 328 КБ |
Предварительный просмотр:
Подписи к слайдам:
Котова О.В. МБОУ СОШ №124 г. Нижний Новгород Прямая линия Кривая линия
На какие две группы можно разделить эти линии?
Проверь себя Прямые линии Кривые линии
Сколько прямых линий можно провести через одну точку? Сколько прямых линий можно провести через две точки?
Проверь себя много линий одна линия
Сколько кривых линий можно провести через одну точку? Сколько кривых линий можно провести через две точки?
Проверь себя много линий много линий
Чем похожи и чем отличаются линии слева и справа?
Проверь себя незамкнутые линии замкнутые линии
Мы узнали Линии бывают прямые и кривые Через одну точку можно провести много прямых и кривых линий Через две точки можно провести только одну прямую линию, но много кривых линий Кривые линии бывают замкнутые и незамкнутые
По теме: методические разработки, презентации и конспекты
Презентация к уроку математики Образовательной системы “Школа 2100”. Подробнее по адресу:http://avtatuzova.ru/news/matematika_1_klass_urok_10_prjamaja_i_krivaja_linii_luch_prezentaci.
Подробнее по адресу:http://avtatuzova.ru/news/matematika_1_klass_urok_10_prjamaja_i_krivaja_linii_luch_prezentaci.
Конспект урока разрабтан к учебнику математики Демидовой Т.Е., Козловой С.А., Тонких А.П. для 1 класса по теме “Прямая и кривая линии. Луч” с использованием ЭОР.
Конспект урока с использованием ЭОР.
урок по математике 1 класс, УМК Гармония.
Презентацию можно использовать при подготовке к 1 классу по курсу “Математика”.
Технологическая карта урока “Точка. Прямая и кривая линии”предназначена в помощь учителю, для подготовки к уроку математики в 1 классе.
“>
Какая линия ограничивает фигуру круг. Рэмп «геометрическая фигура круг
Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..
Давайте сначала рассмотрим, какие у круга бывают части и как они называются.
- Окружность — линия, ограничивающая круг.
- Дуга — часть окружности.
- Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
- Хорда — отрезок, соединяющий две точки окружности.
- Сегмент — часть круга, ограниченная хордой и дугой.
- Сектор — часть круга, ограниченная двумя радиусами и дугой.
Интересующие нас величины и их обозначения:
Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.
- Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
- Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
- Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.
Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.
Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.
Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).
И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.
И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.
Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.
1. Даны диаметр D и длина дуги L
; длина хорды ;
высота сегмента ; центральный угол .
2. Даны диаметр D и длина хорды X
; длина дуги ;
высота сегмента ; центральный угол .
Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол .
3. Даны диаметр D и центральный угол φ
; длина дуги ;
длина хорды ; высота сегмента .
4. Даны диаметр D и высота сегмента H
; длина дуги ;
длина хорды ; центральный угол .
6. Даны длина дуги L и центральный угол φ
; диаметр ;
длина хорды ; высота сегмента .
8. Даны длина хорды X и центральный угол φ
; длина дуги ;
диаметр ; высота сегмента .
9. Даны длина хорды X и высота сегмента H
; длина дуги ;
диаметр ; центральный угол .
10. Даны центральный угол φ и высота сегмента H
; диаметр ;
длина дуги ; длина хорды .
Внимательный читатель не мог не заметить, что я пропустил два варианта:
5. Даны длина дуги L и длина хорды X
7. Даны длина дуги L и высота сегмента H
Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?
Задача эта сводится к решению уравнений:
; — в варианте 5
; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем . Всё то, что я тут длинно рассказываю, она делает за микросекунды.
Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:
длина окружности ;
площадь круга ;
площадь сектора ;
площадь сегмента ;
И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.
Урок математики в 1 классе с ГУО на тему: «Геометрическая фигура: круг»
Цель: Познакомить с геометрической фигурой – кругом. Учить отличать круг от других геометрических фигур и правильно его называть. Закрепить названия цветов. Воспитывать уважительное отношение друг к другу.
I Организационный момент.
1. Кто ходит в гости по утрам,
Тот поступает мудро!
Тарам-парам, тарам-парам,
На то оно и утро!
Дети, какое сейчас время суток? (утро)
Следом за утром приходит … (день)
Часто из гостей возвращаются, когда наступает….(вечер) (С помощью картинок)
2. Посмотрите внимательно на картинки, что на них общее? Чем они все похожи? (на всех картинках нарисовано солнце)
II. Сообщение темы.
Солнце круглое. Сегодня на уроке мы познакомимся с геометрической фигурой – кругом. Поучимся отличать его от других фигур, будем находить предметы круглой формы.
III. Знакомство с фигурой.
1.К нам на урок пришёл гость – Винни-Пух. Он прилетел на воздушных шарах. (Детям раздаются воздушные шары) Шар круглый. (Предложить обвести шар ладонью, пальцем.)
2. Посмотрите на Винни-Пуха, какие части тела у него круглые?
3. Вини-Пух очень любит покушать, и поэтому принёс с собой набор посуды (плоскостные изображения посуды круглой и квадратной формы). Но Вини-Пух любит есть только из посуды круглой формы. Помогите выбрать посуду круглой формы.
4. Пока Вини-Пух добирался до нас, у него разбилось несколько тарелок. Помогите, склейте их! (Дети собирают разрезную картинку)
Какой формы тарелка?
5. Посмотрите вокруг, найдите круглые предметы в нашем классе.
IV. Физ. минутка (хороводная игра)
Ровным кругом друг за другом
Мы идём за шагом шаг.
Дружно вместе все на месте
Делаем вот так!
(Водящий выбирается по очереди)
V. Закрепление изученного
1. У Вини-Пуха много друзей. Он принёс их портреты. (Изображения из геометрических фигур. Рассматриваем, обговариваем, кто это).
Скажите, что у них круглое?
2. Детям раздаются наборы геом.фигур. Найдите круг. (Тактильное обследование, прокатить круг по столу). Обговорить цвет и размер фигур.
Почему круг катится? (потому что нет углов)
Почему колёса круглые? (потому что нет углов, они могут катиться)
3. Выкладывание по образцу изображения из набора геом. фигур. (Друг Винни)
VI. Работа в тетради.
- Пальчиковая гимнастика.
- Объяснение задания.
- Работа в тетради.
VII. Итог: С какой фигурой познакомились? Чем занимались на уроке?
Сегодня мы будем делать цыплёнка. Каким цветом цыпленок? Правильно, жёлтый. Из всех кругов выбери только желтые круги. Потом отложи отдельно голубые круги и зеленые.
Сначала просто выкладываем цыплёнка на бумаге без клея, чтобы у малыша было понимание того, что мы делаем, это также поможет избежать ошибок при работе с клеем.
Большой жёлтый круг будет туловищем цыпленка. Куда мы его положим? (предлагаем ребенку самому выбрать место на листе бумаги).
Кружок поменьше будет головой. Где у нашего цыплёнка будет голова? (ребёнок пусть снова сам выберет место, в какую сторону будет смотреть цыплёнок: вверх на небо и солнце или вниз на травку, может он будет клевать зернышки. Помогайте малышу фантазировать, предлагайте варианты. Маленьким можно подсказать, посоветовать, но не настаивайте, пусть он сам сделает выбор)
Где маленький чёрный кружок? Это будет глаз. Маленький треугольник — клюв, два одинаковых треугольника — лапки. Разложи фигуры на свои места.
Чего не хватает нашему цыпленку? Правильно, крыльев! У нас есть ещё 2 жёлтых круга, один мы отложим — это будет солнце, а из второго сделаем крылья. Как ты думаешь, как из одного круга сделать два крыла? (с этим справятся дети от трёх лет. Пусть ребёнок подержит круг в руках, повертит, приложит к бумаге, возможно, у него появится ответ).
Мы разрежем круг напополам. Для этого давай найдем центр круга. Где центр (середина) у круга? (можно дать ребенку карандаш и предложить самому найти и отметить центр с тыльной (не цветной!) стороны листа. Даже если точка не в центре, а где-то рядом, ничего страшного, похвалите кроху! Если ребёнок мал, сделайте все сами, объясняя каждое действие).
Через центр теперь проведем прямую линию, которая разделит круг напополам. По этой линии мы разрежем наш круг на две части. Получилось два крыла (обязательно разрезайте через точку (центр), указанную ребёнком, во-первых, ребёнок будет чувствовать, что его мнение важно для вас и вы прислушиваетесь к нему, а во-вторых — аппликация будет более художественной)
В ходе занятия для детей постарше можно объяснить, что такое полукруг (или вспомнить эту фигуру)
Посмотри, какие фигуры у нас получились. Это фигура называется полукруг. Пол круга — полукруг (повторяем несколько раз и предлагаем повторить название)
Где будут крылышки у нашего цыплёнка?
Цыплёнка выложили на бумаге, теперь можно приклеить его.
Цыплёнок готов.
Давай возьмём большие зелёные круги (или 1 круг) — это будет наша травка. Как ты думаешь, как из круга сделать травку? Правильно, снова разрезать напополам (повторяем шаги, как с крылышками: даём ребёнку отметить центр, разрезаем и приклеиваем снизу). Чтобы травка была натуральнее, можно сделать небольшие надрезы по округлой стороне.
На небо приклеиваем солнышко.
Облака можно сделать разными способами:
1. Наклеить кружки внахлёст, формируя облако. Разный размер кружков сделает форму облака более натуральной.
2. Разрезать круги напополам и также наклеивать внахлёст.
У нас получилось по-другому: Поля захотела сложить круги напополам и приклеить только одну половину круга. Таким образом мы уже делали другие поделки и этот вариант ей понравился.
Когда бумага окончательно высохнет, можно дорисовать солнечные лучи и цветы на травке карандашом. Можно сделать это пластилином. Пусть малыш выбирает сам.
Форма круга является интересной с точки зрения оккультизма, магии и древних значений, придаваемых ей людьми. Все мельчайшие составляющие вокруг нас — атомы и молекулы — имеют круглую форму. Солнце круглое, Луна круглая, наша планета тоже круглая. Молекулы воды — основы всего живого — тоже имеют круглую форму. Даже природа создает свою жизнь в кругах. Например, можно вспомнить про птичье гнездо — птицы вьют его также в этой форме.
Данная фигура в древних помыслах культур
Круг — это символ единства. Он присутствует в разных культурах во многих мельчайших деталях. Мы даже не придаем столько значения этой форме, как это делали наши предки.
Издавна круг — это знак бесконечной линии, который символизирует время и вечность. В дохристианскую эпоху он был древним знаком колеса солнца. Все точки в эквивалентны, линия круга не имеет ни начала, ни конца.
А центр круга был источником бесконечного вращения пространства и времени для масонов. Круг — конец всех фигур, недаром в нем была заключена тайна творения, по мнению масонов. Форма циферблата часов, имеющая тоже такую форму, обозначает собой непременное возвращение в точку отправления.
Эта фигура имеет глубокий магический и мистический состав, которым его наделили многие поколения людей из разных культур. Но что собой представляет круг как фигура в геометрии?
Что такое окружность
Часто понятие круга путают с понятием окружности. Это немудрено, ведь они между собой очень тесно взаимосвязаны. Даже названия их схожи, что вызывает много путаницы в незрелых умах школьников. Чтобы разобраться, «кто есть кто», рассмотрим эти вопросы подробнее.
По определению, окружностью является такая кривая, которая замкнута, и каждая точка которой находится равноудалённо от точки, именуемой центром окружности.
Что необходимо знать и чем уметь пользоваться, чтобы построить окружность
Чтобы построить окружность, достаточно выбрать произвольную точку, которую можно обозначить как О (именно так в большинстве источников именуются центр окружности, не будем отходить от традиционных обозначений). Следующим этапом идет использование циркуля — инструмента для черчения, который состоит из двух частей с закрепленными на каждой из них либо иглой, либо пишущим элементом.
Эти две части соединены между собой шарниром, что позволяет выбирать произвольный радиус в определенных границах, связанных с длиной этих самых частей. С помощью данного прибора в произвольную точку О устанавливается остриё циркуля, а карандашом уже очерчивается кривая, которая из итоге получается окружностью.
Какими величинами характеризуется окружность
Если соединить при помощи линейки центр окружности и любую произвольную точку на кривой, полученной в результате работы циркулем, мы получим Все такие отрезки, именуемые радиусами, будут равны. Если же соединить при помощи линейки прямой линией две точки на окружности и центр, мы получим ее диаметр.
Для окружности также характерно вычисление ее длины. Чтобы ее найти, необходимо знать либо диаметр, либо радиус окружности и воспользоваться формулой, представленной на рисунке ниже.
В этой формуле С — длина окружности, r — радиус окружности, d — диаметр, а число Пи — константа со значением 3,14.
Кстати, константа Пи была вычислена как раз из окружности.
Оказалось, что независимо от того, каков диаметр круга, соотношение длины окружности и диаметра одинаковое, равное примерно 3,14.
В чем же главное отличие круга от окружности
По сути, окружность — это линия. Она не является фигурой, она является кривой замкнутой линией, не имеющей ни конца, ни начала. А то пространство, что расположено внутри нее — это пустота. Простейшим примером окружности выступает обруч или, по-иному, хула-хуп, который дети используют на занятии физической культуры или же взрослые, для того чтобы создать себе стройную талию.
Теперь мы подошли к понятию того, что такое круг. Это в первую очередь фигура, то есть некое множество точек, ограниченных линией. В случае круга этой линией выступает окружность, рассмотренная выше. Выходит, что круг — это окружность, в середине которой не пустота, а множество точек пространства. Если натянуть на хула-хуп ткань, то мы уже не сможем его крутить, ведь он будет уже не окружностью — его пустота замещена тканью, куском пространства.
Перейдем непосредственно к понятию круга
Круг — геометрическая фигура, которая является частью плоскости, ограниченной окружностью. Для него также характерны такие понятия, как радиус и диаметр, рассмотренные выше при определении окружности. И вычисляются они точно таким же образом. Радиус круга и радиус окружности являются идентичными по размеру. Соответственно, длина диаметра тоже аналогична в обоих случаях.
Так как круг является частью плоскости, то для него характерно наличие площади. Вычислить ее можно снова-таки при помощи радиуса и числа Пи. Формула выглядит следующими образом (см. рисунок ниже).
В данной формуле S — площадь, r — радиус круга. Число Пи — снова та же константа, равная 3,14.
Формула круга, для вычисления которой возможно также использовать диаметр, изменяется и принимает вид, представленный на следующем рисунке.
Одна четвертая появляется из того, что радиус — это 1/2 диаметра. Если радиус в квадрате, выходит, что соотношение преобразуется до вида:
r*r = 1/2*d*1/2*d;
Круг — это фигура, в которой можно выделить отдельные части, например сектор. Выглядит он как часть круга, которая ограничена отрезком дуги и его двумя радиусами, проведенными из центра.
Формула, которая позволяет вычислить площадь данного сектора, представлена на нижеследующем рисунке.
Использование фигуры в задачах с многоугольниками
Также круг — геометрическая фигура, которая часто используется в комплекте с другими фигурами. Например, такими как треугольник, трапеция, квадрат или ромб. Нередко встречаются задачи, где нужно найти площадь вписанного круга или, наоборот, описанного вокруг определенной фигуры.
Вписанный круг является таким, который соприкасается со всеми сторонами многоугольника. С каждой стороной любого многоугольника у окружности должна быть точка соприкосновения.
Для определенного вида многоугольника определение радиуса вписанной окружности вычисляется по отдельным правилам, которые доступно объясняются в курсе геометрии.
Можно привести для примера несколько из них. Формула круга, вписанного в многоугольники, может вычисляться следующим образом (ниже на фото приведено несколько примеров).
Несколько простых примеров из жизни, для того чтобы закрепить понимание разницы между кругом и окружностью
Перед нами Если он открыт, то железная каемка люка — это окружность. Если он закрыт, то крышка выступает в роли круга.
Окружностью также можно назвать любое кольцо — золотое, серебряное или бижутерию. Кольцо, которое держит на себе связку ключей, — тоже окружность.
А вот круглый магнит на холодильнике, тарелка или блинчики, испеченные бабушкой, -это круг.
Горлышко бутылки или банки при виде сверху — это окружность, а вот крышка, которая закроет это горлышко, при том же виде сверху является кругом.
Таких примеров можно привести множество, и для усвоения такого материала их нужно приводить, чтобы дети лучше улавливали связь теории с практикой.
Тема урока
Геометрические фигуры
Что такое геометрическая фигура
Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.
Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.
Точка и прямая — это основные геометрические фигуры, расположенные на плоскости.
К самым простым геометрическим фигурам на плоскости принадлежат — отрезок, луч и ломаная линия.
Что такое геометрия
Геометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.
Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник.
В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.
Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости.
К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия.
Точка
Из выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам. И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений. Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры.
В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D ….
А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике. Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Прямая
Как и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела.
Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком.
Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч.
Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча. Данные лучи являются дополнительными.
Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
Задание
Какая ломаная линия называется незамкнутой?
Как обозначается прямая?
Как называется ломаная линия, у которой четыре замкнутых звена?
Какое название имеет ломаная линия с тремя замкнутыми звеньями?
Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой. Примером замкнутой ломаной является любой многоугольник.
Плоскость
Как точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией. Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Угол
Фигура, которая имеет два луча и вершину, называется углом. Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.
Задание:
1. Как в тексте обозначают угол?
2. Какими единицами можно измерить угол?
3. Какие бывают углы?
Параллелограмм
Параллелограмм — это четырехугольник, противолежащие стороны которого попарно параллельны.
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником.
Квадрат — это тот же параллелограмм, у него и углы и стороны равны.
Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны.
Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом.
Трапеция
При рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной.
Окружность и круг
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Треугольник
Также к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно. Любой треугольник имеет три вершины и три стороны.
Задание: Какой треугольник называют вырожденным?
Многоугольник
К многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия.
В многоугольнике все точки, которые соединяют отрезки, являются его вершинами. А отрезки, из которых состоит многоугольник, являются его сторонами.
А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром. Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
«Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
«Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
Узнайте о замкнутой кривой | Chegg.com
Если C — простая замкнутая кривая, тогда линейный интеграл F⃗ \ vec {F} F вокруг C обозначается как
∮F⃗⋅dr⃗ \ oint \ vec {F} \ cdot d \ vec {r} ∮F⋅dr
Где F⃗ \ vec {F} F — функция векторной точки, а r⃗ \ vec {r} r — уравнение кривой C.
Пусть C — простая замкнутая кривая, тогда линейный интеграл F⃗ \ vec {F} F вдоль C равен
∮cF⃗ ∙ dr⃗ = ∮c (F1dx + F2dy + F3dz) \ oint_ {c} \ vec {F} \ bullet d \ vec {r} = \ oint_c (\ F_1dx + F_2 dy + F_3dz) ∮c F ∙ dr = ∮c (F1 dx + F2 dy + F3 dz)
Вызываетсяциркуляция F⃗ \ vec {F} F вокруг кривой C.Линейный интеграл по простой замкнутой кривой не зависит от пройденного пути, поскольку он имеет одну и ту же начальную и конечную точки. Интеграл, вычисленный в направлении против часовой стрелки, имеет положительный знак, а интеграл, вычисленный в направлении по часовой стрелке, имеет отрицательный знак, но значения обоих интегралов одинаковы. Пусть C обозначает простую замкнутую кривую в направлении против часовой стрелки, а C ‘обозначает простую замкнутую кривую в направлении по часовой стрелке, линейный интеграл по простой замкнутой кривой равен
∮cF⃗ ∙ dr⃗ = −∮c1F⃗ ∙ dr⃗ \ oint_ {c} \ vec {F} \ bullet d \ vec {r} = — \ oint_ {c_1} \ vec {F} \ bullet d \ vec {r} ∮c F ∙ dr = −∮c1 F ∙ dr
Пусть A и B — любые две точки на кривой.Пусть C₁ и C₂ — кривые, показанные на рисунке между точками A и B.
Начиная с точки A, линейный интеграл F⃗ \ vec {F} F вдоль кривой C, направленной против часовой стрелки, равен
∮cF⃗ ∙ dr⃗ = ∮c1F⃗ ∙ dr⃗ + ∮c2F⃗ ∙ dr⃗ \ oint_ { c} \ vec {F} \ bullet d \ vec {r} = \ oint_ {c_1} \ vec {F} \ bullet d \ vec {r} + \ oint_ {c_2} \ vec {F} \ bullet d \ vec {r} ∮c F ∙ dr = ∮c1 F ∙ dr + ∮c2 F ∙ dr
Если мы начнем с точки B, линейный интеграл от F⃗ \ vec {F} F вдоль кривой C ‘, которая по часовой стрелке определяется выражением
∮cF⃗ ∙ dr⃗ = ∮c1F⃗ ∙ dr⃗ + ∮c2F⃗ ∙ dr⃗ \ oint_ {c} \ vec {F} \ bullet d \ vec {r} = \ oint_ {c_1} \ vec {F} \ bullet d \ vec {r} + \ oint_ {c_2} \ vec {F} \ bullet d \ vec {r} ∮c F ∙ dr = ∮c1 F ∙ dr + ∮c2 F ∙ dr
−∮c2F⃗ ∙ dr⃗ − ∮c1F⃗ ∙ dr⃗- \ oint_ {c_2} \ vec {F} \ bullet d \ vec {r} — \ oint_ {c_1} \ vec {F} \ bullet d \ vec {r } −∮c2 F ∙ dr − ∮c1 F ∙ dr
= — (∮c2F⃗ ∙ dr⃗ − ∮c1F⃗ ∙ dr⃗) = — \ begin {pmatrix} \ oint_ {c_2} \ vec {F} \ пуля d \ vec {r} — \ oint_ {c_1} \ vec {F} \ bullet d \ vec {r} \ end {pmatrix} = — (∮c2 F ∙ dr − ∮c1 F ∙ dr )
= −∮c2F⃗ ∙ dr⃗ = — \ oint_ {c_2} \ vec {F} \ bullet d \ vec {r} = — ∮c2 F ∙ dr
∴ ∮cF⃗ ∙ dr⃗ = −∮c1F⃗ ∙ dr⃗ \ поэтому \ oint_ {c} \ vec {F} \ bullet d \ vec {r} = — \ oint_ {c_1} \ vec {F} \ bullet d \ vec {r} ∴∮c F ∙ dr = −∮c1 F ∙ dr
5.Дорожки
Пути — это кривые (известные как кривые Безье). Пути просты в изучении и использовании в GIMP. Чтобы понять их концепции и механизм, посмотрите глоссарий Кривая Безье или Википедия [ WKPD-BEZIER ]. Инструмент «Пути» очень мощный, он позволяет создавать сложные конструкции. формы. Чтобы использовать инструмент Paths в GIMP, вы должны сначала создайте путь, а затем обведите его.
В GIMP термин «обводка» означает применить к контуру определенный стиль (цвет, ширина, узор…).
Путь имеет две основные цели:
Вы можете преобразовать замкнутый путь в выделение.
Любой путь, открытый или закрытый, может быть пройден ; то есть нарисованные на изображении различными способами.
Рисунок 7.10. Иллюстрация четырех разных путей создания
Начните с рисования контура вашего пути; план может быть изменен позже (см. Инструмент Контуры).Для начала выберите инструмент «Контуры» одним из следующих способов:
Когда выбран инструмент Контуры, курсор мыши превращается в указатель (стрелку) с кривой. Щелкните левой кнопкой мыши по изображению, чтобы создать первую точку на пути. Двигаться указатель мыши на новую точку и щелкните левой кнопкой мыши, чтобы создать другую точка связана с предыдущей точкой. Хотя вы можете создать столько по вашему желанию, вам нужно всего два балла, чтобы узнать о Пути.При добавлении точек у курсора мыши появляется маленький «+» рядом с кривой, которая указывает, что щелчок добавит новый точка. Когда курсор мыши находится рядом с отрезком линии, «+» Изменится на крест со стрелками; как инструмент перемещения.
Подведите курсор мыши к отрезку линии, щелкните левой кнопкой мыши и перетащите отрезок линии. Происходят два события.
Сегмент линии изгибается и изгибается при вытягивании.
Каждый сегмент линии имеет начальную и конечную точки. четко обозначен. «Линия направления» сейчас проекты из каждой конечной точки для отрезка линии, который был взолнованный.
Изогнутый отрезок линии оставляет конечную точку в том же направлении, что и «направляющая линия» покидает конечную точку. Длина «линия направления» определяет, насколько далеко отрезок линии проецируется вдоль «линии направления» перед поворотом в сторону другая конечная точка.Каждая «направляющая линия» имеет пустую квадратная коробка (называемая ручкой) на одном конце. Щелкните и перетащите маркер на изменить направление и длину «направляющей линии».
Рисунок 7.11. Внешний вид дорожки при манипулировании ею
Путь состоит из двух компонентов: прямых и изогнутых. сегменты. Черные квадраты — это опорные точки, открытый кружок указывает выбранный якорь, а два открытых квадрата — маркеры, связанные с выбранным якорем.
Рисование линий и кривых | Rhino 3-D моделирование
Рисование линий и кривых | 3-D моделирование RhinoКривая Rhino похожа на кусок проволоки. Он может быть прямым или изогнутым, а может быть открытым или закрытым.
Поликривая — это несколько сегментов кривой, соединенных вместе встык.
Rhino предоставляет множество инструментов для рисования кривых. Вы можете рисовать прямые линии, полилинии, состоящие из соединенных отрезков, дуг, окружностей, многоугольников, эллипсов, спиралей и спиралей.
Вы также можете рисовать кривые, используя контрольные точки кривой, и рисовать кривые, проходящие через выбранные точки.
См .: Википедия: Кривая.
Линии и полилинии
Линии — это кривая степени 1 без изгибов. Полилиния — это серия соединенных вместе отрезков прямых или дуг.
Линия
Нарисуйте один линейный сегмент.
LineThroughPt
Проведите линию через любую комбинацию точек, контрольных точек и объектов облака точек.
Ломаная линия
Нарисуйте многосегментную полилинию с параметрами для сегментов линии и дуги, вспомогательных линий отслеживания и закрытия.
Многоугольник
Нарисуйте многоугольник с указанным количеством сторон с параметрами вписанного / описанного, по краю, в форме звезды, по кривой и по вертикали.
Прямоугольник
Нарисуйте прямоугольную замкнутую полилинию из с опциями для начала в центре, трех точек, вертикали и закругленных с дугой или коническими углами.
См .: Википедия: Line.
Кривые произвольной формы
Кривые произвольной формы в Rhino являются кривыми NURBS. Кривая NURBS определяется своим порядком, набором взвешенных контрольных точек и вектором узла.
Rhino предлагает множество методов для создания кривых произвольной формы.
Изгиб
Нарисуйте кривую по точкам.
HandleCurve
Построение цепочек кривых Безье с помощью маркеров редактирования.
InterpCrv
Постройте кривую через выбранные места.
InterpCrvOnSrf
Построить кривую через точки на поверхности.
Эскиз
Перетащите мышь, чтобы нарисовать кривую.
См .: Википедия: Неоднородный рациональный B-сплайн.
Кривые конического сечения
Кривые конического сечения были сначала определены как пересечение: прямого кругового конуса с переменным углом при вершине; плоскость, перпендикулярная элементу конуса.В зависимости от того, меньше ли угол 90 градусов, равен ему или больше, мы получаем эллипс, параболу или гиперболу. Дуга — это часть круга. Команды Rhino позволяют рисовать определенные коники, а общая команда Conic позволяет рисовать конические кривые произвольной формы. Коники степени 2.
Коническая
Нарисуйте кривую конического сечения с параметрами начала, конца, вершины и значения rho.
Дуга
Нарисуйте дугу с параметрами центра, начала, угла и направления.
Круг
Нарисуйте круг из центра и радиуса, диаметра, точек на окружности и длины окружности.
Эллипс
Нарисуйте замкнутую эллиптическую кривую из точек фокусировки, центра и краев, ограничивающего прямоугольника и вокруг кривой.
Гипербола
Нарисуйте гиперболическую кривую из точек фокусировки, вершин или коэффициента.
Парабола
Нарисуйте параболическую кривую от фокуса и вершины или конечной точки.
См .: Википедия: Conic.
Спираль и спираль
Спираль — это кривая на плоскости, которая огибает фиксированную центральную точку на постоянно увеличивающемся или уменьшающемся расстоянии от точки.
Спираль — это трехмерная кривая, которая вращается вокруг оси на постоянном или непрерывно изменяющемся расстоянии при движении параллельно оси.
Спираль
Нарисуйте спиральную кривую с вариантами количества поворотов, шага, вертикали, реверса и вокруг кривой.
Спираль
Нарисуйте спиральную кривую с вариантами количества поворотов, шага, плоской, вертикальной и круговой кривой.
См .: Википедия: Спираль.
См. Также
Создание кривых из других объектов
Редактировать кривые
Rhinoceros 5 © 2010-2015 Robert McNeel & Associates.17 сентября 2015 г.
Открыть тему с навигацией
Там, где «простые кривые» становятся сложнее, чем вы думаете
Занятия математиков могут показаться нормальным людям любопытными и странными. Иногда они тратят огромную энергию на доказательство результатов, которые кажутся очевидными. Один из таких результатов называется теоремой Жордана. Все мы знаем, что круг имеет внутреннюю и внешнюю стороны, и что это свойство также справедливо для гораздо большего набора замкнутых кривых.
«Простая замкнутая кривая» — это замкнутая непрерывная петля на плоскости, которая не пересекает себя. Такую искаженную версию круга также называют кривой Жордана в честь французского математика Камиля Жордана, который первым доказал некоторые из ее ключевых свойств.
Теорема Жордановой кривой утверждает, что каждая простая замкнутая кривая, независимо от ее сложности или извилистости, делит плоскость на две области: внутреннюю и внешнюю.Теорема кажется настолько тривиальной, что не требует доказательства. Но такие результаты могут быть гораздо более глубокими, чем может показаться на первый взгляд, и в некоторых случаях вещи, которые кажутся очевидными, могут оказаться ложными.
Богемный ученый
Бернард Больцано, богемский математик, философ и священник, был первым, кто поставил задачу кривой в явной форме. Он был убежден в необходимости ввести строгость в математический анализ.Он утверждал, что для замкнутой петли на плоскости линия, соединяющая точку, заключенную в петле (внутри), с точкой, удаленной от нее (снаружи), должна пересекать петлю. Это кажется достаточно очевидным, но Больцано понял, что это нетривиальная проблема.
Первое доказательство теоремы о кривой появилось во влиятельной книге Джордана Cours d’analyse, впервые опубликованной в 1882 году. Теорема легко формулируется и легко доказывается для кривых, которые являются многоугольниками, состоящими из отрезков прямых.
Однако для общих кривых это довольно сложно доказать, поскольку «простые» кривые могут обладать некоторыми причудливыми свойствами, такими как неровности повсюду без определенного направления или фрактальность по своей природе, как граница снежинки. Из-за этого трудно отличить, какие точки находятся внутри, а какие снаружи. Доказательство использует передовые идеи из раздела математики, известного как топология.
Вдохновение для художников
«Задача коммивояжера», или TSP, ищет самый короткий маршрут, который может выбрать продавец, чтобы посетить несколько городов и вернуться в исходную точку.Решением этой оптимизационной задачи является жорданова кривая. Такие изгибы вдохновляли художников.
Профессор Роберт Бош из Оберлинского колледжа в Огайо использует результаты теории оптимизации для создания художественных изображений с помощью этих простых циклов. На иллюстрации изображена скульптура «Объятие» от Bosch, где простая замкнутая кривая разделяет две области, представленные металлами разного цвета. Bosch решил проблему TSP с 726 городами, чтобы сформировать границу в этой скульптуре.
Интуиция служит неоценимым средством открытия новой математики, но она также может сбить нас с пути. При доказательстве, казалось бы, очевидных результатов всегда требуется строгость.
Что касается кривых Иордана, великий немецкий математик Феликс Кляйн сформулировал проблемы следующим образом: «Каждый знает, что такое кривая, пока он не изучит достаточно математики, чтобы запутаться из-за бесчисленного количества возможных исключений.”
Питер Линч — почетный профессор школы математики и статистики UCD — ведет блог на thatsmaths.com
эталонный запрос — кратчайшая замкнутая кривая для проверки сферы
Джеймс Венк и я только что закончили работу, доказывающую гипотезу Залгаллера о проверке сфер для замкнутых кривых:
Самая короткая замкнутая кривая для проверки сферы.2 $ внутри своей выпуклой оболочки имеет длину $ L (\ gamma) \ geq 4 \ pi $. Равенство справедливо только тогда, когда $ \ gamma $ состоит из 4 полукругов длиной $ \ pi $, расположенных в форме бейсбольного шва, как предположил Залгаллер в 1996 году.
Доказательство, которое занимает 38 страниц, использует некоторые понятия из более ранней работы по этой проблеме, которые я упоминал в моем последнем посте ниже, вместе с другими идеями из интегральной геометрии, выпуклого анализа, геометрической теории меры и геометрической теории узлов. Кроме того, мы выводим ряд формул для проверки эффективности кривых, которые можно проверить с помощью записной книжки Mathematica , которую мы предоставили.2 $ пересекает $ \ gamma $. Например, горизонт линейного сегмента — это область области, показанной на рисунке выше. В данной статье мы определяем эффективность (инспекция) $ \ gamma $ как $$ E (\ gamma): = \ frac {H (\ gamma)} {L (\ gamma)}. $$ Мы хотим показать, что $ L (\ gamma) \ geq 4 \ pi $. Поскольку $ \ gamma $ замкнуто, $ H (\ gamma) \ geq 8 \ pi $. Итак, достаточно показать, что $ E (\ gamma) \ leq 2 $. Для этого отметим, что, поскольку $ H $ аддитивен, для любого разбиения $ \ gamma $ на подмножества $ \ gamma_i $, $ i \ in I $, $$ E (\ gamma) = \ sum_i \ frac {H (\ gamma_i)} {L (\ gamma)} = \ sum_i \ frac {L (\ gamma_i)} {L (\ gamma)} E (\ gamma_i) \ leq \ sup_i E (\ gamma_i).2 $, который называется (конус), разворачивающийся $ \ gamma $. Эта операция восходит к работе Кантареллы, Куснера и Салливана о толщине узлов. Оказывается, $ Е (\ гамма) = Е (\ тильда \ гамма). $$ Кроме того, поскольку $ \ gamma $ минимально, отсюда следует, что $ \ tilde \ gamma $ локально выпукло относительно относительно $ o $. Следовательно, он допускает разбиение на сегменты, которые мы называем спиралями , которые являются максимальными подмножествами $ \ tilde \ gamma $ с монотонным расстоянием от $ o $. Доказано, что эффективность любой спирали не превосходит $ 2 $, что дает требуемое неравенство $ L (\ gamma) \ leq 4 \ pi $.Доказательство основано на вычислении $ E $ для отрезков прямых, многоугольных аппроксимаций и вариационной процедуры.
Приведенные выше аргументы составляют первую половину статьи. Вторая половина посвящена характеристике случая, когда $ L (\ gamma) = 4 \ pi $. Эта часть статьи становится более аналитической и требует более точных оценок эффективности. Основная идея здесь заключается в том, что если $ L (\ gamma) = 4 \ pi $, то $ E (\ gamma) = 2 $, что, в свою очередь, дает $ E (\ tilde \ gamma_i) = 2 $ для всех спиралей в развертывание $ \ gamma $.Мы показываем, что $ E (\ tilde \ gamma_i) = 2 $ только тогда, когда $ \ tilde \ gamma_i $ имеет постоянное расстояние $ \ sqrt2 $ от $ o $, что, в свою очередь, приводит к тому, что $ \ gamma $ должно иметь постоянное расстояние $ \ sqrt2 $ тоже из $ o $, либо лежать на сфере радиуса $ \ sqrt2 $. Наконец, мы показываем, что $ \ gamma $ должна состоять из $ 4 $ полукругов, используя формулу типа Крофтона Бляшке-Сантало для длины сферических кривых и технику доказательств классической теоремы о $ 4 $ вершинах, которая была развита далее Умехара и Торбергссон.
Короче говоря, как и ожидалось в конце моего последнего поста, доказательство полного результата действительно потребовало значительных усилий, помимо оценок, полученных в более ранней работе. Предположения Zalgaller относительно открытых контрольных кривых до сих пор остаются нерешенными. Также естественно рассматривать версии проблемы с более высокой размерностью. Некоторые из описанных выше методов применимы во всех измерениях, но для расширения результата потребуется больше идей.
Curve Geometry | The Grasshopper Primer, третье издание
1.4.1. КРИВАЯ ГЕОМЕТРИЯ
NURBS (неоднородные рациональные B-сплайны) — это математические представления, которые могут точно моделировать любую форму от простой 2D линии, круга, дуги или прямоугольника до самой сложной трехмерной органической поверхности произвольной формы или твердого тела. Благодаря своей гибкости и точности NURBS-модели могут использоваться в любом процессе — от иллюстраций и анимации до производства.
Поскольку кривые являются геометрическими объектами, они обладают рядом свойств или характеристик, которые можно использовать для их описания или анализа.Например, у каждой кривой есть начальная координата, а у каждой кривой есть конечная координата. Когда расстояние между этими двумя координатами равно нулю, кривая замыкается. Кроме того, каждая кривая имеет несколько контрольных точек, если все эти точки расположены в одной плоскости, кривая в целом является плоской. Некоторые свойства применяются к кривой в целом, в то время как другие применяются только к определенным точкам на кривой. Для Например, планарность — это глобальное свойство, а касательные векторы — локальное свойство. Кроме того, некоторые свойства применимы только к некоторым типам кривых.До сих пор мы обсуждали некоторые из компонентов примитивной кривой Grasshopper, такие как линии, круги, эллипсы и дуги.
- Линия
- Полилиния
- Круг
- Эллипс
- Arc
- Кривая NURBS
- Polycurve
- Конечная точка
- Точка редактирования
- Контрольная точка
1.4.1.1. NURBS CURVES
Степень: Степень — это целое положительное число.Обычно это число 1, 2, 3 или 5, но может быть любым положительным целым числом. Степень кривой определяет диапазон влияния контрольных точек на кривую; где чем выше степень, тем больше диапазон. Линии и полилинии NURBS обычно имеют степень 1, окружности NURBS — степень 2, а большинство кривых произвольной формы — степень 3 или 5.
Контрольные точки: Контрольные точки представляют собой список как минимум степени + 1 балл. Один из самых простых способов изменить форму кривой NURBS — переместить ее контрольные точки.
Вес: Контрольным точкам присвоен номер, называемый весом. Веса обычно являются положительными числами. Когда все контрольные точки кривой имеют одинаковый вес (обычно 1), кривая называется нерациональной, в противном случае кривая называется рациональной. Большинство кривых NURBS нерациональны. Несколько кривых NURBS, таких как круги и эллипсы, всегда рациональны.
Узлы: Узлы — это список чисел (степень + N-1), где N — количество контрольных точек.
Точки редактирования: Точки на кривой, вычисленные при средних значениях узлов.Точки редактирования похожи на контрольные точки, за исключением того, что они всегда расположены на кривой, и перемещение одной точки редактирования обычно изменяет форму всей кривой (перемещение одной контрольной точки меняет форму кривой только локально). Точки редактирования полезны, когда вам нужно, чтобы точка внутри кривой проходила точно через определенное место.
NURBS кривых узлов в результате разной степени:
A D 1 Кривая NURBS ведет себя так же, как полилиния.Кривая D 1 имеет узел для каждой контрольной точки.
D 2 Кривые NURBS обычно используются только для аппроксимации дуг и окружностей. Сплайн пересекает контрольный многоугольник на полпути каждого сегмента.
D 3 — это наиболее распространенный тип кривой NURBS, используемый по умолчанию в Rhino. Вы, вероятно, хорошо знакомы с визуальным развитием сплайна, даже если узлы кажутся странными.
1.4.1.2. КОМПОНЕНТЫ СОЕДИНИТЕЛЯ GRASSHOPPER
Примеры файлов, сопровождающих этот раздел: http://grasshopperprimer.com/appendix/A-2/1_gh-files.html
Grasshopper имеет набор инструментов для выражения более сложных типов кривых Rhino, таких как кривые Нурбса и полигональные кривые. Эти инструменты можно найти на вкладке Кривая / Сплайны.
Кривая Нурбса (Кривая / Сплайн / Кривая Нурбса): компонент кривой Нурбса строит кривую NURBS из контрольных точек.Вход V определяет эти точки, которые можно описать неявно, выбрав точки из сцены Rhino или наследовав изменчивые данные от других компонентов. Вход Nurbs Curve-D устанавливает степень кривой.
Interpolate Curve (Curve / Spline / Interpolate): Интерполированные кривые ведут себя немного иначе, чем кривые NURBS. V-вход для компонента аналогичен компоненту NURBS в том, что он запрашивает определенный набор точек для создания кривой.Однако при использовании метода интерполированной кривой результирующая кривая фактически будет проходить через эти точки независимо от степени кривой. В компоненте кривой NURBS мы могли достичь этого только тогда, когда степень кривой была установлена на единицу. Также, как и компонент кривой NURBS, вход D определяет степень результирующей кривой. Однако в этом методе для ввода градусов принимаются только нечетные пронумерованные значения. Опять же, P-вход определяет, является ли кривая периодической. Вы начнете видеть некоторую закономерность в выходных данных для многих компонентов кривой, поскольку выходы C, L и D обычно определяют результирующую кривую, длину и область кривой соответственно.
Kinky Curve (Curve / Spline / Kinky Curve): компонент извилистой кривой позволяет вам управлять определенным пороговым значением угла A, при котором кривая переходит от изогнутой линии к гладкой интерполированной кривой. Следует отметить, что вход A требует ввода в радианах.
Полилиния (кривая / сплайн / полилиния): полилиния — это набор сегментов линии, соединяющих две или более точек, результирующая линия всегда будет проходить через ее контрольные точки; аналогично интерполированной кривой.Подобно типам кривых, упомянутым выше, V-вход компонента Polyline определяет набор точек, которые будут определять границы каждого линейного сегмента, составляющего полилинию. C-вход компонента определяет, является ли полилиния открытой или замкнутой кривой. Если положение первой точки не совпадает с положением последней точки, будет создан линейный сегмент, чтобы замкнуть цикл. Вывод для компонента Polyline отличается от вывода в предыдущих примерах тем, что единственной результирующей является сама кривая.
путей — SVG 2
путей — SVG 2Содержание
- 9.1. Введение
- 9.2. Элемент «путь»
- 9.3. Данные пути
- 9.3.1. Общая информация о данных пути
- 9.3.2. Указание данных пути: свойство «d»
- 9.3.3. «moveto» подает команду
- 9.3.4. Команда «closepath»
- 9.3.4.1. Завершающая сегмент операция закрытия пути
- 9.3.5. «lineto» управляет
- 9.3.6. Кубическая кривая Безье дает команду
- 9.3.7. Квадратичная кривая Безье дает команду
- 9.3.8. Команды эллиптической дуги
- 9.3.9. Грамматика данных пути
- 9.4. Направленность трассы
- 9.5. Примечания по реализации
- 9.5.1. Параметры эллиптической дуги вне допустимого диапазона
- 9.5.2. Отраженные контрольные точки
- 9.5.3. Сегменты пути нулевой длины
- 9.5.4. Обработка ошибок в данных пути
- 9.6. Расстояние по трассе
- 9.6.1. Атрибут pathLength
- 9.7. Интерфейсы DOM
- 9.7.1. Интерфейс SVGPathElement
9.1. Введение
Путь представляет собой контур фигуры, которую можно заливать или погладил. Путь также можно использовать в качестве обтравочного контура для описания анимация или позиционирование текста. Путь может использоваться более чем для одного из эти функции одновременно.(Видеть Серверы заливки, обводки и покраски, Обрезка и маскирование, Анимация (‘animateMotion’), и текст на пути.)
Путь описывается с использованием концепции текущей точки. В аналогия с рисованием на бумаге, текущая точка может быть думал как расположение ручки. Положение пера могут быть изменены, а контур фигуры (открытый или закрытый) может отслеживаться перетаскиванием по прямым линиям или кривые.
Пути представляют собой геометрию контура объекта, определяется в терминах перейти к (установить новую текущую точку), От до (начертить прямую), от до (начертить кривая с использованием кубической кривой Безье), arc (эллиптическая или дуги окружности) и closepath (замкнуть текущую shape, подключившись к последним командам moveto ).Составные пути (т. Е. Путь с несколькими подпутьями) являются можно разрешить такие эффекты, как «дырки от бублика» в объектах.
В этой главе описываются синтаксис, поведение и DOM. интерфейсы для путей SVG. Различные примечания по реализации для SVG пути можно найти в реализации элемента «path» Заметки.
Путь определяется в SVG с помощью элемента «path».
Все основные формы описаны с точки зрения их эквивалентный путь — это какова их форма как тропинка.(Эквивалентный путь Элемент «path» — это просто сам путь.) Чтобы определить основные формы как эквивалентные пути, определена завершающая сегмент операция замыкания пути, который в настоящее время не может быть представлен в синтаксисе основного пути.
9.2. Элемент «путь»
‘ path ‘
- Категории:
- Графический элемент, визуализируемый элемент, элемент формы
- Модель содержимого:
- Любое количество следующих элементов в любом порядке: clipPath, маркер, маска, скрипт, стиль
- Атрибуты:
- атрибуты aria — ‘aria-activedescendant’, ‘aria-atomic’, ‘aria-autocomplete’, ‘aria-busy’, ‘aria-checked’, ‘aria-colcount’, ‘aria-colindex’ , ‘aria-colspan’, ‘aria-controls’, ‘aria-current’, ‘aria -hibitedby’, ‘aria-details’, ‘aria-disabled’, ‘aria-dropeffect’, ‘aria-errormessage’, ‘ aria-extended, aria-flowto, aria-grabbed, aria-haspopup, aria-hidden, aria-invalid, aria-keyshortcuts, aria-label, aria- labelledby ‘,’ aria-level ‘,’ aria-live ‘,’ aria-modal ‘,’ aria-multiline ‘,’ aria-multiselectable ‘,’ aria-Ориентация ‘,’ aria-owns ‘,’ aria-placeholder ‘ , ‘aria-posinset’, ‘aria-press’, ‘aria-readonly’, ‘aria-related’, ‘aria-required’, ‘aria-roledescription’, ‘aria-rowcount’, ‘aria-rowindex’, ‘aria-rowspan’, ‘aria-selected’, ‘aria-setsize’, ‘aria-sort’, ‘aria-valuemax’, ‘aria-valuemin’, ‘aria-valuenow’, ‘aria -valuetext ‘,’ role ‘
- атрибутов условной обработки -‘ requiredExtensions ‘,’ systemLanguage ‘
- основных атрибутов -‘ id ‘,’ tabindex ‘,’ lang ‘,’ xml: space ‘,’ class ‘,’ style ‘
- глобальные атрибуты событий — oncancel, oncanplay, oncanplaythrough, onchange, onclick, onclose, oncuechange, ondblclick, ondrag, ondragend, ondragenter, ondragexit, ondragleave, ondragover, ondragstart, ondrop, ondurationchange, onemptied, onended, onerror, onfocus, oninput, oninvalid, onkeydown ‘,’ onkeypress ‘,’ onkeyup ‘,’ onload ‘,’ onloadeddata ‘,’ onloadedmetadata ‘,’ onloadstart ‘,’ onmousedown ‘,’ onmouseenter ‘,’ onmouseleave ‘,’ onmousemove ‘,’ onmouseout ‘,’ onmouseover ‘, onmouseup, onmousewheel, onpause, onplay, onplaying, onprogress, onratechange, onreset, onresize, onscroll, onseeke d ‘,’ onseeking ‘,’ onselect ‘,’ onshow ‘,’ onstalled ‘,’ onsubmit ‘,’ onsuspend ‘,’ ontimeupdate ‘,’ onggle ‘,’ onvolumechange ‘,’ onwaiting ‘
- атрибуты событий элемента документа -‘ oncopy ‘,’ oncut ‘,’ onpaste ‘
- графические атрибуты событий -‘ onfocusin ‘,’ onfocusout ‘
- атрибуты презентации —
- ‘ pathLength ‘
- Свойства геометрии:
- Интерфейсы DOM:
Контур формы для элемента «путь» задается с помощью d имущество.См. Данные о пути ниже.
9.3. Данные пути
9.3.1. Общая информация о данных пути
Путь определяется включением «пути» элемент, для которого свойство d указывает данные пути. Данные пути содержат переместиться на , линейно на , кривая на (как кубическая, так и квадратичный Безье), arc и closepath инструкции.
Пример треугольника01 указывает путь в форме треугольника. (В M обозначает переход с на , L s обозначают линии до s, а z обозначает ближний путь ().
Пример треугольника01
Просмотреть этот пример как SVG (только для браузеров с поддержкой SVG)
Данные пути могут содержать символы новой строки и, следовательно, могут быть разбит на несколько строк для удобства чтения.Новые строки внутри атрибутов в разметке будут нормализованы до пробела символы при разборе.
Синтаксис данных пути краток, чтобы позволить минимальный размер файла и эффективная загрузка, поскольку многие файлы SVG будут преобладать их данные пути. Некоторые из способов, которыми SVG попытки минимизировать размер данных пути следующие:
- Все инструкции выражаются одним символом (например, moveto выражается как M ).
Избыточный пробел и разделители (например, запятые) могут быть устраненным; например, следующее содержит ненужные мест:
м 100100 л 200200Более компактно это можно выразить как:
M100 100L200 200Буква команды может быть удалена, если идентичная команда в противном случае ему предшествовало бы письмо; например, следующие содержит ненужную вторую команду «L»:
M 100200 L 200100 L -100-200Более компактно это можно выразить как:
M 100200 L 200100-100-200- Для большинства команд есть абсолютные и относительные доступные версии (прописные буквы означают абсолютные координаты, строчные буквы означают относительные координаты).
- Альтернативные формы от до доступны для оптимизировать частные случаи горизонтальных и вертикальных линий (абсолютное и относительное).
- Альтернативные формы кривой доступны для оптимизировать особые случаи, когда некоторые из контрольных точек на текущем сегменте может быть определена автоматически из контрольные точки на предыдущем сегменте.
Синтаксис данных пути представляет собой префиксную нотацию (т. Е. Команды за которыми следуют параметры).Единственная допустимая десятичная точка — это Юникод U + 0046 FULL STOP («.») Символ (также называемый в Юникоде как PERIOD, точка и десятичная точка) и никаких других разделителей разрешены символы [UNICODE]. (Например, следующее недопустимое числовое значение в потоке данных пути: «13,000,56». Вместо этого скажите: «13000,56».)
Для относительных версий команд все координаты значения относятся к текущей точке в начале команда.
В таблицах ниже используются следующие обозначения описать синтаксис заданной команды пути:
- (): группировка параметров
- +: требуется 1 или несколько заданных параметров
В описании команд пути cpx и cpy представляют координаты текущей точки.
9.3.2. Указание данных пути: свойство «d»
| Имя: | д |
|---|---|
| Значение: | нет | |
| Начальный: | нет |
| Применимо к: | «путь» |
| Унаследовано: | № |
| процентов: | НЕТ |
| Медиа: | визуал |
| Вычисленное значение: | как указано |
| Анимация: | да |
Свойство d используется для определения формы элемента «путь».
Значение none указывает, что нет данные пути для элемента. Для элементов «path» это означает, что элемент не отображает и не влияет на ограничивающую рамку предка элементы контейнера.
Путь состоит из нескольких сегментов, и каждая команда, либо явная или неявно, кроме moveto или closepath, определяет один сегмент пути .
Все координаты и длины, указанные в данных пути, должны рассматриваться как в пользовательских единицах измерения в текущей пользовательской системе координат.
Значение
Для анимации два значения свойства d могут быть только гладко интерполируется, когда строки данных пути содержат та же структура, (т.е. точно такое же количество и типы данных пути команды, расположенные в том же порядке). Если указана анимация и списки команд данных пути имеют разную структуру, тогда значения должны быть интерполированный с помощью дискретный тип анимации.
Если список команд данных пути имеет одинаковую структуру, то каждая параметр для каждой команды данных пути должен быть интерполированный отдельно как вещественные числа. Флаги и логические значения должны быть интерполированы как дроби от нуля до единицы, с учетом любого ненулевого значения быть значением один / истина.
Решено, что «d станет атрибутом презентации (без имени изменить) со строкой данных пути в качестве значения «в Лондон Встреча редакторов.
В следующих разделах перечислены команды, которые можно использовать. в строках данных пути. Те что рисовать отрезки прямых линий, включая команды lineto ( л , л , H , H , V и v ) и команды закрытия пути ( Z и z ). Эти три группы команд рисуют кривые:
- Кубический Команды Безье ( C , c , S и с ).Кубический отрезок Безье определяется по начальной, конечной и двум контрольным точкам.
- Квадратичная Команды Безье ( Q , q , T и т ). Квадратичный отрезок Безье — это определяется начальной точкой, конечной точкой и одним элементом управления точка.
- Эллиптический команды arc ( A и a ). Сегмент эллиптической дуги рисует сегмент эллипса.
9.3.3.
«moveto» командуетКоманды «moveto» ( M или м ) необходимо установить новую начальную точку и новая текущая точка.Эффект такой, как если бы «перо» подняли и переместили в новое место. Сегмент данных пути (если он есть) должен начинаться с «moveto» команда. Последующие команды «moveto» (т. Е. Когда «moveto» не первая команда) представляют собой начало нового подпуть :
| Команда | Имя | Параметры | Описание |
|---|---|---|---|
| M (абсолютное) m (относительное) | moveto | (х у) + | Начните новый вложенный путь с заданными координатами (x, y). M (верхний регистр) означает, что абсолютное координаты последуют; м (строчные) указывает, что последуют относительные координаты. Если moveto за которыми следуют несколько пар координат, последующие пары рассматриваются как неявные команды lineto. Следовательно, неявный lineto команды будут относительными, если moveto является относительным, и absolute, если moveto является абсолютным. Если относительный ход ( м ) появляется как первый элемент пути, тогда он рассматривается как пара абсолютных координат.В этом случае последующие пары координат рассматриваются как относительные даже если начальное движение интерпретируется как абсолютное движение. |
Когда используется относительная команда m , позиция перемещена в ( cpx + x , копий + y ).
9.3.4. Команда
«closepath»«Ближний путь» ( Z или z ) завершает текущий подпуть, возвращая его в исходную точку.Автоматический от текущей точки к начальной проводится прямая линия текущего подпути. Этот сегмент пути может быть нулевым длина.
Если за «closepath» сразу следует «moveto», то «moveto» определяет начальную точку следующего подпути. Если за «closepath» сразу следует любая другая команда, то следующий подпуть начинается в той же начальной точке, что и текущий подпуть.
Когда подпуть заканчивается «закрытым путем», он отличается по поведению. из того, что происходит, когда «вручную» закрывает подпуть через команда «lineto» в способе соединения «штрих-линия» и «штрих-линейный колпачок».С «closepath» конец последнего сегмента подпути «соединяется» с началом начального сегмент подпути, использующий текущее значение «stroke-linejoin». Если вместо этого вы «вручную» закроете подпуть через «lineto» команда, начало первого сегмента и конец последнего сегменты не соединяются, а вместо этого каждый закрывается с помощью текущее значение «stroke-linecap». В конце команды новая текущая точка устанавливается на начальная точка текущего подпути.
| Команда | Имя | Параметры | Описание |
|---|---|---|---|
| Z или z | ближний путь | (нет) | Закройте текущий подпуть, подключив его обратно к текущему начальная точка подпути (см. выше). Поскольку Z и Z Команды не принимают параметров, они имеют идентичный эффект. |
Замкнутый подпуть должен быть закрыт команда «closepath», она «соединяет» первый и последний сегменты пути.Любой другой путь — это открытый подпуть .
Закрытый подпуть отличается по поведению из открытого подпути, конечная координата которого является начальной точкой подпути. Первый и последний сегменты открытого подпути не будут соединены, даже если конечной координатой последнего сегмента пути является начальная точка подпути. Это приведет к первому и последнему сегменты контура ограничиваются текущим значением stroke-linecap вместо того, чтобы соединяться с использованием текущего значения stroke-linejoin.
Если за «closepath» сразу следует «moveto», затем «moveto» определяет начальную точку следующий подпуть. Если за «closepath» сразу следует любой другая команда, то следующий подпуть должен начинаться с той же начальной точки как текущий подпуть.
9.3.4.1. Завершающая сегмент операция закрытия пути
Чтобы представить основные формы как эквивалентные пути, должен быть способ закрыть изогнутые формы без введения дополнительного прямолинейного участка (даже если этот сегмент будет иметь нулевую длину).Для этой цели здесь определяется операция закрытия сегмента.
Завершение сегмента закрытие пути операция комбинирует с предыдущей командой пути, с двумя эффектами:
- Это гарантирует, что конечная точка координат предыдущей команды точно совпадает начальная точка текущего подпути.
- Он соединяет конечную и начальную точки подпути, делая его замкнутым подпутьем.
Завершающие сегменты операции закрытия пути в настоящее время не поддерживаются как команду в синтаксисе данных пути.Рабочая группа предложила такой синтаксис для будущих версий спецификации.
9.3.5.
«линето» командуетРазличные команды «lineto» рисуют прямые линии от от текущей точки к новой:
| Команда | Имя | Параметры | Описание |
|---|---|---|---|
| L (абсолютное) l (относительное) | линето | (х у) + | Проведите линию от текущей точки до заданной (x, y) координата, которая становится новой текущей точкой. L (верхний регистр) указывает, что абсолютное координаты последуют; л (строчные буквы) указывает, что последуют относительные координаты. Число пары координат могут быть указаны для рисования ломаной линии. В конце команды новая текущая точка устанавливается на предоставленный окончательный набор координат. |
| H (абсолютное) h (относительное) | горизонтальная линия | х + | Рисует горизонтальную линию от текущей точки. H (верхний регистр) указывает что последуют абсолютные координаты; ч (нижний регистр) указывает, что относительные координаты будут следить. Может быть указано несколько значений x (хотя обычно это не имеет смысла). H или h команда эквивалентна л или л команда с 0 указанным для координаты y. В конце команды новая текущая точка берется из окончательного значения координаты. |
| В (абсолютное) В (относительное) | вертикальная линия | г + | Рисует вертикальную линию от текущей точки. V (верхний регистр) означает, что последуют абсолютные координаты; в (нижний регистр) указывает, что относительные координаты будут следить. Может быть указано несколько значений y (хотя обычно это не имеет смысла). A В или В команда эквивалентна л или л команда с 0 указанным для координаты x.В конце команды новая текущая точка берется из окончательного значения координаты. |
Когда используется относительная команда l , конечная точка линии ( cpx + x , копий + y ).
Когда используется относительная команда h , конечная точка линии ( cpx + x , копеек ). Это означает что команда h с положительным значением x value рисует горизонтальную линию в направлении положительной оси x.
Когда используется относительная команда v , конечная точка линии ( cpx , копий + y ).
9.3.6. Кубическая кривая Безье дает команду
Кубические команды Безье следующие:
| Команда | Имя | Параметры | Описание |
|---|---|---|---|
| C (абсолютный) c (относительный) | кривой до | (х1 у1 х2 у2 х у) + | Рисует кубическую кривую Безье по текущему указать на (x, y), используя (x1, y1) в качестве контрольной точки на начало кривой и (x2, y2) в качестве контрольной точки в конец кривой. C (прописные) указывает, что последуют абсолютные координаты; c (нижний регистр) указывает, что относительный координаты последуют. Несколько наборов координат могут указать, чтобы нарисовать полибезье. В конце команда, новая текущая точка становится последней (x, y) пара координат, используемая в полибезье. |
| S (абсолютный) s (относительный) | сокращение / плавная кривая до | (x2 y2 x y) + | Рисует кубическую кривую Безье по текущему указать на (x, y).Предполагается, что первая контрольная точка отражение второй контрольной точки на предыдущей команду относительно текущей точки. (Если нет предыдущая команда или если предыдущая команда не была C, c, S или s, предположим, что первая контрольная точка совпадает с текущей точкой.) (x2, y2) — второй элемент управления точка (т. е. контрольная точка в конце кривой). S (верхний регистр) означает, что абсолютное координаты последуют; с (строчные буквы) указывает, что последуют относительные координаты.Несколько наборы координат могут быть указаны для рисования полибезье. В конце команды новый текущая точка становится последней используемой парой координат (x, y) в полибезье. |
При родственнике c или c используется команда, каждая из относительных пар координат вычисляется так же, как и в команде m . Например, конечная контрольная точка кривой обе команды: ( cpx + x , копий + y ).
Пример cubic01 показывает некоторые простое использование кубических команд Безье в пути. В пример использует внутреннюю таблицу стилей CSS для назначения стиля характеристики. Обратите внимание, что контрольной точкой для команды «S» является вычисляется автоматически как отражение контрольной точки для предыдущей команды «C» относительно начальной точки Команда «S».
Пример cubic01
Просмотреть этот пример как SVG (только браузеры с поддержкой SVG)
На следующем рисунке показано, как кубический Безье кривые меняют свою форму в зависимости от положения контрольные точки.Первые пять примеров иллюстрируют один кубический отрезок пути Безье. Пример внизу справа показана команда «C», за которой следует команда «S».
Просмотр
этот пример как SVG (только браузеры с поддержкой SVG)
9.3.7. Квадратичная кривая Безье дает команду
Квадратичные команды Безье следующие:
| Команда | Имя | Параметры | Описание |
|---|---|---|---|
| Q (абсолютный) q (относительный) | квадратичная кривая Безье до | (x1 y1 x y) + | Рисует квадратичную кривую Безье по текущему укажите на (x, y), используя (x1, y1) в качестве контрольной точки. Q (верхний регистр) указывает, что абсолютное координаты последуют; q (строчные) указывает, что последуют относительные координаты. Несколько наборы координат могут быть указаны для рисования полибезье. В конце команды новый текущая точка становится последней используемой парой координат (x, y) в полибезье. |
| T (абсолютное) t (относительное) | Сокращение / гладкая квадратичная кривая Безье до | (х у) + | Рисует квадратичную кривую Безье по текущему указать на (x, y).Контрольной точкой считается отражение контрольной точки на предыдущей команде относительно текущей точки. (Если нет предыдущего команда или если предыдущая команда не была Q, q, T или t, предположим, что контрольная точка совпадает с текущей точки.) T (прописные буквы) означает, что последуют абсолютные координаты; т (нижний регистр) указывает, что относительные координаты будут следить. В конце команды новая текущая точка становится последней парой координат (x, y), используемой в полибезье. |
При родственнике q или t используется команда, каждая из относительных пар координат вычисляется так же, как и в команде m . Например, конечная контрольная точка кривой обе команды: ( cpx + x , копий + y ).
Пример quad01 показывает некоторые простое использование квадратичных команд Безье внутри контура. Обратите внимание, что контрольная точка для команды «T» вычисляется автоматически как отражение контрольной точки для предыдущая команда «Q» относительно начальной точки «T» команда.
Пример quad01
Просмотреть этот пример как SVG (только для браузеров с поддержкой SVG)
9.3.8. Команды эллиптической кривой дуги
| SVG 2 Требование: | Упростите рисование дуг в синтаксисе пути SVG. |
|---|---|
| Разрешение: | Упростите создание дуг в путях. |
| Назначение: | Чтобы облегчить авторам запись данных пути с дугами вручную. |
| Владелец: | Кэмерон (ACTION-3151) |
Команды эллиптической дуги следующие:
| Команда | Имя | Параметры | Описание |
|---|---|---|---|
| A (абсолютный) a (относительный) | эллиптическая дуга | (rx ry x-axis-rotation big-arc-flag sweep-flag x г) + | Рисует эллиптическую дугу от текущей точки до ( x , y ).Размер и ориентация эллипса определяется двумя радиусами ( RX , Ry ) и x-axis-rotation , которая указывает, как эллипс в целом поворачивается в градусах относительно текущего система координат. Центр ( сх , г. cy ) эллипса вычисляется автоматически, чтобы удовлетворить ограничения, налагаемые другие параметры. флаг с большой дугой и развертка-флаг способствует автоматическому расчеты и помогают определить, как нарисована дуга. |
Когда используется относительная команда , конечная точка дуги составляет ( cpx + x , копий + y ).
Пример arcs01 показывает некоторые простое использование команд дуги внутри контура.
Пример arcs01
Просмотреть этот пример как SVG (только для браузеров с поддержкой SVG)
Команда эллиптической дуги рисует часть эллипса. который должен соответствовать следующим ограничениям:
- дуга начинается в текущей точке
- дуга заканчивается в точке ( x , л )
- эллипс имеет два радиуса ( rx , ry )
- ось абсцисс эллипса повернута на x-ось-поворот градус относительно x-оси текущая система координат.
В большинстве случаев на самом деле есть четыре разные дуги. (два разных эллипса, каждый с двумя разными дугами) которые удовлетворяют этим ограничениям. флаг с большой дугой и флаг развертки указывает, какой из четырех дуги нарисованы следующим образом:
- Из четырех возможных свипов дуги два будут представлять размах дуги не менее 180 градусов ( «большая дуга»), а два будут представлять длину дуги менее чем или равный 180 градусам («малая дуга»).Если флаг с большой дугой — это ‘1’, затем один из двух будут выбраны более крупные развертки дуги; в противном случае, если флаг с большой дугой — это «0», один из меньших будут выбраны развертки дуги,
- Если sweep-flag равен «1», то дуга будет быть нарисованным в направлении «положительного угла» (т. е. эллипс формула x = cx + rx * cos (тета) и y = cy + ry * sin (theta) равно оценивается так, что тета начинается под углом, соответствующим текущей точке и увеличивается положительно, пока дуга достигает (x, y)).Значение 0 заставляет дугу рисовать направление «отрицательный угол» (т. е. тета начинается под углом значение, соответствующее текущей точке, и уменьшается до тех пор, пока дуга достигает (x, y)).
Ниже показаны четыре комбинации флаг с большой дугой и развертка и четыре разные дуги, которые будут построены на основе значения этих флагов. Для каждого случая следующие данные пути использовалась команда:
где «?,?» заменяется на «0,0» «0,1» «1,0» и «1,1» на сгенерируйте четыре возможных случая.
Просмотр этот пример как SVG (только браузеры с поддержкой SVG)
См. Раздел Параметры эллиптической дуги, выходящие за пределы допустимого диапазона. для подробных примечаний по реализации для команды эллиптической дуги данных пути.
Приложение «Замечания по реализации» имеет соответствующие формулы для программного обеспечения, которое необходимо преобразовать Обозначение дуги SVG в формате, в котором используются центральные точки и дуги.
9.3.9. Грамматика для данных пути
Данные пути SVG соответствуют следующей грамматике EBNF.
svg_path :: = wsp * moveto? (перейти к drawto_command *)?
drawto_command :: =
двигаться
| близкий путь
| Lineto
| horizontal_lineto
| vertical_lineto
| кривая
| smooth_curveto
| quadratic_bezier_curveto
| smooth_quadratic_bezier_curveto
| эллиптическая_ дуга
moveto :: =
("M" | "m") wsp * последовательность_координат
closepath :: =
("Z" | "z")
lineto :: =
("L" | "l") wsp * последовательность_координат
horizontal_lineto :: =
("H" | "h") wsp * последовательность_координат
vertical_lineto :: =
("V" | "v") wsp * последовательность_координат
curveto :: =
("C" | "c") wsp * curveto_coordinate_sequence
последовательность_координат_кривой :: =
Coordinate_pair_triplet
| (тройка_координат запятая? последовательность_координат_координат)
smooth_curveto :: =
("S" | "s") wsp * smooth_curveto_coordinate_sequence
smooth_curveto_coordinate_sequence :: =
Coordinate_pair_double
| (Coordinate_pair_double comma_wsp? smooth_curveto_coordinate_sequence)
quadratic_bezier_curveto :: =
("Q" | "q") wsp * quadratic_bezier_curveto_coordinate_sequence
quadratic_bezier_curveto_coordinate_sequence :: =
Coordinate_pair_double
| (пара_координат, двойная запятая? wsp? quadratic_bezier_curveto_coordinate_sequence)
smooth_quadratic_bezier_curveto :: =
("T" | "t") wsp * последовательность_координат
эллиптическая_дуга :: =
("A" | "a") wsp * elliptical_arc_argument_sequence
elliptical_arc_argument_sequence :: =
elliptical_arc_argument
| (эллиптическая_дуга_аргумент запятая_всп? эллиптическая_дуга_аргумент_последовательность)
эллиптический_дуговой_аргумент :: =
число comma_wsp? число comma_wsp? число comma_wsp
флаг comma_wsp? флаг comma_wsp? Coordin_pair
двойной_координат :: =
ordin_pair comma_wsp? Coordin_pair
Coordin_pair_triplet :: =
ordin_pair comma_wsp? ordin_pair comma_wsp? Coordin_pair
последовательность_координат :: =
Coordin_pair | (пара_координат, запятая_wsp? последовательность_пар_координат)
последовательность_координат :: =
координата | (координата запятая? последовательность_координат)
пара_координат :: = координата запятая_wsp? координировать
координата :: = знак? номер
знак :: = "+" | "-"
число :: = ([0-9]) +
flag :: = ("0" | "1")
comma_wsp :: = (wsp + ","? wsp *) | ("," wsp *)
wsp :: = (# x9 | # x20 | #xA | #xC | #xD)
Обработка EBNF должна потреблять как можно больше заданного Производство EBNF по мере возможности, останавливаясь в момент, когда встречается персонаж, который больше не удовлетворяет производство.Таким образом, в строке «М 100-200» первая координата для «moveto» потребляет символы «100» и останавливается при встрече со знаком минус, потому что знак минус не может следовать за цифрой при производстве «координаты». В в результате первая координата будет «100», а вторая координата будет «-200».
Аналогично для строки «M 0.6.5» первая координата «moveto» потребляет символы «0,6» и останавливается на встречает вторую десятичную точку, потому что производство «координата» допускает только одну десятичную точку.Результат что первая координата будет «0,6», а вторая координата будет «.5».
Обратите внимание, что EBNF разрешает строку данных пути в d должно быть пустым. Это не ошибка, вместо этого он отключает отображение пути. Отрисовка также отключается, когда свойство d имеет значение none.
Если данные пути не соответствуют грамматике, значит, данные пути ошибочны. (см. Обработка ошибок).
9,4. Направленность пути
Некоторые функции, например ориентация маркеров и формы ограничения строк, определяются в терминах направление пути на заданном расстоянии вдоль пути или на начало или конец отдельного сегмента.
Направление пути в указанном расстояние по пути определяется следующим образом:
- Если заданное расстояние равно нулю, то направление пути равно направление в начале первый сегмент пути.
- В противном случае, если данное расстояние является длиной пути, то направление пути — это направление в конце пути последний сегмент.
- В противном случае, если данное расстояние по пути встречается на пути
граница сегмента, то направление пути — это
направление в начале
отрезок на заданном расстоянии, учитывая, что каждый отрезок
быть конечной точкой эксклюзивно.
Это будет «пройти мимо» сегменты нулевой длины и выберите более поздний сегмент, если расстояние находится на границе между двумя сегментами ненулевой длины.
- В противном случае заданное расстояние по пути будет посередине. отрезка пути ненулевой длины. Направление — это просто направление кривой в этой точке. Если точка лежит на разрыве, например куспид в сегменте Безье, то направление не определено; в таком случае, направление между входящим и исходящим направлениями вокруг неоднородности должен быть использован.
Направление в начале сегмента пути определяется следующим образом:
- Если длина всего пути, которому принадлежит сегмент, равна нулю, то направление в начале сегмента указывает в том же направлении, что и положительная ось абсцисс.
- В противном случае, если сегмент пути имеет нулевую длину и сегмент не имеют любые предшествующие сегменты ненулевой длины, то направление в начало сегмента такое же, как направление в конце отрезка.
- В противном случае, если сегмент пути имеет нулевую длину и есть ненулевые сегмент длины, предшествующий этому сегменту, затем направление в начале этот сегмент такой же, как и направление в конце ближайшего предшествующий сегмент ненулевой длины.
- В противном случае сегмент пути имеет ненулевую длину. Направление на начало сегмента — это просто направление, выходящее из начала сегмента точка.
Направление в конце пути сегмент определяется следующим образом:
- Если длина всего пути, которому принадлежит сегмент, равна нулю, то направление в конце сегмента указывает в том же направлении, что и положительная ось абсцисс.
- В противном случае, если сегмент пути имеет нулевую длину и сегмент не есть следующие сегменты ненулевой длины, то направление в конец сегмента совпадает с направление в начале сегмента.
- В противном случае, если сегмент пути имеет нулевую длину и есть ненулевые сегмент длины, следующий за этим сегментом, затем направление в конце этот сегмент такой же, как и направление в начале ближайшего следующий сегмент ненулевой длины.
- В противном случае сегмент пути имеет ненулевую длину. Направление на конец сегмента — это просто направление, ведущее к концу сегмента точка.
9,5. Примечания по реализации
Соответствующий пользовательский агент SVG должен реализовывать функции, использующие данные пути. по следующим реквизитам:
9.5.1. Параметры эллиптической дуги вне допустимого диапазона
Для всех параметров эллиптической дуги разрешены произвольные числовые значения. (кроме логических флагов), но пользовательские агенты должны внести следующие корректировки для недопустимых значений при рендеринге кривых или вычислении их геометрии:
Если конечная точка ( x , y ) сегмента совпадает с текущей точкой (е.g., конечная точка предыдущего отрезка), тогда это эквивалентно полностью исключению сегмента эллиптической дуги.
Если rx или ry равно 0, тогда эта дуга рассматривается как отрезок прямой («lineto»), соединяющий конечные точки.
Если rx или ry имеют отрицательные знаки, они опущены; вместо этого используется абсолютное значение.
Если rx , ry и x-axis-rotation таковы, что нет решения (в основном, эллипс недостаточно большой, чтобы дотянуться до от текущей точки до новой конечной точки) затем эллипс увеличивается равномерно, пока не будет ровно одно решение (пока эллипс как раз достаточно большой).
См. Раздел приложения Коррекция радиусов за пределами допустимого диапазона для математической формулы для этой операции масштабирования.
Это снисходительное, но последовательное обращение с выходом за пределы допустимого диапазона values гарантирует, что:
- Неизбежные приближения, исходящие от компьютера арифметика не может вызвать допустимый набор значений, записанных одним Реализация SVG будет считаться недействительной при чтении другая реализация SVG. В противном случае это было бы проблема для общих граничных случаев, таких как полукруглый дуга.
- Непрерывная анимация, вызывающая передачу параметров из-за недопустимых значений не проблема. Движение остается непрерывным.
9.5.2. Отраженные контрольные точки
Команды S / s и T / t указывают, что первая контрольная точка данный кубический сегмент Безье вычисляется по формуле отражение последней контрольной точки предыдущего сегмента пути относительно текущей точки. Точная математика выглядит как следует.
Если текущая точка ( curx , cury ) и конечная контрольная точка предыдущего отрезка пути ( oldx2 , oldy2 ), затем отраженная точка (т.е.е., ( новыйx1 , newy1 ), первая контрольная точка текущего сегмента пути):
(newx1, newy1) = (curx - (oldx2 - curx), cury - (oldy2 - любопытный))
= (2 * curx - старыйx2, 2 * cury - oldy2)
9.5.3. Сегменты тракта нулевой длины
Сегменты пути с нулевой длиной недействительны, и повлияет на рендеринг в следующих случаях:
- Если маркеры указаны, то маркер рисуется на каждая применимая вершина, даже если данная вершина является конечная точка отрезка пути нулевой длины и даже если Команды moveto следуют друг за другом.
- Как указано в Stroke Properties, заглушки должны быть окрашены для подпути нулевой длины, когда stroke-linecap имеет значение круглый или квадратный.
9.5.4. Обработка ошибок в данных пути
Нераспознанное содержимое в потоке данных пути (т. Е. содержимое, не являющееся частью грамматики данных пути) является ошибка. В таком случае необходимо использовать следующие правила обработки ошибок:- Общее правило обработки ошибок в данных пути: что пользовательский агент SVG должен отображать элемент «путь» вверх в (но не включая) команду пути, содержащую первая ошибка в спецификации данных пути.Это будет предоставить пользователю или разработчику визуальную подсказку о где ошибка может быть в спецификации данных пути. Это правило сильно препятствует созданию недействительных Данные пути SVG.
- Если команда данных пути содержит неверный набор параметры, то отображается заданная команда данных пути до последнего правильно определенного сегмента пути включительно, даже если этот сегмент пути является подкомпонентом команда данных составного пути, например «lineto» с несколько пар координат.Например, для пути строка данных ‘M 10,10 L 20,20,30’, есть нечетное количество параметров для команды «L», которая требует четного количество параметров. Пользовательский агент требуется для рисования строка от (10,10) до (20,20), а затем выполнить ошибку отчет с ‘L 20 20’ это последний правильно определенный сегмент спецификации данных пути.
- По возможности, все пользовательские агенты SVG должны сообщать все ошибки пользователю.
9.6.Расстояние по тропе
Различные операции, включая текст на траектории и анимацию движения и различные инсульты операции, требуют, чтобы пользовательский агент вычислял расстояние по геометрии графического элемента, например «путь».
Существует точная математика для вычисления расстояния вдоль пути, но формулы очень сложные и требуют существенного вычисление. Рекомендуется, чтобы продукты авторинга и пользователь агенты используют алгоритмы, которые дают столь же точные результаты, как возможный; однако, чтобы учесть различия в реализации и помочь при расчетах расстояний получить результаты, которые приблизительное намерение автора, можно использовать атрибут «pathLength» предоставить авторский расчет общей длины путь, чтобы пользовательский агент мог масштабировать расстояние вдоль пути вычислений по отношению «pathLength» к собственному пользовательскому агенту вычисленное значение для общей длины пути.
Операция «moveto» в элементе «path» определяется как нулевая длина. Только различные «lineto», «curveto» и «arcto» команды участвуют в расчетах длины пути.
9.6.1. Атрибут «pathLength»
Имя Значение Начальное значение Анимационный длина пути <номер> (нет) да Авторский расчет полной длины путь в пользовательских единицах.Это значение используется для калибровки собственное расстояние по пути пользовательского агента расчеты с автором. Пользовательский агент будет масштабируйте все вычисления расстояния вдоль пути по соотношению «pathLength» пользователю собственное вычисленное значение общей длины пути агента. «PathLength» потенциально влияет вычисления текста по пути, анимация движения и различные инсультные операции.
Нулевое значение допустимо и должно рассматриваться как бесконечный масштабный коэффициент.Значение нуля, масштабируемое бесконечно, должно оставаться нулевым, в то время как любое непроцентное значение больше чем ноль должно стать + Infinity.
Отрицательное значение — ошибка (см. Обработка ошибок).
«pathLength» не влияет на процент расчет расстояния вдоль пути.
9,7. DOM интерфейсы
9.7.1. Интерфейс SVGPathElement
Объект SVGPathElement представляет «путь» в DOM.
[Exposed = Window]
interface SVGPathElement : SVGGeometryElement {
}; .