Кривая Гильберта vs Z-order / Хабр
Неоднократно доводилось слышать мнение, что из всех заметающих кривых. именно кривая Гильберта наиболее перспективна для пространственной индексации. Мотивируется это тем, что она не содержит разрывов и потому в некотором смысле “хорошо устроена”. Так ли это на самом деле и при чем здесь пространственная индексация, разберёмся под катом.
Завершающая статья из цикла:
- Почему не работает прямолинейный подход при
пространственной индексации заметающими кривыми - Презентация алгоритма
- 3D и очевидные оптимизации
- 8D и перспективы в OLAP
- 3D на сфере, как это выглядит
- 3D на сфере, benchmarks
- Как насчет индексации неточечных объектов?
Кривая Гильберта обладает замечательным свойством — расстояние между двумя последовательными точками на ней всегда равно единице (шагу текущей детализации, если точнее).
- понижения размерности (управление цветовой палитрой)
- повышения локальности доступа в многомерном индексировании (здесь)
- в конструировании антенн (здесь)
- кластеризации таблиц (DB2)
Что касается пространственных данных, свойства кривой Гильберта позволяют увеличить локальность ссылок и повысить эффективность кэша СУБД, как здесь, где перед использованием таблицы рекомендуют дополнить её колонкой с вычисленным значением и отсортировать по этой колонке.
В пространственном поиске кривая Гильберта присутствует в Гильбертовых R-деревьях, где основная идея (очень грубо) — когда приходит время расщепить страницу на двух потомков — сортируем все элементы на странице по значениям центроидов и делим пополам.
Но нас больше интересует другое свойство кривой Гильберта — это самоподобная заметающая кривая. Что позволяет использовать ее в индексе на основе B-дерева. Речь идёт о способе нумерации дискретного пространства.
- Пусть задано дискретное пространство размерности N.
- Допустим также, что у нас есть некоторый способ нумерации всех точек этого пространства.
- Тогда, для индексации точечных объектов достаточно поместить в индекс на основе B-дерева номера точек в которые попали эти объекты.
- Поиск в таком пространственном индексе зависит от способа нумерации и в конечном счете сводится к выборке по индексу из интервалов значений.
- Заметающие кривые хороши своим самоподобием, которое позволяет порождать относительно небольшое количество таких подинтервалов, тогда как прочие способы (например, подобие строчной развёртки) требует огромного числа подзапросов, что делает такую пространственную индексацию малоэффективной.
Итак, откуда берётся это интуитивное ощущение, что кривая Гильберта хороша для пространственной индексации? Да в ней нет разрывов, расстояние между любыми последовательными точками равно шагу дискретизации. Ну и что? Какова связь между этим фактом и потенциально высокой производительностью?
Ну и что? Какова связь между этим фактом и потенциально высокой производительностью?
В самом начале мы сформулировали правило — «хороший» метод нумерации минимизирует суммарный периметр страниц индекса. Речь идёт о страницах B-дерева, на которых в конце концов окажутся данные. Другими словами — производительность индекса определяется числом страниц, которые придётся прочитать. Чем меньше страниц приходится в среднем на запрос эталонного размера, тем выше (потенциальная) производительность индекса.
С этой точки зрения кривая Гильберта выглядит очень перспективно. Но это интуитивное ощущение на хлеб не намажешь, поэтому проведём численный эксперимент.
- рассмотрим 2 и 3 -мерные пространства
- возьмём квадратные/кубические запросы разных размеров
- для серии случайных запросов одного типа и размера подсчитаем среднее/дисперсию числа заметённых страниц, в серии 1000 запросов
- будем исходить из того, что в каждом узле пространства лежит точка.
 Можно набросать случайных данных и проверить на них, но тогда возникли бы вопросы к качеству этих случайных данных. А так мы имеем вполне объективный показатель “пригодности”, пусть и далёкий от любого реального набора данных
Можно набросать случайных данных и проверить на них, но тогда возникли бы вопросы к качеству этих случайных данных. А так мы имеем вполне объективный показатель “пригодности”, пусть и далёкий от любого реального набора данных - на странице помещается 200 элементов, важно чтобы это была бы не степень двойки, что привело бы к вырожденному случаю
- сравним между собой кривую Гильберта и Z-curve
Вот так это выглядит в виде графиков.
Теперь стоит хотя бы из любопытства посмотреть как при фиксированном размере запроса (2D 100X100) ведет себя число прочитанных страниц в зависимости от размера страницы.
Хорошо заметны “ямы” в Z-order, соответствующие размерам 128, 256 и 512. И “ямки” в 192, 384, 768. Не такие уж и большие.
Как мы видим, разница может достигать 10%, но почти везде это в пределах статистической погрешности. Тем не менее везде кривая Гильберта ведёт себя лучше чем Z-кривая. Не сильно, но лучше. По-видимому, эти 10% и есть оценка сверху потенциального эффекта, которого можно достичь, перейдя на кривую Гильберта. Стоит ли овчинка выделки? Попробуем узнать.
Тем не менее везде кривая Гильберта ведёт себя лучше чем Z-кривая. Не сильно, но лучше. По-видимому, эти 10% и есть оценка сверху потенциального эффекта, которого можно достичь, перейдя на кривую Гильберта. Стоит ли овчинка выделки? Попробуем узнать.
Реализация.
Использование кривой Гильберта в пространственном поиске сталкивается с рядом трудностей. Например, само вычисление ключа из 3 координат занимает (у автора) около 1000 тактов, примерно в 20 раз больше, чем то же для zcurve. Возможно, существует какой то более эффективный метод, кроме того есть мнение, что уменьшение числа прочитанных страниц окупает любое усложнение работы. Т.е. диск — более дорогой ресурс чем процессор. Поэтому мы будем в первую очередь ориентироваться именно на чтения буферов, а времена просто примем к сведению.
Что касается алгоритма поиска. Вкратце, он базируется на двух идеях —
- Индекс представляет собой B-дерево с его страничной организацией.
 Если мы хотим логарифмического доступа к первому элементу выдачи, то должны подобно бинарному поиску использовать стратегию “разделяй и властвуй”. Т.е. необходимо на каждой итерации в среднем поровну делить запрос на подзапросы.
Если мы хотим логарифмического доступа к первому элементу выдачи, то должны подобно бинарному поиску использовать стратегию “разделяй и властвуй”. Т.е. необходимо на каждой итерации в среднем поровну делить запрос на подзапросы.Из самоподобия заметающих кривых следует, что если взять квадратную (кубическую) решетку, выходящую из начала координат с шагом в степень двойки, то любой элементарный куб в этой решетке содержит один интервал значений. Следовательно, рассекая поисковый запрос по узлам этой решетки можно разбить исходный произвольный подзапрос на непрерывные интервалы. После чего каждый из этих интервалов вычитывается из дерева.
- Если этот процесс не остановить, он порежет исходный запрос вплоть до интервалов из одного элемента, это не то, чего бы нам хотелось. Критерий остановки таков — запрос режется на подзапросы до тех пор, пока целиком не умещается на одной странице B-дерева.
 Как только уместился — проще прочитать страницу целиком и отфильтровать ненужное. Как узнать что уместились? У нас есть минимальная и максимальная точки подзапроса, равно как и текущая и последняя точки страницы.
Как только уместился — проще прочитать страницу целиком и отфильтровать ненужное. Как узнать что уместились? У нас есть минимальная и максимальная точки подзапроса, равно как и текущая и последняя точки страницы.Ведь в начале обработки подзапроса мы делаем поиск в B-дереве минимальной точки подзапроса и получаем листовую страницу, на которой остановился поиск и текущее положение в ней.
Всё это одинаково справедливо и для кривой Гильберта и для Z-order. Однако:
- для кривой Гильберта нарушен порядок — левая нижняя точка запроса вовсе не обязательно меньше правой верхней (для двумерного случая)
- мало того, совершенно не обязательно максимум и/или минимум подзапроса находится в одном из его углов, он необязательно вообще лежит в пределах запроса
- следовательно, настоящий диапазон значений может быть гораздо шире поискового запроса, в худшем случае, это весь экстент слоя, если вам удалось попасть в область вокруг центра
Это приводит к тому, что необходимо модифицировать исходный алгоритм.
Для начала изменился интерфейс работы с ключом.
- bitKey_limits_from_extent — этот метод вызывается один раз в начале поиска для определения настоящих границ поиска. На вход принимает координаты поискового экстента, отдаёт минимальное и максимальное значения диапазона поиска.
- bitKey_getAttr — на вход принимает интервал значений подзапроса и также исходные координаты поискового запроса. Возвращает маску из следующих значений
- baSolid — этот подзапрос целиком лежит внутри поискового экстента, его не надо расщеплять, а можно значения из интервала целиком помещать в выдачу
- baReadReady — минимальный ключ интервала подзапроса лежит внутри поискового экстента, можно делать поиск в B-дереве. В случае zcurve этот бит взводится всегда.
- baHasSmth — если этот бит не взведён, данный подзапрос целиком расположен вне поискового запроса и должен быть проигнорирован. В случае Z-order этот бит взводится всегда.

Модифицированный алгоритм поиска выглядит так:
- Заводим очередь подзапросов, изначально в этой очереди один единственный элемент — экстент (а также минимальный и максимальный ключи диапазона), найденный с помощью вызова bitKey_limits_from_extent
- Пока очередь не пуста:
- Достаем элемент с вершины очереди
- Получаем информацию о нём с помощью bitKey_getAttr
- Если не взведен baHasSmth, игнорируем этот подзапрос
- Если взведен baSolid, вычитываем весь диапазон значений прямо в resultset и переходим к следующему подзапросу
- Если взведен baReadReady, выполняем поиск в B-дереве по минимальному значению в подзапросе
- Если не взведен baReadReady или для этого запроса не срабатывает критерий остановки (он не помещается на одной странице)
- Вычисляем минимальное и максимальное значения диапазона подзапроса
- Находим разряд ключа, по которому будем резать
- Получаем два подзапроса
- Помещаем их в очередь, сначала тот, что с бОльшими значениями, затем второй
Рассмотрим на примере запроса в экстенте [524000,0,484000 …525000,1000,485000].
Вот так выглядит исполнение запроса для Z-order — ничего лишнего.
Subqueries — все порождённые подзапросы, results — найденные точки,
lookups — запросы к B-дереву.
Поскольку диапазон пересекает 0x80000, стартовый экстент получается размером в весь экстент слоя. Всё самое интересное слилось в центре, рассмотрим поподробнее.
Обращают на себя внимание «скопления» подзапросов на границах. Механизм их возникновения примерно таков — допустим, очередной разрез отсёк от границы поискового экстента узкую полоску, например, шириной 3. Причем, в этой полоске даже нет точек, но мы то этого не знаем. А проверить сможем только в тот момент, когда минимальное значение диапазона подзапроса попадёт в пределы поискового экстента. В результате алгоритм станет резать полоску вплоть до подзапросов размером в 2 и 1 и только тогда сможет сделать запрос к индексу чтобы убедиться, что там ничего нет. Или есть.
Или есть.
На число прочитанных страниц это не влияет, все такие проходы по В-дереву приходятся на кэш, но объем проделанной работы впечатляет.
Ну что же, осталось выяснить сколько в действительности было прочитано страниц и сколько времени всё это заняло. Следующие значения получены на тех же данных и тем же способом, что и ранее. Т.е. 100 000 000 случайных точек в [0…1 000 000, 0…0, 0…1 000 000].
Замеры проводились на скромной виртуальной машине с двумя ядрами и 4 Гб ОЗУ, поэтому времена не имеют абсолютной ценности, а вот числам прочитанных страниц по прежнему можно доверять.
Времена показаны на вторых прогонах, на разогретом сервере и виртуальной машине. Количества прочитанных буферов — на свеже-поднятом сервере.
| NPoints | Nreq | Type | Time(ms) | Reads | Hits |
|---|---|---|---|---|---|
| 1 | 100 000 | zcurve rtree hilbert |
. 36 36.38 .63 |
1.13307 1.83092 1.16946 |
3.89143 3.84164 88.9128 |
| 10 | 100 000 | zcurve rtree hilbert |
.38 .46 .80 |
1.57692 2.73515 1.61474 |
7.96261 4.35017 209.52 |
| 100 | 100 000 | zcurve rtree hilbert |
.48 .50 … 7.1 * 1.4 |
3.30305 6.2594 3.24432 |
31.0239 4.9118 465.706 |
| 1 000 | 100 000 | zcurve rtree hilbert |
1.2 1.1 … 16 * 3.8 |
13.0646 24.38 11.761 |
165.853 7.89025 1357.53 |
| 10 000 | 10 000 | zcurve rtree hilbert |
5. 5 54.2 … 135 * 14 |
65.1069 150.579 59.229 |
651.405 27.2181 4108.42 |
| 100 000 | 10 000 | zcurve rtree hilbert |
53.3 35…1200 * 89 |
442.628 1243.64 424.51 |
2198.11 186.457 12807.4 |
| 1 000 000 | 1 000 | zcurve rtree hilbert |
390 300…10000* 545 |
3629.49 11394 3491.37 |
6792.26 3175.36 36245.5 |
где
Npoints — среднее число точек в выдаче
Nreq — число запросов в серии
Type — ‘zcurve’ — исправленный алгоритм с гиперкубами и разбором numeric, используя его внутреннюю структуру,;’rtree’- gist only 2D rtree; ‘hilbert’ — тот же алгоритм что и для zcurve, но для кривой Гильберта, (*) — для того, чтобы сравнить время поиска приходилось уменьшать серию в 10 раз для того, чтобы страницы умещались в кэш
Time(ms) — среднее время выполнения запроса
Reads — среднее число чтений на запрос. Самая важная колонка.
Самая важная колонка.
Shared hits — число обращений к буферам
* — разброс значений вызван высокой нестабильностью результатов, если нужные буфера успешно находились в кэше, то наблюдалось первое число, в случае массовых промахов — второе. Фактически, второе число характерно для заявленного Nreq, первое — в 5-10 раз меньшего.
Выводы
Немного удивляет, что “наколеночная” оценка преимуществ кривой Гильберта дала довольно точную оценку реального положения дел.
Видно, что на запросах, где размер выдачи соизмерим или более размера страницы, кривая Гильберта начинает вести себя лучше по числу промахов мимо кэша. Выигрыш, впрочем, составляет единицы процентов.
С другой стороны, интегральное время работы для кривой Гильберта примерно вдвое хуже оного у Z-кривой. Допустим, автор выбрал не самый эффективный способ вычисления кривой, допустим, что-то можно было сделать поаккуратнее. Но ведь вычисление кривой Гильберта объективно тяжелее Z-кривой, для работы с ней действительно надо предпринимать существенно больше действий. Ощущение такое, что отыграть это замедление с помощью нескольких процентов выигрыша в чтении страниц не удастся.
Ощущение такое, что отыграть это замедление с помощью нескольких процентов выигрыша в чтении страниц не удастся.
Да, можно сказать, что в высококонкурентной среде каждое чтение страницы обходится дороже десятков тысяч вычислений ключа. Но ведь число успешных попаданий в кэш у кривой Гильберта заметно больше, а они проходят через сериализацию и в конкурентной среде тоже чего-то стоят.
Итого
Вот и подошло к концу эпическое повествование о возможности и особенностях пространственных и/или многомерных индексов на основе самоподобных заметающих кривых, построенных на B-деревьях.
За это время (кроме того, что такой индекс реализуем) мы выяснили что по сравнению с традиционно применяемым в данной области R-деревом
- он компактнее (объективно — за счет лучшей средней заполняемости страниц)
- быстрее строится
- не использует эвристик (т.е. это именно алгоритм)
- не боится динамических изменений
- на малых и средних запросах работает быстрее.

Проигрывает на больших запросах (только при избытке памяти под кэш страниц) — там, где выдаче участвуют сотни страниц.
При этом R-дерево работает быстрее т.к. фильтрация происходит только на периметре, обработка которого заметающими кривыми заметно тяжелее.
В обычных условиях конкуренции за память и на таких запросах наш индекс заметно быстрее R-дерева. - Без изменения алгоритма работает с ключами любой (разумной) размерности
- При этом возможно применение разнородных данных в одном ключе, например, времени, класса объекта и координат. При этом не надо настраивать никаких эвристик, в худшем случае, если диапазоны данных сильно различается, просядет производительность.
- Пространственные объекты ((многомерные) интервалы) трактуются как точки, пространственная семантика обрабатывается в границах поисковых экстентов.
- Допускается смешение интервальных и точных данных в одном ключе, опять же вся семантика выносится наружу, алгоритм не меняется
- Всё это не требует вмешательства в синтаксис SQL, введения новых типов, …
Если хочется, можно написать обёртывающее расширение PostgreSQL.
- И да, выложено под лицензией BSD, допускающей почти полную свободу действий.
Кривые Гильберта | Компьютерная графика
Кривые Гильберта впервые были описаны в 1891 году немецким математиком Давидом Гильбертом.
Кривая Гильберта — это непрерывная кривая, заполняющая пространство. Эти кривые также являются фракталами, они самоподобны; если вы увеличите масштаб и внимательно посмотрите на часть кривой более высокого порядка, то вы увидите, что она выглядит так же, как сама кривая.
Самый простой способ понять, как строится кривая Гильберта, следующий. Представьте, что у вас есть длинный кусок веревки и вы хотите расположить веревку на плоской сетке с квадратными ячейками. Ваша цель состоит в том, чтобы веревка пересекала стороны каждого квадрата сетки ровно один раз.
Не разрешается, чтобы веревка пересекала сама себя.
Есть много способов сделать это, однако кривые Гильберта имеют некоторые дополнительные интересные свойства. Чтобы понять эти свойства, мы должны внимательнее посмотреть на то, как они строятся рекурсивно.
Чтобы понять эти свойства, мы должны внимательнее посмотреть на то, как они строятся рекурсивно.
Рекурсия
Основным элементом кривой Гильберта является П-образный элемент.
Здесь у нас квадратная сетка 2×2. Начнем с левого верхнего угла и проведем веревку через другие три квадрата сетки, закончив в правом верхнем углу.
Теперь представьте, что мы удваиваем размер сетки, получая сетку 4×4.
Мы можем представить эту сетку 4×4 в виде набора 4 = 2×2 сеток, каждая из которых имеет размер 2×2 (как набор матрешек).
Мы хотим пересечь сетку более высокого уровня в таком порядке 0->1->2->3 (это показано большими желтыми стрелками), а затем внутри этой сетки используем все тот же П-образный шаблон обхода для каждой из сеток меньшего уровня.
Эта запутанная и извилистая кривая проходит через каждый квадрат сетки.
Если вы вернетесь назад, к кривой на сетке , приведенной выше, то увидите, что она построена из кривых для четырех сеток , размещенных по П-образному образцу…
Вот некоторые кривые Гильберта по возрастанию порядка:
От 1D к 2D
Здесь все становится немного интереснее. Вместо того чтобы использовать веревку, представим, что мы по сетке располагаем измерительную ленту.
Вместо того чтобы использовать веревку, представим, что мы по сетке располагаем измерительную ленту.
Поскольку лента извивается и разворачивается в противоположном направлении вокруг сетки, получается интересное свойство. Если сопоставить расстоянию d , отмеренному лентой, пару координат (x,y) точек на исходной сетке, то получится, что другие отметки на ленте (близкие к d) соответствуют координатам, близким к (x,y).
Мы получили полезную функцию перехода от размерности 1 к двум измерениям, она сохраняет свойство локальности (примеч. Проекция, сохраняющая свойство локальности — линейное проективное отображение, которое оптимально сохраняет структуру окрестности точки из области определения).
Близкие значения d соответствуют близким значениям .
Замечание. Обратное не всегда верно (что неизбежно при отображении двух измерений на одно измерение). Обязательно будут случаи, когда точки с геометрически близкими координатами (x,y) будут соответствовать сильно отличающимся значениям на ленте d. Тем не менее, за исключением этих случаев, кривые Гильберта также неплохо работают и на обратных отображениях.
Тем не менее, за исключением этих случаев, кривые Гильберта также неплохо работают и на обратных отображениях.
Ниже можно увидеть квадрат, раскрашенный с использованием кривой Гильберта. Цвета, близкие друг к другу на спектре, имеют близкие координаты (x,y).
(Близкие координаты (x,y) не всегда соответствуют близким цветовым оттенкам цвета по причине, описанной выше, хотя часто это так. Отсутствие непрерывности наиболее заметно вдоль двух границ. Некоторые интересные обходы этого ограничения были придуманы, больше об этом — позже).
Более высокие размерности
Построение кривых Гильберта может быть сделано и для более чем двух измерений. Одномерная линия может быть закручена в стольких измерениях, сколько вы можете себе представить.
Вариант трехмерной кривой показан слева. В этом случае точки на кривой, численно близкие друг к другу, также близки в трехмерном пространстве.
Легко увидеть, как это может быть распространено на более высокие измерения.
Практическое применение
Функции Гильберта могут помочь в индексировании пространственных баз данных; при поиске записи, близкой по географическому положению они дают возможность определить приоритет для поиска.
Кроме баз данных эти кривые иногда используются в обработке изображений. При преобразовании изображения в оттенки серого через сглаживание черного и белого значения, превосходящие критические, могут быть перенесены с помощью использования гильбертовой кривой так, что на рисунке крайности будут менее очевидными для глаз.
В более высоких размерностях они могут быть использованы для планирования задач в компьютерных программах с параллельной обработкой данных, преобразования многомерного распределения задач в одномерное и привязки близких задач к точкам размещения с более высоким уровнем близости.
Исследования
Ранее уже говорилось, что не все в кривых Гильберта идеально. (Точки с близкими значениями d имеют схожие значения (x,y), но обратное не всегда верно).
(Точки с близкими значениями d имеют схожие значения (x,y), но обратное не всегда верно).
Это свойство было бы невероятно полезно, например, при осуществлении эффективного доступа к данным. Давайте представим, что у вас есть некоторые данные, хранящиеся в цифровом виде (точки их размещения с очень большим временем доступа), и требуется их индексация и доступ к ним эффективным образом, что нужно сделать географически. Как известно, преобразование координат (x,y) в значения d не может гарантировать, что близкие значения d расположены в непосредственной близости. Большую часть времени да, но время от времени нет.
Чтобы избежать этого, вместо простого индексирования данных на одной кривой Гильберта, данные переводятся на множество гильбертовых кривых (как правило, полученных вращением и горизонтальными/вертикальными сдвигами одной кривой).
Кривые Гильберта
Это статья о кривых Гильберта. Кривые Гильберта названы в честь немецкого математика Давида Гильберта . Впервые они были описаны в 1891 году. Кривая Гильберта представляет собой непрерывную кривую заполнения пространства. Они также фрактальны и самоподобны; Если вы увеличите масштаб и внимательно посмотрите на участок кривой более высокого порядка, то узор, который вы увидите, будет выглядеть точно так же, как он сам. Простой способ представить себе создание кривой Гильберта — это представить, что у вас есть длинная веревка, и вы хотите положить ее на сетку квадратов на столе. Ваша цель — накинуть нить на доску так, чтобы нить прошла через каждый квадрат доски только один раз. |
Строка не может пересекаться сама с собой. Существует множество шаблонов для достижения этого эффекта, но кривые Гильберта обладают некоторыми дополнительными интересными свойствами. Чтобы понять эти свойства, нам нужно более подробно рассмотреть, как они определяются рекурсивно. |
Кривая Гильберта, вписывающаяся в сетку 8 x 8 , показана слева. |
Рекурсия
Основным элементом кривой Гильберта является U-образная форма. Посмотрите на изображение слева. Здесь у нас есть квадратная сетка 2 x 2 . Мы начинаем с нашей «нити» в верхнем левом углу и протягиваем ее через три других квадрата в сетке, чтобы закончить в верхнем правом углу. |
Теперь представьте, что мы удвоили размер сетки, чтобы сделать 4 x 4 сетка. Мы можем представить эту сетку 4 x 4 как вложенный набор сеток 2 x 2 , каждая из которых имеет размер 2 x 2 (как набор матрешек). Мы хотим пройти по сетке на высоком уровне, следуя грубому шаблону 0->1->2->3 (показанному большими желтыми стрелками), а затем внутри каждой из этих сеток по более точному самоподобному шаблону обхода через каждую из меньших сеток. |
Результат показан слева. Этот запутанный и извилистый узор проходит через каждый квадрат сетки. |
Если вы прокрутите назад вверх, чтобы посмотреть на изображение кривой 8 x 8 , нарисованное выше, вы увидите, что оно следует образцу четырех сеток 4 x 4 , нарисованных U-образно… |
Вот несколько изображений кривых Гильберта с постоянно увеличивающейся плотностью:
1D в 2D
Теперь становится немного интереснее. Вместо того, чтобы использовать кусок веревки, представьте, что мы наматываем на сетку измерительную ленту. |
Поскольку лента извивается и закручивается по сетке дважды, она создает интересное свойство: мы обнаружим, что если мы преобразуем расстояние ( d ), показанное на рулетке, в пару (x,y ) координат на сетке, то обнаруживаем, что другие отметки на рулетке (близкие к d ) имеют очень близкие координаты (x,y) .
Мы создали полезную функцию сопоставления между одномерным и двухмерным измерениями, которая хорошо сохраняет локальность.
Аналогичные значения d имеют аналогичные значения (x,y) ПРИМЕЧАНИЕ Обратное не всегда может быть верным (что неизбежно при отображении из двух измерений в одно измерение). Обязательно будут случаи, когда (x,y) геометрически близкие координаты, имеющие неблизкие значения при измерении вдоль ленты d . Однако, в отсутствие этих выбросов, кривые Гильберта, на самом деле, хорошо справляются и с обратными характеристиками. Справа вы можете увидеть радугу, нарисованную с помощью кривой Гильберта. Цвета, близкие друг к другу в спектре, имеют схожие координаты (x, y) . (близкие координаты (x,y) не всегда имеют одинаковые оттенки цвета по описанной выше причине, хотя часто имеют. Разрывы наиболее заметны вдоль степеней двух границ. Некоторые интересные обходные пути для это ограничение было изобретено — об этом позже. |
Пристальный взгляд
Ниже приведен график пифагорейского расстояния между всеми ячейками на кривой Гильберта 16 x 16 и контрольной точкой образца (отмечена красной линией). По оси x отложено одномерное расстояние d , измеренное вдоль ленты. По оси ординат показано расстояние между точкой, изображенной на оси абсцисс, и контрольной точкой (отмечена красной линией).
Как видите, когда значение d близко к нашей контрольной точке, расстояния до других точек близки к d мал, и чем дальше мы удаляемся от красной линии, тем в среднем становится больше расстояние. Это не идеально, но довольно хорошо, учитывая, как плохо это могло бы выглядеть, если бы мы просто двигали ленту зигзагом вперед и назад, как гигантскую доску для лотков и лестниц
, по шкале от 0 до 255, где ноль — начало ленты, а 255 — конец ленты.
Ниже приведен еще один пример, на этот раз с контрольной точкой на 138 единицах вдоль кривой.
Как и прежде, чем дальше от контрольной точки, тем больше становится расстояние между парами координат (x,y) . И, как и прежде, значения d , близкие к контрольной точке, сопоставляются с координатами, близкими к (x,y) координатам контрольной точки.
Вот тепловая карта, показывающая расстояние между всеми парами значений d . Чем ярче цвет, тем больше расстояние. Верхний левый угол сетки представляет собой расстояние между d=0, d=0. Каждый пиксель сдвигается вправо на n представляет d=n, и каждый пиксель перемещается вниз на м. представляет d=m, а цвет каждого пикселя представляет пифагорово расстояние между двумя точками d=n, d=m на 2D-плоскости.
(Приведенные выше графики эквивалентны горизонтальным срезам этой сетки с оттенком цвета, представляющим высоту графика).
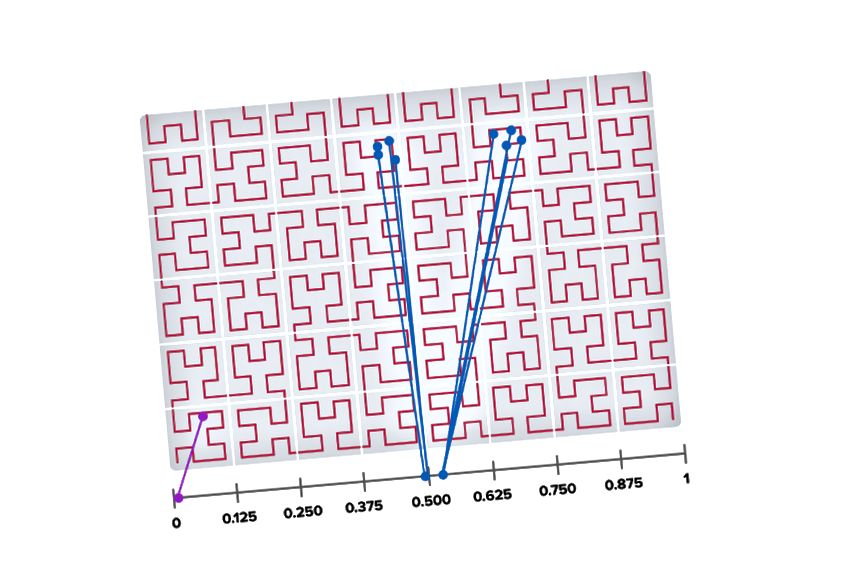
Обратите внимание на темную полосу по всей передней диагонали. Это показывает, что для всех значений d значения, численно близкие к d расположены с координатами (x, y) в непосредственной близости.
Более высокие размеры
Характеристики кривых Гильберта могут быть распространены более чем на два измерения. 1D-линия может быть обернута в столько измерений, сколько вы можете себе представить. Слева показана визуализация кривой в 3D-контейнере. В этой форме точки на линии, численно близкие друг к другу, близки и в трехмерном пространстве. Легко понять, как это можно распространить на более высокие измерения. |
Практическое использование
Кривые Гильберта не просто круто выглядят, это очень полезные конструкции. Функции Гильберта могут помочь в построении индексов для пространственных баз данных; при поиске записи в близком географическом местоположении они могут помочь определить приоритет для изучения. Помимо работы с базой данных, они иногда используются в процессе обработки изображений. При преобразовании изображения в шкалу серого путем сглаживания черных и белых пикселей переносимые значения пороговой обработки могут быть перенесены вперед, и с помощью кривой Гильберта излишки могут быть распределены по схеме, менее очевидной для глаза. В более высоких размерностях их можно использовать для реализации планирования задач в вычислительных приложениях с параллельной обработкой. Преобразование многомерного распределения задач в одномерное пространство и назначение связанных задач местоположениям с более высоким уровнем близости. |
Текущие исследования
Помните, я упоминал ранее, что, хотя и в порядке, функции обратного поиска кривых Гильберта не идеальны? (Места с похожими значениями d также имеют аналогичные (x,y) значений, но обратное не всегда верно?)
Эта функция была бы невероятно полезна, например, для обеспечения эффективного доступа к данным. Давайте представим, что у вас есть некоторые данные, хранящиеся в цифровом холодном хранилище (местоположение с очень большим временем доступа), и вы хотите эффективно индексировать и получить к ним доступ для географического поиска. Как мы знаем, преобразование координаты (x,y) в значение d может не гарантировать, что аналогичные значения d расположены в непосредственной близости. Большую часть времени да, но иногда нет.
Большую часть времени да, но иногда нет.
Чтобы противодействовать этому, а не просто индексировать данные по одной кривой Гильберта, данные переводятся в набор кривых Гильберта (обычно это сочетание поворотов и горизонтальных/вертикальных перемещений одной и той же кривой). Таким образом, путем объединения результатов сглаживаются любые неблагоприятные края от ступенчатых изменений вокруг границ 2 n .
XKCD
Наконец, ни одна статья о кривых Гильберта не может быть написана без ссылки на Карту Интернета Рэндалла
Полный список всех статей можно найти здесь. Нажмите здесь, чтобы получать уведомления о новых статьях по электронной почте.
Кривые Гильберта в App Store
Описание
Потрясающий трактат о кривой Гильберта и многих новых обобщениях. Для старшеклассников, колледжей и людей, интересующихся математикой, с более чем 130 динамическими иллюстрациями/анимациями.
Кривые Гильберта — это уникальное приложение в форме книги, которое показывает, объясняет и позволяет вам исследовать и играть с одной из самых известных и элегантных математических конструкций — кривой Гильберта, заполняющей пространство. Он показывает, как сопоставить точки сегмента прямой с каждой точкой внутри квадрата в виде непрерывной кривой. Вы можете сделать анимированный бесконечный зум в его построении или изучить карту в интерактивном режиме с разными уровнями точности, чтобы понять, как она работает как непрерывная кривая.
Но это только первая дюжина страниц. Затем в этом 160-страничном приложении/книге исследуются и иллюстрируются способы обобщения построения кривой Гильберта в удивительный набор заполняющих пространство кривых, путей, узоров и плиток, начиная от фрактальных кривых вертушки и заканчивая полукривыми домино. с почти везде линейными границами до квадратов с нечеткой вершиной. Попутно он объясняет или доказывает пройденное математическое путешествие.
Он представляет собой анимированную мета-Гильбертову конструкцию, которая показывает, как границы бесконечной последовательности заполняющих пространство плиток кривых с фрактальными границами могут сходиться к набору кривых Гильберта. Здесь есть даже невиданные ранее конструкции в виде полудомино, некоторые из узоров которых можно легко спутать с коврами, корзинами или глиняной посудой коренных американцев или других коренных народов. Одна только иллюстрация показывает более 77 000 возможных кривых, заполняющих пространство, полудомино, каждая из которых состоит из миллионов строк, основанных на перечислении всех возможных самоотрицательных мотивов «усиков». Большинство этих красивых, привлекающих внимание узоров являются математическими открытиями, представленными здесь впервые.
Разработанное для старшеклассников и студентов колледжей, профессиональных математиков и всех интересующихся математикой людей, интересующихся двухмерными шаблонами проектирования и заполняющими пространство кривыми и/или фракталами, приложение представляет вам более 130 иллюстраций в виде 160-страничный электронный документ под названием «Снаружи внутри и изнутри». Дуглас МакКенна, иллюстратор, автор, исследователь и программист, отмеченный наградами разработчик программного обеспечения, художник-математик, пионер фракталов и исследователь заполняющих пространство кривых, чья карьера началась с рисования иллюстраций заполняющих пространство кривых для отца фракталов Бенуа Мандельброта. .
Дуглас МакКенна, иллюстратор, автор, исследователь и программист, отмеченный наградами разработчик программного обеспечения, художник-математик, пионер фракталов и исследователь заполняющих пространство кривых, чья карьера началась с рисования иллюстраций заполняющих пространство кривых для отца фракталов Бенуа Мандельброта. .
Но это приложение не использует (и не может) использовать файлы PDF или другие векторные файлы для иллюстраций, не зависящих от разрешения. Вместо этого он внутренне самостоятельно набирает текст и математику во время запуска приложения в соответствии с высочайшими стандартами (качество TeX), в то же время предоставляя читателю независимо масштабируемые изображения, встроенные в текст. Большинство этих изображений параметризуются с помощью различных элементов управления или анимированы, чтобы вы могли взаимодействовать с визуальными конструкциями и лучше понимать их. Многие иллюстрации с десятками миллионов связанных линий могут быть построены на лету и сильно увеличены независимо от текста, чтобы вы могли исследовать и понимать мириады мельчайших деталей и структуры.
Представляя собой десятилетний опыт написания, исследований, набора текста и другой разработки программного обеспечения, это приложение представляет собой окончательный визуальный трактат по теме, которая однозначно подходит для точного рисования только с помощью компьютера.
Версия 1.2
Исправлено еще несколько мелких ошибок в нескольких иллюстрациях полудомино, которые возникали при отображении сеток.
Рейтинги и обзоры
6 оценок
Сногсшибательно!
Замечательное приложение Дуга Маккенны «Кривые Гильберта» — это доступное и увлекательное введение в мир кривых, заполняющих пространство.
Он прост в использовании и наполнен великолепными, интерактивными, процедурно сгенерированными изображениями. Настоятельно рекомендуется!
Новаторский. Абсолютно единственный в своем роде.
Единственное сообщение в своем роде. Без равных.
Впечатляющий
Необыкновенное исследование и интересное техническое достижение.
Разработчик, компания Mathemaesthetics, Inc., указала, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Данные не собираются
Разработчик не собирает никаких данных из этого приложения.
Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста.


 )
)