Критерии манна уитни онлайн: Расчет критерия Манна-Уитни

Классификации психологических задач и методов их решения — МАГИСТРАТУРА

Е.В.Сидоренко и О.Ю.Ермолаев предложили следующую классификацию задач и методов их решения

Задачи	Условия	Методы
1. Выявление различий в уровне исследуемого признака	a)    Две выборки испытуемых	Q критерий Розенбаума  U критерий Манна-Уитни φ — критерий (угловое преобразование Фишера)
	b)   Три и больше выборок испытуемых	S критерий Джонкира H критерий Крускала-Уоллиса
Задачи	Условия	Методы
2.  Оценка сдвига значений исследуемого признака	a)    Два замера на одной и той же выборке испытуемых	Критерий Макнамары T критерий Вилкоксона G критерий знаков φ критерий (угловое преобразование Фишера) t –критерий Стьюдента
	b)   Три и более замеров на одной и той же выборке испытуемых	χ2r  критерий Фридмана L критерий тенденций Пейджа t –критерий Стьюдента
3. Выявление различий в распределении признака	a)        При сопоставлении эмпирического распределения с теоретическим	χ2 критерий Пирсона λ критерий Колмогорова — Смирнова t –критерий Стьюдента
	b)    При сопоставлении двух эмпирических распределений	χ2 критерий Пирсона λ критерий Колмогорова — Смирнова φ критерий (угловое преобразование Фишера)
4.   Выявление степени согласованности изменений	a)    Двух признаков	φ коэффициент корреляции Пирсона η корреляционное отношение Пирсона τ коэффициент корреляции Кендела ρ коэффициент ранговой корреляции Спирмена

Классификация сдвигов и критериев оценки их статистической достоверности

Виды сдвигов	Объект сопоставлений	Условия		Критерии оценки достоверности сдвига
		Количество замеров	Количество групп
1. Временные, ситуационные, умозрительные, измерительные	Одни и те же показатели, измеренные у одних и тех же испытуемых в разное время, в разных ситуациях в разных представляемых условиях или разными способами	2	1	G — критерий знаков; Т — критерий Вилкоксона
		З и более	1	L — критерий тенденций Пейджа; χ2r — критерий Фридмана
2. Сдвига под влиянием эксперименталь-ных воздействий	Одни и те же показатели, измеренные у одних и тех же испытуемых до и после воздействия: а) при отсутствии контрольной группы	2	1	G — критерий знаков; Т — критерий Вилкоксона
		3 и более	1	L — критерий тенденций Пейджа; χ2r— критерий Фридмана
	6) при наличии контрольной группы	2	2	Вариант 1 — сопоставление значений «до» и «после» отдельно по экспериментальной и контрольной группам: G — критерий знаков; Т — критерий Вилкоксона Вариант 2 — сопоставление сдвигов в двух группах: Q — критерий; U — критерий Манна-Уитни; φ* — критерий Фишера
		З и более	2	Сопоставление значений отдельно по экспериментальной и контрольной группам: L, — критерий тенденций Пейджа; χ2, — критерий Фридмана
3. Структурные сдвиги	Разные показатели одних и тех же испытуемых	2	1	G — критерий знаков; Т — критерий Вилкоксона
		З и более	1	L — критерий тенденций Пейджа; χ2r — критерий Фридмана

Q критерий Розенбаума

Позволяет оценить различие между двумя выборками по какому-либо признаку

Предназначен для работы с данным, полученным в ранговой, интервальной и шкале отношений

В каждой из выборок должно быть не менее 11 испытуемых

Объемы выборок примерно должны совпадать

U критерий Манна-Уитни Online расчет
Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо признака, количественно измеренного.  Он позволяет выявлять различия между малыми выборками, когда n1,n2≥3 или n1=2, n2≥5

В каждой выборке должно быть не менее 3 наблюдений: n1,n2 ≥ З; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.
В каждой выборке должно быть не более 60 наблюдений; n1, n2 ≤ 60.

H критерий Крускала-Уоллиса

Является обобщением U-критерия Манна-Уитни на случай k несвязанных выборок (k>2) и предназначен для оценки различий одновременно между тремя, четырьмя и т.д. выборками по уровню какого-либо признака.

S критерий Джонкира

Этот критерий предназначен для выявления тенденций изменения признака при переходе от выборки к выборке при сопоставлении трех и более выборок.

Объемы выборок должны совпадать

Нижний порог — не менее 3 выборок и не менее 2 наблюдений в каждой выборке. Верхний порог в существующих таблицах — не более 6 выборок и не более 10 наблюдений в каждой из них.

Критерий Макнамары:

Предназначен для работы с данными, полученными в  дихотомической шкале

Для зависимых выборок

Количество испытуемых при измерениях рекомендуется выбрать в количестве не менее 10-15 человек.

G критерий знаков Online расчет

Предназначен для работы с данными, полученными в шкале наименований или порядковой. 

Количество измерений [5; 300]

Для зависимых выборок

T критерий Вилкоксона Online расчет

Применяется для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых.
Минимальное количество испытуемых, прошедших измерения в двух условиях — 5 человек. Максимальное количество испытуемых — 50 человек

 χ²_r  Критерий Фридмана

Применяется для сопоставления показателей, измеренных в c условиях (c≥3) на одной и той же выборке из n испытуемых.

Нижний порог: не менее 2-х испытуемых (n≥2), каждый из которых прошел не менее 3-х замеров (с≥3).

L критерий тенденций Пейджа

Применяется для для сопоставления показателей, измеренных в трех и более условиях на одной и той же выборке испытуемых. Критерий позволяет выявить тенденции в изменении величин признака при переходе от условия к условию.
К сожалению, имеющиеся таблицы критических значений рассчитаны только на небольшую выборку (n ≤ 12) и ограниченное количество сопоставляемых замеров (с < 6)

t –критерий Стьюдента

Применяется для для оценки различий величин средний значений двух выборок, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных выборок, причем выборки могут быть не равны по величине.

Для применения t-критерия Стьюдента необходимо соблюдать следующие условия:
1. Измерение может быть проведено в шкале интервалов и отношений.
2. Сравниваемые выборки должны быть распределены по нормальному закону.

Анализ элементного состава отдельных видов Sedum (Rhodiola) spp. и Orthilia secunda | Тернинко

1. Yang M., Lee H. S., Hwang M. W., Jin M. Effects of Korean red ginseng (Panax Ginseng Meyer) on bisphenol A exposure and gynecologic complaints: single blind, randomized clinical trial of efficacy and safety. BMC Complement Altern Med. 2014;25(14):265. DOI: 10.1186/1472-6882-14-265.

2. Drozdoff L., Klein E., Kiechle M., Paepke D. Use of biologically based complementary medicine in breast and gynecological cancer patients during systemic therapy. BMC complementary and alternative medicine. 2018;18(1):1–7. DOI: 10.1186/s12906-018-2325-3.

3. Della Corte L., Noventa M., Ciebiera M., Magliarditi M., Sleiman Z., Karaman E., Catena U., Salvaggio C., Falzone G., Garzon S. Phytotherapy in endometriosis: an up-to-date review. J Complement Integr Med. 2020;17(3):1–12. DOI: 10.1515/jcim-2019-0084.

4. Cesar G. Fraga. Relevance, essentiality, and toxicity of trace elements in human health. Molecular Aspects of Medicine. 2005;26:235–244. DOI: 10.1016/j.mam.2005.07.013.

5. Ciosek Ż., Kot K., Kosik-Bogacka D., Łanocha-Arendarczyk N., Rotter I. The Effects of Calcium, Magnesium, Phosphorus, Fluoride, and Lead on Bone Tissue. Biomolecules. 2021;11(4):506. DOI: 10.3390/biom11040506.

6. Шугалей И. В., Гарабаджиу А. В., Илюшин М. А., Судариков А. М. Некоторые аспекты влияния алюминия и его соединений на живые организмы. Экологическая химия. 2012;21(3):168–172.

7. Yokel R. A. Aluminum reproductive toxicity: a summary and interpretation of scientific reports. Critical Reviewsin Toxicology. 2020;50(7):551–593. DOI: 10.1080/10408444.2020.1801575.

8. Румянцев А. Г., Захарова И. Н., Чернов В. М., Тарасова И. С., Заплатников А. Л., Коровина Н. А., Боровик Т. Э., Звонкова Н. Г., Мачнева Е. Б., Лазарева С. И., Васильева Т. М. Распространенность железодефицитных состояний и факторы, на нее влияющие. Медицинский совет. 2015;6:62–66. DOI: 10.21518/2079-701X-2015-6-62-66.

9. Keats E. C., Haider B. A., Tam E., Bhutta Z. A. Multiple‐micronutrient supplementation for women during pregnancy. Cochrane Database of Systematic Reviews. 2019;3. DOI: 10.1002/14651858.cd004905.pub6.

10. Абашин С. Ю. Железодефицит у женщин и возможности его коррекции. Онкогинекология. 2015;1:63–69.

11. Ендина А. В., Гладилин Г. П. Регуляция обмена железа у женщин репродуктивного возраста с доброкачественной патологией тела матки, осложненной кровотечением. Фундаментальные исследования. 2013;7(1):87–90.

12. Геворгян А. П., Сибирская Е. В. Первичная дисменорея с позиции сегодняшнего дня. Проблемы репродукции. 2018;24(6):32–38. DOI: 10.17116/repro20182406132.

13. Назаренко Е. Г. Магний и женская репродуктивная система. Медицинский совет. 2019;7:119–125. DOI: 10.21518/2079-701X-2019-7-119-125.

14. Ахмеджанова З. И., Жиемуратова Г. К., Данилова Е. А., Каримов Д. А. Макро- и микроэлементы в жизнедеятельности организма и их взаимосвязь с иммунной системой (обзор литературы). Журнал теоретической и клинической медицины. 2020;1:16–21.

15. Громова О. А., Торшин И. Ю., Хаджидис А. К. Анализ молекулярных механизмов воздействия железа (II), меди, марганца в патогенезе железодефицитной анемии. Клиническая фармакология и фармакоэкономика. 2010;1:1–9.

16. Prasad A. S. Zinc in Human Health: Effect of Zinc on Immune Cells. Molecular Medicine. 2008;14(5-6):353–357. DOI: 10.2119/2008-00033.

17. Олина А. А., Садыкова Г. К. Значение дефицита цинка в формировании нарушений репродуктивного здоровья (обзор литературы). Пермский медицинский журнал. 2015;32(5):138–143. DOI: 10.17816/pmj325138-143.

18. Ayana G., Moges T., Samuel A. Dietary zinc intake and its determinants among Ethiopian children 6–35 months of age. BMC Nutrition. 2018;4(30):1–6. DOI: 10.1186/s40795-018-0237-8.

19. Государственная фармакопея Российской Федерации XIV издание: официальный текст. М.: Федеральная электронная медицинская библиотека; 2018. Доступно по: http://www.femb.ru/femb/pharmacopea.php. Ссылка активна на 30.03.2021.

20. Коденцова В. М. Витамины и минералы как фактор предупреждения дефектов развития плода и осложнений беременности. Медицинский совет. 2016;9:106–114. DOI: 10.21518/2079-701X-2016-9-106-114.

21. Куркин В. А. Родиола розовая (золотой корень): стандартизация и создание лекарственных препаратов: монография. Самара: ООО «Офорт»: ГБОУ ВПО СамГМУ Минздрава России; 2015. 240 с.

Онлайн-калькулятор: критерий Манна-Уитни

  Professional  Статистика

или критерий Уилкоксона-Манна-Уитни).

Как было указано в t-тесте для двух выборок, вы можете применить t-критерий , если выполняются следующие предположения:

• Две выборки независимо и случайным образом взяты из исходной совокупности(й).
• Что шкала измерения для обоих образцов имеет свойства шкалы равных интервалов.
• Можно разумно предположить, что исходная совокупность(я) имеет нормальное распределение.

Однако иногда ваши данные не соответствуют второму и/или третьему требованию. Например, нет ничего, что указывало бы на нормальное распределение или на неодинаковую шкалу интервалов, т. е. расстояние между соседними значениями нельзя считать постоянным. Но вы все еще хотите выяснить, является ли разница между двумя выборками существенной. В таких случаях можно использовать

U-критерий Манна-Уитни , непараметрическая альтернатива t-тесту.

В статистике U-критерий Манна-Уитни (также называемый критерием Манна-Уитни-Уилкоксона (MWW), критерием суммы рангов Уилкоксона или критерием Уилкоксона-Манна-Уитни (WMW)) является непараметрическим критерием нулевого гипотеза о равновероятности того, что случайно выбранное значение из одной выборки будет меньше или больше, чем случайно выбранное значение из второй выборки ¹ , или . Однако он также используется в качестве замены t-критерия независимых групп с нулевой гипотезой о том, что медианы двух популяций равны .

Кстати, на самом деле есть два теста — U-критерий Манна-Уитни и критерий суммы рангов Уилкоксона. Они были разработаны независимо и используют разные меры, но статистически эквивалентны.

Предположения теста Манна-Уитни:

• Две выборки взяты случайным образом и независимо друг от друга;
• Что зависимая переменная по своей сути непрерывна — способна в принципе, если не на практике, производить измерения, выполненные с точностью до n-го знака после запятой;
• Меры в двух выборках обладают свойствами по крайней мере порядковой шкалы измерения , так что имеет смысл говорить о «больше чем», «меньше чем» и «равно». ²

Как видите, этот непараметрический тест не предполагает (и не требует) выборок из нормально распределенных совокупностей. Такие тесты также называются тестами без распространения .

Предостережение

Уже некоторое время известно, что критерий Уилкоксона-Манна-Уитни равен 9На 0011 отрицательно влияет неоднородность дисперсии, когда размеры выборки не равны .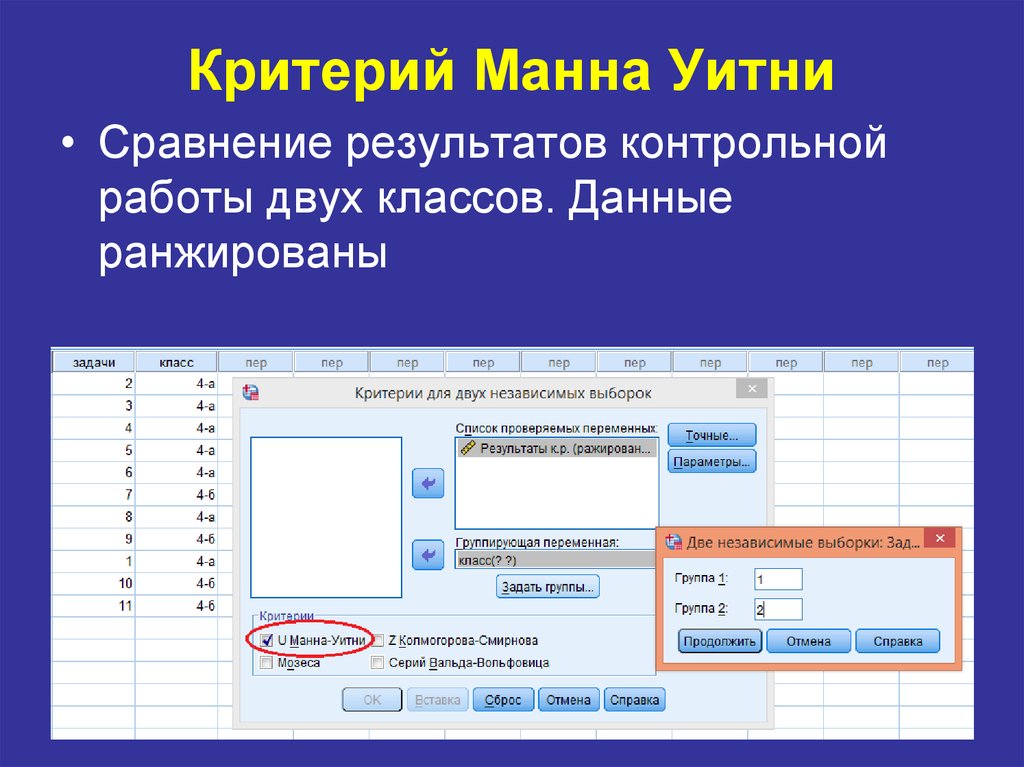 Однако даже при равных размерах выборок очень небольшие различия между дисперсиями генеральной совокупности приводят к тому, что критерий Уилкоксона-Манна-Уитни для большой выборки становится слишком либеральным , то есть фактическая частота ошибок типа I для Критерий Манна-Уитни увеличивался по мере увеличения размера выборки. ³ .

Следовательно, вы должны помнить, что этот тест верен, только если два распределения совокупности одинаковы (включая однородность дисперсии), за исключением смещения местоположения .

Метод

Метод заменяет необработанные значения их соответствующими рангами. При этом некоторых результатов можно добиться с помощью простой математики. Например, общая сумма рангов уже известна из общего размера и равна . Следовательно, средний ранг равен .

Общая идея состоит в том, что если нулевая гипотеза верна и выборки существенно не различаются, то ранги в некоторой степени сбалансированы между A и B, и средний ранг для каждой выборки должен приближаться к общему среднему рангу, а суммы рангов должны приблизительно и соответственно.

Расчет

Чтобы выполнить тест, сначала вам нужно рассчитать показатель, известный как U, для каждого образца.

Вы начинаете с объединения всех значений из обеих выборок в один набор, сортировки их по значению и присвоения ранга каждому значению (в случае ничьей каждому значению присваивается средний ранг). Ранги идут от 1 до N, где N — сумма размеров и . Затем вы вычисляете сумму рангов для значений каждой выборки и .

Теперь вы можете рассчитать U как

Для небольших размеров выборки вы можете использовать табличные значения. Вы берете минимум двух Us, а затем сравниваете его с критическим значением, соответствующим размерам выборки и выбранному уровню значимости. В учебниках по статистике критические значения обычно приводятся в таблицах для размеров выборки до 20.

Для больших размеров выборки можно использовать z-критерий. Было показано, что U примерно нормально распределено, если оба размера выборки равны или больше 5 (в некоторых источниках говорится, что если ⁴ ).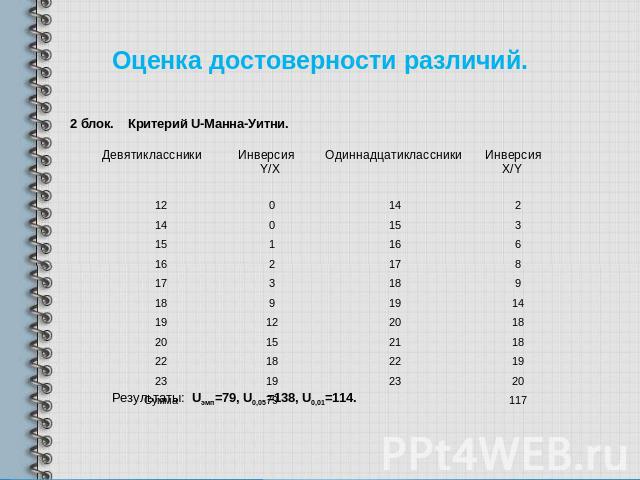

,
где

В случае ничьей формула для стандартного отклонения принимает вид

где g количество групп связей, tj количество связанных рангов в группе j .

Приведенный ниже калькулятор использует z-критерий. Конечно, существует ограничение на размер выборки (оба размера выборки должны быть равны или больше 5), но это, вероятно, не является большим ограничением для реальных случаев.

U-критерий Манна-Уитни

26 21 22 26 1922 26 25 21 23 23 23 18 22 22 22

Образец A

18 21 21 20 20 29 20 20 20 21 21 25 17 18 19

Образец B

Покажите ранги Таблицы

ПРОТИВАЦИЯ

цифры после десятичной точка: 2

Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.

U для образца A

U для образца B

U среднее

U стандартное отклонение

 

Z-показатель (абсолютное значение)

 

Уровень достоверности ненаправленной гипотезы

 

Уровень достоверности направленной гипотезы

 

---

U-критерий Манна-Уитни ↩

1. Подраздел 11а. Тест Манна-Уитни ↩

2. Глупые или бессмысленные поступки, которые делают люди при анализе данных: 2. Использование теста Уилкоксона-Манна-Уитни для устранения неоднородности дисперсии ↩

3. Статистика: 2.3 U-тест Манна-Уитни ↩

URL-адрес скопирован в буфер обмена

Похожие калькуляторы

• • Стьюдентный критерий для двух выборок
• • Стьюдентный критерий для парных выборок
• • Статистика PlanetCalc
• • P-значение
• Раздел статистики
• Статистика Fermat0 32 калькулятора )

  #Mann-Whitney #statistics Mann-Whitney непараметрическая значимость нулевой гипотезы Статистика U Test

  PlanetCalc, Манн-Уитни Тест

 TIMUR  2020-12-14 20:58:11

Манн-Уитни Тест U в Статистике SPSS | Установка, процедура и интерпретация

Введение

U-критерий Манна-Уитни используется для сравнения различий между двумя независимыми группами, когда зависимая переменная либо порядковая, либо непрерывная, но не имеет нормального распределения. Например, вы можете использовать U-тест Манна-Уитни, чтобы понять, различаются ли отношения к дискриминации в оплате труда, где отношения измеряются по порядковой шкале, в зависимости от пола (т. е. вашей зависимой переменной будет «отношение к дискриминации в оплате труда», а вашей независимой переменная будет «пол», которая имеет две группы: «мужской» и «женский»). В качестве альтернативы вы можете использовать U-критерий Манна-Уитни, чтобы понять, различаются ли зарплаты, измеренные по непрерывной шкале, в зависимости от уровня образования (т. е. вашей зависимой переменной будет «зарплата», а вашей независимой переменной будет «образовательный уровень», что имеет две группы: «средняя школа» и «университет»). U-критерий Манна-Уитни часто считают непараметрической альтернативой независимому t-критерию, хотя это не всегда так.

В отличие от t-теста для независимых выборок, U-критерий Манна-Уитни позволяет вам делать разные выводы о ваших данных в зависимости от ваших предположений о распределении ваших данных. Эти выводы могут варьироваться от простого определения того, различаются ли две популяции, до определения различий в медианах между группами. Эти разные выводы зависят от формы распределения ваших данных, о чем мы расскажем позже.

В нашем расширенном руководстве по U-тесту Манна-Уитни мы проведем вас через все шаги, необходимые для понимания того, когда и как использовать U-критерий Манна-Уитни, покажем вам необходимые процедуры в SPSS Statistics, а также как интерпретировать результаты и сообщать о них. . Вы можете получить доступ к этому расширенному руководству по U-тестированию Манна-Уитни, подписавшись на Laerd Statistics. В этом кратком руководстве мы покажем вам основы U-критерия Манна-Уитни с использованием одной из процедур SPSS Statistics, когда нарушается критическое предположение этого теста. Прежде чем мы покажем вам, как это сделать, мы объясним различные предположения, которым должны соответствовать ваши данные, чтобы U-критерий Манна-Уитни дал вам достоверный результат.

Далее мы обсудим эти предположения.

Статистика SPSS

Предположения

Когда вы выбираете анализ данных с помощью U-критерия Манна-Уитни, часть процесса включает в себя проверку того, что данные, которые вы хотите проанализировать, действительно могут быть проанализированы с использованием U-критерия Манна-Уитни. Вы должны сделать это, потому что использовать U-критерий Манна-Уитни уместно только в том случае, если ваши данные «проходят» четыре предположения, которые необходимы для того, чтобы U-критерий Манна-Уитни дал вам достоверный результат. На практике проверка этих четырех допущений просто увеличивает время анализа, требуя от вас нажатия еще нескольких кнопок в SPSS Statistics при выполнении анализа, а также еще немного обдумывания ваших данных, но это не сложная задача.

Прежде чем мы познакомим вас с этими четырьмя допущениями, не удивляйтесь, если при анализе ваших собственных данных с помощью SPSS Statistics одно или несколько из этих допущений будут нарушены (т. е. не выполнены). Это не редкость при работе с реальными данными, а не с примерами из учебников, которые часто только показывают, как выполнять U-критерий Манна-Уитни, когда все идет хорошо! Однако не волнуйтесь. Даже если ваши данные не соответствуют определенным предположениям, часто есть решение, позволяющее обойти это. Во-первых, давайте взглянем на эти четыре предположения:

• Предположение №1: Ваша зависимая переменная должна измеряться на порядковом или непрерывном уровне . Примеры порядковых переменных включают пункты Лайкерта (например, 7-балльная шкала от «полностью согласен» до «полностью не согласен»), среди других способов ранжирования категорий (например, 5-балльная шкала, объясняющая, насколько покупателю понравилось продукт в диапазоне от «Не очень» до «Да, много»). Примеры непрерывные переменные включают время пересмотра (измеряется в часах), интеллект (измеряется с помощью показателя IQ), успеваемость на экзамене (измеряется от 0 до 100), вес (измеряется в кг) и так далее. Вы можете узнать больше о порядковых и непрерывных переменных в нашей статье: Типы переменных.
• Предположение №2: Ваша независимая переменная должна состоять из двух категориальных , независимых групп . Примеры независимых переменных, которые соответствуют этому критерию, включают пол (2 группы: мужчина или женщина), статус занятости (2 группы: работающий или безработный), курение (2 группы: да или нет) и так далее.
• Предположение №3: Вы должны иметь независимость наблюдений , что означает отсутствие связи между наблюдениями в каждой группе или между самими группами. Например, в каждой группе должны быть разные участники, при этом ни один участник не может входить более чем в одну группу. Это скорее проблема дизайна исследования, чем то, что вы можете проверить, но это важное предположение U-критерия Манна-Уитни. Если ваше исследование не соответствует этому предположению, вам нужно будет использовать другой статистический тест вместо U-критерия Манна-Уитни (например, критерий знакового ранга Уилкоксона).
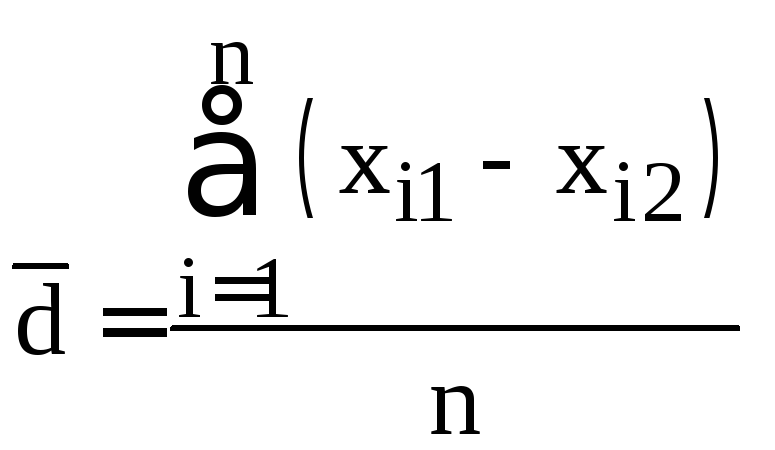  Если вы не уверены, соответствует ли ваше исследование этому допущению, вы можете воспользоваться нашим селектором статистических тестов, который является частью нашего расширенного контента.
• Предположение № 4: U-критерий Манна-Уитни можно использовать, когда ваши две переменные не распределены нормально . Однако, чтобы знать, как интерпретировать результаты U-критерия Манна-Уитни, вы должны определить, соответствуют ли ваши два распределения (т. е. распределение оценок для обеих групп независимой переменной, например, «мужчины» и «женщины» для независимой переменной «пол») имеют ту же форму . Чтобы понять, что это значит, взгляните на диаграмму ниже:
  

  Copyright 2013. Laerd Statistics

  
  На двух приведенных выше диаграммах распределение баллов для «мужчин» и «женщин» имеет одинаковую форму . На диаграмме слева вы не можете видеть распределение баллов для «мужчин» (показано синим цветом на диаграмме справа), потому что два распределения идентичны (т.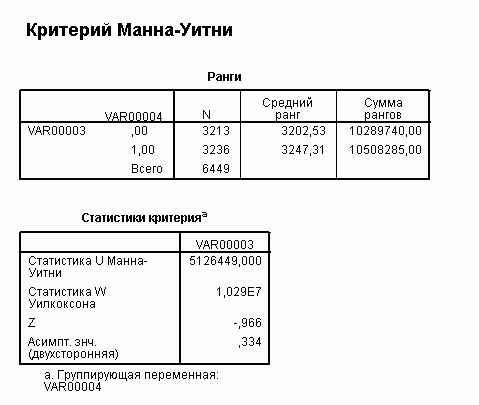 е. оба распределения идентичны, поэтому они «на друг над другом» на диаграмме, с распределением самцов синего цвета под распределением самок красного цвета). Однако на диаграмме справа, несмотря на то, что оба распределения имеют одинаковая форма , они имеют другое расположение (т. е. распределение одной из групп независимой переменной имеет более высокие или более низкие значения по сравнению со вторым распределением – в нашем примере самки имеют «более высокие» значения, чем самцы, общий).

  Когда вы анализируете свои собственные данные, крайне маловероятно, что ваши два распределения будут идентичными, но они могут иметь одинаковую (или «похожую») форму. Если они имеют одинаковую форму, вы можете использовать SPSS Statistics для проведения U-критерия Манна-Уитни для сравнения медианы вашей зависимой переменной (например, показателя вовлеченности) для двух групп (например, мужчин и женщин) независимой переменной (например, пола), которая вас интересует. Однако, если ваши два распределения имеют различную форму , вы можете использовать U-критерий Манна-Уитни только для сравнения средних рангов .

  Таким образом, при выполнении U-критерия Манна-Уитни необходимо также использовать SPSS Statistics, чтобы определить, имеют ли два ваших распределения одинаковую форму или другой формы . Для этого потребуется выполнить еще несколько процедур в SPSS Statistics, но это простой пошаговый процесс, который мы покажем вам в нашем расширенном руководстве по U-тесту Манна-Уитни. В этом кратком руководстве мы покажем вам, как выполнить U-критерий Манна-Уитни, предполагая, что ваши два распределения не имеют одинаковой формы, так что вы можете сравнивать только средние ранги, а не медианы.

Вы можете проверить предположение №4 с помощью SPSS Statistics. Прежде чем сделать это, вы должны убедиться, что ваши данные соответствуют предположениям № 1, № 2 и № 3, хотя для этого вам не требуется SPSS Statistics. Просто помните, что если вы не проверите предположение № 4, вы не будете знать, правильно ли вы сравниваете средние ранги или медианы, а результаты, полученные при выполнении U-критерия Манна-Уитни, могут быть недействительными. Вот почему мы посвящаем ряд разделов нашего расширенного руководства по U-тестированию Манна-Уитни, чтобы помочь вам сделать это правильно. Вы можете узнать больше о допущении № 4 и о том, что вам нужно будет интерпретировать, в разделе 9.0011 Предположения нашего расширенного руководства по U-тестированию Манна-Уитни, доступ к которому можно получить, подписавшись на Laerd Statistics.

В разделе «Процедура тестирования в SPSS Statistics» этого «краткого руководства» мы иллюстрируем процедуру SPSS Statistics для выполнения U-критерия Манна-Уитни, предполагая, что ваши два распределения имеют разную форму и вам нужно интерпретировать средние ранги, а не медианы. . Во-первых, мы приводим пример, который мы используем для объяснения процедуры U-теста Манна-Уитни в SPSS Statistics.

SPSS Statistics

Пример

Концентрация холестерина (разновидность жира) в крови связана с риском развития сердечно-сосудистых заболеваний, так что более высокие концентрации холестерина указывают на более высокий уровень риска, а более низкие концентрации указывают на более низкий уровень уровень риска. Если вы снизите концентрацию холестерина в крови, риск развития сердечно-сосудистых заболеваний может быть снижен. Избыточный вес и/или отсутствие физической активности повышают концентрацию холестерина в крови. И физические упражнения, и потеря веса могут снизить концентрацию холестерина. Однако неизвестно, что лучше всего подходит для снижения концентрации холестерина: физические упражнения или снижение веса. Поэтому исследователь решил выяснить, что более эффективно для снижения уровня холестерина: физические упражнения или меры по снижению веса. С этой целью исследователь набрал случайную выборку неактивных мужчин, которые были классифицированы как имеющие избыточный вес. Затем эта выборка была случайным образом разделена на две группы: группа 1 подвергалась диете с контролем калорийности (т. е. группа «диеты»), а группа 2 выполняла программу упражнений и тренировок (т. Чтобы определить, какая программа лечения была более эффективной, концентрации холестерина сравнивали между двумя группами в конце программ лечения.

SPSS Statistics

Настройка в SPSS Statistics

В SPSS Statistics мы ввели значения концентрации холестерина, нашей зависимой переменной, под именем переменной Cholesterol. Затем мы создали группирующую переменную с именем Group, которая представляла нашу независимую переменную. Поскольку у нашей независимой переменной было две группы — «диета» и «упражнения», мы присвоили группе диеты значение «1», а группе упражнений значение «2». Если вы не пометите две группы, SPSS Statistics не сможет различить их, и U-критерий Манна-Уитни не запустится.

Примечание. В SPSS Statistics есть две разные процедуры для выполнения U-критерия Манна-Уитни: процедура Непараметрические критерии > Независимые выборки и Устаревшие диалоговые окна > 2 независимых выборки .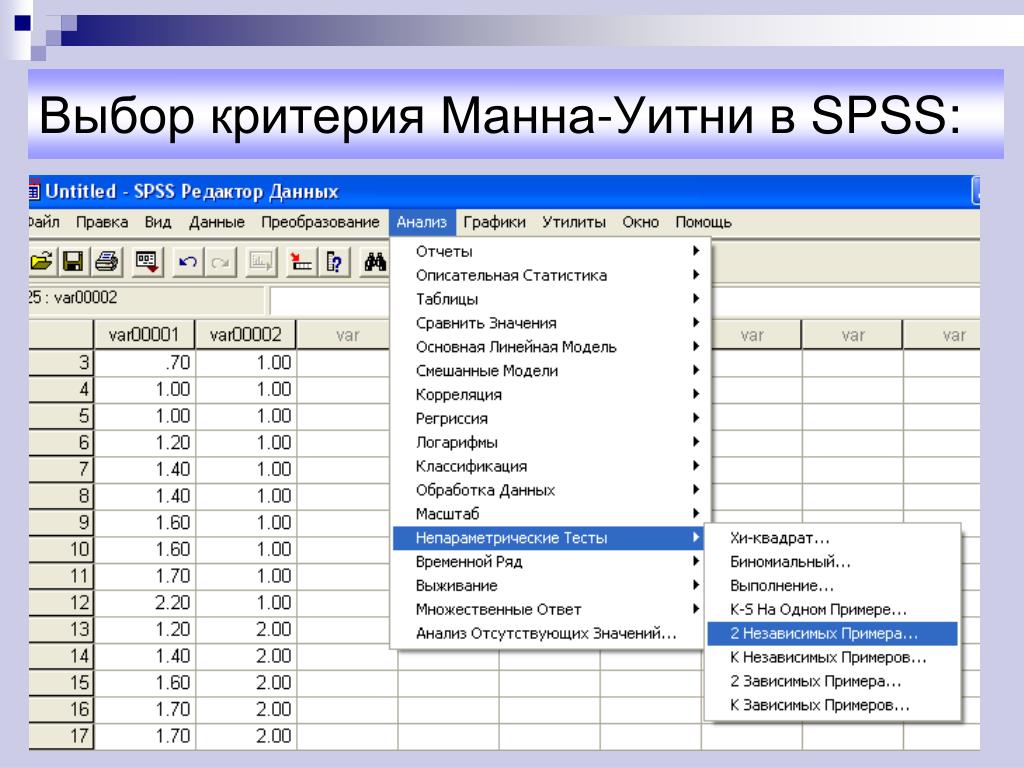 То, как мы объяснили настройку данных выше, относится к обеим процедурам , когда ваша зависимая переменная непрерывна , что мы и рассмотрим в следующем разделе «Процедура тестирования» в разделе «Статистика SPSS». Однако, если вы используете Непараметрические тесты > Независимые выборки вам необходимо внести изменения в настройку данных, если ваша зависимая переменная порядковая (т. е. в отличие от непрерывной ). Мы объясняем, как это сделать, в нашем расширенном руководстве по U-тестированию Манна-Уитни, доступ к которому вы можете получить, подписавшись на Laerd Statistics.

В нашем расширенном руководстве по U-тестированию Манна-Уитни мы покажем вам все шаги, необходимые для правильного ввода данных в SPSS Statistics для запуска U-теста Манна-Уитни как для Непараметрические критерии > Независимые выборки и Устаревшие диалоговые окна > 2 независимых выборки Процедуры, описанные в примечании выше.

SPSS Statistics

Процедура тестирования в SPSS Statistics

Если вы читали предположение № 4 ранее, вы должны знать, что процедура SPSS Statistics при анализе ваших данных с использованием U-критерия Манна-Уитни отличается в зависимости от формы двух распределения вашей независимой переменной. В нашем примере, где нашей зависимой переменной является концентрация холестерина, холестерин, мы имеем в виду два распределения независимой переменной, группы (т. группа упражнений). В приведенных ниже 10 шагах мы покажем вам, как анализировать ваши данные с помощью U-критерия Манна-Уитни в SPSS Statistics, когда эти два распределения имеют другая форма , и, следовательно, вы должны сравнивать средние ранги вашей зависимой переменной, а не медианы .

Чтобы использовать SPSS Statistics, чтобы определить, имеют ли ваши два распределения одинаковые или разные формы , или если вы хотите знать, как использовать SPSS Statistics для выполнения U-критерия Манна-Уитни, когда ваши два распределения имеют та же форма , так что вам нужно сравнить медианы , а не означает ранги , вам потребуется доступ к разделу Процедуры нашего расширенного руководства по тестированию Манна-Уитни U (примечание: вы можете сделать это, подписавшись на Laerd Statistics). Кроме того, приведенные ниже 10 шагов также показывают, как выполнить U-критерий Манна-Уитни с использованием процедуры Legacy Dialogs > 2 Independent Samples в SPSS Statistics. Как мы объясняли ранее, в SPSS Statistics есть две разные процедуры для выполнения U-критерия Манна-Уитни: Непараметрические критерии > Независимые выборки и Legacy Dialogs > 2 Independent Samples . Мы рекомендуем процедуру Непараметрические тесты > Независимые выборки , если ваши два распределения имеют одинаковую форму , потому что ее немного проще выполнить, но процедура Устаревшие диалоги > 2 независимых выборки подойдет, если ваши два распределения имеют разные формы . Мы покажем вам обе процедуры в нашем расширенном руководстве по U-тесту Манна-Уитни.

В конце 9 шагов ниже мы покажем вам, как интерпретировать результаты этого теста, используя средних рангов .

Примечание. Следующая процедура идентична для SPSS Statistics версий с 17 по 28 , а также для подписной версии SPSS Statistics , где версия 28 и подписная версия являются последними версиями статистики SPSS. Однако в версии 27 и подписки версии , SPSS Statistics представила новый вид своего интерфейса под названием « SPSS Light », заменив предыдущий вид для версий 26 и более ранних версий , который назывался « SPSS Standard ». Таким образом, если у вас есть SPSS Statistics версии 27 или 28 (или подписка версии SPSS Statistics), следующие изображения будут светло-серыми, а не синими. Тем не менее, процедура идентичен .

1. Щелкните A nalyze > N onparametric Tests > L egacy Dialogs > 2 I ndependent Samples. .. в верхнем меню, как показано ниже:

   Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

2. Вам будет представлено диалоговое окно Two-Independent-Samples Tests , как показано ниже:

   Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

3. Перенесите зависимую переменную Cholesterol в поле T est Variable List: box, а независимую переменную Group в поле
   G rouping Variable: с помощью кнопки или путем перетаскивания переменных в поле коробки.

   Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

   Примечание. Убедитесь, что флажок M ann-Whitney U установлен в области «Тип теста» и G rouping Переменная: прямоугольник выделен желтым цветом (как показано выше). Если он не выделен желтым цветом, просто щелкните курсором в поле G rouping Variable:, чтобы выделить его.

1. Нажмите на кнопку.