Гиперболические и обратные им функции MatLab
Арифметические операторы и функции
Операторы отношения и их функции
Логические операторы
Специальные символы
Системные переменные и константы
Функции поразрядной обработки
Функции обработки множеств
Функции времени и даты
Элементарные функции
Алгебраические и арифметические функции
Тригонометрические и обратные им функции
Гиперболические и обратные им функции
Функции округления и знака
Функции комплексного аргумента
Что нового мы узнали?
Наряду с тригонометрическими функциями в математических расчетах часто используются и гиперболические функции. Ниже приводится список таких функций, определенных в системе MATLAB. Функции вычисляются для каждого элемента массива. Входной массив допускает комплексные значения. Все углы в тригонометрических функциях измеряются в радианах.
acosh(X)
— возвращает гиперболический арккосинус для каждого элемента X.
»Y= acosh (0.7)
Y =
0 + 0.7954i
acoth(X) — возвращает гиперболический арккотангенс для каждого элемента X. Пример:
»Y = acoth (0.1)
Y=
0.1003 + 1.5708i
acsch(X) — возвращает гиперболический арккосеканс для каждого элемента X. Пример:
» Y = acsch(1)
Y =
0.8814
asech(X) — возвращает гиперболический арксеканс для каждого элемента X. Пример:
» Y = asech(4)
Y =
0
+ 1.
3181i
asinh(X) — возвращает гиперболический арксинус для каждого элемента X. Пример:
» Y = asinh (2.456)
Y =
1.6308
atanh(X)
— возвращает гиперболический арктангенс для каждого элемента X. Пример:
» Х=[0.84 0.16 1.39];
» atanh (X)
ans =
1.2212 0.1614 0.9065 + 1.5708i
cosh(X) — возвращает гиперболический косинус для каждого элемента X. Пример:
» Х=[1 23];
» Cosh(X)
ans =
1.
5431
3.7622 10.0677
coth(X)
— возвращает гиперболический котангенс для каждого элемента X. Пример:
» Y = coth(3.987)
Y =
1.0007
csch(x) — возвращает гиперболический косеканс для каждого элемента X. Пример:
» Х=[2 4.678 5:0.987 1 3];
» Y = csch(X)
Y =
0.2757
0.0186 0.0135
0.8656
0.8509 0.0998
sech(X) — возвращает гиперболический секанс для каждого элемента X. Пример:
» X=[pi/2 pi/4 pi/6 pi];
» sech(X)
ans =
0.
3985
0.7549 0.8770 0.0863
sinh(X) — возвращает гиперболический синус для каждого элемента X. Пример:
»
X=[pi/8 pi/7 pi/5 pi/10];
» sinh(X)
ans =
0.4029 0.4640 0.6705 0.3194
tanh(X)
— возвращает гиперболический тангенс для каждого элемента X. Пример:
» X=[pi/2 pi/4 pi/6 pi/10];
»tanh(X)
ans =
0.9172
0.6558 0.4805 0.3042
Следующий m-файл-сценарий строит графики ряда гиперболических функций:
syms x
subplot(2,2,l).
ezplot(sinh(x).[-4
4]).xlabel(«).grid on
subplot(2,2.2).ezplot(cosh(x).[-4 4]).xlabel(»).grid on
subp1ot(2.2,3).ezplot(tanh(x).[-4 4]).grid on
subplot(2.2.4).ezplot(sech(x).[-4 4]).grid on
Нетрудно заметить, что гиперболические функции в отличие от тригонометрических не являются периодическими. Выбранные для графического представления функции дают примеры характерных нелинейностей.
В другом файле использованы команды для построения графиков ряда обратных гиперболических функций:
syms x
subplot(2,2.1).ezplot(asinh(x).[-4 4]).xlabel(«).grid on
subplot(2.2.2),ezp1ot(acosh(x).[0 4]).
2x = 1$
ФУНКЦИИ ОТРИЦАТЕЛЬНЫХ АРГУМЕНТОВ
sh(-x) = -sh x
ch(-x) = ch x
th(-x) = -th x
csch(-x) = -csch x
sech(-x) = sech x
cth(-x) = -cth x
ФОРМУЛЫ СЛОЖЕНИЯ
sh (x ± y) = sh x ch y ± ch x sh y
ch (x ± y) = ch x ch y ± sh x sh y
th(x ± y) = (th x ± th y)/(1 ± th x.th y)
cth(x ± y) = (cth x cth y ± l)/(cth y ± cth x)
ФОРМУЛЫ ДВОЙНЫХ УГЛОВ
sh 2x = 2 sh x ch x
ch 2x = ch2x + sh2x = 2 ch2x — 1 = 1 + 2 sh2x
th 2x = (2th x)/(1 + th2x)
ФОРМУЛЫ ПОЛОВИННЫХ УГЛОВ
$\text{sh} \frac{x}{2} = \pm \sqrt{\frac{\text{ch} x — 1}{2}}$ [+ если x > 0, — если x
$\text{ch} \frac{x}{2} = \sqrt{\frac{\text{ch} x + 1}{2}}$
$\text{th} \frac{x}{2} = \pm \sqrt{\frac{\text{ch} x — 1}{\text{ch} x + 1}}$ [+ если x > 0, — если x
$= \frac{\text{sh} x}{\text{ch} x — 1} = \frac{\text{ch} x + 1}{\text{sh} x}$
ФОРМУЛЫ КРАТНОСТИ УГЛОВ
sh 3x = 3 sh x + 4 sh3 x
ch 3x = 4 ch3 x — 3 ch x
th 3x = (3 th x + th3 x)/(1 + 3 th2x)
sh 4x = 8 sh3 x ch x + 4 sh x ch x
ch 4x = 8 ch4 x — 8 ch2 x + 1
th 4x = (4 th x + 4 th3 x)/(1 + 6 th2 x + th4 x)
СТЕПЕНИ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
sh2x = ½ch 2x — ½
ch2 x = ½ch 2x + ½
sh3x = ¼sh 3x — ¾sh x
ch3 x = ¼ch 3x + ¾ch x
sh4x = 3/8 — ½ch 2x + 1/8ch 4x
ch4 x = 3/8 + ½ch 2x + 1/8ch 4x
СУММА, РАЗНИЦА И УМНОЖЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
sh x + sh y = 2 sh ½(x + y) ch ½(x — y)
ch x + ch y = 2 ch ½(x + y) ch ½(x — y)
ch x — ch y = 2 sh ½(x + y) sh ½(x — y)
sh x sh y = ½(ch (x + y) — ch (x — y))
ch x ch y = ½(ch (x + y) + ch (x — y))
sh x ch y = ½(sh (x + y) + sh (x — y))
ВЫРАЖЕНИЕ ГИПЕРБОЛТЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ДРУГИЕ
В следующем мы принимаем, что x > 0.
2}}$
ГРАФИКИ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
y = sh x
y = ch x
y = th x
y = cth x
y = sech x
y = csch x
ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Если x = sh y, тогда y = sh-1 a называется обратным гиперболическим синусом of x. Аналогично определяются и другие обратные гиперболические функции. Обратные гиперболические функции являются многозначными, но в случае обратных тригонометрических функций мы ограничимся основными значениями, при которых их можно рассматривать как однозначные.
Ниже приведен список основных значений [если не указано иное] обратных гиперболических функций, выраженных через логарифмические функции, которые принимаются в качестве вещественных.
2} + 1})$ $x \neq 0$
ОТНОШЕНИЯ МЕЖДУ ОБРАТНЫМИ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ
csch-1 x = sh-1 (1/x)
sech-1 x = ch-1 (1/x)
cth-1 x = th-1 (1/x)
sh-1(-x) = -sh-1x
th-1
cth-1 (-x) = -cth-1x
csch-1 (-x) = -csch-1x
ГРАФИКИ ОБРАТНЫХ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
y = sh-1x
y = ch-1x
y = th-1x
y = cth-1x
y = sech-1x
y = csch-1x
ОТНОШЕНИЯ МЕЖДУ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ и ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
| sin(ix) = i sh x | cos(ix) = ch x | tan(ix) = i th x |
| csc(ix) = -i csch x | sec(ix) = sech x | cot(ix) = -i cth x |
| sh(ix) = i sin x | ch(ix) = cos x | th(ix) = i tan x |
| csch(ix) = -i csc x | sech(ix) = sec x | cth(ix) = -i cot x |
ПЕРИОДИЧНОСТЬ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
In the following k is any integer.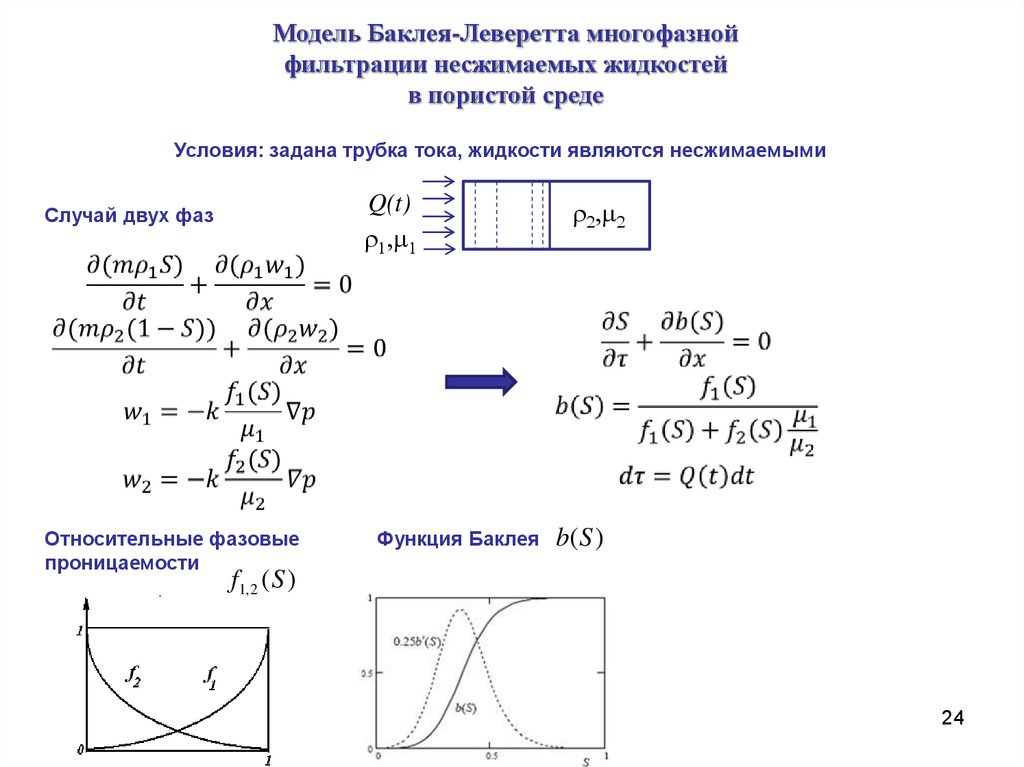
sh (x + 2kπi) = sh x csch (x + 2kπi) = csch x
ch (x + 2kπi) = ch x sech (x + 2kπi) = sech x
th (x + kπi) = th x cth (x + kπi) = cth x
ОТНОШЕНИЕ МЕЖДУ ОБРАТНЫМИ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ И ОБРАТНЫМИ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
| sin-1 (ix) = ish-1x | sh-1(ix) = i sin-1x |
| cos-1 x = ±i ch-1 x | ch-1x = ±i cos-1x |
| tan-1(ix) = i th-1x | th-1(ix) = i tan-1x |
| cot-1(ix) = -i cth-1x | cth-1 (ix) = -i cot-1x |
| sec-1 x = ±i sech-1x | sech-1 x = ±i sec-1x |
| csc-1(ix) = -i csch-1x | csch-1(ix) = -i csc-1x |
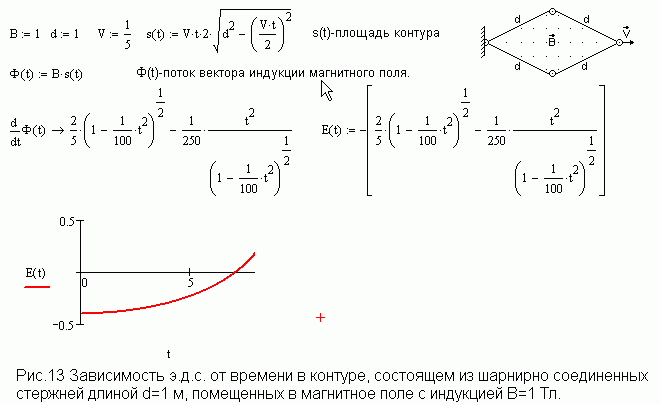
Определение 4.11.3 Другие гиперболические функции $ $ \ eqalign {\ tanh x & = {\ sinh x \ over \ cosh x} \ cr \ coth х & = {\ сп х \ над \ зп х} \ кр \sech x &= {1\over\cosh x}\cr \csch x &= {1\over\sinx x}\cr} $$ Область определения $\coth$ и $\csch$ равна $x\neq 0$, а область определения остальные гиперболические функции — это все действительные числа. Графики показаны на рисунке 4.11.1 $\квадрат$
| $\cosh$ | $\sin$ | $\tanh$ |
| $\sech$ | $\csch$ | $\coth$ |
Рисунок 4.11.1. Гиперболические функции.
Конечно, гиперболические функции не очень похожи на тригонометрические функции графически. Но у них есть аналоги свойства, начиная со следующего тождества.
Теорема 4.11.4. Для всех $x$ в $\R$ $\ds \cosh ^2 x -\sinh ^2 x = 1$.
92 t-1}=\pm\sinh t$. Так что для некоторых
подходящие $t$, $\cosh t$ и $\sinh t$ — координаты типичного
точка на гиперболе. На самом деле получается, что $t$ в два раза больше
площадь, показанная на первом графике
рисунок 4.11.2. Даже
это аналогично тригонометрии; $\cos t$ и $\sin t$ – это
координаты типичной точки на единичной окружности, а $t$ дважды
площадь, показанная на втором графике рисунка 4.11.2.
Рисунок 4.11.2. Геометрические определения sin, cos, sinh, ch: $t$ в два раза больше заштрихованного площади на каждом рисунке. 9{-x }\over 2} =\cosh x$. $\qed$
Поскольку $\cosh x > 0$, $\sinh x$ возрастает и, следовательно, инъективен, поэтому
У $\sinh x$ есть обратный $\arcsinh x$. Кроме того, $\sinh x > 0$, когда
$x>0$, поэтому $\cosh x$ инъективен на $[0,\infty)$ и имеет (частичный)
обратный, $\arccosh x$. Другие гиперболические функции имеют обратные
также, хотя $\arcsech x$ является лишь частично обратным.
Мы можем вычислить производные этих функций, поскольку у нас есть другие
обратные функции.
2}}$.
92+1})$.)
Пример 4.11.2 Вычислите следующие пределы:
а. $\ds \lim_{x\to \infty} \cosh x$
б. $\ds \lim_{x\to \infty} \sinh x$
в. $\ds \lim_{x\to \infty} \tanh x$
д. $\ds \lim_{x\to \infty } (\cosh x -\sinh x)$
(отвечать)
Пример 4.11.3 Покажите, что диапазон $\tanh x$ равен $(-1,1)$. Какие являются диапазонами $\coth$, $\sech$ и $\csch$? (Используйте тот факт, что они являются обратными функциями.) 92 х$. Вычислить производные остальных гиперболических функций.
Пример 4.11.8 Каковы области определения шести обратных гиперболических функции?
Пример 4.11.9 Нарисуйте графики всех шести обратных гиперболических функции.
Элементарные функции комплексной переменной. Элементарные функции комплексного переменного дробно-рациональные функции показательная функция показательная функция логарифмическая функция тригонометрические и гиперболические функции
, стр.
6
11 Основные функции комплексной переменной
Напомним определение комплексного показателя -. Затем
расширение серии Maclaurin. Радиус сходимости этого ряда равен +∞, а это означает, что комплексный показатель аналитичен на всей комплексной плоскости и
(exp z)» = exp z; exp 0 = 1. (2)
Первый равенство здесь следует, например, из теоремы о почленном дифференцировании для степенного ряда 9.0003
11.1 Trigonometric and hyperbolic functions
Sine complex variable called the function
Cosine of a complex variable there is a function
Hyperbolic sine of a complex variable defined like this:
Гиперболический косинус комплексной переменной есть функция
Отметим некоторые свойства вновь введенных функций.
A. Если x∈ ℝ, то cos x, sin x, ch x, sh x∈ ℝ.
Б. Между тригонометрическими и гиперболическими функциями существует следующая связь:
cos iz = ch z; sin из = ish z, ch iz = cos z; ш из = исин з.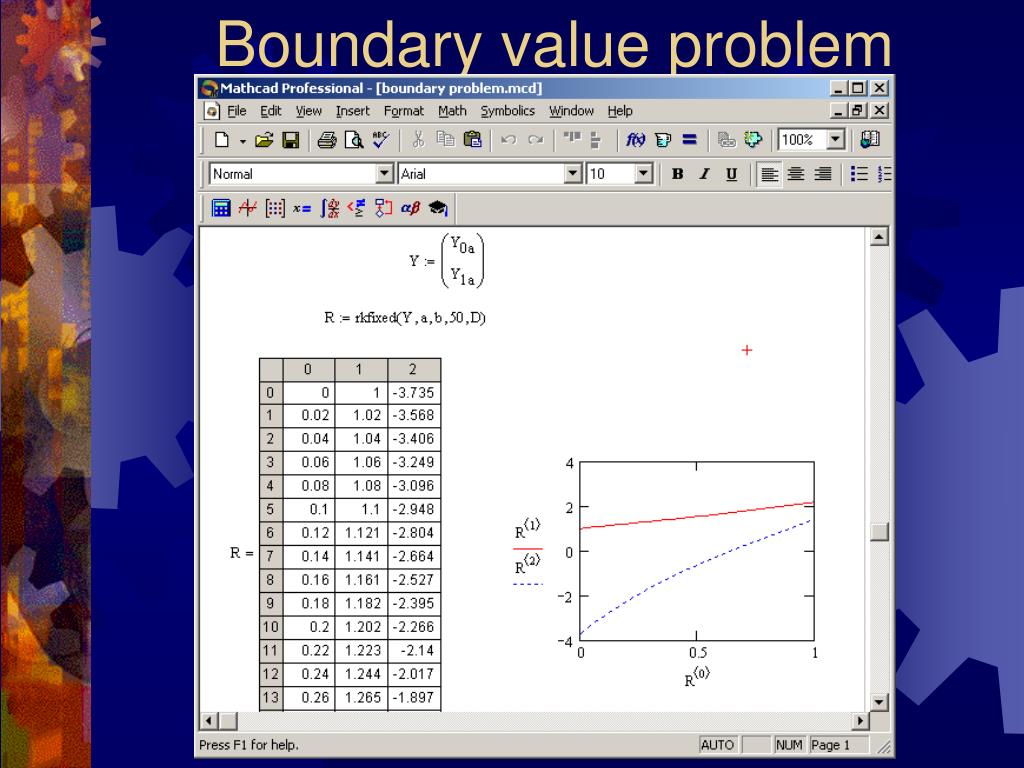
Б. Основные тригонометрические и гиперболические тождества :
cos 2 z + sin 2 z = 1; ч 2 з-ш 2 з = 1.
Доказательство основного гиперболического тождества.
Основное тригонометрическое тождество следует из основного гиперболического тождества при учете связи между тригонометрическими и гиперболическими функциями (см. свойство Б)
D Формулы сложения :
В частности,
D. Для вычисления производных тригонометрических и гиперболических функций следует применить теорему о почленном дифференцировании степенного ряда. Получаем:
(cos z)»=-sin z;(sin z)»=cos z; (ч з)»= ш з; (ш з)» = ч з.
E. Функции cos z, ch z четные, а функции sin z, sh z нечетные.
Г. (Частота) Функция e z является периодической с периодом 2π i. Функции cos z, sin z являются периодическими с периодом 2π, а функции ch z, sh z — с периодом 2πi. При этом
Применяя формулы суммы, получаем
Z .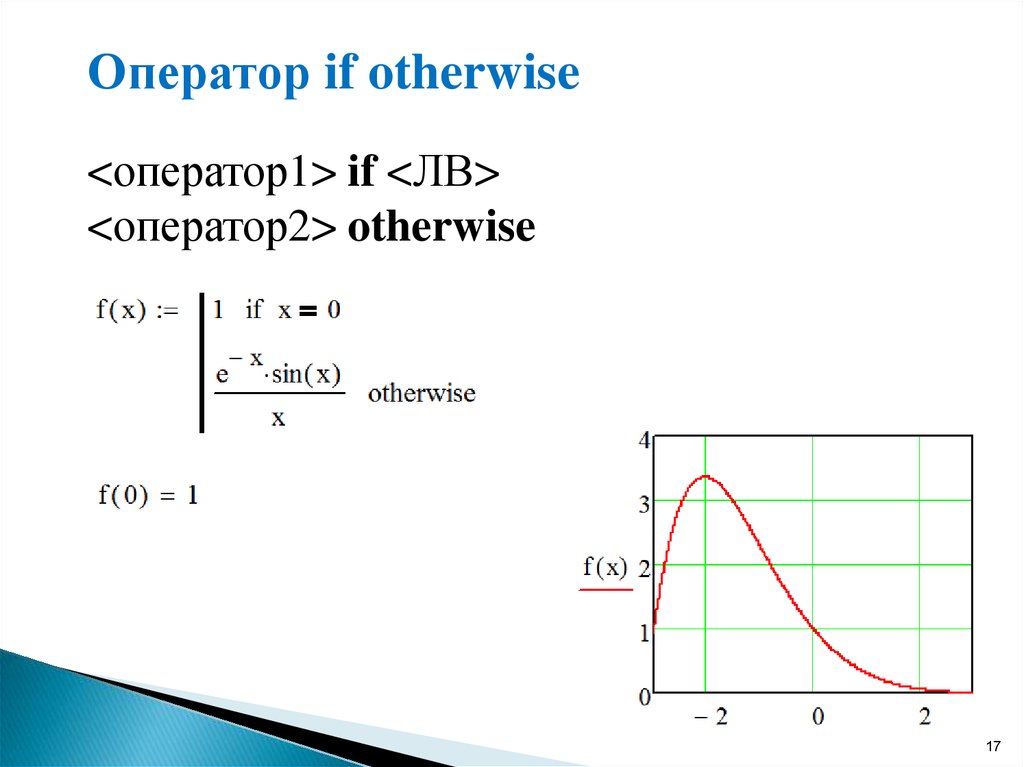
Разложения на действительную и мнимую части :
Если однозначная аналитическая функция f (z) биективно отображает область D в область G, то D называется областью однолистности.
И. Домен D k = (x + iy | 2π k≤ y
Доказательства. Из соотношения (5) следует, что отображение exp: D k → ℂ инъективно. Пусть w — любое ненулевое комплексное число. Тогда, решив уравнения е х = | ш | и е iy = w/| ш | с вещественными переменными x и y (y выбирается из полуинтервала при n > 1 отличен от нуля во всех точках, кроме z = 0. Записывая w и z в экспоненциальном виде в формуле (4), получаем из формулы (5 ) что комплексные числа Z\ и z2 такие, что где k — целое число, отображаются в одну точку w. Следовательно, при n > 1 отображение (4) не является однолистным на плоскости z. Простейший пример области в котором отображение z = zn однолистно, является сектором, где а — любое действительное число. В области (7) отображение (4) является конформным. — многозначным, так как для каждого комплексного числа z = r1 в Ф 0 можно задайте n различных комплексных чисел так, чтобы их n-я степень была равна z: Заметим, что многочлен степени n от комплексной переменной z — это функция, где заданы комплексные числа, причем ао Ф 0.
Многочлен любой степени является аналитической функцией на всей комплексной плоскости 2.3 Дробно-рациональная функция Дробно-рациональная функция — это функция вида где) — многочлены комплексной переменной ле з. Дробно-рациональная функция аналитична на всей плоскости, кроме тех точек, в которых знаменатель Q (z) обращается в нуль. Пример 3. Функция Жуковского __ является аналитической во всей плоскости z, исключая точку z = 0. Выясним, при каких условиях на область комплексной плоскости функция Жуковского, рассматриваемая в этой области, будет однолистной. M Пусть точки Z) и zj переводятся функцией (8) в одну точку. Тогда, для, получаем, что Значит, для однолистности функции Жуковского необходимо и достаточно выполнения условия. Пример области, удовлетворяющей условию однолистности (9) — внешний вид круга | г | > 1. Поскольку производная функции Жуковского Элементарные функции комплексного переменного Дробно-рациональные функции Степенная функция Показательная функция Логарифмическая функция Тригонометрическая и гиперболическая функции отличны от нуля везде, кроме точек, то отображение области, осуществляемое этой функцией, будет конформная (рис.
13). Обратите внимание, что внутренняя часть единичного диска | I также является областью однолистности функции Жуковского. Рис. 13 2.4. Показательная функция Показательная функция ez определяется для любого комплексного числа z = x + zy следующим образом: При x = 0 получаем формулу Эйлера: Опишем основные свойства показательной функции: 1. При вещественном z, это определение совпадает с обычным. В этом можно убедиться непосредственно, положив y = 0 в формуле (10). 2. Функция ez аналитична на всей комплексной плоскости, и для нее сохраняется обычная формула дифференцирования. 3. Теорема сложения сохраняется для функции e. Положим 4. Функция ez периодична с мнимым основным периодом 2xi. Действительно, для любого целого k С другой стороны, если то из определения (10) следует, что откуда следует, что или где n — целое число. Полоса не содержит ни одной пары точек, связанных соотношением (12), поэтому из проведенного исследования следует, что отображение w = e» является однопрямым в полосе (рис.
14). В качестве производной это отображение конформно Замечание Функция rg однолистна в любой полосе 2.5 Логарифмическая функция Из уравнения, в котором задано неизвестное, получаем Следовательно, функция, обратная функции, определена для любого и представляется формулой где Эта многозначная функция называется логарифмической и обозначается следующим образом.Тогда получаем формулу 2.6 для Ln z.Тригонометрические и гиперболические функции Из формулы Эйлера (11) для вещественных y получаем Откуда Определим тригонометрические функции sin z и cos z для любых комплексных числа z с помощью следующих формул: Интересными свойствами обладают синус и косинус комплексного аргумента. Перечислим основные из них: Функции sinz и cos z: 1) при действительных x z-x совпадают с обычными синусами и косинусами; 2) являются аналитика по белому оле комплексная плоскость; 3) подчиняются обычным формулам дифференцирования: 4) периодичны с периодом 2т; 5) sin z — нечетная функция, cos z — четная; 6) сохраняются обычные тригонометрические соотношения.