ЛБ_6
Дисциплина: Теоретические основы статистических исследований
Лабораторная работа №6
Корреляционный анализ
При проведении корреляционного анализа различают параметрические и непараметрические методы анализа наличия зависимости.
1. Параметрические методы оценки корреляции. Коэффициент линейной корреляции Пирсона
Коэффициент линейной корреляции отражает меру линейной зависимости между двумя переменными. Предполагается, что переменные измерены в интервальной или количественной шкале.
1.1. Реализация в SPSS
Для того, чтобы рассчитать коэффициент линейной корреляции Пирсона необходимо использовать следующую последовательность команд:
В результате чего, откроется диалоговое
окно (рис.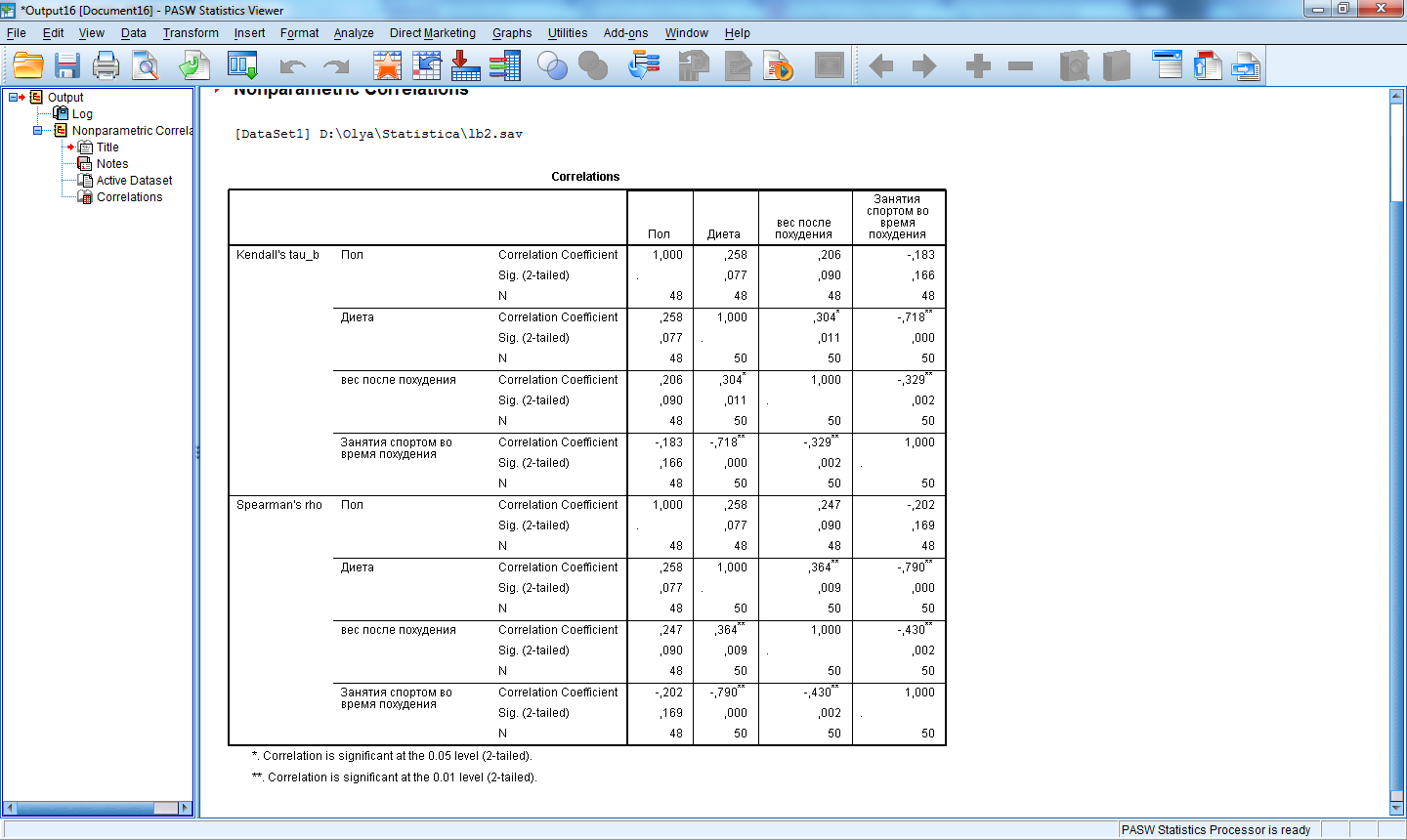 1), в котором необходимо указать
переменные, для которых будет рассчитан
коэффициент корреляции Пирсона. И
установить флажок в поле Pearson.
1), в котором необходимо указать
переменные, для которых будет рассчитан
коэффициент корреляции Пирсона. И
установить флажок в поле Pearson.
Рис.1. Диалоговое окно Bivariate Correlations
После нажатия на кнопку ОК на экран будет выведена матрица корреляций Пирсона для указанных переменных.
Пример расчета коэффициентов линейной корреляции Пирсона для переменных height, weight_1, index_1 приведен на рис.2.
Рис.2. Матрица коэффициентов корреляции Пирсона
Значимая положительная корреляция в этой таблице наблюдается для всех переменных. Например, коэффициент корреляции между переменными height и weight, равный 0,732 (уровень значимости р=0,001), говорит о тесной положительной связи между этими переменными. Т.е. Чем больше рост респондента, тем больше его вес.
1. 2. Реализация в STATISTICA
2. Реализация в STATISTICA
Для того, чтобы рассчитать коэффициент линейной корреляции Пирсона необходимо использовать следующую последовательность команд:
Statistics (Статистики) – Basic Statistics and Tables (Основные статистики и таблицы) – Correlation matrices (Корреляционные матрицы)
В результате откроется диалоговое окно (рис.3.), в котором необходимо указать переменные для расчета линейного коэффициента корреляции Пирсона
Рис.3. Диалоговое окно Product-Moment and Partial Correlations
После нажатия на кнопку Summary: Correlations на экран будет выведена корреляционная матрица.
Пример расчета коэффициентов линейной
корреляции Пирсона для переменных
height, weight_1,
index_1 приведен на рис. 4.
4.
Рис.4. Матрица коэффициентов корреляции Пирсона
2. Непараметрические методы оценки корреляции.
Коэффициенты Спирмена и Кенделла
Оба показателя, основаны на корреляции не самих значений рассматриваемых признаков, а их рангов. С их помощью можно изучать и измерять связь не только между количественными, но и качественными (атрибутивными) признаками, ранжированными определенным образом.
2.1. Реализация в SPSS
Для того, чтобы рассчитать коэффициенты ранговой корреляции Спирмена и Кенделла, необходимо использовать следующую последовательность команд:
Analyze (Анализ) – Correlate (Корреляция) – Bivariate (Двумерная)
В открывшемся диалоговом окне Bivariate Correlations (рис.1.)
установить флажок в поле Kendall’s tau—b и Spearman.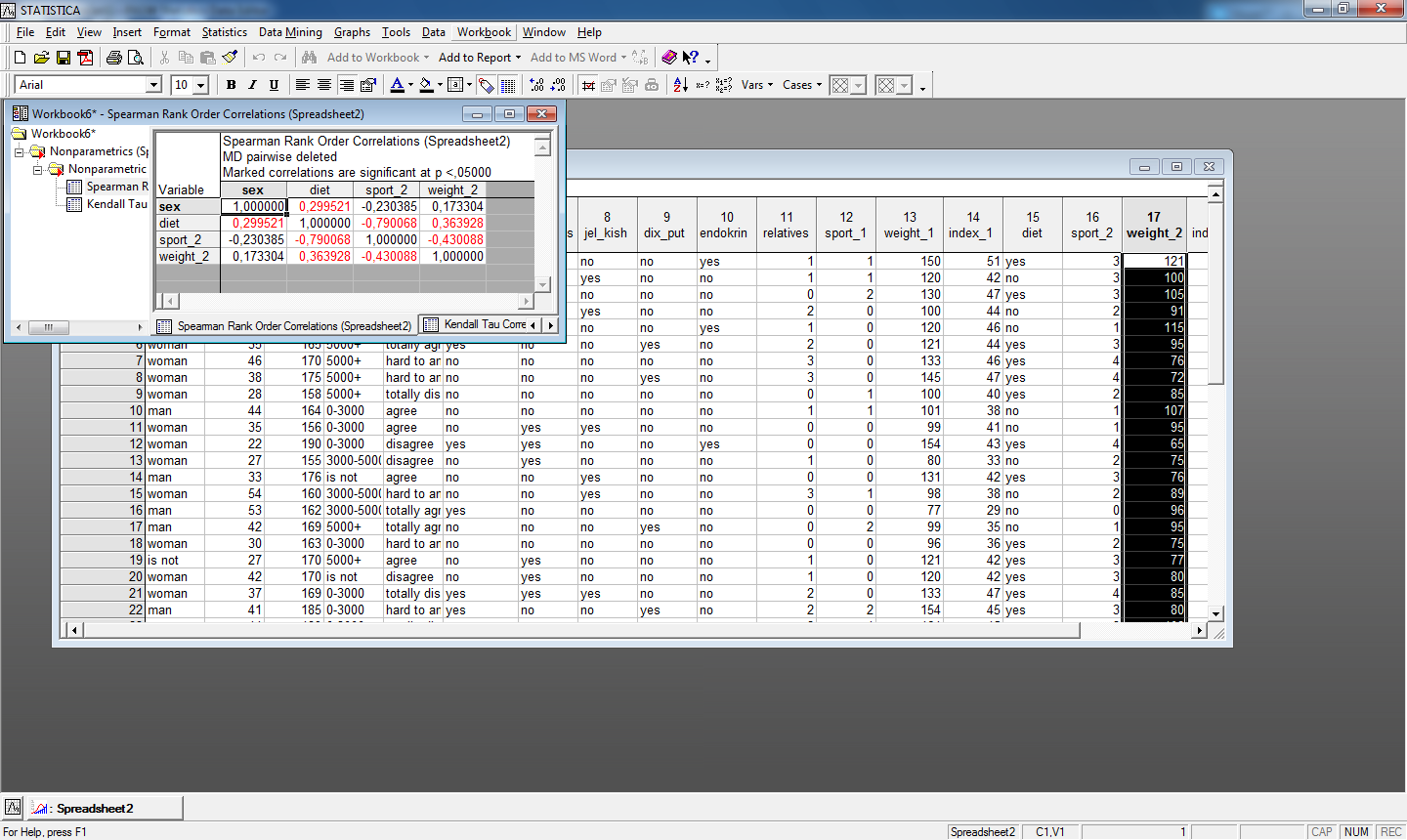 После
нажатия на кнопку ОК на экран будет
выведена матрица корреляций Спирмена
и Кендалла для указанных переменных.
После
нажатия на кнопку ОК на экран будет
выведена матрица корреляций Спирмена
и Кендалла для указанных переменных.
Пример расчета коэффициентов ранговой корреляции Спирмена и Кендалла для переменных sex, diet, weight_2, sport_2 приведен на рис.5.
Рис.5. Матрица корреляций Спирмена и Кенделла
Из полученной матрицы видно, что переменные diet и sport_2 имеют тесную обратную связь. Т.к. переменная diet принимает два значения: 1- соблюдает и 2-не соблюдает, то коэффициент корреляции равный -0,718 по Кендаллу и -0,79 по Спирмену можно трактовать так: если респондент при программе похудения придерживался диеты, то он чаще занимался спортом. Также обратную корреляцию имеет пара переменных sport_2 и weight_2, что можно трактовать так: чем больше респондент занимался спортом, участвуя в программе похудения, тем меньше стал вес после программы похудения.
Значительную прямую корреляцию имеют
пары переменных: sex и diet
(учитывая кодировку данных переменных
это означает, что женщины соблюдают
диету чаще, чем мужчины), weight_2
и diet (учитывая кодировку
переменной diet – если
респондент не соблюдал диету во время
программы похудения, то его вес после
программы похудения окажется выше).
2.2. Реализация в STATISTICA
Для того, чтобы рассчитать коэффициенты ранговой корреляции Спирмена и Кенделла, необходимо использовать следующую последовательность команд:
Statistics (Статистики) – Nonparametrics (Непараметрические) –
Correlations (Корреляции)
В результате чего откроется диалоговое окно (рис.6.), в котором необходимо указать переменные, для которых будут рассчитаны коэффициенты корреляции.
Рис.6. Диалоговое окно Correlations
После нажатия на кнопку Spearman rank
Пример расчета коэффициентов ранговой
корреляции Спирмена и Кендалла для
переменных sex, diet,
weight_2, sport
приведен соответственно на рис. 7. и
рис.8.
7. и
рис.8.
Рис.7. Матрица корреляций Спирмена
Рис.8. Матрица корреляций Кендалла
Полученные результаты схожи с результатами расчета коэффициентов ранговой корреляции в пакете SPSS.
3. Частные корреляции. Выявление ложных корреляций.
На практике иногда возникают ситуации, когда в результате корреляционного анализа обнаруживаются логически необъяснимые, противоречащие объективному опыту исследователя корреляции между двумя переменными (например, оказывается, что между уровнем дохода респондентов и количеством детей в семье существует статистически значимая зависимость). В этом случае говорят о так называемой ложной корреляции, исследовать которую помогают частные коэффициенты корреляции.
3.1. Реализация в SPSS
В SPSS коэффициент частной корреляции можно рассчитать используя следующую последовательность команд:
Analyze (Анализ) – Correlate (Корреляции) – Partial (Частные)
В результате откроется диалоговое окно
(рис. 9.), в котором необходимо ввести в
поле Variables переменные
для которых нужно вычислить коэффициент
корреляции, а в окно Controlling for – переменную,
значение которой нужно исключить
9.), в котором необходимо ввести в
поле Variables переменные
для которых нужно вычислить коэффициент
корреляции, а в окно Controlling for – переменную,
значение которой нужно исключить
Рис.9. Диалоговое окно Partial Correlations
После нажатия на кнопку ОК на экран будет выведена матрица частных коэффициентов корреляции.
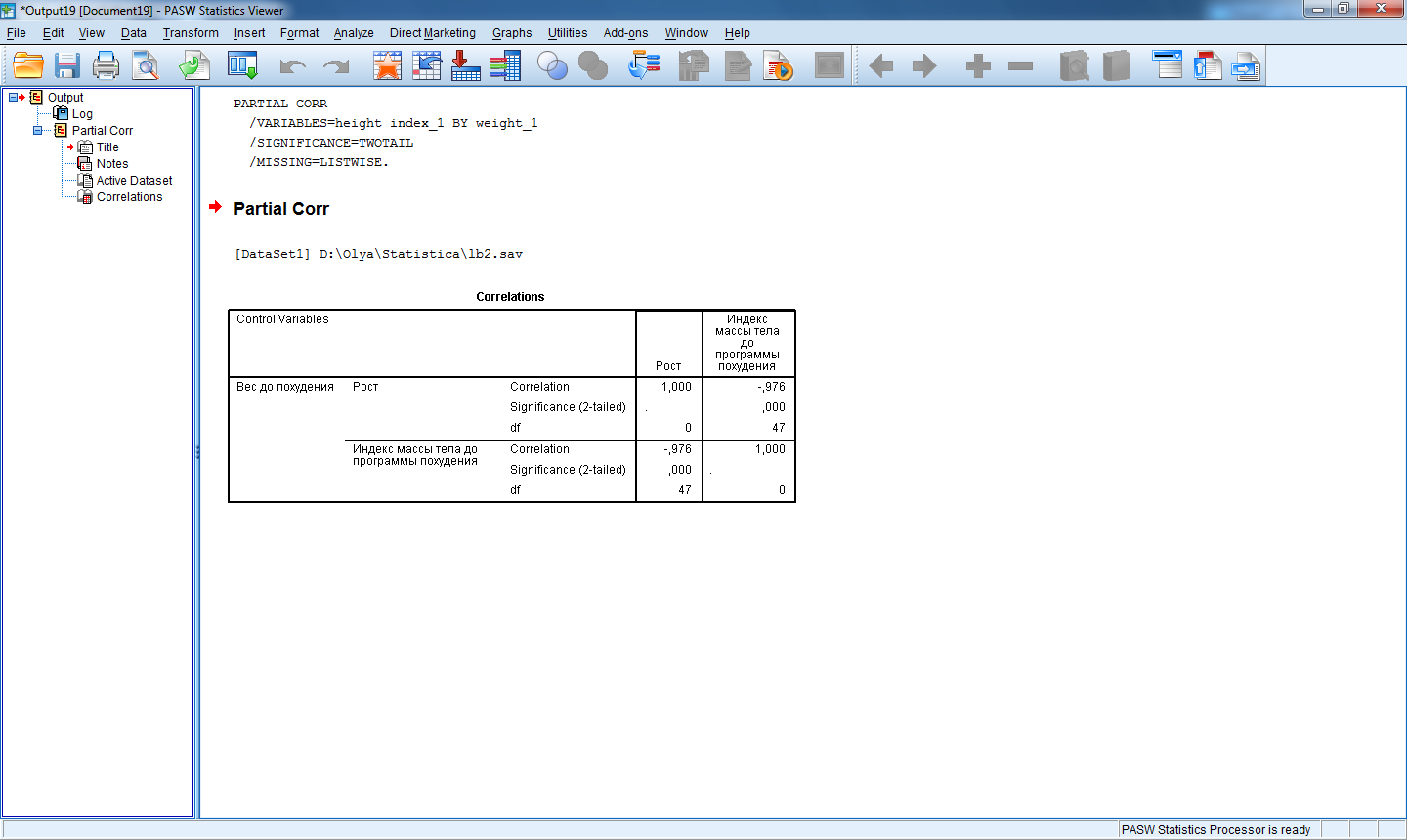
Пример расчета коэффициентов частной корреляции для переменных height и index_1 за исключением переменной weight_1 приведен на рис.10.
Рис.10. Матрица коэффициентов частной корреляции.
Рассчитанный коэффициент корреляции
с высокой точностью (p<0,001)
говорит о том, что существует тесная
обратная связь между переменными height
и index_1 (за исключением
переменной weight_1), т.е. чем
выше рост респондента, тем ниже его
индекс массы тела. Заметим, что коэффициент
линейной корреляции Пирсона для этих
переменных с высокой точностью (p=0,001)
давал значение 0,45 (рис.2.), что свидетельствует
о прямой связи переменных.
Заметим, что коэффициент
линейной корреляции Пирсона для этих
переменных с высокой точностью (p=0,001)
давал значение 0,45 (рис.2.), что свидетельствует
о прямой связи переменных.
3.2. Реализация в STATISTICA
Для того, чтобы рассчитать коэффициент частной корреляции необходимо использовать следующую последовательность команд:
Statistics (Статистики) – Basic Statistics and Tables (Основные статистики и таблицы) – Correlation matrices (Корреляционные матрицы)
В открывшемся диалоговом окне Product—Moment and Partial Correlations (рис.3.) необходимо перейти на вкладку Advanced / plot где, щелкнув на кнопку Partial correlations. В открывшемся окне, в поле First list указать переменные для которых нужно вычислить коэффициент корреляции, а в поле
После нажатия на кнопку ОК на экран будет выведена матрица частных коэффициентов корреляции.
Пример расчета коэффициентов частной корреляции для переменных height и index_1 за исключением переменной weight_1 приведен на рис.11.
Рис.11. Матрица коэффициентов частной корреляции.
Индивидуальное задание:
Для имеющихся данных в пакетах MS Excel (или Mathcad), SPSS и Statistica рассчитать:
значение ковариации и коэффициента корреляции Пирсона,
коэффициенты корреляции Спирмена и Кенделла,
корреляционную матрицу,
коэффициент множественной корреляции ,
коэффициент частной корреляции,
коэффициент детерминации,
коэффициент конкордации.
Сделать выводы о наличии или отсутствии
связи в каждом конкретном случае и о ее
силе.
Факторный анализ с матрицей корреляций Спирмена на входе
*(Вопрос) Как выполнить факторный анализ с матрицей коэффициентов корреляции Спирмена на входе?.
*(Ответ) Размещён в SPSSX-L 05.02.2002. Автор: Marta Garcia-Granero.
* Во-первых, сгенерируем данные для примера.
INPUT PROGRAM.
- VECTOR X(10).
- LOOP #I = 1 TO 100.
- LOOP #J = 1 TO 10.
- COMPUTE X(#J) = UNIFORM(5).
- END LOOP.
- END CASE.
- END LOOP.
- END FILE.
END INPUT PROGRAM.
execute.
* Создание корреляционной матрицы, подходящей для команды FACTOR.
* Это гибрид из двух разных файлов.
* Если вы будете выполнять синтаксис шаг за шагом, легко увидите, что он делает.
* Директория temp на диске C: должна существовать.
* Исходные матрицы корреляций:
* Можно также использовать и корреляции Кендала
* (для порядковых переменных) вместо Спирмена.
CORRELATIONS
/VARIABLES=x1 TO x10
/MATRIX=OUT('c:\\temp\\corr1_.sav')
/MISSING=PAIRWISE .
NONPAR CORR
/VARIABLES=x1 TO x10
/PRINT=SPEARMAN
/MATRIX=OUT('c:\\temp\\corr2_. sav')
/MISSING=PAIRWISE .
* Преобразования файлов.
GET FILE='c:\\temp\\corr2_.sav'.
EXECUTE .
SELECT IF(rowtype_ ~= 'N').
EXECUTE .
RECODE rowtype_ ('RHO'='CORR') .
EXECUTE .
SAVE OUTFILE='c:\\temp\\corr2_.sav'.
GET FILE='c:\\temp\\corr1_.sav'.
EXECUTE .
SELECT IF($casenum<4).
EXECUTE .
ADD FILES /FILE=*
/FILE='c:\\temp\\corr2_.sav'.
EXECUTE.
* Получили и сохраняем окончательную матрицу (пригодную для команды FACTOR).
SAVE OUTFILE='c:\\temp\\c_matrix.sav'.
* Теперь - факторный анализ.
* Я указала опции, которые обычно использую
* (метрика KMO, MSA, каменистая осыпь, проверка Бартлетта,
* вращение Варимакс с отсортированными нагрузками; вывод малых нагрузок подавляется)
* Modify them if needed.
FACTOR
/MATRIX=IN(cor='c:\\temp\\c_matrix.sav')
/ANALYSIS x1 TO x10
/PRINT KMO AIC EXTRACTION ROTATION
/FORMAT SORT BLANK(0.4)
/PLOT EIGEN
/CRITERIA MINEIGEN(1) ITERATE(25)
/EXTRACTION PC
/CRITERIA ITERATE(25)
/ROTATION VARIMAX
/METHOD=CORRELATION .
* Разумеется, этот случайный набор данных некоррелирован и малопригоден для факторного анализа.
sav')
/MISSING=PAIRWISE .
* Преобразования файлов.
GET FILE='c:\\temp\\corr2_.sav'.
EXECUTE .
SELECT IF(rowtype_ ~= 'N').
EXECUTE .
RECODE rowtype_ ('RHO'='CORR') .
EXECUTE .
SAVE OUTFILE='c:\\temp\\corr2_.sav'.
GET FILE='c:\\temp\\corr1_.sav'.
EXECUTE .
SELECT IF($casenum<4).
EXECUTE .
ADD FILES /FILE=*
/FILE='c:\\temp\\corr2_.sav'.
EXECUTE.
* Получили и сохраняем окончательную матрицу (пригодную для команды FACTOR).
SAVE OUTFILE='c:\\temp\\c_matrix.sav'.
* Теперь - факторный анализ.
* Я указала опции, которые обычно использую
* (метрика KMO, MSA, каменистая осыпь, проверка Бартлетта,
* вращение Варимакс с отсортированными нагрузками; вывод малых нагрузок подавляется)
* Modify them if needed.
FACTOR
/MATRIX=IN(cor='c:\\temp\\c_matrix.sav')
/ANALYSIS x1 TO x10
/PRINT KMO AIC EXTRACTION ROTATION
/FORMAT SORT BLANK(0.4)
/PLOT EIGEN
/CRITERIA MINEIGEN(1) ITERATE(25)
/EXTRACTION PC
/CRITERIA ITERATE(25)
/ROTATION VARIMAX
/METHOD=CORRELATION .
* Разумеется, этот случайный набор данных некоррелирован и малопригоден для факторного анализа.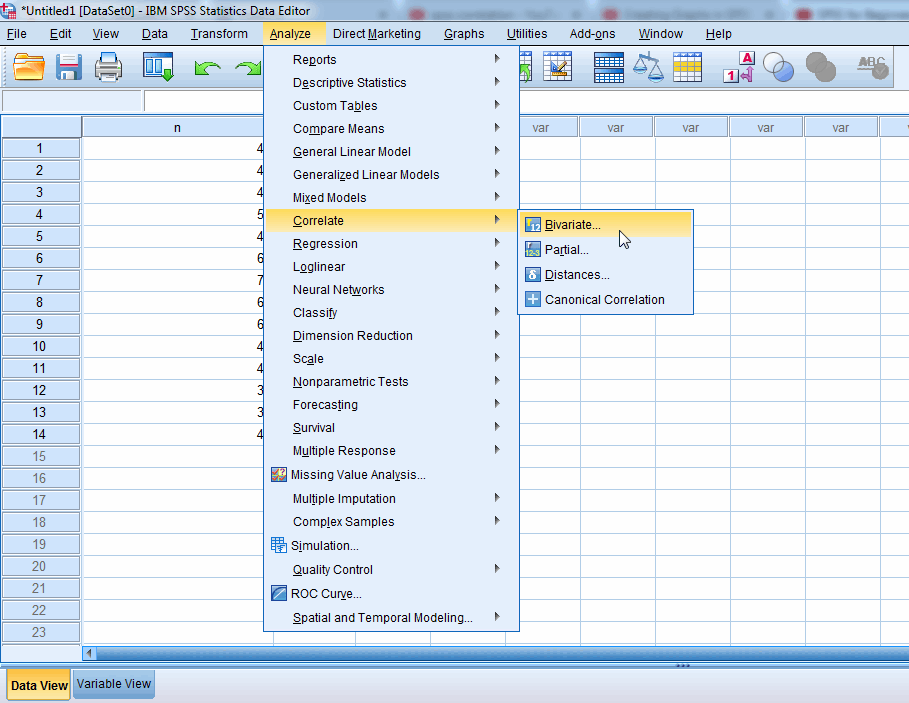 * В частности, метрики KMO и MSA весьма низки, а проверка Бартлетта незначима.
* В частности, метрики KMO и MSA весьма низки, а проверка Бартлетта незначима.
Корреляция Спирмена. Частная корреляция.
Корреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Коэффициент корреляции Спирмена (Spearman rank correlation coefficient) — мера линейной связи между случайными величинами. Корреляция Спирмена является ранговой, то есть для оценки силы связи используются не численные значения, а соответствующие им ранги. Коэффициент инвариантен по отношению к любому монотонному преобразованию шкалы измерения.Коэффициент ранговой корреляции Спирмена — это непараметрический метод, который используется с целью статистического изучения связи между явлениями.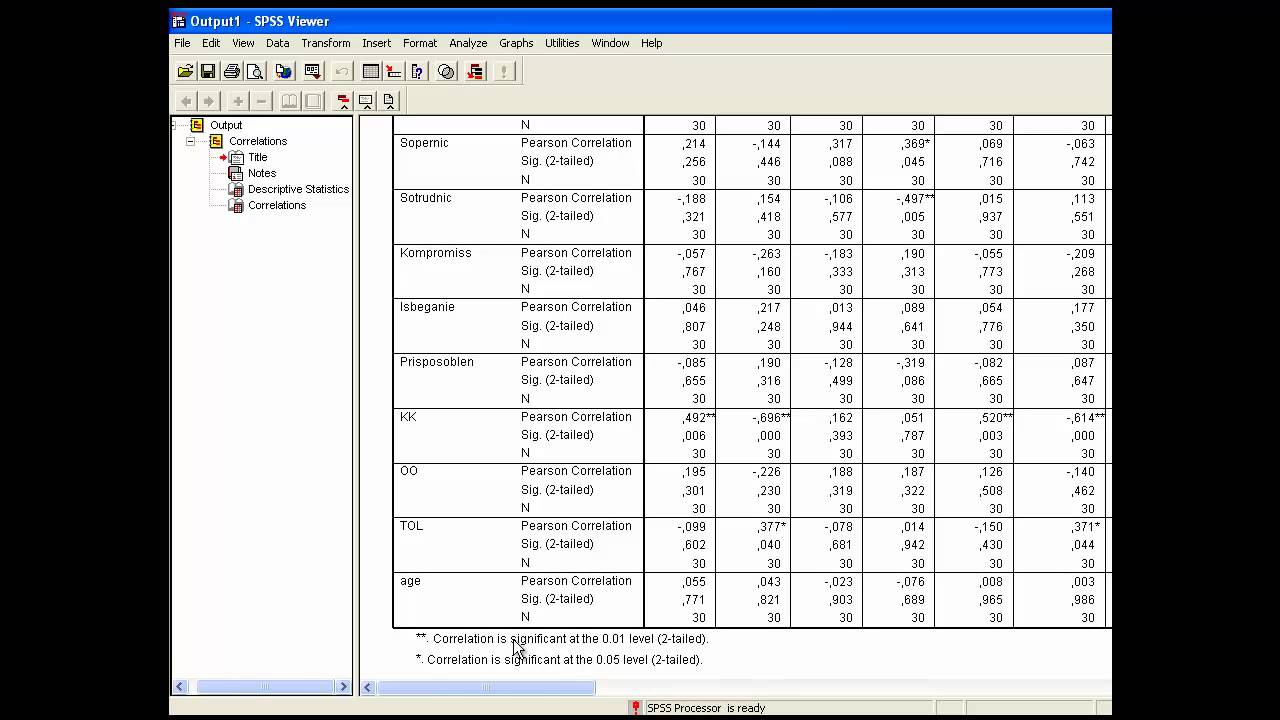 В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.
В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.
Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:
1) Сопоставать каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию).
2) Определить разности рангов каждой пары сопоставляемых значений.
3) Возвести в квадрат каждую разность и суммировать полученные результаты.
4) Вычислить коэффициент корреляции рангов по формуле:.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
где — сумма квадратов разностей рангов, а — число парных наблюдений.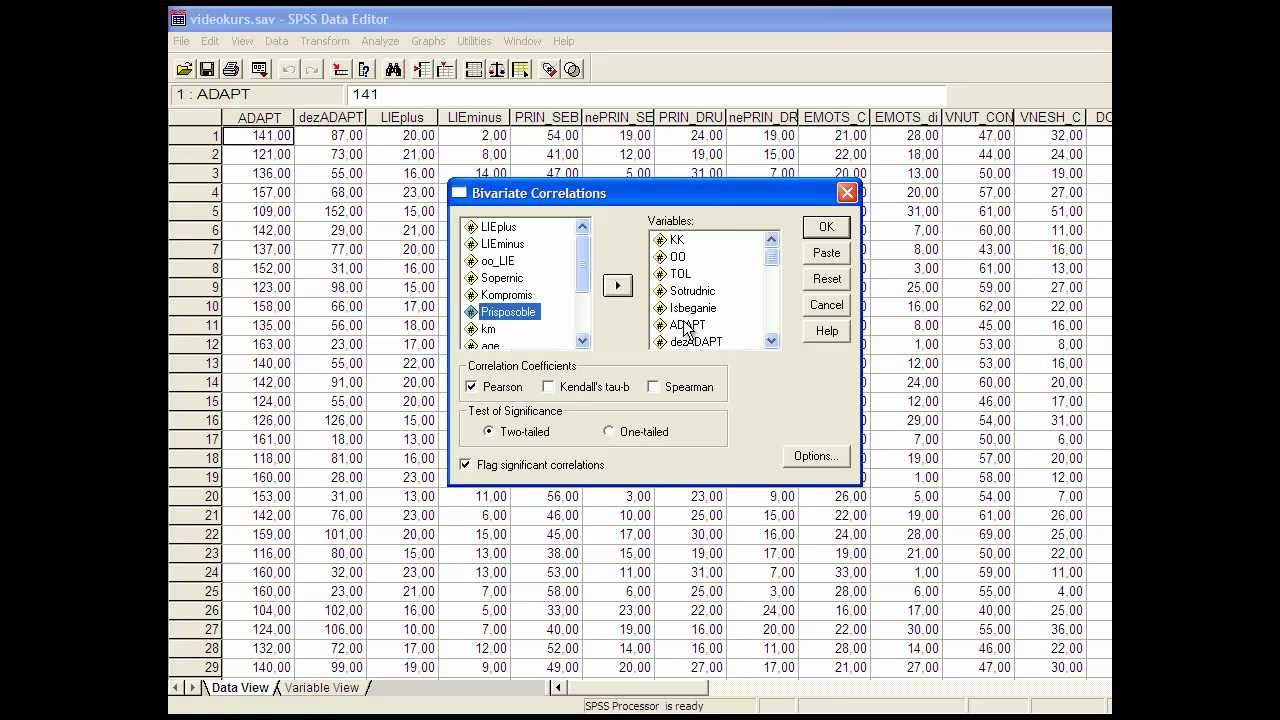
При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента равные 0,3 и менее, показателями слабой тесноты связи; значения более 0,4, но менее 0,7 — показателями умеренной тесноты связи, а значения 0,7 и более — показателями высокой тесноты связи.
Мощность коэффициента ранговой корреляции Спирмена несколько уступает мощности параметрического коэффициента корреляции.
Коэффицент ранговой корреляции целесообразно применять при наличии небольшого количества наблюдений. Данный метод может быть использован не только для количественно выраженных данных, но также и в случаях, когда регистрируемые значения определяются описательными признаками различной интенсивности.
Частная корреляция.Корреляция между двумя переменными, вычисленная после устранения влияния всех других переменных, называется частной корреляцией. Например, длина волос может коррелировать с ростом человека (чем выше человек, тем короче волосы), однако эта зависимость становится слабой или совсем исчезает, если устранить влияние пола наблюдаемых людей, поскольку женщины обычно ниже ростом и чаще имеют более длинные волосы, чем мужчины.
В случае статистической связи нескольких случайных переменных величин — выражение зависимости одной из этих величин (предиктанда) от одной из других величин (предикторов) при условии, что остальные предикторы сохраняют постоянные значения. Для простейшего случая трех случайных переменных величин Χ, Υ, Ζ, связанных линейной корреляцией, коэффициент частной корреляции rX, Y, Z между X и Υ выражается так:
где rX Z, rX Y и т. д. — коэффициенты линейной корреляции между парами соответствующих переменных, вычисленные независимо от третьей переменной.
Если исследовать достаточно большую совокупность мужчин и сопоставить размер их обуви с уровнем образованности, то между этими двумя переменными можно заметить хоть и небольшую, но в то же время значимую корреляцию. Это корреляция может послужить примером так называемой ложной корреляции. Здесь статистически значимый коэффициент корреляции является не проявлением некоторой причинной связи между двумя рассматриваемыми переменными, а в большей степени обусловлен некоторой третьей переменной.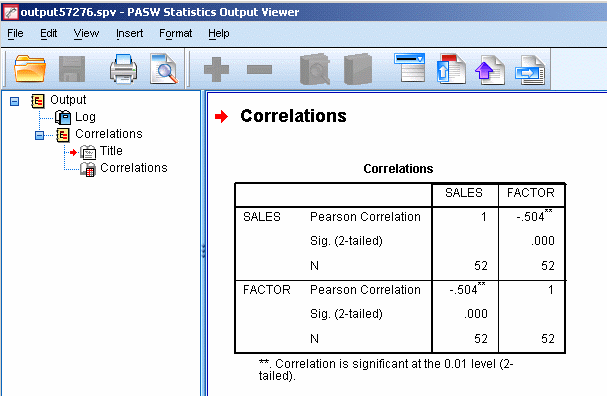
В рассматриваемом примере такой переменной является рост. С одной стороны существует некоторая незначительная корреляция между ростом и уровнем образованности, а с другой — вполне объяснимая и логичная связь между ростом и размером обуви. Вместе эти две корреляции приводят к упоминавшейся ложной корреляции. Для исключения одной такой искажающей переменной необходим расчёт так называемой частной корреляции.
Если присвоить коррелирующим переменным индексы 1 и 2, а искажающей переменной — индекс 3, и попарно рассчитать корреляционный коэффициент (Пирсона) r12,r13, и r23 , то для частных корреляционных коэффициентов получим:
Достаточно давно в социологических исследованиях, проводимых в Германии, выяснялось отношение населения к приезжим рабочим-иностранцам. Для этого было сформулировано несколько отдельных вопросов. Ответы на вопросы суммировались. Сумма могла принимать значения от 0 до 30, причём большее значение соответствует более негативному отношению к приезжим рабочим.
Среди многочисленных дополнительных переменных учитывались: возраст опрашиваемых и частота посещения церкви. Последней характеристике были присвоены значения от 1 (никогда) до 6 (по меньшей мере, 2 раза в неделю). Небольшая выборка из оригинальных данных опроса (35 респондентов с этими тремя переменными) наводится в файле kirche.sav. Откройте этот файл, если Вы хотите самостоятельно провести следующие расчёты.
Если подсчитать корреляции между этими тремя переменными, то при выборе коэффициентов Пирсона для анализа взаимосвязи, получатся следующие результаты закроем глаза на то, что одна из переменных, а именно частота посещения церкви, имеет порядковую шкалу):
Correlations (Корреляции)
|
ALTER (Возраст) |
GAST (Приезжий) |
KIRCHE (Церковь) |
||
|
ALTER (Возраст) |
Pearson Correlation (Корреляция по Пирсону) Sig. |
1,000 35 |
,468″ ,005 35 |
,779″ ,000 35 |
|
GAST (Приезжий) |
Pearson Correlation (Корреляция по Пирсону) Sig. (2-tailed) (Значимость (2-сторонняя)) N |
,468″ ,005 35 |
1,000 35 |
,432** ,010 35 |
|
KIRCHE (Церковь) |
Pearson Correlation (Корреляция по Пирсону) Sig. (2-tailed) (Значимость (2-сторонняя)) N |
,779″ ,000 35 |
,432″ ,010 35 |
1,000 35 |
«* Correlation is significant at the . 01 level (2-tailed). Корреляция является закономерной на уровне 0,01 (2-стороння).
01 level (2-tailed). Корреляция является закономерной на уровне 0,01 (2-стороння).
Принимая во внимание полярность, полученные результаты можно трактовать, к примеру, таким образом, что частые посещения церкви коррелируют с отрицательным отношением к приезжим рабочим (r = 0,432). Прежде, чем поставить в упрёк церкви враждебность по отношению к иностранцам, нужно учесть влияние возраста. Он также коррелирует с враждебным отношением к иностранным рабочим (r = 0,468) и сильно коррелирует с частотой посещения церкви (r = 0.779). Таким образом, возникает подозрение, что возраст является искажающим признаком, виновным в ложной корреляции между частотой посещения церкви и отрицательным отношением к иностранным рабочим. Докажем это путём расчёта частных корреляционных коэффициентов.
- Откройте файл kirche.sav.
- Выберите в меню Analyse… (Анализ) Correlate… (Корреляция) Partial… (Частная)
Откроется диалоговое окно Partial Correlations (Частные корреляции).
- Перенесите переменные gast и kirche в поле признаков, а переменную alter в поле контрольных переменных и оставьте предварительную установку для двухстороннего теста значимости.
При помощи щелчка на кнопке Options… (Опции) наряду с традиционной обработкой пропущенных значений, Вы можете организовать расчёт среднего значения, стандартного отклонения и вывод «корреляций нулевого порядка» (то есть простых корреляционных коэффициентов).
В случае одной искажающей переменной, как в приведенном примере, возможен расчёт частной корреляции первого порядка, при наличии нескольких искажающих переменных, SPSS выдаёт корреляции высших порядков.
- Начните расчёт щелчком на кнопке ОК. Вязкие просмотра появится следующий результат:
|
Partial correlation coefficients (Частичные корреляционные коэффициенты) |
||
|
Controlling for. |
LTER Возраст) |
|
|
GAST (Приезжий) |
GAST ( Приезжий) 1,0000 ( 0) P= , |
KIRCHE (Церковь) ,1215 ( 32) P= ,494 |
|
KIRCHE (Церковь) |
,1215 ( 32) P= ,494 |
1,0000 ( 0) P= , |
Вас, возможно, удивит, что в данном случае всё ещё выводится старый вариант таблицы результатов, соответствующий прежним версиям SPSS. Результаты включают: частный корреляционный коэффициент, число степеней свободы (число наблюдений минус 3) и уровень значимости. Исходя из полученных результатов, можно сделать вывод, что при исключении искажающей переменной alter больше не наблюдается существенной корреляции между частотой посещения церкви и отрицательным отношением к иностранным рабочим.
Рис. 15.3: Диалоговое окно Partial Correlations (Частичные корреляции)
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимостьАнализ надежности
При помощи разнообразных критериев определяется, какие задания (переменные) можно считать надежными, а какие нет.
Ø в список «переменные» вносим все переменные (метрические, порядковые), которые хотим проверить на надежность; Ø в графе «модель» выбираем модель проверки на надежность – альфа: · Альфа – коэффициент внутренней согласованности, значения близкие «1» означает высокую внутреннюю согласованность, значения близкие «0» и отрицательным значениям – свидетельствуют о несогласованности данного вопроса с остальными вопросами теста. · Деление пополам – делит группу вопросов на 2 части и считает коэффициент корреляции между ними.
· Гутман – определение нижней границы пригодности.
· Параллельно – оценка максимального правдоподобия пригодности теста при условии наличия одинаковых дисперсий пунктов.
· Строго параллельно – оценка максимального правдоподобия пригодности теста при условии наличия одинаковых средних значений пунктов и одинаковых дисперсий пунктов.
· Метки объектов – вопросы будут отображены с метками.
Ø галочки в меню «статистика»: масштаб, масштабировать если пункт удален, средние, вариации, корреляции (в подгруппе «итоги»), корреляции (в подгруппе «между пунктами»).
· Деление пополам – делит группу вопросов на 2 части и считает коэффициент корреляции между ними.
· Гутман – определение нижней границы пригодности.
· Параллельно – оценка максимального правдоподобия пригодности теста при условии наличия одинаковых дисперсий пунктов.
· Строго параллельно – оценка максимального правдоподобия пригодности теста при условии наличия одинаковых средних значений пунктов и одинаковых дисперсий пунктов.
· Метки объектов – вопросы будут отображены с метками.
Ø галочки в меню «статистика»: масштаб, масштабировать если пункт удален, средние, вариации, корреляции (в подгруппе «итоги»), корреляции (в подгруппе «между пунктами»).
Сводка обработки наблюдений
1. N – количество респондентов.Статистики пригодности
1. Альфа Кронбаха – статистика надежности внутренней согласованности: · Больше 0,9 – отличная; · Больше 0,8 – хорошая; · Больше 0,7 – приемлемая; · Больше 0,6 – сомнительная; · Больше 0,5 – малопригодная; · Меньше 0,5 – недопустимая. 2. Альфа Кронбаха, основанная на стандартизованных пунктах – статистика надежности с учетом стандартизации пунктов. 3. Количество пунктов – количество заданий (переменных) проверяемых на надежность.
2. Альфа Кронбаха, основанная на стандартизованных пунктах – статистика надежности с учетом стандартизации пунктов. 3. Количество пунктов – количество заданий (переменных) проверяемых на надежность.Матрица корреляций между пунктами
1. Корреляция (r) – два органа считаются коррелируемые если изменение одного из них сопровождается большим или меньшим изменением другого в том же направлении – Ф.Гальтон. Коэффициент Пирсона всегда лежит в пределах от -1 (отрицательная корреляция) до 1 (положительная корреляция). Значения близкие 0 свидетельствует о том, что переменные практически не коррелируемы между собой.
Итоговые статистики пунктов
1. Средние пунктов – средние арифметические значения всех пунктов. 2. Дисперсии пунктов – вспомогательная величина для стандартного отклонения. 3. Межпунктовые корреляции – см. выше.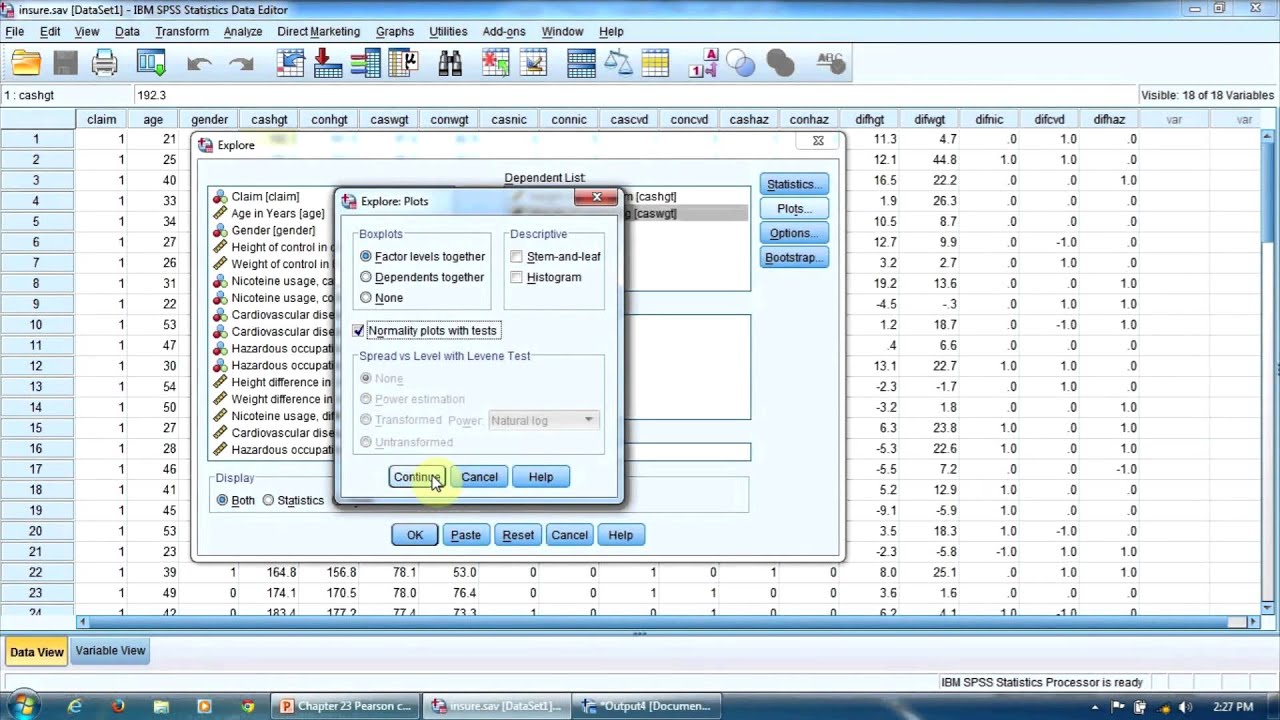 · Максимум. · Максимум / Минимум. · Дисперсия. · Количество пунктов.
· Максимум. · Максимум / Минимум. · Дисперсия. · Количество пунктов.Общие статистики пунктов
1. Среднее шкалы при удалении пункта – величина, характеризующая надежность заданий, и ее повышение при удалении конкретной переменной. 2. Дисперсия шкалы при удалении пункта – величина, характеризующая надежность заданий, и ее повышение при удалении конкретной переменной. 3. Общая корреляция коррелированных пунктов – это главная в этой таблице величина, характеризующая надежность заданий, и ее повышение при удалении конкретной переменной. Нам необходимо удалить из списка «переменных» все те переменные, которые имеют в этом столбике значения меньше чем 0,2 (условно), включая все отрицательные значения. После чего повторить проверку заданий на надежность. 4. Квадрат коэффициента множественной корреляции – величина, характеризующая надежность заданий, и ее повышение при удалении конкретной переменной.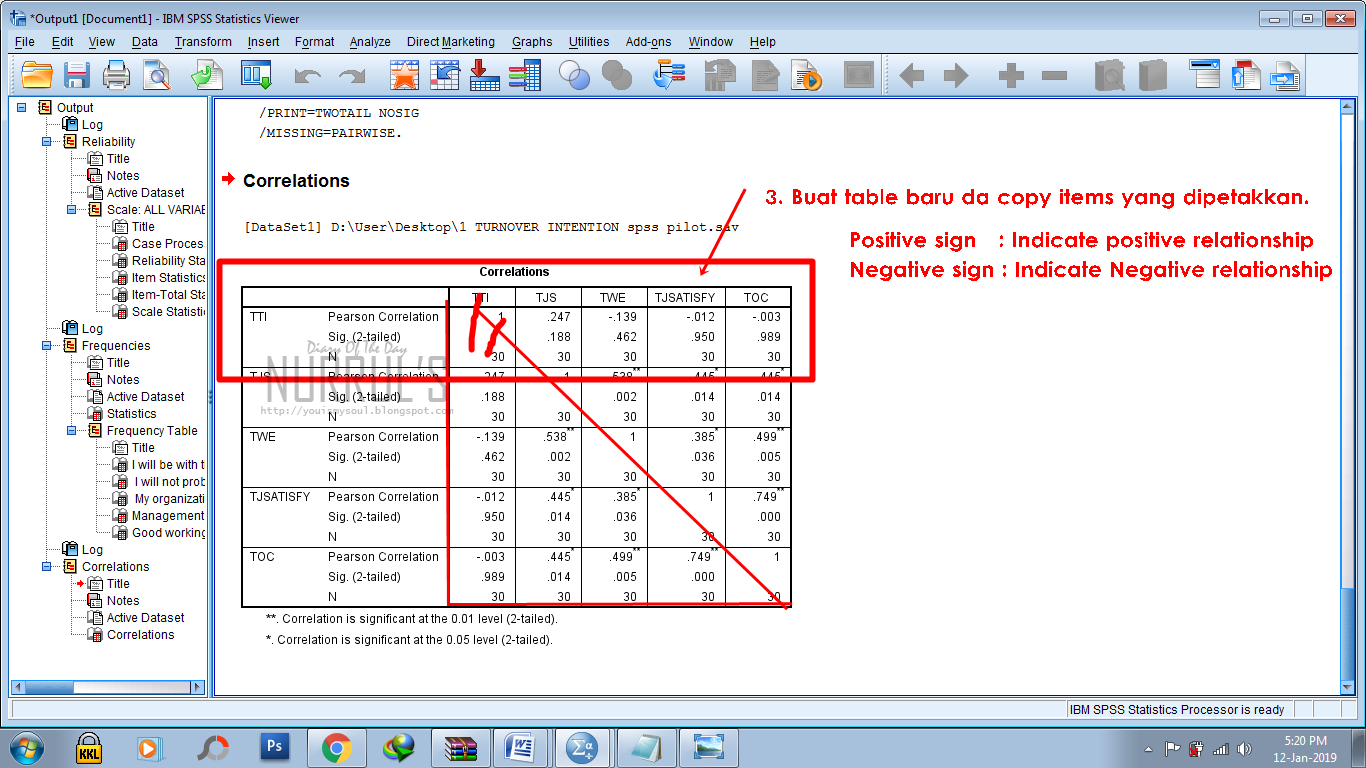 5. Альфа Кронбаха при удалении пункта – статистика надежности внутренней согласованности всех переменных при удалении конкретного задания.
5. Альфа Кронбаха при удалении пункта – статистика надежности внутренней согласованности всех переменных при удалении конкретного задания.Статистики шкалы
1. Среднее (арифметическое) – сумма всех значений деленное на их количество.
2. Дисперсия – вспомогательная величина для стандартного отклонения.
3. Стд. отклонение (от среднего) – величина, характеризующая изменчивость (равняется квадратному корню из дисперсии).
4. Количество пунктов – количество переменных.
Ø в список «переменные» вносим все переменные (метрические, порядковые), которые в первом анализе дали корреляцию больше 0,2; Ø в графе «модель» выбираем модель проверки на надежность – деление пополам; Ø галочки в меню «статистика»: масштаб, масштабировать если пункт удален, средние, вариации, корреляции (в подгруппе «итоги»), корреляции (в подгруппе «между пунктами»).

Быстрый способ проверки надежности теста путем определения коэффициента корреляции между 2-мя частями теста. Стоит все же провести повторное тестирование и сделать проверку на ретестовую надежность (чаще всего используют при делении на четные и не четные вопросы).
Сводка обработки наблюдений (данная таблица уже была рассмотрена выше)
Статистики пригодности
1. Альфа Кронбаха – статистика надежности внутренней согласованности: · Больше 0,9 – отличная; · Больше 0,8 – хорошая; · Больше 0,7 – приемлемая; · Больше 0,6 – сомнительная; · Больше 0,5 – малопригодная; · Меньше 0,5 – недопустимая. 2. Количество пунктов – количество заданий (переменных) проверяемых на надежность. 3. Корреляция между формами – приближенное значение надежности шкал, рассчитанное в предположении, что она содержит 5 элементов. 4. Коэффициент Спирмена-Брауна – коэффициент показывает корреляцию между 2-мя частями теста (стоит обратить внимание на: равно ли количество вопросов или нет): · Больше 0,9 – отличная; · Больше 0,8 – хорошая; · Больше 0,7 – приемлемая; · Больше 0,6 – сомнительная; · Больше 0,5 – малопригодная; · Меньше 0,5 – недопустимая. 5. Коэффициент половинного расщепления Гутмана – аналог выше наведенного коэффициента.
5. Коэффициент половинного расщепления Гутмана – аналог выше наведенного коэффициента.Матрица корреляций между пунктами (данная таблица уже была рассмотрена выше)
Итоговые статистики пунктов (данная таблица уже была рассмотрена выше)
Общие статистики пунктов (данная таблица уже была рассмотрена выше)
Меню статистики: · Элемент – средние значения и их стандартное отклонение. · Масштаб – общее среднее значение, дисперсия, стандартное отклонение и количество пунктов в сумме. · Масштаб если пункт удален – альфа для каждого из пунктов. · Средние – средние значения для всех пунктов. · Вариации – средние для дисперсий всех пунктов. · Ковариации – вычисления ковариаций между каждой переменной и суммой всех остальных. · Корреляции – вычисления корреляций между каждой переменной и суммой всех остальных. · Корреляции – корреляционная матрица для всех пунктов.
· Ковариации – ковариационная матрица для всех пунктов.
· Т квадрат – сравнения различий между средними значениями всех пунктов.
· Тьюки тест – проверка линейности зависимости.
· Корреляции – корреляционная матрица для всех пунктов.
· Ковариации – ковариационная матрица для всех пунктов.
· Т квадрат – сравнения различий между средними значениями всех пунктов.
· Тьюки тест – проверка линейности зависимости.· Меню АNOVA
★ Тест ранговой корреляции Спирмена
Пользователи также искали:
коэффициент ранговой корреляции спирмена, корреляция спирмена statistica, на чем основан тест ранговой корреляции спирмена, подсчет корреляции спирмена, ранговая корреляция спирмена, тест ранговой корреляции спирмена excel, тест ранговой корреляции спирмена онлайн, вычислите значение непараметрического коэффициента ранговой корреляции спирмена, Спирмена, спирмена, корреляции, ранговой, Тест, тест, коэффициента, корреляция, ранговая корреляция спирмена, подсчет корреляции спирмена, корреляция спирмена statistica, excel, онлайн, основан, коэффициент, ранговая, подсчет, вычислите, значение, непараметрического, statistica, Тест ранговой корреляции Спирмена, на чем основан тест ранговой корреляции спирмена, коэффициент ранговой корреляции спирмена, вычислите значение непараметрического коэффициента ранговой корреляции спирмена, тест ранговой корреляции спирмена онлайн, тест ранговой корреляции спирмена excel, тест ранговой корреляции спирмена,
23. 11.2020 Ирина Тюрина
11.2020 Ирина Тюрина
С ноября 2020 года доступна новая версия программно-методического комплекса – Статкласс 1.7. Для образовательных учреждений с действующей академической лицензией переход на новую версию Статкласс 1.7 предоставляется бесплатно и для ее заказа достаточно заполнить форму.
Что нового?
В новой версии Статкласс 1.7 обновлено аналитическое ядро программного решения – IBM SPSS Statistics до 27 версии. Базовая комплектация программного решения Статкласс включает теперь функционал не только обновленного базового модуля SPSS Statistics Base, но и дополнительные процедуры подготовки данных (ранее модуль Data Preparation) и более широкие возможности для выборочных оценок, с использованием метода бутсреп (ранее модуль Bootstrapping).
Наряду с калькулятором объема выборки обновленная версия Статкласс, после включения в нее 27 версии SPSS, включает теперь процедуры расчета мощности статистических критериев при разных объемах выборок и, наоборот, расчета объемов выборок для желаемой мощности критерия. Эти процедуры помогут на лабораторных занятиях по прикладной статистике использовать теперь дополнительные инструменты оценки достаточного количества наблюдений для проверки той или иной гипотезы.
Меню процедуры Анализ статистической мощности. IBM SPSS Statistics 27
Для оценки объема выборки в общем случае преподавателям или студентам необходимо будет выбрать вид эффекта (например, это может быть гипотеза о среднем значении, о доле, о коэффициенте корреляции, или о влиянии предиктора в регрессионной модели), указать ожидания величины эффекта в стандартизированных или абсолютных значениях, пороговый уровень значимости, при котором нулевая гипотеза должна быть отвергнута, и желаемую мощность (т. е. надежность достижения порогового уровня значимости в том случае, если эффект указанного размера действительно присутствует в генеральной совокупности).
е. надежность достижения порогового уровня значимости в том случае, если эффект указанного размера действительно присутствует в генеральной совокупности).
Диалог процедуры Анализ статистической мощности для оценки корреляции Пирсона. Требуемая мощность: 0,8, ожидаемый выборочный коэффициент корреляции = 0,25 (соответствующий гипотезе h2), коэффициент, соответствующий гипотезе H0 = 0, двусторонняя проверка, уровень значимости 0,05. IBM SPSS Statistics 27
На выходе будет получена оценка требуемого размера выборки.
Расчет объема выборки/мощности доступен в обновленной версии для следующих видов гипотез: [HTML_REMOVED] [HTML_REMOVED] Об одном среднем значении [HTML_REMOVED] О двух выборочных средних в независимых выборках [HTML_REMOVED] О двух выборочных средних в связанных выборках [HTML_REMOVED] О значимости фактора в однофакторной ANOVA (включая контрасты и парные сравнения) [HTML_REMOVED] Об одной доле [HTML_REMOVED] О двух долях в связанных выборках [HTML_REMOVED] О двух долях в независимых выборках [HTML_REMOVED] О величине коэффициента корреляции Пирсона [HTML_REMOVED] О ранговой корреляции Спирмена [HTML_REMOVED] О частной корреляции [HTML_REMOVED] О влиянии предиктора в модели линейной регрессии [HTML_REMOVED]
В процедуры сравнения средних и однофакторного дисперсионного анализа (ANOVA ) в обновленной версии SPSS добавлен расчет стандартизированных мер величины эффекта. В отличие от статистической значимости, меры эффекта не пытаются доказать существование эффекта, а пытаются оценить его размер. Эффект может измеряться в абсолютном выражении, а может быть стандартизирован. В IBM SPSS Statistics размер эффекта для средних и ранее оценивался в некоторых «продвинутых» процедурах линейных моделей, однако с 27 версии наиболее популярные тесты для средних из базового модуля также могут возвращать оценку величины эффекта и ее 95% доверительный интервал. Новые возможности стали доступны теперь в процедурах: t-проверки для одной выборки, для независимых выборок и для связанных выборок, а также процедуре Однофакторный дисперсионный анализ (One-way ANOVA) и оцениваемые контрасты.
В отличие от статистической значимости, меры эффекта не пытаются доказать существование эффекта, а пытаются оценить его размер. Эффект может измеряться в абсолютном выражении, а может быть стандартизирован. В IBM SPSS Statistics размер эффекта для средних и ранее оценивался в некоторых «продвинутых» процедурах линейных моделей, однако с 27 версии наиболее популярные тесты для средних из базового модуля также могут возвращать оценку величины эффекта и ее 95% доверительный интервал. Новые возможности стали доступны теперь в процедурах: t-проверки для одной выборки, для независимых выборок и для связанных выборок, а также процедуре Однофакторный дисперсионный анализ (One-way ANOVA) и оцениваемые контрасты.
Запрос вывода оценки величины эффекта при проверке гипотезе о среднем значении. IBM SPSS Statistics 27
Оценки величины эффекта – Коэна и Хеджеса и их доверительные интервалы в выводе процедуры t-критерия для среднего. IBM SPSS Statistics 27
В обновленной версии программного решения Статкласс, где в качестве аналитического ядра будет поставляться новая, 27-й версии IBM SPSS, появилась распространенная мера согласованности двух классификаций -взвешенная каппа Коэна, при расчете которой учитывается порядок категорий.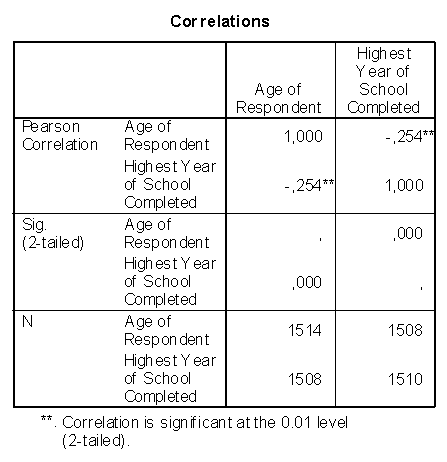 При анализе данных экспертных оценок теперь можно измерить, насколько схожи два эксперта в классификации объектов на заданное число групп. Или, например, насколько соответствует классификация, сделанная прогностической моделью реальным классам объектов.
При анализе данных экспертных оценок теперь можно измерить, насколько схожи два эксперта в классификации объектов на заданное число групп. Или, например, насколько соответствует классификация, сделанная прогностической моделью реальным классам объектов.
Начиная с 27-й версии SPSS пользователь может запрашивать построение матрицы корреляций, без дублирования значений относительно главной диагонали.
Матрица корреляции без дублирования элементов. IBM SPSS Statistics 27
Теперь верхнюю часть треугольника матрицы корреляции можно оставить пустой и не перегружать таким образом таблицу избыточными числовыми значениями. Дополнительно можно сделать матрицу еще более компактной, убрав элементы главной диагонали, не несущие в себе полезной информации.
В новой версии IBM SPSS в популярных процедурах построения частотных таблиц и кросстабуляций появилась возможность в один клик делать вывод более компактным, а получаемые таблицы – готовыми к публикации.
Диалоговое окно Таблицы сопряженности: вывод в ячейках. IBM SPSS Statistics 27
IBM SPSS Statistics 27
Например, с помощью опции Создать таблицу стилей АРА в диалоговом окне Вывод в ячейках можно вывести готовую кросс-таблицу, оформленную в стиле АРА. Итоговая таблица в стиле АРА будет очищена от вспомогательных элементов и заголовков строк и столбцов, а статистики получат компактные наименования, что позволит сократить время на редактирование таблиц, предназначенных для научных публикаций в международных журналах.
В 27 версии SPSS в Мастере диаграмм появился новый встроенный шаблон для создания пузырьковых диаграмм, на которых можно одномоментно отразить связь сразу 4-х переменных: две количественных переменных задают оси диаграммы, еще одна количественная — задает размер точки (или в данном случае — пузырька), а с помощью категориальной переменной пузырьки можно раскрасить по категориям. Возможность построения таких диаграмм в SPSS была давно, но для этого требовалось использовать встроенный язык GPL (Graphic Production Language). Теперь построить диаграмму можно достаточно быстро, без написания кода.
Диалог Мастера диаграмм с настройками размера пузырька для диаграммы разброса. IBM SPSS Statistics 27
В установках по умолчанию для форматирования диаграмм в новой версии SPSS появился предпросмотр диаграмм. Меняя ту или иную установку, пользователь сразу видит, как, приблизительно, она отразится на внешнем виде будущей диаграммы.
Диалог системных настроек Диаграмм. IBM SPSS Statistics 27
Кроме этого, у пользователей SPSS появилась теперь возможность быстро переключаться между предустановленными стилями диаграмм. Нужный стиль можно выставить как в глобальных настройках системы (Правка – Параметры), так и выбрать индивидуально в диалоге Мастера диаграмм. Например, зная, что диаграмму предстоит опубликовать в черно-белом исполнении, в Мастере диаграмм, при построении графика можно выбрать предустановленный стиль Publication Gray.
Диалог Мастера диаграмм с настройками внешнего вида диаграмм. IBM SPSS Statistics 27
На всех панелях инструментов в новой версии SPSS по умолчанию появилась кнопка сквозного поиска, которая существенно облегчит поиск нужных функций в SPSS, в справке и наверняка пригодится в образовательных учреждениях при его изучении. Как это работает? При вводе текста в строку поиска SPSS ищет введенный термин среди меню и разделов он-лайн справки. Так, например, при вводе «коррел» в окне появится список процедур (диалоговых окон), в названии которых есть слово «корреляция», а также разделы справки, в том числе — примеры кейс-стади, в которых говорится про корреляционный анализ. Выбор соответствующего пункта списка сразу же открывает либо соответствующее диалоговое окно, либо браузер со страницей справочной системы.
Как это работает? При вводе текста в строку поиска SPSS ищет введенный термин среди меню и разделов он-лайн справки. Так, например, при вводе «коррел» в окне появится список процедур (диалоговых окон), в названии которых есть слово «корреляция», а также разделы справки, в том числе — примеры кейс-стади, в которых говорится про корреляционный анализ. Выбор соответствующего пункта списка сразу же открывает либо соответствующее диалоговое окно, либо браузер со страницей справочной системы.
Диалог сквозного поиска в IBM SPSS Statistics 27
Вместе с новым SPSS и установкой Статкласс 1.7 теперь будет разворачиваться и более современная версия интерпретатора Python – 3.8.2. Разумеется, вместе с этой версией устанавливаются и соответствующие адаптированные библиотеки, обеспечивающие интеграцию Python и SPSS.
Таким образом, приобретая Статкласс 1.7. преподаватели, научные сотрудники и студенты вузов получат гораздо больше функционала, чем раньше.
Если Вы хотите воспользоваться новыми возможностями Статкласс 1. 7, мы подберем Вам оптимальную комплектацию и вариант лицензирования. Наряду с локальными и конкурентными лицензиями вузы могут приобрести специальные лицензии с домашними установками для преподавателей и студентов, которые в условиях дистанционного обучения приобрели еще большее значение для эффективного освоения в процессе обучения статистических компетенций.
Заказать консультацию Вы можете, заполнив контактную форму.
7, мы подберем Вам оптимальную комплектацию и вариант лицензирования. Наряду с локальными и конкурентными лицензиями вузы могут приобрести специальные лицензии с домашними установками для преподавателей и студентов, которые в условиях дистанционного обучения приобрели еще большее значение для эффективного освоения в процессе обучения статистических компетенций.
Заказать консультацию Вы можете, заполнив контактную форму.
Об авторе
Ирина Тюрина
Predictive Solutions
1
Первый слайд презентации: Описательная статистика в SPSS : 1
Изображение слайда
Изображение для работы со слайдом
2
Слайд 2: Описательная статистика в SPSS : 1
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
3
Слайд 3: Описательная статистика в SPSS : 1
Изображение слайда
Изображение для работы со слайдом
4
Слайд 4: Описательная статистика в SPSS : 2
Изображение слайда
Изображение для работы со слайдом
5
Слайд 5: Описательная статистика в SPSS : 2
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
6
Слайд 6: Описательная статистика в SPSS : 2
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
Изображение для работы со слайдом
7
Слайд 7: Проверка на нормальность распределения в SPSS
Изображение слайда
Изображение для работы со слайдом
Реклама. Продолжение ниже
Продолжение ниже
8
Слайд 8: Проверка на нормальность распределения в SPSS
Изображение слайда
Изображение для работы со слайдом
9
Слайд 9: Проверка на нормальность распределения в SPSS
Изображение слайда
Изображение для работы со слайдом
10
Слайд 10: Проверка на нормальность распределения в SPSS
Изображение слайда
Изображение для работы со слайдом
11
Слайд 11: Параметрические и непараметрические критерии
Все критерии различий условно подразделены на две группы: параметрические и непараметрические критерии. Критерий различия называют параметрическим, если он основан на конкретном типе распределения генеральной совокупности (как правило, нормальном) или использует параметры этой совокупности (средние, дисперсии и т.д.).
Критерий различия называют непараметрическим, если он не базируется на предположении о типе распределения генеральной совокупности и не использует параметры этой совокупности. Поэтому для непараметрических критериев предлагается также использовать такой термин как «критерий, свободный от распределения».
При нормальном распределении генеральной совокупности параметрические критерии обладают большей мощностью по сравнению с непараметрическими. Иными словами, они способны с большей достоверностью отвергать нулевую гипотезу, если последняя неверна. По этой причине в тех случаях, когда выборки взяты из нормально распределенных генеральных совокупностей, следует отдавать предпочтение параметрическим критериям. Однако, как показывает практика, подавляющее большинство данных, получаемых в психологических экспериментах, не распределены нормально, поэтому применение параметрических критериев при анализе результатов психологических исследований может привести к ошибкам в статистических выводах.
Критерий различия называют параметрическим, если он основан на конкретном типе распределения генеральной совокупности (как правило, нормальном) или использует параметры этой совокупности (средние, дисперсии и т.д.).
Критерий различия называют непараметрическим, если он не базируется на предположении о типе распределения генеральной совокупности и не использует параметры этой совокупности. Поэтому для непараметрических критериев предлагается также использовать такой термин как «критерий, свободный от распределения».
При нормальном распределении генеральной совокупности параметрические критерии обладают большей мощностью по сравнению с непараметрическими. Иными словами, они способны с большей достоверностью отвергать нулевую гипотезу, если последняя неверна. По этой причине в тех случаях, когда выборки взяты из нормально распределенных генеральных совокупностей, следует отдавать предпочтение параметрическим критериям. Однако, как показывает практика, подавляющее большинство данных, получаемых в психологических экспериментах, не распределены нормально, поэтому применение параметрических критериев при анализе результатов психологических исследований может привести к ошибкам в статистических выводах. В таких случаях непараметрические критерии оказываются более мощными, т.е. способными с большей достоверностью отвергать нулевую гипотезу.
Итак, при оценке различий в распределениях, далеких от нормального, непараметрические критерии могут выявить значимые различия, в то время как параметрические критерии таких различий не обнаружат.
Важно отметить, что,
во-первых, непараметрические критерии выявляют значимые различия и в том случае, если распределение близко к нормальному;
во-вторых, при вычислениях вручную непараметрические критерии являются значительно менее трудоемкими, чем параметрические.
В таких случаях непараметрические критерии оказываются более мощными, т.е. способными с большей достоверностью отвергать нулевую гипотезу.
Итак, при оценке различий в распределениях, далеких от нормального, непараметрические критерии могут выявить значимые различия, в то время как параметрические критерии таких различий не обнаружат.
Важно отметить, что,
во-первых, непараметрические критерии выявляют значимые различия и в том случае, если распределение близко к нормальному;
во-вторых, при вычислениях вручную непараметрические критерии являются значительно менее трудоемкими, чем параметрические.
Изображение слайда
12
Слайд 12: Корреляция
Корреляция (от лат.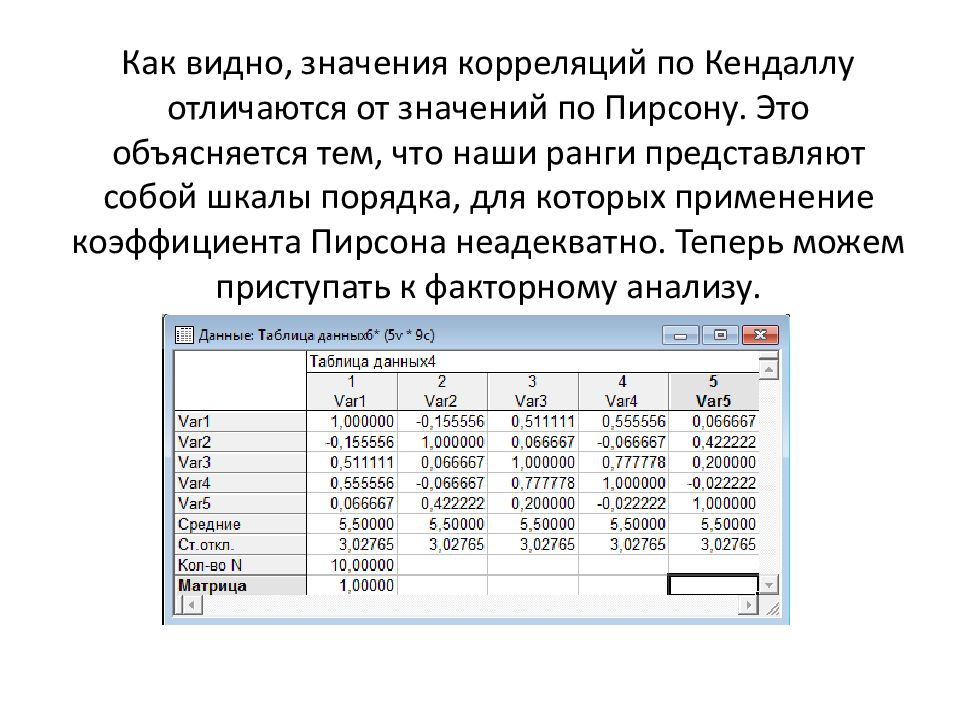 correlatio «соотношение, взаимосвязь») или корреляционная зависимость — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.[1]
correlatio «соотношение, взаимосвязь») или корреляционная зависимость — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.[1]
Изображение слайда
Изображение для работы со слайдом
13
Слайд 13: Корреляция. Коэффициент корреляции Пирсона
Только для нормального распределения! Только для количественной шкалы
Изображение слайда
Изображение для работы со слайдом
14
Слайд 14: Корреляция. Коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона
Только для нормального распределения! Только для количественной шкалы или шкалы интервалов.
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
Реклама. Продолжение ниже
15
Слайд 15: Корреляция. Коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона
Уровень значимости статистического теста (р) — допустимая для данной задачи вероятность ошибки первого рода (ложноположительного решения, false positive ), то есть вероятность отклонить нулевую гипотезу, когда на самом деле она верна.
Изображение слайда
Изображение для работы со слайдом
16
Слайд 16: Корреляция. Коэффициент корреляции Пирсона
Уровень значимости статистического теста (р) — допустимая для данной задачи вероятность ошибки первого рода (ложноположительного решения, false positive ), то есть вероятность отклонить нулевую гипотезу, когда на самом деле она верна.
Изображение слайда
Изображение для работы со слайдом
17
Слайд 17: Корреляция. Коэффициент корреляции Спирмена
Используется, если хотя бы одна из коррелируемых шкал не распределена нормально. Количественной шкалы, шкалы интервалов или порядковые шкалы.
Изображение слайда
Изображение для работы со слайдом
18
Слайд 18: Корреляция. Коэффициент корреляции Спирмена
Коэффициент корреляции Спирмена
Используется, если хотя бы одна из коррелируемых шкал не распределена нормально. Количественной шкалы, шкалы интервалов или порядковые шкалы.
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
19
Слайд 19: Корреляция. Коэффициент корреляции Спирмена
Коэффициент корреляции Спирмена
Изображение слайда
Изображение для работы со слайдом
20
Слайд 20: Корреляция. Коэффициент корреляции Хи квадрат Пирсона
Номинальные шкалы.
Изображение слайда
Изображение для работы со слайдом
21
Слайд 21: Корреляция. Коэффициент корреляции Хи квадрат Пирсона
Коэффициент корреляции Хи квадрат Пирсона
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
22
Слайд 22: Корреляция. Коэффициент корреляции Хи квадрат Пирсона
Изображение слайда
Изображение для работы со слайдом
23
Слайд 23: Различие между группами
Изображение слайда
Изображение для работы со слайдом
24
Слайд 24: Различие между группами.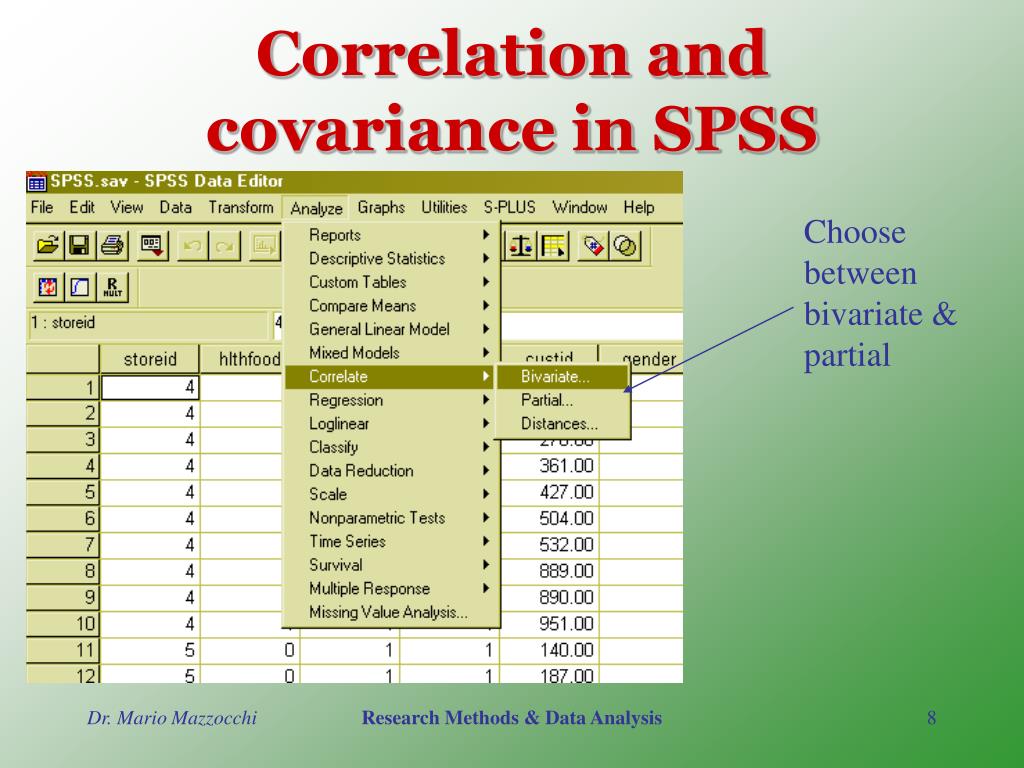 Т-критерий
Т-критерий
Только для нормального распределения! Только для количественной
Изображение слайда
Изображение для работы со слайдом
25
Слайд 25: Различие между группами. Т-критерий
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
26
Слайд 26: Различие между группами. Т-критерий
Т-критерий
Изображение слайда
Изображение для работы со слайдом
27
Слайд 27: Различие между группами. Критерий Манна-Уитни
Используется, если хотя бы одна из коррелируемых шкал не распределена нормально. Количественной шкалы, шкалы интервалов или порядковые шкалы.
Изображение слайда
Изображение для работы со слайдом
28
Слайд 28: Различие между группами. Критерий Манна-Уитни
Критерий Манна-Уитни
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
29
Слайд 29: Различие между группами. Критерий Манна-Уитни
Изображение слайда
Изображение для работы со слайдом
30
Слайд 30: Различие «до» и «после»
Изображение слайда
Изображение для работы со слайдом
31
Слайд 31: Различие «до» и «после». Т-критерий
Т-критерий
Только для нормального распределения! Только для количественной шкалы или шкалы интервалов.
Изображение слайда
Изображение для работы со слайдом
32
Слайд 32: Различие «до» и «после». Т-критерий
Изображение слайда
Изображение для работы со слайдом
33
Слайд 33: Различие «до» и «после».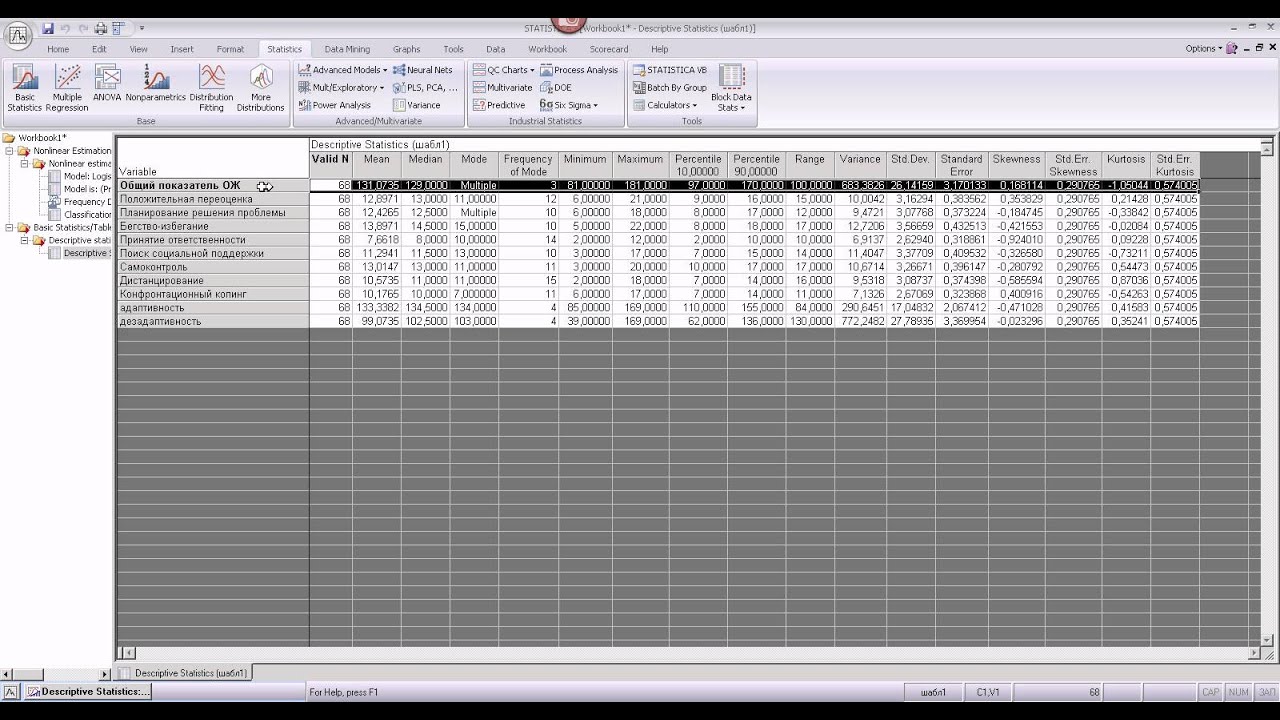 Т-критерий
Т-критерий
Изображение слайда
Изображение для работы со слайдом
34
Слайд 34: Различие «до» и «после». Критерий Вилкоксона
Используется, если хотя бы одна из коррелируемых шкал не распределена нормально. Количественной шкалы, шкалы интервалов или порядковые шкалы.
Изображение слайда
Изображение для работы со слайдом
35
Слайд 35: Различие «до» и «после». Критерий Вилкоксона
Критерий Вилкоксона
Изображение слайда
Изображение для работы со слайдом
36
Слайд 36: Различие «до» и «после». Критерий Вилкоксона
Изображение слайда
Изображение для работы со слайдом
37
Последний слайд презентации: Описательная статистика в SPSS : 1: Различие «до» и «после». Критерий Вилкоксона
Критерий Вилкоксона
Изображение слайда
Изображение для работы со слайдом
ЛБ_6
Дисциплина: Теоретические основы статистических исследований
Лабораторная работа № 6
Корреляционный анализ
При проведении корреляционного анализа
различают параметры и
непараметрические методы анализа
наличие зависимости.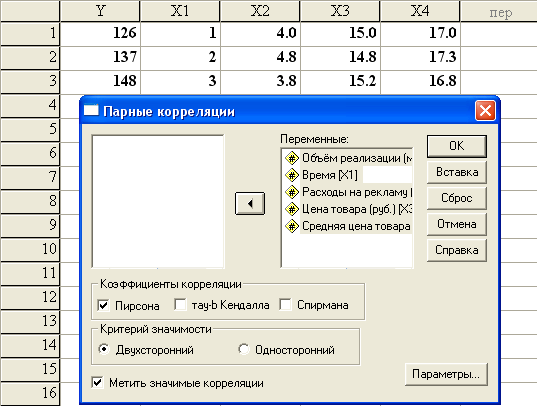
1. Параметрические методы оценки корреляции.Коэффициент линейной корреляции Пирсона
Коэффициент линейной корреляции отражает меру линейной зависимости между двумя переменными. Предполагается, что переменные измерены в интервальной или количественной шкале.
1.1. Реализация в SPSS
Для того, чтобы рассчитать коэффициент линейной корреляции Пирсона необходимо использовать следующую последовательность команд:
Анализ (Анализ) — Коррелят (Корреляция) — Двумерная (Двумерная)
В результате чего, откроется диалоговое окно (рис.1), в котором указать необходимо переменные, для которых будет рассчитан коэффициент корреляции Пирсона. И установить флажок в поле Pearson .
Рис .1. Диалоговое окно Двумерное Корреляции
После нажатия кнопки ОК на экран
будет выведена матрица корреляций
Пирсона для указанного числа.
Пример расчета коэффициентов линейной корреляции Пирсона для числа рост, вес_1, index_1 приведен на рис.2.
Рис.2. Матрица коэффициентов корреляции Пирсона
Значимая положительная корреляция в в этой таблице присутствует для всех сумма. Например, коэффициент корреляции между переменными высотой и вес, равный 0,732 (уровень значимости р = 0,001), говорит о тесной положительной связи между этим переменными. Т.е. Чем больше рост респондента, тем больше его вес.
1.2. Реализация в STATISTICA
Для того, чтобы рассчитать коэффициент линейной корреляции Пирсона необходимо использовать следующую последовательность команд:
Статистика (Статистики) — Базовая Статистика и Таблицы (Основные статистики и таблицы) — Корреляция матрицы (Корреляционные матрицы)
В результате откроется диалоговое окно
(рис.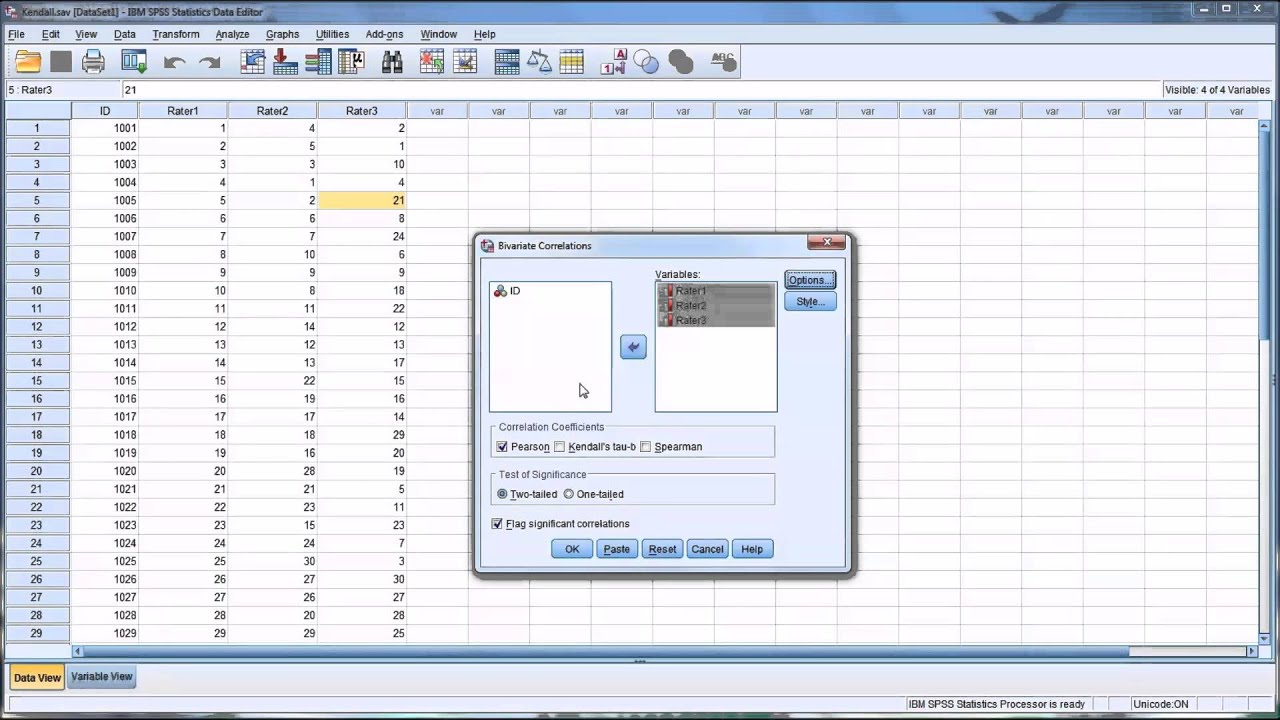 3.), в котором указать необходимо
переменные для расчета линейного
коэффициент корреляции Пирсона
3.), в котором указать необходимо
переменные для расчета линейного
коэффициент корреляции Пирсона
Рис .3. Диалоговое окно Продукт-Момент и Частично Корреляции
После нажатия на кнопку Резюме : Корреляции на экран будет выведена корреляционная матрица.
Пример расчета коэффициентов линейной корреляции Пирсона для числа рост, вес_1, index_1 приведен на рис.4.
Рис.4. Матрица коэффициентов корреляции Пирсона
2. Непараметрические методы оценки корреляции.
Коэффициенты Спирмена и Кенделла
Оба показателя, основаны на корреляции
не самих значений рассматриваемых
признаки, а их рангов. С их помощью
можно изучать и измерять связь не только
между количественными, но и качественными
(атрибутивными) признаками, ранжированными
определенным образом.
2.1. Реализация в SPSS
Для того, чтобы рассчитать коэффициенты ранговой корреляции Спирмена и Кенделла, необходимо использовать следующую последовательность команд:
Анализ (Анализ) — Коррелят (Корреляция) — Двумерная (Двумерная)
В открывшемся диалоговом окне Двумерное Корреляции (рис.1.) установить флажок в поле Kendall ’ s тау — б и Копейщик . После нажать на кнопку ОК на экран будет выведена матрица корреляций Спирмена и Кендалла для указанного числа.
Пример расчета коэффициентов ранговой корреляции Спирмена и Кендалла для пол секс, диета, вес_2, спорт_2 приведен на рис.5.
Рис.5. Матрица корреляций Спирмена и Кенделла
Из полученной матрицы видно, что
переменные диета и спорт_2
имеют тесную обратную связь. Т.к.
переменная диета принимает
два значения: 1- соблюдает и 2-не соблюдает,
то коэффициент корреляции равный -0,718
по Кендаллу и -0,79 по Спирмену можно
трактовать так: если респондент при
программе похудения придерживался
диеты, то он чаще занимался спортом.
Также обратную корреляцию имеет пара
числа sport_2 и weight_2,
что можно трактовать так: чем больше
респондент занимался спортом, участвуя
в программе похудения, тем меньше стал
вес после программы похудения.
Т.к.
переменная диета принимает
два значения: 1- соблюдает и 2-не соблюдает,
то коэффициент корреляции равный -0,718
по Кендаллу и -0,79 по Спирмену можно
трактовать так: если респондент при
программе похудения придерживался
диеты, то он чаще занимался спортом.
Также обратную корреляцию имеет пара
числа sport_2 и weight_2,
что можно трактовать так: чем больше
респондент занимался спортом, участвуя
в программе похудения, тем меньше стал
вес после программы похудения.
Значительную прямую корреляцию имеют пары объем: секс и диета (учитывая кодировку данных число это означает, что женщины соблюдают диету чаще, чем мужчины), вес_2 и диета (учитывая кодировку вариант диеты — если респондент не соблюдал диету во время программы похудения, то его вес после программы похудения укрепленного выше).
2.2. Реализация в STATISTICA
Для того, чтобы рассчитать коэффициенты ранговой корреляции Спирмена и Кенделла, необходимо использовать следующую последовательность команд:
Статистика (Статистики) — Непараметрические данные (Непараметрические) —
Корреляции (Корреляции)
В результате чего откроется диалоговое
окно (рис. 6.), в котором указать необходимо
переменные, для которых будут рассчитаны
коэффициенты корреляции.
6.), в котором указать необходимо
переменные, для которых будут рассчитаны
коэффициенты корреляции.
Рис.6. Диалоговое окно Корреляции
После нажатия кнопки Spearman ранг R на экран будет выведена матрица корреляций Спирмена, а после других кнопки Kendall Tau — матрица корреляций Кенделла.
Пример расчета коэффициентов ранговой корреляции Спирмена и Кендалла для пол секс, диета, weight_2, спорт приведен соответственно на рис.7. и рис.8.
Рис.7. Матрица корреляций Спирмена
Рис.8. Матрица корреляций Кендалла
Полученные результаты схожи с результатами расчета коэффициентов ранговой корреляции в пакете SPSS.
3. Частные корреляции.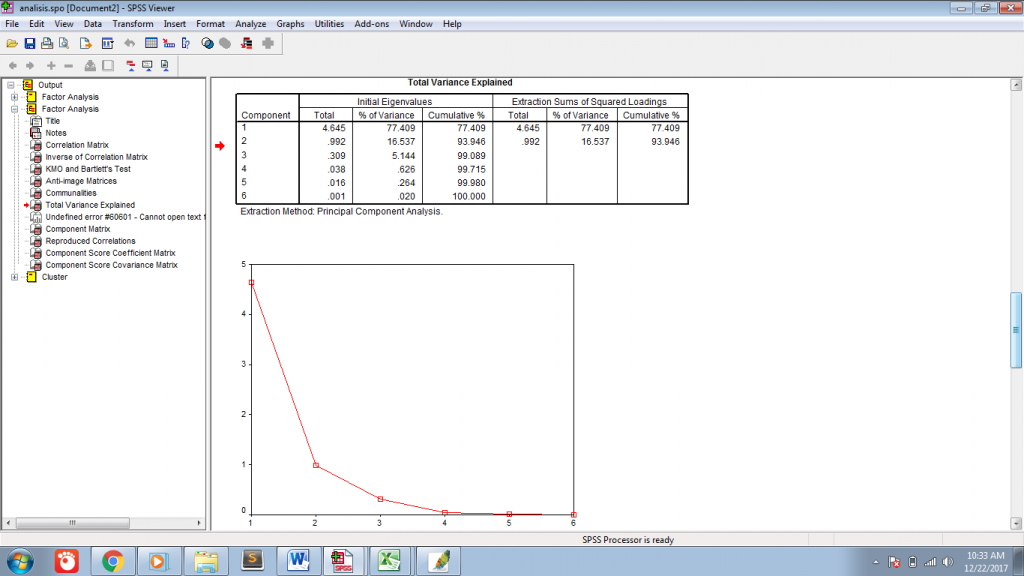 Выявление ложных
корреляций.
Выявление ложных
корреляций.
На практике иногда возникает ситуации, когда в результате корреляционного анализа обнаруживаются логически необъяснимые, противоречащие объективному опыту исследователя корреляции между двумя переменными (например, оказывается, что между уровнем дохода респондентов и есть детей в семье существует статистически значимая зависимость).В этом случае говорят о так называемой ложной корреляции, исследовать которую обеспечивают частные коэффициенты корреляции.
3.1. Реализация в SPSS
В SPSS коэффициент частной корреляции можно рассчитать используя соответствующую последовательность команд:
Анализ (Анализ) — Коррелят (Корреляции) — Частично (Частные)
В результате откроется диалоговое окно (рис.9.), в котором достигается достижение в поле Переменные переменные для которых нужно вычислить коэффициент корреляции, а в окно Контроллинг для — переменную, значение которой нужно исключить
Рис. 9. Диалоговое окно Частичное
Корреляции
9. Диалоговое окно Частичное
Корреляции
После нажатия кнопки ОК на экран будет выведена матрица частных коэффициентов корреляции.
Пример расчета коэффициентов частной корреляции для чисел высота и index_1 за исключением вариант веса_1 приведен на рис.10.
Рис.10. Матрица коэффициентов частной корреляции.
Рассчитанный коэффициент корреляции с высокой точностью (p <0,001) говорит о том, что существует тесная обратная связь между переменными высотой и index_1 (за исключением вариант веса_1), т.е. чем выше рост респондента, тем ниже его индекс массы тела. Заметим, что коэффициент линейной корреляции Пирсона для этих размер с высокой точностью (p = 0,001) давал значение 0,45 (рис.2.), что свидетельствует о прямой связи чис.
3.2. Реализация в STATISTICA
Для того, чтобы рассчитать коэффициент частная корреляции необходимо использовать следующая последовательность команд:
Статистика (Статистики) — Базовая Статистика и Таблицы (Основные статистики и таблицы) — Корреляция матрицы (Корреляционные матрицы)
В открывшемся диалоговом окне Продукт — Момент и Частично Корреляции (рис. 3.)
необходимо перейти на вкладку Дополнительно / участок где, щелкнув на
кнопку Частично корреляции . В открывшемся
окно, в поле Первый список указать переменные для которых нужно
вычислить коэффициент корреляции, а в
поле Второе список — переменную, значение которой нужно
исключить.
3.)
необходимо перейти на вкладку Дополнительно / участок где, щелкнув на
кнопку Частично корреляции . В открывшемся
окно, в поле Первый список указать переменные для которых нужно
вычислить коэффициент корреляции, а в
поле Второе список — переменную, значение которой нужно
исключить.
После нажатия кнопки ОК на экран будет выведена матрица частных коэффициентов корреляции.
Пример расчета коэффициентов частной корреляции для чисел высота и index_1 за исключением вариант веса_1 приведен на рис.11.
Рис.11. Матрица коэффициентов частной корреляции.
Индивидуальное задание:
Для обмена данными в пакетах MS Excel ( или Mathcad) , SPSS и Statistica рассчитать:
значение ковариации и коэффициент корреляции Пирсона,
коэффициенты корреляции Спирмена и Кенделла,
корреляционная матрицу,
коэффициент множественной корреляции ,
коэффициент частной корреляции,
коэффициент детерминации,
коэффициент конкордации.
Сделать выводы о наличии или отсутствии связи в каждом конкретном случае и о ее силе.
23.11.2020 Ирина Тюрина
С ноября 2020 года доступна новая версия программно-методического комплекса — Статкласс 1.7. Для образовательных учреждений с действующей академической лицензией переход на новую версию Статкласс 1.7 предоставляется бесплатно и для ее заказа заполнить форму.
Что нового?
В новой версии Статкласс 1.7 обновленное аналитическое ядро программного решения — IBM SPSS Statistics до 27 версии. Базовая комплектация программного обеспечения Статкласс включает теперь функционал не только обновленного модуля SPSS Statistics Base, но и дополнительные процедуры подготовки данных (ранее модуль Data Preparation) и более широкие возможности для выборочных оценок, с использованием метода бутсреп (ранее модуль начальной загрузки).
Наряду с калькулятором выборки обновленная версия Статкласс, после включения в нее 27 версии SPSS, включает теперь процедуры расчета мощности критериев при разных объемах выборок и, наоборот. Эти процедуры на лабораторных занятиях по прикладной статистике использовать теперь дополнительные инструменты измерения количества наблюдений для проверки или иной гипотезы.
Меню процедуры Анализ статистической мощности.IBM SPSS Statistics 27
Для оценки выборки в общем случае преподавателям или студентам необходимо выбрать вид эффекта (например, это может быть гипотеза о среднем значении, о доле, о коэффициенте корреляции, или о влиянии предиктора в регрессионной модели), указать ожидания величины эффекта в стандартизированных или абсолютных значенийх, пороговый уровень значимости, при котором нулевая гипотеза должна быть отвергнута, и желаемую мощность (т.е. надежность достижения порогового уровня значимости в случае, если эффект достижения размера действительно присутствует в генеральной совокупности).
Диалог процедуры Анализ статистической мощности для оценки корреляции Пирсона. Требуемая мощность: 0,8, ожидаемый выборочный коэффициент корреляции = 0,25 (соответствующий гипотезе h2), коэффициент, соответствующий гипотезе H0 = 0, двусторонняя проверка, уровень значимости 0,05. IBM SPSS Statistics 27
На выходе будет получена оценка большого размера выборки.
Расчет объема выборки / мощности в обновленной версии для следующих видов гипотез: [HTML_REMOVED] [HTML_REMOVED] Об одном среднем значении [HTML_REMOVED] О двух выборочных средних в независимых выборках [HTML_REMOVED] О двух выборочных средних в соответствующих выборках [HTML_REMOVED] О значимости фактора в однофакторной ANOVA (включая контрасты и парные сравнения) [HTML_REMOVED] Об одном доле [HTML_REMOVED] О двух долях в связанных выборках [HTML_REMOVED] О двух долях в независимых выборках [HTML_REMOVED] О величине коэффициента корреляции Пирсона [HTML_REMOVED] О ранговой корреляции Спирмена [HTML_REMOVED] О частной корреляции [HTML_REMOVED] О влиянии предиктора в модели линейной регрессии [HTML_REMOVED]
В процедурах среднего и однофакторного дисперсионного анализа (ANOVA) в обновленной версии SPSS добавлен расчет стандартизированных мер анализа величины эффекта. В отличие от статистической значимости, меры эффект не пытается доказать существование эффекта, а пытаются оценить его размер. Эффект может измеряться в абсолютном выражении, а может быть стандартизирован. В IBM SPSS Statistics размер эффекта для средних и ранее оценивался в некоторых «продвинутых» процедурахх линейных моделей, с 27 версией наиболее популярные тесты для средних из базового модуля также возвращать оценку эффекта и ее 95% доверительный интервал. Новые возможности стали доступны теперь в процедуре: t-проверки для одной выборки, для независимых выборок и для соответствующего выбора Однофакторный дисперсионный анализ (односторонний дисперсионный анализ) и оцениваемые контрасты.
Запрос вывода оценки эффекта при проверке гипотезе о среднем значении. IBM SPSS Statistics 27
Оценки эффекта эффекта — Коэна и Хеджеса и их доверительные интервалы в выводе процедуры t-критерия для среднего. IBM SPSS Statistics 27
В обновленной версии программного решения Статкласс, где в качестве аналитического ядра будет поставляться новая 27-й версии IBM SPSS, появилась распространенная мера согласованности двух классификаций -взвешенная каппа Коэна, при расчете которой учитывается порядок категорий. При анализе данных экспертных оценок теперь можно измерить, насколько схожи два эксперта в классификации объектов на заданное число групп. Или, например, соответствует классификация, сделанная прогностической моделью реальным классам объектов.
При анализе данных экспертных оценок теперь можно измерить, насколько схожи два эксперта в классификации объектов на заданное число групп. Или, например, соответствует классификация, сделанная прогностической моделью реальным классам объектов.
Начиная с 27-й версии SPSS пользователь может запрашивать построение матрицы корреляций, без дублирования значений относительно главного диагонали.
Матрица корреляции без дублирования элементов. IBM SPSS Statistics 27
Теперь верхнюю часть треугольника матрицы корреляции можно оставить пустой и не перегружать таким образом таблицу избыточными числовыми значениями.Дополнительно можно сделать матрицу еще более компактной, убрав элементы главной диагонали, не несущие в себе полезной информации.
В новой версии IBM SPSS в популярных процедурах построения частотных таблиц и кросстабуляций появилась возможность в один клик делать вывод более компактным, а получаемые таблицы — готовыми к публикации.
Диалоговое окно Таблицы сопряженности: вывод в ячейках.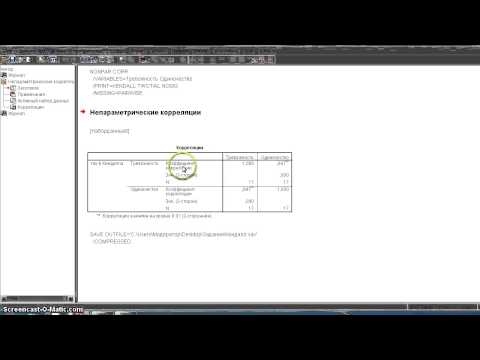 IBM SPSS Statistics 27
IBM SPSS Statistics 27
Например, с помощью опции Создать таблицу стилей АРА в диалоговом окне Вывод в ячейках можно вывести готовую кросс-таблицу, оформленную в стиле АРА.Итоговая таблица в стиле АРА будет очищена от вспомогательных элементов и заголовков строк и столбцов, а статистика позволит получить компактные наименования, что позволит сократить время на редактирование таблиц, предназначенных для научных публикаций в международных журналах.
В 27 версии SPSS в Мастере диаграмм появился новый встроенный шаблон для создания пузырьковых диаграмм сразу, на которых можно одномоментно отразить связь 4-х чисел: две количественных длины задают оси диаграммы, еще одна количественная — задает размер точки (или в данном случае — пузырька) , а с помощью категориальной пузырьки можно раскрасить по категориям.Возможность построения таких диаграмм в SPSS была давно, но для этого требовалось использовать встроенный язык GPL (язык производства графики). Теперь построить диаграмму можно достаточно быстро, без написания кода.
Диалог Мастера диаграмм с настройками размера пузырька для диаграмм разброса. IBM SPSS Statistics 27
В установках по умолчанию для форматирования диаграмм в новой версии SPSS появился предпросмотр диаграмм. Меняя ту или иную установку, пользователь сразу видит, как, приблизительно, она отразится на внешнем виде будущей диаграммы.
Диалог системных настроек Диаграмм. IBM SPSS Statistics 27
Кроме этого для пользователей SPSS появилась возможность быстро переключаться между предустановленными диаграммами. Нужный стиль можно выставить как в глобальных настройках системы (Правка — Параметры), так и выбрать индивидуально в диалоге Мастера диаграмм. Например, зная, что диаграмму предстоит опубликовать в черно-белом исполнении, в Мастере диаграмм, при построении графика можно выбрать предустановленный стиль Publication Gray.
Диалог Мастера диаграмм с настройками внешнего вида диаграмм. IBM SPSS Statistics 27
На всех панелях инструментов в версии SPSS по умолчанию появилась кнопка сквозного поиска, которая упрощает поиск нужных функций в SPSS, в справке и наверняка пригодится в образовательных учреждениях при его изучении. Как это работает? При вводе текста в строку поиска SPSS ищет введенный термин среди меню и разделов он-лайн справки. Так, например, при вводе «коррел» в окне появляется список процедур (диалоговых окон), в названии которых есть слово «корреляция», а также разделы справки, в том числе — примеры кейс-стади, в говорится про корреляционный анализ.Выбор нужного меню списка сразу же открывает либо соответствующее диалоговое окно, либо браузер со страницей справочной системы.
Диалог сквозного поиска в IBM SPSS Statistics 27
Вместе с новым SPSS и установкой Статкласс 1.7 теперь будет разворачиваться и более современная версия интерпретатора Python — 3.8.2. Разумеется, вместе с этой версией устанавливаются и соответствующие адаптированные библиотеки, обеспечивающие интеграцию Python и SPSS.
Таким образом, приобретая Статкласс 1.7. преподаватели, научные сотрудники и студенты вузов получат гораздо больше функционала, чем раньше.
Если Вы хотите использовать возможности Статкласс 1. 7, мы подберем Вам оптимальную комплектацию и вариант лицензирования. Наряду с локальными и конкурентными лицензиями вузы могут приобрести специальные лицензии с домашними установками для преподавателей и студентов, которые в условиях дистанционного обучения приобрели еще большее значение для эффективного использования в процессе обучения статистических компетенций.Заказать консультацию Вы можете, заполнив контактную форму.
7, мы подберем Вам оптимальную комплектацию и вариант лицензирования. Наряду с локальными и конкурентными лицензиями вузы могут приобрести специальные лицензии с домашними установками для преподавателей и студентов, которые в условиях дистанционного обучения приобрели еще большее значение для эффективного использования в процессе обучения статистических компетенций.Заказать консультацию Вы можете, заполнив контактную форму.
Об авторе
Ирина Тюрина
Решения для прогнозирования
★ Тест ранговой корреляции Спирмена
Пользователи также искали:
коэффициент ранговой корреляции спирмена, корреляция спирмена statistica, на чем основан тест ранговой корреляции спирмена, подсчет корреляции спирмена, ранговая корреляция спирмена, тест ранговой корреляции спирмена excel, тест ранговой корреляции спирмена онлайн, вычислите значение непараметрического коэффициента ранговой корреляции спирмена, Спирмена, спирмена, корреляции, ранговой, Тест, тест коэффициент, корреляция, ранговая корреляция спирмена, подсчет корреляции спирмена, корреляция спирмена statistica, отличиться онлайн, основан, коэффициент, ранговая, подсчет, вычислите, значение, непараметрического, статистика, Тест ранговой корреляции Спирмена, на чем основан тест ранговой корреляции спирмена, коэффициент ранговой корреляции спирмена, вычислите значение непараметрического коэффициента ранговой корреляции спирмена, тест ранговой корреляции спирмена онлайн, тест ранговой корреляции спирмена excel, тест ранговой корреляции спирмена,
Корреляция Спирмена. Частная корреляция.
Частная корреляция.
Корреляция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменение одной из этих величин приводит к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Коэффициент корреляции Спирмена (коэффициент ранговой корреляции Спирмена) — мера линейной связи между случайными величинами.Корреляция Спирмена является ранговой, то есть для оценки силы связи используются не численные значения, соответствующие им ранги. Коэффициент инвариантен по отношению к любому монотонному преобразованию шкалы измерения. Коэффициент ранговой корреляции Спирмена — это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя различными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.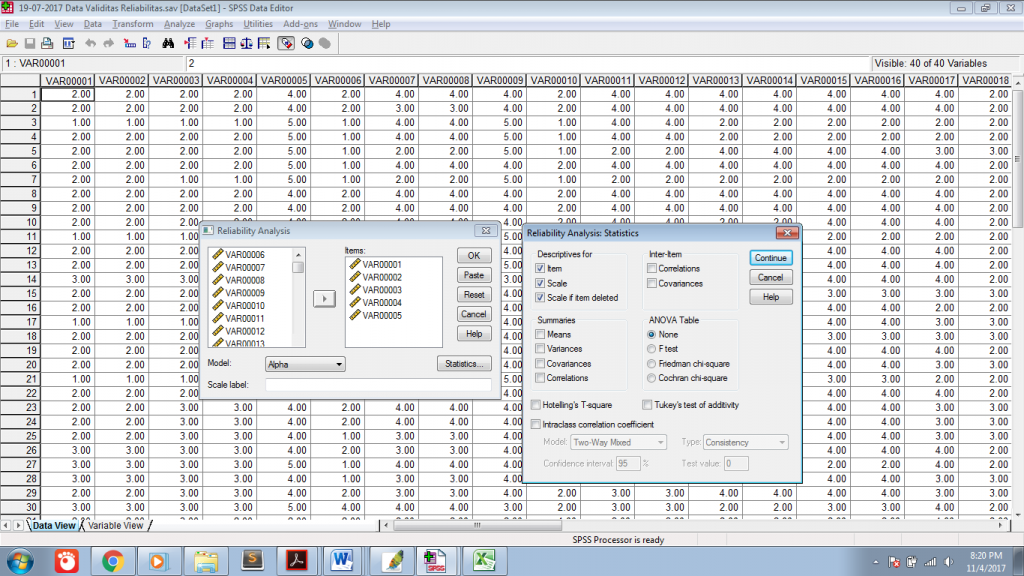
Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:
1) Сопоставать каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию).
2) Определить разности рангов каждой пары сопоставляемых значений.
3) Возвести в квадрат каждую разность и суммировать полученные результаты.
4) Вычислить коэффициент корреляции рангов по формуле :.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам.Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
где — сумма квадратов разностей рангов, а — число парных наблюдений.
При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения показателя слабой связи тесноты связи; значения более 0,4, но менее 0,7 — показателями высокой тесноты связи, а значения 0,7 и более — показателями высокой тесноты связи.
Мощность коэффициента ранговой корреляции Спирмена несколько уступает параметрического коэффициента корреляции.
Коэффицент ранговой корреляции целесообразно применить при наличии небольшого количества наблюдений. Данный метод может быть использован не только для количественно выраженных данных, но и в других случаях, когда регистрируются значения параметров описательными параметрами.
Частная корреляция. Корреляция между двумя переменными, вычисленная после воздействия всех других чисел, называется частной корреляцией. Например, волосы могут коррелировать с ростом человека (чем выше человек, тем короче волосы), однако эта зависимость становится слабой или совсем исчезает, если устранить влияние пола наблюдаемых людей, поскольку обычно ниже ростом и имеют более длинные волосы, чем мужчины. В случае нескольких случайных величин — выражение одной из этих величин (предиктанда) от одного из других величин (предикторов) при условии, что остальные предикторы сохраняют постоянные значения.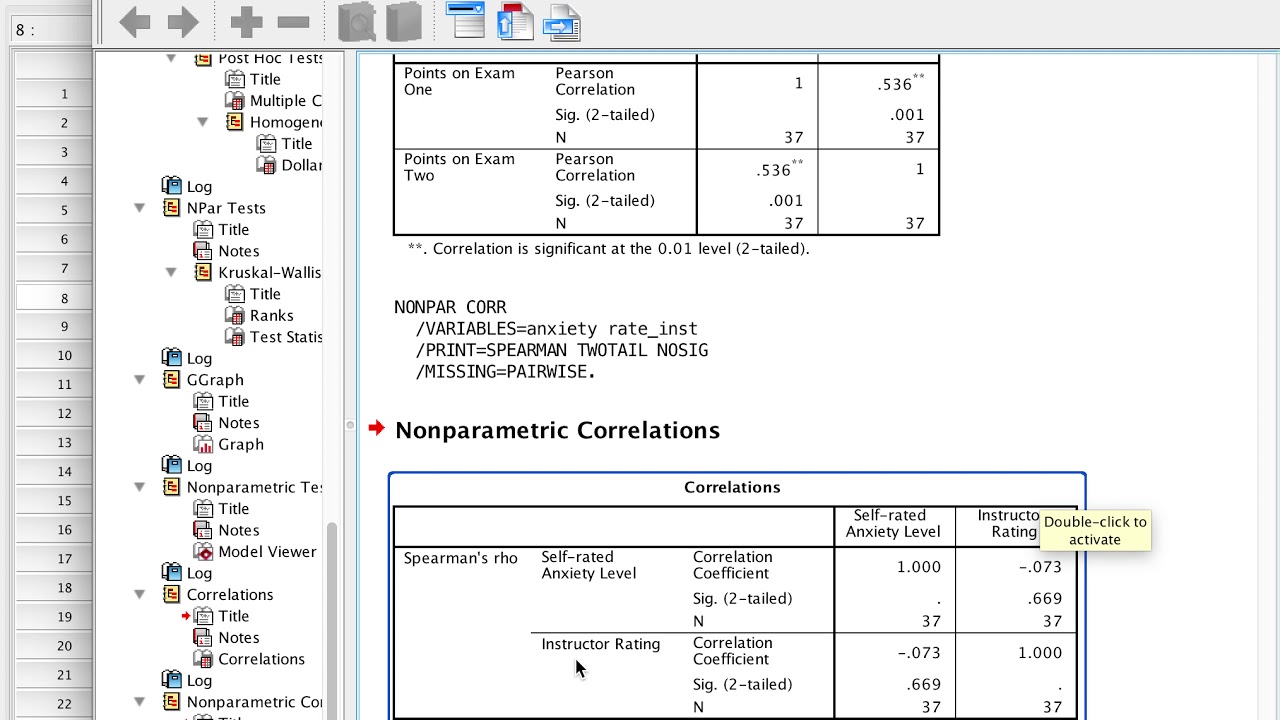 Коэффициент частной корреляции rX, Y, Z между X, Y, Z между X, выражается так:
Коэффициент частной корреляции rX, Y, Z между X, Y, Z между X, выражается так:
где rX Z, rX Y и т. д. — коэффициенты линейной корреляции между парами чисел, вычисленные независимо от третьей переменной.
Если исследовать достаточно большую совокупность мужчин и сопоставить размер обуви с уровнем образованности, то между этими двумя переменными можно хоть и небольшую, но в то же время значимую корреляцию.Это корреляция может послужить примером так называемой ложной корреляции. Здесь статистически значимый коэффициент корреляции является не проявлением некоторой причинной связи между двумя рассматриваемыми переменными, а в большей степени обусловленной другой переменной.
В рассматриваемом примере такой образец является рост. С одной стороны существует некоторая незначительная корреляция между ростом и уровнем образования, а с другой — вполне объяснимая и логичная связь между ростом и размером обуви. Вместе эти две корреляции приводят к возникновению ложной корреляции. Для исключения такой альтернативной необходимой расчёт так называемой частной корреляции.
Вместе эти две корреляции приводят к возникновению ложной корреляции. Для исключения такой альтернативной необходимой расчёт так называемой частной корреляции.
Если использовать коррелирующие переменные индексы 1 и 2, изменяющуюся переменную — индекс 3, и попарно рассчитать корреляционный коэффициент (Пирсона) r12, r13, и r23, то для частных корреляционных коэффициентов получим:
Достаточно давно в социологических исследованиях, проводимых в Германии, значительно выросло отношение населения к приезжим рабочим-иностранцам.Для этого было сформулировано несколько отдельных вопросов. Ответы на вопросы суммировались. Сумма могла принимать значения от 0 до 30, причём большее значение соответствует более негативному отношению к приезжим рабочим.
Среди номеров дополнительных учитывались: возраст опрашиваемых и частота посещения церкви. Последнейике были присвоены значения от 1 (никогда) до 6 (по меньшей мере, 2 раза в неделю). Небольшая выборка из оригинальных данных опроса (35 респондентов с этими тремя переменными) наводится в файле кирче.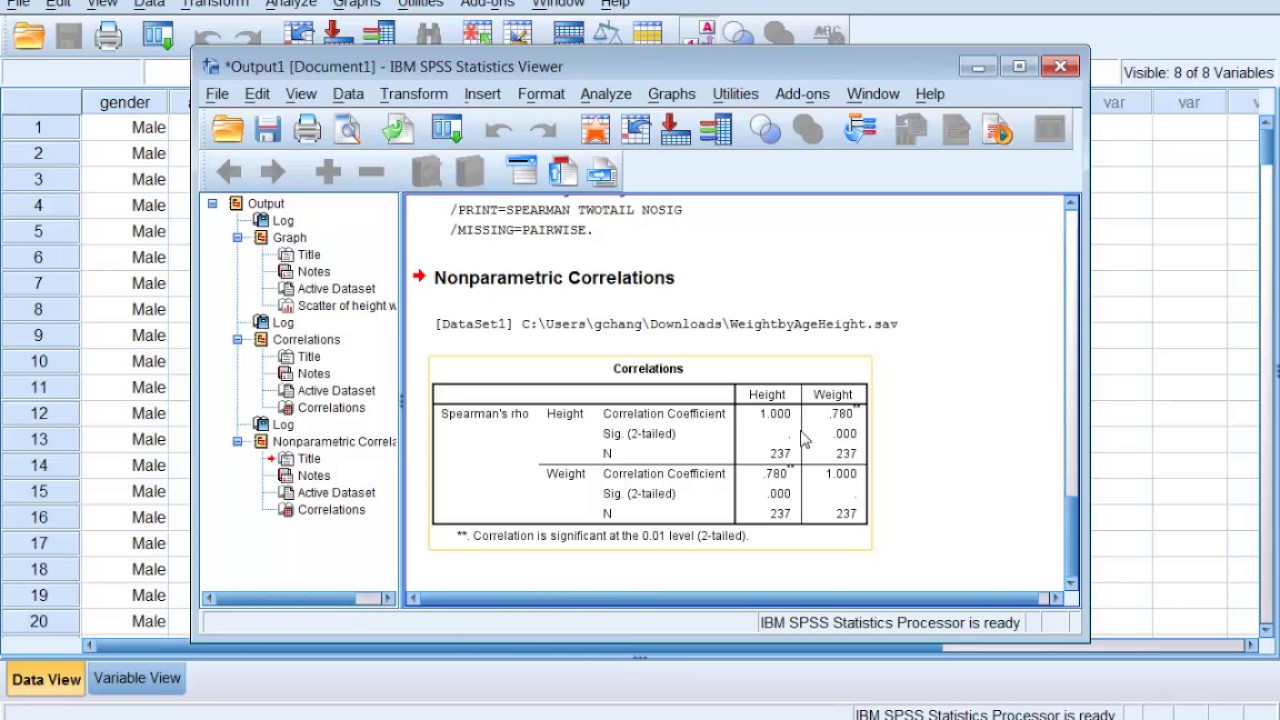 сав. Откройте этот файл, если Вы хотите самостоятельно провести следующие расчёты.
сав. Откройте этот файл, если Вы хотите самостоятельно провести следующие расчёты.
Если подсчитать корреляции между этими тремя переменными, то при выборе коэффициентов Пирсона для анализа взаимосвязи, получатся следующие результаты закроем глаза на то, что одна из частоты посещения церкви, имеет порядковую шкалу):
Корреляции (Корреляции)
ALTER (Возраст) | ГАСТ (Приезжий) | КИРХЕ (Церковь) | ||
ALTER (Возраст) | Корреляция Пирсона (Корреляция по Пирсону) Sig.(2-сторонняя) (Значимость (2-сторонняя)) N | 1 000 35 | , 468 дюймов, 005 35 | , 779 «, 000 35 |
ГАСТ (Приезжий) | Корреляция Пирсона (Корреляция по Пирсону) Sig. | , 468 дюймов, 005 35 | 1 000 35 | , 432 **, 010 35 |
КИРХЕ (Церковь) | Корреляция Пирсона (Корреляция по Пирсону) Sig.(2-сторонняя) (Значимость (2-сторонняя)) N | , 779 «, 000 35 | , 432 «, 010 35 | 1 000 35 |
«* Корреляция значима на уровне 0,01 (2-сторонняя). Корреляция является закономерной на уровне 0,01 (2-стороння).
Принимая во внимание полярность, полученные результаты можно трактовать, к примеру, таким образом, что частые посещения церкви коррелируют с отрицательным отношением к приезжим рабочим (r = 0,432).Прежде, чем поставить в упрёк церкви враждебность по отношению к иностранцам, нужно учесть влияние возраста. Он также коррелирует с враждебным отношением к иностранным рабочим (r = 0,468) и сильно коррелирует с посещением церкви (r = 0,779). Таким образом, возникает подозрение, что является искажающим признаком, виновным в ложной корреляции между посещением церкви и отрицательным отношением к иностранным рабочим. Докажем это путём расчёта частных корреляционных коэффициентов.
Он также коррелирует с враждебным отношением к иностранным рабочим (r = 0,468) и сильно коррелирует с посещением церкви (r = 0,779). Таким образом, возникает подозрение, что является искажающим признаком, виновным в ложной корреляции между посещением церкви и отрицательным отношением к иностранным рабочим. Докажем это путём расчёта частных корреляционных коэффициентов.
- Откройте файл kirche.sav.
- Выберите в меню Анализировать … (Анализ) Сопоставить … (Корреляция) Частично … (Частная)
Откроется диалоговое окно Частные корреляции.
- Перенесите переменные gast и kirche в поле признаков, а переменную альтернативу в поле контрольных чисел и введите предварительную установку для двухстороннего теста значимости.
При помощи щелчка на кнопке Опции… (Параметры) стандартной обработкой пропущенных значений, Вы можете организовать расчёт среднего значения, стандартного отклонения и вывод «корреляций нулевого порядка» (то есть простых корреляционных коэффициентов).
В одной из иллюстраций, приведенных в примере, приведен пример расстановки частных корреляций первого порядка, SPSS выдаёт корции высших порядков.
- Начните расчёт щелчком на кнопке ОК.Вязкие просмотр появится следующий результат:
Коэффициенты частичной корреляции (Частичные корреляционные коэффициенты) | ||
Контроллинг для … A (Контрольная переменная) ( | LTER Возраст) | |
GAST (Приезжий) | ГАСТ (Приезжий) 1,0000 (0) P =, | KIRCHE (Церковь), 1215 (32) P =, 494 |
КИРХЕ (Церковь) | , 1215 (32) P =, 494 | 1,0000 (0) P =, |
Вас, возможно, удивит, что в данном случае всё ещё выводится старый вариант результатов, соответствующий прежним версиям SPSS. Результаты включают: частный корреляционный коэффициент, число степеней свободы (число наблюдений минус 3) и уровень значимости. Исходя из полученных результатов, можно сделать вывод.
Результаты включают: частный корреляционный коэффициент, число степеней свободы (число наблюдений минус 3) и уровень значимости. Исходя из полученных результатов, можно сделать вывод.
Рис. 15.3: Диалоговое окно Partial Correlations (Частичные корреляции)
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимостьЭкспериментальная психология и статистика для психологов.(Лекция 2)
1. Экспериментальная психология и статистика для психологов (лекция 2)
к.полит.н. Зеликсон Денис ИгоревичПлан лекции
1.
2.
3.
4.
5.
Корреляции между переменными
Линейная регрессия
Хи-квадрат
Т-статистика
Непараметрические методы
Вопрос 1.
 Научная проблема в психологии
Научная проблема в психологии не формируется путем:
1. Наблюдений за явлениями
2. Выведений гипотез из теории
3. Анализа практических проблем
4.Развития отдельной школы (культурноисторический подход)
Вопрос 2. К видум экспериментальных
исследования в психологии не относится:
1. Лонгитюдное исследование
2. Межсубъектный эксперимент
3. Квазиэксперимент
4. Внутрисубъектный эксперимент
Вопрос 3. К критерием опросника
отношение:
1. Надежность и наличие нескольких шкал
2. Объективность и наличие одной шкалы
3. Валидность и наличие нескольких шкал
4. Валидность, надежность и объективность
Вопрос 4.Надежность опросников
определяется критерием
1. Хи-квадрат однородность
2. Альфа-Кронбаха
3. R-Спирмена
4. Тест-ретест
Вопрос 4. При нормальном
распределении, M = 20 и SD = 4, результат
опросника в 10 примен в Z, равной?
1. Z = 2,5
2.
 Z = 1,8
Z = 1,8 3. Z = -2,5
4. Z = — 2,2
Вопрос 5. Ошибка первого рода — это:
1. Неверное принятие H0 в силу низкой
статистической значимости
2. Верное принятие H0 в силу низкой
статистической значимости
3.Неверное отклонение h2 при верной h2
4. Неверное принятие h2 при верной H0
Вопрос 6. К элементам описательной
статистики не относится:
1. Статистическая значимость
2. Размах
3. Медиана
4. Стандартное оклонение
1. Корреляции между переменными
Корреляция — ассоциация (взаимосвязь) между
переменными.
линейная и линейная
монотонная и не монотонная
Коэффициент корреляции — статистический
показатель вероятностной связи между двумя
переменными
говорит об одномоментном двух
или более психологических феноменов
не говорит о причинно-следственной связи
между феноменами
Монотонная и не монотонная связь
Коэффициент корреляции
Z статистика и корреляции
Возможные направления связи
Частная корреляция
переменные связаны между собой через
третью переменную
третья переменная питает взаимосвязь
первых двух
исключаем влияющую альтернативную на
корреляцию первых двух
Коэффициент корреляции и величина эффекта
коэффициент корреляции = величина эффекта
сила — вероятность получения значимой
корреляции
Планирование корреляционного
исследования
Корреляционная матрица исследования
Коэффициент детерминации
величина изменчивости одной изза изменчивости другой
коэффициент корреляции (R2)
Статистические критерии для корреляции
Пирсона
интервальные переменные
нормальное распределение (не
обязательно)
мера линейной связи
Спирмена и Кендалла
порядковые или порядковая и
интервальная переменные
нелинейная связь
Phi-коэффициент сопряженности
номинальные переменные
необходимо равенство количества
номинальных данных
Корреляция Пирсона в SPSS
анализ
корреляции
парные
перенос переменной в правую таблицу
Пирсона
ОК
Корреляция Спирмена и Кендалла в SPSS
анализ
корреляции
парные
перенос переменной в правую таблицу
Спирмена и / или Кендалла
ОК
Phi-коэффициент сопряженности в SPSS
анализ
описательные статистики
таблицы сопряженности
перенос переменной в правую таблицу
статистика
ФИ и и В Крамера
продолжить
ОК
2.
 Линейная регрессия
Линейная регрессия Множественная регрессия
выявление наиболее связанных
факторов с каким-либо феноменом
возможность делать предсказания об
изменение феномена
способ обработки данных, когда другие методы
недоступны
Методы линейной регрессии
ввод: все переменные в уравнении
пошагово: комбинация включения и
исключение
удалить: поочередное значимых удаление
факторов
Вывод данных
F — критерий Фишера
R — коэффициент множественной корреляции
R2 — коэффициент детерминации
B — коэффициент регрессии
b — стандартизированный коэффициент
регрессии
Линейная регрессия в SPSS
анализ
регрессия
линейная
перенос переменной в правую таблицу
(зависимая)
перенос переменной в правую таблицу
(независимые)
метод (ввод, удалить, пошагово)
ОК
3.Хи-квадрат
Назначение критерия
значение номинальных чисел
можно использовать для номинальных и
ранговых (низкий, средний, высокий)
1.
 сравнение выборки с
сравнение выборки с теоретическим: кто чаще … мужчины (1) или
женщины (0)?
2. сравнение наблюдаемых распределений частот:
зависит ли предпочтение в чем-то (1, 2, 3 …) от
пола (0 или 1)?
3. сравнение одного события среди других событий
со случайным распределением: наблюдается ли
закономерность в чередовании (1, 1, 0, 1, 0…)
чего-либо?
Хи-квадрат и размер эффекта
ФИ и В Крамера
Хи-квадрат и мощность
Планирование исследования
Вывод данных
Хи-квадрат Пирсона
степени свободы: количество количества
градаций минус 1
асс. значимость: вероятность случайной
связи
Хи-квадрат независимости в SPSS
анализ
описательные статистики
таблицы сопряженности
перенос переменной в правую таблицу
(строки)
перенос переменной в правую таблицу
(столбцы)
статистика
Хи-квадрат Фи и V Крамера (Ета)
продолжить
вывести кластеризированные.
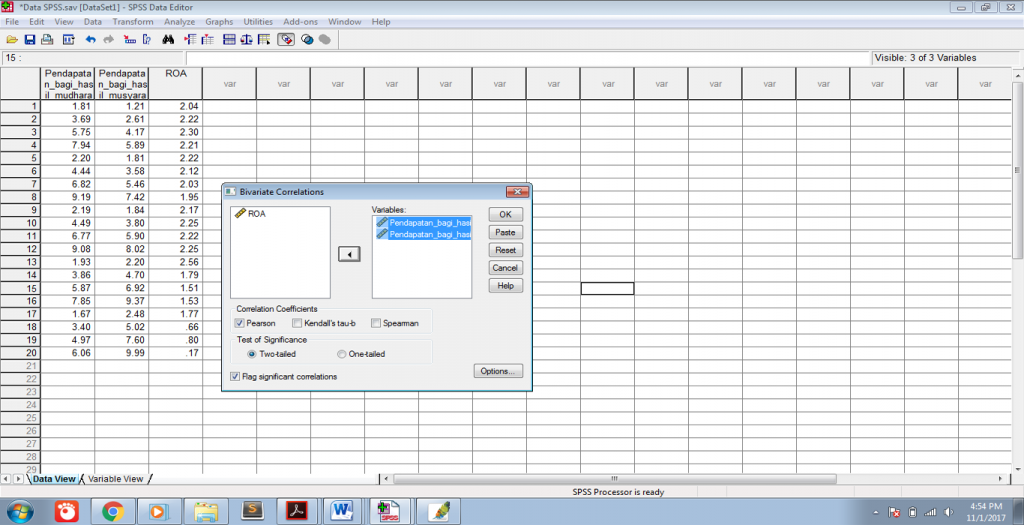 …
… ОК
4. Т-статистика
Назначение t-статистики
для независимок (среднее значение
двух выборок)
для парных выборок (до и после)
одновыборочный (среднее значение с
эталоном)
t-критерий для независимых выборок
проверяет гипотезу о том, отличаются ли
средние значения двух ГС между собой
а) дисперсии выборок при этом примерно
одинаковы
б) графическое изображение не отличается
от нормального
если а) и б) не выполняются, то используем
критерий Манна-Уитни
F — критерий который показывает равенство
дисперсий выборок (p> 0,05)!
t-критерий для независимых выборок и
мощность
t критерий для парных выборок
проверяет гипотезу о том, отличаются ли
средние значения двух выборок («до» и
«После»)
а) данные положительно коррелируют
б) графическое изображение не отличается
от нормального
если а) не выполняется, то используем tкритерий для независимых выборок
если б) не выполняется, то используем
критерий Уилкоксона
t-критерий для парных выборок и мощность
t-критерий для независимых выборок в SPSS
анализ
сравнение средних
T-критерий для независимых выборок
перенос переменной в правую таблицу
(проверяемые)
перенос переменной в правую таблицу
(группа)
задать группу
продолжить
ОК
t-критерий для парных выборок в SPSS
анализ
сравнение средних
T-критерий для парных выборок
перенос переменной в правую таблицу
продолжить
ОК
5.
 Непараметрические методы
Непараметрические методы Условия применения критериев
Манн-Уитни: две независимые выборки
Уилкоксона: две зависимые выборки
Краскела-Уоллеса:> 2 независимых выборок
Фридмана:> 2 зависимых выборок
распределение по признаку в ГС
отличается от нормального
различия в дисперсиях тогда, когда их не
должно быть
маленькая выборка
наличие выбросов
Манн-Уитни в SPSS
анализ
непараметрические степень
устаревшие диалоговые окна
критерий для двух независимых выборок
перенос переменной в правую таблицу
перенос групп в правую таблицу
задать группы (1, 2)
ОК
Уилкоксон в SPSS
анализ
непараметрические степень
устаревшие диалоговые окна
критерий для двух связанных выборок
перенос переменной в правую таблицу
ОК
Краскела-Уоллеса в SPSS
анализ
непараметрические степень
устаревшие диалоговые окна
критерий для К независимый выборок
перенос переменной в правую таблицу
перенос групп в правую таблицу
задать группы (1, 2, 3)
ОК
Исследование гемограмм пациентов
Исходные данные
Импорт из Excel в STATISTICA
Визуальный анализ
Диаграмма рассеяния
Способ 1
Способ 2
Средство Кисть
Диаграмма Вороного
Описательный (дескрипитивный) анализ гемограмм
Анализ выбросов
Корреляционный анализ
Корреляции Пирсона
Корреляции Спирмена и Кендалла
Исследование эффективности лечения: введение новой модели
Цель дальнейшего исследования
Проверка гипотезы о нормальности
Сравнение выборок
Какой метод лечения более эффективен?
Есть ли существенное различие состояний до и после лечения?
Исходные данные
Исходная таблица данных в формате Excel.
Содержит информацию о 150 пациентах.
Четыре столбца содержат значения показателей их гемограмм — эритроцитов (в 10 12 / л), тромбоцитов (10 9 / л), лейкоцитов (10 9 / л), гемоглобина (г / л).
Импорт из Excel в STATISTICA
Шаг 1. При попытке открытия файла системы STATISTICA (через меню Файл / Открыть) программа предложит нам на выбор несколько вариантов.
Выберем второй пункт.
Шаг 2. Далее необходимо выбрать номер таблицы в таблице Excel, который содержит нужную нам информацию. Сделать это очень просто.
Выбреем Лист 1 и нажмём ОК.
Шаг 3. Далее вам необходимо:
указать диапазон значений во внешнем файле, который будет импортирован;
решить, надо ли импортировать наблюдений и число;
сохранить (или нет) формат ячеек из исходной таблицы.

Поставим галочки во все поля и нажмём ОК.
Шаг 4. Теперь в программе STATISTICA открыта таблица.
Сохраним её под именем Гемограмма.sta.
Шаг 4. Введём дополнительную информацию о параметре.
Для этого выберем в пункт Данные / Все характеристики число .
В появившемся диалоге Редактор спецификаций число можно: указать длинные имена, коды пропущенных данных, добавить новые переменные или удалить старые и т.д.
Визуальный анализ
Вначале данные нужно увидеть…
Система STATISTICA включает широкий спектр графических методов для визуального представления результатов исследования. Все графические средства STATISTICA возможность выбора встроенного аналитического метода анализа и содержат большой набор, позволяющий пользователю интерактивно управлять отображением информации на экране.
Диаграмма рассеяния
Построим диаграмму рассеяния для переменных Тромбоциты . Сделать это очень просто.
Из медицинской практики известно, что увеличение числа тромбоцитов в крови может привести к тромбозу.
Для больных со слишком большим уровнем тромбоцитов в крови построим диаграмму рассеяния Номер пациента и Тромбоциты .
Врач определяет критический уровень количества тромбоцитов в крови для проведения операции.Пусть это значение равно 250.
Проведём горизонтальную прямую, соответствующему значению.
Это можно сделать двумя способами.
Способ 1
Выберем из раскрывающегося списка пункта Параметры графика . В появившемся окне перейдём на закладку Ось: Дополнительные риски .
Выберем Ось — Левая Х , укажем Положение = 250, поставим галочку в окне сетка.
Можно также настроить тип и толщину линии. Для внесения изменений нажмём на кнопку Сетка .
В итоге на диаграмме рассеяния отображается прямая Тромбоциты = 250.
Способ 2
Воспользуемся панелью Графические инструменты .
Выберем рисование стрелки и соответствующую прямую на графике
Как и раньше, можно настраивать опции построенного объекта.
Теперь выделим пациентов, количество тромбоцитов в крови которых превышает данный уровень.
Для этого воспользуемся средством Кисть .
Средство Кисть
Средство Кисть является очень важным для визуального анализа данных.
Нажмём на кнопку 2M Закрашивание на панели инструментов.
Выделим точки, соответствующие наблюдения, лежащим выше, прямой Тромбоциты = 250.
Если мы теперь откроем таблицу Редактор данных графика , то отмеченные наблюдения будут выделены красным цветом.
Диаграмма Вороного
Построим диаграмму Вороного по переменным Гемоглобин и Тромбоциты . Сделать это очень просто.
На диаграмме Вороного значения двух чисел X и Y изображаются, как на диаграмме рассеяния, а затем пространство между отдельными точками данных делится границами, окружающими каждую точку данных, на области по следующему принципу: каждая точка области находится ближе к заключенной внутри точки данных, чем к любой другой соседней точке данных.
Приведем пример практического использования диаграммы Вороного.
Предположим, что на анализ поступил новый больной.
Для назначения лечения было бы полезно знать, какая гемограмма ему наиболее близка. Это можно сделать с помощью диаграммы Вороного.
Пусть в поступившей гемограмме указаны значения: Тромбоциты = 220 и Гемоглобин = 105. Проведём на графике соответствующие прямые; точка пересечения прямого будет соответствовать новому пациенту.
Проведём на графике соответствующие прямые; точка пересечения прямого будет соответствовать новому пациенту.
Выявим наблюдение, которое является «хозяином» области, которое попадает данное наблюдение.
Для этого воспользуемся средством Кисть .
Описательный (дескриптивный) анализ гемограмм
Вычислим описательные статистические значения для чисел, значения информации о гемограммах. Сделать это очень просто.
Шаг 1. Запустим модуль Основные статистики и таблицы .
Выберем пункт Описательные статистики . Нажмём ОК .
Шаг 2. Выбор числа
Шаг 3. На вкладке Дополнительно укажем интересующие нас статистики.
Нажав OK , получим таблицу с описательными статистиками.
Описательные статистики по группам
Достаточно часто необходимость вычислить описательные статистики отдельно по каждой группе наблюдений.
Например, вычислим средние значения показателей гемограммы отдельно для каждой группы, а также для мужчин и для женщин.
Шаг 1. В диалоге Основные статистики и таблицы выберем пункт Группировка и однофакторный ДА .
В окне Внутригрупповые статистики и корреляции перейдём на вкладку Списки таблиц .
Шаг 2. Выберем группирующие переменные.
Шаг 3. Выберем зависимые переменные.
Нажмём на кнопку OK в диалоге Внутригрупповые статистики и таблицы .
В рабочей книге STATISTICA появится таблица, содержащая значения средних по группам.
Анализ выбросов
Выбросами резко выделяются наблюдения, например, пациенты с избыточным числом тромбоцитов.
Выявление выбросов осуществляется посредством двумерных диаграмм размаха.
Построим диаграмму размаха по типу Тромбоциты .
Выберем в меню пункт Графики / 2M Графики / Диаграммы размаха . В появившемся окне перейдём на вкладку Дополнительно .
Укажем переменные.
Пока что мы не будем указывать группирующую переменную.
Отметьте, что вкладка на Дополнительно окна 2M Диаграмма размаха Вы можете настроить эффекты наблюдений — выбросов (например, Вы можете указать Коэффициент выбросов ).
Нажмём ОК в диалоге 2M Диаграмма размаха .
На диаграмме размаха отмечены четыре выброса — три «слишком больших» значения и одно «слишком маленькое».
Визуально анализируя диаграмму размаха.
Определим, какие именно наблюдения выбросами. Один из способов нам уже известен — можно построить диаграмму рассеяния для числа Номер наблюдения и Тромбоциты и при помощи средства Кисть привлечь нужные наблюдения.
Опишем другой способ. Расположим наблюдения по убыванию модели Тромбоциты .
Для этого выберем из пункта Данные / Отсортировка .
В появившемся окне укажем параметры Ключа 1 .
После кнопки OK наблюдения в исходной таблице данных расположены в порядке убывания стоимости Тромбоциты .
Теперь мы можем определить, какие наблюдения выбросами — это первые три и последнее наблюдения в таблице.Итак, «нестандартный» уровень тромбоцитов в крови выявлен у пациентов номер 71, 87, 79 и 97.
Теперь вновь вызовем диалог 2M Диаграмма размаха и зададим в окне Переменные в качестве группирующей переменную Пол .
Например, значение Тромбоциты = 300, исчезающий выбросом для наблюдений, рассмотренных вместе, оказывается «нормальным» при рассмотрении только группы женщин.Есть и примеры обратного: значение Тромбоциты = 73 выбросом для группы мужчин, но при рассмотрении всех наблюдений оно оказывается «нормальным».
Корреляционный анализ
Вычислим корреляции между переменными Var4 — Var7 . Сделать это очень просто.
Корреляции Пирсона
Запустим модуль Основные статистики и таблицы . В появившемся окне выберем пункт Парные и частные корреляции .
Отобразится окно Парные и частные корреляции .
Нажмём на кнопку Квадратная матрица и укажем переменные.
После нажатия кнопки OK в диалоге Парные и рабочие корреляции в рабочей книге добавится таблица с коэффициентами корреляции между указанными переменными.
Итак, почти все переменные попарно зависимы; исключение составляет пара Эритроциты — Тромбоциты .
Корреляции Спирмена и Кендалла
Шаг 1. Запустим модуль Непараметрическая статистика . Выберем пункт Корреляции Спирмена, тау Кендалла, гамма .
В появившемся диалоге Ранговые корреляции перейдём на вкладку Дополнительно .
Шаг 2. Зададим переменные.
Шаг 3. Нажмём на кнопку Спирмена R в диалоге Ранговая корреляция .
Теперь вернёмся в окно Ранговая корреляция и нажмём на кнопку Тау Кендалла .
Обратите внимание: коэффициент корреляции Спирмена между переменными Эритроциты и Тромбоциты оказался статистически значимым, в то время как коэффициенты корреляции Кендалла — нет. Это объясняется тем, что коэффициент корреляции Спирмена сильнее реагирует на несогласие ранжировок.
Визуально проанализируем зависимость между переменными.С этой целью построим Матричный график .
Нажмём на кнопку Матричный график в диалоге Ранговые корреляции .
Другой способ построения подобного графика: можно выбрать из меню пункт Графика / Матричные графики.
Исследование эффективности лечения: введение новой модели
Введем новую переменную, характеризующую эффективность лечения.
В качестве меры эффективности лечения выберем размещение
,
где — состояние пациента до лечения (девятая переменная в таблице), — состояние пациента после лечения (десятая переменная в таблице).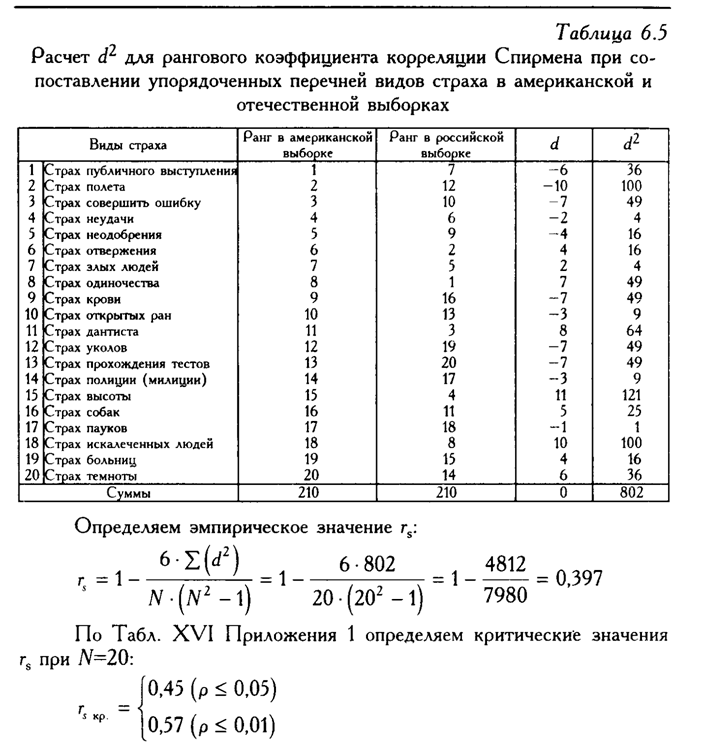
Эта величина обладает свойствами:
1) Чем ближе значение к 1, тем эффективнее лечение. В крайнем случае, когда пациент поступил в предсмертном состоянии (10), а после лечения оказался абсолютно здоров (100), значение равно 0.9.
2) Чем ближе значение к -1, тем менее эффективно лечение. В крайнем случае, когда пациент поступил абсолютно здоровым (100), а после лечения оказался в предсмертном состоянии (10), значение равно -0.9.
3) Значение = 0 означает, что состояние пациента не изменилось.
Добавим в таблицу новую переменную, назовём её Эффективность , укажем формат отображения, зададим формулу для её вычислений.
В итоге в таблице появится новый столбец.
Цель дальнейшего исследования
Целью исследования, которое мы сейчас проведём, является ответом на следующие вопросы:
1) Какой метод лечения более эффективен?
2) Есть ли существенное различие состояний до пациентов и после лечения?
Проверка гипотезы о нормальности для эффективности Эффективность
Для ответа на поставленные вопросы можно использовать T-критерий переменной Эффективность . Этот критерий требует нормальности распределения, поэтому использование проверим гипотезу о нормальности.
Этот критерий требует нормальности распределения, поэтому использование проверим гипотезу о нормальности.
Сначала проверим визуальными методами.
Построим гистограмму по переменной Эффективность . Для этого выберем из меню пункт Графика / Гистограммы .
На вкладке Дополнительно укажем: Распределение = Нормальное , количество категорий — 7 (приблизительное значение двоичного логарифма от 150, то есть от количества наблюдений), выберем переменную — Эффективность .
Гипотеза нормальности кажется очень неправдоподобной (особенно «плохо» выглядят крайние столбцы).
Тот же вывод следует сделать по нормальному вероятностному графику.
Если наблюдаемые значения (откладываемые по оси X) были распределены нормально, то все значения на графике попали на прямую линию. Однако этого не наблюдается.
Теперь вычислим некоторые описательные характеристики для модели .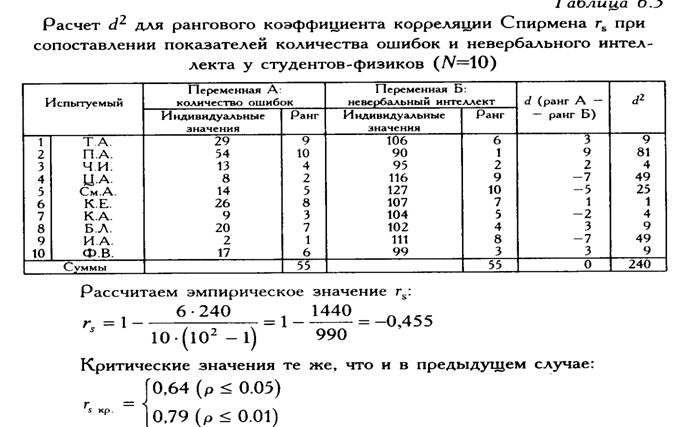
На вкладке Дополнительно диалог Описательные статистики поставим галочки в полях Асимметрия , стандартная ошибка асимметрии , Эксцесс , Стандартная ошибка эксцесса .
Нажмём ОК .
Судя по значению Асимметрии , распределение Эффективность можно считать нормальным (0 «почти что» содержится в интервале Ассиметрия ± ошибка Стандартная Асимметрии ).
Но судя по значению Эксцесса , гипотезу о нормальности следует отклонить. Как правило, если найдена хотя бы одна существенная «нестыковка», гипотезу смело отклоняется, в то время как соответствие даже всем известным критериям ещё не влечёт справедливость гипотезы.
В заключении обратимся к модулю Подгонка распределений .
Выберем пункт Нормальное в левом столбце, нажмём ОК .
В появившемся окне укажем в качестве альтернативы Эффективность .
Нажмём ОК .
Обратите внимание: значение p = 0,00031, то есть значительно меньше на 5%. Это значит, что гипотезу о нормальности следует отклонить.
Итак, окончательный вывод: Распределение отличия Показатель от нормального распределения.
Сравнение выборок
И первый, и второй вопросы, поставленные задачи в Цели исследования, задайте время выполнения сравнения выборок.Будем отвечать на вопросы в порядке их постановки.
1) Какой метод лечения более эффективен?
С точки зрения прикладной статистики, оценка сводится к сравнительным характеристикам Эффективность по группам I и II (сравнение независимых выборок).
Как мы уже использовали методы непараметрической статистики.
Шаг 1. Запустим модуль Непараметрическая статистика .
Выберем пункт Сравнение двух независимых групп .
Шаг 2. Укажем переменные.
Обратите внимание: коды для группирующей модели (I и II) автоматически появляются в соответствующих окошках.
Шаг 3. Нажмём на кнопку U-критерий Манна — Уитни .
Обратите внимание на p-уровень: 0,63. Гипотезу о равенстве функций распределения отклонить нельзя.Поэтому выявить явное преимущество одного из методов не удалось.
Неявное преимущество можно построить на основе сравнения диаграмм размаха по образцу Эффективность .
Если мы хотим сравнить, вполне разумно рассмотрение категоризованных диаграмм размаха.
Для этого выберем в пункт Графики / категоризованные графики / Диаграмма размаха .
Укажем переменные для этого графика
На вкладке Дополнительно уменьшим количество Y-категорий до 4.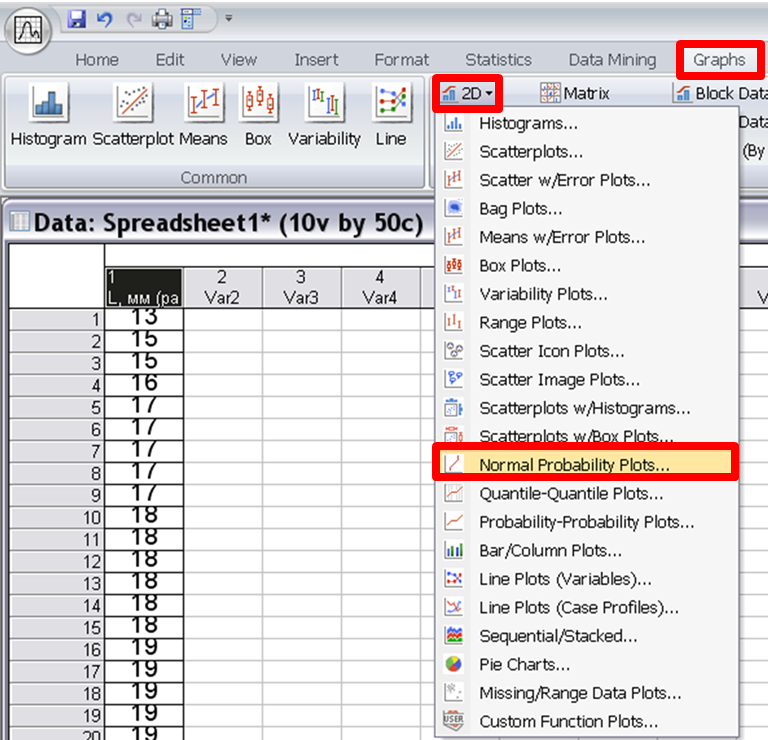
Нажмём ОК .
2) Есть ли существенное различие состояний до пациентов и после лечения?
Это уже задача сравнения парных повторных наблюдений.
Как и прие на первый вопрос, мы воспользуемся непараметрическими методами.
Шаг 1. Запустим модуль Непараметрическая статистика .
Выберем пункт сравнение Двух зависимых чисел .
Шаг 2. Укажем переменные.
Шаг 3. Нажмём на кнопку Критерий знаков .
Вернёмся в диалоге Сравнение двух чисел и нажмём на кнопку Критерий Вилкоксона .
Интерпретация результатов : гипотезу об однородности отвергнуть и принять альтернативу доминирования. Улучшить лечение среднего значения состояния после лечения.
Улучшить лечение среднего значения состояния после лечения.
Связанные определения:
Выборочное среднее, среднее значение выборки
Дисперсия (рассеяние, разброс)
Дисперсия выборки (выборочная дисперсия)
Коэффициент вариации
Максимум
Математическое ожидание дискретной случайной величины
Математическое ожидание непрерывной случайной величины
Меры дисперсии 905 Параметры разброса
Минимум
Мода
Описательные статистики
Описательный анализ
Параметры рассеяния
Параметры центральной тенденции
Среднее значение
Среднеквадратичное отклонение популяции
Стандартная ошибка среднего
Стандартное отклонение
В начало
Содержание портала
Основы программирования в R
Распределение количественных показателей и проверка распределения на нормальность
Иногда в процессе анализа данных мы сталкиваемся с необходимой типом распределения. Решить эту задачу непросто: нет такого универсального статистического теста, который позволяет однозначно тип распределения, за исключением случаев, когда оно является нормальным. Распределение данных можно сравнить с нормальным распределением. Требование нормального распределения данных лежит в основе некоторых статистических тестов и моделей; плюс, при визуальном сравнении с нормальным распределением удобно отмечать всякие особенности распределения (скошенность, наличие длинных хвостов и прочее).
Начнем с визуального анализа. Например, наложим на гистограмму, построенную для показателя, график плотности нормального распределения с установленным обязательством.
Напоминание 1. О графике плотности распределения можно думать как о «сглаженной» гистограмме с большим числовым столбцов.
set.seed (123) # для воспроизводимости
x <- sample (seq (1, 200), 100) # показатель x
hist (x) # гистограмма x график (плотность (x)) # график плотности x Напоминание 2. Нормальное распределение задается согласно: математическое ожидание и стандартным отклонением. Математическое ожидание отвечает за среднее значение (значение, относительно которого симметричен график плотности распределения), стандартное отклонение - за разброс значений вокруг среднего.
Нормальное распределение задается согласно: математическое ожидание и стандартным отклонением. Математическое ожидание отвечает за среднее значение (значение, относительно которого симметричен график плотности распределения), стандартное отклонение - за разброс значений вокруг среднего.
# add = TRUE - чтобы картинки к уже нарисованным
кривая (dnorm (x, mean = 2, sd = 1), xlim = c (-10, 10), col = "зеленый")
кривая (dnorm (x, mean = -1, sd = 1), xlim = c (-10, 10), col = "blue", add = TRUE)
кривая (dnorm (x, mean = 2, sd = 3), xlim = c (-10, 10), col = "red", add = TRUE) Теперь попробуем совместить на гистограмму и график плотности нормального распределения с предусмотренным графиком.Загрузим базу данных с прошлого занятия.
библиотека (иностранная)
df <- read.dta ("CPDS.dta")
библиотека (dplyr)
df <- df%>% filter (год> = 2014) # выберем данные Построим гистограмму для показателя vturn (явка на выборы) и наложим на нее график плотности нормального распределения с обяз. Какие параметры считать размер? Среднее значение, равное среднему значению показателя vturn , и стандартное отклонение, равное стандартному отклонению vturn .
Какие параметры считать размер? Среднее значение, равное среднему значению показателя vturn , и стандартное отклонение, равное стандартному отклонению vturn .
# freq = FALSE - обязательно, так как нужны не абсолютные частоты, а вероятности
hist (df $ vturn, main = "Гистограмма явки", freq = FALSE, col = "помидор")
# na.rm = TRUE - не учитываем пропуски (NA)
кривая (dnorm (x, mean = mean (df $ vturn, na.rm = TRUE),
sd = sd (df $ vturn, na.rm = TRUE)),
col = "blue", add = TRUE) Как кажется, распределение явки на нормальное. А теперь проверим формально.
Один из статистических критериев, позволяющий проверить нормальность распределения данных, это критерий Шапиро-Уилка .С помощью этого критерия проверяется нулевая гипотеза, которая состоит в том, что данные распределены нормально .
shapiro.test (df $ vturn) ##
## Тест нормальности Шапиро-Уилка
##
## data: df $ vturn
## W = 0,97094, значение p = 0,09848 P-value> 0,05, следовательно, вероятность того, что нулевая гипотеза верна при условии использования данных, не мала. На данных на уровне значимости 5% (0,05) нет оснований отвергнуть нулевую гипотезу о том, что данные распределены нормально.Показатель явки имеет нормальное распределение.
На данных на уровне значимости 5% (0,05) нет оснований отвергнуть нулевую гипотезу о том, что данные распределены нормально.Показатель явки имеет нормальное распределение.
Связь между качественными переменными: таблицы сопряженности и критерий хи-квадрат
С таблицами мы уже знакомы. Познакомимся с таблицами напряженности - таблицами, которые иллюстрируют совместное напряжение. Построим таблицу сопряженности (таблица сопряженности) для двух признаков: poco (принадлежность к пост-коммунистическим странам) и gov_party (тип партийной) системы.
ctab <- таблица (df $ poco, df $ gov_party)
Посмотреть (ctab) По полученной таблице сопряженности можно определить, например, что число пост-коммунистических стран с гегемонией правых / центристских партий равно 4.
Связь между качественными переменными можно визуализировать с помощью мозаичного графика (мозаичный сюжет). Подробнее о мозаичном графике см. здесь и здесь. Для этого потребуется библиотека vcd .
здесь и здесь. Для этого потребуется библиотека vcd .
# install.packages ("vcd")
библиотека (vcd)
мозаика (poco ~ gov_party, data = df) Перекрывающие друг друга названия по оси x все портят, но идея понятна: с помощью мозаичной графики мы можем визуализировать таблицу сопряженности.Темно-серый цвет соответствует пост-коммунистическим странам, светло-серый - всем остальным. Разбивка на пять блоков по горизонтали - разбивка по значениям модели gov_party (гегемония правых / центристских партий, доминирование левых партий и прочие).
Чтобы все совсем стало понятно, поправим подписи по оси x.
ang_labels <- c (0, 0, 0, 0, 0) # углы
pos_labels = rep ("right", 5) # позиции названий
args = list (set_varnames = c (poco = "", gov_party = "")) # убираем подписи к осям
мозаика (poco ~ gov_party, data = df, rot_labels = ang_labels, just_labels = pos_labels,
labeling_args = args) Проблему длинных подписей можно решать по-разному. Мы пока на время воспользуемся основным, но не самым красивым: добавим аргумент
Мы пока на время воспользуемся основным, но не самым красивым: добавим аргумент abbreviate = TRUE , и все подписи будут сокращены по первому буквам:
мозаика (poco ~ gov_party, data = df, rot_labels = ang_labels, just_labels = pos_labels,
labeling_args = args, abbreviate = TRUE) А теперь проверим формально, есть ли связь между этими признаками (принадлежность к пост-коммунистическим странам и типовой системе). Воспользуемся критерием хи-квадрат.Нулевая гипотеза: признаки не связаны (независимы) .
chisq.test (таблица (df $ poco, df $ gov_party)) ## Предупреждение в chisq.test (table (df $ poco, df $ gov_party)): хи-квадрат
## приближение может быть неверным ##
## Тест хи-квадрат Пирсона
##
## данные: таблица (df $ poco, df $ gov_party)
## X-квадрат = 6,3478, df = 4, значение p = 0,1746 P-value> 0,05, следовательно, вероятность того, что нулевая гипотеза верна при условии использования данных, не мала. На основе данных на уровне значимости 5% (0,05) нет оснований отвергнуть нулевую гипотезу о том, что признаки независимой оценки. Тип партийной системы и принадлежность к пост-коммунистическим странам не связаны.
На основе данных на уровне значимости 5% (0,05) нет оснований отвергнуть нулевую гипотезу о том, что признаки независимой оценки. Тип партийной системы и принадлежность к пост-коммунистическим странам не связаны.
Замечание. R выдал предупреждение Аппроксимация хи-квадрата может быть неверной . (Пояснение, возможно, будет понятно не всем, но его можно смело пропустить и посмотреть, как решается эта проблема). При расчете ожидаемых частот для расчета ожидаемого значения хи-квадрат получилось, что некоторые ожидаемые частоты в ячейках таблицы сопряженности меньше 5, и таких ячеек много.В такой ситуации p-value не может быть посчитан точно. Для решения проблемы нужно дописать аргумент simulate.p.value = TRUE , тогда R будет считать p-значение по-другому, используя симуляции (см. Справку и документацию).
Связь между количественными переменными: диаграммы рассеяния и коэффициенты корреляции
Напоминание про корреляции. Коэффициент корреляции К.Пирсона - показатель линейной связи между двумя переменными, измеренными в количественной шкале.Коэффициент корреляции принимает значения от -1 до 1. Отрицательные значения коэффициента корреляции свидетельствуют об обратных величинах одной переменной значения другой величины, положительные значения коэффициента корреляции - о прямой связи между переменными (с величиной одной переменной значения другой величины). изменяются). Если коэффициент корреляции Пирсона между переменными равенством 0, это не всегда означает, что между ними нет - связь между ними может просто быть нелинейной (например, квадратичной).Коэффициент корреляции показывает только связь между переменными, а не зависимость (Y зависит от X) и не влияет (X влияет на Y).
Коэффициент корреляции К.Пирсона - показатель линейной связи между двумя переменными, измеренными в количественной шкале.Коэффициент корреляции принимает значения от -1 до 1. Отрицательные значения коэффициента корреляции свидетельствуют об обратных величинах одной переменной значения другой величины, положительные значения коэффициента корреляции - о прямой связи между переменными (с величиной одной переменной значения другой величины). изменяются). Если коэффициент корреляции Пирсона между переменными равенством 0, это не всегда означает, что между ними нет - связь между ними может просто быть нелинейной (например, квадратичной).Коэффициент корреляции показывает только связь между переменными, а не зависимость (Y зависит от X) и не влияет (X влияет на Y).
Коэффициент корреляции Ч.Спирмена также используется для измерения связи между двумя переменными, измеренными в количественной шкале, преимущественно в порядковой (). Коэффициент корреляции Спирмена, в отличие от коэффициента Пирсона, устойчивым к наличию нетипичных значений.
Связи между количественными переменными можно представить в виде корреляционной матрицы.Корреляционная матрица всегда симметричная (коэффициент самой корреляции между переменными X и Y коэффициент корреляции между переменными Y и X), и на главной диагонали такие матрицы стоят 1 (корреляция переменной с собой равна 1).
Диаграммы рассеяния (диаграммы рассеяния)
Допустим, мы хотим посмотреть на связь между переменными gov_left1 и gov_right1. Построим диаграмму рассеяния (диаграмма рассеяния).
участок (df $ gov_left1, df $ gov_right1) По диаграмме рассеяния видно, что связь между переменными обратная (чем больше x, тем меньше y) и, скорее всего, сильная.
Как можно заметить, особой красотой этот график не отличается. График скучный. Что мы можем сделать? Во-первых, подписать оси.
участок (df $ gov_left1, df $ gov_right1,
xlab = "Левые партии (% от общего числа)", ylab = "Правые партии (% от общего числа)") Во-вторых, мы можем добавить цвета. Допустим, мы хотим разделить страны на пост-коммунистические и не пост-коммунистические и отразить это на графике. То есть точки, соответствующие пост-коммунистическим странам и точки, соответствующие всем остальным странам будут отличаться по цвету.
str (df $ poco) # проверим, какие значения принимает poco ## Фактор с 2 уровнями «Нет», «Посткоммунистический»: 1 1 1 1 1 1 2 2 1 1 ... цветов <- c ("синий", "красный") [df $ poco] # устанавливаем цвета по группирующей замене
сюжет (df $ gov_left1, df $ gov_right1,
xlab = "Левые партии (% от общего числа)",
ylab = "Правые партии (% от общего числа)",
col = цвета, lwd = 2) # lwd - толщина линии, в нашем случае толщина окружностей для точек По умолчанию R использует «пустые» точки.Но тип точек можно менять, добавляя аргумент pch . Список маркеров для точек см. здесь.
Матрица диаграмм рассеяния (матрица рассеяния)
Иногда в ходе предварительного анализа бывает нужно посмотреть на связь «всего со всем».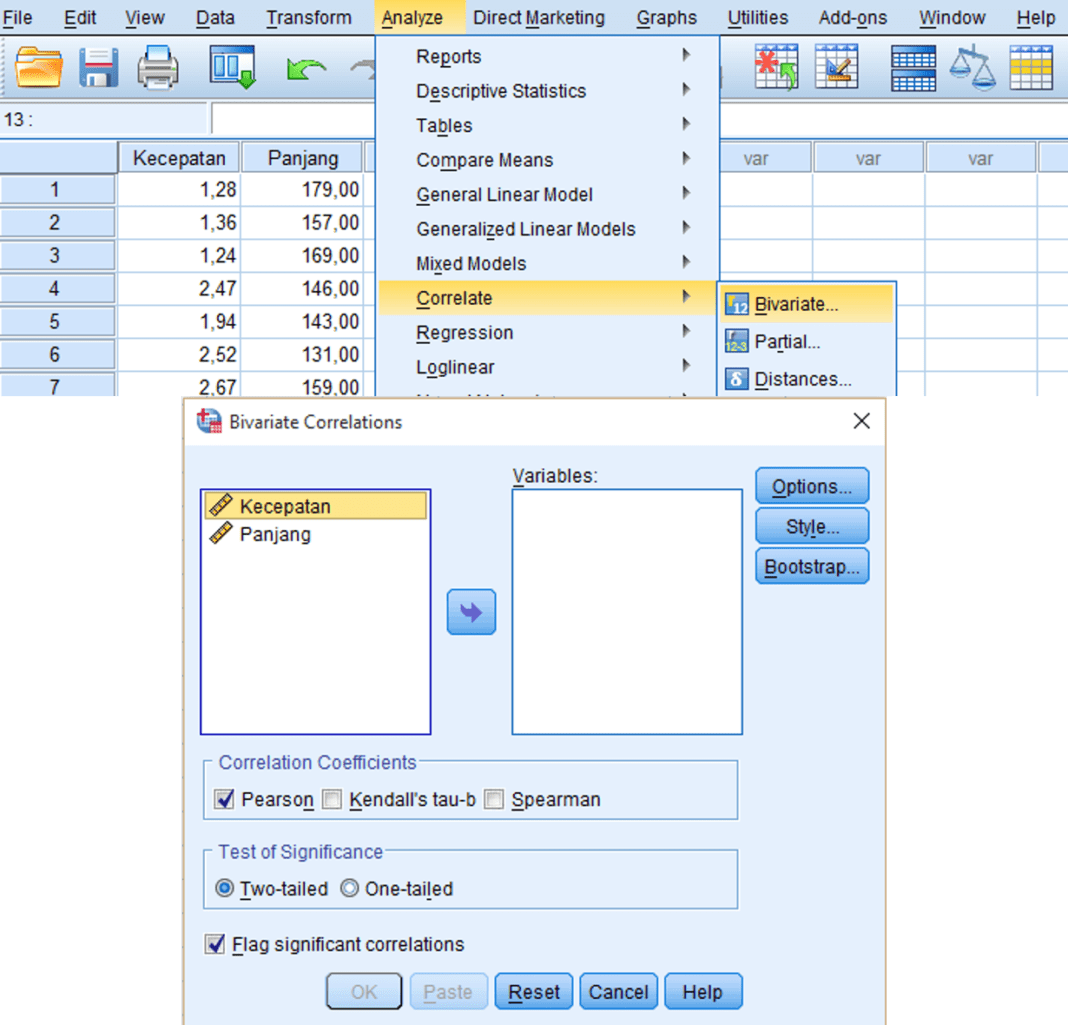 Для этого удобно использовать матрицу диаграмм рассеяния.
Для этого удобно использовать матрицу диаграмм рассеяния.
Построим диаграммы для процентов голосов за разные партии.
пар (df [10:12], col = colors) # выбираем столбцы 10-12 На пересечении названий находятся диаграммы рассеяния, соответствующие парам показателей.
А теперь проиллюмируем то же самое, но более красочно. Для этого потребуется библиотека вагон .
# install.packages ("автомобиль")
библиотека (машина)
# диагональ - что стоит на диагонали
# smooth = FALSE - обычная регрессия,
# smooth = TRUE - лессовая регрессия
scatterplotMatrix (df [10:12], diagonal = "гистограмма", smooth = FALSE) Диагональ этой матрицы показывает разные графики, отражающие показатели, например, гистограммы или ящики с усами.На сами диаграммы рассеяния добавляется регрессионная прямая (прямой вид y = kx + b, при k <0 наклон прямой отрицательный, связь между x и y обратная, при k> 0 наклон прямой положительный, связь между x и y прямая).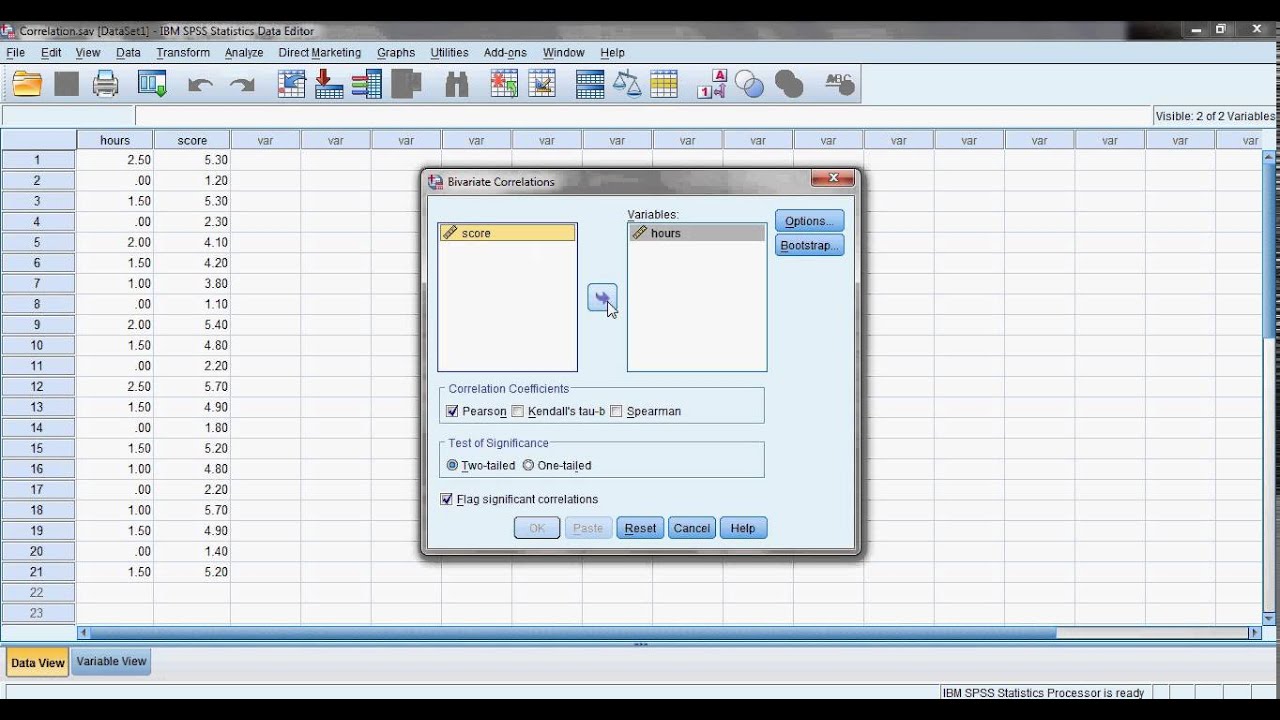 Можно также добавить кривую взвешенной регрессии ( лессовая регрессия от локально взвешенная регрессия ). Логика ее построения (в очень упрощенном виде) такая:
Можно также добавить кривую взвешенной регрессии ( лессовая регрессия от локально взвешенная регрессия ). Логика ее построения (в очень упрощенном виде) такая:
- все значения x разбиваем на много маленьких интервалов
- на каждом интервале строим регрессионную прямую
- «сглаживаем» получившуюся ломаную линию, чтобы получить гладкую кривую
Наведем красоту на графике выше:
# создадим вектор с названиями чисел
labs <- c («Правый», «Центр», «Левый»)
# рег.line = FALSE - нет регрессионной прямой, оставим только гладкий (кривая лесса)
# var.labels - названия терми на диагонали
# cex.labels - размер шрифта для надписей
# main - название графика
scatterplotMatrix (df [10:12], diagonal = "гистограмма", smooth = TRUE,
reg.line = FALSE,
var.labels = labs,
cex.labels = 1.3,
main = "Соотношение долей сторон") Еще один вариант симпатичного графика для корреляций - разноцветный график, созданный с помощью пакета gclus .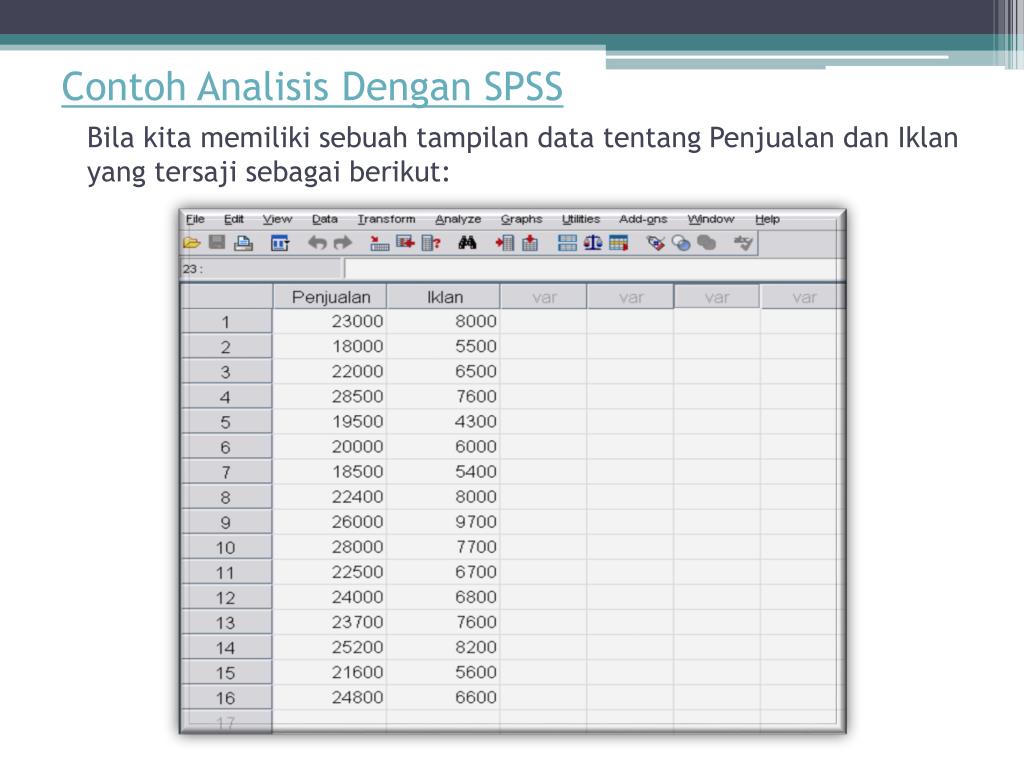
библиотека (gclus)
# получим вектор коэффициентов корреляции (по модулю)
coeffs <- abs (cor (df [10:12]))
# зададим цвета (автоматическое разбиение по вектору коэффициентов)
цвета <- dmat.color (coeffs)
# отсортируем так, чтобы графики, где связь наибольшая,
# были ближе к диагонали
order <- order.single (коэфф.)
# строим сам график
# разрыв - расстояние между графиками в матрице
cpairs (df [10:12], order, panel.colors = colors, gap = .5,
main = "Соотношение долей сторон") Корреляционный анализ
Для начала посмотрим на коэффициент корреляции между какими-нибудь двумя переменными:
кор (df $ gov_left1, df $ gov_right1) ## [1] -0.7110288 Если бы в одной из чисел были пропущенные значения (NA), коэффициент корреляции бы не рассчитался. Тут можно действовать по аналогии с расчетом среднего значения:
cor (df $ gov_left1, df $ gov_right1, use = "complete.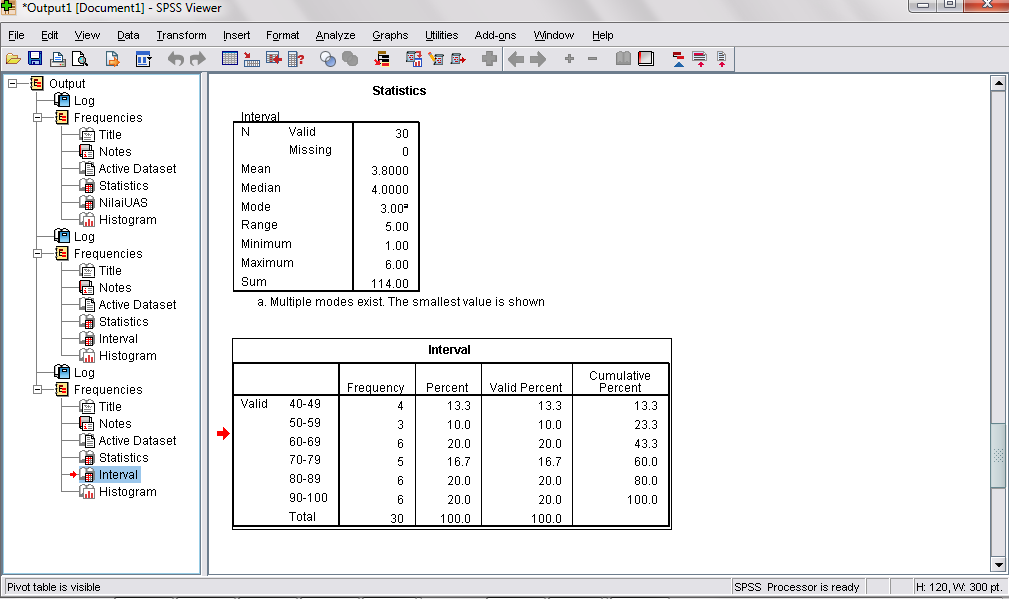 obs") # использовать все, кроме NA (полные наблюдения)
obs") # использовать все, кроме NA (полные наблюдения) ## [1] -0,7110288 Как известно, существуют разные коэффициенты корреляции. Самые распространенные - линейный коэффициент корреляции Пирсона, коэффициент ранговой корреляции Спирмена и коэффициент ранговой корреляции Кендалла.По умолчанию коэффициент Пирсона, остальные можно получить, прописав дополнительный аргумент:
cor (df $ gov_left1, df $ gov_right1, method = "spearman") # коэфф. Спирмена ## [1] -0.7136618 Проверить значимость коэффициента корреляции - проверить нулевую гипотезу о том, что истинный коэффициент корреляции равен 0.
corr <- cor.test (df $ gov_left1, df $ gov_right1)
корр ##
## Корреляция продукта и момента Пирсона
##
## данные: df $ gov_left1 и df $ gov_right1
## t = -8.4602, df = 70, значение p = 2,595e-12
## альтернативная гипотеза: истинная корреляция не равна 0
## 95-процентный доверительный интервал:
## -0. 8093747 -0.5738938
## примерные оценки:
## cor
## -0.7110288
8093747 -0.5738938
## примерные оценки:
## cor
## -0.7110288 В выдаче мы видим две важные вещи: значение коэффициента корреляции (выборочные оценки) и pvalue. В нашем случае pvalue <0,05, следовательно, на 5% уровне значимости есть основания отвергнуть нулевую гипотезу о соотношении коэффициента корреляции нулю. Раз эту гипотезу отвергаем, что коэффициент корреляции не 0, а следовательно, между процентом левых и правых партий действительно есть.
Выдача R представляет собой список (список):
ул. (корр) ## Список из 9
## $ statistic: Именованное число -8,46
## ..- attr (*, "имена") = chr "t"
## $ параметр: Именованный int 70
## ..- attr (*, "имена") = chr "df"
## $ p.value: число 2.6e-12
## $ оценка: Именованное число -0,711
## ..- attr (*, "имена") = chr "cor"
## $ null.value: Именованное число 0
## ..- attr (*, "имена") = chr "корреляция"
## $ альтернатива: chr "двухсторонний"
## $ method: chr "Соотношение продукта и момента Пирсона"
## $ data. имя: chr "df $ gov_left1 и df $ gov_right1"
## $ conf.int: атомарный [1: 2] -0,809 -0,574
## ..- attr (*, "conf.level") = число 0,95
## - attr (*, "класс") = chr "htest"
имя: chr "df $ gov_left1 и df $ gov_right1"
## $ conf.int: атомарный [1: 2] -0,809 -0,574
## ..- attr (*, "conf.level") = число 0,95
## - attr (*, "класс") = chr "htest" А значит, из него можно вызвать отдельные элементы.
coeff <- corr $ оценка # коэффициент
pvalue <- corr $ p.value # p-значение
коэфф; pvalue ## cor
## -0.7110288 ## [1] 2.595076e-12 Если хотим посмотреть на корреляцию «всего со всем», указать столбцы в базе (переменные) и получить корреляционную матрицу:
cor (df [10:12]) ## gov_right1 gov_cent1 gov_left1
## gov_right1 1.0000000 -0,4403955 -0,7110288
## gov_cent1 -0.4403955 1.0000000 -0.2413104
## gov_left1 -0.7110288 -0.2413104 1.0000000 Для того, чтобы получить корреляционную матрицу и значимость коэффициентов в ней, нужно постараться. Загрузим библиотеку Hmisc .
# install. packages ("Hmisc")
библиотека (Hmisc)
# Внимание: функция привередничает - требует матрицу, а не просто столбцы из базы
rcorr (as.matrix (df [10:12]))
packages ("Hmisc")
библиотека (Hmisc)
# Внимание: функция привередничает - требует матрицу, а не просто столбцы из базы
rcorr (as.matrix (df [10:12])) ## gov_right1 gov_cent1 gov_left1
## gov_right1 1.00 -0,44 -0,71
## gov_cent1 -0,44 1,00 -0,24
## gov_left1 -0,71 -0,24 1,00
##
## n = 72
##
##
## П
## gov_right1 gov_cent1 gov_left1
## gov_right1 0,0001 0,0000
## gov_cent1 0,0001 0,0411
## gov_left1 0,0000 0,0411 Но то, что мы увидели, немного не похоже на то, что хотелось бы показать другим. Единой таблички с коэффициентами и значимостью нет. Действительно, в R есть некоторые проблемы с корреляционными матрицами.
Воспользуемся уже написанной функцией, доступной по ссылке, и немного модифицируем ее. Чтобы воспользоваться этой функцией, помимо уже установленного нами пакета Hmisc потребуется библиотека xtable . Как и stargazer она используется для выгрузки выдач R в html или LaTeX.
# install. packages ("xtable")
packages ("xtable") Скопируем код для функций с сайта в R-файле (New RScript) и назовем его корреляцию .R . Модифицируем код: в качестве аргумента функции corstars добавим файл (про написание собственных функций поговорим).
corstars <-function (x, method = c ("pearson", "spearman"), removeTriangle = c ("upper", "lower"), result = c ("none", "html", "latex") ), файл) А также допишем в строки 46 и 47 файл = файл :
if (result [1] == "html") print (xtable (Rnew), type = "html", file = file)
иначе print (xtable (Rnew), type = "latex", file = file) Это нужно для того, чтобы R не просто вывел результат в консоль, но и сохранил код для таблички в отдельный файл.
Добавим также строку require (xtable) , например, после require (Hmisc) , иначе R не поймет, откуда брать функцию xtable . Теперь сохраним все изменения в файле correlation. и загрузим его сюда: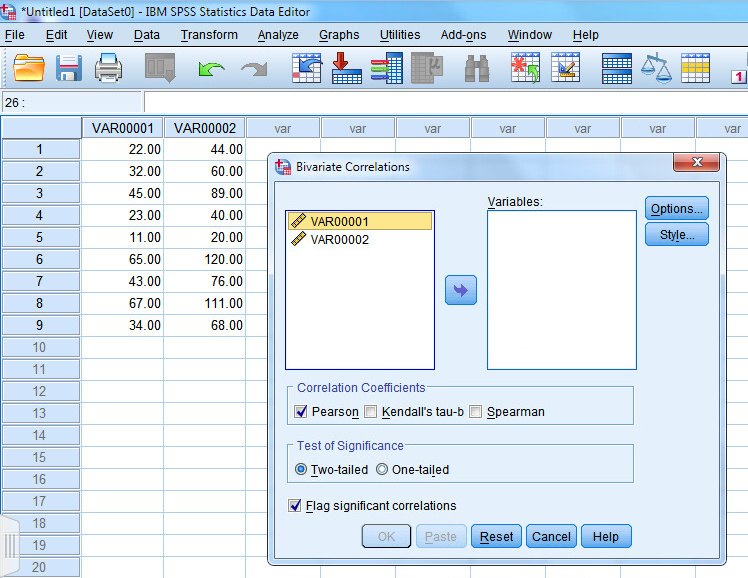 R
R
источник ("correlation.R") Теперь R знает, что из этого файла можно брать функции, и не будет ругаться, если встретит незнакомое (не встроенное в базовые библиотеки) название.
Финальный аккорд:
# сохраняем результат в файле корр.htm - могу открыть через браузер иди Word
corstars (x = df [10:12], method = "pearson", removeTriangle = "upper",
result = "html", file = "corrtable.htm") .
 (2-tailed) (Значимость (2-сторонняя)) N
(2-tailed) (Значимость (2-сторонняя)) N .. A (Контрольная переменная) (
.. A (Контрольная переменная) (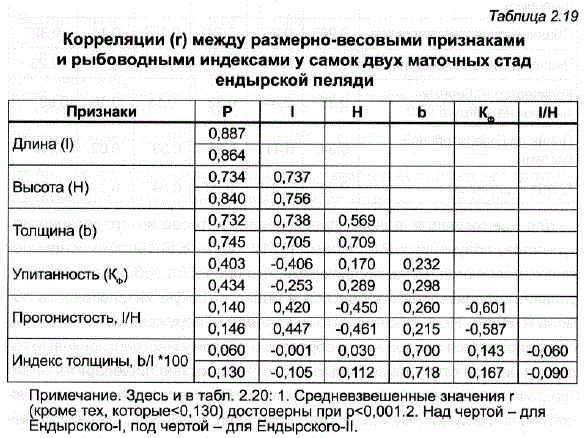
 (2-сторонняя) (Значимость (2-сторонняя)) N
(2-сторонняя) (Значимость (2-сторонняя)) N