Конические поверхности.
Определение. Конической называется поверхность, которую образует множество всех прямых (образующих), проходящих через каждую точку некоторой кривой (направляющей), и через некоторую точку O (вершину).
Выберем декартову СК так, чтобы начало координат совпадало с вершиной конической поверхности F. Пусть F(x,y,z)=0 – уравнение поверхности F в этой СК. Поскольку мы рассматриваем только поверхности второго порядка, то F – многочлен второй степени от 3 переменных. Тогда функция двух переменных
j(x,y)=F(x,y,c)
будет также многочленом второй степени для любого cÎR, а система
j(x,y)=0,
z=c
будет задавать сечение поверхности F плоскостью
 Получающуюся в сечении кривую g выберем в качестве
Получающуюся в сечении кривую g выберем в качестве
направляющей. Т.к. j(x,y)– многочлен 2 степени, то g – кривая 2 порядка. Если g – центральная, то можем считать, что ось Oz проходит через ее центр.
Предположим сначала, что направляющая – эллипс
g: + –1=0, (*)
z=c
Пусть M(x1,y1,z1) – произвольная точка поверхности F. Тогда вся прямая OM должна лежать на поверхности. Ее параметрическое уравнение:
x= x1t,
OM: y= y1t,
z= z1t.
Пусть она пересекает направляющую g в точке Mo(xo
,yo,c). Тогда ее координаты должны удовлетворять уравнению прямой OM:xo= x1t, xo= x1c/z1,
yo= y1t, Þ yo= y1c/z1,
c= z1.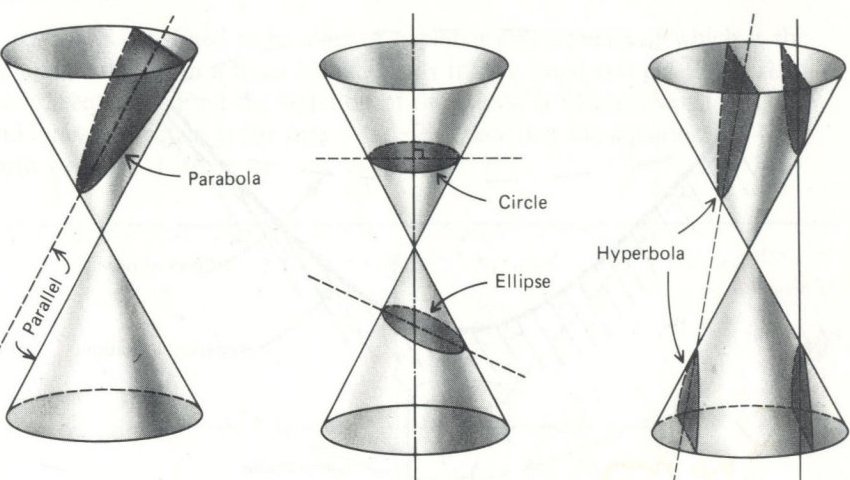 t=c/z1.
t=c/z1.
А теперь подставим найденные выражения в уравнение эллипса:
+ –1=0.
Домножим это уравнение на z1/c, и получим
+ –=0. (2)
Обратно, пусть координаты точки M(x1,y1,z1) удовлетворяют уравнению (2). Тогда этому уравнению удовлетворяют и координаты любой точки на прямой
+ –=t2( + –)=t2·0=0,
а подставив в (2) z=c, получим уравнение эллипса (*). Значит, (2) и есть уравнение конической поверхности. Опуская индексы, окончательно получаем каноническое уравнение конуса.
+ –=0.
Аналогично, если направляющая кривая – это гипербола
––1=0,
z=c ,
получим уравнение конической поверхности
––=0 Û – + +=0.
Это такой же «эллиптический» конус, только ось его будет не Oz, а Oz¢.
Пусть теперь направляющая g – это парабола
x 2 =2py,
z=c .
Тогда тем же способом получим уравнение
x2 =yz. (**)
Повернем СК на 45о вокруг оси Ox. Тогда формулы замены координат имеют вид
x=x¢,
y= (y¢+z¢),
z= (–y¢+z¢).
Подставим эти формулы в (**), и обозначив a2 =p/c, получим
x2 =a2(–y¢2 +z¢2) Û + y¢2 – z¢2 =0.
Таким образом, уравнение (**) тоже определяет конус, ось которого является биссектрисой угла yOz.
Мы уже говорили в предыдущей главе, что эллипс, гипербола и парабола – это конические сечения. Теперь мы в этом убедились.
Если направляющей служит пара прямых, то коническая поверхность представляет собой пару плоскостей, обязательно пересекающихся или совпадающих, т.к. обе плоскости должны проходить через начало координат. Эти поверхности относятся также к цилиндрическим и они были рассмотрены в предыдущем параграфе.
Итак, мы установили, что существуют 4 типа конических поверхностей:
1. Конус + –=0.
2. Пара пересекающихся плоскостей a2x2 –b2y2 =0 .
3. Пара мнимых пересекающихся плоскостей a2x2 +b2y2 =0 .
4. Пара совпадающих плоскостей x2 =0.
Дата добавления: 2020-02-05; просмотров: 253; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
§ 13. Конические поверхности
Определение 2.3.Конической поверхностьюназывается множе-
ство прямых (образующих), проходящих через некоторую точку (вершину) и пересекающих некоторую линию (направляющую)(рис.21).
45
Коническая ПВП— коническая поверхность с направляющей,
являющейся КВП.
Рис. 21. Рис. 22.
Выведем уравнение конической поверхности в случае, когда вершина совпадает с началом прямоугольной системы координат OXY, а направляющей служит эллипс:
Возьмем на поверхности конуса произвольную точку М1(х1,у1,z1)
(рис. 22}. Тогда параметрическое уравнение
прямой OM1имеют вид:
22}. Тогда параметрическое уравнение
прямой OM1имеют вид:
х=х1t, y=y1t, z=z1t.
Прямая ОМ1пересекает направляющую в точке M(x,у,с), следова-
тельно, с=z1t, т.е.t=с/z1. Значит, х=х1t=(х1с)/z1, у=(су1)/z1.
Точка M принадлежит эллипсу, поэтому
=1
46
Умножим обе части последнего выражения на z12/c2, получаем
(*)
Так как соотношению (*) удовлетворяет любая точка поверхнос-
ти, то
(2.3)
— уравнение конической поверхности
Рис. 23. Рис. 24.
В частности, если а=b, то получаем уравнение прямого круго-
вого конуса
х2+у2—k2z2=0, (**)
где
k2=а2/с2.
Плоскость, параллельная плоскости ХОУ, пересекает конус (**)
по окружности. Например, плоскость z=1 пересекает конус (**) по окружности х2+y2=k2. Если немного наклонить эту плоскость, то в сечении получается эллипс (рис. 23).
47
Плоскости, параллельные плоскостям OYZ и OXZ, пересекают
конус по гиперболам (рис.24). Например, в сечении конуса (**)
плоскостью х=b, получаем кривую
b2+y2-k2z2=0, т.е.
Если секущая плоскость параллельна образующей конуса, то в
сечении получается парабола (рис. 24). Поэтому эллипс, гипербола и парабола называются коническими сечениями.
Определение 2.4.Поверхность называетсяповерхностью враще-
ния,если она вместе с каждой своей точкой
содержит и всю окружность, полученную
вращением этой точки вокруг некоторой
фиксированной прямой, называемойосью
вращении.
F(y,z)=0 (*)
(рис. 25). Найдем уравнение по-
верхности вращения, образован-
ной вращением кривой l вокруг
оси OZ. Возьмем произволь-
ную точку М1(x1,у1,z1) на полу-
ченной поверхности и проведем
через нее плоскость, перпенди
кулярную оси OZ. Обозначим точ
ки Р(0,0,z1) и М(0,у,z). Ради-
ности
равен: R=М1Р=РМ,
т.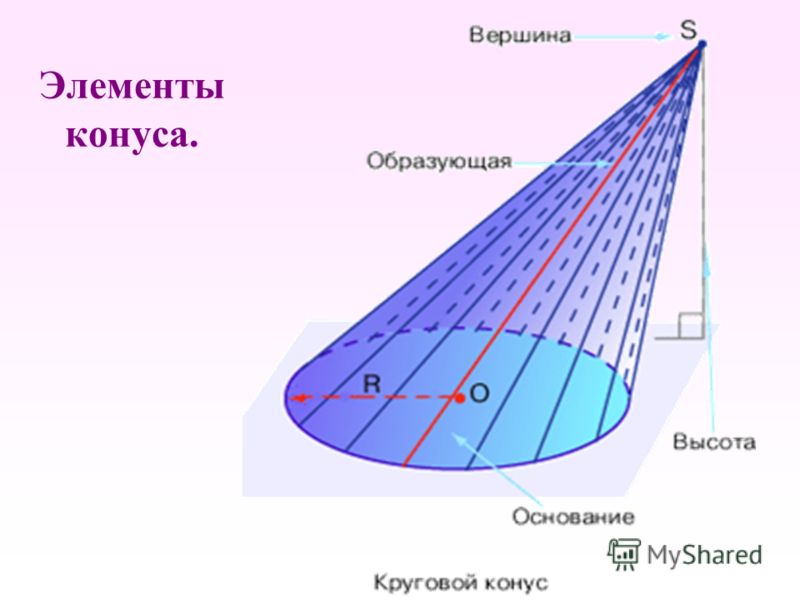 е.
е.
Откуда
48
(**)
Так как точка М принадлежит кривой l, то, подставляя значение у из (**) в уравнение (*), получаем. Этому уравнению удовлетворяют все точки поверхности, значит,
(2.4)
— искомое уравнение поверхности вращения.
Заметим, что знак в (2.4) выбирается таким образом, чтобы в
соответствующих точках, он совпадал со знаком ординаты у кривой l.
Аналогичным образом можно получить, что уравнение
задает поверхность вращения, образованную вращением кривой
F(x,z)=0 вокруг оси OZ.
Коническая поверхность вычисляется по формуле. Площадь полной поверхности конуса равна
Геометрия является разделом математики, изучающим структуры в пространстве и отношение между ними. В свою очередь она также состоит из разделов, и одним из них является стереометрия. Она предусматривает изучение свойств объемных фигур, находящихся в пространстве: куба, пирамиды, шара, конуса, цилиндра и др.
В свою очередь она также состоит из разделов, и одним из них является стереометрия. Она предусматривает изучение свойств объемных фигур, находящихся в пространстве: куба, пирамиды, шара, конуса, цилиндра и др.
Конус — это тело в евклидовом пространстве, которое ограничивает коническая поверхность и плоскость, на которой лежат концы ее образующих. Его образование происходит в процессе вращения прямоугольного треугольника вокруг любого из его катетов, поэтому он относится к телам вращения.
Составляющие конуса
Различают следующие виды конусов: косой (или наклонный) и прямой. Косым называется тот, ось которого пересекается с центром его основания не под прямым углом. По этой причине высота в таком конусе не совпадает с осью, так как она является отрезком, который опущен из вершины тела на плоскость его основания под углом 90°.
Тот конус, ось которого расположена перпендикулярно к его основанию, называется прямым. Ось и высота в таком геометрическом теле совпадают по причине того, что вершина в нем расположена над центром диаметра основания.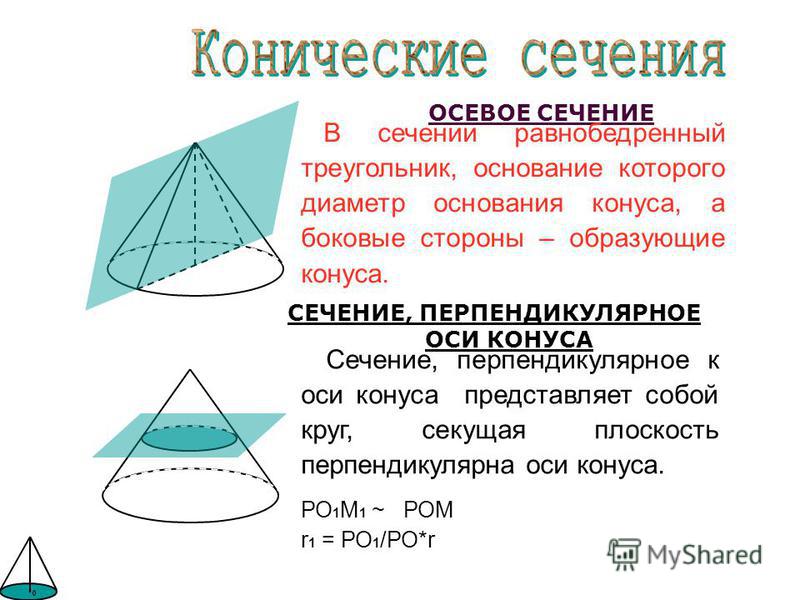
Конус состоит из следующих элементов:
- Круга, являющегося его основанием.
- Боковой поверхности.
- Точки, не лежащей в плоскости основания, называющейся вершиной конуса.
- Отрезков, которые соединяют точки круга основания геометрического тела и его вершину.
Все эти отрезки являются образующими конуса. Они наклонные к основанию геометрического тела, и в случае прямого конуса их проекции равны, так как вершина равноотдалена от точек круга основания. Таким образом, можно сделать вывод, что в правильном (прямом) конусе образующие равны, то есть имеют одинаковую длину и образуют одинаковые углы с осью (или высотой) и основанием.
Так как в косом (или наклонном) теле вращения вершина смещена по отношению к центру плоскости основания, образующие в таком теле имеют разную длину и проекцию, поскольку каждая из них находится на разном расстоянии от двух любых точек круга основания. Кроме того, углы между ними и высотой конуса также будут отличаться.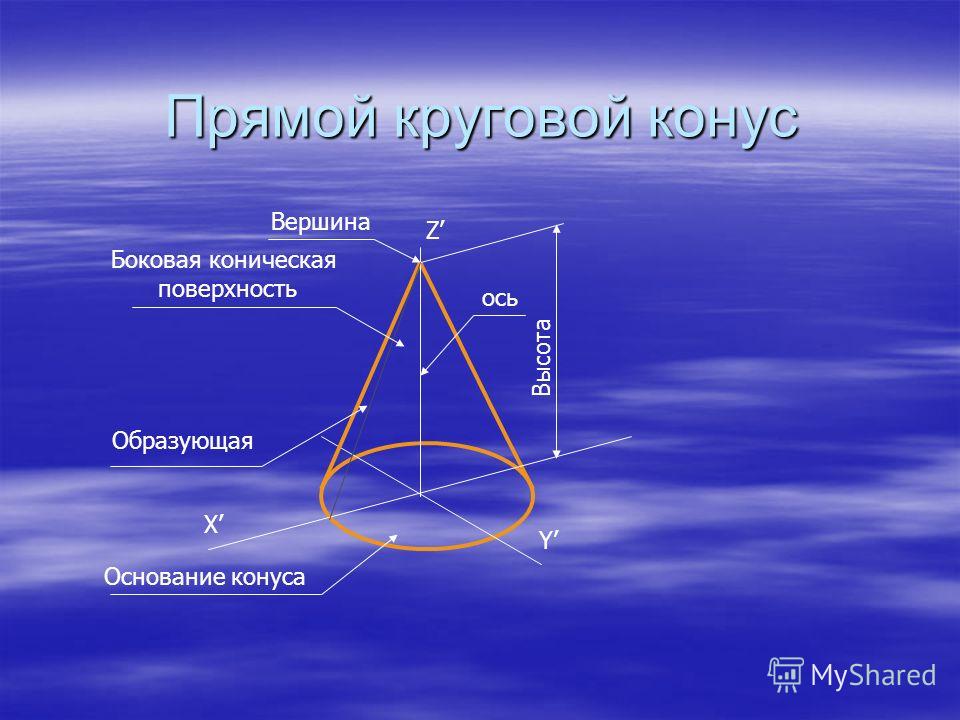
Длина образующих в прямом конусе
Как написано ранее, высота в прямом геометрическом теле вращения перпендикулярна плоскости основания. Таким образом, образующая, высота и радиус основания создают в конусе прямоугольный треугольник.
То есть, зная радиус основания и высоту, при помощи формулы из теоремы Пифагора, можно вычислить длину образующей, которая будет равна сумме квадратов радиуса основания и высоты:
l 2 = r 2 + h 2 или l = √r 2 + h 2
где l — образующая;
r — радиус;
h — высота.
Образующая в наклонном конусе
Исходя из того, что в косом, или наклонном конусе образующие имеют не одинаковую длину, рассчитать их без дополнительных построений и вычислений не получится.
Прежде всего необходимо знать высоту, длину оси и радиус основания.
r 1 = √k 2 — h 2
где r 1 — это часть радиуса между осью и высотой;
k — длина оси;
h — высота.
В результате сложения радиуса (r) и его части, лежащей между осью и высотой (r 1), можно узнать полную сформированного образующей конуса, его высотой и частью диаметра:
где R — катет треугольника, образованного высотой, образующей и частью диаметра основания;
r — радиус основания;
r 1 — часть радиуса между осью и высотой.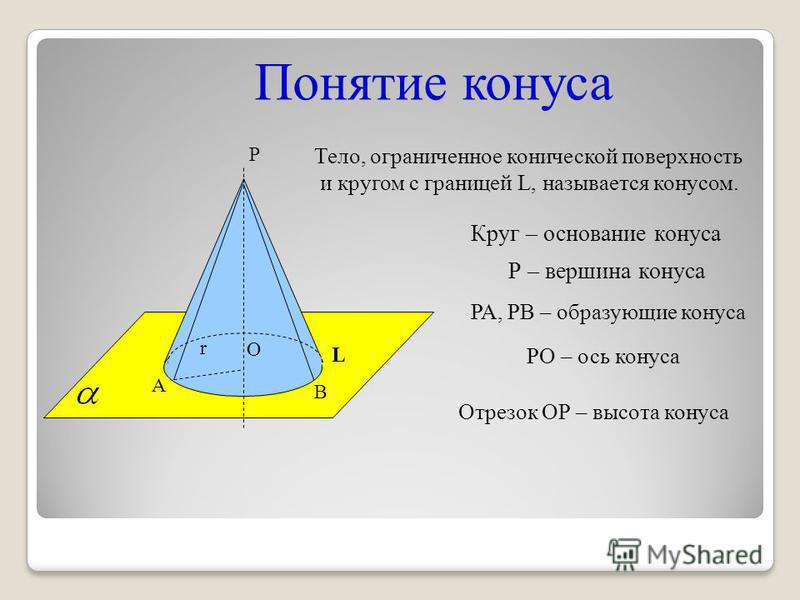
Пользуясь все той же формулой из теоремы Пифагора, можно найти длину образующей конуса:
l = √h 2 + R 2
или, не производя отдельно расчет R, объединить две формулы в одну:
l = √h 2 + (r + r 1) 2 .
Несмотря на то, прямой или косой конус и какие вводные данные, все способы нахождения длины образующей всегда сводятся к одному итогу — использованию теоремы Пифагора.
Сечение конуса
Осевым называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание — это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.
Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.
Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие — оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.
Площадь сечения
Упомянутое ранее осевое сечение конуса представляет собой треугольник. Исходя из этого, его площадь можно рассчитать по формуле площади треугольника:
S = 1/2 * d * h или S = 1/2 * 2r * h
где S — это площадь сечения;
d — диаметр основания;
r — радиус;
h — высота.
В косом, или наклонном конусе сечение по оси также является треугольником, поэтому в нем площадь сечения рассчитывается аналогично.
Объем
Поскольку конус является объемной фигурой в трехмерном пространстве, то можно вычислить его объем. Объемом конуса называется число, которое характеризует это тело в единице измерения объема, то есть в м 3 . Расчет не зависит от того, прямой он или косой (наклонный), так как формулы для двух этих видов тел не отличаются.
Объемом конуса называется число, которое характеризует это тело в единице измерения объема, то есть в м 3 . Расчет не зависит от того, прямой он или косой (наклонный), так как формулы для двух этих видов тел не отличаются.
Как указано ранее, образование прямого конуса происходит вследствие вращения прямоугольного треугольника по одному из его катетов. Наклонный же, или косой конус образуется иначе, поскольку его высота смещена в сторону от центра плоскости основания тела. Тем не менее такие отличия в строении не влияют на методику расчета его объема.
Расчет объема
Любого конуса выглядит следующим образом:
V = 1/3 * π * h * r 2
где V — это объем конуса;
h — высота;
r — радиус;
π — константа, равная 3,14.
Для расчета высоты тела необходимо знать радиус основания и длину его образующей. Поскольку радиус, высота и образующая объединяются в прямоугольный треугольник, то высоту можно рассчитать по формуле из теоремы Пифагора (a 2 + b 2 = c 2 или в нашем случае h 2 + r 2 = l 2 , где l — образующая). Высота при этом будет рассчитываться путем извлечения квадратного корня из разности квадратов гипотенузы и другого катета:
Высота при этом будет рассчитываться путем извлечения квадратного корня из разности квадратов гипотенузы и другого катета:
a = √c 2 — b 2
То есть высота конуса будет равна величине, полученной после извлечения квадратного корня из разности квадрата длины образующей и квадрата радиуса основания:
h = √l 2 — r 2
Рассчитав таким методом высоту и зная радиус его основания, можно вычислить объем конуса. Образующая при этом играет важную роль, так как служит вспомогательным элементом в расчетах.
Аналогичным образом, если известна высота тела и длина его образующей, можно узнать радиус его основания, извлекая квадратный корень из разности квадрата образующей и квадрата высоты:
r = √l 2 — h 2
После чего по той же формуле, что указана выше, рассчитать объем конуса.
Объем наклонного конуса
Так как формула объема конуса одинакова для всех видов тела вращения, отличие в его расчете составляет поиск высоты.
Для того чтобы узнать высоту наклонного конуса, вводные данные должны включать длину образующей, радиус основания и расстояние между центром основания и местом пересечения высоты тела с плоскостью его основания. Зная это, можно с легкостью рассчитать ту часть диаметра основания, которая будет являться основанием прямоугольного треугольника (образованного высотой, образующей и плоскостью основания). После чего, снова используя теорему Пифагора, произвести расчет высоты конуса, а впоследствии и его объема.
Зная это, можно с легкостью рассчитать ту часть диаметра основания, которая будет являться основанием прямоугольного треугольника (образованного высотой, образующей и плоскостью основания). После чего, снова используя теорему Пифагора, произвести расчет высоты конуса, а впоследствии и его объема.
Мы знаем, что такое конус, попробуем найти площадь его поверхности. Зачем нужно решать такую задачу? Например, нужно понять, сколько теста пойдет на изготовление вафельного рожка? Или сколько кирпичей понадобится, чтобы сложить кирпичную крышу замка?
Измерить площадь боковой поверхности конуса просто так не получится. Но представим себе все тот же рожок, обмотанный тканью. Чтобы найти площадь куска ткани, нужно разрезать и разложить ее на столе. Получится плоская фигура, ее площадь мы сможем найти.
Рис. 1. Разрез конуса по образующей
Сделаем так же с конусом. «Разрежем» его боковую поверхность вдоль любой образующей, например, (см. рис. 1).
Теперь «размотаем» боковую поверхность на плоскость. Получаем сектор. Центр этого сектора — вершина конуса, радиус сектора равен образующей конуса, а длина его дуги совпадает с длиной окружности основания конуса. Такой сектор называется разверткой боковой поверхности конуса (см. рис. 2).
Получаем сектор. Центр этого сектора — вершина конуса, радиус сектора равен образующей конуса, а длина его дуги совпадает с длиной окружности основания конуса. Такой сектор называется разверткой боковой поверхности конуса (см. рис. 2).
Рис. 2. Развертка боковой поверхности
Рис. 3. Измерение угла в радианах
Попробуем найти площадь сектора по имеющимся данным. Сперва введем обозначение: пусть угол при вершине сектора в радианах (см. рис. 3).
С углом при вершине развертки нам придется часто сталкиваться в задачах. Пока же попробуем ответить на вопрос: а не может ли этот угол получиться больше 360 градусов? То есть не получится ли так, что развертка наложится сама на себя? Конечно же, нет. Докажем это математически. Пусть развертка «наложилась» сама на себя. Это означает, что длина дуги развертки больше длины окружности радиуса . Но, как уже было сказано, длина дуги развертки есть длина окружности радиуса . А радиус основания конуса, разумеется, меньше образующей, например, потому, что катет прямоугольного треугольника меньше гипотенузы
Тогда вспомним две формулы из курса планиметрии: длина дуги .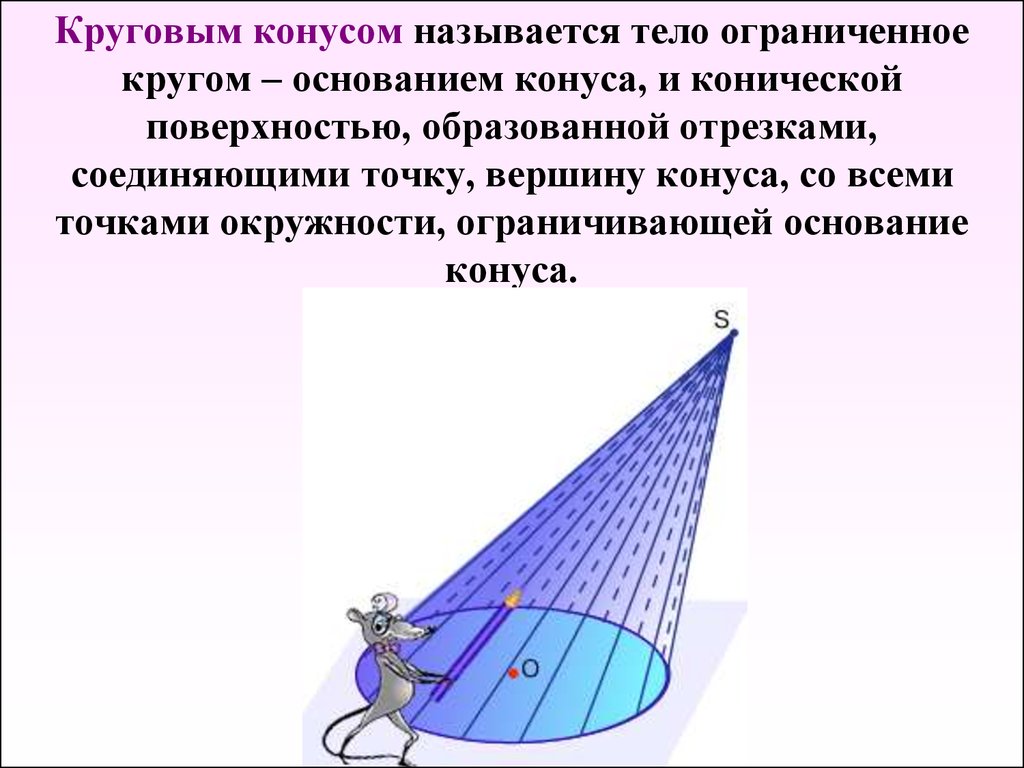 Площадь сектора: .
Площадь сектора: .
В нашем случае роль играет образующая , а длина дуги равна длине окружности основания конуса, то есть . Имеем:
Окончательно получаем: .
Наряду с площадью боковой поверхности можно найти и площадь полной поверхности. Для этого к площади боковой поверхности надо прибавить площадь основания. Но основание — это круг радиуса , чья площадь по формуле равна .
Окончательно имеем: , где — радиус основания цилиндра, — образующая.
Решим пару задач на приведенные формулы.
Рис. 4. Искомый угол
Пример 1 . Разверткой боковой поверхности конуса является сектор с углом при вершине. Найти этот угол, если высота конуса равна 4 см, а радиус основания равен 3 см (см. рис. 4).
Рис. 5. Прямоугольный треугольник, образующий конус
Первым действием, по теореме Пифагора, найдем образующую: 5 см (см. рис. 5). Далее, мы знаем, что .
Пример 2 . Площадь осевого сечения конуса равна , высота равна . Найти площадь полной поверхности (см. рис. 6).
Найти площадь полной поверхности (см. рис. 6).
Сегодня мы расскажем вам о том, как найти образующую конуса, что частенько требуется в школьных задачках по геометрии.
Понятие образующей конуса
Прямой конус — это фигура, которая получается в результате вращения прямоугольного треугольника вокруг одно из его катетов. Основание конуса образует круг. Вертикальное сечение конуса — это треугольник, горизонтальное — круг. Высотой конуса является отрезок, соединяющий вершину конуса с центром основания. Образующей конуса является отрезок, который соединяет вершину конуса с любой точкой на линии окружности основания.
Так как конус образуется вращением прямоугольного треугольника, то получается, что первым катетом такого треугольника является высота, вторым — радиус круга, лежащего в основании, а гипотенузой будет образующая конуса. Нетрудно догадаться, что для расчета длины образующей пригодится теорема Пифагора. А теперь подробнее о том, как найти длину образующей конуса.
Находим образующую
Легче всего понять, как найти образующую, можно на конкретном примере. Допустим, даны такие условия задачи: высота равна 9 см., диаметр круга основания составляет 18 см. Необходимо найти образующую.
Итак, высота конуса (9 см.) — это один из катетов прямоугольного треугольника, с помощью которого был образован данный конус. Второй катет будет являться радиусом круга основания. Радиус — это половина диаметра. Таким образом, делим данный нам диаметр пополам и получаем длину радиуса: 18:2 = 9. Радиус равен 9.
Теперь найти образующую конуса очень легко. Так как она является гипотенузой, то квадрат ее длины будет равен сумме квадратов катетов, то есть сумме квадратов радиуса и высоты. Итак, квадрат длины образующей = 64 (квадрат длины радиуса) + 64 (квадрат длины высоты) = 64×2 = 128. Теперь извлекаем квадратный корень из 128. В итоге получаем восемь корней из двух. Это и будет образующая конуса.
Как видите, ничего сложного в этом нет. Для примера мы взяли простые условия задачи, однако в школьном курсе они могут быть и сложнее. Помните, что для расчета длины образующей вам нужно выяснить радиус круга и высоту конуса. Зная эти данные, найти длину образующей легко.
Помните, что для расчета длины образующей вам нужно выяснить радиус круга и высоту конуса. Зная эти данные, найти длину образующей легко.
Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.
Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».
Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».
А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2 (16). Мы тоже расскажем о ней.
Элементы конуса. Конус. Основные понятия. Площадь поверхности конуса. Обработка конических поверхностей с применением конусной линейки
Рассмотрим какую-либо линию l (кривую или ломаную), лежащую в некоторой плоскости (рис. 386, а, б), и произвольную точку М, не лежащую в этой плоскости. Всевозможные прямые, соединяющие точку М со всеми точками линии образуют поверхность а; такая поверхность называется конической поверхностью, точка вершиной, линия — направляющей, прямые образующими. На рис. 386 мы не ограничиваем поверхность а ее вершиной, но представляем себе ее простирающейся неограниченно в обе стороны от вершины.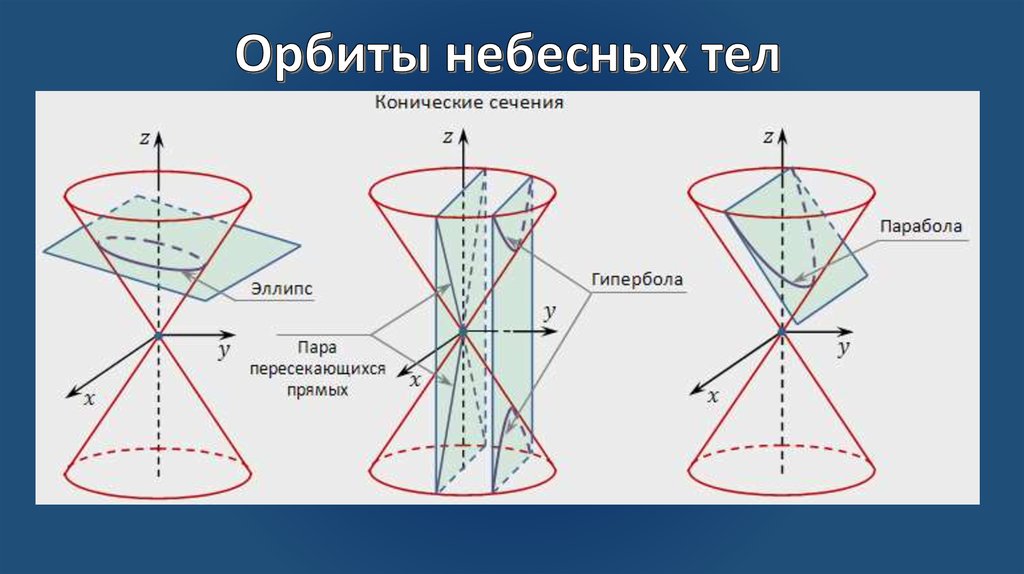
Если коническую поверхность рассечь какой-либо плоскостью, параллельной плоскости направляющей , то в сечении получим линию (кривую или ломаную, в зависимости от того, была ли кривой или ломаной линия ), гомотетичную линии l, с центром гомотетии в вершине конической поверхности. Действительно, отношение любых соответствующих отрезков образующих будет постоянным:
Итак, сечения коническои поверхности плоскостями, параллельными плоскости направляющей, подобны и подобно расположены, с центром подобия в вершине конической поверхности; это же верно для любых параллельных плоскостей, не проходящих через вершину поверхности.
Пусть теперь направляющая — замкнутая выпуклая линия (кривая на рис. 387, а, ломаная на рис. 387, б). Тело, ограниченное с боков конической поверхностью, взятой между ее вершиной и плоскостью направляющей, и плоским основанием в плоскости направляющей, называется конусом (если -кривая линия) или пирамидой (если -ломаная).
Пирамиды классифицируются по числу сторон многоугольника, лежащего в их основании.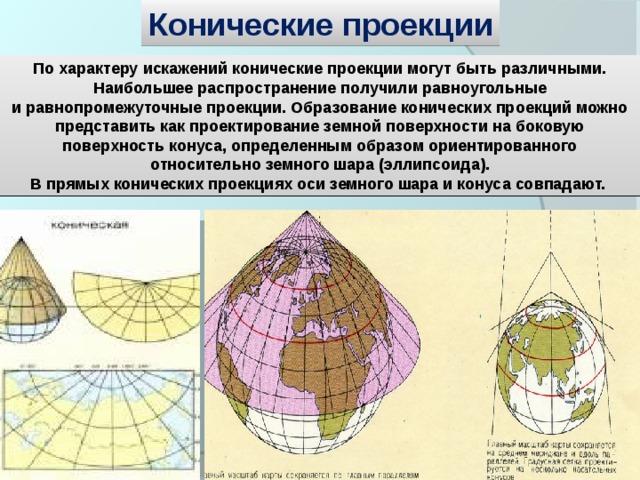 Говорят о треугольной, четырехугольной и вообще -угольной пирамидах. Заметим, что -угольная пирамида имеет грань: боковых граней и основание. При вершине пирамиды мы имеем -гранный угол с плоскими и двугранными углами.
Говорят о треугольной, четырехугольной и вообще -угольной пирамидах. Заметим, что -угольная пирамида имеет грань: боковых граней и основание. При вершине пирамиды мы имеем -гранный угол с плоскими и двугранными углами.
Они соответственно называются плоскими углами при вершине и двугранными углами при боковых ребрах. При вершинах основания мы имеем трехгранных углов; их плоские углы, образованные боковыми, ребрами и сторонами основания, называются плоскими углами при основании, двугранные углы между боковыми гранями и плоскостью основания — двугранными углами при основании.
Треугольная пирамида иначе называется тетраэдром (т. е. четырехгранником). Любая из ее граней может быть принята за основание.
Пирамида называется правильной при выполнении двух условий: 1) в основании пирамиды лежит правильный многоугольник,
2) высота, опущенная из вершины пирамиды на основание, пересекает его в центре этого многоугольника (иначе говоря, вершина пирамиды проектируется в центр основания).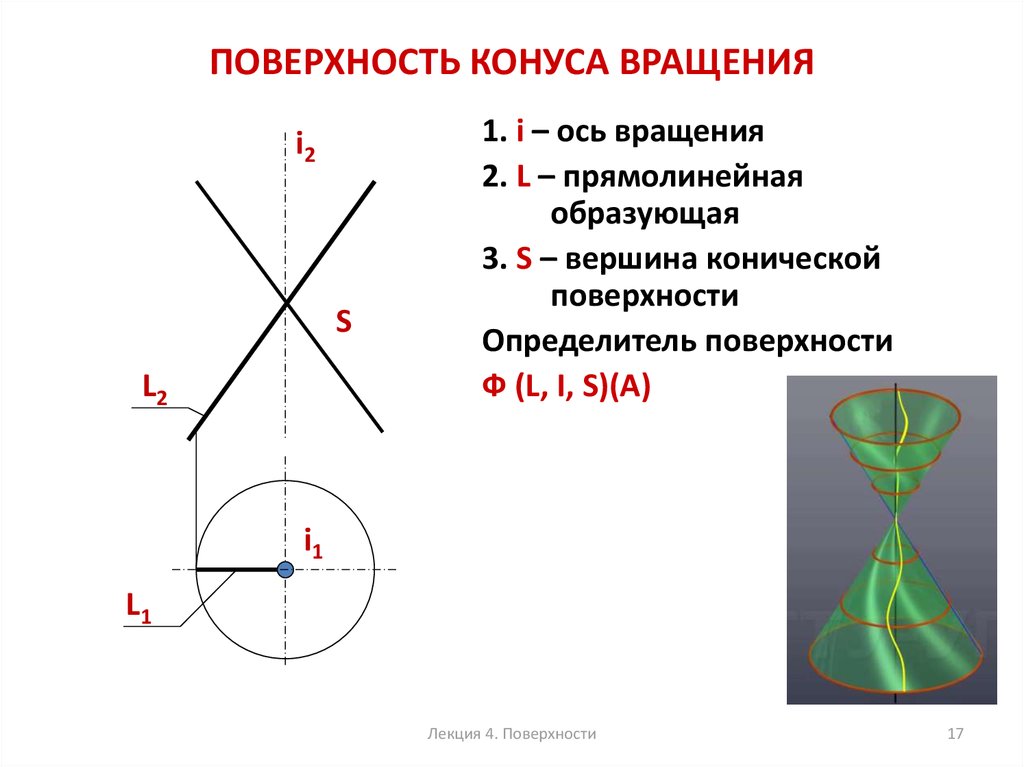
Заметим, что правильная пирамида не является, вообще говоря, правильным многогранником!
Отметим некоторые свойства правильной -угольной пирамиды. Проведем через вершину такой пирамиды высоту SO (рис. 388).
Повернем всю пирамиду как целое вокруг этой высоты на угол При таком повороте многоугольник основания перейдет сам в себя: каждая из его вершин займет положение соседней. Вершина пирамиды и ее высота (ось вращения!) останутся на месте, и поэтому пирамида как целое совместится сама с собой: каждое боковое ребро перейдет в соседнее, каждая боковая грань совместится с соседней, каждый двугранный угол при боковом ребре также совместится с соседним.
Отсюда вывод: все боковые ребра равны между собой, все боковые грани суть равные равнобедренные треугольники, все двугранные углы при основании равны, все плоские углы при вершине равны, все плоские углы при основании равны.
Из числа конусов в курсе элементарной геометрии мы изучаем прямой круговой конус, т. е. такой конус, основание которого круг, а вершина проектируется в центр этого круга.
Прямой круговой конус показан на рис. 389. Если проведем через вершину конуса высоту SO и повернем конус вокруг этой высоты на произвольный угол, то окружность основания будет скользить сама по себе; высота и вершина останутся на месте, поэтому при повороте на любой угол конус совместится сам с собой. Отсюда видно, в частности, что все образующие конуса равны между собой и одинаково наклонены к плоскости основания. Сечения конуса плоскостями, проходящими через его высоту, будут равнобедренными треугольниками, равными между собой. Весь конус получается от вращения прямоугольного треугольника SOA вокруг его катета (который становится высотой конуса). Поэтому прямой круговой конус является телом вращения и также называется конусом вращения. Если не оговорено противное, мы для краткости в дальнейшем говорим просто «конус», понимая под этим конус вращения.
Сечения конуса плоскостями, параллельными плоскости его основания, суть круги (хотя бы потому, что они гомотетичны кругу основания).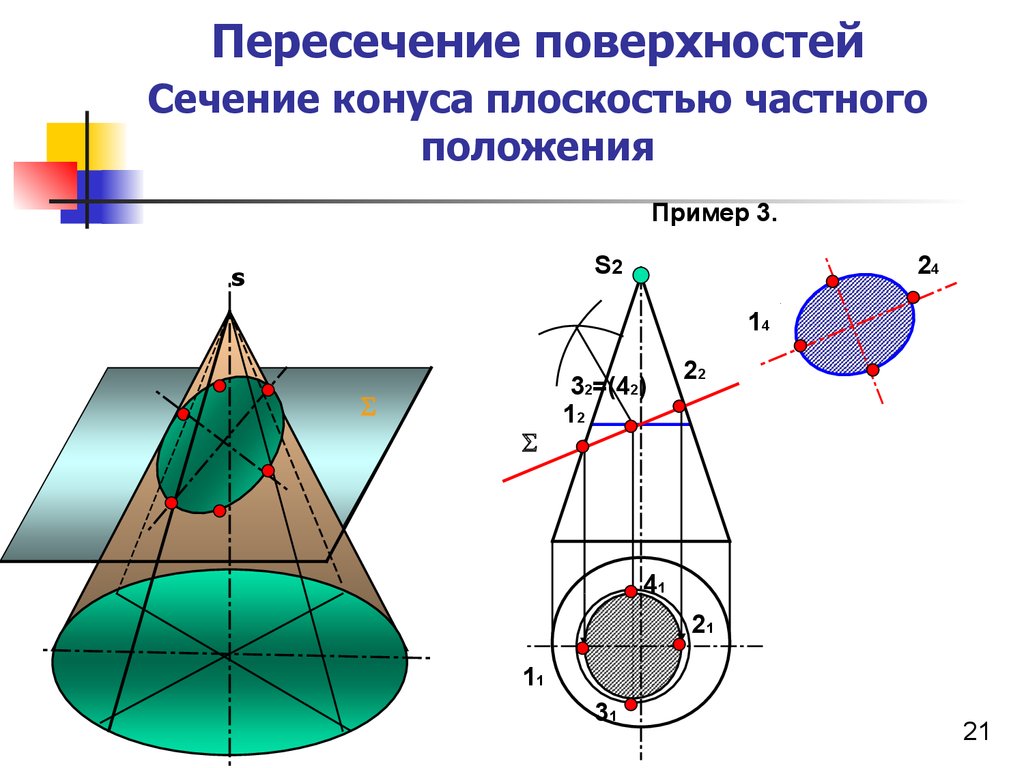
Задача. Двугранные углы при основании правильной треугольной пирамиды равны а. Найти двугранные углы при боковых ребрах.
Решение. Обозначим временно сторону основания пирамиды через а. Проведем сечение пирамиды плоскостью, содержащей ее высоту SO и медиану основания AM (рис. 390).
Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга,- вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания (рис. 1) Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса. Все образующие конуса равны друг другу. Поверхность конуса состоит из основания и боковой поверхности.
Рис. 1
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. Наглядно прямой круговой конус можно представлять себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси (рис.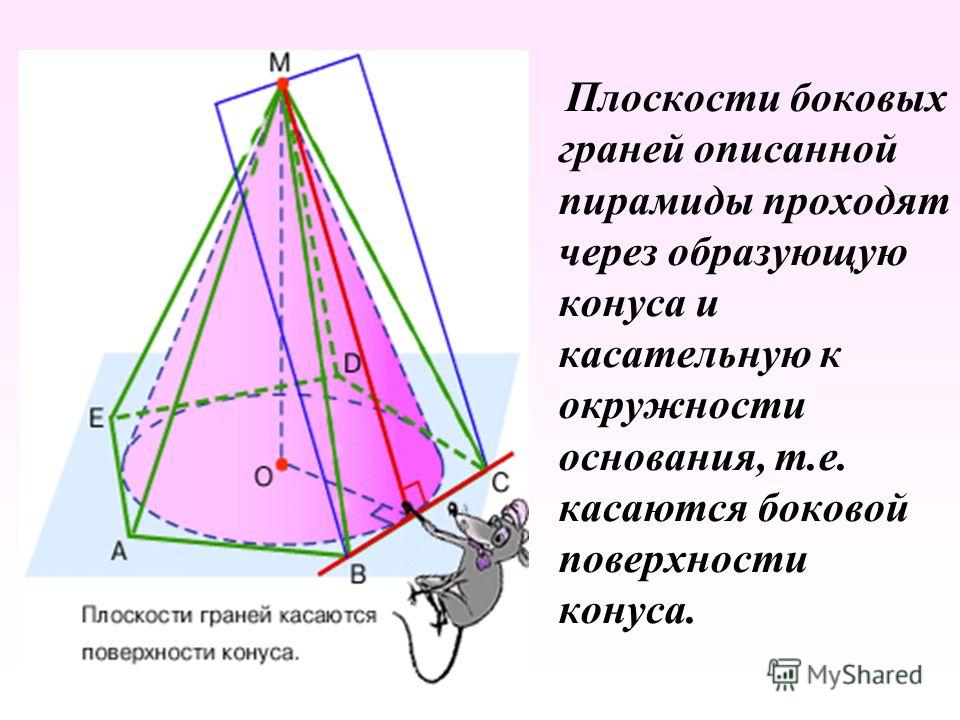 2).
2).
Рис. 2
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту.
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 3). В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса (рис. 4).
Рис. 3 Рис. 4
Площадь поверхности конуса
Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав ее по одной из образующих (рис. 2,а,б). Разверткой боковой поверхности конуса является круговой сектор (рис. 2,6), радиус которого равен образующей конуса, а длина дуги сектора — длине окружности основания конуса.
За площадь боковой поверхности конуса принимается площадь ее развертки. Выразим площадь Sбок боковой поверхности конуса через его образующую l и радиус основания r.
Выразим площадь Sбок боковой поверхности конуса через его образующую l и радиус основания r.
Площадь кругового сектора — развертки боковой поверхности конуса (рис.2) — равна (Пl2а)/360, где а — градусная мера дуги ABA», поэтому
Sбок = (Пl2а)/360. (*)
Выразим а через l и r. Так как длина дуги ABA» равна 2Пr (длине окружности основания конуса), то 2Пr = Пlа/180, откуда a=360r/l. Подставив это выражение в формулу (*), получим:
Sбок = Пrl. (**)
Таким образом, площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Для вычисления площади Sкон полной поверхности конуса получается формула: Sкон = Пr (l + r). (***)
Усеченный конус
Возьмем произвольный конус и проведем секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей представляет собой конус, а другая называется усеченным конусом. Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усеченного конуса, а отрезок, соединяющий их центры, — высотой усеченного конуса.
Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усеченного конуса, а отрезок, соединяющий их центры, — высотой усеченного конуса.
Часть конической поверхности, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключенные между основаниями, называются образующими усеченного конуса. Все образующие усеченного конуса равны друг другу (докажите это самостоятельно).
Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую: Sбок = П (r + r1) l.
Дополнительная информация о конусе
1. В геологии существует понятие «конус выноса». Это форма рельефа, образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину.
2. В биологии есть понятие «конус нарастания». Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.
3. «Конусами» называется семейство морских моллюсков подкласса переднежаберных. Раковина коническая (2–16 см), ярко окрашенная. Конусов свыше 500 видов. Живут в тропиках и субтропиках, являются хищниками, имеют ядовитую железу. Укус конусов очень болезнен. Известны смертельные случаи. Раковины используются как украшения, сувениры.
4. По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на 1 млн. жителей (чаще в южных странах). Этого бы не случалось, если бы везде были громоотводы, так как образуется конус безопасности. Чем выше громоотвод, тем больше объем такого конуса. Некоторые люди пытаются спрятаться от разрядов под деревом, но дерево не проводник, на нем заряды накапливаются и дерево может быть источником напряжения.
5. В физике встречается понятие «телесный угол». Это конусообразный угол, вырезанный в шаре. Единица измерения телесного угла – 1 стерадиан. 1 стерадиан – это телесный угол, квадрат радиуса которого равен площади части сферы, которую он вырезает.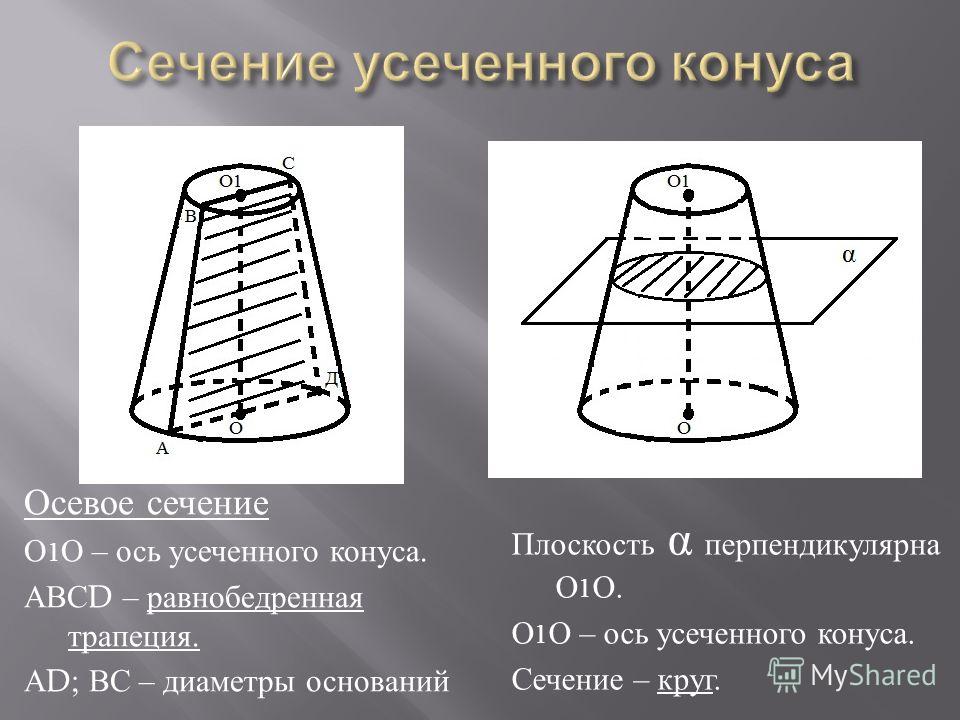 Если в этот угол поместить источник света в 1 канделу (1 свечу), то получим световой поток в 1 люмен. Свет от киноаппарата, прожектора распространяется в виде конуса.
Если в этот угол поместить источник света в 1 канделу (1 свечу), то получим световой поток в 1 люмен. Свет от киноаппарата, прожектора распространяется в виде конуса.
Конус (с греческого «konos») – сосновая шишка. Конус знаком людям с глубокой древности. В 1906 году была обнаружена книга «О методе», написанная Архимедом (287-212 гг. до н. э.), в этой книге дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед говорит, что это открытие принадлежит древнегреческому философу Демокриту (470-380 гг. до н.э.), который с помощью данного принципа получил формулы для вычисления объема пирамиды и конуса.
Конус (круговой конус) – тело, которое состоит из круга – основание конуса, точки, не принадлежащей плоскости этого круга, – вершины конуса и всех отрезков, соединяющих вершину конуса и точки окружности основания. Отрезки, которые соединяют вершину конуса с точками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.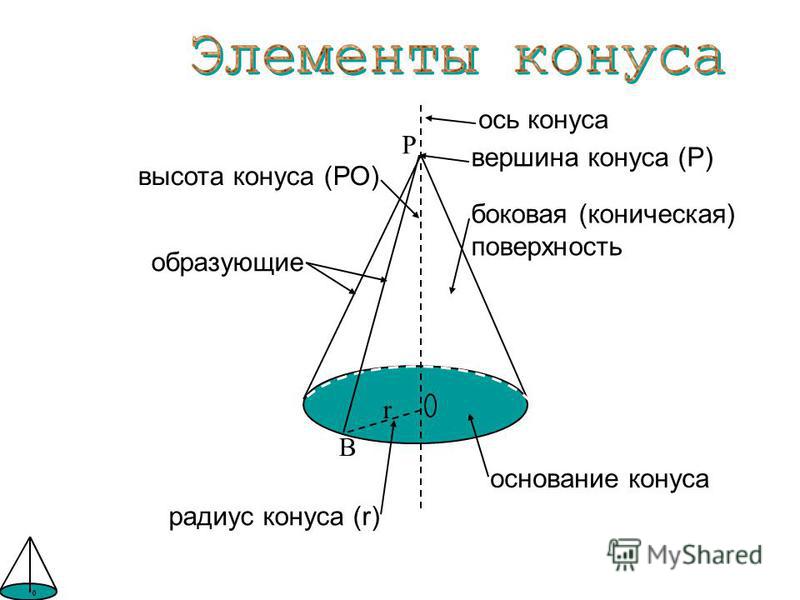
Конус называется прямым, если прямая, которая соединяет вершину конуса с центром основания, перпендикулярна плоскости основания. Прямой круговой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси.
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого конуса называется прямая, содержащая его высоту.
Сечение конуса плоскостью, проходящей через образующую конуса и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью конуса.
Плоскость, перпендикулярная оси конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса.
Плоскость, перпендикулярная оси конуса отсекает от него меньший конус. Оставшаяся часть называется усечённым конусом.
Объём конуса равен трети произведения высоты на площадь основания. Таким образом, все конусы, опирающиеся на данное основание и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
Таким образом, все конусы, опирающиеся на данное основание и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
Площадь боковой поверхности конуса можно найти по формуле:
S бок = πRl,
Площадь полной поверхности конуса находится по формуле:
S кон = πRl + πR 2 ,
где R – радиус основания, l – длина образующей.
Объём кругового конуса равен
V = 1/3 πR 2 H,
где R – радиус основания, Н – высота конуса
Площадь боковой поверхности усеченного конуса можно найти по формуле:
S бок = π(R + r)l,
Площадь полной поверхности усеченного конуса можно найти по формуле:
S кон = πR 2 + πr 2 + π(R + r)l,
где R – радиус нижнего основания, r – радиус верхнего основания, l – длина образующей.
Объём усечённого конуса можно найти следующим образом:
V = 1/3 πH(R 2 + Rr + r 2),
где R – радиус нижнего основания, r – радиус верхнего основания, Н – высота конуса.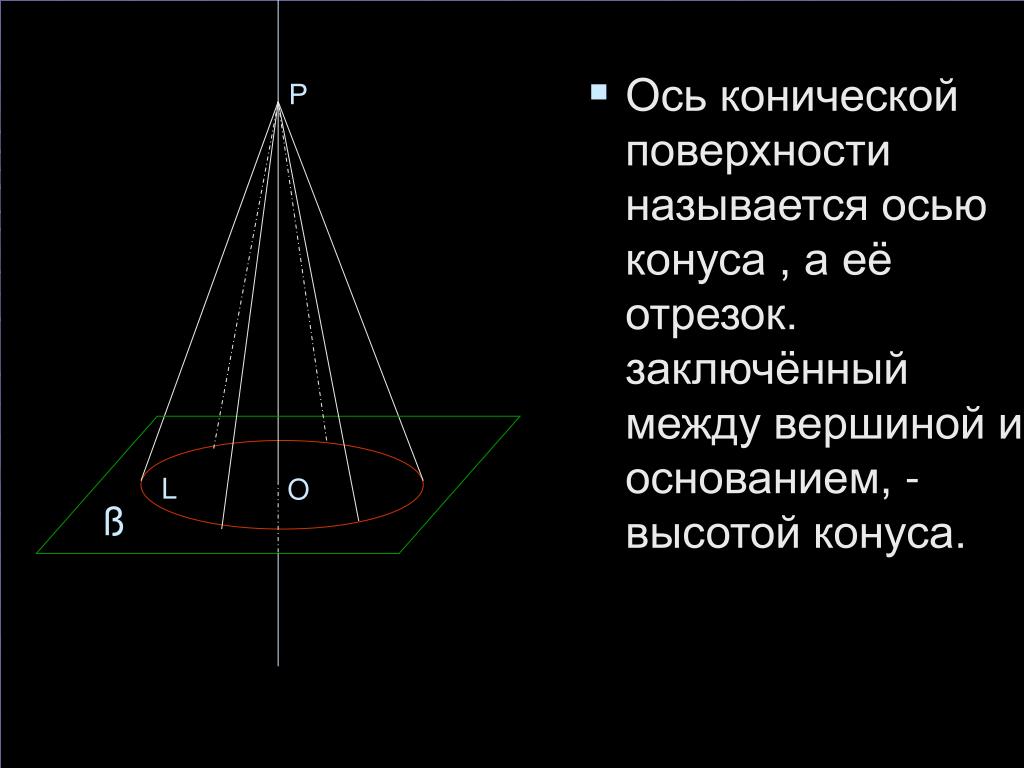
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Определения:
Определение 1. Конус
Определение 2. Круговой конус
Определение 3. Высота конуса
Определение 4. Прямой конус
Определение 5. Прямой круговой конус
Теорема 1. Образующие конуса
Теорема 1.1. Осевое сечение конуса
Объем и площади :
Теорема 2. Объем конуса
Теорема 3. Площадь боковой поверхности конуса
Усеченный конус :
Теорема 4. Сечение, параллельное основанию
Определение 6. Усеченный конус
Теорема 5. Объем усеченного конуса
Теорема 6. Площадь боковой поверхности усеченного конуса
Определние
Тело ограниченное с боков конической поверхностью, взятой между её вершиной и плоскостью направляющей, и плоским основанием направляющей, образованным замкнутой кривой, называется конусом.
Основные понятия
Круговым конусом называют тело, которое состоит из круга (основания), точки, не лежащей в плоскости основания (вершины) и всех отрезков соединяющих вершину с точками основания.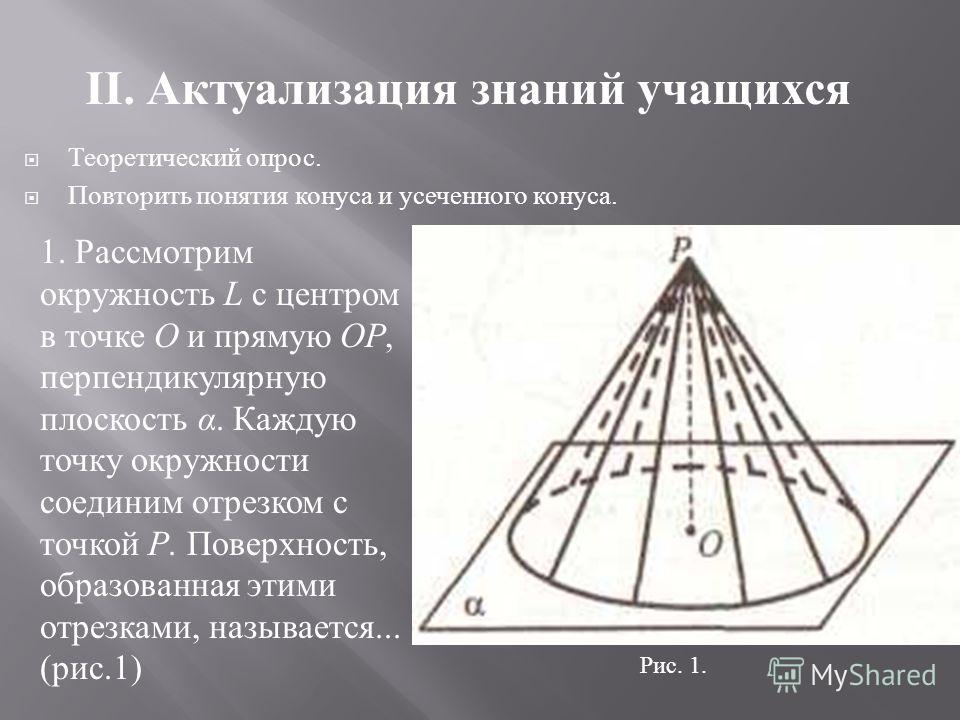
Прямым конусом называется конус, высота которого основанием содержит центр основания конуса.
Рассмотрим какую-либо линию (кривую, ломаную или смешанную)(например, l ), лежащую в некоторой плокости, и произвольную точку (например, М), не лежащую в этой плоскости. Всевозможные прямые, соединяющие точку М со всеми точками данной линии l , образуют поверхность, называемую канонической . Точка М является вершиной такой поверхности, а заданная линия l — направляющей . Все прямые соединяющие точку М со всеми точками линии l , называют образующими .
Каноническая поверхность не ограничивается ни её вершиной, ни направляющей. Она простирается неограниченно в обе стороны от вершины. Пусть теперь направляющая — замкнутая выпуклая линия. Если направляющая — ломаная линия, то тело, ограниченное с боков канонической поверхностью, взятой между её вершиной и плокостью направляющей, и плоским основанием в плоскости направляющей, называется пирамидой .
Если же направляющая — кривая или смешанная линия, то тело, ограниченное с боков канонической поверхностью, взятой между её вершиной и плокостью направляющей, и плоским основанием в плоскости направляющей, называется конусом или
Определение 1 . Конусом называют тело, состоящее из основания — плоской фигуры, ограниченной замкнутой линией (кривой или смешанной), вершины — точки, не лежащей в плокости основания, и всех отрезков, соединяющих вершину со всевозможными точками основания.
Все прямые, проходящие через вершину конуса и любую из точек кривой, ограничивающей фигуру основания конуса, называются образующими конуса. Чаще всего в геометрических задачах под образующей прямой имеется ввиду отрезок этой прямой, заключенный между вершиной и плоскостью основания конуса.
Основание ограниченной смешанной линией — это очень редкий случай. Он сдесь указан только потому, что он может быть рассмотрен в геометрии. Чаще рассматривается случай с криволинейной направляющей. Хотя, что случай с произвольной кривой, что случай со смешанной направляющей, мало чем полезен и в них сложно вывести какие-любо закономерности. Из числа конусов в курсе элементарной геометрии изучается прямой круговой конус.
Хотя, что случай с произвольной кривой, что случай со смешанной направляющей, мало чем полезен и в них сложно вывести какие-любо закономерности. Из числа конусов в курсе элементарной геометрии изучается прямой круговой конус.
Известно, что окружность есть частный случай замкнутой кривой линии. Круг — плоская фигура, ограниченная окружностью. Принимая окружность за направляющую, можно определеить круговой конус.
Определение 2 . Круговым конусом называют тело, которое состоит из круга (основания), точки, не лежащей в плоскости основания (вершины) и всех отрезков соединяющих вершину с точками основания.
Определение 3 . Высота конуса — перпендикуляр, опущенный из вершины на плокость основания конуса. Можно выделить конус, высота которого падает в центр плоской фигуры основания.
Определение 4 . Прямым конусом называется конус, высота которого основанием содержит центр основания конуса.
Если связать эти два определения, мы получим конус, основание котрого есть круг, а высота падает в центр этого круга.
Определение 5 . Прямым круговым конусом называют конус, основание котрого есть круг, а высота его соединяет вершину и центр основания данного конуса.
Такой конус получается вращением прямоугольного треугольника вокруг одного из катетов. Поэтому прямой круговой конус является телом вращения и называется также конусом вращения. Если не оговорено противное, то для краткости в дальнейшем говорим просто конус.
Итак приведем некоторые свойства конуса:
Теорема 1 . Все образующие конуса равны. Доказательство. Высота МО перпендикулярна всем прямым основания по определению перпендикулярной прямой к плокости. Поэтому треугольники МОА, МОВ и МОС являются прямоугольными и равны по двум катетам (МО — общая, ОА=ОВ=ОС — радиусы основания. Поэтому равны и гипотенузы, т.е. образующие.
Радиус основания конуса иногда называют радиусом конуса . Высота конуса называется также осью конуса , поэтому любое сечение, проходящее через высоту называется осевым сечением .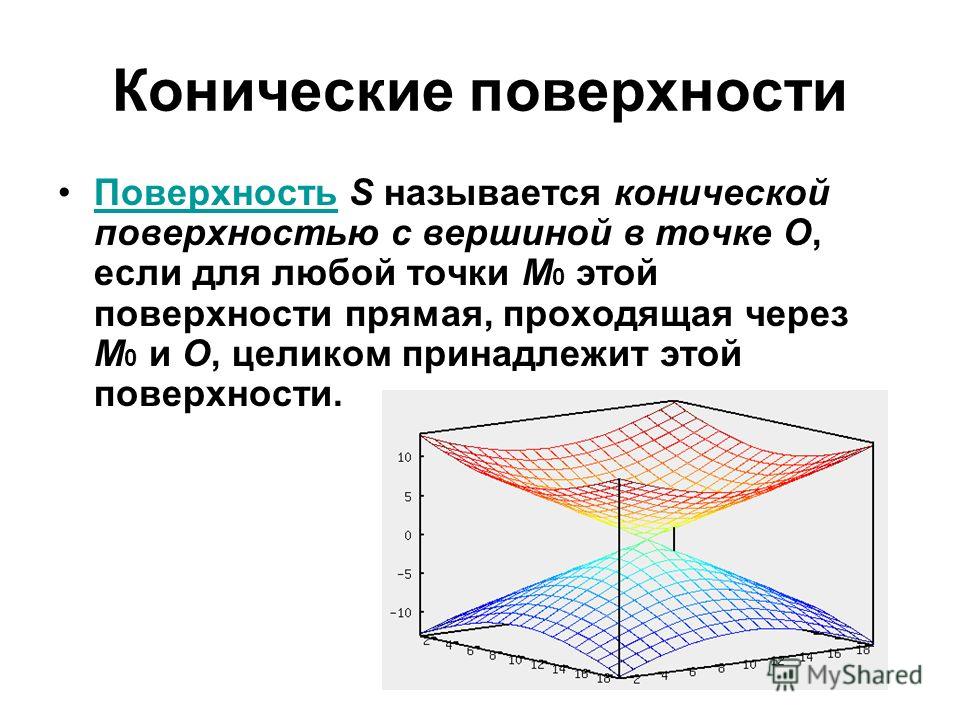 Любое осевое сечение пересекает основание по диаметру (т.к. прямая, по которой пересекаются осевое сечение и плокость основания, проходит через центр окружности) и образует равнобедренный треугольник.
Любое осевое сечение пересекает основание по диаметру (т.к. прямая, по которой пересекаются осевое сечение и плокость основания, проходит через центр окружности) и образует равнобедренный треугольник.
Теорема 1.1. Осевое сечение конуса есть равнобедренный треугольник. Так треугольник АМВ является равнобедренным, т.к. две его стороны МВ и МА есть образующие. Угол АМВ является углом при вершине осевого сечения.
Сегодня мы расскажем вам о том, как найти образующую конуса, что частенько требуется в школьных задачках по геометрии.
Понятие образующей конуса
Прямой конус — это фигура, которая получается в результате вращения прямоугольного треугольника вокруг одно из его катетов. Основание конуса образует круг. Вертикальное сечение конуса — это треугольник, горизонтальное — круг. Высотой конуса является отрезок, соединяющий вершину конуса с центром основания. Образующей конуса является отрезок, который соединяет вершину конуса с любой точкой на линии окружности основания.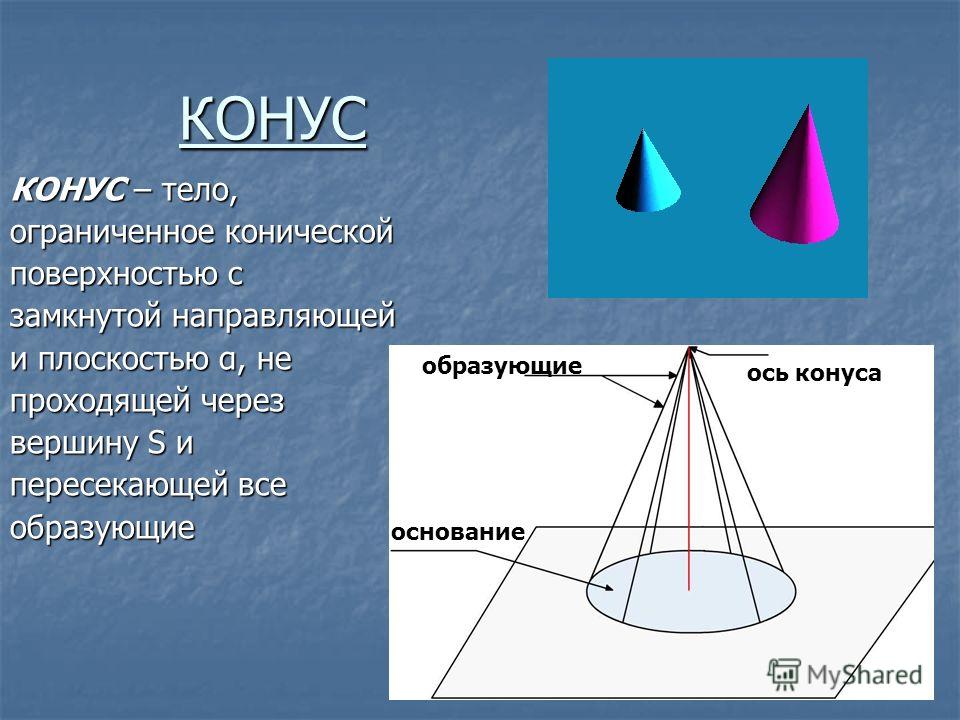
Так как конус образуется вращением прямоугольного треугольника, то получается, что первым катетом такого треугольника является высота, вторым — радиус круга, лежащего в основании, а гипотенузой будет образующая конуса. Нетрудно догадаться, что для расчета длины образующей пригодится теорема Пифагора. А теперь подробнее о том, как найти длину образующей конуса.
Находим образующую
Легче всего понять, как найти образующую, можно на конкретном примере. Допустим, даны такие условия задачи: высота равна 9 см., диаметр круга основания составляет 18 см. Необходимо найти образующую.
Итак, высота конуса (9 см.) — это один из катетов прямоугольного треугольника, с помощью которого был образован данный конус. Второй катет будет являться радиусом круга основания. Радиус — это половина диаметра. Таким образом, делим данный нам диаметр пополам и получаем длину радиуса: 18:2 = 9. Радиус равен 9.
Теперь найти образующую конуса очень легко. Так как она является гипотенузой, то квадрат ее длины будет равен сумме квадратов катетов, то есть сумме квадратов радиуса и высоты. Итак, квадрат длины образующей = 64 (квадрат длины радиуса) + 64 (квадрат длины высоты) = 64×2 = 128. Теперь извлекаем квадратный корень из 128. В итоге получаем восемь корней из двух. Это и будет образующая конуса.
Итак, квадрат длины образующей = 64 (квадрат длины радиуса) + 64 (квадрат длины высоты) = 64×2 = 128. Теперь извлекаем квадратный корень из 128. В итоге получаем восемь корней из двух. Это и будет образующая конуса.
Как видите, ничего сложного в этом нет. Для примера мы взяли простые условия задачи, однако в школьном курсе они могут быть и сложнее. Помните, что для расчета длины образующей вам нужно выяснить радиус круга и высоту конуса. Зная эти данные, найти длину образующей легко.
| Деятельность учителя | Деятельность ученика |
3. Объяснение нового материала Цель: ввести новые понятия и свойства конуса. |
|
1. Конус может быть получен вращением
прямоугольного треугольника вокруг одного из
его катетов. (Слайд 8) (Слайд 8)Теперь рассмотрим, как строится конус. Сначала изображаем окружность с центром O и прямую OP, перпендикулярную к плоскости этой окружности. Каждую точку окружности соединим отрезком с точкой P (учитель поэтапно строит конус). Поверхность, образованная этими отрезками, называется конической поверхностью, а сами отрезки – образующими конической поверхности. |
В тетрадях строят конус. |
| (диктует определение) (Слайд 9) Тело, ограниченной конической поверхностью и кругом с границей L, называется конусом. | Записывают определение. |
Коническая поверхность называется боковой
поверхностью конуса, а круг – основанием
конуса. Прямая OP, проходящая через центр
основания и вершину, называется осью конуса. Ось конуса перпендикулярна плоскости основания.
Отрезок OP называется высотой конуса. Точка P
называется вершиной конуса, а образующие
конической поверхности – образующими конуса.
Ось конуса перпендикулярна плоскости основания.
Отрезок OP называется высотой конуса. Точка P
называется вершиной конуса, а образующие
конической поверхности – образующими конуса.
|
На чертеже подписывают элементы конуса. |
| Назовите две образующие конуса и сравните их? | PA и PB, они равны. |
| Почему образующие равны? | Проекции наклонных равны как радиусы окружности, значит и сами образующие равны. |
| Запишите в тетради: свойства конуса: | (Слайд 10) |
| 1. Все образующие конуса равны. Назовите
углы наклона образующих к основанию? Сравните их. |
Углы: PСО, PDO. |
| 2. Углы наклона образующих к основанию
равны. Назовите углы между осью и
образующими? |
СРО и DPO |
| 3. Углы между осью и образующими равны. Назовите
углы между осью и основанием? |
POC и POD. |
| 4. Углы между осью и основанием прямые. Мы будем рассматривать только прямой конус. |
|
| 2. Рассмотрим сечение конуса различными
плоскостями. Что представляет собой секущая плоскость, проходящая через ось конуса? |
Треугольник. |
| Какой это треугольник? | Он равнобедренный. |
| Почему? | Две его стороны являются образующими, а они равны. |
| Что представляет собой основание данного треугольника? | Диаметр основания конуса. |
| Такое сечение называется осевым. (Слайд
11) Начертите в тетрадях и подпишите это
сечение. Что представляет собой секущая плоскость, перпендикулярная оси OP конуса? |
Круг. |
| Где расположен центр этого круга? | На оси конуса. |
| Это сечение называется круговым
сечением.(Сдайл 12) Начертите в тетрадях и подпишите это сечение. Существуют и другие виды сечений конуса, которые не являются осевыми и не параллельны основанию конуса.  Рассмотрим их на примерах. (Слайд 13) Рассмотрим их на примерах. (Слайд 13) |
Чертят в тетрадях. |
| 3. Теперь выведем формулу полной
поверхности конуса. (Слайд 14) Для этого боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав ее по одной из образующих. |
|
| Что является разверткой боковой поверхности конуса? (чертит на доске) | Круговой сектор. |
| Что является радиусом этого сектора? | Образующая конуса. |
| А длина дуги сектора? | Длина окружности. |
| За площадь боковой поверхности конуса принимается площадь ее развертки. (Слайд 15) | , где – градусная мера
дуги. |
| Чему равна площадь кругового сектора? | |
| Значит, чему равна площадь боковой
поверхности конуса? Выразим через и . (Слайд 16) |
|
| С другой стороны эта же дуга
представляет собой длину окружности основания
конуса. Чему она равна? Откуда . |
|
| Подставляя в
формулу боковой поверхности конуса получим, . Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. . Запишите эти формулы. |
Записывают: , . |
| 4. Название: Решение задач на нахождение элементов конуса. | |
№ 547.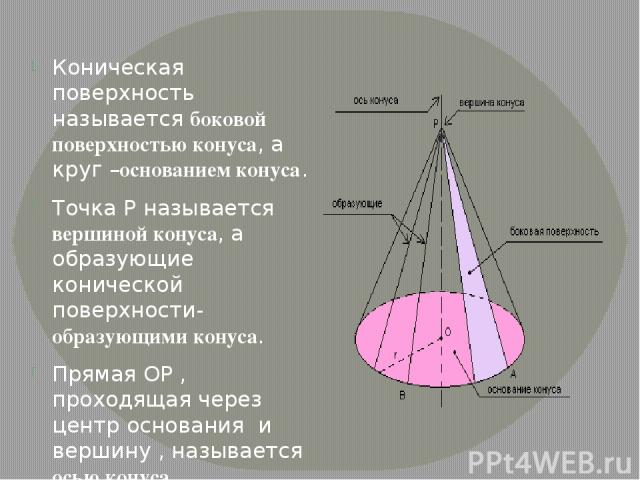 (решаем у доски). (Слайд 17) (решаем у доски). (Слайд 17) |
Дано: см, см. Найти: . Решение: – прямоугольный. , , |
| № 548 (а) (Слайд 18) | Дано: см, Найти: . Решение: – прямоугольный. Т.к. , то PO = 6 см. , , см, , см2. Ответ: см2 |
| № 549(а) (Слайд 19) | Дано: , h
= 8 дм. Найти: РО1 Решение: => => . дм. Ответ: дм. |
| № 550 (Слайд 20) | Дано: конус, –
прямоугольный, см. Найти: . Решение: – равнобедренный (PA = PB как образующие) => углы при основании равны 450; – прямоугольный, => ,
т. , см2. Ответ: 25 см2. |
| 5. Подведение итогов урока | |
| Решите задачу устно: дано: R = 3, H = 4. Найти: L. Итак, мы с вами познакомились с понятием конуса, его элементов и научились решать задачи на нахождение элементов конуса. Вопрос о конусе важен, так как конические детали имеются во многих машинах и механизмах, носовая часть самолетов и ракет имеет коническую форму. |
(Слайд 21) L = 5 |
Тела вращения 9 класс онлайн-подготовка на Ростелеком Лицей
Тела вращения
Одним из первых величайших изобретений человечества был гончарный круг. С его помощью стало возможным в большом количестве создавать посуду и другие изделия из керамики.
Поскольку гончарный круг во время работы вращается, то в результате его работы получаются изделия особой формы – они симметричны относительно вертикальной оси (см. рис. 1).
рис. 1).
Рис. 1. Гончарные изделия симметричны относительно вертикальной оси
Такие тела, что вполне логично, называют телами вращения, ведь их можно получить, вращая плоскую фигуру вокруг некоторой оси.
Известный нам цилиндр можно получить, вращая вокруг вертикальной оси прямоугольник (см. рис. 2).
Рис. 2. Цилиндр получается вращением вокруг вертикальной оси прямоугольника
Конус можно получить, вращая вокруг вертикальной оси равнобедренный (или прямоугольный) треугольник (см. рис. 3).
Рис. 3. Конус получается вращением вокруг вертикальной оси равнобедренного или прямоугольного треугольника
Шар можно получить, вращая вокруг вертикальной оси круг (см. рис. 4).
Рис. 4. Шар получается вращением вокруг вертикальной оси круга
Отличие тел вращения от многогранников
Поскольку объекты, имеющие форму тел вращения, встречаются довольно часто (в строительстве, архитектуре и вообще в быту), мы будем подробно изучать свойства этих тел. В частности, научимся вычислять характеристики их элементов, площадь поверхности и объем таких тел.
В частности, научимся вычислять характеристики их элементов, площадь поверхности и объем таких тел.
Главным отличием тел вращения от многогранников является отсутствие вершин, ребер или граней, т. е. поверхность тел вращения не образована пересечением нескольких плоскостей (см. рис. 5). Именно это различие означает «гладкую» форму тел вращения и «угловатую» форму многогранников. Это, конечно, не строгие математические термины, но они помогают нам легко, «на глаз», различать такие тела.
Рис. 5. Тела вращения отличаются от многогранников отсутствием вершин, ребер или граней
При этом многогранники нам помогут получить и доказать различные свойства тел вращения. Вспомните, что мы приближали окружность правильными многоугольниками (см. рис. 6).
Рис. 6. Приближение окружности правильными многоугольниками
Точно так же можно поступить и с телами вращения – например, призма, в основании которой лежит правильный многоугольник с большим количеством вершин, будет очень похожа на цилиндр, пирамида – на конус (см. рис. 7).
рис. 7).
Рис. 7. Приближение призмы (основание – правильный многоугольник) и пирамиды
С шаром чуть сложнее, но его тоже можно приближать различными многогранниками (см. рис. 8).
Рис. 8. Приближение шара
Так, футбольный мяч обычно представляет собой многогранник, гранями которого являются пяти- и шестиугольники (см. рис. 9). И этот многогранник настолько хорошо приближает сферу, что позволяет футболистам играть футбол и даже использовать поговорку: «Мяч круглый».
Рис. 9. Футбольный мяч представляет собой многогранник, гранями которого являются пяти- и шестиугольники
Правильные многогранники
Может возникнуть вопрос – почему с шаром не сделать так же, как с кругом. Почему не взять правильный многогранник и не увеличивать в нем количество граней до тех пор, пока не получится тело, очень похожее на шар?
Оказывается, проблема в том, что правильных многогранников не так много. Если существуют правильные многоугольники с любым количеством вершин, то правильных многогранников существует всего видов.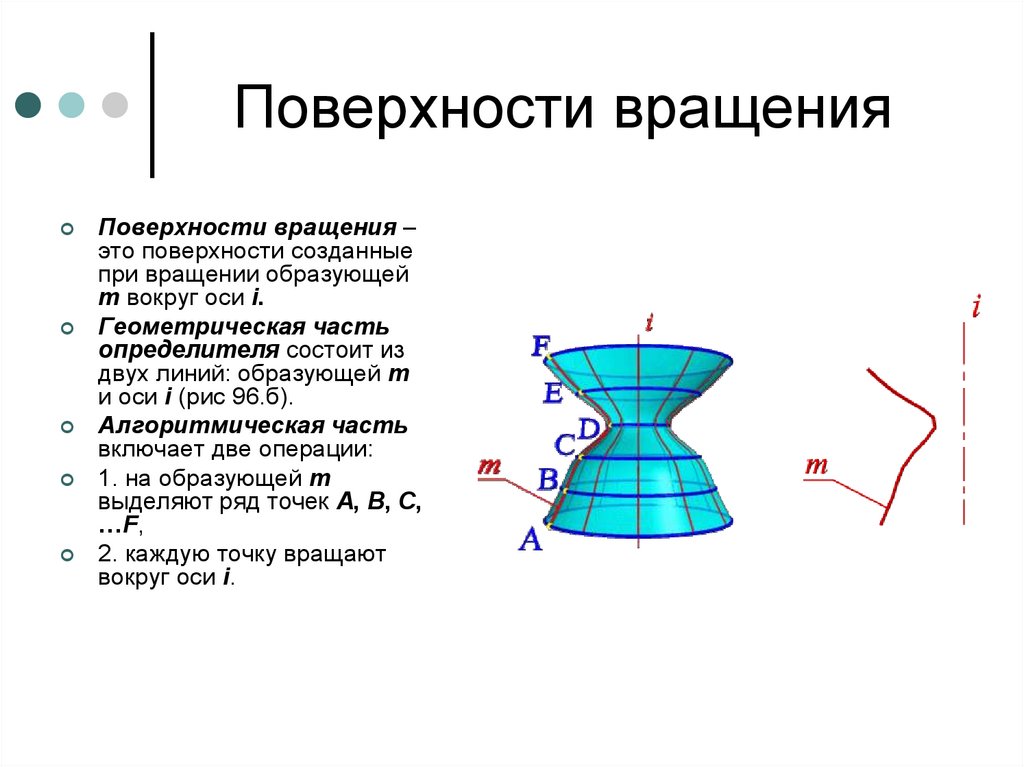 Посмотрим, почему так получается.
Посмотрим, почему так получается.
Пусть правильный многогранник имеет граней, каждая из которых представляет собой правильный n-угольник. И пусть в каждой вершине сходится ребер, а в многограннике всего вершин и ребер.
Мы можем сказать, что , (в каждой вершине сходится не меньше ребер).
Т. к. каждая грань содержит ребер, то:
( появляется, т. к. каждое ребро принадлежит двум граням (см. рис. 10), и мы его посчитали раза).
Рис. 10. Каждое ребро принадлежит двум граням
Аналогично, т. к. в каждой вершине сходится ребер, то:
( появляется, т. к. каждое ребро соединяет вершины (см. рис. 11) и мы опять его посчитали раза).
Рис. 11. Каждое ребро соединяет вершины
Вспомним теорему Эйлера для многогранников:
Подставим полученные равенства:
Т. к. правая часть должна быть положительной, то левая часть тоже положительная:
Или:
Если , то:
Значит, либо , либо должно быть равно или .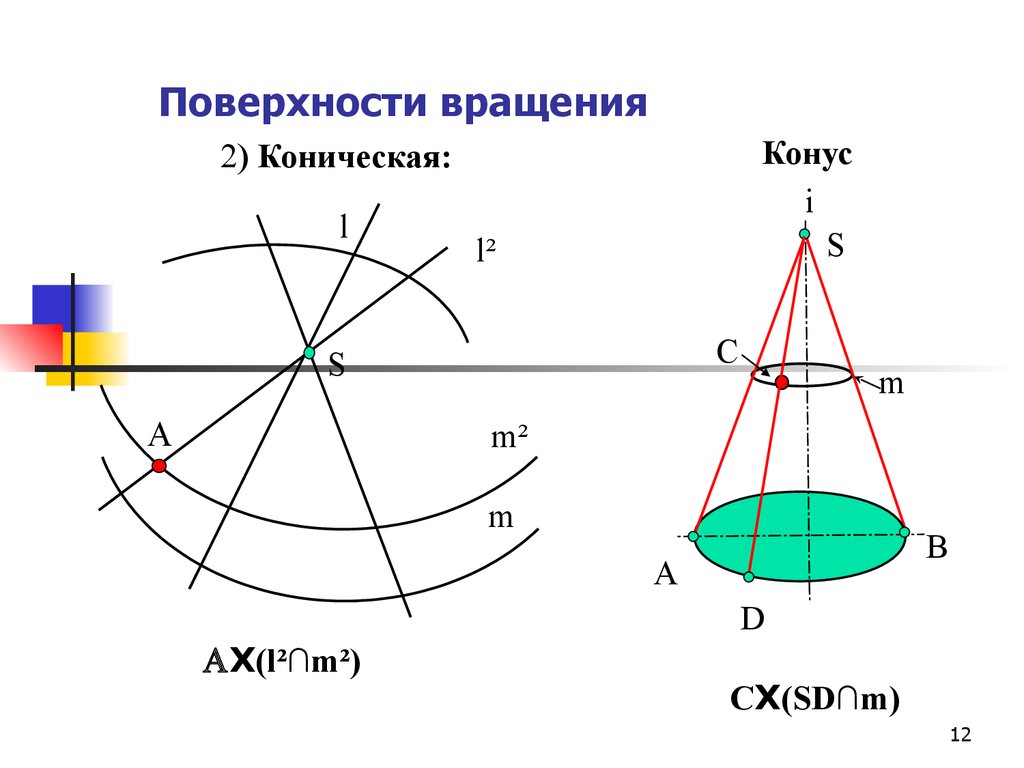
Пусть , тогда:
Откуда:
Возможные варианты:
1. Если :
Откуда:
Это тетраэдр (см. рис. 12).
Рис. 12. Тетраэдр
2. Если , :
Откуда:
Это октаэдр (см. рис. 13).
Рис. 13. Октаэдр
3. Пусть , :
Откуда:
Это икосаэдр (см. рис. 14).
Рис. 14. Икосаэдр
4. Пусть :
Откуда:
Т. е. единственный возможный вариант: :
Откуда:
Это куб (см. рис. 15).
Рис. 15. Куб
Осталось рассмотреть два случая: . Поскольку в неравенстве и симметричны, то все случаи будут рассматриваться аналогично. Случаи и мы уже рассмотрели.
5. Единственный новый случай: :
Откуда:
Это додекаэдр (см. рис. 16).
Рис. 16. Додекаэдр
Мы рассмотрели все возможные варианты, других правильных многогранников нет (см. рис. 17).
рис. 17).
Рис. 17. Правильные многогранники
Поэтому провести аналогию с приближением окружности правильными многоугольниками для правильных многогранников не получится. Это не значит, что шар нельзя приблизить многогранниками – можно, мы уже приводили пример футбольного мяча. Но эти многогранники не будут правильными.
Цилиндр
Возьмем прямоугольник и будем его вращать вокруг стороны (см. рис. 18).
Рис. 18. Получение цилиндра вращением прямоугольника вокруг стороны
Сверху и снизу у нас получатся два круга. Их мы будем называть верхним и нижним основаниями цилиндра (см. рис. 19).
Рис. 19. Верхнее и нижнее основания цилиндра
Радиусы этих кругов одинаковы и равны длинам отрезков и . Эти радиусы оснований также будем называть и радиусом самого цилиндра (см. рис. 20).
Рис. 20. Радиус цилиндра
Кроме основания, у нас получилась поверхность, созданная вращением отрезка . Она называется боковой поверхностью цилиндра или просто цилиндрической поверхностью (см. рис. 21).
Она называется боковой поверхностью цилиндра или просто цилиндрической поверхностью (см. рис. 21).
Рис. 21. Боковая поверхность цилиндра (цилиндрическая поверхность)
Боковая поверхность состоит из вертикальных отрезков, параллельных друг другу. Они называются образующими цилиндра (см. рис. 22). Любая образующая является высотой цилиндра.
Рис. 22. Образующая цилиндра
Какие бывают цилиндры
На самом деле, мы дали определение не произвольного цилиндра, а одного из видов – прямого кругового (см. рис. 23). Название вполне объяснимое: «прямой», так как образующие перпендикулярны основаниям, «круговой», так как в основании лежат круги.
Рис. 23. Прямой круговой цилиндр
Более общее определение цилиндра такое. Если взять две одинаковые кривые и разместить их в параллельных плоскостях, то вместе с семейством параллельных образующих, которые соединяют точки этих кривых, они образуют цилиндр (см. рис. 24). Само семейство параллельных образующих называется цилиндрической поверхностью (см. рис. 25).
рис. 24). Само семейство параллельных образующих называется цилиндрической поверхностью (см. рис. 25).
Рис. 24. Образование цилиндра
Рис. 25. Цилиндрическая поверхность
Понятно, что цилиндр может быть прямым (см. рис. 26) или наклонным (см. рис. 27) (в зависимости от угла наклона образующих к плоскости основания).
Рис. 26. Прямой цилиндр
Рис. 27. Наклонный цилиндр
Также вид цилиндра может определяться кривой, которая лежит в основаниях. Например, эллиптический (см. рис. 28). При таком определении призма тоже будет частным случаем цилиндра (см. рис. 29).
Рис. 28. Эллиптический цилиндр
Рис. 29. Призма как частный случай цилиндра
Но все же в подавляющем большинстве случаев под цилиндром мы будем подразумевать именно прямой круговой цилиндр.
Формулы цилиндра
Как мы уже говорили, цилиндр можно приближать правильной призмой, увеличивая количество вершин в основании последней.
Вспомним, что объем любой призмы равен произведению площади основания на высоту.
Тогда объем цилиндра как предельного случая призмы тоже можно вычислить по этой формуле:
Т. к. основание цилиндра – круг, то площадь основания находится по формуле площади круга:
А объем цилиндра тогда вычисляется по формуле:
Площадь боковой поверхности цилиндра тоже легко находится. Развернем боковую поверхность – получим прямоугольник (см. рис. 30).
Рис. 30. Развертка цилиндрической поверхности
Высота этого прямоугольника равна высоте цилиндра, а длина равна длине окружности основания. Таким образом, площадь боковой поверхности вычисляется по формуле:
Конус
Можно провести аналогию с приближением цилиндра призмой для конуса: приближать его правильной пирамидой.Но конус также является фигурой вращения.Чтобы его получить, рассмотрим прямоугольный треугольник и начнем его вращать вокруг катета (см.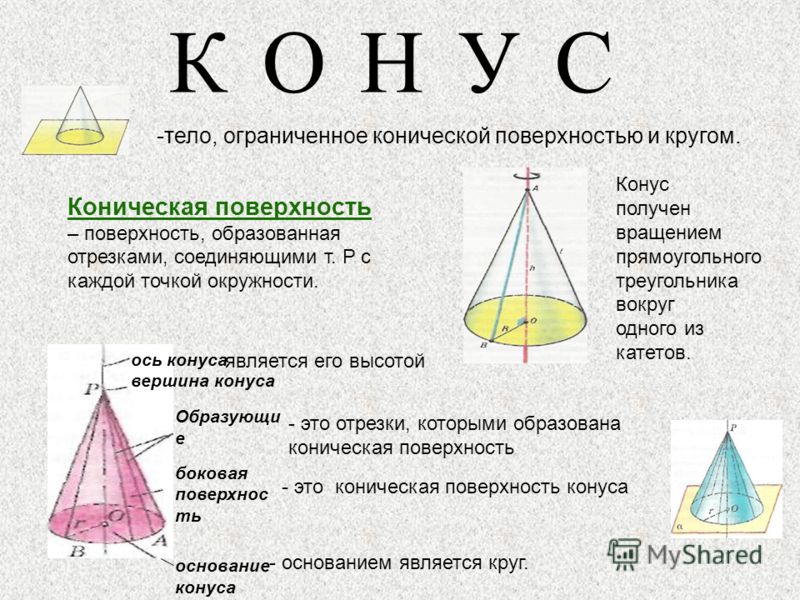 рис. 31).
рис. 31).
Рис. 31. Получение конуса вращением прямоугольного треугольника вокруг катета
Катет опишет круг – основание конуса – и будет, соответственно, радиусом конуса (рис. 32).
Рис. 32. Катет является радиусом конуса
А при вращении гипотенузы образуется боковая поверхность конуса, другое название – коническая поверхность (см. рис. 33). Отрезки, из которых состоит коническая поверхность, как и в случае цилиндра, называются образующими.
Рис. 33. Боковая поверхность конуса (коническая поверхность)
Вершина – это вершина конуса, – ось конуса, которая является и высотой (см. рис. 34).
Рис. 34. Вершина и ось (высота) конуса
Какие бывают конусы
И снова, как и в ситуации с цилиндром, мы дали определение одному из видов конуса – прямому круговому конусу (см. рис. 35).
Рис. 35. Прямой круговой конус
Более общее определение такое. Рассмотрим точку в пространстве и кривую. Соединим выбранную точку со всеми точками этой кривой (см. рис. 36). Семейство этих образующих – коническая поверхность (см. рис. 37). Вместе с частью плоскости, которую ограничивает кривая, коническая поверхность образует конус (см. рис. 38).
Соединим выбранную точку со всеми точками этой кривой (см. рис. 36). Семейство этих образующих – коническая поверхность (см. рис. 37). Вместе с частью плоскости, которую ограничивает кривая, коническая поверхность образует конус (см. рис. 38).
Рис. 36. Образование конуса
Рис. 37. Коническая поверхность
Рис. 38. Коническая поверхность образует конус вместе с частью плоскости, которую ограничивает кривая
Понятно, что конус может быть прямым (см. рис. 39) (если у основания есть центр симметрии и вершина конуса проецируется в этот центр симметрии), а может быть наклонным (см. рис. 40).
Рис. 39. Прямой конус
Рис. 40. Наклонный конус
Также ясно, что, в зависимости от кривой в основании, конус может быть круговым, эллиптическим (см. рис. 41) и т. д. Более того, при таком определении даже пирамида является частным случаем конуса (см. рис. 42).
Рис. 41. Эллиптический конус
Рис. 42. Пирамида как частный случай конуса
Но в подавляющем большинстве задач мы будем встречаться именно с прямым круговым конусом.
Формулы конуса
Объем любой пирамиды вычисляется по формуле:
Эту же формулу можно использовать для вычисления объема конуса как предельного случая правильной пирамиды.
Поскольку площадь основания – это площадь круга, то объем конуса вычисляется по формуле:
Развертка конической поверхности представляет собой не прямоугольник, как у цилиндра, а круговой сектор (см. рис. 43).
Рис. 43. Развертка конической поверхности
Вспомним, как вычисляется площадь сектора. Пусть есть сектор радиуса длиной дуги (см. рис. 44).
Рис. 44. Сектор радиуса длиной дуги
Длина всей окружности равна:
Площадь сектора во столько раз меньше площади целого круга, во сколько длина дуги меньше длины всей окружности:
Рассмотрим конус с образующей и радиусом основания (см. рис. 45).
Рис. 45. Конус с образующей и радиусом основания
Теперь для вычисления боковой поверхности конуса разрежем ее по одной из образующих и развернем.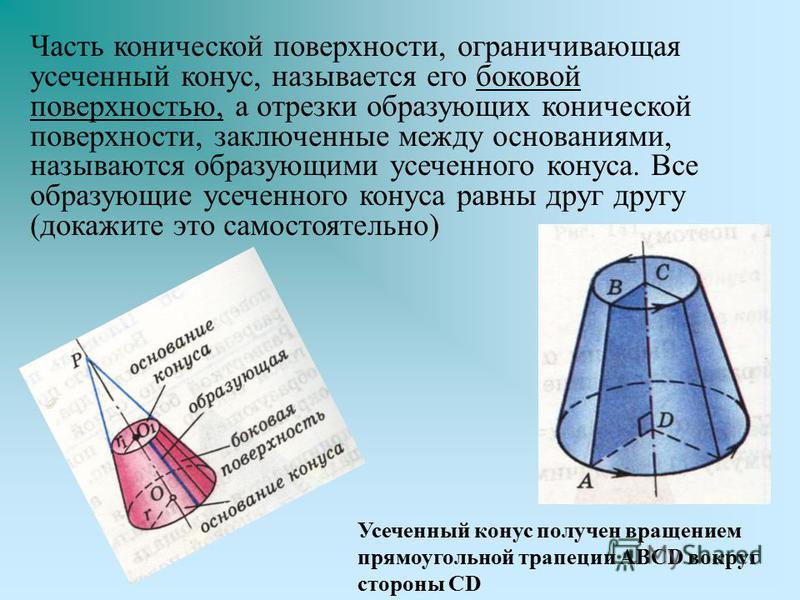 Получим круговой сектор (см. рис. 46).
Получим круговой сектор (см. рис. 46).
Рис. 46. Развертка конуса с образующей и радиусом основания
Радиусом сектора является образующая конуса , а длина дуги равна длине окружности основания конуса:
Найдем площадь сектора:
Это и есть формула боковой поверхности конуса:
Посмотрим на еще один предельный случай. Понятно, что у конуса образующая всегда больше радиуса основания . Если ее уменьшать и таким образом приближать к , то высота конуса будет стремиться к нулю. Тогда сама коническая поверхность будет стремиться к кругу, лежащему в основании (см. рис. 47).
Рис. 47. Приближение образующей конуса к радиусу основания
Тогда неудивительно, что формула боковой поверхности конуса при стремлении к превращается в формулу площади круга, лежащего в основании конуса:
Шар
Переходим к рассмотрению третьего тела вращения – шара (см. рис. 48). Шар во многом является трехмерным аналогом круга. Они имеют идентичные определения, которые мы рассмотрим чуть позже.
Они имеют идентичные определения, которые мы рассмотрим чуть позже.
Рис. 48. Шар
Кроме этого, границы шара и круга имеют отдельные названия. Это достаточно необычно для фигур. Например, граница квадрата так и будет называться – граница или периметр квадрата. Граница же круга называются окружностью, а граница шара называется сферой (см. рис. 49).
Рис. 49. Сфера и окружность
Можно представлять дело ровно наоборот: не окружность – это граница круга, а круг – это часть плоскости, ограниченная окружностью. Точно так же не сфера – граница шара, а шар – часть пространства, ограниченная сферой.
На самом деле для всех четырех фигур (см. рис. 50) существуют свои строгие независимые определения:
- Окружность – множество точек плоскости, удаленных от данной точки на данное расстояние.
- Круг – множество точек плоскости, удаленных от данной точки не более чем на данное расстояние.
- Сфера – множество точек пространства, удаленных от данной точки на данное расстояние.
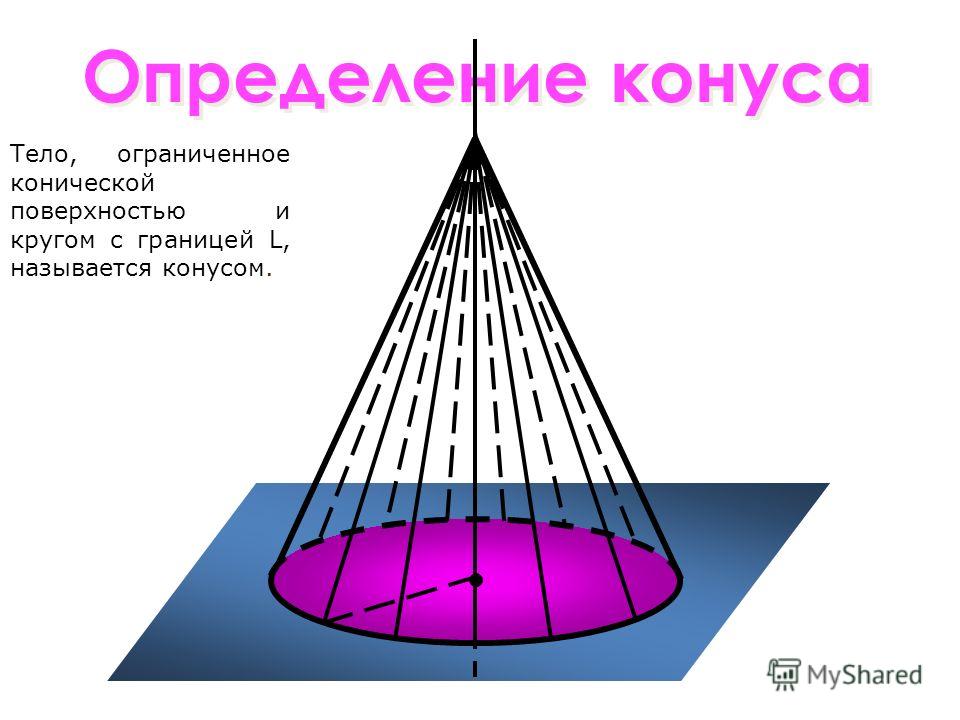
- Шар – множество точек пространства, удаленных от данной точки не более чем на данное расстояние.
Рис. 50. Слева направо: окружность, круг, сфера, шар
Почему шар называется фигурой вращения, тоже понятно. Его можно получить вращением круга (или даже достаточно полукруга) вокруг своего диаметра (см. рис. 51).
Рис. 51. Получение шара вращение круга вокруг своего диаметра
Расстояние от любой точки сферы до центра называется радиусом сферы и шара (см. рис. 52).
Рис. 52. Радиус сферы и шара
Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром. Понятно, что, как и в случае круга, диаметр равен двум радиусам.
Объем шара
Вопрос объема и площади поверхности шара (т. е. площади сферы) решается немного сложнее, чем для цилиндра и конуса. Начнем с объема.
Попробуем найти объем шара радиуса . Для удобства оставим только половину шара (см.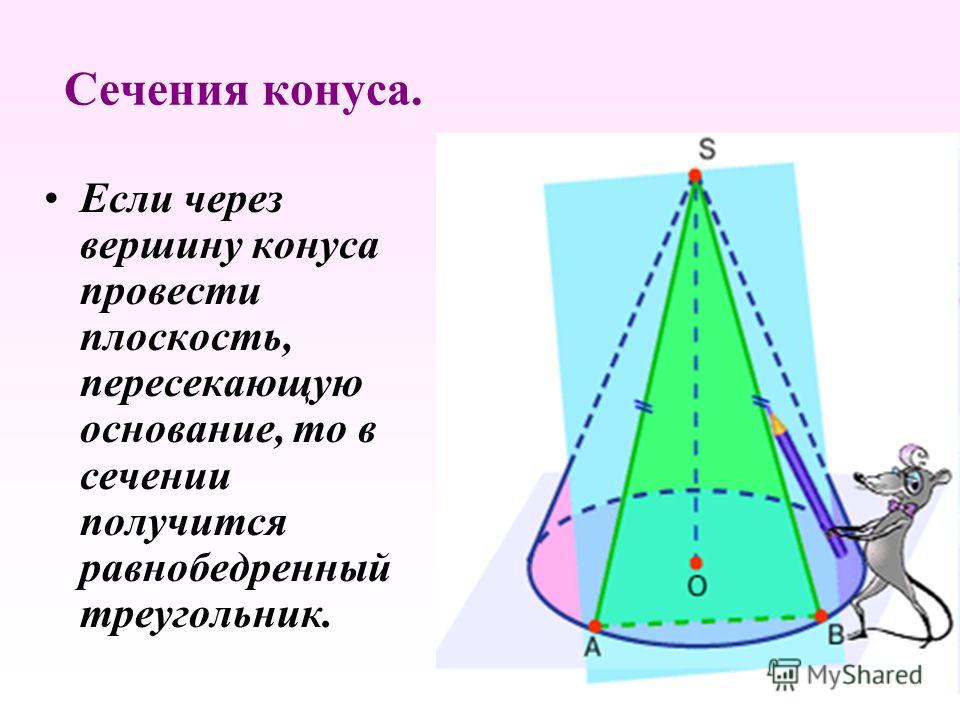 рис. 53), и если нам удастся найти ее объем, то умножим потом результат на два.
рис. 53), и если нам удастся найти ее объем, то умножим потом результат на два.
Рис. 53. Половина шара радиуса
Положим полушар на плоскость и рядом поставим цилиндр, высота и радиус которого равны , т. е. высоты у обоих тел одинаковые (см. рис. 54).
Рис. 54. Полушар и цилиндр с равными высотами и радиусами на плоскости
Помните, что более простая фигура ставится рядом с более сложной, чтобы применить принцип Кавальери для сравнения их объемов (Многогранники. Виды многогранников. Объём).
Основания у обоих тел – это равные круги радиуса . Но если мы пересечем фигуры плоскостью (см. рис. 55), то равенство площадей пропадает.
Рис. 55. Пересечение полушара и цилиндра плоскостью
Явно сечение у цилиндра больше, чему у половины шара. Найдем площадь сечения половины шара. Пусть расстояние между плоскостями равно (см. рис. 56).
Рис. 56. Расстояние между плоскостями равно
Тогда радиус сечения мы найдем по теореме Пифагора:
Тогда площадь сечения (см. рис. 57):
рис. 57):
Рис. 57. Площадь сечения
При этом площадь сечения цилиндра равна:
Значит, чтобы площадь сечения цилиндра стала равна площади сечения половины шара, нужно вычесть из него величину , т. е. круг радиуса .
Внутри круга радиуса построим круг радиуса . Площадь полученного кольца (см. рис. 58):
Т. е. равна площади сечения половины шара.
Рис. 58. Кольцо
Осталось подобрать тело, у которого будут такие сечения. Нетрудно догадаться, что таким телом будет цилиндр, из которого вырезали перевернутый конус, основание которого совпадает с верхним основанием цилиндра (см. рис. 59).
Рис. 59. Цилиндр, из которого вырезали перевернутый конус, основание которого совпадает с верхним основанием цилиндра
Посмотрим на ситуацию еще раз. Два тела стоят на плоскости . Первое – половина шара радиуса . Второе – цилиндр радиуса и высоты , в котором вырезана полость в виде перевернутого конуса. Радиус основания и высота конуса тоже равны .
Если провести плоскость параллельно плоскости на расстоянии , то мы получим два сечения – круг и кольцо, площади которых одинаковы и равны:
Но тогда, по принципу Кавальери, эти тела имеют равные объемы. Объем сконструированного нами тела равен разности объемов цилиндра и конуса:
Мы нашли объем половины шара. Осталось его умножить на два и получить объем шара:
Площадь поверхности шара
Попробуем теперь определить площадь поверхности шара (площадь сферы). Основная идея будет следующей. Если есть тонкая пленка, то объем такой пленки равен произведению ее площади на толщину:
Если так окажется, что мы знаем объем и толщину пленки, то можем найти ее площадь:
Рассмотрим теперь шар радиуса . Покрасим его слоем краски толщиной (см. рис. 60). Радиус окрашенного шара равен .
Рис. 60. Шар радиуса покрашен слоем краски толщиной
Объем слоя краски можно вычислить как разность объемов окрашенного и неокрашенного шаров:
Найдем площадь слоя краски – разделим объем на :
Если мы говорим о площади поверхности шара радиуса, то это соответствует нашей задаче с краской, толщина слоя которой . Тогда формула приобретает вид:
Тогда формула приобретает вид:
Это и есть формула площади поверхности шара (площади сферы):
Заключение
1. Цилиндр очень похож на призму и имеет такую же формулу для вычисления объема:
Развертка цилиндрической поверхности – это прямоугольник, ее площадь рассчитывается по формуле:
2. Конус очень похож на пирамиду и имеет такую же формулу для вычисления объема:
Развертка конической поверхности – это сектор, ее площадь рассчитывается по формуле:
где – образующая конуса.
3. Объем шара рассчитывается по формуле:
Площадь его поверхности, т. е. сферы, рассчитывается по формуле:
Список литературы
- Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 9 класс. Учебник. – М.: «Просвещение», 2017.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 9 класс. Учебник. – М.: «Просвещение», 2018.
- Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия, 9 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru (Источник)
- Интернет-портал yoclever.org (Источник)
- Интернет-портал math5school.ru (Источник)
Домашнее задание
- Найти объем цилиндра, радиус которого равен , а высота равна радиусу.
- Найти объем конуса, радиус основания которого равен , а высота вдвое больше радиуса основания.
- Объемы двух шаров относятся как . Найти отношение площадей их поверхностей.
Площадь поверхности конуса
Горячая математикаобщий площадь поверхности из конус есть сумма площадей его основания и боковой (боковой) поверхности.
площадь боковой поверхности конуса – это площадь только боковой или боковой поверхности.
Поскольку конус тесно связан с пирамида , формулы для их площадей связаны.
Помните, формула площади боковой поверхности пирамиды 1 2 п л а общая площадь поверхности 1 2 п л + Б .
Поскольку основанием конуса является круг, подставляем
2
π
р
за
п
а также
π
р
2
за
Б
куда
р
это радиус основания цилиндра.
Итак, формула для площадь боковой поверхности прямого конуса л . С . А знак равно π р л , куда л — наклонная высота конуса .
Пример 1:
Найдите площадь боковой поверхности прямого конуса, если радиус 4 см, а наклонная высота 5 см.
л
. С
.
А
знак равно
π
(
4
)
(
5
)
знак равно
20
π
≈
62,82
см
2
С
.
А
знак равно
π
(
4
)
(
5
)
знак равно
20
π
≈
62,82
см
2
Формула для общая площадь поверхности прямого конуса
Т
.
С
.
А
знак равно
π
р
л
+
π
р
2
.
Пример 2:
Найдите площадь полной поверхности прямого конуса, если радиус 6 дюймов, а наклонная высота 10 дюймы.
Т . С . А знак равно π ( 6 ) ( 10 ) + π ( 6 ) 2 знак равно 60 π + 36 π знак равно 96 π дюймы 2 ≈ 301,59 дюймы 2
SCIRP Открытый доступ
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и медико-биологические науки.

- Бизнес и экономика
- Химия и материаловедение.
- Информатика. и общ.
- Науки о Земле и окружающей среде.
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по тематике
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Опубликуйте у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
- Подача статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. org org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
| Недавно опубликованные статьи |
| Недавно опубликованные статьи |
Оценка ветровой энергии 17 станций штата Рио-де-Жанейро, Бразилия, тематическое исследование за 2020–2021 годы()
Лаиса Прата Морейра Фернандес, Лаис Феррейра Назарет, Ярло Энрике Друмонд Пирес Паскоаль, Карлос Эдуардо Фидель де Соуза и Силва, Андре Луис Ксавьер Гимарайнш Насри, Педро Скарпини Гомес Гнапп, Густаво Раймес Богеа Феликс, Рохерио Габриэль де Кастро Москейра, Карлос Альберто Хуниор Москейра де Оливейра, Сара Налия де Оливейра Коста, Ханс Шмидт Сантос
Журнал библиотеки открытого доступа Том 9 № 9, 14 сентября 2022 г.

DOI: 10.4236/oalib.1109215 13 загрузок 63 просмотров
Антиоксидантные свойства и антимикробная активность экстрактов двух съедобных грибов, Pleurotus sajor caju и Schizophyllum commune ()
Суджат Аль-Азад, Вивиан Чонг Ай Пинг
Достижения в области биологических наук и биотехнологий Том 13 № 9, 14 сентября 2022 г.
DOI: 10.4236/абб.2022.139023 8 загрузок 43 просмотров
Эпидемиологические аспекты диабетической ретинопатии в Центре применения диплома специализированных исследований в области офтальмологии (Cadeso)/Donka-Conakry()
Сонасса Диане, Ибрахима Фофана, Тьерно Мадиу Бах, Мусса Диавара, Закари Адаму Туре, Оскар Адебайо Тонухеуа, Тамба Мина Миллимуно, Северин Бони
Достижения в области инфекционных заболеваний Том 12 № 3, 14 сентября 2022 г.

DOI: 10.4236/помощь.2022.123039 7 загрузок 52 просмотров
Гаплотипы MDR1 и полиморфизм G2677T/A предсказывают ответ на иматиниб у тунисских пациентов с хроническим миелоидным лейкозом()
Мариам Аммар, Соня Ктари, Моэз Медхаффар, Ханен Гоззи, Моэз Эллуми, Аднен Хаммами, Халед Зегал, Лобна Бен Махмуд
Journal of Biosciences and Medicines Vol.10 No.9, 14 сентября 2022 г.
DOI: 10.4236/jbm.2022.109009 7 загрузок 33 просмотров
Насилие, связанное с выборами, в Нигерии: перспективы здравоохранения, образования и безопасности.
 Качественное исследование()
Качественное исследование()Гамалиэль Аджоку, Оби Питер Адигве
Открытый журнал социальных наук Том 10 № 10, 14 сентября 2022 г.
DOI: 10.4236/jss.2022.1010010 4 загрузки 38 просмотров
Уровни тяжелых металлов и потенциальные экологические риски, оцененные на участке агроэкосистемы в тропическом регионе()
Люк Календеле Лундеми, Стефани Салуму Неема, Эммануэль Казингуву Атибу, Криспин Кьела Муладжи, Тьерри Табу Тангу, Камилла Ипей Нсиманда, Роберт Буэя Суами, Мари Онококо Эсако, Дьедонне Эюль’Анки Мусибоно, Фернандо Пьедаде Карвальо
Журнал геонаук и охраны окружающей среды Том 10 № 9, 14 сентября 2022 г.
DOI: 10.
 4236/gep.2022.109003
15 загрузок 149Просмотры
4236/gep.2022.109003
15 загрузок 149Просмотры
Подпишитесь на SCIRP
Свяжитесь с нами
| клиент@scirp.org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
Площадь поверхности конуса – формула, вывод, примеры
Площадь поверхности конуса – это площадь, занимаемая поверхностью конуса. Конус представляет собой трехмерную фигуру с круглым основанием. Это означает, что основание состоит из радиуса или диаметра. Расстояние между центром основания и самой верхней частью конуса (конечно, в случае с мороженым эта часть находится внизу) является высотой конуса. Мы можем найти площадь поверхности конуса двумя способами — полной площадью поверхности и площадью криволинейной поверхности конуса.
Мы можем найти площадь поверхности конуса двумя способами — полной площадью поверхности и площадью криволинейной поверхности конуса.
В этой статье мы узнаем, как вычислить площадь поверхности конуса. Общая площадь поверхности включает в себя как изогнутую, так и плоскую круглую площадь, тогда как площадь изогнутой поверхности включает площадь только изогнутой поверхности. Мы рассмотрим формулу и решим несколько примеров для лучшего понимания концепции.
| 1. | Какова площадь поверхности конуса? |
| 2. | Площадь поверхности конуса Формула |
| 3. | Изогнутая поверхность конуса |
| 4. | Расчет площади поверхности конуса |
| 5. | Часто задаваемые вопросы о площади поверхности конуса |
Какова площадь поверхности конуса?
Площадь, занимаемая поверхностью/границей конуса, называется площадью поверхности конуса. Она всегда измеряется в квадратных единицах. Складывание множества треугольников и вращение их вокруг оси дает форму конуса. Поскольку он имеет плоское основание, он имеет общую площадь поверхности, а также площадь изогнутой поверхности. Мы можем классифицировать конус как прямой круговой конус или наклонный конус. Вершина в прямом круглом конусе обычно находится вертикально над центром основания, тогда как вершина конуса в наклонном конусе не находится вертикально над центром основания.
Она всегда измеряется в квадратных единицах. Складывание множества треугольников и вращение их вокруг оси дает форму конуса. Поскольку он имеет плоское основание, он имеет общую площадь поверхности, а также площадь изогнутой поверхности. Мы можем классифицировать конус как прямой круговой конус или наклонный конус. Вершина в прямом круглом конусе обычно находится вертикально над центром основания, тогда как вершина конуса в наклонном конусе не находится вертикально над центром основания.
Площадь поверхности конуса Формула
Поскольку конус имеет криволинейную поверхность, мы можем выразить площадь его криволинейной поверхности, а также общую площадь поверхности. Конус имеет два вида площади поверхности:
- Общая площадь поверхности
- Изогнутая поверхность
Если радиус основания конуса равен «r», а наклонная высота конуса равна «l», площадь поверхности конуса определяется как:
- Общая площадь поверхности, T = πr(r + л) квадратных единиц
- Площадь криволинейной поверхности, S = πrl квадратных единиц
Применяя теорему Пифагора о конусе, мы можем найти связь между площадью поверхности конуса и его высотой. Мы знаем, h 2 + r 2 = l 2 , где h — высота конуса, r — радиус основания, а l — наклонная высота конуса.
Мы знаем, h 2 + r 2 = l 2 , где h — высота конуса, r — радиус основания, а l — наклонная высота конуса.
⇒ l = √(h 2 + r 2 )
Таким образом,
- Общая площадь поверхности по высоте может быть определена как T = πr(r + l) = T = πr(r + √(ч 2 + р 2 )).
- Площадь искривленной поверхности конуса по высоте может быть выражена как S = πrl = πr(√(h 2 + r 2 )).
Изогнутая поверхность конуса
Мы обсудили формулу для нахождения площади криволинейной поверхности конуса, теперь давайте разберемся в ее значении. Как и другие трехмерные фигуры, конус также имеет как плоские, так и криволинейные поверхности. Площадь изогнутой поверхности конуса относится только к изогнутой части конуса, отличной от круглого плоского основания. Чтобы найти площадь криволинейной поверхности конуса, мы умножаем радиус и наклонную высоту конуса на pi(π). Выведем формулу площади криволинейной поверхности конуса ниже.
Выведем формулу площади криволинейной поверхности конуса ниже.
Площадь криволинейной поверхности конуса Формула
Площадь криволинейной поверхности конуса может быть определена путем нахождения площади сектора по формуле
Площадь сектора (в пересчете на длину дуги) = (длина дуги × радиус)/ 2 = ((2πr) × l)/2 = πrl.
∴ Площадь криволинейной поверхности конуса, S = πrl единиц 2 .
Расчет площади поверхности конуса
Возьмем конус высотой «h», радиусом основания «r» и высотой наклона «l». Чтобы определить площадь поверхности образования конуса, мы вырезаем конус из центра, который выглядит как сектор круга (плоская форма).
Общая площадь поверхности конуса = площадь основания конуса + площадь изогнутой поверхности конуса
⇒ Общая площадь поверхности конуса = πr 2 + πrl = πr (r + l).
∴ Полная площадь поверхности конуса, T = πr (r + l) ед. криволинейная поверхность конуса.
Пример: Найдите общую площадь поверхности и площадь криволинейной поверхности конуса, радиус которого равен 7 дюймам, а наклонная высота равна 3 дюймам. (Используйте π = 22/7).
Мы знаем, что площадь полной поверхности конуса равна πr (r + l), а площадь боковой поверхности конуса равна πrl. Учитывая, что: r = 7 дюймов, l = 3 дюйма и π = 22/7. Таким образом, общая площадь поверхности конуса T = πr (r + l) = (22/7) × 7 × (7 + 3) = (22/7) × 7 × 10 = 22 × 10 = 220 в 2 .
∴ Общая площадь поверхности конуса 220 2 .
Площадь криволинейной поверхности конуса, S = πrl = (22/7) × 7 × 3 = 66 в 2 . ∴ Площадь изогнутой поверхности конуса составляет 66 дюймов 2 .
Давайте рассмотрим еще несколько примеров площади поверхности конуса для более глубокого понимания.
Часто задаваемые вопросы о площади поверхности конуса
Какова площадь поверхности конуса?
Мера площади, занимаемой поверхностью конуса, называется площадью поверхности конуса. Существует два типа площади поверхности конуса, которые можно разделить на общую площадь поверхности и площадь криволинейной поверхности конуса.
Существует два типа площади поверхности конуса, которые можно разделить на общую площадь поверхности и площадь криволинейной поверхности конуса.
Как найти площадь поверхности конуса?
Площадь поверхности конуса можно найти, выполнив следующие шаги:
- Шаг 1: Определите заданные значения радиуса, наклонной высоты и высоты конуса.
- Шаг 2: Используйте соответствующую формулу для расчета площади поверхности. Если необходимо найти общую площадь поверхности конуса, используйте формулу πr (r + l) квадратных единиц, а если нужно найти площадь криволинейной поверхности конуса, используйте формулу πrl квадратных единиц.
- Шаг 3: Упростите и запишите ответ в квадратных единицах.
Что такое площадь криволинейной поверхности конуса?
Площадь криволинейной поверхности конуса известна как площадь криволинейной поверхности конуса. Формула для расчета площади криволинейной поверхности конуса: πrl, где «r» — радиус основания, а «l» — наклонная высота конуса. При этом мы не рассматриваем площадь основания конуса, имеющего форму круга.
При этом мы не рассматриваем площадь основания конуса, имеющего форму круга.
Какова площадь криволинейной поверхности правильного круглого конуса?
Прямой круглый конус определяется как конус, осью которого является линия, соединяющая вершину и середину круглого основания. Таким образом, площадь криволинейной поверхности прямого круглого конуса определяется как πrl, где «r» — радиус основания, а «l» — наклонная высота. С точки зрения высоты, площадь изогнутой поверхности прямого круглого конуса определяется как πr(√(h 2 + r 2 )) где «h» — высота правильного круглого конуса.
Как найти площадь поверхности конуса с наклонной высотой и диаметром?
Полную площадь поверхности конуса с наклонной высотой и диаметром конуса можно найти по формуле T = π(D/2) ((D/2) + l), где D — диаметр, а l — наклонная высота. Площадь криволинейной поверхности конуса с наклонной высотой и диаметром можно найти по формуле S = π(D/2)l, где D — диаметр, а l — наклонная высота.
Как найти полную площадь поверхности конуса?
Полную площадь поверхности конуса можно найти, выполнив следующие шаги:
- Шаг 1: Проверьте значения, указанные в вопросе.
- Шаг 2: Подставьте значения радиуса и наклонной высоты в формулу πr (r + l). В случае, если наклонная высота не указана, мы записываем значение наклонной высоты через высоту конуса «h», подставляя l = √(h 2 + r 2 ), что дает значение, T = πr(r + √(h 2 + r 2 )) где «r» — радиус конуса, а «h» — высота конуса.
- Шаг 3: Теперь найдите значение общей площади поверхности.
- Шаг 4: Запишите окончательный ответ в квадратных единицах.
Как найти площадь криволинейной поверхности конуса?
Площадь криволинейной поверхности конуса можно найти, используя следующие шаги:
- Шаг 1: Запишите значения, указанные в вопросе.

- Шаг 2: Подставить значения радиуса и наклонной высоты заданного вопроса в формулу πrl. В случае, если наклонная высота не указана, мы записываем значение наклонной высоты через высоту конуса «h», подставляя l = √(h 2 + r 2 ), что дает значение S = πr√(h 2 + r 2 ), где «r» — радиус конуса, а «h» — высота конуса.
- Шаг 3: Теперь найдите значение площади криволинейной поверхности и запишите ответ в квадратных единицах.
Что произойдет с площадью поверхности конуса, если наклонную высоту и радиус основания удвоить?
Площадь поверхности конуса зависит от радиуса основания и его наклонной высоты. Таким образом, общая площадь поверхности и площадь криволинейной поверхности конуса увеличиваются в четыре раза, когда наклонная высота и радиус основания удваиваются как:
- Общая площадь поверхности = πr (r + l) = π(2r) (2r + 2l) = 4πr (r + l) = 4 × исходная общая площадь поверхности.

- Площадь криволинейной поверхности = πrl = π(2r)(2l) = 4πrl = 4 × исходная площадь криволинейной поверхности, где «r» — исходный радиус, а «l» — исходная наклонная высота конуса.
Справочник по классу Geom_ConicalSurface — Open CASCADE Technology Documentation
Описывает конус. Конус определяется половинным углом (может быть отрицательным) при вершине и позиционируется в пространстве с помощью системы координат (объект gp_Ax3) и опорного радиуса следующим образом: Подробнее…
#include
| Geom_ConicalSurface (const gp_Ax3 &A3, const Standard_Real Ang, const Standard_Real Radius) | |||||
A3 defines the local coordinate system конической поверхности. Ang – полуугол конической поверхности. Его абсолютное значение находится в диапазоне ]0, PI/2[. D1V) ориентирован в сторону «внешней области» поверхности. Подробнее… D1V) ориентирован в сторону «внешней области» поверхности. Подробнее… | |||||
| Geom_ConicalSurface (const gp_Cone &C) | |||||
| More… | |||||
| void | SetCone (const gp_Cone &C) | ||||
| Set | |||||
| void | SetRadius (const Standard_Real R) | ||||
| Изменяет радиус конической поверхности в плоскости размещения (Z = 0, V = 0). Локальная система координат не изменяется. Поднимается, если R < 0,0. Подробнее... | |||||
| void | SetSemiAngle (const Standard_Real Ang) | ||||
Изменяет полуконический угол конической поверхности. Полуугол может быть отрицательным. Его абсолютное значение Abs(Ang) находится в диапазоне ]0,PI/2[. Вызывает ConstructionError, если Abs(Ang) < Разрешение от gp или Abs(Ang) >= PI/2 — Разрешение. Подробнее… Полуугол может быть отрицательным. Его абсолютное значение Abs(Ang) находится в диапазоне ]0,PI/2[. Вызывает ConstructionError, если Abs(Ang) < Разрешение от gp или Abs(Ang) >= PI/2 — Разрешение. Подробнее… | |||||
| gp_Cone | Cone () const | ||||
| Возвращает те же непереходные геометрические свойства, что и <> конус с теми же свойствами, что и <>. More… | |||||
| Standard_Real | UReversedParameter (const Standard_Real U) const override | ||||
| Eeturn 2.PI — U. More… | |||||
| Standard_Real | VReversedParameter (const Standard_Real V) const override | ||||
Вычисляет параметр u (или v) на измененной поверхности при изменении ее параметрического направления u (или v) на противоположное для любой точки параметра u U ( или параметра v) на этом конусе. В случае конуса эти функции возвращают соответственно: Подробнее… В случае конуса эти функции возвращают соответственно: Подробнее… | |||||
| виртуальная пустота | VReverse() override | ||||
| Изменяет ориентацию этого конуса в параметрическом направлении v. Границы поверхности не изменяются, но параметрическое направление v меняется на обратное. As a consequence, for a cone: More… | |||||
| virtual void | TransformParameters (Standard_Real &U, Standard_Real &V, const gp_Trsf &T) const override | ||||
| Computes the parameters on the трансформируемая поверхность для преобразования точки параметров U,V на | |||||
| virtual gp_GTrsf2d | ParametricTransformation (const gp_Trsf &T) const override | ||||
Returns a 2d transformation used to find the new parameters of a point on the transformed surface. Подробнее… Подробнее… | |||||
| gp_Pnt | Apex () const | ||||
| Вычисляет вершину этого конуса. Он находится на отрицательной стороне оси вращения этого конуса, если полуугол при вершине положительный, и на положительной стороне «главной оси», если полуугол отрицательный. Подробнее… | |||||
| void | СПАСИТЕЛЬСКИЙ ИСПОЛЬЗОВЫЙ ИСПОЛЬЗОВЫЙ ИСПОЛЬЗОВЫЙ ИСПОЛЬЗОВЫЙ. V2 = Реальныйпоследний. U1 = 0 и U2 = 2*PI. More… | ||||
| void | Coefficients (Standard_Real &A1, Standard_Real &A2, Standard_Real &A3, Standard_Real &B1, Standard_Real &B2, Standard_Real &B3, Standard_Real &C1, Standard_Real &C2, Standard_Real &C3, Standard_Real &D) const | ||||
Возвращает коэффициенты неявного уравнения квадрики в абсолютной декартовой системе координат: Эти коэффициенты нормированы. Подробнее… Подробнее… | |||||
| Standard_Real | RefRadius () const | ||||
| Возвращает базовый радиус этого конуса. Базовый радиус — это радиус окружности, образованной пересечением этого конуса и его базовой плоскости (т. е. плоскости, определяемой началом координат, «X
Direction» и «Y Direction» локальной системы координат этого конуса). Если вершина этого конуса находится в начале локальной системы координат этого конуса, возвращаемое значение равно 0. Подробнее… | |||||
| Standard_Real | SemiAngle () const | ||||
| Возвращает полуугол этого конуса. Внимание! Полуугол может быть отрицательным. Подробнее… | |||||
| Standard_Boolean | IsUClosed () const override | ||||
возвращает True Подробнее. .. .. | |||||
| Standard_Boolean | IsVClosed() const override | ||||
| возвращает значение False. Подробнее… | |||||
| Standard_Boolean | IsUPeriodic () const override | ||||
| Возвращает True Подробнее… | |||||
| Standard_Boolean | IsVPeriodic () const override | ||||
| Возвращает Подробнее… | |||||
| Handle< Geom_Curve > | UIso (const Standard_Real U) const override | ||||
Строит изопараметрическую линию U этой конусной линии. Начало этой линии находится в опорной плоскости этого конуса (т. е. в плоскости, определяемой началом координат, «Направлением X» и «Направлением Y» локальной системы координат этого конуса). Подробнее… е. в плоскости, определяемой началом координат, «Направлением X» и «Направлением Y» локальной системы координат этого конуса). Подробнее… | |||||
| Ручка< Geom_Curve > | VIso (const Standard_Real V) const override | ||||
| Строит изопараметрическую окружность V этого конуса. Это окружность на этом конусе, расположенная в плоскости координаты Z V*cos(Semi-Angle) в локальной системе координат этого конуса. «Ось» этой окружности является осью вращения этого конуса. Его начальная точка определяется «направлением X» этого конуса. Предупреждение Если изопараметрическая окружность V находится близко к вершине этого конуса, радиус окружности становится очень маленьким. Можно иметь круг с радиусом, равным 0,0. Подробнее… | |||||
| void | D0 (const standard_real u, const standard_real v, gp_pnt & p) const revide | ||||
| 515151. | |||||
| void | D1 (const strand_real u, const standard_real v, gp_pnt & p, gp_vec & d1u, gp_vec & d1v gp_pnt & p, gp_vec & d1u, gp_vec & d1v gp_pnt & p, gp_vec & d1u, gp_vec & d1v). производные по направлениям U и V. Подробнее… | ||||
| void | D2 (const Standard_Real U, const Standard_Real V, gp_Pnt &P, gp_Vec &D1U, gp_Vec &D1V, gp_Vec &D2U, gp_Vec &D2V, gp_Vec &D2UV) const override | ||||
| Computes the текущая точка, первая и вторая производные по направлениям U и V. Подробнее… | |||||
| void | , gp_Vec &D2U, gp_Vec &D2V, gp_Vec &D2UV, gp_Vec &D3U, gp_Vec &D3V, gp_Vec &D3UUV, gp_Vec &D3UVV) переопределение константы | ||||
Вычисляет текущую точку, первую, второй и третий производные в направлениях U и V. More … More … | |||||
| GP_VEC | |||||
| GP_V_VEC | |||||
| GP_V_V_V_V_V_V_VEC | |||||
| GP_V_V_V_V_V_V_V_V_V_VEC | |||||
| Вычисляет производную порядка Nu в параметрическом направлении u и Nv в параметрическом направлении v в точке параметров (U, V) этого конус. Исключения Standard_RangeError, если: Подробнее… | |||||
| void | Transform (const gp_Trsf &T) override | ||||
| Применяет преобразование T к Conse. Подробнее… | |||||
| Handle< Geom_Geometry > | Copy () const override | ||||
Создает новую копию этого объекта. Подробнее… Подробнее… | |||||
| виртуальная пустота | DumpJson (Standard_OStream &theOStream, Standard_Integer theDepth=-1) const override | ||||
| Выгружает мое содержимое в поток. More… | |||||
| Public Member Functions inherited from Geom_ElementarySurface | |||||
| void | SetAxis (const gp_Ax1 &theA1) | ||||
| Changes the main axis (ZAxis) of the elementary surface. Подробнее… | |||||
| void | SetLocation (const gp_Pnt &theLoc) | ||||
| Изменяет систему координат локальной поверхности. Подробнее… | |||||
| void | SetPosition (const gp_Ax3 &theAx3) | ||||
1 901 Изменение локальной системы координат поверхности. Подробнее… Подробнее… | |||||
| const gp_Ax1 & | Axis () const | ||||
| Возвращает главную ось поверхности (ZAxis). Подробнее… | |||||
| const gp_Pnt & | Location() const | ||||
| Возвращает точку локальной системы координат поверхности. Подробнее… | |||||
| const gp_Ax3 & | Position () const | ||||
| Возвращает локальную систему координат поверхности. Подробнее… | |||||
| виртуальная пустота | UReverse() override | ||||
Изменяет параметрическое направление U поверхности на обратное. Подробнее… Подробнее… | |||||
| GeomAbs_Shape | Continuity () const override | ||||
| Подробнее… | |||||
| Standard_Boolean | IsCNu (const Standard_Integer N) const override | ||||
| | |||||
| Standard_Boolean | IsCNv (const Standard_Integer N) const override | ||||
| 1 Возвращает 9. Подробнее… | |||||
| Ручка< Geom_Surface > | URReversed () const | ||||
Изменяет направление U параметризации  Подробнее… Подробнее… | |||||
| Handle< Geom_Surface > | VReversed() const | ||||
| | 9015 Границы поверхности не изменяются. Копия |||||
| virtual Standard_Real | UPeriod () const | ||||
| Возвращает период u этой параметрической поверхности. Поднимается, если поверхность не упериодична. Подробнее… | |||||
| virtual Standard_Real | VPeriod () const | ||||
| Возвращает период параметрической поверхности в этом направлении. повышается, если поверхность не является периодической. Подробнее… | |||||
| gp_Pnt | Значение (const Standard_Real U, const Standard_Real V) const | ||||
1 точка на поверхности вычисл. Подробнее… Подробнее… | |||||
| void | Зеркало (const gp_Pnt &P) | ||||
| Выполняет преобразование геометрии относительно центра симметрии P. Подробнее… | |||||
| void | Зеркало (const gp_Ax1 &A1) | ||||
| Подробнее… | |||||
| void | Mirror (const gp_Ax2 &A2) | ||||
| Выполняет преобразование геометрии относительно плоскости. Размещение оси A2 определяет плоскость симметрии: (Location, XDirection, YDirection). Подробнее… | |||||
| void | Вращение (const gp_Ax1 &A1, const Standard_Real Ang) | ||||
| Вращение геометрии | 1 A1 — ось вращения. Ang — угловое значение поворота в радианах. Подробнее… Ang — угловое значение поворота в радианах. Подробнее… | ||||
| void | Scale (const gp_Pnt &P, const Standard_Real S) | ||||
| 1 Scales ametry 90.1501 Scales ametry S — значение масштабирования. Подробнее… | |||||
| void | Преобразование (const gp_Vec &V) | ||||
| Преобразование геометрии. V — вектор переноса. Подробнее … | |||||
| void | Translate (const gp_pnt & p1, const gp_pnt & p2) | ||||
| 51. Подробнее… | |||||
| Handle< Geom_Geometry > | Mirrored (const gp_Pnt &P) const | ||||
| Handle< Geom_Geometry > | Mirrored (const gp_Ax1 &A1) const | ||||
| Handle< Geom_Geometry > | Зеркальный (const gp_Ax2 &A2) const | ||||
| Handle< Geom_Geometry > | Повернутый (const gp_Ax1 &A1, const Standard_Real Ang)0151 | ||||
| Handle< Geom_Geometry > | Scaled (const gp_Pnt &P, const Standard_Real S) const | ||||
| Handle< Geom_Geometry > | Transformed (const gp_Trsf &T) const | ||||
| Handle< Geom_Geometry > | Translation (const gp_Vec &V) const | ||||
| Handle< Geom_Geometry > | Перевод (const gp_pnt & p1, const gp_pnt & p2) const | ||||
| Standard_Transient () | |||||
| STANDER_TRANSIENT () | |||||
| 50150150150150150150150150150150150150150150150150150150150150150150150150150150150150159 | . | ||||
| Standard_Transient (const Standard_Transient &) | |||||
| Конструктор копирования — ничего не делает. Подробнее… | |||||
| Standard_Transient & | operator= (const Standard_Transient &) | ||||
| Оператор присваивания, необходимый для предотвращения копирования счетчика ссылок. Подробнее… | |||||
| виртуальный | ~Standard_Transient () | ||||
| Деструктор должен быть виртуальным. Подробнее… | |||||
| виртуальная пустота | Удалить () const | ||||
Освобождение памяти для переходных классов. Подробнее… Подробнее… | |||||
| virtual const opencascade::handle< Standard_Type > & | DynamicType () const | ||||
| 1 Возвращает дескриптор объекта | 1 9 Подробнее… | ||||
| Standard_Boolean | IsInstance (const opencascade::handle< Standard_Type > &theType) const | ||||
| Возвращает истинное значение, если это экземпляр Type. Подробнее… | |||||
| Standard_Boolean | IsInstance (const Standard_CString theTypeName) const | ||||
| 9 Подробнее… | |||||
| Standard_Boolean | IsKind (const opencascade::handle< Standard_Type > &theType) const | ||||
Возвращает true, если это экземпляр Type или экземпляр любого класса, наследуемого от Type. Обратите внимание, что множественное наследование не поддерживается механизмом OCCT RTTI. Подробнее … Обратите внимание, что множественное наследование не поддерживается механизмом OCCT RTTI. Подробнее … | |||||
| Стандарт_BOOLEAN | ISKIND (CONST STANDER_CSTRING THETYPENAME) Const | ||||
| . Обратите внимание, что множественное наследование не поддерживается механизмом OCCT RTTI. Подробнее… | |||||
| Standard_Transient * | This () const | ||||
| Возвращает неконстантный указатель на этот объект. Для защиты от создания дескриптора объектов, выделенных в стеке, или вызова из конструктора будет вызываться исключение Standard_ProgramError, если счетчик ссылок равен нулю. Подробнее… | |||||
| Standard_Integer | GetRefCount () const | ||||
Получить счетчик ссылок этого объекта. Подробнее… Подробнее… | |||||
| void | IncrementRefCounter () const | ||||
| Увеличивает счетчик ссылок этого объекта. Подробнее… | |||||
| Standard_Integer | DecrementRefCounter () const | ||||
| этот счетчик уменьшает объекты; возвращает уменьшенное значение. Подробнее… | |||||
| static const char * | get_type_name () | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 type0150 Возвращает описание этого объекта. Подробнее… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| static const opencascade::handle< Standard_Type > & | get_type_descriptor () | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Возвращает дескриптор типа класса Standard_Transient. Подробнее … Подробнее … | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Защищенные атрибуты, унаследованные от GEOM_ELEMENTARYSURPARCE | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| GP_AX3 | . Конус определяется половинным углом (может быть отрицательным) при вершине и позиционируется в пространстве с помощью системы координат (объект gp_Ax3) и базового радиуса следующим образом:
◆ Geom_ConicalSurface() [1/2]
A3 определяет локальную систему координат конической поверхности. Ang – полуугол конической поверхности. Его абсолютное значение находится в диапазоне ]0, PI/2[. Радиус — это радиус круга Viso в плоскости размещения конической поверхности, определенной с помощью «XAxis» и «YAxis». «ZDirection» A3 определяет направление оси симметрии поверхности. Если точка расположения A3 является вершиной поверхности Radius = 0 . Поднят, если радиус < 0,0 или Abs(Ang) < разрешение из gp или Abs(Ang) >= PI/2 — разрешение ◆ Geom_ConicalSurface() [2/2]
Создает ConicalSurface из непереходного gp_Cone. ◆ Вершина()
Вычисляет вершину этого конуса. Он находится на отрицательной стороне оси вращения этого конуса, если полуугол при вершине положительный, и на положительной стороне «главной оси», если полуугол отрицательный. ◆ Границы()
Коническая поверхность бесконечна в направлении V, поэтому V1 = Realfirst из Standard и V2 = RealLast. Реализует Geom_Surface. ◆ Коэффициенты()
Возвращает коэффициенты неявного уравнения квадрики в абсолютной декартовой системе координат: Эти коэффициенты нормированы. A1.X**2 + A2.Y**2 + A3.Z**2 + 2.(B1.X.Y + B2.X.Z + B3.Y.Z) + 2.(C1.X + C2.Y + C3.Z) + D = 0,0 ◆ Конус()
Возвращает постоянный конус с теми же геометрическими свойствами, что и ◆ Копировать()
Создает новый объект, который является копией этого конуса. Реализует Geom_Geometry.
Вычисляет точку P (U, V) на поверхности. P (U, V) = Loc + (RefRadius + V * sin (Полуугол)) * (cos (U) * XDir + sin (U) * YDir) + V * cos (Полуугол) Angle) * ZDir Geom_ConicalSurface::RefRadius Standard_Real RefRadius() const Возвращает опорный радиус этого конуса. Базовый радиус – это радиус окружности, образованной… где Loc — начало плоскости размещения (ось X, ось Y) XDir — направление оси X, а YDir — направление оси Y. Реализует Geom_Surface.
Вычисляет текущую точку и первые производные по направлениям U и V. Реализует Geom_Surface.
Вычисляет текущую точку, первую и вторую производные по направлениям U и V. Реализует Geom_Surface.
Вычисляет текущую точку, первую, вторую и третью производные по направлениям U и V. Реализует Geom_Surface.
Вычисляет производную порядка Nu в параметрическом направлении u и Nv в параметрическом направлении v в точке параметров (U, V) этого конуса.
Реализует Geom_Surface. ◆ DumpJson()
Выгружает содержимое меня в поток. Реализовано заново из Geom_ElementarySurface. ◆ IsUClosed()
возвращает True. Реализует Geom_Surface. ◆IsUPeriodic()
Возвращает True. Реализует Geom_Surface. ◆ IsVClosed()
возвращает значение False. Реализует Geom_Surface. ◆ IsVPeriodic()
Возвращает ложь. Реализует Geom_Surface. ◆ Параметрическое преобразование ()
Возвращает двумерное преобразование, используемое для поиска новых параметров точки на преобразованной поверхности. me->Transformed(T)->Value(U’,V’) та же точка, что и me->Value(U,V).Transformed(T) Где U’,V’ получаются путем преобразования U,V с преобразованием 2d, возвращаемым me->ParametricTransformation(T) Этот метод возвращает масштаб по оси U с T.ScaleFactor Повторно реализован из Geom_Surface. ◆ RefRadius()
Возвращает опорный радиус этого конуса. ◆ Полуугол()
Возвращает полуугол при вершине этого конуса. Внимание! Полуугол может быть отрицательным. ◆ SetCone()
Установите ◆ SetRadius()
Изменяет радиус конической поверхности в плоскости размещения (Z = 0, V = 0). Локальная система координат не изменяется. Поднимается, если R < 0,0. ◆ SetSemiAngle()
Изменяет полуугол конической поверхности. Полуугол может быть отрицательным. Его абсолютное значение Abs(Ang) находится в диапазоне ]0,PI/2[. Вызывает ConstructionError, если Abs(Ang) < Разрешение от gp или Abs(Ang) >= PI/2 — Разрешение. ◆ Преобразование()
Применяет преобразование T к этому конусу. Реализует Geom_Geometry. ◆ Параметры преобразования ()
Вычисляет параметры на преобразованной поверхности для преобразования точки параметров U,V на me->Transformed(T)->Value(U’,V’) та же точка, что и me->Value(U,V).Transformed(T) Где U’,V’ новые значения U,V после вызова me->TransformParameters(U,V,T) Этот метод умножает V на T. Переработано из Geom_Surface. ◆ UIso()
Строит U изопараметрическую линию этого конуса. Начало этой линии находится в опорной плоскости этого конуса (т.е. в плоскости, определяемой началом координат, «Направлением X» и «Направлением Y» локальной системы координат этого конуса). Реализует Geom_Surface. ◆ URReversedParameter()
Eeturn 2. Реализует Geom_ElementarySurface. ◆ VIso()
Строит изопараметрическую окружность V этого конуса. Это окружность на этом конусе, расположенная в плоскости координаты Z V*cos(Semi-Angle) в локальной системе координат этого конуса. «Ось» этой окружности является осью вращения этого конуса. Его начальная точка определяется «направлением X» этого конуса. Предупреждение Если изопараметрическая окружность V находится близко к вершине этого конуса, радиус окружности становится очень маленьким. Можно иметь круг с радиусом, равным 0,0. Реализует Geom_Surface. ◆ VReverse()
Изменяет ориентацию этого конуса в параметрическом направлении v.
Повторно реализовано из Geom_ElementarySurface. ◆ VReversedParameter()
Вычисляет параметр u (или v) на модифицированной поверхности при изменении ее параметрического направления u (или v) на противоположное для любой точки параметра u U (или параметра v V) на этом конусе. В случае конуса эти функции возвращают соответственно:
Реализует Geom_ElementarySurface. 92 \конец{выравнивание*} между самолетами \начать{выравнивать*} z=0\qquad\text{ и }\qquad z=\frac{3-x}{2}\tag{1} \конец{выравнивание*} мы рассматриваем параметрическое представление $\Phi(t,\varphi)$ $\mathcal{C}$ \начать{выравнивать*} \Phi(t,\varphi) =\begin{pmatrix} x\\ y\\ z\end{pmatrix} =\begin{pmatrix} t\cos \varphi \\ t \sin \varphi\\ t \end{pmatrix}\qquad\qquad \begin{matrix}0\leq \varphi \leq 2\pi\\0\leq t \leq \frac{3}{2+\cos\varphi}\end{matrix}\tag{2} \конец{выравнивание*} Комментарий:
$$ $$
$\endgroup$ 3 $\begingroup$
92}\cdot 2\sqrt3\pi=\sqrt{15}\pi$. $\endgroup$ 3 Зарегистрируйтесь или войдите в системуЗарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя адрес электронной почты и пароль Опубликовать как гостьЭлектронная почта Обязательно, но не отображается Опубликовать как гостьЭлектронная почта Требуется, но не отображается Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie . Площадь поверхности конусаПервым шагом в определении площади поверхности конуса является измерение радиуса круглой части конуса. Следующим шагом является нахождение площади круга или основания. Площадь круга в 3,14 раза больше квадрата радиуса ( πr 2 ). Теперь вам нужно найти площадь самого конуса. Для этого необходимо измерить сторону (наклонную высоту) конуса. Убедитесь, что вы используете ту же форму измерения, что и радиус. Теперь вы можете использовать измерение стороны, чтобы найти площадь конуса. Формула площади конуса в 3,14 раза больше радиуса, умноженного на сторону ( πrl ). Таким образом, площадь поверхности конуса равна площади круга плюс площадь конуса, и окончательная формула определяется как: SA = πr 2 + πrl Площадь криволинейной (боковой) поверхности конуса = πrl Пример 1: Конус имеет радиус 3 см и высоту 5 см. Найдите общую площадь поверхности конуса. L 2 = H 2 + R 2 | 2 + 3 2 06 | 686 2 2 9 2 + 3 25 + 3 2 9008 2 + 3 2 9. 2 2 2 . l = √(34) l = 5,83 см А площадь поверхности конуса равна: + L) С. : Общая площадь поверхности конуса составляет 375 квадратных дюймов. Substitute l = 4r and π = 3 Таким образом, радиус основания конуса равен 5 дюймам. Пример 3: Какова общая площадь поверхности конуса, если его радиус = 4 см, а высота = 3 см. As in the previous example the slant can be determined using Pythagoras: Вставка l = 5 получим: +5) Пример 4: Наклонная высота конуса 20см. Площадь кривой поверхности = πrl Пример 5: Высота и радиус конуса 5 ярдов и 7 ярдов. Найдите площадь боковой поверхности данного конуса. Шаг 1 : Step 2 : Lateral surface area: Итак, площадь боковой поверхности конуса = 189,03 квадратных ярда. Пример 6: Круглый конус имеет высоту 15 дюймов и радиус основания 20 дюймов. Какова площадь боковой поверхности конуса? Решение: The lateral surface area of cone is given by: Example 7: Найдите полную площадь поверхности конуса, радиус основания которого равен 3 см, а высота перпендикуляра равна 4 см. Чтобы найти общую площадь поверхности конуса, нам нужна наклонная высота конуса, а не перпендикулярная высота. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
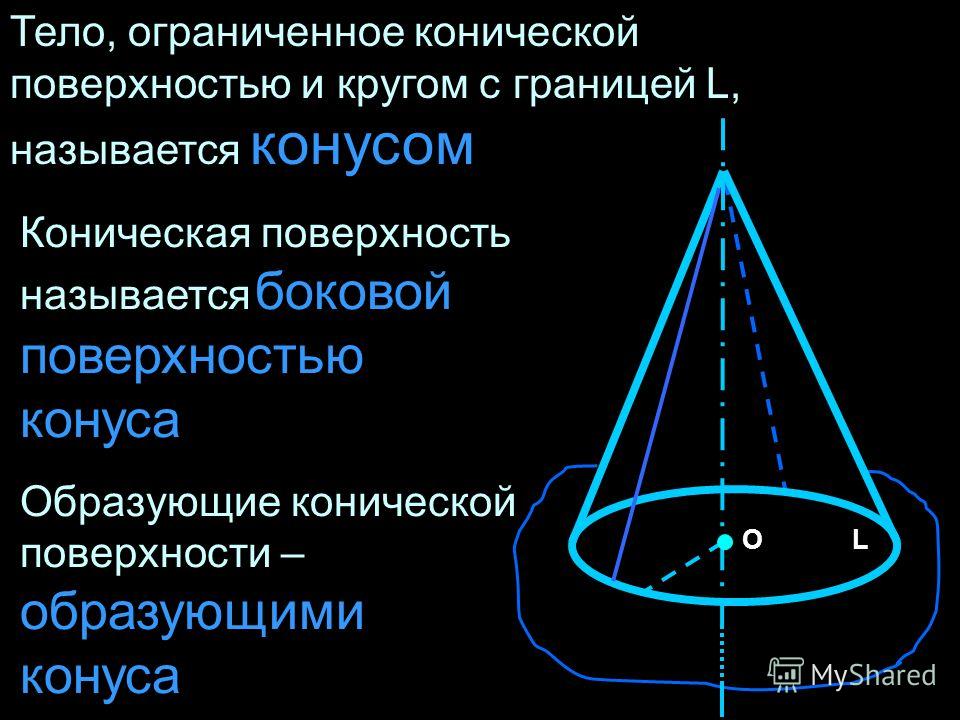 Они равны.
Они равны. е. PO = AO = 5 см;
е. PO = AO = 5 см;