Действительные и комплексные числа MatLab
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная /
- База знаний /
- CAD / CAM /
Урок 2. Установка системы и первые навыки работы
Установка и файловая система MATLAB
Запуск MATLAB и работа в режиме диалога
Новый и старый
облик системы MATLAB 6.0
Операции строчного редактирования
Команды управления окном
MATLAB в роли суперкалькулятора
О переносе строки в
сессии
Основные объекты MATLAB
Понятие о математическом выражении
Действительные
и комплексные числа
Константы и системные переменные
Текстовые комментарии
Переменные и присваивание им значений
Уничтожение
определений переменных
Операторы и функции
Применение оператора : (двоеточие)
Сообщения об ошибках
и исправление ошибок
Форматы чисел
Формирование векторов и матриц
Особенности задания
векторов и матриц
Объединение малых матриц в большую
Удаление столбцов и строк матриц
Дефрагментация рабочей области
Сохранение рабочей области сессии
Ведение дневника
Загрузка рабочей области сессии
Завершение вычислений и работы с системой
Завершение вычислений
Завершение работы с системой
Что нового мы узнали?
Число —
простейший объект языка MATLAB, представляющий количественные
данные. Числа можно считать константами, имена которых совпадают с их значениями.
Числа используются в общепринятом представлении о них. Они могут быть целыми,
дробными, с фиксированной и плавающей точкой. Возможно представление чисел в
хорошо известном научном формате с указанием мантиссы и порядка числа.
Числа можно считать константами, имена которых совпадают с их значениями.
Числа используются в общепринятом представлении о них. Они могут быть целыми,
дробными, с фиксированной и плавающей точкой. Возможно представление чисел в
хорошо известном научном формате с указанием мантиссы и порядка числа.
0
2
-3
2.301 0.00001 123.45бе-24
-234.456е10
Как нетрудно заметить, в мантиссе чисел целая часть отделяется от дробной не
запятой, а точкой, как принято в большинстве языков программирования. Для отделения
порядка числа от мантиссы используется символ е. Знак «плюс» у чисел
не проставляется, а знак «минус» у числа называют
унарным минусом.
Пробелы между символами в числах не допускаются.
Числа могут быть
комплексными: z
=Rе(x)+Im(x)*i. Такие числа содержат
действительную Re(z) и мнимую Im(z) части. Мнимая часть имеет множитель
i
или
j,
означающий корень квадратный из -1:
3i
2j
2+3i
-3.141i
-123.456+2.7e-3i
Функция real (z) возвращает действительную часть комплексного числа, Re(z),
a функция imag(z) — мнимую, Im(z). Для получения модуля комплексного числа используется
функция abs(z), а для вычисления фазы — angle(Z). Ниже даны простейшие примеры
работы с комплексными числами:
»i
ans=
0 +1.0000i
» j
ans =
0 + 1.0000i
» z=2+3i
z =
2.
» abs(z)
ans
=
3.6056
» real(z)
ans=
2
» imag(z)
ans =
3
» angle(z)
ans =
0.9828
В MATLAB не принято делить числа на целые и дробные, короткие и длинные и т. д., как это принято в большинстве языков программирования, хотя задавать числа в таких формах можно. Вообще же операции над числами выполняются в формате, который принято считать форматом с двойной точностью.
Такой формат удовлетворяет подавляющему большинству требований к численным расчетам, но совершенно не подходит для символьных вычислений с произвольной (абсолютной) точностью. Символьные
вычисления MATLAB может выполнять с помощью специального пакета расширения Symbolic
Math Toolbox.
Символьные
вычисления MATLAB может выполнять с помощью специального пакета расширения Symbolic
Math Toolbox.
Нравится
Твитнуть
Теги MatLab САПР
Сюжеты MatLab
Знакомство с матричной лабораторией MATLAB MatLab
8073 0
Визуализация и графические средства MatLab
9565 0
Техническая документация по системе MatLab
6096 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster.ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2207 s
Комплексные числа/функции и мат. пакеты : Околонаучный софт
| trarbish |
| ||
19/05/14 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| trarbish |
| ||
19/05/14 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| trarbish |
| ||
19/05/14 |
| ||
| |||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| trarbish |
| ||
19/05/14 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 7 ] |
Модераторы: Karan, Toucan, PAV, maxal, Супермодераторы
Комплексные числа в Matlab и Octave
Matlab и Octave имеют следующие примитивы для сложных номера:
октава: 1> помогите j j — встроенная константа - Встроенная переменная: I - Встроенная переменная: J - Встроенная переменная: я - Встроенная переменная: j Чисто мнимое число, определяемое как `sqrt (-1)'.«Я» и «Дж» формы являются истинными константами и не могут быть изменены. «я» и «дж» формы подобны обычным переменным и могут использоваться для других целей. Однако, в отличие от других переменных, они снова предполагают их специальные предопределенные значения, если они очищены *Примечание Статус переменных::. Дополнительная справка по встроенным функциям, операторам и переменным доступна в электронной версии руководства. Используйте команду `help -i
' для поиска в указателе руководств. Справка и информация об Octave также доступны в Интернете. на http://www.octave.org и через [email protected] список рассылки. октава: 2> квадрат (-1) ответ = 0 + 1i октава:3> помогите реально real — это встроенная функция сопоставления - Функция отображения: реальная (Z) Верните действительную часть Z. См. также: imag и conj. ... октава:4> справка изображение imag — это встроенная функция сопоставления - Функция отображения: изображение (Z) Верните мнимую часть Z как действительное число. 2 ответ = 5 >> угол (z) ответ = 1.1071
Теперь давайте сделаем полярную форму:
>> г = абс (г)
р =
2,2361
>> тета = угол (z)
тета =
1.1071
Любопытно, что он не определен по умолчанию в Matlab (хотя он есть в
Октава). Его можно легко вычислить в Matlab как e=exp(1) .
Ниже приведены некоторые примеры с использованием мнимых экспонент:
>> г * ехр (j * тета)
ответ =
1 + 2и
>> г
г =
1 + 2и
>> г/абс(г)
ответ =
0,4472 + 0,8944i
>> ехр(j*тета)
ответ =
0,4472 + 0,8944i
>> z/conj(z)
ответ =
-0,6 + 0,8i
>> ехр(2*j*тета)
ответ =
-0,6 + 0,8i
>> изображение(журнал(г/абс(г)))
ответ =
1.1071
>> тета
тета =
1.1071
>>
Вот некоторые манипуляции с двумя комплексными числами:
>> х1 = 1; >> х2 = 2; >> у1 = 3; >> у2 = 4; >> z1 = x1 + j * y1; >> z2 = x2 + j * y2; >> z1 z1 = 1 + 3i >> z2 z2 = 2 + 4и >> z1*z2 ответ = -10 +10i >> z1/z2 ответ = 0,7 + 0,1i
Еще одна вещь, которую следует отметить в синтаксисе Matlab, заключается в том, что транспонирование
оператор ‘ (для векторов и матриц) сопрягает как
а также транспонирует. Использовать .’ транспонировать без
спряжение:
Использовать .’ транспонировать без
спряжение:
>>х = [1:4]*j
х =
0 + 1i 0 + 2i 0 + 3i 0 + 4i
>> х'
ответ =
0 - 1и
0 - 2и
0 - 3i
0 - 4и
>> х.'
ответ =
0 + 1i
0 + 2i
0 + 3i
0 + 4i
Следующий раздел:
Функционирование полиномов в MATLAB
Предыдущий раздел:
Решающие линеарные уравнения с использованием Matrices
Раздельные номера. чем сложение, вычитание и умножение комплексных чисел, потому что трудно разделить число на мнимое число. Для
деление комплексных чисел , нам нужно найти член, на который мы можем умножить числитель и знаменатель, который исключит мнимую часть знаменателя, чтобы мы получили действительное число в знаменателе. В этой статье мы узнаем о делении комплексных чисел, делении комплексных чисел в полярной форме, делении мнимых чисел и делении сложных дробей.
| 1. | Что такое деление комплексных чисел? |
| 2. | Шаги для деления комплексных чисел |
| 3. | Деление комплексных чисел в полярной форме |
| 4. | Часто задаваемые вопросы о делении комплексных чисел |
Что такое деление комплексных чисел?
Деление комплексных чисел математически аналогично делению двух действительных чисел. Если \(z_1=x_1+iy_1\) и \(z_2=x_2+iy_2\) являются двумя комплексными числами, то деление комплексных чисел \(z_1\) и \(z_2\) математически записывается как: 92}\справа)\конец{выровнено}\]
Шаги для деления комплексных чисел
Теперь, когда мы знаем, что такое деление комплексных чисел, давайте обсудим этапы деления комплексных чисел. Чтобы разделить два комплексных числа, выполните указанные шаги:
- Сначала вычислите сопряженное комплексное число, стоящее в знаменателе дроби.
 2\theta_2)}\\&=\frac{r_1}{r_2}\left[\cos(\theta_1-\theta_2)+i\sin( \theta_1-\theta_2)\right]\\&=r\left(\cos\theta+i\sin\theta\right)\end{выровнено}\]
2\theta_2)}\\&=\frac{r_1}{r_2}\left[\cos(\theta_1-\theta_2)+i\sin( \theta_1-\theta_2)\right]\\&=r\left(\cos\theta+i\sin\theta\right)\end{выровнено}\]Где \(\theta=\theta_1-\theta_2\) и \(r=\dfrac{r_1}{r_2}\).
Таким образом, деление комплексных чисел \(z_{1}=r_1\left(\cos\theta_1+i\sin\theta_1\right)\) и \(z_{2}=r_2\left(\cos\) theta_2+i\sin\theta_2\right)\) в полярной форме определяется как частное \(\dfrac{r_1\left(\cos\theta_1+i\sin\theta_1\right)}{r_2\left(\cos \theta_2+i\sin\theta_2\right)}\).
Рассчитывается по формуле:
\[\begin{aligned}\dfrac{z_1}{z_2}&=r\left(\cos\theta+i\sin\theta\right)\end{aligned} \]
Важные замечания по делению комплексных чисел
- Чтобы разделить комплексное число a+ib на c+id, умножьте числитель и знаменатель дроби a+ib/c+id на c−id и упростите.
- Сопряженным комплексом z = a+ib является a−ib.
- Модуль комплексного числа z = a+ib равен |z| = √(а 2 + б 2 )
Темы, связанные с делением комплексных чисел
- Умножение комплексных чисел
- Полярная форма комплексных чисел
- Комплексное сопряжение
Деление комплексных чисел Примеры
Пример 1: Выразите комплексное число (5+√2i)/(1−√2i) в виде a+ib, используя формулу деления комплексных чисел.
 2}\\&=\dfrac{16+38i}{68}\\&=\dfrac{4} {17}+\dfrac{19}{34}i\end{align}\]
2}\\&=\dfrac{16+38i}{68}\\&=\dfrac{4} {17}+\dfrac{19}{34}i\end{align}\]Ответ: 3+4i на 8-2i = \(\dfrac{4}{17}+\dfrac{19}{34}i\)
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по делению комплексных чисел
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о делении комплексных чисел
Что такое деление комплексных чисел в алгебре?
Деление комплексных чисел математически похоже на деление двух действительных чисел. Если \(z_1=x_1+iy_1\) и \(z_2=x_2+iy_2\) являются двумя комплексными числами, то деление комплексных чисел \(z_1\) и \(z_2\) математически записывается как:
\[ \dfrac{z_1}{z_2}=\dfrac{x_1+iy_1}{x_2+iy_2}\].

 пакеты
пакеты пакеты
пакеты пакеты
пакеты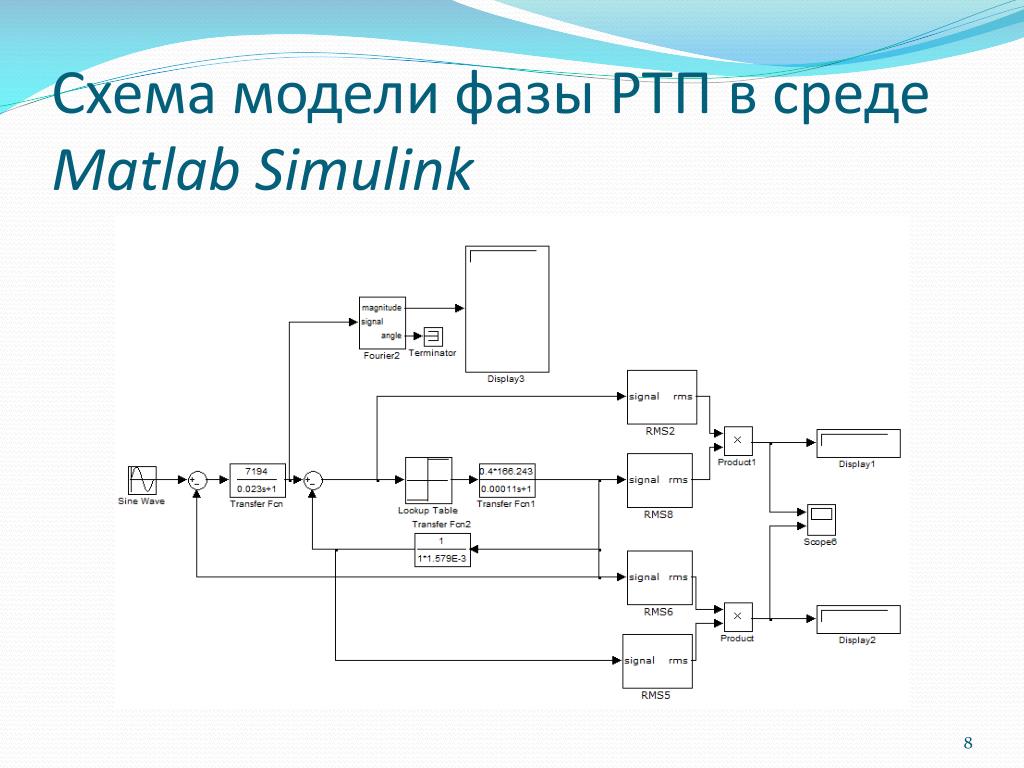 пакеты
пакеты
 Тогда под корнем будет как раз .
Тогда под корнем будет как раз . пакеты
пакеты
 Боюсь, что в каждом конкретном случае придётся разбираться отдельно.
Боюсь, что в каждом конкретном случае придётся разбираться отдельно.