ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ.
ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ.
ПРОЕКЦИИ ТОЧКИ. КОМПЛЕКСНЫЙ ЧЕРТЕЖ.
Чтобы построить изображение предмета, сначала изображают отдельные его элементы в виде простейших элементов пространства. Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.д
Правила построения изображений на чертежах в инженерной графике основываются на методе проекций. Одно изображение (проекция) геометрического тела не позволяет судить о его геометрической форме или форме простейших геометрических образов, составляющих это изображение. Таким образом, нельзя судить о положении точки в пространстве по одной ее проекции; положение ее в пространстве определяется двумя проекциями.
Рассмотрим пример построения проекции точки А, расположенной в пространстве двугранного угла (рис. 60). Одну из плоскостей проекции расположим горизонтально, назовем ее
 П2=A2;
П2=A2;Проецирующие лучи АА1 и АА2 взаимно перпендикулярны и создают в пространстве проецирующую плоскость АА1АА2, перпендикулярную обеим сторонам проекций. Эта плоскость пересекает плоскости проекций по линиям, проходящим через проекции точки А.
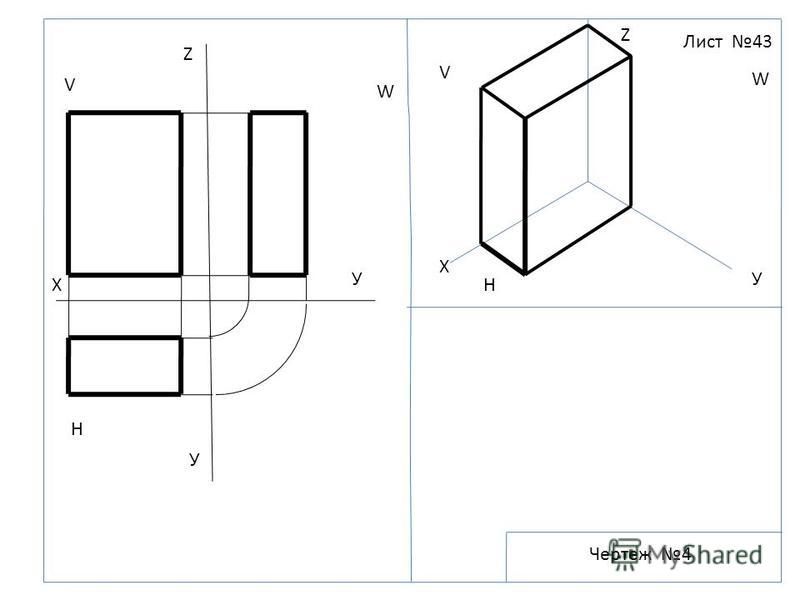
Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П1 с фронтальной плоскостью П2 вращением вокруг оси П2/П1 (рис. 61, а). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси П 2/П1. Прямая А1А2, соединяющая горизонтальную А1 и фронтальную А2 проекции точки, называется вертикальной линией связи.
Полученный плоский чертеж называется комплексным чертежом.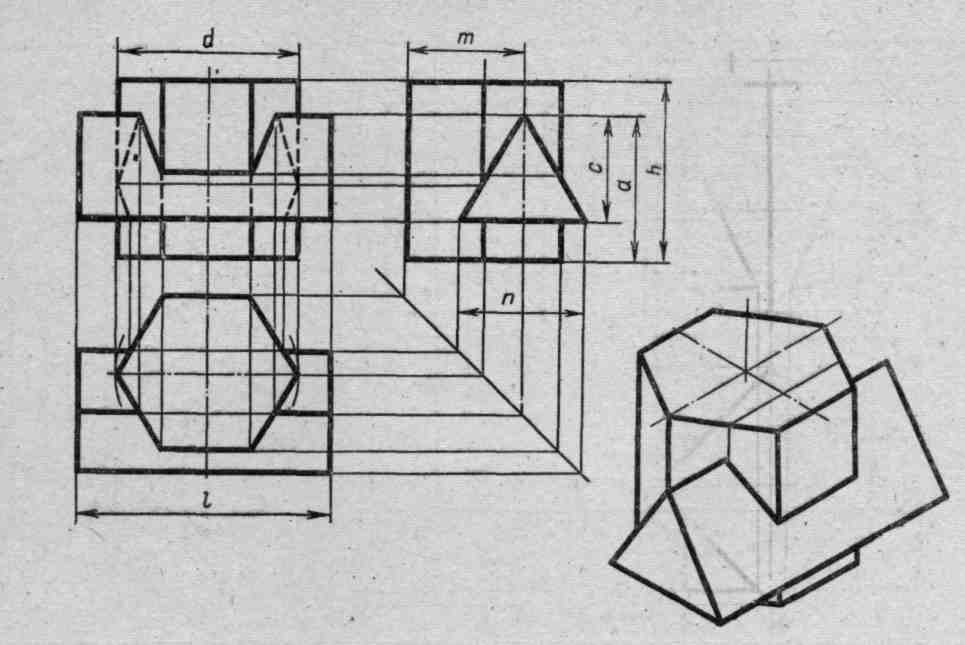 Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.
Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.
Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки а относительно этих плоскостей (рис. 61, б) ее высотой h (АА1 =h)
Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П1 и фронтальной плоскости проекций П2 (рис. 62, а). В результате пересечения фронтальной П 2 и профильной П3 плоскостей проекций получаем новую ось П2/П3, которая располагается на комплексном чертеже параллельно вертикальной линии связи A1A2 (рис. 62, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А2 новой линией связи, которую называют горизонталь-
ной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A1A2 _|_ А2А1 и А2А3, _|_ П2/П3.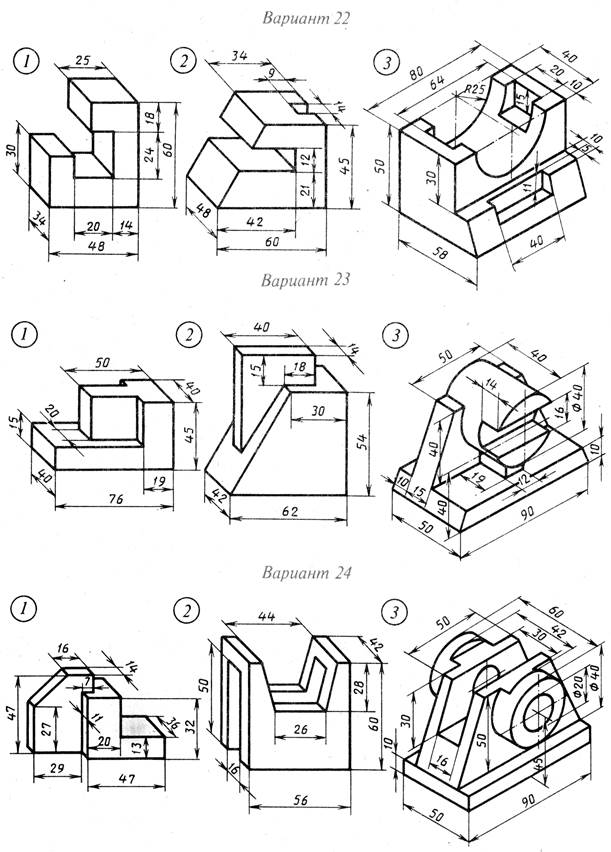
Положение точки в пространстве в этом случае характеризуется ее широтой
Полученный комплексный чертеж точки называется трехпроек-ционным.
В трехпроекционном чертеже глубина точки АА2 проецируется без искажений на плоскости П1и П2 (рис. 62, а). Это обстоятельство позволяет построить третью — фронтальную проекцию точки А по ее горизонтальной А1 и фронтальной А2 проекциям (рис. 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A2A3 _|_A2A1. Затем в любом месте на чертеже провести ось проекций П2/П3 _|_ А2А3, измерить глубину f точки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П 2/П3. Получим профильную проекцию А3 точки А.
Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.
Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рис. 62, в). В тех случаях, когда условиями задачи этого не требу-
ется, проекции точек могут быть даны без изображения осей (рис. 63, а, б). Такая система называется безосновой. Линии связи могут также проводиться с разрывом (рис. 63, б).
Расположение проекций точек на комплексном чертеже зависит от положения точки в пространстве трехмерного угла. Рассмотрим некоторые случаи:
Две точки в пространстве могут быть расположены по-разному. В отдельном случае они могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают.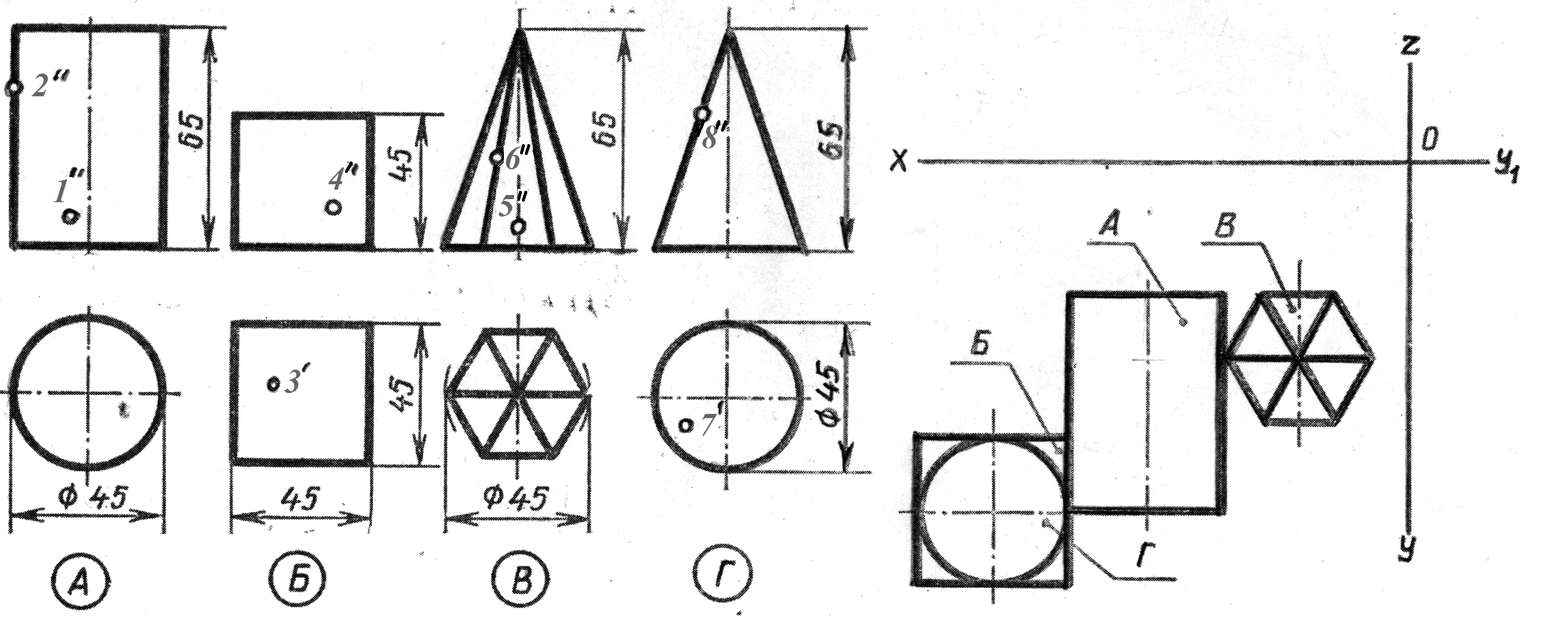 Такие точки называются конкурирующими. На рис. 64, а приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости П1 [А1 == В1]. Такие точки называются горизонтально конкурирующими. Если проекции точек A и В совпадают на плоскости
Такие точки называются конкурирующими. На рис. 64, а приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости П1 [А1 == В1]. Такие точки называются горизонтально конкурирующими. Если проекции точек A и В совпадают на плоскости
П2 (рис. 64, б), они называются фронтально конкурирующими. И если проекции точек А и В совпадают на плоскости П3 [А3 == B3] (рис. 64, в), они называются профильно конкурирующими.
По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующих точек будет видима та, у которой больше высота, у фронтально конкурирующих — та, у которой больше глубина, и у профильно конкурирующих — та, у которой больше широта.
Свойства трехпроекционного чертежа точки позволяют по горизонтальной и фронтальной ее проекциям строить третью на другие плоскости проекций, введенные взамен заданных.
На рис. 65, а показаны точка А и ее проекции — горизонтальная А1 и фронтальная А2. По условиям задачи необходимо произвести замену плоскостей П2. Новую плоскость проекции обозначим П4 и расположим перпендикулярно П1. На пересечении плоскостей П1 и П4 получим новую ось П1
Поскольку новая плоскость П4 заменяет фронтальную плоскость проекции П2, высота точки А изображается одинаково в натуральную величину и на плоскости П2, и на плоскости П4.
Это обстоятельство позволяет определить положение проекции A4, в системе плоскостей П1 _|_ П4 (рис. 65, б) на комплексном чертеже. Для этого достаточно измерить высоту точки на заменяемой плоско-
65, б) на комплексном чертеже. Для этого достаточно измерить высоту точки на заменяемой плоско-
сти проекции П2, отложить ее на новой линии связи от новой оси проекций — и новая проекция точки А4 будет построена.
Если новую плоскость проекций ввести взамен горизонтальной плоскости проекций, т. е. П4 _|_ П2 (рис. 66, а), тогда в новой системе плоскостей новая проекция точки будет находиться на одной линии связи с фронтальной проекцией, причем А2А4 _|_. В этом случае глубина точки одинакова и на плоскости П1, и на плоскости П4. На этом основании строят А4 (рис. 66, б) на линии связи А2А4 на таком расстоянии от новой оси П1/П4 на каком А1 находится от оси П2/П1.
Как уже отмечалось, построение новых дополнительных проекций всегда связано с конкретными задачами. В дальнейшем будет рассмотрен ряд метрических и позиционных задач, решаемых с применением метода замены плоскостей проекций. В задачах, где введение одной дополнительной плоскости не даст желаемого результата, вводят еще одну дополнительную плоскость, которую обозначают П
Три основные плоскости проекций (П1_|_П2 _|_ П3) могут рассматриваться и как координатные плоскости. Тогда оси проекций становятся координатными осями: осью абсцисс х, П1/П3 —осью координат у,П2/П3 —осью аппликат z.
Тогда оси проекций становятся координатными осями: осью абсцисс х, П1/П3 —осью координат у,П2/П3 —осью аппликат z.
Начало координат (точка О) располагается в точке пересечения осей координат (рис. 68, а).
Чтобы отнести точку А к натуральной системе координат Oxyz, надо построить ортогональную проекцию точки А на плоскости хОу. Затем проекцию А1 ортогонально проецировать на ось х в точку Ах. Тогда получим пространственную координатную ломаную АА1АХО, отрезки которой параллельны осям координат и соответственно называются: ОАХ — отрезком абсциссы; АХ А1 — отрезком ординат; А1А — отрезком аппликаты.
Измерив координатные отрезки единицей длины l, получим три отвлеченных числа — три координаты точки А:
х = OAX абсцисса; у = AxA1— ордината; z = AA1 — аппликата.
Если точка задана своими координатами А (х, у, z), то можно построить ее комплексный чертеж, задав соответствующую единицу длины l (например, l = 1 мм). Абсцисса точки определяет положение
вертикальной линии связи (рис. 68, б). Горизонтальная проекция точки определяется величиной ординаты, а фронтальная — величиной аппликаты.
Контакты для заказа чертежей
Справочная по строит. черч.
Телефон
89042493591
кроме выходных
задать вопрос, узнать о возможности, сроках и цене изготовления чертежей можно по аське:
587-149-933
Новости:
Открылся наш сайт
Здесь вы можете заказать красивые цветы из ткани на платье и заколки.
ЧЕРЧЕНИЕ. Школьный интернет-учебник — Проецирование 2-3
Комплексным чертежом называют изображения предмета, составленные из двух или более связанных между собой ортогональных проекций изображаемого геометрического образа (рис.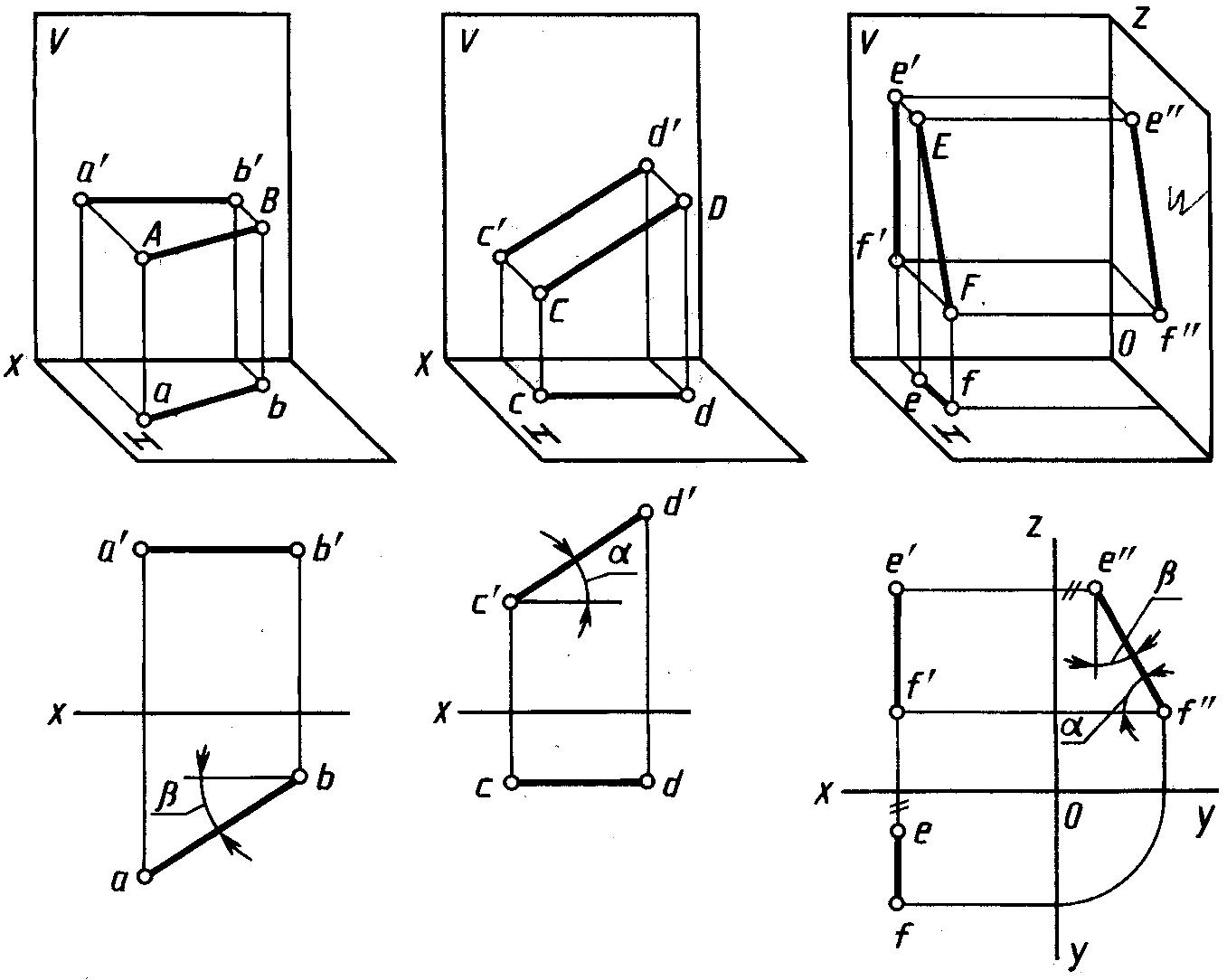 1).
1).
Рис. 1. Наглядное изображение предмета
Фронтальную проекцию называют видом спереди, или главным видом. Главный вид, получаемый на фронтальной плоскости проекций, является исходным, он должен давать наиболее полное представление о форме и размерах предмета. Предмет располагают так, чтобы на чертеже большая часть его элементов изображалась как видимая. Корпусные детали (кронштейны, передние и задние бабки, корпуса кранов и вентилей, трубопроводов, насосов, редукторов) на главном изображении (виде) показывают в рабочем положении, т. е. в положении, которое деталь занимает при эксплуатации. Детали, находящиеся при работе в различных положениях, вычерчивают в положении, которое преобладает в процессе изготовления. Поэтому такие детали, как валы, оси, шпиндели, шкивы, штифты и др., имеющие цилиндрическую или коническую форму и обрабатываемые на токарных станках в горизонтальном положении, изображают с горизонтально расположенной осью. (Можно посмотреть здесь). Как было сказано на прошлом уроке, горизонтальная проекция (вид сверху) располагается под фронтальной, а профильная (вид слева) — справа от фронтальной и на одном уровне с ней. Нарушать это правило расположения проекций нельзя. Такое расположение проекций называют проекционной связью.
(Можно посмотреть здесь). Как было сказано на прошлом уроке, горизонтальная проекция (вид сверху) располагается под фронтальной, а профильная (вид слева) — справа от фронтальной и на одном уровне с ней. Нарушать это правило расположения проекций нельзя. Такое расположение проекций называют проекционной связью.
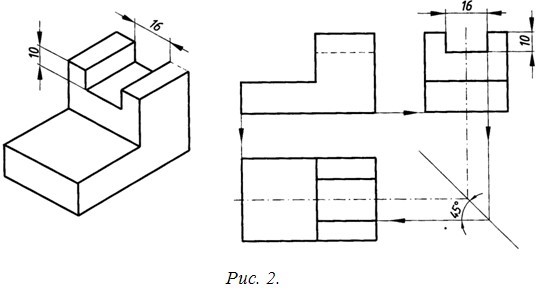
Рис.2. Комплексный чертеж
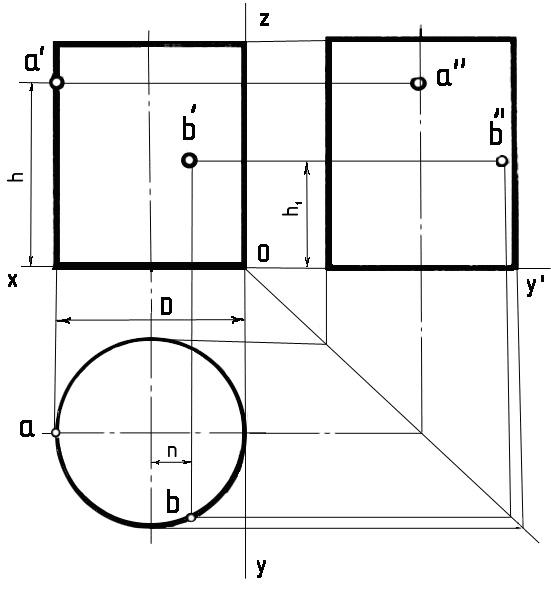
Проекционная связь показана на рис. 2 тонкими сплошными линиями, которые называются линиями связи. При проведении линий связи между горизонтальной и профильной проекциями удобно пользоваться вспомогательной прямой, которую проводят под углом 45° от осей в правой нижней четверти. Линии связи, идущие от вида сверху, доводят до вспомогательной прямой. Из точек пересечения с нею восставляют перпендикуляры для построения вида слева.
Так строят чертежи в прямоугольных проекциях. Используя размеры детали и перенося их с имеющихся видов на достраиваемый, можно построить чертеж детали любой сложности.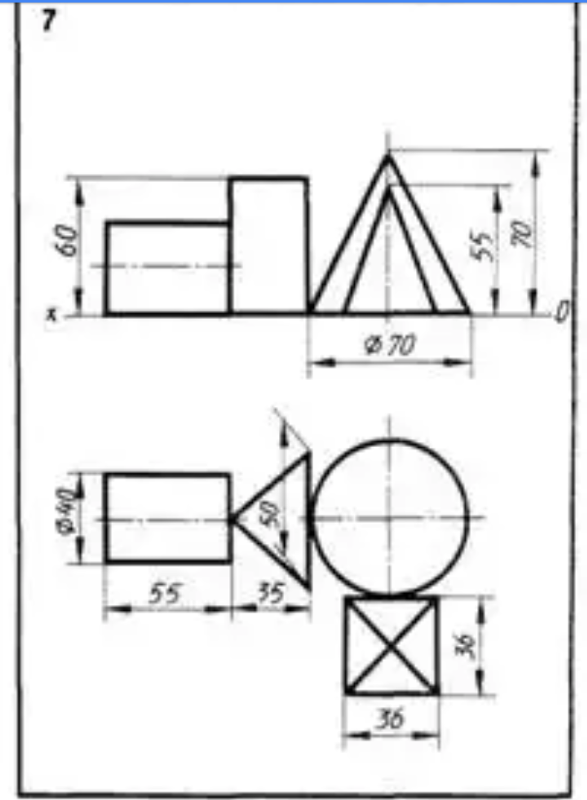
Построение чертежа
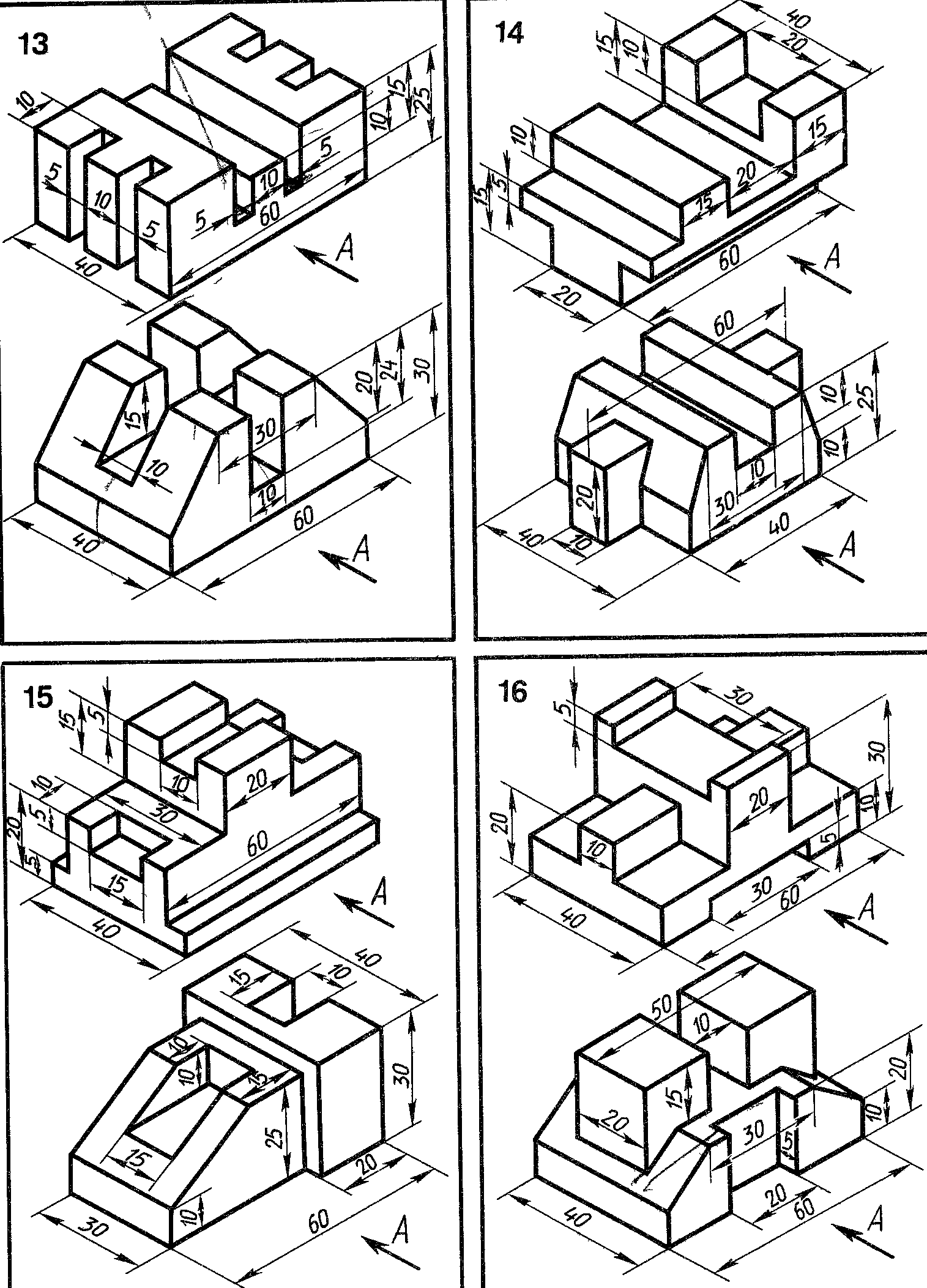
В учебной практике иногда приходится выполнять задания, связанные с увеличением или уменьшением количества изображений на чертеже, например строить третий вид по двум имеющимся.
Построение третьего вида предмета сводится к построению третьих видов его отдельных элементов (точек, линий, плоских фигур) и отдельных частей. Для этой цели, изучая чертеж, определяют форму, размеры и положение этих частей на предмете. Таким образом, вначале осуществляется чтение чертежа. После этого приступают к графическим построениям, вычерчивая последовательно один за другим те или иные элементы предмета.
На рисунке 3 показана последовательность построения вида слева по двум заданным: главному и сверху. Перенос размеров с вида сверху на достраиваемый вид осуществлен с помощью постоянной прямой чертежа.
Рис. 3
Иногда при построении отсутствующего на чертеже вида применение постоянной прямой не обязательно. Для переноса размеров с одного вида на другой можно воспользоваться циркулем или линейкой (см. рис. 3, размер, обозначен звездочкой).
Для переноса размеров с одного вида на другой можно воспользоваться циркулем или линейкой (см. рис. 3, размер, обозначен звездочкой).
В заключение нужно удалить линии построения и обвести чертеж.
Компоновка чертежа
Компоновка чертежа (или композиция чертежа) выражается в гармоничном сочетании отдельных элементов изображения в выбранном масштабе с заданным форматом бумаги. Компоновкой чертежа также называется размещение изображений, размеров и надписей на поле чертежа (т.е. внутри рамки).
Начинающие чертежники строят чертеж, как правило, без учета площади листа бумаги. В итоге чертеж либо не помещается в отведенном ему поле, либо занимает только его часть.
Поскольку мы воспринимаем изображение не само по себе, не изолированно, а вместе с листом, на котором оно расположено, то между величинами изображения и листа должна существовать определенная пропорциональная зависимость, или, как говорят художники, композиционное равновесие.
Простейший способ достижения равновесия в чертеже – это равномерное распределение проекций (но не за счет нарушения проекционной связи!). Из рисунка 4 легко понять суть этого требования.
Рис.4. Компоновка проекций на чертеже
Но здесь могут быть и неожиданности. На рисунке 5 проекция валика размещена строго посередине листа. Несмотря на это, изображение кажется сдвинутым вниз.
Рис.5. Деталь на чертеже кажется смещенной
Это объясняется особенностью восприятия изображений нашим глазом: горизонтальные линии нам представляются длиннее вертикальных, верхняя половина предмета – больше нижней. Поэтому изображение валика следовало бы расположить несколько выше середины листа. По той же причине верхние части некоторых типографических знаков делают меньше нижних, но мы их видим равными (рис. 6).
Рис.6. Компоновка типографических знаков
Поверните рисунок и вы убедитесь в этом (посмотрите здесь).
Это относится и к ряду букв и цифр чертежного шрифта. Взгляните на рисунок 7.
Рис.7. Компоновка круга в квадрате
Кажется, будто небольшой черный круг расположен в глубине квадрата, большой круг выдвинут на первый план и только третий круг лежит в плоскости квадрата. Этот пример поможет вам определить соотношение толщины и размеров линий, цифр, надписей и других элементов чертежа при его выполнении, т. е. выдержать равновесие между черным и белым.
На рисунке 8 легко увидеть, какая компоновка чертежа выполнена композиционно правильно.
Рис.8. Компоновка размерных линий на чертеже
Стрелки чертежей на рис. 8, а) и в) несоизмеримы с проекциями: первые — велики, вторые — слишком малы, цифры — также. Кроме того, на рис. 8, а) они «прижаты» к своим проекциям, на рис. 8, в), напротив, «оторваны» от них. Правильно исполнен чертеж на рис. 8, б). В нем зрительно все уравновешено и создаются благоприятные условия для глаза при его движении по изображению.
Законы композиции проявляются во всех видах искусств: в архитектуре, скульптуре, живописи, музыке, фотографии и т. п.
Количество изображений
Выбор числа изображений является важным этапом выполнения чертежей. Он заключается в нахождении положения детали на главном изображении и необходимого числа видов, которые позволят полно и точно отобразить внешнюю и внутреннюю форму, а также размеры предмета.
Количество видов должно быть наименьшим, но полностью выявляющим форму предмета.
Выбор положения детали в главном изображении должен давать наиболее полное представление о форме и размерах детали: на главном виде должна быть максимально представлена информация о форме.
Обычно деталь показывают в положении, которое она занимает при обработке. Поэтому ось деталей, получаемых точением (например, валы), располагают горизонтально. Это облегчает рабочему изготовление детали по чертежу, так как и на чертеже и на станке он видит ее в одинаковом положении.
Выбор положения детали на главном изображении в значительной степени определяет количество изображений на чертеже. Предмет стараются располагать так, чтобы большая часть его элементов на главном виде изображалась как видимая.
Форма детали, представленной на рисунке 9 выявляется одним видом при правильном выборе главного изображения (главного вида).
Рис. 9.
Для передачи формы детали (рис. 10) необходимы два вида. Одним, главным видом не возможно показать глубину пазов утолщенной части детали.
Рис. 10.
Форму детали, показанной на рисунке 11 выявляют тремя изображениями. Даже два вида детали не будет полно определять форму.
Рис. 11.
Иллюстрированный самоучитель по созданию чертежей › Проекции точки. Комплексный чертеж. › Элементы трехпроекционного комплексного чертежа точки [страница — 41] | Самоучители по инженерным программам
Элементы трехпроекционного комплексного чертежа точки
Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции.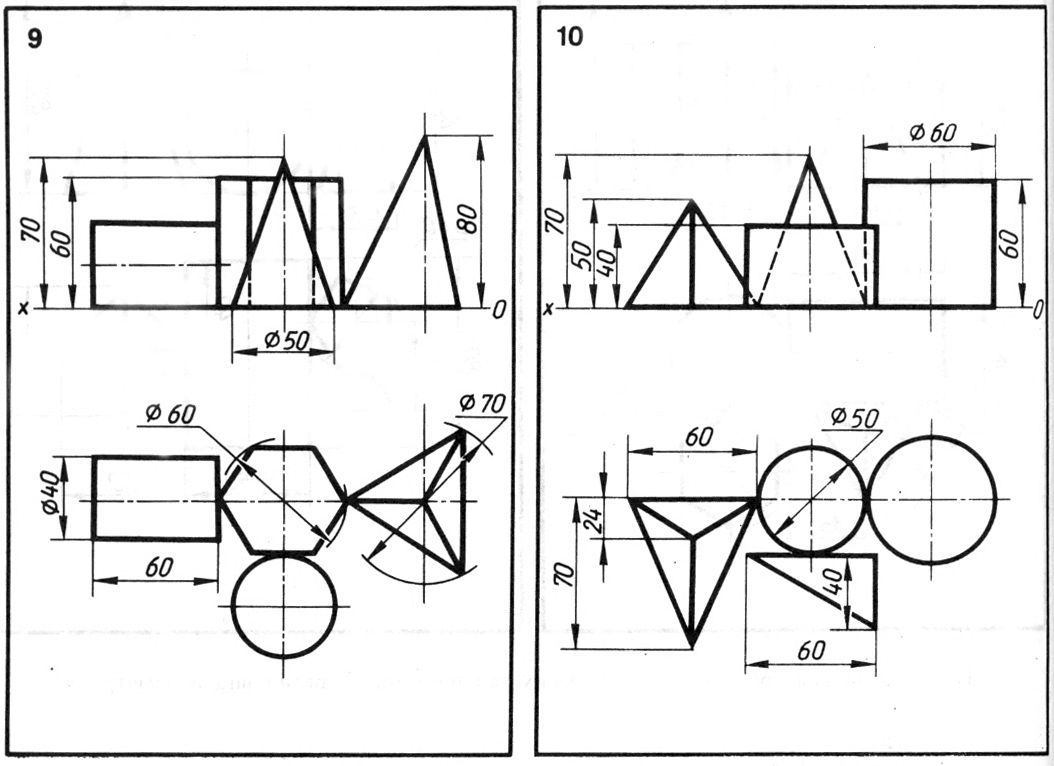 Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П1 и фронтальной плоскости проекций П2 (рис. 62, а). В результате пересечения фронтальной П2 и профильной П3 плоскостей проекций получаем новую ось П2/П3, которая располагается на комплексном чертеже параллельно вертикальной линии связи A1A2 (рис. 62, б). Третья проекция точки А – профильная – оказывается связанной с фронтальной проекцией А2 новой линией связи, которую называют горизонтальной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A1A2 _|_ А2А1 и А2А3, _| _ П2/П3.
Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П1 и фронтальной плоскости проекций П2 (рис. 62, а). В результате пересечения фронтальной П2 и профильной П3 плоскостей проекций получаем новую ось П2/П3, которая располагается на комплексном чертеже параллельно вертикальной линии связи A1A2 (рис. 62, б). Третья проекция точки А – профильная – оказывается связанной с фронтальной проекцией А2 новой линией связи, которую называют горизонтальной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A1A2 _|_ А2А1 и А2А3, _| _ П2/П3.
Рис. 62
62
Положение точки в пространстве в этом случае характеризуется ее широтой – расстоянием от нее до профильной плоскости проекций П3, которое обозначим буквой р.
Полученный комплексный чертеж точки называется трехпроекционным.
В трехпроекционном чертеже глубина точки АА2 проецируется без искажений на плоскости П1и П2 (рис. 62, а). Это обстоятельство позволяет построить третью – фронтальную проекцию точки А по ее горизонтальной А1 и фронтальной А2 проекциям (рис. 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A2A3 _|_A2A1. Затем в любом месте на чертеже провести ось проекций П2/П3 _|_ А2А3, измерить глубину f точки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П2/П3. Получим профильную проекцию А3 точки А.
Получим профильную проекцию А3 точки А.
Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.
Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рис. 62, в). В тех случаях, когда условиями задачи этого не требуется, проекции точек могут быть даны без изображения осей (рис. 63, а, б). Такая система называется безосновой. Линии связи могут также проводиться с разрывом (рис. 63, б).
Рис. 63
«Выполнение комплексного чертежа геометрических тел»
ПРАКТИЧЕСКАЯ РАБОТА № 4
Тема: Выполнение комплексного чертежа геометрических тел
Цель работы: Освоить практические навыки построения комплексных
чертежей и аксонометрических проекций геометрических
тел с нахождением проекций точек и линий,
принадлежащих поверхности данного геометрического
тела
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Согласно рабочей учебной программе и календарно-тематическому плану данная практическая работа выполняется во время учебного занятия № 9-10 в рамках Темы 2. 1 Метод проекций. Комплексный чертеж.
1 Метод проекций. Комплексный чертеж.
Для выполнения практической работы предоставляется рабочее место, методические указания по выполнению практической работы.
ТЕОРЕТИЧЕСКАЯ СПРАВКА
Для выполнения графической работы по построению комплексных чертежей и аксонометрических проекций геометрических тел с нахождением проекций точек и линий, принадлежащих поверхности данного геометрического тела необходимо проработать по учебнику следующие темы:
— Методы проекцирования. Эпюр Монжа. Проецирование плоскости. Способы преобразования проекций: разобрать упражнения по построению проекции точки и отрезка прямой по заданным координатам на плоскости чертежа и в наглядном пространственном изображении методом прямоугольного параллельного проецирования, применяемое для приобретения навыков дальнейшего выполнения графических работ по построению комплексного чертежа модели и изображению ее в пространстве.
— Аксонометрические проекции. Поверхности и тела. Сечение геометрических тел плоскостями: разобрать упражнения на построение проекций плоских фигур для приобретения навыков для дальнейшего выполнения графических работ по построению комплексного чертежа модели и упражнения по определению натуральной величины плоских фигур тремя способами.
Изображения предметов на чертежах выполняют методом прямоугольного (ортогонального) проецирования. При этом изображаемый предмет располагают между глазом наблюдателя и плоскостью проекций, через все точки предмета проводят проецирующие лучи под прямым углом к плоскости проекций и получают прямоугольную (ортогональную) проекцию на плоскости.
Наиболее полное представление о предмете дает проецирование на три взаимно перпендикулярные плоскости проекций.
За основу построений предлагается выбрать тела вращения или гранные тела (на усмотрение преподавателя).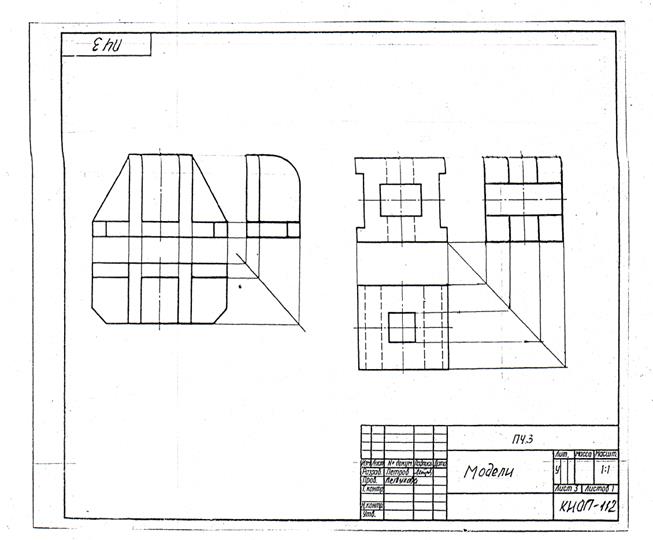
Компоновка осей эпюра производится произвольно.
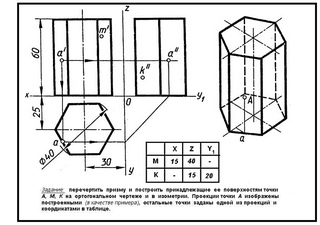
На образце выполнения задания (рисунке 2) в качестве примера показано выполнение проекций призмы, пирамиды, цилиндра, конуса и построение заданных на их поверхностях точек, а также изображена построенная по ним аксонометрическая проекция с изображением точек в пространстве.
ЗАДАНИЕ
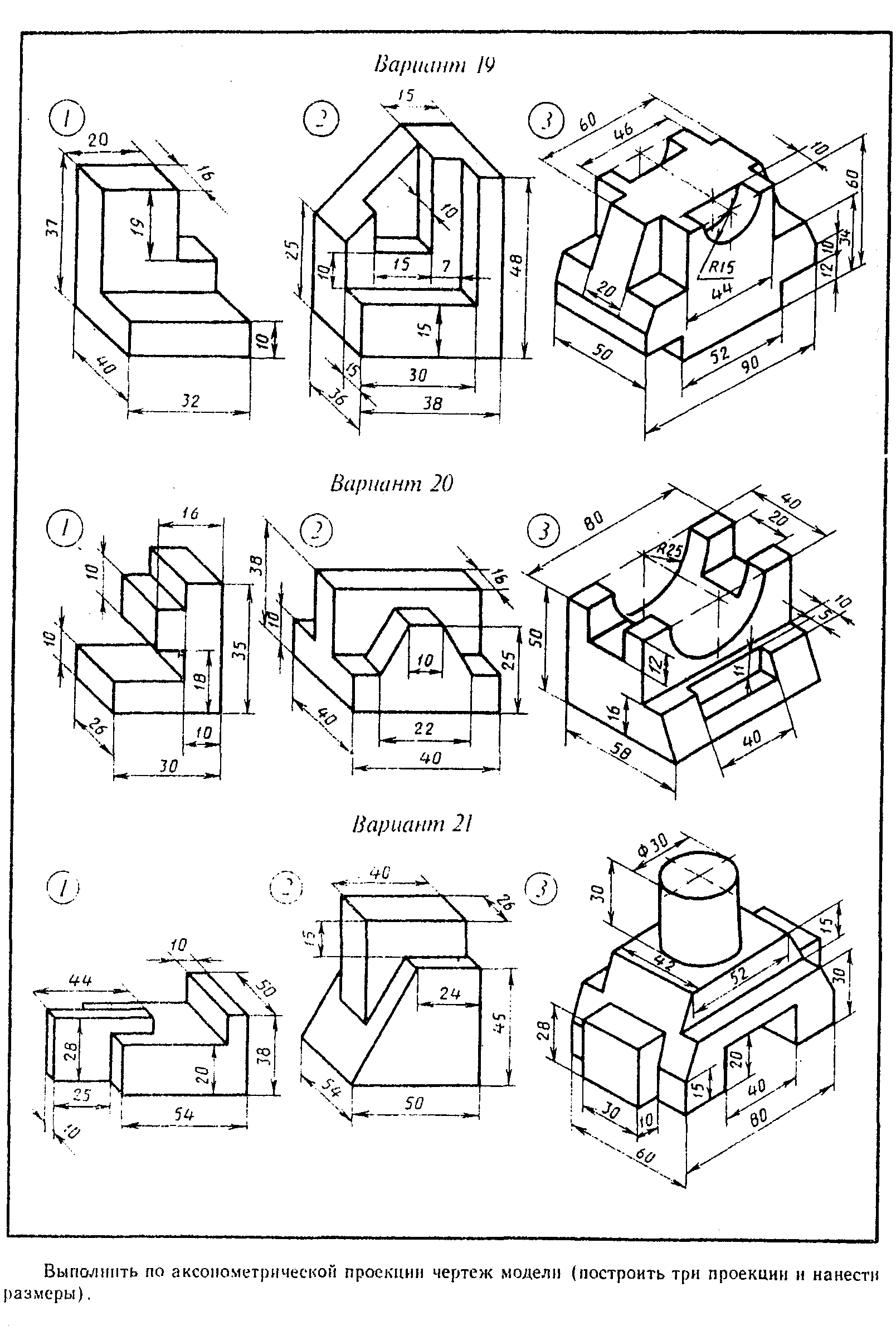
На листе формата А4 построить в трех проекциях комплексный чертеж геометрических тел в масштабе 1:1, по заданным размерам своего варианта (таблица 1) и условию рисунка 1. Найти проекции точек расположенных на их поверхностях. По выполненным чертежам построить аксонометрические проекции геометрических тел с нахождением точек в пространстве.
Рисунок 1 – Условия для выполнения задания
Таблица 1 – Варианты задания
УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ1 Ознакомьтесь с вариантом задания;
2 Произвольно выберите расположение осей эпюра;
3 Постройте в тонких линиях три проекции геометрических тел по заданным размерам;
4 Проставьте размеры;
5 Выберите расположение осей октанта;
6 Выполните аксонометрическую проекцию построенных геометрических тел;
7 Постройте заданные на поверхностях тел точки, по образцу выполненных точек А и В;
8 Обведите контуры тел в октанте и на эпюре;
9 Заполните основную надпись.
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАННИЯ
Пример выполнения задания представлен на рисунке 2.
Рисунок 2 – Пример выполнения задания
КОНТРОЛЬНЫЕ ВОПРОСЫ
1 Какие аксонометрические проекции Вы знаете?
2 Под каким углом располагаются оси аксонометрических проекций друг к другу?
3 Как выполняется изометрия и диметрия проекций?
4 Какие они имеют коэффициенты искажения по осям?
5 Какие геометрические тела, изображены на рисунке 1?
6 Какие поверхности будут проецироваться на горизонтальную плоскость без искажения?
7 Какие поверхности будут проецироваться на фронтальную плоскость без искажения?
8 Какие поверхности будут проецироваться на горизонтальную плоскость в виде прямой?
9 Почему проекции цилиндра и конуса на фронтальной и профильной проекции одинаковы?
10 Для изображения каких геометрических тел лучше выбирать диметрию?
1.
 Глава 6. Проекции точки. Комплексный чертеж
Глава 6. Проекции точки. Комплексный чертеж
Чтобы построить изображение предмета, сначала изображают отдельные его элементы в виде простейших элементов пространства. Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.д
Правила построения изображений на чертежах в инженерной графике основываются на методе проекций. Одно изображение (проекция) геометрического тела не позволяет судить о его геометрической форме или форме простейших геометрических образов, составляющих это изображение. Таким образом, нельзя судить о положении точки в пространстве по одной ее проекции; положение ее в пространстве определяется двумя проекциями.
Рассмотрим пример построения проекции точки А, расположенной в пространстве двугранного угла (рис. 60). Одну из плоскостей проекции расположим горизонтально, назовем ее горизонтальной плоскостью проекций и обозначим буквой П1. П2=A2;
П2=A2;
Проецирующие лучи АА1 и АА2взаимно перпендикулярны и создают в пространстве проецирующую плоскость АА1АА2, перпендикулярную обеим сторонам проекций. Эта плоскость пересекает плоскости проекций по линиям, проходящим через проекции точки А.
Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П1с фронтальной плоскостью П2 вращением вокруг оси П2/П1 (рис. 61, а). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси П2/П1. Прямая А1А2, соединяющая горизонтальную А1и фронтальную А2проекции точки, называется вертикальной линией связи.
Полученный плоский чертеж называется комплексным чертежом. Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.
Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.
Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки а относительно этих плоскостей (рис. 61, б) ее высотой h (АА1 =h) и глубиной f(AA2 =f), то эти величины на комплексном чертеже существуют как отрезки вертикальной линии связи. Это обстоятельство позволяет легко реконструировать чертеж, т. е. определить по чертежу положение точки относительно плоскостей проекций. Для этого достаточно в точке А2 чертежа восстановить перпендикуляр к плоскости чертежа (считая ее фронтальной) длиной, равной глубине f. Конец этого перпендикуляра определит положение точки А относительно плоскости чертежа.
Комплексные чертежи линий — презентация онлайн
Лекции по начертательнойгеометрии
Комплексные чертежи линий
2. Разновидности линий
РАЗНОВИДНОСТИ ЛИНИЙЛинии: прямые, ломаные и кривые.
С их помощью строят изображения
предметов на чертеже.
Ломаные и кривые линии могут быть
плоскими и пространственными;
замкнутыми и незамкнутыми.
Прямые: общего положения,
линии уровня, проецирующие.
3. Кривая а(1, 2, 3, 4, 5)
Для построения чертежа кривой линии а необходимозафиксировать на ней достаточное количество точек.
Спроецировать эти точки. Затем соединить проекции точек
плавной кривой.
4. Проекции окружности а(а1, а2) замкнутая, плоская кривая
5. Ломаная а(А, В, С, D)
Ломаная а(А, В, С, D) состоит из отрезков прямых, имеющих общиевершины [АВ], [BC], [CD]. Для построения чертежа ломаной
достаточно спроецировать ее вершины. Затем соединить проекции
вершин отрезками прямых.
6. ПРЯМЫЕ ЛИНИИ Свойства прямой линии
Через любые две различные точкипроходит одна и только одна прямая.
Две различные прямые могут иметь
не более одной общей точки.
7. Положение прямых в пространстве
• Прямые общего положения — не параллельны и неперпендикулярны ни одной плоскости проекций.
• Прямые уровня – параллельны плоскостям проекций:
– фронталь (f) — параллельна П2
– горизонталь (h) — параллельна П1
– профильная прямая (p) — параллельна П3
• Проецирующие прямые — перпендикулярны
плоскостям проекций:
горизонтально-проецирующая – перпендикулярна П1
фронтально-проецирующая – перпендикулярна П2
профильно-проецирующая – перпендикулярна П3
8. Прямая общего положения l(А,В)
Прямая, не параллельная и не перпендикулярная ниодной из плоскостей проекций (П1 ,П2, П3), называется
прямой общего положения.
Разности координат точек (А,В), задающих прямую l, не
равны нулю.
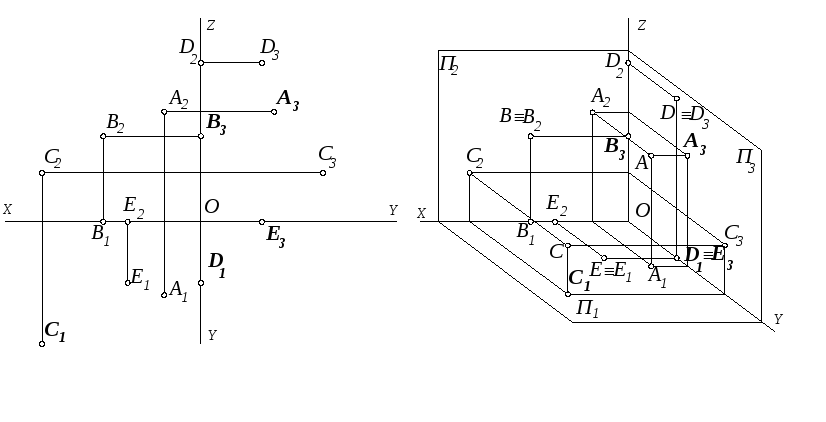
9. Построение комплексного чертежа прямой l по разности координат двух ее точек А и В. Три проекции точки А заданы.
10. Определение положения вертикальной линии связи для проекций точки В
Координата X точки В меньше координаты X точки А. Отмеряем30 мм вправо (так как координата X увеличивается влево) и
проводим вертикальную линию связи для нахождения проекций
точки В.
11. Построение фронтальной проекции (В2) точки В
Точка В выше точки А на 15 мм. Отмеряем вверх отфронтальной проекции (А2) точки А по линии связи
разность высот и фиксируем фронтальную проекцию (В2)
точки В.
12. Построение горизонтальной проекции (В1) точки В
Координата Y точки В меньше координаты Y точки А на 20 мм.Отмеряем 20 мм по вертикальной линии связи вверх от уровня А1
(так как точка В ближе к плоскости П2, чем точка А) и фиксируем
горизонтальную проекцию (В1) точки В.
13. Построение профильной проекции (В3) точки В
Из В2 проводим горизонтальную линию связи.
Отмеряем разность координат YA-YB = 2 0 мм
по линии связи от А3 влево, так как на плоскости П3
координаты Y нарастают вправо.
14. Построение проекций прямой l
На плоскости П2 проводим фронтальную проекцию l2 прямой l черезфронтальные проекции её точек А2 и В2.
На плоскости П1 проводим горизонтальную проекцию l1 прямой l через
горизонтальные проекции её точек А1 и В1.
На плоскости П3 проводим профильную проекцию l3 прямой l через
профильные проекции её точек А3 и В3.
15. Прямые уровня занимают частное положение Горизонталь — линия параллельная П1
α – угол наклона прямой к П1β – угол наклона прямой к П2
γ – угол наклона прямой к П3
Так как горизонталь h(h2,h3,h4) параллельна плоскости П1, ее отрезок [AB]
проецируется на эту плоскость в натуральную величину (без искажения)
IABI=IA1B1I. Углы наклона горизонтали к плоскостям проекций П2 (β)
и П3 (γ) проецируются на П1 в натуральную величину.
16.
 Построить комплексный чертеж прямой по разности координат двух ее точек А и В. Три проекции точки А заданы. Так как разность высот точек линии равна нулю, линия параллельна
Построить комплексный чертеж прямой по разности координат двух ее точек А и В. Три проекции точки А заданы. Так как разность высот точек линии равна нулю, линия параллельнаплоскости П1 — горизонталь. Построение чертежа горизонтали следует
начинать с фронтальной проекции (h3).
Она составляет угол 90° с вертикальной линией связи.
17. Построение фронтальной проекции (h3) горизонтали
Координата X точки В меньше координаты X точки А. Отмеряем 25 ммвправо (так как координата X увеличивается влево) и проводим
вертикальную линию связи для нахождения проекций точки В. На высоте
точки А фиксируем фронтальную проекцию В2.
18. Построение горизонтальной проекции (h2) горизонтали
Координата Y точки В больше координаты Y точки А на 15 мм. Отмеряем15 мм по вертикальной линии связи вниз от уровня А1 (так как точка В
дальше от плоскости П2, чем точка А) и фиксируем горизонтальную
проекцию (В1) точки В. Через А1 и В1 проводим h2.

19. Построение профильной проекции (h4) горизонтали
Из В2 проводим горизонтальную линию связи. Отмеряемразность координат YB -YA = 15 мм по линии связи от А3 вправо,
так как на плоскости П3 координаты Y нарастают вправо, и
фиксируем В3. Через А3 и В3 проводим профильную проекцию
(h4) горизонтали.
20. Фронталь — линия параллельная плоскости П2
Так как фронталь f(f1,f2,f3) параллельна плоскости П2, ее отрезок [AB]проецируется на эту плоскость в натуральную величину (без
искажения) IABI=IA2B2I. Углы наклона фронтали к плоскостям
проекций П1 (α) и П3 (γ) проецируются на П2 в натуральную
величину.
21. Построить комплексный чертеж прямой по разности координат двух ее точек А и В. Две проекции точки А заданы.
Так как разность глубин точек линии равна нулю, линияпараллельна плоскости П2 — фронталь. Построение чертежа
фронтали следует начинать с горизонтальной проекции (f1).
Она составляет угол 90° с вертикальной линией связи.

22. Построение горизонтальной проекции (f1) фронтали
Координата X точки В меньше координаты X точки А. Отмеряем 30 ммвправо (так как координата X увеличивается влево) и проводим
вертикальную линию связи для нахождения проекций точки В.
На пересечении перпендикуляра из А1 и вертикальной линии связи
фиксируем горизонтальную проекцию В1. Через А1 и В1 проводим f1.
23. Построение фронтальной проекции (f2) фронтали
Точка В выше точки А на 15 мм. Отмеряем вверх отфронтальной проекции (А2) точки А по линии связи
разность высот и фиксируем фронтальную проекцию (В2)
точки В. Через А2 и В2 проводим f2.
24. Построение профильной проекции (f3) фронтали
Из В2 и А2 проводим горизонтальные линии связи. Зафиксируем В3 .Проводим профильную проекцию (f3) под углом 90° к линии связи
так как разность координат YB -YA = 0 мм. В пересечении f3 и
горизонтальной линии связи из А2, определим А3.
25. Профильная прямая — линия параллельная плоскости П3
Так как профильная прямая p(p1,p2, p3) параллельна плоскости П3, ееотрезок [AB] проецируется на эту плоскость в натуральную величину
(без искажения) IABI=IA3B3I.
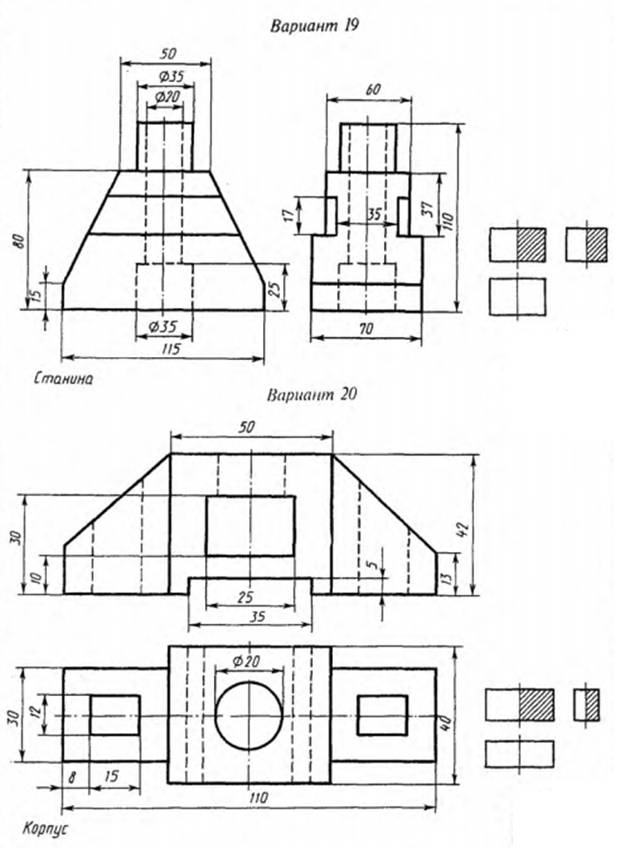 Углы наклона профильной прямой к
Углы наклона профильной прямой кплоскостям проекций П1 (α) и П2 (β) проецируются на П3 в
натуральную величину.
26. Построить комплексный чертеж прямой по разности координат двух ее точек А и В. Три проекции точки А заданы.
Так как разность широт точек линии равна нулю, линия параллельнаплоскости П3 — профильная прямая. Построение чертежа профильной
прямой начнём с фронтальной проекции (p2). Она составляет угол 0°
с вертикальной линией связи.
27. Построение фронтальной проекции (p2) профильной прямой p
Точка А выше точки В на 15 мм. Отмеряем вниз от фронтальнойпроекции (А2) точки А по линии связи разность высот и фиксируем
фронтальную проекцию (В2) точки В. Через А2 и В2 проводим
фронтальную проекцию (p2) профильной прямой p.
28. Построение горизонтальной проекции (p1) профильной прямой p
Координата Y точки В больше координаты Y точки А. Отмеряем 20мм в сторону увеличения координаты Y (по вертикальной линии
связи) и фиксируем горизонтальную проекцию (В1) точки В.
 Через
ЧерезА1 и В1 проводим горизонтальную проекцию (p1) профильной
прямой p.
29. Построение профильной проекции (p3) профильной прямой p
Из В2 проводим горизонтальную линию связи. Отмеряем разностькоординат YB -YA = 20 мм по линии связи от А3 вправо, так как на
плоскости П3 координаты Y нарастают вправо, и фиксируем В3. Через
А3 и В3 проводим профильную проекцию (p3) профильной прямой p.
30. Условие обратимости комплексного чертежа линии уровня
Двух проекционный комплексный чертеж линии уровняобратим только в том случае, если он содержит проекцию
прямой на параллельную ей плоскость проекций.
Проецирующие прямые занимают частное положение
Горизонтально-проецирующая прямая перпендикулярна
горизонтальной плоскости проекций (П1)
IABI
IABI
∆X=0
∆Y=0
А,В — горизонтально конкурирующие точки.
Точка В выше точки А.
32. Построить комплексный чертеж прямой q(AB) по разности координат двух ее точек А и В.
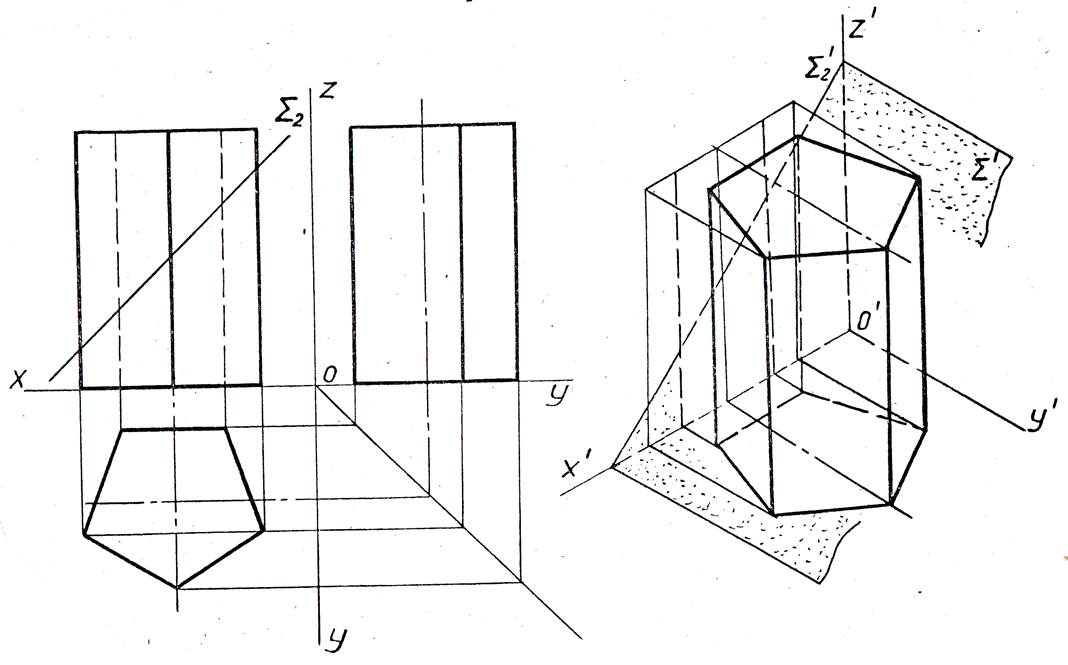 Проекции точки А не заданы. Так как разность широт и глубин точек линии равна нулю, линия
Проекции точки А не заданы. Так как разность широт и глубин точек линии равна нулю, линияперпендикулярна плоскости П1 – горизонтально проецирующая.
Построение чертежа горизонтально проецирующей линии следует
начинать с горизонтальной проекции (q1). Вся линия q(AB) на плоскость П1
проецируется в точку.
33. Построение горизонтальной проекции (q1) горизонтально проецирующей прямой q
Мысленно делим свободное пространство на три плоскости П1, П2 иП3. На П1 фиксируем горизонтальную проекцию (q1) горизонтально
проецирующей прямой q.
34. Построение фронтальной проекции (q2)
Из q1 проводим вертикальную линию связи и фиксируем на нейфронтальную проекцию (В2) точки В так как высота (координата Z)
точки В больше высоты точки А.
35. Построение фронтальной проекции (q2)
Отмеряем вниз по линии связи разность высот точек А и В (20 мм)и наносим на чертёж фронтальную проекцию (А2) точки А. Через
А2 и В2 проводим фронтальную проекцию (q2) прямой q.

36. Построение профильной проекции (q3)
Расстояние от В2 до В3выбираем
из условия компоновки
чертежа
Из В2 и А2 проводим горизонтальные линии связи. Фиксируем на
плоскости П3 профильную проекцию (В3) точки В. Через В3 проводим
профильную проекцию (q3) прямой q под углом 90° к горизонтальной
линии связи. В пересечении q3 с горизонтальной линией связи из А2
находим А3.
Фронтально-проецирующая прямая
перпендикулярна фронтальной плоскости (П2)
IABI
IABI
А,В — фронтально конкурирующие точки.
Точка В ближе к наблюдателю (дальше от П2) точки А.
38. Построить комплексный чертеж прямой i(AB) по разности координат двух ее точек А и В. Проекции точки А не заданы.
Так как разность широт и высот точек линии равна нулю, линияперпендикулярна плоскости П2 – фронтально проецирующая.
Построение чертежа фронтально проецирующей следует начинать с
фронтальной проекции (i2). Вся линия i(AB) на плоскость П2 проецируется в
точку.
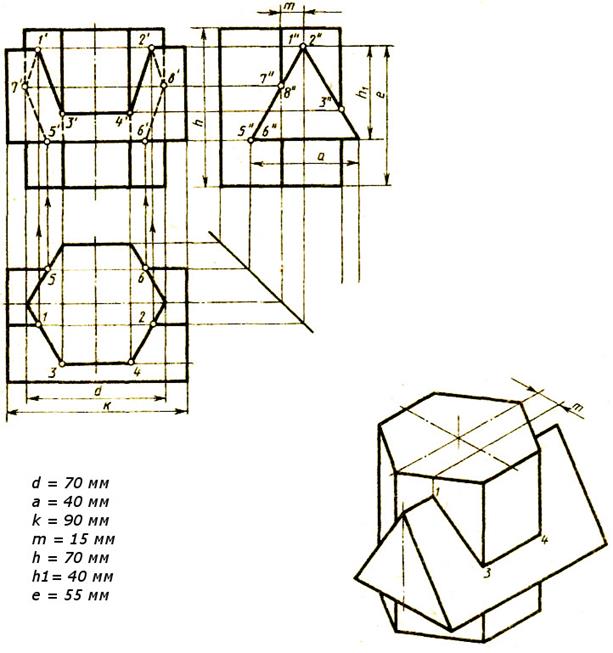
39. Построение фронтальной проекции (i2) фронтально проецирующей прямой i
Мысленно делим свободное пространство на три плоскости П1, П2и П3. На П2 фиксируем фронтальную проекцию (i2) фронтально
проецирующей прямой i.
40. Построение горизонтальной проекции (i1)
Из i2 проводим вертикальную линию связи и фиксируем наней горизонтальную проекцию (В1) точки В, так как глубина
(координата Y) точки В больше глубины точки А..
41. Построение горизонтальной проекции (i1) фронтально проецирующей прямой i
Отмеряем вверх по линии связи разность глубин точек А и В (20мм)и наносим на чертёж горизонтальную проекцию (А1) точки А. Через
А1 и В1 проводим горизонтальную проекцию (i1) прямой i..
42. Построение профильной проекции (i3) фронтально проецирующей прямой i
Из В2 и А2 проводим горизонтальную линию связи. Фиксируем наплоскости П3 профильную проекцию (В3) точки В. Отмеряем влево по
линии связи разность глубин точек А и В (20 мм) и фиксируем
профильную проекцию А3 точки В.
 Через В3 и А3 проводим профильную
Через В3 и А3 проводим профильнуюпроекцию (i3) фронтально проецирующей прямой i.
Профильно проецирующая прямая g(g1,g2,g3)
IABI
IABI
∆Y=0
∆Z=0
А,В — профильно конкурирующие точки
Точка А дальше от плоскости П3, чем точка В.
44. Построить комплексный чертеж прямой g(АВ) по разности координат двух ее точек А и В. Проекции точки А не заданы.
Так как разность глубин и высот точек линии равна нулю, линияперпендикулярна плоскости П3 – профильно проецирующая.
Построение чертежа профильно проецирующей следует начинать с
профильной проекции (g3). Вся линия g(AB) на плоскость П3 проецируется
в точку.
45. Построение профильной проекции (g3) профильно проецирующей прямой g(А,В)
Мысленно делим свободное пространство на три плоскостиП1, П2 и П3. На П3 фиксируем профильную проекцию (g3)
профильно проецирующей прямой g(А,В). Оставить место для
построений на П1 и П2!
46. Построение фронтальной проекции (g2) профильно проецирующей прямой g
Из g3 проводим горизонтальную линию связи и фиксируем на нейфронтальную проекцию (А2) точки А, так как широта (координата X)
точки А больше широты точки В.
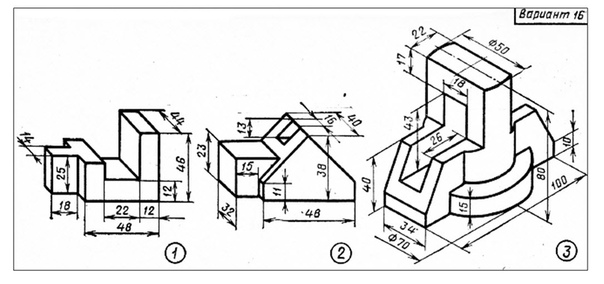 .
.47. Построение фронтальной проекции (g2) профильно проецирующей прямой g
Отмеряем вправо по линии связи разность широт точек А и В(20мм) и фиксируем фронтальную проекцию В2 точки В.
Через В2 и А2 проводим фронтальную проекцию (g2)
профильно проецирующей прямой g.
48. Построение горизонтальной проекции (g1) профильно проецирующей прямой g
Из А2 и В2 проводим вертикальной линии связи. Фиксируемгоризонтальную проекцию (А1) точки А. Координаты Y точки В и точки А
одинаковы. Через А1 и проводим горизонтальную проекцию (g1)
профильно проецирующей прямой p под углом 90° к линии связи.
Фиксируем горизонтальную проекцию (В1) точки В.
49. Относительное положение прямых в пространстве
1. Параллельныеm
m1
n
n1
m2
m1
n2
n1
У параллельных прямых одноимённые проекции
параллельны (m1 II n1), (m2 II n2).
50. Параллельность линий уровня
Линии уровня параллельны, если параллельныих проекции на параллельную им плоскость
51.
 Параллельность линий уровня •Линии уровня параллельны, если параллельны
Параллельность линий уровня •Линии уровня параллельны, если параллельныих проекции на параллельную им плоскость
52. Относительное положение прямых в пространстве
2. Пересекающиесяa
b
K
a1
b1
K1
a2
b2
K2
a1
b1
K1
У пересекающихся прямых проекции точки пересечения
(К1), (К2) должны принадлежать одной линии связи.
53. Относительное положение прямых в пространстве
3. Скрещивающиесясм. на П1
12
3
=(4
)
a2 2 2
22
a1 41
b1
31 (21)=11
см. на П2
Одна из скрещивающихся прямых
может быть выше (ниже)
относительно П1 и дальше (ближе)
b2 относительно П2. Положение
скрещивающихся прямых
определяется с помощью
горизонтально (1, 2) и фронтально
(3, 4) конкурирующих точек
соответственно.
Точки пересечения проекций
находятся на разных линиях связи.
Относительно П1 – b над a
Относительно П2 – b перед a
54.
 Скрещивающиеся прямые Точки пересечения проекций скрещивающихся
Скрещивающиеся прямые Точки пересечения проекций скрещивающихсяпрямых находятся на разных линиях связи
55. Относительное положение точек и прямых линий
Точка может принадлежать прямой линии. В этом случаепроекции точки, принадлежащие проекциям прямой,
должны принадлежать одной линии связи.
56. Точка 1 выше прямой m
57. Точка 4 ближе к П2 ,чем прямая m. Точка 4 за прямой m.
58. Определение длины отрезка прямой и углов его наклона к плоскостям проекций способом прямоугольного треугольника
Натуральная величина IABI отрезка [AB] прямой общего положения накомплексном чертеже может быть определена как гипотенуза прямоугольного
треугольника, одним катетом которого будет проекция отрезка, а другим разность недостающих координат концов отрезка.
59. Определить на комплексном чертеже истинную величину отрезка [AB] и углы наклона его к плоскостям П1 и П2.
Натуральная величина IABI отрезка [AB] прямой общего положения накомплексном чертеже может быть определена как гипотенуза прямоугольного
треугольника, одним катетом которого будет проекция отрезка, а другим разность недостающих координат концов отрезка.
60. Определение истинной величины IABI отрезка [AB] и угла α наклона его к плоскости П1.
1. Определяем разность высот (ΔZ) концов отрезка [AB] прямой общегоположения.
2. Проводим направление катета прямоугольного треугольника, одним
катетом которого будет горизонтальная проекция (A1B1) отрезка [AB].
61. Определение истинной величины IABI отрезка [AB] и угла α наклона его к плоскости П1.
3. На направлении катета откладываем разность высот (ΔZ) концовотрезка [AB] и фиксируем вершину треугольника А0.
4. Соединив вершину прямоугольного треугольника А0 с вершиной В1,
получим истинную величину IABI отрезка [AB]
и угол α наклона его к плоскости П1
62. Определение истинной величины IABI отрезка [AB] и угла β наклона его к плоскости П2.
1. Определяем разность глубин (Δy) концов отрезка [AB] прямой общегоположения.
2. Проводим направление катета прямоугольного треугольника, одним
катетом которого будет фронтальная проекция (A2B2) отрезка [AB].

63. Определение истинной величины IABI отрезка [AB] и угла β наклона его к плоскости П2.
3. На направлении катета откладываем разность глубин (Δy) концовотрезка [AB] и фиксируем вершину треугольника B0.
4. Соединив вершину прямоугольного треугольника B0 с вершиной A2,
получим истинную величину IABI отрезка [AB]
и угол β наклона его к плоскости П2
64. Найти истинную длину ломаной линии IABCDEI= мм. Построить на [CD] точку К по условию: ICK I=20 мм.
Истинная длина отрезков проецирующих прямых IABI =IA1B1I; IВСI =IВ1С1I.Для отрезка [CD] прямой общего положения — гипотенуза IC0D1I прямоугольного
треугольника, одним катетом которого будет проекция отрезка [C1D1] , а другим разность высот концов отрезка. Для отрезка фронтали [DЕ] истинная длина
IDЕI =ID2Е2I
Проецирование на три взаимно перпендикулярные плоскости проекции
Существует множество деталей, информацию о форме которых невозможно передать двумя проекциями чертежа (рис. 75).
75).
Для того чтобы информация о сложной форме детали была представлена достаточно полно, используют проецирование на три взаимно перпендикулярные плоскости проекции: фронтальную — V, горизонтальную — H и профильную — W (читается «дубль вэ»).
Система плоскостей проекций представляет собой трехгранный угол с вершиной в точке О. Пересечения плоскостей трехгранного угла образуют прямые линии — оси проекций (OX, OY, OZ) (рис. 76).
В трехгранный угол помещают предмет так, чтобы его формообразующая грань и основание были бы параллельны соответственно фронтальной и горизонтальной плоскостям проекций. Затем через все точки предмета проводят проецирующие лучи, перпендикулярные всем трем плоскостям проекций, на которых получают фронтальную, горизонтальную и профильную проекции предмета. После проецирования предмет удаляют из трехгранного угла, а затем горизонтальную и профильную плоскости проекций поворачивают на 90* соответственно вокруг осей ОХ и OZ до совмещения с фронтальной плоскостью проекции и получают чертеж детали, содержащий три проекции.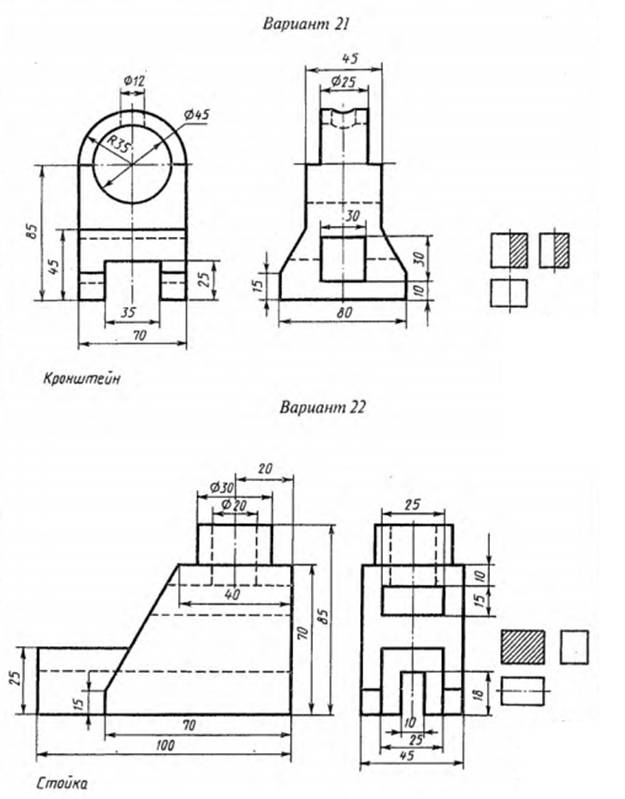
Рис. 75. Проецирование на две плоскости проекций не всегда дает
полное представление о форме предмета
Рис. 76. Проецирование на три взаимно перпендикулярные
плоскости проекций
Три проекции чертежа взаимосвязаны друг с другом. Фронтальная и горизонтальная проекции сохраняют проекционную связь изображений, т. е. устанавливаются проекционные связи и между фронтальной и горизонтальной, фронтальной и профильной, а также горизонтальной и профильной проекциями (см. рис. 76). Линии проекционной связи определяют местоположение каждой проекции на поле чертежа.
Во миогнх странах мира принята другая система прямо- угольного проецирования на три взаимно перпендикулярные плоскости проекций, которая условно называется «американская» (см. Приложение 3). Основное eе отличие состоит в том, что по-иному, относительно проецируемого объекта, в пространстве располагается трехгранный угол и в других направлениях разворачиваются плоскости проекций. Поэтому горизонтальная проекция оказывается над фронтальной, а профильная проекция — справа от фронтальной.
Поэтому горизонтальная проекция оказывается над фронтальной, а профильная проекция — справа от фронтальной.
Форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения и выполнения чертежей нужно знать, как изображаются геометрические тела в системе трех проекций на производстве (табл. 7). (Чертежи, содержащие три проекции, называются комплексными чертежами.)
7. Комплексные и производственные чертежи деталей простой геометрической формы
П p и м e ч а н и я: 1. В зависимости от особенностей производственного процесса на чертеже изображают определенное число проекций. 2. На чертежах принято давать наименьшее, но достаточное число изображений для определения формы предмета. Число изображений чертежа можно уменьшить, используя условные знаки s, l, ? которых вы уже знаете.
ортогональных проекций
ортогональных проекций Графический языкКогда вы впервые научились читать нашу письменную речь, вы прошли через это в логическом порядке.
 Вы выучили алфавит, затем выучили
простые слова. Вы не могли выучить простые слова, пока не узнали буквы
которые их сформировали. Позже в ваш словарный запас были добавлены более сложные слова
и процесс продолжился.
Вы выучили алфавит, затем выучили
простые слова. Вы не могли выучить простые слова, пока не узнали буквы
которые их сформировали. Позже в ваш словарный запас были добавлены более сложные слова
и процесс продолжился.То же самое можно применить и к изучению графического языка.Графический язык можно разбить на «алфавит» точек, линии и плоскости. Твердые объекты состоят из следующих элементов: точек представляющие углы, линии, представляющие края, и плоскости, представляющие поверхности.
От инженеров требуется проектировать, пересматривать, анализировать и / или создавать сложные части или системы. Эти части или системы задуманы или существуют в трехмерная среда. До появления трехмерного твердотельного моделирования это было сложно точно определить эти части в трехмерном пространстве.К отображать эти объекты на двухмерном носителе, таком как лист бумаги, обычно проектировщик создает проекцию детали.
Проекции строятся при просмотре объекта с воображаемым прозрачным
плоскость, помещенная между наблюдателем и объектом.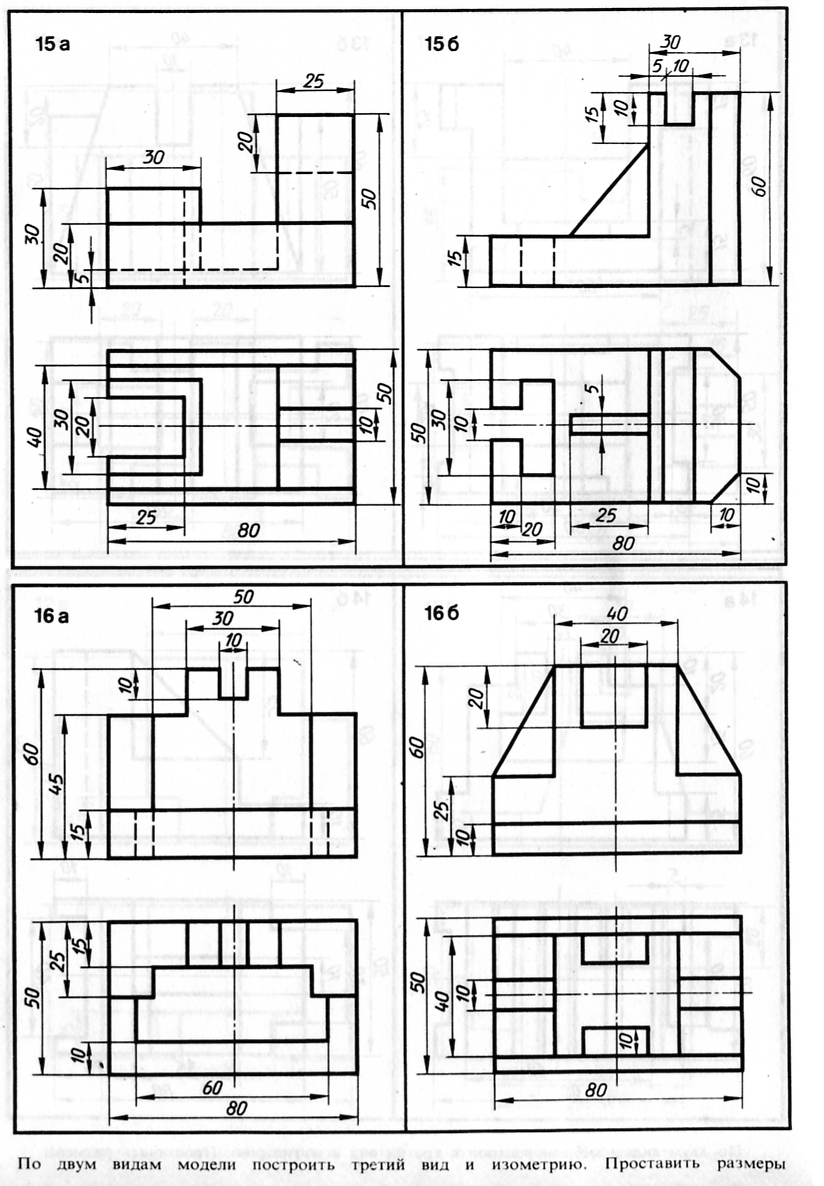 Изображение объекта
проецируется на эту воображаемую плоскость, определяемую как плоскость проекции.
Двумерное представление или вид объекта — это
результат.
Изображение объекта
проецируется на эту воображаемую плоскость, определяемую как плоскость проекции.
Двумерное представление или вид объекта — это
результат.
При представлении технических рисунки.Наше внимание будет сосредоточено на конкретном типе, известном как орфографическая проекция. Ортографическая проекция — это представление чаще всего используется инженерами. Ортогональные виды позволяют описание точного размера и формы объекта.
Самая простая функция, которую вы можете отобразить графически, — это точка в пространстве. К продемонстрировать понятие ортогональной проекции, мы начнем с демонстрации проекции единственная точка в пространстве.
Система орфографической проекции классифицируется по
отношения, образованные между наблюдателем, плоскостью проекции и
объект.[РИСУНОК 3-1] Обратите внимание, что
линия обзора (также называемая линией проекции) перпендикулярна
на плоскость проекции. Эта связь должна существовать для проекции
быть орфографической проекцией. Изображение точки O проецируется на
плоскость проекции и двухмерный вид точки могут быть
нарисовано.
Эта связь должна существовать для проекции
быть орфографической проекцией. Изображение точки O проецируется на
плоскость проекции и двухмерный вид точки могут быть
нарисовано.
Чтобы полностью определить объект, необходимо как минимум два ортогональных вида. обязательный. В зависимости от сложности детали можно выбрать три или более ракурса. обязательный. Чтобы пример был простым, и продемонстрировать задействованную теорию, мы продолжим рассматривать один точку в пространстве и покажите три вида в ортогональной проекции.
Теория стеклянной коробкиТеория стеклянной коробки обычно используется в качестве наглядного пособия при определении орфографическая проекция. Представьте себе коробку с прозрачными стенками, содержит точку О. Шесть плоскостей, составляющих коробку, определяется как основные проекционные плоскости. Предполагается, что точка имеет фиксированное положение внутри коробки. [РИСУНОК 3-2] Точка проецируется на три поверхности, образующие вверх по коробке: верхняя или H (горизонтальная) плоскость, передняя или «F» (фронтальная) плоскость, а правая сторона или «P» (профиль) самолет.
 Наблюдатель имеет разное положение для каждого из трех представлений.
так, чтобы линия обзора была перпендикулярна плоскости, на которой
проекция делается.
Наблюдатель имеет разное положение для каждого из трех представлений.
так, чтобы линия обзора была перпендикулярна плоскости, на которой
проекция делается.Эти три точки зрения должны быть представлены так, чтобы возникла логическая взаимосвязь. поддерживается. Плоскости проекции просто развернуты, поэтому они находятся на в той же плоскости, т.е. чтобы их можно было нарисовать на двухмерном носителе, таком как бумага. Чтобы поддерживать взаимосвязь между видами, плоскости проекции не могут быть разделены, только развернуты по краям, созданным пересечение плоскостей.
Фактические плоскости, составляющие стеклянную коробку, обычно не отображаются в виде
часть готового рисунка. Эти самолеты — воображаемые самолеты, представленные
чтобы передать теорию. Линии сгиба часто включаются в рисунок и будут
быть показаны в примерах в виде фантомных линий (штрих-пунктирная линия). В
линии сгиба, также называемые ссылочными
линии, на самом деле линии, в которых плоскости, составляющие воображаемый
коробка пересекается.
Положение точки можно определить по трем параметрам.
Точка расположена на определенной высоте внутри рамки. Вершина поле обозначено буквой «H», чтобы идентифицировать его как «горизонтальный плоскости «, и указывается размер Dh. Это расстояние определяет местонахождение точки по горизонтали в пространстве и определяется как расстояние от горизонтальная плоскость (Dh). Вы также можете считать это расстояние от в сверху коробки в точку.
Точка также имеет фиксированную глубину внутри рамки. Передняя часть коробки обозначен буквой «F», чтобы идентифицировать его как фронтальную плоскость.Размерность Df показано положение точки относительно фронтальной самолет. Точка O расположена на фиксированном расстоянии (Df) позади лобной самолет.
Наконец, точка также должна располагаться относительно одной из сторон.
коробки,
измерение ширины. Правая сторона коробки помечена буквой «P», чтобы идентифицировать ее как плоскость профиля. Показан размер Dp для определения местоположения
точка . Точка O расположена на фиксированном расстоянии Dp слева от правой стороны.
профиль
самолет.
Точка O расположена на фиксированном расстоянии Dp слева от правой стороны.
профиль
самолет.
Обратите внимание, что точка могла быть расположена относительно трех других самолеты, которые также составляют коробку.Расстояние от нижней части box можно было дать, например, вместо Dh. Это более стандартно однако измерять сверху, чтобы найти точку. Также предпочтительно чтобы точка располагалась спереди, а не сзади. Просто поскольку вид детали снизу или сзади обычно не представлен, нижний а задние контрольные плоскости обычно не используются для определения местоположения точек. Слева и виды объектов с правой стороны являются обычным явлением, поэтому при поиске точки из Плоскость профиля обычно используется как с левой, так и с правой стороны.Индексы Dpr и Dpl часто используются, чтобы указать, располагается относительно правой или левой плоскости проекции.
The Df, Расстояния Dp и Dh всегда отсчитываются от линии сгиба (или справочные линии).
На [РИСУНОК 3-3] орфографические
показана проекция одной точки.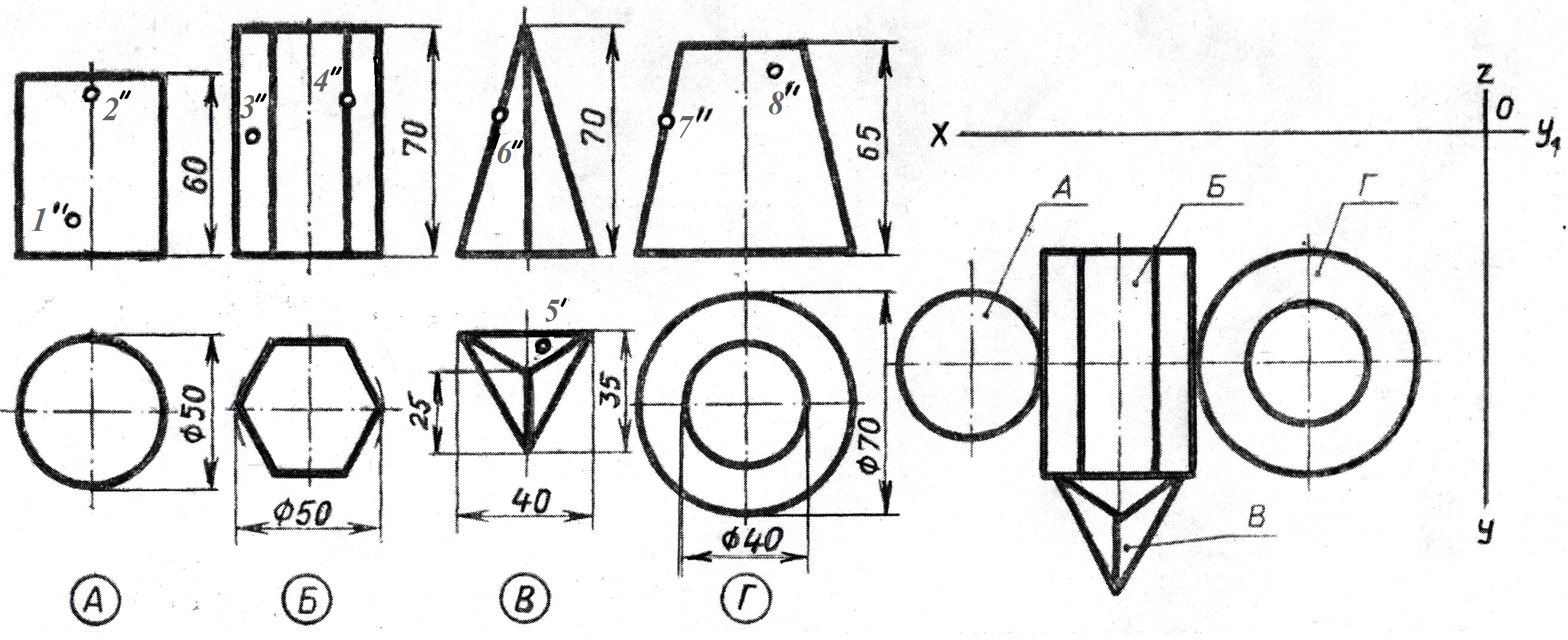 Положение наблюдателя
схематично показано, что он находится на измеримом расстоянии от выступа
самолет. Ортографически проецировать изображение любого геометрического объекта
больше точки, наблюдатель следует рассматривать как бесконечное
расстояние от плоскости проекции.Исходя из этого предположения, строки
прицел будут параллельны друг другу. [ФИГУРА
3-4] Мы расширим наш пример, чтобы показать орфографические
проекция линии в пространстве.
Положение наблюдателя
схематично показано, что он находится на измеримом расстоянии от выступа
самолет. Ортографически проецировать изображение любого геометрического объекта
больше точки, наблюдатель следует рассматривать как бесконечное
расстояние от плоскости проекции.Исходя из этого предположения, строки
прицел будут параллельны друг другу. [ФИГУРА
3-4] Мы расширим наш пример, чтобы показать орфографические
проекция линии в пространстве.
Чтобы закрепить теорию орфографической проекции, большая часть начальных проблемы будут проблемами «отсутствующего обзора». Вам дадут два из трех основные представления и попросили построить отсутствующий вид. Ты должен понять что два представления должны быть известны для построения дополнительных представлений.Один орфографический вид содержит только два измерения. Все три измерения должно быть известно, иначе объект не определен.
Рассмотрим вид спереди одной приведенной точки. Вы знаете высоту точки (Dh) и положение
точки относительно одной из плоскостей профиля (Dp). Но нет ничего, чтобы указать, насколько далеко
точка находится за фронтальной плоскостью (Df). Эта глубина (Df) должна быть указана для определения положения
точка. Если бы был вид сверху, было бы известно Df.Только после этого можно было нарисовать недостающую сторону (профиль).
Посмотреть.
Но нет ничего, чтобы указать, насколько далеко
точка находится за фронтальной плоскостью (Df). Эта глубина (Df) должна быть указана для определения положения
точка. Если бы был вид сверху, было бы известно Df.Только после этого можно было нарисовать недостающую сторону (профиль).
Посмотреть.
Чтобы на самом деле построить этот вид сбоку, сначала осознайте, что Dh известен. Высота точки в вид сбоку будет таким же, как на данном виде спереди. Просто спроецируйте высоту по горизонтали строительная линия. Затем поймите, что Df также известен. Дело в определенное фиксированное расстояние за фронтальной плоскостью. Вы можете увидеть это расстояние (оно указано) на виде сверху. Расстояние, на которое точка находится за фронтальной плоскостью (Df) одинаково независимо от того, смотрите ли вы на точку сверху или сбоку.Перенести это расстояние от вид сверху на вид сбоку (всегда не забывая измерять от линии сгиба). Затем вы заполните отсутствует вид и решить проблему.
Линии и поверхностиЛиния определяется двумя точками в пространстве.
 Это может проявляться по-разному
в зависимости от относительного положения зрителя.
Это может проявляться по-разному
в зависимости от относительного положения зрителя.Если зритель выбирает положение так, чтобы линия его взгляда была параллельна к линии, линия будет отображаться как одна точка в пространстве.В этом случае, линия перпендикулярна плоскости, на которую она проецируется.
Если линия просматривается перпендикулярно направлению взгляда в данной строке будет отображаться истинная длина (TL). В этом в случае, если линия параллельна плоскости, на которую она проецируется. Помни это нужно предположить, что наблюдатель находится на бесконечном расстоянии от проекции плоскости так, чтобы линии взгляда были параллельны друг другу.
Если смотреть на линию так, что она составляет угол, отличный от 90 градусов, с плоскость проекции, она будет выглядеть в укороченном виде.Это будет искаженный вид линии, и длина линии в этом виде будет короче чем его истинная длина, но больше точки.
Линии в пространстве можно классифицировать в зависимости от их отношения к
основные проекционные плоскости. Мы определим три различных типа
линии.
Мы определим три различных типа
линии.
Нормальная линия — это линия в пространстве, параллельная двум основным плоскости и перпендикулярно третьему. Следовательно, учитывая три основных просмотров (H, F, P), линия должна отображаться TL в двух видах.В оставшихся вид, он будет отображаться как точка.
Наклонная линия — это линия в пространстве, параллельная одному из трех основные взгляды. Он не параллелен и не перпендикулярен двум другим взгляды. Линия будет отображаться как TL на одном виде, поскольку она параллельна одному из проекционные плоскости. В оставшихся двух он будет выглядеть в укороченном виде. взгляды.
Косая линия — это линия в пространстве, которая не параллельна и не перпендикулярна. на любой из основных самолетов. В принципе, он будет выглядеть в укороченном виде. взгляды.
Чтобы завершить наш графический алфавит, мы должны включить плоские поверхности. Самолет
можно определить в пространстве несколькими способами. Три неколинеарных точки
(точки, которые не лежат на одной линии), определяют плоскую поверхность.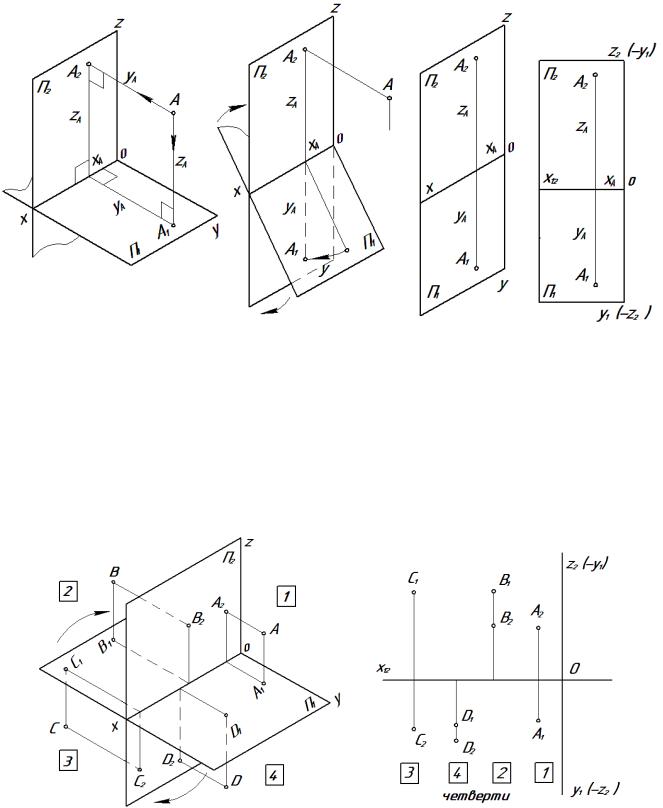 Любая прямая и точка, не лежащая на этой прямой, аналогичным образом определяют поверхность плоскости. А
плоскость также может быть определена двумя параллельными линиями или двумя пересекающимися
линии.
Любая прямая и точка, не лежащая на этой прямой, аналогичным образом определяют поверхность плоскости. А
плоскость также может быть определена двумя параллельными линиями или двумя пересекающимися
линии.
Плоская поверхность может иметь любую конкретную форму, то есть поверхность на объекте. Также можно предположить, что оно будет продолжаться бесконечно во всех направлениях.Для После обсуждения предположим, что простая плоскость определяется тремя точками в пространстве. Точки соединяются, образуя плоскую поверхность в форме треугольник. Вы можете использовать один из треугольников для рисования из вашего набора в качестве наглядного пособия.
Так же, как линия может выглядеть по-разному в зависимости от положения наблюдатель, так что может плоская поверхность. Рассмотрим поверхность с фиксированным треугольная форма.
Если наблюдатель смотрит на поверхность так, что линии взгляда параллельны
к самолету, он или она будет видеть самолет как единую линию.Учитывая
ортогональная проекция плоскости в этом виде, плоскость будет
перпендикулярно плоскости проекции. Говорят, что это прямой вид на самолет. Есть бесконечное количество позиций в
который этот вид можно увидеть.
Говорят, что это прямой вид на самолет. Есть бесконечное количество позиций в
который этот вид можно увидеть.
Если наблюдатель смотрит на поверхность так, что линии взгляда перпендикулярно плоскости, он или она увидит плоскость в ее истинном размере и форма. Это будет верно, если плоская поверхность проецируется на плоскость проекции параллельна ему.Для того, чтобы неподвижная плоскость в пространстве выглядела истинной size (TS), есть только две позиции, где наблюдатель мог бы быть расположена; 180 град.
Существует бесконечное количество видов, на которых поверхность будет казаться укороченной. Самолет будет казаться укороченным в любом ракурсе, где
поверхность не параллельна и не перпендикулярна плоскости проекции.
Архитектурные чертежи: 8 мастерских параллельных проекций
Архитекторы: Продемонстрируйте свой следующий проект через Architizer и подпишитесь на нашу вдохновляющую новостную рассылку .
Аксонометрические чертежи — мощный инструмент для визуального представления сложных пространственных схем. Их уникальная точка зрения позволяет создавать наглядные рисунки, которые представляют трехмерное пространство на двухмерной поверхности. При параллельных проекциях обычные законы перспективы не действуют: нет сдвига в масштабе, как это было бы через объектив камеры или через наши глаза. Хотя эти рисунки часто имеют идеальные пропорции и размеры, они особенно убедительны, поскольку находятся между реальностью и невозможностью: человеческий глаз никогда не видит пространство таким образом.
Эта коллекция рассматривает несколько применений техники параллельной проекции, каждый раз используемой художниками и архитекторами для передачи больших идей. Готовясь к участию в конкурсе One Drawing Challenge, исследуйте эти увлекательные архитектурные представления и визуализируйте свои собственные…
Изображение через Pinterest
Изображение с FANTASTIC OFFENSE в Twitter
Правительственный центр округа Ориндж , автор Пол Рудольф, Гошен, штат Нью-Йорк.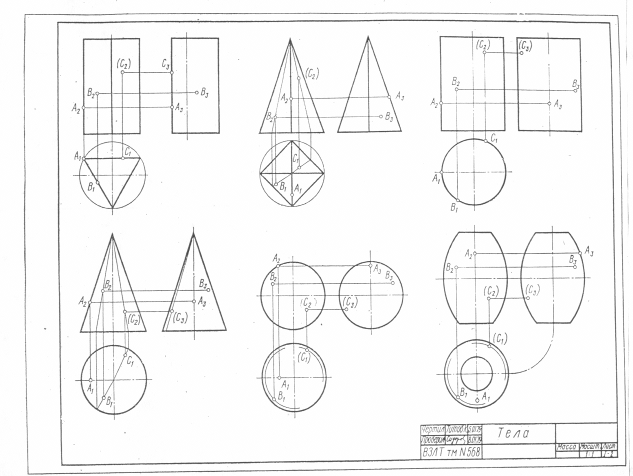
Мастерские ручные рисунки Рудольфа свидетельствуют о силе комбинирования изобразительных техник для передачи различных аспектов здания. Аксонометрический вид и перспектива сечения работают в тандеме, чтобы передать выступающие прямолинейные объемы внешнего фасада, а также внутреннее пространство внутри них. Две приведенные выше параллельные проекции необычны по-разному — первая вращает весь чертеж в пространстве, чтобы обеспечить вид с земли, который представляет здание с правдоподобной человеческой точки зрения.Второй дает нам вид с высоты птичьего полета, показывая 87 многоуровневых крыш, через которые дневной свет проникает во все здание.
АЛЬБОМ «Bff016» от SET Architects, Милан, Италия
На этой паре рисунков показано пространство вместе и разорванное. Использование аксонометрической проекции показывает не только то, как пространство выглядит и может быть населенным, но и очевидную простоту дизайна. На чертеже установка разбивается на четыре основных компонента: пол, содержимое, конструкция и крыша, демонстрируя модульность и воспроизводимость конструкции.
Изображения через Høyblokka Revisited
Høyblokka Revisited by Kolab Arkitekten + Kollaboratoriet, Осло, Норвегия
Принимая участие в конкурсе дизайнеров, предлагая дизайнерам переосмыслить культурно значимое здание в Норвегии, компания Kollaboratoriet предложила решение, которое выразилось в этих простых, но ярких рисунках. Используя аксонометрический рисунок, зритель получает четкое представление о том, как отдельные единицы функционируют в пределах всего жилого комплекса.
Изображения через ArchEyes
Неофутуристические рисунки Яна Каплицкого, Лондон, Великобритания
Эти дальновидные и творческие рисунки — работа независимой практики Каплицкого, Future Systems, с 1970-х по 1990-е годы. Он был известен тем, что сказал: «Наличие 65 идей для одной задачи — не признак творчества. Это просто пустая трата энергии ». Эти подробные рисунки иллюстрируют интерес Каплицкого к преобразованию идей в отдельные, легко читаемые рисунки.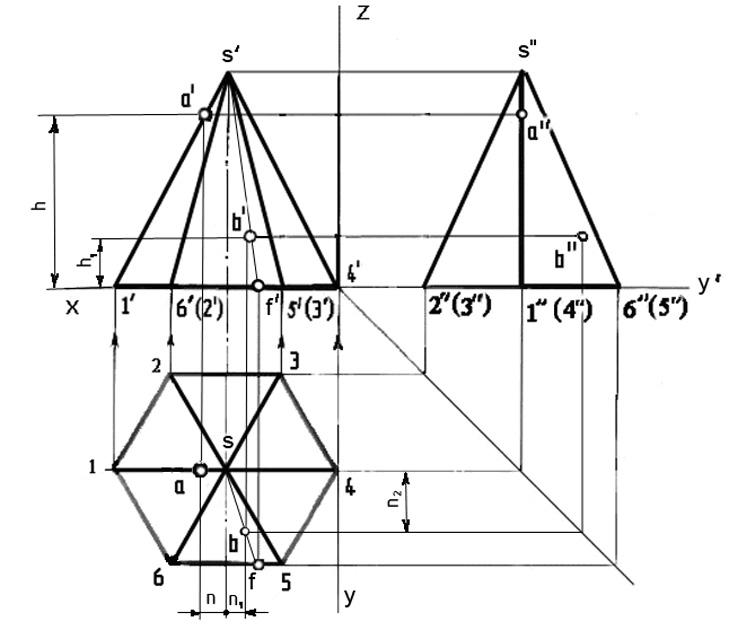 Уникальный вид чертежей позволяет зрителю понять форму и функции каждого искусно выполненного проекта.
Уникальный вид чертежей позволяет зрителю понять форму и функции каждого искусно выполненного проекта.
Социально-культурный центр by fala atelier, Рейноса, Испания
Fala ателье, игриво именующее себя «практикой наивной архитектуры», создает рисунки с уникальным радостным качеством. Этот персонаж пронизывает все проекты фирмы — от чертежа до воплощенного дизайна. Эти рисунки передают основную концепцию проекта с помощью чистых линий и продуманных цветовых пятен.Аксонометрическое изображение этого сложного пространства дает ощущение целостности проекта, представляя каждую из 49 комнат как часть более крупной экосистемы.
© Архитектура BRIO
Дом у ручья и Прибрежный дом от Architecture BRIO, Индия
Река является неотъемлемой частью идентичности обоих домов. Архитектура BRIO использует разнесенную аксонометрическую проекцию, чтобы показать каждый дом по отношению к его окружению. В то время как детализированная проекция дома парит над землей, черный силуэт прямо под ним указывает на положение дома в ландшафте.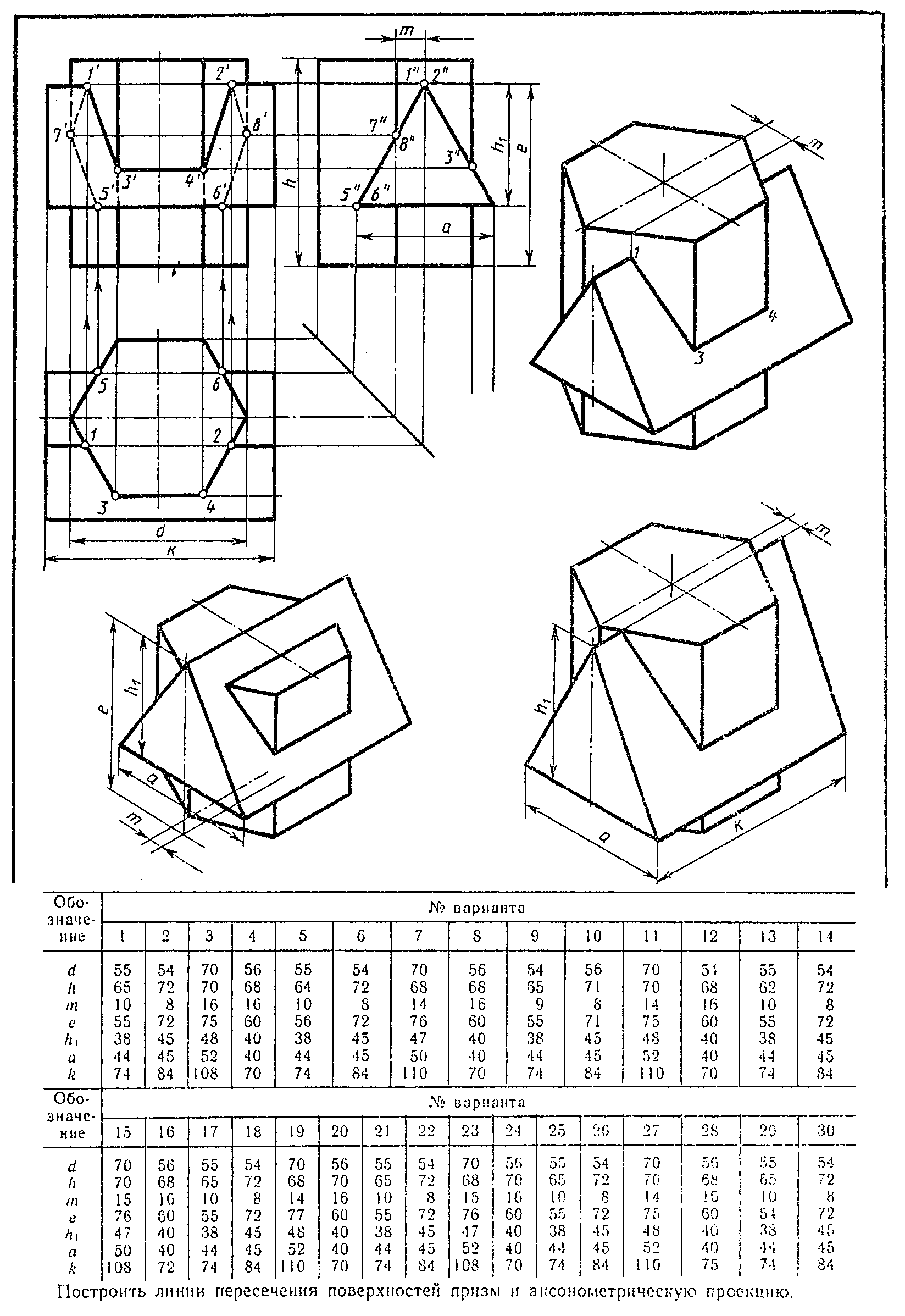 Благодаря использованию аксонометрии в разобранном виде рисунок успешно предоставляет информацию о самом доме и его положении в ландшафте, не подвергая опасности ни то, ни другое.
Благодаря использованию аксонометрии в разобранном виде рисунок успешно предоставляет информацию о самом доме и его положении в ландшафте, не подвергая опасности ни то, ни другое.
Образы через Socks
Ранние коллажи (1967–1970) Даниэля Либескинда
Трудно представить себе какую-либо из зубчатых, очень скульптурных архитектур Даниэля Либескинда когда-либо существующую в двухмерной плоскости. Тем не менее, когда Либескинд был студентом Cooper Union в 1960-х годах, его профессора поощряли его исследовать пересечение визуального искусства и архитектуры с помощью коллажей и других рисунков.
Повернутые на 30 градусов сетки служат якорем для сложной геометрии Либескинда, которая восхищает пространственной неоднозначностью и бросает вызов обычной логике измерения, которую мы ожидаем от аксонометрических проекций. Сочетание этих двух вещей создает необычные и очень убедительные произведения, мастерски стирающие грань между искусством и архитектурой.
Туан Цзе Ху от Drawing Architecture Studio, Пекин, Китай
Этот набор рисунков от DAS демонстрирует, что аксонометрические проекции не обязательно предназначены для представления пространств упорядоченным и логичным способом.Эти полуфантастические рисунки окрестностей Пекина используют изобразительную технику как инструмент, демонстрирующий городской динамизм.
Рисунок следует правилам параллельной проекции, но применяет его к городу с нескольких точек зрения, создавая нелогичное пространственное расположение. Красочные здания, выдавленные из сетки в суматошном великолепии, успешно передают не только реальность застроенной среды, но и нечто большее: улавливают феноменологию городской жизни..
A F.E., глядя вдоль Arrow A.
E.E. смотрит вдоль стрелки B.
Апиан.
Первый вид, который S нарисовал для AP. Этого нет в инструкциях, но без него FE очень сложно нарисовать. Стрелка A показывает, что три стороны шестиугольника видны в FE, а A P. построено так, что три стороны шестиугольника. стороны видны (поверните шестиугольник на 30 * в AE, и будут видны только две стороны) A P. также используется для определения ширины pnsm в E..
построено так, что три стороны шестиугольника. стороны видны (поверните шестиугольник на 30 * в AE, и будут видны только две стороны) A P. также используется для определения ширины pnsm в E..
A F.E., глядя вдоль Arrow A.
E.E. смотрит вдоль стрелки B.
Апиан.
3R0 УГЛОВОЕ ПРОЕКЦИЯ
Рис. 10/14
ПРОЕКЦИЯ НА 1-Й УГОЛ F.E.
Рис. 10/15
На рис. 10/15 показаны «следующие виды усеченной пирамиды в 1-й угловой проекции. Углы пирамиды пронумерованы от 1 до 4 для облегчения идентификации на каждом возвышении.
A F.E. смотрит по стрелке.
Апиан.
ПРОЕКЦИЯ НА 1-Й УГОЛ F.E.
Для этого типа задач разумно сначала нарисовать требуемые виды, как если бы пирамида была завершена. Еще раз необходимо нарисовать A.E., чтобы можно было нарисовать наклонную грань на A.E., а затем точки 1.2. 3 и 4 можно снова спроецировать на план. Затем точки 1 и 3 проецируются на F.E., а точки 2 и 4 — на
. E.E.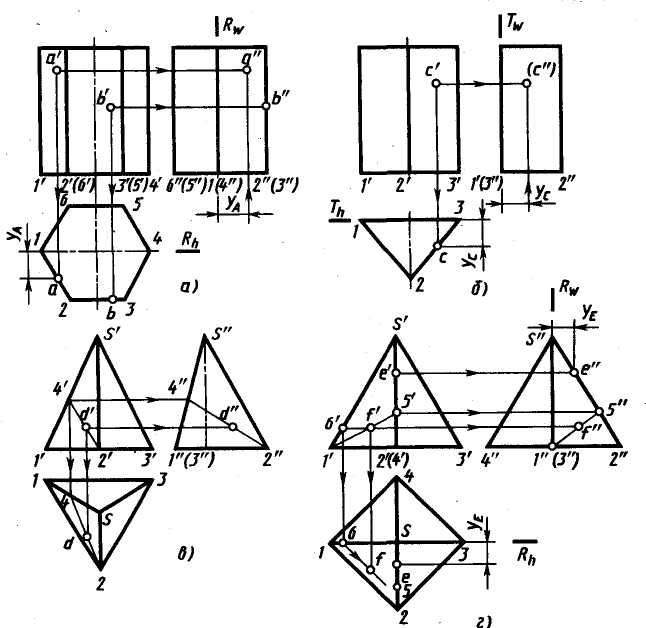 Точки 2 и 4 могут быть спроецированы с E.E. на
Точки 2 и 4 могут быть спроецированы с E.E. на
F.E. и точки 1 и 3 из F.От E. до E.E.Обратите внимание, что после того, как A.E. нарисован, можно нарисовать наклонную грань на всех трех видах без каких-либо дополнительных измерений
Фиг.10/15
На рис. 10/16 показаны следующие виды восьмиугольной пирамиды в проекции под третьим углом. Пирамида лежит набок.
A F.E. смотрит по стрелке.
Апиан
Чтобы нарисовать пирамиду, лежащую на боку, сначала нарисуйте ее вертикально, а затем переверните. Это делается с помощью компаса, как показано.Если строится план пирамиды, стоящей вертикально, это облегчает поиск положений углов пирамиды на плане, когда она перевернута.
3R0 УГЛОВОЕ ПРОЕКЦИЯ
3R0 УГЛОВОЕ ПРОЕКЦИЯ
На рис. 10/17 показан следующий вид * шестиугольной пирамиды, нарисованной в 3-м угловом ограждении. Вершина пирамиды срезана под углом A &, а нижняя под углом 30 °.
Подросток F.E. в направлении стрелки.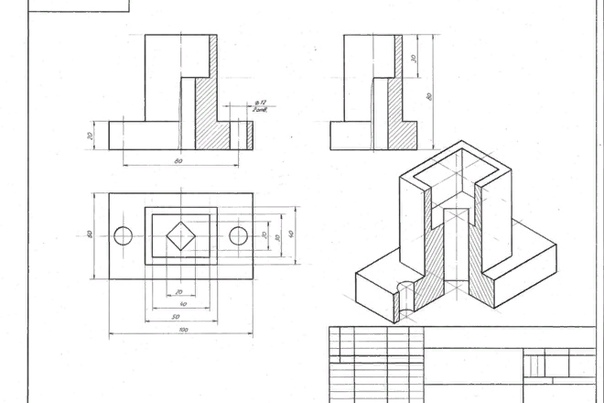
План.
Ан А.Проектируется по плану на 3ЦП.
Что касается F »g. 15.10. пирамида сначала рисуется, как если бы она была закончена, на всех четырех видах. Затем на КЭ рисуется нижняя секущая плоскость. Точки, где она пересекает углы, затем проецируются поперек ВЕ и до плана. Точка, где она пересекает центральный угол на КЭ, не может быть спроецирована прямо на план и должна быть проецироваться через EE (следуйте стрелкам).
Затем рисуется верхняя секционная плоскость на E.E.и точки, где он пересекает углы, проецируются на F.E. и до плана.
Большинство этих углов можно спроецировать прямо с плана на AE. Исключение составляют точки в центральном углу, и их (размеры ab c и d) можно перенести из любого удобного источника, в данном случае цилиндра FE
* конусы
На рис. 10/18 показаны следующие виды цилиндра в проекции 1-го угла.
A. F.E. видно по стрелке.Апиан.
AP проецируется с F. E. под углом 46 °. Если план разделен на несколько полос, можно измерить ширину цилиндра на любой из этих полос.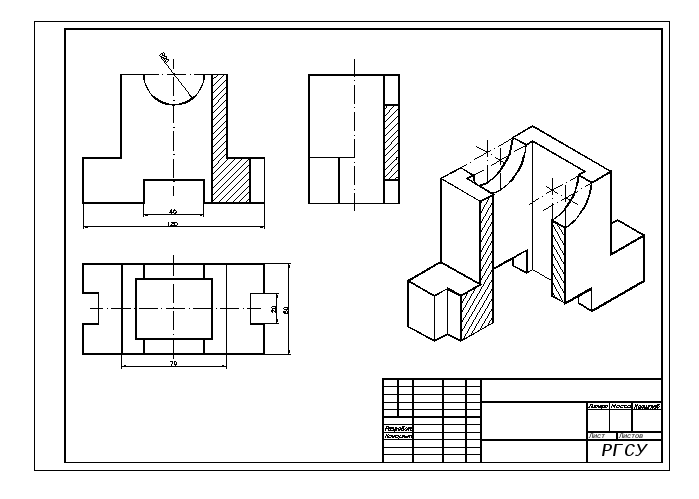 Исполнительные положения каждой из полос могут быть спроецированы на FE, а затем поперек AP. Ширина цилиндра на каждом из stnps переносится с плана на A P. с разделителями, измеренными с каждой стороны от центральной линии. (показана только одна сторона). Затем точки соединяются аккуратной кривой от руки.
Исполнительные положения каждой из полос могут быть спроецированы на FE, а затем поперек AP. Ширина цилиндра на каждом из stnps переносится с плана на A P. с разделителями, измеренными с каждой стороны от центральной линии. (показана только одна сторона). Затем точки соединяются аккуратной кривой от руки.
ПРОЕКЦИЯ 1-Й УГОЛ
ПРОЕКЦИЯ НА 1-Й УГОЛ
- Рис. 10/18
На Рис. 10/19 показаны следующие виды цилиндра, нарисованного в 3-й угловой проекции. Цилиндр лежит на боку, и один конец отрезан от 30® и другой конец на 60 дюймов в.д., если смотреть в направлении стрелки. В-в., если смотреть слева от FE Apian
Проекция A.P. с плана под углом 60 ° Восточная восточная долгота разделена на несколько полос.Полосы выступают со стороны восточной восточной долготы.E до F.E. и до плана Они тоже проецируются от E.E. к плану на 45? Точки проекторов «F.E.» и «E.E.» пересекаются на плане (в точках a, b, c и d и т. Д.), Образуя очертания двух эллипсов на плане.
Очертания эллипсов на точке A P находятся путем проецирования полос на точку A P и последующего переноса измерений 1, 2, 3. и т. Д. С точки E.E. на точку доступа с разделителями.
На рис. 10/20 показаны следующие виды изогнутого цилиндра в проекции 1-го угла
.А F.E. видно по стрелке.
Апиан
На этом чертеже используется «другой метод построения AP из предыдущих двух примеров. Вместо того, чтобы быть разделенным на» поездки, цилиндр разделен на 12 равных сегментов. Тезы отмечены на стенках цилиндра цифрами от 1 до 12. Эллипсы, сформированные на AP, находятся путем построения пересечений проекторов с номерами от 1 до 12 от FE и из конструкции, проведенной по линии с AP. Проекторы пересекаются в 1 ‘, 2’.3 * и т. Д. Обратите внимание, что на E.E. номер 1 находится в верхней части круга, в то время как на конструкции (и, следовательно, на A.P.) номер 1 находится справа. Это, конечно, то, что вам следует ожидать
ПРОЕКЦИЯ НА 1-Й УГОЛ
(Только строительство)
Рис. 10/20
10/20
ПРОЕКЦИЯ 1-Й УГОЛ
(только строительство)
Рис.10/20
На рис. 10/21 показаны следующие виды цилиндра в 3-й угловой проекции. Основание цилиндра срезано под углом 30 °, а цилиндр наклонен под углом 60 ° в F.E.
A F.E., если смотреть в направлении стрелки. E.E. вид слева от F.E.
Апиан. ПРОЕКЦИЯ ТРЕТИЙ УГОЛ
ПЛАН
Цилиндр разделен на двенадцать равных сегментов. Это делается на отдельном вспомогательном фасаде и плане, которые построены специально для этой цели. Эллипсы находятся путем нанесения пересечений проекторов из точек 1 и 1,2, 2, 3, 3, 4 и 4. и т. Д.
ПЛАН
(только строительство)
Фиг.21.10
(только строительство)
Фиг.10/21
r (только Construelion)
ПРОЕКЦИЯ 1-Й УГОЛ
ПРОЕКЦИЯ ПЕРВОГО УГЛА
На рис. 10/22 показаны следующие виды конуса, нарисованного в проекции 1-го угла.
A F.E., если смотреть в направлении стрелки
Апиан
План разбит на полосы. Эти полосы проецируются поперёк к восточному востоку и, следовательно, к атому.Ширину основания конуса на поверхности этих полос измеряют на плане с разделителями и переносят на AP.Затем точки соединяются аккуратной кривой от руки.
Эти полосы проецируются поперёк к восточному востоку и, следовательно, к атому.Ширину основания конуса на поверхности этих полос измеряют на плане с разделителями и переносят на AP.Затем точки соединяются аккуратной кривой от руки.
СЧл
На рис. 10/23 показаны следующие виды конуса, нарисованного в 3-й угловой проекции. Конус лежит на боку.
A F.E., если смотреть в направлении стрелки.
Апиан
Конус сначала рисуется вертикально вверх, а затем его переворачивают на бок. Вместо того, чтобы делиться на полосы, как раньше, он делится на 12 равных сегментов. Они пронумерованы от 1 до 12 на двух конструкциях, проведенных в соответствии с буквой F.E. и E. E. Эллипсы, образованные на E.E. и плане, находятся путем нанесения пересечений проекторов из этих построек. Они пересекаются в 12 *. 3 \ и т. Д. На ВП и на плане.
Более подробно геометрия конусов исследуется в следующей главе.
Разделы
Предположим, вы рисуете коробку. Вы рисуете прямоугольник в ортогональной проекции и довольны результатом. Но кто-то приходит и говорит вполне разумно. Хороший рисунок, но после эл.коробка — это всего лишь контейнер, и вы не показали, что внутри коробки; конечно, это важно «. И, конечно, он прав. Часто бывает важно показать, что находится внутри объекта, а также показать внешнее. В ортогональной проекции это обслуживается секцией е.
Но кто-то приходит и говорит вполне разумно. Хороший рисунок, но после эл.коробка — это всего лишь контейнер, и вы не показали, что внутри коробки; конечно, это важно «. И, конечно, он прав. Часто бывает важно показать, что находится внутри объекта, а также показать внешнее. В ортогональной проекции это обслуживается секцией е.
ПЛАН ПРОЕКЦИИ НА ТРЕТИЙ УГОЛ_
ПЛАН ПРОЕКЦИИ НА ТРЕТИЙ УГОЛ_
На рис. 10/24 показаны два рисунка »блока aame: один без сечения i, а другой« с разрезом ». На верхнем чертеже ни на одном из ортогональных видов не видно, что блок является пустотелым.На нижнем левом изометрическом виде блок вырезан по высоте, и сразу видно, что этот блок полый. Нижний правый вид показывает вырезанный блок, нарисованный в ортогональной проекции. Опять же, гораздо опаснее увидеть, что блок является пустотелым.
Внимательно обратите внимание на следующие мл:
1. Внешний вид с разрезом нарисован с отсутствующей половиной блока, но без отображения других видов.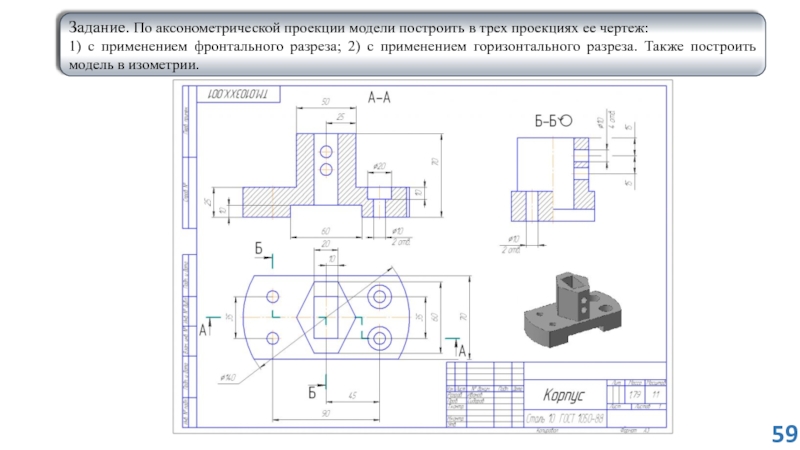 Они сохраняют свой нормальный полный контур.
Они сохраняют свой нормальный полный контур.
2. Точка, в которой делается разрез, обозначается секущей плоскостью.Это нарисовано тонкой цепочкой, пунктирной линией, которая утолщается там, где она меняет направление, и на короткое расстояние в конце. Стрелки указывают направление проецирования сечения.
3. Если плоскость разреза прорезает твердый материал, материал заштрихован под углом 45 *.
4. При проецировании разреза остальные видимые элементы, которые можно увидеть с другой стороны плоскости разреза, также отображаются на разрезе.
6. На разделе не принято рисовать скрытые двойки.
Существует множество правил, касающихся секционирования, но большинство из них применяется к инженерному чертежу, а не к геометрическому чертежу. По этой причине они находятся во втором
ПРОЕКЦИЯ ТРЕТЬЕГО УГЛА
- 1-Й УГОЛ
Рис. 10/26
Рис 10/25
Рис. 10/25 «как сечение шестиугольника
Задача этого типа содержит все характеристики вспомогательных отметок, и те же методы используются для проецирования этого разреза.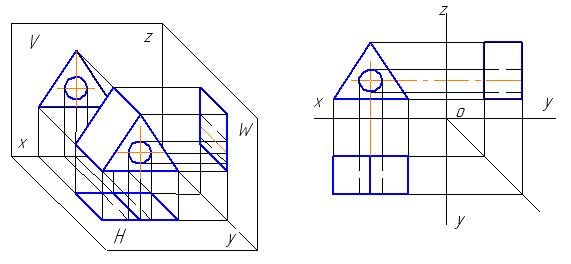
Иногда вопросы, заданные в экзаменационных работах, не касаются конкретного раздела, но для поиска решения необходимо использовать те же методы.
Фиг.10/26
На рис. 10/26 показан кувшин для сливок, имеющий форму усеченной шестиугольной пирамиды. Задача состоит в том, чтобы найти истинную форму крышки.
Решение состоит в том, чтобы спроецировать «секцию» (или A E.) из наклонной вершины пирамиды. Сначала нарисуйте F.E .., затем план. Истинную ширину a и b можно измерить на плане, и эти измерения перенести на «секцию» с разделителями.
Рис. 10/27 »как« действие, проецируемое куском толстостенной трубы, прикрепленной к прямоугольному основанию. Помимо F.E., должен быть нарисован план. Выбираются точки по окружности кругов на стержне, и эти точки проецируются вниз на плоскость сечения, а затем поперек на само сечение. Центральная линия является удобной точкой отсчета, поэтому расстояние от каждой точки до центральной линии измеряется разделителями и переносится на соответствующую линию проекции на разрезе.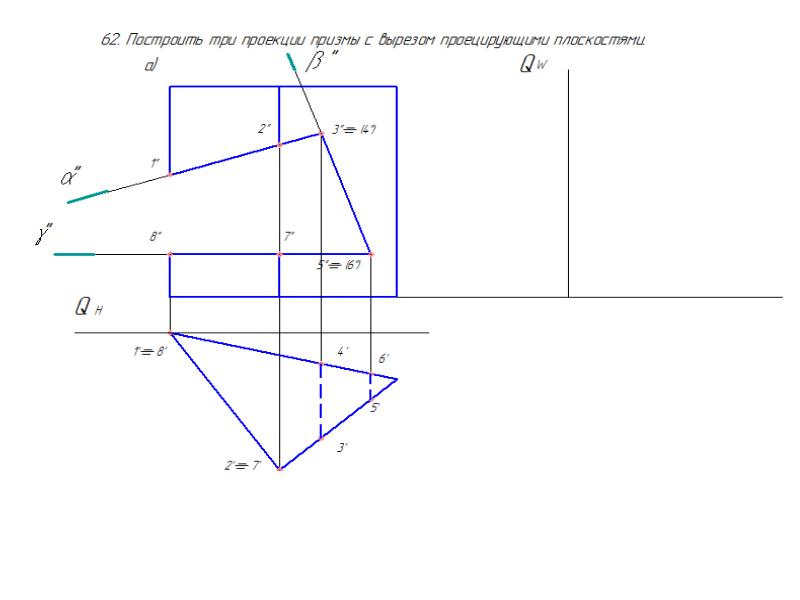 Для наглядности показаны только семь точек, но. конечно, все точки по окружности должны быть измерены и перенесены.
Для наглядности показаны только семь точек, но. конечно, все точки по окружности должны быть измерены и перенесены.
Из этого чертежа следует отметить два момента. Во-первых, штриховка сечения не рисуется на 45 *. Это потому, что штриховка будет параллельна большей части контура. В этом типе случая можно выбрать угол, отличный от 45 *. Во-вторых, обратите внимание, что штриховка выполняется только там, где плоскость сечения (или разреза) действительно прорезает твердый материал.
ПРОЕКЦИЯ НА ТРЕТИЙ УГОЛ
ПРОЕКЦИЯ ТРЕТЬЕГО УГОЛА
Наконец. На рис. 10/28 показано сечение торцевого ключа. На одном конце имеется шестигранная выемка для гайки или головки болта, а на другом — квадратная выемка для крепления стержня. Круглый профиль снова разбивается на части, чтобы можно было измерить точки вдоль его окружности и перенести измерения на сечение через плоскость сечения. Точки, где план сечения пересекает шестиугольные и прямоугольные розетки, проецируются на сечение, и любые измерения, которые необходимо выполнить, определяются путем проецирования назад на одну из конечных отметок. Они отмечены значком. б. c и d Размеры внешнего профиля отмечены (от t до 8
Они отмечены значком. б. c и d Размеры внешнего профиля отмечены (от t до 8
Для наглядности показана только половина измерений. С другой половиной разбираются так же. Конические разрезы рассматриваются в следующей главе Разделы, применяемые к инженерным чертежам, рассматриваются в части 2 этой книги.
Фиг.10/28
Упражнения 10 (Все вопросы задаются в единицах Импехеля)
1. На рис. 1. показана квадратная призма диаметром 20 мм и длиной 50 мм, опирающаяся одним из углов на горизонтальную плоскость. Нарисуйте в натуральную величину следующие виды и покажите все скрытые детали.
(а) Заданная отметка
(b) Конечная отметка в направлении стрелки E.
(c) Спроектированный план под видом (a).
North Waste / n Экзаменационная комиссия средней школы
2. На рис. 2 показан вид спереди и изометрический эскиз светоотражателя из листового металла для марионетки
.Фиг.10/28
Нарисуйте всю площадку, заданную переднюю высоту и спроецируйте на нее полный и торцевой вид отражателя.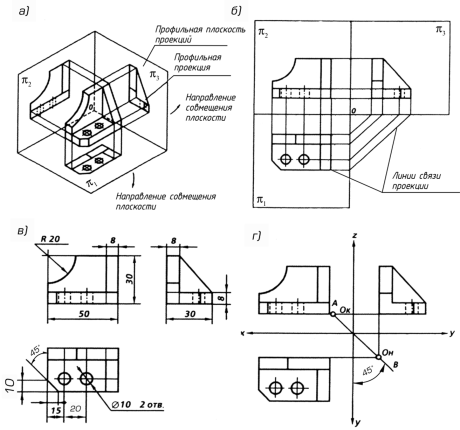 Нарисуйте. также истинная форма поверхности отмечена ABCO.
Нарисуйте. также истинная форма поверхности отмечена ABCO.
Толщиной металла можно пренебречь. Экзаменационная комиссия Wast Midlands
Рис. 2
Рис 2
14. План и высота специального углового кронштейна показаны на рис. 14.
(a) Нарисуйте в натуральную величину данные виды и спроецируйте вспомогательный план на линию земли X, -Y ,.
(b) Используя вспомогательный план в (a) выше, спроецируйте вспомогательную возвышенность на линии земли X, -Yt.
Показать все скрытые детали. Ассоциированная экзаменационная комиссия
16.На рис. 16 показан увеличенный вид удлинительной ножки для торцевого ключа.
Нарисуйте в масштабе 4: 1 в ортогональной проекции под первым углом:
(а) заданная высота;
(c) истинная форма сечения в плоскости разреза XX.
Оксфордские местные экзамены z
РАЗМЕРЫ В ММ
15. Два вида поворотного блока, показанного на рис. 15. Нарисуйте данные виды и нарисуйте высоту по XY, если смотреть в направлении стрелки A. Скрытые края должны быть показаны. Кембриджские местные экзамены
Скрытые края должны быть показаны. Кембриджские местные экзамены
РАЗМЕРЫ В мм Рис.16
РАЗМЕРЫ В мм Рис.16
17. На фиг. 17 показан вид и план отливки углового плинтуса, форма которого симметрична относительно AA.
Нарисуйте вторую отметку в направлении стрелки B.
Нарисуйте вертикальный разрез на плоскости разреза AA. Скрытые детали обязательны для всех видов. Объединенный совет южных университетов
РАЗМЕРЫ В ММ
Fio.17
- РАЗМЕРЫ В мм
Типы проекций для проектирования машин и инструментов
Графическая проекция играет важную роль в машинном черчении и проектировании. Для понимания трехмерной структуры можно использовать различные типы проекции. Здесь мы обсудим важные типы прогнозов, включая их преимущества и недостатки.
Параллельная проекция
Когда вы смотрите на машину, вы видите, что у нее есть плоскости, основанные на параллельных линиях.Например, токарный станок имеет прямоугольную основу, которая представляет собой комбинацию параллельных линий.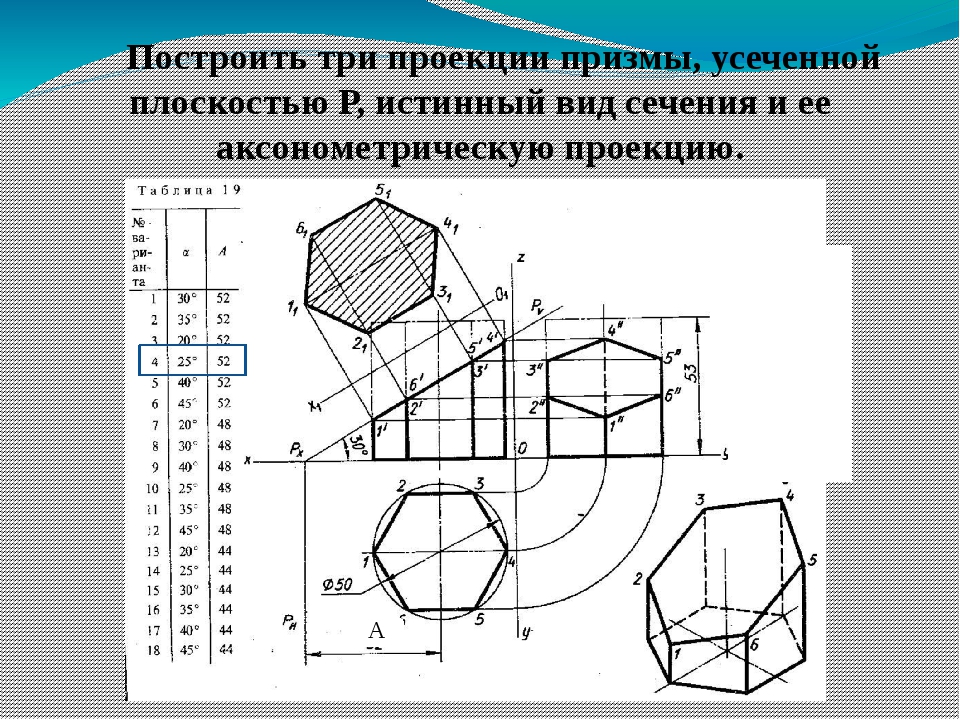 Если параллельные линии нарисованы, чтобы представить параллельные линии, фактически присутствующие на машине, мы называем это параллельной проекцией. Этот тип проекции широко используется чертежниками и архитекторами для создания чертежей и схем.
Если параллельные линии нарисованы, чтобы представить параллельные линии, фактически присутствующие на машине, мы называем это параллельной проекцией. Этот тип проекции широко используется чертежниками и архитекторами для создания чертежей и схем.
Ортографическая проекция — самая распространенная параллельная проекция из-за ее простоты. Он представлен с использованием трех представлений; вид спереди, вид сбоку и вид сверху. С точки зрения графики, вам нужно нарисовать объект в плоскости XY, плоскости YZ и плоскости ZX по отдельности.
Чтобы нарисовать вид спереди, вы просто представляете, как объект выглядит спереди. Не думайте о наклоне объекта, просто нарисуйте все, что он выглядит. Аналогичным образом можно нарисовать вид объекта сверху и сбоку (см. Изображение).
С помощью этой проекции можно получить точные измерения, поскольку все виды нарисованы в одном масштабе. Однако он не обеспечивает реалистичной проекции трехмерной модели; кроме того, чтобы почувствовать дизайн объекта, требуется несколько представлений.
Ортографическую проекцию можно нарисовать двумя способами: первой угловой проекцией и третьей угловой проекцией.Оба они имеют отличия только в позиционировании различных взглядов. В проекции под первым углом вид спереди помещается в первый квадрант; вид сверху и сбоку помещены на четвертый и второй квадранты соответственно. В проекции под третьим углом третий квадрант используется для обзора спереди; тогда как вид сверху и сбоку помещены на второй и четвертый квадранты.
Аксонометрическая проекция — это разновидность ортогональной проекции. Рисование объекта в этом методе несколько сложно, потому что
требуется только одно изображение для рисования трехмерной структуры объекта на плоской бумаге.Предположим, вы используете проектор, и объект расположен перед линиями проектора. Теперь вы можете увидеть изображение трехмерного объекта на двухмерной плоскости сразу за объектом. Эта проекция есть не что иное, как аксонометрическая проекция.
Аксонометрическая проекция подразделяется на три категории в зависимости от ориентации объекта.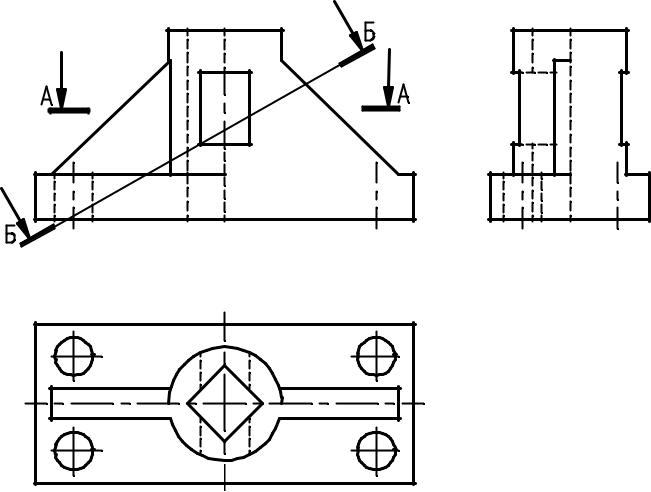
Первый и самый удобный вид — изометрический. В этом типе проекции углы между тремя осями равны. Как показано на диаграмме, если мы спроецируем куб на двумерную поверхность, вы увидите, что все три стороны AB, AC и AD равны.
Второй тип — диаметральная проекция, в которой только два угла между осями равны. Вы можете увидеть диаграмму, на которой только две стороны AB и AC равны.
Третья — триметрическая проекция, которую можно нарисовать с использованием трех осей, имеющих разные углы между ними. Это наиболее распространенный тип аксонометрической проекции, и объект можно разместить в любом месте по отношению к наблюдателю.
Все эти методы используются для проектирования мебели и конструкций. Аксонометрическая проекция лучше подходит для прямоугольных конструкций, чем для криволинейных объектов.
Наклонная проекция сравнительно проще, чем аксонометрическая. Для рисования любого объекта требуется только одно изображение и традиционное оборудование. В этом методе сначала нужно нарисовать вид спереди или вид сбоку, а затем нарисовать остальную часть объекта по отношению к нему.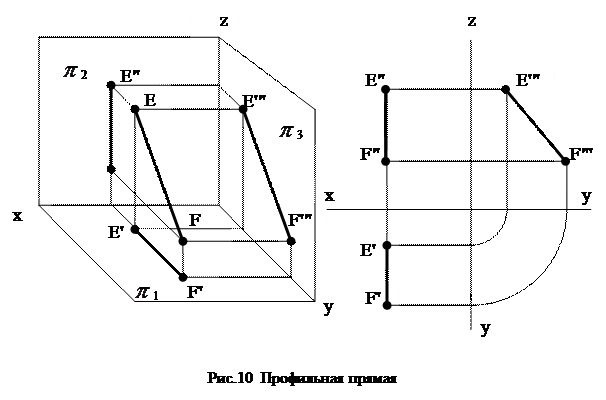
- Нарисуйте объект спереди или сбоку, как в ортогональной проекции.
- Измерения, проведенные в обратном направлении, должны быть в масштабе, равном половине фактического измерения.
- Линии, проведенные назад, должны иметь угол от 300 до 450; однако это удобно, если вы используете 450 углов.
Косая проекция делится на два типа в зависимости от масштабирования.
Первая — это кавалерийская проекция, в которой длина по осям X и Z нанесена в масштабе 1: 1, и для длины оси Y не требуется масштабирования. Его очень легко рисовать, и он часто используется для рисования объекта, когда вы можете использовать только свои руки, например, рисовать куб на доске. Чаще всего этот тип
используется в оборонительных сооружениях.
Другой тип — выступ для шкафа. В отличие от кавалерийской проекции, этот метод использует масштаб 2: 1 для рисования длин в направлениях X и Z соответственно. Кроме того, длины по оси Y также должны быть правильно масштабированы.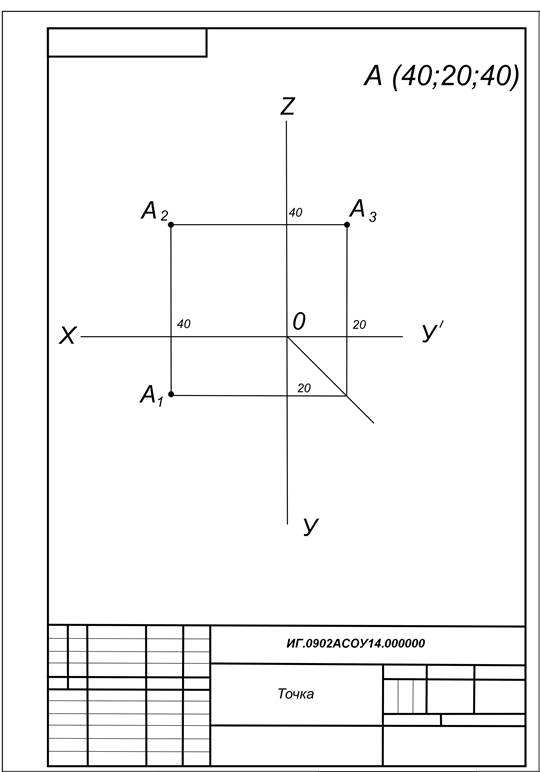 Эта проекция очень полезна в мебельной промышленности.
Эта проекция очень полезна в мебельной промышленности.
В перспективной проекции не используются параллельные линии для проецирования объекта, это проекция вдоль линий, выходящих из одной точки. Из-за этого ближняя часть кажется больше, чем дальняя.Это очень похоже на работу наших глаз в отношении восприятия глубины. Например, когда мы видим железнодорожную линию, кажется, что она сходится к одной точке, называемой точкой схода. При использовании этой проекции вид объекта кажется более реалистичным.
Вы можете использовать любой тип проекции для рисования объекта на плоской поверхности. Однако для этого требуется хорошее воображение, чтобы объект стал более реалистичным. Масштабирование должно выполняться правильно, чтобы избежать искажений. Всегда используйте зажимы, чтобы жестко закрепить чертежный лист на столе.Кроме того, используйте чистое оборудование, чтобы нарисовать аккуратное и чистое изображение.
Ссылки
Авиационные чертежи Методы иллюстрации — Ортографическая проекция
Прикладная геометрия
Геометрия — это раздел математики, который имеет дело с линиями, углами, фигурами и некоторыми предполагаемыми свойствами в пространстве.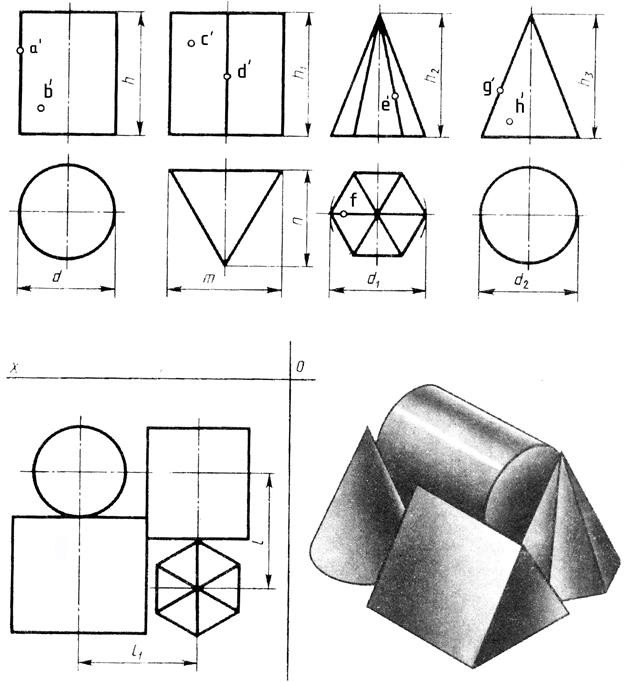 Прикладная геометрия, используемая в рисовании, использует эти свойства для точного и правильного графического представления объектов. В прошлом рисовальщики использовали различные инструменты с различными масштабами, формами и кривыми для создания своих рисунков.Сегодня компьютерные графические программы, показывающие чертежи, обеспечивают практически любой масштаб, форму и кривую, какие только можно вообразить, что устарели, и потребность в дополнительных инструментах отпала.
Прикладная геометрия, используемая в рисовании, использует эти свойства для точного и правильного графического представления объектов. В прошлом рисовальщики использовали различные инструменты с различными масштабами, формами и кривыми для создания своих рисунков.Сегодня компьютерные графические программы, показывающие чертежи, обеспечивают практически любой масштаб, форму и кривую, какие только можно вообразить, что устарели, и потребность в дополнительных инструментах отпала.
Для графической иллюстрации объектов используется ряд методов. Наиболее распространены орфографические проекции, графические рисунки, диаграммы и блок-схемы.
Ортогональные проекционные чертежи
Чтобы показать точный размер и форму всех частей сложных объектов, необходимо несколько видов.Это система, используемая в ортогональной проекции.
В ортогональной проекции существует шесть возможных видов объекта, поскольку все объекты имеют шесть сторон: переднюю, верхнюю, нижнюю, заднюю, правую и левую. На рис. 2‑12 (а) показан объект, помещенный в прозрачную коробку с шарнирами по краям. Проекции по бокам коробки — это виды, если смотреть прямо на объект с каждой стороны. Если очертания объекта нарисованы на каждой поверхности и коробка открыта, как показано на (b), а затем уложена плоско, как показано на (c), в результате получится ортогональная проекция с шестью ракурсами.
На рис. 2‑12 (а) показан объект, помещенный в прозрачную коробку с шарнирами по краям. Проекции по бокам коробки — это виды, если смотреть прямо на объект с каждой стороны. Если очертания объекта нарисованы на каждой поверхности и коробка открыта, как показано на (b), а затем уложена плоско, как показано на (c), в результате получится ортогональная проекция с шестью ракурсами.
Для четкого изображения объекта редко требуется показывать все шесть ракурсов; поэтому рисуются только те виды, которые необходимы для иллюстрации требуемых характеристик объекта. Чаще всего встречаются одно-, двух- и трехкурсные чертежи. Независимо от количества использованных видов, расположение обычно такое, как показано на рисунке 2-12, с видом спереди в качестве основного вида. Если показан вид справа, он будет справа от вида спереди. Если показан вид слева, он будет слева от вида спереди.Виды сверху и снизу, если они есть, будут показаны в их соответствующих положениях относительно вида спереди.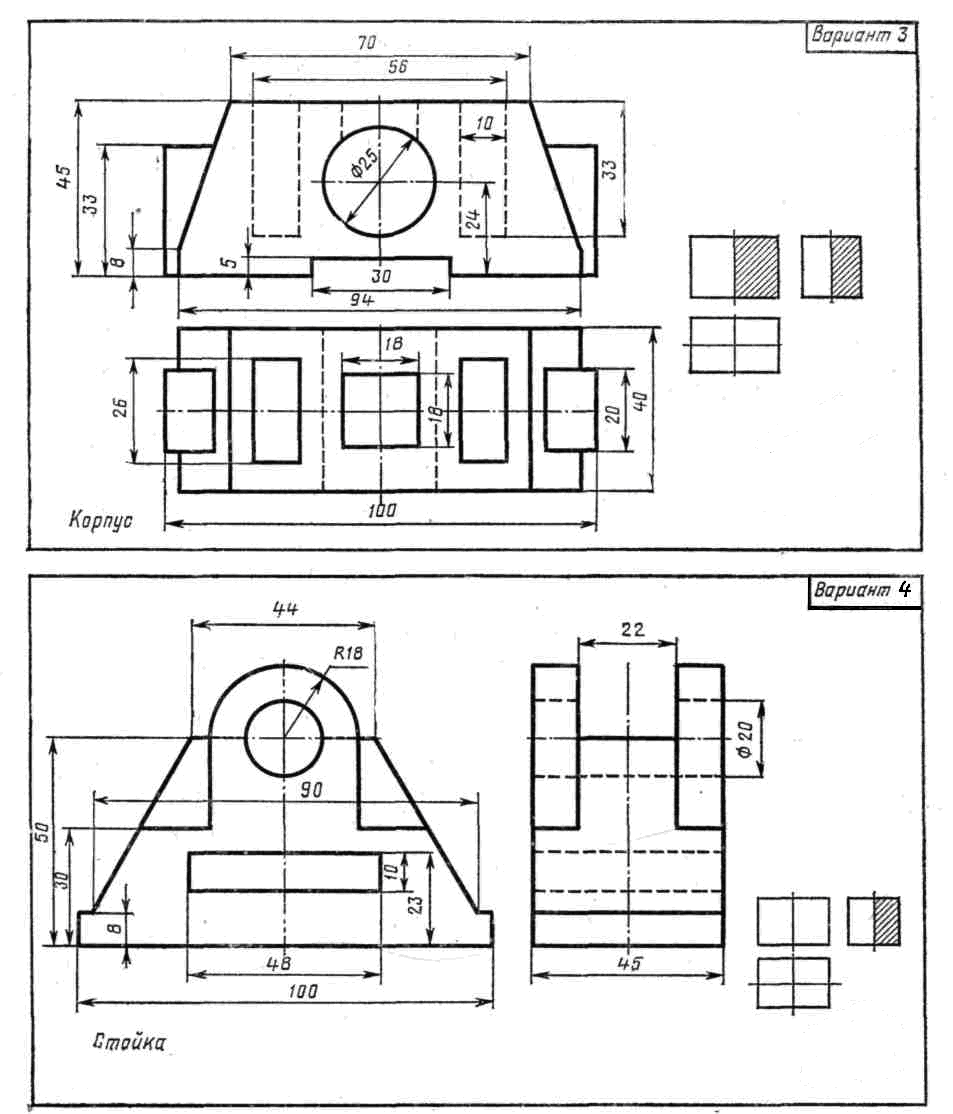
Чертежи с одним видом обычно используются для объектов одинаковой толщины, таких как прокладки, регулировочные шайбы и пластины. В размерных заметках указана толщина, как показано на Рисунке 2-13. Чертежи с одним видом также обычно используются для цилиндрических, сферических или квадратных деталей, если все необходимые размеры могут быть правильно показаны на одном виде.
Рисунок 2-13. Чертеж одного вида.Когда пространство ограничено и необходимо показать два вида, симметричные объекты часто представляются половинными видами, как показано на рис. 2-14.
Рисунок 2-14. Симметричный объект с внешней половиной вида.Чертежи самолета редко показывают более двух основных или полных видов объекта. Вместо этого обычно будет один полный вид и один или несколько подробных видов или видов в разрезе.
Полетный механик рекомендует
дополнительных обзоров — базовое чтение чертежей
- ДОПОЛНИТЕЛЬНОЕ ОБОРУДОВАНИЕ, ВИД СПЕРЕДИ
- ДОПОЛНИТЕЛЬНОЕ ОБОРУДОВАНИЕ ВИД СВЕРХУ
- ДОПОЛНИТЕЛЬНОЕ ОБОРУДОВАНИЕ, ВИД БОКОВОЙ
- ЭСКИЗ ДОПОЛНИТЕЛЬНЫЕ ВИДЫ
Когда объект имеет наклонную или наклонную поверхность, обычно невозможно показать наклонную поверхность на орфографическом чертеже без искажений.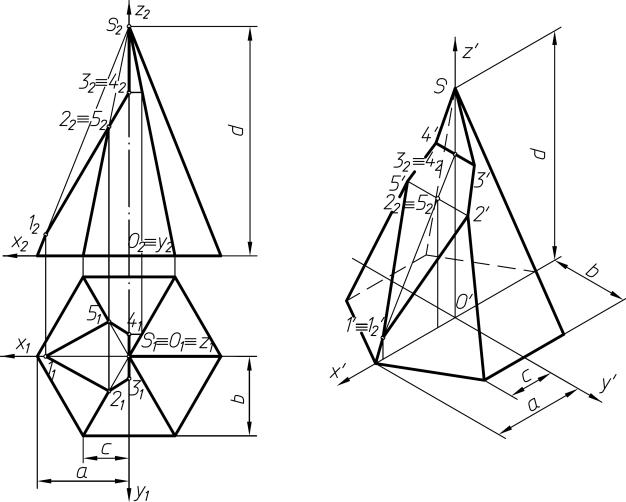 Чтобы представить более точное описание любой наклонной поверхности, обычно требуется дополнительный вид, известный как вспомогательный вид.
Чтобы представить более точное описание любой наклонной поверхности, обычно требуется дополнительный вид, известный как вспомогательный вид.
Вспомогательный вид — это просто «вспомогательный» вид, который показывает наклонную часть объекта, как она есть на самом деле. Получается, что проект. объект так, чтобы истинный размер и форма поверхности (или поверхностей) были видны такими, какие они есть на самом деле.
Вспомогательные виды обычно встречаются на многих типах промышленных чертежей.
Вспомогательное оборудование, вид спередиЕсть три основных типа вспомогательных видов.В первом типе вспомогательный вид проецируется из вида спереди трехразмерного (ортогонального) чертежа. Во втором и третьем типах чертежей вспомогательные виды проецируются сверху и сбоку.
Вот вспомогательный вид спереди простого объекта с наклонной поверхностью.
Обратите внимание, что линии проекции перпендикулярны наклонной поверхности первого вида, и что на вспомогательном виде показана только наклонная поверхность объекта. · Остальная часть объекта опущена, однако для ясности иногда показаны части прилегающих · поверхностей. Также обратите внимание, что наклонные поверхности видов сверху и сбоку укорачиваются из-за искажения, тогда как поверхность вспомогательного вида имеет истинный или фактический размер.
· Остальная часть объекта опущена, однако для ясности иногда показаны части прилегающих · поверхностей. Также обратите внимание, что наклонные поверхности видов сверху и сбоку укорачиваются из-за искажения, тогда как поверхность вспомогательного вида имеет истинный или фактический размер.
Чтобы набросать вспомогательный вид, вы начинаете с орфографии. видов объекта и добавьте линии проекции, перпендикулярные (90 ◦ ) наклонной поверхности, добавив опорную линию на любом удобном расстоянии от вида с наклонной поверхностью.
Затем расстояние CB на вспомогательном виде устанавливается такой же длины, как соответствующее расстояние на одном из ортогональных видов; в этом примере это вид сбоку. На этом вспомогательный вид завершен.
Вспомогательное оборудование, вид сверху Вспомогательный элемент вида сверху разработан так же, как вспомогательный элемент вида спереди, за исключением того, что вспомогательный элемент проецируется с вида сверху.
Будет ли проецироваться дополнительный вид спереди, сверху или сбоку, зависит от положения объекта или от того, какая поверхность объекта наклонена.В этом примере вид сверху наклонен. Следовательно, вспомогательный вид должен проецироваться с вида сверху.
Опять же, обратите внимание на то, что наклонные поверхности, показанные на видах спереди и сбоку, не показаны по истинной длине.
Вспомогательный вид сбокуВспомогательные элементы, вид сбоку, нарисованы так же, как вспомогательные элементы, вид спереди и сверху. Опять же, место проецирования вспомогательного вида зависит от положения объекта или от того, какая поверхность объекта наклонена.
Очевидно, что это очень простые примеры вспомогательных представлений, которые представлены, чтобы познакомить вас с концепцией дополнительных представлений.
По мере того, как объекты с наклонными поверхностями становятся более сложными, вспомогательные виды предоставляют средства представления объектов в их истинном размере и форме.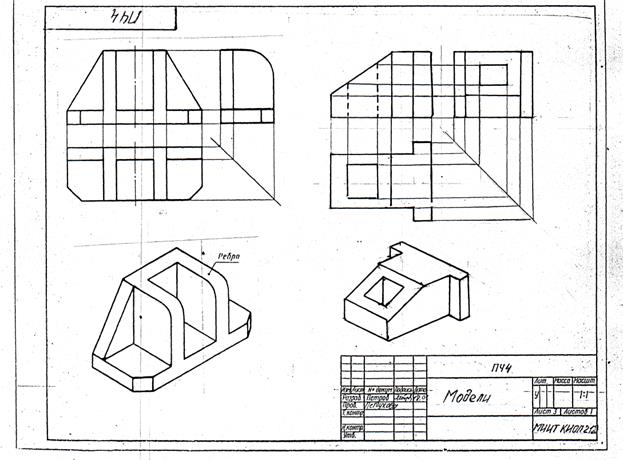
Для выполнения следующих задач требуется дополнительный вид. Нарисуйте необходимые вспомогательные виды в отведенных местах.
Практика рисования 1
Практика рисования 2
В этой задаче круглое отверстие центрируется на наклонной поверхности и просверливается сквозь объект. Отверстие в. вид спереди и сбоку из-за искажения. Он появится в его истинной форме на вспомогательном виде. Помните, что вспомогательная проявляется с точки зрения наклонной поверхности. Завершите вспомогательный вид.
Практика рисования 3
В этой задаче в объекте частично вырезано квадратное отверстие.Завершите вспомогательный вид.
Викторина
Указания: Завершите вспомогательный вид в отведенном месте.
Ортографическая проекция: определение и примеры — математический класс [видео 2021]
Различные виды
Обычно чертеж в ортогональной проекции состоит из трех разных видов: вид спереди, вид сверху и вид сбоку.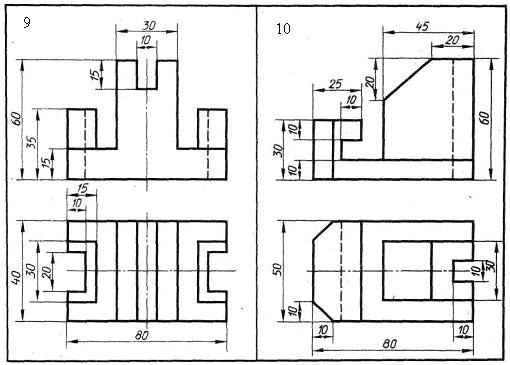 Иногда для ясности используется больше просмотров. Вид сбоку обычно является правой стороной, но если используется левая сторона, это отмечается на чертеже.
Иногда для ясности используется больше просмотров. Вид сбоку обычно является правой стороной, но если используется левая сторона, это отмечается на чертеже.
Чтобы нарисовать один из видов объекта, используйте линии для отображения изменений глубины. Например, рассмотрим этот объект с его правосторонней ортогональной проекцией:
Обратите внимание, что есть линии, в которых есть какие-либо изменения глубины в структуре; это изменяет правый боковой вид трехмерного объекта на двухмерное изображение. Следующие два изображения показывают вид спереди и вид сверху одного и того же объекта:
Размеры
В реальной ортогональной проекции все виды включаются на одну страницу.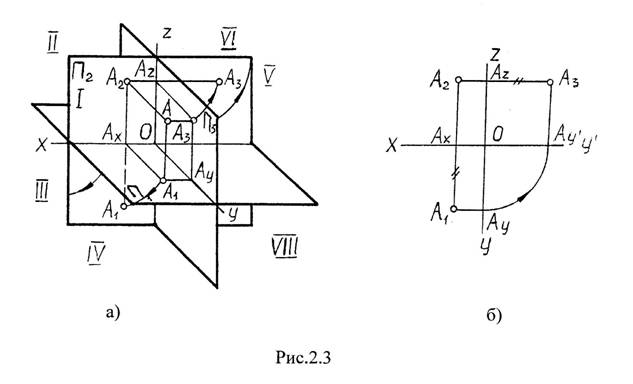 Обычно вид спереди находится в нижнем левом углу страницы, вид сверху — в верхнем левом углу, а вид справа — в правом нижнем углу. Для всех трех рисунков используется один и тот же масштаб, а их длина, ширина и высота выровнены.
Обычно вид спереди находится в нижнем левом углу страницы, вид сверху — в верхнем левом углу, а вид справа — в правом нижнем углу. Для всех трех рисунков используется один и тот же масштаб, а их длина, ширина и высота выровнены.
Иногда изометрический рисунок объекта включается в правый верхний угол. Изометрический чертеж — это вид объекта под углом, так что можно увидеть все различные виды объекта.Хотя изометрический рисунок двухмерный, он кажется трехмерным. Изометрический рисунок не нужно рисовать в масштабе или совмещать с тремя ортогональными проекционными рисунками.
Часто чертеж ортогональной проекции включает измерения размеров каждого из видов. Это позволяет человеку, создающему дизайн, масштабировать его по желанию дизайнера. На этом изображении показана фактическая ортогональная проекция показанного ранее объекта:
Пример
Рассмотрим другой пример.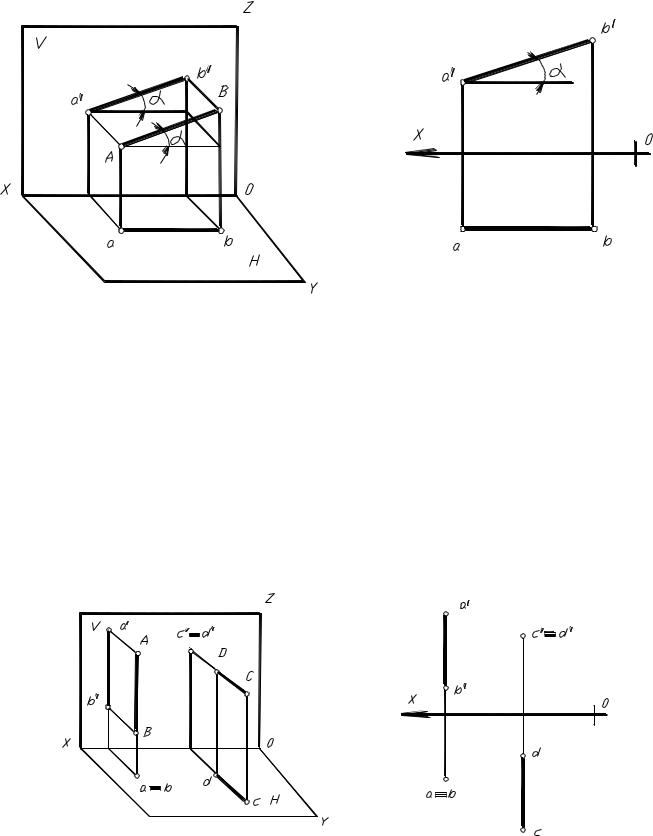 Предположим, вы хотите создать набор ступенек, по которым можно добраться до верхней полки шкафа. Вы знаете, что есть три ступеньки, и знаете, какой высоты они должны быть и размеры каждой ступени. Проблема только в том, что вы не можете построить их самостоятельно. Хорошей новостью является то, что вы можете создать ортогональную проекцию своих шагов и представить ее строителю, и они могут построить ее для вас на основе вашего ортогонального чертежа, показанного на изображении:
Предположим, вы хотите создать набор ступенек, по которым можно добраться до верхней полки шкафа. Вы знаете, что есть три ступеньки, и знаете, какой высоты они должны быть и размеры каждой ступени. Проблема только в том, что вы не можете построить их самостоятельно. Хорошей новостью является то, что вы можете создать ортогональную проекцию своих шагов и представить ее строителю, и они могут построить ее для вас на основе вашего ортогонального чертежа, показанного на изображении:
На изображении мы видим, что вам нужен набор ступеней, каждая из которых имеет высоту десять дюймов, глубину двенадцать дюймов и длину 36 дюймов.Строителю это не должно быть слишком сложно. Благодаря этому рисунку у вас будет свой набор шагов в кратчайшие сроки!
Резюме урока
Ортографические проекции — это двухмерные чертежи различных видов трехмерного объекта.