Комплексно сопряженная матрица: fkn+antitotal | студентам & программистам

комплексно-сопряженные матрицы : Высшая алгебра

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

sadomovalex	комплексно-сопряженные матрицы 16. 05.2007, 16:22
22/04/06 144 СПб (Тула)	добрый день пусть — комплексная матрица размера , , . Рассмотрим определители и . Но с другой стороны . Сравнивая выражения определителей, получаем что должно выполняться условие , т.е. — т.е. вещественная и мнимая части комплексной матрицы перестановочны между собой. Где тут ошибка

PAV	16. 05.2007, 16:39
Супермодератор 29/07/05 8248 Москва	А разве у нас уже из равенства определителей двух матриц следует равенство самих матриц?

sadomovalex	16. 05.2007, 16:55
22/04/06 144 СПб (Тула)	нет не следует, но смущает выражение под определителем и то что результаты в конечном счете равны, т.е.

RIP	16. 05.2007, 17:45
Заслуженный участник 11/01/06 3734	Если , вещественные матрицы, то . В частности, если , то определители равны. В нашем случае так и есть, поскольку

sadomovalex	17. 05.2007, 09:33
22/04/06 144 СПб (Тула)	спасибо RIP но остается следующий вопрос: пусть , и действительный матрицы и . Возможна ли ситуация, когда

Brukvalub	17. 05.2007, 09:46
Заслуженный участник 01/03/06 13626 Москва	Ответ очевиден — да. Достаточно прибавлять к диагональной матрице разные верхне-треугольные матрицы с нулями на главной диагонали

PAV	17. 05.2007, 09:48
Супермодератор 29/07/05 8248 Москва	Разумеется, может. Из самых общих соображений. Допустим, Вы зафиксировали матрицы и , а все элементов матрицы считаете независимыми неизвестными переменными. Равенство определителей — это одно линейное соотношение, которое (за исключением отдельных вырожденных ситуаций) уменьшит число переменных на 1. Проще говоря, из этого равенства можно выразить один элемент матрицы через остальные, после чего эти остальные переменных можно задавать как угодно. (Еще раз — за исключением отдельных вырожденных ситуаций, связанных с равенством некоторых выражений нулю).

Brukvalub	17.05.2007, 09:53
Заслуженный участник 01/03/06 13626 Москва	PAV писал(а): . ..это одно линейное соотношение… Наверное, правильнее будет говорить об одном нелинейном соотношении?

PAV	17.05.2007, 10:01
Супермодератор 29/07/05 8248 Москва	Ну да, конечно, я не очень удачно выразился. Я имел в виду, что это равенство одно. Если уже фиксированы все элементы матрицы , кроме одного, то мы имеем простое линейное соотношение на этот один оставшийся элемент. Добавлено спустя 1 минуту 48 секунд: Которое может при неудачном выборке остальных оказаться вырожденным, т.е. коэффициент при этом одном параметре равен нулю. Тогда плохо, ибо от него ничего не зависит. В остальных случаях все хорошо, значение этого параметра определяется однозначно.

sadomovalex	17.05.2007, 10:36
22/04/06 144 СПб (Тула)	спасибо за ответы, с темой разобрались

lt3km	17. 05.2007, 14:43
10/12/05 43 МГУ	Тут есть еще одно рассуждение, если вспомнить, что матрицы это координаты векторов во внешней алгебре, то можно получить формулы сложения определителей по последней строке в случае когда матрицы отличаются только в одной строке.

Brukvalub	17. 05.2007, 14:52
Заслуженный участник 01/03/06 13626 Москва	lt3km писал(а): …можно получить формулы сложения определителей по последней строке в случае когда матрицы отличаются только в одной строке. Так все и так знают, что определитель является полилинейной и кососимметрической функцией строк (столбцов) матрицы. Это доказывается совсем по-детски, без привлечения всяких там внешних или внутренних алгебр.

bot	17. 05.2007, 15:18
Заслуженный участник 21/12/05 5819 Новосибирск	Brukvalub писал(а): Так все и так знают, что определитель является полилинейной и кососимметрической функцией строк (столбцов) матрицы. Это доказывается совсем по-детски, без привлечения всяких там внешних или внутренних алгебр. А также с добавлением ещё одного свойства может служить системой аксиом для задания определителя, при этом достаточно рассматривать его только лишь как функцию столбцов (или, наоборот, строк).

lt3km	17.05.2007, 17:56
10/12/05 43 МГУ	Да, согласен. Забыл первый курс

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 14 ]

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Найти:

Решение в MathCAD

множение двух векторов V1 и V2;
M*V

M*V

Умножение матрицы M на вектор V;
M1*M2

M1*M2

Умножение двух матриц M1 и M2;
V/Z

V/Z

Деление вектора V на скаляр Z;
M/Z

M/Z

Деление матрицы M на скаляр Z;
M-1

M^-1

Обращение матрицы M;
Mn

M^n

Возведение матрицы M в степень n;
| V |

Ѕ V

Вычисление квадратного корня из μV;
| M|

Ѕ M

Вычисление определителя матрицы M;
VT

V Ctrl !

Транспонирование вектора V;
MT

M Ctrl !

Транспонирование матрицы M;
V1xV2

V1 Ctrl* V2

Кросс – умножение двух векторов V1 и V2;
V

V ”

Получение комплексно – сопряженного вектора;
M

M ”

Получение комплексно – сопряженной матрицы;
?V

Alt $ V

Вычисление суммы элементов вектора V;
V

V Ctrl –

Векторизация вектора V;
M

M Ctrl –

Векторизация матрицы M;
M

M Ctrl ^n

Выделение n–го столбца матрицы M;
Vn

V [ n

Выделение n–го элемента вектора V;
Mm,n

M [(m,n)

Выделение элемента (m, n) матрицы M.

Под понятием “векторизация” подразумевается одновременное проведение математических операций в их скалярном значении над всеми элементами вектора или матрицы, помеченными векторизации. Это можно понимать и как возможность параллельных вычислений.
Если А и В – векторы, то А*В даёт скалярное произведение этих векторов. Но то же произведение под знаком векторизации создает новый вектор, каждый j-й элемент которого есть произведение j –х элементов векторов А и В. Векторизация позволяет использовать скалярные операторы и функции с массивами.
2.2 Векторные и матричные функции.

Существует также ряд встроенных векторных и матричных функций. Приведем векторные функции, входящие в систему Math CAD:
lenght (V)

возвращает длину вектора;
last (V)

возвращает индекс последнего элемента;
max (V)

возвращает максимальный по значению элемент;
min (V)

возвращает минимальный по значению элемент;
Re (V)

возвращает вектор действительных частей вектора с комплексными элементами;
Im (V)

возвращает вектор мнимых частей вектора с комплексными элементами;
ε (i, j, k)

полностью асимметричный тензор размерности три.

<< Назад   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 Вперед >>

Conjugate transpose

Марко Табога, доктор философии

В матричной алгебре часто бывает, что нам нужно и транспонировать, и взять комплексное сопряжение матрицы. Результат последовательного применения эти две операции называются сопряженным транспонированием (или эрмитовым транспонированием). В математической литературе для обозначения этого двойного числа используются специальные символы. операция.

Содержание

1. Definition

2. Symbols

3. Properties

4. Hermitian matrix

5. Solved exercises

   1. Exercise 1

   2. Exercise 2

Definition

Сопряженное транспонирование матрицы это матрица определенный где обозначает транспонирование, а черта над чертой обозначает комплексное сопряжение.

Помните, что комплексно-сопряженная матрица получается путем взятия комплексное сопряжение каждого из его элементов (см. лекцию о сложные матрицы).

В определении мы использовали тот факт, что порядок транспонирования и сопряжения не имеет значения: является ли знак мнимого часть записи о переключается до или после перемещения записи в другую позицию не изменить конечный результат.

Пример Определите матрицу Его сопряженный остров его сопряженное транспонирование

Символы

Несколько различных символов используются в литературе в качестве альтернативы символ, который мы использовали до сих пор.

Наиболее распространенными альтернативами являются символ (для Эрмитов):

и кинжал:

Свойства

Свойства сопряженной транспозиции являются непосредственными следствиями свойства транспонирования и сопряжения. Поэтому перечислим некоторые из них без доказательств.

Для любых двух матриц а также таким образом, что описанные ниже операции корректно определены и любой скаляр , у нас есть это

Эрмитова матрица

Матрица, равная своей сопряженной транспонированной, называется эрмитовой (или самосопряженный). Другими словами, эрмитов тогда и только тогда если

Пример Рассмотрим матрицу затем его сопряженное транспонирование как есть следствие является эрмитовым.

Обозначим через в -й запись и по в -й запись . По определению сопряженного транспонирования мы есть

Следовательно, эрмитов тогда и только тогда если для каждый а также , откуда также следует, что диагональные элементы должны быть действительными: их комплексная часть должна быть равна нулю, чтобы удовлетворить

Решенные упражнения

Ниже вы можете найти несколько упражнений с поясненными решениями.

Упражнение 1

Пусть вектор быть определен по

Вычислить продукт

Раствор

Конъюгат, транспонированный это

и продукт

Упражнение 2

Пусть матрица быть определен по

Вычислите его сопряженное транспонирование.

Решение

У нас есть что

Как цитировать

Пожалуйста, указывайте как:

Taboga, Marco (2021). «Сопряженное транспонирование», Лекции по матричной алгебре. https://www.statlect.com/matrix-алгебра/conjugate-transpose.

Конъюгированное транспонирование

Марко Табога, доктор философии

В матричной алгебре часто бывает, что нам нужно и транспонировать, и взять комплексное сопряжение матрицы. Результат последовательного применения эти две операции называются сопряженным транспонированием (или эрмитовым транспонированием). В математической литературе для обозначения этого двойного числа используются специальные символы. операция.

Table of contents

1. Definition

2. Symbols

3. Properties

4. Hermitian matrix

5. Solved exercises

   1. Exercise 1

   2. Exercise 2

Определение

Сопряженное транспонирование матрицы это матрица определенный где обозначает транспонирование, а черта над чертой обозначает комплексное сопряжение.

Помните, что комплексно-сопряженная матрица получается путем взятия комплексное сопряжение каждого из его элементов (см. лекцию о сложные матрицы).

В определении мы использовали тот факт, что порядок транспонирования и сопряжения не имеет значения: является ли знак мнимого часть записи о переключается до или после перемещения записи в другую позицию не изменить конечный результат.

Пример Определите матрицу Его сопряженный остров его сопряженное транспонирование

Символы

Несколько различных символов используются в литературе в качестве альтернативы символ, который мы использовали до сих пор.

Наиболее распространенными альтернативами являются символ (для Эрмитов):

и кинжал:

Свойства

Свойства сопряженной транспозиции являются непосредственными следствиями свойства транспонирования и сопряжения.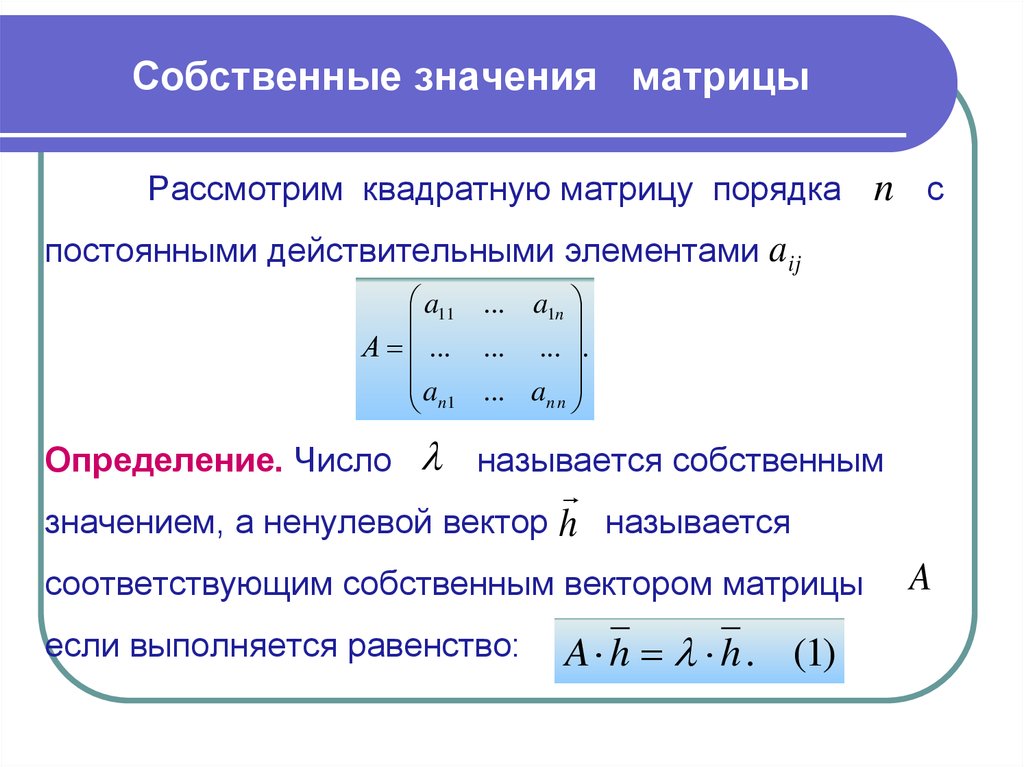 Поэтому перечислим некоторые из них без доказательств.

Для любых двух матриц а также таким образом, что описанные ниже операции корректно определены и любой скаляр , у нас есть это

Эрмитова матрица

Матрица, равная своей сопряженной транспонированной, называется эрмитовой (или самосопряженный). Другими словами, эрмитов тогда и только тогда если

Пример Рассмотрим матрицу затем его сопряженное транспонирование как есть следствие является эрмитовым.

Обозначим через в -й запись и по в -й запись . По определению сопряженного транспонирования мы есть

Следовательно, эрмитов тогда и только тогда если для каждый а также , откуда также следует, что диагональные элементы должны быть действительными: их комплексная часть должна быть равна нулю, чтобы удовлетворить

Решенные упражнения

Ниже вы можете найти несколько упражнений с поясненными решениями.