Задача №1. Перевод из одной системы в другую, сравнение чисел в различных системах.
Автор материалов — Лада Борисовна Есакова.
Системы счисления и их разновидности.
Система счисления – это способ представления, записи чисел с помощью письменных знаков. Количество этих самых знаков (цифр), используемых для записи чисел, называется основанием системы счисления.
Различных систем счисления у разных народов существовало великое множество. Но все их можно поделить на непозиционные и позиционные. Позиционные системы в свою очередь подразделяются на однородные и смешанные.
1. Непозиционные системы счисления.
В непозиционных системах счисления число, обозначаемое цифрой, не зависит от положения цифры в записи числа.
Самым простым примером непозиционной системы счисления является единичная (унарная) система счисления. Это запись числа с помощью повторения зарубок на дощечке или узелков на веревке. Все зарубки, узелки или другие «цифры» абсолютно одинаковы, а потому их порядок не имеет значения, число получается простым суммированием количества символов.
Унарной системой счисления до сих пор пользуются маленькие дети, показывая количество на пальцах.
Еще одной используемой до сих пор почти непозиционной системой счисления является Римская:
Она названа почти непозиционной, потому что в Римской системе, кроме обычного сложения цифр в числе, действует правило: если младшая цифра стоит слева от старшей, она вычитается из суммы.
Т.е. число , а число
Непозиционных систем счисления известно очень много, но мы завершим на этом их рассмотрение. Использование непозиционных систем неудобно, а для очень больших чисел практически невозможно, и к тому же нет возможности записать дроби.
2. Позиционные системы счисления.
В позиционных системах счисления число, обозначаемое цифрой, зависит от положения цифры в записи числа.
Самой популярной позиционной системой является, конечно же, десятичная.
Мы видим, что числа 15 и 51 имеют совсем разные значения, хотя состоят из одних и тех же цифр. Разница обусловлена положением цифры в числе.
Разница обусловлена положением цифры в числе.
Но десятичная система ничем не лучше и не хуже другой позиционной системы, она просто привычная. Число 10 выбрано основанием по количеству пальцев на двух руках (для удобства счета). Однако, в Китае популярной была пятиречная система счисления (по количеству пальцев на одной руке), а двадцатиричная система использовалась у Ацтеков, Майя и некоторых народов Африки (по количеству пальцев на ногах и руках).
Еще одной известной позиционной системой счисления является двенадцатиричная (считали фаланги пальцев (кроме большого) на руке. Элементы двенадцатиричной системы сохранились в Англии: 1 фут = 12 дюймов, 1 шиллинг = 12 пенсов.
Ну и, наконец, незаменимая в наш компьютерный век двоичная система. Почему именно двоичная? Да потому что у компьютера только 2 «пальца», точнее два состояния: «есть ток», «нет тока».
2.1. Однородные системы счисления.
В однородной системе в каждой позиции числа может находиться любая цифра. Примером может быть запись числа в любой позиционной системе счисления (десятичной, двоичной и пр.). Т.е. когда мы пишем число в десятичной системе, в любой позиции мы можем написать цифру от 0 до 9.
Примером может быть запись числа в любой позиционной системе счисления (десятичной, двоичной и пр.). Т.е. когда мы пишем число в десятичной системе, в любой позиции мы можем написать цифру от 0 до 9.
2.2. Смешанные системы счисления.
В смешанной системе счисления набор используемых цифр может отличаться в зависимости от позиции. В качестве примера удобно рассмотреть запись времени в формате ЧЧ.ММ.СС (часы.минуты.секунды). В качестве часов может быть использовано число от 00 до 23, в качестве минут и секунд – число от 00 до 59.
Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита.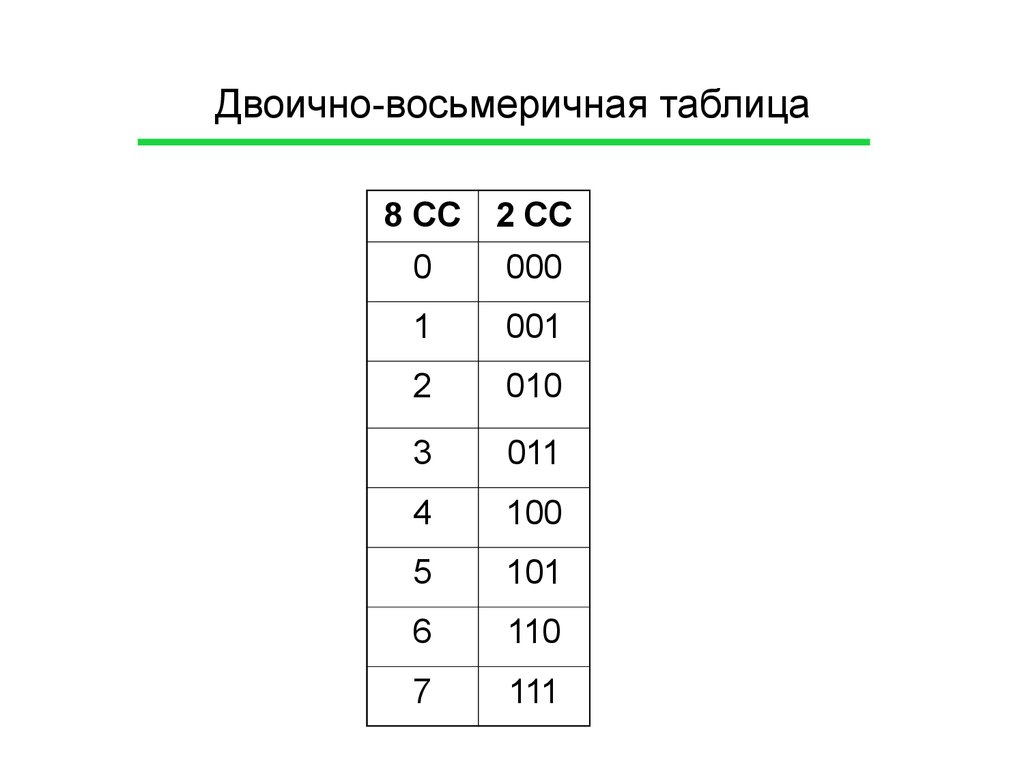 Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания.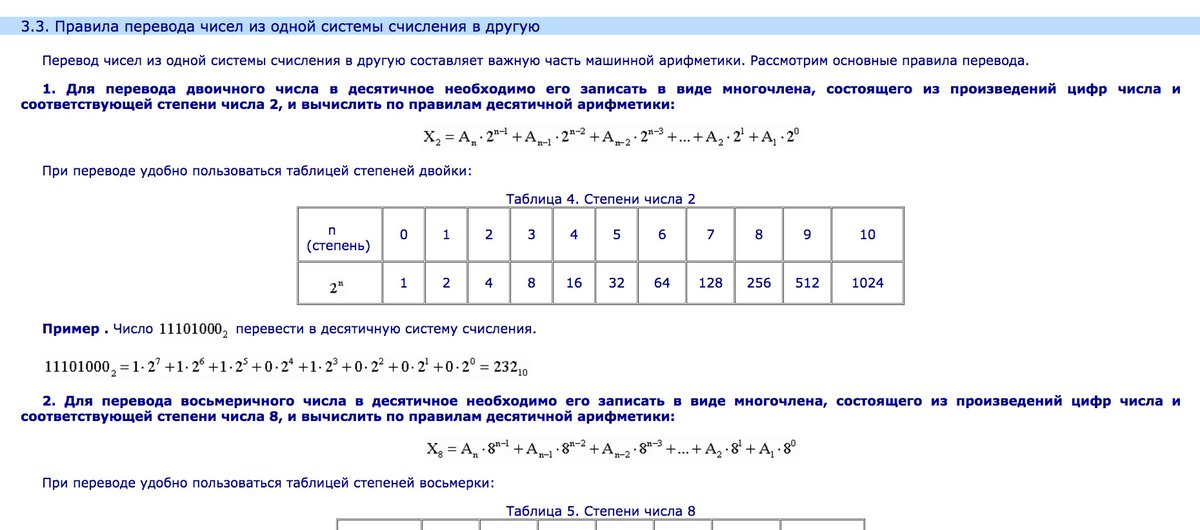 В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т. е.
е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Десятичные дроби и смешанные числа в разных системах счисления.
Автор — Лада Борисовна Есакова.
Перевод целых чисел из одной системы счисления в другую обычно не вызывает проблем. А вот необходимость перевести десятичную дробь или смешанное число (число с целой и дробной частью) из системы в систему часто ставит в тупик даже сильных учеников.
1. Перевод смешанного числа в десятичную систему счисления из любой другой.
Для перевода смешанного числа в десятичную систему из любой другой следует пронумеровать разряды числа, начиная с нуля, справа налево от младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.
Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.
Пример 1.
Переведите число 105,4 из восьмеричной системы в десятичную.
Решение:
Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :
Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа:
Ответ:
2. Перевод десятичных дробей из десятичной системы счисления в любую другую.
Для перевода десятичной дроби из десятичной системы в любую другую следует умножать дробь, а затем дробные части произведений, на основание новой системы пока дробная часть не станет равной 0 или до достижения указанной точности. Затем целые части выписать, начиная с первой.
Пример 2
Переведите десятичное число 0,816 в двоичную систему с точностью до сотых.
Решение:
Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на 2 и выписываем целые части, начиная с первой:
Ответ:
Пример 3.
Переведите десятичное число 0,8125 в восьмеричную систему.
Решение:
Умножаем дробь 0,8125, а затем дробную часть произведения (0,5) на 8 и выписываем целые части, начиная с первой:
Ответ:
3. Перевод смешанных чисел из десятичной системы счисления в любую другую
Если необходимо перевести смешанное число из десятичной системы в любую другую, следует перевести целую и дробную части, а затем записать, разделив десятичной запятой.
Пример 4.
Сколько единиц в двоичной записи десятичного числа 14,125?
Решение:
Переведем целую часть числа в двоичную систему:
Переведем дробную часть числа в двоичную систему:
Соединим целую и дробную части:
14,12510 = 1110,0012
Количество единиц равно 4.
Ответ: 4
Перевод чисел из разных систем счисления с помощью MS Excel
14576
Осуществить перевод чисел из разных систем исчисления можно различными способами.
Как бы там ни было, в рамках данной статьи рассмотрим способ перевода из разного рода систем счисления с помощью табличного процессора MS Excel. С помощью MS Excel существует возможность осуществить перевод из:
восьмеричной в двоичную с помощью функции ВОСЬМ.В.ДВ (OCT2BIN);
восьмеричной в десятичную с помощью функции ВОСЬМ.В.ДЕС (OCT2DEC);
восьмеричной в шестнадцатеричную с помощью функции ВОСЬМ.В.ШЕСТН (OCT2HEX);
двоичной в восьмеричную с помощью функции ДВ.В.ВОСЬМ (BIN2OCT);
двоичной в десятичную с помощью функции ДВ.В.ДЕС (BIN2DEC);
двоичной в шестнадцатеричную с помощью функции ДВ.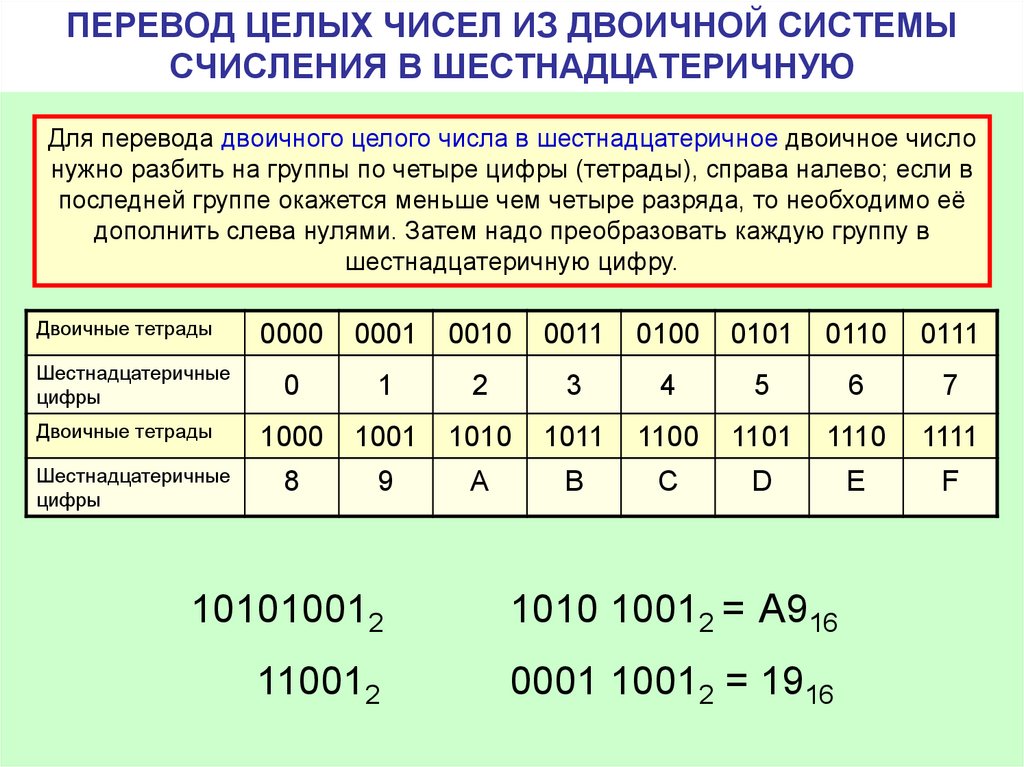 В.ШЕСТН (BIN2HEX);
В.ШЕСТН (BIN2HEX);
десятичной в восьмеричную с помощью функции ДЕС.В.ВОСЬМ (DEC2OCT);
десятичной в двоичную с помощью функции ДЕС.В.ДВ (DEC2BIN);
десятичной в шестнадцатеричную с помощью функции ДЕС.В.ШЕСТН (DEC2HEX);
шестнадцатеричной в восьмеричную с помощью функции ШЕСТН.В.ВОСЬМ (HEX2OCT);
шестнадцатеричной в двоичную с помощью функции ШЕСТН.В.ДВ (HEX2BIN);
шестнадцатеричной в десятичную с помощью функции ШЕСТН.В.ДЕС (HEX2DEC);
Перевод из восьмеричной системы в двоичную
[spoiler]Поскольку основание восьмеричной системы является степенью для двоичной, то перевод между этими двумя системами достаточно тривиальная задача. Достаточно осуществить перевод каждой цифры из восьмеричной системы в двоичную справа на лево. Соответствие цифр двух система представлено в таблице.
| Двоичная система | Восьмеричная система |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Например, 235 в восьмеричной системе равно: 5=101, 3=011, 2=010 и результат равен 010011101 или 10011101 (начальные нули в двоичной системе можно опустить).
Для осуществления данного преобразования с помощью MS Excel следует воспользоваться функцией ВОСЬМ.В.ДВ или OCT2BIN, если у Вас установлена англоязычная версия MS Excel.
Результатом будет одно и то же число, просто оно может быть записано с нулями вначале или без них.[/spoiler]
Перевод из восьмеричной системы в десятичную
[spoiler]Для перевода из восьмеричной системы в десятичную, число необходимо представить в виде суммы произведений степеней основания восьмеричной системы счисления на соответствующие цифры в разрядах восьмеричного числа.
Например, число 235 будет равняться = 5*8(в нулевой степени) + 3*8(в первой степени) + 2*8(во второй степени) = 5*1+3*8+2*64=157
Для осуществления данного преобразования с помощью MS Excel следует воспользоваться функцией ВОСЬМ.В.ДЕС или OCT2DEC, если у Вас установлена англоязычная версия MS Excel.
[/spoiler]
Перевод из восьмеричной системы в шестнадцатеричную
[spoiler]Наиболее простой способ «ручного» перевода чисел из восьмеричной системы в шестнадцатеричную состоит в том, чтобы с начала перевести число в двоичную, а затем уже в шестнадцатеричную системы счисления.
С помощью MS Excel такой перевод предельно прост, как, впрочем, и остальные варианты, достаточно воспользоваться функцией ВОСЬМ.В.ШЕСТН или OCT2HEX, если у Вас установлена англоязычная версия MS Excel.
[/spoiler]
Перевод из двоичной системы в восьмеричную
[spoiler]Достаточно простой перевод. Разбиваем двоичное число на триады начиная справа, если в последней триаде недостает цифр, просто дописываем нули. Например, переведем число 1001001. Для удобства представим его как 001 001 001. После перевода триад, согласно таблице:
| Двоичная система | Восьмеричная система |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
В восьмеричной системе получаем число: 111.
Перевод с помощью MS Excel следует воспользоваться функцией ДВ.В.ВОСЬМ или BIN2OCT, если работа ведется в англоязычной версии офиса.
[/spoiler]
Перевод из двоичной системы в десятичную
[spoiler]Для такого перевода необходимо число в двоичной системе счисления представить в виде суммы произведения степеней основания (начиная с нуля) на соответствующие цифры в разрядах двоичного числа.
Переведем число 001001001 в десятичную систему счисления. 1*2(в степени 6)+ 0*2(в степени 5)+ 0*2(в степени 4)+ 1*2(в степени 3)+ 0*2(в степени 2)+ 0*2(в степени 1)+ 1*2(в степени 0) = 64+0+0+8+0+0+1 = 73.
Перевод с помощью MS Excel следует воспользоваться функцией ДВ.В.ДЕС или BIN2DEC, если работа ведется в англоязычной версии офиса.
[/spoiler]
Перевод из двоичной системы в шестнадцатеричную
[spoiler]Перевод из двоичной системы счисления в шестнадцатеричную несколько схож из переводом из двоичной в восьмеричную, однако, в этом случае число в двоичной системе счисления необходимо разбивать на тетрады, т. е. кодирование осуществляется четырьмя битами, а не тремя. И перевод производится согласно таблице:
е. кодирование осуществляется четырьмя битами, а не тремя. И перевод производится согласно таблице:
| Двоичная система | Шестнадцатеричная система |
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Переведем число 1001001, предварительно запишем его как: 0100 1001, что равняется 49.
Перевод с помощью MS Excel следует воспользоваться функцией ДВ.В.ШЕСТН или BIN2HEX, если работа ведется в англоязычной версии офиса.
[/spoiler]
Перевод из десятичной системы в восьмеричную
[spoiler]Для осуществления данного перевода необходимо произвести операцию деления и пошагового перевода в соответствии с алгоритмом:
- Делится десятичное число на 8. Частное от деления остается для следующего шага, а остаток от деления записывается как бит числа в восьмеричной системе счисления (справа на лево).
- Если частное не равно 0, то повторяется первый шаг, однако в качестве делимого берется уже частное. Новый остаток записывается в число в восьмеричной системе счисления справа на лево.
Шаги выполнять до тех пор, пока частное не станет равно 0, а остаток от деления меньше 8.
Для примера возьмем число 157.
157/8 = частное 19, остаток 5
19/8 = частное 2, остаток 3
2/8=частное 0, остаток 2
Итого, записав справа на лево числа, получаем: 235.
Перевод с помощью MS Excel следует воспользоваться функцией ДЕС.В.ВОСЬМ или DEC2OCT, если работа ведется в англоязычной версии офиса.
[/spoiler]
Перевод из десятичной системы в двоичную
[spoiler]Перевод осуществляется путем деления числа на 2 и перевода в соответствии с алгоритмом:
- Делится десятичное число на 2. Частное от деления остается для следующего шага, а остаток от деления записывается как бит числа в двоичной системе счисления (справа на лево).
- Если частное не равно 0, то повторяется первый шаг, однако в качестве делимого берется уже частное. Новый остаток записывается в двоичное число справа на лево.
Процедура выполняется до тех пор пока частное не станет равно 0, а остаток от деления – 1.
Возьмем число 157.
157/2 = частное 78, остаток 1
78/2 = частное 39, остаток 0
39/2 = частное 19, остаток 1
19/2 = частное 9, остаток 1
9/2= частное 4, остаток 1
4/2 =частное 2, остаток 0
2/2 = частное 1, остаток 0
1/2 = частное 0, остаток 1
Итог: 10011101
Для осуществления перевода с помощью MS Excel следует воспользоваться функцией ДЕС.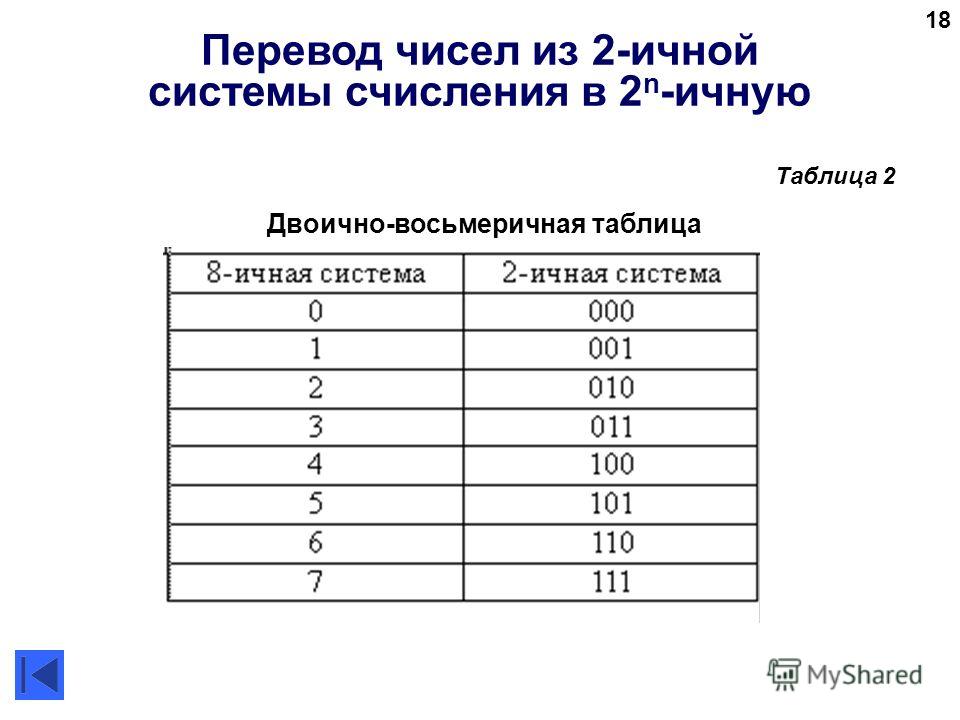 В.ДВ или DEC2BIN, если работа ведется в англоязычной версии офиса.
В.ДВ или DEC2BIN, если работа ведется в англоязычной версии офиса.
[/spoiler]
Перевод из десятичной системы в шестнадцатеричную
[spoiler]Алгоритм перевода из десятичной системы в шестнадцатеричную аналогичен уже описанным выше алгоритмам перевода в двоичную или восьмеричную систему, однако в качестве делителя здесь следует брать число 16, итак:
- Делится десятичное число на 16. Частное от деления остается для следующего шага, а остаток от деления записывается как бит числа в двоичной системе счисления (справа на лево).
- Если частное не равно 0, то повторяется первый шаг, однако в качестве делимого берется уже частное. Новый остаток записывается в шестнадцатеричное число справа на лево.
Процедура выполняется до тех пор пока частное не станет равно 0, а остаток от деления – меньше 16.
Не лишнем будет привести таблицу соответствия цифр в десятичной и шестнадцатеричной системе счисления:
| Десятичная система | Шестнадцатеричная система |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
Число 157 в шестнадцатеричной системе будет:
157/16 = частное 9 остаток 13
9/16 = частное 0 остаток 9
И ответ 9D (поскольку 13 соответствует D).
Для осуществления перевода с помощью MS Excel следует воспользоваться функцией ДЕС.В.ШЕСТН или DEC2HEX, для англоязычной версии офиса.
[/spoiler]
Перевод из шестнадцатеричной системы в восьмеричную
[spoiler]При ручном переводе чисел из шестнадцатеричной системы в восьмеричную число переводят в двоичную систему счисления, а затем уже в восьмеричную в соответствии с описанными здесь правилами.
Для осуществления перевода с помощью MS Excel следует воспользоваться функцией ШЕСТН.В.ВОСЬМ или HEX2OCT, для англоязычной версии офиса.
Внимание! В формуле числа в шестнадцатеричной системе счисления следует записывать в кавычках, т.к. в противном случае число будет восприниматься как ссылка на ячейку.[/spoiler]
Перевод из шестнадцатеричной системы в двоичную
[spoiler]В двоичную систему счисления перевод крайне прост и аналогичен переводу в восьмеричную систему счисления, однако, здесь числа переводятся справа налево и дополняются до 4 разрядов в соответствии с таблицей:
| Двоичная система | Шестнадцатеричная система |
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Например, число 9D будет равно: 10011101.
Для осуществления перевода с помощью MS Excel следует воспользоваться функцией ШЕСТН.В.ДВ или HEX2BIN, для англоязычной версии офиса.
Внимание! В формуле числа в шестнадцатеричной системе счисления следует записывать в кавычках, т.к. в противном случае число будет восприниматься как ссылка на ячейку.[/spoiler]
Перевод из шестнадцатеричной системы в десятичную
[spoiler]Перевод производится по аналогии с переводами из восьмеричной и двоичной системы, однако, в данном случае для степеней будет основания будет число 16. Т.е. десятеричное число представляется в виде суммы произведения цифр шестнадцатеричного числа на 16 в степени разряда, начиная с 0. Таблица соответствия чисел десятичной и шестнадцатеричной систем представлена ниже.
| Десятичная система | Шестнадцатеричная система |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
Перевод числа 9D равняется = 9*16 (в степени 1) + 13* 16 (в степени 0) = 9*16+13*1 = 157.
Для осуществления перевода с помощью MS Excel следует воспользоваться функцией ШЕСТН.В.ДЕС или HEX2DEC, для англоязычной версии офиса.
[/spoiler]
Еще записей в тему?
Если честно, некоторые могут быть не свежие:)
БОЛЬШЕ МАТЕРИАЛОВ
Как перевести числа из восьмеричной системы счисления в двоичную. Как перевести числа из восьмеричной системы счисления в двоичную Перевод чисел из любой системы счисления в десятичную систему счисления
Автор Eternal aum задал вопрос в разделе Другие языки и технологии
перевод чисел в двоичную,восьмеричную системы счисления и получил лучший ответ
Ответ от Емил Иванов[гуру]
// Посмотри ответ пользователя Gennady!
// Задача: 100 (10) =? (2).
(* «Перевести 100 (из 10-чной) в 2-ичную систему счисления! «,
я случайно услышал, когда я прошел мимо уличного стола кафе «Markrit»,
(у угла улиц «Патриарх Евтимий» и «Князь Борис» в Софии) 05 июня 2009.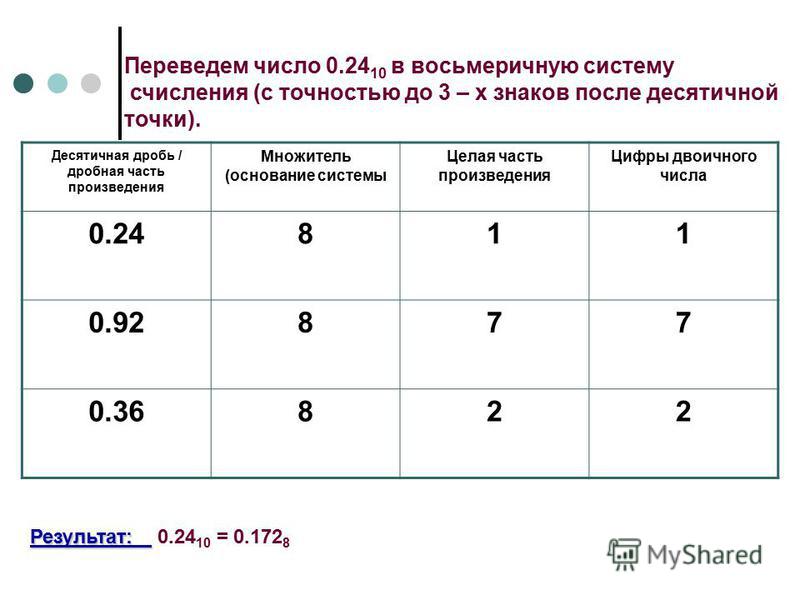 *)
*)
Решение (которое я говорил вслух, потому что мне пришлось ждать много проезжающих мимо машин вдоль бульвара) :
І способ — число 100 делится на 2 (пока не получиться 1), а остатки от деления формируют число снизу-вверх (слева-направо) .
100:2 = 50 I 0
50:2 = 25 I 0
25:2 = 12 I 1
12:2 = 6 I 0
6:2 = 3 І 0
3:2 = 1 I 1
1:2 = 1 I 1
100 (10) = 1100100 (2)
II способ — число разлагается по степеням числа 2, начиная с максимальной меньшей числа 100 степени (числа 2).
(Если степени числа 2 заранее не известны, можно исчислить:
2 на 7 степени 128
2 на 6 степени 64
2 на 5 степени 32
2 на 4 степени 16
2 на 3 степени 8
2 на 2 степени 4
2 на 1 степени 2
2 на 0 степени 1).
1. 64 64 + 32 64 + 32 + 16 > 100 (отсюда и 16 не слагаемое)
…
64 + 32 + 4 = 100 (4 является третьим слагаемым — число 100 получено) .
2. На разряд** каждого слагаемого (из т. 1) записать в число цифра 1,
на остальные разряды** записать 0.
** Разряд числа соответствует степени числа 2.
** Для примера, 2 разряд соответствует 2-ой степени числа 2,
где должно быть 1, так как число 4 (2-ой степени числа 2) слагаемое.)
100 (10) = 64 +32 +4 = 1100100 (2)
// Так как 2 на 3 степени 8,
для быстрого превращения числа:
1. из 2-ичной в 8-ичную систему счисления,
можно:
— сгруппировать цифры 2-ичного числа в тройках;
— записывать полученную 8-ичную цифру в каждую из тройках.
100 (10) = 1 100 100 (2) = 144 (8)
2. из 8-ичной в 2-ичную сестему счисления,
можно записывать каждую 8-ичную цифру 3 цифрами 2-ичной системы счисления.
100 (10) = 144 (8) = 1 100 100 (2)
Ответ от Котенок [новичек]
используй Калькулятор на компе и все проблемы))))
Ответ от Александр Радько [активный]
У калькулятора в винде смени вид на инженерный))
тогда указывай модель телефона, пробуй что-то из этого ссылка
,
Ответ от Gennady [гуру]
Доброго времени суток.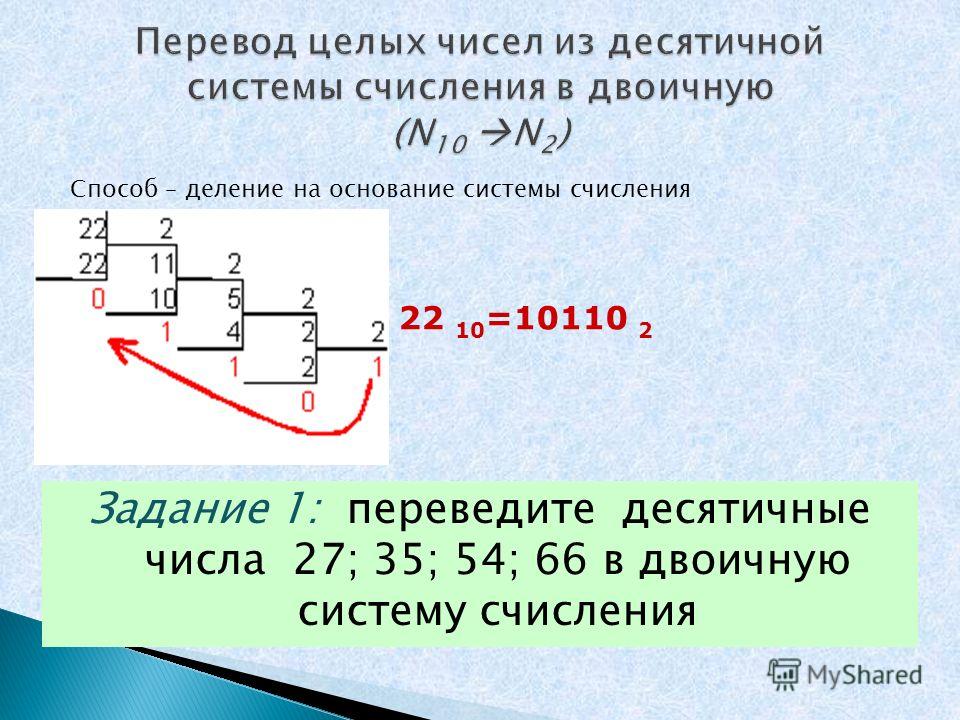 0 = 1*8 + 1*4 + 0*2 + 1*1 = 8 + 4 + 0 + 1 = 13
0 = 1*8 + 1*4 + 0*2 + 1*1 = 8 + 4 + 0 + 1 = 13
Перевод из, допустим, восьмеричной системы в пятиричную надо делать через десятичную по этим правилам.
Если вы это осознаете, вам не понадобится мобила на экзамене.
Удачи!
Для микросхем компьютера важно лишь одно. Либо сигнал есть (1), либо его нет (0). Но записывать программы в двоичном коде — дело нелегкое. На бумаге получаются очень длинные комбинации из нулей и единиц. Человеку их тяжело.
Использование привычной всем десятичной системы в компьютерной документации и программировании очень неудобно. Преобразования из двоичной в десятичную системы и обратно — весьма трудоемкие процессы.
Происхождение восьмеричной системы, так же как и десятичной, связывают со счетом на пальцах. Но считать нужно не пальцы, а промежутки между ними. Их как раз восемь.
Решением проблемы стала восьмеричная . По крайней мере на заре компьютерной техники. Когда разрядность процессоров была невелика. Восьмеричная система позволила с легкостью переводить как двоичные числа в восьмеричные, так и наоборот.
Восьмеричная система позволила с легкостью переводить как двоичные числа в восьмеричные, так и наоборот.
Восьмеричная система счисления — система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Преобразование
Для того чтобы перевести число в двоичное, необходимо заменить каждую цифру восьмеричного числа на тройку из двоичных цифр. Важно лишь запомнить, какая двоичная комбинация соответствует цифрам числа. Их совсем немного. Всего восемь!
Во всех системах счисления, кроме десятичной, знаки читаются по одному. Например, в восьмеричной системе число 610 произносится «шесть, один, ноль».
Если вы хорошо знаете систему счисления, то можно и не запоминать соответствие одних чисел другим.
Двоичная система ничем не отличается от любой другой позиционной системы. Каждый разряд числа имеет . Как только предел достигнут, текущий разряд обнуляется, а перед ним появляется новый. Только одно замечание. Предел этот очень мал и равен единице!
Только одно замечание. Предел этот очень мал и равен единице!
Все очень просто! Ноль предстанет группой из трех нулей — 000, 1 обернется последовательностью 001, 2 превратится в 010 и т.д.
В качестве примера попробуйте преобразовать восьмеричное число 361 в двоичное.
Ответ — 011 110 001. Или, если отбросить незначащий ноль, то 11110001.
Перевод из двоичной системы в восьмеричную аналогичен описанному выше. Только начинать разбиение на тройки нужно с конца числа.
С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую. Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже.
Результат уже получен!
Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
Тогда число 6372 можно представить в следующем виде:
6372=6000+300+70+2 =6·10 3 +3·10 2 +7·10 1 +2·10 0 .
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
Тогда число 1287.923 можно представить в виде:
1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10 -1 +2·10 -2 +3·10 -3 .
В общем случае формулу можно представить в следующем виде:
Ц n ·s n +Ц n-1 ·s n-1 +…+Ц 1 ·s 1 +Ц 0 ·s 0 +Д -1 ·s -1 +Д -2 ·s -2 +. ..+Д -k ·s -k
..+Д -k ·s -k
где Ц n -целое число в позиции n , Д -k — дробное число в позиции (-k), s — система счисления.
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления — из множества цифр {0,1}, в шестнадцатеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E | 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
1 ·2 6 +0 ·2 5 +1 ·2 4 +1 ·2 3 +1 ·2 2 +0 ·2 1 +1 ·2 0 +0 ·2 -1 +0 ·2 -2 +1 ·2 -3 =64+16+8+4+1+1/8=93.125
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3 . Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Здесь A -заменен на 10, B — на 11, C — на 12, F — на 15.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4 . Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 0 | 2 | 1 | |||||
| 0 |
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111 . Следовательно можно записать:
1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111 . Следовательно можно записать:
159 10 =10011111 2 .
Пример 5 . Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147 (см. Рис. 2). Следовательно можно записать:
615 10 =1147 8 .
Пример 6 . Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7 . Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0 | 0.428 | |
| x | 2 | |
| 0 | 0.856 | |
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0 | 0.848 | |
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011 .
Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011 .
Следовательно можно записать:
0.214 10 =0.0011011 2 .
Пример 8 . Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0 | 0.25 | |
| x | 2 | |
| 0 | 0.5 | |
| x | 2 | |
| 1 | 0.0 |
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Следовательно, получился следующий результат:
0.125 10 =0.001 2 .
Пример 9 . Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
0. 214 10 =0.36C8B4 16 .
214 10 =0.36C8B4 16 .
Пример 10 . Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0 | 0.768 | |
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Получили:
0.512 10 =0.406111 8 .
Пример 11 . Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Далее объединяя эти результаты получим:
159.125 10 =10011111.001 2 .
Пример 12 . Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим.
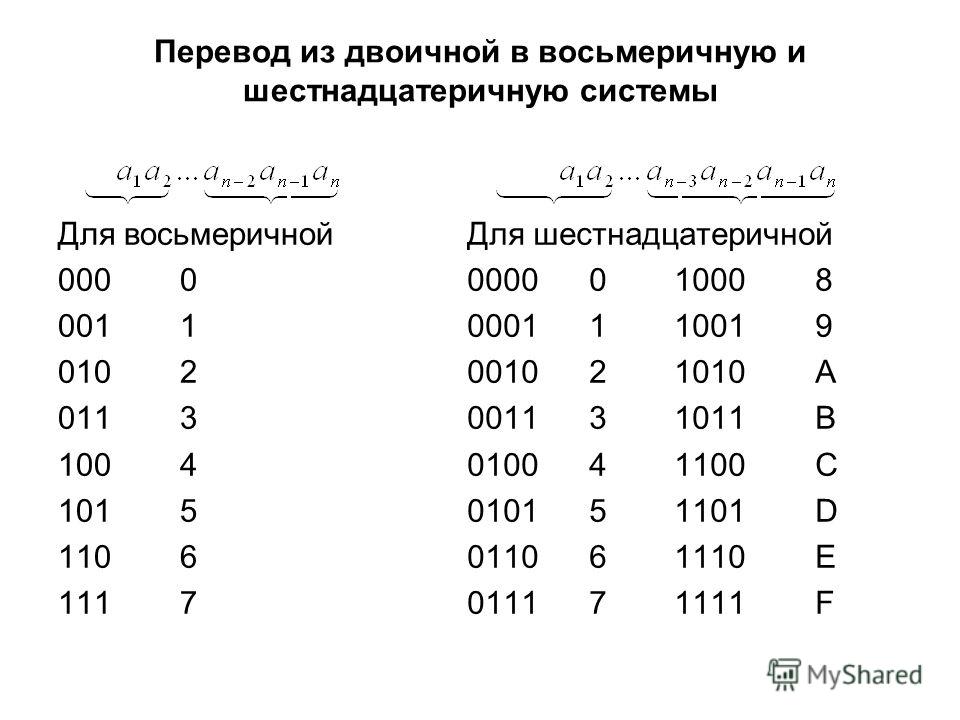
Перевод чисел из двоичной СС в 8-ричную и 16-ричную и обратно
1. Перевод из двоичной системы счисления в шестнадцатеричную:
исходное число разбивается на тетрады (т.е. 4 цифры), начиная с справа для целых чисел и слева для дробных. Если количество цифр исходного двоичного числа не кратно 4, оно дополняется слева нулями до 4 для целых чисел и справа для дробных;
каждая тетрада заменяется шестнадцатеричной цифрой в соответствии с таблицей.
1. 10011 2 = 0001 0011 2 = 13 16
2. 0,1101 2 =
0,D 16 .
2. Из
шестнадцатеричной системы счисления
в двоичную:
каждая
цифра шестнадцатеричного числа
заменяется тетрадой двоичных цифр в
соответствии с таблицей. Если в таблице
двоичное число имеет менее 4 цифр, оно
дополняется слева нулями до 4;
Если в таблице
двоичное число имеет менее 4 цифр, оно
дополняется слева нулями до 4;
1. 13 16 = 0001 0011 2 = 10011 2
2. 0,2А 16 =
0,0010 1010 2 = 0,0010101 2 .
3. Из
двоичной системы счисления в восьмеричную
исходное число разбивается на триады (т.е. 3 цифры), начиная с справа для целых чисел и слева для дробных. Если количество цифр исходного двоичного числа не кратно 3, оно дополняется слева нулями до 3 для целых чисел и справа для дробных;
каждая триада заменятся восьмеричной цифрой в соответствии с таблицей
1. 1101111001.1101 2 =001 101 111 001.110 100 2 = 1571,64
2. 11001111.1101 2 = 011 001 111.110 100 2 = 317, 64 8
4. Для перевода восьмеричного числа в двоичную систему счисления
каждая цифра восьмеричного числа заменяется триадой двоичных цифр в соответствии с таблицей. Если в таблице двоичное число имеет менее 3 цифр, оно дополняется слева нулями до 3 для целых чисел и справа до 3 для дробных;
незначащие
нули в результирующем числе отбрасываются.
1. 305,4 8 = 011 000 101 , 100 2 = 11000101,1 2
2. 2516,1 8 = 010 101 001 110 , 001 2 = = 10101001110,001 2
5. Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.
1. 175,24 8 = 001 111 101 , 010 100 2 = 0111 1101 , 0101 2 = 7D,5 16
2. 426,574 8 = 100 010 110 , 101 111 100 2 = 0001 0001 0110 , 1011 1110 2 =116,BE
3. 0,0010101 2 = 0,0010 1010 2 = 0,2A 16 .
4. 7B2,E 16 = 0111 1011 0010 ,1110 2 = 11110110010,111 2
5. 11111111011,100111 2 = 0111 1111 1011,1001 1100 2 = 7FB,9C 16
6. 110001,10111 2 = 0011 0001,1011 1000 2 = 31,B8 16
Задачи на Системы счисления
4
Задачи на системы счисления
Найти сумму чисел 378 и 648 в восьмеричной системе счисления.
Найти сумму чисел 3A16 и 648 в восьмеричной системе счисления.

Найти сумму чисел 378 и B416 в восьмеричной системе счисления.
Найти разность чисел 6358 и 4768 в восьмеричной системе счисления.
Чему равна сумма чисел 438 и 5616?
Количество значащих нулей в двоичной записи десятичного числа 126 равно:
1) 1 2) 2 3) 3 4) 0
Перевести число 15FC16 в десятичную систему счисления.
Перевести число 1011012 в десятичную систему счисления.
Перевести число 101,112 в десятичную систему счисления.
Перевести десятичную дробь 0,1875 в двоичную и восьмеричную системы счисления.
Перевести двоичное число 1101111010111011112 в шестнадцатеричную систему счисления.

Дано а = D716, b = 3318. Какое из чисел c, записанных в двоичной системе, отвечает условию a < c < b?
1) 110110012 2) 110111002 3) 110101112 4) 110110002
Количество цифр в двоичной записи десятичного числа, которое можно представить в виде 2 + 8 + 16 + 64 + 128 + 256 + 512, равно:
1) 7 2) 8 3) 9 4) 10
Укажите через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ запишите в десятичной системе счисления.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
Укажите наименьшее основание системы счисления, в которой запись числа 19 трехзначна.

В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание.
В таблице ниже представлена часть кодовой таблицы ASCII:
Символ | 1 | 5 | A | B | Q | a | b |
Десятичный код | 49 | 53 | 65 | 66 | 81 | 97 | 98 |
Шестнадцатеричный код | 31 | 35 | 41 | 42 | 51 | 61 | 62 |
Каков шестнадцатеричный код символа «q» ?
1) 7116 2) 8316 3) А116 4) В316
Сколько единиц в двоичной записи числа 195?
1) 5 2) 2 3) 3 4) 4
Количество значащих нулей в двоичной записи десятичного числа 128 равно:
1) 6 2) 7 3) 8 4) 0
Как представлено число 8310 в двоичной системе счисления?
1) 10010112 2) 11001012 3) 10100112 4) 1010012
Как представлено число 2510 в двоичной системе счисления?
1) 10012 2) 110012 3) 100112 4) 110102
Сколько единиц в двоичной записи десятичного числа 194,5?
1) 5 2) 6 3) 3 4) 4
Вычислите сумму двух двоичных чисел x и y, если x = 10101012 и y = 10100112.

1) 100101102 2) 110010102 3) 101001102 4) 101010002
Вычислите значение суммы 102 + 108 + 1016 в двоичной системе счисления.
1) 101000102) 11110 3) 11010 4) 10100
Вычислите сумму чисел X и Y, если X = 1101112, Y = 1358. Результат представьте в двоичном виде.
1) 11010100 2) 10100100 3)10010011 4) 10010100
Значение выражения 1016 + 108·102 в двоичной системе счисления равно:
1) 10102 2) 110102 3) 1000002 4) 1100002
Дано а = 5716, b = 1678.
 Какое из чисел c,
записанных в двоичной системе, отвечает
условию a < c < b?
Какое из чисел c,
записанных в двоичной системе, отвечает
условию a < c < b?
1) 10001102 2) 10001112 3) 11001112 4) 11101112
Дано а = 2128, b = 14316. Какое из чисел c, записанных в двоичной системе, отвечает условию a < c < b?
1) 110000110 2) 100100011 3) 101100011 4) 1110111
Дано А = 9D16, B = 2378. Какое из чисел C, записанных в двоичной системе, отвечает условию A < C < B?
1) 10011010 2) 10011110 3) 10011111 4) 11011110
В таблице ниже представлена часть кодовой таблицы ASCII:
Символ | 1 | 5 | A | B | P | a | b |
Десятичный код | 49 | 53 | 65 | 66 | 80 | 97 | 98 |
Шестнадцатеричный код | 31 | 35 | 41 | 42 | 50 | 61 | 62 |
Каков шестнадцатеричный код символа «p»?
1) 71 2) 70 3) А1 4) В3
В таблице ниже представлена часть кодовой таблицы ASCII:
Символ | 1 | 5 | A | B | a | b | r |
Десятичный код | 49 | 53 | 65 | 66 | 97 | 98 | 114 |
Шестнадцатеричный код | 31 | 35 | 41 | 42 | 61 | 62 | 72 |
Каков шестнадцатеричный код символа «R»?
1) A0 2) 72 3) А2 4) 52
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием 4 оканчивается на 11.

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
В системе счисления с некоторым основанием десятичное число 49 записывается в виде 100. Укажите это основание.
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 80, запись которых в системе счисления с основанием 5 оканчивается на 10.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на 5.
В системе счисления с некоторым основанием десятичное число 129 записывается в виде 1004. Укажите это основание.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 40 оканчивается на 4.
Укажите, сколько раз используется цифра 3 при записи чисел 13, 14, 15, …, 22, 23 в системе счисления с основанием 4.
Укажите, сколько раз используется цифра 2 при записи чисел 13, 14, 15, …, 22, 23 в системе счисления с основанием 3.
В непозиционной системе счисления, которая называется системой остатков (СО), в качестве оснований выбираются взаимно простые числа, например, p1=3, p2=5, p3=7. При этом диапазон однозначного представления чисел равен произведению оснований (в приведенном примере p1∙p2∙p3 = 105, т. е. однозначно представляются все числа от 0 до 104). Любое число в этом диапазоне записывается остатками от целочисленного деления этого числа на выбранные основания. Например, число A = 19 запишется в СО с основаниями 3, 5, 7 так: A = (1, 4, 5). Укажите, какая из записей соответствует числу 5, записанному в системе остатков с основаниями 3, 5, 7.
1) (3, 0, 2) 2) (2, 0, 2) 3) (2, 0, 5) 4) (5, 5, 5)
В непозиционной системе счисления, которая называется системой остатков (СО), в качестве оснований выбираются взаимно простые числа, например, p1=3, p2=5, p3=7.
 При этом диапазон однозначного
представления чисел равен произведению
оснований (в приведенном примере p1∙p2∙p3 = 105,
т. е. однозначно представляются все
числа от 0 до 104). Любое число в этом
диапазоне записывается остатками от
целочисленного деления этого числа на
выбранные основания. Например, число A = 19
запишется в СО с основаниями 3, 5, 7 так: A = (1, 4, 5).
Укажите, какая из записей соответствует
числу 3, записанному в системе остатков
с основаниями 3, 5, 7.
При этом диапазон однозначного
представления чисел равен произведению
оснований (в приведенном примере p1∙p2∙p3 = 105,
т. е. однозначно представляются все
числа от 0 до 104). Любое число в этом
диапазоне записывается остатками от
целочисленного деления этого числа на
выбранные основания. Например, число A = 19
запишется в СО с основаниями 3, 5, 7 так: A = (1, 4, 5).
Укажите, какая из записей соответствует
числу 3, записанному в системе остатков
с основаниями 3, 5, 7.
1) (3, 0, 0) 2) (0, 3, 3) 3) (0, 2, 4) 4) (3, 3, 3)
В саду 100 фруктовых деревьев — 14 яблонь и 42 груши. Найдите основание системы счисления, в которой указаны числа.
Найдите основание системы счисления, в которой выполнено следующее сложение: 144 + 24 = 201.
Найдите основание системы счисления, в которой выполнено следующее умножение: 3213 = 1043.

Дано А=9516, B=2278. Какое из чисел C, записанных в двоичной системе, отвечает условию A<C<B?
1) 10011010 2) 10010111 3) 10010110 4) 11010110
Вычислите сумму чисел x и y при x = 1D16, y = 728.
Результат представьте в двоичной системе счисления.
1) 100011112 2) 11001012 3) 1010112 4) 10101112
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 32, запись которых в системе счисления с основанием три оканчивается на 10.
Запишите число 5678 в двоичной системе счисления.
1) 1011111012 2) 1001101112 3) 1011101112 4) 10001101112
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 100, запись которых в системе счисления с основанием 5 оканчивается на 11.

Дано а = 2528, b = AC16. Какое из чисел c, записанных в двоичной системе, отвечает условию a < c < b?
1) 10101011 2) 10101010 3) 10101111 4) 10101100
Вычислите сумму чисел x и y, при x = A616, y = 758.
Результат представьте в двоичной системе счисления.
1) 110110112 2) 111100012 3) 111000112 4) 100100112
В системе счисления с некоторым основанием число 17 записывается в виде 101. Укажите это основание.
Сколько единиц содержится в двоичной записи десятичного числа 173?
1) 7 2) 5 3) 6 4) 4
Вычислите сумму чисел x и y, при x = A116, y = 11012.
 Результат представьте в десятичной
системе счисления.
Результат представьте в десятичной
системе счисления.
1) 204 2) 152 3) 183 4) 174
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 39 оканчивается на 3.
Даны два числа: a = DD16, b = 3378. Какое из чисел c, записанных в двоичной системе, удовлетворяет неравенству a < c < b?
1) 11011110 2) 10111010 3) 11101101 4) 11101111
Чему равна сумма чисел x и y, если x = 2D16, y = 578.
1) 100001002 2) 10111002 3) 2728 4) 8416
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в системе счисления с основанием 5 оканчивается на 3.

Тестовые задания по теме «Виды систем счисления и арифметические действия в них»
ГБПОУ города Москвы «Спортивно-педагогический колледж»
Департамента спорта и туризма города Москвы
преподаватель информатики и ИКТ: Макеева Е.С.
Тестовые задания по теме «Виды систем счисления и арифметические действия в них»
Тест 1. Системы счисления
Цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9:
римские 2) арабские 3) греческие 4) русские
В римской системе счисления цифра 5 обозначается:
I 2) V 3) X 4)L
В римской системе счисления цифра 10 обозначается:
I 2) V 3) X 4) L
В римской системе счисления цифра L обозначает:
50 2) 100 3) 1000 4) 5
В римской системе счисления цифра C обозначает:
50 2) 100 3) 1000 4) 10
В римской системе счисления цифра M обозначает:
50 2) 100 3) 1000 4) 10
В римской системе счисления число LIX обозначает:
59 2) 61 3) 110 4) 5110
В римской системе счисления число CLIV обозначает:
104 2) 154 3) 1514 4) 1504
Как записывается число 55 в римской системе счисления?
VV 2) XV 3) LV 4) CV
Как записывается число 2012 в римской системе счисления?
MMXII 2) MM00XII 3) 2M00XII
В шестнадцатеричной системе счисления цифра С обозначает:
10 2) 11 3) 12 4) 13
В шестнадцатеричной системе счисления 13 записывается цифрой:
B 2) С 3) D 4) F
Переведите десятичное число 7 в двоичную систему счисления:
101 2) 1110 3) 1111 4) 111
Восьмеричное число 21 в десятичной системе счисления:
13 2) 15 3) 17 4) 24
Переведите десятичное число 47 в восьмеричную систему счисления:
37 2) 57 3) 65 4) 75
Шестнадцатеричное число 3А в десятичной системе счисления:
45 2) 51 3) 58 4) 74
Переведите десятичное число 63 в шестнадцатеричную систему счисления:
3В 2) 315 3) F3 4) 3F
Как записывается двоичное число 11011110 двумя шестнадцатеричными цифрами?
CA 2) DE 3) FB 4) BE
Тест 2. Двоичная система счисления
Двоичная система счисления
Переведите двоичное число 1110 в десятичную систему счисления:
14 2) 7 3) 11 4) 111
Переведите двоичное число 101010 в десятичную систему счисления:
222 2) 42 3) 52 4) 121
Переведите двоичное число 110110 в десятичную систему счисления:
66 2) 112 3) 54 4) 312
Переведите двоичное число 100000000 в десятичную систему счисления:
128 2) 512 3) 256 4) 1024
Переведите двоичное число 11111111 в десятичную систему счисления:
1023 2) 127 3) 255 4) 511
Переведите десятичное число 15 в двоичную систему счисления:
1110 2) 11111 3) 10000 4) 1111
Переведите десятичное число 21 в двоичную систему счисления:
10101 2) 11111 3) 10001 4) 11101
Переведите десятичное число 98 в двоичную систему счисления:
1110111 2) 1100010 3) 1000001 4) 1100101
Переведите десятичное число 129 в двоичную систему счисления:
10000001 2) 11111111 3) 10010101 4) 11101001
Переведите десятичное число 257 в двоичную систему счисления:
100000001 2) 11111111 3) 100000011 4) 110000000
Тест 3. Сложение и умножение в двоичной системе счисления
Сложение и умножение в двоичной системе счисления
В двоичной системе счисления 1+1=
2 2) 10 3) 11 4) 1
Сложите в двоичной системе счисления числа 101+111=
1100 2) 212 3) 1110 4) 1000
Сложите в двоичной системе 100 + 10 =
110 2) 101 3) 110 4) 1010
Сложите в двоичной системе 1111 + 101 =
10110 2) 10101 3) 11100 4) 10100
Сложите в двоичной системе 1011 + 1101 =
11000 2) 10100 3) 11100 4) 10110
Умножьте в двоичной системе счисления числа 11011=
1001 2) 11000 3) 10010 4) 10001
Умножьте в двоичной системе 1101 11 =
101001 2) 100111 3) 111000 4) 101100
Умножьте в двоичной системе 1011 11 =
101101 2) 101001 3) 111001 4) 100001
Умножьте в двоичной системе 1010 101 =
110010 2) 101001 3) 111001 4) 101101
Умножьте в двоичной системе 1001 110 =
111000 2) 101000 3) 110110 4) 101100
Тест 4.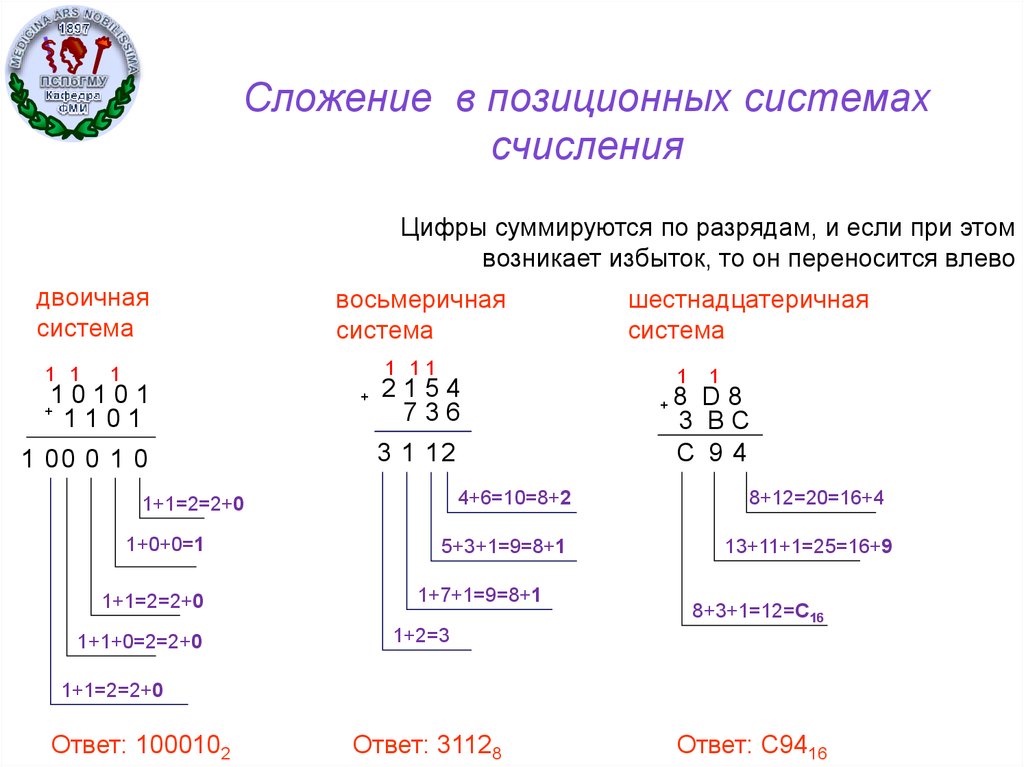 Восьмеричная система счисления
Восьмеричная система счисления
Переведите восьмеричное число 10 в десятичную систему счисления:
7 2) 9 3) 8 4) 10
Переведите восьмеричное число 53 в десятичную систему счисления:
40 2) 43 3) 64 4) 344
Переведите восьмеричное число 76 в десятичную систему счисления:
56 2) 496 3) 448 4) 62
Переведите восьмеричное число 125 в десятичную систему счисления:
75 2) 85 3) 105 4) 92
Переведите восьмеричное число 257 в десятичную систему счисления:
175 2) 128 3) 390 4) 168
Переведите десятичное число 8 в восьмеричную систему счисления:
10 2) 71 3) 100 4) 9
Переведите десятичное число 17 в восьмеричную систему счисления:
15 2) 10001 3) 21 4) 23
Переведите десятичное число 23 в восьмеричную систему счисления:
11011 2) 27 3) 18 4) 25
Переведите десятичное число 55 в восьмеричную систему счисления:
67 2) 76 3) 66 4) 77
Переведите десятичное число 64 в восьмеричную систему счисления:
46 2) 77 3) 101 4) 100
Тест 5. Шестнадцатеричная система счисления
Шестнадцатеричная система счисления
Переведите шестнадцатеричное число 10 в десятичную систему счисления:
16 2) 1000 3) 15 4) 20
Переведите шестнадцатеричное число A1 в десятичную систему счисления:
160 2) 2576 3) 176 4) 161
Переведите шестнадцатеричное число F8 в десятичную систему счисления:
240 2) 248 3) 304 4) 3848
Переведите шестнадцатеричное число ABC в десятичную систему счисления:
2748 2) 2560 2) 188 4) 2750
Переведите шестнадцатеричное число 12С в десятичную систему счисления:
250 2) 300 3) 400 4) 288
Переведите десятичное число 16 в шестнадцатеричную систему счисления:
F1 2) 1000 3) 61 4) 10
Переведите десятичное число 25 в шестнадцатеричную систему счисления:
91 2) 19 3) 52 4) 265
Переведите десятичное число 65 в шестнадцатеричную систему счисления:
41 2) 14 3) 52 4) 65
Переведите десятичное число 520 в шестнадцатеричную систему счисления:
256 2) 802 3) 502 4) 208
Переведите десятичное число 550 в шестнадцатеричную систему счисления:
126 2) 206 3) 226 4) 622
Тест 6.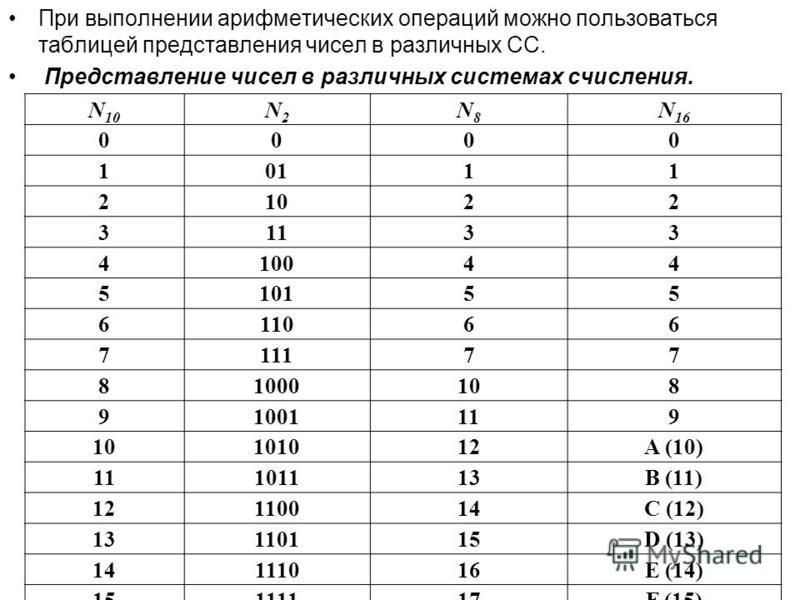 Перевод из восьмеричной и шестнадцатеричной систем счисления в двоичную
Перевод из восьмеричной и шестнадцатеричной систем счисления в двоичную
Переведите восьмеричное число 75 в двоичную систему счисления.
Переведите восьмеричное число 246 в двоичную систему счисления.
Переведите восьмеричное число 5431 в двоичную систему счисления.
Переведите двоичное число 110010 в восьмеричную систему счисления.
Переведите двоичное число 101100001 в восьмеричную систему счисления.
Переведите двоичное число 111001100010 в восьмеричную систему счисления.
Переведите шестнадцатеричное число D5 в двоичную систему счисления.
Переведите шестнадцатеричное число 13F в двоичную систему счисления.
Переведите шестнадцатеричное число E98 в двоичную систему счисления.
Как записывается двоичное число 10011111 двумя шестнадцатеричными цифрами?
Запишите двумя шестнадцатеричными цифрами двоичное число 10000001.
Запишите двумя шестнадцатеричными цифрами двоичное число10100011.
Ответы к тесту по теме «Виды систем счисления и арифметические действия в них».
Тест 1
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
2 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 3 | 3 | 4 | 3 | 2 | 3 | 4 | 2 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
Тест 2. | 1 | 2 | 3 | 3 | 3 | 4 | 1 | 2 | 1 | 1 |
Тест 3 | 2 | 1 | 3 | 4 | 1 | 3 | 2 | 4 | 1 | 3 |
Тест 4 | 3 | 2 | 4 | 2 | 1 | 1 | 3 | 2 | 1 | 4 |
Тест 5 | 1 | 4 | 2 | 1 | 2 | 4 | 2 | 1 | 4 | 3 |
Тест 6
1 | 2 | 3 | 4 | 5 | 6 |
111101 | 10100110 | 101100011001 | 62 | 541 | 7142 |
7 | 8 | 9 | 10 | 11 | 12 |
11010101 | 100111111 | 111010011000 | 9F | 81 | A3 |
Опубликовано в группе «УРОКИ, КИМы, ИГРЫ, практикумы, творческие задания по ИНФОРМАТИКЕ, МАТЕМАТИКЕ и другим дисциплинам.»
Лекция №4. Выполнение типовых заданий части 2.
Лекция №4. Выполнение типовых заданий части 2.
Ответом к заданиям этой части (В1–В10) является набор символов, которые следует записать в бланк ответов № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждый символ пишется в отдельной клеточке.
Задание В1 требует от учеников наличия некоторых знаний из курса комбинаторики. Мы покажем общий способ решения заданий данного типа. Если Вам ранее не попадались подобные задачи, рекомендуем наверстывать упущенное.
Задача B1: Сигнальное устройство в течение одной секунды передает 1 из 3 возможных сигналов. Сколько различных сигналов может передать устройство за 4 секунды?
Решение: Покажем наиболее простой способ решения задачи. Очевидно, что в первую, вторую, третью и четвертую секунду устройство может передать любой из 3 возможных сигналов. Тогда общее число возможных сигналов за 4 секунды вычисляется по следующей формуле: 3*3*3*3=34=81 (в комбинаторике эта формула является одной из основных).
Тогда общее число возможных сигналов за 4 секунды вычисляется по следующей формуле: 3*3*3*3=34=81 (в комбинаторике эта формула является одной из основных).
Ответ. 81.
Задание B2. Для того, чтобы решить задание В2, нам придется вспомнить правила работы с блок-схемами. Строго говоря, блок-схема это еще не программирование, но работа с ними находится на ближайшей ступени к нему. Рекомендуем обратить особое внимание на данный элемент.
Задача В2: Дана блок-схема. Чему будет равна переменная b после ее выполнения?
Решение: Поясним каждую из трех составляющих приведенной блок-схемы. Первый (верхний) прямоугольник — задание начальных значений. Ромб — условие, в случае выполнения которого происходит один переход (ветвь Да), а в случае невыполнения — другой переход (ветвь Нет). Второй (нижний) прямоугольник — выполнение заданных в нем действий. Рассмотрим блок-схему пошагово:
1) a=256, b=0
2) Проверка: а=0. Нет. Поэтому, переход по стрелке «Нет»
3) а=256/2=128, b=0+128=128
4) Проверка: а=0. Нет. Поэтому, переход по стрелке «Нет»
Нет. Поэтому, переход по стрелке «Нет»
5) а=128/2=64. b=128+64=192
…
И так далее. До тех пор, пока а не станет равно 1. После выполнения блок-схемы b равно 255
Ответ: 255.
Задание В3. Одним из разделов, обязательно входящих в курс информатики является «Системы счисления». При должном внимании, он не вызывает особых трудностей у учеников. Задание В3 потребует от учеников вспомнить курс «Систем счисления».
Задача В3: Десятичное число 49 в системе счисления с неким основанием записывается как 100. Найти это основание.
Решение: Рассмотрим двоичную систему счисления: десятичное число 4 записывается в ней как 100. В восьмеричной системе счисления: десятичное число 64 записывается как 100. В шестнадцатеричной: десятичное число 256 записывается как 100. Аналогично, десятичное число 49 в семеричной системе счисления записывается как 100.
Ответ: 7.
Выполним задание В4. Ограничимся лишь общими указаниями (так как в части А имеются подобные задания).
Задача В4: Сколько различных решений имеет уравнение
J /\ ¬K /\ L /\ ¬M /\ (N \/ ¬N) = 0
где J, K, L, M, N – логические переменные?
В ответе не нужно перечислять все различные наборы значений J, K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов.
Решение: Обратите внимание на то, что выражение (N \/ ¬N) — истинно при любом N. Из максимально возможного числа наборов логических переменных исключите те, при которых уравнение не имеет смысла.
Ответ: 30.
Задание B5 вновь потребует от учеников применить знания об исполнителе Робот. Рассмотрим это задание.
Задача В5: Дан исполнитель Робот, выполняющий следующие команды: вправо, влево, вверх, вниз по бесконечной клетчатой доске. Робот выполнил следующую программу:
влево
вверх
вверх
влево
вниз
вправо
вправо
вправо
Сколько команд минимально нужно выполнить роботу, чтобы вернуться в начальную клетку?
Решение: 2 команды (вниз, влево)
Ответ: 2.
Для того, чтобы решить задание В6 — от учеников потребуется применить логическое мышление. Решим задачу.
Задача В6: На одной улице стоят в ряд 4 дома, в которых живут 4 человека: Алексей, Егор, Виктор и Михаил. Известно, что каждый из них владеет ровно одной из следующих профессий: Токарь, Столяр, Хирург и Окулист, но неизвестно, кто какой и неизвестно, кто в каком доме живет. Однако, известно, что:
1) Токарь живет левее Столяра
2) Хирург живет правее Окулиста
3) Окулист живет рядом со Столяром
4) Токарь живет не рядом со Столяром
5) Виктор живет правее Окулиста
6) Михаил не Токарь
7) Егор живет рядом со Столяром
8) Виктор живет левее Егора
Выясните, кто какой профессии, и кто где живет, и дайте ответ в виде заглавных букв имени людей, в порядке слева направо. Например, если бы в домах жили (слева направо) Константин, Николай, Роман и Олег, ответ был бы: КНРО
Решение: Приведем верную схему:
Токарь | Окулист | Столяр | Хирург |
Алексей | Михаил | Виктор | Егор |
Ответ: АМВЕ
Задания B7-B10 объединяет то, что для их решения от учеников потребуется лишь умение строить логические рассуждения.
Задача В7: У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 256 Кбит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 32 Кбит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 5 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу.
Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 512 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей?
В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.
Ответ: 1296
Задача В8: Строки (цепочки латинских букв) создаются по следующему правилу. Первая строка состоит из одного символа – латинской буквы «А». Каждая из последующих цепочек создается такими действиями: в очередную строку сначала записывается буква, чей порядковый номер в алфавите соответствует номеру строки (на i-м шаге пишется «i»-я буква алфавита), к ней слева дважды подряд приписывается предыдущая строка.
Вот первые 4 строки, созданные по этому правилу:
(1) A
(2) AAB
(3) AABAABC
(4) AABAABCAABAABCD
Латинский алфавит (для справки):
ABCDEFGHIJKLMNOPQRSTUVWXYZ
Запишите шесть символов подряд, стоящие в седьмой строке со 117-го по 122-е место (считая слева направо).
Ответ: AABAAB
Задача В9: На месте преступления были обнаружены четыре обрывка бумаги. Следствие установило, что на них записаны фрагменты одного IP-адреса. Криминалисты обозначили эти фрагменты буквами А, Б, В и Г.
Восстановите IP-адрес.
В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.
Ответ: ВБГА
Задача В10: В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” в запросе используется символ |, а для логической операции “И” – &.
№ Запрос
1 канарейки | щеглы | содержание
2 канарейки & содержание
3 канарейки & щеглы & содержание
4 разведение & содержание & канарейки & щеглы
Ответ: 4321.
как преобразовать десятичное 64 в восьмеричное
Как записать 64 в восьмеричное (основание 8)?
64 равно 100 в восьмеричной форме
| ||||||||||||||||
Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа. Калькулятор преобразования десятичной базы. Здесь вы можете найти ответ на такие вопросы, как: как преобразовать десятичное 64 в восьмеричное или десятичное в восьмеричное преобразование.
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| 10 | A | 12 | 1010 |
| 11 | B | 13 | 1011 |
| 12 | C | 14 | |
| 13 | 9000|||
| 13 | 9000|||
| 13 | 9000|||
| 13 | 9000 | ||
| 13 | 0009 | 1101 | |
| 14 | E | 16 | 1110 |
| 15 | F | 17 | 1111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 16 | 10 | 20 | 10000 |
| 17 | 11 | 21 | 10001 |
| 18 | 12 | 0008 2210010 | |
| 19 | 13 | 23 | 10011 |
| 20 | 14 | 24 | 10100 |
| 21 | 15 | 25 | 10101 |
| 22 | 16 | 26 | 10110 |
| 23 | 17 | 27 | 10111 |
| 24 | 18 | 30 | |
| 0008 11000 | |||
| 25 | 19 | 31 | 11001 |
| 26 | 1A | 32 | 11010 |
| 27 | 1B | 33 | 11011 |
| 28 | 1C | 34 | 11100 |
| 29 | 1D | 35 | 11101 |
| 30 | 1E | 36 | 111110 |
| 31 | 1F | 37 | 11111 |
| Dec | Hex | Oct | Bin | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | |||||||||||
| 33 | 21 | 41 | 100001 | |||||||||||
| 34 | 22 | 42 | 100010 | |||||||||||
| 35 | 23 | 43 | ||||||||||||
| 100011 | ||||||||||||||
| 36 | 24 | 44 | 100100 | |||||||||||
| 37 | 25 | 45 | 100101 | |||||||||||
| 38 | 26 | 46 | 100110 | |||||||||||
| 39 | 27 | 47 | 100111 | |||||||||||
| 40 | 28 | 50 | 101000 | |||||||||||
| 41 | 2951 | 101001 | 29 | 51 | 101001 | 51 | 101001 | 0009|||||||
| 42 | 2A | 52 | 101010 | |||||||||||
| 43 | 2B | 53 | 101011 | |||||||||||
| 44 | 2C | 54 | 101100 | |||||||||||
| 45 | 2D | 55 | 101101 | |||||||||||
| 46 | 2E | 56 | 101110 | |||||||||||
| 47 | 2F | 57 | 101111 | 2F | 57 | 101111 | 0060
| 110009 |
9000
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 240 | F0 | 360 | 11110000 | |
| 241 | F1 | 361 | 11110001 | |
| 242 | F2 | 362 | 11110010 | |
| 243 | F3 | 363 | 11110011 | |
| 244 | F4 | 364 | 11101009 | 0009 |
| 245 | F5 | 365 | 11110101 | |
| 246 | F6 | 366 | 11110110 | |
| 247 | F7 | 367 | 11110111 | |
| 248 | F8 | 370 | 11111000 | |
| 249 | F9 | 371 | 11111001 | |
| 250 | FA | 372 | 0008 11111010 | |
| 251 | FB | 373 | 11111011 | |
| 252 | FC | 374 | 11111100 | |
| 253 | FD | 375 | 11111101 | |
| 254 | FE | 376 | 11111110 | |
| 255 | FF | 377 | 111111111999910 |
Номерная базовая конвертер
Пожалуйста, перейдите на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
- 100011000000 binary to octal
- 15104 decimal to binary
- binary to octal
- 11110111100 binary to decimal
- 2700 octal to decimal
- 25 decimal to binary
- 1101000000 binary to decimal
- F1 hexadecimal в восьмеричное
- шестнадцатеричное в десятичное
Десятичный 64 в восьмеричном | работа, решение
Как написать 64 в восьмеричной системе?
64 записывается как 100 в восьмеричном формате
Преобразование из/в десятичное в двоичное. Преобразование десятичных чисел. Возможно, вы обратились к нам в поисках ответов на такие вопросы, как: Десятичное число 64 в восьмеричном | работа, решение или преобразование из десятичного в восьмеричное. Используйте калькулятор ниже, чтобы преобразовать в / из основных базовых систем.
Чтобы использовать этот калькулятор, просто введите значение в любом поле слева.
С помощью этого конвертера вы можете получить ответы на такие вопросы, как:
- Что такое 64 в двоичном формате?
- Что такое 64 в шестнадцатеричном формате?
- Что такое 64 в восьмеричной системе?
- Как преобразовать 64 в двоичный файл?
- Как преобразовать 64 в двоичный файл? И так далее.

Decimal to Binary Chart — Including Hexa and Octal
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 110999 | 110999 | 110999 | 110 | 110 | 110999 | 110999 | 7 | 7 | 111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| 10 | A | 12 | 1010 |
| 11 | B | 13 | 1011 |
| 12 | C | 14 | 9009 |
| 13 | D | 9 | |
| 13 | D | 9 9007 | 0008 1101 |
| 14 | E | 16 | 1110 |
| 15 | F | 17 | 1111 |
| Dec | Hex | Oct | Bin | |||||
|---|---|---|---|---|---|---|---|---|
| 16 | 10 | 20 | 10000 | |||||
| 17 | 11 | 21 | 10001 | |||||
| 18 | 12 | 22 | ||||||
| 18 | 12 | 22 | ||||||
| 10010 | ||||||||
| 19 | 13 | 23 | 10011 | |||||
| 20 | 14 | 24 | 10100 | |||||
| 21 | 15 | 25 | 10101 | |||||
| 22 | 16 | 26 | 10110 | |||||
| 23 | 17 | 27 | 10111 | |||||
| 24 | 18 | 30 | 18 | 30 | 9000 | 0009 | ||
| 25 | 19 | 31 | 11001 | |||||
| 26 | 1A | 32 | 11010 | |||||
| 27 | 1B | 33 | 11011 | |||||
| 28 | 1C | 34 | 11100 | |||||
| 29 | 1d | 35 | 11101 | |||||
| 30 | 36 | 11110 | 1F | 37 | 11111 |
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | |
| 33 | 21 | 41 | 100001 | |
| 34 | 22 | 42 | 100010 | |
| 35 | 23 | 43 | 100011 | |
| 36 | 24 | 44 | 100100 | |
| 37 | 25 | 45 | 100101 | |
| 38 | 26 | 46 | 100110 | |
| 39 | 27 | 47 | 100111 | |
| 40 | 28 | 50 | 101000 | |
| 41 | 29 | 51 | 101001 | 51 | 101001 | 0007 | 42 | 2A | 52 | 101010 |
| 43 | 2B | 53 | 101011 | |
| 44 | 2C | 54 | 101100 | |
| 45 | 2D | 55 | 101101 | |
| 46 | 2E | 56 | 101110 | |
| 47 | 2F | 8 57101111 |
| Dec | Hex | Oct | Bin | ||||
|---|---|---|---|---|---|---|---|
| 48 | 30 | 60 | 110000 | ||||
| 49 | 31 | 61 | 110001 | ||||
| 50 | 32 | 62 | 110010 | ||||
| 51 | 33 | 63 | 110011 | ||||
| 52 | 34 | 64 | 110100 | 64 | 110100 | 64 | 1101009 | 9000
| 53 | 35 | 65 | 110101 | ||||
| 54 | 36 | 66 | 110110 | ||||
| 55 | 37 | 67 | 110111 | ||||
| 56 | 38 | 70 | 111000 | ||||
| 57 | 39 | 71 | 111001 | ||||
| 58 | 3A | 72 | 111010999 | ||||
| 111010999 | |||||||
| 111010 | |||||||
| 1110109 | |||||||
| 111010 | |||||||
| 3B | 73 | 111011 | |||||
| 60 | 3C | 74 | 111100 | ||||
| 61 | 3D | 75 | 111101 | ||||
| 62 | 3E | 76 | 111110 | ||||
| 63 | 3F | 77 | 111111 |
Образцы преобразования базы
- 1000100000 Бинарный2858
- E8 hexadecimal to binary
- 31400 octal to decimal
- EC00 hexadecimal to binary
- 20 in binary
- 375 octal to hexadecimal
- B0 hexadecimal to decimal
Disclaimer
While every effort is made to обеспечить точность информации, представленной на этом веб-сайте, мы не даем никаких гарантий в отношении этой информации.
Двоичный, десятичный, шестнадцатеричный, октябрь
Двоичный, десятичный, шестнадцатеричный, октябрьПри работе с ИТ важно знать двоичные, шестнадцатеричные и восьмеричные числа.
| Десятичный | Двоичный | Шестнадцатеричный | Восьмеричный | Двоичный код в восьмеричный | Двоичный код в шестнадцатеричный |
Десятичный (основание 10)
Числа состоят из десяти цифр 0,1,2,3,4,5,6,7,8,9
Местные значения показаны ниже
10 0 =1
10 1 =10
10 2 =10 * 10 =100
10 3 =10* 10 * 10 =1000
10 4 =10 * 10 * 10 * 10 =10000
10 5 =10 * 10 * 10 * 10 * 10 =100000
ДВОИЧНЫЙ (основание 2)
Номера состоят только из двух цифр 0,1
Местные значения показаны ниже
2 0 =1
2 1 =2
2 2 =2 * 2 =4
2 3 =2 * 2 * 2 =8
2 4 = 2 * 2 * 2 * 2 = 16
2 5 = 2 * 2 * 2 * 2 * 2 = 32
2 6 = 2 * 2 * 2 * 2 * 2 * 2 = 64
2 7 = 2 * 2 * 2 * 2 * 2 * 2 * 2 = 128
Следует использовать следующий шаблон для преобразования двоичных чисел в десятичные числа и десятичных чисел в двоичные числа. Всегда не забывайте считать справа налево вместо слева направо. Также обратите внимание, что значение каждого разряда удваивается справа налево.
Всегда не забывайте считать справа налево вместо слева направо. Также обратите внимание, что значение каждого разряда удваивается справа налево.
| 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Вышеизложенное следует запомнить. Позже это будет важно помнить при определении количества подсетей и хостов в подсетях. Поэтому этот навык необходимо практиковать и закреплять как можно чаще. Вот несколько примеров задач.
Пример 1 (двоично-десятичный)
11001011 = 128 + 64 + 8 + 2 + 1 = 203
| 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
Написав диаграмму и поместив 1 и 0 под нужными местами в диаграмме, все, что осталось, это сложить значения разрядов, под которыми стоят 1, и сумма будет значением десятичного числа.
Пример 2 (двоично-десятичный)
01011110 = 64 + 16 + 8 + 4 + 2 = 94
| 2 7 | 2 6 | 2 5 | 2 6 3 |
|---|
3664
Чтобы преобразовать десятичные числа в двоичные числа, ставьте 1 в разрядных значениях до тех пор, пока все разрядные значения с 1 не составят сумму. Если какой-либо пронумерованный разряд добавляет значение, превышающее десятичное число, в эти разрядные значения следует вставлять 0.
Пример 3 (десятичный в двоичный)138 = 10001010 или
| 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
Другим методом преобразования десятичных чисел в двоичные является метод остатка. Разделите десятичное число на 2 и запишите 1, если есть остаток, или 0, если остатка нет. Затем разделите ответ на 2 и запишите 1, если есть остаток, или 0, если остатка нет. Процесс деления продолжается до тех пор, пока не останется 8 битов или разрядных значений 1 или 0. Не забудьте записать 1 и 0 в обратном порядке справа налево.
Разделите десятичное число на 2 и запишите 1, если есть остаток, или 0, если остатка нет. Затем разделите ответ на 2 и запишите 1, если есть остаток, или 0, если остатка нет. Процесс деления продолжается до тех пор, пока не останется 8 битов или разрядных значений 1 или 0. Не забудьте записать 1 и 0 в обратном порядке справа налево.
Пример 4 (десятичный в двоичный)
218 = 11011010
| 218 | ÷ | 2 | = | 109 | остаток | 0 | 109 | ÷ | 2 | = | 54 | остаток | 1 | 54 | ÷ | 2 | = | 27 | остаток | 0 |
|---|---|---|---|---|---|---|
| 27 | ÷ | 2 | = | 13 | остаток | 1 | 13 | ÷ | 2 | = | 6 | остаток | 1 | 6 | ÷ | 2 | = | 3 | остаток | 0 | 3 | ÷ | 2 | = | 1 | остаток | 1 | 1 | ÷ | 2 | = | 0 | остаток | 1 |
Работу можно проверить, поместив 1 и 0 обратно в таблицу и сложив значения мест, которые имеют 1.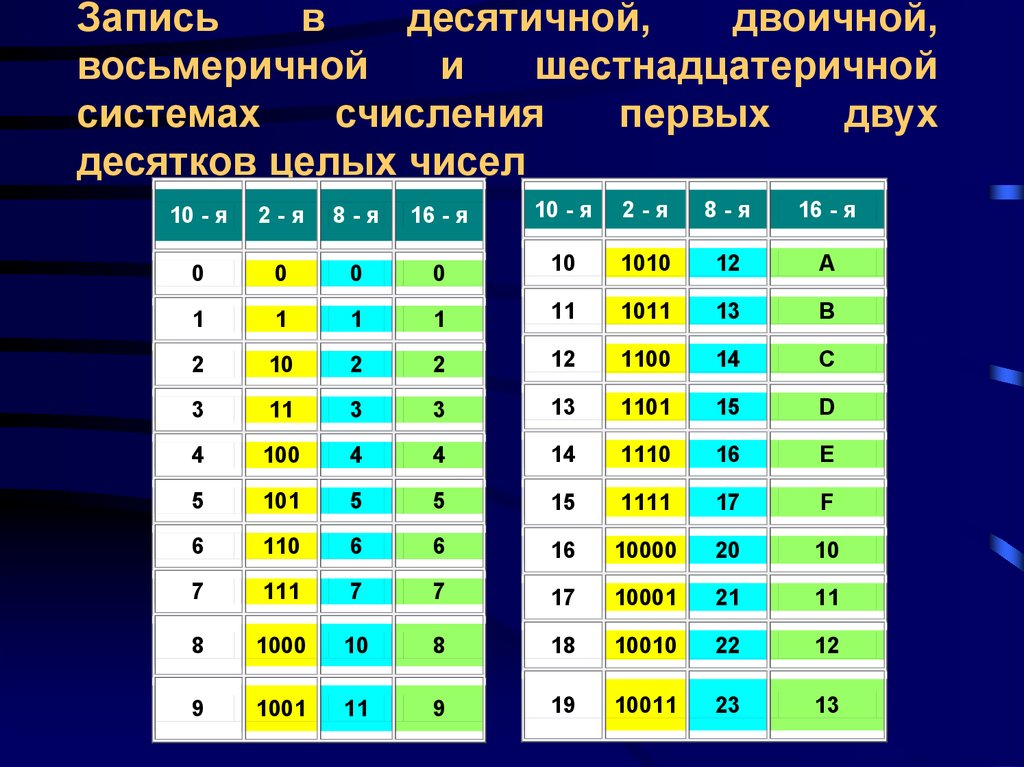
Проверка ответа (218) 128 + 64 + 16 + 8 + 2
| 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 6|
|---|---|---|---|---|---|---|---|
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Шестнадцатеричный (основание 16)
Шестнадцатеричный перевод с греческого означает «шестнадцать».
Hexa=6 (шестиугольник, гексаграмма и т. д.)
Десятичный=10
Шестнадцатеричный=16
В шестнадцатеричной системе к стандартным арабским цифрам от 0 до 9 добавляется 6 букв, чтобы дать вам систему счисления с основанием 16 вместо десяти.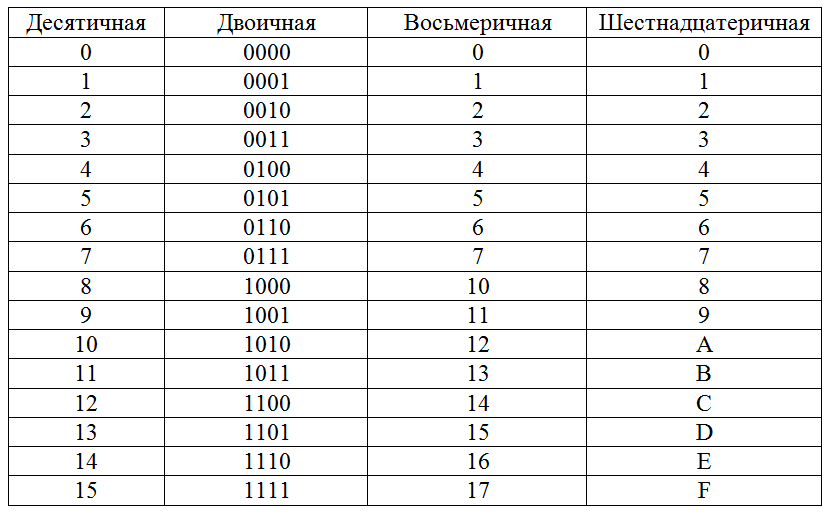
Числа состоят из шестнадцати цифр 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F
Местные значения показаны ниже
16 0 =1
16 1 =16
16 2 = 16 * 16 = 256
16 3 =16 * 16 * 16 = 4069
Подсчет в шестнадцатеричном формате:
Сосчитайте от 0 до 9, затем сосчитайте A, B, C, D, E, F.
Затем вы достигаете 10 (шестнадцатеричное 10, что соответствует десятичному 16).
Посчитайте еще раз: 11, 12, 13, 14, 15, 16, 17, 18, 19, затем используйте 1 и букву: 1A, 1B, 1C, 1D, 1E, 1F.
Затем вы достигаете 20 (шестнадцатеричное число 20, которое соответствует десятичному числу 32).
Это будет продолжаться вечно. Например,
Пример 1 (шестнадцатеричный в десятичный)
B0 в шестнадцатеричном формате = 176 в десятичном формате:
(B[шестнадцатеричный] * 16[десятичный]) + (0 * 1).
Поскольку B равно 11 в десятичном виде, это уравнение принимает вид
. (11 * 16) + (0 * 1) = 11 * 16 = 176.
(11 * 16) + (0 * 1) = 11 * 16 = 176.
| 16 2 | 16 1 | 16 0 |
|---|---|---|
| 256 | 16 | 1 |
| 0 | Б | 0 |
| 11*16 | 0 |
Пример 2 (шестнадцатеричный код в десятичный)
D4 в шестнадцатеричном формате = 212 в десятичном формате:
(D[шестнадцатеричный] * 16[десятичный]) + (4 * 1).
Поскольку D равно 13 в десятичном виде, это уравнение принимает вид
.
(13 * 16) + (4 * 1) = 208 + 4 = 212.
| 16 2 | 16 1 | 16 0 |
|---|---|---|
| 256 | 16 | 1 |
| 0 | Д | 4 |
| 13*16 | 4 |
Вот еще несколько примеров
Шестигранник.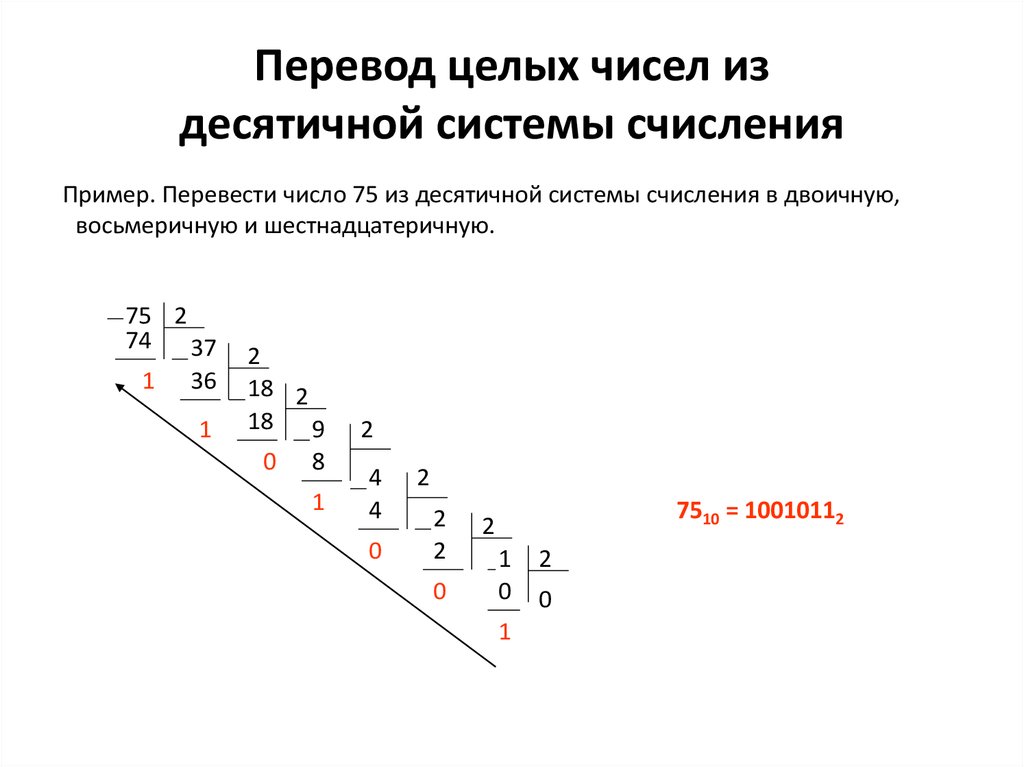 | = | Шестнадцатеричный. уравнение | = | Десятичное уравнение | = | Десятичный |
| С8 | = | (С*16) + (8*1) | = | (12*16) + (8*1) | = | 200 |
| ТФ | = | (Ф * 16) + (Ф * 1) | = | (15*16) + (15*1) | = | 255 |
| 100 | = | (1 * 16 * 16) + (0 * 16) + (0 * 1) | = | (1 * 16 * 16) + (0 * 16) + (0 * 1) | = | 256 |
Пример 6 (десятичный в шестнадцатеричный)
218 в десятичном формате = DA в шестнадцатеричном формате
| 218÷16 = 13 | Д | 218-(13*16) =218 — 208 = 10 | А |
|---|
Пример 7 (десятичный в шестнадцатеричный)
178 в десятичной системе = B2 в шестнадцатеричной системе:
178 = (11 * 16) + (2 * 1) =
(В * 16[шестн. ]) + (2 * 1) =
]) + (2 * 1) =
БИ 2.
Вот еще несколько примеров
| Десятичный | = | Десятичное уравнение | = | Шестнадцатеричный. уравнение | = | Шестнадцатеричный. |
| 48 | = | (3*16) + (0*1) | = | (3*10) + (0*1) | = | 30 |
| 513 | = | (2 * 16 * 16) + (0 * 16) + (1 * 1) | = | (2 * 10 * 10) + (0 * 10) + (1 * 1) | = | 201 |
| 1000 | = | (3*16*16) + (14*16) + (8*1) | = | (3*10*10) + (Е*10) + (8*1) | = | 3E8 |
Вот еще несколько чисел в шестнадцатеричном и десятичном виде.
Попробуйте преобразовать одну форму в другую и обратно, пока не освоитесь с процессом.
| Шестигранник. | Декабрь | . | Шестнадцатеричный. | Декабрь | . | Шестнадцатеричный. | декабря |
| 0 | 0 | 10 | 16 | С8 | 200 | ||
| 1 | 1 | 11 | 17 | Ф0 | 240 | ||
| 2 | 2 | 19 | 25 | ФФ | 255 | ||
| 9 | 9 | 1А | 26 | 100 | 256 | ||
| А | 10 | 1Б | 27 | 3E8 | 1000 | ||
| Б | 11 | 1F | 31 | 1000 | 4 096 | ||
| С | 12 | 20 | 32 | 10000 | 65 536 | ||
| Д | 13 | 32 | 50 | 100000 | 1 048 576 | ||
| Е | 14 | 64 | 100 | ФФФФФФ | 16 777 215 | ||
| Ф | 15 | А0 | 160 | 1000000 | 16 777 216 |
Есть два преимущества шестнадцатеричной системы для компьютеров:
1. Вы можете хранить больше информации в том же пространстве. В шестнадцатеричном коде с двумя цифрами вы можете выразить числа от 0 до 255. В десятичном коде с двумя цифрами вы можете считать от 0 до 99.
Вы можете хранить больше информации в том же пространстве. В шестнадцатеричном коде с двумя цифрами вы можете выразить числа от 0 до 255. В десятичном коде с двумя цифрами вы можете считать от 0 до 99.
2. Шестнадцатеричное (с основанием 16) легко преобразуется в двоичное (с основанием 2), используемое компьютерами. Двузначное шестнадцатеричное число может находиться в диапазоне от 0 до 255, что может быть выражено восемью цифрами двоичного кода (один байт).
Восьмеричный (основание 8)
Octa=6 (октагон, октаграмма, октава и т. д.)
INumbers состоят из восьми цифр 0,1,2,3,4,5,6,7
Значения мест показаны ниже
8 0 =1
8 1 =8
8 2 =8 * 8 = 64
8 3 = 8 * 8 * 8 = 512
8 4 =8 * 8 * 8 * 8 = 4096
8 5 =8 * 8 * 8 * 8 =32768
Подсчет в шестнадцатеричном формате:
Пример 1 (восьмерично-десятичный)
1025 в восьмеричном = 533 в десятичном
(1 * 512) + (0 * 64) + (2 * 8) + (5 * 1)
| 8 5 | 8 4 | 8 3 | 8 2 | 8 1 | 8 0 | ||
|---|---|---|---|---|---|---|---|
| 32768 | 4096 | 512 | 64 | 8 | 1 | ||
| 0 | 0 | 1 | 0 | 2 | 5 | ||
Пример 2 (восьмерично-десятичный)
25170 в восьмеричном = 10872 в десятичном
(2 * 4096) + (5 * 512) + (1 * 64) + (7 * 8) + (0 * 1)
| 8 5 | 8 4 | 8 3 | 8 2 | 8 1 | 8 0 | ||
|---|---|---|---|---|---|---|---|
| 32768 | 4096 | 512 | 64 | 8 | 1 | ||
| 0 | 2 | 5 | 1 | 7 | 0 | ||
Двоичный код в восьмеричный
Если мы сравним разрядность восьмеричного числа с двоичным, вы должны увидеть шаблон
| 2 9 | 28 | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
|---|---|---|---|---|---|---|---|---|---|
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 8 3 | 8 2 | 8 1 | 8 0 |
|---|---|---|---|
| 512 | 64 | 8 | 1 |
Каждая группа из три двоичных числа соответствуют одному восьмеричному числу .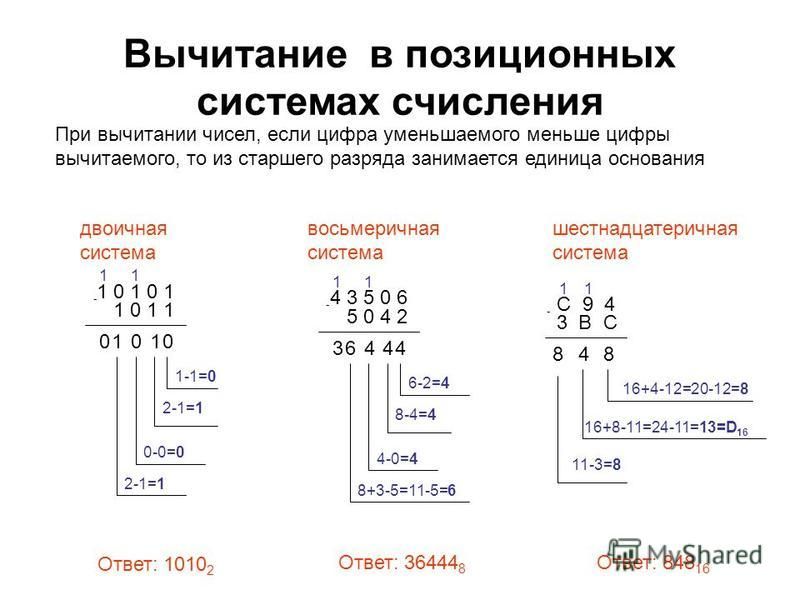
Пример 1
Двоичное число 101011 = 53 восьмеричное
101 | 011 |
5 | 3 |
Пример 2
Двоичный 10010111 = 227 восьмеричный
10 | 010 | 111 |
2 | 2 | 7 |
Пример 3
Двоичный 101011100 = 534 восьмеричный
101 | 011 | 100 |
5 | 3 | 4 |
Двоичный код в шестнадцатеричный
Если мы сравним разрядность восьмеричного числа с двоичным, вы должны увидеть шаблон
| 2 9 | 28 | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
|---|---|---|---|---|---|---|---|---|---|
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 16 2 | 16 1 | 16 0 |
|---|---|---|
| 256 | 16 | 1 |
Каждая группа из четырех двоичных чисел соответствует одному шестнадцатеричному.
Пример 1
Двоичное число 101001 = 29 шестнадцатеричных
10 | 1001 |
2 | 9 |
Пример 2
Двоичный 10010111 = 97 шестнадцатеричный
1001 | 0111 |
9 | 7 |
Пример 3
Двоичный 01011010 = 5A шестнадцатеричный
0101 | 1010 |
5 | 10 |
5 | А |
Пример 3
Двоичный 10111110 = BE шестнадцатеричный
1011 | 1110 |
11 | 14 |
Б | Е |
6.
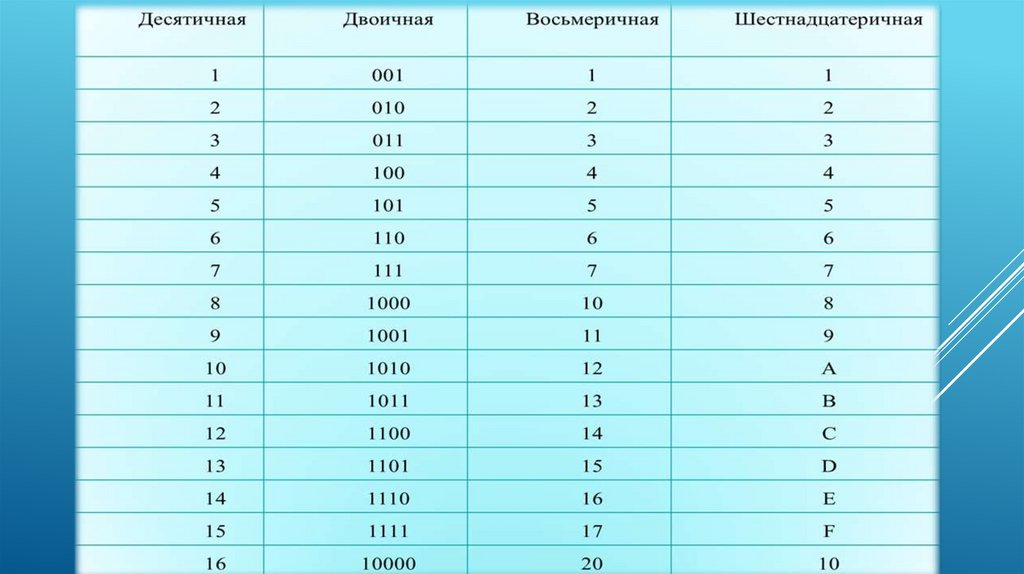 12. Двоичные, восьмеричные, десятичные, шестнадцатеричные числа 90) = 64 + 0 + 16 + 0 + 4 + 2 + 1 = 87, поэтому 1010111 в двоичном формате равно десятичному числу 87.
12. Двоичные, восьмеричные, десятичные, шестнадцатеричные числа 90) = 64 + 0 + 16 + 0 + 4 + 2 + 1 = 87, поэтому 1010111 в двоичном формате равно десятичному числу 87. В приложении введите dec0b1010111 и увидите, что результат равен 87. Код «0b» используется для обозначения числа как двоичного числа. Чтобы преобразовать 87 обратно в двоичный формат, введите bin87. Калькулятор должен отобразить 0b1010111. Число, следующее за кодом «0b», является двоичным эквивалентом 87.
Примеры
Преобразование каждого десятичного числа в двоичное.
1) 105
2) 224
3) 100
Решения для калькулятора
Введите «bin» перед каждым числом.
1) корзина(105)
2) корзина(224)
3) корзина(100)
Примеры
Преобразование каждого двоичного числа в десятичное число.
1) 1101001
2) 11100000
3) 1100100
Решения для калькулятора
Введите «dec» перед каждым аргументом и обозначьте двоичное число как «0b».
1) уб(0b1101001)
2) уб(0b11100000)
3) уб(0b1100100)
90).
Чтобы увидеть это преобразование в приложении, введите oct8 и увидите, что на дисплее отображается 0o10, что означает, что десятичное число 8 эквивалентно 10 в восьмеричной системе счисления. Код «0o» означает, что следующее число является восьмеричным числом.
Чтобы преобразовать восьмеричное число 10 обратно в десятичное, введите dec0o10. Результат 8.
Примеры
Преобразование каждого десятичного числа в восьмеричное.
1) 105
2) 224
3) 100
Решения для калькулятора
Введите «oct» перед каждым аргументом.
1) окт(105)
2) окт(224)
3) окт(100)
Примеры
Преобразование каждого восьмеричного числа в десятичное.
1) 151
2) 340
3) 144
Решения для калькулятора
Введите «dec» перед каждым аргументом и обозначьте восьмеричное число «0o».
1) десят(0o151)
2) десят(0o340)
3) десят(0o144)
Преобразование десятичного числа в шестнадцатеричное и наоборот
Шестнадцатеричная система счисления – это система счисления с основанием 16. Он использует 16 символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F) для представления числа. В отличие от восьмеричной и двоичной систем, здесь используются первые шесть букв алфавита (A, B, C, D, E и F). Это означает, что после 9 система считает A для 10, B для 11, C для 12, D для 13, E для 14 и F для 15. Подсчет от 15 заменяет последнюю цифру.
Например, десятичное число 17 выражается как 11 в шестнадцатеричной системе. Чтобы увидеть его в приложении, введите hex17, и приложение отобразит 0x11. Первые два символа «0x» означают, что следующее число является шестнадцатеричным числом. Чтобы преобразовать шестнадцатеричное число 11 обратно в десятичное, введите dec0x11, и результатом будет 17.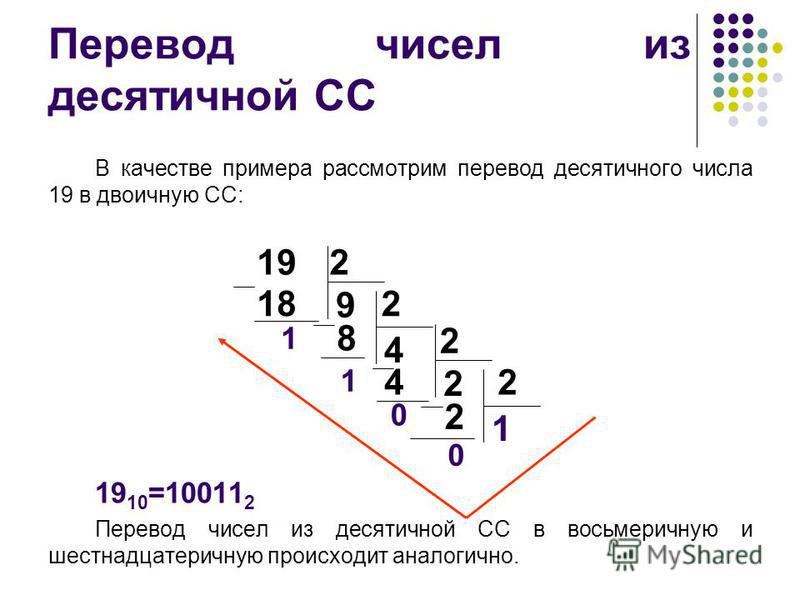
Примеры
Преобразование каждого десятичного числа в шестнадцатеричное.
1) 105
2) 224
3) 100
Решения для калькулятора
Введите «hex» перед каждым аргументом.
1) hex105
2) hex224
3) hex100
Примеры
Преобразование каждого шестнадцатеричного числа в десятичное.
1) 69
2) E0
3) 64
Решения для калькулятора
Введите «dec» перед каждым аргументом и обозначьте шестнадцатеричное число «0x».
1) десят (0x69)
2) десят (0xE0)
3) десят (0x64)
Преобразование между системами счисления
Не забудьте ввести код «0b» для преобразования двоичного числа, «0o» для преобразования восьмеричного числа и «0x» для преобразования шестнадцатеричного числа.
Примеры
1) Преобразовать 10011001 в шестнадцатеричный формат.
2) Преобразовать 1234E в двоичный формат.
3) Преобразование A045 в восьмеричное.
4) Преобразовать 012576 в двоичный формат.
5) Преобразовать 101011 в восьмеричное.
Решения для калькулятора
1) Тип: hex(0b10011001)
Двоичный код 10011001 эквивалентен 99 в шестнадцатеричном формате.
2) Тип: bin(0x1234E)
Шестнадцатеричное число 1234E эквивалентно 10010001101001110.
4) Тип: bin0o012576
Восьмеричное число 012576 эквивалентно 1010101111110 в двоичном формате.
5) Тип: oct0b101011
Двоичное число 101011 эквивалентно восьмеричному числу 53.
СЛЕДУЮЩИЙ: 6.13. комплексные числа>
Список содержимого
Преобразователь десятичного числа в восьмеричное
Чтобы использовать этот преобразователь десятичного числа в восьмеричное , вы должны ввести десятичное значение, например 245, в левое поле ниже, а затем нажать кнопку «Преобразовать». Конвертер даст вам восьмеричный эквивалент заданного десятичного числа.
Конвертер даст вам восьмеричный эквивалент заданного десятичного числа.
Десятичное значение (макс.:
Восьмеричное значение преобразование подкачки: Octal To Decimal Converter
Преобразование десятичного числа в восьмеричное приводит к базовым числам
Десятичная система счисления
Десятичная система счисления является наиболее часто используемой и стандартной системой в повседневной жизни. В качестве основы (основания) используется число 10. Следовательно, он имеет 10 символов: цифры от 0 до 9; а именно 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.
Как одна из старейших известных систем счисления, десятичная система счисления использовалась многими древними цивилизациями. Трудность представления очень больших чисел в десятичной системе была преодолена индо-арабской системой счисления. Индо-арабская система счисления дает позиции цифрам в числе, и этот метод работает с использованием степени основания 10; цифры возводятся до n -й власти, в соответствии со своим положением.
Например, возьмем число 2345,67 в десятичной системе:
- Цифра 5 стоит на позиции единиц (10 0 , что равно 1),
- 4 стоит на позиции десятков (10 1 )
- 3 стоит на позиции сотен (10 2 )
- 2 находится в позиции тысяч (10 3 )
- При этом цифра 6 после запятой находится в десятых долях (1/10, что равно 10 -1 ), а 7 находится в сотых (1/100, то есть 10 -2 ) позиции
- Таким образом, число 2345,67 можно также представить следующим образом: (2 * 10 3 ) + (3 * 10 2 ) + (4 * 10 1 ) + (5 * 10 0 ) + (6 * 10 -1 ) + (7 * 10 -2 )
Восьмеричная система счисления
Восьмеричная система счисления (или сокращенно октальная) использует число 8 в качестве основы (основания). В качестве системы счисления с основанием 8 она использует восемь символов: числа от 0 до 7, а именно 0, 1, 2, 3, 4, 5, 6 и 7. Хотя она использовалась некоторыми индейскими племенами до 20 века. , восьмеричная система стала популярной на заре вычислительной техники как язык компьютерного программирования. Это связано с тем, что восьмеричная система сокращает двоичную систему за счет упрощения длинных и сложных цепочек двоичных изображений, используемых компьютерами.
Хотя она использовалась некоторыми индейскими племенами до 20 века. , восьмеричная система стала популярной на заре вычислительной техники как язык компьютерного программирования. Это связано с тем, что восьмеричная система сокращает двоичную систему за счет упрощения длинных и сложных цепочек двоичных изображений, используемых компьютерами.
Восьмеричная система в основном используется для двоичного счета в группах по три: каждая восьмеричная цифра представляет три двоичных цифры. Поскольку 8 равно 2 в третьей степени (2 3 ), восьмеричная система стала идеальной аббревиатурой от двоичной для машин, которые используют размеры слов, кратные трем, то есть 6-битные, 12-битные, 24-битные или 36-битные. кусочек. В настоящее время большинство современных систем используют шестнадцатеричный формат, а не восьмеричный. Однако восьмеричные числа являются важной частью базовых знаний в области электроники.
Как преобразовать десятичную в восьмеричную
Преобразование десятичного числа в восьмеричное может быть достигнуто путем применения алгоритма повторного деления и остатка. Проще говоря, десятичное число многократно делится по основанию 8. Между этими делениями остатки дают восьмеричный эквивалент в обратном порядке.
Проще говоря, десятичное число многократно делится по основанию 8. Между этими делениями остатки дают восьмеричный эквивалент в обратном порядке.
Вот как шаг за шагом преобразовать десятичное число в восьмеричное:
- Шаг 1 : Если заданное десятичное число меньше 8, восьмеричный эквивалент такой же. Если данное число больше 7, разделите число на 8.
- Шаг 2 : Запишите остаток.
- Шаг 3 : Разделите часть до десятичной точки вашего частного еще раз на 8.
- Шаг 4 : Запишите остаток.
- Шаг 5 : Продолжайте этот процесс деления на 8 и записывая остатки до тех пор, пока последняя десятичная цифра, которая у вас останется, не будет меньше 8.
- Шаг 6 : Когда последняя десятичная цифра меньше 8, частное будет меньше 0, а остаток будет самой цифрой.
- Шаг 7 : Последний остаток, который вы получите, будет старшей цифрой вашего восьмеричного значения, а первый остаток шага 3 будет младшей значащей цифрой.
 Поэтому, когда вы записываете остатки в обратном порядке — начиная снизу со старшей цифры и идя вверх — вы достигнете восьмеричного значения данного десятичного числа.
Поэтому, когда вы записываете остатки в обратном порядке — начиная снизу со старшей цифры и идя вверх — вы достигнете восьмеричного значения данного десятичного числа.
Теперь применим эти шаги, например, к десятичному числу (501) 10
Шаг 1: Поскольку 501 больше 7, разделите на 8. 501 ÷ 8 = 62,625 Шаг 2: Чтобы вычислить остаток, нужно часть после запятой умножить на 8. 0,625 * 8 = 5 Таким образом, первый остаток (и наименее значащая цифра в восьмеричном числе) равен 5. Шаг 3: Разделите 62 (часть частного до запятой) на 8. 62 ÷ 8 = 7,75 Шаг 4: Рассчитайте остаток. 0,75 * 8 = 6 Шаг 5: Разделите целую часть последнего частного на 8. 7 ÷ 8 = 0,875 Шаг 6: Рассчитайте остаток. 0,875 * 8 = 7 (Обратите внимание, что когда вы достигли числа, меньшего, чем система счисления 8 на шаге 3, остаток 7 уже был очевиден. Это потому, что если десятичное число меньше 8, восьмеричный эквивалент имеет то же значение.) Шаг 7: Остатки, написанные снизу вверх, дают вам восьмеричное число (765) 9.5551 8 Таким образом, (765) 8 равно (501) 10
Примеры преобразования десятичной дроби в восьмеричную
Пример 1: (1465) 10 = (2671) 8
Пример 2: (8) 10 = (10) 8
8 ÷ 8 = 1 Остаток 0 1 ÷ 8 = 0,125 0,125 * 8 = 1 (Остаток 1) Прочитайте остаток от наиболее значимого к наименее - снизу вверх: 10.
Пример 3: (10) 10 = (12) 8
10 ÷ 8 = 1,25 0,25 * 8 = 2 (Остаток 2) 1 ÷ 8 = 0,125 (Остаток 1) Прочитайте остаток от наиболее значимого к наименее - снизу вверх: 12.
Пример 4: (1234) 10 = (2322) 8
1234 ÷ 8 = 154,25 (Остаток 2) 154 ÷ 8 = 19,25 (Остаток 2) 19 ÷ 8 = 2,375 (Остаток 3) 2 ÷ 8 = 0,25 (Остаток 2) Восьмеричное число 2322.
Таблица преобразования десятичных чисел в восьмеричные
| Десятичные числа | Восьмеричные числа |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 | 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 10 |
| 9 | 11 |
| 10 | 12 |
| 11 | 13 |
| 12 | 14 |
| 13 | 15 |
| 14 | 16 | 17 |
| 20 | |
| 17 | 21 |
| 18 | 22 |
| 19 | 23 |
| 20 | 24 |
| 21 | 25 |
| 22 | 26 |
| 23 | 27 |
| 24 | 30 |
| 25 | 31 | 26 | 32 |
| 26 | 32 |
| 33 | |
| 28 | 34 |
| 29 | 35 |
| 30 | 36 |
| 31 | 37 |
| 32 | 40 |
| 33 | 41 |
| 34 | 42 |
| 35 | 43 |
| 36 | 44 |
| 37 | 45 |
| 37 | 45 |
| 37 | 45 |
| 37 | 45 |
| 46 | |
| 39 | 47 |
| 40 | 50 |
| 41 | 51 |
| 42 | 52 |
| 43 | 53 |
| 44 | 54 |
| 45 | 55 |
| 46 | 56 |
| 47 | 57 |
| 48 | 60 |
| 48 | 60 |
| 48 | 60 |
| 48 | 60 |
| 61 | |
| 50 | 62 |
| 51 | 63 |
| 52 | 64 |
| 53 | 65 |
| 54 | 66 |
| 55 | 67 |
| 56 | 70 |
| 57 | 71 |
| 58 | 72 |
| 59 | 9000 |
| 59 | |
| 59 | |
| 59 | |
| 74 | |
| 61 | 75 |
| 62 | 76 |
| 63 | 77 |
| 64 | 100 |
| Decimal | Octal | ||
|---|---|---|---|
| 65 | 101 | ||
| 66 | 102 | ||
| 67 | 103 | ||
| 68 | |||
| 105 | |||
| 70 | 106 | ||
| 71 | 107 | ||
| 72 | 110 | ||
| 73 | 111 | ||
| 74 | 112 | ||
| 75 | 113 | ||
| 76 | 114 | ||
| 77 | 115 | ||
| 78 | 110009 | ||
| 117 | |||
| 79 0009 | 117 | ||
| 11000 | 0010|||
| 80 | 120 | ||
| 81 | 121 | ||
| 82 | 122 | ||
| 83 | 123 | ||
| 84 | 124 | ||
| 85 | 125 | ||
| 86 | 126 | ||
| 87 | 127 | ||
| 88 | 130 | ||
| 131 | |||
| 132 | |||
| 132 | 0009 | ||
| 91 | 133 | ||
| 92 | 134 | ||
| 93 | 135 | ||
| 94 | 136 | ||
| 95 | 137 | ||
| 96 | 140 | ||
| 97 | 141 | ||
| 98 | 142 | ||
| 99 | 143 | ||
| 144 | |||
| 101 | 14499 | ||
| 101 | 140009 | 145 | |
| 102 | 146 | ||
| 103 | 147 | ||
| 104 | 150 | ||
| 105 | 151 | ||
| 106 | 152 | ||
| 107 | 153 | ||
| 108 | 154 | ||
| 109 | 155 | ||
| 110 | 156 | ||
| 111 | 157 | ||
| 112 | 160 | ||
| 113 | 161 | ||
| 114 | 162 | ||
| 115 | 163 | ||
| 116 | 164 | ||
| 117 | 165 | ||
| 118 | 166 | ||
| 119 | 167 | ||
| 120 | 170 | ||
| 121 | 171 | ||
. 0009 0009 | 172 | ||
| 123 | 173 | ||
| 124 | 174 | ||
| 125 | 175 | ||
| 126 | 176 | ||
| 127 | 177 | ||
| 128 | 200 |
| Десятичный | Восьмеричный | |
|---|---|---|
| 129 | 201 | |
| 130 | 202 | |
| 131 | 203 | |
| 132 | 204 | |
| 133 | 205 | |
| 134 | 206 | |
| 135 | 207 | |
| 136 | 210 | |
| 137 | 211 | |
| 138 | 212 | |
| 139 | 213 | |
| 140 | 214 | |
| 141 | 215 | |
| 141999 | 215 | |
| 1410009 | 215 | |
| 142 | 216 | |
| 143 | 217 | |
| 144 | 220 | |
| 145 | 221 | |
| 146 | 222 | |
| 147 | 223 | |
| 148 | 224 | |
| 149 | 225 | |
| 150 | 226 | |
| 151 | 227 | |
| 230 | ||
| 153 | 231 | |
| 154 | 232 | |
| 155 | 233 | |
| 156 | 234 | |
| 157 | 235 | |
| 158 | 236 | |
| 159 | 237 | |
| 160 | 240 | |
| 161 | 241 | |
| 162 | 242 | 2419 |
| 162 | 242 | 0009 |
| 163 | 243 | |
| 164 | 244 | |
| 165 | 245 | |
| 166 | 246 | |
| 167 | 247 | |
| 168 | 250 | |
| 169 | 251 | |
| 170 | 252 | |
| 171 | 253 | |
| 172 | ||
| 255 | ||
| 174 | 256 | |
| 175 | 257 | |
| 176 | 260 | |
| 177 | 261 | |
| 178 | 262 | |
| 179 | 263 | |
| 180 | 264 | |
| 181 | 265 | |
| 182 | 266 | |
| 183 | 267 | |
| 183 | 267 | 2669 |
| 183 | 267 | 2669 |
| 183 | 267 | 2669 |
| 184 | 270 | |
| 185 | 271 | |
| 186 | 272 | |
| 187 | 273 | |
| 188 | 274 | |
| 189 | 275 | |
| 190 | 276 | |
| 191 | 277 | |
| 192 | 300 |
. 0069 Окталь 0069 Окталь | |
|---|---|
| 193 | 301 |
| 194 | 302 |
| 195 | 303 |
| 196 | 304 |
| 197 | 305 |
| 198 | 306 |
| 199 | 307 |
| 200 | 310 |
| 201 | 311 |
| 202 | 312 |
| 203 | 313 |
| 204 | 314 |
| 205 | 315 |
| 206 | 316 |
| 207 | 317 |
| 208 | 320 |
| 209 | 321 |
| 210 | 322 |
| 211 | 323 |
| 212 | 324 |
| 213 | 324|
| 213 | 9325 |
| 214 | 326 |
| 215 | 327 |
| 216 | 330 |
| 217 | 331 |
| 218 | 332 |
| 219 | 333 |
| 220 | 334 |
| 221 | 335 |
| 222 | 336 |
| 337 | |
| 223 | 337 |
| 223 | 337 | 224 | 340 |
| 225 | 341 |
| 226 | 342 |
| 227 | 343 |
| 228 | 344 |
| 229 | 345 |
| 230 | 346 |
| 231 | 347 |
| 232 | 350 |
| 233 | 351 |
| 234 | 351|
| 234 | 9352 |
| 235 | 353 |
| 236 | 354 |
| 237 | 355 |
| 238 | 356 |
| 239 | 357 |
| 240 | 360 |
| 241 | 361 |
| 242 | 362 |
| 243 | 363 |
| 244 | 364 |
| 364 | 0007 | 245 | 365 |
| 246 | 366 |
| 247 | 367 |
| 248 | 370 |
| 249 | 371 |
| 250 | 372 |
| 251 | 373 |
| 252 | 374 |
| 253 | 375 |
| 254 | 376 | 9 | 377 |
Преобразование десятичной системы в восьмеричную – введение, примеры и часто задаваемые вопросы
Сначала мы должны узнать об обеих системах сумм. Число с основанием 8 является восьмеричным числом, а разнообразие с основанием 10 является десятичным числом. Здесь мы научимся преобразованию десятичного числа в восьмеричное. Это то же самое, что преобразовать любое десятичное число в двоичное или десятичное в шестнадцатеричное.
Число с основанием 8 является восьмеричным числом, а разнообразие с основанием 10 является десятичным числом. Здесь мы научимся преобразованию десятичного числа в восьмеричное. Это то же самое, что преобразовать любое десятичное число в двоичное или десятичное в шестнадцатеричное.
При преобразовании десятичной системы в двоичную мы делим сумму на 2, при десятичной системе счисления в шестнадцатеричную мы делим сумму на 16. В случае метода преобразования десятичной системы в восьмеричную мы делим сумму на 8 и записываем остаток в обратном порядке. чтобы призвать эквивалентное восьмеричное число.
Десятичная система счисления наиболее знакома широкой публике. Это основание 10, которое имеет всего 10 символов — 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. В то время как восьмеричная система является одной из систем счисления для представления чисел. Это основание 8, которое имеет только 8 символов, таких как 0, 1, 2, 3, 4, 5, 6 и 7.
Обзор восьмеричного числа
лучше сначала иметь хорошее представление об Octal. Итак, в математике восьмеричная система счисления, которую тоже довольно часто называют окталем. Проще говоря, эта система использует 8 в качестве основы для расчета, а не число 10. Таким образом, то, что представляет число 10 в обычной системе счисления, представлено 8 в восьмеричной системе счисления.
Итак, в математике восьмеричная система счисления, которую тоже довольно часто называют окталем. Проще говоря, эта система использует 8 в качестве основы для расчета, а не число 10. Таким образом, то, что представляет число 10 в обычной системе счисления, представлено 8 в восьмеричной системе счисления.
Теперь, что касается десятичной системы счисления, в обычной системе счисления десятичная всегда представлена цифрой 10, но в восьмеричной системе счисления она снова представлена цифрой 8. Если вам может быть интересно, что если 10 представлено цифрой 8 в восьмеричная система счисления, тогда как насчет 100. Опять же, это просто, 100 — это 10 умножить на 10, и аналогичным образом для восьмеричной системы счисления получается 8 умножить на 8, то есть 65. Итак, 100 в обычном система счисления становится 64 в восьмеричной системе счисления.
В десятичной системе, как сказано выше, каждое число имеет основание десять. Итак, возьмем в качестве примера семьдесят четыре, 74.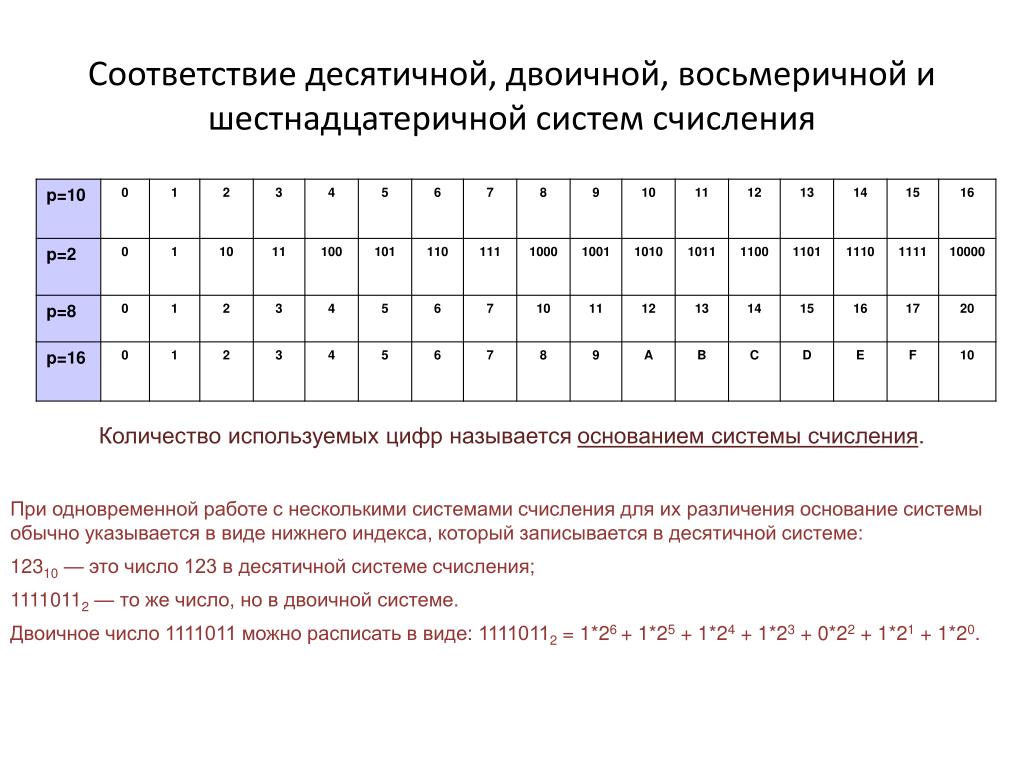 Таким образом, это означает 7, умноженное на 10 в степени 1, и сложение. 4 умножьте на 10 в степени 0.
Таким образом, это означает 7, умноженное на 10 в степени 1, и сложение. 4 умножьте на 10 в степени 0.
Теперь давайте посмотрим на восьмеричную систему счисления того же числа, которое равно 74, что означает умножение 8 на 8, а затем добавление 8 в степень 1, а затем снова добавление 2.
О восьмеричной системе счисления можно узнать гораздо больше, и если вы хотите узнать об этой системе счисления, нажмите на эту ссылку.
Преобразование десятичного числа в восьмеричное
Существует много методов преобразования десятичного числа в восьмеричное, некоторые из которых обсуждаются здесь:
Евклидов метод последовательного деления на 8: Математик Евклид. Все, что вам нужно сделать здесь, это разделить исходное число на степень 8, которая должна быть наибольшей степенью 8. Делая это, вы будете получать напоминания, что вам нужно делать с этими напоминаниями, так это делите меньшие степени числа 8 последовательно, пока, наконец, не останется 1.
 Формирование восьмеричных чисел осуществляется с помощью частных и записывается в порядке, который генерируется алгоритмами.
Формирование восьмеричных чисел осуществляется с помощью частных и записывается в порядке, который генерируется алгоритмами.Метод последовательного умножения на 8: Этот метод также полезен для преобразования десятичной дроби в восьмеричную. Во-первых, все, что вам нужно сделать, это умножить десятичную дробь на 8. Какой бы результат ни получился, его целая часть становится первой цифрой восьмеричной дроби. Теперь сделайте то же самое с дробной частью числа, то есть умножьте его на число 8, пока, наконец, оно не станет равным нулю. Иногда эти два заданных метода, то есть евклидов метод последовательного деления на 8 и метод последовательного умножения на 8.
Преобразование десятичной системы счисления в восьмеричную
Давайте узнаем, как преобразовать десятичную систему счисления в восьмеричную. Существуют различные прямые или косвенные методы преобразования десятичного числа в восьмеричное (метод преобразования десятичного числа в восьмеричное). В косвенном методе нам нужно преобразовать десятичное число в другую систему счисления (например, двоичную или шестнадцатеричную), затем мы можем преобразовать их в двоичные числа, преобразовав каждую цифру в двоичные числа из шестнадцатеричной и используя группировку из восьмеричной системы счисления.
В косвенном методе нам нужно преобразовать десятичное число в другую систему счисления (например, двоичную или шестнадцатеричную), затем мы можем преобразовать их в двоичные числа, преобразовав каждую цифру в двоичные числа из шестнадцатеричной и используя группировку из восьмеричной системы счисления.
Пример — преобразование десятичного числа 98 в восьмеричное число
Сначала преобразуйте его в двоичное или шестнадцатеричное число.
= (98) 10
= (1×2 6 + 1×2 5 + 0x2 4 + 0x2 3 + 0x2 2 + 1×2 1 + 0 x 2 0 ) 10 или (6 x 16 1 +2×16 0 ) 10
Поскольку основания двоичного и шестнадцатеричного чисел равны 2 и 16 соответственно, вы получаете
= (1100010) 2
или (62) 16
Затем преобразуйте каждую цифру шестнадцатеричного числа в 4 бита двоичного числа, одновременно преобразуя каждую группу из трех битов из наименее значащих в двоичное число.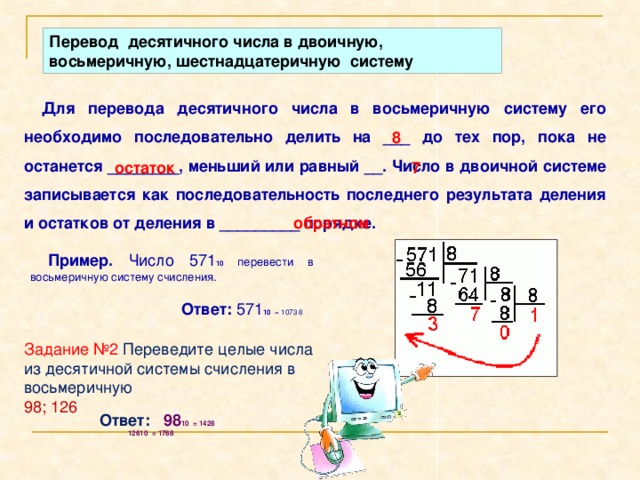
= (001 100 010) 2
OR (0110 0010) 2
= (001 100 010) 2
= (1 4 2) 1 =. 8 Но есть два прямых метода преобразования десятичного числа в восьмеричное — преобразование с остатком и преобразование с делением. Они объясняются следующим образом. Это простой метод, который включает в себя деление числа, которое нужно преобразовать. Пусть десятичное число равно N, а затем разделите это число на 8, потому что основание восьмеричной системы счисления равно 8. Запишите значение остатка, который может быть — 0, 1, 2, 3, 4, 5, 6, или 7. Снова делим оставшееся десятичное число, пока оно не станет 0, и отмечаем каждый остаток выполненного шага. Затем запишите остаток снизу вверх (или в обратном порядке), который также будет эквивалентен восьмеричному числу данного десятичного числа. Возьмите десятичное число как делимое. Разделите число на 8 (поскольку 8 является основанием восьмеричного числа, здесь делитель). Сохранить остаток в массиве (и это будет: 0, 1, 2, 3, 4, 5, 6 или 7 из-за делителя 8). Повторяйте два предыдущих шага, пока сумма не станет больше нуля. Выведите упомянутый массив в обратном порядке (что также будет эквивалентно восьмеричному числу заданного десятичного числа). Делимое (здесь — заданное десятичное число) здесь есть число, которое также делится, делитель (здесь основание восьмеричного числа, т. Пример. Чтобы преобразовать десятичное число 210 в восьмеричное число Поскольку мы знаем, что данное число является десятичным целым числом, поэтому, просто используя описанный выше алгоритм, мы выполняем короткое деление на 8 с остатком. Division Remainder (R) 210 / 8 = 26 2 26 / 8 = 3 2 3 / 8 = 0 3 Теперь запишем остаток снизу вверх (в обратном порядке) эквивалентное восьмеричное число для десятичного целого числа 210. Для десятичной дробной части метод поясняется следующим образом. Пусть десятичная дробь также является частью M, тогда мы умножаем это число на 8, потому что основание для восьмеричной системы счисления равно 8. Запишите значение целого числа часть, которая будет — 0, 1, 2, 3, 4, 5, 6 и 7. Снова мы умножаем оставшееся десятичное дробное число, пока оно не станет 0, а затем отмечаем каждую целую часть для результата каждого шага. После этого запишите отмеченные результаты целой части, которая будет эквивалентной дробью восьмеричной части заданного десятичного числа. Это процедура преобразования дробного десятичного числа, алгоритм приведен ниже. Возьмем десятичное число как произведение. Умножьте это число на 8 (8 — основание восьмеричного числа, поэтому здесь умножьте). Сохраните значение целой части результата в массиве (это будет: 0, 1, 2, 3, 4, 5, 6 и 7 из-за множителя 8). Повторяйте два вышеуказанных шага до тех пор, пока число не станет равным нулю. Распечатайте массив (который будет похож на дробное восьмеричное число до заданного десятичного дробного числа). Пример — преобразование десятичного дробного числа 0,14086 Поскольку мы знаем, что данное число является десятичным дробным числом, поэтому, просто используя описанный выше алгоритм, мы выполняем короткое умножение на 8 с целой частью. Умножение Результирующая целочисленная часть 0,14086 .7 1951 9552 (a) Преобразование с остатком (для целочисленной части)
 Это процедура преобразования целого десятичного числа, алгоритм приведен ниже.
Это процедура преобразования целого десятичного числа, алгоритм приведен ниже.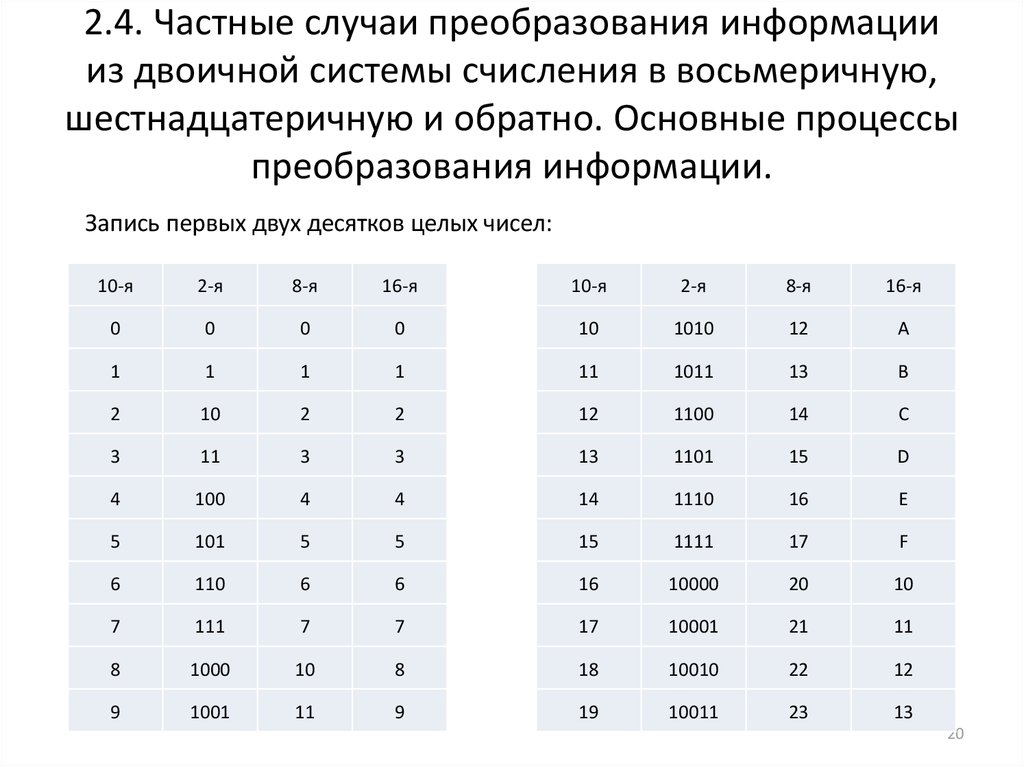 е. 8) в числе, на которое делится делимое, и частное — это результат деления.
е. 8) в числе, на которое делится делимое, и частное — это результат деления.
(b) Преобразование с остатком (для дробной части)

25 в восьмеричное число. 25 x 8 = 0,126989139131313131313 9000 3 


 н.э.
н.э.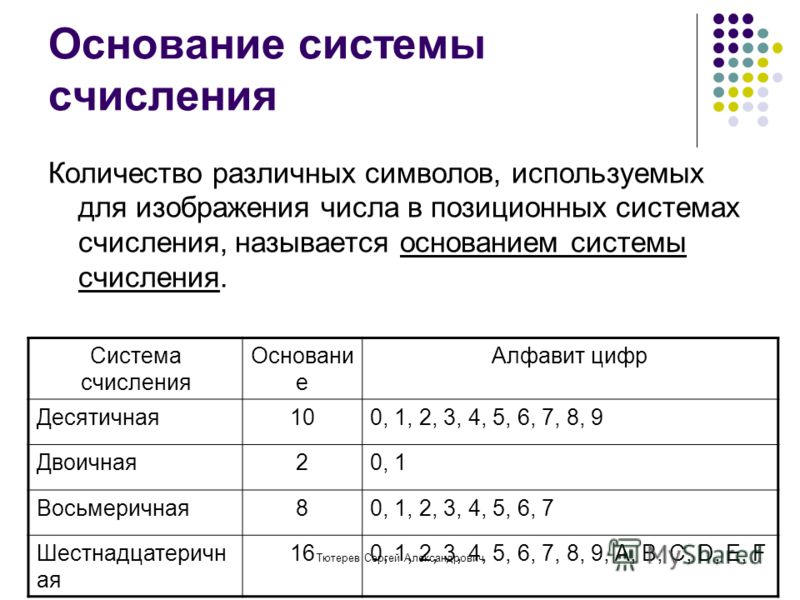 0008 31
0008 31