Лаб 12. ВектМатр в MathCad
Лабораторная работа 4-5
Тема: Использование векторных и матричных операций для решения задач в системе MathCad
Задание:
Задать два вектора X и Y с пятью элементами двумя способами. Элементы первого вектора – произвольно заданные числа. Элементы 2 –го вектора вычисляются по формуле: .
Выполнить следующие преобразования: элементы вектора Х удвоить, элементы вектора Y увеличить на 1.
Получить вектор Z, равный сумме векторов X и Y. Найти скалярное произведение векторов X и Y.
Задать два вектора X и Y из трех элементов. Найти их скалярное и векторное произведения, используя соответствующие «кнопки» на панели инструментов «
Задать две квадратные матрицы А и В одинаковых размеров (не больше 5). Получить: сумму матриц, разность матриц, произведение, определитель каждой из матриц.
Найти обратные матрицы. Произвести проверку того, что обратные матрицы вычислены верно.
Найти скалярное произведение первой строчки матрицы А на ее последний столбик.
Преобразовать матрицу А по правилу: элементы умножить на максимальный элемент этой матрицы (воспользоваться функцией мax из мастера функций).
Преобразовать матрицу В по правилу: элементы каждой строчки умножить на максимальный элемент этой строчки (воспользоваться функцией мax из мастера функций).
Найти суммы элементов в каждом из столбиков матрицы А.
Найти суммы элементов в каждом из строк матрицы А.
Найти сумму всех элементов матрицы А.
Соединить (дописывая справа) матрицы в одну матрицу D. Из второй строки матрицы D получить вектор K.
Повторить пункт 12, но соединение организовать дописыванием вниз.
Определить функцию . Определить функцию с именем — как производную от функции Fun.
Построить две матрицы, у одной матрицы элементы должны вычисляться по формуле: . У другой матрицы элементы , где t1 и t2 — переменные, принимающих значения из промежутка (каждая из своего промежутка значений). Заметим, что размеры матрицы V зависят от выбранных промежутков и шагов.
Порядок выполнения работы
Загрузить систему Mathcad.
Познакомиться с методическим указанием.
Выполнить задание.
Подготовить отчет. В отчет включить разделы: тема, ход работы, вывод.
Сдать работу преподавателю.
Методические указания
Задание векторов и матриц
Векторы могут рассматриваться как матрицы, состоящие из одного столбца. Существуют две возможности задания векторов и матриц:
С помощью индексированных переменных. Любая индексированная переменная, индексами которой являются переменные, принимающие целочисленные значения из некоторого промежутка, уже представляют собой вектор или матрицу.
Пример. Требуется задать вектор x, состоящий из 6 элементов. Элементам этого вектора присвоить значения индексов.
Решение:
А) задать индексированный промежуток для переменной i:i := 0..5 (знак .. появляется после набора ;)
В) присвоить элементам вектора х значения индексов (к индексу можно перейти с помощью символа — левой квадратной скобки, либо с помощью кнопки на панели инструментов):
xi := i
C) «распечатать» вектор:
С помощью использования команды Matrix. Взять эту команду можно либо из меню «Insert»(а), либо на панели инструментов «Matrix»(в), как это показано на рис.1. В открывшемся диалоговом окне «Insert Matrix» необходимо указать число строк и число столбцов. В нашем примере число строк равно 6, а число столбцов равно 1. Решение предыдущего примера в этом случае сводится к последовательности действий:
х:=
выполнить команду Matrix;
задать параметры в диалоговом окне «Insert Matrix»;
заполнить шаблон, который откроется после нажатия кнопки «Ok».
P.S. Диалоговое окно «Insert Matrix» содержит кнопку «Delete». Если выделен один из элементов матрицы, эта кнопка позволяет удалить число строк (находящихся ниже выделенного элемента) и столбцов (находящихся справа от выделенного элемента), которое будет указано в полях диалогового окна. Аналогично с помощью команды «Insert» можно вставить заданное число строк и столбцов.
Рис.1. Вызов диалогового окна «Insert Matrix» для создания матрицы с помощью команды «Matrix»
Операции с векторами и матрицами, матричные функции
С матрицами могут производиться как численные, так и символьные вычисления. Операции с матрицами в системе MathCad обозначаются так, как это принято в математике: —, +, *, … . На рис. 2 показаны назначение некоторых команд, расположенных на панели инструментов «Matrix».Х-1 – получить обратную матрицу
|X| — вычислить детерминант
МТ – транспонировать
М< > — из матрицы взять вектор-столбец
v – получить сумму элементов
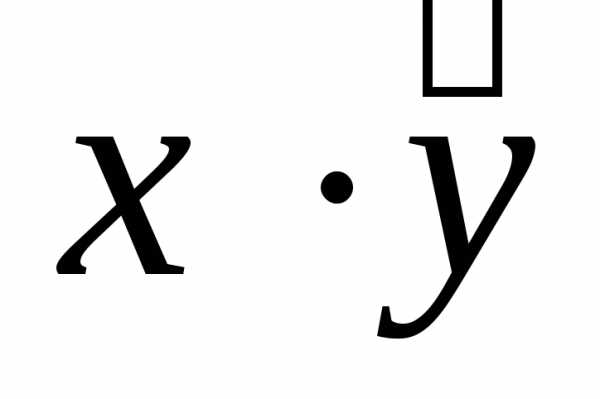 -скалярное
произведение векторов
-скалярное
произведение векторов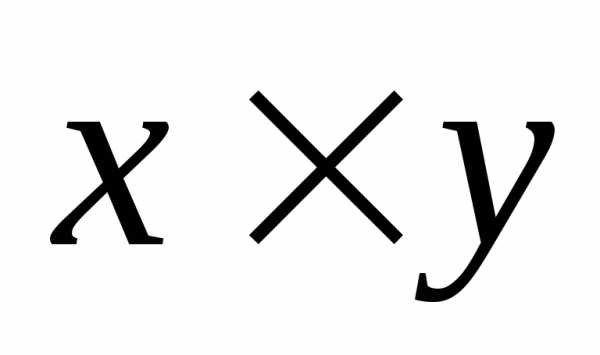
Рис.2. Назначение некоторых команд, расположенных на панели инструментов «Matrix».
Помимо этого, система MathCad представляет большое количество функций для работы с векторами и матрицами. Воспользоваться этими функциями можно с помощью мастера функций f(x) , обратиться к которому можно с помощью команды, как это показано на рис.3.
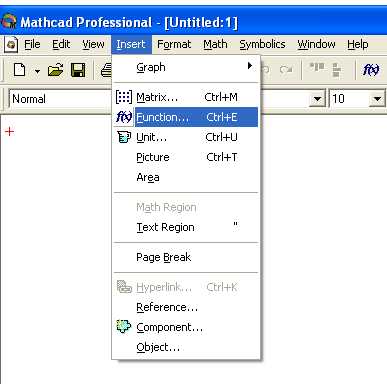
Рис.3. Вызов мастера функций
Вызов мастера функций открывает диалоговое окно, как это показано на рис.4. В этом окне следует открыть категорию «Vector and Matrix», как это показано на рис.4. В окне «Function Name» перечислены имена функций для выбранной категории в алфавитном порядке. А внизу комментарии по их назначению и использованию.
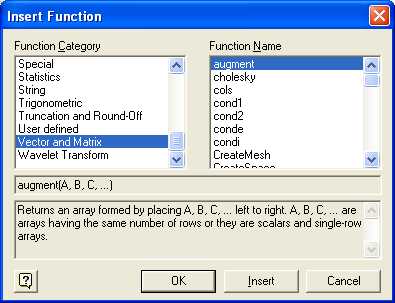
Рис.4. Диалоговое окно мастера функций
Формирование из вектора диагональной матрицы
Формирование матрицы заданного размера с элементами
d i,j =F(i,j),
где F – определенная функция
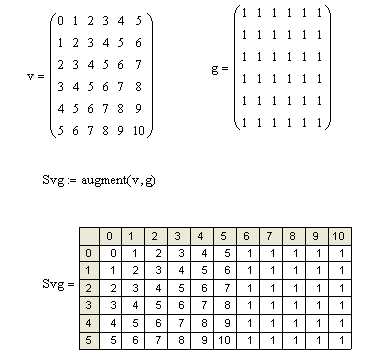
Соединение двух матриц в одну матрицу (рядом –функция augment, друг под другом — функция stack)
Выделение подматрицы из матрицы v
Формирование вектора из матрицы по его номеру
Преобразование прямоугольных координат в цилиндрические координаты и наоборот
Рис.5. Примеры использования функций и операторов для работы с векторами и матрицами
Контрольные вопросы
Какие операции представлены на панели инструментов «Matrix»?
Как задать вектор? Как задать матрицу?
Как задать матрицу с элементами, вычисленными по формулам?
- Найти функцию еlement.и пояснить ее назначение?
Найти функцию rank.и пояснить ее назначение?
Как из матрицы получить вектор – столбец? Вектор-строчку?
Как получить обратную матрицу?
Когда обратную матрицу вычислить нельзя?
Как проверить, вычислена ли обратная матрица правильно?
Где взять функции для работы с матрицами?
Как создать единичную матрицу?
studfiles.net
Работа с матрицами и векторами в MathCAD. Задачи линейной алгебры — Студопедия.Нет
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Курганский государственный университет»
Кафедра «Автоматизация производственных процессов»
ОСНОВЫ ИНЖЕНЕРНЫХ РАСЧЁТОВ
Методические указания к комплексу лабораторных, практических и контрольных работ по курсу «Основы инженерных расчётов»
для студентов направлений подготовки
15.03.04 Автоматизация технологических процессов и производств
(профиль «Автоматизация технологических процессов и производств
(машиностроение)»),
27.03.04 Управление в технических системах (профиль «Системы и
технические средства автоматизации и управления»)
Курган 2018
Кафедра: «Автоматизация производственных процессов»
Дисциплина: «Основы инженерных расчётов»
Составил: к.т.н., доцент Е.К. Карпов.
Утверждены на заседании кафедры 21 декабря 2017 г.
Рекомендованы методическим советом
университета __________ 20__ г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ…………………………………………………………………………..4
1 Представление результатов вычислений. Управление вычислениями…………4
2 Работа с матрицами и векторами в MathCAD. Задачи линейной алгебры…….8
3 Создание графиков в MathCAD. Двумерные графики и трехмерные графики13
4 Встроенные функции MathCAD для решения обыкновенных уравнений и систем. Решение систем дифференциальных уравнений………………………..15
5 Первая программа и обработка информации из внешнего файла…………….16
6 Циклы и операторы. Программы с ветвлениями и рекурсивные вычисления.19
7 Задания для контрольной работы……………………………………………….21
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ………………………………31
ВВЕДЕНИЕ
Целью освоения дисциплины «Основы инженерных расчётов» является приобретение студентами знаний о применении систем компьютерной математики для автоматизации инженерно-технической деятельности и ознакомление с наиболее популярными современными математическими пакетами. Практическое введение в MathCAD и освоение технически структурного программирования в объёме, достаточном для использования этой системы при изучении соответствующих разделов высшей математики, общетехнических и специальных дисциплин.
Изучение приведённых далее материалов позволит студентам узнать о современных средствах автоматизации математических расчётов, получить навыки для решения задач математического моделирования, вычислительных задач математического анализа, построения геометрических фигур различной степени сложности, решения задач, связанных с матрицами, и исследованием динамических систем.
Также методические указания содержат задания для контрольной работы студентов заочной формы обучения и материалы, необходимые для её выполнения.
Представление результатов вычислений. Управление вычислениями
Программный пакет MathCAD обладает встроенной математической палитрой, представляющей собой набор специализированных панелей для работы с различными типами данных, вычислений, графических построений и программирования. Наиболее простой способ знакомства с ними состоит в практическом освоении каждой из них в процессе решения тех или иных задач. В первой главе сделан упор на самые простые вычисления панели калькулятора и работу с различными типами данных. Также показана возможность создания своих функций, основываясь на которой необходимо будет выполнять задания к этой и последующим главам.
На рисунке 1 представлены примеры различных выражений, написанных с помощью программы MathCAD. Примеры а) и б) — это арифметические выражения, операндами которых являются числовые константы, заданные в десятичной (а) и в шестнадцатеричной (б) системах счисления. Результаты вычисления этих выражений — числовые константы, формат представления которых пользователь может выбрать по своему усмотрению.
Пример в) — это алгебраическое выражение, операндами которого являются константы и переменные числового типа. Результат вычисления этого выражения — число, определяемое значениями числовых переменных a, b и c.
В примере г) используется один из операторов суммирования элементов числовых рядов. Операнд этого оператора использует функцию, возвращающую значение синуса угла, заданного с использованием переменной α и предопределенной переменной π;
Пример д) — логическое выражение, использующее операторы сравнения “больше” и “не равно” и логические операторы “отрицания” и “конъюнкции”. Результатом вычисления этого выражения будет одно из двух логических значений: «истина» или «ложь» в зависимости от значений переменных x, y, z.
Пример е) иллюстрирует возможность использования логического выражения в качестве операнда арифметического выражения. Такая возможность в системе MathCAD существует, так как логические константы «истина» и «ложь» ассоциируются с числовыми константами «1» и «0», соответственно.
Примеры ж) и з) иллюстрируют использование операторов интегрирования и дифференцирования.
Рисунок 1 – Примеры различных выражений
На рисунке 2 приведены результаты различных вычислений, произведённых с числовыми типами данных. Выражение а) иллюстрирует возможность различного форматирования результата вычисления выражения числового типа; б) возможность использования в одном выражении чисел, заданных в различных системах счисления; в) содержит примеры использования в выражениях комплексных чисел и встроенных функций для их обработки.
Рисунок 2 – Результаты вычислений над числовыми типами
Строковый тип данных используется для хранения и работы с текстовой информацией. В программе MathCAD существует большое количество функций для работы с ними. На рисунке 3 приведены результаты работы некоторых из них.
Функция concat (от англ. concatenation — слияние) обеспечивает объединение нескольких текстовых строк в одну.
Функция num2str преобразует число в текстовую строку, состоящую из цифр этого числа, а функция str2num производит обратное преобразование (в последнем случае исходная строка символов должна содержать только цифры).
Функция strlen определяет длину (число символов) строки.
Функция substr выделяет из заданной строки подстроку, начиная с символа, номер которого задается вторым параметром функции. Длина выделяемой подстроки задается третьим параметром функции.
Функция str2vec формирует вектор ASCII-кодов символов заданной строки, а функция vec2str формирует строку символов по заданным их ASCII-кодам (коды могут быть представлены в любой системе счисления).
Функция IsString возвращает логическое значение «истина», если ее аргумент имеет строковый тип данных, и значение «ложь» в противном случае.

Рисунок 3 – Работа со строковым типом данных
Важной частью работы с программным пакетом MathCAD является возможность определять функции и использовать их в дальнейшем. На рисунке 4 а) определена пользовательская функция SqTrap, предназначенная для расчета площади трапеции, размеры которой определяются формальными аргументами а, b и h. Предлагается три различных способа обращения к этой функции для расчета площади трапеции с основаниями 1м и 2м и высотой Зм: в первом случае фактические аргументы заданы числовыми константами, во втором — определенными ранее переменными х, у и z, а в третьем — числовыми константами и выражением.
Рисунок б) иллюстрирует возможность использования имени функции в качестве параметра другой функции.

Рисунок 4 – Создание функций
Рисунок в) содержит примеры обработки данных логического типа. Переменная А определена с помощью логического выражения и при заданных значениях переменных х, у и z получила значение «ложь», которое отображается числовым значением “0”. Встроенная функция if() анализирует значение логического выражения, заданного ее первым аргументом, и если оно «истинно», возвращает второй параметр, а в противном случае — третий.
Применение функций при решении практических задач можно использовать в следующих задачах:
— требуется рассчитать мгновенное значение тока, полученного в результате однополупериодного выпрямления синусоидального тока i в различные моменты времени:
,
чтобы вычислить значение выпрямленного тока в другие моменты времени, достаточно в самом первом выражении изменить значение t и задать режим вычислений;
— определить скорость равноускоренного движения точки через 4 секунды от начала вычислений:
,
чтобы вычислить значение скорости в любой момент времени, необходимо просто задать это время в созданной функции. Начальная скорость и ускорение задаются константами.
Задания к главе 1:
1) введите все примеры с рисунков главы в MathCAD;
2) разработайте пользовательскую функцию, реализующую специализированный калькулятор для расчёта длины отрезка прямой, заданного координатами x, y, z его граничных точек;
3) создайте 4 переменных строкового типа, содержащие Ваши фамилию, имя, отчество (латинскими буквами) и год рождения. Используя встроенные функции группы «string»:
а) определите переменную fullname, содержащую Ваше полное имя;
б) определите количество символов в строке fullname;
в) определите первый и последний символы строки fullname;
г) выделите подстроку fitstname из строковой переменной fullname;
д) определите ASCII-коды цифр, образующих Ваш год рождения;
е) определите, имеет ли строковый тип данных переменная, хранящая Ваш год рождения;
ж) преобразуйте строковую переменную (год рождения) в соответствующую ей переменную числового типа;
4) разработайте пользовательскую функцию, которая принимает в качестве параметров две строковых переменных А и В и целое число n, а возвращает строку, в которой строка В вставлена в строку А между n-м и (n+1)-м её символами, Если хотя бы один из параметров А, В имеет не строковый тип данных, или если значение параметра n превышает длину строки А, функция должна возвратить строку «Error»;
5) пусть задана переменная строкового типа произвольной длины, последние четыре символа которой — цифры, представляющие год (например, «Konstantin P. Philimonov, esquire, was burn in 1982»). Разработайте пользовательскую функцию, модифицирующую такую переменную путем увеличения «года» на заданное число;
6) решите 9 и 17 варианты заданий 1 и 2 из контрольной работы, опираясь на пример, приведённый в конце данных методических указаний.
Работа с матрицами и векторами в MathCAD. Задачи линейной алгебры
В MathCAD для работы с матрицами и векторами предназначена специальная панель инструментов Matrix (рисунок 5). Чтобы отобразить панель Matrix необходимо щелкнуть по кнопке на математической панели Math.
Рисунок 5 – Панель инструментов Matrix
Рассмотрим назначение некоторых из кнопок панели Matrix:
– создание новой матрицы;
– ввод элемента массива;
– формирование обратной матрицы;
– вычисление определителя матрицы;
– определение столбца матрицы: А<j>– j-й столбец матрицы;
– транспонирование матрицы;
– определение ранжированной переменной: j=m..n;
– вычисление скалярного произведения векторов;
– вычисление векторного произведения векторов.
В примере на рисунке 6 определена переменная А — она получила значение матрицы размерностью 4х6, элементами которой являются константы числового и строкового типов. Строки и столбцы этой матрицы пронумерованы, начиная с нуля, так как переменная ORIGIN имеет нулевое значение (по умолчанию). После переопределения этой переменной соответственно изменилась и нумерация элементов матрицы.
Ниже на том же рисунке иллюстрируется возможность использования переменных и функций в качестве элементов массивов. Заметим, что переменная р и функция g(х) должны быть определены до определения массива В. При вычислении значения переменной В элементы массива р, g(р), и g(1) получили соответствующие числовые значения. В качестве индексов элементов массива использованы три различных математических выражения. При использовании индексных выражений необходимо следить, чтобы они возвращали целочисленные значения, не выходящие за пределы допустимых значений, соответствующих текущему значению переменной ORIGIN. В данном примере строки матрицы B пронумерованы от нуля до двух, а столбцы — от нуля до трех.
Массив D определен путем присвоения значений отдельным его элементам. Если к моменту определения некоторого элемента массива сам массив еще не определен, он будет создан автоматически. Размерность этого массива будет соответствовать значению индекса определяемого элемента, а все «предшествующие» элементы массива получат нулевые значения. Если определяется элемент существующего массива, и индекс элемента выходит за пределы его размерности, массив соответственно «расширяется» с возможным добавлением “нулевых” элементов.
Индексы элементов массива Е определены целочисленными ранжированными переменными і и j, а значения элемента массива Еi,j вычисляются с помощью выражения, включающего эти переменные в качестве операндов.
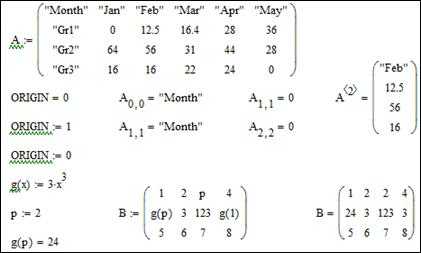
Рисунок 6 – Способы определения матриц
На рисунке 7 приведены примеры применения операторов для работы с векторами и матрицами: а) – любой двуместный арифметический оператор, операндами которого являются массив и скаляр, применяется ко всем элементам массива, в результате чего изменяются лишь значения элементов массива, а его структура сохраняется.
Если оба операнда — массивы (пример б), то тривиальными являются только операторы сложения и вычитания и лишь в том случае, если оба массива имеют одинаковую размерность.

Рисунок 7 – Применение операторов для работы с векторами и матрицами
Пример в) иллюстрирует применение оператора «| |» с различными операндами. В этом операторе допускается использование только двух видов операндов-массивов: вектор — в этом случае вычисляется его модуль, и квадратная матрица — в этом случае вычисляется ее определитель.
Пример г). Если два вектора (одинаковой размерности) объединены оператором умножения (*), будет вычислено их скалярное произведение. Если два трехэлементных вектора объединены оператором (х), будет определен новый вектор — результат векторного произведения исходных векторов. Этот вектор имеет модуль, равный произведению модулей исходных векторов на синус угла между ними, и описывает направленный отрезок, перпендикулярный плоскости расположения исходных векторов.
Если операндами оператора умножения (*) являются не векторы, а матрицы (пример д), этот оператор выполняет умножение матриц, в результате которого формируется новая матрица.
Пример е) иллюстрирует применение оператора возведения массива в степень. Операндом такого оператора может быть только квадратная матрица, а показатель степени может быть только целочисленным скаляром. При этом нулевая степень матрицы трактуется как единичная матрица, первая степень — сама исходная матрица, другие положительные степени матрицы трактуются в смысле операции матричного умножения, минус первая степень — обратная матрица (результатом умножения которой на исходную матрицу является единичная матрица), прочие отрицательные степени матрицы – соответствующие положительные степени обратной матрицы.
В примере ж) показаны операторы транспонирования массивов и суммирование элементов векторов. Следует обратить внимание на оператор транспонирования вектора: в результате формируется матрица, состоящая из одной строки. Обращение к элементам такой матрицы производится с использованием двойного индекса.
Применение матричных исчислений при решении практических задач можно продемонстрировать, произведя расчёт электрической цепи с помощью уравнений Кирхгофа.
Рассмотрим цепь, изображенную на рисунке 8. Требуется рассчитать токи во всех ветвях различными методами.

Рисунок 8 – Пример электрической цепи для расчёта
Рассчитаем токи во всех ветвях с помощью уравнений Кирхгофа. Зададим данные:
где mE, aE — модуль и аргумент (в радианах) значения ЭДС, заданной в показательной форме;
mZ3, aZ3 — модуль и аргумент сопротивления Z3.
Для наглядности все величины, заданные в показательной форме, переведём в алгебраическую форму. Это можно будет и не делать, так как Mathcad это делает автоматически
Далее составим систему уравнений по законам Кирхгофа. Зададим в системе MathCAD матрицы А и В.
Для нахождения вектора искомых токов записываем
,
где A-1 – операция вычисления матрицы, обратной А.
Результат вычисления токов вы ведем на экран:
Теперь выполним тот же самый расчёт методом контурных токов.
Примем обход всех независимых контуров по часовой стрелке и обозначим контурные токи I11, I22, I33.
Запишем ZK и EK в системе MathCAD, где ZK – матрица сопротивлений системы контурных уравнений, IK – вектор-столбец контурных токов, EK – вектор столбец контурных ЭДС.
Тогда исходные контурные токи можно получить:
Получим токи ветвей.
Методы расчёта дали один и тот же результат, следовательно, расчёты верны. Наиболее простым для данной цепи является метод контурных токов.
Задания к главе 2:
1) введите все примеры с рисунков главы в MathCAD;
2) сформируйте таблицы значений двух функций: у(х) = 2/(sin3(х)+2) и z(х) = 5sin(4х/3) для х = -180o…180o с шагом в 6o;
3) используя оператор численного дифференцирования, сформируйте таблицы значений 1-й, 2-й и 3-й производных функции z(х)=х3 + 3х5 для х = [-5…5];
4) создайте копию матрицы А, вставьте дополнительный столбец между вторым и третьим столбцами, заполните его произвольными значениями, удалите левый столбец и верхнюю строку;
5) создайте вектор-столбец из 5 элементов (ряд натуральных чисел от 1 до 5). Определите значение 3-го элемента столбца. Создайте матрицу-строку из 5 элементов (ряд натуральных чисел от 6 до 10). Определите значение 3-го элемента строки;
6) сформируйте векторы S, С, S2 и С2, элементы которых содержат значения функций соответственно sin(х)‚ cos(х), sin2(х) и cos2(х), где х — дискретно заданный угол в диапазоне от 0 до 360° с шагом 18°;
7) определите квадратную матрицу Z размерностью 12х12, в которой каждый элемент равен сумме значений своих индексов, если их произведение не превышает 64, иначе – произведению индексов. Постройте пространственный график по данным матрицы Z;
8) решите 5 и 13 варианты заданий 3 и 4 из контрольной работы, опираясь на пример, приведённый в конце данных методических указаний.
studopedia.net
Основы работы в MathCAD — Стр 2

Такие графики задаются нажатием кнопки с изображением графика в полярных координатах. Обозначение переменных не изменяется. На рис. 7 приведено построение фигуры Лисажу в полярных координатах.
Задача 5. Построить самостоятельно фигуру Лисажу.
Трехмерные графики.
В Маткад можно строить различные трехмерные графики: поверхности, уровней, столбиковые диаграммы и т. п. Для примера построим график поверхности, описываемой
функцией z = 55x 2 + 25y 2 для 0<= x <=40, 0<= y <=50.
1.Прежде всего, нужно определить узлы, в которых будет вычисляться функция. Запишем:
i:= 0..40 j:=0..50
После этой записи функция будет вычисляться в точках с координатами i=0, j=0: i=0, j=1 и т.д.
2.Нужно установить связь аргументов х и у с узлами. Мы запишем
x i =i yj =j
3.Запишем саму функцию z(x, y)= 55x 2 + 25y 2
4.Определим матрицу ординат, по которым будет строиться график: M i , j = z(x i , y j).
5.После этого вызовем график поверхности с панели графиков и поставим в нижнем правом углу М. Затем, выйдя из графика, щелкнем курсором. График будет построен.
На рис .8 показано построение этого графика.
Рис.8. Пространственный график в Маткад.
Введя курсор внутрь графика, и щелкнув мышью, мы снова вызовем трехстраничное окно, в котором можно установить все параметры графика.
На странице Viev (вид) устанавливается тип графика: Display as – показывать в виде (поверхности, линии уровней, столбиковой диаграммы), тип осей Axis (в виде непосредственно осей, в виде плоскостей, отсутствие осей), показ заднего плана (Back
Planes): показывать (Show), заполнять цветом поверхность (Fill Color) и кромку(Edge Color) и угол, под которым показываются оси координат.
В зависимости от выбранного типа графика меняется набор надписей на остальных страницах. Например, для графика Surface Plot (график поверхности) на странице Color and Lines (цвет и линии) нанесены надписи: Shading( затенение).
На странице Axis(оси) нанесены те же, что и для случая плоских графиков надписи, но теперь уже для трех осей: Gird Lines – нанесение сетки координат, Numbered – оцифровка соответствующей оси, Autoscale- автоматическая разметка осей, Shove Markers – показать метки по осям, Autogird — автоматический показ сетки координат,
Numbers of Grids — оцифровка сетки.
Задача 6. Построить график функции, приведенной в тексте, выбрав зеленый цвет поверхности, розовый цвет заднего плана, угол представления 45 градусов и оцифрованные оси.
Построить для той же функции график уровней и столбиковую диаграмму.
Задача 7. Построить график функции z = 3×3 −4y 2 для 0 <= x <= 3 , 0<= y <= 4.
ЛАБОРАТОРНАЯ РАБОТА №3. ДЕЙСТВИЯ НАД МАТРИЦАМИ В МАТКАД.
Понятие о встроенных функциях Маткад.
Большинство задач в Маткад решаются с помощью так называемых встроенных функций, т.е. с помощью заранее составленных программ решения той или иной задачи.
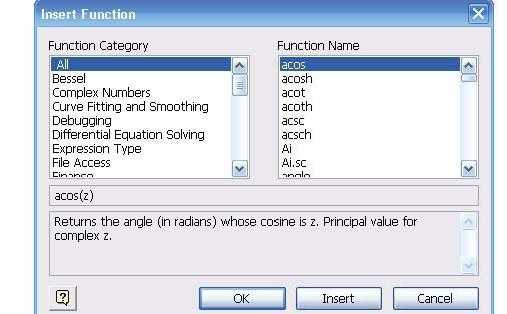
Каждая такая программа имеет свое имя, по которому она вызывается. Имя можно набирать с клавиатуры, но можно и вызывать с помощью кнопки f(x). Нажав эту кнопку, мы вызовем панель Insert Function (вставить функцию), в которой имеется два поля: Function Category (тип функции) и Function Name (имя функции). Выбрав тип и имя, и нажав кнопку ОК, мы вызовем данную функцию (Рис.1).
Рис.1.Панель вызова функции
Пусть, например, нужно найти синус числа 45. Вызвав панель вставки функции, выберем категорию Trigonometric и название sin, нажмем ОК. На экране появится шаблон со словом sin внутри и скобками. Вставив в скобки число 45, нажмем «=». Получим
sin(45)=0.851. Можно было бы набрать левую часть на клавиатуре и, после нажатия знака =, получить тот же ответ.
Аналогично используются и другие встроенные функции Маткад.
В Маткад массивы могут записываться в виде векторов (одномерные массивы), в виде матриц (двумерные массивы) и в виде таблиц. Мы рассмотрим пока только запись матриц и векторов. Для действий над ними имеется панель Matrix (матрица), показанная на рис. 2.
Рис.2. Панель матриц
Для ввода матриц и векторов нажмем кнопку панели матриц и вызовем этим окно ввода Insetrt Matrix (ввести матрицу), показанное на рис.3.
Рис.3. Окно ввода матриц и векторов.
Рис.4. Шаблон вектора.
При вводе вектора в графе columns (столбцы) следует проставить 1, а в графе rows(строки) проставить размер вектора. Появится шаблон, показанный на рис. 4.
Ниже представлено три пятиэлементных массива-вектора: Два из них – численные, третий – буквенный, четвертый состоит из выражений.
При задании буквенных массивов и массивов – выражений необходимо предварительно присваивать им численные значения (за каждой буквой в компьютере должно стоять число). После задания выражений вектора можно, записав его имя и поставив знак =, получить его значение. Рисунок лишний раз иллюстрирует, что Маткад различает строчные и заглавные буквы.

Над векторами определены показанные на рис.5.. операции сложения и вычитания, транспонирования, умножения по математическим правилам умножения матриц. Знак транспонирования следует вводить с панели Matrix (матрица).
Порядковый номер элемента, который является его адресом, называется индексом. Нижняя граница индексации задается значением системной переменной ORIGIN,
которая может принимать значение 0 или 1.
Рис.5. Запись векторов в Маткад.
Имя массива увязано с именами индексированных переменных, значениями которых являются элементы массива. Для этого достаточно в виде подстрочного индекса указать индекс элемента. Например, если третий из представленных массивов имеет имя V, то его элементами при ORIGIN=0 будут индексированные переменные: v0=0 V1=b ,w3= d, W4= x.
При задании ORIGIN=1, получим: v1 =0, V1=a, w3=c, W4=x3 – x5.
Задача 1. Ввести все векторы рис.5 и произвести над ними все действия, проведенные на рисунке. Матрицы в Маткаде вводятся так же, как и векторы, но число столбцов в них больше единицы. Элементами матрицы могут быть также числа, буквы, выражения. Как и в случае векторов, буквенные элементы и элементы – выражения должны быть предварительно определены численно. На рис.6 показаны различные способы ввода матриц.
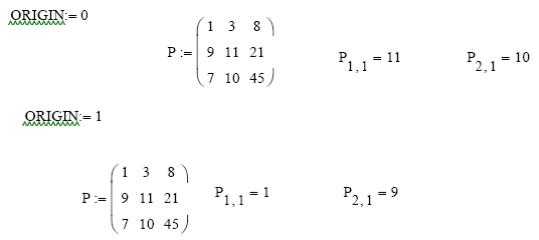
Рис.6. Ввод матриц.
Задача 2. Ввести все матрицы, приведенные на рис.6.
Элементы матриц являются индексированными переменными, имена которых совпадают с именами матриц. Для каждой индексированной переменной указываются два индекса: один — для номера строки, другой — для номера столбца. Например, для матрицы W средний элемент обозначается как W1,1 а последний как W2,2. (Индексы набираются через запятую). На рис.7 показано изменение индексации при различных значениях переменной ORIGIN.(Набирается обязательно заглавными буквами).
Рис.7. Роль переменной ORIGIN
В Маткад определены следующие действия над векторами и матрицами:
А) | сложение – вычитание, |
В) | скалярное и векторное умножение, |
Г) | обращение, |
Д) | транспонирование, |
Е) | сортировка, |
Ж) | выделение столбцов. |
Они выполняются с использованием следующих кнопок панели Matrix:
кнопка индексации элементов матрицы,
кнопка обращения матрицы,
кнопка скалярного произведения векторов и матриц
кнопка транспонирования матрицы,
кнопка векторного произведения двух векторов
кнопка сложения векторов
кнопка выделения столбца матрицы кнопка вычисления детерминанта матрицы.
На рис.8 приведены все эти действия над матрицами, приведенными на рис.6.

Задача.3: Произвести над матрицами все действия, показанные на рис.8.
Рис.8. Действия над матрицами
Задача.4: Ввести две произвольные матрицы. Перемножить. Например:
Проверьте на бумаге правильность произведенных выше действий
Рис.9. Пример выполнения задачи 4
Обращение и вычисление определителя возможно только для квадратных матриц.
Задача 5.. Введите произвольную квадратную матрицу, найдите обратную ей и вычислите определитель, используя показанные выше кнопки встроенных операторов.
Рис.10. Пример выполнения задачи 5.
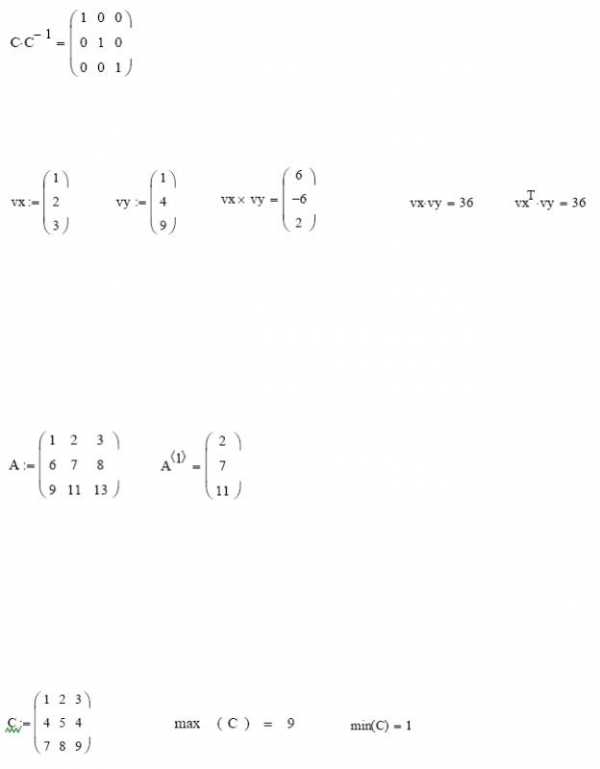
Как известно, умножение матрицы на обратную дает единичную матрицу. Проверим, правильно ли было проведено обращение
Задача 6. Найти скалярное и векторное произведения двух заданных трехэлементных векторов: Проверить на бумаге правильность вычислений.
Рис.11. Пример выполнения задачи 6.
Проверим правильность скалярного умножения, перемножив vxТ и vy . Получили также 36.
При рассмотрении матриц больших размеров удобно выделять их столбцы. Мы будем использовать его в модулях 2 и 3 при решении сложных задач.
Задача 7. Используя кнопку выделения столбцов, выделите столбцы произвольной матрицы, например:
Рис.12. Пример выполнения задачи 7.
В Маткаде имеется большое количество встроенных функций для действий над матрицами и векторами. Рассмотрим некоторые из них.
Вычисление максимального и минимального элементов матрицы или вектора производится с помощью встроенных функций Max(A )и Min(A).
Задача 8 . Вычислить максимальный и минимальный элемент произвольной матрицы, например:
Рис13. Вычисление максимального и минимального элемента матрицы.
Определение количества столбцов и строк в матрице удобно для проверки действий над многомерными матрицами и векторами. Оно производится с помощью
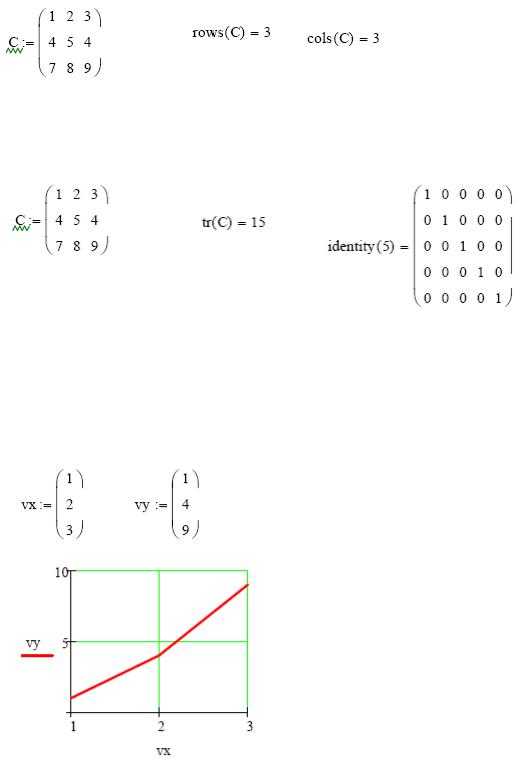
встроенных функций Cols(A)- число столбцов матрицы А и Rows(A)- Число строк матрицы А.
Задача 9. Определить число строк и столбцов в произвольной матрице, например
Рис.13. Пример выполнения задачи 9.
Единичная матрица размером N формируется встроенной функцией Idenfity(N), а след матрицы – встроенной функцией . tr(A):
Рис.14. Формирование единичной матрицы и вычисление следа матрицы.
Графики матричных и векторных зависимостей.
В Маткаде возможно построение графиков по данным, записанным в векторной и матричной форме. На рис.15 показано построение двумерного графика по данным векторов vx и vy, а на рис.16. – построение трехмерного графика по заданным в матрице аргументам и вектору функции.
Рис.15. Построение двумерного графика по векторным данным.
Заданы двумерная матрица аргументов S и вектор значений функции этих аргументов Y.Показано построение графика.
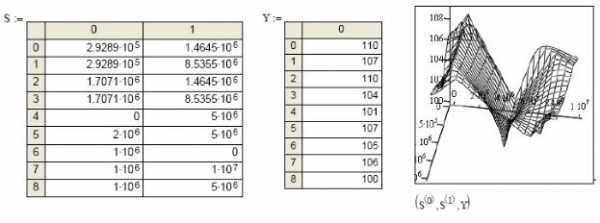
Рис.16.Трехмерный график данных, записанных в векторной форме.
Операции над матрицами в аналитической (символьной) форме.
Системы компьютерной алгебры снабжаются специальным процессором для выполнения аналитических (символьных) вычислений. Его основой является ядро, хранящее всю совокупность формул и формульных преобразований, с помощью которых производятся аналитические вычисления. Чем больше этих формул в ядре, тем надежней работа символьного процессора и тем вероятнее, что поставленная задача будет решена, разумеется, если такое решение существует в принципе (что бывает далеко не всегда).
Ядро символьного процессора Маткад — несколько упрощенный вариант ядра известной системы символьной математики Maple V фирмы Waterloo Maple Software , у которой MathSoft (разработчик Маткада) приобрела лицензию на его применение, благодаря чему Маткад стал системой символьной математики.
Введение в систему Маткад символьных вычислений придает ей качественно новые возможности. Символьные вычисления выполняются, в конечном счете, столь же просто для пользователя, как, скажем, вычисление квадрата х.
Операции, относящиеся к работе символьного процессора, содержатся в подменю позиции Symbolic (Символика) главного меню.
Чтобы символьные операции выполнялись, процессору необходимо указать, над каким выражением эти операции должны производиться, т е надо выделить выражение. Для ряда операций следует не только указать выражение, к которому они относятся, но и наметить переменную, относительно которой выполняется та или иная символьная операция.
Само выражение в таком случае не выделяется, ведь и так ясно, что если маркер ввода выделяет переменную какого-либо выражения, то это выражение уже отмечено наличием в нем выделяемой переменной
Символьные операции разбиты на пять характерных разделов. Это операции с выражениями, операции с переменными, операции с матрицами, операции преобразования, стиль эволюции. Первыми идут наиболее часто используемые операции Они могут выполняться с выражениями, содержащими комплексные числа или имеющими решения в комплексном виде
В данной лабораторной работе мы рассмотрим только операции с матрицами. В дальнейшем будут рассмотрены и другие символьные операции.
Символьный процессор системы Маткад обеспечивает проведение в символьном виде трех наиболее распространенных матричных операций транспонирования и обращения матриц, а также вычисления их детерминанта.
При символьных вычислениях, прежде всего, следует вызвать панель символьных
вычислений нажатием кнопки на математической панели.
После этого появится панель символьных вычислений, показанная на рис.17

Рис.17. Панель символьных вычислений
Для символьных операций над матрицами нам понадобится только предпоследняя строка этого окна, с помощью кнопок которой и производятся транспонирование, обращение матрицы и нахождение ее определителя.
Задача 10. Используя кнопки панели символьных вычислений, провести аналитическое транспонирование и обращение произвольной матрицы, например:
Рис.18. Пример символьного решения матричных задач.
ЛАБОРАТОРНАЯ РАБОТА №4. РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ В МАТЕМАТИЧЕСКОМ ПАКЕТЕ «Маткад».
Алгебраические уравнения в Маткаде решаются как численными, так и аналитическими методами. В данной лабораторной работе будут рассмотрены оба метода
Численное решение системы линейных алгебраических уравнений .
При численном решении систем линейных уравнений используется специальный вычислительный блок, открываемый служебным словом — директивой Given. Блок имеет следующую структуру:
Задание начальных приближений
Given
Уравнения
Ограничительные условия выражения с функцией find
studfiles.net
Урок 13. Обработка статистических данных в Mathcad
В этом и последующих уроках мы будем работать со статистическими данными. Эти данные будем рассматривать как два вектора одинаковой длины, один из которых включает в себя независимые переменные, а второй — зависимые.
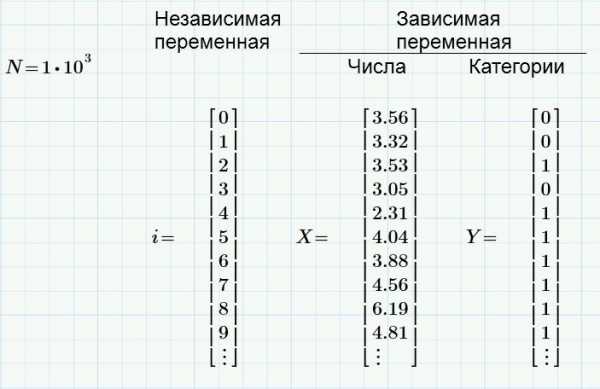
Выше находятся три вектора, каждый из которых включает в себя 1000 элементов. Отображены только первые несколько элементов. Чтобы просмотреть другие элементы, следует щелкнуть по трем точкам внизу столбца чисел, чтобы появился ползунок — квадрат на серой линии:

Первый вектор включает в себя независимую переменную. Вектор X содержит действительные числа, Y — нули и единицы — категории, которые служат для обозначения да/нет, орел/решка и т.п. Эти данные сгенерированы в Mathcad. Как это сделано, мы рассмотрим в конце урока.
Категории и действительные числа в статистике рассматриваются по-разному. Однако, в некоторых случаях такое разделение не совсем ясно — данные можно отнести к любой из двух групп.
Данные выше составляют генеральную совокупность из 1000 точек. В какой-то момент мы рассматривает выборку из этой генеральной совокупности. Часто мы хотим получить представление о свойствах генеральной совокупности, изучая выборку.
Описание данных
Рассмотрим сначала действительные числа. В первую очередь, для описания набора данных используются параметры:
(а) среднее арифметическое X_;
(б) среднеквадратическое (стандартное) отклонение S.
Среднее арифметическое показывает, где находится центр распределения, а среднеквадратическое отклонение (сокращенно СКО) — ширину распределения. Иногда используются и другие параметры, такие как медиана и эксцесс. Эти параметры можно найти в меню Функции -> Статистические:
Среднее арифметическое зависимой переменной X:
СКО переменной X:
Функция в Mathcad:
(В статистике среднее арифметическое обычно обозначается буквой с черточкой над ней. В Mathcadтакая черточка используется с другой целью, поэтому для обозначения среднего арифметического мы используем нижнее подчеркивание.)
Теперь рассмотрим выборку — только первые десять элементов. Условимся обозначать генеральную совокупность заглавной буквой, а выборку — маленькой:
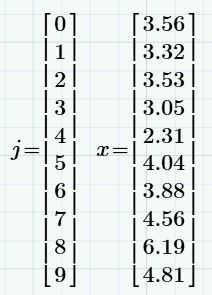
Среднее арифметическое и СКО выборки можно использовать оценки этих же величин для генеральной совокупности:
Здесь у нас в выборке участвуют 10 элементов — такое число часто принимается за минимум выборки. Немного лучшую оценку СКО дает величина:
Здесь мы делили на (n-1) вместо n. Встроенная функция Mathcad:
Ниже находятся два графика, которые показывают некоторые характеристики распределения. Первый — это график в декартовых координатах, известный как диаграмма рассеяния. Он показывает точки данных и границы 2?:
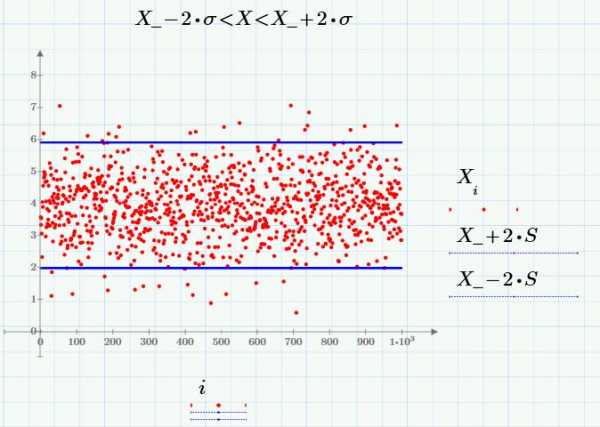
Правило двух сигма в статистике гласит, что для нормального распределения 5% данных будут лежать вне границ 2? от среднего арифметического.
Второй график — гистограмма. Она показывает число точек данных, попавших в различные интервалы. Как его построить, мы обсудим в дальнейшем:
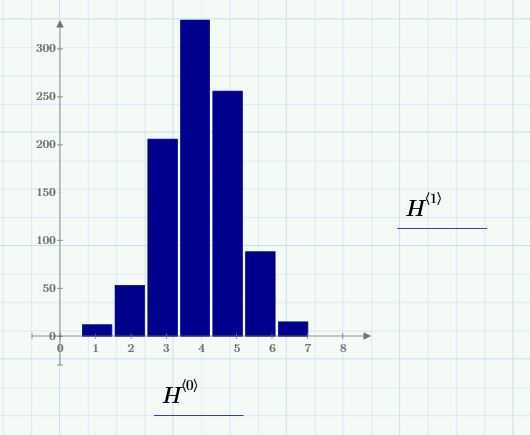
Различные наборы данных можно получить, нажав [Ctrl+F5]. Это займет время, поскольку пересчитывается весь документ.
Теперь рассмотрим данные категорий. Предположим, что мы рассматриваем результат подбрасывания монеты: «1» — орел, «0» — решка. Из нашего набора данных мы можем получить вероятность выпадения орла. Следует внимательно применять арифметические операции к данным категорий, но в нашем выборе между «0» и «1» мы можем легко получить долю единиц, найдя среднее арифметическое вектора Y:
Это вероятность выпадения орла. Заметьте, что считать нужно от 0 до (N-1), чтобы учесть N точек.
Для небольшой выборки ее среднее арифметическое может существенно отличаться от среднего совокупности:
Вы можете получать различные наборы данных в выборке каждый раз, нажимая [Ctrl+F5]. Попробуйте сделать это несколько раз. Для «0» и «1» нужна выборка, по крайней мере, из 30 точек, чтобы получить примерное представление о вероятности. Для надежных результатов при рассмотрении категорий нужны большие выборки — часто это тысячи точек.
Случайные числа
Данные выше были получены с использованием генераторов случайных чисел Mathcad. Они находятся в меню Функции -> Все функции -> Случайные числа. Наиболее важные из них — это равномерное и нормальное распределение.
Равномерное распределение
Случайное число между 0 и x можно получить с помощью функции:
Здесь нажатие [Ctrl+F5] также даст новое значение. Чтобы получить набор случайных чисел, нужно задать диапазон:
На диаграмме рассеяния видно, что распределение действительно равномерное:
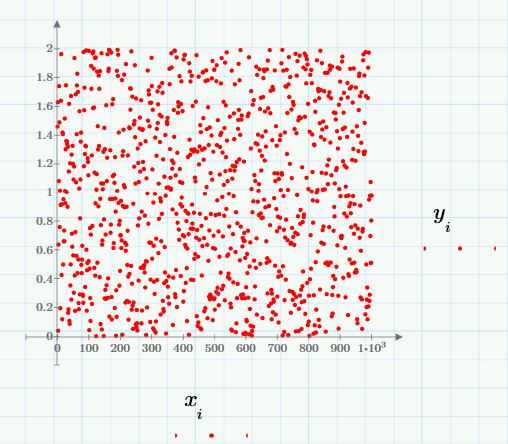
Проверим это еще раз с помощью гистограммы:
Выходными значениями функции гистограммы являются два вектора-столбца. Столбец «0» содержит центры интервалов, а столбец «1» — число элементов в каждом интервале:
При построении графика используйте тип «Столбцы»:
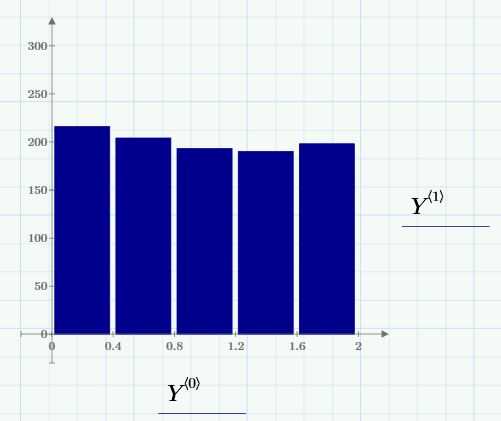
Получается равномерное распределение, как и ожидалось.
Нормальное распределение
Случайные числа с нормальным распределением генерирует функция rnorm(). Она содержит три параметра: число точек, среднее арифметическое и СКО. Создадим набор большого числа точек:
Построим гистограмму с 30 интервалами:
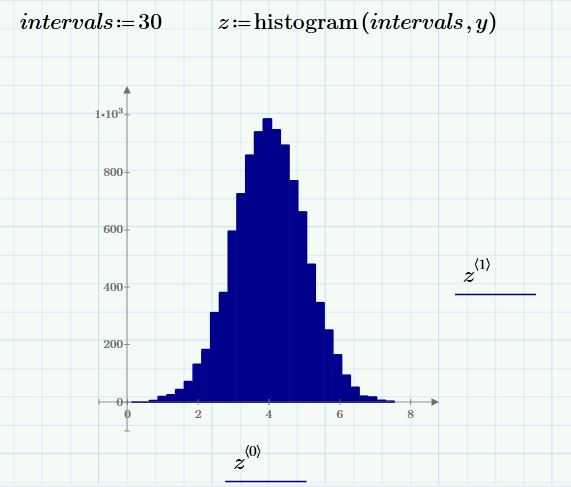
Такой колоколообразный график соответствует нормальному распределению.
Резюме
- Данные включают в себя набор векторов одинаковой длины. Первый вектор — независимая переменная, второй (третий, четвертый,…) — может быть переменной категорий, или включать в себя действительные числа. Полный набор данных формирует генеральную совокупность. Любая ее часть называется выборкой.
- Поведение данных можно описать с помощью среднего арифметического и среднеквадратического отклонения. (Для категорий можно определить лишь вероятность.) В Mathcad есть функции mean() и stdev() для их вычисления. Чтобы оценить стандартное отклонение генеральной совокупности по выборке, используйте Stdev().
- Обычно одна из двадцати точек выходит за пределы границ, отстоящих по обе стороны от среднего арифметического на 2?. Это можно проверить по диаграмме рассеяния или по гистограмме. Гистограмма формируется с помощью функции histogram(intervals,x), выходом которой является матрица с двумя столбцами: столбец «0» содержит данные для оси Xграфика, столбец «1» — для оси Y. Извлечь эти столбцы по отдельности можно с помощью команды Матрицы и таблицы -> Операции с векторами/матрицами.
- Мы рассмотрели два генератора случайных чисел Mathcad. Функция rnd(3) дает случайное значение с равномерным распределением в промежутке 0<x<3. Функция rnorm(x,X_,S) дает случайное значение с нормальным распределением со средним X_ и СКО S. Генератор случайных чисел дает новые значения каждый раз при пересчете [Ctrl+F5].
Другие интересные материалы
sapr-journal.ru
MathCAD — Стр 2
Такие графики задаются нажатием кнопки с изображением графика в полярных координатах. Обозначение переменных не изменяется. На рис. 7 приведено построение фигуры Лисажу в полярных координатах.
Задача 5. Построить самостоятельно фигуру Лисажу.
Трехмерные графики.
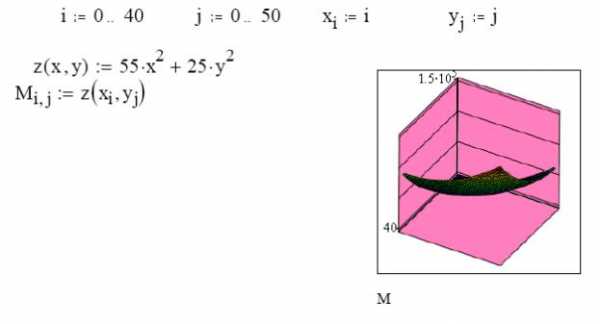
В Маткад можно строить различные трехмерные графики: поверхности, уровней, столбиковые диаграммы и т. п. Для примера построим график поверхности, описываемой
функцией z = 55x 2 + 25y 2 для 0<= x <=40, 0<= y <=50.
1.Прежде всего, нужно определить узлы, в которых будет вычисляться функция. Запишем:
i:= 0..40 j:=0..50
После этой записи функция будет вычисляться в точках с координатами i=0, j=0: i=0, j=1 и т.д.
2.Нужно установить связь аргументов х и у с узлами. Мы запишем
x i =i yj =j
3.Запишем саму функцию z(x, y)= 55x 2 + 25y 2
4.Определим матрицу ординат, по которым будет строиться график: M i , j = z(x i , y j).
5.После этого вызовем график поверхности с панели графиков и поставим в нижнем правом углу М. Затем, выйдя из графика, щелкнем курсором. График будет построен.
На рис .8 показано построение этого графика.
Рис.8. Пространственный график в Маткад.
Введя курсор внутрь графика, и щелкнув мышью, мы снова вызовем трехстраничное окно, в котором можно установить все параметры графика.
На странице Viev (вид) устанавливается тип графика: Display as – показывать в виде (поверхности, линии уровней, столбиковой диаграммы), тип осей Axis (в виде непосредственно осей, в виде плоскостей, отсутствие осей), показ заднего плана (Back
Planes): показывать (Show), заполнять цветом поверхность (Fill Color) и кромку(Edge Color) и угол, под которым показываются оси координат.
В зависимости от выбранного типа графика меняется набор надписей на остальных страницах. Например, для графика Surface Plot (график поверхности) на странице Color and Lines (цвет и линии) нанесены надписи: Shading( затенение).
На странице Axis(оси) нанесены те же, что и для случая плоских графиков надписи, но теперь уже для трех осей: Gird Lines – нанесение сетки координат, Numbered – оцифровка соответствующей оси, Autoscale- автоматическая разметка осей, Shove Markers – показать метки по осям, Autogird — автоматический показ сетки координат,
Numbers of Grids — оцифровка сетки.
Задача 6. Построить график функции, приведенной в тексте, выбрав зеленый цвет поверхности, розовый цвет заднего плана, угол представления 45 градусов и оцифрованные оси.
Построить для той же функции график уровней и столбиковую диаграмму.
Задача 7. Построить график функции z = 3×3 −4y 2 для 0 <= x <= 3 , 0<= y <= 4.
ЛАБОРАТОРНАЯ РАБОТА №3. ДЕЙСТВИЯ НАД МАТРИЦАМИ В МАТКАД.
Понятие о встроенных функциях Маткад.
Большинство задач в Маткад решаются с помощью так называемых встроенных функций, т.е. с помощью заранее составленных программ решения той или иной задачи.
Каждая такая программа имеет свое имя, по которому она вызывается. Имя можно набирать с клавиатуры, но можно и вызывать с помощью кнопки f(x). Нажав эту кнопку, мы вызовем панель Insert Function (вставить функцию), в которой имеется два поля: Function Category (тип функции) и Function Name (имя функции). Выбрав тип и имя, и нажав кнопку ОК, мы вызовем данную функцию (Рис.1).
Рис.1.Панель вызова функции
Пусть, например, нужно найти синус числа 45. Вызвав панель вставки функции, выберем категорию Trigonometric и название sin, нажмем ОК. На экране появится шаблон со словом sin внутри и скобками. Вставив в скобки число 45, нажмем «=». Получим
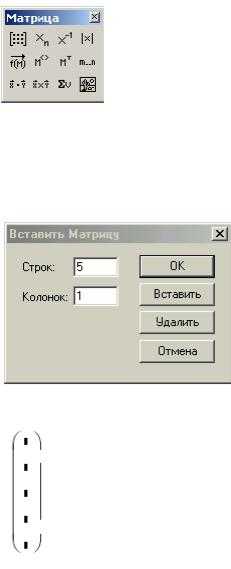
sin(45)=0.851. Можно было бы набрать левую часть на клавиатуре и, после нажатия знака =, получить тот же ответ.
Аналогично используются и другие встроенные функции Маткад.
В Маткад массивы могут записываться в виде векторов (одномерные массивы), в виде матриц (двумерные массивы) и в виде таблиц. Мы рассмотрим пока только запись матриц и векторов. Для действий над ними имеется панель Matrix (матрица), показанная на рис. 2.
Рис.2. Панель матриц
Для ввода матриц и векторов нажмем кнопку панели матриц и вызовем этим окно ввода Insetrt Matrix (ввести матрицу), показанное на рис.3.
Рис.3. Окно ввода матриц и векторов.
Рис.4. Шаблон вектора.
При вводе вектора в графе columns (столбцы) следует проставить 1, а в графе rows(строки) проставить размер вектора. Появится шаблон, показанный на рис. 4.
Ниже представлено три пятиэлементных массива-вектора: Два из них – численные, третий – буквенный, четвертый состоит из выражений.
При задании буквенных массивов и массивов – выражений необходимо предварительно присваивать им численные значения (за каждой буквой в компьютере должно стоять число). После задания выражений вектора можно, записав его имя и поставив знак =, получить его значение. Рисунок лишний раз иллюстрирует, что Маткад различает строчные и заглавные буквы.

Над векторами определены показанные на рис.5.. операции сложения и вычитания, транспонирования, умножения по математическим правилам умножения матриц. Знак транспонирования следует вводить с панели Matrix (матрица).
Порядковый номер элемента, который является его адресом, называется индексом. Нижняя граница индексации задается значением системной переменной ORIGIN,
которая может принимать значение 0 или 1.
Рис.5. Запись векторов в Маткад.
Имя массива увязано с именами индексированных переменных, значениями которых являются элементы массива. Для этого достаточно в виде подстрочного индекса указать индекс элемента. Например, если третий из представленных массивов имеет имя V, то его элементами при ORIGIN=0 будут индексированные переменные: v0=0 V1=b ,w3= d, W4= x.
При задании ORIGIN=1, получим: v1 =0, V1=a, w3=c, W4=x3 – x5.
Задача 1. Ввести все векторы рис.5 и произвести над ними все действия, проведенные на рисунке. Матрицы в Маткаде вводятся так же, как и векторы, но число столбцов в них больше единицы. Элементами матрицы могут быть также числа, буквы, выражения. Как и в случае векторов, буквенные элементы и элементы – выражения должны быть предварительно определены численно. На рис.6 показаны различные способы ввода матриц.

Рис.6. Ввод матриц.
Задача 2. Ввести все матрицы, приведенные на рис.6.
Элементы матриц являются индексированными переменными, имена которых совпадают с именами матриц. Для каждой индексированной переменной указываются два индекса: один — для номера строки, другой — для номера столбца. Например, для матрицы W средний элемент обозначается как W1,1 а последний как W2,2. (Индексы набираются через запятую). На рис.7 показано изменение индексации при различных значениях переменной ORIGIN.(Набирается обязательно заглавными буквами).
Рис.7. Роль переменной ORIGIN
В Маткад определены следующие действия над векторами и матрицами:
А) | сложение – вычитание, |
В) | скалярное и векторное умножение, |
Г) | обращение, |
Д) | транспонирование, |
Е) | сортировка, |
Ж) | выделение столбцов. |
Они выполняются с использованием следующих кнопок панели Matrix:
кнопка индексации элементов матрицы,
кнопка обращения матрицы,
кнопка скалярного произведения векторов и матриц
кнопка транспонирования матрицы,
кнопка векторного произведения двух векторов
кнопка сложения векторов
кнопка выделения столбца матрицы кнопка вычисления детерминанта матрицы.
На рис.8 приведены все эти действия над матрицами, приведенными на рис.6.

Задача.3: Произвести над матрицами все действия, показанные на рис.8.
Рис.8. Действия над матрицами
Задача.4: Ввести две произвольные матрицы. Перемножить. Например:
Проверьте на бумаге правильность произведенных выше действий
Рис.9. Пример выполнения задачи 4
Обращение и вычисление определителя возможно только для квадратных матриц.
Задача 5.. Введите произвольную квадратную матрицу, найдите обратную ей и вычислите определитель, используя показанные выше кнопки встроенных операторов.
Рис.10. Пример выполнения задачи 5.
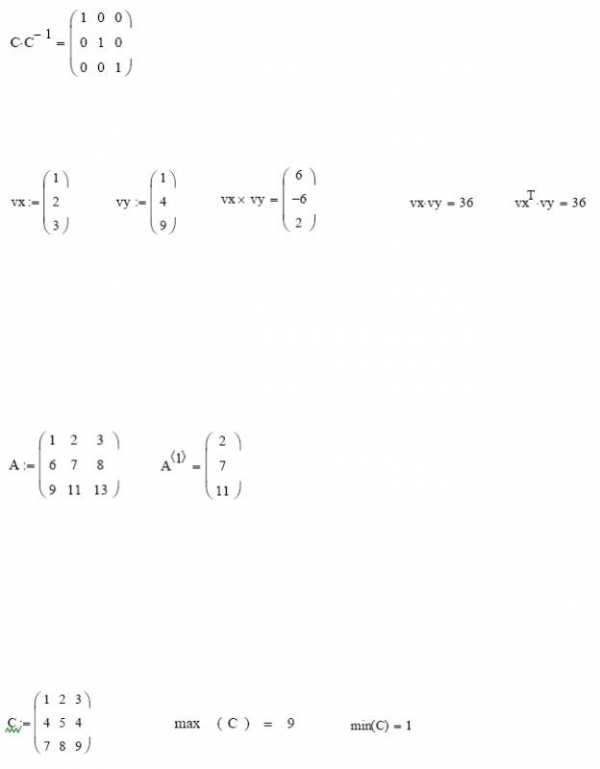
Как известно, умножение матрицы на обратную дает единичную матрицу. Проверим, правильно ли было проведено обращение
Задача 6. Найти скалярное и векторное произведения двух заданных трехэлементных векторов: Проверить на бумаге правильность вычислений.
Рис.11. Пример выполнения задачи 6.
Проверим правильность скалярного умножения, перемножив vxТ и vy . Получили также 36.
При рассмотрении матриц больших размеров удобно выделять их столбцы. Мы будем использовать его в модулях 2 и 3 при решении сложных задач.
Задача 7. Используя кнопку выделения столбцов, выделите столбцы произвольной матрицы, например:
Рис.12. Пример выполнения задачи 7.
В Маткаде имеется большое количество встроенных функций для действий над матрицами и векторами. Рассмотрим некоторые из них.
Вычисление максимального и минимального элементов матрицы или вектора производится с помощью встроенных функций Max(A )и Min(A).
Задача 8 . Вычислить максимальный и минимальный элемент произвольной матрицы, например:
Рис13. Вычисление максимального и минимального элемента матрицы.
Определение количества столбцов и строк в матрице удобно для проверки действий над многомерными матрицами и векторами. Оно производится с помощью
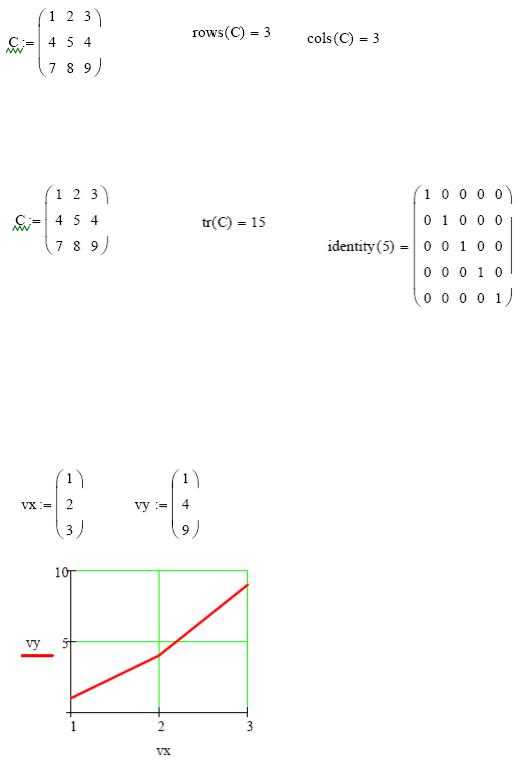
встроенных функций Cols(A)- число столбцов матрицы А и Rows(A)- Число строк матрицы А.
Задача 9. Определить число строк и столбцов в произвольной матрице, например
Рис.13. Пример выполнения задачи 9.
Единичная матрица размером N формируется встроенной функцией Idenfity(N), а след матрицы – встроенной функцией . tr(A):
Рис.14. Формирование единичной матрицы и вычисление следа матрицы.
Графики матричных и векторных зависимостей.
В Маткаде возможно построение графиков по данным, записанным в векторной и матричной форме. На рис.15 показано построение двумерного графика по данным векторов vx и vy, а на рис.16. – построение трехмерного графика по заданным в матрице аргументам и вектору функции.
Рис.15. Построение двумерного графика по векторным данным.
Заданы двумерная матрица аргументов S и вектор значений функции этих аргументов Y.Показано построение графика.
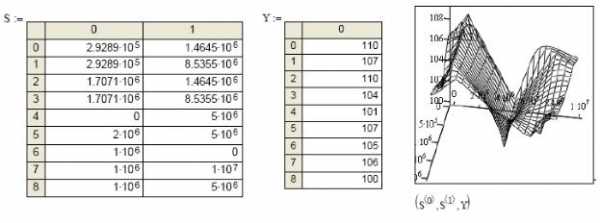
Рис.16.Трехмерный график данных, записанных в векторной форме.
Операции над матрицами в аналитической (символьной) форме.
Системы компьютерной алгебры снабжаются специальным процессором для выполнения аналитических (символьных) вычислений. Его основой является ядро, хранящее всю совокупность формул и формульных преобразований, с помощью которых производятся аналитические вычисления. Чем больше этих формул в ядре, тем надежней работа символьного процессора и тем вероятнее, что поставленная задача будет решена, разумеется, если такое решение существует в принципе (что бывает далеко не всегда).
Ядро символьного процессора Маткад — несколько упрощенный вариант ядра известной системы символьной математики Maple V фирмы Waterloo Maple Software , у которой MathSoft (разработчик Маткада) приобрела лицензию на его применение, благодаря чему Маткад стал системой символьной математики.
Введение в систему Маткад символьных вычислений придает ей качественно новые возможности. Символьные вычисления выполняются, в конечном счете, столь же просто для пользователя, как, скажем, вычисление квадрата х.
Операции, относящиеся к работе символьного процессора, содержатся в подменю позиции Symbolic (Символика) главного меню.
Чтобы символьные операции выполнялись, процессору необходимо указать, над каким выражением эти операции должны производиться, т е надо выделить выражение. Для ряда операций следует не только указать выражение, к которому они относятся, но и наметить переменную, относительно которой выполняется та или иная символьная операция.
Само выражение в таком случае не выделяется, ведь и так ясно, что если маркер ввода выделяет переменную какого-либо выражения, то это выражение уже отмечено наличием в нем выделяемой переменной
Символьные операции разбиты на пять характерных разделов. Это операции с выражениями, операции с переменными, операции с матрицами, операции преобразования, стиль эволюции. Первыми идут наиболее часто используемые операции Они могут выполняться с выражениями, содержащими комплексные числа или имеющими решения в комплексном виде
В данной лабораторной работе мы рассмотрим только операции с матрицами. В дальнейшем будут рассмотрены и другие символьные операции.
Символьный процессор системы Маткад обеспечивает проведение в символьном виде трех наиболее распространенных матричных операций транспонирования и обращения матриц, а также вычисления их детерминанта.
При символьных вычислениях, прежде всего, следует вызвать панель символьных
вычислений нажатием кнопки на математической панели.
После этого появится панель символьных вычислений, показанная на рис.17

Рис.17. Панель символьных вычислений
Для символьных операций над матрицами нам понадобится только предпоследняя строка этого окна, с помощью кнопок которой и производятся транспонирование, обращение матрицы и нахождение ее определителя.
Задача 10. Используя кнопки панели символьных вычислений, провести аналитическое транспонирование и обращение произвольной матрицы, например:
Рис.18. Пример символьного решения матричных задач.
ЛАБОРАТОРНАЯ РАБОТА №4. РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ В МАТЕМАТИЧЕСКОМ ПАКЕТЕ «Маткад».
Алгебраические уравнения в Маткаде решаются как численными, так и аналитическими методами. В данной лабораторной работе будут рассмотрены оба метода
Численное решение системы линейных алгебраических уравнений .
При численном решении систем линейных уравнений используется специальный вычислительный блок, открываемый служебным словом — директивой Given. Блок имеет следующую структуру:
Задание начальных приближений
Given
Уравнения
Ограничительные условия выражения с функцией find
studfiles.net
MathCAD — это просто! Часть 10. Работа с векторами и матрицами
Снова здравствуйте. Мы с вами успели вполне успешно закончить со школьной алгеброй, и, значит, можем переходить к более сложным вещам — например, к тому разделу математики, который в университетах обычно называют линейной алгеброй. Конечно, раздел этот весьма и весьма обширен, и нечего даже думать о том, чтобы охватить хотя бы большую его часть. Тем не менее, нам с вами, я так думаю, кое-что из него научиться использовать практически вполне по силам — к примеру, мы можем научиться работать в MathCAD’е с векторами и матрицами. Эти два понятия — важнейшие математические абстракции, роль которых трудно переоценить в научно-техническом прогрессе. Ведь именно применение векторов и векторного анализа позволило в свое время Оливеру Хевисайду сократить количество уравнений Максвелла, описывающих электромагнитное поле, с двух десятков до всего лишь четырех. До векторного анализа, я так думаю, мы с вами в свое время еще доберемся, ну, а пока займемся более прозаическими вещами. Какими именно? Думаю, все станет ясно, если вы продолжите читать эту статью.
Немного об элементах матриц
Хотя дальше мы будем иметь дело и с векторами, и с матрицами, я краткости ради буду говорить просто «матрица», подразумевая, что под вектором мы будем иметь в виду частный случай матрицы, а именно ту ее разновидность, которая представляет собой одиночный столбец. Если же вектор будет представлять собой строку, то это будет специально оговорено. Впрочем, думаю, до этого дело вряд ли дойдет. С матрицами, вообще говоря, мы с вами работать уже немного умеем. Ну, не то чтобы прямо так вот работать — по крайней мере, вводить их в MathCAD’е мы уже вводили. Тем не менее, думаю, будет не лишним напомнить, что ввести в рабочую область матрицу можно с помощью кнопки Matrix or Vector, расположенной на панели Matrix, либо с помощью сочетания горячих клавиш Ctrl+M. Впрочем, мы с вами пока не затрагивали один небольшой, но крайне важный момент, а именно как обращаться в вычислениях не к матрице целиком, а к отдельным ее элементам. Сделать это, на самом деле, очень просто. Пусть у нас задана квадратная матрица X размером два на два элемента. Верхний левый элемент будет иметь индексы 0,0; нижний правый, соответственно, будет иметь индексы 1,1. То есть, как видите, элементы матрицы нумеруются с нуля. Это, в общем-то, довольно удобно, однако, если для вас привычнее нумеровать их с единицы, или, скажем, с 1024-х, то можно поменять значение встроенной переменной ORIGIN, введя в самом начале документа MatchCAD в строку (без кавычек). Или, соответственно, «ORIGIN := 1024». Можно поменять значение переменной и в окне опций MathCAD’а, выбрав в меню Tools пункт Worksheet options и на вкладке Built-In Variables поменяв значение переменной ORIGIN на нужное вам.
Так вот, вернемся к нашим элементам матрицы. Чтобы «вынуть» из нее первый элемент, нужно написать следующее: X0, 0. Для того, чтобы записать индексы внизу от имени переменной, которая обозначает матрицу, можно воспользоваться кнопкой Subscript со все той же панели инструментов для матричных и векторных вычислений или с клавиатуры перейти в нижний индекс клавишей «[» (русское «х»). Обратите внимание, что для разделения индексов, обозначающих строку и столбец, используется запятая. Элементы матрицы можно не только извлекать из матрицы, заданной таблично. Вы можете задать несколько элементов с соответствующими индексами по ходу вычисления, а после уже MathCAD самостоятельно сформирует из них матрицу (но только когда вы зададите уже все ее элементы — в противном случае незаданным элементам будут присвоены нулевые значения). Вы можете использовать ранжированные переменные для задания элементов матрицы. Временами это бывает не просто удобно, а очень удобно. Так, к примеру, можно задать для матрицы X следующую формулу, описывающую значения каждого ее элемента i-й строки и j-го столбца: Xi, j := i * j. Перед таким определением элементов матрицы остается только определить диапазон, в котором будут изменяться i и j. Я для примера взял значения i := 0..5 и j := 0..5, но вы, конечно же, можете установить любой другой нужный вам диапазон в зависимости от требований вашей задачи, решаемой с помощью матриц в среде MathCAD.
Операции над матрицами
Конечно, у применения матриц в реальных задачах существует множество интересных и не очень аспектов, однако все они рано или поздно упираются в необходимость проведения с матрицами простых алгебраических операций. Проводить их вручную — задача трудоемкая, и можно потратить время с гораздо большей пользой, переложив рутинную работу на MathCAD. Для начала познакомимся с теми функциями, которые собственно никаких математических операций не выполняют, но при этом являются весьма важными в действиях с матрицами. Эти функции позволяют объединять две матрицы в одну (не складывать матрицы, а просто объединять их элементы) и выделять из матрицы другую матрицу. Первая из функций — augment. Она объединяет две матрицы, имеющие одинаковое число строк, таким образом, что из них образуется одна, в которой элементы этих двух располагаются, что называется, «плечом к плечу». В качестве аргументов этой функции нужны только две объединяемые матрицы. Ее аналог для тех матриц, которые имеют одинаковое число столбцов, и должны быть объединены одна над другой, является функция stack. Ее аргументами тоже должны быть две объединяемые матрицы. Функция же, которая не объединяет, а, напротив, «разрезает» матрицы, имеет название submatrix. Для нее нужно указывать имя матрицы, из которой мы хотим выделить подматрицу, и координаты элементов новой матрицы в старой матрице. То есть для того, чтобы вырезать матрицу 4х4 из верхних левых элементов матрицы размером 5х5, нам нужно вызывать эту функцию со следующими параметрами: submatrix(Y, 0, 4, 0, 4). Здесь Y — это, конечно же, имя матрицы размером 5х5 элементов. Демонстрацию использования всех этих функций применительно к конкретным матрицам можно увидеть на соответствующей иллюстрации к статье.
Теперь, я так думаю, самое время перейти уже к арифметическим операциям над матрицами. Вы увидите, что их использование в MathCAD не потребует от вас никаких специальных знаний в области линейной алгебры — не считая, конечно, общих представлений о том, как работают матричные операции, для понимания того, что может получиться в их итоге. MathCAD хорош для пользователя тем, что позволяет ему работать с векторами и матрицами точно так же, как с обычными скалярами, сиречь переменными, содержащими исключительно и только действительные числа. Попробуйте задать две матрицы (я их назвал aa и bb), а затем применить к ним операцию сложения точно так же, как когда-то применяли ее к обыкновенным числам. Конечно, для того, чтобы матрицы можно было складывать, они должны иметь одинаковые размеры. Точно так же можете попробовать вычесть из одной матрицы другую или перемножить их. Вы увидите, что MathCAD успешно справляется с подобными задачами, не напрягая пользователя излишними вычислениями.
Транспонировать матрицы в MathCAD’е ничуть не сложнее, чем их складывать или перемножать. Вычислять обратные матрицы, впрочем, тоже. Во всех этих задачах помогут соответствующие операторы с Они обозначены на ней теми же значками, что и в учебниках по линейной алгебре, а потому пользователю, хотя бы минимально знакомому с матричным исчислением, все должно быть просто и понятно. Нужно только помнить, что нельзя вычислить обратную матрицу для той матрицы, которая является вырожденной (то есть имеет нулевые или пропорциональные друг другу строки или столбцы). Для того, чтобы не останавливаться излишне подробно на этих простых операциях, просто приведу иллюстрацию, демонстрирующую их практическое использование. Думаю, у читателей не возникнет никаких проблем ни с транспонированием, ни с вычислением обратной матрицы с помощью MathCAD.
Еще одной часто выполняемой операцией является вычисление детерминанта, или определителя матрицы. Думаю, что совсем не огорчу вас известием о том, что в MathCAD и с определителями работать так же просто, как и со всем остальным, связанным с матрицами. За его вычисление отвечает кнопка Determinant, расположенная, конечно же, на панели Matrix. Поскольку детерминант в MathCAD’е, как и вообще в линейной алгебре, обозначается с помощью символов прямых черт, ограничивающих матрицу (или имя переменной, ее обозначающей), то вполне логично, что вставить эти самые прямые черты в текст выражения можно с помощью соответствующей клавиши на клавиатуре: Shift + \. Думаю, этой несложной комбинацией будет пользоваться все же удобнее, чем искать каждый раз нужную кнопку на панели инструментов MathCAD’а.
Внешний вид матриц
Мы с вами, конечно же, далеко еще не закончили свое знакомство с матрицами в MathCAD’е, однако, думаю, на сегодня уже непосредственной математики хватит. В конце статьи я лучше расскажу о том, как можно изменить способ отображения матриц в среде MathCAD — возможно, кому-то из читателей этой статьи эта информация будет полезной и небезынтересной.
Дело в том, что MathCAD может отображать матрицы не только в привычном всем виде чисел, заключенных в скобки, но и в виде таблиц. Если вы используете этот математический пакет для каких-либо статистических расчетов и при этом работаете с большими массивами данных, то, безусловно, такое отображение матриц будет более предпочтительным для вас, чем традиционное. Для изменения способа отображения матриц дважды кликните по нужной матрице и в появившемся окне перейдите на вкладку Display Options. Далее в поле Matrix display style выберите значение Table. Матрица приобретет вид точно такой, как на соответствующей иллюстрации к этой статье.
Внешний вид таблицы можно также настроить далее, кликнув по ней правой кнопкой мыши и выбрав пункт Properties. В появившемся окне можно снять птичку с пункта Show column/row labels, чтобы убрать отображение нумерации строк и столбцов в матрице, представляемой в виде таблицы. На вкладке Data Range можно выбрать диапазон отображаемых строк и столбцов матрицы, что также полезно для матриц, содержащих большое количество элементов.
Ну что ж, на сегодня, думаю, достаточно. Это только начало работы с матрицами — в следующий раз мы поговорим о гораздо более интересных вещах, чем просто сложение, транспонирование и вычисление детерминанта.
© Компьютерная газета
Понравилось это:
Нравится Загрузка…
Похожее
mathcadworld.wordpress.com