Основы программирования MatLab — CodeTown.ru
Здравствуйте, уважаемые читатели! В нашей статье, посвященной основам программирования MatLab, мы познакомимся с синтаксисом этого языка, который мы будем использовать в основном для математических вычислений.
MATLAB — это интерактивная система, в которой основным элементом данных является массив. Это позволяет решать различные задания, связанные с техническими вычислениями, особенно в которых используются вектора и матрицы, в несколько раз быстрее, чем при написании программ с использованием других языков программирования.
Переменные в MATLAB:
Существует несколько типов переменных, вот самые основные из них:
- logical (true – 1, false – 0)
- char – символьная строка
- numeric – массивы чисел с плавающей запятой
- int: int8 (массив 8-разрядных целых чисел со знаком, 1 байт на одно число), также есть int16, int32, int64
- single – массив чисел с плавающей запятой одинарной точности (4 байта на одно число)
- double – массив чисел с плавающей запятой двойной точности (16 знаков)
- structure – структурированный массив полей для хранения данных с именами
Имя переменной:
длина — до 63 символов;
не должно совпадать с именами функций и процедур;
должно начинаться с буквы;
может содержать буквы, цифры, знак подчёркивания;
различаются большие и маленькие буквы.
Задать переменную очень легко:
a=4
Еще например:
>> a=2;b=4;a+b
ans =
6
Как видите, Matlab сам выводит результат операции с 2 переменными.
Массивы:
Начнем с задания одномерных массивов:
Задание в командной строке: x = [1,2,3,4] или x = [1 2 3 4]
Задание отдельных элементов: х(3) = 3
Длину массива можно найти командой: length (x)
Переходим к двумерным массивам:
Задание в командной строке: x = [1,2,3,4;5,6,7,8]
ans =
1 2 3 4
5 6 7 8
Задание отдельных элементов: х(2,3) = 7
Обращение к отдельной р-ой строке массива: у = [р,:]
Обращение к к-ому столбцу массива: у = [:,к]
Команда В=А(:,:) обращается ко всем элементам матрицы, т.е. создаёт копию матрицы А.
Также следует знать о стандартных матрицах:
- zeros(n,m) — матрица из нулей размера nxm
- ones(n,m) – матрица из единиц размера nxm
- rand(n,m) – матрица случайных чисел размера nxm
- eye(n,m) – матрица из единиц на главной диагонали размера nxm
Операторы:
Операторы следует знать, так как без них невозможно освоить все основы программирования на MATLAB. )
)
Внутри каждого уровня операторы имеют равный приоритет и вычисляются в порядке следования слева направо. Порядок вычислений может быть изменён скобками.
Операторы отношения:
меньше-функция lt()меньше или равно-функция le()> -больше-функция gt()>= --функция ge()== -равно-функция eg()~= -не равно-функция ne()
Их приоритет ниже арифметических, но выше логических операторов.
Логические операторы:
- &
-массив: 1- для каждого местоположения, в котором оба элемента имеют значение true (отличны от нуля) и 0 – для всех остальных элементов; функция and() - |
-массив: 1- для каждого местоположения, в котором хотя бы один элемент имеет значение true (отличен от нуля) и 0 – для всех остальных элементов; функция or() - ~
-логическое отрицание для каждого элемента входного массива, А; функция not() - xor
-массив: 1- для каждого местоположения, в котором только один элемент имеет значение true (отличен от нуля) и 0 – для всех остальных элементов
A = [0 1 1 0 1]; B = [1 1 0 0 1]; A&B = 01001 A|B = 11101 ~A = 10010 xor(A,B)=10100
Простые примеры:
Задание матрицы 3 на 4 рандомными числами:
>> rand(3,4)
ans =
0. 8147 0.9134 0.2785 0.9649
0.9058 0.6324 0.5469 0.1576
0.1270 0.0975 0.9575 0.9706
8147 0.9134 0.2785 0.9649
0.9058 0.6324 0.5469 0.1576
0.1270 0.0975 0.9575 0.9706
Далее определим детерминант следующей матрицы:
>> x = [1,2,3,4;5,6,7,8;10,11,12,13;14,15,16,17]
x =
1 2 3 4
5 6 7 8
10 11 12 13
14 15 16 17
>> det(x)
ans =
0
Идем дальше:
Приведем пример перемножения матриц, напомню, что матрицы можно перемножать только в том случае, если число столбцов 1 матрицы совпадает с числом строк 2 матрицы.
>> x = [1,2,4;5,6,7]
X1 =
1 2 4
5 6 7
>> x = [1,2;4,5;6,7]
X2 =
1 2
4 5
6 7
>> x1*x2
ans =
11 14 18
29 38 51
41 54 73
На этом мы сегодня закончим. В следующих статьях мы будем уже подробно разбираться со всеми возможностями MATLAB. И поверьте, возможности эти очень большие.
Если у вас остались вопросы, то задавайте их в комментариях.
Конкатенация (объединение) массивов
ЛАБОРАТОРНАЯ РАБОТА № 1.
ОБЩИЕ ПРИНЦИПЫ РАБОТЫ СИСТЕМЫ MATLAB
Цель работы–ознакомление с системойMatLab,правилами созданиячисловых массивов и приобретение практических навыков по использованию средств системы для работы с ними.
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Название системы MatLab происходит от слов Matrix Laboratory (матричная лаборатория). Пакет ориентирован на обработку массивов данных.
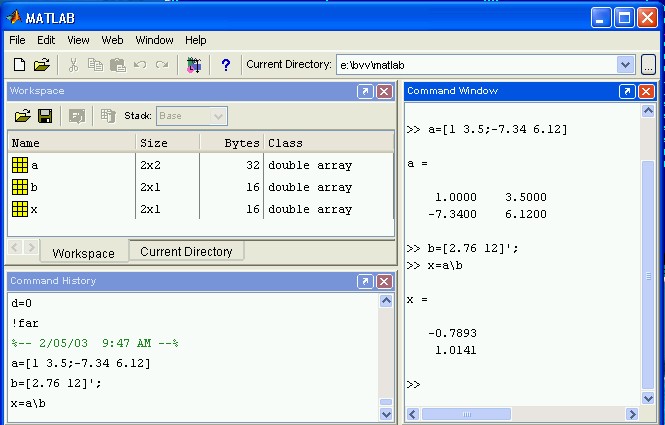
В интерфейс системы MatLab входят следующие панели:
· Command Window (Окно Команд), где проводятся все расчеты и операции;
· Launch Pad (Окно Разделов), где можно получить доступ к различным модулям ToolBox;
· Workspace (Рабочее пространство), где отображается текущий набор переменных, введенных пользователем в командном окне;
· Current Directory (Текущий каталог), где можно установить текущий каталог;
· Command History (История команд), где хранятся команды, набираемые пользователями.
Матричная система MatLab выделяется из других систем тем, что ее операторы и функции имеют операнды в виде векторов и матриц. Так как операции с матрицами могут быть как поэлементными, так и матричными, то в поэлементные операторы добавляется точка. Например, символы точка, звездочка ‘*’ определяют поэлементное умножение массивов, символ звездочка ‘*’ – матричное умножение (табл. 1). Набор любой команды должен заканчиваться нажатием клавиши <Enter>. Действие, выполняемое функцией, применяется ко всем элементам массива, передаваемым в списке входных аргументов.
Справочная информация
Получить справочную информацию можно следующими операторами:
helpwin– справка о разделах и функциях системы MatLab;
helpdesk– общая справка о системе MatLab;
doc <имя_функции>–вывод описания функции в окнеHelp ;help <имя_функции>–краткая информация о функции;
type <имя _функции>–вывод текстаm–файла функции;demo–команда вызова тестовых примеров.
Таблица 1.1 Список арифметических операторов
| Функция | Название | Оператор | Синтаксис |
| Plus | Плюс | + | M1+M2 |
| uplus | Унарный плюс | + | +M |
| minus | Минус | – | M1–M2 |
| uminus | Унарный минус | – | –M |
| mtimes | Матричное умножение | * | M1*M2 |
| times | Поэлементное умножение массивов | .* | M1.*M2 |
| mpower | Возведение в степень матрицы | ^ | M1^x |
| power | Поэлементное возведение в степень массива | .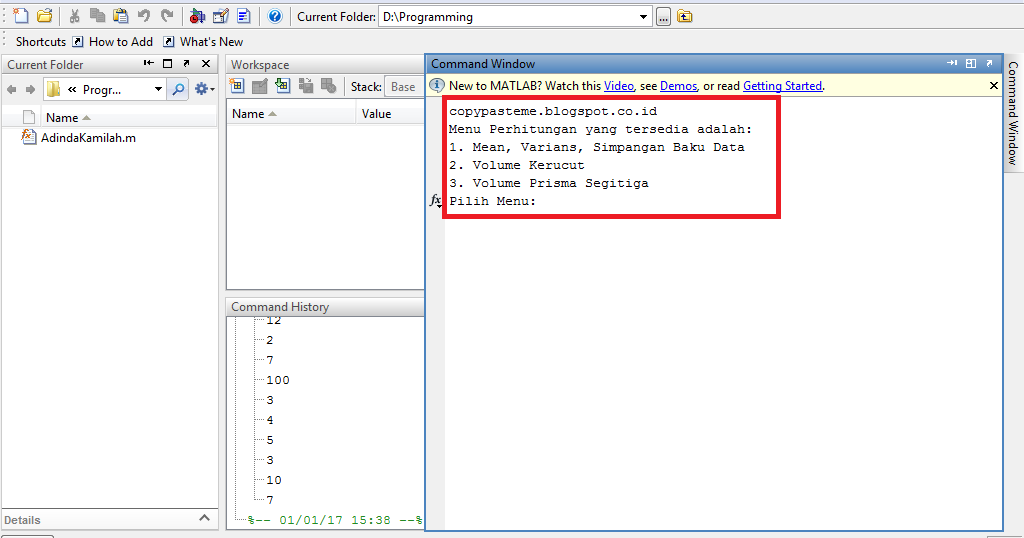 x x
| |
| mldivide | Обратное (справа налево) деление матриц | \ | M1\M2 |
| mrdivide | Деление матриц слева направо | / | M1/M2 |
| ldivide | Деление поэлементное массивов справа налево | .\ | M1.\M2 |
| rdivide | Деление поэлементное массивов слева направо | ./ | M1./M2 |
Для введения комментария используют знак процента – %.
Для создания вектор-строки используются квадратные скобки с перечислением элементов строки через пробел или запятую и специальная конструкция j:i:k с указанием начального значения вектора – j, шага – i и конечного значения вектора – k через двоеточие (если значение шага равно 1, его можно не указывать).
Для создания вектор-столбца элементы вектора перечисляются через точку с запятой в квадратных скобках или транспонируется полученный ранее вектор-строка. Для выполнения операции транспонирования используется одиночная кавычка (‘), которая ставится после индетификатора, определяющего транспонируемую структуру. Для комплексных матриц транспонирование дополняется сопряжением матрицы. Точка с одиночной кавычкой (.’) используется для транспонирования массива без операции сопряжения для комплексных матриц.
Для выполнения операции транспонирования используется одиночная кавычка (‘), которая ставится после индетификатора, определяющего транспонируемую структуру. Для комплексных матриц транспонирование дополняется сопряжением матрицы. Точка с одиночной кавычкой (.’) используется для транспонирования массива без операции сопряжения для комплексных матриц.
Для создания матрицы можно использовать следующие способы ввода элементов в квадратных скобках:
1. По строкам, разделяющимся точкой с запятой;
2. По столбцам, заданным в квадратных скобках;
3. По строкам в интерактивном режиме.
Задание 1. Создать вектор-строку,вектор-столбец и матрицы
Конкатенация (объединение) массивов
С помощью операции конкатенации можно формировать новые массивы из ранее созданных – векторов, матриц, используя эти массивы в качестве своих элементов. Объединять массивы можно по горизонтали и по вертикали.
Объединять массивы можно по горизонтали и по вертикали.
При горизонтальной конкатенации в качестве разделителя массивов в квадратных скобках используется запятая или пробел, например, если В и А – матрицы, то M = [А, В] – горизонтальная конкатенация матриц А и В. А и В должны иметь одинаковое число строк. Горизонтальная конкатенация может быть применена для любого числа матриц в пределах одних скобок [A, B, C].
При вертикальной конкатенации в качестве разделителя массивов в квадратных скобках используется точка с запятой, например, если C и D – матрицы, то M = [C; D] – вертикальная конкатенация матриц C и D. C и D должны иметь одинаковое число столбцов. Вертикальная конкатенация может быть применена для любого числа матриц в пределах одних скобок [C; D; E]. Вертикальная и горизонтальная конкатенация может быть применена в одной операции.
Задание 2. Создать матрицу,используя вертикальную и горизонтальнуюконкатенацию
Задание 3. Создать квадратную единичную матрицу размерностью2
Создать квадратную единичную матрицу размерностью2
Задание 4. Создать вектор-столбец с помощью вертикальной конкатенации
использованием функций rand и randn
Задание 5. Создать матрицу с помощью горизонтальной конкатенации сиспользованием функций ones и zeros
Функция repmat() создает матрицу, копируя исходный массив заданное число раз по вертикали и горизонтали.
B = repmat(A,M,N)–функция создает матрицуB,состоящую изMкопийА по вертикали и N копий А по горизонтали, то есть M N копий массива A (если А – число, функция формирует матрицу размером M N со значением элементов, равных А).
Задание 6. Сформировать матрицуcиспользованием вектор-строки а изтрех элементов
Задание 7. Сформировать матрицу размерностью2 3,все элементыкоторой равны десяти
Сформировать матрицу размерностью2 3,все элементыкоторой равны десяти
Индексация массивов
Элементы массивов обладают двумя свойствами: порядковым номером (индексом) в массиве и собственно значением. Нумерация элементов в системе MatLab начинается с единицы. Для указания индексов элементов массивов используются круглые скобки (ошибка при индексации массива генерируется в том случае, если индекс элемента меньше единицы или больше размера массива).
Задание 8. Задать вектор-строку из четырех элементов и изменить третийэлемент на значение 8
Задание 9. Изменить значение элемента матрицы случайных чиселS,находящегося во второй строке и в четвертом столбце, на 1
Задание 10. Обнулить третий и четвертый столбец из предыдущегопримера
Пустые квадратные скобки удаляют информацию из индексированной структуры.
A(m,:) = [ ] – удаляет строку m из матрицы A. A(:,n) = [ ] – удаляет столбец n из матрицы A.
Сервисные функции
Ниже приведены некоторые функции, необходимые при работе с массивами:
[M,N] = size(<идентификатор_массива>)–возвращает размер массива,где M – число строк; N – число столбцов.
Задание 11. Определить размерность единичной матрицы
max(<идентификатор_массива>) и min(<идентификатор_массива>)–
вычисляет вектор строку, содержащую максимальные или минимальные элементы в каждом столбце матрицы.
Задание 12. Определить максимальные значения матрицы случайныхчисел
Задание 13. Преобразовать матрицу из предыдущего примера в вектор-строку и найти экстремальные значения
Задание 14. Определить длину заданного вектора
Определить длину заданного вектора
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Создать вектор-строку: начальный элемент равен – pi, конечный pi, шаг равен 0.1. Транспонировать строку в столбец.
2. Создать три вектор-строки из 5 элементов fi = [xn, xn-1, xn-2, xn-3, xn-4], где n = 5 для х = 2, 3, 4. Объединить эти строки в матрицу А(3 × 5).
3. Создать три вектор-столбца из 5 элементов арифметической прогрессии. Элемент арифметической прогрессии рассчитывается по формуле:
an = an-1 + d,
где аn–1 – предыдущий элемент; аn – последующий.
Пять элементов вектора формируются, начиная с задания первого элемента а и c использованием шага арифметической прогрессии d для задания последующих элементов:
o Для первого вектор-столбца a = 2; d = 1;
o Для второго вектор-столбца a = 7; d = 2;
o Для третьего вектор-столбца a = 10; d = –2.
1. Объединить эти вектор-столбцы в матрицу В(5 × 3).
B= [a1 a2 a3]
B =
2 7 10
3 9 8
4 11 6
5 13 4
6 15 2
2. Транспонировать матрицу В из предыдущего пункта задания и объединить с матрицей А в матрицу М(6 × 5).
B=B’
B =
2 3 4 5 6
7 9 11 13 15
10 8 6 4 2
M=[B;A]
M =
2 3 4 5 6
7 9 11 13 15
10 8 6 4 2
32 16 8 4 2
243 81 27 9 3
1024 256 64 16 4
Изменение формы и перестановка массивов — MATLAB & Simulink
Основное содержимое
Open Live Script
Многие функции в MATLAB® могут брать элементы существующего массива и помещать их в другую форму или последовательность.
Изменение формы
Функция изменить форму изменяет размер и форму массива. Например, измените матрицу 3 на 4 на матрицу 2 на 6.
А = [1 4 7 10; 2 5 8 11; 3 6 9 12]
А = 3×4
1 4 7 10
2 5 8 11
3 6 9 12
B = изменить форму (A,2,6)
B = 2×6
1 3 5 7 9 11
2 4 6 8 10 12
Пока количество элементов в каждой фигуре одинаково, вы можете преобразовать их в массив с любым количеством измерений. Используя элементы из A , создайте многомерный массив 2 на 2 на 3.
C = изменить форму (A,2,2,3)
C =
С(:,:,1) =
1 3
2 4
С(:,:,2) =
5 7
6 8
С(:,:,3) =
9 11
10 12
Транспонирование и отражение
Распространенной задачей в линейной алгебре является работа с транспонированием матрицы, которое превращает строки в столбцы, а столбцы в строки. Для этого используйте функцию транспонирования
Для этого используйте функцию транспонирования или функцию .' оператор.
Создайте матрицу 3 на 3 и вычислите ее транспонирование.
А = магия(3)
А = 3×3
8 1 6
3 5 7
4 9 2
Б = А.'
В = 3×3
8 3 4
1 5 9
6 7 2
Аналогичный оператор ' вычисляет сопряженное транспонирование для комплексных матриц. Эта операция вычисляет комплексное сопряжение каждого элемента и транспонирует его. Создайте комплексную матрицу 2 на 2 и вычислите ее сопряженное транспонирование.
А = [1+i 1-i; -я я]
А = Комплекс 2×2 1.0000 + 1.0000i 1.0000 - 1.0000i 0,0000 - 1,0000i 0,0000 + 1,0000i
B = A'
B = Комплекс 2×2 1.0000 - 1.0000i 0.0000 + 1.0000i 1.0000 + 1.0000i 0.0000 - 1.0000i
flipud переворачивает строки матрицы сверху вниз, а fliplr переворачивает столбцы слева направо.
А = [1 2; 3 4]
А = 2×2
1 2
3 4
B = флипуд (A)
B = 2×2
3 4
1 2
С = флиплр(А)
С = 2×2
2 1
4 3
Сдвиг и поворот
Вы можете сдвинуть элементы массива на определенное количество позиций, используя функцию circshift . Например, создайте матрицу 3 на 4 и сдвиньте ее столбцы вправо на 2. Второй аргумент [0 2] указывает circshift сдвинуть строки на 0 позиций и сдвинуть столбцы на 2 позиции вправо.
А = [1 2 3 4; 5 6 7 8; 9 10 11 12]
А = 3×4
1 2 3 4
5 6 7 8
9 10 11 12
B = круговое смещение (A,[0 2])
B = 3×4
3 4 1 2
7 8 5 6
11 12 9 10
Чтобы сдвинуть строки A вверх на 1 и сохранить столбцы на месте, укажите второй аргумент как [-1 0] .
C = круговой сдвиг (A, [-1 0])
C = 3×4
5 6 7 8
9 10 11 12
1 2 3 4
Функция rot90 может повернуть матрицу против часовой стрелки на 90 градусов.
А = [1 2; 3 4]
А = 2×2
1 2
3 4
B = rot90(A)
B = 2×2
2 4
1 3
Если вы повернете еще 3 раза, используя второй аргумент для указания количества поворотов, вы получите исходную матрицу А .
С = rot90(B,3)
С = 2×2
1 2
3 4
Сортировка
Сортировка данных в массиве также является ценным инструментом, и MATLAB предлагает ряд подходов. Например, функция sort сортирует элементы каждой строки или столбца матрицы отдельно в порядке возрастания или убывания. Создайте матрицу A и отсортируйте каждый столбец A в порядке возрастания.
А = магия(4)
А = 4×4
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
B = сортировка(A)
B = 4×4
4 2 3 1
5 7 6 8
9 11 10 12
16 14 15 13
Сортировать каждую строку в порядке убывания.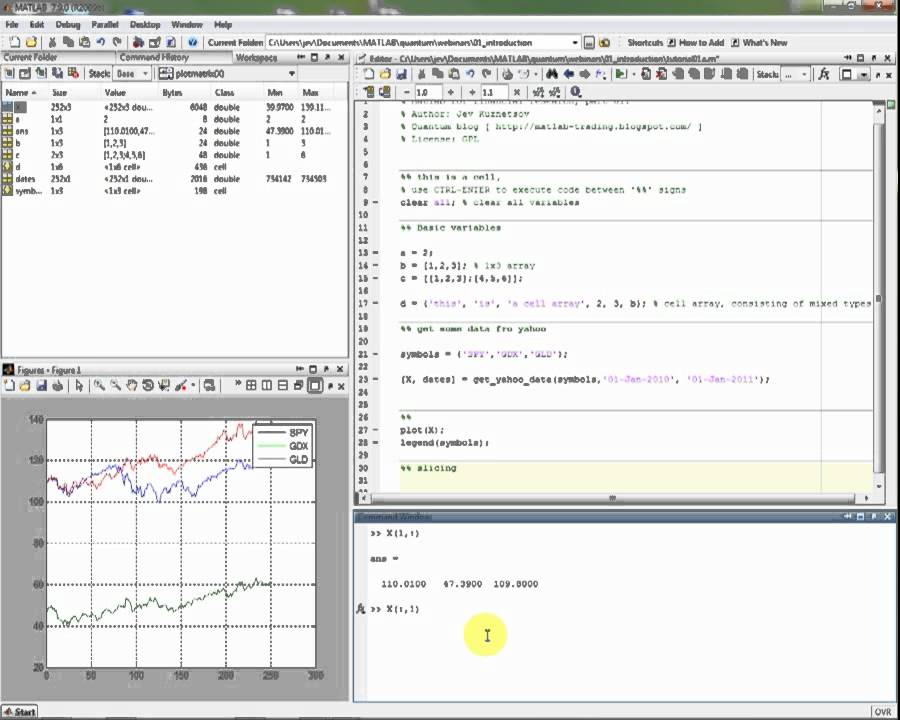 Значение второго аргумента
Значение второго аргумента 2 указывает, что вы хотите сортировать построчно.
C = сортировка (A, 2, «по убыванию»)
C = 4×4
16 13 3 2
11 10 8 5
12 97 6
15 14 4 1
Чтобы отсортировать целые строки или столбцы относительно друг друга, используйте функцию sortrows . Например, отсортируйте строки A в порядке возрастания в соответствии с элементами в первом столбце. Позиции строк меняются, но порядок элементов в каждой строке сохраняется.
D = сортировка(A)
D = 4×4
4 14 15 1
5 11 10 8
9 7 6 12
16 2 3 13
- Удаление строк или столбцов из матрицы
- Индексирование массива
У вас есть модифицированная версия этого примера. Хотите открыть этот пример со своими правками?
Вы щелкнули ссылку, соответствующую этой команде MATLAB:
Запустите команду, введя ее в командном окне MATLAB. Веб-браузеры не поддерживают команды MATLAB.
Веб-браузеры не поддерживают команды MATLAB.
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Свяжитесь с местным офисом
- Пробная версия программного обеспечения
- Пробная версия программного обеспечения
- Обновления продукта
- Обновления продукта
Создание массивов объектов и работа с ними — MATLAB и Simulink
Перейти к содержимомуОсновное содержание
Построение и объединение массивов объектов; гетерогенные массивы
Построение массивов объектов, эталонных объектов и их свойств из массивов,
и проектировать иерархии классов, которые поддерживают формирование разнородных (смешанных
класс) массивы.
Functions
empty | Create empty array of specified class |
Classes
matlab.mixin.Heterogeneous | Superclass for heterogeneous array formation |
Topics
Создание массивов объектов
- Создание массивов объектов
Создание массивов объектов в конструкторе и возврат массива в качестве выходного аргумента. - Инициализировать массивы объектов
MATLAB ® вызывает конструктор класса без аргументов для инициализации элементов массива с объектом по умолчанию. - Инициализировать массивы объектов дескриптора
MATLAB использует объект по умолчанию для инициализации пустых элементов массива объектов дескриптора. - Пустые массивы
Пустые массивы не имеют элементов, но относятся к определенному классу.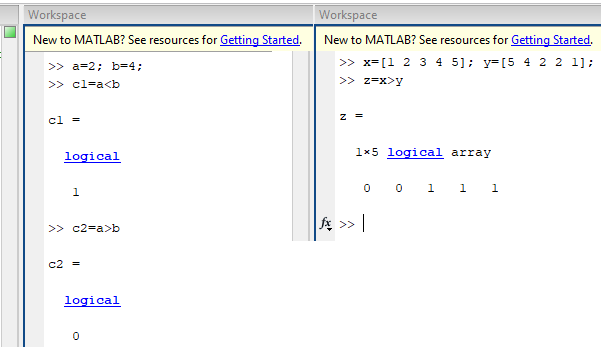
- Доступ к динамическим свойствам в массивах
Доступ к динамическим свойствам в массивах объектов путем обращения к отдельным объектам.
Объединение массивов
- Методы объединения
Вы можете объединять объекты в массивы. - Объединение объектов разных классов
MATLAB следует определенным правилам, когда вы пытаетесь создать массив с объектами разных классов.
Преобразователи объектов и массивы классов
- Неявное преобразование классов
MATLAB может неявно преобразовывать объекты в другой класс для конкатенации, присвоение с индексом, проверка свойств и проверка аргументов. - Преобразователи объектов
Вы можете преобразовать объект одного класса в объект другого класса. - Определение класса массива
Вы можете определить класс массива.