Как в черчении обозначается радиус: Радиус окружности — что такое, формула, как найти ⚪

Радиус окружности — что такое, формула, как найти ⚪

Поможем понять и полюбить математику

Начать учиться

199.3K

Решить задачу можно по-разному: посчитать на калькуляторе, взять алгоритм из похожей задачки, списать у одноклассника. Самый эффективный и радостный — запомнить формулу и прийти к ответу самому. В этой статье расскажем про способы поиска радиуса окружности.

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — часть плоскости, которая лежит внутри окружности. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Если известна длина

, где C — длина окружности.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Если известен диаметр окружности

, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

 

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ прямоугольника.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

, где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

, где a — сторона квадрата.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

, где a, b, с — стороны треугольника, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

, где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

, где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

 

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

Как найти периметр квадрата

К следующей статье

483.1K

Теорема Пифагора

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Обозначение диаметра, радиуса, квадрата, конусности, уклона и дуги

На чертежах используются следующие знаки:  – диаметр, R – радиус, – квадрат,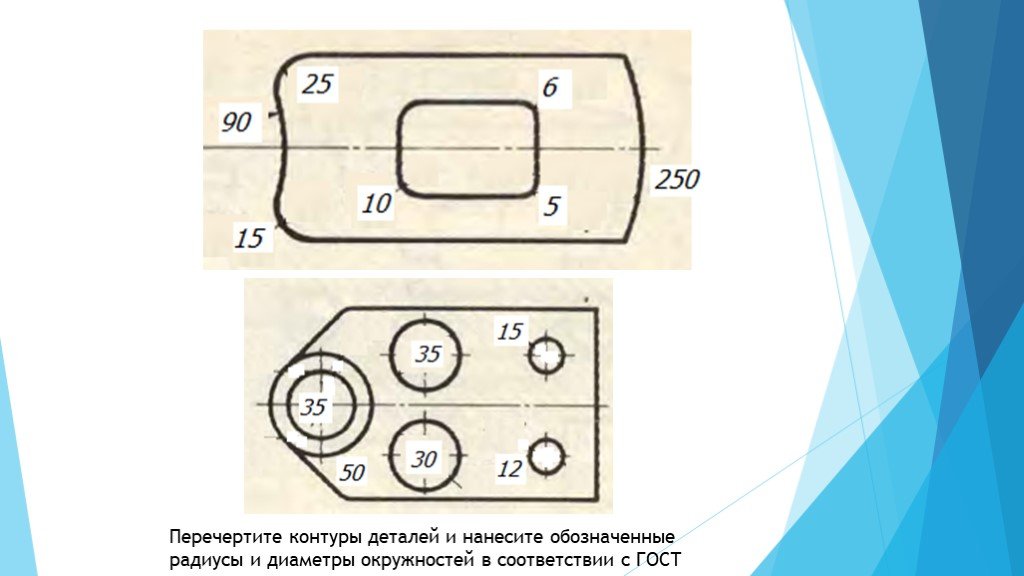

– уклон, – конусность,  – дуга, относительные размеры которых по отношению к цифрам показаны на рис. 2.11.

Диаметр. Цилиндрические поверхности обозначаются на чертежах знаком , который представляет собой окружность, пересеченную прямой линией. Высота и наклон прямой линии одинаковы с высотой и наклоном цифр размерного числа, а диаметр окружности равен 5/7 высоты цифр. Наносится знак диаметра над размерной линией перед размерным числом.

Обозначение диаметра цилиндрической поверхности рекомендуется наносить на том изображении, где ось ее проецируется в линию, т.е. между образующими (см. рис. 2.81). При этом размерную линию разрешается проводить с обрывом независимо от того, изображена ли окружность полностью или частично. Обрыв размерной линии производится дальше центра окружности. Размещение обозначения диаметра на окружности допускается (см. рис. 2.86).

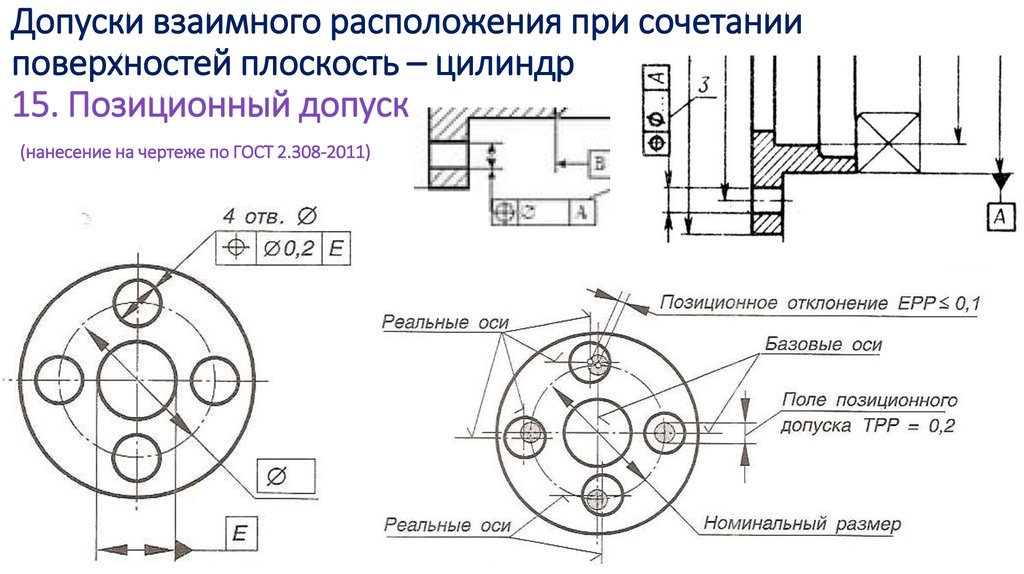
Если деталь имеет несколько одинаковых цилиндрических отверстий, то размер дают один раз с указанием общего их числа (рис. 2.88).

Рис.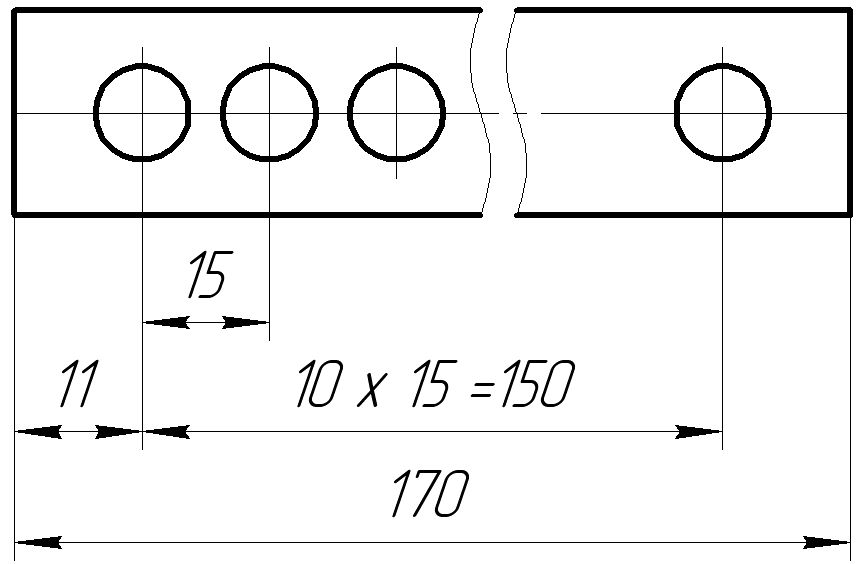 2.88

В таблице 2.6 приведен нормальный ряд чисел, установленный ГОСТ 6636–69* для использования при выборе размера диаметра.

Таблица 2.6

0,5	3	11	21	35	52	78	105	155	210	310	410
0,8	3,5	12	22	36	55	80	110	160	220	320	420
1	4	13	23	38	58	82	115	165	230	330	430
1,2	4,5	14	24	40	60	85	120	170	240	340	440
1,5	5	15	25	42	62	88	125	175	250	350	450
1,8	6	16	26	44	65	90	130	180	260	360	460
2	7	17	28	45	68	92	135	185	270	370	470
2,2	8	18	30	46	70	95	140	190	280	380	480
2,5	9	19	32	48	72	98	145	195	290	390	490
2,8	10	20	34	50	75	100	150	200	300	400	500

Р адиус.

Перед размерным числом, определяющим радиус, обязательно пишется прописная латинская буква R (например, R25). Высота этой буквы и высота размерного числа должны быть одинаковыми.

На рис. 2.89 приведены примеры нанесения наружных дуг окружностей, а на рис. 2.90 – внутренних.

Размерная линия радиуса наносится на том изображении, где дуга проецируется в истинном виде. Из рис. 2.89 и рис. 2.90 следует, что размерная линия радиуса должна располагаться в направлении истинного радиуса и оканчиваться одной стрелкой, примыкающей к контурной (или выносной) линии.

Рис. 2.90

Нанесение размерных чисел при различных положениях размерных линий на чертеже определяется удобством чтения чертежа.

При проведении нескольких размерных линий радиусов из одного центра они не должны располагаться на одной прямой (рис. 2.91).

В случае, если необходимо указать центр дуги большого радиуса, допускается приближать его, выполняя размерную линию с изломом под углом 90° (рис. 2.92).

П ри необходимости положение центра дуги задается пересечением центровых или выносных линий (рис. 2.93).

Если на чертеже радиусы скруглений, сгибов и других подобных элементов одинаковы или какой-либо радиус является преобладающим, то вместо нанесения этих значений на изображение рекомендуется выносить их в технические требования в виде записей «Радиусы скруглений 4 мм»; «Внутренние радиусы сгибов 10 мм»; «Неуказанные радиусы 8 мм» и др.

Нормальные радиусы скруглений, установленные для использования ГОСТ 10948–64, приведены в таблице 2.7.

Таблица 2.7

Извлечение радиуса из технических чертежей — Werk24

Радиусы могут определять внутреннюю и внешнюю криволинейные поверхности детали. Он также используется для отображения скруглений, предназначенных для усиления краев на соединительных гранях.

Буква «R», как показано, широко используется в чертежах и является сокращением от слова «Радиус». Радиус — это расстояние от центра окружности до окружности окружности.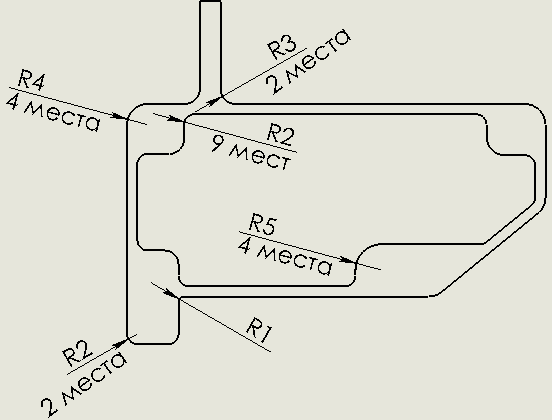 Он всегда ставится перед числом. Например, R50 означает, что круг имеет радиус 50 мм.

Количество

Некоторые индикаторы радиусов описывают несколько радиусов на чертеже. (например, 3xR5). Эта информация доступна в атрибуте количество .

Размер

Размер радиуса доступен в атрибуте размер . Это объект W24Size.

Допуск

Радиусы допускаются так же, как и меры. Имейте в виду, что мин./макс. допуски для радиусов встречаются чаще, чем для мер. Если специальные допуски не определены, применяются общие_допуски. Вся эта информация доступна в атрибут size_tolerance , объект W24SizeTolerance .

Единица измерения

Различие между метрическими и имперскими мерами. Возвращается перечисление W24UnitLength .

Модель

• Запрос радиусов: W24AskVariantGDTs
• Получение радиусов: W24AskVariantGDTsResponse

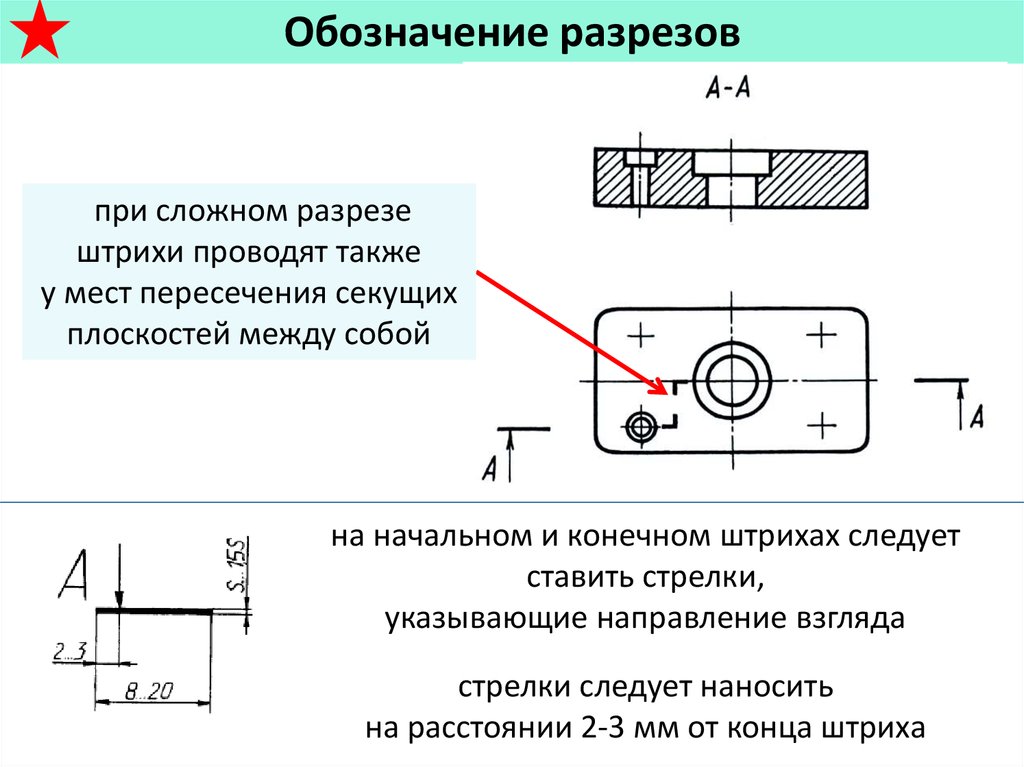
Доступ к извлеченной информации можно получить с помощью модели W24Radius.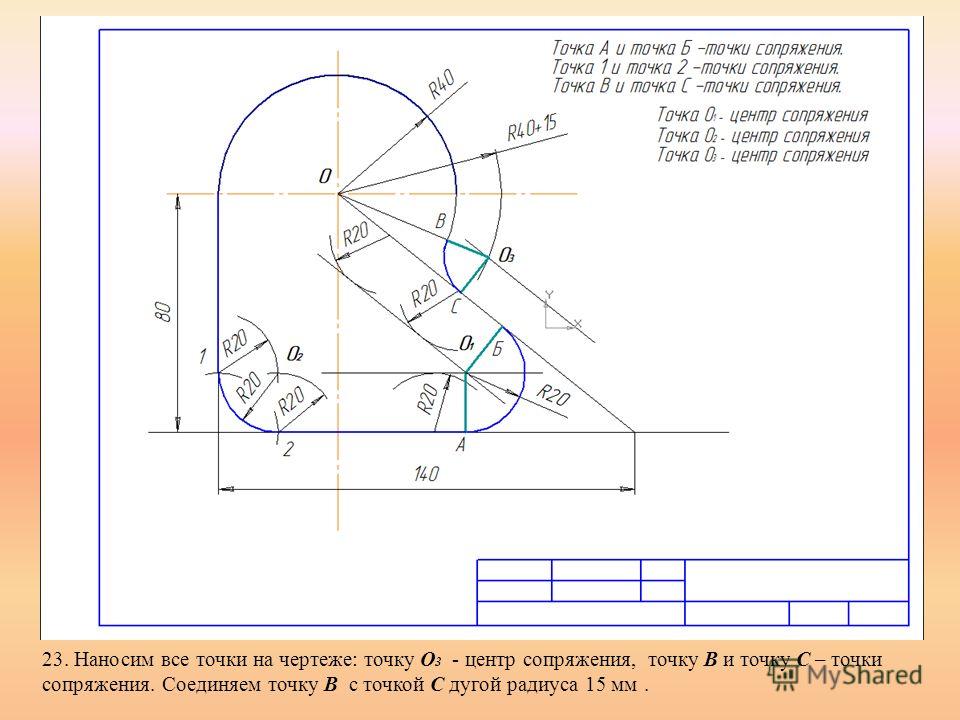

W24Radius

Элемент радиуса

Атрибуты: radius_id: Уникальный идентификатор UUID4. Это можно использовать для предоставления автоматизированной обратной связи об изменениях клиентов.

 метка: Метка радиуса.
уверенность: Werk24 рассчитывает внутреннюю оценку достоверности для
    радиус действия. В зависимости от вашего варианта использования вы можете захотеть
    учитывать или отбрасывать малодостоверные радиусы. Это значение
    позволяет вам это сделать. Диапазон значений от 0,0 до 1,0
 

Свойства

Определения

• W24FeatureCoordinate (объект) : Координатная точка
  Атрибуты: x: позиция x, нормированная по ширине миниатюры
  y: позиция y, нормированная по высоте миниатюры.

• X (номер)

• y (номер)

• 9002 W24FEATEPOSTPOSTION .
  009
  009.
  009.
  009. 9009.10014. 9009.1009. 9009.1009. 9009.1009. 9009.1009. 9009.1009. 9009.1009. 9009.1009. . . . . . 9002. эскизы, нормализованные по ширине и высоте каждого эскиза.
  Положение каждого объекта указано в виде списка координат. Если в списке всего два элемента, вы имеете дело со строкой. Если их четыре или более, вы смотрите на полигон.
  Атрибуты: страница: Положение объекта на миниатюре страницы
  лист: Положение объекта на миниатюре листа
  sectional: Положение объекта на миниатюре сечения.

• лист (массив)

  • Элементы : См. #/definitions/W24FeatureCoordinate .

• холст (массив)

  • Элементы : См. #/definitions/W290Feature1Coordinate.

• секционная (массив)

  • Элементы : См. #/definitions/W2901Co .

• W24SizeType (строка) : Перечисление, описывающее различные типы размера. Должен быть одним из: ['NOMINAL', 'DIAMETER', 'WIDTHS_ACROSS_FLATS'] .

• W24Size (объект) : абстрактный базовый класс для размеров
  Атрибуты: blurb: аннотация для человеческого потребления
  size_type: Тип размера для десериализации Единица прикреплена к родительскому объекту, который также определяет допуск.

• аннотация (строка)

• size_type : См.

• nominal_size (номер)

• W24Sizetolerancetype (Строка) : ENUMED COLERATES. Должен быть одним из: ['APPROXIMATION', 'FIT_SIZE_ISO', 'GENERAL_TOLERANCES', 'MINIMUM', 'MAXIMUM', 'OFF_SIZE', 'ТЕОРЕТИЧЕСКИ_ТОЧНО', 'ССЫЛКА'] .

• W24SizeTolerance (объект) : Абстрактный базовый класс для охвата допусков
  Атрибуты: blurb (str): строковое представление для человеческого восприятия
  toleration_type (W24SizeToleranceType): toleration_type (W24SizeToleranceType).

• toleration_type : См. #/definitions/W24SizeToleranceType .

• аннотация (строка)

• W24UnitLength (строка) : Перечисление поддерживаемых единиц длины. Должен быть одним из: ['METER', 'DECIMETER', 'CENTIMETER', 'MILLIMETER', 'FOOT', 'INCH', 'MICRO_INCH'] .

• W24RadiusLabel (объект) : Метка радиуса
  Атрибуты: аннотация: Строковое представление радиуса для человеческого восприятия
  количество: Количество аннотированного радиуса, например, 2 x R94 возвращает количество0063 size: Размер радиуса, указанный на чертеже.
  size_tolerance: Сведения о допуске радиуса. Пожалуйста, имейте в виду, что радиусы могут иметь специальные допуски. Если на чертеже ничего не указано, применяются общие допуски. Единица
  : единицы длины размера и size_tolerance. В большинстве случаев это будет миллиметр (МЕТРИЧЕСКАЯ СИСТЕМА) или дюйм (ИМПЕРАЦИОННАЯ СИСТЕМА), и он будет соответствовать всему чертежу. Исключения очень редки, но есть.

• аннотация (строка)

• качество (целое число) : По умолчанию: 1 .

• Размер : См. #/definitions/W24Размер .

• size_tolerance : По умолчанию: {'toleration_type': 'GENERAL_TOLERANCES', 'blurb': '', 'standard': None, 'standard_class': None, 'deviation_lower': Noneupper' : Нет, 'tolerance_grade': Нет} .

• блок : См. #/definitions/W24UnitLength .

Запрос Radii

Python

 из werk24 import Hook, W24AskVariantRadii
из werk24.models.techread импорт W24TechreadMessage
из werk24.utils импортировать w24_read_sync
от . импортировать get_drawing_bytes
def recv_radii (сообщение: W24TechreadMessage) -> Нет:
    """ Распечатайте радиусы, когда мы их получили
    """
    если message.is_successful:
        печать (сообщение.payload_dict)
    еще:
        print("Произошли исключения: {message.exceptions}")
если __name__ == "__main__":
    # получить байты отрисовки из файла или буфера
    Drawing_bytes = get_drawing_bytes()
    # определите, какую информацию вы хотите получать от API
    # и что делать, когда информация станет доступной.
    hooks = [Hook(ask=W24AskVariantRadii(), function=recv_radii)]
    # отправить запрос в API Werk24
    w24_read_sync (drawing_bytes, крючки)
 

Диаметр, радиус и длина окружности (видео и практика)

СтенограммаЧасто задаваемые вопросы Практика

Привет, ребята! Добро пожаловать в это видео о радиусе, диаметре и длине окружности.

Круги существуют столько же, сколько существует Земля. Люди могли видеть естественные круги, наблюдая за луной, солнцем и другими различными природными круглыми формами.

Первое технологическое изобретение с использованием круглой формы, однако, не было до 3500 г. до н.э., и это было изобретение гончарного круга. Затем, 300 лет спустя, их использовали для колес колесниц. Когда люди начали видеть ценность и использование объектов круглой формы, они начали изучать круги.

Такие термины, как радиус , диаметр и окружность , помогают нам отслеживать различные измерения окружности.

Итак, теперь давайте посмотрим, что представляет собой каждое из этих измерений.

Определения

Середина окружности

Сначала давайте определим середину , чтобы вы поняли, о чем я говорю, когда я на нее ссылаюсь. Вот круг:

Середина — это точный центр круга, где находится точка.

Теперь давайте посмотрим на другие термины.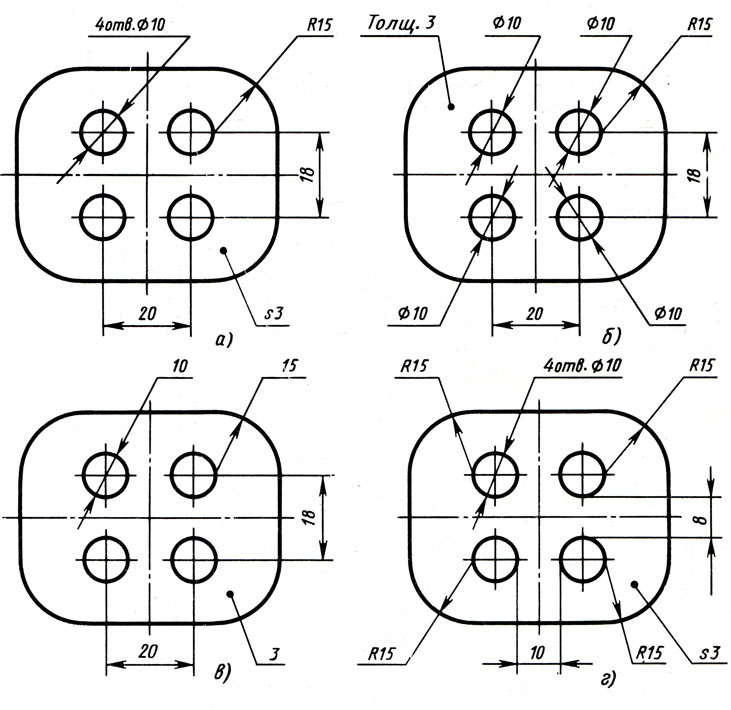

Радиус круга

Радиус — это длина от середины круга до внешнего края круга. Радиус обозначается строчной буквой \(r\).

Диаметр круга

Диаметр — это полная длина круга, проходящая от края через середину до другой стороны. То есть вся эта длина прямо здесь. Диаметр круга обозначается буквой \(d\).

Окружность круга

Окружность — это расстояние вокруг внешнего края этого круга. Окружность обозначается заглавной буквой \(C\).

Окружность сравнима с периметром фигуры, такой как параллелограмм . Если бы вы разрезали линию круга, как если бы это была нить, и выложили ее по размеру. Эта длина будет эквивалентна окружности. Однако, поскольку круг имеет непрерывную кривую, мы используем слово окружность , а не периметр , чтобы отличить его.

Теперь, когда мы рассмотрели, что такое радиус, диаметр и длина окружности, давайте посмотрим, как их рассчитать.

Расчеты

Если бы кто-то просто вручил вам лист бумаги с кружком на нем…. Ну, на самом деле, это было бы довольно странно.

Но допустим, мы хотим найти радиус, диаметр и длину окружности, и все, что у нас есть, это линейка.

Для начала проще всего взять линейку и измерить от самого центра круга расстояние между внешним краем. Это будет диаметр.

Допустим, что когда мы измерили, мы получили длину 9 см для диаметра.

Ну, мы знаем, что если наш радиус проходит от середины до внешнего края, то все, что нам нужно сделать, чтобы найти длину нашего радиуса, это разделить длину диаметра на 2.

Итак, когда мы берем 9 и делим на 2 получаем длину радиуса 4,5см.

Формула радиуса

Формула радиуса может быть записана как \(r=\frac{d}{2}\)

Формула диаметра

Формула диаметра может быть записана как \(d=2r\)

Формула длины окружности

Формула длины окружности: \(C=\pi \times d\), или она может быть записана как \(C=2\times \pi \times r\). Любой работает!

Теперь вы можете спросить: «Откуда взялось число пи и почему мы вдруг получаем длину окружности, если умножаем это число пи на наш диаметр? Кто это решил?» Если вы не задаете этот вопрос… Вы должны, и я все равно отвечу на него.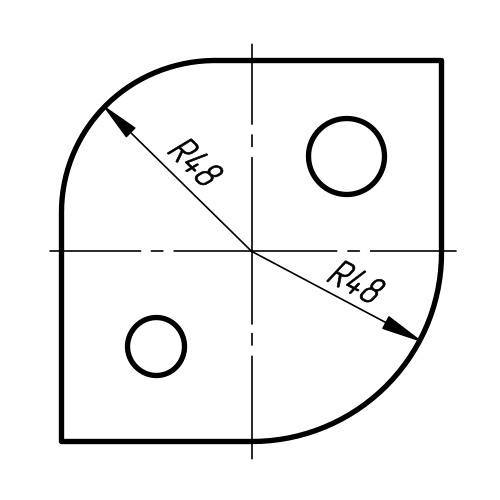

Пи — это символ, который мы используем в математике для обозначения числа 3,14. А на самом деле это просто пи, округленное до сотых. Пи на самом деле не имеет ни конца, ни предсказуемой закономерности. Это просто продолжается.

Однако, когда вы видите символ \(\pi\), обычно (и в нашем случае) будет достаточно 3.14.

Пи — это не случайное число, которое придумали математики и заявили: «Мы будем каждый раз умножать диаметр на число и называть его окружностью». Наоборот, было обнаружено, что пи есть константа 9.0057 отношение между окружностью и диаметром.

Именно поэтому и как мы получили формулу длины окружности.

Теперь возьмем круг диаметром 9 см и радиусом 4,5 см и посчитаем длину окружности.

Я собираюсь использовать формулу с диаметром для этого.

Итак, длина окружности равна (я просто перепишу формулу, чтобы помочь нам следить за нашей работой), \(C=\pi \times d\), равно pi, умноженному на диаметр. Итак, теперь все, что нам нужно сделать, это подставить наше число для диаметра. Это равно, а также мы сказали, что пи равно 3,14, \(C=(3,14)(9\text{ см})=28,26\text{ см}\).

А вот и наш ответ! Теперь, чтобы попрактиковаться, попробуйте нарисовать круг на листе бумаги и измерьте его диаметр линейкой. Затем найдите свой радиус и длину окружности.

Надеюсь, это видео было для вас полезным.

Увидимся в следующий раз!

Часто задаваемые вопросы

Q

Каков радиус окружности?

A

Если бы мы измеряли расстояние от центра круга до внешнего края этого круга, мы бы нашли радиус. Подумайте о часах; если бы одна из стрелок была достаточно длинной, чтобы достать до края часов, эту стрелку можно было бы считать радиусом часов – независимо от того, сколько сейчас времени!

Q

Что такое радиус и диаметр?

A

В то время как радиус окружности проходит от центра к краю, диаметр проходит от края к краю и проходит через центр. Диаметр круга по существу делит фигуру пополам.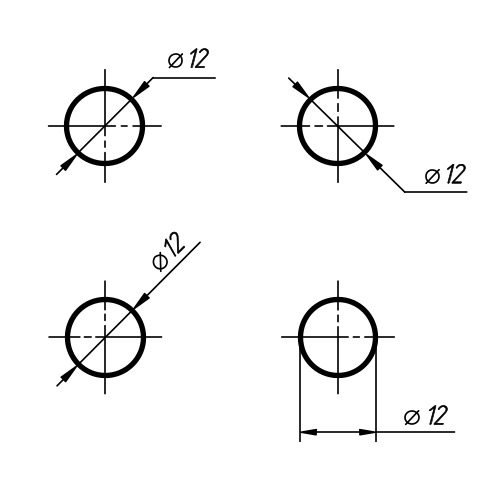 Радиус и диаметр — близкие друзья — радиус круга равен половине длины его диаметра (или: диаметр круга в два раза больше длины его радиуса).

Q

Как называется радиус?

A

Радиус — это отрезок. Следовательно, у него есть две конечные точки: точка в центре круга и точка на краю круга, с которым мы его соединили. Имея все это в виду, мы знаем, что называть радиус так же, как и все сегменты линии: имена обеих конечных точек перечислены рядом (часто с чертой над двумя буквами).

Q

Является ли радиус половиной диаметра?

А

Да! Если вы помните только один факт о кругах, пусть это будет он. Просверлите это в своем уме! Радиус равен половине длины диаметра.

Q

Как найти радиус и диаметр?

A

Если мы знаем только радиус круга, мы просто умножим это значение на 2, чтобы получить диаметр \((d=2r)\). Точно так же, если мы знаем только диаметр круга, мы делим его на 2 и получаем радиус \((r=\frac{d}{2})\)!

Но что, если мы не при задании ни одного из этих значений? Чтобы определить радиус или диаметр круга, нам нужно знать либо его длину окружности, либо его площадь.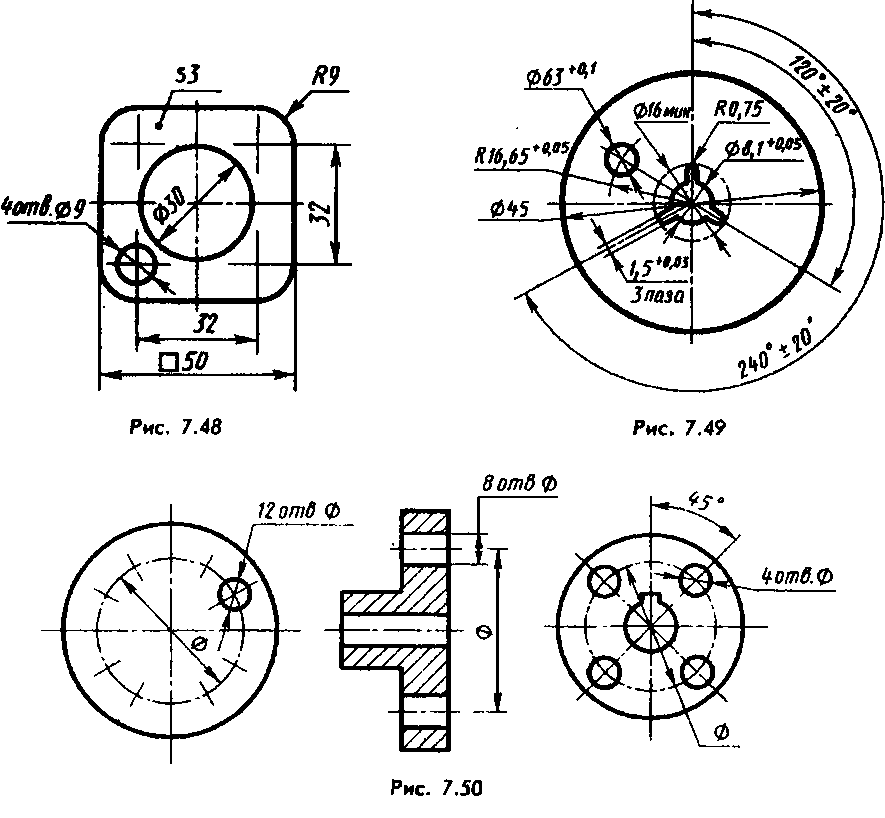 92\)

\(±3=r\)

(Обратите внимание, что квадратный корень из 9 может быть либо 3, либо -3. Поскольку мы имеем дело с реальным кругом, мы будем просто использовать

\( d=2r=6\text{ дюймов}\)

Q

Как рассчитать длину окружности

A

его радиус. Затем мы используем соответствующее значение в этом уравнении: \(C=2πr\) (где « r » представляет радиус, конечно)

Пример. Найдите длину окружности этого круга:

\(r=\frac{10\text{ единиц}}{2}=5\text{ единиц}\)

\(C=2πr=2π\times5= 10π\text{ единиц}\)

Q

Почему длина окружности \(2πr\)?

A

Мы знаем, что длина окружности — это длина всего внешнего края круга. (Можно думать об этом так: длина окружности для кругов равна периметру для треугольников, прямоугольников, пятиугольников и т. д.!) Имея это в виду, давайте переставим переменные в уравнении \(C=2πr\), чтобы получить \ (С=2r\timesπ\). Помните, что \(2r=d\) (где d представляет собой диаметр), поэтому мы могли бы переписать это уравнение еще раз: \(C=d\timesπ\). Другими словами, мы можем обернуть нить (длина которой равна диаметру) вокруг круга 3,1415926… раз.

Q

Как мы используем длину окружности в повседневной жизни?

A

Область применения окружности в повседневной жизни поистине безгранична! Однако одним из примеров является определение размера шины, необходимой для велосипеда или автомобиля. Другим примером может быть определение количества древесины в дереве: для очень-очень старого дерева было бы довольно сложно измерить диаметр основания дерева; но было бы просто обернуть веревку вокруг основания и измерить окружность. Затем вы можете использовать это измерение окружности и «реконструировать» уравнение окружности, чтобы определить диаметр дерева. С помощью этого измерения (и высоты дерева) мы могли бы найти объем древесины внутри этого дерева. Опять же, список примеров можно продолжать бесконечно, поэтому следите за другими способами использования окружности на протяжении всей своей жизни!

Q

Чем отличается длина окружности от диаметра?

A

Окружность – это длина одного полного «круга» вокруг окружности, а диаметр – это длина отрезка, делящего окружность пополам. Думайте об окружности как о внешнем измерении, а о диаметре — как о внутреннем измерении круга!

Q

Является ли диаметр половиной длины окружности?

А

Нет! Помните, что уравнение \(C=2πr\) можно переписать так: \(C=2r\timesπ\), \(C=d\timesπ\) или \(C=d\). Итак, возможно, мы могли бы сказать, что диаметр равен 3,14159.26… ^й окружности…

Q

Является ли диаметр длиной?

A

Если длина определяется как расстояние между двумя точками, тогда да, диаметр является длиной. Диаметр окружности измеряет расстояние между двумя самыми дальними точками окружности.

Практические вопросы

Вопрос №1:

 
Определите длину окружности.

23,16 см

24,14 см

25,12 см

26,11 см

Показать ответ

Ответ:

Длину окружности можно рассчитать по одной из следующих формул: \(C=𝜋d\) или \(C=2)𝜋 .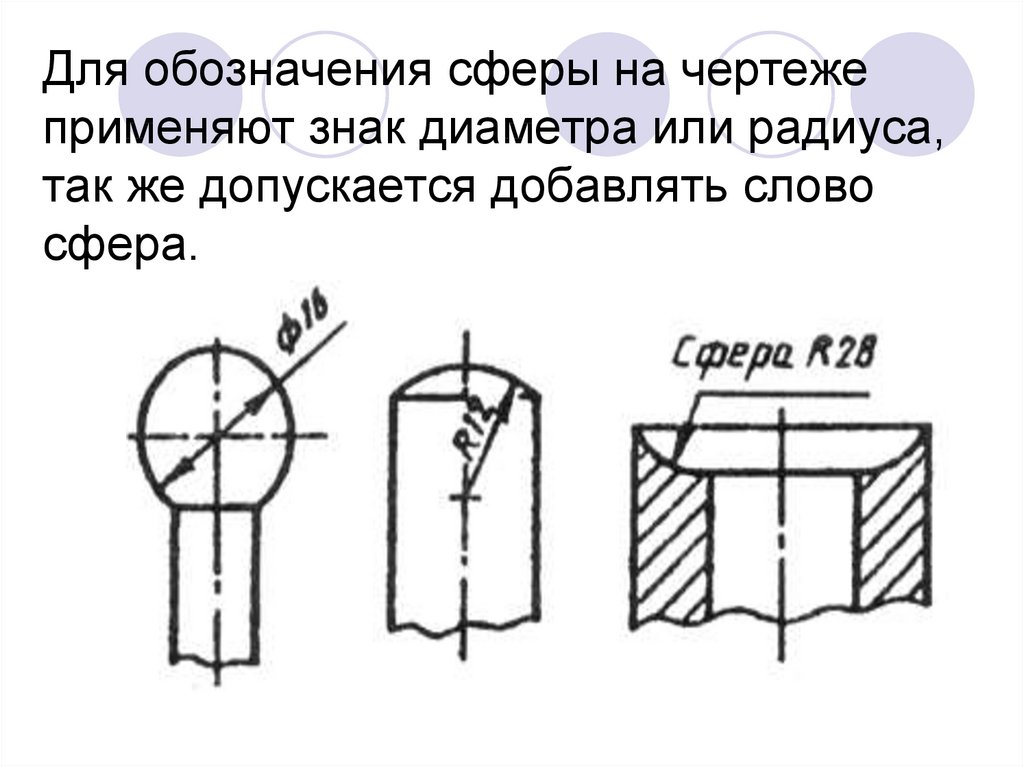

Мы знаем, что диаметр круга равен 8 см, а приближенное число пи равно 3,14, поэтому мы можем подставить эти значения в формулу \(C=𝜋d\). Формула принимает вид \(C=(3.14)(8)\), что упрощается до 25.12. Длина окружности 25,12 см.

Скрыть ответ

Вопрос № 2:

 
Определите радиус окружности, если длина окружности составляет двадцать три дюйма. Округлите ответ до сотых.

3,66 дюйма

4,65 дюйма

3,44 дюйма

4,76 дюйма

Показать ответ

Ответ:

3 Мы знаем, что длина окружности равна двадцати трем дюймам, поэтому мы можем подставить это значение в формулу \(C=2𝜋r\). Мы также знаем, что приблизительное число пи равно 3,14, поэтому единственное неизвестное нам значение — это 9.0009 р , радиус. Когда C и 𝜋 подставляются в формулу, получается \(23=2(3.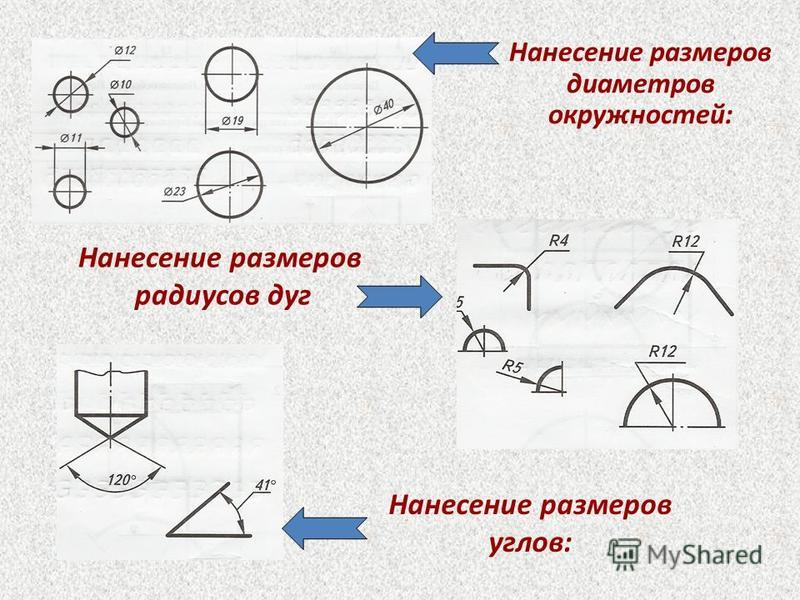 14)r\). Его можно упростить до \(23=6,28r\), а затем обе части уравнения можно разделить на 6,28, чтобы выделить переменную r . 23 разделить на 6,28 равно 3,66 при округлении до сотых. Радиус круга равен 3,66 дюйма.

Скрыть ответ

Вопрос № 3:

 
Если C представляет длину окружности, r представляет радиус, а d представляет диаметр, какая формула неверна?

\(d=2r\)

\(C=𝜋d\)

\(C=2𝜋r\)

\(r=𝜋dC\)

Показать ответ

r=𝜋dC\) неверно, потому что умножение пи, умноженное на диаметр, умноженное на длину окружности, не равно радиусу. Если диаметр известен, то радиус равен половине значения

d .

Скрыть ответ

Вопрос № 4:

 
Велосипеды 1800-х годов сильно отличаются от велосипедов, которые мы видим сегодня. На фотографии ниже заднее колесо велосипеда имеет радиус 9 дюймов, а переднее колесо имеет диаметр 60 дюймов. Используя 3,14 в качестве приближения для пи, какова разница между окружностями переднего и заднего колеса?

161,88 дюйма

151,88 дюйма

171,88 дюйма

131,88 дюйма

Показать ответ

Ответ:

Прежде чем сравнивать переднее и заднее колесо, нам нужно рассчитать длину окружности каждого колеса в отдельности. Длину окружности можно найти по формуле \(C=2𝜋r\) или \(C=𝜋d\). Мы знаем, что радиус заднего колеса равен 9 дюймам, поэтому мы можем подставить его в формулу \(C=2𝜋r\). Формула принимает вид \(C=2𝜋(9)\), что упрощается до 56,52. Передняя шина имеет диаметр 60 дюймов, поэтому мы можем подставить это значение в формулу \(C=𝜋d\). Формула принимает вид \(C=𝜋(60)\), что упрощает 188.4. Теперь, когда мы знаем длину окружности каждого колеса, мы можем просто вычесть 56,52 из 188,4.