Как строить в трехмерной системе координат: Координаты точки и вектора

Содержание

1.9 Построение графиков в трехмерной системе координат

Шаблон графика поверхности обозначается Surface Plot CTRL+2.

Для того чтобы построить график функции от двух переменных (x,y), необходимо вычислить значения функции в узлах сетки системы координат указанных выше переменных. Эти значения функции представляются в виде матрицы, размерность которой определяется числом узлов сетки, определенных по соответствующим переменным.

Рисунок 1.5 Пример построения графика поверхности

1.10 Построение нескольких графиков в одном графическом регионе

Для размещения нескольких графиков в одних и тех же осях координат после введенного в поле значения функции (ось ординат) выражения необходимо нажать запятую на клавиатуре. Появится пустое поле для следующего выражения. Проделать это столько раз, сколько графиков необходимо разместить на чертеже. Аналогично вводятся несколько аргументов по оси абсцисс.

1.11 Форматирование графиков

Для форматирования графиков необходимо дважды щелкнуть левой кнопкой мыши на графике, или щелкнуть правой кнопкой мыши на графике и в контекстном меню выбрать команду

Формат (Format). Затем в появившемся окне изменить параметры графика.

1.12 Решение уравнений

Для решения уравнения с одной неизвестной в системе Mathcad можно воспользоваться встроенной функцией root.

Общий вид функции: root(s(x), x), где s(x) = 0 – решаемое уравнение, x – переменная, значение которой требуется найти.

Например, решение уравнение вида g(x) = f(x) (аналогично g(x) — f(x) = 0) будет найдено следующим образом:

x := 1 (присваиваем начальное значение искомой переменной)

z := root(g(x) – f(x),x)

Переменная z будет содержать решение, которое можно посмотреть, набрав z = .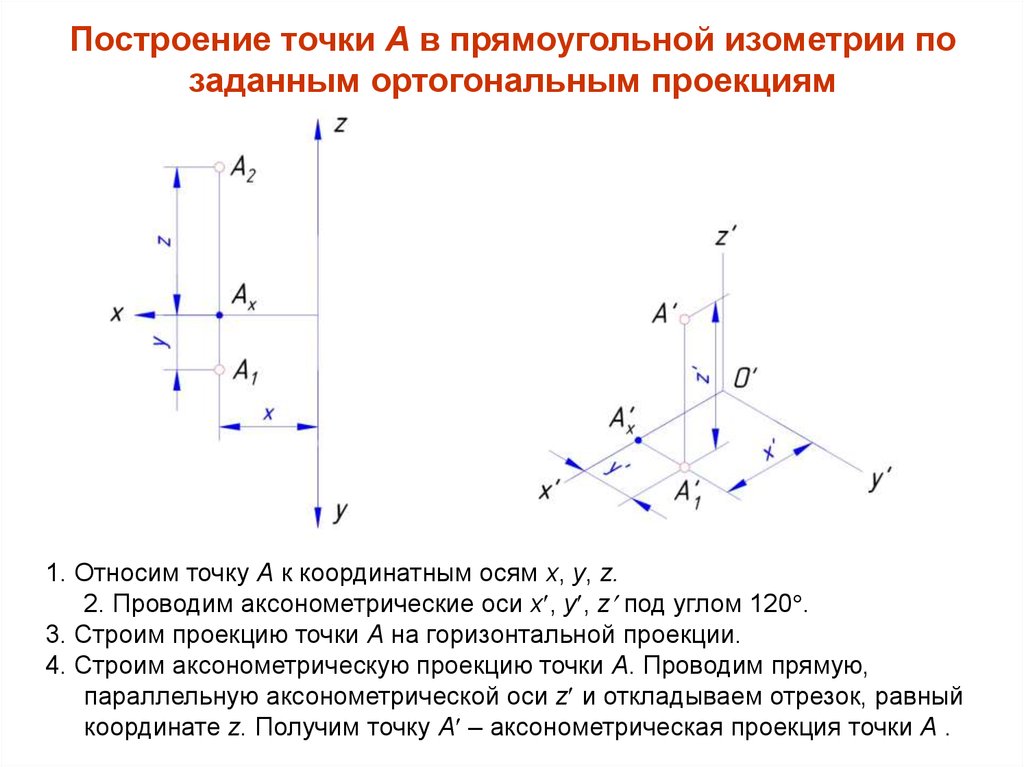

Если уравнение имеет несколько решений, то Mathcad найдет ближайшее к начальному значению искомой переменной. Чтобы отыскать другие решения нужно просто изменить начальное значение.

Порядок выполнения:

Ознакомиться с методическими указаниями к лабораторной работе.
Загрузить программу Mathcad.
Изучить структуру и назначение меню и кнопок панелей инструментов.
Ознакомиться с составом встроенных функций,
Определить в математическом регионе функцию , заданную по варианту в таблице 1.1.
Создать графические регионы и в них построить графики функции , производной и интеграла (в виде ).
Решить графическим и аналитическим методом уравнение вида , коэффициенты a и
b задать по своему усмотрению.
Определить в математическом регионе функцию двух переменных – , заданную по варианту в таблице 1. 1.
Построить график функции двух переменных – в виде поверхности.
Создать текстовые регионы и сделать в них подписи ко всем графикам и расчетам.
Оформить полученные данные в виде рабочего листа Mathcad.
Сохранить файл в папке «Мои документы\ОТМО\», имя файла задать следующим образом: <Группа>.<Фамилия>.<№ лабораторной работы>.
Сдать и защитить работу преподавателю.

Содержание отчёта по лабораторной работе:

Название и цель лабораторной работы.
Задание к лабораторной работе.

Описание результатов выполнения лабораторной работы.
Графики и таблицы значений заданных функций.

Контрольные вопросы:

Назначение пунктов меню и кнопок панелей инструментов системы Mathcad.
Переменная скалярного типа в математическом регионе.
Переменная типа дискретный аргумент в математическом регионе.
Способы описания и вызова функции в системе Mathcad.
Способы построения графиков.
Текстовые регионы системы Mathcad.
Встроенные функции системы Mathcad.
Решение уравнений с помощью встроенных функций системы Mathcad.

Таблица 1.1

№ варианта	Функция одной переменной f(x)	Функция двух переменных F(x,y)
1
2
3
4
5
6
7
8
9	a, b, c задать произвольно
10		a, b задать произвольно
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25	, a, b задать произвольно
26
27
28
29
30

#12.

Как строить трехмерные графики

Смотреть материал на видео

Следующим шагом мы с вами рассмотрим возможности построения трехмерных графиков в пакете matplotlib. Такая возможность появилась, начиная с версии 0.99, поэтому убедитесь, что ваш пакет поддерживает трехмерные графики.

Все дополнительные классы для работы в 3D находятся в модуле:

mpl_toolkits.mplot3d

и вначале мы его импортируем в нашу программу наряду с самим пакетом matplotlib и numpy:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

А, затем, создадим трехмерную систему координат:

fig = plt.figure(figsize=(7, 4))
ax_3d = Axes3D(fig)
 
plt.show()

При выполнении этой простой программы, мы в окне увидим три пространственные оси, которые можно вращать с помощью курсора мышки:

Того же самого результат можно добиться, используя параметр projection при создании системы координат:

fig = plt. figure(figsize=(7, 4))
ax_3d = fig.add_subplot(projection='3d')

Как именно создавать трехмерные оси, зависит от вашего выбора и удобства при написании конкретных программ. Я остановлюсь на втором способе.

После создания координатных осей мы можем в них строить двумерные и трехмерные графики с помощью того же самого набора функций:

plot() – линейный 2D график в трех измерениях;
step() – ступенчатый 2D график в трех измерениях;

scatter() – точеный график 3D график.

Также нам становятся доступными следующие дополнительные функции:

plot_wireframe() – построение каркасной поверхности в 3D;
plot_surface() – построение непрерывной 3D поверхности.

Начнем с самого простого варианта – функции plot() для рисования косинусоиды в трех измерениях:

x = np. linspace(0, 10, 50)
z = np.cos(x)
ax_3d.plot(x, x, z)

То есть, мы здесь по координатам x, y выбираем одни и те же значения, а координата z (вертикаль) – это значение функции. Давайте подпишем оси, чтобы видеть, где какая расположена на этом графике:

ax_3d.set_xlabel('x')
ax_3d.set_ylabel('y')
ax_3d.set_zlabel('z')

Но то, что мы получили, это не совсем трехмерный график. Скорее, это двумерная косинусоида в трех измерениях. Давайте построим настоящее трехмерное изображение, например, вот такой функции:

Первое, что нам здесь нужно сделать – это сформировать двумерную сетку координат по осям x и y:

То есть, должны быть сформированы двумерные массивы x, y, которые для текущей точки с индексами (i, j) возвращают ее координаты в плоскости xy.

Для регулярных сеток эти массивы можно сформировать следующим образом. Определим множество координат x (для столбцов) и y (для строк), например, так:

x = [1, 2, 3]
y = [2, 5, 6, 8]

А, затем, используя функцию meshgrid() сформируем регулярную сетку на основе этих данных:

xgrid, ygrid = np.meshgrid(x, y)

На выходе получим двумерные массивы со значениями:

То есть, смотрите, теперь для любой пары индексов (i, j) мы легко сможем получить координаты точки в плоскости xy:

(xgrid[1, 2], ygrid[1, 2]) = (3, 5)
(xgrid[3, 0], ygrid[3, 0]) = (1, 8)

Но зачем было так все усложнять? Почему бы не использовать одномерные массивы x, y вместо двумерных xgrid, ygrid? Дело в том, что одномерные массивы, которые описывают расположение строк и столбов, могут формировать только регулярные сетки, то есть, прямоугольные. А что, если нужно сформировать гексагональную сетку, которая выглядит, следующим образом:

Здесь уже не получится обойтись указанными одномерными массивами, а нужно прописывать узлы двумерными массивами. Именно поэтому, в общем случае, и реализовано отображение через двумерные массивы трехмерных графиков.

Итак, давайте теперь построим полноценный трехмерный график синусоиды на регулярной сетке. Для этого мы сначала сформируем координаты узлов в плоскости xy:

x = np.arange(-2*np.pi, 2*np.pi, 0.2)
y = np.arange(-2*np.pi, 2*np.pi, 0.2)
xgrid, ygrid = np.meshgrid(x, y)

А, затем, вычислим значения синусоиды в этих узлах:

zgrid = np.sin(xgrid) * np.sin(ygrid) / (xgrid * ygrid)

Если для вывода такого графика воспользоваться функцией plot_wireframe():

ax_3d.plot_wireframe(xgrid, ygrid, zgrid)

то результат будет следующий:

Как видите, мы получили полноценный каркасный трехмерный график синусоиды. Или же можно построить полноценную поверхность в виде синусоиды, используя функцию plot_surface():

ax_3d. plot_surface(xgrid, ygrid, zgrid)

Фактически, только этим две эти функции и отличаются друг от друга: первая строит 3D-каркас, а вторая 3D-поверхность.

У этих функций есть следующие параметры для настройки внешнего вида графика:

Параметр	Описание
x, y, z	2D массивы для построения трехмерных графиков.
rcount, ccount	Максимальное число элементов каркаса по координатам x и y (по умолчанию 50).
rstride, cstride	Величина шага, с которым будут выбираться элементы из массивов x, y (параметры rstride, cstride и rcount, ccount – взаимоисключающие).
color	Цвет графика
cmap	Цветовая карта графика

Например, если установить параметры:

ax_3d.plot_surface(xgrid, ygrid, zgrid, rstride=5, cstride=5, cmap='plasma')

то получим следующий вид нашей синусоиды:

В заключение этого занятия приведу пример построения этого же графика набором точек, используя функцию scatter():

ax_3d.scatter(xgrid, ygrid, zgrid, s=1, color='g')

Увидим следующий результат:

Вот так в базовом варианте можно выполнять построения трехмерных графиков в пакете matplotlib. Этой информации достаточно для большинства прикладных задач.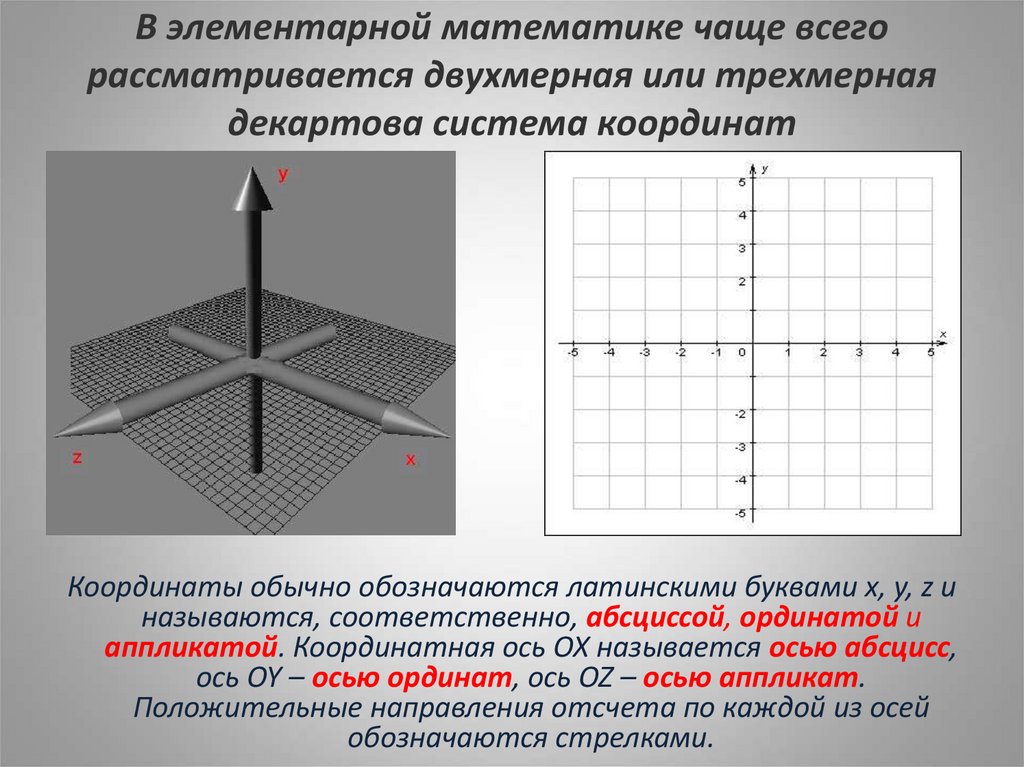 Ну а если потребуется реализовать что-то особенное, тогда прямой путь к документации:

https://matplotlib.org/stable/api/_as_gen/mpl_toolkits.mplot3d.axes3d.Axes3D.html

Видео по теме

#1. Установка пакета и основные возможности

#2. Функция plot для построения и оформления двумерных графиков

#3. Отображение нескольких координатных осей в одном окне

#4. Граничные значения осей и локаторы для расположения меток на них

#5. Настраиваем формат отображения меток у координатных осей

#6. Делаем логарифмический масштаб у координатных осей

#7. Размещаем стандартные текстовые элементы на графике

#8. Добавляем легенду и рисуем геометрические фигуры на графиках

#9. Рисуем ступенчатые, стековые, stem и точечные графики

#10.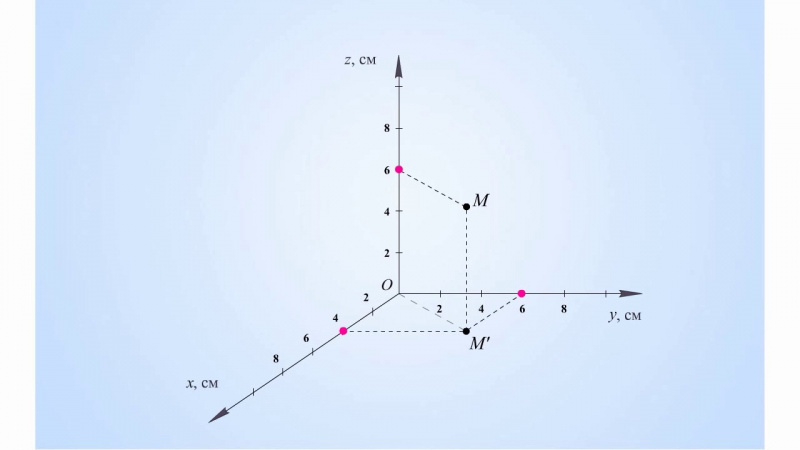 Рисуем гистограммы, столбчатые и круговые диаграммы

#11. Показ изображений и цветовых сеток

#12. Как строить трехмерные графики

#13. Рисуем линии уровня функциями contour, contourf и tricontour, tricontourf

#14. Создаем анимацию графиков Классы FuncAnimation и ArtistAnimation

Система координат — документация MMDetection3D 1.0.0rc4

Горячие клавиши

Обзор

MMDetection3D использует три различные системы координат. Наличие разных систем координат в обществе обнаружения 3D-объектов необходимо, потому что для различных устройств сбора 3D-данных, таких как LiDAR, камера глубины и т. д., системы координат не согласованы, и разные наборы 3D-данных также следуют разным форматам данных. . Ранние работы, такие как SECOND, VoteNet, преобразовывают необработанные данные в другой формат, формируя соглашения, которым также следуют некоторые более поздние работы, что делает преобразование между системами координат еще более сложным. | / | / | / |/ влево —— 0 ——> x вправо | | | | в ты вниз 9| / | / | / |/ влево —— 0 ——> x вправо

Определение систем координат в этом руководстве на самом деле больше, чем просто определение трех осей . Для коробки в форме \((x, y, z, dx, dy, dz, r)\) наши системы координат также определяют, как интерпретировать размеры коробки \((dx, dy, dz)\) и угол рыскания \(r\).

Ниже показаны три системы координат:

Три цифры вверху — это трехмерные системы координат, а три цифры внизу — вид с высоты птичьего полета.

В будущем мы будем придерживаться трех систем координат, определенных в этом уроке.

Определение угла рыскания

Пожалуйста, обратитесь к Википедии за стандартным определением угла рыскания. При обнаружении объекта мы выбираем ось в качестве оси гравитации и опорное направление на плоскости \(\Pi\), перпендикулярное оси гравитации, тогда опорное направление имеет угол рыскания, равный 0, и другие направления на \(\ Pi\) имеют ненулевые углы рыскания в зависимости от его угла с опорным направлением.

В настоящее время для всех поддерживаемых наборов данных аннотации не включают угол тангажа и угол крена, что означает, что нам нужно учитывать только угол рыскания при прогнозировании блоков и расчете перекрытия между блоками.

В MMDetection3D все три системы координат являются правыми системами координат, что означает, что направление возрастания угла рыскания направлено против часовой стрелки, если смотреть с отрицательного направления оси гравитации (ось направлена в глаза).

На рисунке ниже показано, что в этой правосторонней системе координат, если мы установим положительное направление оси x в качестве опорного направления, то положительное направление оси y будет иметь угол рыскания \(\frac {\пи} {2}\). 9| / | / | / |/ влево (рыскание=пи) —— 0 ——> x вправо (рыскание=0)

Для ящика значение угла отклонения от курса равно его направлению минус опорное направление. Во всех трех системах координат в MMDetection3D базовым направлением всегда является положительное направление оси x, в то время как направление прямоугольника определяется как параллельное оси x, если его угол рыскания равен 0. Определение рыскания угол коробки показан на рисунке ниже. 9| /|\ | ____|____ | | | | | | | | __|____|____|____|______\ x вправо | | | | / | | | | | |____|____| |

Определение размеров коробки

Определение размеров коробки нельзя отделить от определения угла рыскания. В предыдущем разделе мы сказали, что направление прямоугольника определяется как параллельное оси x, если его угол рыскания равен 0. Тогда, естественно, размер ящика, соответствующий оси x, должен быть \(dx \). Однако в некоторых наборах данных это не всегда так (мы обратимся к этому позже). 9_________ /|\ | | | | | | | | | | | ды | |____|____|____\ направление коробки (рысканье=0) | | | | / __|____|____|____|_________\ x справа | | | | / | |____|____| | дх |

Связь с необработанными системами координат поддерживаемых наборов данных

KITTI

Необработанная аннотация KITTI находится в системе координат камеры, см. get_label_anno. В MMDetection3D для обучения моделей на основе LiDAR на KITTI данные сначала преобразуются из системы координат камеры в систему координат LiDAR, см.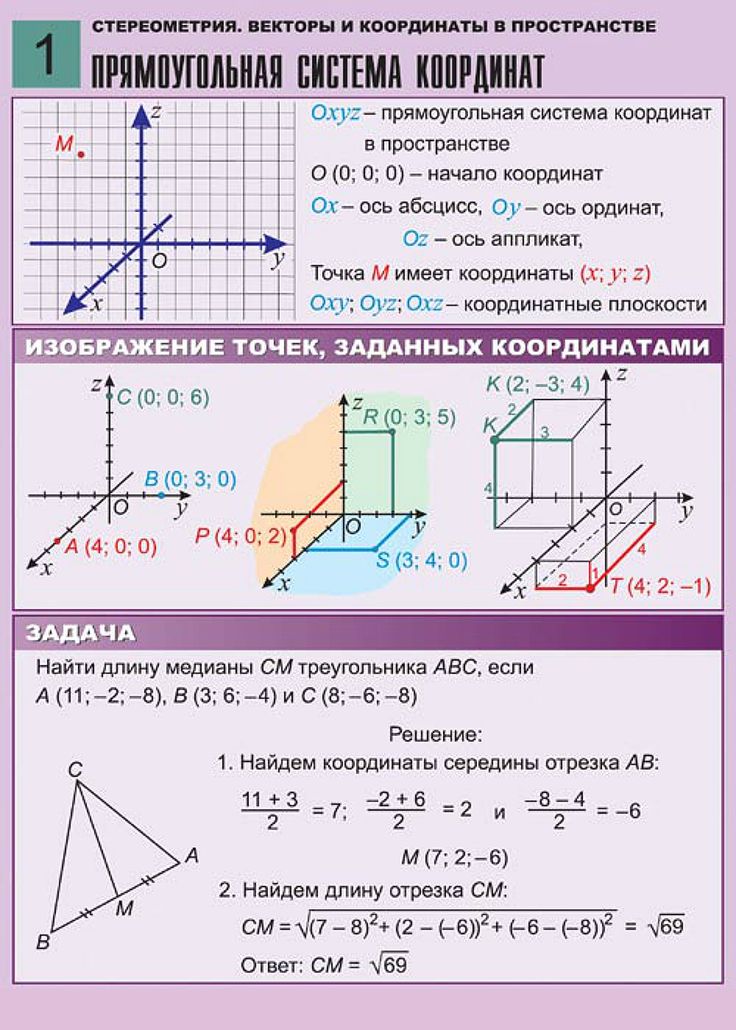 get_ann_info. Для обучения моделей на основе зрения данные хранятся в системе координат камеры.

Во ВТОРОМ, система координат LiDAR для блока определяется следующим образом (вид с высоты птичьего полета):

Для каждого блока размеры равны \((w, l, h)\) и опорное направление для угла рыскания является положительным направлением оси y. Для получения более подробной информации обратитесь к репозиторию.

Наша система координат LiDAR имеет два изменения:

Угол рыскания определяется как правосторонний, а не левосторонний для согласованности;
Размеры коробки равны \((l, w, h)\) вместо \((w, l, h)\), поскольку \(w\) соответствует \(dy\) и \(l\) соответствует \(dx\) в KITTI.

Waymo

Мы используем данные формата KITTI набора данных Waymo. Поэтому KITTI и Waymo также используют одну и ту же систему координат в нашей реализации.

NuScenes

NuScenes предоставляет набор инструментов для оценки, в котором каждый блок упакован в экземпляр Box . Система координат ящика отличается от нашей системы координат LiDAR тем, что первые два элемента размера ящика соответствуют \((dy, dx)\) или \((w, l)\) соответственно, а не обратного. Дополнительные сведения см. в руководстве по NuScenes.

Читатели могут обратиться к комплекту разработки NuScenes для определения блока NuScenes и реализации оценки NuScenes.

Lyft

Lyft использует тот же формат данных, что и NuScenes, поскольку используется система координат.

Дополнительную информацию см. на официальном веб-сайте.

ScanNet

Необработанные данные ScanNet представляют собой не облако точек, а сетку. Данные выборки облака точек находятся в нашей системе координат глубины. Для задачи обнаружения ScanNet аннотации прямоугольников выровнены по оси, а угол рыскания всегда равен нулю. Поэтому направление угла рыскания в нашей системе координат глубины не имеет значения для ScanNet.

SUN RGB-D

Необработанные данные SUN RGB-D представляют собой не облако точек, а изображение RGB-D.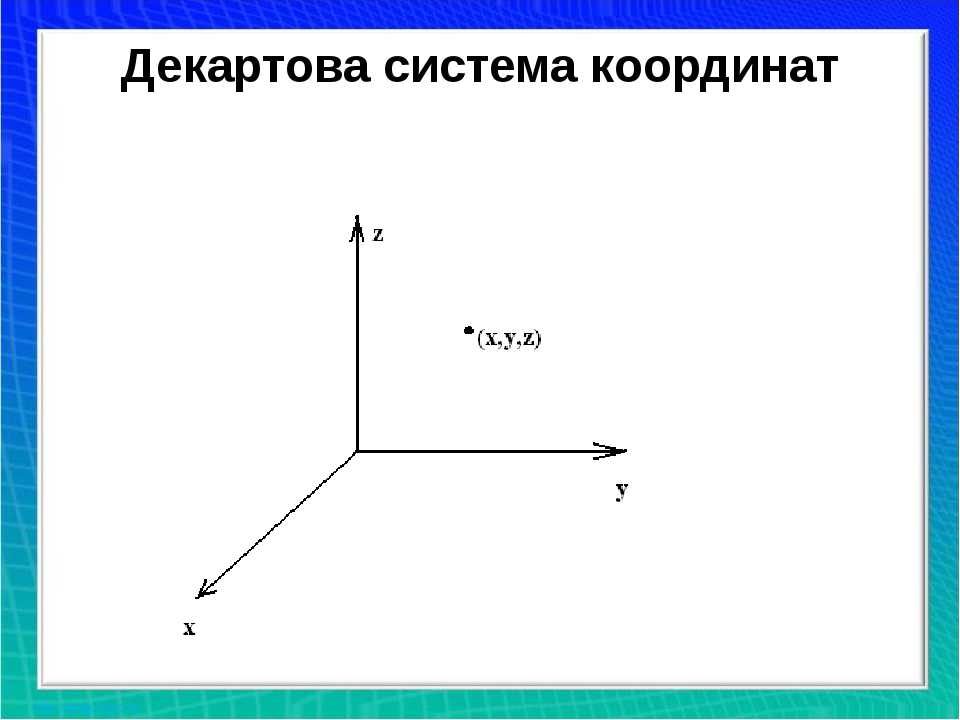 С помощью обратной проекции мы получаем соответствующее облако точек для каждого изображения, которое находится в нашей системе координат «Глубина». Однако аннотация не входит в нашу систему и поэтому требует преобразования.

Для преобразования необработанных аннотаций в аннотации в нашей системе координат глубины см. файл sunrgbd_data_utils.py.

S3DIS

S3DIS использует ту же систему координат, что и ScanNet в нашей реализации. Однако S3DIS — это набор данных, предназначенный только для задачи сегментации, и, таким образом, ни одна аннотация не зависит от системы координат.

Примеры

Преобразование прямоугольника (между различными системами координат)

В качестве примера возьмем преобразование между системой координат нашей камеры и системой координат LiDAR:

Во-первых, для точек и центров прямоугольников координаты до и после преобразования удовлетворяют следующее соотношение:

\(x_{LiDAR}=z_{камера}\)
\(y_{LiDAR}=-x_{камера}\)
\(z_{LiDAR}=-y_{камера}\)

Тогда размеры коробки до и после преобразования удовлетворяют следующему соотношению:

\(dx_{LiDAR}=dx_{камера}\)
\(dy_{LiDAR}=dz_{камера}\)
\(dz_{LiDAR}=dy_{камера}\)

Наконец, угол рыскания также должен быть преобразован:

См. приведенный здесь код для более подробной информации.

Вид с высоты птичьего полета

BEV поля системы координат камеры равно \((x, z, dx, dz, -r)\), если 3D-поле равно \((x, y, z, dx, dy, дз, г)\). Инверсия знака угла рыскания связана с тем, что положительное направление оси гравитации системы координат камеры указывает на землю.

Подробнее см. код здесь.

Вращение ящиков

Мы устанавливаем вращение всех видов ящиков против часовой стрелки вокруг оси гравитации. Поэтому, чтобы повернуть 3D-блок, мы сначала вычисляем новый центр блока, а затем добавляем угол поворота к углу рыскания.

Подробнее см. код здесь.

Часто задаваемые вопросы

В2: В каждой системе координат все три оси указывают точно вправо, вперед и на землю соответственно?

Нет. Например, в KITTI нам нужна калибровочная матрица при преобразовании из системы координат камеры в систему координат LiDAR.

Q3: Как влияет на оценку разность фаз \(2\pi\) в угле рыскания ящика?

При расчете IoU разность фаз \(2\pi\) в угле рыскания приведет к тому же квадрату, что не повлияет на оценку.

Для оценки предсказания углов, такой как метрика NDS в NuScenes и метрика AOS в KITTI, угол предсказанных блоков будет сначала стандартизирован, поэтому разность фаз \(2\pi\) не изменит результат.

Q4: Как влияет на оценку разность фаз \(\pi\) в угле рысканья ящика?

При расчете IoU разность фаз \(\pi\) в угле рыскания приведет к тому же квадрату, что не повлияет на оценку.

Однако для оценки предсказания угла это приведет к прямо противоположному направлению.

Просто подумайте о машине. Угол рыскания — это угол между направлением передней части автомобиля и положительным направлением оси x. Если к этому углу добавить \(\pi\), то передняя часть автомобиля станет задней.

Для таких категорий, как барьер, передняя и задняя части не имеют разницы, поэтому разность фаз \(\pi\) не повлияет на оценку угла предсказания.

Объяснение базовой теории 3D — разработка игр

В этой статье объясняются все основные теории, которые полезно знать, когда вы начинаете работать с 3D.

3D — это, по сути, представление фигур в трехмерном пространстве с системой координат, используемой для расчета их положения.

WebGL использует правую систему координат — ось x направлена вправо, ось y направлена вверх, а ось z направлена за пределы экрана, как показано на рисунке выше.

Различные типы объектов строятся с использованием вершин. Вершина — это точка в пространстве, имеющая собственное трехмерное положение в системе координат и обычно некоторую дополнительную информацию, которая ее определяет. Каждая вершина описывается следующими атрибутами:

Положение : Идентифицирует его в трехмерном пространстве ( x , y , z ).
Цвет : Содержит значение RGBA (R, G и B для красного, зеленого и синего каналов, альфа для прозрачности — все значения находятся в диапазоне от 0,0 до 1,0 ).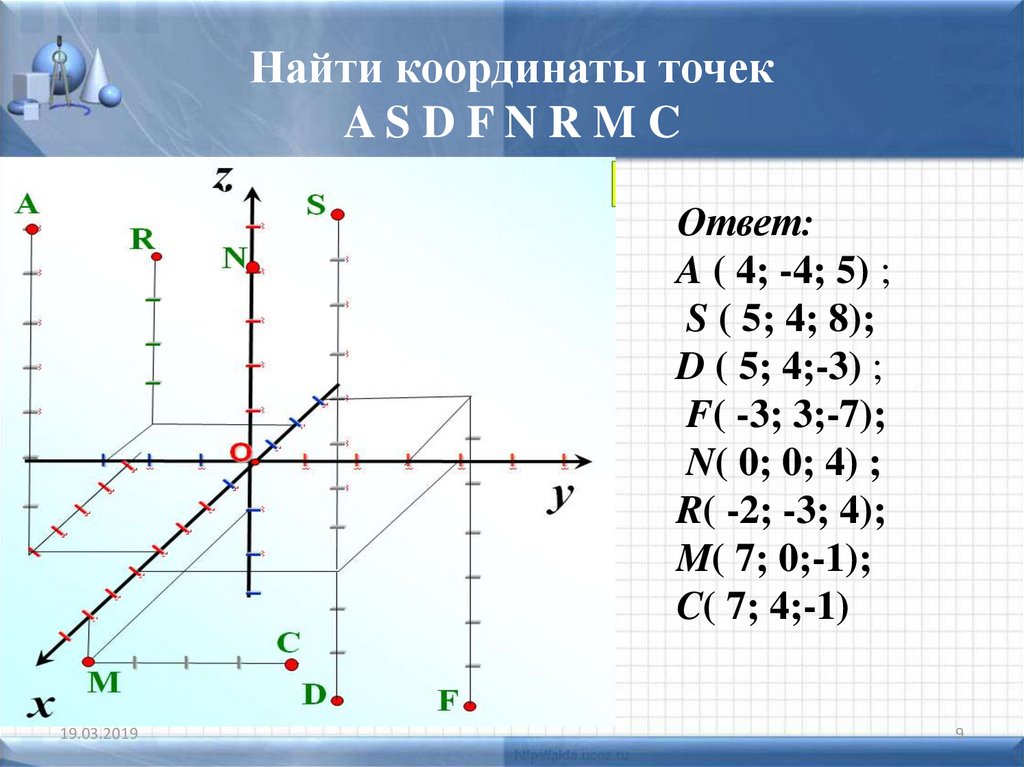
Normal: Способ описания направления вершины.
Текстура : 2D-изображение, которое вершина может использовать для украшения поверхности, частью которой она является, вместо простого цвета.

Вы можете построить геометрию, используя эту информацию — вот пример куба:

Грань заданной формы представляет собой плоскость между вершинами. Например, куб имеет 8 разных вершин (точек в пространстве) и 6 разных граней, каждая из которых состоит из 4 вершин. Нормаль определяет, в какую сторону направлена грань. Кроме того, соединяя точки, мы создаем ребра куба. Геометрия строится из вершины и грани, а материал — это текстура, использующая цвет или изображение. Если мы соединим геометрию с материалом, мы получим сетку.

Конвейер рендеринга — это процесс подготовки изображений и их вывода на экран. Конвейер рендеринга графики берет 3D-объекты, построенные из примитивов , описанных с использованием вершин , применяет обработку, вычисляет фрагментов и визуализирует их на 2D-экране как пикселей .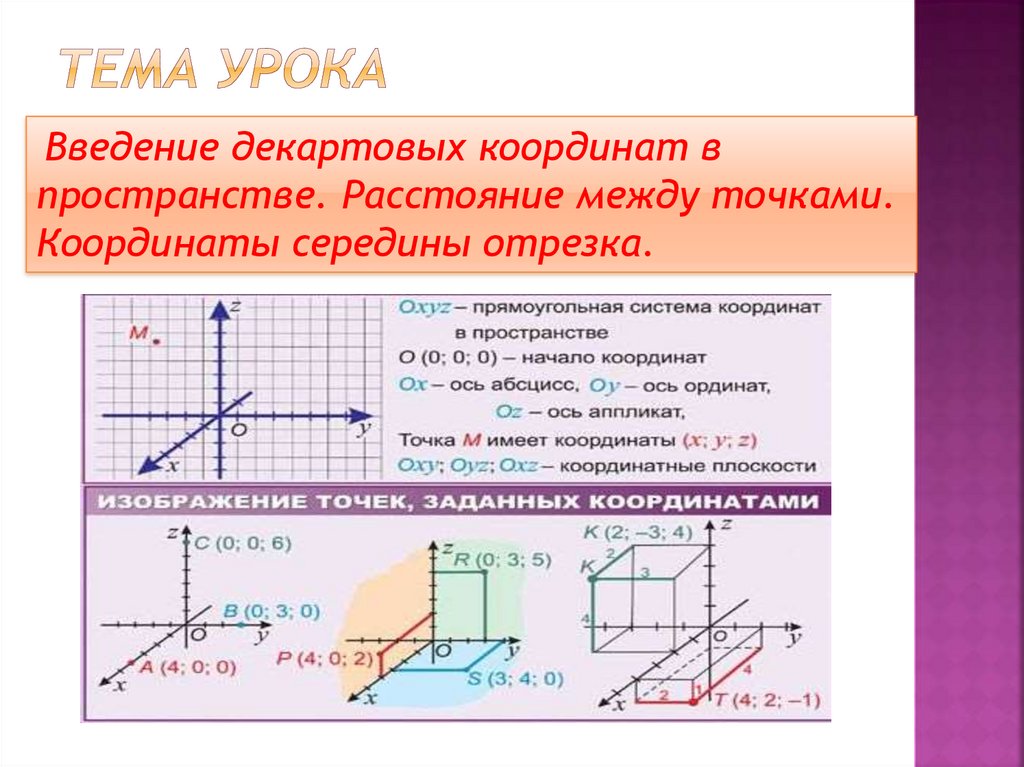

Терминология, используемая на диаграмме выше, следующая:

A Примитив : Вход в конвейер — он построен из вершин и может быть треугольником, точкой или линией.
A Фрагмент : Трехмерная проекция пикселя, которая имеет все те же атрибуты, что и пиксель.
A Пиксель : Точка на экране, расположенная в сетке 2D, которая содержит цвет RGBA.

Обработку вершин и фрагментов можно запрограммировать — вы можете написать свои собственные шейдеры, управляющие выводом.

Обработка вершин заключается в объединении информации об отдельных вершинах в примитивы и установке их координат в трехмерном пространстве для просмотра зрителем. Это как сфотографировать подготовленный вами пейзаж — сначала нужно разместить объекты, настроить камеру, а затем сделать снимок.

Эта обработка состоит из четырех этапов: первый включает в себя размещение объектов в мире и называется преобразованием модели . Затем есть преобразование вида , которое отвечает за позиционирование и настройку ориентации камеры в 3D-пространстве. У камеры есть три параметра — местоположение, направление и ориентация — которые должны быть определены для вновь созданной сцены.

Трансформация проекции (также называемое преобразованием перспективы) затем определяет настройки камеры. Он настраивает то, что может видеть камера — в конфигурацию входит поле зрения , соотношение сторон и дополнительные ближние и дальние плоскости . прочитайте параграф «Камера» в статье Three.js, чтобы узнать об этом.

Последним шагом является преобразование окна просмотра , которое включает в себя вывод всего для следующего шага конвейера рендеринга.

Растеризация преобразует примитивы (соединенные вершины) в набор фрагментов.

Эти фрагменты, представляющие собой 3D-проекции 2D-пикселей, выравниваются по пиксельной сетке, поэтому в конечном итоге их можно распечатать как пиксели на 2D-экране на этапе слияния вывода.

Обработка фрагментов фокусируется на текстурах и освещении — рассчитывает окончательные цвета на основе заданных параметров.

Текстуры

Текстуры — это 2D-изображения, используемые в 3D-пространстве, чтобы объекты выглядели лучше и реалистичнее. Текстуры объединяются из отдельных элементов текстуры, называемых текселями, так же, как элементы изображения объединяются из пикселей. Применение текстур к объектам на этапе обработки фрагментов конвейера рендеринга позволяет нам корректировать его, оборачивая и фильтруя при необходимости.

Обтекание текстурами позволяет повторять 2D-изображение вокруг 3D-объекта. Фильтрация текстур применяется, когда исходное разрешение или изображение текстуры отличаются от отображаемого фрагмента — оно будет уменьшено или увеличено соответственно.

Освещение

Цвета, которые мы видим на экране, являются результатом взаимодействия источника света с поверхностными цветами материала объекта. Свет может поглощаться или отражаться. Стандартная модель освещения Фонга , реализованная в WebGL, имеет четыре основных типа освещения:

Рассеянный : Далекий направленный свет, подобный солнцу.
Specular : Точка света, как лампочка в комнате или фонарик.
Ambient : Постоянный свет применяется ко всему на сцене.
Emissive : Свет, излучаемый непосредственно объектом.

На этапе обработки вывода все фрагменты примитивов из 3D-пространства преобразуются в 2D-сетку пикселей, которые затем выводятся на экран.

При объединении вывода также применяется некоторая обработка для игнорирования информации, которая не нужна — например, не рассчитываются параметры объектов, которые находятся за пределами экрана или за другими объектами и, следовательно, не видны.

Теперь вы знаете основную теорию трехмерных манипуляций. Если вы хотите перейти к практике и увидеть несколько демонстраций в действии, воспользуйтесь приведенными ниже руководствами:

Создание базовой демонстрации с помощью Three.

Как строить в трехмерной системе координат: Координаты точки и вектора — урок. Геометрия, 11 класс.