Функции и Графики — сайт по математике и не только!!! ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ Всё о Математических функциях и их графиках…
Широкое применение нашла логарифмическая функция в астрономии: Например по ней изменяется величина блеска звезд, если сравнивать характеристики блеска отмеченные глазом и с помощью приборов, то можно составить следующий график: Здесь по вертикальной оси отложим блеск звезд в единицах Гиппарха (распределение звезд по субъективным характеристикам (на глаз) на 6 групп), а на горизонтальной — показания приборов. По графику видно, что объективные и субъективные характеристики не пропорциональны, а прибор регистрирует возрастание блеска не на одну и ту же величину, а в 2,5 раза. Эта зависимость выражается логарифмической функцией.
Ещё одно применение логарифмической функции можно найти, если рассматривать логарифмическую спираль.
Спираль, по определению — это плоская линия, образованная движущейся точкой, которая удаляется по определенному закону от начала луча, равномерно вращающегося вокруг своего начала.
Например, подобно оценки блеска звезд в предыдущем пункте, оценивается громкость шума. Единицей громкости служит «бел», практически его десятая доля – децибел. Последовательные степени громкости 1 бел, 2 бела и т.д. – составляют для нашего слуха арифметическую прогрессию. Физическая сила этих шумов составляет геометрическую прогрессию со знаменателем 10. Разности громкости в 1 бел соответствует отношение силы шумов 10. Это значит, что выраженная в белах громкость шума, равна десятичному логарифму его физической силы.
Заметим, что в физике, при проведении научных, экспериментальных расчетов показательная, логарифмическая функции, экспонента и логарифмы применяются очень широко, но как правило не как описание отдельного процесса или комплекса процессов, а входят в состав сложных уравнений и систем уравнений и формул, описывающих данный процесс.
Также широкое применение нашла логарифмическая функция и 
О логарифмическом масштабе
О логарифмическом масштабе
Обозначим две задачи, которые периодически возникают в практике волновых аналитиков (рисунок 1).
Задача №1. На некотором рынке волна I соединила уровни 100 и 400. Третья волна стартовала на отметке 250 и достигла цели в 1000. Как соотносятся волны I и III?
Задача №2. На некотором рынке волна А соединила уровни 400 и 100. Волна С, которая началась на отметке 250, составляет 161.8% от А. На каком уровне завершается волна С?
Рисунок 1 — волновые формации в обычных координатах.
Рисунок 2 — волновые формации в логарифмических координатах.
Действующие волны в наших задачах весьма значительны (цены изменяются в разы) — на таких расстояниях нужно использовать логарифмический масштаб. Перестроим наш график в логарифмический (рисунок 2) и обозначим разворотные точки a-d (не путайте с волнами зигзага).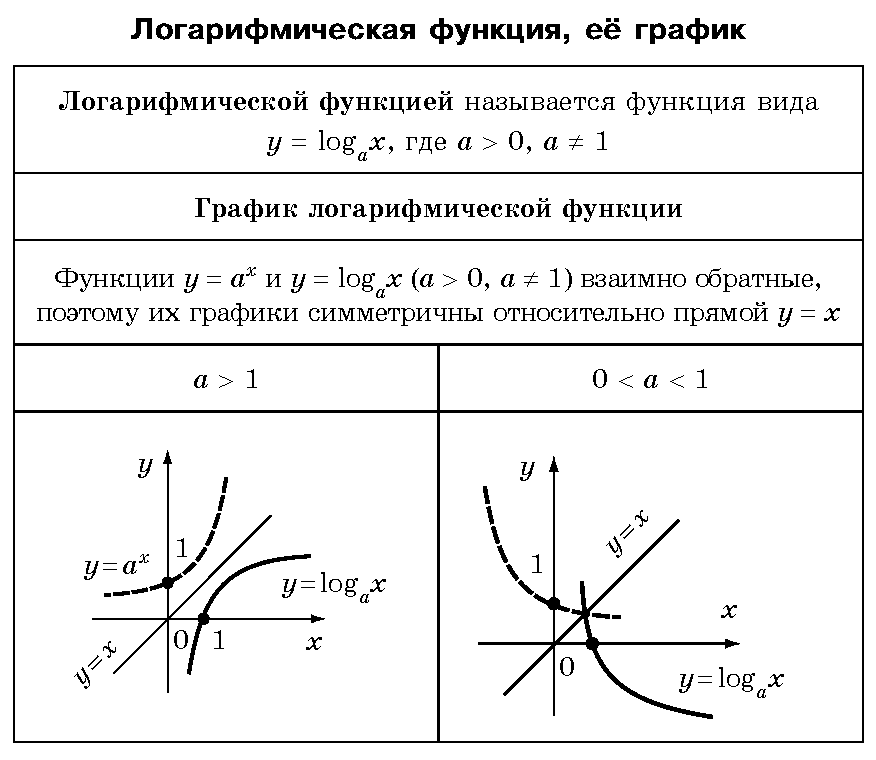
Пропорции между волнами находим из уравнения:
Решения: в первой задаче третья волна равна первой — ln(1000/250)/ln(400/100)=1.
Во второй задаче ответ 26.5 пунктов, поскольку ln(250/26.5)/ln(400/100)=1.618. Эта задача имеет решение и при соотношении С=2.618А и даже при С=4.236А.
Когда использовать логарифмическую шкалу?
В известных книгах по волновой теории вопрос применения логарифмов толком не прояснён. Так или иначе признаётся, что прогресс цивилизации идёт логарифмически, а рост на 10 пунктов с уровня 10 и аналогичный рост с уровня 100 это два принципиально разных движения, которые не могут иметь одинаковый размер. Но где граница между традиционным арифметическим и логарифмическим масштабами?
На просторах сети можно встретить указание использовать логарифмы если изменение котировок превышает 3 раза. На первый взгляд, это логично, но при детальном рассмотрении появляется одна важная нестыковка — как поступать с волнами старших порядков, которые не укладываются в установленные рамки.
Неужели придётся использовать сразу две шкалы — логарифмическую для глобальных разметок и обычную на каждый день?
Следующий пример наглядно поясняет всю противоречивость такого подхода. На рисунке 3 слева показан график курса доллара с 2014-го года в логарифмическом масштабе, а справа — традиционный ценовой график с лета 2015-го. Во втором случае мы имели полное право рисовать импульс с растянутой пятой, хотя логарифмы явно запрещали этот сценарий, ибо предполагаемая волна 3 оказалась короче первой, а растяжения не выполнялись от слова совсем.
Рисунок 3 — график USDRUB в логарифмических и обычных координатах.
Чтобы избежать подобных конфликтов и соблюсти единообразие я советую всегда использовать логарифмическую шкалу. Она универсальна. На старших фреймах она единственная покажет правильные пропорции между волнами и ей нет никакой альтернативы. Если ценовые изменения незначительны, то логарифмические пропорции совпадут с обычными арифметическими, так что мы ничего не нарушим и при этом нам не придётся переключаться с одного масштаба на другой.
Отмечу, что некоторые аналитики допускают возможность измерения волн не только в логарифмах, но и в разах или процентах. На мой взгляд, подобный подход является в чистом виде самодеятельностью и не имеет под собой никаких теоретических обоснований. Кроме того, совершенно не понятно как построить такие волны на графике.
Почему используется именно логарифм?
Давайте посмотрим откуда берутся логарифмические координаты. Как было сказано, рост на 10 пунктов с уровня 10 и аналогичный рост с уровня 100 это два разных движения. Чем выше поднимается рынок, тем проще ему расти относительно стартовой точки. Если мы планируем избавиться от этого казуса, нам придётся разбить всё движение на бесконечно мелкие части и поднимать точку отсчёта на каждом шаге.
Возьмём два дискретных процесса. Первый из них моделирует подвижную точку отсчёта — значение x начинается с единицы и на каждом шаге прирастает на k% от предыдущего. Второй процесс линейный – значение y начинается с нуля и на каждом шаге увеличивается на k% от единицы.
Теперь найдём такое преобразование, которое свяжет процессы X и Y при бесконечно малом k.
Переход от обычной шкалы к логарифмической наглядно проиллюстрирован на рисунке 4. В линейном процессе (справа) размер шага постоянный и не зависит от того, с какого уровня начинается изменение цены. Логарифмический процесс (слева) избавлен от этого недостатка — чем больше текущее значение цены, тем больше дискретный шаг.
Рисунок 4 — сравнение процессов изменения цены в разных масштабах.
Как можно понять, логарифмический масштаб скрадывает изменения цены, сделанные в верхней части графика и растягивает тренды из «подвала». Так, волна роста по индексу Доу с 1974-го по 2001-ый год в обычной системе координат превысила 1200% от волны роста с 1942-го по 1966-ой годы. В логарифмах эти волны соотносятся в пропорции 1.27.
Изображение на главной странице взято из фотобанка Лори
Графические логарифмические функции
Горячая математика Функция
у
знак равно
журнал
б
Икс
является обратной функцией
экспоненциальная функция
у
знак равно
б
Икс
.
Рассмотрим функцию у знак равно 3 Икс . Это можно представить в виде графика:
График обратной функции любой функции есть отражение графика функции относительно прямой у знак равно Икс . Итак, график логарифмической функции у знак равно журнал 3 ( Икс ) что является обратной функцией у знак равно 3 Икс является отражением приведенного выше графика относительно линии у знак равно Икс .
Икс 1 9 1 3 1 3 9 27 81 у знак равно журнал 3 Икс − 2 − 1 0 1 2 3 4
Область определения функции — это множество всех положительных действительных чисел.
Когда база не записывается, считать, что журнал является базовым 10 .
Икс 1 1000 1 100 1 10 1 10 100 1000 у знак равно журнал Икс − 3 − 2 − 1 0 1 2 3
Логарифмическая функция,
у
знак равно
журнал
б
(
Икс
)
,
можно сдвинуть
к
единицы по вертикали и
час
единицы по горизонтали с уравнением
у
знак равно
журнал
б
(
Икс
+
час
)
+
к
.
Вертикальный сдвиг
Если к > 0 , график будет смещен вверх.
Если к < 0 , график будет смещен вниз.
Горизонтальный сдвиг
Если час > 0 , график будет смещен влево.
Если час < 0 , график будет смещен вправо.
Рассмотрим логарифмическую функцию у знак равно [ журнал 2 ( Икс + 1 ) − 3 ] . Это можно получить, переведя родительский граф у знак равно журнал 2 ( Икс ) Пару раз.
Рассмотрим график функции
у
знак равно
журнал
2
(
Икс
)
.
С час знак равно 1 , у знак равно [ журнал 2 ( Икс + 1 ) ] это перевод у знак равно журнал 2 ( Икс ) на одну единицу влево.
В настоящее время, к знак равно − 3 . График у знак равно [ журнал 2 ( Икс + 1 ) ] будет смещен 3 единицы вниз, чтобы получить у знак равно [ журнал 2 ( Икс + 1 ) ] − 3 .
Вы можете вспомнить, что логарифмические функции определены только для положительных действительных чисел.
Это связано с тем, что для отрицательных значений соответствующее показательное уравнение не имеет решения. Например,
3
Икс
знак равно
−
1
не имеет действительного решения, поэтому
журнал
3
(
−
1
)
не определено.
Итак, как насчет такой функции, как у знак равно журнал 4 ( − Икс ) ?
Это определено только для отрицательных значений Икс .
Найдите значения функции для нескольких отрицательных значений Икс . Для упрощения расчета вы можете использовать экспоненциальную форму уравнения, 4 у знак равно − Икс .
Икс − 1 − 2 − 4 − 8 − 16 − 32 у знак равно журнал 4 ( − Икс ) или же 4 у знак равно − Икс 0 1 2 1 1 1 2 2 2 1 2
Нанесите точки и соедините их плавной кривой.
Вы можете видеть, что график является отражением графика функции у знак равно журнал 4 ( Икс ) о у -ось.
Как создавать логарифмические и полулогарифмические графики в Excel
Автор Амир М. Бохлули
Полулогарифмические и логарифмические графики могут помочь вам обнаружить новые взаимосвязи между вашими данными. Вот как их создать в Excel.
Полулогарифмические и логарифмические графики являются полезными инструментами для анализа и нахождения связей между экспоненциальными и степенными функциями. Логарифмические графики могут дать вам представление о взаимосвязи между вашими данными, которая не очевидна на простом графике.
В то время как полулогарифмический график является логарифмическим только по одной оси, логарифмический график является логарифмическим по обеим осям.
Каждый из этих графиков имеет свое собственное применение. С помощью Excel вы можете создавать полулогарифмические и логарифмические диаграммы и графики несколькими щелчками мыши для дальнейшего анализа ваших данных. Читайте дальше, чтобы узнать, как создавать такие графики в Excel.
Как создать полулогарифмический график в Excel
Полулогарифмический график — это график, имеющий одну из двух осей в логарифмическом масштабе. Обычно ось Y является логарифмической. Это означает, что линии сетки оси Y будут экспоненциальными, а линии сетки оси X останутся ровными.
В качестве примера в этой таблице у нас есть количество клеток в среде клеточной культуры в эксперименте в разные дни. Цель состоит в том, чтобы нанести эти данные на полулогарифмический график. Если вы не знакомы с созданием графиков в Excel, прочитайте нашу статью о том, как создавать графики в Excel, чтобы лучше понять этот процесс.
- Выбрать всю таблицу. В этом примере это будут ячейки с A1 по B7 .
- Перейдите в меню Вставить .
- В разделе Charts щелкните Insert Scatter (X, Y) или Bubble Chart .
- Выберите Разброс с плавными линиями и маркерами .
Теперь у вас есть точечная диаграмма ваших данных. Теперь пришло время сделать его полубревенчатым.
- Выберите только что созданную диаграмму.
- Дважды щелкните ось Y.
- На панели Format Axis справа перейдите на вкладку Параметры оси .
- В Опции оси отметьте Логарифмическая шкала .
Вот ваш полулогарифмический график! Обратите внимание, что теперь график представляет собой прямую линию.
Вы также можете изменить базу с 10 по умолчанию на любое другое число, которое вам больше подходит. Это связано с тем, что количество ячеек в таблице данных было экспоненциальным, так как они на самом деле являются степенями шести.
Вы можете улучшить читаемость графика, изменив основание логарифма с 10 на 6.
Как создать логарифмическую диаграмму в Excel
Логарифмический график — это график, обе оси которого представлены в логарифмическом масштабе. Таким образом, линии сетки для осей X и Y на этом графике экспоненциальны и неравномерны. Давайте посмотрим на график log-log в действии на примере.
В аналогичном примере у нас есть количество клеток в разные дни, но на этот раз дни также экспоненциальны. Таблица данных, подобная этой, практически требует логарифмического графика.
Как и в предыдущем примере, выберите таблицу и создайте для нее точечную диаграмму. Если вы хотите узнать больше о точечных диаграммах, прочитайте нашу статью о том, как сделать точечную диаграмму в Excel, чтобы узнать, что это такое и когда вы должны ее использовать.
После того, как вы создали точечную диаграмму, измените ось Y так, как вы научились в предыдущем разделе. Вы можете видеть, что график по-прежнему не является прямой линией.
Это связано с тем, что ось X (номер дня в этом примере) также является экспоненциальной.
- Выберите график.
- Дважды щелкните ось X.
- На панели Формат оси щелкните Параметры оси .
- В разделе «Параметры оси» отметьте Логарифмическая шкала .
Теперь обе ваши оси расположены в логарифмическом масштабе, и вы можете видеть, что ваш график также стал прямой линией. Это связано с тем, что данные по обеим осям являются экспоненциальными.
Учитывая, что все данные на оси X представляют собой степени двойки, то изменение основания логарифма на два даст вам лучшее изображение этого графика.
Логарифмические графики в Excel
Полулогарифмические и логарифмические графики — это полезные активы, которые могут помочь вам обнаружить новые отношения между вашими данными. Эти инструменты широко используются в различных областях, и хотя они не видны сразу в настройках диаграммы, Excel также может создавать полулогарифмические и логарифмические графики.