Как решить систему уравнений в матлабе: Решение СЛАУ и матрицы в Matlab

1.11 Решение систем линейных уравнений

MATLAB позволяет работать с объектами линейной алгебры, т. е. векторами и матрицами, настолько просто, насколько это вообще возможно.

Яркий пример этому – решение систем линейных уравнений.

Пример:

Пусть дана система линейных уравнений

Решить систему с применением оператора обратного деления матриц < \ >.

Решение:

В матричной записи система имеет вид Ах = b, где

A = , b = , х =

– соответственно матрица из коэффициентов при незвестных, вектор-столбец из свободных членов и вектор-столбец из неизвестных.

Введем матрицу А и вектор-столбец свободных членов b:

>> А=[1 3 0;-2 -2 5;1 0 -5]

А =

1 3 0

-2 -2 5

1 0 -5

>> b=[-2;10;-9]

b =

-2

10

-9

Известно, что система имеет единственное решение, если определитель матрицы А не равен нулю (│A│ = det(A) ≠ 0). Вычислим определитель матрицы А:

>> disp(det(A))

-5

Определитель не равен нулю. Находим решение системы с помощью оператора обратного деления матриц < \ >:

>> x=А\b

x =

1

-1

2

Проверим полученное решение x₁ = 1, x₂

= -1, x₃ = 2 подстановкой в систему уравнений:

>> disp(A*x)

-2.0000

10.0000

-9.0000

В результате проверки получен вектор-столбец свободных членов. Значит, система решена верно.

Найдем теперь решение системы х = A^-1b с помощью обратной матрицы. Вначале вычислим обратную матрицу A^-1:

>> A1=inv(A)

A1 =

-2.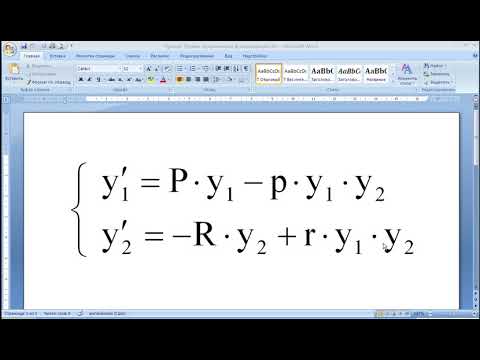 0000 -3.0000 -3.0000

1.0000 1.0000 1.0000

-0.4000 -0.6000 -0.8000

Находим решение системы:

>> A1*b

ans =

1.0000

-1.0000

2.0000

Отметим, что решение системы с помощью обратной матрицы требует больше времени и памяти, к тому же этот способ может дать большую погрешность решения. Поэтому для решения линейных систем рекомендуется применять оператор обратного деления < \ >.

Пример:

Решить систему линейных уравнений

Решение:

>> A=[1 3 0;-2 -2 5;1 0 5]

A =

1 3 0

-2 -2 5

1 0 5

>> b=[-2 10 -9]

b =

-2 10 -9

>> disp(det(A))

35

Находим решение системы:

>> x=A\b’

x =

-7.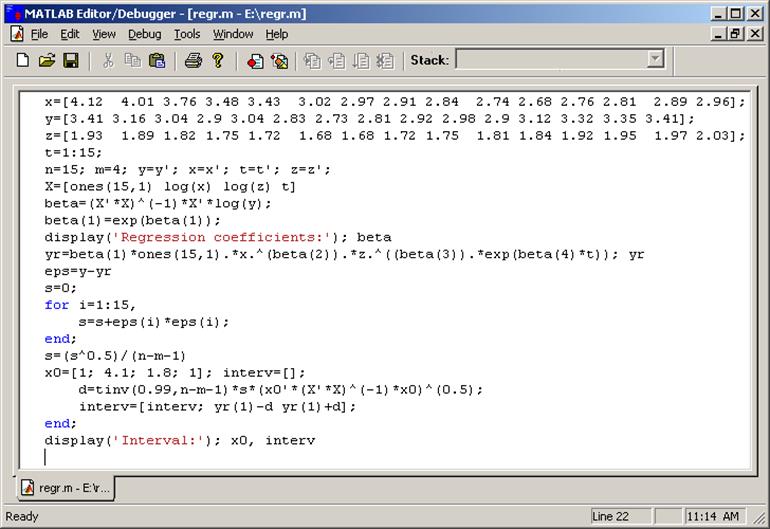 5714

1.8571

-0.2857

Заметим, что обратное деление произведено на вектор-столбец b‘, поскольку вектор b введен как вектор-строка. Получили приближенное решение системы. Вычислим обратную матрицу A^-1:

>> disp(inv(A))

-0.2857 -0.4286 0.4286

0.4286 0.1429 -0.1429

0.0571 0.0857 0.1143

Точное решение системы и точная обратная матрица выражаются через рациональные дроби:

>> format rat

>> x=A\b’

x =

-53/7

13/7

-2/7

>> disp(inv(A))

-2/7 -3/7 3/7

3/7 1/7 -1/7

2/35 3/35 4/35

1. Какие окна имеет интерфейс MATLAB и каково их назначение

2. Какова структура командного окна Command Window

3. Как называется отображение в командном окне сеанса работы с системой На какие зоны подразделяется текстовое поле окна Command Window

4. Для чего служат в MATLAB клавиши <↑> и <↓>

5. Для чего применяется команда disp

6. Как можно ввести слишком длинную команду в окне Command Window

7. Какая информация сохраняется в окнах Command History и Workspase после применения команды очистки экрана clc

8. Как получить справку по выбранной команде MATLAB

9. В каких форматах представляются в MATLAB вещественные числа

10. Какие форматы отображения вещественных чисел используются в MATLAB

11. Как в в MATLAB осуществляются операции с комплексными числами

12. В чем измеряются аргументы встроенных тригонометрических функций

13. Какая команда осуществляет векторизацию символьного выражения

14. Как MATLAB реагирует на ошибки ввода

15. Как обнаружить и устранить семантическую ошибку ввода

16. Как в MATLAB создаются векторы и матрицы

17. Как осуществляется просмотр и редактирование переменных в окне Workspase

18. Как в MATLAB осуществляются матричные и поэлементные операции над векторами и матрицами

19. Что вычисляют команды dot и cross

20. Как решается система линейных уравнений с помощью оператора обратного деления < \ >

Элементарные средства решения СЛУ MatLab

Урок 16. Численные методы Элементарные средства решения СЛУ
Функции для решения систем линейных уравнений с ограничениями
Решение СЛУ с разреженными матрицами
Точное решение, метод наименьших квадратов и сопряженных градиентов
Двунаправленный метод сопряженных градиентов
Устойчивый двунаправленный метод
Метод сопряженных градиентов
Квадратичный метод сопряженных градиентов
Метод минимизации обобщенной невязки
Квазиминимизация невязки — функция qmr

Вычисление нулей функции одной переменной
Минимизация функции одной переменной
Минимизация функции нескольких переменных
Аппроксимация производных
Аппроксимация Лапласиана
Аппроксимация производных конечными разностями
Вычисление градиента функции
Численное интегрирование
Метод трапеций
Численное интегрирование методом квадратур
Работа с полиномами
Умножение и деление полиномов
Вычисление полиномов
Вычисление производной полинома
Решение полиномиальных матричных уравнений
Разложение на простые дроби
Решение обыкновенных дифференциальных уравнений
Решатели ОДУ
Использование решателей систем ОДУ
Описание системы ОДУ
Дескрипторная поддержка параметров решателя
Пакет Partial Differential Equations Toolbox
Что нового мы узнали?

Решение систем линейных уравнений (СЛУ) относится к самой массовой области применения матричных методов, описанных в уроках 10-12.

В этом разделе вы найдете ответы на вопросы, каким образом применяются указанные методы и какие дополнительные функции имеет система MATLAB для решения систем линейных уравнений.

Как известно, обычная СЛУ имеет вид:

а ₁₁ X ₁ , а ₁₂ ,X ₂ …, а _1n X _n =b ₁

Здесь а ₁₁ , а, ₂ ,…, а _пп — коэффициенты, образующие матрицу А, которые могут иметь действительные или комплексные значения,

x ₁ , х ₂ ,. .., х _п — неизвестные, образующие вектор X, и b ₁ , b ₂ ,…, b _п — .свободные члены (действительные или комплексные), образующие вектор В. Эта система может быть представлена в матричном виде как АХ=В, где А — матрица коэффициентов уравнений, X — искомый вектор неизвестных и В — вектор свободных членов. В зависимости от вида матрицы А и ее характерных особенностей MATLAB позволяет реализовать различные методы решения.

Для реализации различных алгоритмов решения СЛУ и связанных с ними матричных операций применяются следующие операторы:

+,-,*,/, \, *, ‘ . Как отмечалось ранее, MATLAB имеет два различных типа арифметических операций — поэлементные и для массивов (векторов и матриц) в целом. Матричные арифметические операции определяются правилами линейной алгебры.

Арифметические операции сложения и вычитания над массивами выполняются поэлементно. Знак точки «.» отличает операции над элементами массивов от матричных операций. Однако, поскольку операции сложения и вычитания одинаковы для матрицы и элементов массива, знаки «.+» и «.-» не используются. Рассмотрим другие операторы и выполняемые ими операции.

* — матричное умножение; С = А*В — линейное алгебраическое произведение матриц А и В:

 

Для случая нескалярных А и В число столбцов матрицы А должно равняться числу строк матрицы В. Скаляр может умножаться на матрицу любого размера.

 / — правое деление. Выражение Х=В/А дает решение ряда систем линейных уравнений АХ=В, где А — матрица размера тхп и В — матрица размера nxk;

 \ — левое деление. Выражение Х=В\А дает решение ряда систем линейных уравнений ХА=В, где А — матрица размера тхп и В — матрица размера nxk. Если А — квадратная матрица, то А\В — примерно то же самое, что и inv(A)*B, в остальных случаях возможны варианты, отмеченные ниже.

Если А — матрица размера пхп, а В — вектор-столбец с п компонентами или матрица с несколькими подобными столбцами, тогда Х=А\В — решение уравнения АХ=В, которое находится хорошо известным методом исключения Гаусса.

Если А — матрица размера тхп и тхп, а В представляет собой вектор-столбец с m компонентами или матрицу с несколькими такими столбцами, тогда система оказывается недоопределенной или переопределенной и решается на основе минимизации второй нормы невязок. -1.

 ‘ — транспонирование матрицы, то есть замена строк столбцами и наоборот. Например, А’ — транспонированная матрица А. Для комплексных матриц транспонирование дополняется комплексным сопряжением. Транспонирование при решении СЛУ полезно, если в матрице А переставлены местами столбцы и строки.

При записи СЛУ в матричной форме необходимо следить за правильностью записи матрицы А и вектора В. Пример (в виде m-файла):

	А-[2  1	0	1:
	1    -3	2	4;
	-5    0	-1	-7:
	1    -6	2	6]:
	В=[8  9	-5	0]:
	Х1=В/А
	Х2=В*А ^ -1
	X3=B*inv(A)

Эта программа выдает результаты решения тремя способами:

X1 =

3. 0000 -4.0000-1.00001.0000

Х2 =

3.0000 -4.0000-1.00001.0000

X3 =

3.0000 -4.0000-1.00001.0000

Как и следовало ожидать, результаты оказываются одинаковыми для всех трех методов. При решении систем линейных уравнений, особенно с разреженной матрицей коэффициентов, полезно применение функций colmmd (colamd), symmmd (symamd), описанных ранее в уроке 12.

 

Нравится

Твитнуть

MATLAB Tutor, часть 10

MATLAB Tutor, часть 10

Репетитор MATLAB

Часть 10.

Решение линейных задач Системы

Предположим, мы хотим решить линейную система

        x 2y +    z =  0
               2 года 8z =  8
     -4x + 5y + 9z = -9

Мы можем решить эту систему за несколько способы в MATLAB; вы узнаете два из них в этой части и еще один в следующей часть.

1. Сначала нам нужно сохранить коэффициенты системы в матрице, а правый вектор в другой матрице. Введите

        A = [1 -2 1
                0 2 -8
               -4 5 9]
        b = [0; 8; -9]

   , а затем введите

        X = A\b

   Три числа, которые вы видите, являются значениями решения x , y и z .

2. Вы можете легко проверить, решение правильное. Матричный продукт A умножить на X должно быть равно правая сторона b . Имеет ли это? Проверьте это.
3. Если у вас есть символьная математика MATLAB Toolkit, вы также можете использовать команду «решить» для решения вышеуказанной системы. Введите

        syms x y z
        eq1 = ‘x — 2*y + z = 0’;
        eq2 = ‘2*y — 8*z = 8’;
        eq3 = ‘-4*x + 5*y + 9*z = -9’;
        [x,y,z] = решить(eq1, eq2, eq3)

4. Если у вас есть система с меньше уравнений, чем неизвестных, можно найти символьное решение для некоторых переменных в терминах других, которые мы могли бы назвать «свободными» переменными. Рассмотрим следующую систему из трех уравнений с четырьмя неизвестными.

           x 2 года + г + 2н =  0
                 2 года 8z +    w  =  8
        -4x + 5y + 9z —    w  = -9

   Мы можем вычислить x , y и z через w . Последняя запись в команде «решить» сообщает, для каких переменных нужно решить, и следовательно, какая переменная будет свободной. Введите

        syms x y z w
        eq1 = ‘x — 2*y + z + 2* w = 0’;
        eq2 = ‘2*y — 8*z + w = ​​8’;
        eq3 = ‘-4*x + 5*y + 9*z — w = -9’;
        [x,y,z] = решить(eq1, eq2, eq3, ‘x,y,z’)

5. Попробуйте те же два метода решение по системе

          x + 4y + 3z = 10
        2x +   y   z =  -1
        3x   y 4z = 11

   О чем говорят результаты? Мы рассмотрим этот пример более внимательно в следующей части.

---

| Главная | Материалы | линейная алгебра | Содержание модуля | Назад | Вперед |

модули на math.duke.edu

Copyright CCP и автор(ы), 1999 г.

решить-уравнение-в-Matlab — Google Такой

AlleVideosBilderBücherMapsNewsShopping

Такой вариант

Описание. S =solve( eqn , var ) решает уравнение eqn для переменной var . Если вы не укажете var , функция symvar определяет переменную для решения. Например, Solve(x + 1 == 2, x) решает уравнение x + 1 = 2 относительно x.

Equations and systems solver — MATLAB solve — MathWorks

www. mathworks.com › … › Mathematics › Equation Solving

Hervorgehobene Snippets

Solve Algebraic Equations — MATLAB & Simulink — MathWorks

www.mathworks. com › … › Решение уравнений

Решайте уравнения аналитически, возвращайте полные решения и визуализируйте результаты.

Решить уравнение · Возврат полного решения к… · Визуализация и построение решений…

Ähnliche Fragen

Как вы используете уравнения в MATLAB?

Как решить уравнения с двумя переменными в MATLAB?

Как решить матричное уравнение в MATLAB?

Решение уравнений — MATLAB и Simulink — MathWorks

www.mathworks.com › … › Математика

Вы можете решать алгебраические уравнения, дифференциальные уравнения и дифференциально-алгебраические уравнения (ДАУ). Решите алгебраические уравнения, чтобы получить точную …

Решение символьных уравнений — MATLAB & Simulink — MathWorks

www.mathworks. com › help › matlabmobile › solvi…

Решите квадратное уравнение, используя функцию решения. Решите квадратное уравнение, не указывая переменную для решения. Функция решения выбирает x для …

Численное решение уравнений — MATLAB & Simulink — MathWorks

www.mathworks.com › … › Решение уравнений

Численное решение уравнений с произвольно высокой точностью, использование диапазонов поиска, и визуализировать результаты.

Решение системы линейных уравнений — MATLAB & Simulink — MathWorks

www.mathworks.com › … › Решение уравнений

Решение системы линейных уравнений с помощью решения · syms x y z eqn1 = 2*x + y + z == 2; eqn2 = -x + y — z == 3; eqn3 = x + 2*y + 3*z == -10; · sol =solve([eqn1, eqn2, …

Matlab Tutorial — 51 — Решение алгебраических уравнений символьно

www.youtube.com › смотреть

24.03.2018 · MathTutorDVD.comУзнайте, как решать линейные алгебраические системы уравнений с помощью .