Как решать тройные интегралы: Вычисление тройных интегралов: теория и примеры

Содержание

Вычисление тройных интегралов: теория и примеры

Понятие тройного интеграла
Вычисление тройного интеграла путём уменьшения кратности
Расстановка пределов интегрирования при переходе к последовательности трёх интегралов
Замена переменных в тройном интеграле и цилиндрические координаты
Тройной интеграл в сферических координатах
Приложения тройного интеграла

Тройные интегралы – это аналог двойного интеграла для функции трёх переменных, заданной как f(M) = f(x, y, z).

Записывается тройной интеграл так:

Здесь V – пространственная (трёхмерная) фигура, ограниченная плоскостями, выражения которых (равенства) даны в задании вычисления тройного интеграла. V называют также замкнутой ограниченной областью трёхмерного пространства.

Вычислить тройной интеграл

— значит найти число, равное объёму тела V или, что то же самое — области V.

Практически каждый может понять смысл вычисления тройного интеграла «на своей шкуре». Точнее — «под шкурой», а ещё точнее — по своим органам дыхания — лёгким. Вне зависимости от того, знаете ли вы об этом или не знаете, в лёгких человека свыше 700 миллионов альвеол — пузырьковых образований, оплетённых сетью капилляров. Через стенки альвеол происходит газообмен. Поэтому можно рассуждать так: объём газа в лёкгих, можно представить в виде некоторой компактной области. А состоит этот объём из маленьких объёмов, сосредоточенных в альвеолах. Ключевую роль в этом сравнении играет именно огромное количество альвеол в лёгких: как мы увидим в следующем абзаце, через такое «огромное количество малостей» математически как раз и формулируется понятие тройного интеграла.

Почему именно тройной интеграл служит для нахождения объёма тела

V? Пусть область V разбита на n произвольных областей Δvi, причём под этим обозначением подразумевается не только каждая маленькая область, но и её объём.

В каждой такой маленькой области выбрана произвольная точка Mi, а f(Mi) — значение функции f(M) в этой точке. Теперь будем максимально увеличивать число таких маленьких областей, а наибольший диаметр Δvi — наоборот, уменьшать. Можем составить интегральную сумму вида

Если функция f(M) = f(x, y, z) непрерывна, то будет существовать предел интегральных сумм вида, указанного выше. Этот предел и называется тройным интегралом.

В этом случае функция f(M) = f(x, y, z) называется интегрируемой в области V; V — областью интегрирования; x, y, z — переменными интегрирования, dv (или dx dy dz) — элементом объёма.

Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.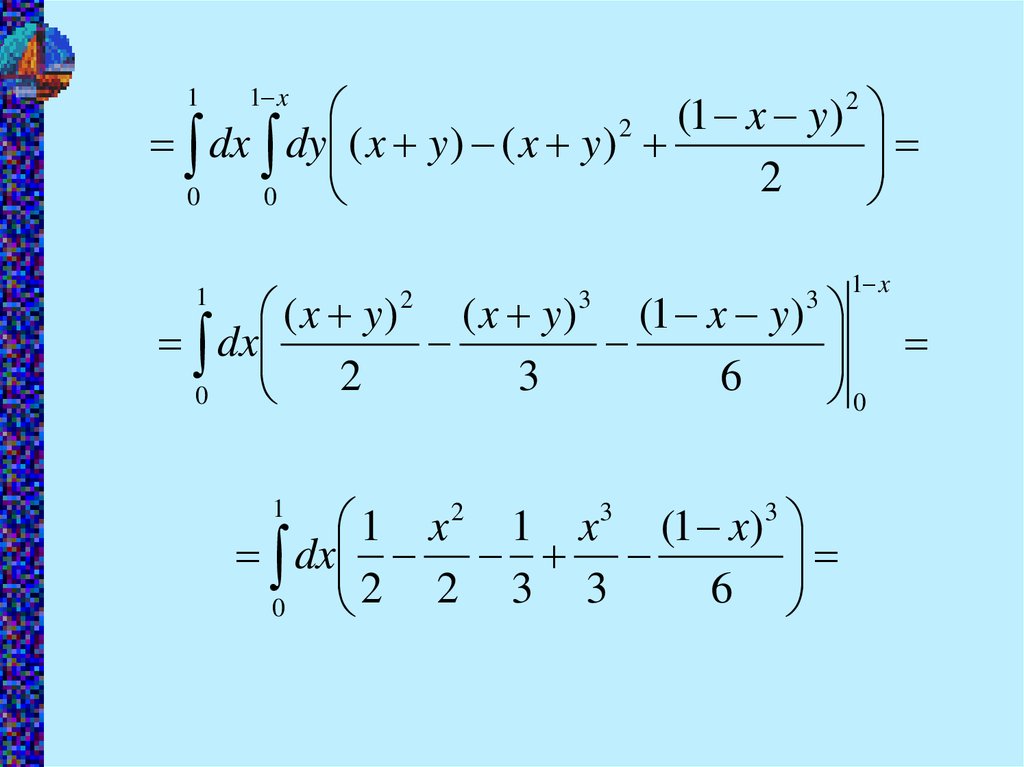

Рассмотрим трёхмерную область V. Снизу и сверху (то есть по высоте) эта область ограничена поверхностями z = z1(x, y) и z = z2(x, y). С боковых сторон (то есть по ширине) область ограничена поверхностями y = y1(x) и y = y2(x). И, наконец, по глубине (если Вы смотрите на область в направлении оси

Ox) — поверхностями x = a и x = b

Чтобы применять переход к интегралам меньшей кратности, требуется, чтобы трёхмерная область V была правильной. Она правильна тогда, когда прямая, параллельная оси Oz, пересекает границу области V не более чем в двух точках. Правильными трёхмерными областями являются, например, прямоугольный параллелепипед, эллипсоид, тетраэдр. На рисунке ниже — прямоугольный параллелепипед, который встретится нам в первом примере на решение задач.

Чтобы наглядно представить отличие правильности от неправильности, добавим, что поверхности области по высоте у правильной области не должны быть вогнуты вовнутрь. На рисунке ниже — пример неправильной области

V — однополостный гиперболоид, поверхность которого прямая, параллельная оси Oz (красного цвета), пересекает более чем в двух точках.

Мы будем рассматривать только правильные области.

Итак, область V — правильная. Тогда для любой функции f(x, y, z), непрерывной в области V, справедлива формула

Эта формула позволяет свести вычисление тройного интеграла к последовательному вычислению внутреннего определённого интеграла по переменной z (при постоянных x и y) и внешнего двойного интеграла по двумерной области D.

Переходя от двойного интеграла к повторному, получаем следующую формулу для вычисления тройного интеграла:

Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три определённых интеграла.

Вычисляются эти интегралы от самого внутреннего (по переменной z) к самому внешнему (по переменной x). Для удобства восприятия последовательности вычислений три «вложенных» интеграла можно записать так:

Из этой записи уже однозначно видно, что:

сначала нужно интегрировать функцию f(x, y, z) по переменной z, а в качестве пределов интегрирования взять уравнения z = z1(x, y) и z = z2(x, y) поверхностей ограничивающих область V снизу и сверху;
получившийся на предыдущем шаге результат интегрировать по переменной y, а в качестве пределов интегрирования взять уравнения

y = y1(x) и y = y2(x) поверхностей, ограничивающих область V с боковых сторон;
получившийся на предыдущем шаге результат интегрировать по переменной x, а в качестве пределов интегрирования взять уравнения x = a и x = b поверхностей, ограничивающих область V по глубине.

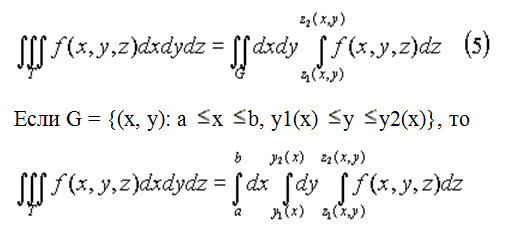
Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу

—

последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.

Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла. В нашем случае применяем формулу 10 из таблицы интегралов:

Вычислим второй интеграл — по переменной y (применяя формулу 7 из таблицы интегралов):

Теперь вычисляем самый внешний интеграл — по переменной x (применяя все ту же формулу 7):

Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.

Пример 2. Вычислить тройной интеграл

где V — параллелепипед, ограниченный плоскостями x = − 1, x = + 1, y = 0, y = 1, z = 0, z = 2.

Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:

Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:

Вычисляем интеграл «в серединке» — по переменной y. Получаем;

Теперь вычисляем самый внешний интеграл — по переменной x:

Ответ: данный тройной интеграл равен -2.

Пример 3. Вычислить тройной интеграл

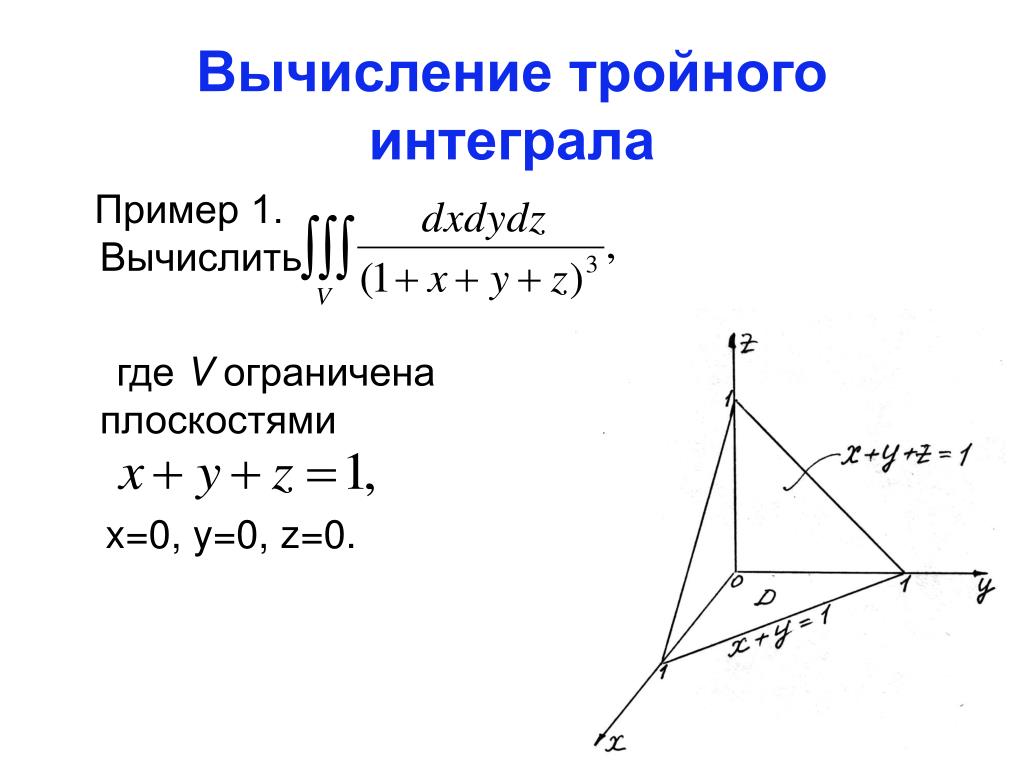
где V — пирамида, ограниченная плоскостью x + y + z = 1 и координатными плоскостями x = 0, y = 0, z = 0. Область V проецируется на плоскость xOy в треугольник D, как показано на рисунке ниже.

Решение. Расставим сначала пределы интегрирования. Для интеграла по переменной z нижний предел интегрирования задан однозначно: z = 0. Чтобы получить верхний предел, выразим z из x + y + z = 1. Получаем 1 − x − y. Для интеграла по переменной y нижний предел интегрирования задан однозначно: y = 0. Для получения верхнего предела выразим y из x + y + z = 1, считая при этом, что z = 0 (так как линия расположена в плоскости xOy). Получаем: 1 − x.

Сводим данный тройной интеграл к последовательности трёх определённых интегралов:

Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:

Вычисляем средний интеграл — по переменной y. Получаем:

Наконец, вычисляем самый внешний интеграл — по переменной x:

Ответ: данный тройной интеграл равен 1/8.

Вычислить тройной интеграл самостоятельно, а затем посмотреть решение

Пример 4. Вычислить тройной интеграл

где V — пирамида, ограниченная плоскостью x + y + z = 1 и координатными плоскостями x = 0, y = 0, z = 0.

Посмотреть правильное решение и ответ.

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Интеграл

Бывает, что студенты, у которых не вызывает особых трудностей непосредственное вычисление интегралов, не могут освоиться в расстановке пределов интегрирования при переходе от тройного интеграла к последовательности трёх определённых интегралов. В этом деле действительно требуется некоторая натренированность. В первом примере область интегрирования V представляла собой параллелепипед, с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно заданы уравнениями плоскостей. Во втором примере — пирамида: здесь уже требовалось чуть больше подумать и выразить один из пределов из уравнения. А если область V ограничивают не плоские поверхности? Нужно, конечно, определённым образом осмотреть область V.

Начнём с примера «пострашнее», чтобы почувствовать «обстановку, приближенную к боевой».

Пример 5. Расставить пределы интегрирования при переходе от тройного интеграла, в котором область V — эллипсоид

Решение. Пусть центр эллипсоида — начало координат, как показано на рисунке выше. Посмотрим на эллипсоид снизу. Снизу его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена ниже плоскости xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение со знаком минус будет нижним пределом интегрирования по переменной z:

Теперь посмотрим на эллипсоид сверху. Здесь его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена выше оси xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение будет верхним пределом интегрирования по переменной z:

Проекцией эллипсоида на плоскость xOy является эллипсоид. Его уравнение:

Чтобы получить нижний предел интегрирования по переменной y, нужно выразить y из уравнения эллипсоида и взять полученное выражение со знаком минус:

Для верхнего предела интегрирования по переменной y то же выражение со знаком плюс:

Что касается интегрирования по переменной x, то область V ограничена по глубине плоскостями. Следовательно, пределы интегрирования по переменной x можно представить как координаты задней и передней границ области. В случае эллипсоида ими будут взятые с отрицательным и положительным знаками величины длин полуоси a: x1 = − a и x2 = a.

Таким образом, последовательность интегралов для вычисления объёма эллипсоида следующая:

где «игрек первое», «игрек второе», «зет первое» и «зет второе» — полученные выше выражения. Если у Вас есть желание и отвага вычислить этот интеграл и, таким образом, объём эллипсоида, то вот ответ: 4πabc/3.

Следующие примеры — не такие страшные, как только что рассмотренный. При этом они предполагают не только расстановку пределов интегрирования, но и вычисление самого тройного интеграла. Проверьте, чему вы научились, следя за решением «страшного» примера. Думать при расстановке пределов всё равно придётся.

Пример 6. Вычислить тройной интеграл

если область интегрирования ограничена плоскостями x + y = 1, x + 2y = 4, y = 0, y = 1, z = 1, z = 5.

Решение. «Курортный» пример по сравнению с примером 5, так как пределы интегрирования по «игрек» и «зет» определены однозначно. Но придётся разобраться с пределами интегрирования по «иксу». Проекцией области интегрирования на плоскость xOy является трапеция ABCD.

В этом примере выгоднее проецировать трапецию на ось Oy, иначе, чтобы вычислить тройной интеграл, на придётся разделить фигуру на три части. В примере 4 мы начинали осмотр области интегрирования снизу, и это обычный порядок. Но в этом примере мы начинаем осмотр сбоку или, если так проще, положили фигуру набок и считаем, что смотрим на неё снизу. Можем найти пределы интегирования по «иксу» чисто алгебраически. Для этого выразим «икс» из первого и второго уравнений, данных в условии примера. Из первого уравения получаем нижний предел 1 − y, из второго — верхний 4 − 2y. Сведём данный тройной интеграл к последовательности трёх определённых интегралов:

Внимание! В этом примере самый внешний интеграл — не по переменной «икс», а по переменной «игрек», а «средний» — по переменной «икс»! Здесь мы применили смену порядка интегрирования, с которой ознакомились при изучении двойного интеграла. Это связано с тем, что, как уже говорилось, мы начали осмотр области интегрирования не снизу, а сбоку, то есть спроецировали её не на ось Ox, на на ось Oy.

Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:

Вычисляем средний интеграл — по переменной x. Получаем:

Наконец, вычисляем самый внешний интеграл — по переменной y:

Ответ: данный тройной интеграл равен 43.

Пример 7. Вычислить тройной интеграл

если область интегрирования ограничена поверхностями x = 0, y = 0, z = 2, x + y + z = 4.

Решение. Область V (пирамида MNRP) является правильной. Проекцией области V на плоскость xOy является треугольник AOB.

Нижние пределы интегрирования по всем переменным заданы в условии примера. Найдём верхний предел интегирования по «иксу». Для этого выразим «икс» из четвёртого уравнения, считая «игрек» равным нулю, а «зет» равным двум. Получаем x = 2. Найдём верхний предел интегирования по «игреку». Для этого выразим «игрек» из того же четвёртого уравнения, считая «зет» равным двум, а «икс» — переменной величиной. Получаем y = 2 − x. И, наконец, найдём верхний предел интегрирования по переменной «зет». Для этого выразим «зет» из того же четвёртого уравнения, считая «игрек» и «зет» переменными величинами. Получаем z = 4 − x − y.

Сведём данный тройной интеграл к последовательности трёх определённых интегралов:

Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:

Вычисляем средний интеграл — по переменной y. Получаем:

Вычисляем самый внешний интеграл — по переменной x и окончательно находим данный тройной интеграл:

Ответ: данный тройной интеграл равен 2.

Если проекцией области интегрирования на какую-либо из координатных плоскостей является круг или часть круга, то тройной интеграл проще вычислисть, перейдя к цилиндрическим координатам. Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами (r, φ, z), где r — расстояние от начала координат до проекции N точки M на плоскость xOy, φ — угол между вектором ON и положительным направлением оси Ox, z — аппликата точки M (рисунок ниже).

Прямоугольные координаты x, y, z с цилиндрическими координатами r, φ, z связывают формулы

x = rcosφ,

y = rsinφ,

z = z.

Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно подынтегральную функцию выразить в виде функции переменных r, φ, z:

То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:

Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:

Пример 8. Вычислить тройной интеграл

переходом к цилиндрическим координатам, где V — область, ограниченная поверхностями и .

Решение. Так как область V на плоскость xOy проектируется в круг , то координата φ изменяется в пределах от 0 до 2π, а координата r — от r=0 до r=1. Постоянному значению в пространстве соответствует цилиндр . Рассматривая пересечение этого цилиндра с областью V, получаем изменение ординаты z от z = r² до z = 1. Переходим к цилиндрическим координатам и получаем:

Ответ: данный тройной интеграл равен π/6.

Если область интегрирования в тройном интеграле представляет собой шар или часть шара, то проще вычислить тройной интеграл в сферических координатах. В сферических координатах точку M характеризуют три величины (ρ, φ, θ), где ρ — расстояние от точки M до начала координат 0, φ — угол между вектором ON и положительным направлением оси Ox (N — проекция точки M на плоскость xOy), θ — угол между вектором OM и положительным направлением оси Oz.

Сферические координаты связаны с прямоугольными декартовыми координатами соотношениями

x = ρsinθcosφ,

y = ρsinθsinφ,

z = ρcosθ.

Элемент объёма в сферических координатах выражается следующим образом:

Таким образом, переход от прямоугольных декартовых координат в тройном интеграле к сферическим координатам осуществляется по формуле:

Чтобы вычислить тройной интеграл в сферических координатах, нужно поступить так же, как при вычислениях в прямоугольных декартовых и цилиндрических координатах — перейти к повторным интегралам (последовательности трёх определённых интегралов):

Пример 9. Вычислить тройной интеграл

переходом к сферическим координатам, где V — область, ограниченная неравенствами и .

Решение. Снизу область интегрирования ограничена конической поверхностью , а сверху — сферой . Так как область интегирования представляет собой часть шара, перейдём к сферическим координатам. Перепишем подынтегральную функцию:

Учитывая, что , получаем

Расставим пределы интегрирования и перепишем последний полученный интеграл в виде трёх повторных интегралов. По рисунку видно, что , , . Поэтому

Итак, тройной интеграл вычислен. Так как все три интеграла — независисмые друг от друга, мы смогли интегрировать каждый отдельно и результаты перемножить.

Вычисление объёма тела. Объём области V равен тройному интегралу по этой области, если подынтегральная функция равна 1:

Вычисление массы неоднородного тела. Массу неоднородного тела с плотностью ρ = ρ(x, y, z) можно вычислить по формуле:

Статические моменты материального тела. Статические моменты относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z) можно вычислить по формулам:

Моменты инерции материального тела. Моменты инерции относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z) можно вычислить по формулам:

Моменты инерции относительно осей Ox, Oy, Oz определяются по формулам:

Центр тяжести материального тела. Координаты центра массы C(xc, yc, zc) материального тела с плотностью ρ = ρ(x, y, z) определяются по формулам:

Пример 10. Вычислить объём тела, ограниченного поверхностями , , .

Решение. Одна их поверхностей — — цилиндрическая поверхность (образующая параллельна оси Oz), то есть проекция области на плоскость xOy совпадает с фигурой, которую ограничивает линия , или . Эта линия изображена на рисунке ниже.

Таким образом, записываем тройной интеграл в цилиндрических координатах и вычисляем его:

Ответ: объём тела равен 176 единиц объёма.

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Кратные и криволинейные интегралы

Кратные и криволинейные интегралы

Вычисление двойных интегралов
Двойные интегралы в полярных координатах
Вычисление тройных интегралов
Вычисление криволинейных интегралов
Интегралы по замкнутому контуру, формула Грина
Вычисление поверхностных интегралов

Поделиться с друзьями

Двойные и тройные интегралы

Двойные и тройные интегралы даются трудно всем студентам. Одна из причин — это отсутствие возможности качественно строить области интегрирования.
Из воображения их брать удается не многим специалистам. Что касается нахождения объемов, образованных пересечением плоскостей, то здесь эта проблема становится еще большей.
Другое дело, что часто кратные интегралы начинают изучать когда студенты только что научились находить определенные интегралы.
Всем Вам помогут в учебе готовые ответы индивидуальной работы.
Приведенные ниже 10 примеров научат Вас решать задание разной сложности.

ВАРИАНТ — 19

Двойной интеграл

ЗАДАНИЕ 1.14 Поменять порядок интегрирования в двойном интеграле:

Решение: Из интеграла выписываем область интегрирования, которая ограничена кривыми

где (y — 1)²=1 — x², x²+(y — 1)²=1.
Получили нижний полукруг с центром в точке O (0;1) и радиусом R=1.
Выражаем полученные функции через переменную y:
, отсюда перед радикалом стоит знак «+» поскольку часть круга находится в правой (положительной по x) части полплоскости;
y=e^x, отсюда x=ln (y).
Выполняем построение рисунка к задаче, это служит доброй подсказкой при выполнении заданий

Как изменять пределы интегрирования Вас по-видимому учили.
Если не все знают, то просто мнимо проведите прямую и выпишите закон за которым изменяются края при прохождении кривой снизу вверх, или слева направо. Таким образом Вы будете знать и количество областей разбития, и функции, которые ограничивают площадь или объем тела.
При изменении порядка интегрирования нашу область разбили на две области: D=D₁+D₂.
Расставим пределы интегрирования в каждой области:

Еще раз внимательно пересмотрите рисунок и попробуйте проанализировать почему так.
При изменении порядка интегрирования получим два двойных интеграла
На этом и все объяснения к первой задаче.

ЗАДАНИЕ 2.13 Найти площадь плоской фигуры, заданной следующими условиями, : xy=1, xy=2, 6y=7-x.
Решение: Сначала выполняем построение кривых, чтобы понять площадь какой фигуры ищем

Дальше видим, что область интегрирования нужно разбивать на три части.
Есть другой вариант, более легкий с точки зрения практической реализации.
Можно найти площадь между двумя красными кривыми и от нее отнять площадь в области D₂ между красной и синей кривыми. В результате получим разницу двух двойных интегралов.
Но здесь пойдем более длинным по пути, описанный попробуйте реализовать самостоятельно.
Первое, что нам нужно — это определить в каких точках графика кривые пересекают друг друга.
Найдем точки пересечения графиков 1 и 3 функций:
складываем систему из двух уравнений

и находим решение

Пересечение второй и третьей функций дают систему уравнений

для определения двух точек

Заданную область будем разбивать на три области: D=D₁+D₂+D₃.
Расставим пределы интегрирования в каждой области:

Через двойной интеграл вычисляем площадь фигуры, ограниченной заданными кривыми:
Интеграл в итоге дает много логарифмов, которые группируем.
Приближенно площадь поверхности равна 1,12 единиц квадратных.

ЗАДАНИЕ 3.12 Вычислить двойной интеграл по области D, ограниченной указанными линиями:
D: y=2x³, y=0, x=1.
Решение: Найдем точки пересечения графиков заданных функций : 2x³=0, x=0.
Изобразим графически область интегрирования

Расставим пределы в заданной области D:

Вычислим двойной интеграл по области D, ограниченной указанными линиями:
Напомним, что это есть лишь двойной интеграл.
Площадь имеет место лишь в тех случаях, когда функция интегрирования равна единице.

ЗАДАНИЕ 4.11 Вычислить двойной интеграл, используя полярные координаты:

Решение: Запишем область интегрирования, которая ограничена кривыми

где
Получили круг с центром в точке O (0;0) и радиусом ровным ругаю из трех (верхняя половина).
Изобразим полукруг в декартовой и полярной системе координат

Перейдем к полярной системе координат (СК), используя следующую замену переменных :

Следует помнить, что дополнительно нужно вычислить якобиан перехода от декартовой к полярной СК:

Он важен, поскольку на него нужно домножити подинтегральную функцию, выраженную в новых координатах
Найдем вид подинтегральной функции в полярной системе координат :

Запишем пределы интегрирования в полярной СК:

Осталось вычислить двойной интеграл:

Интеграл равен I=7*Pi/3.
То, что интеграл содержит число Pi лишь подтверждает правильность вычислений, ведь для круговых форм это распространено.

ЗАДАНИЕ 5.10 Вычислить площадь области D, ограниченной указанными линиями:
D: y=x²+2, x=2, y=x

Решение: Расставим пределы в заданной области D:

Построим кривые, чтобы представить фигуру площадь которой мы ищем.

Здесь есть два варианта: сложный — когда внутренний интеграл за переменной x предусматривает нахождение площади, через сумму двойных интегралов по 2 или 3 областям.
Мы же пойдем легким по пути и определим площадь заштрихованной фигуры с помощью одного двойного интеграла.
Вычислим площадь криволинейной трапеции, ограниченной указанными линиями:

Площадь равна S=14/3 единиц квадратных.
Как видите — выбор порядка интегрирования может существенно сэкономить время при написании контрольной работы, на экзамене или практических заданиях. Для сравнения попробуйте вычислить первым временем и сравнить масштаб выполненных работ.

ЗАДАНИЕ 6.9 Используя двойной интеграл, вычислить, перейдя к полярным координатам, площадь плоской фигуры : (x²+y²)²=a²(2x²+3y²).
Решение: Один из предыдущих примеров содержал переход к полярной системе координат :

и был найден якобиан переходу I=r.
Определим пределы интегрирования :

Пределы интегрирования:
Их легко определить в полярной СК — радиус изменяется от нуля к кривой, которая ограничивает площадь, а угол изменяется от 0 до 360 градусов.
Это Вы должны знать при вычислении подобных заданий.
Вычислим площадь плоской фигуры:

Под интегралом пришлось понижать степень синуса за известной тригонометрической формулой. На пратиці Вы такие случаи рассматривали, то же здесь мы Вам ничего нового не открываем.

ЗАДАНИЕ 7.8 Найти объем тела, заданного поверхностями, что его ограничивают:
y=7-x²-z², , y=0.
Решение: Половину 3d рисунка тела изобразим графически — это хорошая подсказка, которая развивает воображение.

Вычислим объем тела, которое ограничивает эти две поверхности (то есть рисунок разрезали пополам для наглядного отражения)+ снизу плоскостью y=0.
Чтобы упростить интегралы объем тела найдем как разницу объемов параболоида и конуса (см. рис.).

Расставим пределы в заданной области D₁ (круг радиусом ):

Найдем объем параболоида:

При нахождении двойного интегралу целесообразно перейти к полярной СК, поскольку обе фигуры образованы вращением кривой вокруг оси Oy.
Расставим пределы в области D₂ (круг радиусом R=1):

Вычислим объем конуса:

Он равен V=Pi/3 единиц кубических.
Здесь также во время интегрирования перешли к полярной СК.
Последним шагом найдем объем тела, которое находится между параболоидом и конусом, :
Разница объемов равна V=145*Pi/6=75,88 единиц кубических.

Тройной интеграл

ЗАДАНИЕ 8.7 Расставить пределы интегрирования в тройном интеграле , если область V ограничена указанными поверхностями:
V: y=2x, y=1 , x+y+z=3.
Нарисовать область интегрирования.
Решение: В плоскости Oxy уравнение прямых запишем следующим образом: y=1, x=y/2, x=3-y.
Уравнение плоскости в пространстве запишем в виде: z=3-y-x.
Построим пространственный рисунок тела и его проекцию в декартовую плоскость
Как видно из рисунку область тела D, что проектируется на плоскость Oxy, разбивается на две части:
D=D₁+D₂, поэтому пределы интегрирования расставляем следующим образом:

На основе проведенного анализа записываем пределы в тройной интеграл
Внимательно разберите как изменятся пределы, если интегрировать за переменной y во внутреннем интеграле.
Легко убедиться, что получим сумму из трех тройных интегралов.

ЗАДАНИЕ 9.6 Вычислить тройные интегралы: где область интегрирования ограничена:
Решение: Область являет собой параллелепипед, который изображен ниже

Это значительно упрощает интегрирование
Детали вычислений хорошо расписаны в формулах, потому здесь важно лишь правильно подставить пределы и не ошибиться при грустит.

ЗАДАНИЕ 10.5 Используя тройной интеграл, вычислить объем тела, ограниченного поверхностями:

Нарисовать область интегрирования.
Решение: Прежде всего выполняем построение к условию, в крайнем случае старайтесь схематически нарисовать область интегрирования

Дальше записываем пределы интегрирования, учитывая выполненный рисунок:

Через тройной интеграл находим объем тела:

Превращения не сложны и их разберите самостоятельно.
Объем ровный 16 куб. од.
На этом индивидуальная работа из повторных интегралов выполнена.
Больше примеров на двойные и тройные интегралы Вы можете найти в следующих материалах.

∫∫∫ Тройной интеграл — Калькулятор Он-лайн

Калькуляторы онлайн/ Решение интегралов/ Тройных

Примеры

Найдём решение тройного интеграла от функции f(x, y, z).

Введите вверхние и нижние пределы для области интегрирования и подинтегральную функцию для тройного интеграла. 2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x): Интегральный синус от x
Ci(x): Интегральный косинус от x
Shi(x): Интегральный гиперболический синус от x
Chi(x): Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа: вводить в виде 7. 3; — возведение в степень
x + 7: — сложение
x — 6: — вычитание
15/7: — дробь

Другие функции:

asec(x): Функция — арксеканс от x
acsc(x): Функция — арккосеканс от x
sec(x): Функция — секанс от x
csc(x): Функция — косеканс от x
floor(x): Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
ceiling(x): Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
sign(x): Функция — Знак x
erf(x): Функция ошибок (или интеграл вероятности)
laplace(x): Функция Лапласа
asech(x): Функция — гиперболический арксеканс от x
csch(x): Функция — гиперболический косеканс от x
sech(x): Функция — гиперболический секанс от x
acsch(x): Функция — гиперболический арккосеканс от x

Постоянные:

pi: Число «Пи», которое примерно равно ~3. 14159..
e: Число e — основание натурального логарифма, примерно равно ~2,7183..
i: Комплексная единица
oo: Символ бесконечности — знак для бесконечности

Тройные интегралы

Альфашкола
Статьи
Тройные интегралы

Имеют те же свойства, что и двойные интегралы (линейность, аддитивность, формулы среднего значения и т.д.)

I. Вычисление тройных интегралов с помощью повторного интегрирования

1. Предположим, что функция f(x, y, z) непрерывна в рассматриваемой области T.

Пусть сначала T = [a, b; c, d; e, f] — прямоугольный параллелепипед, проектирующийся на плоскость yz в прямоугольник R = [c, d; e, f]. Тогда

Заменяя в (1) двойной интеграл повторным, получим

Вычисление тройного интеграла сводится к последовательному вычислению трёх определённых интегралов.

Если первые два интеграла в (2) объединить в двойной, то будем иметь

где P = [a, b; c, d] — проекция параллелепипеда T на плоскость xy.

Заметим, что в этих случаях можно менять роли переменных.

2. Пусть область T заключена между плоскостями x = a и x = b, причём каждое сечение области T плоскостью x=const, a ≤ x ≤ b представляет собой квадрируемую фигуру G(x)(рис. 1). Тогда

3. Пусть теперь тело T представляет собой «цилиндрический брус», ограниченный снизу и сверху, соответственно, поверхностями z = z1(x, y) и z = z2(x, y), проектирующиеся на плоскость xy в некоторую квадрируемую фигуру G (рис. 2), z1(x, y) и z2(x, y) — непрерывны в G. Тогда

Отметим, что наряду с указанными формулами имеют место и им подобные, получающиеся перестановкой переменных x, y и z.

II. Замена переменных в тройном интеграле состоит в переходе от переменных x, y, z к новым переменным u, v, w по формулам

Если выполняются условия

то имеет место формула

Формулы (6) называют криволинейными координатами (u, v, w) в области T. Рассмотрим примеры криволинейных координат.

1. Цилиндрические координаты представляют соединение полярных координат в плоскости xy с обычной декартовой аппликатой z (рис. 3).

Пусть M(x, y, z) — произвольная точка в пространстве xyz, P — проекция точки M на плоскость xy. Точка M однозначно определяется тройкой чисел (r,φ,z), где (r,φ) — полярные координаты точки P, z — аппликата точки M. Формулы, связывающие их с декартовыми, имеют вид

2. Сферические координаты. Пусть M(x, y) — произвольная точка в пространстве xyz, P — проекция точки M на плоскость xy. Точка M однозначно задаётся тройкой чисел (r,θ,φ), где r — расстояние точки M до точки 0, θ — угол между лучами OM и OZ, φ — полярный угол точки P на плоскости xy. Тройка чисел (r,θ,φ) называется сферическими координатами точки M.

Они связаны с прямоугольными формулами

Якобиан отображения

Иногда используются обобщённые сферические координаты.
Объём V кубируемой области T (кубического тела) в пространстве xyz выражается формулой

Переходя в этом равенстве к новым переменным по формулам (6), получим выражение объёма области T в криволинейных координатах

Пусть T — материальное тело (кубируемая область) с плотностью

Тогда

Пример1. Вычислить объём тела, ограниченного поверхностями: x2 + y2 + z2 = a2, x2 + y2 — ax = 0.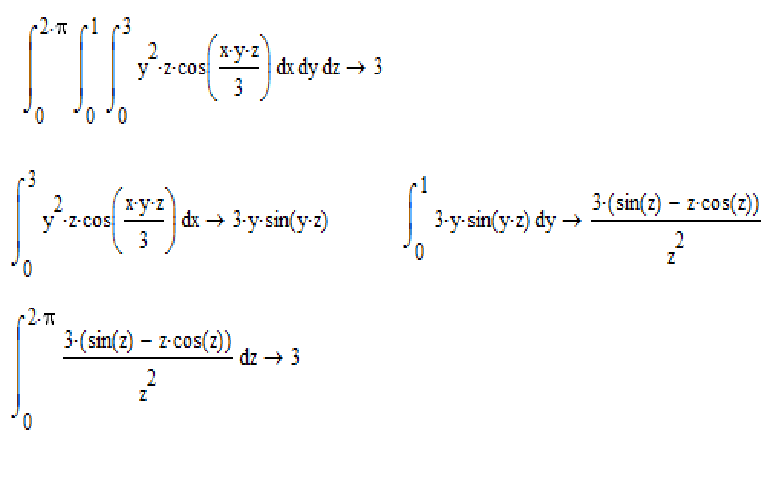 2}}\) вырезанная цилиндром, проектируется в область

Перейдём в интеграле к цилиндрическим координатам по формулам (8). При этом уравнение окружности x? + y? — ax = 0 преобразуется в кривую

Таким образом

Пример 2. Вычислить интеграл

Решение. Перейдём в интеграле к сферическим координатам по формулам (9). Тогда область интегрирования можно задать неравенствами

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Дмитрий Владимирович Замков

Репетитор по математике

Стаж (лет)

Образование:

Самарский государственный экономический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 7-11 классов. Использую смешанную методику преподавания. Западная методика обучения вкупе с российской, около индивидуальная форма. Отличительными особенностями моего преподавания является нестандартность, выстраивание теплой и веселой атмосферы с учеником.

Елена Николаевна Чехлякова

Репетитор по математике

Стаж (лет)

Образование:

Самарский педагогический институт им.В.В.Куйбышева

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 5-11 классов с 10-летним стажем работы. Успешно готовлю к ОГЭ, ЕГЭ (имеются высокие результаты-100 — 96 баллов), ВПР. Помогаю справиться с трудностями в обучении. На занятиях работаю на результат, создаю ситуацию успеха. Стараюсь всегда достигать поставленных целей и задач.

Евгения Юрьевна Накисько

Репетитор по математике

Стаж (лет)

Образование:

Российский химико-технологический университет им. Д.И.Менделеева

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по химии 7-11. Я специалист в области химических наук, имею 2 ступени высшего образования (бакалавриат, магистратура), оконченных с отличием по специальности Общая и Аналитическая химия. На данный момент обучаюсь в аспирантуре РХТУ им. Д.И. Менделеева на кафедре Коллоидной химии. За время обучения получила опыт практической деятельности (поэтому отлично знаю о технике построения лабораторного эксперимента, следовательно, легко разбираю задачи сложной части ОГЭ), занимаюсь как со студентами, так и со школьниками. Работаю по самостоятельно разработанной программе, которую периодически дополняю. Опыт работы 2,5 года. Средний балл, получаемый моими учениками по химии: 4,6. Средний балл сдачи экзаменов: от 75 и выше.

Тройные интегралы. Вычисление объема тела

Похожие презентации:

Тройные интегралы. (Лекция 16)

Вычисление тройных интегралов

Понятие интеграла по фигуре. Выделение частных случаев: двойной интеграл, тройной интеграл. Свойства интегралов

Масса неоднородного тела. Тройной интеграл. (Лекция 2-3)

Тройной интеграл

Вычисление тройных интегралов. Цилиндрические координаты. (Семинар 32)

Приложения тройных интегралов. (Лекция 2.4)

Тройные интегралы. Вычисление тройных интегралов. Декартовы прямоугольные координаты. (Семинар 31)

Тройные интегралы. Вычисления объёма тела

ТРОЙНЫЕ ИНТЕГРАЛЫ.
ВЫЧИСЛЕНИЕ ОБЪЕМА
ТЕЛА.
Понятие тройного интеграла вводиться
аналогично понятию двойного
интеграла.
Пусть функция f(x,y,z) определена в
ограниченной замкнутой области T,
которая принадлежит трехмерному
пространству с определенной
декартовой системой координат Oxyz.
Разобьем заданную область на n
частей, которые не имеют общих
внутренних точек и объемы которых
равны соответственно.
В каждой такой элементарной области
возьмем произвольную точку Pi(xi,yi,zi)
n
составим интегральную
сумму ∑f(xi,yi,zi)dVi
Тройной интеграл в общем виде записывается следующим
образом:
f(x,y,z) – подынтегральная функция трех переменных.
dxdydz – произведение дифференциалов.
T – область интегрирования – пространственное тело
ограниченное множеством поверхностей.
Вычислить тройной интеграл – это значит найти ЧИСЛО:
В соответствии с общим смыслом интегрирования,
произведение dxdydz равно бесконечно малому объему dV
элементарного тела.
Тройной интеграл объединяет все эти бесконечно малые
частички по области , в результате чего получается
интегральное (суммарное) значение объёма тела:
Как решать тройной
интеграл?
Пример 1.
С помощью тройного интеграла вычислить объем тела,
ограниченного поверхностями
Варианты ответа:
1)
2)
3)
4)
С помощью тройного интеграла вычислить объем тела,
ограниченного поверхностями
1)используем формулу
Сначала
изобразим параллельную ортогональную проекцию тела на
координатную плоскость XOY.
2) выясняем, чем тело ограничено с сверху, чем снизу и
выполняем пространственный чертёж.
z=y² параболический цилиндр
расположенный
над плоскостью XOY и
проходящий через
ось OX:
3)Выбираем порядок обхода тела: Двигаемся по OZ
Двигаемся по OY
=>
Двигаемся по OX
Решение свелось к двойному интегралу, используем
формулу:
Ответ: 1)
Пример 2.
Вычислить с помощью тройного интеграла объем тела,
ограниченного указанными поверхностями. Выполнить
чертёж.
Варианты ответа:
1)
2)
3)
4)
Решим систему
получены
две прямые, лежащие в плоскости
параллельные оси
Изобразим проекцию тела на плоскость
XOY:
Искомое тело ограниченно
плоскостью z=0
снизу и
параболическим цилиндром
z=1-x² сверху:
Составим порядок обхода тела: Двигаемся по OZ
Двигаемся по OY
Двигаемся по OX
При интегрировании по «игрек» – «икс» считается константой,
поэтому константу целесообразно сразу вынести за знак интеграла.
Ответ: 2)
Пример 3.
Вычислить с помощью тройного интеграла объём тела,
ограниченного поверхностями
Выполнить чертёжи данного тела и его проекции на
плоскость XOY.
Варианты отета:
1)
2)
3)
4)
Решение: придерживаемся того же порядка действий: в
первую очередь рассматриваем уравнения, в которых
отсутствует переменная «зет». Оно здесь одно.
Проекция цилиндрической поверхности
на
плоскость
представляет собой «одноимённую» окружность.
Плоскости
ограничивают искомое тело снизу и
сверху («высекают» его из цилиндра) и проецируются в круг
Плоскость
пересекает цилиндр
под косым
углом, в результате чего получается эллипс.
Из уравнения
вычислим значения функции
(«высоту») в напрашивающихся точках
Проекция тела на плоскость XOY представляет собой круг, и это
весомый аргумент в пользу перехода к цилиндрической системе
координат:
Найдём уравнения поверхностей в цилиндрических координатах:
порядок обхода тела:
Ответ: 3)
Пример 4.
С помощью тройного интеграла вычислить объём заданного
тела:
, где   – произвольное положительное
число.
неравенство
задаёт шар с центром в начале
координат радиуса , а неравенство
–
«внутренность» кругового цилиндра с осью симметрии
радиуса
.
Таким образом, искомое тело ограничено
круговым цилиндром сбоку и симметричными относительно
плоскости
сферическими сегментами сверху и снизу.
Варианты ответа:
1)
2)
3)
4)
Порядок обхода:
Решаем методом подведения под знак дифференциала:
Ответ: 4)

English Русский Правила

Тройные интегралы. Вычисление объема тела презентация, доклад

Слайд 1Текст слайда:

ТРОЙНЫЕ ИНТЕГРАЛЫ. ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА.

Слайд 2Текст слайда:

Понятие тройного интеграла вводиться аналогично понятию двойного интеграла.
Пусть функция f(x,y,z) определена в ограниченной замкнутой области T, которая принадлежит трехмерному пространству с определенной декартовой системой координат Oxyz. Разобьем заданную область на n частей, которые не имеют общих внутренних точек и объемы которых равны соответственно.
В каждой такой элементарной области возьмем произвольную точку Pi(xi,yi,zi)
n
составим интегральную сумму ∑f(xi,yi,zi)dVi
i=1

Слайд 3Текст слайда:

Тройной интеграл в общем виде записывается следующим образом:

f(x,y,z) – подынтегральная функция трех переменных.
dxdydz – произведение дифференциалов.
T – область интегрирования – пространственное тело ограниченное множеством поверхностей.
Вычислить тройной интеграл – это значит найти ЧИСЛО:

В соответствии с общим смыслом интегрирования, произведение dxdydz равно бесконечно малому объему dV элементарного тела.
Тройной интеграл объединяет все эти бесконечно малые частички по области , в результате чего получается интегральное (суммарное) значение объёма тела:

Слайд 4Текст слайда:

Как решать тройной интеграл?

Пример 1.
С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями Варианты ответа:
1) 2) 3) 4)
С помощью тройного интеграла вычислить объем тела, ограниченного поверхностями
1)используем формулу Сначала изобразим параллельную ортогональную проекцию тела на координатную плоскость XOY.
2) выясняем, чем тело ограничено с сверху, чем снизу и выполняем пространственный чертёж.
z=y² параболический цилиндр расположенный
над плоскостью XOY и проходящий через
ось OX:

Слайд 5Текст слайда:

3)Выбираем порядок обхода тела: Двигаемся по OZ
Двигаемся по OY =>
Двигаемся по OX

Решение свелось к двойному интегралу, используем формулу:

Ответ: 1)

Слайд 6Текст слайда:

Пример 2.
Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Выполнить чертёж.
Варианты ответа:
1) 2) 3) 4)
Решим систему получены

две прямые, лежащие в плоскости параллельные оси
Изобразим проекцию тела на плоскость XOY:
Искомое тело ограниченно плоскостью z=0
снизу и
параболическим цилиндром z=1-x² сверху:

Слайд 7Текст слайда:

Составим порядок обхода тела: Двигаемся по OZ
Двигаемся по OY
Двигаемся по OX

При интегрировании по «игрек» – «икс» считается константой, поэтому константу целесообразно сразу вынести за знак интеграла.

Ответ: 2)

Слайд 8Текст слайда:

Пример 3.
Вычислить с помощью тройного интеграла объём тела, ограниченного поверхностями
Выполнить чертёжи данного тела и его проекции на плоскость XOY.
Варианты отета:
1) 2) 3) 4)
Решение: придерживаемся того же порядка действий: в первую очередь рассматриваем уравнения, в которых отсутствует переменная «зет». Оно здесь одно. Проекция цилиндрической поверхности на плоскость
представляет собой «одноимённую» окружность.
Плоскости ограничивают искомое тело снизу и сверху («высекают» его из цилиндра) и проецируются в круг
Плоскость пересекает цилиндр под косым углом, в результате чего получается эллипс.
Из уравнения вычислим значения функции («высоту») в напрашивающихся точках

Слайд 9Текст слайда:

Проекция тела на плоскость XOY представляет собой круг, и это весомый аргумент в пользу перехода к цилиндрической системе координат:

Найдём уравнения поверхностей в цилиндрических координатах:

порядок обхода тела:

Ответ: 3)

Слайд 10Текст слайда:

Пример 4.
С помощью тройного интеграла вычислить объём заданного тела: , где – произвольное положительное число.
неравенство задаёт шар с центром в начале координат радиуса , а неравенство – «внутренность» кругового цилиндра с осью симметрии радиуса . Таким образом, искомое тело ограничено круговым цилиндром сбоку и симметричными относительно плоскости сферическими сегментами сверху и снизу.
Варианты ответа:
1) 2) 3) 4)

Порядок обхода:

Слайд 11Текст слайда:

Решаем методом подведения под знак дифференциала:

Ответ: 4)

Скачать презентацию

Исчисление III. Тройные интегралы

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 4-5: Тройные интегралы

Теперь, когда мы знаем, как интегрировать по двумерной области, нам нужно перейти к интегрированию по трехмерной области. Мы использовали двойной интеграл для интегрирования по двумерной области, поэтому неудивительно, что мы будем использовать тройной интеграл для интегрирования по трехмерной области. Обозначение общих тройных интегралов:

. \[\iiint\limits_{E}{{f\left( {x,y,z} \right)\,dV}}\]

Давайте начнем с простой интеграции с коробкой,

\[B = \left[ {a,b} \right] \times \left[ {c,d} \right] \times \left[ {r,s} \right]\]

Обратите внимание, что при использовании этого обозначения мы перечисляем $x$ первым, $y$ вторым и $z$ третьим. 9{{\,b}}{{f\left( {x,y,z} \right)dx}}\,dy}}\,dz}}\]

Обратите внимание, что здесь мы интегрировали сначала по $x$, затем по $y$ и, наконец, по $z$, но на самом деле нет смысла интегрировать в таком порядке. Существует 6 различных возможных порядков выполнения интеграла, и порядок, в котором вы выполняете интеграл, будет зависеть от функции и порядка, который, по вашему мнению, будет самым простым. Однако мы получим один и тот же ответ независимо от порядка.

Давайте сделаем быстрый пример этого типа тройного интеграла.

Пример 1. Вычислите следующий интеграл. \[\iiint\limits_{B}{{8xyz\,dV}} \hspace{0,5in} B = \left[ {2,3} \right] \times \left[ {1,2} \right] \ раз \влево[ {0,1} \вправо]\]

Показать решение

Чтобы подчеркнуть, что порядок не имеет значения, давайте воспользуемся порядком, отличным от указанного выше. Считаем интеграл в следующем порядке. {{\,2}}{{10y\,dy}} = 15\конец{выравнивание*}\]

Прежде чем перейти к более общим областям, давайте получим хорошую геометрическую интерпретацию тройного интеграла, чтобы мы могли использовать его в некоторых следующих примерах.

Факт

Объем трехмерной области $E$ определяется интегралом,

\[V = \iiiint\limits_{E}{{\,dV}}\]

Теперь перейдем к более общим трехмерным областям. У нас есть три различных возможности для общей области. Вот набросок первого варианта.

В этом случае мы определяем область $E$ следующим образом:

\[E = \left\{ {\left( {x,y,z} \right)|\left( {x,y} \right) \in D,\,\,\,{u_1}\left( {x,y} \right) \le z \le {u_2}\left( {x,y} \right)} \right\}\]

где $\left( {x,y} \right) \in D$ — запись, означающая, что точка $\left( {x,y} \right)$ лежит в области $ D$ из $xy$-плоскости. В этом случае мы вычислим тройной интеграл следующим образом:

\[\iiint\limits_{E}{{f\left( {x,y,z} \right)\,dV}} = \iint\limits_{D}{{\left[ {\int_{{\, {u_1}\left( {x,y} \right)}}^{{\,{u_2}\left( {x,y} \right)}}{{f\left( {x,y,z} \right)\,dz}}} \right]\,dA}}\]

, где двойной интеграл можно вычислить любым из методов, которые мы видели в предыдущих парах разделов. Другими словами, мы можем сначала проинтегрировать по $x$, мы можем сначала проинтегрировать по $y$, или мы можем использовать полярные координаты по мере необходимости.

Пример 2. Вычислите $\displaystyle \iiint\limits_{E}{{2x\,dV}}$, где $E$ — область под плоскостью $2x + 3y + z = 6$, которая лежит в первый октант.

Показать решение

Сначала мы должны определить октант . Точно так же, как двухмерная система координат может быть разделена на четыре квадранта, трехмерная система координат может быть разделена на восемь октантов. Первый октант — это октант, в котором все три координаты положительны.

Вот набросок самолета в первом октанте.

Теперь нам нужно определить область $D$ в $xy$-плоскости. Мы можем получить визуализацию области, притворившись, что смотрим прямо на объект сверху. То, что мы видим, будет областью $D$ в $xy$-плоскости. Таким образом, $D$ будет треугольником с вершинами в точках $\left({0,0} \right)$, $\left({3,0} \right)$ и $\left ( {0,2} \справа)$. Вот набросок $D$.

Теперь нам нужны пределы интегрирования. Поскольку мы находимся под плоскостью и в первом октанте (то есть мы над плоскостью $z = 0$) у нас есть следующие пределы для $z$.

\[0 \le z \le 6 — 2x — 3y\]

Мы можем проинтегрировать двойной интеграл по $D$, используя любой из следующих двух наборов неравенств.

\[\начать{матрицу} \begin{выровнено} & \,\,\,\,\,\,0\le x\le 3 \\ & 0\le y\le -\frac{2}{3}x+2 \\ \end{выровнено} & \hspace{0,5 дюйма} & \begin{выровнено} & 0\le x\le -\frac{3}{2}y+3 \\ & \,\,\,\,\,\,0\le y\le 2 \\ \конец{выровнено} \\ \конец{матрица}\] 93\\ & = 9\конец{выравнивание*}\]

Давайте теперь перейдем ко второй возможной трехмерной области, с которой мы можем столкнуться для тройных интегралов. Вот набросок этого региона.

Для этой возможности мы определяем область $E$ следующим образом:

\[E = \left\{ {\left( {x,y,z} \right)|\left( {y,z} \right) \in D,\,\,\,{u_1}\left( {y,z} \right) \le x \le {u_2}\left( {y,z} \right)} \right\}\]

Итак, область $D$ будет областью в плоскости $yz$. Вот как мы будем вычислять эти интегралы. 9{{\,{u_2}\left( {y,z} \right)}}{{f\left( {x,y,z} \right)\,dx}}} \right]\,dA}} \]

Как и в первом случае, у нас будет два варианта выполнения двойного интеграла в плоскости $yz$, а также возможность использования полярных координат, если это необходимо.

Пример 3. Определить объем области, лежащей за плоскостью $x + y + z = 8$ и перед областью в плоскости $yz$, ограниченной $\displaystyle z = \ frac{3}{2}\,\,\sqrt y $ и $\displaystyle z = \frac{3}{4}y$.

Показать решение

В данном случае нам дали $D$, так что нам не нужно особо работать, чтобы его найти. Вот набросок области $D$, а также краткий набросок плоскости и кривых, определяющих $D$, спроецированных за плоскость, чтобы мы могли понять, с какой областью мы имеем дело. похоже.

Теперь с графиком региона выше все в порядке, но он не показывает нам, что это за регион. Итак, вот набросок самого региона. 94 = \frac{{49}}{5}\end{align*}\]

Теперь нам нужно взглянуть на третью (и последнюю) возможную трехмерную область, с которой мы можем столкнуться для тройных интегралов. Вот набросок этого региона.

В этом последнем случае $E$ определяется как

\[E = \left\{ {\left( {x,y,z} \right)|\left( {x,z} \right) \in D,\,\,\,{u_1}\left( {x,z} \right) \le y \le {u_2}\left( {x,z} \right)} \right\}\]

и здесь область $D$ будет областью в плоскости $xz$. Вот как мы будем вычислять эти интегралы. 92}\) и плоскость $y = 8$.

Показать решение

Вот эскиз тела $E$. 2} = 4\]

Эта область, как и подынтегральная функция, похоже, предполагают, что мы должны использовать что-то вроде полярных координат. Однако мы находимся в плоскости $xz$ и видим только полярные координаты в плоскости $xy$. Это не является проблемой. Мы всегда можем «перевести» их на плоскость $xz$ со следующим определением.

\ [x = r \ cos \ theta \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} z = r \ sin \ theta \]

Поскольку в регионе нет $y$, мы будем использовать $z$ вместо $y$ во всех формулах. Обратите внимание, что эти определения также приводят к формуле 9{{\,2\pi}}{{\frac{{128}}{{15}}\,d\theta}}\\ & = \frac{{256\sqrt 3 \,\pi}}{{ 15}}\конец{выравнивание*}\]

Примеры тройных интегралов — Math Insight

Пример 1

Длина стороны куба равна 4. Пусть один угол лежит на начало координат и смежные углы лежат на положительных $x$, $y$ и $z$ оси. 2 \le \frac{1}{2} \label{shadow} \end{выравнивание} удовлетворен. Это неравенство описывает тень рожка мороженого, которая представляет собой множество точек $(x,y)$, лежащих на диске радиуса $1/\sqrt{2}$, как показано ниже. 92}} дз\,ди\,дх. \конец{выравнивание*} Мы не будем пытаться вычислить этот интеграл в прямоугольной форме. координаты. Как только вы научитесь заменять переменные в тройных интегралах, вы сможете прочитайте, как вычислить интеграл, используя сферические координаты.

Пример 4

Найти объем тетраэдра, ограниченного координатой плоскости и плоскости через $(2,0,0)$, $(0,3,0)$ и $(0,0,1)$.

Загрузка апплета

Тетраэдр. Тетраэдр ограничен координатными плоскостями ($x=0$, $y=0$ и $z=0$) и плоскостью, проходящей через три точки (2,0,0), (0,3,0 ) и (0,0,1).

Дополнительная информация об апплете.

Решение : Мы знаем уравнения для трех поверхностей тетраэдра, так как они являются уравнениями для координатных плоскостей: $x=0$, $y=0$ и $z=0$. В качестве начального шага мы можем найти уравнение для наклонной плоскости. Вы можете следить процедура во втором примере формирующей плоскости, чтобы вычислить, что плоскость задается уравнением \начать{выравнивать} 3x + 2y + 6z = 6. \label{plane_equation} \end{выравнивание}

Чтобы найти пределы тетраэдра, мы снова воспользуемся методом теней, но на этот раз будем считать ось $y$ вертикальной осью. Вы можете представить, что солнце, отбрасывающее тень, находится в какой-то точке далеко на положительной оси $y$.

При такой ориентации тень тетраэдра является максимальным диапазоном $x$ и $z$ по тетраэдру. Поскольку тетраэдр расширяется в направлениях $x$ и $z$ при уменьшении $y$, тень тетраэдра является в точности основанием тетраэдра в плоскости $xz$ (плоскость $y=0$), который представляет собой треугольник, изображенный ниже.

К интегралу по этой тени подходим как к двойному интегралу. В этой тени (и, следовательно, в самом тетраэдре) полный пробег $z$ равен \начать{выравнивать*} 0 \le z \le 1. \конец{выравнивание*} Чтобы найти диапазон $x$ для каждого значения $z$, вы можете рассчитать по фигуре тени, что верхний предел $x$ — это линия $z=1-x/2$ или $x=2 (1-я)$. Учитывая, что нижний предел $x$ равен нулю, диапазон $x$ в тени для заданного $z$ равен \начать{выравнивать*} 0 \le x \le 2(1 — z). \конец{выравнивание*} В качестве альтернативы вы могли видеть, что верхний предел $x$ соответствует плоскость, заданная уравнением \eqref{plane_equation} при $y=0$. Подключаем $y=0$ в уравнение \eqref{plane_equation} дает $3x + 6z=6$ или $x = 2(1-z)$.

Для каждого значения $x$ и $z$ в тени нам нужно проинтегрировать $y$ снизу вверх (рассматривая $y$ как вертикальную ось). С этой точки зрения низ находится в плоскости $y=0$, а верх — наклонная плоскость уравнения \eqref{plane_equation}, которое мы можем решить для $y$ записать как $y=3(1-x/2-z)$. Следовательно, для заданных $z$ и $x$ диапазон $y$ \начать{выравнивать*} 0 \le y \le 3\left(1 — \frac{x}{2} — z\right). \конец{выравнивание*}

Чтобы найти объем, интегрируем функцию 1 по этой области: \начать{выравнивать*} &\int_0^1 \int_0^{2(1-z)} \int_0^{3(1-x/2-z)} dy \, dx \, dz\\ &\qquad = \int_0^1 \int_0^{2(1-z)} 3\left(1 — \frac{x}{2} — z \right) dx \, дз\\ &\qquad = \int_0^1 3\left. 1\right.\\ &\qquad = 3\left(1 — 1 +\frac{1}{3}\right) = 3\left(\frac{1}{3}\right) = 1. \конец{выравнивание*} 9{3(1-x/2-z)} dy \, dx \, dz, \конец{выравнивание*} так что порядок будет $dx \, dy \, dz$.

Решение : Один из способов изменить порядок интегрирования — построить график тетраэдра из пределов интеграла, а затем повторить процедуру примера 4, но пусть тень отбрасывается от положительного $x$ -ось. Вместо этого мы проиллюстрируем альтернативную процедуру вычисления новых пределов непосредственно из неравенств старых пределов.

Если $y$ будет средним интегралом, нам нужны пределы $y$ через $z$ (независимо от $x$).

Для данного $z$, насколько большим может быть диапазон $y$? Из приведенных выше пределов мы знать \начать{выравнивать*} 0 \le y \le 3\left(1 — \frac{x}{2} — z\right). \конец{выравнивание*} Диапазон самый большой, когда $x=0$, поэтому \начать{выравнивать*} 0 \le y \le 3\влево(1 — z\вправо) \конец{выравнивание*}

Затем, учитывая $z$ и $y$, нам нужно знать диапазон $x$. следующее соотношение должно оставаться верным: \начать{выравнивать*} y \le 3\left(1 — \frac{x}{2} — z\right). \конец{выравнивание*} Мы можем переписать это соотношение в терминах $x$ как \начать{выравнивать*} \frac{3x}{2} \le 3 — 3z -y, \конец{выравнивание*} или же \начать{выравнивать*} x \le 2\left(1 — z — \frac{y}{3}\right). \конец{выравнивание*} 9{2(1-z-y/3)} dx\, dy \, dz. \конец{выравнивание*}

Другие примеры

Другие примеры вычисления тройных интегралов можно найти на страницах, описывающих теневой метод и метод сечений для определения границ интегрирования.

15.4: Тройные интегралы — Математика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 2612

Гилберт Стрэнг и Эдвин «Джед» Герман
OpenStax

Цели обучения

Распознать, когда функция трех переменных является интегрируемой по прямоугольному блоку.
Вычислите тройной интеграл, представив его в виде повторного интеграла.

Распознайте, когда функция трех переменных интегрируема в замкнутой и ограниченной области. 93\) как

\[B = \big\{(x,y,z)\,|\,a \leq x \leq b, \, c \leq y \leq d, \, e \leq z \leq f \большой\}. \nonumber \]

Мы следуем той же процедуре, что и ранее. Разделим интервал $[a,b]$ на $l$ подинтервалов $[x_{i-1},x_i]$ одинаковой длины $\Delta x$ с

\[\ Delta x = \dfrac{x_i — x_{i-1}}{l}, \nonumber \]

разделить интервал $[c,d]$ на $m$ подинтервалов $[y_{i -1}, y_i]$ одинаковой длины $\Delta y$ с

\[\Delta y = \dfrac{y_j — y_{j-1}}{m}, \nonumber \] 9*)\,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber \], если этот предел существует.

Когда тройной интеграл существует на $B$, функция $f(x,y,z)$ называется интегрируемой на $B$. Кроме того, тройной интеграл существует, если $f(x,y,z)$ непрерывен на $B$. Поэтому в наших примерах мы будем использовать непрерывные функции. 2)\, dx \, dy \, dz. \номер\] 92 yz \,dV \nonumber \]

где $B = \big\{(x,y,z)\,|\, — 2 \leq x \leq 1, \, 0 \leq y \leq 3 , \, 1 \leq z \leq 5 \big\} $, как показано на рисунке $\PageIndex{2}$.

Рисунок $\PageIndex{2}$: вычисление тройного интеграла по заданному прямоугольному блоку.

Решение

Порядок не указан, но повторный интеграл можно использовать в любом порядке без изменения уровня сложности. Выберите, скажем, сначала интегрировать $y$, затем $x$, а затем $z$.

93 =18(9-0) =162.\end{align*}\]

Упражнение $\PageIndex{1}$

Вычисление тройного интеграла

\[\iiint_B z \, \sin \, x \, \cos \, y \, dV\nonumber \]

где $B = \big\{(x,y,z)\,|\,0 \leq x \leq \pi, \, \ dfrac{3\pi}{2} \leq y \leq 2\pi, \, 1 \leq z \leq 3 \big\}$.

Подсказка

Выполните действия, описанные в предыдущем примере.

Ответить

\[\iiint_B z \, \sin \, x \, \cos \, y \, dV = 8 \nonumber \] 9{u_2(y,z)} f(x,y,z) \, dx \right] \, dA. 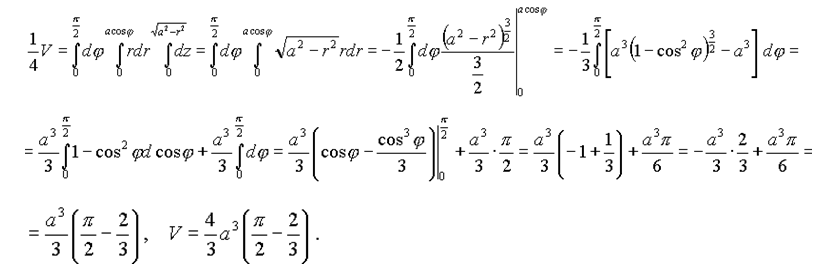\nonumber \]

Обратите внимание, что область $D$ на любой из плоскостей может относиться к типу I или типу II, как описано ранее. Если $D$ в $xy$-плоскости относится к типу I (рис. $\PageIndex{4}$), то

\[E = \big\{(x,y,z) \,|\,a \leq x \leq b, \, g_1(x) \leq y \leq g_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big \}. \nonumber \]

Рисунок $\PageIndex{4}$: Блок $E$, где проекция $D$ на $xy$-плоскость имеет тип I.

Тогда тройной интеграл становится 9{z=u_2(x,y)} f(x,y,z)\,dz \, dx \, dy. \nonumber \]

Пример $\PageIndex{3A}$: вычисление тройного интеграла по общей ограниченной области

Вычисление тройного интеграла функции $f(x,y,z) = 5x — 3y\ ) над сплошным тетраэдром, ограниченным плоскостями \(x = 0, \, y = 0, \, z = 0$ и $x + y + z = 1$.

Решение

На рисунке $\PageIndex{6}$ показан объемный тетраэдр $E$ и его проекция $D$ на $xy$-плоскость.

Рисунок $\PageIndex{6}$: тело $E$ имеет проекцию $D$ на $xy$-плоскость типа I.

9{z=1-x-y}(5x — 3y)\,dz \, dy \, dx = \dfrac{1}{12}.\nonumber \]

Так же, как мы использовали двойной интеграл \[\iint_D 1 \ ,dA \nonumber \] чтобы найти площадь общей ограниченной области $D$ мы можем использовать \[\iiint_E 1\,dV \nonumber \] чтобы найти объем общей сплошной ограниченной области $E$ . Следующий пример иллюстрирует метод.

Пример $\PageIndex{3B}$: нахождение объема путем вычисления тройного интеграла

Найдите объем правильной пирамиды с квадратным основанием в плоскости $xy$ $[-1, 1] \times [-1,1]$ и вершина в точке $(0, 0, 1)$, как показано на следующем рисунке.

Рисунок $\PageIndex{7}$: Нахождение объема пирамиды с квадратным основанием.

Решение

В этой пирамиде значение $z$ меняется от 0 до 1 и на каждой высоте $z$ поперечное сечение пирамиды при любом значении $z$ равно квадрату

\[[-1 + z, \, 1 — z] \times [-1 + z, \, 1 — z].\nonumber \]

Следовательно, объем пирамиды равен \[\iiint_E 1\ ,dV\nonumber \] где

\[E = \big\{(x,y,z)\,|\,0 \leq z \leq 1, \, -1 + z \leq y \leq 1 — z, \, -1 + z \leq x \leq 1 — z \big\}. {x=3} \int_{y=-\sqrt{92}} 1\,dz \, dy \, dx \\ = 36 \pi \,\text{кубических единиц}. \конец{выравнивание*}\]

Изменение порядка интегрирования

Как мы уже видели в двойных интегралах по общим ограниченным областям, изменение порядка интегрирования делается довольно часто для упрощения вычислений. При тройном интеграле по прямоугольному ящику порядок интегрирования не меняет уровень сложности вычисления. Однако с тройным интегралом по общей ограниченной области выбор подходящего порядка интегрирования может немного упростить вычисления. Иногда изменение полярных координат также может быть очень полезным. Здесь мы демонстрируем два примера. 9{z=y} f(x,y,z)\,dz\,dy\,dx. \nonumber \]

Порядок интегрирования здесь первый относительно z , затем y , а затем x . Выразите этот интеграл, изменив порядок интегрирования так, чтобы он был сначала по $x$, затем по $z$, а затем по $y$. Убедитесь, что значение интеграла такое же, если мы допустим $f (x, y, z) = xyz$.

Решение

Лучший способ сделать это — нарисовать область $E$ и ее проекции на каждую из трех координатных плоскостей. Итак, пусть 9{2\pi} \dfrac{64}{15} \,d\theta = \dfrac{128\pi}{15}\nonumber \]

Среднее значение функции трех переменных

Напомним, что мы нашли среднее значение функции двух переменных путем вычисления двойного интеграла по области на плоскости и последующего деления на площадь области. Точно так же мы можем найти среднее значение функции от трех переменных, вычислив тройной интеграл по сплошной области и затем разделив его на объем твердого тела.

Среднее значение функции трех переменных

Если $f(x,y,z)$ интегрируема по сплошной ограниченной области $E$ с положительным объемом $V \, (E),$, то среднее значение функции равно

\[f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \, dV. \nonumber \]

Обратите внимание, что объем равен

\[V \, (E) = \iiint_E 1 \,dV. {z=1-xy} (xy + 8z + 20 ) \, dz \, dy \, dx = \dfrac{147}{40}. \номер\] 9{z=1-x-y} 1 \,dz \, dy \, dx = \dfrac{1}{6}. \nonumber \]

Следовательно, среднее значение равно

\[ T_{ave} = \dfrac{147/40}{1/6} = \dfrac{6(147)}{40} = \dfrac{441} {20} \, \text{°}\text{C} \nonumber \].

Упражнение $\PageIndex{6}$

Найдите среднее значение функции $f(x,y,z) = xyz$ по кубу со стороной 4 единицы в первом октанте с одной вершина в начале координат и ребра параллельны осям координат.

Подсказка: Выполните действия, описанные в предыдущем примере.
Ответить: $f_{ср.} = 8$

Эта страница под названием 15.4: Тройные интегралы распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Странгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
ОпенСтакс
Лицензия
CC BY-NC-SA
Версия лицензии
4,0
Программа OER или Publisher
ОпенСтакс
Показать страницу Содержание
нет
Теги
1. автор @ Эдвин «Джед» Герман
2. автор@Гилберт Странг
3. Фубини там
4. источник@https://openstax. org/details/books/calculus-volume-1
5. тройной интеграл

Как вычислять повторные тройные интегралы — Криста Кинг Математика

Что такое тройной повторный интеграл?

Повторные интегралы — это двойные или тройные интегралы, пределы интегрирования которых уже указаны.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее. 92\дВ???

Вместо тройного повторного интеграла (где слово повторный указывает на наличие пределов интегрирования) мы просто называем его тройным интегралом. Поскольку мы не можем решить тройной интеграл, не найдя пределы интегрирования, мы вычислим пределы интегрирования для каждой переменной, а затем добавим их в тройной интеграл, чтобы превратить его в тройной повторный интеграл. 2???, ???y=0??? и ???х=2???. 92\право]???.

Поскольку объем, для которого мы рассчитываем, находится в верхней части области, показанной выше, в плоскости ???xy???, мы знаем, что нижний предел интегрирования для ???z??? ???0???. Так как объем лежит под ???z=x+y-1???, то верхний предел интегрирования будет ???x+y-1???, значит, ???z??? определяется на интервале ???[0,x+y-1]???.

Вообще говоря, мы накладываем самые сложные пределы интегрирования на самый внутренний интеграл и простейшие пределы интегрирования на самый внешний интеграл. Поскольку пределы интегрирования для ???z??? определены в терминах двух переменных, мы поместим их в самый внутренний интеграл. Пределы интегрирования для ???y??? определяются в терминах одной переменной, поэтому они будут следующими. Поскольку пределы интегрирования для ???x??? являются константами, они будут последними в самом внешнем интеграле. 98\право]???

???\frac{7}{27}(512)+\frac{7}{40}(1,024)-\frac{7}{24}(256)???

???7(256)\влево[\frac{1}{27}(2)+\frac{1}{40}(4)-\frac{1}{24}\right]???

???1792\влево(\frac{2}{27}+\frac{1}{10}-\frac{1}{24}\right)???

???1,792\left[\frac{2}{27}\left(\frac{80}{80}\right)+\frac{1}{10}\left(\frac{216}{216) }\right)-\frac{1}{24}\left(\frac{90}{90}\right)\right]???

???1,792\влево(\frac{160}{2,160}+\frac{216}{2,160}-\frac{90}{2,160}\right)???

???1,792\влево(\фракция{286}{2160}\вправо)???

???1,792\влево(\frac{143}{1,080}\вправо)???

???891\влево(\frac{143}{540}\вправо)???

???\фракция{127,413}{540}???

???\frac{4,719}{20}???

Это значение тройного интеграла.

Получить доступ к полному курсу Calculus 3

Начать

Изучайте математикуКриста Кинг 6 февраля 2021 г. математика, учитесь онлайн, онлайн-курс, онлайн-математика, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерное исчисление, исчисление iii, исчисление 3, исчисление iii, вычисление 3, повторные тройные интегралы, повторные интегралы, тройные интегралы, кратные интегралы

0 лайков

15.5 Тройные интегралы

Неудивительно, что мы также можем делать тройные интегралы — интегралы по трехмерной области. Простейший Приложение позволяет нам вычислять объемы альтернативным способом.

Чтобы аппроксимировать объем в трех измерениях, мы можем разделить трехмерную область на маленькие прямоугольные блоки, каждый $\Delta x\times\Delta y\times\Delta z$ с объемом $\Дельта х\Дельта у\Дельта z$. 2 =1.\кр }$$ $\квадрат$ 92) \; dV$ является максимальным.

Тройной интеграл – определение, общие формы и примеры

С помощью тройных интегралов мы теперь можем расширить наше понимание повторных интегралов до выражений и функций с тремя переменными. Мы можем использовать тройные интегралы для вычисления объема и массы различных объектов — важных компонентов, необходимых нам в физике, проектировании конструкций и других областях. Вот почему важно понимать тройные интегралы, если мы хотим работать с настройками, в которых теперь есть три переменных компонента. Тройные интегралы представляют собой повторение функций с тремя переменными, $\boldsymbol{f(x, y, z)}$. Вместо интегрирования нашей функции по заданной площади мы теперь интегрируем ее по трехмерной фигуре, имеющей объем. На этом этапе важно, чтобы вы были знакомы с тем, как мы настраиваем и оцениваем повторные и двойные интегралы. Откройте встроенные ссылки в отдельной вкладке или окне, если вам нужно немедленно освежить в памяти. В этой статье мы покажем вам, как мы можем визуализировать и понять, что представляют собой тройные интегралы. Мы также подробно объясним, как вычислять различные тройные интегралы. К концу обсуждения вы также должны научиться решать задачи, связанные с тройными интегралами. Вы готовы? Давайте начнем с визуализации тройных интегралов в трехмерных системах координат, а затем используем эти представления для их определения.

Что такое тройной интеграл?

Тройной интеграл — это повторный интеграл с тремя переменными и по трехмерной области. Мы можем рассматривать определение тройных интегралов как расширение определения двойных интегралов, но на этот раз мы интегрируем по объему, а не по площади. Подобно двойным интегралам, мы можем начать с простого тройного интеграла: разделить прямоугольное пространство на меньшие прямоугольники со следующими размерами: $\Delta x \times \Delta y \times \Delta z$. {b} f(x, y, z) \phantom{x} dxdydz \end{выровнено} Это обычная форма, с которой мы столкнемся при работе с тройными интегралами, но в целом существует шесть возможных форм для тройных интегралов. Теперь давайте посмотрим, как изменится выражение для тройного интеграла, когда мы будем работать с более сложными областями, такими как показанная ниже. Предположим, что сейчас мы интегрируем функцию по общей области $S$. На изображении выше показана область $S$ в пространстве, параллельная оси $z$. Эта область ограничена областью, обозначенной как $T$, и является проекцией $S$ на плоскость $xy$. \begin{align}T &= \{(x, y, z) | (x, y) \in T, z_1(x, y) \leq z \leq z_2(x, y)\}\end{aligned} Это обозначение выделяет условия для $S$ и $T$, а также пределы интегрирования для $z$, определяемые двумя другими переменными: $x$ и $y$. Мы используем эти ограничения для определения тройного интеграла от $f(x, y, z)$ по пространству $S$. \begin{aligned}\int \int \int_S f(x, y, z) \phantom{x} dV &= \int \int \int_{z_1(x, y)}^{z_2(x, y)} \фантом{х} dA\конец{выровнено} Как мы узнали в прошлом, мы интегрируем оставшийся двойной интеграл по $dA$, интегрируя по $x$, а затем по $y$. {z_2(x, y)} \phantom{x} dA\end{выровнено} Есть еще две возможные трехмерные фигуры, с которыми можно столкнуться при работе с тройными интегралами: пространство, имеющее проецируемую область на плоскость $xz$, и пространство, которое можно спроецировать на плоскость $yz$. \begin{align}\boldsymbol{xz}\textbf{-plane} &: \{S = {(x, z) \in T, y_1(x, z) \leq y_2(x, z)}\}\ \\boldsymbol{yz}\textbf{-плоскость} &: \{S = {(y, z) \in T, x_1(y, z) \leq x_2(y, z)}\}\end{aligned} Теперь мы работаем с тремя переменными, каждый раз проецируя двумерную фигуру. Это означает, что мы ожидаем шесть возможных повторных интегралов в декартовой форме, и мы можем найти все шесть комбинаций, поменяв местами $dx$, $dy$ и $dz$. 9{\ displaystyle {\ text {Результирующая функция выражена в $z $}}}} dz \ end {выровнено} Подобно двойным интегралам, границы самого внутреннего интеграла определяются остальными переменными. Эти границы представляют собой область, которую мы помечаем как $T$. Теперь, когда мы показали вам различные способы определения тройных интегралов, пришло время узнать, как мы можем установить пределы интегрирования для тройных интегралов и, в конечном итоге, научиться их вычислять.

Как решать тройные интегралы?

Используйте повторную форму тройного интеграла, чтобы вычислить функцию относительно $x$, $y$ и $z$. Вот несколько общих советов, которые следует помнить при работе с тройными интегралами:

Правильно настройте три пары пределов интегрирования.
Интегрировать функцию по самой внутренней переменной – от самой внутренней к самой внешней.
При интеграции функций работайте только с одной переменной, а остальные переменные рассматривайте как константы.
Оцените полученное выражение в заданных границах, затем повторите процесс, пока мы не проинтегрируем его три раза подряд.

Сложность процесса на самом деле будет зависеть от заданных значений. Как и ожидалось, интегрирование функции $f(x, y, z)$ по прямоугольному блоку будет простым. Это становится более сложной задачей, когда нам нужно интегрировать более сложный регион. В этом разделе мы покажем вам примеры, которые помогут вам понять процесс тройной интеграции. 9{2} 2xyz \phantom{x} dxdydz$ и фактически равно $96$. Давайте теперь рассмотрим более сложный пример — вычисление тройных интегралов по более сложной области.

Нахождение тройного интеграла по общей области

При работе с тройными интегралами, включающими более сложные области, важно учитывать проекцию, которую образует область относительно плоскостей $xy$, $xz$ или $yz$ — в зависимости от того, что подходит для нашей задачи. Поработаем над $\int \int \int_{S} z \phantom{x}dV$, где $S$ — объемная фигура, ограниченная следующими плоскостями: $x = 0$, $y = 0$, $ z = 0$ и $x + y + z = 4$. Полезнее всего набросать два графика: 1) реальную сплошную область $S$ и 2) проекцию $S$ на плоскость (в нашем случае мы будем использовать плоскость $xy$). Теперь левый график представляет собой тетраэдр, определяющий объем, по которому мы интегрируем $z$. Из графика видно, что относительно $x$ наши границы лежат в диапазоне от $z = 0$ до $z = 4-x –y$. 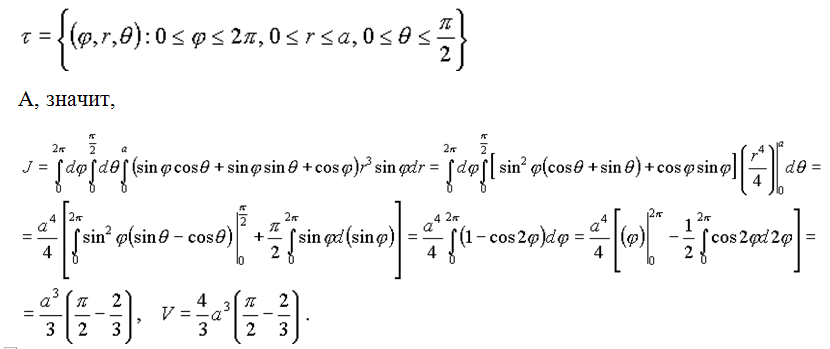{4 – x – y} z \phantom{x}dzdydx$ равно равна $\dfrac{32}{3}$ или приблизительно равна $10,67$. Вы получаете повесить его? Не волнуйтесь, мы подготовили для вас больше примеров — от тройных интегралов с прямоугольными ящиками до интегралов со сложными областями. Когда вы будете готовы работать над другими задачами, перейдите к следующему разделу, чтобы освоить процесс вычисления тройных интегралов! 92} \phantom{x}dV$ равно $\dfrac{324\pi}{5}$ или приблизительно равно $203,58$. Вы также можете попробовать настроить тройной интеграл в декартовой форме и убедиться, что они возвращают одно и то же значение! Пример 4 Одним из важных применений тройных интегралов является нахождение массы, моментов и центра масс твердого тела. Мы можем представить эти компоненты с помощью тройных интегралов, показанных ниже.

9{1}\\&= \dfrac{32\rho}{7} \end{выровнено}

Масса	\begin{align}m &= \int \int \int_{S} \rho(x, y, z) \phantom{x}dV\end{align}
Моменты	\begin{align}M_{yz} &= \int \int \int_{S} x\rho(x, y, z) \phantom{x}dV\\M_{xz} &= \int \int \ int_{S} y\rho(x, y, z) \phantom{x}dV\\M_{xy} &= \int \int \int_{S} z\rho(x, y, z) \phantom{ х}dV\конец{выровнено}
Центр масс	\begin{align}\overline{x} &= \dfrac{M_{yz}}{m} \\\overline{y} &= \dfrac{M_{xz}}{m}\\ \overline{z } &= \dfrac{M_{xy}}{m} \end{align}

Теперь, когда у нас есть моменты, а также масса объекта, мы можем найти координаты его центра масс, используя уравнение $(\overline{x}, \overline{y}, \overline{z}) = \left(\dfrac{M_{yz}}{m}, \dfrac{M_{xz}}{m}, \dfrac{M_{xy}}{m}\right)$.

\begin{выровнено} \boldsymbol{\overline{x}}\end{выровнено}	\begin{выровнено} \boldsymbol{\overline{y}}\end{выровнено}	\begin{выровнено} \boldsymbol{\overline{z}}\end{выровнено}
\begin{align}\overline{x}&= \dfrac{M_{yz}}{m}\\&= \dfrac{\dfrac{128\rho}{7}}{\dfrac{32\ rho}{5}}\\&= \dfrac{20}{7}\end{выровнено}	\begin{align}\overline{x}&= \dfrac{M_{xz}}{m}\\&= \dfrac{0}{\dfrac{32\rho}{5}}\\&= 0 \end{выровнено}	\begin{align}\overline{z}&= \dfrac{M_{xy}}{m}\\&= \dfrac{\dfrac{32\rho}{7}}{\dfrac{32\rho} {5}}\\&= \dfrac{5}{7}\end{выровнено}
\begin{aligned}\boldsymbol{(\overline{x}, \overline{y}, \overline{z})} &= \left(\dfrac{20}{7}, 0, \dfrac{ 5}{7}\справа) \end{выровнено}

Это означает, что центр масс твердого тела находится в точке $\left(\dfrac{20}{7}, 0, \dfrac{5}{7}\right)$. Эта задача показывает лишь одно из многих приложений тройных интегралов.

Как решать тройные интегралы: Вычисление тройных интегралов: теория и примеры

Вычисление тройных интегралов: теория и примеры

Вычислить тройной интеграл самостоятельно, а затем посмотреть решение

Двойные и тройные интегралы

Двойной интеграл

Тройной интеграл

∫∫∫ Тройной интеграл — Калькулятор Он-лайн

Тройные интегралы

Тройные интегралы. Вычисление объема тела

Тройные интегралы. Вычисление объема тела презентация, доклад

Исчисление III. Тройные интегралы

Раздел 4-5: Тройные интегралы

Факт

Примеры тройных интегралов — Math Insight

Пример 1

Пример 4

Загрузка апплета

Другие примеры

15.4: Тройные интегралы — Математика LibreTexts

Цели обучения

Упражнение \(\PageIndex{1}\)

Пример \(\PageIndex{3A}\): вычисление тройного интеграла по общей ограниченной области

Пример \(\PageIndex{3B}\): нахождение объема путем вычисления тройного интеграла

Изменение порядка интегрирования

Среднее значение функции трех переменных

Среднее значение функции трех переменных

Упражнение \(\PageIndex{6}\)

Как вычислять повторные тройные интегралы — Криста Кинг Математика

Что такое тройной повторный интеграл?

Получить доступ к полному курсу Calculus 3

15.5 Тройные интегралы

Тройной интеграл – определение, общие формы и примеры

Что такое тройной интеграл?

Как решать тройные интегралы?

Нахождение тройного интеграла по общей области

Добавить комментарий Отменить ответ