Как определить точку пересечения прямой с плоскостью
Точка пересечения прямой и плоскости
Рассмотрим пошаговую инструкцию построения точки пересечения прямой общего положения с плоскостью общего положения.Отметим, что построение точки пересечения прямой и плоскости — это одна из основ решения задач по предмету начертательная геометрия, не освоив которую дальнейшее понимание предмета будет достаточно трудным.
Порядок построения точки пересечения прямой и плоскости
1. Заключим прямую а во вспомогательную фронтально-проецирующую плоскость (плоскость перпендикулярную фронтальной плоскости проекции). На фронтальной проекции она сольется с прямой а. Очевидно, что линия m пересечения этой плоскости с плоскостью треугольника АВС на фронтальной проекции так же будет сливаться с прямой а (а=m).
2. Определим фронтальные проекции двух точек этой линии m: точки 1 и 2.
3. Найдем их горизонтальные проекции.
4. Соединим горизонтальные проекции точек 1 и 2 — получим горизонтальную проекцию прямой m (которая является линией пересечения вспомогательной плоскости с плоскостью треугольника АВС, и соответственно принадлежит обеим плоскостям). Так как прямая а принадлежит вспомогательной плоскости, и прямая m принадлежит ей же, то точка пересечения этих прямых К и есть точка пересечения прямой а с плоскостью треугольника АВС.
5. С помощью линии связи найдем фронтальную проекцию точки пересечения К.
6. Осталось только определить видимость прямой а. Это можно сделать с помощью метода конкурирующих точек.
Обратите внимание, что мы начали поиск точки пересечения прямой с плоскостью с того, что заключили прямую а во вспомогательную фронтально-проецирующую плоскость. Точно таким же образом можно было заключить прямую а в горизонтально-проецирующую плоскость, и тогда бы построения начались как бы «снизу вверх», но смысл остался бы точно таким же, как и конечное решение — точка пересечения прямой с плоскостью.
Внимание! Для этой темы есть видеоурок.
Вы можете сказать «спасибо!» автору статьи:
пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»
или запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи
или создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение.
А вот это — не реклама. Это напоминание, что каждый из нас может сделать. Если хотите — это просьба. Мы действительно им нужны:
Автор комментария: Дмитрий
Дата: 2012-08-16
Очень легко и понятно вы описали как найти точку пересечения прямой и плоскости, мегареспект!
Автор комментария: Алексндр
Дата: 2012-11-02
Да, теперь осилил
Автор комментария: Студент
Дата: 2012-11-14
Сделайте нормальные чертежи.
Без анимации пошаговые.
Оставляйте адрес, может вам и будет подарок. Новый год ведь скоро 🙂
Автор комментария: Михаил
Дата: 2013-01-31
А вот нечего торопиться. Надо покушать как следует, сесть и всмотреться в гифку. Тогда и познаешь дзен. 🙂
Не торопиться, быть сытым и выспавшимся — да, это отличное подспорье. Спасибо за то, что указали на столь важные моменты. Да прибудет с вами сила, Михаил!
Автор комментария: Настя
Дата: 2013-03-08
Помогите пожалуста. у меня плоскость перпендикулярна фронтальной плоскости проекции и задана следами, а прямая горизонтальна горизонтальной плоскости проекций
Автор комментария: Евгений
Дата: 2014-12-21
Это простооо кул,все понятно,мегареспект вам!!
Автор комментария: Георгий
Дата: 2014-12-28
4. Соединим горизонтальные проекции точек 1 и 2 — получим горизонтальную проекцию прямой m (которая является точкой пересечения вспомогательной плоскости с плоскостью треугольника АВС.
Тут надо исправить: прямая не может являться точкой. Также отсутствует закрывающая скобка.
Автор комментария: Дмитрий
Дата: 2015-05-01
Я всё равно ничего не понял. Хоть на первый взгляд это более толковое объяснение решения, чем пишут в книгах — там ваще мрак.
Автор комментария: Лиля
Дата: 2015-09-22
Высший класс! Ключевое предложение для понимания сути: «Заключим прямую а во вспомогательную фронтально-проецирующую плоскость . «
Эмм. Это сарказм? 🙂 Если да, то в свое оправдание могу сказать лишь то, что терминология должна быть вам в некоторой мере знакома. С меня лишь графический порядок решения. Но с другой стороны давать его в абсолютном отрыве от теории тоже нехорошо. Указанная в вашем комментарии фраза пригодится вам на экзамене, или как минимум на защите данной работы. Но для графического решения прямо сейчас она не так важна. Просто выполняйте по шагам.
Автор комментария: Лия
Дата: 2015-10-22
Автор комментария: Василий
Дата: 2016-10-13
Спасибо огромное.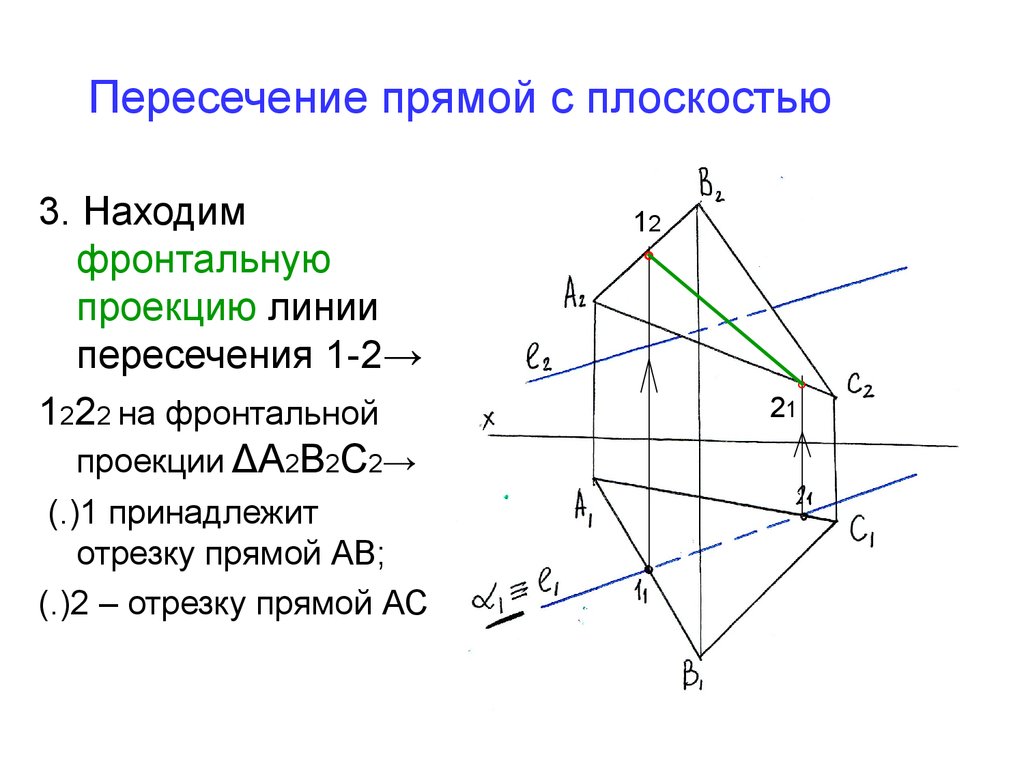
Всё доходчиво и ясно!
Автор комментария: Олег
Дата: 2016-11-17
Как быть если прямая на П2 перпендикулярна Ох, а на П1 в точку проэцируется?
Добавьте свой комментарий:
zakaz@triv >Наша страница в ВК:
работаю преподавателем инженерной графике в техникуме.очень понравился раздел по практике применения. Хотелось бы узнать приемы преподавания начертательной геометрии в соответствие с новыми образовательными стандартами
Для определения точки пересечения прямой с плоскостью пользуемся следующим алгоритмом: прямую заключаем во вспомогательную плоскость, находим линию пересечения этих двух плоскостей (заданной и вспомогательной), и линия пересечения плоскостей в пересечении с заданной прямой даст искомую точку. Последним этапом в построении является определение видимости прямой при помощи конкурирующих точек.
Пример1. Плоскость задана следами (рис.70)
Рис.70
1. Для построения точки пересечения прямой lс плоскостью необходимо через прямую провести вспомогательную плоскость частного положения, например, фронтально-проецирующую β π2, l» fоβ, fоβ – собирающий след, hоβх (рис.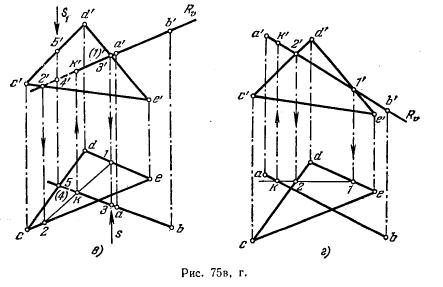
71).
Рис.71
2. Строим линию пересечения MN заданной и вспомогательной плоскости М’=hоα∩ hоβ, N»= fоβ∩ fоα (рис.72).
Рис.72
3. Определяем точку пересечения К заданной прямой l с линией пересечения MN. К’=М’N’∩l ‘, К» – в пересечении линии проекционной связи, проведенной из К’ и l ».
4. Видимость прямой l в случае задания плоскости следами не определяем.
Пример 2. Пересечение прямой с проецирующей плоскостью (рис.73).
При построении точки пересечения прямой с проецирующей плоскостью задача упрощается, т.к. одна из проекций искомой точки будет лежать на собирающем следе. На рис.73 дана горизонтально-проецирующая плоскость. Искомая точка К будет одновременно принадлежать плоскости α и прямой а.
Рис.73
Пример 3. Плоскость задана плоской фигурой (рис.74).
Рис.74
Через прямую l проводим вспомогательную плоскость частного положения, например, горизонтально-проецирующую β π1.
l‘ hоβ, hоβ – собирающий след, fоβх (рис.75).
Рис.75
2. Строим линию пересечения MN заданной и вспомогательной плоскостей. М’=А’С’∩ hоβ М» А»С» и N’=В’С’∩ hоβ N» »ѻ (рис. 76).
3. Строим точку пересечения К заданной прямой l с линией пересечения МN. К»= М»N»∩l». К’ находится в пересечении линии проекционной связи, проведенной из К» и М’N’.
4. Определяем видимость прямой относительно ΔАВС с помощью конкурирующих точек.
Определяем видимость относительно плоскости π2 .Отметим фронтальную проекцию 1» совпадающую с 2». Горизонтальную проекцию 2′ отметим на А’С’, а 1′ на l’. Горизонтальная проекция 1′ лежит перед 2′, следовательно, фронтальная проекция 2» не видима относительно π2. Точка 1 лежит на прямой l, она видима на π2, следовательно, фронтальная проекция l» от 1″2» до К» видима, в точке К» видимость меняется на противоположную.
Определим видимость прямой l относительно плоскости π1. Отметим горизонтальную проекцию 3′, совпадающую с горизонтальной проекцией М’. М» А»С» уже отмечена, 3» l’‘. Фронтальная проекция М» лежит выше фронтальной проекции 3», следовательно, точка М видима относительно π1. Точка 3 лежит на l, следовательно, от М’≡3′ до К’, горизонтальная проекция l’ невидима. В горизонтальной проекции К’ видимость меняется на противоположную. За границами ΔАВС прямая l везде видима.
Рис.76
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9466 — | 7449 — или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
С помощю этого онлайн калькулятора можно найти точку пересечения прямой и плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямой и плоскости задайте вид уравнения прямой («канонический» или «параметрический» ), введите данные в уравнения прямой и плоскости и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Точка пересечения прямой и плоскости − теория, примеры и решения
- Содержание
- 1. Точка пересечения плоскости и прямой, заданной в каноническом виде.
- 2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
- 3. Примеры нахождения точки пересечения прямой и плоскости.
1. Точка пересечения плоскости и прямой, заданной в каноническом виде
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямая L1:
| , | (1) |
| α: Ax+By+Cz+D=0. | (2) |
Найти точку пересечения прямой L1 и плоскости α (Рис.1).
Запишем уравнение (1) в виде системы двух линейных уравнений:
| , | (3) |
| (4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
l1y−p1z=l1y1−p1z1. | (6) |
Решим систему линейных уравнений (2), (5), (6) с тремя неизвестными x, y, z. Для этого в уравнении (2) переведем свободный член в правую часть уравнения и запишем эту систему в матричном виде:
| (7) |
Как решить систему линейных уравнений (11)(или (2), (5), (6)) посмотрите на странице Метод Гаусса онлайн или на примерах ниже. Если система линейных уравнениий (7) несовместна, то прямая L1 и плоскость α не пересекаются. Если система (7) имеет множество решений, то прямая L1 лежит на плоскости α. Единственное решение системы линейных уравнений (7) указывает на то, что это решение определяет координаты точки пересечения прямой L1 и плоскости α.
Замечание. Если прямая задана параметрическим уравнением, то уранение прямой нужно приводить к каноническому виду и применить метод, описанный выше, или же
2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
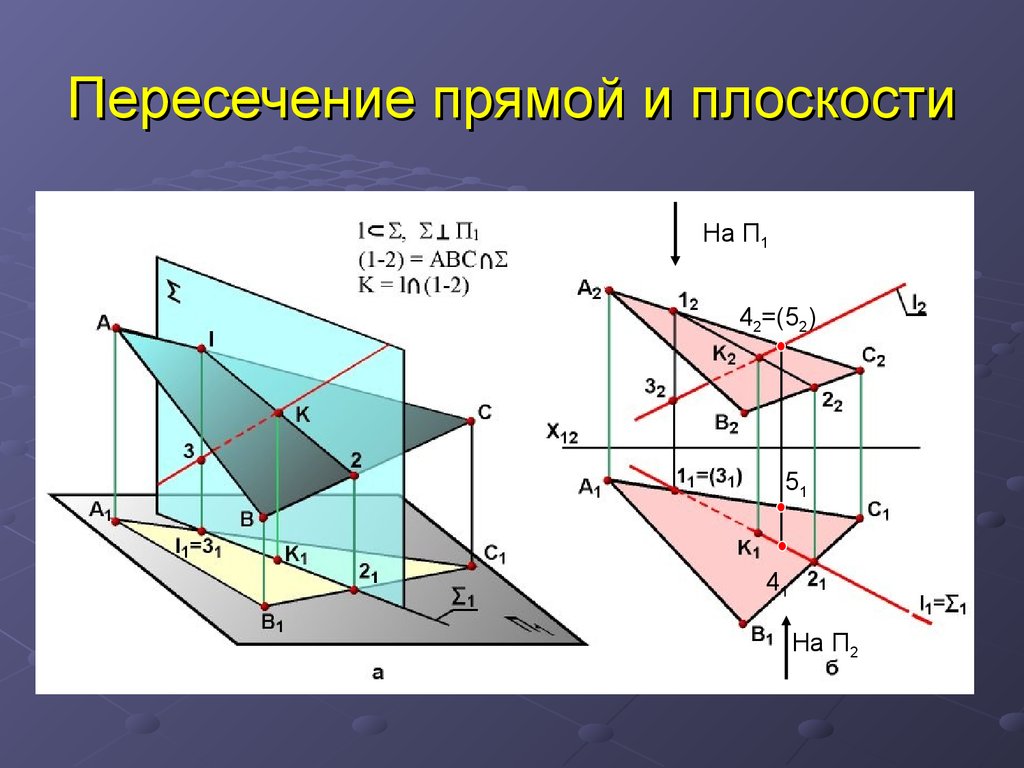
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L1 в параметрическом виде:
| (8) |
| α: Ax+By+Cz+D=0. | (9) |
Задачу нахождения нахождения точки пересечения прямых L1 и плоскости α можно решить разными методами.
Метод 1. Приведем уравнения прямой L1 к каноническому виду.
Для приведения уравнения (8) к каноническому виду, выразим параметр t через остальные переменные:
| (10) |
Так как левые части уравнений (10) равны, то можем записать:
| (11) |
Далее, для нахождения точки пересечения прямой и плоскости нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямой L1 и плоскости α решим совместно уравнения (8) и (9).
Из уравнений (8) подставим x, y, z в (9):
| (13) |
Откроем скобки и найдем t:
| (14) |
Если числитель и знаменатель в уравнении (14) одновременно равны нулю, то это значит, что прямая L1 лежит на полскости α. Если в уравнении (14) числитель отличен от нуля, а знаменатель равен нулю, то прямая и плоскость параллельны.
Если же числитель и знаменатель в уравнении (14) отличны от нуля, то прямая и плоскость пересекаются в одной точке. Для нахождения координат точки пересечения прямой L1 и плоскости α подставим полученное значение t из (14) в (8).
3. Примеры нахождения точки пересечения прямой и плоскости.
Пример 1. Найти точку пересечения прямой L1:
| (15) |
| α: 7x−5y+2z+19=0. | (16) |
Представим уравнение (15) в виде двух уравнений:
| (17) |
| (18) |
Сделаем перекрестное умножение в уравнениях (17) и (18):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| 3x−y=11, | (19) |
2y−3z=−22.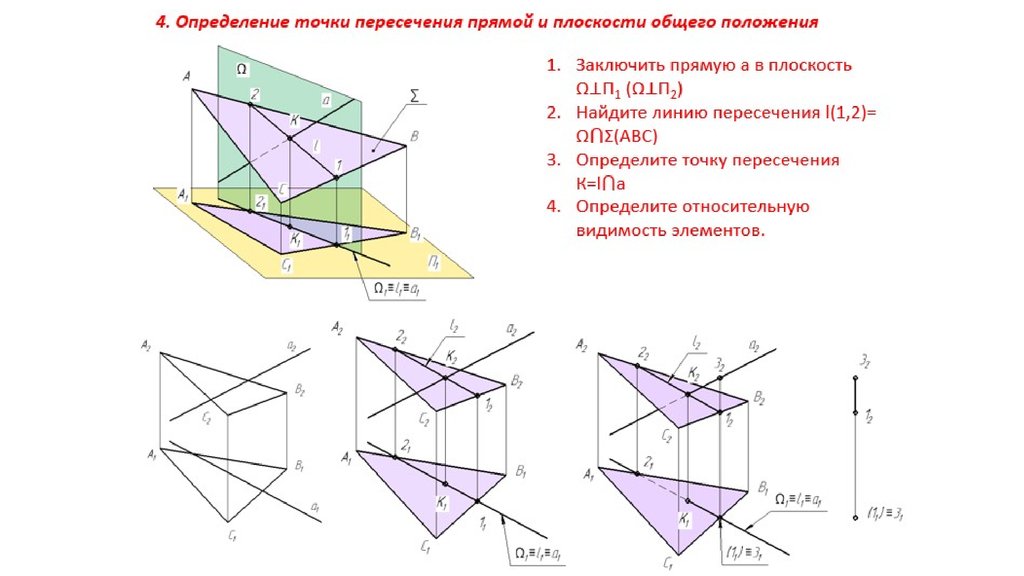 | (20) |
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (19) и (20). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (19) и (20):
| (21) |
Решим систему линейных уравнений (21) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −7/3:
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на 4/3:
Второй этап.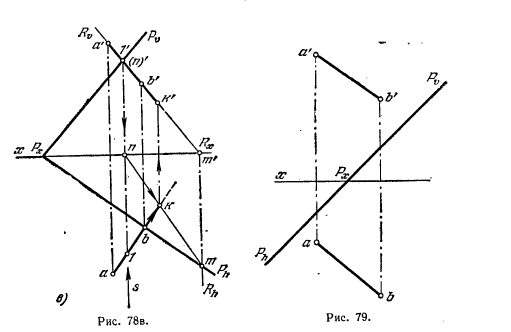
Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −3/2:
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 1/2:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
Ответ. Точка пересечения прямой L1 и плоскости α имеет следующие координаты:
| M (37/2, 89/2, 37). |
Пример 2. Найти точку пересечения прямой L1:
| (22) |
| α: 6x+2y+z+7=0. | (23) |
Представим уравнение (22) в виде двух уравнений:
| (24) |
| (25) |
Сделаем перекрестное умножение в уравнениях (24) и (25):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| −5x−y=8, | (26) |
4y+5z=23. | (27) |
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (26) и (27). Переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (26) и (27):
| (28) |
Решим систему линейных уравнений (21) отностительно x, y, z. Для этого построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 3 со строкой 1, умноженной на 6/5:
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на −1/5:
Из расширенной матрицы восстановим систему линейных уравнений:
| (29) |
Легко можно заметить, что последнее уравнение в (29) несовместна, так как несуществуют такие x, y, z чтобы выполнялось это равенство.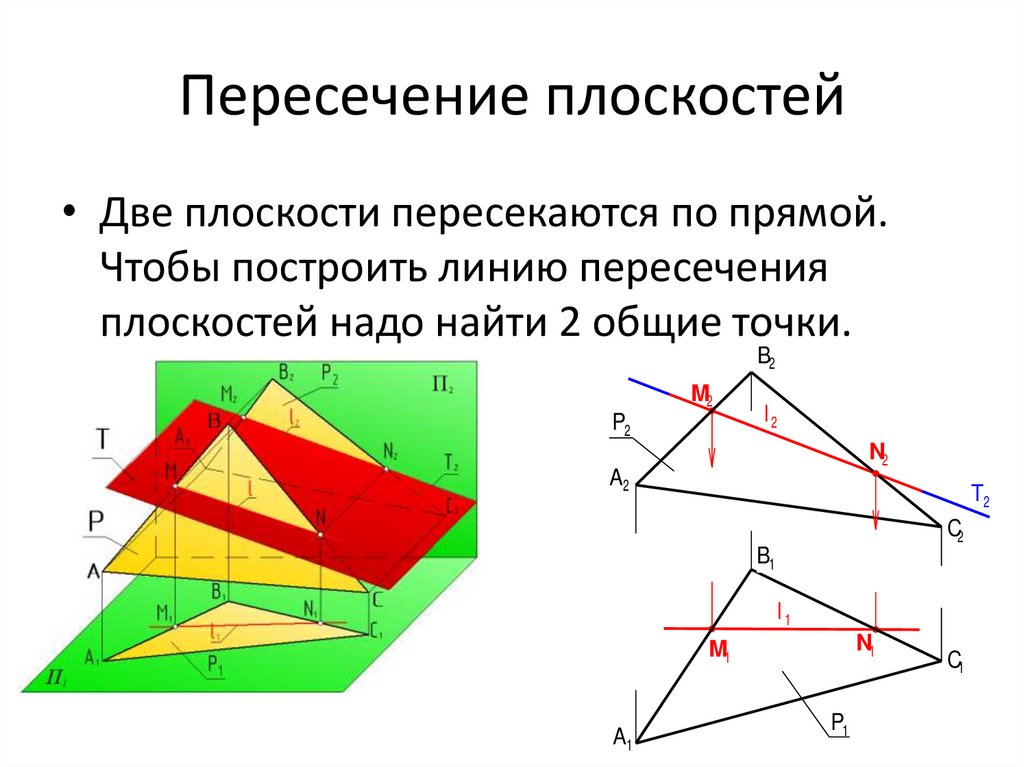
Следовательно система линейных уравнений (2), (26) и (27) несовместна. Тогда прямая L1 и плоскость α не пересекаются, т.е. они параллельны.
Ответ. Прямая L1 и плоскость α параллельны, т.е. не имеют общую точку.
Пример 3. Найти точку пересечения прямой в параметрическом виде L1:
| (30) |
| α: 2x+y−z+11=0. | (31) |
Решение. Для нахождения точки пересечения прямой L1 и плоскости α нужно найти такое значение t, при котором точка M(x, y, z) удовлетворяет уравнению (31). Поэтому подставим значения x, y, z из (30) в (31):
| 2(1+2t)+(−5−5t)−(8−t)+11=0. |
| 2+4t−5−5t−8+t+11=0. | (32) |
Упростив уравнение, получим:
0t=0.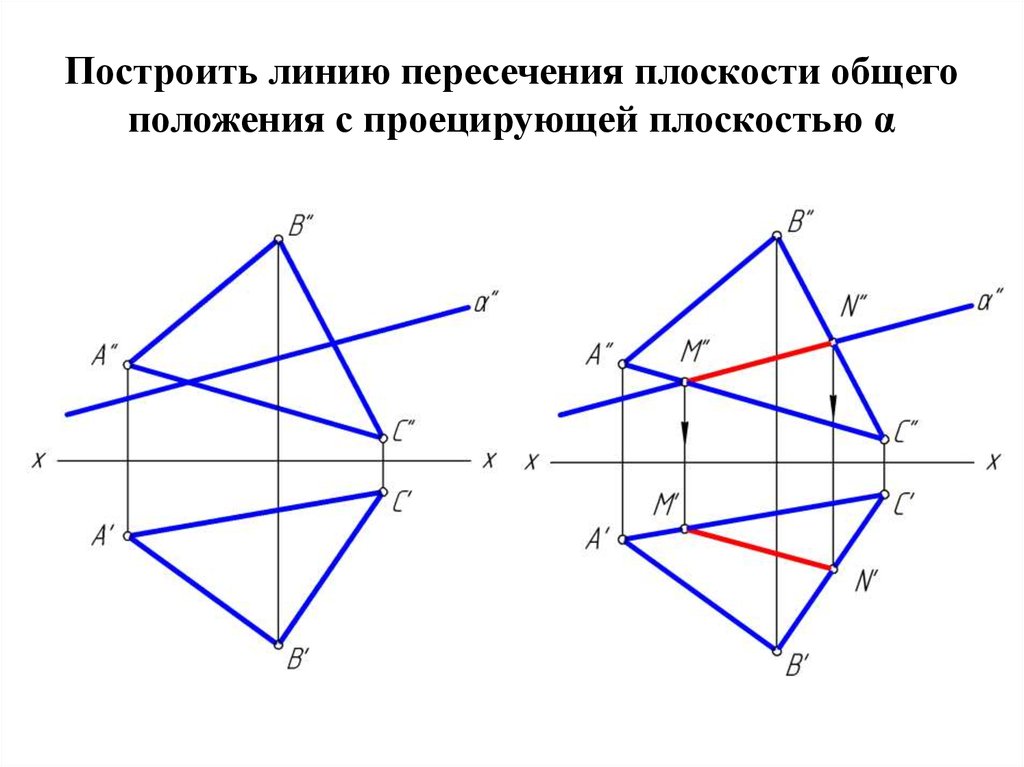 | (33) |
Как видим, любое значение t удовлетворяет уравнению (33), т.е. любая точка на прямой L1 удовлетворяет уравнению плоскости α. Следовательно прямая L1 лежит на плоскости α.
Ответ. Прямая L1 лежит на плоскости α.
Определение точки пересечения прямой с плоскостью
Для определения точки пересечения прямой с плоскостью пользуемся следующим алгоритмом: прямую заключаем во вспомогательную плоскость, находим линию пересечения этих двух плоскостей (заданной и вспомогательной), и линия пересечения плоскостей в пересечении с заданной прямой даст искомую точку. Последним этапом в построении является определение видимости прямой при помощи конкурирующих точек.
Пример1. Плоскость задана следами (рис.70)
Рис.70
1.
Для построения точки пересечения прямой l с плоскостью необходимо через прямую
провести вспомогательную плоскость
частного положения, например,
фронтально-проецирующую βπ2, l»fоβ,
fоβ – собирающий след, hоβх
(рис.
71).
Рис.71
2. Строим линию пересечения MN заданной и вспомогательной плоскости М’=hоα∩ hоβ, N»= fоβ∩ fоα (рис.72).
Рис.72
3. Определяем точку пересечения К заданной прямой l с линией пересечения MN. К’=М’N’∩l ‘, К» – в пересечении линии проекционной связи, проведенной из К’ и l ».
4. Видимость прямой l в случае задания плоскости следами не определяем.
Пример 2. Пересечение прямой с проецирующей плоскостью (рис.73).
При построении точки пересечения прямой с проецирующей плоскостью задача упрощается, т.к. одна из проекций искомой точки будет лежать на собирающем следе. На рис.73 дана горизонтально-проецирующая плоскость. Искомая точка К будет одновременно принадлежать плоскости α и прямой а.
Рис.73
Пример
3.
Плоскость
задана плоской фигурой (рис.74).
Рис.74
Через прямую l проводим вспомогательную плоскость частного положения, например, горизонтально-проецирующую βπ1.l‘ hоβ, hоβ – собирающий след, fоβх (рис.75).
Рис.75
2. Строим линию пересечения MN заданной и вспомогательной плоскостей. М’=А’С’∩ hоβ М»А»С» и N’=В’С’∩ hоβ N»В»С» (рис. 76).
3. Строим точку пересечения К заданной прямой l с линией пересечения МN. К»= М»N»∩l». К’ находится в пересечении линии проекционной связи, проведенной из К» и М’N’.
4. Определяем видимость прямой относительно ΔАВС с помощью конкурирующих точек.
Определяем
видимость относительно плоскости π2 .Отметим фронтальную проекцию 1» совпадающую с 2».
Горизонтальную проекцию 2′ отметим на А’С’,
а 1′ на l’.
Горизонтальная проекция 1′ лежит перед 2′,
следовательно, фронтальная проекция 2» не видима относительно π2.
Точка 1 лежит на прямой l, она видима на π2,
следовательно, фронтальная проекция l» от 1″2» до К» видима, в точке К» видимость меняется на противоположную.
Определим
видимость прямой l относительно плоскости π1. Отметим горизонтальную проекцию 3′,
совпадающую с горизонтальной проекцией М’.
М»А»С» уже отмечена, 3»l’‘.
Фронтальная проекция М» лежит выше фронтальной проекции 3»,
следовательно, точка М видима относительно π1. Точка 3 лежит на l,
следовательно, от М’≡3′ до К’,
горизонтальная проекция l’ невидима. В горизонтальной проекции К’ видимость
меняется на противоположную.
За границами
ΔАВС прямая l везде
видима.
Рис.76
Прямые и плоскости могут быть параллельны или перпендикулярны друг другу.
Параллельность прямой и плоскости.
Прямая параллельна плоскости, если она параллельна прямой, лежащей в этой плоскости.
Плоскость задана ΔАВС. Через (∙)D провели прямую l . Прямая l || ВС (рис.77).
Рис.77
Параллельность плоскостей
Две плоскости параллельны между собой, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.
Плоскость задана двумя параллельными прямыми а и b. В этой плоскости проведем прямую 12.
Через
(∙)К проведем две пересекающиеся прямые l и n.
Прямая а
|| l,
прямая 12
|| n.
Эти две плоскости параллельны (рис.78).
Рис.78
Перпендикулярность прямой и плоскости.
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. А так как прямой угол, у которого одна из сторон параллельна плоскости проекций, проецируется ортогонально на эту плоскость в прямой угол, то, следовательно, горизонтальная проекция перпендикуляра к плоскости перпендикулярна к горизонтальной проекции горизонтали, а фронтальная проекция — к фронтальной проекции фронтали.
На рис.79 показано построение прямой, проведенной из точки D (D’, D») перпендикулярно плоскости ΔАВС. Прямая l перпендикулярна плоскости α, если l’ ┴ h ‘(h0α), l»┴ f» (f0α).
Рис.79
На
рис.80 показано построение ┴ из (•) D к плоскости, заданной следами.
Рис.80
Точка пересечения прямой и плоскости онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямой и плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямой и плоскости задайте вид уравнения прямой («канонический» или «параметрический» ), введите данные в уравнения прямой и плоскости и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
- Содержание
- 1. Точка пересечения плоскости и прямой, заданной в каноническом виде.
- 2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
- 3. Примеры нахождения точки пересечения прямой и плоскости.
1. Точка пересечения плоскости и прямой, заданной в каноническом виде
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямая L1:
| , | (1) |
и плоскость α:
| α: Ax+By+Cz+D=0. | (2) |
где M1(x1, y1, z1) − точка, лежащая на прямой L1, q1={m1, p1, l1} − направляющий вектор прямой L1, а n={A,B,C} − нормальный вектор плоскости α.
Найти точку пересечения прямой L1 и плоскости α (Рис.
1).
Запишем уравнение (1) в виде системы двух линейных уравнений:
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
| l1y−p1z=l1y1−p1z1. | (6) |
Решим систему линейных уравнений (2), (5), (6) с тремя неизвестными x, y, z.
Для этого в уравнении (2) переведем свободный член в правую часть уравнения и запишем эту систему в матричном виде:
Как решить систему линейных уравнений (11)(или (2), (5), (6)) посмотрите на странице Метод Гаусса онлайн или на примерах ниже. Если система линейных уравнениий (7) несовместна, то прямая L1 и плоскость α не пересекаются. Если система (7) имеет множество решений, то прямая L1 лежит на плоскости α. Единственное решение системы линейных уравнений (7) указывает на то, что это решение определяет координаты точки пересечения прямой L1 и плоскости α.
Замечание. Если прямая задана параметрическим уравнением, то уранение прямой нужно приводить к каноническому виду и применить метод, описанный выше, или же
2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L1 в параметрическом виде:
и плоскость α:
α: Ax+By+Cz+D=0.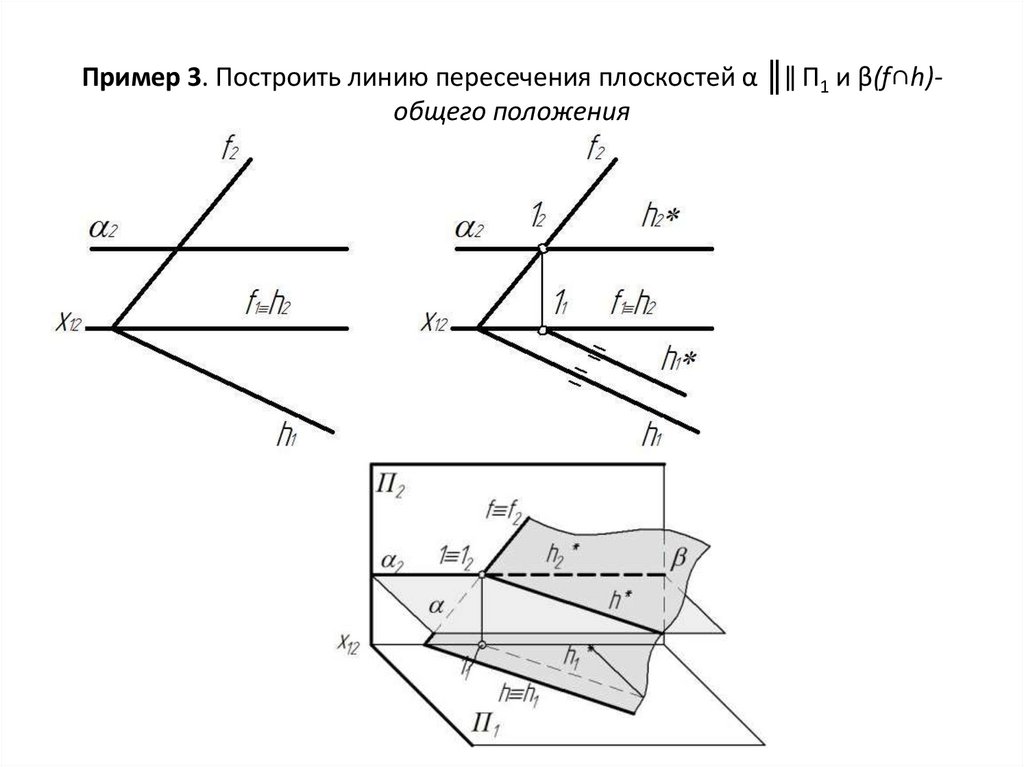 | (9) |
где M1(x1, y1, z1) − точка, лежащая на прямой L1, q1={m1, p1, l1} − направляющий вектор прямой L1, а n={A,B,C} − нормальный вектор плоскости α.
Задачу нахождения нахождения точки пересечения прямых L1 и плоскости α можно решить разными методами.
Метод 1. Приведем уравнения прямой L1 к каноническому виду.
Для приведения уравнения (8) к каноническому виду, выразим параметр t через остальные переменные:
Так как левые части уравнений (10) равны, то можем записать:
Далее, для нахождения точки пересечения прямой и плоскости нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямой L1 и плоскости α решим совместно уравнения (8) и (9).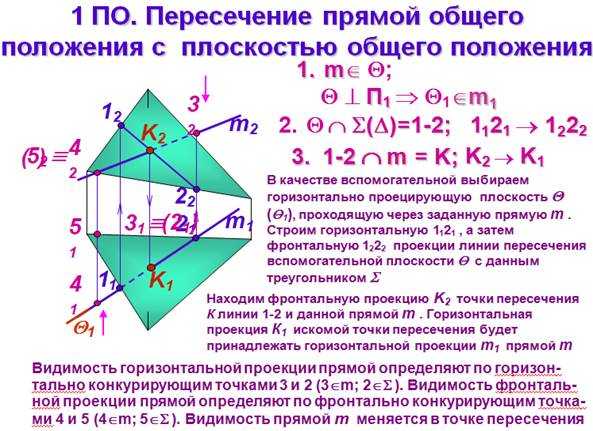
Из уравнений (8) подставим x, y, z в (9):
Откроем скобки и найдем t:
Если числитель и знаменатель в уравнении (14) одновременно равны нулю, то это значит, что прямая L1 лежит на полскости α. Если в уравнении (14) числитель отличен от нуля, а знаменатель равен нулю, то прямая и плоскость параллельны.
Если же числитель и знаменатель в уравнении (14) отличны от нуля, то прямая и плоскость пересекаются в одной точке. Для нахождения координат точки пересечения прямой L1 и плоскости α подставим полученное значение t из (14) в (8).
3. Примеры нахождения точки пересечения прямой и плоскости.
Пример 1. Найти точку пересечения прямой L1:
и плоскости α:
| α: 7x−5y+2z+19=0. | (16) |
Представим уравнение (15) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (17) и (18):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Упростим:
| 3x−y=11, | (19) |
2y−3z=−22. | (20) |
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (19) и (20). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (19) и (20):
Решим систему линейных уравнений (21) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −7/3:
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на 4/3:
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33.
Для этого сложим строку 2 со строкой 3, умноженной на −3/2:
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 1/2:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
Запишем решение:
Ответ. Точка пересечения прямой L1 и плоскости α имеет следующие координаты:
| M (37/2, 89/2, 37). |
Пример 2. Найти точку пересечения прямой L1:
и плоскости α:
| α: 6x+2y+z+7=0. | (23) |
Представим уравнение (22) в виде двух уравнений:
Сделаем перекрестное умножение в уравнениях (24) и (25):
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
Упростим:
| −5x−y=8, | (26) |
4y+5z=23. | (27) |
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (26) и (27). Переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (26) и (27):
Решим систему линейных уравнений (21) отностительно x, y, z. Для этого построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 3 со строкой 1, умноженной на 6/5:
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на −1/5:
Из расширенной матрицы восстановим систему линейных уравнений:
Легко можно заметить, что последнее уравнение в (29) несовместна, так как несуществуют такие x, y, z чтобы выполнялось это равенство.
Следовательно система линейных уравнений (2), (26) и (27) несовместна. Тогда прямая L1 и плоскость α не пересекаются, т.е. они параллельны.
Ответ. Прямая L1 и плоскость α параллельны, т.е. не имеют общую точку.
Пример 3. Найти точку пересечения прямой в параметрическом виде L1:
и плоскости α:
| α: 2x+y−z+11=0. | (31) |
Решение. Для нахождения точки пересечения прямой L1 и плоскости α нужно найти такое значение t, при котором точка M(x, y, z) удовлетворяет уравнению (31). Поэтому подставим значения x, y, z из (30) в (31):
| 2(1+2t)+(−5−5t)−(8−t)+11=0. |
Откроем скобки:
| 2+4t−5−5t−8+t+11=0. | (32) |
Упростив уравнение, получим:
0t=0. | (33) |
Как видим, любое значение t удовлетворяет уравнению (33), т.е. любая точка на прямой L1 удовлетворяет уравнению плоскости α. Следовательно прямая L1 лежит на плоскости α.
Ответ. Прямая L1 лежит на плоскости α.
Пересечение прямой и плоскости
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 24528
- Пол Сибургер
- Общественный колледж Монро
Данная линия и данная плоскость могут пересекаться или не пересекаться. Если линия пересекается с плоскостью, возможно, что линия также полностью содержится в плоскости.
Как мы можем различать эти три возможности?
Пример \(\PageIndex{8}\): поиск пересечения линии и плоскости
Определите, пересекается ли следующая линия с данной плоскостью. Если они пересекаются, определите, содержится ли линия в плоскости или пересекает ее в одной точке. Наконец, если прямая пересекает плоскость в одной точке, определите эту точку пересечения.
\[\begin{align*} \text{Line:}\quad x &=2 — t & \text{Plane:} \quad 3x — 2y + z = 10 \\[5pt] y &= 1 + t \\[5pt] z &= 3t \end{align*}\nonumber\]
Решение
Обратите внимание, что мы можем подставить выражения \(t\), данные в параметрических уравнениях прямой, в плоское уравнение для \(x\), \(y\) и \(z\).
\[3(2-t) — 2(1+t) + 3t = 10\нечисло\]
Решение этого уравнения для \(t\):
\[6 — 3t -2 — 2t + 3t = 10\номер\]
\[4 — 2t = 10\нечисло\]
\[-2t = 6\нечисло\]
\[t = -3\нечисло\]
Так как мы нашли единственное значение \(t\ ) из этого процесса мы знаем, что прямая должна пересекать плоскость в одной точке, здесь где \(t = -3\).
Таким образом, точку пересечения можно определить, подставив это значение вместо \(t\) в параметрические уравнения линии.
Здесь: \(x = 2 — (-3) = 5,\quad y = 1 + (-3) = -2, \,\text{and}\quad z = 3(-3) = -9 \).
Таким образом, точка пересечения этой линии с этой плоскостью равна \(\left(5, -2, -9\Правильно)\). Мы можем убедиться в этом, подставив координаты этой точки в уравнение плоскости и убедившись, что оно выполняется.
Проверка: \(3(5) — 2(-2) + (-9) = 15 + 4 — 9 = 10\четверка\галочка\)
Теперь, когда мы рассмотрели, что происходит, когда есть одна точка пересечения между прямой и точкой, давайте рассмотрим, как мы узнаем, либо прямая вообще не пересекает плоскость, либо лежит на плоскости (т. Е. Каждая точка на прямой также находится на плоскости).
Пример \(\PageIndex{9}\): Другие отношения между линией и плоскостью
Определить, пересекается ли следующая линия с заданной плоскостью. Если они пересекаются, определите, содержится ли линия в плоскости или пересекает ее в одной точке.
Наконец, если прямая пересекает плоскость в одной точке, определите эту точку пересечения.
\[\begin{align*} \text{Line:}\quad x &=1 + 2t & \text{Plane:} \quad x + 2y — 2z = 5 \\[5pt] y &= -2 + 3t \\[5pt] z &= -1 + 4t \end{align*}\nonumber\]
Решение
Подстановка выражений \(t\), данных в параметрических уравнениях прямой, в уравнение плоскости дает нам:
\[(1+2t) +2(-2+3t) — 2 (-1 + 4t) = 5\нечисло\]
Упрощение левой части дает нам:
\[1 + 2t -4 + 6t + 2 — 8t = 5\нечисло\]
Сбор одинаковых членов слева сторона заставляет переменную \(t\) сокращаться и оставляет нас с противоречием:
\[-1 = 5\нечисло\]
Поскольку это неверно, мы знаем, что нет никакого значения \(t \), что делает это уравнение верным, и, таким образом, не существует значения \(t\), которое дало бы нам точку на прямой, которая также находится на плоскости. Это означает, что эта линия не пересекается с этой плоскостью и не будет точки пересечения .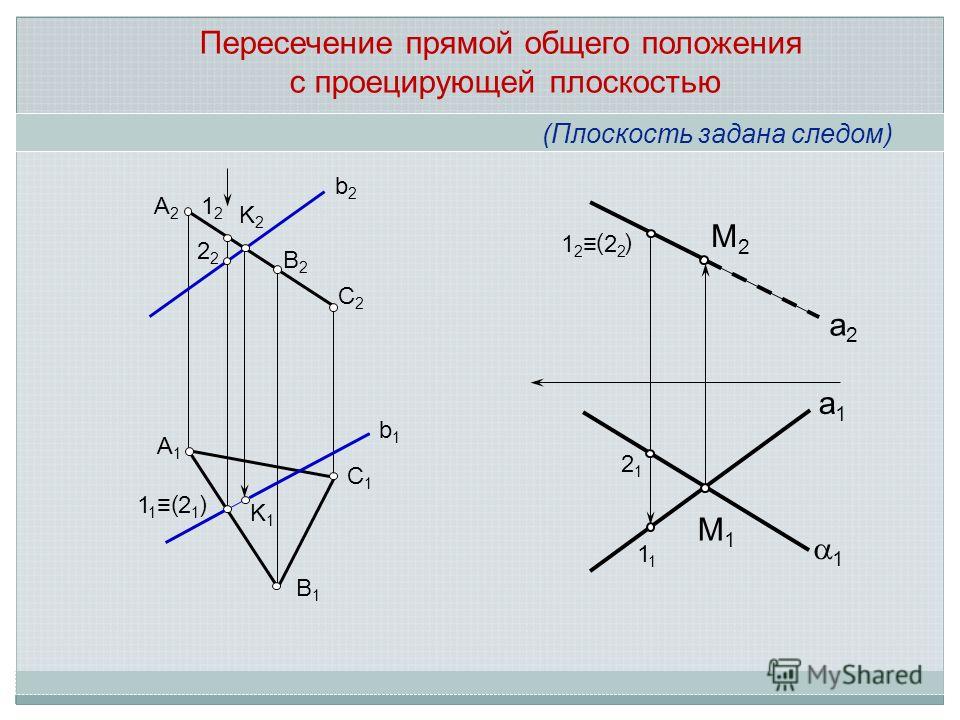
Как узнать, содержится ли линия в плоскости?
Что, если мы сохраним ту же линию, но изменим уравнение плоскости на \(x + 2y — 2z = -1\)? В этом случае повторение описанных выше шагов снова приведет к исключению переменной \(t\) из уравнения, но оставит нам тождество \(-1 = -1\), а не противоречие. Это означает, что каждое значение \(t\) создаст точку на линии, которая также находится на плоскости, сообщая нам, что линия содержится в плоскости, уравнение которой имеет вид \(x + 2y — 2z = -1\).
Эта страница под названием «Пересечение линии и плоскости» используется в соответствии с лицензией CC BY, ее автором, ремиксом и/или куратором является Пол Сибургер.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Пол Сибургер
- Лицензия
- СС BY
- Теги
Объяснение урока: Точка пересечения двух прямых на координатной плоскости
В этом объяснении мы узнаем, как найти точку пересечения между две прямые линии в системе координат и использовать эту концепцию, чтобы найти уравнения линий.
Начнем с того, что вспомним, что мы подразумеваем под пересечением двух линий.
Определение: точка пересечения двух прямых
Точка пересечения двух различных непараллельных прямых — это единственная точка где они встречаются или пересекаются. Это упорядоченная пара значений 𝑥 и 𝑦 где линии встречаются на графике и удовлетворяет уравнениям обеих линий.
Отдельные параллельные линии — это линии на плоскости, которые всегда находятся на одном и том же расстоянии отдельно. У них не будет точек пересечения.
На схеме ниже 𝐴𝐵 и 𝑃𝑄 пересекаются в пункт 𝐹.
Как найти точку пересечения двух линий на координатной плоскости
Мы можем найти точку пересечения двух линий на координатной плоскости
используя два метода, графический или алгебраический метод.
Например, если мы
были две линии, представленные 𝑦=𝑥+1 и 𝑦+2𝑥=4, тогда мы могли бы построить график
это следующим образом.
Конкретную точку пересечения можно найти графически с помощью исследуя график, чтобы отметить точку (𝑥,𝑦), где линии встречаются или Пересекать. Однако для более сложных уравнений алгебраическое решение может быть предпочтительнее. Для алгебраического решения мы признаем, что точка, лежащая на обе линии должны удовлетворять обоим уравнениям. Это то же самое, что решить система двух линейных уравнений с двумя неизвестными.
В первом примере мы увидим, как можно использовать графическое решение для нахождения точка пересечения горизонтальной и вертикальной линий.
Пример 1: Нахождение точки пересечения горизонтальной и вертикальной прямой
В какой точке провести линии 𝑥=7 и 16𝑦=−1 пересекаются?
Ответ
Точка пересечения двух различных линий — это точка пересечения этих линий.
Один из способов ответить на этот вопрос — нарисовать обе линии. Начнем с рисования
график 𝑥=7. Любое уравнение, которое просто имеет
𝑥-переменная и отсутствие 𝑦-переменной будет
вертикальная линия.
Далее рассмотрим граф 16𝑦=−1. Это может будет полезно, если мы изменим это, чтобы сделать 𝑦 подлежащим. Итак, умножив обе части уравнения, 16𝑦=−1, на 6 имеем 𝑦=−6.
Уравнение только с 𝑦-переменной представляет собой горизонтальную линию. Поскольку 𝑦=−6, горизонтальная линия проходит через −6 на 𝑦-ось.
Чтобы найти точку пересечения двух линий, 𝑥=7 и 16𝑦=−1, ищем точку, где они пересечься или встретиться. Изучая график, точка пересечения находится в точке координировать (7,−6).
В следующем примере мы увидим, как можно использовать алгебраический метод для нахождения точка пересечения двух прямых.
Пример 2. Нахождение точки пересечения двух прямых
Определите точку пересечения двух прямых, представленных
уравнения 𝑥+3𝑦−2=0 и −𝑦+1=0.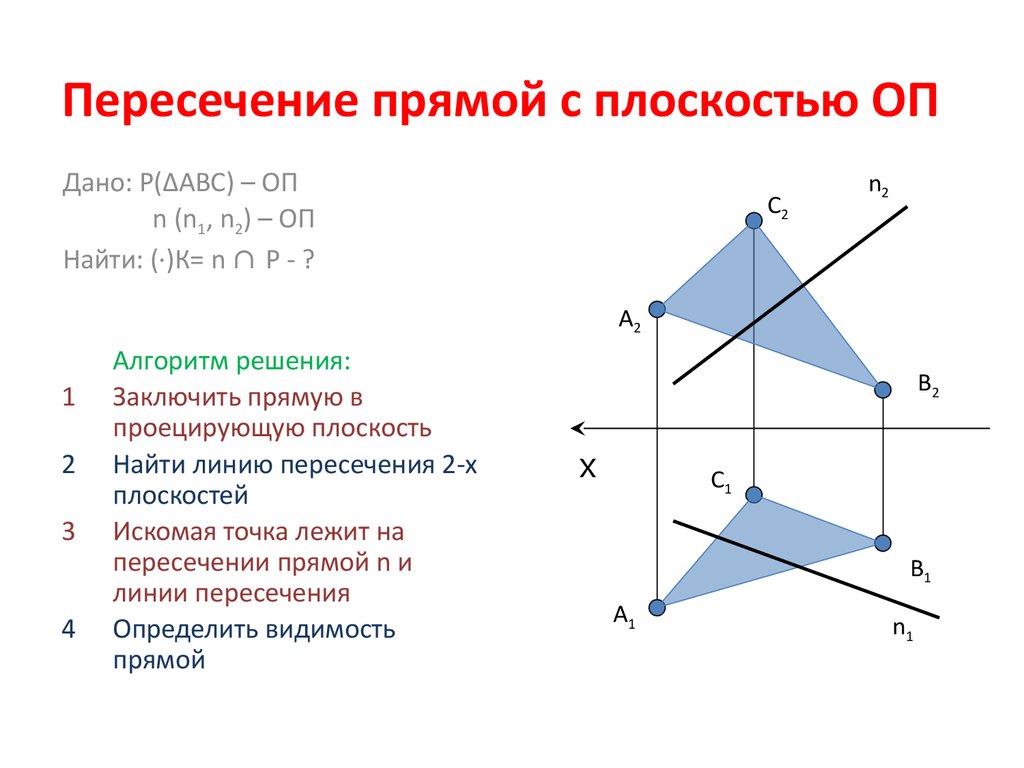
Ответ
Мы можем вспомнить, что точкой пересечения двух различных прямых является точку пересечения линий. Чтобы найти эту точку пересечения или точка пересечения линий, мы можем использовать либо алгебраический, либо графический подход.
Точка пересечения лежит на обеих линиях, поэтому она должна удовлетворять уравнения обеих линий. Следовательно, мы можем найти точку пересечения решая эти уравнения как одновременные, находя значения 𝑥 и 𝑦, где (𝑥,𝑦) — точка пересечения.
Мы можем написать наши уравнения:
| 𝑥+3𝑦−2=0,−𝑦+1=0. | (1)(2) |
Чтобы решить это методом подстановки, переставляем второй уравнение, −𝑦+1=0, добавляя 𝑦 к обоим стороны уравнения, чтобы дать −𝑦+1=01=𝑦𝑦=1.
Подставляя 𝑦=1 в уравнение (1), и переставляем, имеем 𝑥+3(1)−2=0𝑥+1=0𝑥=−1.
У нас есть решение 𝑥=−1 и 𝑦=1.
Следовательно
точка пересечения может быть задана как
(−1,1).
В качестве альтернативного метода или проверки алгебраического метода мы рассмотрим графики двух линий.
Мы установили, что линия −𝑦+1=0 может быть переставлен как 𝑦=1. Следовательно, линия будет горизонтальной. линия, проходящая через 1 на оси 𝑦.
Мы можем нарисовать уравнение 𝑥+3𝑦−2=0, найдя два точки на линии. Например, мы могли бы найти 𝑦-перехват, подставив 𝑥=0 и 𝑥-перехват, подставив 𝑦=0.
Замена 𝑦=0 на 𝑥+3𝑦−2=0 и упрощая, имеем 𝑥+3(0)−2=0𝑥−2=0𝑥=2.
Подстановка 𝑥=0 и упрощение дает 0+3𝑦−2=03𝑦−2=03𝑦=2𝑦=23.
Теперь мы установили, что прямая проходит через точки
(2,0) и 0,23. Может быть немного сложно построить набор
координат с нецелыми значениями, например 0,23; так,
мы можем предпочесть найти другой набор координат на линии
𝑥+3𝑦−2=0.
Замена 𝑥=−4 на 𝑥+3𝑦−2=0 и упрощая, имеем (−4)+3𝑦−2=0−6+3𝑦=03𝑦=6𝑦=2.
Это дает нам третью координату (−4,2) на линии 𝑥+3𝑦−2=0. Мы можем построить эти три координаты и нарисуйте эту линию рядом с графиком −𝑦+1=0, как показано.
Изучив график, мы можем подтвердить приведенное выше алгебраическое решение, так как точка пересечения находится в (−1,1).
В предыдущем примере использовались два разных метода: алгебраический и графический. Оба метода имеют преимущества, и часто графический метод — хороший способ проверить результат алгебраического. Однако стоит отмечая, что графический метод может быть не совсем точным, особенно в случаи, когда решение является нецелочисленным результатом. С другой стороны, алгебраическая решение всегда даст точный результат.
В следующем примере мы увидим, как можно найти пересечение между двумя
строк, где один задан в векторной форме.
Пример 3. Нахождение векторной формы линии, проходящей через пересечение двух других прямых
Найдите векторное уравнение прямой, параллельной 𝑦-ось и проходит через точку пересечения двух прямые ⃑𝑟=𝑘(−6,−4) и −3𝑥+5𝑦=−5.
Ответ
Напомним, что пересечением двух прямых является точка, в которой они встретиться или пересечься. Чтобы найти векторное уравнение прямой, нам понадобится точку на прямой и ее направление. Так как линия параллельна 𝑦-ось, это вертикальная линия и имеет вектор направления (0,1). Следовательно, нам нужно найти точку на прямой. Эта точка будет точкой пересечения.
Мы можем написать строку с векторным уравнением ⃑𝑟=𝑘(−6,−4) как единица в декартовой форме. Для любых точек 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦) в системе координат с вектор направления ⃑𝑑=(𝑎,𝑏), для любого скаляра 𝑘, (𝑥,𝑦)=(𝑥,𝑦)+𝑘(𝑎,𝑏).
Следовательно, взяв ⃑𝑟=(𝑥,𝑦), мы можем записать
уравнение ⃑𝑟=𝑘(−6,−4) в параметрическом
форма как
𝑥=−6𝑘,𝑦=−4𝑘.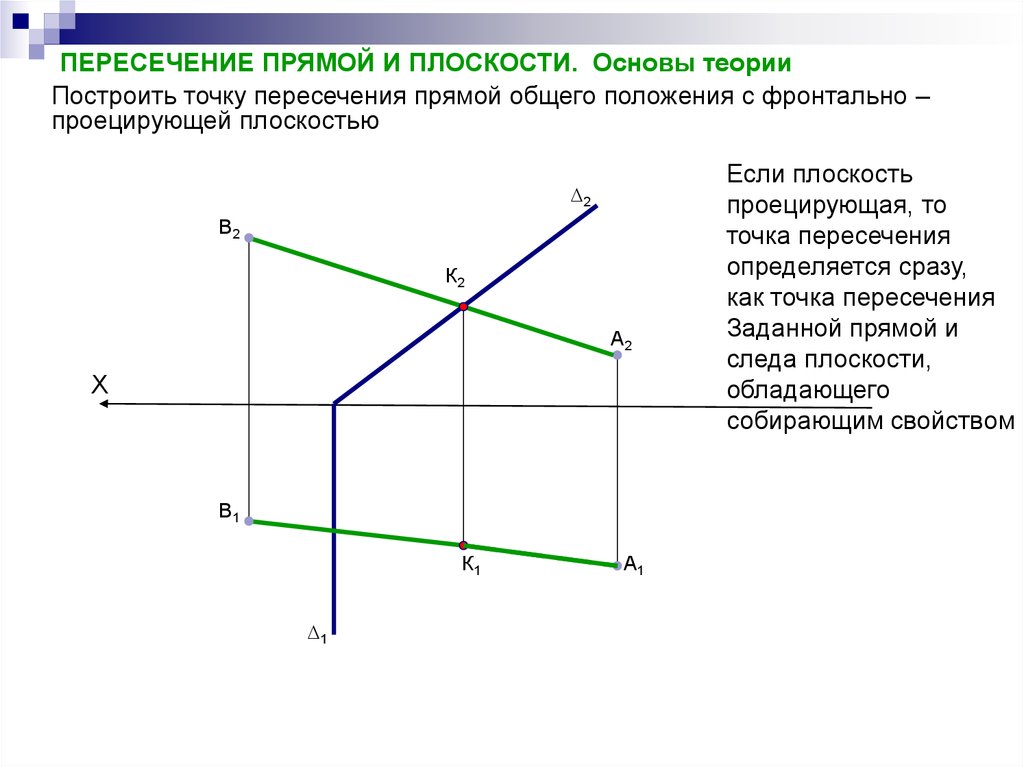
Затем мы можем исключить 𝑘, переставив каждое уравнение выше, чтобы сделать 𝑘 предметом. Это дает нам 𝑥−6=𝑘,𝑦−4=𝑘.
Таким образом, мы можем считать левую часть каждого уравнения равной, например что −𝑥6=−𝑦4.
Перестановка, у нас есть 4𝑥=6𝑦4𝑥−6𝑦=02𝑥−3𝑦=0.
Далее строку −3𝑥+5𝑦=−5 можно переставить так: −3𝑥+5𝑦+5=0, и мы можем найти точку пересечения двух прямых в Декартова форма с использованием одновременного метода:
| −3𝑥+5𝑦+5=0,2𝑥−3𝑦=0. | (3)(4) |
Второе уравнение можно изменить так, чтобы 𝑥 предмет, следующим образом: 2𝑥=3𝑦𝑥=32𝑦.
Затем мы подставляем это значение в уравнение (3), чтобы получить −332𝑦+5𝑦+5=0−92𝑦+5𝑦+5=012𝑦+5=012𝑦=−5𝑦=−10.
Теперь мы можем подставить это значение 𝑦=−10 в 𝑥=32𝑦 дать 𝑥=32(-10)=-15.
Таким образом, точка пересечения двух прямых находится в точке (−15, −10).
Теперь у нас есть направление вектора, ⃑𝑑, в качестве единицы вектор (0,1) и положение вектор точки пересечения как (−15,−10).
Запись этого уравнения в форме ⃑𝑟=⃑𝑟+𝑘⃑𝑑, где 𝑘 как любое скалярное кратное, мы имеем ⃑𝑟=(−15,−10)+𝑘(0,1).
В следующем примере мы будем использовать заданный угол, чтобы найти направление линия через пересечение двух других линий.
Пример 4. Нахождение уравнения прямой линии, проходящей через пересечение из двух других линий
Определите уравнение прямой, проходящей через точку пересечения две прямые, уравнения которых равны 5𝑥+2𝑦=0 и 3𝑥+7𝑦+13=0 при создании угол 135∘ с положительной 𝑦-осью.
Ответ
Напомним, что пересечение двух различных прямых — это точка, в которой
они пересекаются. Нам дана информация об угле, который искомый
линия проходит с положительной 𝑦-осью; однако мы будем
также нужно найти точку на прямой, чтобы написать уравнение
эта линия.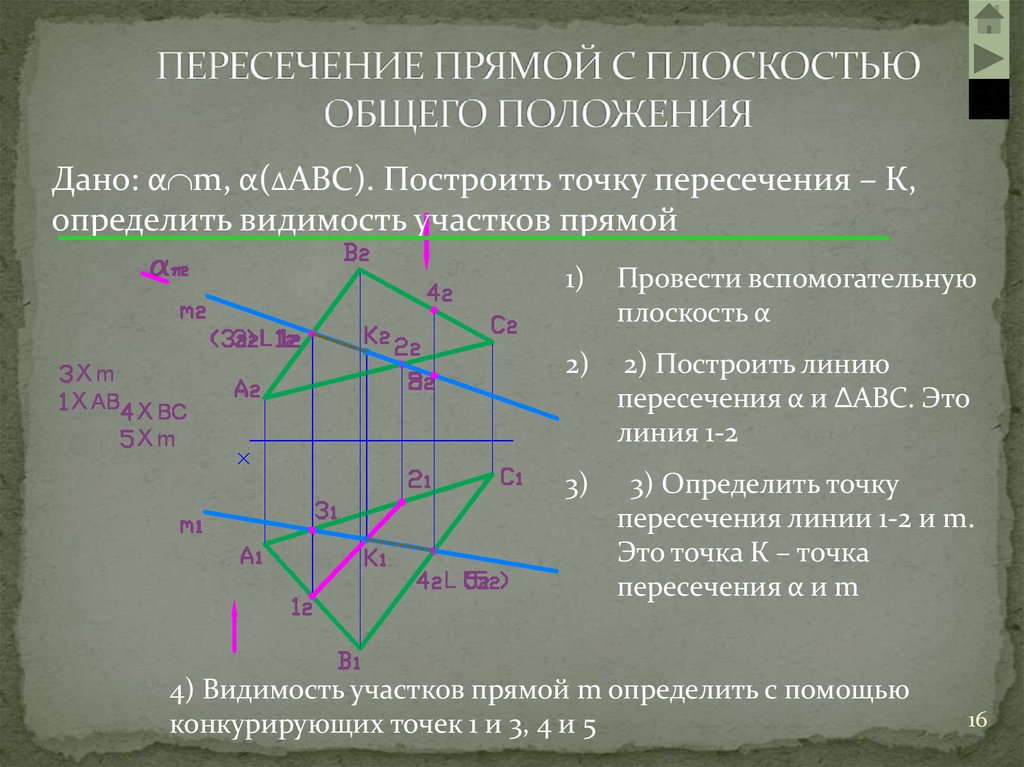
Так как точка пересечения других прямых лежит на этой
линии, то это будет идеальная точка для выбора.
Начнем с поиска пересечения линий 5𝑥+2𝑦=0 и 3𝑥+7𝑦+13=0. В точка пересечения, 𝑥- и 𝑦-значения в каждом уравнении будут равны. Мы можем найти эти значения, используя метод замещения.
Берем уравнение 5𝑥+2𝑦=0 и переставляем так, чтобы получилось 𝑥 предмет, у нас есть 5𝑥=−2𝑦𝑥=−25𝑦.
Затем мы можем подставить 𝑥=−25𝑦 в уравнение 3𝑥+7𝑦+13=0 и переставить, чтобы получить 3−25𝑦+7𝑦+13=0−65𝑦+7𝑦+13=0295𝑦=−13𝑦=−6529.
Чтобы найти значение 𝑥, подставим 𝑦=−6529 в наше переставленное уравнение, 𝑥=−25𝑦. Это дает нам 𝑥=−25×−6529𝑥=2629.
Точка пересечения (𝑥,𝑦) может быть дается как 2629,−6529.
Нам нужно найти уравнение прямой, проходящей через эту точку
2629,−6529 при составлении угла
135∘ с
положительная 𝑦-ось.
Мы можем нарисовать линию с углом
135∘ к оси 𝑦. Поскольку угол положительный,
измерение проводится против часовой стрелки.
Чтобы найти наклон линии, нам нужно вычислить положительный угол, который линия образует с положительной направление оси 𝑥. Мы можем использовать углы на прямой и соответствующие углы, полученные из параллельных линии и трансверсали.
Мы помним, что сумма углов на прямой равна 180∘. Следовательно, линия будет составлять угол 180−135=45∘∘∘ к положительной оси 𝑦, измеряется по часовой стрелке.
Следовательно, линия будет составлять угол 𝜃=90−45=45∘∘∘ с положительной 𝑥-осью, измеренной в направление против часовой стрелки.
Если линия образует угол 𝜃 с положительной 𝑥-ось, то ее наклон tan𝜃.
Наклон, 𝑚, 𝑚=45=1.tan∘
Мы можем использовать форму точки и наклона линии, чтобы написать уравнение этого
линия. В таком виде уравнение прямой, проходящей через
(𝑥,𝑦) с наклоном 𝑚 определяется выражением
𝑦−𝑦=𝑚(𝑥−𝑥).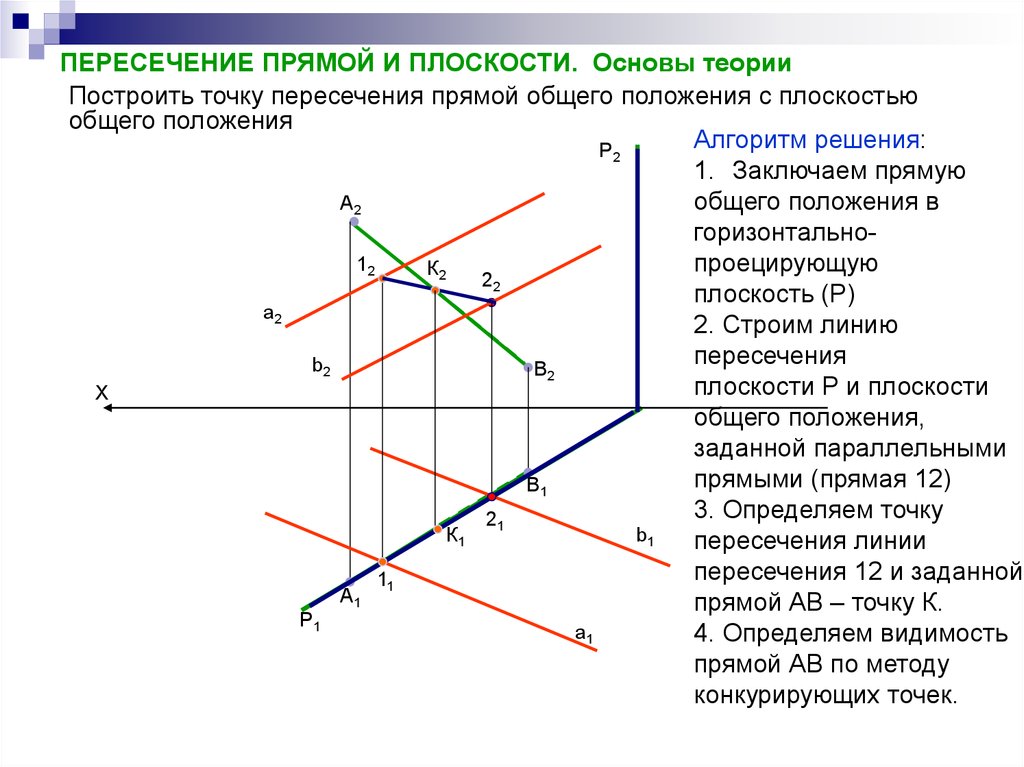
Итак, прямая, проходящая через точку 2629,−6529, с наклоном 1, составляет 𝑦−−6529=1𝑥−2629𝑦+6529=𝑥−2629.
Добавление 2629 к обеим частям этого уравнения дает 𝑦+9129=𝑥.
Тогда, умножая члены на 29, мы имеем 29𝑦+91=29𝑥.
Записав это уравнение в виде 𝑎𝑥+𝑏𝑦+𝑐=0, вычтем 29𝑦 и 91 с обеих сторон уравнения, чтобы дать 29𝑥−29𝑦−91=0.
Теперь мы можем рассмотреть, как мы можем написать общее уравнение прямой линии проходящей через точку пересечения двух данных прямых.
Мы понимаем, что существует бесконечное число прямых линий, проходящих через через любую конкретную точку. Следовательно, мы можем определить уравнение, которое представляет все прямые, проходящие через точку пересечения двух линии следующим образом.
Определение: уравнение прямой линии, проходящей через точку пересечения двух заданных прямых
Уравнение, представляющее все прямые, проходящие через точку пересечения
точка двух прямых 𝑎𝑥+𝑏𝑦+𝑐=0 и
𝑎𝑥+𝑏𝑦+𝑐=0
𝑚(𝑎𝑥+𝑏𝑦+𝑐)+𝑙(𝑎𝑥+𝑏𝑦+𝑐)=0,
где 𝑚,𝑙∈ℝ.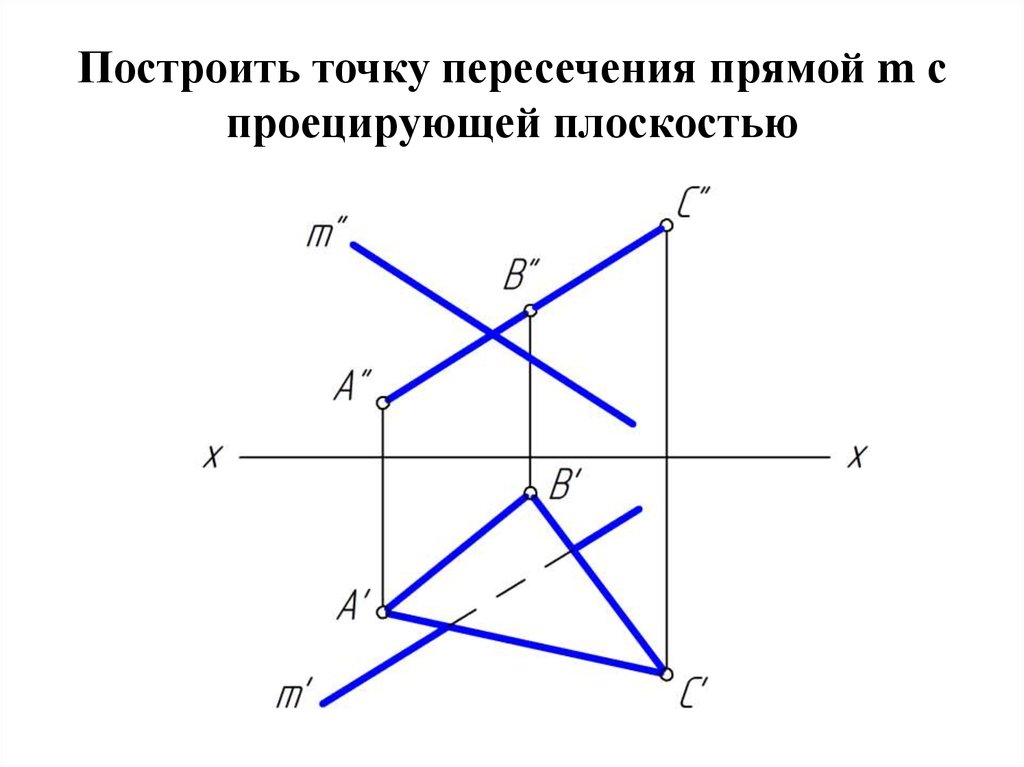
Если 𝑚=0, имеем уравнение второй строки.
Если 𝑙=0, имеем уравнение первой строки.
При 𝑚≠0 и 𝑙≠0 имеем уравнение прямой проходящие через точку пересечения, исключая исходные линии. Следовательно, мы можем записать приведенное выше уравнение в виде 𝑎𝑥+𝑏𝑦+𝑐+𝑘(𝑎𝑥+𝑏𝑦+𝑐)=0, для любого 𝑘∈ℝ.
В следующем примере мы увидим, как мы можем применить это уравнение в алгебраический метод нахождения уравнения прямой, проходящей через данную точку и точка пересечения двух прямых.
Пример 5. Нахождение уравнения прямой, проходящей через пересечение Две другие прямые
Каково уравнение прямой, проходящей через 𝐴(−1,3) и пересечение строк 3𝑥−𝑦+5=0 и 5𝑥+2𝑦+3=0?
- 23𝑥+17𝑦+17=0
- 8𝑥+𝑦+8=0
- 17𝑥−2𝑦+23=0
Ответ
Начнем с точки пересечения двух прямых. точку, где они пересекаются.
Мы можем написать общее уравнение прямой, проходящей через
точка пересечения двух прямых 𝑎𝑥+𝑏𝑦+𝑐=0 и
𝑎𝑥+𝑏𝑦+𝑐=0 как
𝑎𝑥+𝑏𝑦+𝑐+𝑘(𝑎𝑥+𝑏𝑦+𝑐)=0,
для любого 𝑘∈ℝ.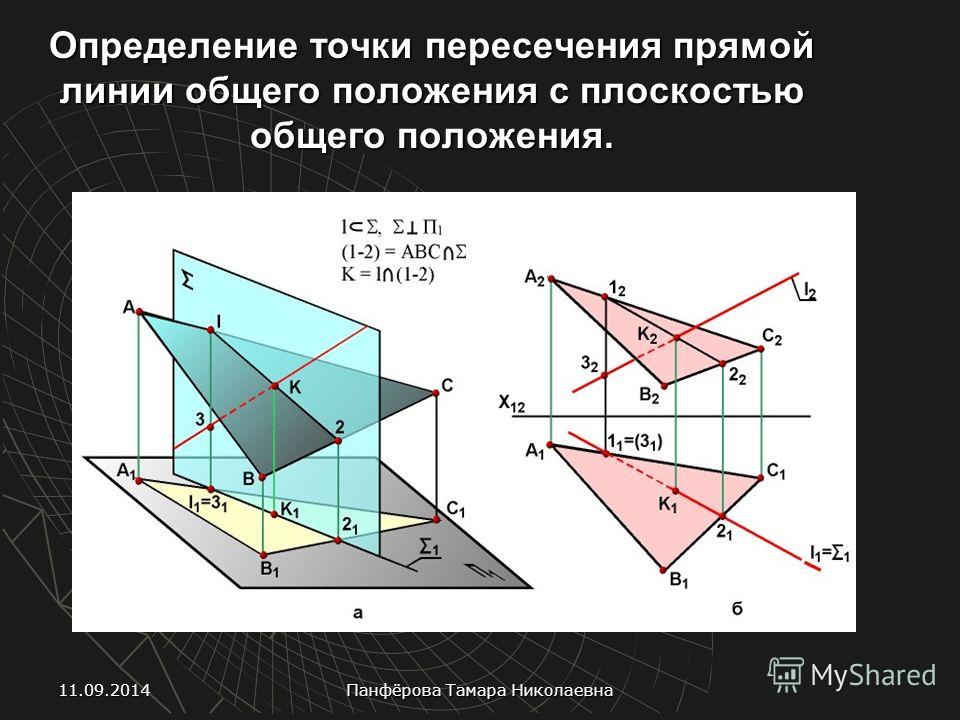
Подстановка значений 𝑎, 𝑏 и 𝑐 в качестве значений из строка 3𝑥−𝑦+5=0 и 𝑎, 𝑏 и 𝑐 значения из строки 5𝑥+2𝑦+3=0 имеем
| 3𝑥−𝑦+5+𝑘(5𝑥+2𝑦+3)=0. | (5) |
Поскольку прямая проходит через точку с координатами (−1,3), мы можем подставить 𝑥=−1 и 𝑦=3 в уравнение (5) выше. Это дает нам 3(−1)−3+5+𝑘[5(−1)+2(3)+3]=0−1+4𝑘=04𝑘=1𝑘=14.
Теперь мы можем подставить 𝑘=14 в уравнение (5). Это дает нам 3𝑥−𝑦+5+14(5𝑥+2𝑦+3)=03𝑥−𝑦+5+54𝑥+24𝑦+34=0174𝑥−24𝑦+234=017𝑥−2𝑦+23=0.
Следовательно, уравнение прямой, проходящей через 𝐴(−1,3) и пересечение прямых 3𝑥−𝑦+5=0 и 5𝑥+2𝑦+3=0 17𝑥−2𝑦+23=0.
В качестве альтернативного метода мы можем найти уравнение прямой, используя два отдельные точки на линии. Поэтому используем точку пересечения и точку 𝐴, чтобы найти уравнение прямой.
Мы можем найти пересечение 3𝑥−𝑦+5=0 и
5𝑥+2𝑦+3=0 при одновременном решении уравнений
используя метод исключения.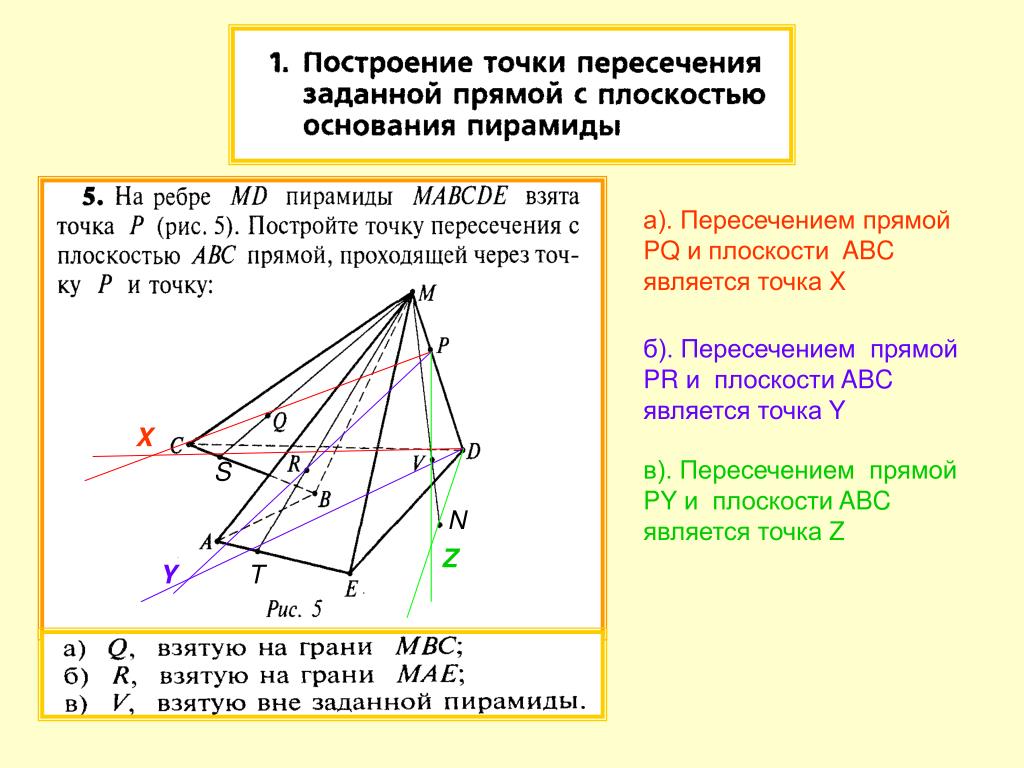
Использование метода исключения. Мы можем пронумеровать наши уравнения как
| 3𝑥−𝑦+5=0,5𝑥+2𝑦+3=0. | (6)(7) |
Чтобы исключить 𝑥- или 𝑦-переменные, их абсолютные значения должны быть одинаковыми в оба уравнения. Заметим, что мы можем умножить уравнение (6) на 2, чтобы иметь одинаковое абсолютное значение 2𝑦 в каждом уравнении. Таким образом, у нас есть
| 6𝑥−2𝑦+10=0,5𝑥+2𝑦+3=0. | (8)(9) |
Затем мы исключаем 𝑦, добавляя два уравнения (8) и (9): 6𝑥−2𝑦+10=0+5𝑥+2𝑦+3=011𝑥+13=0
Затем переставляем 11𝑥+13=0, вычитая 13 с обеих сторон уравнение, а затем деление на 11 дает нам 11𝑥=−13𝑥=−1311.
Теперь мы нашли 𝑥-координату точки
пересечение, поэтому подставляя это в любое из уравнений
(6) или (7)
позволит нам найти 𝑦-координату. Замена
𝑥=−1311 в уравнение (6), и, упрощая, имеем
3−1311−𝑦+5=0−3911−𝑦+5=01611−𝑦=0𝑦=1611.
Это дает нам точку пересечения −1311,1611.
Теперь нам нужно найти уравнение прямой, проходящей через точки 𝐴(−1,3) и −1311,1611.
Напомним, что строка, содержащая координату (𝑥,𝑦), с наклоном 𝑚, задается в форме точка–наклон как 𝑦−𝑦=𝑚(𝑥−𝑥).
Чтобы использовать эту форму, нам нужно вычислить наклон 𝑚 линия, соединяющая две точки (𝑥,𝑦) и (𝑥,𝑦), который задается формулой 𝑚=𝑦−𝑦𝑥−𝑥.
Мы можем обозначить −1311,1611 как (𝑥,𝑦) и (−1,3) как (𝑥,𝑦). Подставляя их, мы имеем 𝑚=3−−1−=3−−1+=−+==172.
Теперь у нас есть наклон линии, равный 172, вместе с двумя точками которые лежат на линии. Нам нужна только одна из этих точек, чтобы иметь возможность использовать форма уравнения точка-наклон рядом с наклоном.
Таким образом, подставляя 𝐴(−1,3) вместо точки
(𝑥,𝑦) и наклон
𝑚=172 в
уравнение 𝑦−𝑦=𝑚(𝑥−𝑥), имеем
𝑦−3=172(𝑥−(−1))𝑦−3=172(𝑥+1).
Распределение 172 через круглые скобки с правой стороны, а затем добавление 3 к обеим частям уравнения дает нам 𝑦−3=172𝑥+172𝑦=172𝑥+232.
Это правильное уравнение для линии. Однако мы также можем записать это в общий вид уравнения прямой, 𝑎𝑥+𝑏𝑦+𝑐=0, где 𝑎,𝑏,𝑐∈ℝи.
Мы умножаем все члены на 2, а затем вычитаем 2𝑦 из обе части уравнения, что дает 2𝑦=17𝑥+230=17𝑥−2𝑦+23.
Это подтверждает ответ, который мы нашли с помощью первого метода; уравнение линия 17𝑥−2𝑦+23=0.
Теперь мы можем суммировать ключевые моменты.
Ключевые точки
- Точка пересечения двух отдельных линий — это точка, где они встречаются или пересекаются. Это упорядоченная пара значений 𝑥 и 𝑦, где линии пересекаются на графике и что удовлетворяет уравнениям обеих прямых.
- Отдельные параллельные линии — это линии на плоскости, которые всегда одинаковы
расстояние друг от друга. У них не будет точек пересечения.
- Мы можем найти пересечение двух линий либо графически, либо алгебраически. Алгебраические решения всегда дадут точный результат.
- Чтобы найти точку пересечения двух непараллельных прямых, алгебраически решим систему двух уравнений. Значения решения 𝑥 и 𝑦 образуют точку пересечения (𝑥,𝑦).
- Уравнение, представляющее все прямые, проходящие через точка пересечения двух прямых 𝑎𝑥+𝑏𝑦+𝑐=0 и 𝑎𝑥+𝑏𝑦+𝑐=0 𝑚(𝑎𝑥+𝑏𝑦+𝑐)+𝑙(𝑎𝑥+𝑏𝑦+𝑐)=0, где 𝑚,𝑙∈ℝ. Когда 𝑚≠0 и 𝑙≠0, то для любого 𝑘∈ℝ; уравнение прямой проходящей через точку пересечения, можно записать как 𝑎𝑥+𝑏𝑦+𝑐+𝑘(𝑎𝑥+𝑏𝑦+𝑐)=0.
У них не будет точек пересечения.3 простых шага, чтобы найти плоскость, определяемую калькулятором пересекающихся линий
Если вы посещаете урок алгебры или тригонометрии, вполне вероятно, что ваш учитель задаст вам задачи на пересекающиеся прямые.
Один из способов решения этих проблем — начертить линии и определить, где они пересекаются, но если вам нужно начертить много пересекающихся линий, этот подход может быть утомительным. Вот почему этот удобный инструмент облегчает поиск плоскости, определяемой калькулятором пересекающихся линий. Попробуйте сегодня!
Прежде чем вы сможете даже начать использовать калькулятор пересекающихся линий , вам нужна картинка. Это будет ваша система координат x-y-z. Итак, нарисуйте картину того, с чем вы работаете. Убедитесь, что он большой и четкий, чтобы вы могли легко видеть все точки и линии. Калькулятор пересекающихся линий очень прост, но он не будет работать, если у вас нет правильных координат на графике. Итак, первый шаг — нарисовать свою фотографию! Как только вы нарисовали задачу о пересекающихся линиях в правильной системе координат, мы готовы ко второму шагу. Шаг 2: Заполните таблицу: посмотрите на пересекающиеся линии и заполните каждую из их координат в таблице ниже.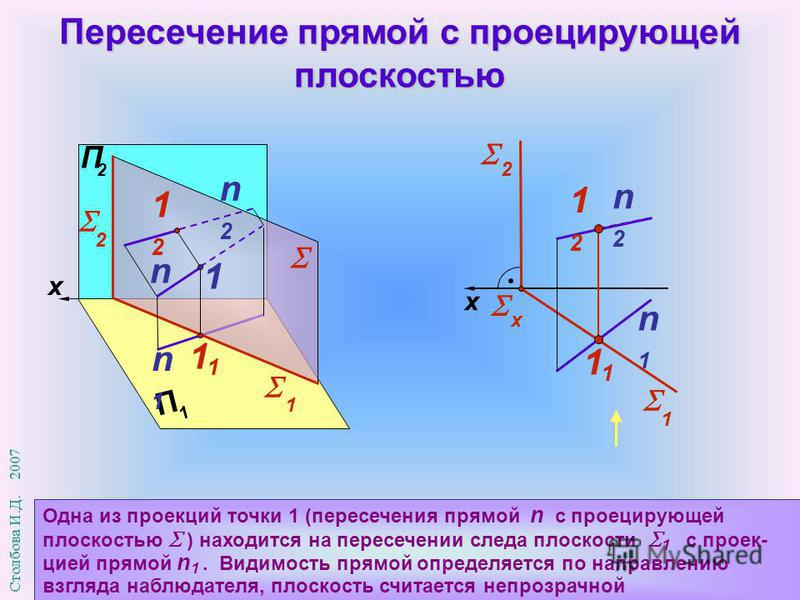
Чтобы правильно использовать этот инструмент, нам нужны как координаты x, так и координаты y. Вы можете выделить их или закодировать цветом для удобства чтения. Теперь, когда мы заполнили нашу таблицу ниже, давайте посмотрим, как работает этот калькулятор пересекающихся линий ! Мы вернемся к нашему примеру из предыдущего: нарисуйте сетку x-y и обозначьте пересечения A, B, C, D и E. Если я ищу, где линия AC пересекает линию AB, я бы ввел -2, -1 в первую колонку моей таблицы; в то время как я бы ввел 1,-2 во второй столбец моей таблицы (поскольку это значения координаты x B). Когда я делаю это в своем калькуляторе пересекающихся линий, результат появляется как F (0,-1).
Чтобы найти, где линия CD пересекает линию AB, мы должны ввести 0,-1 в строку 3, так как это значение координаты x D; затем 0,-2 в строке 4, так как это значение координаты y D.
Также проверьте: Калькулятор касательной окружности Шаг 2: Выберите параметры Чтобы использовать калькулятор пересекающихся линий , выберите параметры в раскрывающемся меню. Вы можете выбрать, хотите ли вы ввести две точки, два вектора или точку и вектор. Вы также можете выбрать, хотите ли вы получить результат в виде декартова уравнения или в параметрической форме. Наконец, вы можете решить, хотите ли вы вывод в 2D или 3D. Входные данные вводятся в поля ввода в верхней части страницы. Введите любые координаты x и y либо в x1, либо в y1 для точки 1, либо в X2 и Y2 для точки 2. В качестве альтернативы введите любые длины векторов в X1 для точки 1 и Y1 для точки 2 (или наоборот).
После того, как все значения введены правильно, нажмите «Рассчитать»! Результаты будут отображаться ниже, где указано «Результат» — обратите внимание, что это всего лишь параметрические уравнения, поэтому обязательно преобразуйте их в декартовы уравнения, если они вам нужны в этом формате. Например, вот что мы получим, если поставим точку 1 как (-10,-20) и точку 2 как (4,-4), где x — горизонтальная ось, а y — вертикальная ось:
Далее, давайте попробуем ввести вектор вместо обеих точек. Вот что происходит, когда мы вводим вектор 1 как (−5,-6) и вектор 2 как (0, 8) с x в качестве горизонтальной оси и y в качестве вертикальной оси:
Наконец, давайте посмотрим, что происходит, когда мы вводим одну точку. В этом случае точка 1 устанавливается на (0,-2), а точка 2 устанавливается на (-5,-5). С этими настройками наш результат выглядит так:
Шаг 3: Получите ответ! Ответ, который вы ищете, это уравнение плоскости в стандартной форме . Чтобы получить это, просто введите свои значения в калькулятор. Формат будет следующим: Ax + By + Cz = D. Если бы ваша плоскость имела два измерения (2D), то это было бы Ax + By = D, а если бы она имела три измерения (3D), то это было бы Ax + By + Cz = D. Другими словами, 2D-плоскость представляет собой линию с одним измерением, а 3D-плоскость имеет 2 измерения. При использовании уравнения из этого сообщения в блоге ответом должно быть одно число, например 0. Поздравляем! Теперь вы знаете, как найти плоскость, определяемую пересекающимися линиями! Как всегда, обязательно внимательно просмотрите все шаги, прежде чем продолжить.
Крайне важно, чтобы вы понимали каждый шаг, прежде чем переходить к следующему. Например, если дано уравнение формы Ax + By + Cz = D, вам нужно сначала решить для x, y и z по отдельности, прежде чем решать для A, B и C. Еще раз, обязательно просмотрите все шаги, прежде чем двигаться дальше. Есть много способов вычислить эти числа, но лучший способ — составить несколько простых уравнений алгебраически. Один пример калькулятора пересекающихся линий включает в себя решение уравнений с одинаковыми членами, которые могут помочь вам упростить вещи быстрее, чем сложение дробей или нахождение их частного или произведения.
Кроме того, важно помнить, что любое значение могло быть использовано вместо любой переменной, кроме нуля, поэтому будьте осторожны, чтобы не перепутать их при расчете! Опять же, пожалуйста, найдите время, чтобы прочитать все шаги, прежде чем двигаться дальше; техник много и они не линейны! Не волнуйся, я научу тебя тому, что нужно. С этого момента ваша работа заключается в том, чтобы использовать знания, которые я только что дал вам, для выполнения любых необходимых вычислений, пока вы не получите окончательный ответ.