Wolfram Mathematica — Энциклопедия языков программирования
Wolfram Mathematica — система для выполнения вычислений, широко использующаяся во всех областях, требующих технических вычислений.
Mathematica была создана Стефаном Вольфрамом (Stephen Wolfram) и разрабатывается Wolfram Research. Первая версия была выпущена 23 июня 1988 года.
Mathematica предоставляет пользователю огромный инструментарий:
- символьные и численные вычисления,
- библиотеки математических и статистических функций, теории групп и теории чисел,
- работа с графикой, в том числе инструменты визуализации и анимации, обработка и распознавание изображений,
- инструментарий для финансовых вычислений, анализа текстовых и графических данных и т.д.
- база данных математической, научной и социально-экономической информации,
- встроенный язык программирования, поддерживающий функциональный, процедурный и объектно-ориентированный стили прогграммирования.
- средства создания программ и пользовательских интерфейсов, параллельных вычислений, подключения внешних DLL и т.д.
Одним из базовых принципов встроенного языка Mathematica является представление любых сущностей в виде списков. Например, сумма чисел — это список с головным элементом Plus. Операции Map и Apply позволяют заменять головные элементы списков и применять заданное выражение к каждому элементу списка.
Элементы синтаксиса:
| Комментарии, которые не могут быть вложенными | (* … *) |
|---|---|
| Регистрозависимость | да |
| Регулярное выражение идентификатора переменной | [_a-zA-Z][_a-zA-Z0-9]* |
| Регулярное выражение идентификатора функции | [_a-zA-Z][_a-zA-Z0-9]* |
| Присваивание значения переменной | a=b, a:=b(отложенное или ленивое присвоение) |
| Объявление переменной | (происходит в месте ее первого использования) |
| Объявление переменной с присваиванием значения | <varname> = <value>; |
| Группировка выражений | ( . .. ) |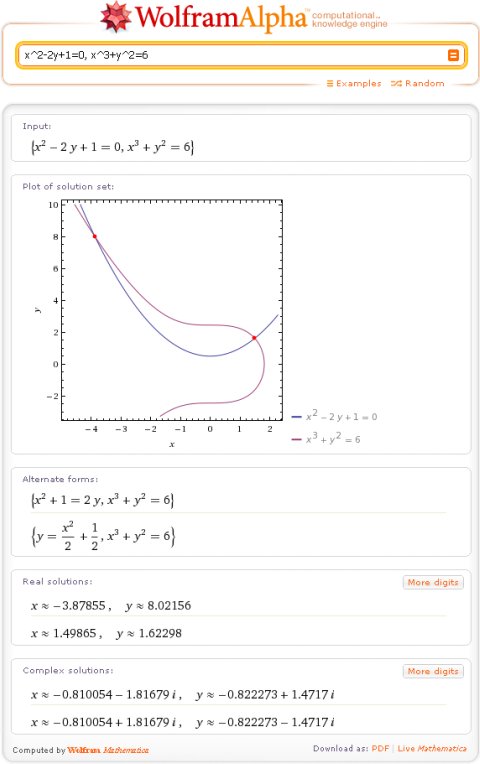
| Блок | [ … ] |
| Равенство | == |
| Неравенство | != |
| Сравнение | < > >= <= |
| Определение функции | f[x_, y_, z_] := (x + y + z) |
| Вызов функции | f[x, y, z] |
| Вызов функции без параметров | f[] |
| Последовательность | ; |
| Если — то | If[condition, trueBlock] |
| Если — то — иначе | If[condition, trueBlock, falseBlock] |
| Бесконечный цикл | While[1<2, loopBody] |
| Цикл с предусловием | While[condition, loopBody] |
| Цикл for — next для диапазона целых чисел с инкрементом на 1 | For[i = 0, i < 10, i++, loopBody] |
| Цикл for — next для диапазона целых чисел с декрементом на 1 | For[i = 10, i > 0, i—, loopBody] |
Примеры:
Квадратное уравнение:
Пример для версий
Wolfram Mathematica 7.
Факториал:
Пример для версий Mathics 0.4, Wolfram Mathematica 7.0.1.0, Wolfram Mathematica 8.0.4
Используется встроенная функция вычисления факториала !. Do — один из способов реализации циклов; выполняет первый аргумент для всех значений, заданных вторым аргументом, а именно: для всех i от 0 до 16 с шагом 1.
Do[Print[i, "! = ", i!] , {i, 0, 16, 1}]
Числа Фибоначчи:
Пример для версий Mathics 0.4, Wolfram Mathematica 7.0.1.0, Wolfram Mathematica 8.0.4
Print обязательно завершает вывод переносом строки, поэтому для того, чтобы вывести все числа Фибоначчи в одной строке, их нужно накопить в переменной msg
<> — оператор конкатенации; он работает только с явными строками, поэтому результат вызова Fibonacci нужно явно перевести в строку функцией ToString.msg = "";
Do[msg = msg <> ToString[Fibonacci[i]] <> ", " , {i, 16} ];
Print[msg, "..."];
Hello, World!:
Пример для версий Mathics 0.4, Wolfram Mathematica 7.0.1.0, Wolfram Mathematica 8.0.4
Функция Print выводит свои аргументы в основной выходной поток. Потоки могут быть вложенными, и для удобства копирования результатов лучше пользоваться для вывода одним потоком.
Print["Hello, World!"];
Hello, World!:
Пример для версий
Mathics 0.4,
Wolfram Mathematica 7.0.1.0,
Wolfram Mathematica 8.
В этом случае создается временная строковая переменная. В конце строки нет символа “;”, и значение этой переменной выводится отдельным Out, что не всегда удобно.
"Hello, World!"
Факториал:
Пример для версий Wolfram Mathematica 8.0.4
Используется рекурсивное определение факториала. Обратите внимание на то, что при определении функции ее аргумент дополняется символом _.
Fact[n_] := If[n == 0, 1, Fact[n - 1]*n]; For[i = 0, i <= 16, i++, Print[i, "! = ", Fact[i]]];
Числа Фибоначчи:
Пример для версий Mathics 0.4
Этот пример использует функцию Riffle, которая в данном случае перемежает элементы массива чисел Фибоначчи копиями строки “,”.
StringJoin[Riffle[Map[ToString, Table[Fibonacci[i], {i,16}]], ", "]] <> "..."
Факториал:
Пример для версий
Wolfram Mathematica 8.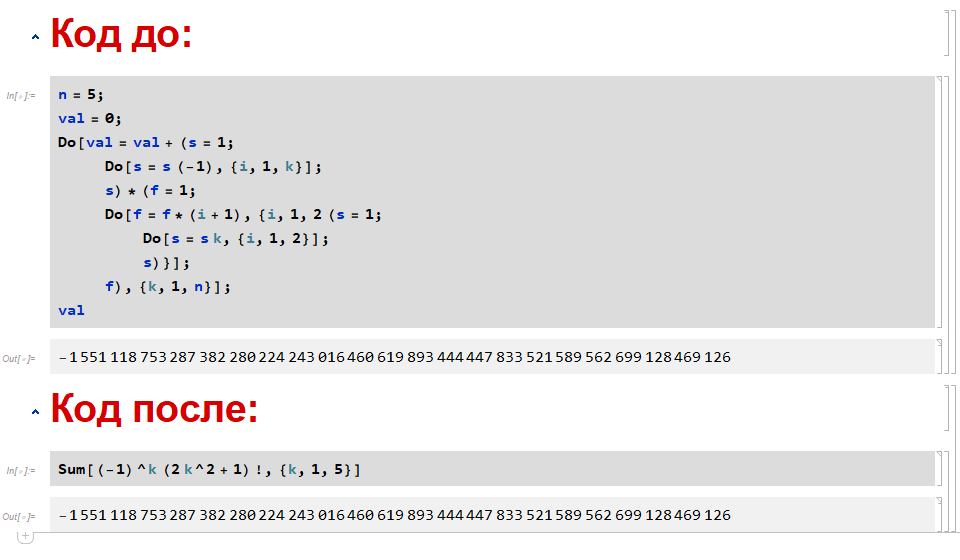
0.4
Символу f[x] ставится в соответствие список (List[…]) первых x натуральных чисел, генерируемый функцией Range[x], в которой головная часть List заменяется на Times при помощи функции Apply[head, expr], записанной здесь как head@@expr.
Здесь использованы две парадигмы программирования, реализованные в Wolfram: во-первых, с помощью шаблонного выражения x_ число, вписанное в квадратные скобки, подставляется в соответствующее место справа от знака отсроченного присваивания := . Во-вторых, функциональная парадигма позволила избавить код от громоздких процедурных конструкций и придти к похожей на математическую записи.
fact[x_]:=Times@@Range[x];
Обработка спектров в программном пакете Wolfram Mathematica — Комбинационное рассеяние света
После непосредственного проведения КР эксперимента необходимо извлечь информацию из полученных данных не только качественно, но также и количественно. Для этого обычно применяются такие программные пакеты как PeakFit, Origin и другие.
Один из них Wolfram Mathematica.
Преимущество этого программного пакета заключается в именно пакетной обработке данных, то есть в возможности обрабатывать последовательно, с помощью одного заданного начального условия, сразу большое количество файлов с данными эксперимента при разных внешних параметрах (температуре, давлении). Для удобства и точности подгонки, полученные подогнанные данные одного спектра одновременно являются начальными для следующего.
Для удобства и исключения каких либо неясностей при пакетной обработке спектров, в программе из имени файла считывается внешний параметр (температура, давление). Оно должно быть специфично — содержать в себе температуру в кельвинах, при которой был проведен данный эксперимент. Само имя файла следует разбить на несколько частей, например с помощью символа «_».
Пример текста программы, написанной в Wolfram Mathematica, для обработки данных КР :
При обработке спектров важную роль играет выбор модели для подгонки контуров.
Ниже представлен фрагмент программы, где описывается одиннадцать функций подгонки, и два коэффициента Бозе – Эйнштейна (nbes, nbeas — для стоксовой и антистоксовой компоненты):
*При использовании в вычислениях физических констант нет необходимости вводить их численное значение. Достаточно в начале программы подключить пакет Physical Constants используя следующую запись:
Самой распространенной и используемой во многих работах, ввиду универсальности, является модель Лоренца. Однако при описании низкочастотного диапазона спектра рекомендуется пользоваться функцией подгонки Harmonic (функция затухающего гармонического осциллятора). Кроме того, при работе с функцией Harmonic нет необходимости отдельно учитывать температурный фактор Бозе – Эйнштейна, ввиду того, что он является одним из составляющих этой функции. Ниже мы опишем два примера программы с использованием моделей для подгонки Harmonic и Lorentz:
1. Пример текста программы с использованием модели подгонки спектров Harmonic:
Полный текст программы:
Описание работы программы по шагам:
Задаем (MyPath) и выбираем(SetDirectory) директорию, в которой хранится папка с нужными нам файлами с экспериментальными данными
Выбираем тип и расширение файлов (*.
txt)
Формируем форму вывода в файл
Здесь задаем модель для подгонки. Условие If присутствует вследствие того, что для функции Harmonic существует два варианта (для стоксовой и антистоксовой компоненты)
Задаем начальные данные для подгонки первого спектра
i1, v1,w1 – интенсивность, частота и ширина первой линии соответственно
i2, v2,w2 – интенсивность, частота и ширина второй линии соответственно
c, b – параметры базовой линии (наклон и уровень по оси Oy).
Значения Sfrom, Sto, Szero определяют
Sfrom и Sto – вырезают частотный интервал для подгонки (в данном случае это 0 – 130 cm-1)
Szero – значение на оси ординат, на котором закреплена ось абсцисс.
Далее следует цикл Do, перебирающий по одному файлу iName из указанной папки за один шаг. Выводится название файла
……- начало цикла
— окончание цикла
В данном случае в цикле участвуют файлы с 1 по 100.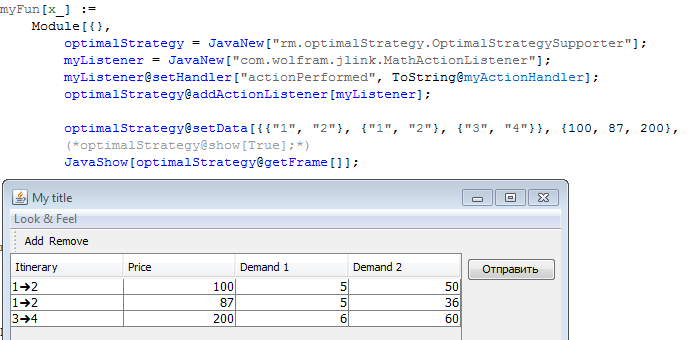
В этой строке происходит разбор имени файла на элементы (с помощью двух функций ToExpression и StringSplit) и считывание значения переменной T (температура, давление) из имени файла (iName). Стоит отметить, что имя файла должно быть специфично — содержать в себе температуру в кельвинах, при которой был проведен данный эксперимент. Само имя файла следует разбить на несколько частей, например с помощью символа «_».
Вывод значения T.
Считывание данных из выбранного файла с помощью функции ReadList и присвоение им имени FullData.
Выбираем нужный нам диапазон данных с помощью функции Select и присваиваем ему имя Data.
Функция FindFit является базовой функцией подгонки в Wolfram Mathematica. Максимальное число итераций – 5000.
*Здесь и далее символ /. означает подстановку значений, указанных после этого знака в выражение, стоящее до знака.
Вывод на экран исходных данных (Epilog-> Point [Data]) функцией Plot, полученных линий в отдельности (условие If[]), подогнанного спектра (model/.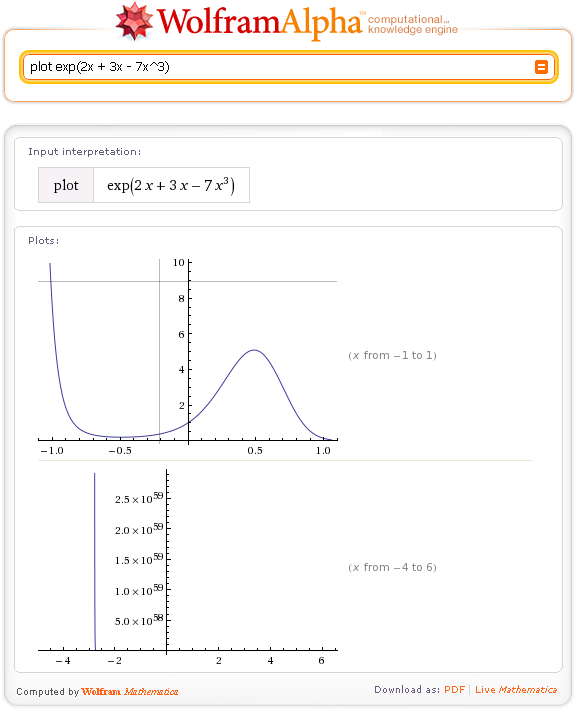
fit)
AxesOrigin – интервал значений по оси Ox
PlotRange – интервал значений по оси Oy
PlotStyle – совокупность параметров графика
Axes->True – видимость осей
Thickness – толщина линий
AxesLabel – подписи по осям.
Выделение подогнанных значений по точкам (функция Evaluate), соответственно данным из файла (iName).
Вычисляем разницу между подогнанными значениями и экспериментальными данными.
Вывод на экран значения Diff – погрешности подгонки (функция ListLinePlot)
PlotRange – интервал значений по оси Ox
AxesOrigin – точка пересечения осей
FillingAxis – заполнение цветом области под графиком.
Присвоение массиву подогнанных значений имени tmp.
Дополнение массива ResultData массивом tmp на каждом шаге цикла (функция Append).
Вывод на экран массива значений tmp.
Окончание работы цикла.
Вывод на экран полученных значений в табличной форме с помощью функции TableForm.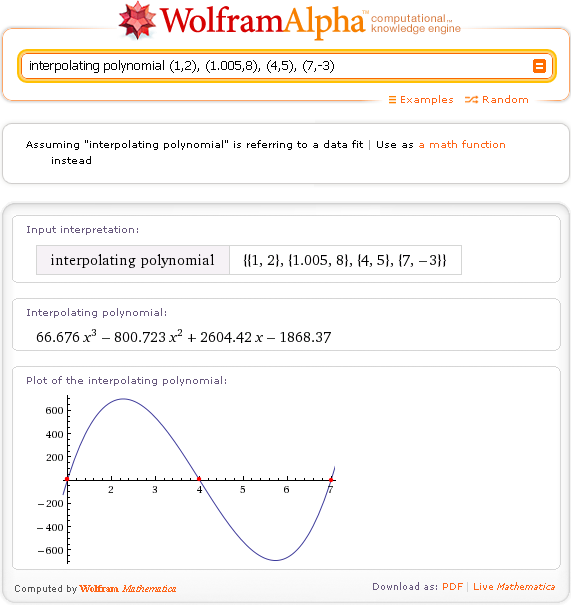
2. Пример текста программы с использованием модели подгонки спектров Lorentz:
Программа, описанная в данном параграфе, по своей структуре практически полностью соответствует программе, описанной ранее, за исключением модели подгонки.
Вследствие того, что при использовании модели подгонки Lorentz нужно отдельно учитывать температурный фактор Бозе — Эйнштейна, в тексте программы появился новый фрагмент.
Задается массив чисел с именем BoseFactor. Он заполняется нулями, имеет два столбца и колличество строк такое же, как и у массива FullData.
Задается массив элементов Eva1, который является фактором Бозе — Эйнштейна для стоксовой компоненты спектра (вычисляется для каждой точки массива FullData (массив экспериментальных данных)). Запись x-> FullData [[1; ;,1]] означает, что в выражении Eva1 переменная x принимает все значения первого столбца массива элементов FullData.
Вычисляется массив с именем Diff1с помощью массива Eva1 (фактора Бозе — Эйнштейна).
Данная запись означает, что второй столбец массива FullData поэлементно делится на массив факторов Бозе — Эйнштейна.
— присвоение значений каждому столбцу массива BoseFactor. первый столбец равенпервому стобцу массива экспериментальных данных Fulldata. Второму столбцу присваивается значение Diff1. Diff1 имеет смысл интенсивности в каждой точке экспериментального спектра, домноженную на обратный температурный фактор Бозе — Эйнштейна.
— выбор интересующего нас спектрального диапазона с помощью функции Select. Аналогичная строка присутствует и в тексте программы, представленной в П.1, но исходным массивом там служит массив экспериментальных данных FullData.
Программа, описанная в данном разделе
2, {x, 1, 7}]| Out [1] = |
Некоторые хорошо известные последовательности встроены в:
| в [2]: = | ⨯ Table[Fibonacci[x], {x, 1, 7}] |
| Out[2]= |
Define a recursive sequence using RecurrenceTable:
(Note the use { x , мин , макс } обозначения.
)
| In[1]:= | ⨯ RecurrenceTable[{a[x] == 2 a[x - 1], a[1] == 1}, a, {x, 1, 8}] |
| OUT [1] = |
Вычислить общее количество последовательности:
| в [2]: = | ⨯ [%] | ⨯ [%] | ⨯ [%] | ⨯ |
| Out[2]= |
Вычислить сумму последовательности из ее производящей функции:
| в [1]: = | ⨯ Сумма [i + 1), {I, 1, 10}] |
| Out [1] = |
Используйте ESCsumtESC для заполняемой формы:
| In[2]:= | ⨯ \!\( \*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(10\)]\(i \((i + 1)\)\)\) |
| Out[2]= |
Вы можете делать неопределенные и кратные суммы:
| In[3]:= | ⨯ \!\( \*UnderoverscriptBox[\(\[Сумма]\), \(i = 1\), \(n\)]\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 1\), \(n\)]i\ j\)\) |
| Out[3]= |
Рассчитайте функцию генерирования для последовательности:
| в [1]: = | ⨯ FindsequenceFunction [{2, 4, 6, 8}, N] |
| OUT OUT OUT [1] |
. ]= | 92], {x, 0, 8}]
| Out[1]= |
O[x] 9 представляет члены более высокого порядка, которые были опущены; Используйте нормальное, чтобы усеть этот термин:
| в [2]: = | ⨯ Нормальный [%] |
| Out [2] = |
Функция Series возвращает степенной ряд в терминах производных:
| в [3]: = | ⨯ Серия [2 F [x] - 3, {x, 0, 3}] |
| [3] = |
| In[1]:= | ⨯ \!\( \*UnderoverscriptBox[\(\[Сумма]\), \(n = 0\), \(\[Бесконечность]\)] \*SuperscriptBox[\(0.5\), \(n\)]\) |
| Out[1]= |
БЫСТРЫЙ СПРАВОЧНИК: Целочисленные последовательности »
КРАТКАЯ СПРАВКА: Расширение серии »
›
Включите JavaScript для взаимодействия с контентом и отправки форм на веб-сайтах Wolfram.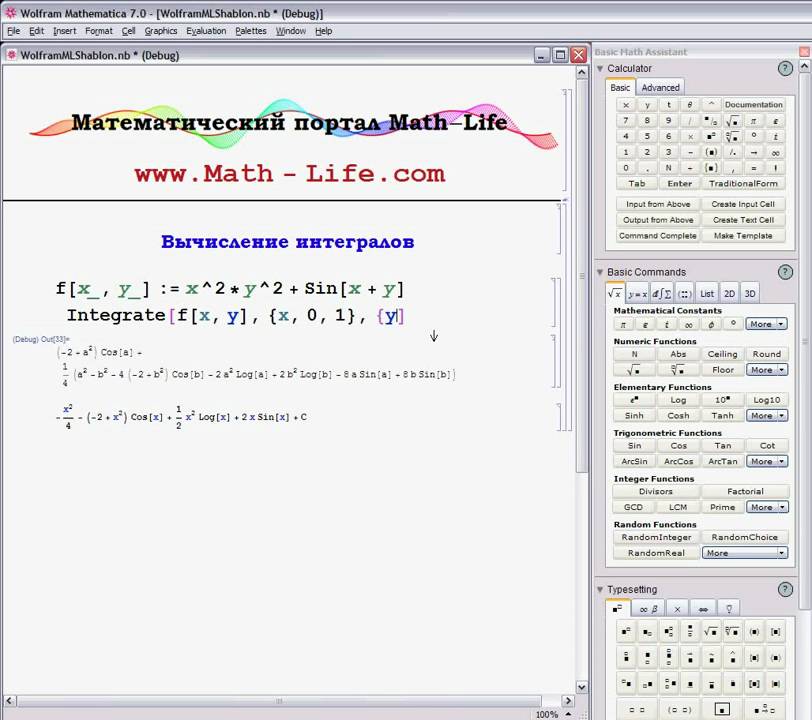
Узнайте, как »
Представляем Wolfram|Alpha Notebook Edition — Стивен Вольфрам Письма
Следующий большой шаг для Wolfram|Alpha
Wolfram|Alpha пользуется огромным успехом у студентов. Будь то колледж или старшая школа, Wolfram|Alpha стал для студентов повсеместным способом получить ответы. Но это одноразовый процесс: учащийся вводит вопрос, который он хочет задать (скажем, по математике), и Wolfram|Alpha дает ему ответ (обычно богато контекстуализированный). Это невероятно полезно, особенно в сочетании с возможностями пошагового решения.
Но что, если не нужен однократный ответ? Что, если кто-то хочет построить (или проработать) целое вычисление? Что ж, именно для этого мы создали Mathematica и весь ее интерфейс ноутбука. И за более чем 30 лет именно так во всем мире было сделано бесчисленное количество изобретений и открытий. Это также то, как учили поколения студентов более высокого уровня.
Но как насчет студентов, которые еще не готовы использовать Mathematica? Что, если бы мы могли взять мощь Mathematica (и того, что сейчас называется Wolfram Language), но объединить ее с простотой Wolfram|Alpha?
Вот что мы сделали в Wolfram|Alpha Notebook Edition.
Он построен на огромной технологической башне, но он позволяет любому студенту — без изучения синтаксиса и чтения документации — немедленно создавать или работать с вычислениями. Просто введите ввод так же, как в Wolfram|Alpha. Но теперь вы не просто получаете однократный ответ. Вместо этого все находится в блокноте Wolfram Notebook, где вы можете сохранять и использовать предыдущие результаты, а также создавать или обрабатывать все вычисления:
Сила записных книжек
Возможность использовать ввод в произвольной форме в стиле Wolfram|Alpha — это то, что открывает Wolfram|Alpha Notebook Edition для широкого круга учащихся. Но именно использование среды ноутбука делает ее уникально ценной для образования. Потому что, имея возможность работать с вещами в последовательности шагов, учащиеся действительно вовлечены в вычисления, которые они делают.
Попробуйте один шаг. Посмотрите, что происходит. Измените его, если хотите. Поймите вывод. Посмотрите, как это вписывается в следующий шаг.
А затем — прямо в блокноте — посмотрите, как все ваши шаги сочетаются друг с другом, чтобы дать окончательные результаты. А затем сохраните свою работу в записной книжке, чтобы продолжить или просмотреть то, что вы сделали, в другой раз.
Но блокноты предназначены не только для хранения вычислений. Они также могут содержать текст и структуру. Таким образом, учащиеся могут использовать их не только для выполнения своих вычислений, но и для ведения заметок, а также для объяснения своих вычислений или полученных результатов: студенческая работа: вычислительные эссе. Вычислительное эссе включает в себя как текст, так и вычисления, объединенные для создания повествования, в которое вносят свой вклад как человек, так и компьютер.
Процесс создания вычислительного эссе — отличный способ для студентов увлечься материалом, который они изучают. Вычислительные эссе также могут стать отличной демонстрацией достижений учащихся, а также средством оценки их понимания. И это не просто то, что нужно создать для задания: это активные вычисляемые документы, которые учащиеся могут сохранить и использовать в любое время в будущем.
Но тетради делают не только студенты. В Wolfram|Alpha Notebook Edition записные книжки также являются отличным средством, с помощью которого учителя могут предоставлять материалы ученикам. Опишите концепцию в блокноте, а затем позвольте учащимся исследовать ее, выполняя собственные расчеты прямо в блокноте. Или сделайте блокнот с описанием задания или теста, а затем позвольте учащимся заполнить свою работу (и оцените ее прямо в блокноте).
Wolfram|Alpha Notebook Edition очень часто используется для визуализации концепций. Часто студенты сами просят визуализацию. Но учителя также могут создавать шаблоны для визуализации и позволять учащимся заполнять свои собственные функции или данные для самостоятельного изучения.
Wolfram|Alpha Notebook Edition также поддерживает динамическую интерактивную визуализацию — например, с помощью функции Wolfram Language Manipulate. А в Wolfram|Alpha Notebook Edition учащиеся (и преподаватели!) могут создавать всевозможные динамические визуализации, просто используя естественный язык:
Но что, если вам нужна более сложная интерактивная демонстрация, которую может быть трудно указать? Что ж, Wolfram|Alpha Notebook Edition имеет прямой доступ к демонстрационному проекту Wolfram, который содержит более 12 000 демонстраций.
Вы можете запросить демонстрацию, используя естественный язык, или вы можете просто просмотреть веб-сайт демонстрационного проекта, выбрать демонстрацию, скопировать ее в записную книжку Wolfram|Alpha Notebook Edition, а затем сразу же использовать ее там:
С помощью Wolfram|Alpha Notebook Edition очень легко создавать привлекательный контент. Контент может включать чистые расчеты или визуализации. Но — используя возможности базы знаний Wolfram — он также может включать в себя широкий спектр данных реального мира, будь то страны, химические вещества, слова или произведения искусства. И вы можете получить к нему доступ, используя естественный язык, и работать с ним прямо в блокноте:
Wolfram|Alpha Notebook Edition — отличный инструмент для студентов, который может использовать их на своих компьютерах. Но это также отличный инструмент для лекций и демонстраций в классе (а также для студенческих презентаций). Выберите «Файл» > «Создать» > «Блокнот для докладчика», и вы получите блокнот, настроенный для создания слайд-шоу Wolfram|Alpha Notebook Edition:
Нажмите «Начать презентацию», чтобы начать презентацию.
Но у вас будет не просто слайд-шоу в стиле PowerPoint. Это полностью интерактивное, редактируемое, вычисляемое слайд-шоу. Интерфейсы Manipulate работают. Все сразу редактируется. И вы можете делать вычисления прямо во время презентации, исследуя разные случаи, извлекая разные данные и так далее.
Создание кода на естественном языке
Мы изобрели блокноты более 30 лет назад, и с тех пор они широко используются в системе Mathematica. Но в то время как в блокнотах Mathematica (и Wolfram Desktop) вы (по умолчанию) указываете вычисления в точном синтаксисе и семантике языка Wolfram Language, в блокнотах Wolfram|Alpha Notebook Edition вместо этого вы указываете их, просто используя ввод в произвольной форме в стиле Wolfram|Alpha. .
И действительно, одно из ключевых технических достижений, которое сделало Wolfram|Alpha Notebook Edition возможным, заключается в том, что мы разработали все более надежную технологию преобразования естественного языка в код, которая может перейти от ввода на естественном языке в свободной форме к точный код языка Wolfram Language, который можно использовать для построения вычислений:
По умолчанию Wolfram|Alpha Notebook Edition настроен на отображение сгенерированного им кода языка Wolfram Language.
Вам не нужно смотреть на этот код (и вы можете сделать так, чтобы он всегда был скрыт). Но — к счастью для меня как разработчика языка — студенты находят его очень легким для чтения, часто даже проще, чем математика. А его чтение дает им дополнительную возможность понять, что происходит, и убедиться, что указанные вычисления действительно нужны им.
И у того факта, что Wolfram|Alpha Notebook Edition генерирует код, есть большой побочный эффект: регулярно знакомясь с кодом, который представляет введенный ими естественный язык, учащиеся постепенно усваивают идею выражения вещей на вычислительном языке и концепции. вычислительного мышления.
Если учащийся хочет изменить вычисление при использовании Wolfram|Alpha Notebook Edition, он всегда может отредактировать введенную им информацию в произвольной форме. Но они также могут напрямую редактировать сгенерированный язык Wolfram Language, что дает им реальный опыт работы с языком вычислений.
Что делать дальше? Предиктивный интерфейс
Основная цель Wolfram|Alpha Notebook Edition — обеспечить полное «самообслуживание», чтобы учащиеся всех уровней могли успешно использовать его без какого-либо внешнего обучения или помощи.
Конечно, ввод в свободной форме является ключевой частью достижения этого. Но другая часть — это интерфейс прогнозирования Wolfram|Alpha Notebook Edition, который предлагает, что делать дальше, исходя из того, что сделали студенты.
Введите вычисление, и обычно под полем ввода появляются всплывающие кнопки:
Эти кнопки предлагают направления движения. Здесь пошаговое решение создает расширенную интерактивную версию пошаговой функциональности Wolfram|Alpha Pro — все прямо в блокноте:
Нажмите на связанные вычисления, и вы увидите предложения для различных вычислений, которые вы, возможно, захотите do:
Он предлагает построить подынтегральную функцию и интеграл:
Он также предлагает вам увидеть расширение ряда:
Теперь обратите внимание, что под выводом есть полоса предложений о возможных последующих вычислениях для этого вывода. Щелкните, например, список коэффициентов, чтобы найти список коэффициентов:
Теперь есть новые предложения.
Щелкните, например, по сумме, чтобы найти сумму коэффициентов:
The Math Experience
Wolfram|Alpha Notebook Edition имеет множество функций для улучшения «математического опыта». Например, нажмите кнопку в верхней части блокнота, и вы получите «математическую клавиатуру», которую можно использовать для прямого ввода математических обозначений:
Язык Wolfram Language, лежащий в основе Wolfram|Alpha Notebook Edition, регулярно обрабатывает математические операции, необходимые ведущим математикам мира. Но наличие всей этой сложной математики иногда может привести учащихся в замешательство. Таким образом, в Wolfram|Alpha Notebook Edition есть способы сказать «не усложняйте математику». Например, вы можете настроить его так, чтобы свести к минимуму использование комплексных чисел:
Wolfram|Alpha Notebook Edition также по умолчанию выполняет такие действия, как добавление констант интегрирования к неопределенным интегралам:
Кстати, Wolfram|Alpha Notebook Edition по умолчанию автоматически форматирует математический вывод в элегантном «традиционном учебнике».
Но рядом с каждым выводом всегда есть небольшая кнопка, так что вы можете переключаться между «традиционной формой» и стандартной формой языка Wolfram Language.
В математике довольно часто используется функция, и вы просто говорите: «Я хочу это построить!» Но какой диапазон использовать? В системе Mathematica (или языке Wolfram Language) вам нужно будет это указать. Но в Wolfram|Alpha Notebook Edition всегда есть автоматически выбранный диапазон:
Но поскольку вы можете видеть код языка Wolfram Language, включая диапазон, его легко изменить и указать любой диапазон, который вы хотите.
Что делать, если вы хотите получить интерактивный элемент управления для изменения диапазона или изменения параметра в функции? В Mathematica (или языке Wolfram Language) вам нужно было бы написать Manipulate. Но в Wolfram|Alpha Notebook Edition вы можете создать целый интерактивный интерфейс, просто используя естественный язык:
А поскольку в Wolfram|Alpha Notebook Edition все вычисления Manipulate выполняются непосредственно на вашем локальном компьютере, передача данных по сети не замедляется, поэтому все выполняется на полной скорости.
(Кроме того, если у вас есть долгие вычисления, вы можете просто позволить им продолжать работать на вашем компьютере; нет тайм-аута, как в Wolfram|Alpha в Интернете.)
Многошаговые вычисления
Одна из важных функций Wolfram|Alpha Notebook Edition заключается в том, что он не просто выполняет однократные вычисления; он позволяет вам выполнять многоэтапные вычисления, которые, по сути, включают обмен данными с компьютером, в котором вы регулярно обращаетесь к предыдущим результатам:
Часто бывает достаточно просто рассказать о самом последнем результате и сказать что-то вроде «постройте его как функцию x». Но также довольно часто хочется вернуться к результатам ранее в блокноте. Один из способов сделать это — сказать что-то вроде «предпоследний результат» или использовать метки Out[ n ] для каждого результата. Но еще одна вещь, которую Wolfram|Alpha Notebook Edition позволяет вам делать, — это устанавливать значения переменных, которые затем можно использовать на протяжении всего сеанса:
Также можно определять функции, все с помощью естественного языка:
При работе с многошаговыми вычислениями возникает множество сложных вопросов проектирования и реализации.
Например, если у вас есть традиционный результат для неопределенного интеграла с константой интегрирования, что вы делаете с константой, когда хотите построить результат? (Wolfram|Alpha Notebook Edition последовательно обрабатывает произвольные аддитивные константы на графиках, эффективно устанавливая их равными нулю.)
Также может быть сложно узнать, что относится к чему в «разговоре». Если вы говорите «график», вы пытаетесь построить свой последний результат или вам нужен интерфейс для создания совершенно нового графика? Если вы используете местоимение, например, «сюжет», то потенциально более очевидно, что вы имеете в виду, и у Wolfram|Alpha Notebook Edition больше шансов использовать свои возможности понимания естественного языка, чтобы понять это.
Мир с Wolfram|Alpha Notebook Edition
Было очень приятно видеть, насколько широко Wolfram|Alpha используется студентами. Но в основном это усыновление происходило за пределами классной комнаты. Теперь, с Wolfram|Alpha Notebook Edition, у нас есть инструмент, который можно сразу же использовать в классе, во всем спектре колледжей и довузовских учебных заведений.
И я рад видеть, как это может упростить курсовую работу, углубить понимание, позволить преподавать новые концепции и эффективно предоставить персонального наставника по искусственному интеллекту для каждого студента.
С сегодняшнего дня Wolfram|Alpha Notebook Edition доступен на всех стандартных компьютерных платформах (Mac, Windows, Linux). (Облачная версия также будет доступна в Интернете в ближайшее время.) Колледжи и университеты с полными лицензиями сайта Wolfram Technology System могут автоматически начать использовать Wolfram|Alpha Notebook Edition уже сегодня; в школах с другими лицензиями сайта его можно сразу добавить. Он доступен для школ K–12 и младших колледжей в виде пакетов для занятий или в виде лицензии для сайта. И, конечно же, он также доступен для отдельных учителей, студентов, любителей и других.
(О, и если у вас есть Mathematica или Wolfram Desktop, в будущих версиях также можно будет создавать блокноты «Wolfram|Alpha mode», которые эффективно интегрируют возможности Wolfram|Alpha Notebook Edition.
И в целом существует идеальная совместимость между Wolfram |Alpha Notebook Edition, Mathematica, Wolfram Desktop, Wolfram Cloud, Wolfram Programming Lab и т. д. – обеспечивает беспроблемный опыт для людей, продвигающихся по образовательной и профессиональной карьере.)
Подобно Wolfram|Alpha – и языку Wolfram – Wolfram|Alpha Возможности Notebook Edition будут расширяться и в будущем. Но то, что есть сегодня, уже является замечательным достижением, которое, как мне кажется, изменит многие образовательные учреждения.
Более 31 года назад мы представили Mathematica (и то, что сейчас называется Wolfram Language). Десять лет назад мы представили Wolfram|Alpha. Теперь, сегодня, с выпуском Wolfram|Alpha Notebook Edition, мы впервые пробуем — в контексте образования — совершенно новый подход к вычислениям: полноценную вычислительную среду, управляемую естественным языком. Он не вытесняет Wolfram Language или Wolfram|Alpha, но определяет новое направление, которое со временем принесет мощь вычислений совершенно новой аудитории.