Как поделить отрезок в автокаде на равные части: Как разделить линию в Автокаде. Видеоурок

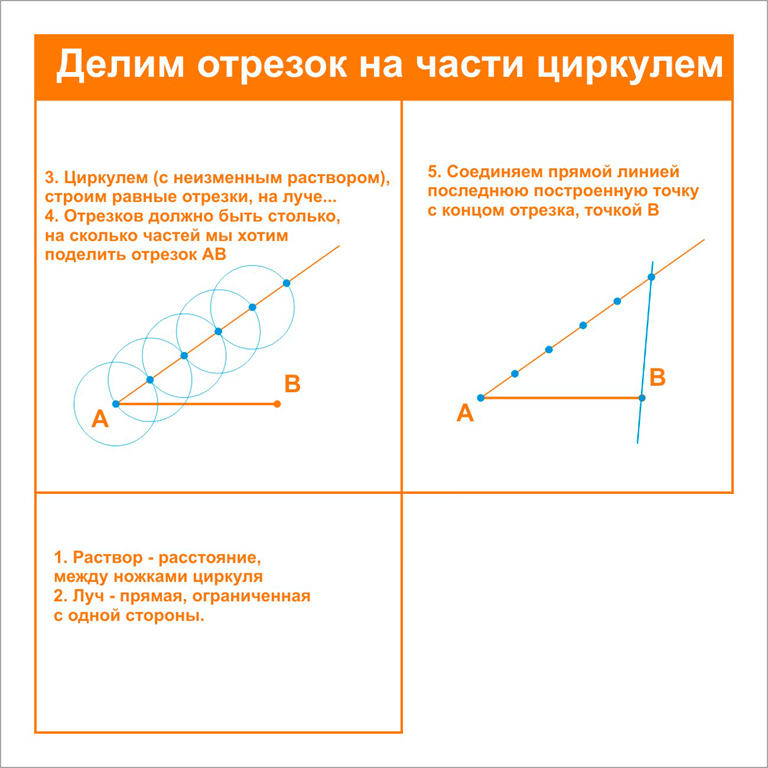
Деление круга на равные части

УчебаМатематикаГеометрия

Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами

Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.

Деление круга на равные по площади части радиусами

Радиус круга

Число частей

Точность вычисления

Знаков после запятой: 2

Угол сектора

 

Длина дуги

 

Длина хорды

 

Деление круга на равные по площади части параллельными хордами

Радиус круга

Число частей

Точность вычисления

Знаков после запятой: 2

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Деление круга на равные части радиусами

Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:

1. Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.

2. Определяем размер дуги сектора, перемножая радиус на угол в радианах

3. Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.

Собственно и всё — мы получили все характеристики для N равных секторов

Деление круга на равные части параллельными хордами

Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.

Деление круга на три равные части двумя хордами

Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.

Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.

y=f(x)

По теореме Пифагора получаем следующую функцию

Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:

Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем

, откуда

Итак, полное выражение

Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)

Таким образом мы можем приравнять

Что дает нам такое финальное уравнение

Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона.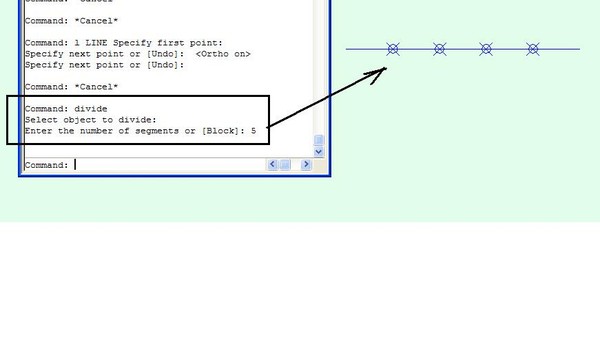 Калькулятор использует метод Ньютона.

Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.

Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Вычисление радиуса по площади круга
• • Круговой сектор
• • Сегмент круга
• • Круг
• • Сколько малых одинаковых окружностей радиуса r можно вписать в большую окружность радиуса R
• • Раздел: Геометрия ( 96 калькуляторов )

 #геометрия #круг Геометрия круг окружность площадь радиус сектор угол хорда

 PLANETCALC, Деление круга на равные части

Timur2020-11-03 14:19:41

Преобразование эллипса в полилинию или группу дуг в AutoCAD

Преобразование эллипса в полилинию или группу дуг в AutoCAD

Добрый день!

В продолжении темы преобразования объектов, которую я начал в сообщении «Преобразование сплайнов в полилинии в AutoCAD» предлагаю сегодня рассмотреть способы преобразования эллипсов в полилинию или группу дуг в AutoCAD.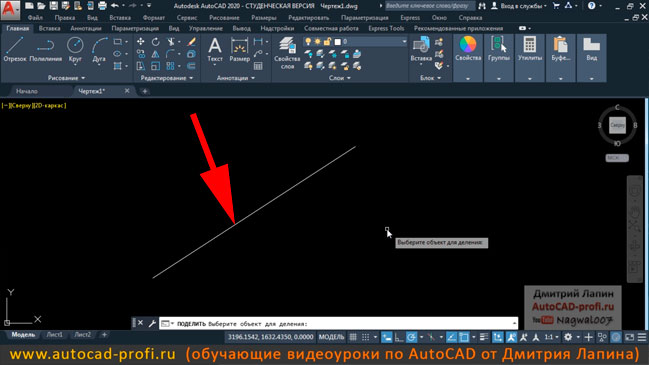

Зачем нужно такое преобразование? Начертить объекты с помощью эллипсов в чертеже легко, но вот использовать их для дальнейших построений практически невозможно. Например, если построить овальную комнату с помощью сплайна, то в итоге все равно придется разбить его на отрезки, чтобы построить стену. Точно также с всевозможными обечайками, баками и другими объектами — при изготовлении эллипсы все равно будут разбиваться на линейные или дуговые сегменты, а потом свариваться в единую поверхность.

Сначала рассмотрим преобразование эллипсов в полилинию, а потом — в дуги.

Преобразование эллипса в полилинию

1. Переменная PELLIPSE 

Перед тем, как начать создавать эллипс, установите значение переменной PELLIPSE равным 1. Эта переменная управляет типом вновь создаваемых эллипсов: 0 — строится реальный эллипс, 1 — создается представление эллипса в виде полилинии.

Точность построения эллипсов с помощью полилиний невысока, но вполне подходит для большинства случаев

Но этот способ годится только для случая, когда вы только собираетесь рисовать эллипсы.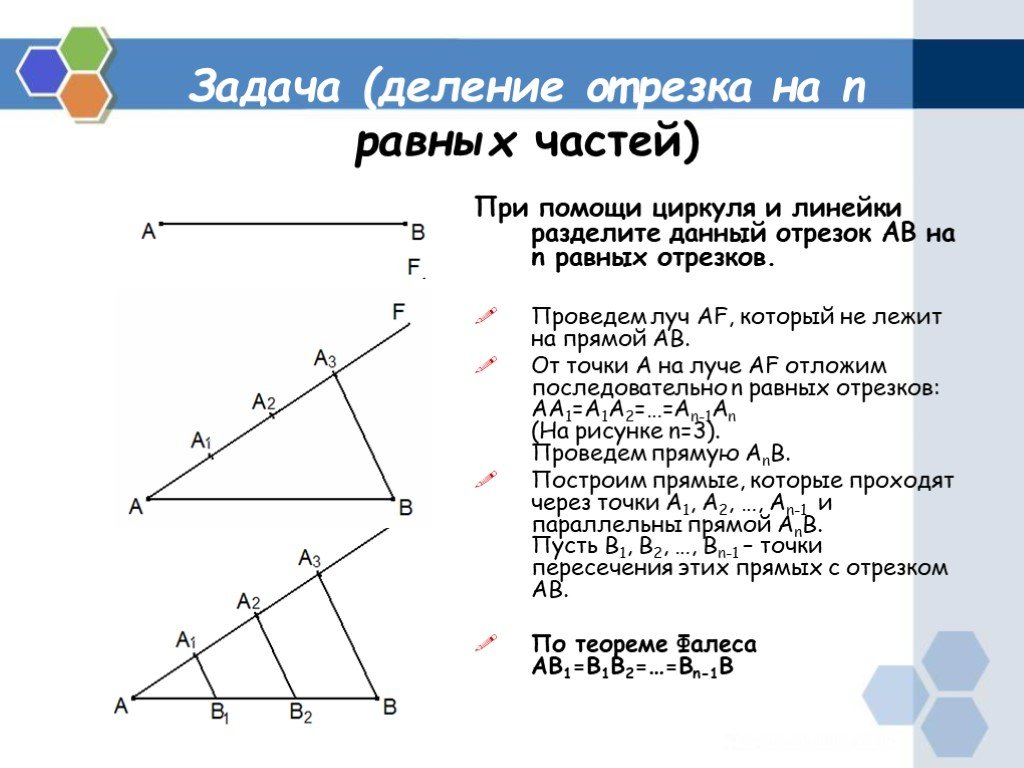 Если вы хотите преобразовать уже созданные, то используйте другой способ

2. Команда ПОДОБИЕ (_OFFSET)

Если построить смещение от эллипса, то вновь созданный эллипс будет построен с помощью сплайна. Т.к. AutoCAD не позволяет создавать нулевое смещение, то необходимо сместить эллипс на некоторое расстояние, удалить исходный эллипс и сместить полученный сплайн обратно. Долго, но представление эллипса с помощью сплайна крайне точное, гораздо выше, чем с помощью полилинии.

О том, как преобразовать сплайн в полилинию я писал в отдельном посте здесь. Управляя параметром точности преобразования можно добиться приемлемого результата по точности построения.

3. Экспорт в формат DXF версии AutoCAD R12

Если сохранить чертеж в формате DXF версии AutoCAD R12, то все эллипсы, которые есть в файле, будут преобразованы в полилинии, поскольку в AutoCAD R12 еще не было понятия эллипсов.

Это самый нежелательный, но самый быстрый способ преобразования. Все эллипсы вычерчиваются с помощью очень маленьких линейных сегментов полилинии, которые занимают большой объем памяти.

Преобразование эллипса в группу дуг

К сожалению, никаких штатных средств преобразования эллипсов в дугу в AutoCAD нет, поэтому придется вспомнить ручное черчение и самостоятельно восстановить дугу. Построения я проводил по классическому справочнику Сергея Бернштейна. 

1. Эллипс из четырех дуг

Способ позволяет построить эллипс из четырех дуг и двух центров.

• Строим эллипс, который хотим представить в виде дуг. Прочерчиваем большую и малые оси эллипса. Расстояние ob — длина большой полуоси, oa — длина малой полуоси.
• Соединяем точки a и b. На полученном отрезке строим точку d, вычислив расстояние ad = ob — oa (разность длин большой и малой полуосей)
• Строим линию, проходящую через середину отрезка bd и перпендикулярный к нему. Пересечение этого отрезка с малой осью даст точку e — центр первой дуги, с большой осью — c — центр второй дуги, с эллипсом — точку f — точку соединения этих дуг.
• Строим дуги из центра e и от точки a до f, из центра c от точки f до b. Остальные дуги получаем операцией симметрии.

Получаем эллипс, вычерченный с помощью четырех дуг. Точность построения невелика, но вполне достаточна для большинства инженерных задач.

2. Эллипс из восьми дуг

Данный способ позволяет построить эллипс из восьми дуг и трех центров.

• Строим эллипс, который хотим представить в виде дуг. Прочерчиваем большую и малые оси эллипса. Расстояние ob — длина большой полуоси, oa — длина малой полуоси.
• Строим отрезки ad, bd и ab. Строим из точки d отрезок, перпендикулярный отрезку ab и продлеваем его до пересечения с малой осью. Полученные точки e и c — центры искомых дуг.
• Строим окружность из точки e радиусом, равным eb. Строим окружность из точки a с радиусом, равным eb. Строим окружность из точки c радиусом, равным cf.
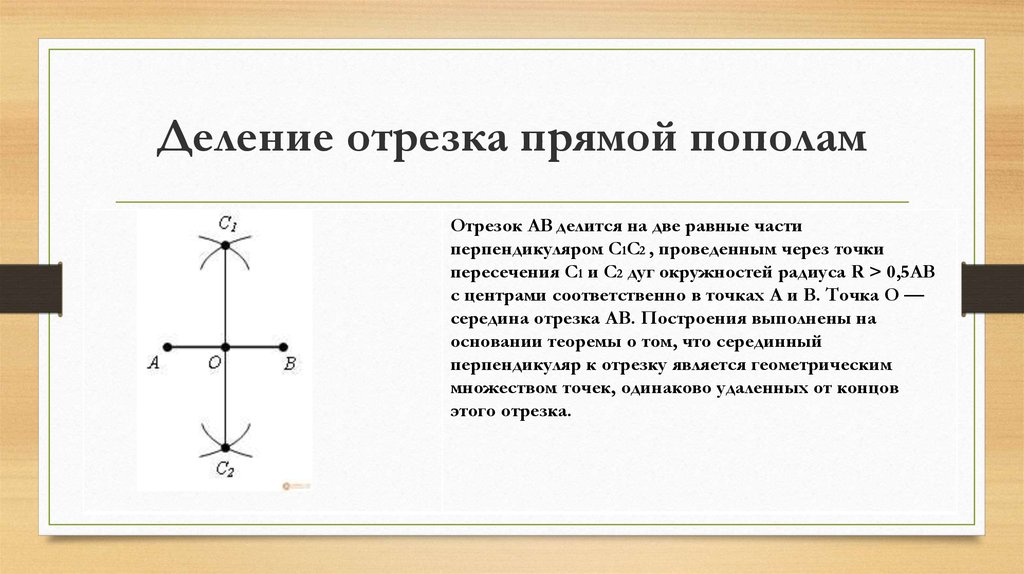  Пересечение окружностей дает точку g — центр третей искомой дуги.
• Строим отрезки ge и от g до пересечения нижней окружности с малой осью. Продлеваем эти отрезки до эллипса — получаем точки h и k, в которых касаются дуги.
• Строим дуги из центров c, e и g. Остальные дуги получаем с помощью симметрии.

Итог такого построения — эллипс, вычерченный из восьми дуг, который точнее повторяет исходную фигуру, чем из четырех дуг.

Процесс геометрических построений можно посмотреть в этом видеоруководстве

С остальными приемами работы в AutoCAD можно ознакомиться на странице блога.

С уважением, Андрей.

---

Как использовать сегменты разделительной линии в AutoCAD (пройдено 100%) 23 марта

5/5 — (117 голосов)

Сегменты разделительной линии Темы статей: AutoCAD разделить | Как использовать сегменты разделительной линии в AutoCAD Привет, ребята, Ранее мы изучили команды X-line и Mline из раскрывающегося меню панели рисования.

Вытяжная панель

На панели рисования доступно множество параметров, связанных с линией.

Мы можем увидеть это, щелкнув раскрывающееся меню рисования.

Подгонка сплайна , Сплайн CV, Несколько точек, Вспомогательная линия, Луч, Мультилиния, Разделение AutoCAD, Измерение , Область, Спираль, Кольцевая, Пометочные облака и т. д. Доступны параметры в раскрывающемся списке панели рисования меню.

Изучим команду AutoCAD разделить.

Разделить сегменты линии в AutoCAD

Команда AutoCAD разделить (Разделить сегменты линии)

Как разделить линию в Автокад?

1 . Эта команда используется для AutoCAD и . Разделите любую линию или объекта на какую-то часть , которую мы хотим.

2. Мы можем вызвать команду «Разделить», выбрав инструмент разделения AutoCAD в раскрывающемся меню панели рисования на вкладке «Главная».

Или просто введите « DIV » в командной строке и нажмите Enter.

3 . Затем выберите линию или объект, который вы хотите разделить.

4 . После выбора объекта AutoCAD спросит, на сколько частей мы хотим разделить линию или объект. Дайте количество частей 1, 2 или по мере необходимости.

5 . Линия или объект автоматически разделятся на равные части и будут показывать точки на линии или объекте.

6 . Для изменения стиля точки, если она очень маленькая или невидимая, перейдите к утилитам ’ и нажмите на раскрывающееся меню.

И выберите « Стиль точки ».

Мы можем изменить стиль точки в диалоговом окне.

Тип наконечника

7 . Мы также можем вставлять свои собственные созданные блоки вместо точек, выбрав опцию « Блок » на панели команд.

8 . Нажмите на блок и дайте имя блоку, который мы создали ранее.

Если вы хотите выровнять блок с объектом, то нажмите на ‘ Да ’, иначе нажмите ‘ Нет ’.

Затем дайте номер деления.

Как создать блок?

1 . Нарисуйте любую форму, которую хотите создать, например, стрелку или что-то еще.

2. затем введите « B » в командной строке.

3 . Нажмите Введите .

4 . Дайте название блока.

5 . Затем нажмите «ОК».

Блок готов к использованию.

Пример сегментов разделительной линии AutoCAD

1 . Например, я хочу разделить линию 3000 мм на 5 частей.

2 . Итак, я выберу разделенную команду из раскрывающегося меню панели рисования.

Или я наберу « DIV » в командной строке и нажму клавишу Enter.

3 . Я выберу линию как объект и дам 5 чисел.

4 . При нажатии на Введите ключ , строка разделится на 5 частей, как показано на рисунке.

Готово.

Узнайте больше о команде AutoCAD «Разделить сегменты линии и измерить» на нашем канале Youtube.

Также прочитайте нашу предыдущую статью

Использование команды РАЗДЕЛИТЬ — Видеоурок по AutoCAD

Из курса: AutoCAD: советы и рекомендации

Видео заблокировано.

Разблокируйте этот курс с бесплатной пробной версией

Присоединяйтесь сегодня, чтобы получить доступ к более чем 20 800 курсам, которые преподают отраслевые эксперты.

Использование команды РАЗДЕЛИТЬ

“

— [Инструктор] Итак, вот еще один совет и прием по AutoCAD. Теперь мы рассмотрим команду разделения, доступную в AutoCAD. Итак, у нас есть для вас новый рисунок, и что мы собираемся сделать, так это разделить нашу линию здесь, которая находится на слое объектов, на группу равных сегментов. И что мы здесь сделаем, так это настроим его так, чтобы он делился на несколько сегментов. Теперь у нас есть еще один совет и трюк AutoCAD, где мы рассмотрели команду измерения, где мы разделили аналогичную линию, но на измеренные сегменты. На этот раз мы собираемся выбрать количество сегментов, а не расстояние для каждого сегмента.