Как определить натуральную величину: Определение натуральной величины отрезка

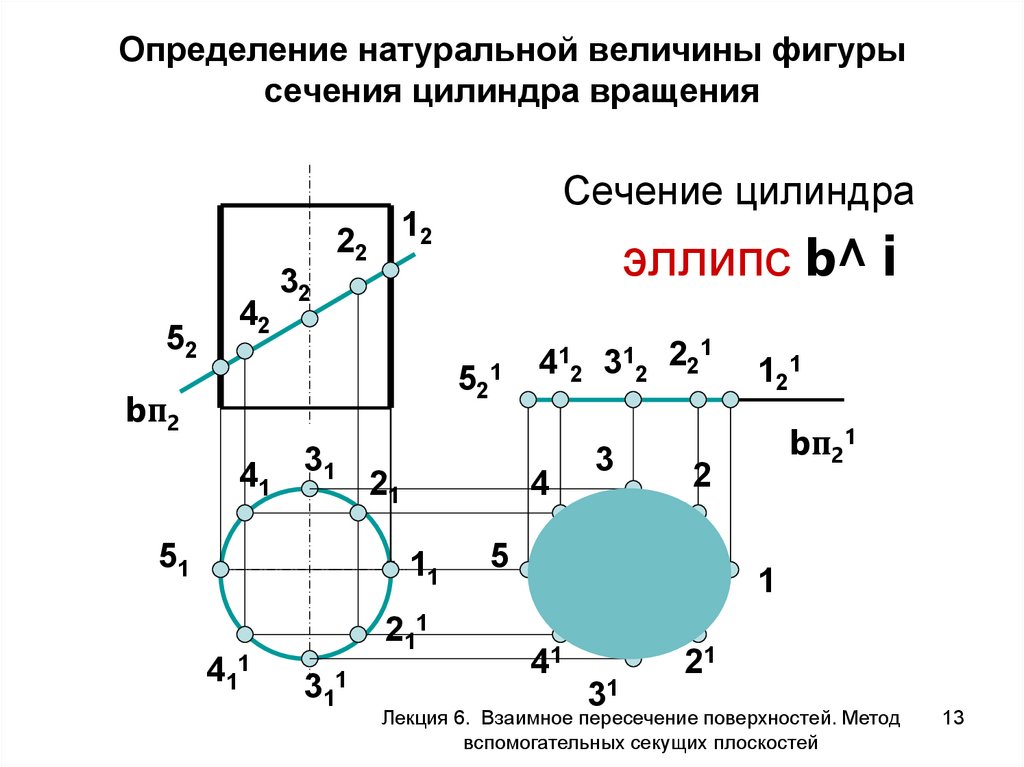
Определение натуральной величины отрезка

Если отрезок параллелен плоскости, то он проецируется на неё без искажений. В остальных случаях для нахождения его натуральной величины применяют метод прямоугольного треугольника или способы преобразования ортогональных проекций.

Содержание

1. Метод прямоугольного треугольника
2. Способ параллельного переноса
3. Поворот вокруг оси

Метод прямоугольного треугольника

Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.

Для того чтобы найти натуральную величину отрезка AB (рисунок выше), строим прямоугольный треугольник A₀A’B’. Его первый катет A’B’ – это горизонтальная проекция AB. Второй катет A’A₀ равен величине Z_A – Z_B, то есть разности удаления точек A и B от горизонтальной плоскости П₁.

Откладываем A’A₀ = Z_A – Z_B перпендикулярно A’B’. Затем проводим гипотенузу A₀B’ треугольника A₀A’B’. На рисунке она обозначена красным цветом. Её величина соответствует настоящей длине AB.

Способ параллельного переноса

Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Например, если перемещать отрезок EF параллельно горизонтальной плоскости П₁, то длина его проекции E’F’ не изменится, когда она займет новое положение E’₁F’₁ (как это показано на рисунке ниже).

Еще одно важное свойство параллельного переноса заключается в том, что при любом перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной плоскости, то её горизонтальная проекция движется по прямой, параллельной оси X.

Пример построения

Чтобы определить действительный размер отрезка EF, на свободном месте чертежа строим его новую горизонтальную проекцию E’₁F’₁ = E’F’ так, чтобы она была параллельна оси X . Затем по линиям связи находим точки E»₁ и F»₁. Расстояние между ними и есть искомая величина, поскольку мы перенесли EF в положение, параллельное фронтальной плоскости.

Метод параллельного переноса, описанный здесь, иногда называют параллельным перемещением. Посмотреть дополнительные примеры и получить более подробную информацию по данной теме можно в этой статье.

Поворот вокруг оси

Для того, чтобы отрезок стал параллелен плоскости проекции и без искажения отразился на ней, он может быть повернут вокруг проецирующей прямой, проходящей через один из его концов.

Пример построения

Определим длину произвольного отрезка MN. Для этого через точку N проводим горизонтально проецирующую прямую i. Вокруг неё поворачиваем MN так, чтобы его проекция M’N’ заняла положение M’₁N’₁, параллельное оси X.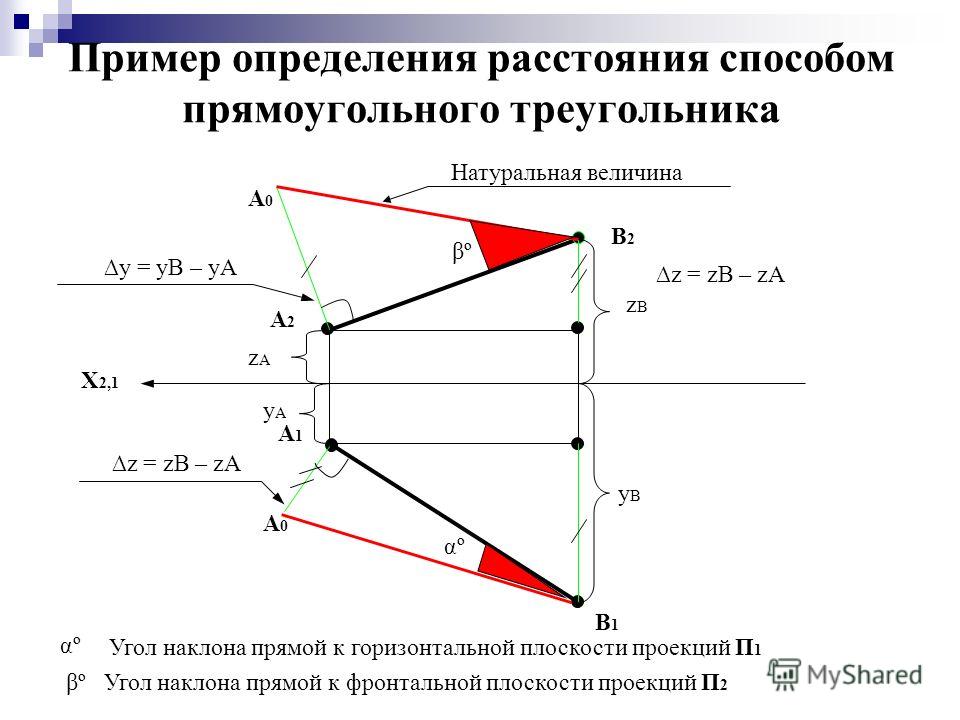

По линиям связи находим точку M»₁. При этом исходим из того, что M» в процессе вращения движется параллельно горизонтальной плоскости.

Точка N не изменит своего положения, так как лежит на оси поворота. Поэтому осталось только соединить N»₁ и M»₁ искомым отрезком. На рисунке он выделен красным цветом.

Более подробную информацию о решении задач методом поворота вокруг оси вы можете получить, ознакомившись со следующим материалом.

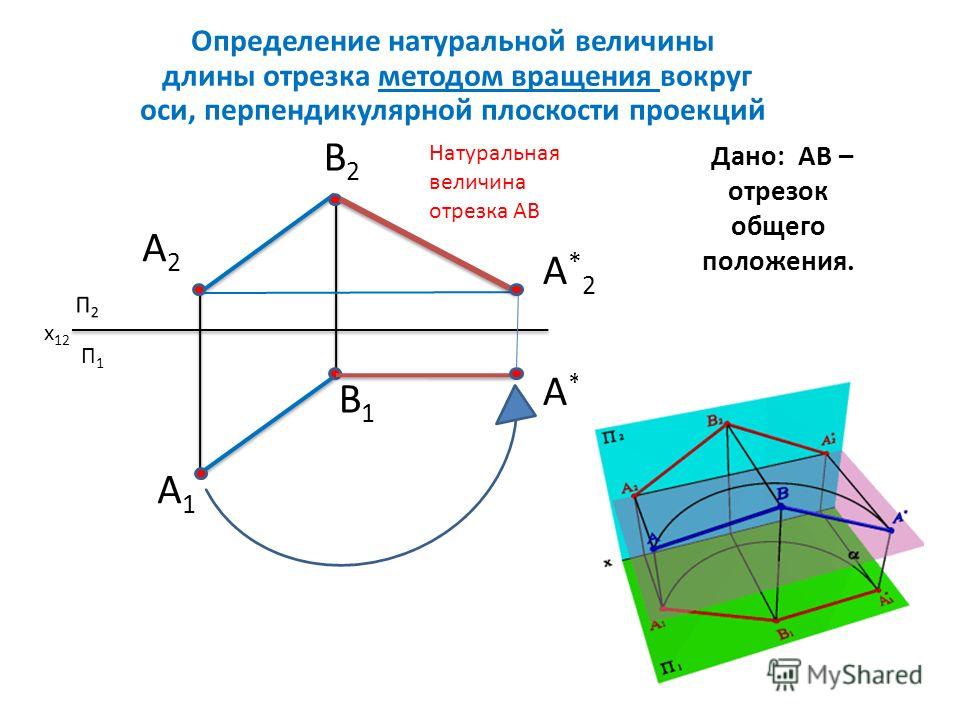
Натуральная величина

Натуральная величина

Натуральная величина — геометрическая характеристика проекции равная исследуемому объекту.

Треугольник (плоская фигура, угол)

Плоская фигура проецируется в натуральную величину при условии параллельности этой фигуры и плоскости проекций. Аналогично, натуральная величина отрезка равна длине проекции, относительно плоскости которой отрезок занимает параллельное положение.

Натуральная величина плоской фигуры занимающей общее положение может быть определена по ортогональной проекции, относительно плоскости которой данная фигура приведена в параллельное положение.

Если исследуется прямой отрезок (линия), то отрезок должен быть приведён к линии уровня и фактически стать параллельным плоскости проекции.

В общем случае, можно использовать два способа: (1) замена плоскостей проекций и (2) плоскопараллельное перемещение. Возможно комбинирование алгоритмов и использование метода прямоугольного треугольника и поворота для совмещения с плоскостью параллельной одной из плоскостей проекций.

Для фигуры занимающей общее положение по отношению к плоскостям проекций, потребуется выполнения двух шагов: (1) приведение к проецирующему положению и (2) приведение к положению уровня. Если фигура занимает положение параллельное плоскости проекции, то проекция этой фигуры будет соответствовать натуральной величине. Проецирующее положение, одновременно, даёт определение угла наклона плоскости к плоскости проекции.

ANGL7896547 метод начертательной геометрии для определения натуральной величины.

Замена плоскостей проекций

Построение натуральной величины треугольника методом замены плоскостей.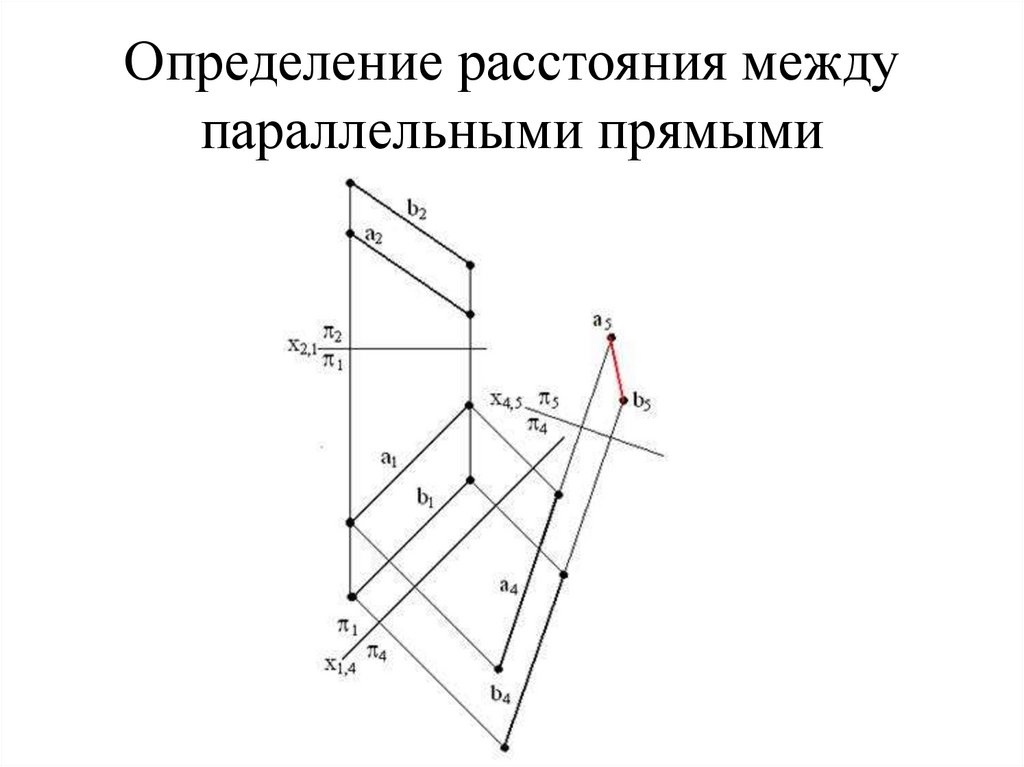

1. На горизонтальной проекции, в треугольнике ABC проведена фронталь f=AF (A₁F₁║OX).
2. Фронтальная проекция f₂ определена по проекционной связи F₁F₂ с условием F₂∈B₂C₂.
3. Замена П₁ на П₄⊥f — в результате ABC занимает положение проецирующее на П₄. A₄B₄C₄ — проецируется в один отрезок, и угол φ соответствует углу наклона плоскости треугольника ABC к фронтальной плоскости проекций П₂.
4. П₅║ABC заменяет П₂. A₅B₅C₅ =ABC — натуральная величина заданного треугольника.

Плоскопараллельное перемещение

1. Плоско-параллельное перемещение до положения f⊥П₁
   ∠γ — наклон плоскости треугольника к фронтальной плоскости проекции.
2. Приведение ABC║П₂

R на первом этапе показывает эквивалентность плоскопараллельного перемещения и метода вращения.

Отрезок прямой линии

Натуральная величина отрезка может быть представлена проекцией относительно которой отрезок занимает параллельное положение. Возможно построение эквивалентного отрезка методом прямоугольного треугольника.

Метод прямоугольного треугольника

На одной из проекций (в примере — горизонтальной) строится прямоугольный треугольник: A₁B₁ — катет (основание), A₁A₀ — катет равный разности координат ΔY_AB, расстояние вдоль оси перпендикулярной к выбранной плоскости. Гипотенуза полученного треугольника равна

натуральной величине отрезка. Угол при основании прямоугольного треугольника равен углу наклона прямой отрезка к горизонтальной плоскости проекции.

Вращение вокруг проецирующей прямой

Вращая отрезок вокруг фронтально (горизонтально) проецирующей прямой, можно перевести его в положение горизонтали (фронтали), тем самым получив натуральную величину на горизонтальной (фронтальной) проекции.

На горизонтальной проекции выполнен поворот точки конца отрезка A вокруг вертикальной оси проходящей через точку B. Вращение выполнено до положения A0
1B
1║OX, B_X=A_X. Фронтальная проекция точки B перемещается вдоль OX сохраняя свою высоту (координату Z) |A0
2B
1|=|AB|.

Замена плоскостей проекций

Построив плоскость проекций параллельно заданному отрезку, можно получить проекцию равную натуральной величине.

Замена плоскостей проекций П

1/П₂→П₄/П₂, П₄║AB. |A₄B₄|=|AB| — натуральная величина отрезка, ∠α=∠α(AB,П₁) — угол наклона прямой к горизонтальной плоскости.

---

Определение истинной величины сечения пирамиды.
Определить натуральную величину.

---

Определение натуральной величины.

Решение задач по начертательной геометрии.

4.8.3: Поиск фактических размеров — K12 LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

8811

Рис. 4.8.3.1

Сэм на окружной ярмарке смотрит на витрины с моделями поездов. Самый маленький из них — это калибр «N» в масштабе 1: 160. Если площадь дисплея составляет 4 фута на 8 футов, какую площадь представляет дисплей?

В этой концепции вы узнаете, как использовать коэффициент масштабирования для определения фактических размеров.

Использование масштабного коэффициента для определения фактических размеров

A   отношение  сравнивает две величины.

Соотношения можно записывать дробями, с двоеточием или со словом «к».

 2/3, 2:3 и «2 к 3» – это соотношения.

Пропорция создается, когда два соотношения оказываются эквивалентными или равными.

1/2=3/6 — пропорция.

A   единица скорости  является сравнением двух измерений, одно из которых имеет значение 1.

55 миль в час, 55 миль/1 час является единицей скорости.

A   единица масштаба   – это коэффициент, с помощью которого размеры реального объекта сравниваются с размерами чертежа или модели в масштабе, которые представляют реальный объект. Ни одно из значений в единицах шкалы не должно равняться 1. 

Единица измерения на карте может выглядеть так: 1/2 дюйма = 100 футам.

Соотношение будет записано как  0,5/100  .

Чтобы изобразить линию длиной 500 футов, в единицах измерения можно нарисовать линию длиной 2 (1/2) дюйма.

Линия длиной 4 дюйма соответствует реальной линии длиной 800 футов.

Масштабы и пропорции единиц могут использоваться для расчета фактических расстояний по картам, чертежам или моделям.

Фактические расстояния могут быть представлены на картах, чертежах или моделях с использованием шкалы единиц измерения.

A  Масштабный коэффициент  похоже на шкалу единиц измерения. Это соотношение, которое сравнивает масштабные размеры с фактическими размерами.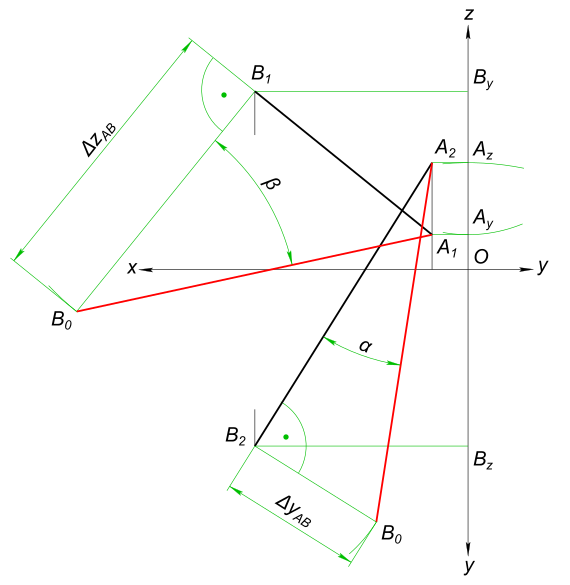 Он отличается тем, что не дает никаких конкретных единиц.

Масштабный коэффициент для чертежа в масштабе может быть 1/200, что означает, что фактический размер в 200 раз больше размера чертежа.

Масштабные коэффициенты можно использовать для определения как масштаба, так и фактических размеров или размеров.

Примеры

Пример 4.8.3.1

Ранее вам дали задачу о демонстрации моделей поездов на ярмарке.

Наименьший из них — N-метр в масштабе 1:160. Если площадь дисплея составляет 4 фута на 8 футов, какую площадь представляет дисплей?

Решение

Сначала запишите коэффициент масштабирования.

масштаб/факт = 1/160

Затем напишите отношения, представляющие неизвестные фактические длину и ширину дисплея, к масштабу длины и ширины дисплея.

Длина=масштаб/фактическая=8/ш

Ширина=масштаб/фактическая=4/л

Затем напишите две пропорции, установив два отношения длины равными друг другу и два отношения ширины равными друг другу.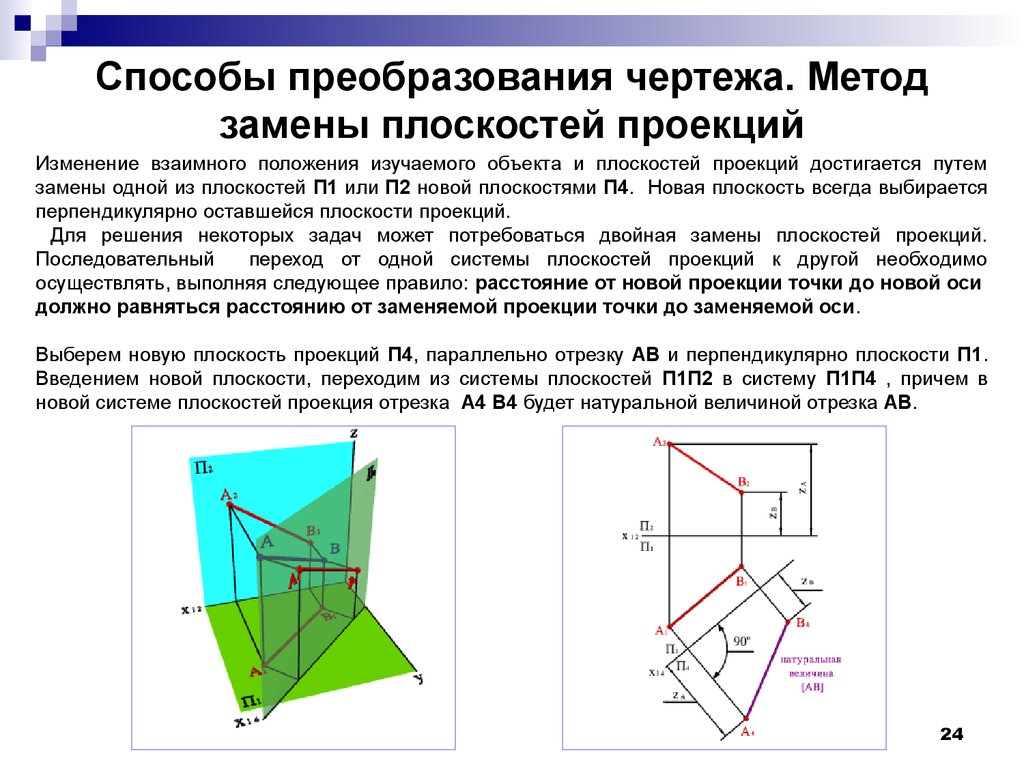 Данной единицей являются футы.

Длина=4/l=1/160

Ширина=8/w=1/160

Затем перемножьте каждое уравнение крест-накрест.

Д=4×160

Д=640 футов

Ш=8×160

Ш=1280 футов

Затем, чтобы найти площадь дисплея, умножьте длину на ширину.

640 футов × 1280 футов = 819 200 квадратных футов

Ответ: 819 200 квадратных футов.

Пример 4.8.3.2

Небольшой самолет с размахом крыла 16 футов. Масштабный коэффициент для модели – 1/48. Найдите размах крыла модели в дюймах.

Решение

Сначала запишите масштабный коэффициент.

масштаб/факт = 1/48

Затем напишите отношение фактической длины размаха крыльев к неизвестной длине размаха крыльев по шкале.

scale/actual=w/16

Затем напишите пропорцию, установив два отношения равными друг другу. Помните, что футы — это единственная единица измерения.

1/48=w/16 

Затем перекрестно умножьте.

48ш=16

ш=13

Затем переведите футы в дюймы.

1/3 фута × (12/1) дюймов/фут=4 дюйма

Ответ: 4 дюйма. Размах крыльев модели самолета составит 4 дюйма.

Пример 4.8.3.3

Самая длинная сторона треугольной клумбы составляет 5,5 метра. Лия хочет сделать чертеж клумбы в масштабе. Масштабный коэффициент для ее рисунка будет 1/20. Какой длины будет самая длинная сторона клумбы на ее рисунке?

Раствор

Сначала запишите коэффициент масштабирования.

масштаб/факт = 1/20

Затем напишите отношение фактической длины стороны к неизвестной масштабной длине стороны.

масштаб/факт = 1/5,5

Затем напишите пропорцию, установив два отношения равными друг другу. Единственная указанная единица – метры.

1/20=1/5,5

метра

Далее умножьте крест.

5,5=20 л

л=0,275 метра

Затем переведите метры в сантиметры.

0,275 метра × (100/1) см/м=2,75 см

Ответ: 27,5 сантиметра.

Пример 4.8.3.4

Муравей, которого заметила Элисон, был слишком мал, чтобы его можно было нарисовать в натуральную величину.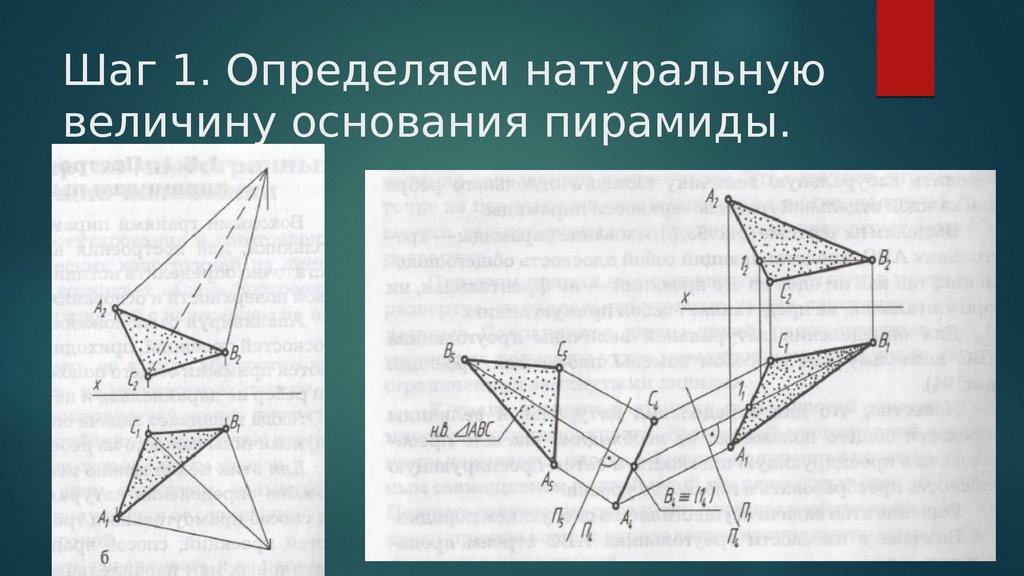 Итак, Элисон сделала рисунок в масштабе, показанный ниже. Масштабный коэффициент для рисунка равен 5. Найдите фактическую длину наблюдаемого муравья Элисон.

Рисунок 4.8.3.2

Решение

Сначала запишите коэффициент масштабирования.

scale/actual=5/1

Затем напишите отношение, представляющее неизвестную фактическую длину муравья к масштабной длине муравья.

масштаб/фактическое значение=2,75/л

Затем напишите пропорцию, установив два отношения равными друг другу. Сантиметры — единственная заданная единица измерения.

5/1=2,75/1 см

Затем перекрестное умножение.

2,75=5 л

л=0,55

л=0,55 см

Затем переведи сантиметры в миллиметры.

0,55 см × (10/1) мм/см=5,5 мм

Пример 4.8.3.5

На приведенном ниже чертеже в масштабе показан прямоугольный ковер. Масштабный коэффициент для чертежа – 1/24. Какова площадь в квадратных футах фактического ковра?

Рисунок 4.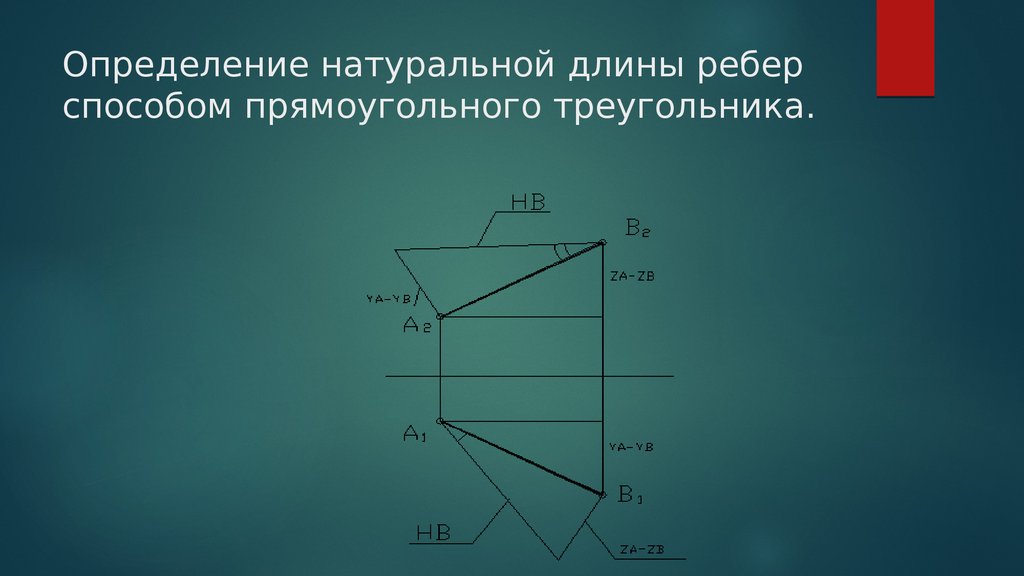 8.3.3

Решение

Сначала запишите коэффициент масштабирования.

масштаб/факт = 1/24

Затем напишите соотношения, представляющие неизвестные фактические длину и ширину ковра к масштабу длины и ширины ковра.

scale/actual=4/1     scale/actual=2/w

Затем напишите две пропорции, установив два отношения длины равными друг другу и два отношения ширины равными друг другу. Данной единицей измерения являются дюймы.

Длина=4/l=12/4

Ширина=2/w=12/4

Затем перемножьте каждое уравнение крест-накрест.

Д=4×24

Д=96 дюймов

Ш=2×24

Ш=48 дюймов

Затем, чтобы найти площадь ковра, умножьте длину на ширину.

96″×48″=4608 кв. дюймов

Ответ: 4608 кв. дюймов.

Обзор

Решите каждую проблему. Имейте в виду, что несколько задач могут состоять из нескольких частей.

1. Кэлвин нарисовал карту своего района. Масштабный коэффициент, который он использовал для своей карты, был 1/800. Фактическое расстояние между домом Кальвина и домом его лучшего друга Фрэнка составляет 80 метров. Каким должно быть расстояние в сантиметрах между этими двумя точками на его масштабном чертеже?
2. Если расстояние от дома Кальвина до парка составляет 40 метров, каково это расстояние в сантиметрах?
3. Если расстояние от дома Кальвина до магазина на углу в два раза больше, чем расстояние от его дома до дома Фрэнка, то каким будет расстояние на карте в сантиметрах?
4. Если бы расстояние от дома Кэлвина до дома его бабушки было на полпути между его домом и домом Фрэнка, каким было бы это расстояние на карте в сантиметрах?
5. Мадлен построила модель лодки. Фактическая длина лодки составляет 24 фута. Масштабный коэффициент, который она использовала для модели, был 1/36. Какой должна быть длина модели лодки в дюймах?
6. Если бы масштабный коэффициент был 1/72, какова была бы длина модели лодки в дюймах?
7. Металлическая труба длиной 2,5 метра. Джош хочет сделать чертеж трубы в масштабе. Масштабный коэффициент для его рисунка будет 1/100. Какой длины в сантиметрах будет металлическая труба на его чертеже?
8. Сидра заметила комнатную муху, которая была слишком мала, чтобы ее можно было нарисовать в натуральную величину. Поэтому она сделала чертеж в масштабе, используя 10 в качестве масштабного коэффициента. Фактическая длина комнатной мухи составляла 8 миллиметров. Какова длина комнатной мухи на рисунке Сидры в миллиметрах?
9. Какова длина комнатной мухи на рисунке Сидры в сантиметрах?
10. Луис сделал масштабную модель собачьей будки, которую собирается построить. Масштабный коэффициент, который он использовал для этой модели, был 1/24. Он хочет, чтобы реальная высота собачьей будки была 6 футов. Какой должна быть высота собачьей будки в его масштабной модели?
11. Жан-Марк использовал масштабный коэффициент 5, чтобы сделать этот масштабный рисунок мотылька.

Рисунок 4. 8.3.4

На рисунке размах крыльев бабочки составляет 3 сантиметра. Каков фактический размах крыльев в миллиметрах у мотылька, которого наблюдал Жан-Марк?

12. Ниже приведен чертеж бассейна в масштабе. На чертеже в масштабе диаметр бассейна составляет 1 (1/2) дюйма. Масштабный коэффициент чертежа – 1/72. Каков фактический диаметр бассейна в футах?

Рисунок 4.8.3.5

13. Барбара сделала масштабную модель монумента Вашингтона. Масштабный коэффициент для ее модели – 1/1332. Высота ее модели составляет 5 дюймов. Какова реальная высота памятника Вашингтону в футах?
14. Ниже приведена карта городского парка. Эта карта была создана с использованием масштабного коэффициента 1/300.

Рисунок 4.8.3.6

1. На карте расстояние между песочницей и качелями 2,5 сантиметра. Какое фактическое расстояние между песочницей и качелями в метрах?
2. На карте расстояние между песочницей и джунглями составляет 1,7 сантиметра.
   Каково фактическое расстояние между песочницей и тренажерным залом в метрах?

15. На приведенном ниже рисунке в масштабе показан пол спальни Джулиана.

Рисунок 4.8.3.7

Масштабный коэффициент для чертежа – 1/200.

1. Каковы размеры фактического этажа в метрах?
2. Какова площадь фактического этажа в квадратных метрах?

Обзор (ответы)

Чтобы просмотреть ответы на обзор, откройте этот файл PDF и найдите раздел 5.13.

Дополнительные ресурсы

Видео:

PLIX Interactive:  Эскиз футбольного стадиона

Практика:  Найти фактические размеры

---

Эта страница под названием 4.8.3: Find Actual Dimensions распространяется по не объявленной лицензии и была создана, изменена и/или курирована CK-12 Foundation с использованием исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   СК12

2. Теги

   1. источник@https://www.ck12.org/c/measurement

Видео с вопросами: расчет размера изображения на основе увеличения и фактического размера ячейки

Стенограмма видео

Студент нарисовал клетку животного, которую он наблюдал под микроскопом. Диаметр клетки, которую они нарисовали, составлял 100 миллиметров, но реальный размер ячейка была 0,01 миллиметра.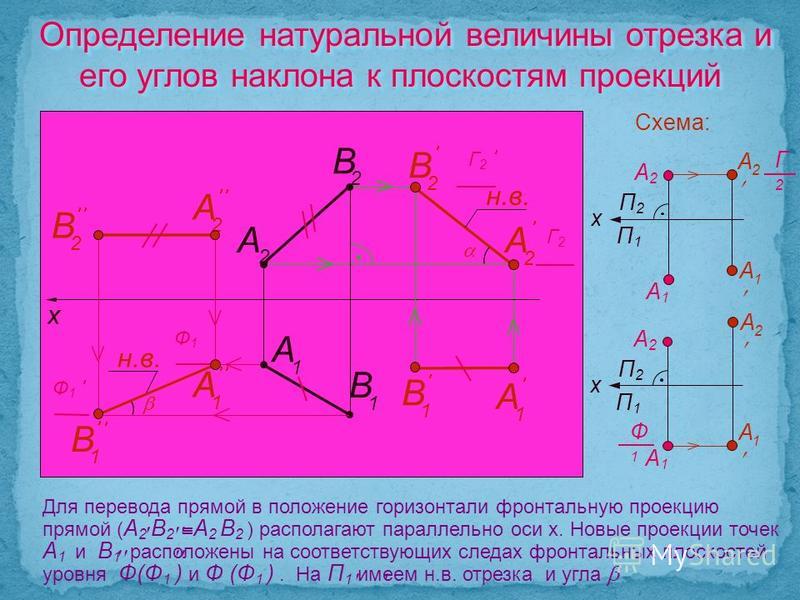 Во сколько раз рисунок был больше реальной клетки?

В этом вопросе мы говорим о том, что рисунок больше, чем объект. нарисовано, что означает, что изображение увеличено. Ученик смог нарисовать клетку, потому что использовал микроскоп с увеличением. изображение ячейки, чтобы ее можно было увидеть.

Увеличение — это процесс визуального увеличения объекта. Когда микроскоп увеличивает объект, он использует для этого увеличительные линзы. В обычном световом микроскопе обычно используются две увеличительные линзы. Ближайшая к предмету линза называется линзой объектива, а линза, на которую просматривается линза окуляра.

Чтобы посмотреть на клетку, ее нужно поместить на предметное стекло. Затем слайд помещается на сцену, и источник света освещает его снизу. через объект на слайде. Затем световые лучи попадают в линзу объектива, которая преломляет их, образуя увеличенное изображение. изображение. Затем световые лучи проходят от этого изображения через линзу окуляра, увеличивая изображение. изображение дальше. Когда мы смотрим в окуляр, мы видим это окончательное увеличенное изображение. Увеличение каждого объектива указано сбоку.

Обычный школьный микроскоп имеет три или четыре объектива от 4х до до 100 раз и линзу окуляра, которая обычно имеет 10-кратное увеличение. Общее увеличение объекта вычисляется путем умножения увеличения линзы окуляра на увеличение используемого объектива. Итак, если бы мы использовали объектив с наименьшим увеличением, увеличение было бы 10 умножить на четыре, что равно 40. При использовании объектива с самым большим увеличением это будет 10, умноженное на 100, что дает нам увеличение в 1000 раз.

Итак, если бы мы использовали самый мощный объектив, чтобы посмотреть на объект размером 0,02 миллиметра в диаметре, какого размера будет окончательное изображение? Чтобы понять, как это вычислить, давайте воспользуемся треугольником уравнения увеличения. Чтобы использовать это, мы просто покрываем переменную, которую хотим узнать, здесь размер изображение. Это оставляет нам 𝐴, умноженное на 𝑀, что означает, что диаметр фактического объекта, умноженное на общее увеличение, равно диаметру изображения. Если мы посмотрим на этот пример, мы умножим диаметр фактического объекта на 0,02. миллиметров, при общем увеличении, 1000. Это дает нам окончательный диаметр изображения 20 миллиметров.

Если бы нас попросили рассчитать увеличение по размеру объекта и размер изображения, как бы мы это вычислили? Итак, мы хотим рассчитать общее увеличение. Итак, мы хотим, чтобы это было по одну сторону от знака равенства. Поэтому нам нужно изменить формулу. На данный момент увеличение умножается на диаметр фактического объект. Чтобы избавиться от этого, оставить увеличение само по себе, мы должны сделать противоположное умножение, то есть деление. Итак, мы делим левую часть на диаметр фактического объекта.

Правило с уравнениями состоит в том, что все, что вы делаете с одной стороной, вы делаете с другой, чтобы держите его сбалансированным. Следовательно, нам также нужно разделить правую часть на диаметр фактического объект. В левой части уравнения диаметр фактического объекта наверху и нижняя компенсация. Затем мы остаемся с уравнением, что общее увеличение равно диаметру изображения. разделить на диаметр фактического объекта. Это также показано в треугольнике увеличения. Если вы закроете 𝑀 для увеличения, останется 𝐼, диаметр изображения, над 𝐴, диаметр фактического объекта.

Давайте рассмотрим пример. Если диаметр изображения составляет 50 миллиметров, а диаметр фактического объекта составляет 0,01 миллиметра, мы можем подставить их в наше уравнение, вот так. Это означает, что общее увеличение равно 50, деленное на 0,01, что составляет 5000. раз. Это уравнение также можно использовать для расчета, во сколько раз больше рисунок.