Учебный элемент по теме «Сопряжение окружностей»
ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ «МНОГОПРОФИЛЬНЫЙ ЛИЦЕЙ»
учебная дисциплина
«ОСНОВЫ ЧЕРЧЕНИЯ»
УЧЕБНЫЙ ЭЛЕМЕНТ № 7
Раздел: Геометрические построения.
Тема раздела: Сопряжение окружностей.
Рассматриваемые вопросы:
— правила выполнения сопряжения;
— сопряжение прямой линии с окружностью;
— внешнее сопряжение двух окружностей;
— внутреннее сопряжение двух окружностей;
— смешанное сопряжение двух окружностей.
с. Амурзет
Внимание!
Учебный элемент (далее УЭ) предназначен для самостоятельного изучения учебного материала, как на уроках, так и при внеаудиторной подготовке.
В структуру УЭ входят четыре части:
Теоретическая часть, часть в которой для приобретения теоретических знаний излагается учебный материал по теме урока.

Практическая часть, для получения первоначального практического опыта дается задание, которое необходимо выполнить по аналогии.
Графическая часть, в этой части для закрепления первоначального опыта и развития умений выполняется индивидуальное задание.
Контрольно-обобщающая часть, выполнение тестовых и контрольных заданий позволяет закрепить теоретические знания и практический опыт, а так же проследить уровень усвоения учебного материала.
Задания и упражнения теоретической и контрольно-обобщающей части выполняются в тетради, задания практической и графической части выполняются на чертежных форматах. Все работы формируются в индивидуальную папку.
Количество и качество выполненных работ является основанием для допуска к итоговой работе, после изучения всего курса «Основы инженерной графики».
Условные обозначения:
ПР— практическая работа;
ГР— графическая работа;
Т/З— тестовое задание;
I.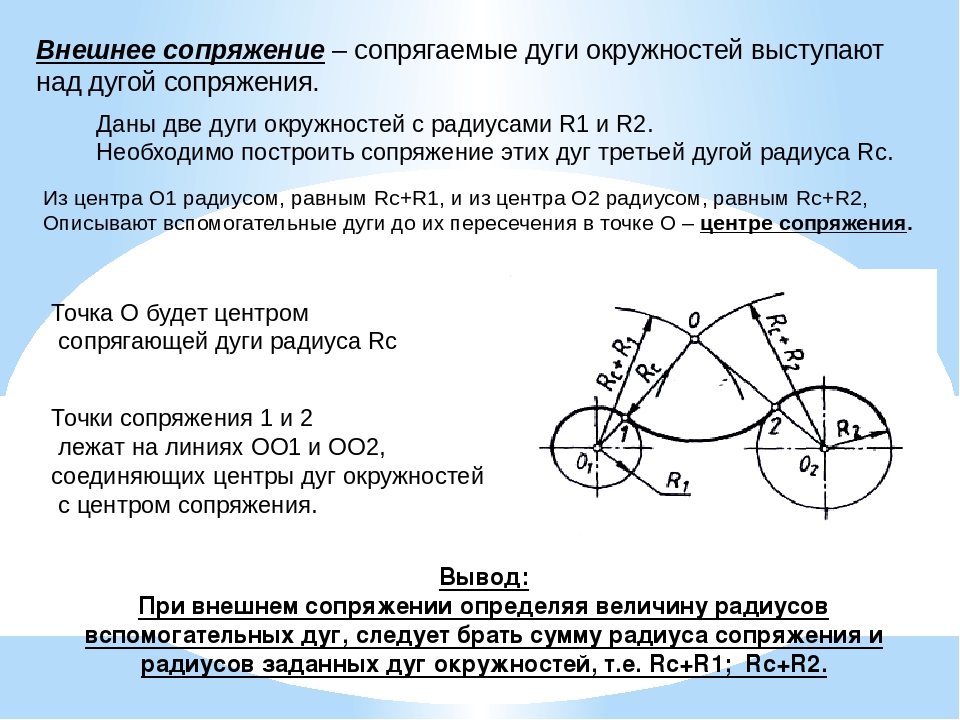 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. Правила выполнения сопряжения
Если радиус сопряжения RC прямой линии и окружности радиусом R задан, то при определении параметров сопряжений следует исходить из следующих положений:
а) множество точек, удаленных от прямой на расстояние Rc, есть две параллельные прямые, отстоящие от заданной на расстояние Rc;
б) множество точек, удаленных от окружности на расстояние Rc, есть две концентрические окружности, радиусы которых равны сумме или разности R и Rc;
в) точки пересечения множеств, указанных в пунктах «а» и «б», являются центрами сопряжений;
г) точка сопряжения с заданной прямой есть основание перпендикуляра, опущенного из центра сопряжения на прямую;
д) точка сопряжения с заданной окружностью лежит на прямой, соединяющей центр этой окружности с центром сопряжения.
По положению центра заданной окружности и центра сопрягающей дуги относительно общей касательной различают внешнее и внутреннее сопряжения.
Если центр окружности и центр сопряжения лежат по разные стороны от касательной, то такое сопряжение считают внешним, а если эти центры располагаются по одну сторону от касательной, — внутренним.
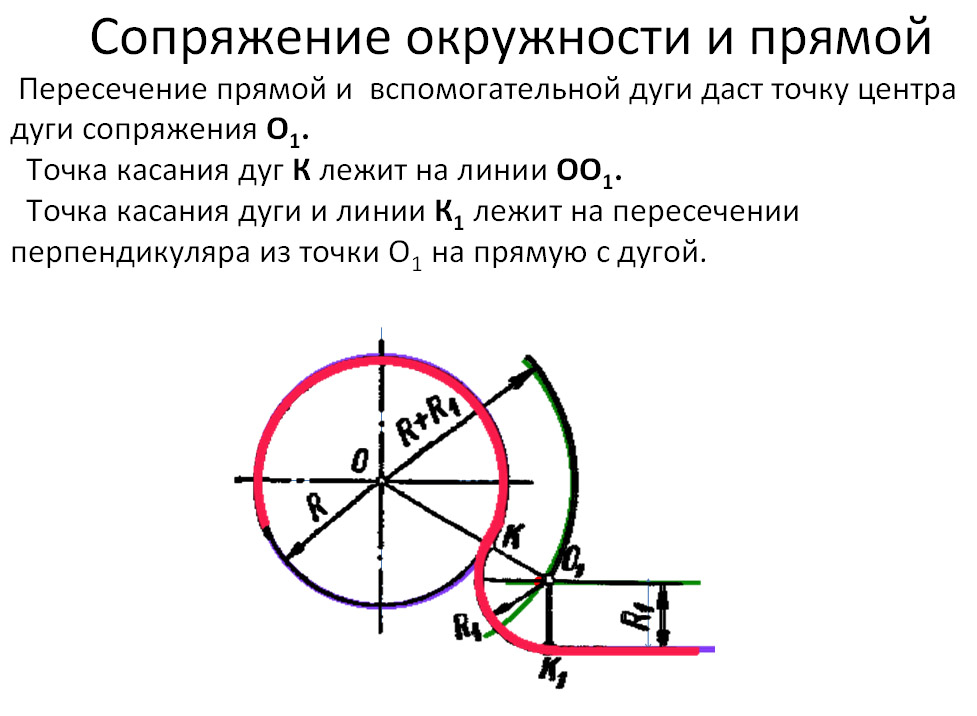
2. Сопряжение прямой линии с окружностью
Задана окружность радиусом R с центром в точке «О» и прямая АВ.
Требуется выполнить внешнее сопряжение окружности и прямой дугой окружности радиусом Rc.
Выбрав на прямой АВ произвольную точку М, восстановим из нее перпендикуляр к АВ и отложим на нем отрезок MN, равный Rc.
Через точку N проведем прямую, параллельную АВ (см. п. «а»).
Из точки «О», как из центра, радиусом R2, равным сумме радиусов R1 и Rc, проведем дугу окружности (см. п. «б»).
Точка С пересечения прямой, проходящей через точку N, с дугой радиусом R2 является центром сопряжения (см. п. «в»).
Из точки С опустим перпендикуляр на АВ. Основание К2 перпендикуляра и будет точкой сопряжения с прямой (см. п. «г»).
п. «г»).
Соединим точки «О» и «С» прямой линией. Пересечение прямой с заданной окружностью определяет точку сопряжения А’, (см. п. «д»).
Завершая построение, следует из центра С радиусом Rc провести дугу окружности от точки K1 до точки К2.
Рисунок 1.
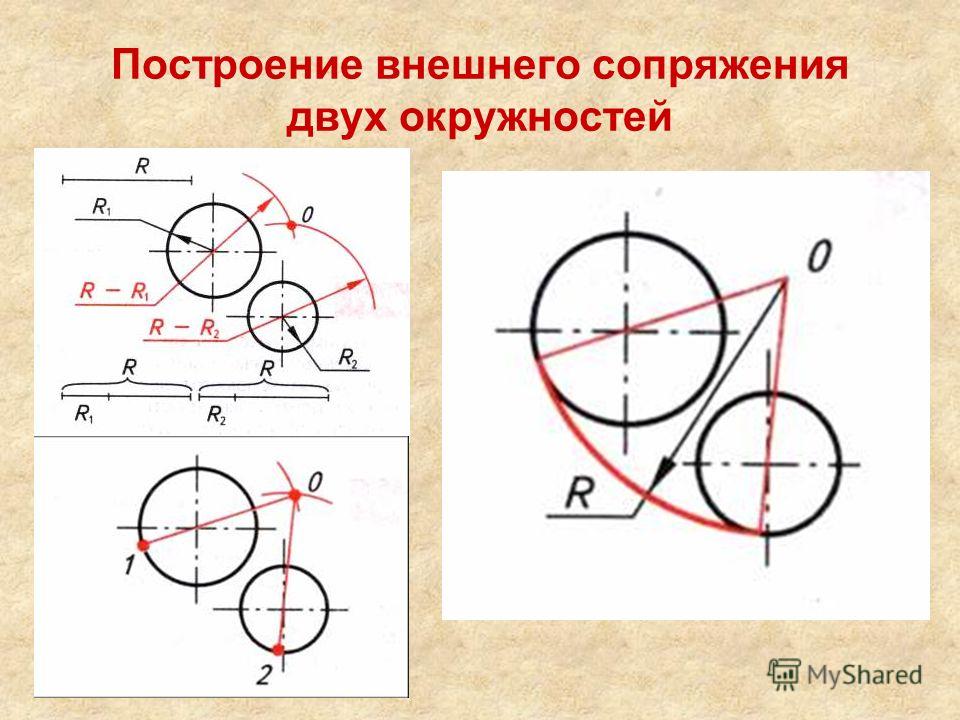
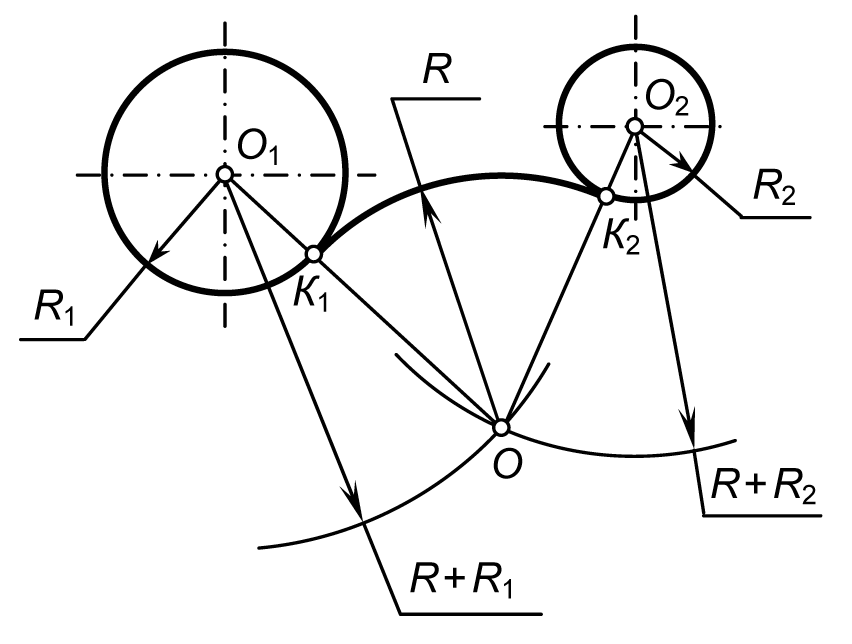
3. Внешнее сопряжение двух окружностей
Заданы окружности с центрами в точках О1 и О2, имеющие радиусы R1 и R2 соответственно.
Требуется выполнить внутреннее сопряжение этих окружностей дугой окружности радиусом RС.
Из центра О1 проводят дугу окружности радиусом R3, равным сумме радиусов R1 и Rc, а из центра О2 — дугу окружности радиусом R4, равным сумме радиусов R2 и RС.
Точка С пересечения этих дуг является центром сопряжения, а точки К1 и К2 пересечения прямых О1С и О2С с соответствующими окружностями- точками сопряжения.
Определив основные параметры сопряжения, можно из центра С между точками К1 и К2 провести дугу окружности радиусом Rc.
Рисунок 2.
4. Внутреннее сопряжение двух окружностей
Если необходимо выполнить внутреннее сопряжение окружностей с радиусами R1, и R2 и центрами соответственно в точкам О1 и О2 , то для определения центра их сопряжения С надо провести дуги окружностей радиусами R3 и R4, равными разностям радиуса сопряжения Rc и соответственно радиусов R1 и R2 заданных окружностей.
Точки К1 и К2 сопряжения будут находиться на продолжении прямых, соединяющих центр С сопряжений с центрами окружностей О1 и О2.
Рисунок 3.
5. Смешанное сопряжение двух окружностей
Если же радиус сопряжения Rc задан и для одной из окружностей (с центром О1 и радиусом R1) следует выполнить внутреннее сопряжение, а для другой (с центром О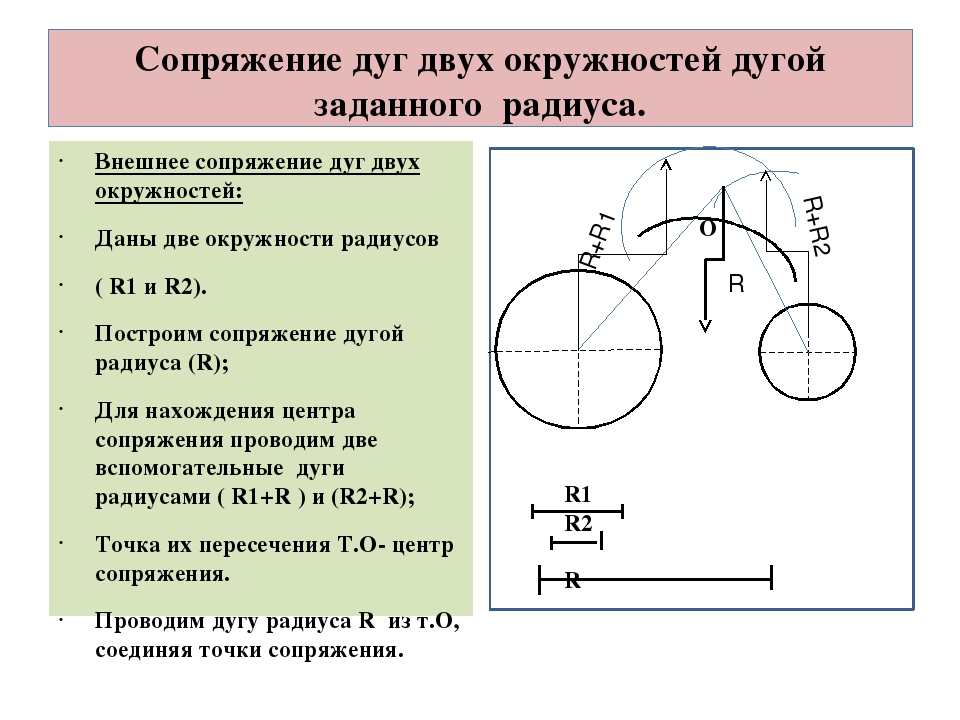
При этом точка сопряжения К1 будет находиться на пересечении прямой О1С с окружностью радиусом R1 , а точка сопряжения К2 — на пересечении окружности радиусом R2 с продолжением прямой О2 С.
Рисунок 4.
II. ПРАКТИЧЕСКАЯ ЧАСТЬ
ПР № 8. Сопряжение окружностей.
Задание 1. По аналогии построить сопряжение окружности и отрезка.— радиус окружности 50.
— радиус сопряжения 15.
Задание 2. По аналогии построить внешнее сопряжение двух окружностей.— радиус окружности 50.
— радиус сопряжения 15.
Задание 3. По аналогии построить внутреннее сопряжение двух окружностей.— радиус окружности 50.
— радиус сопряжения 15.
Задание 4. По аналогии построить смешанное сопряжение двух окружностей.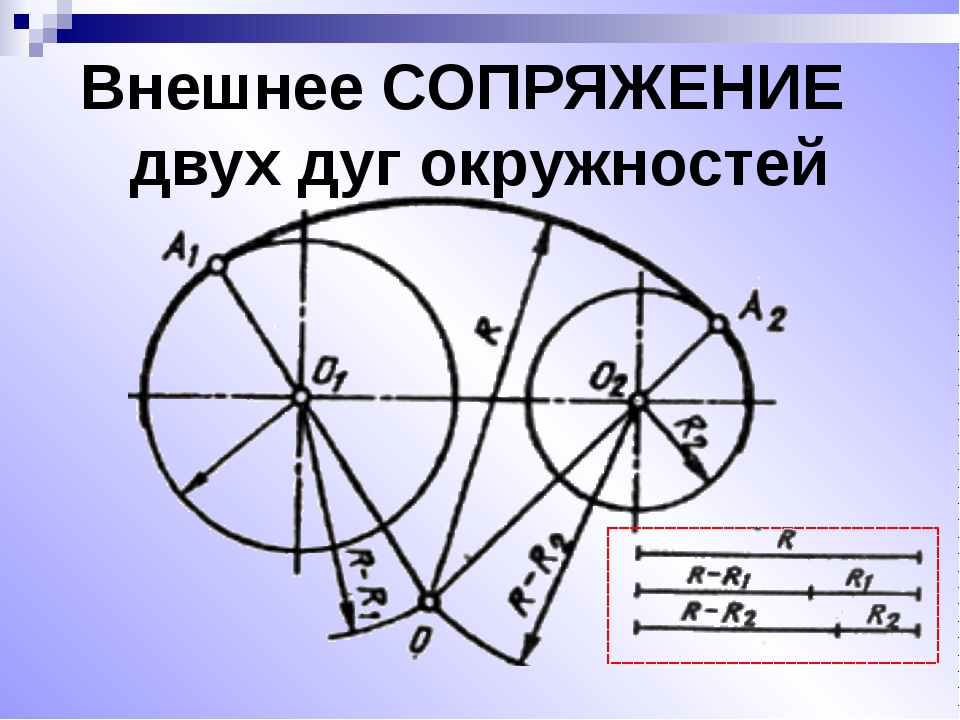
— радиус окружности 50.
— радиус сопряжения 15.
III. ГРАФИЧЕСКАЯ ЧАСТЬ
ГР № 7. Чертеж детали с сопрягаемыми поверхностями.
Задания.
— оформить формат А4.
— выполните чертеж детали с применением приемов сопряжения.
Образец оформления работы.
IV
1. Дать определение сопряжения.
2. Перечислить этапы построения сопряжения.
3. Что такое внешнее сопряжение?
4. Какое сопряжение называется внутренним?
5. Дать определение внешневнутреннего сопряжения.
6. Пересечением каких геометрических множеств точек получается центр дуги, сопрягающей две окружности?
7. Как определить точку сопряжения двух окружностей?
8. Как определить центр дуги, сопрягающей две прямые линии?
Как определить центр дуги, сопрягающей две прямые линии?
9. Как определить точку сопряжения окружности с прямой линией?
10. При пересечении каких геометрических множеств точек получается центр дуги, сопрягающей окружность с прямой линией?
Сопряжения. Виды сопряжений, их элементы, последовательность построений.
Урок черчения в 8 классеТема: Сопряжения. Виды сопряжений, их элементы, последовательность построений.Слайд 1.
Цели: привитие интереса к предмету «Черчение», развитие умений использовать полученные знания в практической деятельности.
Задачи урока:
познакомить обучающихся с применением сопряжений в технических формах;
научить выполнять основные виды сопряжений, понимать принцип построения сопряжений;
развивать логическое мышление, познавательный интерес, умение работать чертежными инструментами; воспитывать точность и аккуратность, внимательность и усидчивость.

Оборудование:
Материалы и инструменты: рабочая тетрадь, чертежная бумага формата А4 и инструменты.
Ход урока
І. Организационный момент (2 мин.)
Учитель:
Добрый день, я приветствую Вас!
На хорошей волне начинаем урок!
Я уверен: все свершится у нас.
И знания пригодятся нам впрок!
Объявление темы и целей урока.
ІІ. Актуализация опорных знаний (5 мин.)
Учитель. В окружающей жизни мы часто встречаемся с предметами, форма которых имеет плавные переходы. Это: мобильные телефоны, автомобили, посуда и др. В предыдущих классах на уроках изобразительного искусства вы выполняли изображения различных животных, фигуры, которых также имели плавные переходы(см.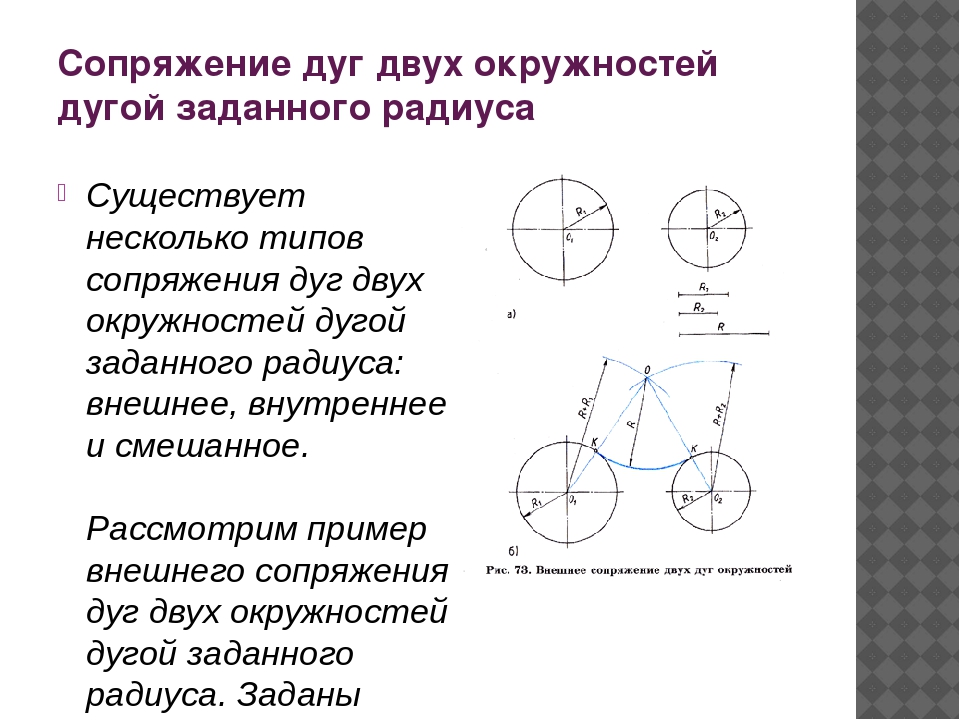 рис. 1).Слайд 2.
рис. 1).Слайд 2.
Рис. 1
ІІІ. Изложение нового материала (10 мин.)
Сопряжением называется плавный переход от одной линии к другой.
Применение сопряжений очень разнообразно и многопланово в технической деятельности человека.
Сопряжения используют:
Слайд 3.
Рис.2Рис.3
(см. рис. 4).
(см. рис.5).Слайд 4.
Рис.4Рис.5
Сопряжения в технических деталях, предметах, изделиях применяют с целью: увеличения прочности, удобного и безопасного обращения, уменьшения коррозии деталей, учета эстетических требований.
При изучении сопряжений очень важно понять принцип их выполнения.
Для построения сопряжения надо найти центры, из которых проводят дуги, т.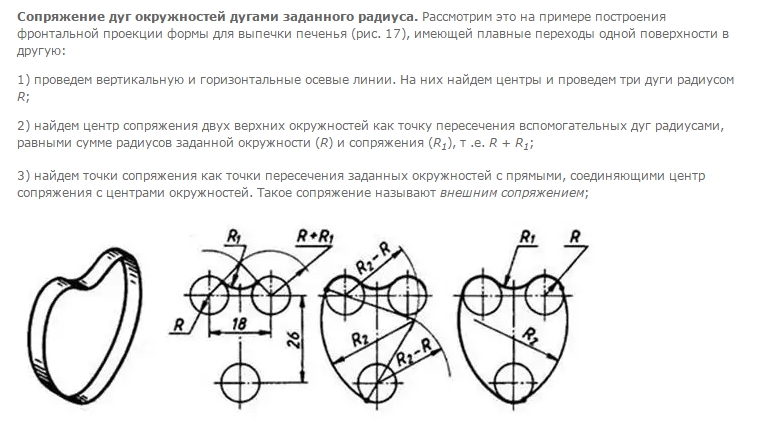 е.центры сопряжений.Необходимо найти также точки, в которых одна линия переходит в другую, т.е.точки сопряжений.Слайд 5.
е.центры сопряжений.Необходимо найти также точки, в которых одна линия переходит в другую, т.е.точки сопряжений.Слайд 5.
Рассмотрим несколько видов сопряжения (обучающиеся делают записи в рабочих тетрадях, выполняют построения вслед за учителем). Слайды 6-9.
На внешнем сопряжениицентры сопрягаемых окружностей находятся за пределами радиуса сопряжения.
На внутреннем сопряжении центры сопрягаемых окружностей находятся внутри радиуса сопряжения.
ІV. Практическая работа(20 мин.)
Выполним заготовки трех изображений фигур, которые будем сопрягать.
Сопряжение двух прямых R15Внешнее сопряжение R10 Внутреннее сопряжение R80
Физкультминутка(2 мин.)(выполняется обучающимися вслед за демонстрацией на мультимедийном проекторе).
Продолжение практической работы.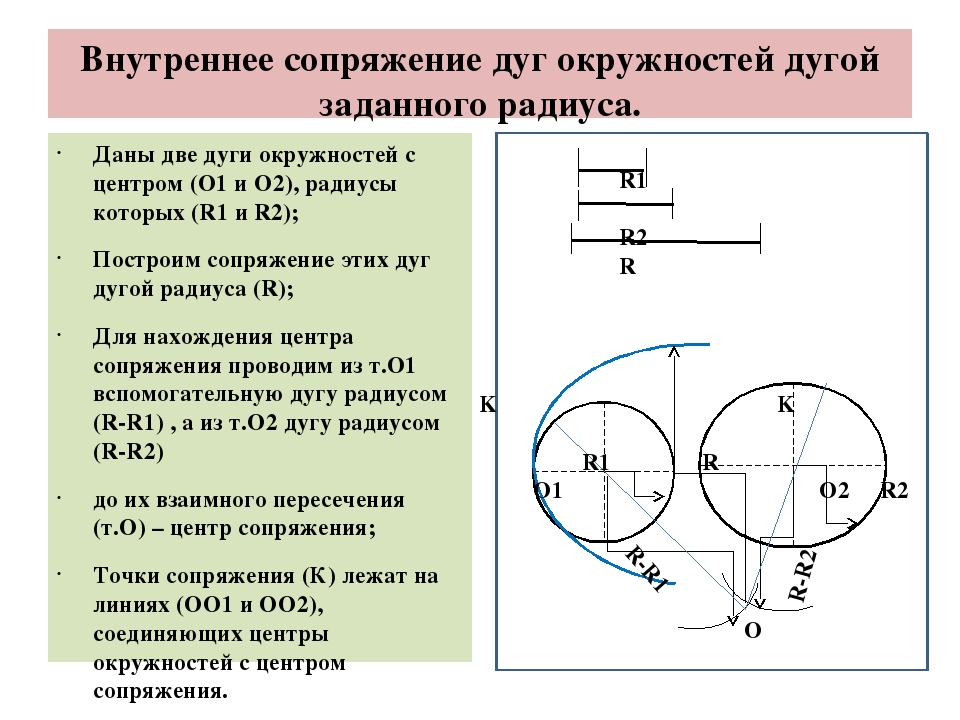
Учащиеся получают карточки-задания (одну на парту – работа в парах) с алгоритмами различных видов сопряжений (Сопряжение двух прямых R15, Внешнее сопряжение R10, Внутреннее сопряжение R80). Слайд 11,12.
По истечении отведенного времени (10 мин.), учитель выявляет учащихся, справившихся с заданием. Затем демонстрирует выполнение данных видов сопряжений на доске.
Алгоритм выполнения сопряжений
Внешнее сопряжение R10
Из центра большей окружности проводим вспомогательные дуги радиусом, равным сумме радиуса сопряжения и радиуса окружности (30+10=40).
Из центра меньшей окружности проводим вспомогательные дуги радиусом, равным сумме радиуса сопряжения и радиуса окружности (20+10=30).
В пересечении этих дуг находим центры сопряжения О1 и О2, соединяем их с центрами сопрягаемых окружностей и находим на них точки сопряжения.
 Затем из этих центров проводим сопрягаемые дуги R10, ограничивая их точками сопряжения.
Затем из этих центров проводим сопрягаемые дуги R10, ограничивая их точками сопряжения.Контур сопряженной фигуры обводим сплошной толстой линией.
Внутреннее сопряжение R80
1. Из центра большей окружности проводим вспомогательные дуги радиусом, равным разнице радиуса сопряжения и радиуса окружности (80-30=50).
2. Из центра меньшей окружности проводим вспомогательные дуги радиусомравным разнице радиуса сопряжения и радиуса окружности (80-20=60).
3. В пересечении этих дуг находим центры сопряжения О1 и О2, соединяем его с центрами сопрягаемых окружностей и находим на них точки сопряжения. Затем из этих центров проводим сопрягаемые дуги R80, ограничивая их точками сопряжения.
4. Контур сопряженной фигуры обводим сплошной толстой линией.
Сопряжение двух прямых (углов) R15
Из вершин трапеции выполняем дугиR15.
 Проводим касательные линии к этим дугам и, на пересечении их, находим центры сопряжений О1, О2, О3, О4.
Проводим касательные линии к этим дугам и, на пересечении их, находим центры сопряжений О1, О2, О3, О4.Из этих центров проводим перпендикуляры к сопрягаемым сторонам углов трапеции, находим точки сопряжения и выполняем сопряжение всех углов R15.
Контур сопряженной фигуры обводим сплошной толстой линией.
Сопряжение окружности и прямой,
двух параллельных прямых R10
Проводим вспомогательные линии, на удалении от прямых на расстоянии радиуса сопряжения R10.
Из центра окружности проводим вспомогательные дуги радиусом, равным сумме радиуса сопряжения и радиуса окружности (20+10=30) до пересечения с вспомогательными линиями.
Из полученных центров сопряжения проводим перпендикуляры к линиям и к окружности,находим точки сопряжения и выполняем сопряжение R10.
Контур сопряженной фигуры обводим сплошной толстой линией.

V. Итог урока (5 мин.)
Оценивание работ обучающихся. Рефлексия. Слайд 13.
— Что называется сопряжением?
— Какие виды сопряжений были изучены на уроке?
— Что необходимо построить для выполнения сопряжений?
— Чем отличается внешнее сопряжение от внутреннего?
VI. Домашнее задание (1 мин.)
Изучить §15 пункт 3. Выполнить творческий эскиз « Сопряжение любимого предмета (мобильный телефон, игрушка и т. п.)». Слайд 14.
Заключение
На примере данного урокабыло показано, как можно объяснить детям назначение сопряжений, заинтересовать их примерами на практике через демонстрацию форм предметов с плавными переходами. Представлен алгоритм сопряжения углов, окружности и прямой и двух окружностей. Показан способ применения этих видов сопряжений при построении различных фигур.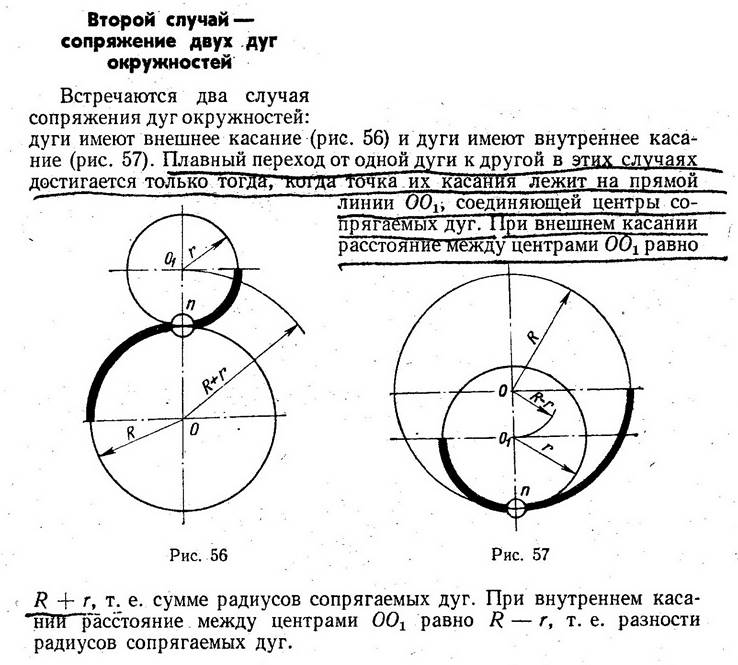
Литература и электронные источники
Программы основного общего образования (ЧЕРЧЕНИЕ 8-9 классы) Министерства образования и науки Донецкой Народной Республики, г. Донецк, 2015 г.
Учебник ЧЕРЧЕНИЕ для 7 – 8 классов, авторы: А.Д. Ботвинников, В.Н. Виноградов, И.С.Вышнепольский М. Просвещение, 1993.
С.К. Боголюбов, А. В. Воинов ЧЕРЧЕНИЕ М. «Машиностроение», 1981.
И.А. Воротников Занимательное ЧЕРЧЕНИЕ М. Просвещение, 1990.
http://festival.1september.ru/articles/567010/.
http://lib.znate.ru/docs/index-248123.htm
Сопряжение дуг двух окружностей с помощью прямой — Студопедия
Суть решения этой задачи состоит в построении внешней или внутренней касательной к данным окружностям (рис. 3.33).
Рисунок 3.33
Для проведения внешней касательной, сопрягающей две окружности радиусов R1 и R2 (а), сначала соединяют центры окружностей, затем отрезок ОО1 делят точкой О2 пополам, а из точки О проводят окружность радиусом (R – R1), равным разности радиусов задаваемых окружностей (в). На этой окружности радиусом О2О засекают точки Е и D (в). Продлив отрезки ОЕ и OD до пересечения с окружностью радиуса R, получают точки сопряжения С и В (г). Соединяют точки Е и D с центром О1. Из точек С и В параллельно отрезкам О1Е и О1D проводят отрезки, сопрягающие две окружности. Точки сопряжения на окружности радиуса R1 можно получить, восстанавливая в точке О1 перпендикуляры к отрезкам О1Е и О1D.
На этой окружности радиусом О2О засекают точки Е и D (в). Продлив отрезки ОЕ и OD до пересечения с окружностью радиуса R, получают точки сопряжения С и В (г). Соединяют точки Е и D с центром О1. Из точек С и В параллельно отрезкам О1Е и О1D проводят отрезки, сопрягающие две окружности. Точки сопряжения на окружности радиуса R1 можно получить, восстанавливая в точке О1 перпендикуляры к отрезкам О1Е и О1D.
Рисунок 3.34
Для построения внутренних касательных, сопрягающих две окружности радиусов R и R1 (рис. 3.34,а), из середины отрезка ОО1 (точки О2) – проводят дугу радиусом О2О, а из центра О проводят дугу радиусом (R+R1), равным сумме радиусов заданных окружностей (б).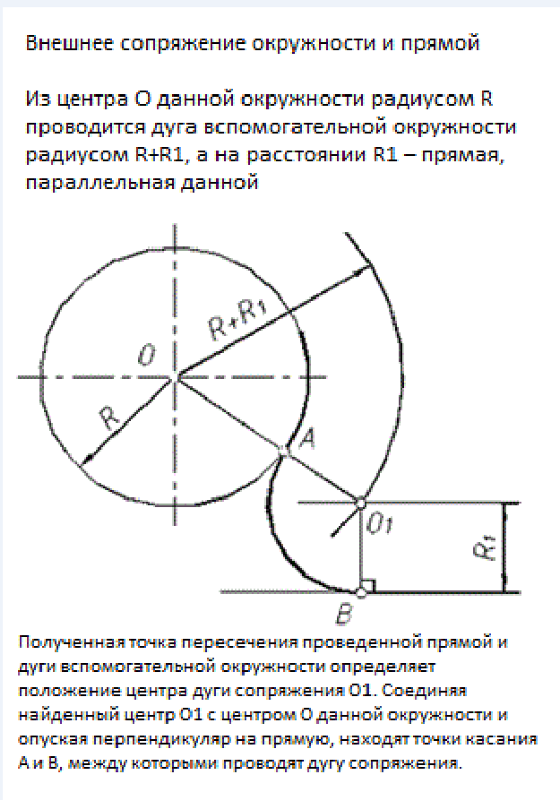 В пересечении этих окружностей отмечают точки Е и D, которые соединяют с точкой О1. Касательные, сопрягающие две окружности, будут параллельны отрезкам ЕО1 и DО1 (в). Построение точек сопряжения ясно из чертежа.
В пересечении этих окружностей отмечают точки Е и D, которые соединяют с точкой О1. Касательные, сопрягающие две окружности, будут параллельны отрезкам ЕО1 и DО1 (в). Построение точек сопряжения ясно из чертежа.
Сопряжение двух окружностей выполняется отрезком прямой, являющейся внутренней или внешней касательной. Построение отрезка выполняется с помощью объектной привязки «Касательная» (Прыжок в тангенс). Выбор точек привязки производится по одну сторону оси симметрии, проходящей через центры окружности (внешнее сопряжение) или по разные стороны (внутреннее сопряжение).
Внутренняя касательная
Внешняя касательная
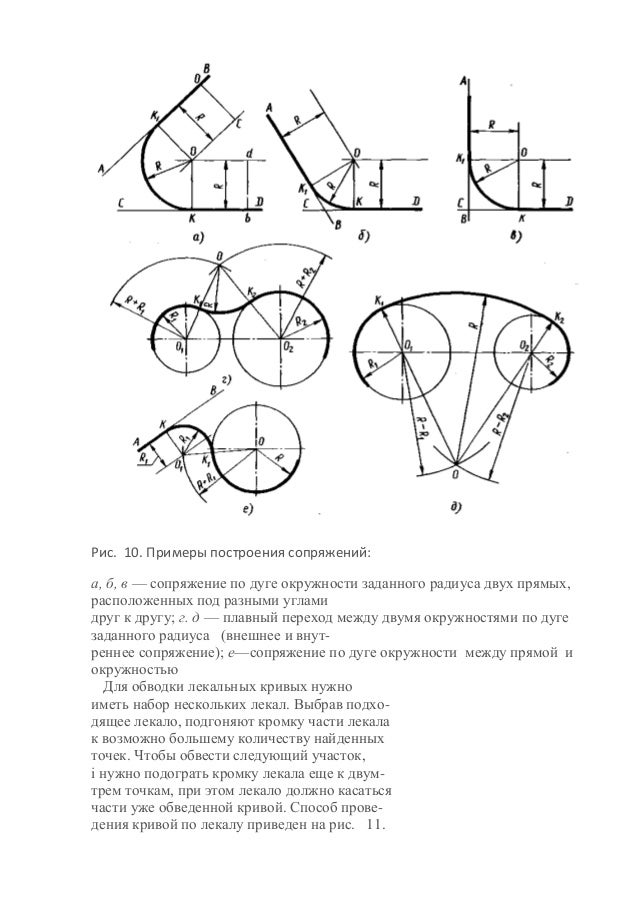
Примеры построения сопряжений — Студопедия
Поэтапный показ решения примеров непосредственно на рисунках дает возможность во многих случаях ограничиваться локаничными пояснениями.
Пример 1. Провести касательную к окружности из произвольной точки А (рис.39).
Провести касательную к окружности из произвольной точки А (рис.39).
Решение основано на положениях 1 и 3 (см. §8).
1. Построить точку С – середину отрезка ОА.
2. Построить точку касания Т. Для этого из центра С через концы отрезка ОА провести вспомогательную окружность и пересечь ее с заданной окружностью.
Пример 2. Внешнее касание двух окружностей. Через точку Т на окружности радиуса R1 провести касательную окружность радиуса R2 (рис. 40).
Решение основано на положении 2.
1. Из центра О1 провести дугу окружности радиусом R1+R2.
2. Построить центр сопряжения О2. Для этого провести прямую О1Т и пересечь ее со вспомогательной дугой.
3. Из центра О2 и через точку Т провести искомую окружность.
Пример 3. Внутреннее касание двух окружностей. Через точку Т на окружности радиуса R1 провести касательную окружность радиуса R2 (рис. 41).
Внутреннее касание двух окружностей. Через точку Т на окружности радиуса R1 провести касательную окружность радиуса R2 (рис. 41).
Решение аналогично примеру 2. Разница лишь в том, что радиус вспомогательной дуги равен R2-R1.
Задачи сопряжения двух линий дугой окружности заданного радиуса решаются в три этапа: построение центра этой дуги, построение двух точек сопряжения и проведение сопрягающей дуги.
Пример 4. Сопряжение двух прямых при помощи дуги окружности радиуса R (рис. 42).1. Построить центр сопряжения С. Для этого провести и пересечь между собой две прямые, отстоящие от заданных прямых на расстоянии R.
2. Построить точки сопряжения Т1 и Т2. Для этого из центра С опустить перпендикуляры на заданные прямые.
3. Из центра С через точки Т1 и Т2 провести сопрягающую дугу.
Пример 5. Сопряжение двух дуг окружностей третьей дугой радиуса R (рис. 43).
43).
1. Построить центр сопряжения С. Для этого провести и пересечь между собой дуги окружностей радиусов R1+R и R2-R.
2. Построить точки сопряжения Т1 и Т2. Для этого провести прямые О1С и О2С и пересечь ими заданные дуги окружностей.
3. Из центра С через точки Т1 и Т2 провести сопрягающую дугу.
Пример 6. Внешнее сопряжение окружности и прямой линии при помощи дуги окружности радиуса R1 (рис. 44).
1. Построить центр сопряжения С. Для этого провести и пересечь между собой прямую, отстоящую от заданной прямой на расстоянии R, и дугу окружности радиуса R+R1.
2. Построить точки сопряжения Т1 и Т2. Для этого провести прямую ОС и пересечь ее с заданной окружностью. После этого из точки С опустить перпендикуляр на заданную прямую.
3. Из центра С через точки Т и Т1 провести сопрягающую дугу.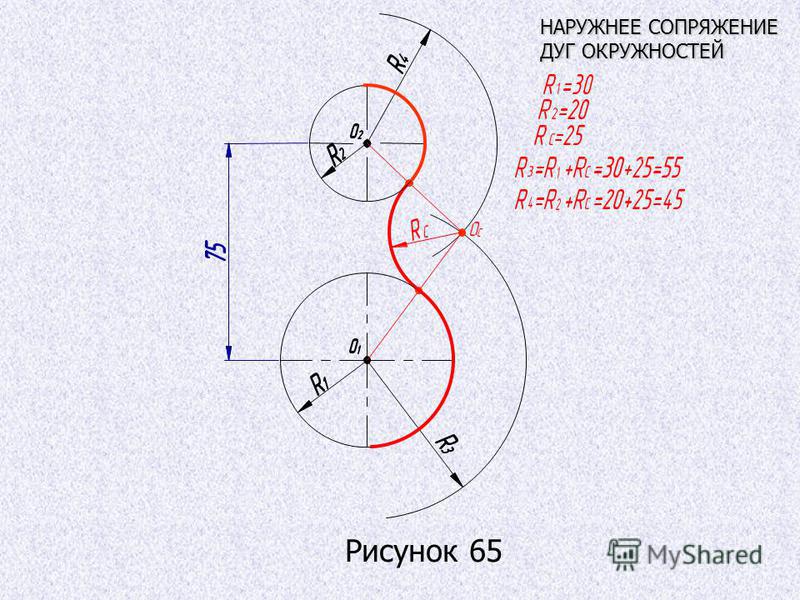
Пример 7. Внутреннее сопряжение окружности и прямой линии при помощи дуги окружности радиуса R1. Вариант 1 (рис. 45).
Решение аналогично примеру 6. Разница лишь в том, что радиус вспомогательной дуги равен R1-R.
Пример 8. Внутреннее сопряжение окружности и прямой линии при помощи дуги окружности радиуса R1. Вариант 2 (рис. 46).Решение аналогично примерам 6 и 7. Разница лишь в том, что радиус вспомогательной дуги равен R-R1.
Пример 9. Внешнее сопряжение двух окружностей при помощи дуги радиуса R (рис. 47).
1. Построить центр сопряжения С. Для этого провести и пересечь между собой дуги окружностей радиусов R1+R и R2+R.
2. Построить точки сопряжения Т1 и Т2. Для этого провести и пересечь между собой прямые О1С и О2С.
3. Из центра С через точки Т1 и Т2 провести сопрягающую дугу.
Пример 10. Внутреннее сопряжение двух окружностей при помощи дуги радиуса R (рис. 48).
Внутреннее сопряжение двух окружностей при помощи дуги радиуса R (рис. 48).
Решение аналогично примеру 9. Разница лишь в том, что радиусы вспомогательных дуг равны R-R1 и R-R2.
Пример 11. Смешанное сопряжение двух дуг окружностей при помощи дуги радиуса R (рис. 49).
Решение аналогично примерам 9 и 10. Разница лишь в том, что радиусы вспомогательных дуг равны R1+R и R-R2.
Задачи на сопряжение двух окружностей общей касательной решаются в три этапа: проведение вспомогательной окружности, построение точек сопряжения и проведение искомой касательной по двум точкам. Решение этих задач основано на положении 4 (§8).
Пример 12. Сопряжение двух окружностей внешней касательной (рис. 50).
1. Из центра большой окружности провести окружность радиуса R2-R1.
2. Построить точки сопряжения Т1 и Т2. Для этого из средней точки О между центрами окружностей провести дугу через центр большой окружности до пересечения ее в точке Т со вспомогательной окружностью. Радиус О2Т в пересечении с большой окружностью даст точку Т2. Радиус из центра О1, параллельный радиусу О2Т2, в пересечении с малой окружностью даст точку Т1.
Радиус О2Т в пересечении с большой окружностью даст точку Т2. Радиус из центра О1, параллельный радиусу О2Т2, в пересечении с малой окружностью даст точку Т1.
3. Провести искомую касательную по двум точкам Т1 и Т2.
Пример 13. Сопряжение двух окружностей внутренней касательной (рис. 51).
Решение аналогично примеру 12. Разница лишь в том, что радиус вспомогательной окружности равен R1+R2.
Сопряжение двух заданных окружностей — Энциклопедия по машиностроению XXL
Сопряжение двух заданных окружностей [c.98]Для пояснения всех последующих построений на рис. 70, б отдельно вынесены элементы геометрических построений контура, распределенные по следующим группам скругление углов, касательные к дугам окружностей, сопряжение прямой и дуги окружности дугой заданного радиуса, сопряжение двух дуг окружностей дугой заданного радиуса, сопряжение двух дуг окружностей дугой, проходящей через заданную точку. [c.91]
[c.91]
Построение сопряжения двух дуг окружностей дугой заданного радиуса. Такой вид сопряжения может быть внешним, внутренним и смешанным. При внешнем сопряжении дуги находятся с внешней стороны дуги сопряжения, т. е. точки сопряжения представляют собой точки перегиба. [c.42]
На рис. 3.39 показан случай смешанного сопряжения двух дуг окружностей третьей дугой заданного радиуса R2, когда рас тояние а между центрами дуг меньше суммы их радиусов R R ). Построения ясны из чертежа. [c.43]
Подсчитаем параметры формы с учетом условий. Прямая /71 не требует параметров положения. Параметр формы (размер а) отрезка этой прямой определяет точку В на оси ох. Прямая П2 задается точкой В и угловым размером (3. Прямая Я4 задана условием о (Я4) и угловым размером 7. Наконец, окружность 03 является сопрягающим элементом в тройке П2 [03] ПА, где Я2 и Я4 заданы параметрами и условиями, отличными от касания. Условия касания 03 и сопрягаемых элементов эквивалентны двум параметрам положения окружности 03.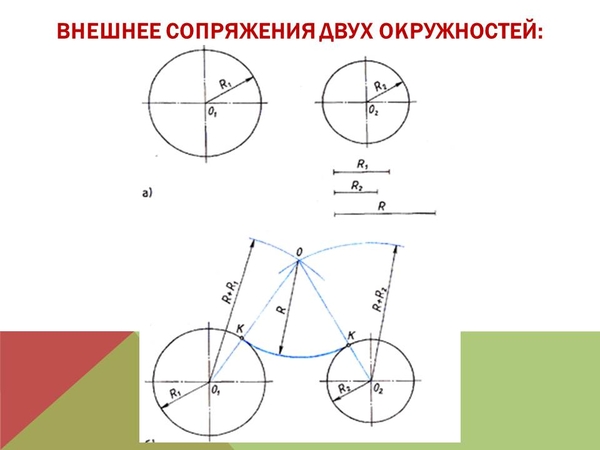 Остается задать ее параметр формы R. Фигура может быть построена по размерам а, р, у, R с помощью алгоритма, реализующего сопряжение двух заданных прямых дугой известного радиуса.
[c.39]
Остается задать ее параметр формы R. Фигура может быть построена по размерам а, р, у, R с помощью алгоритма, реализующего сопряжение двух заданных прямых дугой известного радиуса.
[c.39]
Сопряжение двух дуг окружностей дугой заданного радиуса. Из центров О, и Oj описываются дуги вспомогательной окружности радиусом йз = Л + й, и R =R + R (при внешнем сопряжении, черт. 38) или Rj=R-R и R =R-R (при внутреннем сопряжении, черт. 39). Точка О пересечения этих дуг и будет центром искомой дуги окружности радиуса R. [c.15]
Построение сопряжения двух дуг окружностей радиусов R и Rg дугой заданного радиуса R (случай внешнего касания, рис. 33). Из центра Oi радиусом, равным Rq, и из центра О радиусом, [c.23]
Построение сопряжения двух дуг окружностей радиусов и/ 1 дугой заданно го радиуса — случай внешнего касания (фиг. 24, а). [c.20]Сопряжение двух окружностей дугой заданного радиуса / з.
 [c.443]
[c.443]Сопряжение двух неконцентрических дуг окружностей дугой заданного радиуса (черт. 41). Из заданного центра О, проводится дуга вспомогательной окружности радиусом R =R +R, а из заданного центра Oj — радиусом Лд = — R. Пересечение этих дуг определит иско- [c.15]
При разметке часто встречаются случаи внутреннего сопряжения двух окружностей с дугой заданного радиуса (рис. 37, ж). Центр Oj находят как точку пересечения дуг, проведенных из центров [c.39]Выявление операций, необходимых для построения чертежа, облегчает выбор способа его выполнения. Если нужно вычертить, например, пластину, изображенную на рис. 39, то анализ контура ее изображения приводит нас к выводу, что мы должны применить следующие геометрические построения в пяти случаях провести взаимно перпендикулярные центровые линии (цифра 1 в кружке), в четырех случаях вычертить параллельные линии (цифра 2), вычертить две концентрические окружности (0 50 и 70 мм), в шести случаях построить сопряжения двух параллельных прямых дугами заданного радиуса (цифра 3), а в четырех — сопряжения дуги и прямой дугой радиуса 10 мм (цифра 4), в четырех случаях построить сопряжение двух дуг дугой радиуса 5 мм (цифра 5 в кружке).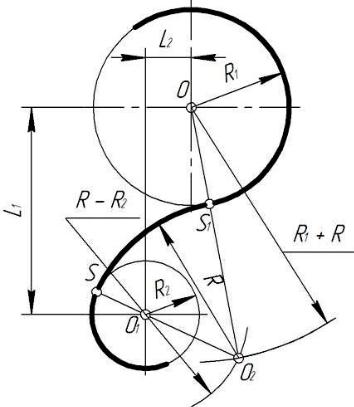 [c.28]
[c.28]
Построить сопряжение двух окружностей дугой заданного радиуса R (рис. 26, а). При внешнем сопряжении центр сопрягающей дуги — точка О — определяется пересечением двух геометрических мест—вспомогательных окружностей радиусов R — -R и проведенных соответственно из центров сопрягаемых дуг, т. е. из точек Ох и Oj. Точки сопряжения Л и В определяются как точки пересечения заданных дуг с прямыми 00 и 00[c.26]
На рис. 38, в показано сопряжение дугой радиуса Я двух окружностей разных диаметров. При этом одной окружности сопрягающая дуга касается внешней стороной, а другой — внутренней. Центр сопряжения О в этом случае будет в точке пересечения окружностей радиусов и / —/ 2-На рис. 39 показано построение сопряжения двух параллельных линий АЕ и ОВ двумя дугами. При этом точки сопряжений О, Е и М заданы. Такая задача может встретиться, например, при построении профиля карниза. Центры сопрягающих дуг Ох и О2 будут расположены в пересечении перпендикуляров к заданным прямым, проведенных из точек О и Е, и прямых, делящих отрезки ОМ и МЕ пополам и перпендикулярных к прямой ОЕ.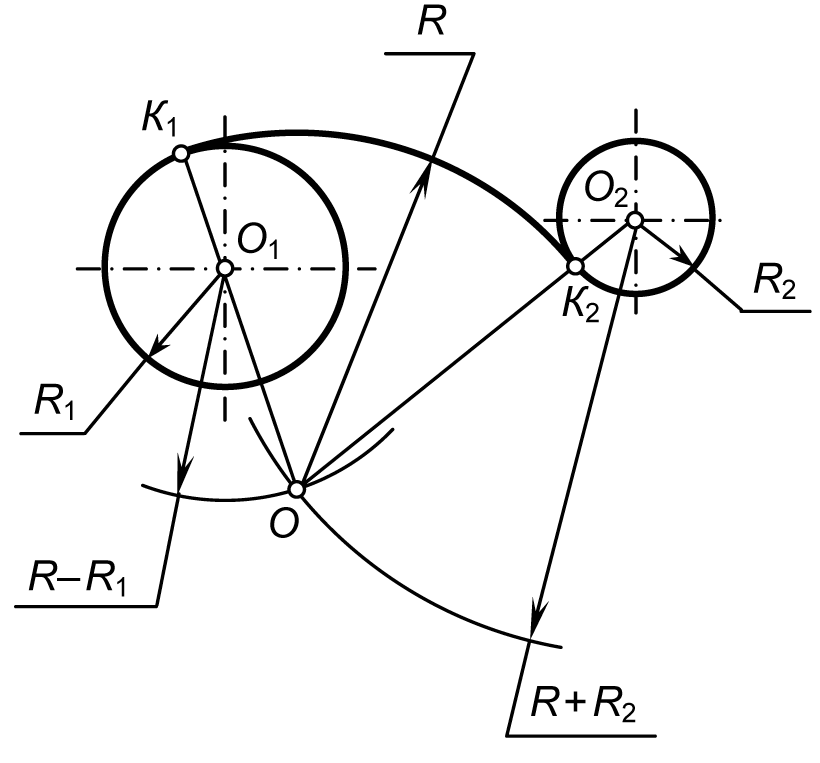 [c.30]
[c.30]
При построении сопряжения двух пересекающихся прямых АВ и СО дугой окружности радиуса В (рис. 73) проводим вспомогательные пря- 73 мые КУ и МР, параллельно заданным прямым на расстоянии, равном радиусу В, и отметим точку О их пересечения. Из точки О, как из центра, проведем окружность радиуса В. Для определения точек сопряжения А и С опустим перпендикуляры из центра О на прямые АВ и СО. [c.48]
Сопряжение двух параллельных прямых дугами окружностей проводится в следующей последовательности. Соединяем точку А с точкой В и продолжаем прямую АВ до пересечения с прямой (точка Б). В точках Л и Б восставляем перпендикуляры к соответствующим прямым. Затем восставляем перпендикуляры к серединам отрезков прямых АВ и ВБ. Точки пересечения этих перпендикуляров и определят центры О1 и О2 сопрягающих окружностей. Из центра 0 радиусом, равным отрезку О1Л, а из центра О2 радиусом ОгБ проводим дуги окружности, которые проходят через точку В и сопрягают заданные прямые (рис.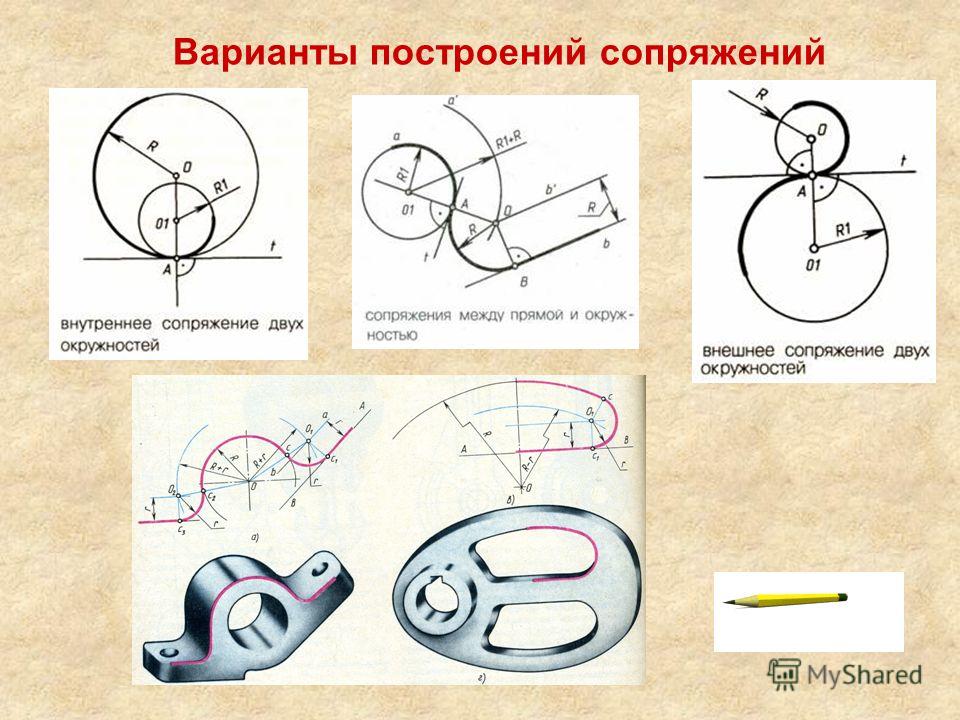 17, в).
[c.27]
17, в).
[c.27]
Сопряжение двух прямых дугой окружности. Все задачи на сопряжение могут быть сведены к двум видам сопряжение двух прямых дугой окружности заданного радиуса и сопряжение двух прямых дугой окружности с условием, что на одной из них задана точка касания. В том и другом случае необходимо построить центр сопрягающей дуги. [c.53]
Сопряжение двух пересекающихся прямых дугой окружности заданного радиуса R (рис. 109). Сопрягающая дуга должна касаться заданных прямых, поэтому ее центр должен быть удален от каждой прямой на величину, равную радиусу R . Проводят две прямые, параллельные заданным и удаленные от них на величину радиуса R , и в пересечении этих прямых отмечают точку О — центр сопрягающей дуги. Из точки О опускают перпендикуляры на каждую из заданных прямых. Основания перпендикуляров — точки А и В — являются точками касания сопрягающей дуги. Такое построение сопряжения справедливо для двух пересекающихся прямых, составляющих любой угол. Для сопряжения сторон прямого угла можно воспользоваться также способом, указанным на рис. 110.
[c.53]
Для сопряжения сторон прямого угла можно воспользоваться также способом, указанным на рис. 110.
[c.53]
Сопряжение двух пересекающихся прямых дугой окружности, проходящей через заданную точку касания А (рис. 111). Известно, что центры дуг, сопрягающих две пересекающиеся прямые, принадлежат биссектрисе угла, образованного этими прямыми. Поэтому, построив биссектрису угла, из точки касания А восстав- [c.53]
Сопряжение двух дуг дугой окружности заданного радиуса. В зависимости от вида касания сопрягающей дуги с двумя заданными сопряжение может быть внешним, внутренним и смешанным. [c.55]
Позволяет выполнить сопряжение двух отрезков, сегментов полилинии, дуг окружностей или окружностей дугой заданного радиуса, а также выполняет сглаживание ребер твердотельных объектов. [c.380]
| Рис. 16.31. Сопряжение двух окружностей дугой заданного радиуса а — внешнее касание б — внутреннее касание в — смешанное касание |
 В н е ш -нее касание (рис. 16.31, а). Центр О3 искомой дуги радиуса Л3 находится на пересечении вспомогательных окружностей, описанных из центров О, и О2 соответствующими радиусами Л, + 7 з и з-
[c.447]
В н е ш -нее касание (рис. 16.31, а). Центр О3 искомой дуги радиуса Л3 находится на пересечении вспомогательных окружностей, описанных из центров О, и О2 соответствующими радиусами Л, + 7 з и з-
[c.447]Сопряжение двух неконцентрических дуг окружностей третьей дугой заданного радиуса (рис. 16.37). Центр О3 дуги Л3 находится на пересечении двух вспомогательных дуг, построенных соответственно из центров О, И О2 радиусами Л, + Л3 и Точки сопряжения Кп М [c.449]
Внешнее сопряжение двух окружностей и радиусов Rj. и / 2 дугой заданного радиуса R (рис. 111). Из центра 0 радиусом Я + Rzi а из центра 0 радиусом Я + Я% проводят дуги до пересечения их в точке О — центре дуги сопряжения. Точки А п В сопряжения лежат на [c.98]
Внутреннее сопряжение двух окружностей радиусов и 2 дугой заданного радиуса Н (рис. 112). Из центра 0 проводят дугу радиусом Я — Я , а из центра 0 — дугу радиусом Я — В пересечении этих дур получают точку О — центр дуги сопряжения. Точ дугу сопряжения радиусом Я. [c.99]
Смешанное сопряжение двух окружностей радиусов и 2 дугой заданного радиуса Н (рис. 114, а, б). Смешанное сопряжение двух данных дуг третьей дугой [c.99]
Условиями возможности решения задач на построение сопряжений двух окружностей радиусов 7 , и дугой заданного радиуса Я являются [c.101]
Сопряжение двух окружностей радиусов и Я2, если задана точка Л сопряжения на одной из окружностей (рис. 116, а, б). Центр дуги сопряжения должен лежать на прямой, проведенной через центр О окружности и заданную точку А сопряжения. Соединяют точку А (рис. 116, а) с центром 0 и откладывают на этой прямой отрезок АС, равный Я . Соединяют точку С с центром 0 . В точке О — середине отрезка СО — восставляют к нему перпендикуляр до пересечения с продол жением прямой О А в точке О — центре дуги сопряжения. Точка В сопряжения лежит на пересечении линии центров 00 с окружностью радиуса Я2. Соединяя точки А и В дугой радиуса Я с центром в точке О, строят внешнее сопряжение заданных окружностей. [c.101]
СОПРЯЖЕНИЕ ДВУХ СТОРОН УГЛА ДУГОЙ ОКРУЖНОСТИ ЗАДАННОГО РАДИУСА [c.35]
При выполнении чертежей деталей, показанных на рис. 58, б, г, е, выполняют построение сопряжения двух сторон угла дугой окружности заданного радиуса. На рис. 58, а выполнено построение сопряжения дугой сторон острого угла, на рис. 58, в — тупого угла, на рис. 58, д — прямого. [c.35]
Сопряжение — это плавное соединение двух объектов дугой заданного радиуса. В качестве сопрягаемых объектов могут быть отрезки, полилинии, окружности, дуги, эллипсы и т. д. Сопряжение двух отрезков (рис. 586) [c.360]
При построении сопряжений двух дуг окружностей третьей дугой заданного радиуса различают внешнее и внутреннее сопря—жения. [c.44]
Для построения сопряжения двух пересекающихся прямых а и Ь под острым углом дугой заданного ридиуса R (рис. 3.25) необходимо определить множество центров окружностей, удаленных от прямых на расстояние R. Для этого на расстоянии R проводят прямые, параллельные заданным, до пересечения в точке О (а). Дуга радиуса R, проведенная из точки О как из центра, и будет дугой сопряжения (б). Основания перпендикуляров, опущенных из точки О на прямые а и Ь, будут точками сопряжения. [c.38]В практике разметки часто встречаются случаи внутреннего сопряжения двух окружностей с дугой заданного радиуса (фиг. 45, б). Центр Ог находят как точку пересечения дуг, проведенных из центров О и Oi радиусами R% — R и Яг — R. Точки и i являются точками пересечения продолжений линий ООг и О1О2 с соответствующими окружностями. [c.60]
Сопряжение двух дашых окружвостей дугой заданного радиуса Ri. При внешнем касании (рис. III.9) из центра Oj окружности радиуса jRi описывается дуга вспомогательной окружности радиусом Ri + R и из центра окружности радиуса R2 — дуга радиусом Rj + R . Точка О3 пересечения этих дуг является центром искомой дуги окружности радиуса Л3. Соединяя центры О3 и Oi, а также Oj и определяют точки касания Ki я К2. [c.128]
Построение сопряжения двух окружностей радиусами длиной Яа и заданн дугой сопряжения радиусом Я [c.53]
Сопряжение двух параллельных прямых дугой окружности, проходящей через заданную точку касания А (рис. 112). Из точки А восставляют перпендикуляр к заданным прямым и на пересечении его со второй прямой отмечают точку В. Отрезок АВ делят пополам и получают точку О — центр сопрягающей дуги окружности радиуса Яе=АВ12. [c.54]
Сопряжение двух неконцентричных дуг окружностей дугой заданного радиуса (рис. 19). Даны две дуги, описанные из центра О, и 0 радиусами и Й2- [c.69]
Сопряжение двух окружностей с заданной точкой Г] на одной из окружностей (рис. IV.50). Из произвольной точки Oi, взятой на прямой 0Г , радиусом 0 Г, проводим дугу с таким расчетом, чтобы она пересекла вторую окружность в двух точках, например I к 2. Соединяя точки 1 и 2, получим радикальную ось, которую продол-жае.м до пересечения с прямой, перпендикулярной ОГ, в точке М (радикальный центр). Из точки AI радиусом AiTi проводим дугу, которая пересечет вторую окрун ность в точке Гг. Это вторая точка сопряжения. Соединяя точку Гг с центром О и продолжая эт/ прямую до прямой ОТ,, получим точку О2 — центр дуги сопряжения Г2Г1. [c.89]
2.10 Построение сопряжения
Лист № 4
Цель задания: ознакомление с правилами построения плавного перехода от одной линии к другой.
Выполнить на листе формата А4 задание «Сопряжение», взяв данные по своему варианту из таблицы 6 (стр. 38-41).
Сопряжением линий называется плавный переход по кривой от одной линии к другой. Точкой сопряжения линий называется общая точка двух сопрягаемых линий, это точка в которой одна линия переходит в другую линию.
Построение сопряжений основано на геометрических понятиях о прямых, касательных к окружностям и на свойствах касающихся между собой окружностей.
Для правильного выполнения чертежей необходимо уметь выполнять построения сопряжений, которые основаны на двух положениях:
1. Для сопряжения прямой линии и дуги необходимо, чтобы центр окружности, которой принадлежит дуга, лежал на перпендикуляре к прямой, восстановленном из точки сопряжения (рисунок 38). При сопряжении прямой линии и кривой прямая должна являться одновременно касательной к кривой.
2. Для сопряжения двух дуг необходимо, чтобы центры окружностей, которым принадлежат дуги, лежали на прямой, проходящей через точку сопряжения и перпендикулярной к общей касательной этих дуг (рисунок 38). Точку сопряжения находят на прямой, соединяющей центры окружностей. Точка сопряжения (В) является границей двух линий, здесь кончается одна линия и начинается другая. Следовательно, точки сопряжения являются вместе с тем и точками касания прямой и дуги или двух дуг.
Рисунок 38 – Построение сопряжений
Рассмотрим построение сопряжений сторон угла (острого, тупого, прямого) дугой заданного радиуса R (рисунок 39).
На рисунке 39а выполнено построение сопряжения сторон острого угла дугой, на рисунке 39б – тупого угла, на рисунке 39в – прямого.
Сопряжение выполняется следующим образом: параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые линии. Точка пересечения этих линий будет центром дуги радиуса R, т.е. центром сопряжения. Из центра О описывают дугу, плавно переходящую в прямые – стороны угла. Дугу заканчивают в точках М и N – это точки сопряжения, они являются основаниями перпендикуляров, опущенных из центра О на стороны угла.
Рисунок 39 – Построение сопряжений
Рассмотрим построение сопряжения дуги с дугой.
Сопряжение двух дуг окружностей может быть внутренним, внешним и смешанным.
При внутреннем сопряжении центры О и О1 сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R (рисунок 40а).
При внешнем сопряжении центры О и О1 сопрягаемых дуг радиусов R1 и R2 находятся вне сопрягающей дуги радиуса R (рисунок 40б).
При смешанном сопряжении центр О1 одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R, а центр О другой сопрягаемой дуги вне её (рисунок 40в).
а) б) в)
Рисунок 40 – Построение сопряжений
Построение внутреннего сопряжения.
Задано:
а) радиусы сопрягаемых окружностей R1 и R2;
б) расстояние l1 и l2между центрами этих дуг;
в) радиус R сопрягающей дуги.
Требуется:
а) определить положение центра О2 сопрягающей дуги;
б) найти точки сопряжения S и S1;
в) провести дугу сопряжения.
Построение сопряжения показано на рисунке 40а. По заданным расстояниям между центрами l1 и l2 на чертеже намечают центры О и О1, из которых описывают сопрягаемые дуги радиусов R1 и R2. Из центра О1 проводят вспомогательную дугу окружности радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R2, а из центра О – радиусом, равным разности радиусов сопрягающей дуги R и сопрягаемой R1. Вспомогательные дуги пересекутся в точке О2 , которая и будет искомым центром сопрягающей дуги.
Для нахождения точек сопряжения точку О2 соединяют с точками О и О1 прямыми линиями. Точки пересечения продолжения прямых О2О и О2О1 с сопрягаемыми дугами являются искомыми точками сопряжения (точки S и S1).
Радиусом R из центра О2 проводят сопрягающую дугу между точками сопряжения S и S1.
Построение внешнего сопряжения.
Задано:
а) радиусы R1 и R2 сопрягаемых дуг окружностей;
б) расстояние l1 и l2между центрами этих дуг;
в) радиус R сопрягающей дуги.
Требуется:
а) определить положение центра О2 сопрягающей дуги;
б) найти точки сопряжения S и S1;
в) провести дугу сопряжения.
Построение внешнего сопряжения показано на рисунке 40б. По заданным расстояниям между центрами l1 и l2 на чертеже намечают центры О и О1, из которых описывают сопрягаемые дуги радиусов R1 и R2. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R1 и сопрягающей R, а из центра О1 – радиусом, равным сумме радиусов сопрягаемой R2 и сопрягающей R. Вспомогательные дуги пересекутся в точке О2, которая и будет искомым центром сопрягающей дуги.
Для нахождения точек сопряжения центры дуг соединяют прямыми линиями ОО2 и О1О2. Эти две прямые пересекают сопрягаемые дуги в точках сопряжения S и S1.
Из центра О2 радиусом R проводят сопрягающую дугу, ограничивая её точками сопряжения S и S1.
Построение смешанного сопряжения.
Задано:
а) радиусы R1 и R2 сопрягаемых дуг окружностей;
б) расстояние l1 и l2между центрами этих дуг;
в) радиус R сопрягающей дуги.
Требуется:
а) определить положение центра О2 сопрягающей дуги;
б) найти точки сопряжения S и S1;
в) провести дугу сопряжения.
Пример смешанного сопряжения приведен на рисунке 41 а,б.
а) б)
Рисунок 41 – Построение сопряжений
По заданным расстояниям между центрами l1 и l2 на чертеже намечают центры О и О1, из которых описывают сопрягаемые дуги радиусов R1 и R2. Из центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягаемой дуги R1 и сопрягающей R, а из центра О1 – радиусом, равным разности радиусов R и R2. Вспомогательные дуги пересекутся в точке О2, которая и будет искомым центром сопрягающей дуги.
Соединив точки О и О2 прямой получают точку сопряжения S1, соединив точки О1 и О2 находят точку сопряжения S. Из центра О2 проводят дугу сопряжения от S до S1.
Таблица 6 – Варианты графической работы на построение сопряжений
Продолжение таблицы 6
Продолжение таблицы 6
Продолжение таблицы 6
Нахождение центра круга или дуги с помощью циркуля и линейки или линейки
На этой странице показано, как найти центр круга или дуги с помощью циркуля и линейки или линейки. Этот метод основан на том, что при любом аккорд круга, серединный перпендикуляр хорды всегда проходит через центр окружности. Применяя это дважды к двум разным хордам, центр устанавливается там, где пересекаются две биссектрисы. Евклидова конструкция
Пошаговые инструкции для печати
Вышеупомянутая анимация доступна как распечатываемый лист с пошаговыми инструкциями, который можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.
Проба
Изображение ниже — это последний рисунок из приведенной выше анимации.
| Аргумент | Причина | |
|---|---|---|
| 1 | RS — хорда круга C | Хорда — это отрезок прямой, соединяющий две точки на окружности. См. Определение аккорда. |
| 2 | AC — биссектриса хорды RS | .AC был нарисован путем построения серединного перпендикуляра RS.См. Метод и доказательство в разделе Построение серединного перпендикуляра отрезка | .
| 3 | BC — серединный перпендикуляр хорды PQ | Как в (1) и (2) |
| 4 | Центр круга лежит на прямой AC. | Серединный перпендикуляр хорды проходит через центр окружности. См. Определение аккорда. |
| 5 | Центр круга лежит на прямой BC. | Как в (4). |
| 6 | Точка C — центр окружности. | Единственная точка, общая для AC и BC. |
— Q.E.D
Попробуйте сами
Щелкните здесь, чтобы распечатать лист, содержащий две задачи по поиску центра. Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатная продукция не защищена авторскими правами.Другие конструкции, страницы на сайте
линий
Уголки
Треугольники
Правые треугольники
Центры треугольника
Окружности, дуги и эллипсы
Полигоны
Неевклидовы конструкции
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Теоремы о круге — Математика GCSE Revision
Теоремы
В этом разделе объясняется теорема окружности, включая касательные, сектора, углы и доказательства.
В видео ниже показаны правила, которые необходимо помнить при построении теорем о кругах.
Равнобедренный треугольник
Два радиуса и хорда образуют равнобедренный треугольник.
Поперечное сечение перпендикулярной хорды
Перпендикуляр от центра окружности к хорде всегда будет делить хорду пополам (разделять его на две равные длины).
Углы, расположенные на одной дуге
Углы, образованные из двух точек на окружности, равны другим углам в той же дуге, образованным из этих двух точек.
Угол полукруга
Углы, образованные проведением линий от концов диаметра круга к его окружности, образуют прямой угол. Итак, c — это прямой угол .
Доказательство
Мы можем разделить треугольник пополам, проведя линию от центра круга до точки на окружности, которой соприкасается наш треугольник.
Мы знаем, что каждая из линий, являющихся радиусом круга (зеленые линии), имеет одинаковую длину. Следовательно, каждый из двух треугольников равнобедренный и имеет пару равных углов.
Но все эти углы вместе должны составлять 180 °, так как они являются углами исходного большого треугольника.
Следовательно, x + y + x + y = 180, другими словами 2 (x + y) = 180.
и поэтому x + y = 90. Но x + y — это размер угла, который мы хотели найти.
Касательные
Касательная к окружности — это прямая линия, которая касается окружности только в одной точке (поэтому она не пересекает окружность, а только касается ее).
Касательная к окружности образует прямой угол с радиусом окружности в точке контакта касательной.
Кроме того, если две касательные нарисованы на окружности и они пересекаются, длины этих двух касательных (от точки, где они касаются круга, до точки, где они пересекаются) будут одинаковыми.
Угол в центре
Угол, образованный в центре круга линиями, исходящими из двух точек на окружности круга, в два раза больше угла, образованного на окружности круга линиями, исходящими из тех же точек. то есть a = 2b .
Доказательство
Возможно, вам придется доказать этот факт:
OA = OX, поскольку оба они равны радиусу круга.Следовательно, треугольник AOX равнобедренный, поэтому ∠OXA = a
. Аналогично, OXB = b
Поскольку в сумме углы в треугольнике равны 180, мы знаем, что ∠XOA = 180 — 2a
Аналогично, ∠BOX = 180 — 2b
Так как углы вокруг точки в сумме составляют 360, мы имеем thatAOB = 360 — ∠XOA — ∠BOX
= 360 — (180 — 2a) — (180 — 2b)
= 2a + 2b = 2 (a + b) = 2 ∠AXB
Теорема об альтернативном сегменте
На этой диаграмме показана теорема об альтернативном сегменте .Короче говоря, красные углы равны друг другу, а зеленые углы равны друг другу.
Доказательство
Возможно, вам придется доказать теорему об альтернативном отрезке:
Мы используем факты о связанных углах
Касательная составляет угол 90 градусов с радиусом окружности, поэтому мы знаем, что ∠OAC + x = 90.
Угол в полукруге равен 90, поэтому ∠BCA = 90.
Углы в треугольнике складываем до 180, поэтому ∠BCA + ∠OAC + y = 180
Следовательно, 90 + ∠OAC + y = 180 и, следовательно, ∠OAC + y = 90
Но OAC + x = 90, поэтому ∠OAC + x = ∠OAC + y
Следовательно, x = y
Циклический четырехугольник
Циклический четырехугольник — это четырехугольная фигура в окружности, каждая вершина (угол) которой касается окружности окружности.Противоположные углы такого четырехугольника в сумме составляют 180 градусов.
Площадь сектора и длина дуги
Если радиус окружности равен r,
Площадь сектора = πr 2 × A / 360
Длина дуги = 2πr × A / 360
Другими словами, площадь сектора = площадь круга × A / 360
длина дуги = длина окружности × A / 360
Для получения дополнительной информации об определениях кругов щелкните здесь
Как найти меру угла
Два луча с одинаковой конечной точкой создают угол.Точка, в которой они пересекаются, называется вершиной. Угол образует часть воображаемого круга. А поскольку круги измеряют 360 градусов, вы можете найти угол, образованный лучами. Вот несколько вещей, которые вы должны знать о том, как найти величину угла.
Четыре типа углов
Есть четыре типа углов. Знание разницы поможет вам оценить размер угла. Вот четыре типа углов и размеров, которые помогут вам классифицировать каждый из них.
Использование транспортира
Лучший способ измерить угол — использовать транспортир. Для этого вы начнете с выстраивания одного луча вдоль линии под углом 0 градусов на транспортире. Затем совместите вершину с серединой транспортира. Следуйте по второму лучу, чтобы определить угол с точностью до градуса.
Углы в треугольниках
Треугольники получили свое название от трех углов, которыми они обладают. Эти три угла в сумме должны составлять 180 градусов. Часто у вас есть измерения двух углов. Однако вам придется вычислить размер третьего угла. Используемое уравнение:
угол A + угол B + угол C = 180 градусов.
Например, у вас есть следующий треугольник. Что такое измерение угла C?
Если вы подставите эти числа в уравнение, вы получите следующее уравнение:
Уголки в четырехугольнике
Квадраты и прямоугольники имеют четыре прямых угла.Если сложить углы, получится 90 + 90 + 90 + 90 = 360. Четырехугольник также имеет четыре угла. Следовательно, углы формы составляют в сумме 360 градусов, даже если нет прямых углов. Чтобы определить недостающий угол четырехугольника, вы можете использовать следующее уравнение:
угол A + угол B + угол C + угол D = 360 градусов.
Посмотрите следующий пример. Можете ли вы определить недостающий угол в этом четырехугольнике?
Чтобы найти недостающий угол, подставьте измерения угла в уравнение:
Независимо от того, работаете ли вы с лучом, треугольником или четырехугольником, существуют методы, которые вы можете использовать, чтобы обнаружить недостающее измерение угла.Если вам интересно, как найти величину угла на луче, треугольнике или четырехугольнике, попробуйте использовать транспортир или уравнения, которые мы обсуждали. Они должны работать и помочь вам немного облегчить жизнь!