Как найти arg z комплексные числа: Как найти модуль и аргумент комплексного числа: онлайн, примеры

Содержание

Геометрия комплексных чисел . Магия математики [Как найти x и зачем это нужно]

Комплексные числа можно представить в виде комплексной же плоскости. Выглядит она так же, как и алгебраическая система координат (x, y), только вместо оси y мы чертим некую мнимую ось, на которой расположены числа 0, ±i, ±2i и так далее. Вот как будут выглядеть на этой плоскости некоторые комплексные величины:

Только что мы выяснили, насколько легко складывать, вычитать и умножать числовые выражения комплексных величин. С их геометрическими представлениями работать ничуть не сложнее: достаточно просто взглянуть на соответствующие точки.

Возьмем, к примеру, сложение:

(3 – 2i) + (–1 + i) = 2 + 3i

Посмотрите на график ниже: точки 0, 3 + 2i, 2 + 3i и –1 + i образуют параллелограмм.

Вы удивитесь, но его вполне достаточно, чтобы сложить комплексные числа

z и w.

Для вычитания z – w возьмем третью точку – w, расположенную симметрично напротив w. А теперь просто сложим z и – w, как показано на графике:

Для умножения и деления нам понадобится измерить комплексные величины. Модулем (или длиной) любого комплексного числа считается длина отрезка от начала координат 0 до точки, соответствующей искомому числу. То есть модуль числа z (обозначается как |z|) есть расстояние от 0 до точки z. Если z = a + bi, тогда, согласно теореме Пифагора, модуль z будет равен

|z| = ?(a? + b?)

На графике ниже хорошо видно, что точка 3 + 2i имеет модуль ?(3? + 2?)

= ?13.

Обратите внимание, что для соответствующего этой точке угла ? tan ? = 2/3. Следовательно, ? = tan^–12/3 ? 33,7° или примерно 0,588 рад.

Точки с модулем, равным 1, складываются в единичную окружность (см. график ниже). Чему будет равно комплексное число, образующее угол ?? Если бы мы находились в более привычной системе координат, нужная нам точка имела бы координаты (cos ?, sin ?) – это нам хорошо известно по предыдущей главе. Значит, здесь получаем cos ? + i sin ?. То есть любая комплексная величина с модулем R соответствует формуле

z = R(cos ? + i sin ?)

что есть не что иное, как тригонометрическое представление этого числа. Забегу немного вперед: в конце главы мы выясним, что равно оно будет

Re^i?.

А вот еще кое-что интересное: при перемножении комплексных чисел будут перемножаться и их модули.

Теорема: Для комплексных величин z₁ и z₂ |z₁z₂| = |z₁| |z₂|. Иными словами, модуль произведения есть произведение модулей.

Например,

|(3 + 2i)(1 – 3i)| = |9 – 7i| = ?(9? + (–7)?)?130 = ?13?10 = |3 + 2i| |1 – 3i

А что насчет угла, привязанного к произведению? Для обозначения угла, образованного комплексным z и «положительной» половиной оси x, обычно используется представление arg z. Так, arg (3 + 2i) = 0,588 рад. Аналогично arg (1 – 3i) = tan^–1 (–3) = –71,56° = –1,249 рад, потому что значение 1 – 3i располагается в квадранте IV, а тангенс его угла ? равен –3.

Обратите внимание, что угол значений (3 + 2i)(1 – 3i) = (9 – 7i) имеет tan^–1 (–7/9) = –37.87° = –0,661 рад, что есть 0,588 + (–1,249). И имеется теорема, которая доказывает, что это совсем не совпадение!

Теорема: Для комплексных величин z₁ и z₂ arg (z₁z₂) = arg (z₁) + arg (z₂

). Другими словами, угол произведения есть сумма углов.

Доказательство этого (оно приведено в «отступлении») основано на некоторых тригонометрических тождествах, рассмотренных нами в предыдущей главе.

Отступление

Доказательство: Возьмем две комплексные величины z₁ и z₂, имеющие модули R₁ и R₂ и углы ?₁ и ?₂ соответственно. Записав их в тригонометрическом представлении, имеем

z₁ = R₁ (cos ?₁ + i sin ?₁)

z₂ = R₂ (cos ?₂ + i sin ?₂)

Тогда на основании тождеств cos (

A + B) и sin (A + B)

z₁ z₂ = R₁(cos ?₁ + i sin ?₁) R₂(cos ?₂ + i sin ?₂) = R₁ R₂ [cos ?₁ cos ?₂ – sin ?₁ sin ?₂ + i(sin ?₁ cos ?₂ + sin ?₂ cos ?₁)] = R₁ R₂ [cos(?₁ + ?₂) + i(sin(?

1 + ?₂))]

Следовательно, z₁z₂ имеет модуль R₁R₂ (что нам уже известно) и угол ?₁ + ?₂, что и требовалось доказать. ?

Обобщим: чтобы умножить комплексные величины, нужно умножить их модули и сложить их углы. К примеру, при умножении некоего числа на i модуль останется прежним, а угол «вырастет» на 90°. Имейте в виду, что при перемножении двух действительных величин положительные числа будут иметь углы, равные 0° (или, что то же самое, 360°), а отрицательные – 180°. Два угла по 180° дадут в сумме 360° – еще одно доказательство, что произведение двух отрицательных величин есть величина положительная. Мнимые же числа имеют углы, равные либо 90°, либо –90° (или 270°). Следовательно, при умножении такого числа на само себя угол должен быть равен 180° (так как 90° + 90° = 180°, а –90° + –90° = –180°, что ничем не отличается от 180°), что соответствует отрицательной величине.

Ну и, наконец, возьмем число z с углом ?: 1/z должно иметь угол –?. (Почему? Да потому что z · 1/z = 1, то есть z и 1/z должны в сумме давать 0°.)

Получается, что при делении комплексных чисел, мы делим их модули и вычитаем их углы: z₁/z₂ имеет модуль R₁/R₂ и угол ?₁ – ?₂.

Комплексные числа — презентация онлайн

Похожие презентации:

Комплексные числа

Теория комплексных чисел. Геометрическая интерпретация комплексного числа. (Тема 3)

Комплексные числа

Теория комплексных чисел. Показательная форма комплексного числа. (Тема 4)

1. Комплексные числа.

Панарад А.Ю.
Кафедра Алгебры, Геометрии и Анализа.
ДВФУ

2. ПЛАН:

1. Основные понятия. Формы записи.
2. Действия над комплексными числами:
a) Сложение комплексных чисел;
b) Вычитание комплексных чисел;
c) Умножение комплексных чисел;
d) Деление комплексных чисел ;
e) Возведение в n-степень;
f) Извлечение корней из комплексных
чисел.

3. Основные понятия.

Определение.
Комплексным числом называется выражение
вида
, z i
где и — действительные числа, а i — мнимая
единица, и
2
i 1
Например, = 6 i или = 1-5i .

Число называется действительной частью
комплексного числа и обозначается Re z,
а мнимой частью и обозначается Im z.

4. Основные понятия.

Два комплексных числа
называются равными
тогда и только тогда,
когда равны их
действительные и
мнимые части.
Два комплексных числа,
отличающихся лишь
знаком мнимой части,
называются комплексносопряженными.
z1 1 1i ;
z 2 2 2i
z1 z 2 1 2 ; 1 2
z1 1 1i
z 2 2 2i

5. Примеры.

Пример 1.
z1 5 3i ;
Пример 2.
z 2 25 / 5 15 / 5i
z 2 5 3i
5 25 / 5
3 15 / 5
Вывод : z1 z 2
z1 5 3i ;
Вывод : z1 и z 2
комплексно сопряженные числа.

6. Геометрическое изображение комплексных чисел.

Всякое комплексное число
можно изобразить точкой
плоскости xOy такой, что
x Re z, y Im z.
И, наоборот, каждую точку
координатной плоскости
можно рассматривать как
образ комплексного
числа.
= i, М(
y
M( ; )
O
x

7.

Геометрическое изображение комплексных чисел.y
M(x;y)
O
x
Плоскость, на которой
изображается
комплексные числа,
называется комплексной
плоскостью.
Ось абсцисс Ox называется
действительной осью.
Ось ординат Oy называется
мнимой осью.

8. Геометрическое изображение комплексных чисел.

y
r OM
M(x;y)
φ
O
x
Комплексное число можно
задавать с помощью
радиус
вектора r OM .
Длина вектора называется
модулем этого числа и
обозначается ф фили r .
Величина угла между
положительным направлением
r
оси Ox и вектором
называется аргументом этого
комплексного числа и
обозначается Arg или
Аргумент комплексного числа
определяется с точностью до
слагаемого

9. Формы записи комплексных чисел.

1. Алгебраическая.
2. Тригонометрическая.
3. Показательная.
Любое комплексное число
можно записать в любой форме.

10. Формы записи комплексных чисел.

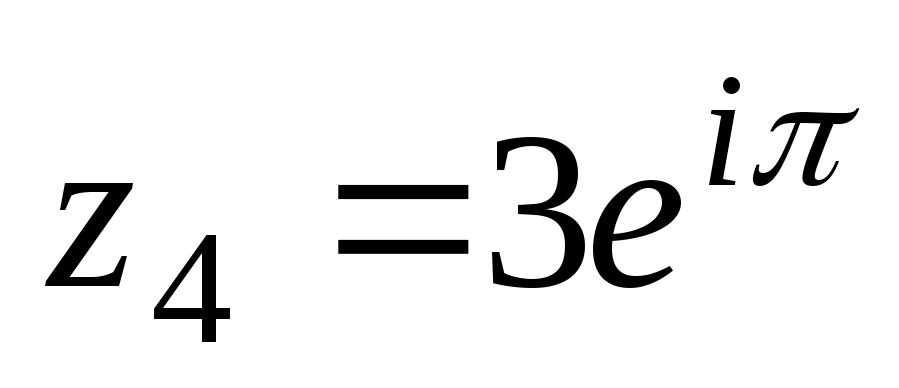Модуль r и аргумент можно
рассматривать как полярные
координаты вектора
r OM
Тогда получаем
x r cos
y r sin
Комплексное число z= i можно
записать в виде
z r cos ir sin
Или
z r (cos i sin )
Запись числa
z= i
называется
алгебраической формой
комплексного числа.
Запись числа z в виде
z=r(cosφ+isinφ)
называется
тригонометрической
формой
комплексного числа.

11. Переход от одной формы к другой.

От алгебраической формы
к тригонометрической
r z x2 y2
x
y
cos
sin
r
r
y
x
Т.к. Arg z arg z 2 k
tg
То
cos cos(arg z 2 k )
sin sin(arg z )
От тригонометрической
формы к алгебраической
x r cos
y r sin

12. При переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить главное значение аргумента, т.е.

arg z
Т.к.
то
arg z
arctg
arg z arctg
arctg
y
tg
x
y
для точек I и IV четвертей ;
x
y
для точек II четверти ;
x
y
для точек III четверти.

13. Пример: Комплексное число изобразить на плоскости и записать в тригонометрической форме

z 2 2i
x 2
y 2
y
2
φ
0
r z x2 y2
2
x
r 22 22 2 2
Для I четверти
y
2
arg z arctg arctg arctg1
x
2
arg z
4
2 2i 2 2 (cos i sin )
4
4

14. Комплексное число можно записать в показательной (или экспонентной) форме

z re
i
Где
arg z
r z и
В силу формулы Эйлера
e i cos i sin
функция
i периодическая с основным периодом
e
2π.
Для записи комплексного числа в показательной
форме надо определить главное значение аргумента
и модуль.

15. 2. Действия над комплексными числами

Суммой двух комплексных
чисел
z1 x1 y1i
z 2 x2 y 2 i
Называется комплексное
число
z1 z 2 ( x1 x2 ) ( y1 y2 )i
Разностью двух комплексных
чисел z1 x1 y1i
z 2 x2 y 2 i
Называется комплексное
число
z1 z 2 ( x1 x2 ) ( y1 y2 )i
Геометрически комплексные числа
складываются и вычитаются, как
векторы.

16. Сложение (вычитание) комплексных чисел

Примеры:
1. z1 4 2i
z 2 5 3i
z1 z 2 (4 5) (2 3)i 1 5i
2.
z1 3 5i
z 2 2 7i
z1 z 2 (3 2) ( 5 ( 7)i 1 2i

17. Произведение и частное комплексных чисел в алгебраической форме.

Произведением двух
комплексных чисел
Частным двух комплексных
чисел
z1 x1 y1i
z1 x1 y1i
z 2 x2 y 2 i
называется комплексное
число
z 2 x2 y 2 i
z z1 z 2 ( x1 x2 y1 y2 ) ( x1 y2 y1 x2 )i
Формула получается путем
перемножения двучленов!
( x1 y1i )( x2 y2i )
называется комплексное число
z1 x1 x2 y1 y2 y1 x2 x1 y2
i
2
2
2
2
На практике
z2
x2 используют
y2
x2 y 2
z
умножение числителя и
знаменателя на число,
сопряженное знаменателю!
( x1 y1i ) ( x2 y2i )
( x2 y 2 i ) ( x2 y 2 i )

18. Произведение и частное комплексных чисел в алгебраической форме.

Произведение:
Частное:
z1 1 2i
z1 1 2i
z 2 3 4i
z2 1 i
z1 z 2 (1 2i ) (3 4i )
1 2i (1 2i )(1 i )
1 i
(1 i )(1 i )
1 3 2i 3 1 4i 2i 4i
4 6i 4i 8i 2 4 10i 8
4 10i
z1 z 2 4 10i
i 1
2
1 2i i 2 3 i
1 1
2
z1 3 1
i
z2 2 2

19.

Произведение и частное комплексных чисел в тригонометрической форме.Произведение чисел
z1 r1 (cos 1 i sin 1 )
z 2 r2 (cos 2 i sin 2 )
Находим по формуле
z1 z 2 r1r2 (cos( 1 2 ) i sin( 1 2 ))
При умножении модули
перемножаются, а
аргументы складываются!
Частное чисел
z1 r1 (cos 1 i sin 1 )
z 2 r2 (cos 2 i sin 2 )
Находим по формуле
z1 r1
(cos( 1 2 ) i sin( 1 2 ))
z 2 r2
При делении модули
делятся, а аргументы
вычитаются!

20. Произведение и частное комплексных чисел в тригонометрической форме.

Произведение:
i sin )
3
3
z 2 5(cos i sin )
z1 z 2 3 5(cos( ) i sin( ))
3
3
z1 3(cos
4
4
z1 z 2 15(cos
i sin )
3
3
Частное:
i sin )
3
3
z2 5(cos i sin )
z1 3
(cos( ) i sin( ))
z2 5
3
3
z1 3(cos
z1 3
2
2
(cos( ) i sin( ))
z2 5
3
3

21. Произведение и частное комплексных чисел в показательной форме.

z1 r1e
i 1
z 2 r2 e
i 2
z1 z 2 r1r2 e
i ( 1 2 )
z1 r1 i ( 1 2)
e
z 2 r2
z1 2e
i
z 2 3e
z1 z 2 6e
z1 2
e
z2 3
i
i
i
2
3
5
6
6

22. Возведение комплексных чисел в степень.

Правило умножения комплексных чисел
позволяет возвести число в n-степень:
z n z z z …
n
Получим Формулу Муавра:
z n r n (cos n i sin n )
Для показательной формы используют формулу:
z n r n e in

23. Возведение комплексных чисел в степень. Пример.

Найти (1 3i ) 9
Запишем число в тригонометрической форме:
r 1 3 2,
arg z arctg 3 ,
3
z 2(cos i sin )
3
3
z 9 (1 3i )9 29 (cos 9
i sin 9 )
3
3
29 (cos 3 sin 3 ) 29 ( 1) 512.

24. Извлечение корней из комплексных чисел в тригонометрической форме.

Определение.
Корнем n-й степени из комплексного числа z называется
комплексное число ω, удовлетворяющее равенству:
n z
Данное действие выполняется над комплексными
n
z
числами в тригонометрической форме.

n различных
корней!
2 k
2 k
n
r (cos i sin ) r (cos
i sin
)
n
n
Получим
n

25. Извлечение корней из комплексных чисел. Пример.

6
Извлечение корней из
комплексных чисел.
Пример.
Найти
z , если z 1
В тригонометрической форме число имеет вид:
1 cos i sin
6
1 cos
2k
2k
i sin
6
6
Используем формулу:
Найдем 6 возможных корней, придавая k последовательно
значения 0,1,2,3,4,5:
3 1
k
1
,
z
cos
i
sin
i
2
k 0, z1 cos i sin
i
2
2
6
6
2 2
5
5
3 1
k 2, z1 cos
i sin
i
6
6
2 2
3
3
k 4, z1 cos
i sin
i
2
2
k 3, z1 cos
7
7
3 1
i sin
i
6
6
2 2
k 5, z1 cos
11
11
3 1
i sin
i
6
6
2 2

English Русский Правила

Аргумент калькулятора комплексных чисел

Поиск инструмента

Поиск инструмента в dCode по ключевым словам:

Просмотр полного списка инструментов dCode

Аргумент комплексного числа

Инструмент для вычисления значения аргумента комплексного числа. Аргументом ненулевого комплексного числа $z$ является значение (в радианах) угла $\theta$ между абсциссой комплексной плоскости и линией, образованной $(0;z)$.

Результаты

Комплексный числовой аргумент — dCode

Теги: Арифметика, Геометрия

dCode и многое другое

Программа dCode бесплатна, а ее инструменты оказывают ценную помощь в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Калькулятор аргументов

Комплексный номер z

Формат результата

Автоматический выбор
Точное значение (когда возможно)
Приблизительное числовое значение
Научное обозначение

См. также: Модуль/величина комплексного числа

Комплекс из калькулятора аргументов и модулей

Аргумент $ \theta $
Модуль/величина $ r $

См. также: Экспоненциальная форма комплексного числа — Аффикс комплексного числа — Сопряжение комплексного числа

Ответы на вопросы (FAQ)

Что такое аргумент комплексного числа? (Определение)

Аргумент представляет собой угол $\theta$, определяющий комплексное число $z$ в комплексной плоскости, отмечен arg или Arg вычисляется по формуле:

$$ \arg(z) = 2\arctan \left( \frac{\Im(z)}{\Re(z) + |z|} \ справа) = \theta \mod 2\pi $$

, где $ \Re(z) $ действительная часть, $ \Im(z) $ мнимая часть и $ |z| $ комплексный модуль $z$.

Как вычислить аргумент комплексного числа?

Чтобы определить аргумент комплексного числа $ z $, примените приведенную выше формулу, чтобы найти $ \arg(z) $.

Пример: Возьмем $ z = 1+i $, действительная часть равна $ 1 $, мнимая часть равна $ 1 $ и модуль комплексного числа $ |z| $ равно $ \sqrt(2) $, поэтому $\arg(z) = 2 \arctan\left(\frac{1}{1 + \sqrt(2)} \right) = \frac{\pi}{4 } $

Результатом вычисления $ \arg(z) $ является значение между $ -\pi $ и $ +\pi $, а тета-значение равно модулю $ 2\pi $

В электричестве аргумент равен эквивалентна фазе (а модуль является действующим значением).

Каковы свойства аргументов? 9n ) \equiv n \times \arg(z) \mod 2\pi $

$ \arg( \frac{1}{z} ) \equiv -\arg(z) \mod 2\pi $

$ \arg( \frac{z_1}{z_2} ) \equiv \arg(z_1) — \arg(z_2) \mod 2\pi $

Если $ a $ строго положительное вещественное число, а $ b $ строго отрицательное действительное число , тогда

$ \arg(a \cdot z) \equiv \arg(z) \mod 2\pi $

$ \arg(b \cdot z) \equiv \arg(z) +\pi \mod 2 \pi $

Какие значения сложных аргументов нужно знать?

Некоторые аргументы тривиальны (аргумент 1, аргумент -1, аргумент i, аргумент -i и т. д.) и их можно запомнить:

— $ \arg( 1 ) = 0 $

— $ \arg( 2 ) = 0 $

— $ \arg( n ) = 0 $ (где $ n $ — положительное действительное число)

— $ \arg(-1) = \pi $

— $ \arg(-2) = \pi $

— $ \arg(-n) = \pi $ (с $ n $ ненулевым положительным вещественным числом)

— $ \arg( i ) = \pi / 2 $

— $ \arg( — i ) = — \pi / 2 $

— $ \arg( 1+i ) = \pi / 4 $

— $ \arg( 1-i ) = — \pi / 4 $

— $ \arg( -1+i ) = 3 \pi / 4 $

— $ \arg( -1-i ) = — 3 \pi / 4 $

Какой аргумент у числа 0?

Аргумент $ 0 $ равен $ 0 $ (число 0 имеет действительную и комплексную часть нуля и, следовательно, является нулевым аргументом).

Что означает аргумент, равный 0?

Если аргумент комплексного числа равен $ \arg(z) = 0 $, то число не имеет мнимой части (это действительное число).

Какой главный аргумент?

Аргумент представляет собой угол, обычно в радианах. Углы повторяются каждые $ 2 \pi $, поэтому их бесконечное количество.

Главный/главный аргумент находится между $-\pi $ и $\pi$ (но некоторые люди берут между $0$ и $2\pi$)

Чтобы вычислить главный аргумент из не- главный аргумент добавить или вычесть $ 2 \pi $ столько раз, сколько необходимо (расчет по модулю $ 2 \pi $)

dCode всегда вычисляет главный аргумент.

Исходный код

dCode сохраняет за собой право собственности на исходный код «Комплексный числовой аргумент». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Аргумент сложного числа», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Комплексного числа». функции «Аргумент» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, script или доступ к API для «Комплексного числового аргумента» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.

Цитировать dCode

Копирование и вставка страницы «Аргумент комплексного числа» или любых его результатов разрешено, если вы цитируете dCode!
Цитировать как источник (библиографию):
Аргумент комплексного числа на dCode.fr [онлайн-сайт], получено 18 февраля 2023 г., https://www.dcode.fr/complex-number-argument

Сводка

Калькулятор аргумента
Комплекс из калькулятора аргумента и модуля
Что такое аргумент комплексного числа? (Определение)
Как вычислить аргумент комплексного числа?
Каковы свойства аргументов?
Какие значения сложных аргументов нужно знать?
Каков аргумент числа 0?
Что означает аргумент, равный 0?
Каков главный аргумент?

Похожие страницы

Комплексное число Модуль/величина
Комплексное число Экспоненциальная форма
Complex Number Conjugate
Complex Number Affix
Pythagore Triple
Rounding Calculator
Knuth’s Arrows
DCODE’S TOOLS LIST

Support

Paypal
Patreon
More

Forum/Help

Ключевые слова

аргумент, комплекс, число, угол, фаза, плоскость, тета

Ссылки

▲

Как найти модуль (абсолютное значение) и аргумент (угол) комплексных чисел?

Комплексная плоскость играет важную роль в математике. Есть два понятия, связанные с комплексными числами: модуль и аргумент. Следующее пошаговое руководство поможет вам научиться находить модуль и аргумент комплексных чисел.

Одна из самых важных особенностей чисел, вещественных или сложных, заключается в том, что они имеют «абсолютное значение». Имейте в виду, что если действительное число положительное или отрицательное, его абсолютное значение $|x|$ равно самому себе. Если $x$ отрицательно, его абсолютное значение $|x|$ является его отрицанием, которое является положительным значением $x$. Потому что $|3|$ равно $3$, а $| –4|$ равно $4$. Удаляет знак у вещественного числа.

См. также

Тождества комплексных чисел
Как решить комплексную плоскость

Пошаговое руководство по модулю и аргументу комплексных чисел

В комплексной плоскости $C$ расстояние от $ z$ до $0$ называется абсолютным значением $|z|$. Это облегчит понимание абсолютного значения действительных чисел. Абсолютное значение $|x|$ действительного числа $x$ можно рассматривать как расстояние от $x$ до $0$ на прямой с действительными числами, так что это облегчит задачу. понять, что такое абсолютное значение. 92}}\)

Аргумент комплексного числа определяется как угол, образованный между действительной осью и комплексным числом, представленным на комплексной плоскости, где действительная ось является началом комплексного числа. Обозначается символами «$θ$» или «$φ$». Он измеряется в радианах, которые являются стандартной единицей измерения.

Точка $P$ обозначает комплексное число на этой диаграмме. Длина $OP$ известна как величина или модуль числа, а угол, под которым $OP$ наклонен от положительной действительной оси, является аргументом точки $P$. 9n)=n\ arg (z)}\)

$Z_1$ и $Z_2$ — это два комплексных числа, которые, как мы можем предположить, обладают следующими свойствами:

$\color{blue} { arg (\frac {z_1}{z_2})=arg (z_1)-arg(z_2)}$

$\color{blue}{arg\ (z_1 z_2)= arg (z_1) + arg (z_2 )}$

Как лучше всего найти аргумент комплексного числа?

По заданному комплексному числу определите действительную и мнимую составляющие.