Js целочисленное деление: Как поделить число нацело в javascript?

javascript — Зачем при записи чисел в конце добавляют .0?

Вопрос задан 6 лет 1 месяц назад

Изменён 5 лет 2 месяца назад

Просмотрен 717 раз

Часто в коде программ числа записываются в виде цифры с .0 на конце. Например:

C: double s = 1.0 / 6.0;

Delphi: var d: Single; begin d := 16.0 + 1.0; end;

JS: var t = 90.0;

Возможны примеры и на других языках, но для начала предлагаю ограничиться этими тремя

Какой смысл несет добавление .0 в данных случаях?
В каких случаях .0 можно опускать, а в каких он меняет логику поведения программы?

• javascript
• c++
• delphi

6

Если говорить в общем, то добавление . 0 к числу, изменяет его тип и превращает его из целого, в дробное (число с плавающей точкой). Такое изменение типа числа влияет на то, как оно будет храниться в памяти и на то, как и какие операции с ним могут выполняться.

В JS добавление .0 абсолютно лишено всякого смысла, т.к. там все числа изначально являются дробными.

В Delphi так же не возникает необходимости вручную приводить целые числа к дробным, т.к. компилятор замечательно справляется с этим самостоятельно, там где это нужно. Операция деления двух целых всегда возвращает дробное число и его невозможно по ошибке присвоить целому. Для особых случаев, когда надо выполнить целочисленное деление, есть специальный оператор div.

А вот в Си и некоторых других языках, и для целочисленного, и для обычного деления используется один и тот же оператор деления

/ который ведёт себя по разному, в зависимости от типа операндов:

• если оба операнда целые, то и в результате деления будет целое (целочисленное деление): double i = 5 / 2; даст 2. 0 (дробная часть результата операции отбрасывается, получается целое число, которое затем приводится к целевому типу double).
• если хоть один из операндов является дробным, то и результат будет дробным: double i = 5 / 2.0; даст 2.5.

В Си, вместо .0 перед числом можно указывать тип числа с плавающей точкой (float/double), т.е. выполнять приведение типа: double i = 5 / (double) 2; такая конструкция используется, если операнд не число, а переменная целочисленного типа:

int k = 2;
double i = 5 / (double) k; // --> i = 2.5

2

В конце литерала нужно добавлять .0 в том случае, если вам важно получить тип с плавающей точкой. Я приведу пример для С/С++, но он также будет актуальным для Java, C# и многих других языков:

double X = 15 / 2; // Выведет 7

Здесь тип переменной — double, так что можно подумать, что в ответе получится 7. 5, но это не так. Поскольку и 15 и 2 не имеют дробной части, они будут считаться целыми числами при вычислении, и для них сначала будет произведено целочисленное деление (15 / 2 = 7), а потом полученный результат будет конвертирован и записан в переменную типа double.

Это можно исправить, добавив пустую дробную часть к одному или к обоим литералам. Если один из операндов является числом с плавающей точкой, то второй операнд тоже будет конвертирован в число с плавающей точкой, и вы получите правильный результат:

double X = 15.0 / 2; // Выведет 7.5

Общее правило для C++ и подобных языков: добавляйте .0 к литералам тогда, когда ожидаете ответ типа float или double. Это поможет избежать неожиданностей.

7

.0 задавать для значения переменной нужно для того, что бы явно показать как компилятору (интерпретатору) языка, так и программисту, что в контексте использования переменной речь идет о дробных числах. Один из возможных примеров тут.

1. Изучайте базовые типы и приемы работы с переменными этих типов для тех платформ и языков, на которых программируете или собираетесь начать программировать.

2. Если у вас есть вероятность, что в результатах ваших вычислений будут задействованы дробные числа — так и работайте с переменными соответствующих типов.

6

В давние времена, когда появился Fortran — первый язык программирования высокого уровня, имеющий транслятор, это были азы, с которых начиналось обучение программированию. Добавление точки после числа сейчас называют неявным приведением типа. Когда надо было получить тип REAL от деления целых, писали Z=(X+0.)/(Y+0.) или Z=7./8.

Это, конечно, было неисчерпаемым источником багов в программах. Тогда считалось несолидным добавлять ноль после точки. Это же целая лишняя дырка в перфокарте!

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Назначение деления (/=) Оператор присваивания division делит переменную на значение правого операнда присваивает результат Последнее изменение:Март 25,2022,автор MDN contributors

Деление (/)Оператор деления(/)образует коэффициент своих операндов,где левый операнд-делитель,а правый-делимое.

Оператор присваивания деления(/=)делит переменную на значение правого операнда и присваивает результат переменной.

Оператор /=сначала делит значение переменной или свойства (в левой части оператора)на значение выражения (в правой части оператора).Затем оператор присваивает переменной или свойству результат этой операции с плавающей точкой.

Присвоение (=)Простой оператор присваивания(=)используется для присвоения значения переменной.Операция присваивания оценивается по присвоенному значению.Для присвоения одного значения нескольким переменным можно использовать цепочку операторов присваивания.

Все числа в javascript являются двойными.Это означает,что по умолчанию целочисленное деление отсутствует.

Знак деления представляет собой тире или двойное тире с точкой вверху и точкой внизу (÷). Это равносильно слову «разделить на». Этот символ встречается в основном в учебниках по арифметике для начальной школы.

Оператор строгого равенства(===)проверяет,равны ли два его операнда,возвращая булевский результат.В отличие от оператора равенства,оператор строгого равенства всегда считает операнды разных типов разными.

Оператор присвоения деления ( /= ) делит переменную на значение правого операнда и присваивает результат переменной.

Try it

Syntax

x /= y // х = х / у

Examples

Использование задания на деление

// Предполагается, что следующая переменная и все операции выполняются по порядку
// бар = 5
bar /= 2     // 2.5
bar /= 2     // 1.25
bar /= 0     // Infinity
bar /= 'foo' // NaN

Specifications

Specification
Спецификация языка ECMAScript # sec-assignment-operators

Browser compatibility

	Desktop	Mobile	Server
	Chrome	Edge	Firefox	Internet Explorer	Opera	Safari	WebView Android	Chrome Android	Firefox для Android	Opera Android	Safari на IOS	Samsung Internet	Deno	Node. js
Division_assignment	1	12	1	3	3	1	4.4	18	4	10.1	1	1.0	1.0	0.10.0

See also

• Операторы присваивания в справочнике JS
• Division operator

---

• 1
• …
• 834
• 835
• 836
• 837
• 838
• …
• 925
• Next

Equality (==)

javascript — Как убедиться, что целочисленное деление дает правильные результаты?

Задавать вопрос

спросил 7 лет, 2 месяца назад

Изменено 2 года, 9 месяцев назад

Просмотрено 1к раз

Я знаю, что вычисления с плавающей запятой могут быть неточными. Например:

 вар х = 100*0,333;
 

Здесь x устанавливается равным 33.300000000000004 , а не 33 . Это может показаться незначительной проблемой, но становится серьезной, если используется округление. Например, Math.ceil(x) будет неправильным — вместо 33 будет получено 34 .

Проблема в том, что мне сказали, что JS не делает большой разницы между целыми числами и числами с плавающей запятой. Поэтому я начинаю беспокоиться, есть ли способ убедиться в правильности интегрального деления.

Обычная формула целочисленного деления в JS выглядит так: Math.floor(n/m) , где n , m — целые числа. Теперь допустим, что м делит на поровну. Поскольку JS обрабатывает каждое число как число с плавающей запятой, n/m вернет число с плавающей запятой. Если это число с плавающей запятой не является точным, но даже немного меньше фактического результата вычисления, то Math. floor(n/m) будет округлено до одного целого числа меньше, чем должно.

Для иллюстрации: если, например, 9/3 дает 2.999999999999999 , а не 3 , то Math.floor(9/3) неправильно даст 1.3 3 2 89018 Ну, на самом деле, Math.floor(9/3) действительно выдает правильные результаты, но это, конечно, только пример; замените 9 и 3 любым неудачным выбором целых чисел.

Может ли случиться такой сценарий? Если да, то есть ли способ обеспечить правильные результаты?

• javascript
• точность с плавающей запятой
• целочисленное деление

7

Может ли случиться такой сценарий?

Нет. Если это целые числа (т.е. числа с плавающей запятой без дробной части) и делятся нацело, то результат будет точным и снова целым числом.
Если делить не нацело, результат всегда будет больше, чем точный результат целочисленного деления. Вы никогда не получите 2.9999999… номер, который должен был быть 3 . Результаты с плавающей запятой настолько точны, насколько это возможно, округление не разрушает общий предварительный порядок.

1

, если вы хотите получить точный результат целочисленного деления. Затем сделайте это

 Math.round((m - m%n)/n)
 

Если значение деления двух чисел должно быть 3, то так и будет. Если значение должно быть 2,999999999999, оно будет таким. Java не делает какого-то странного скрытого округления вверх или вниз. Если вам ВСЕГДА нужно округлить значение в меньшую сторону, используйте Floor (x/y), даже если значение равно 2,9.99999999999999999999999999999999999 он все равно вернется как 2. Вот что делает Флор. То же самое и с потолком. если значение равно 3.0000000000000000000001, то оно будет установлено на 4. Я учу этому в колледже, так оно и должно работать, и оно работает.

2

Зарегистрируйтесь или войдите

Зарегистрироваться с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Целочисленная математика в JavaScript | Джеймс Дарпиниан

Возможно, вы знаете, что все числа в JavaScript являются 64-битными значениями с плавающей запятой двойной точности. Иногда это удобно, и это работает довольно хорошо по умолчанию для начинающих программистов, которых часто смущает целочисленная математика, и это справедливо, когда 1 / 2 = 0 . К сожалению, это замедляет работу. Двойники занимают много памяти, а математика с плавающей запятой медленнее, чем математика с целыми числами на процессорах. Это также неудобно, если вы хотите перенести существующий код на JavaScript, потому что существующий код обычно предполагает использование целочисленной математики.

К счастью, есть способ заставить JavaScript выполнять целочисленные вычисления, и он работает на удивление хорошо!

TL;DR​

Добавить | 0 после каждой математической операции для получения 32-битного целого числа со знаком и >>> 0 для 32-битного целого числа без знака. И храните все свои числа в типизированных массивах вместо массивов JavaScript.

Фон

В JavaScript есть полный набор инструкций по обработке битов. Побитовые операторы и/или/xor/not/shift такие же, как в C, и я понятия не имею, почему они изначально были в JavaScript, потому что они не кажутся очень полезными для веб-разработки. Кроме того, это странно, когда все числа имеют двойную точность с плавающей запятой, верно? Никто не выполняет побитовые операции над числами с плавающей запятой. И JavaScript тоже. На самом деле, JavaScript (концептуально) сначала округлит ваш 64-битный тип double до 32-битного целого числа со знаком, выполнит побитовую операцию, а затем преобразует его обратно в значение двойной точности. Странный!

Все эти преобразования звучат дорого! И, вероятно, так оно и было, еще до asm.js. Разработчики asm.js переносили код C на JavaScript, и странное приведение типов, выполняемое странными побитовыми операторами JavaScript, было как раз тем, что им было нужно для эмуляции целочисленной арифметики C.

Хитрость

Если в C x и y являются целыми числами, то x / y будет выполнять целочисленное деление, округляя результат в меньшую сторону.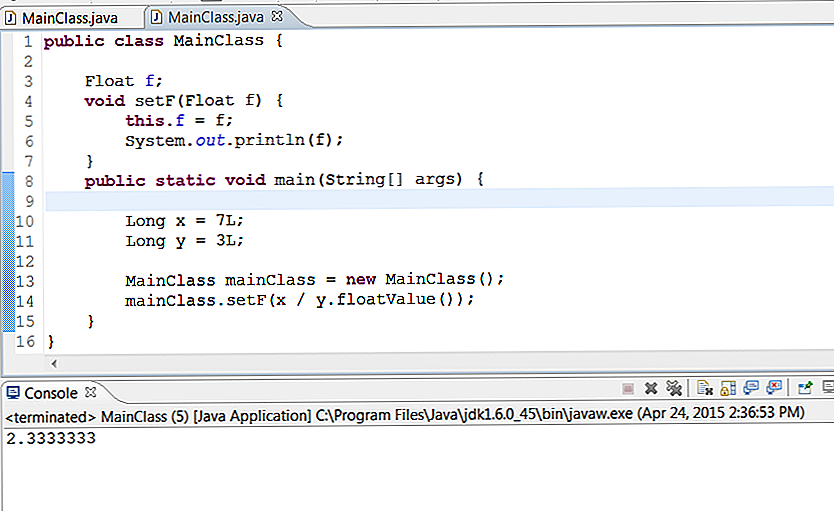 В JavaScript x/y всегда будет делением с плавающей запятой с результатом с плавающей запятой. Но если вы примените побитовый оператор сразу после этого, то результат будет округлен в меньшую сторону, преобразован в целое число, и вы получите то же число, что и C! С большим количеством работы. Конечно, вы не хотите, чтобы ваш побитовый оператор изменил результат, поэтому вы можете выполнить побитовую операцию без операций, например >> 0 или | 0 . No-op в C, конечно, но не в JavaScript из-за целочисленного преобразования.

Как только asm.js начал делать | 0 везде, люди начали очень интересоваться его оптимизацией. Очевидно, что вы можете просто пропустить выполнение инструкции ИЛИ , так как она ничего не делает. Но настоящая работа заключается во всех этих медленных преобразованиях в числа с плавающей запятой и обратно. Получается, что если добавить | 0 после каждой операции ваш JIT-компилятор JavaScript также может пропускать избыточные преобразования и просто все время сохранять ваши числа как целые числа. Когда известно, что входные данные для деления являются целыми числами, и | 0 снова преобразует его в целое число, затем вместо двух преобразований в число с плавающей запятой, инструкции деления с плавающей запятой, а затем преобразования в целое число, JIT может выдать одну команду целочисленного деления, как это сделал бы компилятор C, без вообще изменить результат. Это довольно чудесно!

Подробнее

Все побитовые операторы JavaScript, унаследованные от C, преобразуют свои операнды и результаты в 32-битные целые числа со знаком. Но есть трюк и для целых чисел без знака. В JavaScript есть один дополнительный побитовый оператор, которого нет в C: >>> . По сути, это оператор «беззнакового сдвига вправо», и он особенный, поскольку его результатом является 32-разрядное целое число без знака. Поэтому, когда вам нужно целое число со знаком, вы добавляете | 0 после ваших арифметических операций, а для беззнаковых вы используете >>> 0 .

Все это прекрасно работает для 32-битных целочисленных вычислений, как со знаком, так и без знака. А другие размеры? К сожалению, если вам нужна 64-битная целочисленная математика, вам не повезло. Эти трюки работают для 32-битных чисел, потому что с плавающей запятой двойной точности можно точно представить каждое 32-битное целое число, и выполнение деления с плавающей запятой двух целых чисел меньше 2 ³² , а затем преобразование результата в целое число дает точно такой же результат, как инструкция целочисленного деления в каждом случае. Но полный диапазон 64-битных целых чисел не может быть представлен с плавающей запятой двойной точности. Целые числа, превышающие 2 ⁵³ , могут быть представлены неточно, и числа JavaScript всегда должны вести себя так, как если бы они были представлены значениями с плавающей запятой двойной точности, даже если это не так. Компилятор JIT не может просто незаметно выполнять 64-битные целочисленные вычисления и притворяться, что это числа с плавающей запятой, потому что он получит другие результаты, когда целые числа достаточно велики.

К сожалению, умножение двух 32-битных чисел может дать результат до 2 ⁶⁴ . Когда результат больше 2 ⁵³ , умножение двойной точности с плавающей запятой может давать ответы, отличные от умножения целых чисел, даже если оно впоследствии усекается до 32-битного целого числа. Это не позволяет JavaScript JIT использовать инструкции целочисленного умножения. Для решения этой проблемы был введен Math.imul() . Поэтому для целочисленного умножения вы должны использовать это вместо * оператор, за которым следует | 0 .

ОК, 64-битная версия не работает, как насчет 16-битной и 8-битной? Ну, с одной стороны, вы тоже не можете этого сделать, вся ваша целочисленная математика будет иметь ширину 32 бита. Но, с другой стороны, это не так уж и плохо, потому что ЦП складывает 32-битные числа так же быстро, как и 8-битные. Там, где меньшие типы действительно , дело в использовании памяти. Если вам нужен массив байтов, но вместо этого вы используете массив JavaScript для хранения чисел JavaScript, он будет использовать в 8 раз больше памяти (и в 8 раз больше пропускной способности памяти, и в 8 раз больше места в кэше), потому что каждое число JavaScript составляет 8 байтов. К счастью, в JavaScript есть решение и для этого: типизированные массивы. Типизированные массивы могут содержать 8-битные, 16-битные и 32-битные значения как со знаком, так и без знака. Дополнительным преимуществом является то, что, поскольку типизированные массивы не могут содержать ссылки на объекты, сборщику мусора не нужно сканировать их содержимое, что также повышает производительность.

Дополнительный вопрос: как насчет 32-битной плавающей запятой? Это быстрее, чем 64-битные вычисления с плавающей запятой, и часто используется в 3D-графике. Можем ли мы использовать аналогичный трюк, чтобы JIT-компилятор JavaScript выдавал 32-битные математические инструкции с плавающей запятой? Ответ — да, есть функция Math.fround , используемая для этой цели asm.js. Я никогда не пробовал использовать его сам.

Собираем все вместе

Asm.js использует эти методы для преобразования кода C в JavaScript и приближается к производительности собственных компиляторов C.