Основы программирования на Java
Основы программирования на Java
ОглавлениеВВЕДЕНИЕОСНОВНЫЕ ПОНЯТИЯ 1. ПЕРЕМЕННЫЕ 2. ТИПЫ 2.1. Простые типы 2.  2.1.2. Символы 2.1.3. Тип boolean 2.2. Приведение типов 3. МАССИВЫ 3.1. Многомерные массивы 4. ОПЕРАТОРЫ 4.1. Арифметические операторы 4.1.1. Оператор деления по модулю 4.1.2. Арифметические операторы присваивания 4.1.3. Инкремент и декремент 4.2. Целочисленные битовые операторы и операторы отношений 4.3. Операторы отношений 4.4. Булевы логические операторы 4.5. Тернарный оператор if-then-else 4.6. Приоритеты операторов 5. УПРАВЛЕНИЕ ВЫПОЛНЕНИЕМ ПРОГРАММЫ 5.1. Условный оператор if-else 5.2. Опреатор break 5.3. Оператор switch 5.4. Оператор return 6. ЦИКЛЫ 6.1. Цикл while 6.2. Цикл do-while 6.3. Цикл for 6.4. Оператор continue ОБЪЕКТНО-ОРИЕНТИРОВАННОЕ ПРОГРАММИРОВАНИЕ НА JAVA 7. КЛАССЫ 7.1. Переменные класса 7.2. Оператор new 7.3. Объявление методов 7.4. Вызов метода 7.5. Скрытие переменных 7.6. Конструкторы 7.7. Совмещение методов 7.  8. Ссылка this 8. Ссылка this7.9. Наследование 7.10. Ссылка super 7.11. Замещение методов 7.12. Динамическое назначение методов 7.13. Директива final 7.14. Деструкторы 7.15. Статические методы Директива final, деструкторы и статические методы 7.16. Абстрактные классы 8. ПАКЕТЫ И ИНТЕРФЕЙСЫ 8.1. Пакеты 8.2. Интерфейсы 9. ОБРАБОТКА ИСКЛЮЧЕНИЙ 9.1. Основы механизма исключений 9.2. Типы исключений 9.3. Неперехваченные исключения 9.4. Операторы try и catch 9.5. Несколько разделов catch 9.6. Вложенные операторы try 9.7. Оператор throw 9.8. Оператор throws Операторы throw и throws 9.9. Оператор finally 10. МНОГОПОТОЧНОЕ ПРОГРАММИРОВАНИЕ 10.1. Модель легковесных процессов в Java 10.2. Подпроцесс 10.3. Интерфейс Runnable 10.4. Приоритеты подпроцессов 10.5. Синхронизация 10.6. Методы программного интерфейса легковесных процессов 11.1. Работа с файлами 11.2. Каталоги Классы InputStream и OutputStream 11.  3. Класс InputStream 3. Класс InputStream11.4. Класс OutputStream Файловый поток FilelnputStream и FileOutputStream 11.5. Файловый поток FilelnputStream 11.6. Файловый поток FileOutputStream 12. ПРОГРАММИРОВНИЕ ГРАФИЧЕСКИХ ПОЛЬЗОВАТЕЛЬСКИХ ИНТЕРФЕЙСОВ 12.1. Компоненты 12.2. Класс Container 12.3. Класс Canvas 12.4. Класс Label 12.5. Класс Button 12.6. Класс Checkbox 12.7. Класс CheckboxGroup 12.8. Класс Choice 12.9. Класс List 12.10. Класс Scrollbar 12.11. Класс TextField 12.12. Класс TextArea 12.13. Стратегии размещения компонентов 12.14. Программирование окон – Window 12.15. Программирование меню 12.16. Модель обработки событий от компонентов ЗАКЛЮЧЕНИЕ БИБЛИОГРАФИЧЕСКИЙ СПИСОК |
The Remainder Operator работает с двойниками в Java — The Renegade Coder
Я преподаю в OSU почти два года, и меня всегда поражало, как многому я учусь у своих студентов. Например, в прошлом у меня были студенты, которые писали странные фрагменты кода, которые я не понимал. На данный момент, даже после более чем 300 постов в блогах, нескольких видеороликов на YouTube и даже сбора фрагментов кода с более чем 100 языков, можно подумать, что я все это видел. Ну, недавно я видел студента, использующего оператор остатка (
Например, в прошлом у меня были студенты, которые писали странные фрагменты кода, которые я не понимал. На данный момент, даже после более чем 300 постов в блогах, нескольких видеороликов на YouTube и даже сбора фрагментов кода с более чем 100 языков, можно подумать, что я все это видел. Ну, недавно я видел студента, использующего оператор остатка ( % ) в парном разряде, и с тех пор я совсем не был прежним.
Содержание
Остаток против оператора модуля
Прежде чем я начну рассказ, я хотел бы остановиться и провести различие между оператором остатка и оператором модуля. В Java нет оператора модуля . Вместо этого % — оператор остатка. Для положительных чисел они функционально эквивалентны. Однако, как только мы начнем играть с отрицательными числами, мы увидим удивительную разницу.
Я уже немного рассказывал об этой разнице в статье про шифрование RSA. Тем не менее, я нашел еще один отличный источник, в котором сравнивается оператор «по модулю» в различных языках, включая Java, Python, PHP и C. Например, если мы возьмем
Например, если мы возьмем 3 % 5 , мы получим 3, потому что 5 вообще не входит в 3. Если мы начнем играть с отрицательными числами, результаты будут аналогичными. Например, если мы возьмем 3 % -5 , мы все равно получим три, потому что это все, что осталось.
Между тем, если мы изменим сценарий и сделаем дивиденд отрицательным (в конце концов, остаток является побочным продуктом деления), мы начнем видеть отрицательные остатки. Например, -3 % 5 возвращает -3. Аналогично, -3 % -5 возвращает -3.
Обратите внимание, что во всех этих примерах мы получаем одни и те же результаты с некоторыми вариациями знака. Другими словами, с оператором остатка нас не слишком интересуют знаки. Все, что мы хотим знать, это сколько раз одно число входит в другое число. Затем мы смотрим на делимое, чтобы определить знак.
С другой стороны, у оператора по модулю немного больше нюансов. Во-первых, операнд справа определяет диапазон возможных возвращаемых значений. Если это значение положительное, результат будет положительным. Это немного отличается от нашего оператора остатка.
Если это значение положительное, результат будет положительным. Это немного отличается от нашего оператора остатка.
Между тем, левый операнд определяет направление, в котором мы циклически перемещаемся по диапазону возможных значений. Естественно, это идеально согласуется с оператором остатка, когда оба значения имеют одинаковый знак. К сожалению, в любых других обстоятельствах они совершенно разные:
| Expression | Java (Remainder) | Python (MOD) |
|---|---|---|
3 % 5 | 3 | 3 |
3 % -5 | 3 | -2 |
-3 % 5 | -3 | 2 |
-3 % -5 | -3 | -3 |

Оператор остатка для двойных чисел
Когда мы думаем об операторе остатка, мы часто предполагаем, что он работает исключительно с целыми числами — по крайней мере, до недавнего времени я так понимал. Как оказалось, оператор остатка на самом деле работает с числами с плавающей запятой, и в этом есть смысл.
Вдохновение
Ранее в этом месяце я работал со студентом в лаборатории, который попросил их написать программу обмена монет. В частности, эта программа должна была принимать от пользователя несколько центов и выводить номиналы в американской валюте (например, доллары, полдоллара, четверти, десять центов, пятаки и пенни).
Если вы думаете о том, как решить эту проблему, я дам вам подсказку: вы можете использовать жадный подход. Другими словами, сначала выберите самую большую монету и подсчитайте, сколько из них делится на ваше текущее количество центов. Если вы все сделаете правильно, вам даже не понадобится поток управления. Однако вы можете немного почистить свой код с помощью массива и цикла. Поскольку мне лень писать решение на Java, вот как оно может выглядеть на Python:
Поскольку мне лень писать решение на Java, вот как оно может выглядеть на Python:
цента = 150
доллары = центы // 100
центов %= 100
половина_долларов = центов // 50
центов %= 50
четверти = центы // 25
центов %= 25
десять центов = центы // 10
центов %= 10
никель = центов // 5
центов %= 5
пенни = центы
print(f'{доллары}, {полдоллары}, {четверти}, {даймы}, {пятак}, {пенни}') Во всяком случае, у меня был студент, который интерпретировал центы как доллары и центы. Другими словами, они позволяют своему пользователю вводить суммы в долларах, например, 1,50 доллара, а не 150 центов. Честно говоря, это не так уж и много. Все, что нам нужно сделать, это умножить сумму в долларах на 100 и добавить оставшиеся центы, чтобы получить целое число.
Но это не то, что сделал этот ученик.
Использование удвоения
Если бы мы переписали приведенную выше программу, используя доллары и центы, мы могли бы получить что-то вроде следующего:
цента = 1,50
доллары = центы // 1
центов %= 1
половина_долларов = центов // 0,50
центов% = 0,50
четверти = центы // 0,25
центов% = 0,25
десять центов = центы // 0,10
центов %= .1
никель = центы // 0,05
центов% = 0,05
пенни = центы // 0,01
print(f'{доллары}, {половина_долларов}, {четверть}, {даймс}, {пятак}, {пенни}') И если мы запустим это, мы получим точно такой же результат, как и раньше: один доллар и полдоллара.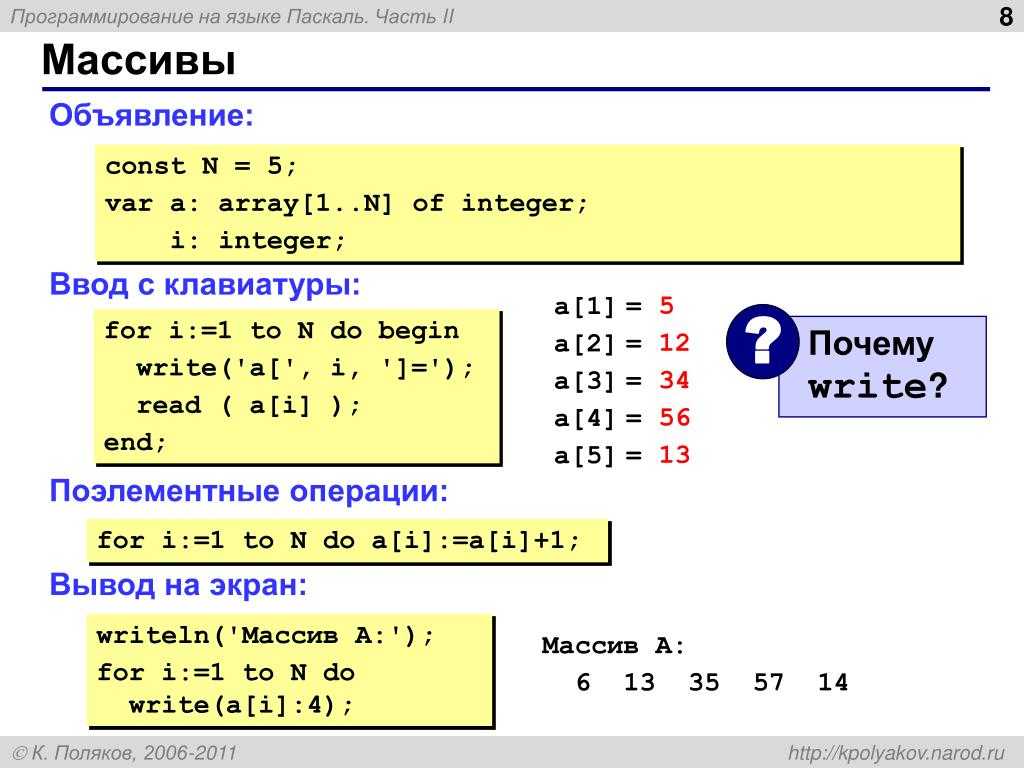 Как это возможно?
Как это возможно?
Как оказалось, вычисление остатка с использованием десятичных дробей вполне допустимо. Все, что нам нужно сделать, это вычислить, сколько раз наше делимое идет полностью на в наш делитель. Например, 0,77 % 0,25 «в идеале» даст 0,02, потому что это максимально близкое значение, которое мы можем получить к 0,77, не переходя больше.
Предостережения
Узнав, что можно взять остаток от десятичной дроби, я сразу же удивился, почему я не знал об этом раньше. Конечно, быстрый поиск в Google покажет вам всевозможные ошибочные действия, которые могут возникнуть.
Например, в предыдущем примере я утверждал, что 0,02 будет остатком от 0,77 и 0,25, и это будет вроде как. Видите ли, в большинстве языков программирования значения с плавающей запятой по умолчанию имеют определенную точность, которая определяется базовой двоичной архитектурой. Другими словами, существуют десятичные числа, которые не могут быть представлены в двоичном виде. Одно из этих чисел является результатом нашего выражения выше:
Одно из этих чисел является результатом нашего выражения выше:
>>> 0,77 % 0,25 0,020000000000000018
При работе с действительными числами мы постоянно сталкиваемся с подобными проблемами. В конце концов, есть удивительное количество десятичных значений, которые не могут быть представлены в двоичном виде. В результате мы получаем сценарии, в которых ошибки округления могут привести к сбою нашего алгоритма изменений. Чтобы доказать это, я переписал приведенное выше решение, чтобы вычислить сдачу для первых 200 центов:
для i в диапазоне (200):
центов = (i//100) + (i/100) % 1
ожидаемый = центы
доллары = центы // 1
центов %= 1
половина_долларов = центов // 0,50
центов% = 0,50
четверти = центы // 0,25
центов% = 0,25
десять центов = центы // 0,10
центов %= . 1
никель = центы // 0,05
центов% = 0,05
пенни = центы // 0,01
фактический = доллары + полдоллара * 0,50 + четверти * 0,25 + десять центов * 0,10 + пятак * 0,05 + пенни * 0,01
печать (f'{ожидаемый}: {фактический}')
1
никель = центы // 0,05
центов% = 0,05
пенни = центы // 0,01
фактический = доллары + полдоллара * 0,50 + четверти * 0,25 + десять центов * 0,10 + пятак * 0,05 + пенни * 0,01
печать (f'{ожидаемый}: {фактический}')
Для вашего здравомыслия я не буду выводить результаты, но поделюсь несколькими суммами в долларах, где этот алгоритм дает сбой: при вычислении пенни: .03 % .01 )
.09 % .05 ) .013 .11 % .14 терпит неудачу при вычислении десятицентовиков: .12 % .1 ) .15 % .1 ) Уже сейчас мы начинаем видеть тревожную часть этих расчеты становятся жертвой ошибок округления. Только за первые 16 центов мы не можем произвести точную сдачу в 50% случаев (без учета 0).
Кроме того, многие ошибки начинают повторяться. Другими словами, я подозреваю, что эта проблема усугубляется с увеличением количества центов, поскольку при этом увеличивается вероятность ошибок округления. Конечно, я пошел дальше и модифицировал программу еще раз, чтобы измерить частоту ошибок:
ошибки = 0
для я в диапазоне (1000000):
центов = (i//100) + (i/100) % 1
ожидаемый = центы
доллары = центы // 1
центов %= 1
половина_долларов = центов // 0,50
центов% = 0,50
четверти = центы // 0,25
центов% = 0,25
десять центов = центы // 0,10
центов %= .1
никель = центы // 0,05
центов% = 0,05
пенни = центы // 0,01
фактический = доллары + полдоллара * 0,50 + четверти * 0,25 + десять центов * 0,10 + пятак * 0,05 + пенни * 0,01
ошибки += 0 если ожидаемо == актуально иначе 1
print(f"{(ошибки/1000000) * 100}% ОШИБКА") Теперь я должен предварить, что этот фрагмент кода сравнивает действительные числа, используя == , что обычно считается плохой практикой. В результате мы можем считать несколько «правильных» решений неправильными. Тем не менее, я думаю, что это достаточно хорошая оценка на данный момент.
В результате мы можем считать несколько «правильных» решений неправильными. Тем не менее, я думаю, что это достаточно хорошая оценка на данный момент.
Когда я запустил его, я обнаружил, что 53,850699999999996% всех расчетов изменений были неверными. По иронии судьбы, даже в моем вычислении ошибки была проблема с округлением.
Следует ли использовать оператор остатка для двойных значений?
На данный момент мы должны задаться вопросом, имеет ли смысл использовать оператор остатка для двойных чисел в Java. В конце концов, если ошибки округления являются такой проблемой, кто вообще может доверять результатам?
Лично моя интуиция подсказала бы избегать этой операции любой ценой. Тем не менее, я немного покопался, и есть несколько способов обойти эту проблему. Например, мы могли бы попробовать выполнить арифметику в другой базе, используя класс, который представляет значения с плавающей запятой в виде строки целых чисел (например, класс Decimal в Python или класс BigDecimal в Java).
Конечно, у такого рода классов есть свои проблемы с производительностью, и невозможно избежать ошибок округления по основанию 10. В конце концов, основание 10 не может представлять такие значения, как одна треть. Тем не менее, вы добьетесь гораздо большего успеха с оставшимся оператором.
В конце концов, я лично не сталкивался с этим сценарием, и я сомневаюсь, что вы тоже столкнетесь. Конечно, если вы здесь, скорее всего, вы столкнулись именно с этой проблемой. К сожалению, у меня нет большого решения для вас.
В любом случае, спасибо, что заглянули. Если вы нашли эту статью интересной, подумайте о том, чтобы поделиться ею. Если вы хотите, чтобы в ваш почтовый ящик попадало больше подобного контента, зайдите на мою страницу с информационным бюллетенем и оставьте свой адрес электронной почты. Кроме того, вы можете поддержать The Renegade Coder, став покровителем или совершив одну из этих странных вещей.
Пока вы здесь, ознакомьтесь с одной из следующих статей по теме:
- Камень, ножницы, бумага с использованием модульной арифметики
- Еще один способ изучить рекурсию
- Разница между заявлениями и выражениями
В противном случае, спасибо, что нашли время, чтобы проверить мой сайт! Я ценю это.
Будучи учеником на протяжении всей жизни и стремящимся учителем, я обнаружил, что не все предметы имеют одинаковое значение. В результате некоторые темы могут остаться незамеченными из-за нехватки времени или других обязательств. Лично я нахожу эти потерянные артефакты довольно забавными для обсуждения. Вот почему я решил запустить целую серию, чтобы сделать именно это. Добро пожаловать в Coding Tangents, сборник статей, посвященных граничным темам разработки программного обеспечения.
В этой серии я расскажу о темах, которые, как мне кажется, интересовали многих моих учеников, но никогда не имели возможности их изучить. Во многих случаях это предметы, которые, как мне кажется, заслуживают большего внимания в классе. Например, вы когда-нибудь получали формальное объяснение модификаторов доступа? Как насчет управления пакетами? Контроль версий?
В некоторых случаях студенты вынуждены изучать эти предметы самостоятельно. Естественно, это создает почву для заблуждений, которые становятся популярными на онлайн-форумах, таких как Stack Overflow и Reddit. В этой серии я надеюсь вернуться к основам, где эти темы могут быть рассмотрены во всей их полноте.
Естественно, это создает почву для заблуждений, которые становятся популярными на онлайн-форумах, таких как Stack Overflow и Reddit. В этой серии я надеюсь вернуться к основам, где эти темы могут быть рассмотрены во всей их полноте.
← Предыдущий пост: [#10] [#12]: Следующий пост →
Recent Posts
ссылка на 29 вещей, которые я бы сказал, только если бы меня похитили29 вещей, которые я бы сказал, только если бы меня похитили
2023 год — это год моего 29-летия, и мальчик, я начал это чувствовать. Во всяком случае, вот обычный ежегодный пост со списком.
Продолжить чтение
ссылка на Почему == Иногда работает со строками в Java?Почему == иногда работает со строками в Java?
Сравнение строк в Java — это всегда кошмар, но знаете ли вы, что использование == иногда может сработать? Да, поздоровайся с еще большим количеством кошмарного топлива.
Продолжить чтение
Модуль в порядке операций
Автор Анна Щепанек, доктор философии
Отзыв от Rijk de Wet
Последнее обновление: 21 ноября 2022 г.
- Что такое модульный оператор?
- Считается ли модуль делением?
- Где модуль в порядке операций?
- Где модуль в PEMDAS?
Задумывались ли вы когда-нибудь над , как по модулю вписывается в порядок операций ? Вы попали по адресу — в этой статье мы объясним все, что вам нужно знать о PEMDAS и модуле. Не знаете, что такое PEMDAS? Продолжай читать!
Что такое оператор по модулю?
Оператор по модулю возвращает остаток от деления одного числа на другое число. Помните, здесь мы имеем дело с целыми числами. В математической записи, если a и n — два целых числа, мы всегда можем найти b и r такие, что
a = b * n + r
, где остаток 0 0 3 r < r равен 900. . Тогда по модулю n = r .
В качестве альтернативы мы можем сказать, что a mod n = r тогда и только тогда, когда n делит a−r без остатка .
Например:
21 по модулю 5 = 1, потому что21 = 4 * 5 + 123 mod 10 = 3потому что23 = 2 * 10 + 33 mod 10 = 3, потому что3 = 0 * 10 + 3
Модуль считается таким же, как деление?
Модуль связан с делением , но не совсем то же самое . Посмотрим:
7 / 2 = 3,5
отличается от
7 мод 2 = 1 .
Существует также операция целочисленного деления (часто обозначаемая двойной косой чертой // , особенно в программировании):
7 // 2 = 3 .
Связь между целочисленным делением и делением по модулю может быть выражена следующим соотношением:
7 = 3 * 2 + 1 .
Как видите, целочисленное деление 7 // 2 отвечает на вопрос «Сколько раз 2 вписывается в 7?» и 7 по модулю 2 отвечает на вопрос «Каков будет остаток при делении 7 на 2?»
Где модуль в порядке операций?
В большинстве языков программирования принято соглашение о том, что оператор по модулю (обозначаемый как % , а не по модулю ) занимает то же место в порядке операций, что и умножение и деление . Следовательно, стоит ПОСЛЕ операций в скобках, но ДО сложения и вычитания . Когда есть модуль и умножение или деление, то операции выполняются от слева направо .
Следовательно, стоит ПОСЛЕ операций в скобках, но ДО сложения и вычитания . Когда есть модуль и умножение или деление, то операции выполняются от слева направо .
Например:
2 * 3 % 4преобразуется в2, потому что у нас есть2 * 3 = 6и6 % 4 = 2.3 % 4 * 2преобразуется в6, потому что у нас есть3 % 4 = 3и3 * 2 = 6.
Однако в математике мы иногда отдаем предпочтение оператору по модулю перед умножением и сложением. Это потому что mod n рассматривается как , указывающее на среду , в которой мы выполняем вычисления — в правильных математических терминах мы называем это кольцом. Следовательно, многие математики согласятся, что выражение 3 mod 4 * 2 подразумевает, что мы выполняем вычисления по модулю 8 , поэтому результатом будет 3 .
Как видите, не всегда очевидно, где находится модуль в порядке операций. Если вы сомневаетесь при работе с новым языком программирования, просто обратитесь к документации или выполните быструю проверку, попросив компьютер (или калькулятор) оценить несколько примеров. Это может потребовать написания небольшого кода, но ваша проблема будет решена немедленно. В математике во избежание путаницы используйте круглые скобки . Столкнувшись с запутанным выражением, проверьте контекст или попросите разъяснений у коллег .
Где модуль в PEMDAS?
PEMDAS — это аббревиатура, которая расшифровывается как Скобки, Экспоненты, Умножение/Деление, Сложение/Вычитание . Он кодирует порядок старшинства при выполнении арифметических операций.
🙋 Не стесняйтесь проверить наш калькулятор сложения, калькулятор длинного вычитания, калькулятор длинного деления, калькулятор умножения и калькулятор степени, чтобы помочь вам в этом!
В некоторых странах используется аббревиатура BEDMAS , обозначающая Скобки, Экспоненты, Деление/Умножение, Сложение/Вычитание .