Новые функции стандартной библиотеки Kotlin 1.5
Рассмотрим изменения стандартной библиотеки, относящиеся к версии Kotlin 1.5.
1. Новые функции коллекции
Допустим, есть список объектов, в каждом из которых имеется свойство, допускающее значение «null». Как получить первое, отличное от «null» значение этого свойства в коллекции?
Обычно с помощью функции mapNotNull() сначала получают коллекцию всех значений, отличных от «null». А затем для получения искомого значения вызывают firstOrNull().
В Kotlin 1.5 имеются функции firstNotNullOf() и firstNotNullOfOrNull(). Функция firstNotNullOf() возвращает первое, отличное от «null» значение переданного селектора либо исключение, когда нет ни одного подходящего элемента. Вторая функция ведет себя аналогично, но в случае отсутствия подходящего элемента возвращает 
firstNotNullOf() работает за две функции: mapNotNull() и first(). Так же и firstNotNullOfOrNull() работает за функции mapNotNull() и firstOrNull().
Проиллюстрируем это кодом:
data class Employee(val name: String, val designation: String?)
val employees = listOf(
Employee("Felix", null),
Employee("Vee", null),
Employee("Ram", "Developer"),
Employee("Vivek", "Senior Developer"),
Employee("Joe", "Developer"),
)
// Старый метод
val firstDesignation = employees.mapNotNull { it.designation }.firstOrNull()
// Метод Kotlin 1.5
val newfirstDesignation = employees.firstNotNullOfOrNull { it.designation }2. Целочисленные типы без знака Ubyte, UShort, UInt и ULong
Они применяются там, где надо, чтобы тип содержал только неотрицательные значения.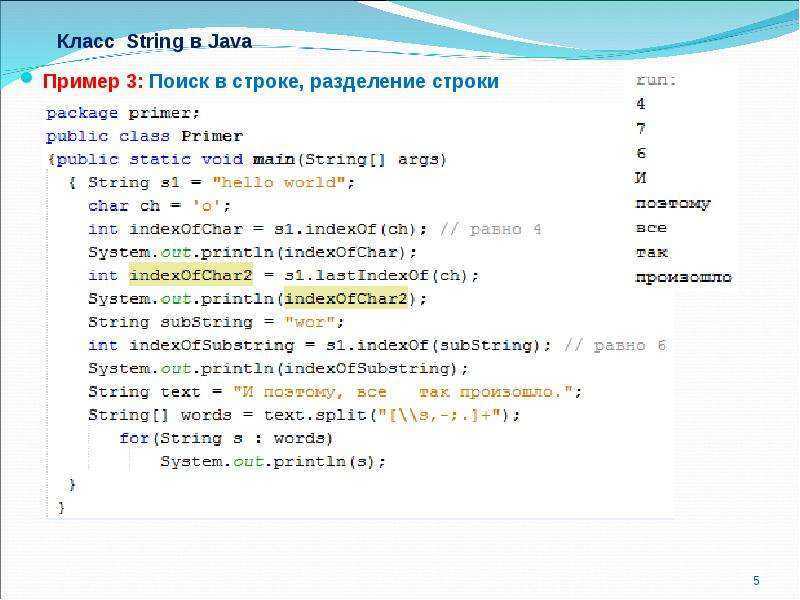 Эти типы более интуитивно понятны в работе на уровне битов и байтов и при манипулировании пикселями в растровой графике, байтами в файле или другими двоичными данными.
Эти типы более интуитивно понятны в работе на уровне битов и байтов и при манипулировании пикселями в растровой графике, байтами в файле или другими двоичными данными.
UByte: 8-разрядное целое число без знака в диапазоне от 0 до 255.UShort: 16-разрядное целое число без знака от 0 до 65 535.UInt: 32-разрядное целое число без знака от 0 до 2³² – 1.ULong: 64-разрядное целое число без знака от 0 до 2⁶⁴ – 1.
3. Целочисленное деление с округлением вниз и оператор mod
Появилась новая функция floorDiv()
(5).floorDiv(3) -> returns 1
(-5).floorDiv(3) -> returns -2
Функция вычисления остатка mod возвращает остаток от деления, а результат при этом округляется вниз. Она совершенно отличается от оператора %, который в Kotlin называется rem.
Вот пример кода:
val a = -4 val b = 3 println(-4 % 3) -> -1 println(a.mod(b)) -> 2
Здесь оператор % возвращает остаток –1. Но a.mod(b) — это разница между a и a.floorDiv(b) * b. Она либо равна нулю, либо имеет тот же знак, что и b, хотя a % b
4. API преобразования символов в целые числа
В Kotlin появились функции, которые делают преобразование отдельных символов в числа более выразительным.
При таком преобразовании во внимание принимается одно из двух: либо код символов для соответствующего символа, либо фактическая цифра, которую представляет символ, выполняя парсинг числа.
И то и другое лаконично выражается с помощью нового API преобразования. Здесь появились преобразования Char, которые разделены на следующие наборы функций с четкими наименованиями:
- Функции для получения кода с целыми числами
Charи построенияCharиз данного кода:
fun Char(code: Int): Char
fun Char(code: UShort): Char
val Char.code: Int
- Функции для преобразования
Charв числовое значение цифры, которую представляет символ:
fun Char.digitToInt(radix: Int): Int
fun Char.digitToIntOrNull(radix: Int): Int?
- Функция-расширение для
Intдля преобразования представляемого им неотрицательного числа, состоящего из одной цифры, в соответствующем видеChar:
fun Int.digitToChar(radix: Int): Char
5. Категория символов в мультиплатформенном коде
Появились функции для проверки свойств символов, доступных в общем коде. С их помощью проверяется символ (это цифра, буква либо цифра или буква) и буква (прописная, строчная или заглавная), а также определено ли его представление в Юникоде или это последовательность ISO.
'1'.isDigit() -> true
'A'.isLetter() -> true
'!'.isLetterOrDigit() -> false
'C'.isLowerCase() -> false
'C'.isUpperCase() -> true
'b'.isTitleCase() -> false
'?'.isDefined() -> true
'\n'.isISOControl() -> true
6. Функции преобразования строк/символов с учетом регистра
В Kotlin 1.5 появился новый, не зависящий от локали API для преобразования текста верхнего/нижнего регистров. «Не зависящий от локали» означает: какими бы ни были языковые настройки в целевой системе, вы получите последовательные результаты преобразования с учетом регистра.
То есть новый API помогает избежать ошибок, обусловленных различными настройками языковых стандартов. Вот старый и новый способы преобразований:
Функции преобразования строк String:
Функции преобразования символов Char:
Нужно преобразование на основе локали? Тогда необходимо прямо указать ее:
“kotlin”.uppercase(Locale.forLanguageTag(“tr-TR”))
7. Строгая версия String?.toBoolean()
Появились также функции String.toBooleanStrict() и String.toBooleanStrictOrNull(). Функция .toBooleanStrict() выбрасывает исключение для всех входных данных, кроме литералов true или false.
Здесь тоже учитывается регистр. Поэтому в примере "true".toBooleanStrict() выдает true, а "True".toBooleanStrict() выбрасывает исключения.
Функция String.toBooleanStrictOrNull() вместо исключения выдаст null для всех входных данных, кроме литералов true или false. И здесь также учитывается регистр.
"true".toBooleanStrictOrNull() -> возвращает true
"True".toBooleanStrictOrNull() -> возвращает null.
Вот и все об изменениях стандартной библиотеки Kotlin. Хотите узнать больше? Воспользуйтесь документацией.
Читайте также:
- Модификатор Kotlin, которого не должно было быть
- Корутины Kotlin: как работать асинхронно в Android
- Как избежать утечек памяти с помощью Kotlin
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Shalu T D: Exploring the Kotlin 1.5 Standard Library
Читайте также
5.15. Арифметические операторы
Java поддерживает семь арифметических операторов, которые работают с любыми числовыми типами:
+ сложение
— вычитание
* умножение
/ деление
% остаток
Java также поддерживает унарный минус (-) для изменения знака числа. Знак может быть изменен оператором следующего вида:
val = -val;
Кроме того, имеется и унарный плюс— например, +3. Унарный плюс включен для симметрии, без него было бы невозможно записывать константы вида +2.0.
5.15.1. Целочисленная арифметика
Целочисленная
арифметика выполняется с дополнением
по модулю 2— то есть
при выходе за пределы своего диапазона
допустимых значений (int
или long) величина приводится
по модулю, равному величине диапазона. Таким образом, в целочисленной арифметике
никогда не происходит переполнения,
встречаются лишь выходы значения за
пределы диапазона.
Таким образом, в целочисленной арифметике
никогда не происходит переполнения,
встречаются лишь выходы значения за
пределы диапазона.
При целочисленном делении происходит округление по направлению к нулю (то есть 7/2 равно 3, а –7/2 равно –3). Деление и остаток для целых типов подчиняются следующему правилу:
(x/y)*y + x%y == x
Следовательно, 7%2 равно 1, а –7%2 равно –1. Деление на ноль или нахождение остатка от деления на 0 в целочисленной арифметике не допускается и приводит к запуску исключения ArithmeticException.
Арифметические операции с символами представляют собой целочисленные операции после неявного приведения char к типу int.
5.15.2. Арифметика с плавающей точкой
Для работы с
плавающей точкой (как для представления,
так и для совершения операций) в Java
используется стандарт IEEE7541985.
В соответствии с ним допускаются как
переполнение в сторону бесконечности
(значение превышает максимально
допустимое для double или
float), так и вырождение в
ноль (значение становится слишком малым
и неотличимым от нуля для double
или float).
Арифметические операции с конечными операндами работают в соответствии с общепринятыми нормами. Знаки выражений с плавающей точкой также подчиняются этим правилам; перемножение двух чисел с одинаковым знаком дает положительный результат, тогда как при перемножении двух чисел с разными знаками результат будет отрицательным.
Сложение двух
бесконечностей с одинаковым знаком
дает бесконечность с тем же знаком. Если
знаки различаются—
ответ равен NaN. Вычитание
бесконечностей с одинаковым знаком
дает NaN; вычитание
бесконечностей с разными знаками дает
бесконечность, знак которой совпадает
со знаком левого операнда. Например,
(-(-)) равно . Результат любой арифметической
операции, в которой участвует величина
NaN, также равен NaN.
При переполнении получается бесконечность
с соответствующим знаком, а при
вырождении— ноль с
соответствующим знаком.
Если -0.0 == 0.0, как же отличить отрицательный ноль, полученный в результате вырождения, от положительного? Его следует использовать в выражении, в котором участвует знак, и проверить результат. Например, если значение x равно отрицательному нулю, то выражение 1/x будет равно отрицательной бесконечности, а если положительному— то положительной бесконечности.
Операции с бесконечностями выполняются по стандартным математическим правилам. Сложение (или вычитание) конечного числа с любой бесконечностью также дает бесконечность. Например, (-+x) дает — для любого конечного x.
Бесконечность
может быть получена за счет соответствующей
арифметической операции или использования
имени бесконечности для объектов типа
float или double:
POSITIVE_INFINITY
или NEGATIVE_INFINITY.
Например, Double.NEGATIVE_INFINITY
представляет значение отрицательной
бесконечности для объектов типа double.
Умножение бесконечности на ноль дает в результате NaN. Умножение бесконечности на ненулевое конечное число дает бесконечность с соответствующим знаком.
Деление, а также деление с остатком может давать бесконечность или NaN, но никогда не приводит к исключениям. В таблице перечислены результаты арифметических операций при различных значениях операндов:
x | y | x/y | x%y |
Конечное | ±0.0 | NaN | |
Конечное | ±0.0 | x | |
±0.0 | ±0.0 | NaN | NaN |
Конечное | NaN | ||
NaN | NaN |
Во всех остальных
отношениях нахождение остатка при
делении с плавающей точкой происходит
аналогично нахождению целочисленного
остатка. Вычисление остатка методом
Math.IEEERemainder
описано в разделе 14.8.
Вычисление остатка методом
Math.IEEERemainder
описано в разделе 14.8.
Python | 8 Примеры оператора остатка Pyhton
Операторы остатка Python используются для вычисления некоторых операндов. Операторы — это специальные символы, которые используются с операндами для выполнения некоторых операций, таких как сложение, вычитание, деление и т. д. Операторы могут обозначаться как «+» для сложения, «-» для вычитания, «/» для деления, «*» для умножения и т. д. В Python оператор модуля представляет собой символ процента (‘%’), который также известен как оператор остатка Python, тогда как существует оператор деления для целого числа как ‘//’, который также работает только с целочисленными операндами возвращает остаток, но в целых числах. Точно так же оператор остатка Python или оператор модуля также возвращает остаток при разделении двух операндов, т. Е. Один операнд делится с другим операндом, что приводит к остатку. Этот оператор остатка используется как для целых чисел, так и для чисел с плавающей запятой.
Синтаксис:
x % y
Дивиденд % Делитель: Остаток получается при делении x на y. Остаток будет целым числом, если оба делимых являются целыми числами. Остаток будет числом с плавающей запятой, если один из делимых или делителей является числом с плавающей запятой.
Примеры оператора напоминания Python
Ниже приведены различные примеры оператора напоминания Python.
Пример №1
Код:
х = 5
у = 2
г = х % у
print ('Remainder is:', r) Вывод:
Объяснение: В приведенном выше примере x = 5 , y = 2, поэтому 5 % 2 , 2 входит в 5 два раза, что дает 4 , поэтому остаток равен 5 – 4 = 1. В Python остаток получается с помощью функции numpy.ramainder() в numpy. Он возвращает остаток от деления двух массивов и возвращает 0, если массив делителей равен 0 (ноль) или если оба массива имеют массив целых чисел. Эта функция также используется для отдельных номеров.
Эта функция также используется для отдельных номеров.
Пример #2
Код:
импортировать numpy как np
п1 = 6
п2 = 4
г = np.остаток (n1, n2)
print ("Дивиденд равен:", n1)
print ("Делитель равен:", n2)
print ("Остаток: ", r) Вывод:
Объяснение: В приведенном выше примере используется функция numpy.remainder() для данного делимого и делителя, чтобы найти остатки двух, что работает аналогично модульный оператор. В этом примере это 6 % 4, 4 входит в 6, один раз, что дает 4, поэтому остаток 6 — 4 = 2.
Пример №3
Код:
импортировать numpy как np
arr1 = np.массив ([7, -6, 9])
массив2 = np.массив ([3, 4, 3])
rem_arr = np.remainder (arr1, arr2)
print ("Массив дивидендов: ", arr1)
print ("Массив делителей: ", arr2)
print ("Массив остатка: ", rem_arr) Вывод:
Объяснение: В приведенном выше примере функция numpy. remainder() может использоваться в списке элементов для вычисления остатка соответствующий элемент в списке или массиве элементов. у нас есть два массива [7 -6 9] и [3 4 3], поэтому 7 % 3,3 переходит в 7 два раза, поэтому остаток равен 1, -6 % 4, 4 входит в 6 один раз, поэтому остаток равен 2, 9 % 3, 3 идет в 9 три раза, так что остаток равен 0. Массив значений остатка будет [1 2 0].
remainder() может использоваться в списке элементов для вычисления остатка соответствующий элемент в списке или массиве элементов. у нас есть два массива [7 -6 9] и [3 4 3], поэтому 7 % 3,3 переходит в 7 два раза, поэтому остаток равен 1, -6 % 4, 4 входит в 6 один раз, поэтому остаток равен 2, 9 % 3, 3 идет в 9 три раза, так что остаток равен 0. Массив значений остатка будет [1 2 0].
Пример #4
Оператор остатка или оператор по модулю используется для нахождения четных или нечетных чисел. Ниже приведен фрагмент кода для печати нечетных чисел от 0 до 20.
Код:
для числа в диапазоне (1, 20):
если (число% 2 != 0):
печать (число) Вывод:
Объяснение: В приведенном выше примере с помощью оператора по модулю печатаются нечетные числа от 0 до 20 из кода; если число делится на 2 и в остатке получается 0, то мы говорим это как четное число; иначе его нечетное число. Если число равно 2, то 2 % 2 дает остаток 0, так что теперь это четное число, а не нечетное; если число равно 3, то 3% 2 дает остаток 1, который 2 переходит в 3 один раз, поэтому дает 2, а остаток 3 — 2 = 1, что не равно нулю, поэтому заданное число 3 нечетно, и с помощью цикла for он будет проверять до 20 чисел и вывести все нечетные числа от 0 до 20. Оператор по модулю или оператор остатка также используется для чисел с плавающей запятой, в отличие от оператора деления ( // ), который используется только для целых чисел и дает остаток также в целочисленной форме.
Если число равно 2, то 2 % 2 дает остаток 0, так что теперь это четное число, а не нечетное; если число равно 3, то 3% 2 дает остаток 1, который 2 переходит в 3 один раз, поэтому дает 2, а остаток 3 — 2 = 1, что не равно нулю, поэтому заданное число 3 нечетно, и с помощью цикла for он будет проверять до 20 чисел и вывести все нечетные числа от 0 до 20. Оператор по модулю или оператор остатка также используется для чисел с плавающей запятой, в отличие от оператора деления ( // ), который используется только для целых чисел и дает остаток также в целочисленной форме.
Пример #5
Код:
a = input("Дивиденд:\n")
фа = поплавок (а)
b = input("Делитель:\n")
fb = плавающая (b)
fr = fa % fb
print ("Остаток", fr) Вывод:
Пример #6
В Python оператор по модулю можно использовать и для отрицательных чисел, что дает тот же остаток, что и для положительных чисел, но отрицательный знак делителя в остатке будет тот же.
Код:
Печать (-5 % 3)
Выход:
Код:
Печать (5 % -3)
Выход:
За кодом:- -5 % 3 = (1 -2*3) % 3 = 1
- 5 % -3 = (-1 * -2 * -3) % 3 = -1
Объяснение: Эти отрицательные числа используют функцию fmod() для нахождения остатка; если какое-либо из чисел среди делимого или делителя отрицательное, то мы можем даже использовать функцию fmod() математической библиотеки, и это также можно использовать для нахождения остатка чисел с плавающей запятой.
Пример #7
Код:
импортировать математику а = -10 б = 3 print(math.fmod(a,b))
Вывод:
Объяснение: В Python оператор по модулю выдает ошибку, когда делитель равен нулю (0). Обычно это дает ZeroDivisionError, поскольку мы знаем, что любое число, деленное на ноль, равно бесконечности (∞).
Пример #8
Код:
p = 10 д = 0 г = р % д печать (г)
Приведенный выше код выдает ошибку, как показано на скриншоте ниже.
Вывод:
Код:
p = 10
д = 0
пытаться:
рем = p * q
печать (рем)
кроме ZeroDivisionError как zde:
print("Невозможно разделить на 0") Эту ошибку можно отловить с помощью блоков try-except, как показано на снимке экрана ниже.
Вывод:
Заключение
В Python оператор по модулю — это оператор для получения остатка от деления двух чисел, известного как делимое и делитель. Этот оператор можно использовать для нахождения остатка как целых чисел, так и чисел типа данных с плавающей запятой. Оператор по модулю также является одним из математических операторов, таких как сложение (+), вычитание (-), деление (//) и т. д. Оператор деления используется только для целых чисел, в отличие от оператора по модулю. И если делитель равен нулю, мы можем обработать его, обработав исключение, используя блок try-except для вывода ошибки.
И если делитель равен нулю, мы можем обработать его, обработав исключение, используя блок try-except для вывода ошибки.
Рекомендуемые статьи
Реализации евклидова деления
Примечание: Эта статья была переведена с помощью автоматического переводчика и одного проход был сделан, чтобы удалить самые большие ошибки.Если вы хотите сделать эту статью читабельной, вы можете сообщать мне об ошибках перевода (слово, предложение, абзац) по связавшись со мной по адресу электронной почты внизу страницы. Спасибо
Принцип
В этой статье обсуждается евклидово деление, фундаментальный предмет, представляющий
отправной точкой для всех вопросов, связанных с простыми числами и факторизацией целых чисел.
Евклидово деление со сложением, вычитанием и умножением является одним из четырех основных
операции над целыми числами. Его цель состоит в том, чтобы попытаться оставить заданную группу элементов справедливой.
относительно ограничения, характеризуемого числом.
Например, пакет с 12 шариками для 3 человек или бабушкин торт.
разрезать на 8 порций, пока нас 6 за столом.
Мы считаем, что в этой статье мы работаем с положительными целыми числами (набор N натуральных чисел), таким образом, это
справедливое распределение иногда невозможно без появления «половинок», «четвертей»,
«третье лицо» или другое… Например, 3 мяча, которые нужно распределить между 2 людьми, дают каждому по 1 мячу.
и мы не пытаемся отрезать последнее… Этот остаток нераспределенный откладывается, это остаток.
Обратите внимание, что на рациональных числах (установите Q) и так далее на действительных числах (очень грубо плавающие числа)
распространение возможно, но может дать что-то с трудом представимое в реальной жизни,
например 10/3 = 3,3333… это означает от 3 до бесконечности, в них сложно разрезать торт
условия…
С математической точки зрения определение евклидова деления натуральных чисел
выглядит следующим образом:
Пусть a и b — целые числа и b отлично от 0, существует единственная пара (q, r) целых чисел
такой как:
- а = бк + р
- г < б
Примечание 1 : Мы находим это понятие справедливого распределения с помощью термина «bq» и
остаток с термином «r».
Примечание 2 : Для целых чисел (набор Z целых чисел, положительных и отрицательных) мы имеем почти
такое же определение. Только второе условие меняется и становится |r| < |б|.
Об имени на условиях евклидова деления «a = bq + r» имеем:
- а это дивиденд
- b это делитель
- q — это частное
- р остаток
Проведение испытаний
В этой статье мы представим некоторые известные реализации евклидова деления и сравните их, чтобы увидеть, какие из них наиболее эффективны и быстрее. Но оценить время и столкнуться с результатами, у нас должна быть небольшая тестовая программа, которая будет измерять время различные реализации деления, а также проверьте три следующих критерия, чтобы избежать предвзятость в тестировании:
- Наборы тестов должны быть согласованными: одно деление соответствует миллисекундам, если мы проверяем
только одно подразделение, мы не можем извлечь соответствующую информацию, потому что времени слишком мало.
 Мы будем
поэтому делайте прогоны в 20 миллионов делений.
Мы будем
поэтому делайте прогоны в 20 миллионов делений. - Наборы тестов должны быть одинаковыми для каждой реализации: для сравнения двух реализаций евклидова деления, он обязательно будет использовать тот же набор тестов, потому что деление с разные методы на разные номера не интересны.
- Создайте несколько тестовых наборов с разными свойствами: идея состоит в том, чтобы протестировать реализации разделение на наборы, имеющие разные свойства, с целью выдвижения сильных и слабых сторон реализации.
Java-класс EuclideTestCaseGenerator отвечает за создание наборов тестов. Этот
будет создавать наборы в соответствии с 3 методами: один с именем «случайный» будет брать случайным образом числа a (
дивиденд) и b (делитель) между 1 и 1000 миллиардов, другой называется «A > B» idem для
«случайный», за исключением того, что a обязательно больше, чем b, и последний назван «custom», такой же, как случайный
с а > 4*b.
Наконец, Java-класс EuclideBench является оркестратором для запуска реализаций
Евклидово деление. Реализации должны реализовывать (как java) интерфейс IEuclide.
Реализации должны реализовывать (как java) интерфейс IEuclide.
источник
Первая реализация
Самый простой способ вычислить евклидово деление опирается на его определение: «сколько раз я могу поставить b в ?». Это приводит к простому и относительно короткому алгоритму. состоящий из вычитания столько раз, сколько это может быть b (делитель) a (делимое), пока не получите остаток меньше b.
public long [] euclid( long a, long b) {
long r = a;
long q = 0;
в то время как (r >= b) {
r = r — b;
q = q + 1;
}
long [] евклид = { q, r };
возврат евклид;
}
На данный момент у нас нет никаких элементов сравнения с другими реализациями, но
поверьте метод наивен :).
Все, что мы видим в этом алгоритме, — это риск не результата, когда a слишком велико по сравнению с b
потому что переменная r в инструкции «r = r — b» не уменьшается достаточно быстро. Сложность
алгоритма равен O(a).
источник
Сложность
алгоритма равен O(a).
источник
Вторая реализация
Чтобы улучшить первую реализацию, может быть интересно закодировать десятичное деление, которое мы
учиться в школе. А для тех, кто не помнит, как это работает, по простой схеме
это намного лучше, чем длинная речь, чтобы запомнить метод… позаботьтесь о том, чтобы схема показала
как выучить молодой французский. По тому уголку света, где вы изучали положение
цифры и визуальные изменения, но общие принципы остаются прежними:
т.е. 87 = 7 * 12 + 3
На уровне реализации метод состоит в умножении b (делитель) на 10 несколько
раз меньше, чем a (делимое), то делаем деление идентично первому
реализации и, наконец, снова с дивидендом остатка от деления
предыдущий шаг.
общедоступный длинный [] евклид( длинный a, длинный b) {
длинный r = а;
long q = 0;
длинное n = 1;
long aux = 0;
в то время как (r >= b) {
в то время как (b * n <= a) {
n *= 10;
}
n /= 10;
aux = b * n;
в то время как (r >= вспомогательный) {
r = r — вспомогательный;
q = q + n;
}
a = r;
n = 1;
}
long [] евклид = { q, r };
возврат евклид;
}
В этой статье мы будем приводить результаты в виде трех таблиц, представляющих прогон
на каждом из трех тестовых наборов (случайный, A > B и A > 4 * B). Важно видеть, что
направление чтения сверху вниз и алгоритмы должны сравниваться только в
контекст пробега. Здесь мы случайно взяли 40 миллионов чисел (2 умножить на 20 миллионов) и
рассчитал время, необходимое наивному и десятичному алгоритму для выполнения 20 миллионов евклидовых
дивизии (это пробег 1). Затем мы взяли другие числа, такие как A > B, и повторили 20
миллион делений (прогон 2), затем то же самое для A > 4 * B (прогон 3).
Важно видеть, что
направление чтения сверху вниз и алгоритмы должны сравниваться только в
контекст пробега. Здесь мы случайно взяли 40 миллионов чисел (2 умножить на 20 миллионов) и
рассчитал время, необходимое наивному и десятичному алгоритму для выполнения 20 миллионов евклидовых
дивизии (это пробег 1). Затем мы взяли другие числа, такие как A > B, и повторили 20
миллион делений (прогон 2), затем то же самое для A > 4 * B (прогон 3).
Все это говорит о том, что мало интереса сравнивать 2 отдельных прогона, потому что наборы данных
отличается, хотя верно то, что мы видим, что время увеличивается между 3 прогонами, этот рост
трудно поддается количественной оценке.
Посмотрим, что будет.
| Случайное | А > В | А > 4 * В | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Работа/проверка | n1 / 150660990 | n2 / 294686702 | n3 / 1221575580 | ||||||
| Наивный | 1,437 | 2,281 | 5,375 | ||||||
| Десятичный | 2,0 | +0,563 | 2,984 | +0,703 | 4,032 | -1,343 | |||
Эта вторая реализация показывает, что наивный метод работает быстрее, когда мы берем случайные значения. или когда a (делимое) больше, чем b (делитель), потому что алгоритм очень прост
и иди быстро. К минусам, когда b в 4 раза меньше, чем a, производительность меняется на обратную и десятичная дробь
метод становится намного быстрее.
или когда a (делимое) больше, чем b (делитель), потому что алгоритм очень прост
и иди быстро. К минусам, когда b в 4 раза меньше, чем a, производительность меняется на обратную и десятичная дробь
метод становится намного быстрее.
В тестовом примере A > B мы можем задаться вопросом, почему выигрыш отсутствует просто потому, что тестовый набор
неадекватный! Проблема возникает из-за распределения чисел при случайной стрельбе. Для
например, если мы выберем число от 0 до 1000, у нас будет 890,99% шанс попасть в 4-значный
число (результаты можно экстраполировать на n цифр), на 4-значных числах мы имеем отношения a / b
очень низкий, поэтому результат A > B неубедителен. Добавляя условие A > 4 * B, мы
искусственно увеличить соотношение, и мы ясно видим выигрыш.
Второй алгоритм меньше зависит от отношения a/b, потому что мы начинаем с умножения на 10 б столько раз, сколько необходимо, чтобы оказаться ближе к а. источник
Третья реализация
Чтобы оптимизировать время вычисления евклидова деления, мы изменим стратегию на
реализация алгоритма, основанного на дихотомии. Этот метод позволяет очень быстро найти
значение, используя старую добрую пословицу «разделяй и властвуй».
Этот метод позволяет очень быстро найти
значение, используя старую добрую пословицу «разделяй и властвуй».
Здесь дихотомический поиск будет сосредоточен на значении q (частное). Подход состоит
первый шаг к ограничению q, затем многократно разрезая этот интервал на две равные части и выбирая
интервал содержит q.
Следует отметить, что эти операции границы и разрезания будут выполняться со степенью 2
или, другими словами, мы используем бинарные операции, облегчающие работу компьютера. 9n
Критерии дихотомии следующие:
- Если b * ((альфа + бета) / 2) <= a, то альфа = (альфа + бета) / 2
- Если b * ((альфа + бета)/2) > а, то бета = (альфа + бета)/2
И это работает! Шаг за шагом мы приближаемся (и находим) частное q. Для большего
подробности, включая математическую демонстрацию метода, см. во французской Википедии.
статья о Евклидовом
деление (раздел бинарного метода). К сожалению, не нашел на английском языке.
общедоступный длинный [] евклид( длинный a, длинный b) {
длинный n = 0;
long aux = b;
if (a < b) {
long [] euclide = { 0, a };
вернуть евклид;
}
в то время как (aux <= a) {
aux = (aux << 1);
n++;
}
long alpha = (1 << (n - 1));
длинный бета = (1 << n);
в то время как (n— > 0) {
aux = (альфа + бета) >> 1;
, если ((aux * b) <= a) {
alpha = aux;
} else {
beta = aux;
}
}
long [] евклид = { альфа, а — (b * альфа) };
возврат евклид;
}
И мы улучшаем производительность. ..
..
С подходом дихотомии мы чувствуем, что «пробел» преодолен. Поскольку десятичный метод позволяет
большой выигрыш при условии, что a (дивиденд) очень велик по сравнению с b
(делитель), здесь создается впечатление обобщённого выигрыша на всех наборах тестов. А это
нормально, потому что мы прошли log2(a).
источник
| Случайное | А > В | А > 4 * В | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Работа/проверка | n4 / 198332981 | n5 / 394652967 | n6 / 13 | ||||||
| Наивный | 1,578 | 2,75 | 5,921 | ||||||
| Десятичный | 2,0 | +0,422 | 3,0 | +0,25 | 4,032 | -1,889 | |||
| Бинарная дихотомия | 1,375 | -0,625 | 2,015 | -0,985 | 3,297 | -0,735 | |||
Четвертая реализация
Всегда стремясь к производительности, мы делаем большой скачок назад в истории цивилизации. так как собираемся вдохновить из технического подразделения в Древнем Египте на реализацию четвертого
алгоритма Евклидова деления.
так как собираемся вдохновить из технического подразделения в Древнем Египте на реализацию четвертого
алгоритма Евклидова деления.
Вопрос: Были ли все египтяне во времена фараонов потенциальными учеными-компьютерщиками?
Никто не знает, кроме их методов умножения
и деление
полагался в основном на числа разложения в степени 2, чтобы выполнить эти 2 операции.
В основном они рассуждали в двоичном формате, чтобы иметь возможность умножать и делить.
- Насчет умножения, целью было преобразовать в бинарный первый оператор (см.
Википедия для этого преобразования), а затем построить таблицу степеней 2, умноженных на
второй оператор (легко, просто умножьте на 2 второй оператор столько раз, сколько хотите), и
наконец, суммируя значения в таблице как «где установлен бит».
Пример с 18 * 9 = ? 18 (двоичный) 9 * 2 (n раз) 0 9 1 18 there is 1, we pick 0 36 0 72 1 144 there is 1, мы выбираем Итак, 18 + 144 = 162 = 18 * 9. 
- Что касается разделения, то египтяне использовали тот же принцип, но в обратном порядке.
Они начали с построения таблицы степеней числа 2, умноженного на делитель (всегда с умножение на 2) до тех пор, пока не получится число больше а (делимое). Затем они восстанавливают «результат в двоичном виде» путем выбора числа, такие как их сложения не превышают a. Этот выбор, начиная с наибольшего числа (самый старший бит).Пример 218 / 6 = ? N 6 * 2 (N Times) Дополнение 5 192 WE Pick, потому что 19218 192 192. because 192 + 96 = 288 et 288 > 218 3 48 X we don’t pick because 192 + 48 > 218 2 24 216 we pick because 192 = 36, остаток r равен 2 (218 — 116). Большинство сайтов в Интернете говорят о разделении Египта как об историческом подходе, а не как о Информатика.
 Таким образом, мы находим принцип работы и много информации, описывающей предмет.
в текстовом виде. К минусам мы не видели примера реализации алгоритма, но это не мешает
неважно, просто сделай это!
Таким образом, мы находим принцип работы и много информации, описывающей предмет.
в текстовом виде. К минусам мы не видели примера реализации алгоритма, но это не мешает
неважно, просто сделай это!общедоступный длинный [] евклид( длинный а, длинный б) {
длинный n = 0;
длинное p = b;
if (a < b) {
long [] euclide = { 0, a };
вернуть евклид;
}
в то время как (p <= a) {
p = (p << 1);
n++;
}
p = (p >> 1);
н—;
long q = (1 << n);
long aux = p; 9n, но и цикл «пока (n > 0)» в центре программы. По сути, эти два алгоритма эквивалентны, один можно переписать в другой. sourceЧто касается производительности, мы снова получаем большую скорость. Конечно, не так сильно, как изменение от от десятичного до дихотомического, но выигрыш в 0,2 с (кроме случайного) в среднем является почетным.
Направление чтения по пробегу (и сверху вниз).
Не сравнивайте два отдельных запуска.Случайный А > В А > 4 * В Работа/проверка n7 / 162438146 n8 / 313167294 n9 / 1211389641 Наивный 1,406 2,781 5,5 Десятичный 2,016 +0,61 3,0 +0,219 3,828 -1,672 Бинарная дихотомия 1,39 -0,626 2,0 -1,0 3,015 -0,813 Бинарный египетский 1,36 -0,03 1,781 -0,219 2,719 -0,296 Пятая реализация
А вот последняя реализация евклидова деления, это метод бинарной дихотомии, дополненной методом Горнера.

На самом деле это просто более изящная переписка египетской дивизии (четвертой реализации), который сам по себе эквивалентен третьему (если следовать…).public long [] евклид( long a, long b) {
long r = a;
long q = 0;
длинный n = 0;
long aux = b;
в то время как (вспомогательный <= a) {
вспомогательный = (вспомогательный << 1);
n++;
}
в то время как (n > 0) {
aux = (aux >> 1);
н—;
q = (q << 1);
if (r >= aux) {
r = r — aux;
q++;
}
}
long [] евклид = { q, r };
возврат евклид;
}По производительности на нашем старом тестовом компьютере AMD 3200 2 Ghz хуже, чем реализации египетской дивизии, посмотреть, нет ли на других машинах (или др.
