Чем отличается диметрия от изометрии. Как сделать аксонометрию. Ограничения аксонометрической проекции
ГОСТ 2.317-68* устанавливает прямоугольные и косоугольные аксонометрические проекции.
Построение аксонометрических проекций заключается в том, что геометрическую фигуру вместе с осями прямоугольных координат, к которым
эта фигура отнесена в пространстве, параллельным (прямоугольным или косоугольным) способами проецируют на выбранную плоскость проекций. Таким образом, аксонометрическая проекция — это проекция на
одну плоскость. При этом направление проецирования выбирают так, чтобы оно не совпадало ни с одной из координатных осей.
При построении аксонометрических проекций изображаемый предмет жестко связывают с натуральной системой координат Oxyz. В целом аксонометрический чертеж получается
состоящим из параллельной проекции предмета, дополненной изображением координатных осей с натуральными масштабными отрезками по этим осям. Название «аксонометрия» и произошло от слов — аксон
— ось и метрео — измеряю.
Виды аксонометрических проекций
Аксонометрические проекции в зависимости от направления проецирования разделяют на:
- косоугольные , когда направление проецирования не перпендикулярно плоскости аксонометрических проекций;
- прямоугольные , когда направление проецирования перпендикулярно плоскости аксонометрических проекций.
В зависимости от сравнительной величины коэффициентов искажения по осям различают три вида аксонометрии:
- изометрия — все три коэффициента искажения равны между собой;
- диметрия — два коэффициента искажения равны между собой и отличаются от третьего;
- триметрия — все три коэффициента искажения не равны между собой.
Прямоугольная изометрия
В прямоугольной изометрии углы между осями равны 120°. При построении изометрической проекции по осям х, у, z и параллельно им откладывают натуральные размеры предмета. Отсюда название «изометрия», что по-гречески означает «равные измерения»
Построение изометрических проекций плоских геометрических фигур
Рассмотрим построение треугольника на горизонтальной плоскости в изометрической проекции.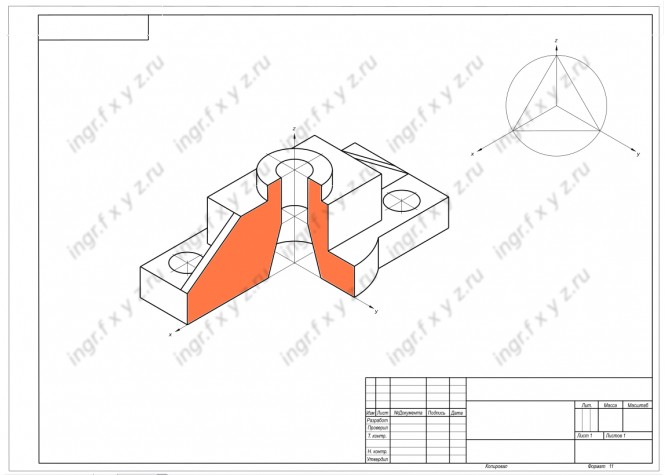 При построении первоначально необходимо определить расположение фигуры относительно начала
координат. Для этого по оси х откладывают расстояние m, равное смещению оси треугольника относительно оси у. Из найденной точки проводят прямую, параллельную оси у, и на ней откладывают отрезок,
равный k — смещению основания треугольника от оси х, получили точку 1. Симметрично точке 1 по прямой, параллельной оси х, в обе стороны откладывают отрезки, равные половине основания треугольника
– найдены точки 3, 4. Из точки 1 по прямой, параллельной оси у, откладывают отрезок, равный высоте треугольника – определена точка 2. Полученные точки соединяют. Аналогично строят фронтальную и
профильную проекцию фигуры.
При построении первоначально необходимо определить расположение фигуры относительно начала
координат. Для этого по оси х откладывают расстояние m, равное смещению оси треугольника относительно оси у. Из найденной точки проводят прямую, параллельную оси у, и на ней откладывают отрезок,
равный k — смещению основания треугольника от оси х, получили точку 1. Симметрично точке 1 по прямой, параллельной оси х, в обе стороны откладывают отрезки, равные половине основания треугольника
– найдены точки 3, 4. Из точки 1 по прямой, параллельной оси у, откладывают отрезок, равный высоте треугольника – определена точка 2. Полученные точки соединяют. Аналогично строят фронтальную и
профильную проекцию фигуры.Аксонометрические проекции применяются для наглядного изображения различных предметов. Предмет здесь изображают так, как его видят (под определенным углом зрения). На таком изображении отражены все три пространственных измерения, поэтому чтение аксонометрического чертежа обычно не вызывает затруднений.
Аксонометрический чертеж можно получить как с помощью прямоугольного проецирования, так и с помощью косоугольного проецирования. Предмет располагают так, чтобы три основных направления его измерений (высота, ширина, длина) совпадали с осями координат и вместе с ними спроецировались бы на плоскость. Направление проецирования не должно совпадать с направлением осей координат, т. е. ни одна из осей не будет проецироваться в точку. Только в этом случае получится наглядное изображение всех трех осей.
Для получения прямоугольных аксонометрических проекций оси координат наклоняют относительно плоскости проекций Р А так, чтобы их направление не совпадало с направлением проецирующих лучей. При косоугольном проецировании можно варьировать как направлением проецирования, так и наклоном координатных осей относительно плоскости проекций. При этом координатные оси в зависимости от их угла наклона к аксонометрической плоскости проекций и направления проецирования будут проецироваться с разными коэффициентами искажения.
§ 26. ПРЯМОУГОЛЬНЫЕ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
Изометрическая проекция отличается большой наглядностью и широко применяется в практике. Координатные оси при получении изометрической проекции наклоняют относительно аксонометрической плоскости проекций так, чтобы они имели одинаковый угол наклона (рис. 236). В этом случае они проецируются с одинаковым коэффициентом искажения (0,82) и под одинаковым углом друг к другу (120°).
В практике коэффициент искажения по осям обычно принимают равным единице, т. е. откладывают действительную величину размера. Изображение получается увеличенным в 1,22 раза, но это не приводит к искажениям формы и не сказывается на наглядности, а упрощает построения.
Изображение получается увеличенным в 1,22 раза, но это не приводит к искажениям формы и не сказывается на наглядности, а упрощает построения.
Аксонометрические оси в изометрии проводят, предварительно построив углы между осями х, у и z (120°) или углы наклона осей х и у к горизонтальной прямой (30°). Построение осей в изометрии с помощью циркуля показано на рис. 237, где радиус R взят произвольно. На рис. 238 показан способ построения осей х и у с использованием тангенса угла 30°. От точки О — точки пересечения аксонометрических осей откладывают влево или вправо по горизонтальной прямой пять одинаковых отрезков произвольной длины и, проведя через последнее деление вертикальную прямую, откладывают на ней вверх и вниз по три таких же отрезка. Построенные точки соединяют с точкой О и получают оси Ох и Оу.
Откладывать (строить) размеры и производить измерения в аксонометрии можно только по осям Ох, Оу и Оz или на прямых, параллельных этим осям.
На рис. 239 показано построение точки А в изометрии по ортогональному чертежу (рис. 239, а). Точка А расположена в плоскости V. Для построения достаточно построить вторичную проекцию а » точки
На рис. 240 показано построение точки В в изометрии. Сначала строят вторичную проекцию точки В на плоскости хОу. Для этого от начала координат по оси Ох откладывают координату Х в (рис. 240, б), получают вторичную проекцию точки b х. Из этой точки параллельно оси Оу проводят прямую и на ней откладывают координату Y B .
Построенная точка b на аксонометрической плоскости будет вторичной проекцией точки В. Проведя из точки b прямую, параллельную оси Oz, откладывают координату Z B и получают точку В, т. е. аксонометрическое изображение точки В. Аксонометрию точки В можно построить и от вторичных проекций на плоскости zОх или zОу.
е. аксонометрическое изображение точки В. Аксонометрию точки В можно построить и от вторичных проекций на плоскости zОх или zОу.
Прямоугольная диметрическая проекция. Координатные оси располагают так, чтобы две оси Ох и Оz имели одинаковый угол наклона и проецировались с одинаковым коэффициентом искажения (0,94), а третья ось Оу была бы наклонена так, чтобы коэффициент искажения при проецировании был в два раза меньше (0,47). Обычно коэффициент искажения по осям Ох и Oz принимают равным единице, а по оси Оу — 0,5. Изображение получается увеличенным в 1,06 раза, но это так же, как и в изометрии, не сказывается на наглядности изображения, а упрощает построение. Расположение осей в прямоугольной диметрии показано на рис. 241. Строят их, откладывая углы 7° 10″ и 41°25″ от горизонтальной линии по транспортиру, или откладывая одинаковые отрезки произвольной длины, как показано на рис. 241. Полученные точки соединить с точкой О .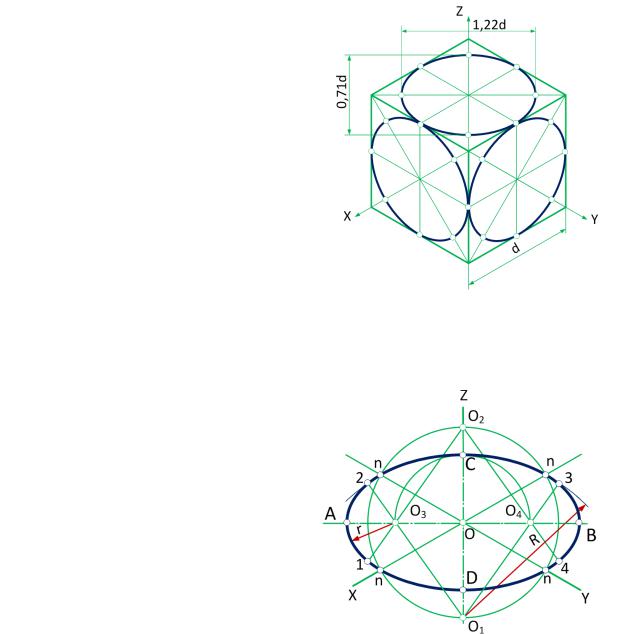
§ 27. КОСОУГОЛЬНЫЕ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
Фронтальная изометрическая проекция. Расположение аксонометрических осей показано на рис. 242. Угол наклона оси Оу к горизонтали обычно равен 45°, но может иметь значение 30 или 60°.
Горизонтальная изометрическая проекция. Расположение аксонометрических осей показано на рис. 243. Угол наклона оси Оу к горизонтали обычно равен 30°, но может иметь значение 45 или 60°. При этом угол 90° между осями Ох и Оу должен сохраняться.
Фронтальную и горизонтальную косоугольные изометрические проекции строят без искажения по осям Ох, Оу и Oz.
Фронтальная диметрическая проекция. Расположение осей показано на рис. 244. Рис. 245 иллюстрирует проецирование осей координат на аксонометрическую плоскость проекций. Плоскость xOz параллельна плоскости Р. Допускается ось Оу проводить под углом 30 или 60° к горизонтали, коэффициент искажения по оси Ох и Oz принят равным 1, а по оси Оу — 0,5.
Рис. 245 иллюстрирует проецирование осей координат на аксонометрическую плоскость проекций. Плоскость xOz параллельна плоскости Р. Допускается ось Оу проводить под углом 30 или 60° к горизонтали, коэффициент искажения по оси Ох и Oz принят равным 1, а по оси Оу — 0,5.
ПОСТРОЕНИЕ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР В АКСОНОМЕТРИИ
Основанием ряда геометрических тел является плоская геометрическая фигура: многоугольник или окружность. Чтобы построить геометрическое тело в аксонометрии, надо уметь строить прежде всего его основание, т. е. плоскую геометрическую фигуру. Для примера рассмотрим построение плоских фигур в прямоугольной изометрической и диметрической проекции. Построение многоугольников в аксонометрии можно выполнять методом координат, когда каждую вершину многоугольника строят в аксонометрии как отдельную точку (построение точки методом координат рассмотрено в § 26), затем построенные точки соединяют отрезками прямых линий и получают ломаную замкнутую линию в виде многоугольника.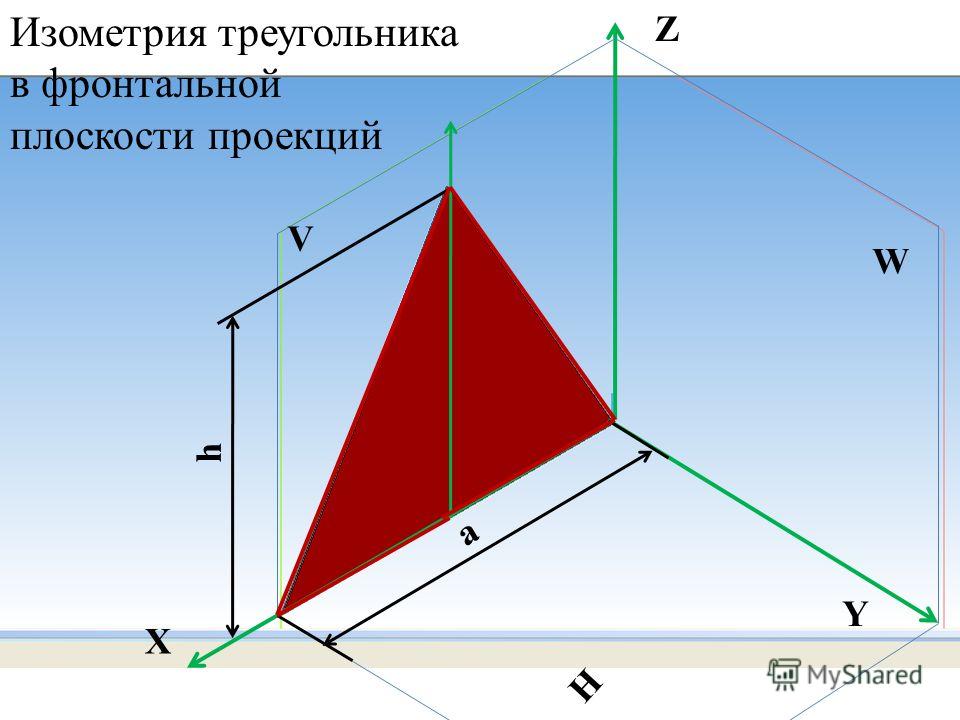
Отображать различные геометрические предметы с помощью чертежей и посредством компьютерной графики можно с применением принципов изометрии и аксонометрии. В чем специфика каждого из них?
Что представляет собой аксонометрия?
Под аксонометрией или аксонометрической проекцией понимается способ графического отображения тех или иных геометрических предметов посредством параллельных проекций.
Аксонометрия
Геометрический предмет в данном случае чаще всего рисуется с использованием определенной системы координат — так, чтобы та плоскость, на которую он проецируется, не соответствовала положению плоскости других координат соответствующей системы. Получается, что предмет отображается в пространстве посредством 2 проекций и выглядит объемно.
При этом по той причине, что плоскость отображения предмета не расположена строго параллельно какой-либо из осей системы координат, отдельные элементы соответствующего отображения могут искажаться — по одному из 3 следующих принципов.
Во-первых, искажение элементов отображения предметов может наблюдаться по всем 3 осям, используемым в системе, в равной величине. В этом случае фиксируется изометрическая проекция предмета, или изометрия.
Во-вторых, искажение элементов может наблюдаться только по 2 осям в равной величине. В этом случае наблюдается диметрическая проекция.
В-третьих, искажение элементов может фиксироваться как различающееся по всем 3 осям. В этом случае наблюдается триметрическая проекция.
Рассмотрим, таким образом, специфику первого типа искажений, формируемых в рамках аксонометрии.
Что представляет собой изометрия?
Итак, изометрия — это разновидность аксонометрии, которая наблюдается при прорисовке предмета в случае, если искажение его элементов по всем 3 осям координат одинаковое.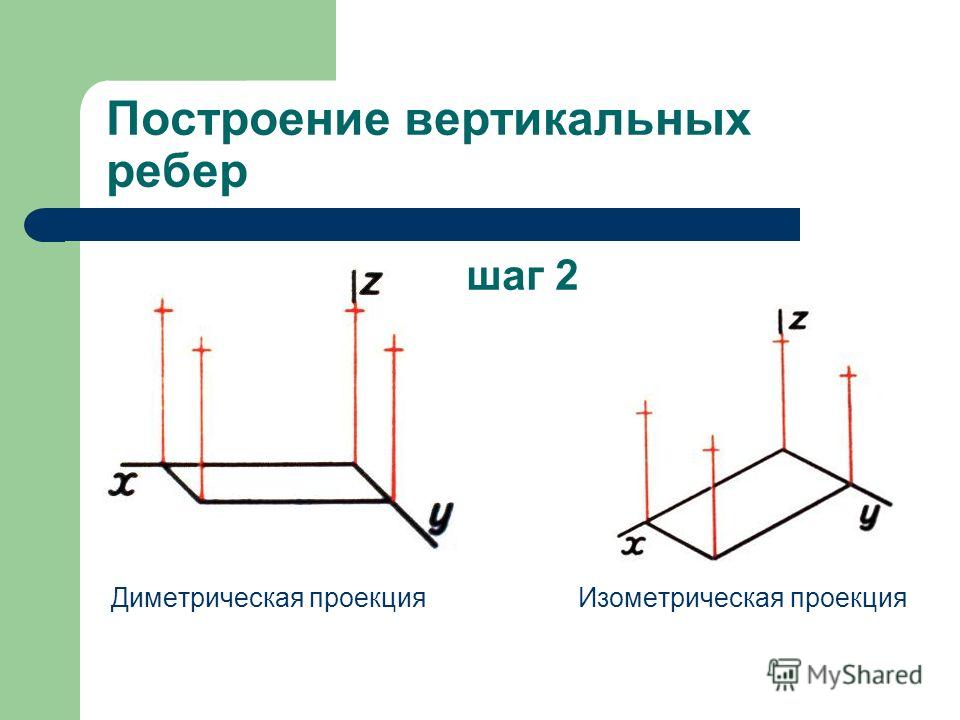
Изометрия
Рассматриваемый вид аксонометрической проекции активно применяется в промышленном проектировании. Он позволяет хорошо просматривать те или иные детали в рамках чертежа. Распространено использование изометрии и при разработке компьютерных игр: с помощью соответствующего типа проекции становится возможным эффективно отображать трехмерные картинки.
Можно отметить, что в сфере современных промышленных разработок под изометрией в общем случае понимается прямоугольная проекция. Но иногда она может быть представлена и в косоугольной разновидности.
Сравнение
Главное отличие изометрии от аксонометрии заключается в том, что первый термин соответствует проекции, являющейся только лишь одной из разновидностей той, которая обозначается вторым термином. Изометрическая проекция, таким образом, существенно отличается от других разновидностей аксонометрии — диметрии и триметрии.
Отобразим более наглядно то, в чем разница между изометрией и аксонометрией, в небольшой таблице.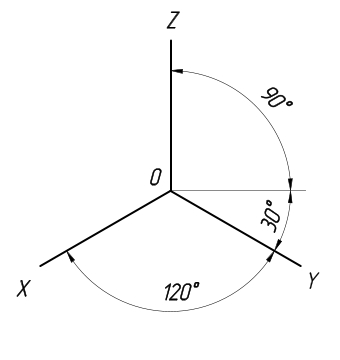
Что такое диметрия
Диметрия представляет собой один из видов аксонометрической проекции. Благодаря аксонометрии при одном объемном изображении можно рассматривать объект сразу в трех измерениях. Поскольку коэффициенты искажений всех размеров по 2-м осям одинаковы, данная проекция и получила название диметрия.
Прямоугольная диметрия
При расположении оси Z» вертикально, при этом оси Х» и Y» образуют с горизонтального отрезка углы 7 градуса 10 минут и 41 градус 25 минут. В прямоугольной диметрии коэффициент искажения по оси Y будет составлять 0,47, а по осям Х и Z в два раза больше, то есть 0,94.
Чтобы осущесвить построение приближенно аксонометрические оси обычной диметрии, необходимо принять, что tg 7 градусов 10 минут равен 1/8, а tg 41 градуса 25 минут равен 7/8.
Как построить диметрию
Для начала необходимо начертить оси, чтобы изобразить предмета в диметрии. В любой прямоугольной диметрии углы, находящиеся между осями Х и Z, равны 97 градусов 10 минут, а между осями Y и Z – 131 градусов 25 минут и между Y и Х – 127 градусов 50 минут.
Теперь требуется нанести оси на ортогональные проекции изображаемого предмета, учитывая выбранное положение предмета для вычерчивания в диметрической проекции. После того, как завершите перенос на объемное ихображение габаритных размеров предмета, можете приступать к чертежу незначительных элементов на поверхности предмета.
Стоит запомнить, что окружности в каждой плоскости диметрии изображаются соответствующими эллипсами. В диметрической проекции без искажения по осям Х и Z большая ось нашего эллипса во всех 3-х плоскостях проекции будет составлять 1,06 диаметра нарисованной окружности. А малая ось эллипса в плоскости ХОZ составляет 0,95 диаметра, а в плоскости ZОY и ХОY – 0,35 диаметра. В диметрической проекции с искажением по осям Х и Z большая ось эллипса равняется диаметру окружности во всех плоскостях. В плоскости ХОZ малая ось эллипса составляет 0,9 диаметра, а плоскостях ZОY и ХОY равны 0,33 диаметра.
Чтобы получить более детально изображение, необходимо выполнить вырез через детали на диметрии.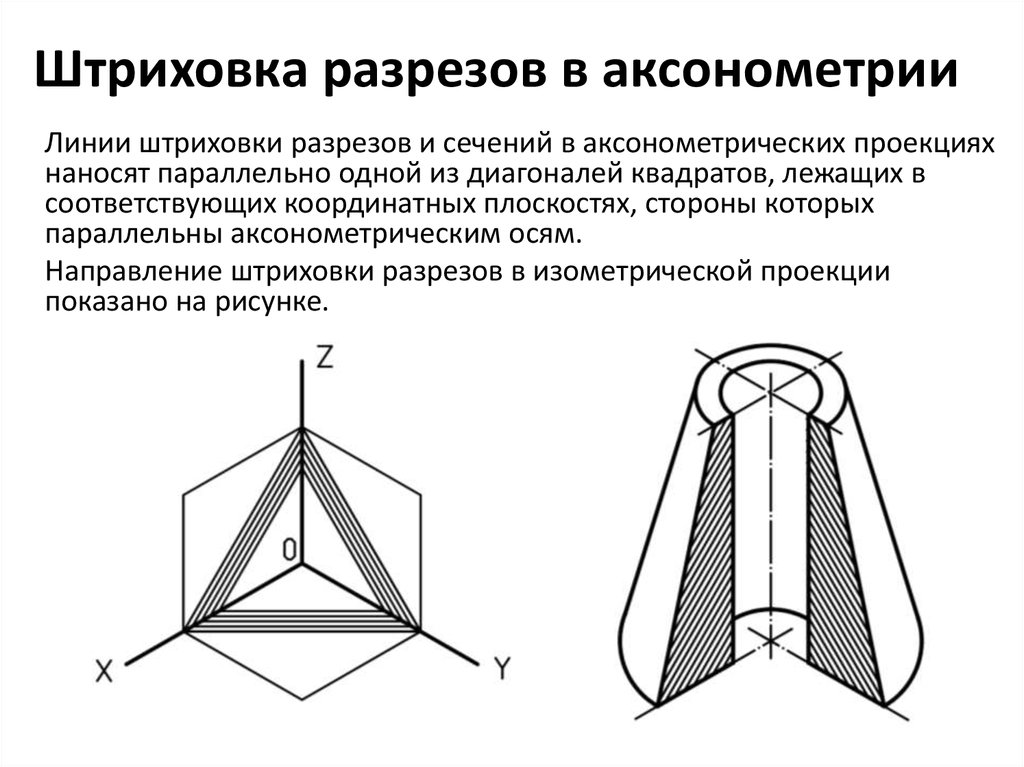 Заштриховку при вычеркивании выреза следует наносить параллельно проведенной диагонали проекции выбранного квадрата на необходимую плоскость.
Заштриховку при вычеркивании выреза следует наносить параллельно проведенной диагонали проекции выбранного квадрата на необходимую плоскость.
Что такое изометрия
Изометрия является одним из видов аксонометрической проекции, где расстояния единичных отрезков на всех 3-х осях одинаковые. Изометрическая проекция активно используется в машиностроительных чертежах, чтобы отобразить внешний вид предметов, а также в разнообразных компьютерных играх.
В математике изометрия известна как преобразование метрического пространства, которое сохраняет расстояние.
Прямоугольная изометрия
В прямоугольной (ортогональной) изометрии аксонометрические оси создают между собой углы, которые равны 120 градусам. Ось Z находится в вертикальном положении.
Как начертить изометрию
Построение изометрии предмета дает возможность получить наиболее выразительное представление о пространственных свойствах изображаемого объекта.
Перед тем, как начать построение чертежа в изометрической проекции, необходимо выбрать такое расположение изображаемого предмета, чтобы были максимально видны его пространственные свойства.
Теперь вам требуется определиться с видом изометрии, которую будете чертить. Существует два ее вида: прямоугольная и горизонтальная косоугольная.
Нарисуйте оси легкими тонкими линиями, чтобы изображение получилось по центру листа. Как уже раньше говорилось, углы в прямоугольном виде изометрической проекции должны составлять 120 градусов.
Начинайте рисовать изометрию с именно верхней поверхности изображения предмета. От углов получившейся горизонтальной поверхности нужно провести две вертикальные прямые и отложить на них соответствующие линейные размеры предмета. В изометрической проекции все линейные размеры по всех трем осям будут оставаться кратны единице. Затем последовательно требуется соединить созданные точки на вертикальных прямых. В результате получиться внешний контур предмета.
Стоит учитывать, что при изображении любого предмета в изометрической проекции видимость криволинейных деталей будет обязательно искажаться. Окружность должна изображаться эллипсом. Отрезок между точками окружности (эллипса) по осям изометрической проекции должен быть равен диаметру окружности, а оси эллипса не будут совпадать с осями изометрической проекции.
Отрезок между точками окружности (эллипса) по осям изометрической проекции должен быть равен диаметру окружности, а оси эллипса не будут совпадать с осями изометрической проекции.
Если изображаемый объект имеет скрытые полости ли сложные элементы, постарайтесь выполнить заштриховку. Она может быть простой либо ступенчатой, все зависит сложности элементов.
Запомните, что все построение должно выполнять строго с применением чертежных инструментов. Применяйте несколько карандашей с разными видами твердости.
Аксонометрия
Аксонометрия (от греч. axcon – ось и metreo – измеряю) дает наглядное изображение предмета на одной плоскости.
Изображение предмета в аксонометрии получается путем параллельного проецирования его на одну плоскость проекций вместе с осями прямоугольных координат, к которым этот предмет отнесен.
Коэффициенты искажения по осям в аксонометрии определяют отношением аксонометрических координатных отрезков к их натуральной величине при одинаковых единицах измерения.
Натуральные коэффициенты искажения обозначают:
- по оси x – u ;
- по оси y – v ;
- по оси z – w .
В зависимости от сравнительной величины коэффициентов искажения по осям различают три вида аксонометрии:
Изометрия – все три коэффициента искажения равны между собой: u=v=w .
Диметрия – два коэффициента искажения равны между собой и отличаются от третьего u=v≠w ; v=w≠u ; u=w≠v .
Триметрия – все три коэффициента искажения не равны между собой: u≠v≠w .
В зависимости от направления проецирования аксонометрические проекции разделяют на прямоугольные (направление проецирования перпендикулярно плоскости аксонометрических проекций) и косоугольные (направление проецирования не перпендикулярно плоскости аксонометрических проекций).
Прямоугольные проекции
Изометрия
Положение аксонометрических осей приведено на рис.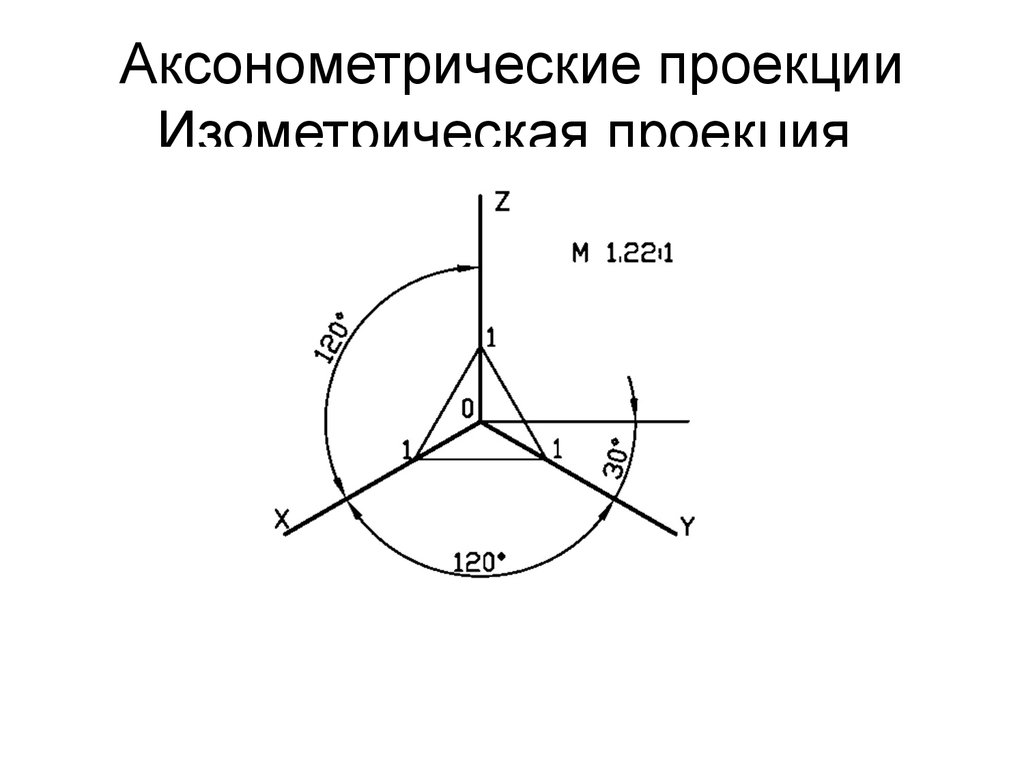 1.
1.
Рис.1. |
Коэффициент искажения по осям x , y , z равен 0,82.
Изометрию для упрощения, как правило, выполняют без искажения по осям x , y , z , т. е. приняв коэффициент искажения равным 1.
Построенное таким образом изображение будет больше самого предмета в 1,22 раза, т.е. масштаб изображения будет М 1,22:1 .
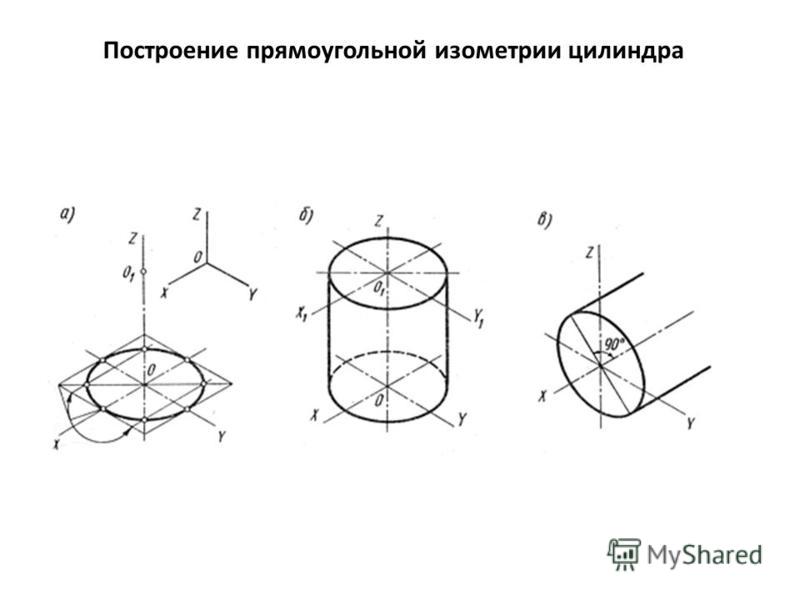
Окружности, лежащие в плоскостях, параллельных плоскостям проекций проецируются на аксонометрическую плоскость проекций в эллипсы (рис.2). Если изометрическую проекцию выполняют без искажения по осям x , y , z , то большая ось эллипсов 1, 2, 3 равна 1,22, а малая ось – 0,71 диаметра окружности. Если изометрическую проекцию выполняют с искажением по осям x , y , z , то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось – 0,58 диаметра окружности.
Пример изометрической проекции детали приведен на рис. 3.
3.
Диметрия
Положение аксонометрических осей приведено на рис.4.
Рис.4. |
Коэффициент искажения по оси y равен 0,47, а по осям x и z – 0,94.
Диметрическую проекцию, как правило, выполняют без искажения по осям x и z и с коэффициентом искажения 0,5 по оси y .
Аксонометрический масштаб будет М 1,06:1 .
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис.5). Если диметрическую проекцию выполняют без искажения по осям x и z , то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 – 0,95, эллипсов 2 и 3 – 0,35 диаметра окружности. Если диметрическую проекцию выполняют с искажением по осям x и z , то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 – 0,9, эллипсов 2 и 3 – 0,33 диаметра окружности.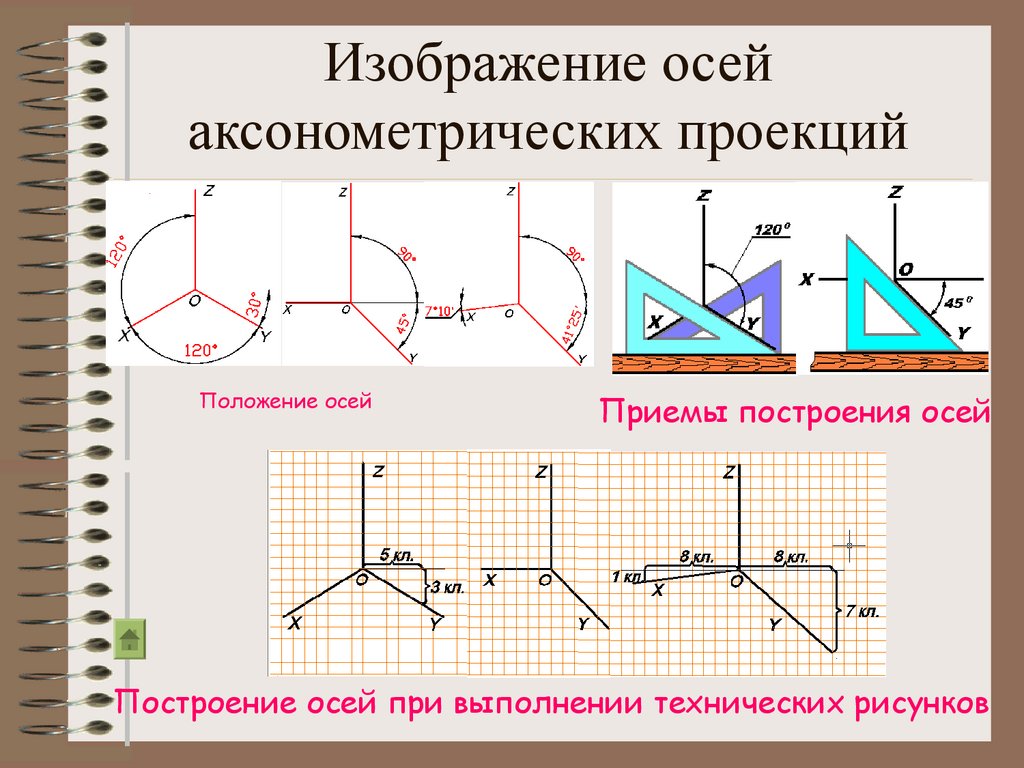
Пример диметрической проекции детали приведен на рис.6.
Косоугольные проекции
Изометрия фронтальная
Положение аксонометрических осей приведено на рис.7.
Допускается применять фронтальные изометрические проекции с углом наклона оси у 30 и 60°.
Фронтальную изометрическую проекцию выполняют без искажения по осям x , y , z .
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис.8). Большая ось эллипсов 2 и 3 равна 1,3, а малая ось – 0,54 диаметра окружности.
Пример фронтальной изометрической проекции детали приведен на рис.9.
Изометрия горизонтальная
Положение аксонометрических осей приведено на рис.10.
Допускается применять горизонтальные изометрические проекции с углом наклона оси y 45 и 60°, сохраняя угол между осями x и y 90°.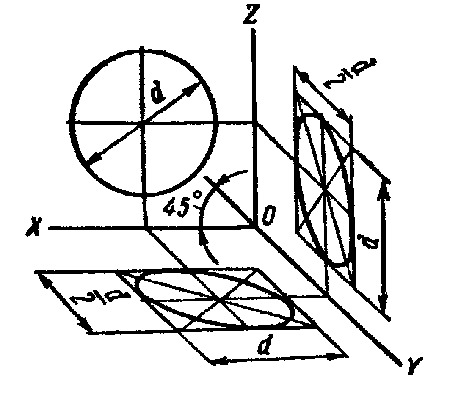
Горизонтальную изометрическую проекцию выполняют без искажения по осям x , y и z .
Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскостям проекций – в эллипсы (рис.11). Большая ось эллипса 1 равна 1,37, а малая ось – 0,37 диаметра окружности. Большая ось эллипса 3 равна 1,22, а малая ось – 0,71 диаметра окружности. Оси фронтальной диметрии
Допускается применять фронтальные диметрические проекции с углом наклона оси у 30 и 60°.
Коэффициент искажения по оси y равен 0,5, а по осям x и z – 1.
Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис. 14). Большая ось эллипсов 2 и 3 равна 1,07, а малая ось – 0,33 диаметра окружности.
14). Большая ось эллипсов 2 и 3 равна 1,07, а малая ось – 0,33 диаметра окружности.
Пример фронтальной диметрической проекции детали приведен на рис.15.
Как сделать аксонометрию. Диметрия и изометрия Аксонометрической фронтальной изометрической проекции
ГОСТ 2.317-68* устанавливает прямоугольные и косоугольные аксонометрические проекции.
Построение аксонометрических проекций заключается в том, что геометрическую фигуру вместе с осями прямоугольных координат, к которым
эта фигура отнесена в пространстве, параллельным (прямоугольным или косоугольным) способами проецируют на выбранную плоскость проекций. Таким образом, аксонометрическая проекция — это проекция на
одну плоскость. При этом направление проецирования выбирают так, чтобы оно не совпадало ни с одной из координатных осей.
При построении аксонометрических проекций изображаемый предмет жестко связывают с натуральной системой координат Oxyz. В целом аксонометрический чертеж получается
состоящим из параллельной проекции предмета, дополненной изображением координатных осей с натуральными масштабными отрезками по этим осям. Название «аксонометрия» и произошло от слов — аксон
— ось и метрео — измеряю.
Название «аксонометрия» и произошло от слов — аксон
— ось и метрео — измеряю.
Виды аксонометрических проекций
Аксонометрические проекции в зависимости от направления проецирования разделяют на:
- косоугольные , когда направление проецирования не перпендикулярно плоскости аксонометрических проекций;
- прямоугольные , когда направление проецирования перпендикулярно плоскости аксонометрических проекций.
В зависимости от сравнительной величины коэффициентов искажения по осям различают три вида аксонометрии:
- изометрия — все три коэффициента искажения равны между собой;
- диметрия — два коэффициента искажения равны между собой и отличаются от третьего;
- триметрия — все три коэффициента искажения не равны между собой.
Прямоугольная изометрия
В прямоугольной изометрии углы между осями равны 120°. При построении изометрической проекции по осям х, у, z и параллельно им откладывают натуральные размеры предмета. Отсюда название
«изометрия», что по-гречески означает «равные измерения»
Отсюда название
«изометрия», что по-гречески означает «равные измерения»
Построение изометрических проекций плоских геометрических фигур
Рассмотрим построение треугольника на горизонтальной плоскости в изометрической проекции. При построении первоначально необходимо определить расположение фигуры относительно начала координат. Для этого по оси х откладывают расстояние m, равное смещению оси треугольника относительно оси у. Из найденной точки проводят прямую, параллельную оси у, и на ней откладывают отрезок, равный k — смещению основания треугольника от оси х, получили точку 1. Симметрично точке 1 по прямой, параллельной оси х, в обе стороны откладывают отрезки, равные половине основания треугольника – найдены точки 3, 4. Из точки 1 по прямой, параллельной оси у, откладывают отрезок, равный высоте треугольника – определена точка 2. Полученные точки соединяют. Аналогично строят фронтальную и профильную проекцию фигуры.
Построение аксонометрических проекций начинают с проведения аксонометрических осей.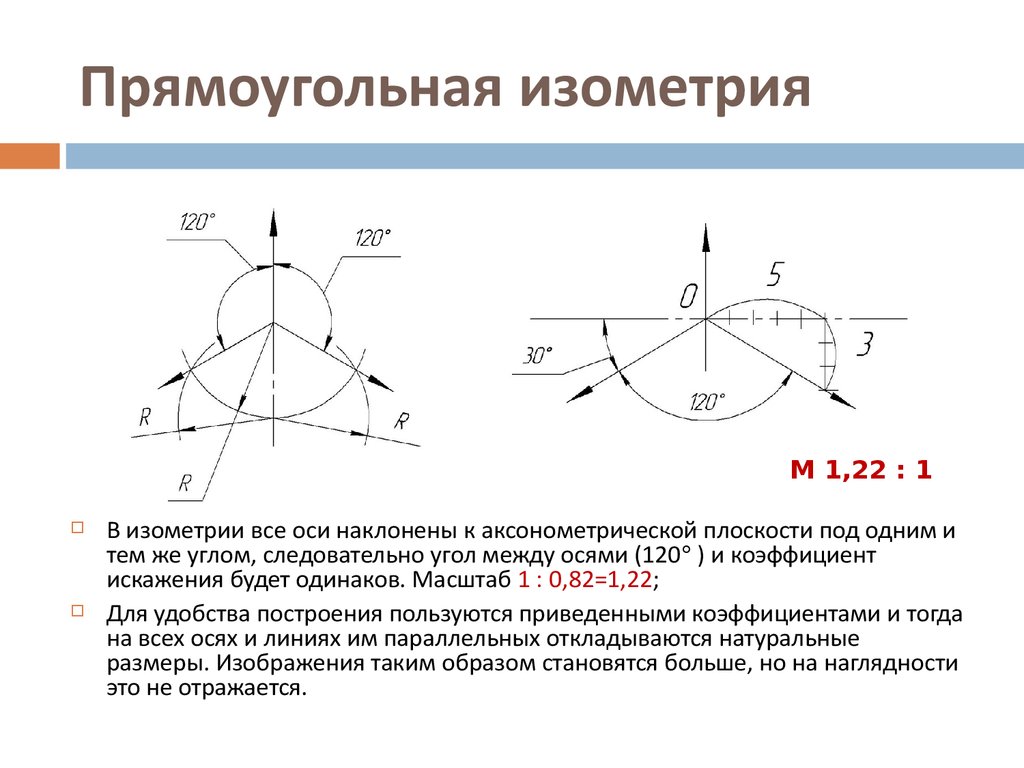
Положение осей. Оси фронтальной ди-метрической проекции располагают, как показано на рис. 85, а: ось х — горизонтально, ось z — вертикально, ось у — под углом 45° к горизонтальной линии.
Угол 45° можно построить при помощи чертежного угольника с углами 45, 45 и 90°, как показано на рис. 85, б.
Положение осей изометрической проекции показано на рис. 85, г. Оси х и у располагают под углом 30° к горизонтальной линии (угол 120° между осями). Построение осей удобно проводить при помощи угольника с углами 30, 60 и 90° (рис. 85, д).
Чтобы построить оси изометрической проекции с помощью циркуля, надо провести ось z, описать из точки О дугу произвольного радиуса; не меняя раствора циркуля, из точки пересечения дуги и оси z сделать засечки на дуге, соединить полученные точки с точкой О.
При построении фронтальной диметрической проекции по осям х и z (и параллельно им) откладывают действительные размеры; по оси у (и параллельно ей) размеры сокращают в 2 раза, отсюда и название «диметрия», что по-гречески означает «двойное измерение».
При построении изометрической проекции по осям х, у, z и параллельно им откладывают действительные размеры предмета, отсюда и название «изометрия», что по-гречески означает «равные измерения».
На рис. 85, в и е показано построение аксонометрических осей на бумаге, разлинованной в клетку. В этом случае, чтобы получить угол 45°, проводят диагонали в квадратных клетках (рис. 85, в). Наклон оси в 30° (рис. 85, г) получается при соотношении длин отрезков 3: 5 (3 и 5 клеток).
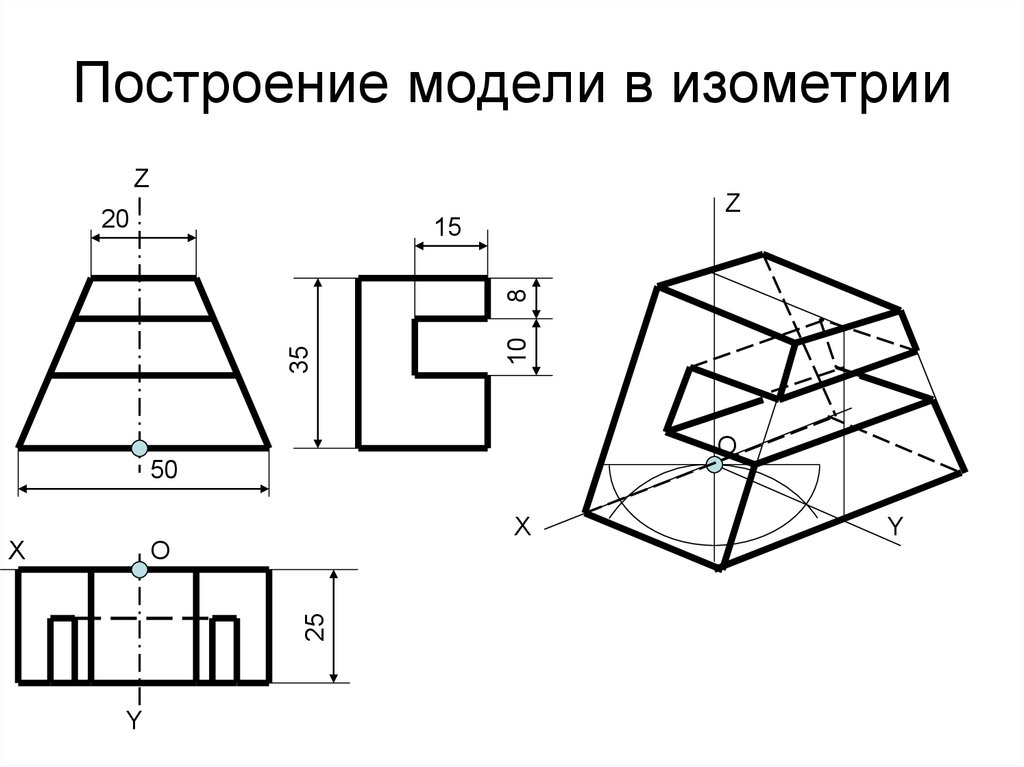
Построение фронтальной диметрической и изометрической проекций . Построить фронтальную диметрическую и изометрическую проекции детали, три вида которой приведены на рис. 86.
Порядок построения проекций следующий (рис. 87):
1. Проводят оси. Строят переднюю грань детали, откладывая действительные величины высоты — вдоль оси z, длины — вдоль оси х (рис. 87, а).
2. Из вершин полученной фигуры параллельно оси v проводят ребра, уходящие вдаль. Вдоль них откладывают толщину детали: для фронтальной ди-метрической проекции — сокращенную в 2 раза; для изометрии — действительную (рис. 87, б).
87, б).
3. Через полученные точки проводят прямые, параллельные ребрам передней грани (рис. 87, в).
4. Удаляют лишние линии, обводят видимый контур и наносят размеры (рис. 87, г).
Сравните левую и правую колонки на рис. 87. Что общего и в чем различие данных на них построений?
Из сопоставления этих рисунков и приведенного к ним текста можно сделать вывод о том, что порядок построения фронтальной диметрической и изометрической проекций в общем одинаков. Разница заключается в расположении осей и длине отрезков, откладываемых вдоль оси у.
В ряде случаев построение аксонометрических проекций удобнее начинать с построения фигуры основания. Поэтому рассмотрим, как изображают в аксонометрии плоские геометрические фигуры, расположенные горизонтально.
Построение аксонометрической проекции квадрата показано на рис. 88, а и б.
Вдоль оси х откладывают сторону квадрата а, вдоль оси у — половину стороны а/2 для фронтальной диметрической проекции и сторону а для изометрической проекции. Концы отрезков соединяют прямыми.
Концы отрезков соединяют прямыми.
Построение аксонометрической проекции треугольника показано на рис. 89, а и б.
Симметрично точке О (началу осей координат) по оси х откладывают половину стороны треугольника а/2, а по оси у — его высоту h (для фронтальной диметрической проекции половину высоты h/2). Полученные точки соединяют отрезками прямых.
Построение аксонометрической проекции правильного шестиугольника показано на рис. 90.
По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. По оси у симметрично точке О откладывают отрезки s/2, равные половине расстояния между противоположными сторонами шестиугольника (для фронтальной диметрической проекции эти отрезки уменьшают вдвое). От точек m и n, полученных на оси у, проводят вправо и влево параллельно оси х отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.
Ответьте на вопросы
1. Как располагают оси фронтальной диметрической и изометрической проекций? Как их строят?
Разновидностью которых являются аксонометрические и, в том числе, изометрические проекции, делятся также на ортогональные (перпендикулярные), с направлением проекции перпендикулярным к плоскости проекции, и косоугольные , с углом между направлением и плоскостью, отличным от прямого. По советским стандартам (см. ) аксонометрические проекции могут быть и ортогональными, и косоугольными . По западным же стандартам, аксонометрические проекции являются только ортогональными, а косоугольные проекции рассматриваются отдельно. В результате, по западным стандартам изометрическая проекция определяется более узко и, помимо равенства масштабов по осям, включает условие равенства 120° углов между проекциями любой пары осей. Во избежание путаницы далее, если не указано иное, под изометрической проекцией будет подразумеваться только прямоугольная изометрическая проекция .
По советским стандартам (см. ) аксонометрические проекции могут быть и ортогональными, и косоугольными . По западным же стандартам, аксонометрические проекции являются только ортогональными, а косоугольные проекции рассматриваются отдельно. В результате, по западным стандартам изометрическая проекция определяется более узко и, помимо равенства масштабов по осям, включает условие равенства 120° углов между проекциями любой пары осей. Во избежание путаницы далее, если не указано иное, под изометрической проекцией будет подразумеваться только прямоугольная изометрическая проекция .
Стандартные изометрические проекции
Прямоугольная (ортогональная) изометрическая проекция
В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°, ось Z» направлена вертикально. Коэффициенты искажения () имеют числовое значение . Как правило, для упрощения построений изометрическую проекцию выполняют без искажений по осям, то есть коэффициент искажения принимают равным 1, в этом случае получают увеличение линейных размеров в раза.
Косоугольная фронтальная изометрическая проекция
Ось Z» направлена вертикально, угол между осью X» и Z» равен 90°, ось Y» с углом наклона 135° (допускается 120° и 150°) от оси Z».
Фронтальная изометрическая проекция выполняется по осям X», Y» и Z» без искажения.
Кривые параллельные фронтальной плоскости проецируются без искажений.
Косоугольная горизонтальная изометрическая проекция
Ось Z» направлена вертикально, между осью Z» и осью Y» угол наклона равен 120° (допускается 135° и 150°), при этом сохраняется угол между осями X» и Y» равным 90°.
Горизонтальную изометрическую проекцию выполняют без искажения по осям X», Y» и Z».
Ограничения аксонометрической проекции
Изометрическая проекция в компьютерных играх и пиксельной графике
Рисунок телевизора в почти-изометрической пиксельной графике. У пиксельного узора видна пропорция 2:1
Примечания
- По ГОСТ 2 .317-69 — Единая система конструкторской документации.
 Аксонометрические проекции.
Аксонометрические проекции. - Здесь горизонтальной называется плоскость, перпендикулярная оси Z (которая является прообразом оси Z»).
- Ingrid Carlbom, Joseph Paciorek. Planar Geometric Projections and Viewing Transformations // ACM Computing Surveys (CSUR) : журнал. — ACM , декабрь 1978. — Т. 10. — № 4. — С. 465-502. — ISSN 0360-0300 . — DOI :10.1145/356744.356750
- Jeff Green. GameSpot Preview: Arcanum (англ.) . GameSpot (29 февраля 2000).(недоступная ссылка — история ) Проверено 29 сентября 2008.
- Steve Butts. SimCity 4: Rush Hour Preview (англ.) . IGN (9 сентября 2003). Архивировано
- GDC 2004: The History of Zelda (англ.) . IGN (25 марта 2004). Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.
Для тoгo чтобы получить аксонометрическую проекцию предмета (рис. 106), необходимо мысленно: поместить предмет в систему координат; выбрать аксонометрическую плоскость проекций и расположить предмет перед ней; выбрать направление параллельных проецирующих лучей, которое не должно совпадать ни с одной из аксонометрических осей; направить проецирующие лучи через все точки предмета и координатные оси до пересечения с аксонометрической плоскостью проекций, получив тем самым изображение проецируемого предмета и координатных осей.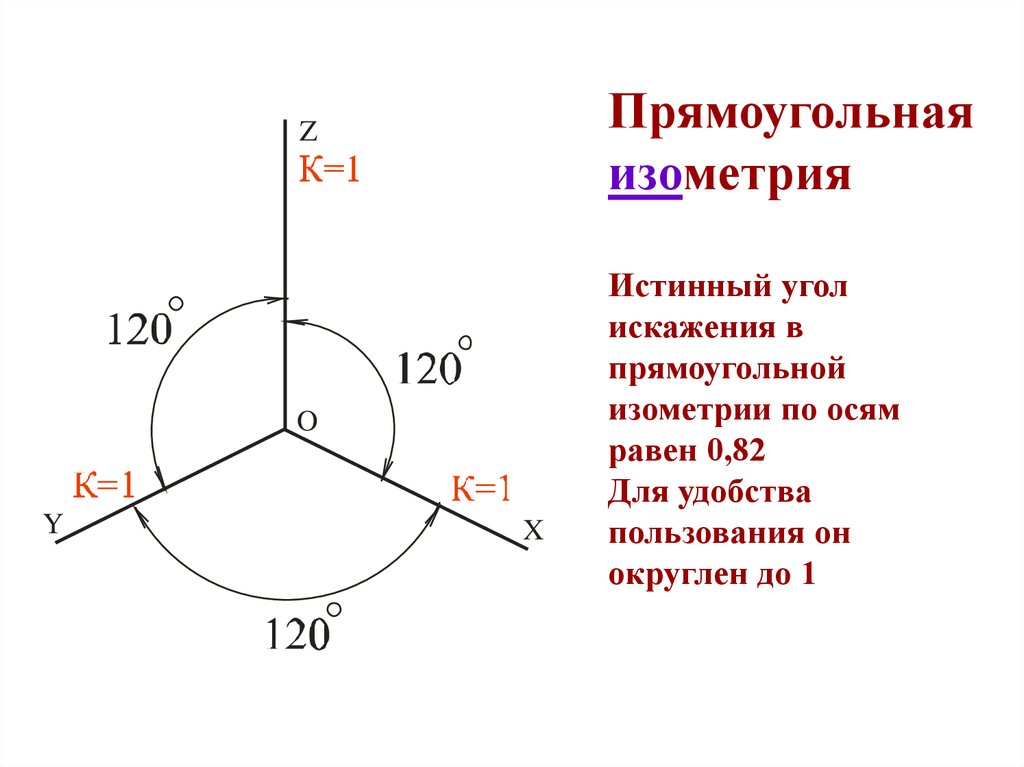
На аксонометрической плоскости проекций получают изображение — аксонометрическую проекцию предмета, а также проекции осей систем координат, которые называют аксонометрическими осями.
Аксонометрической проекцией называется изображение, полученное на аксонометрической плоскости в результате параллельного проецирования предмета вместе с системой координат, которое наглядно отображает его форму.
Система координат состоит из трех взаимно пересекающихся плоскостей, которые имеют фиксированную точку — начало координат (точку О) и три оси (X, У, Z), исходящие из нее и расположенные под прямым углом друг к другу. Система координат позволяет производить измерения по осям, определяя положение предметов в пространстве.
Рис. 106. Получение аксонометрической (прямоугольной изометрической) проекции
Можно получить множество аксонометрических проекций, по- разному располагая предмет перед плоскостью и выбирая при этом различное направление проецирующих лучей (рис.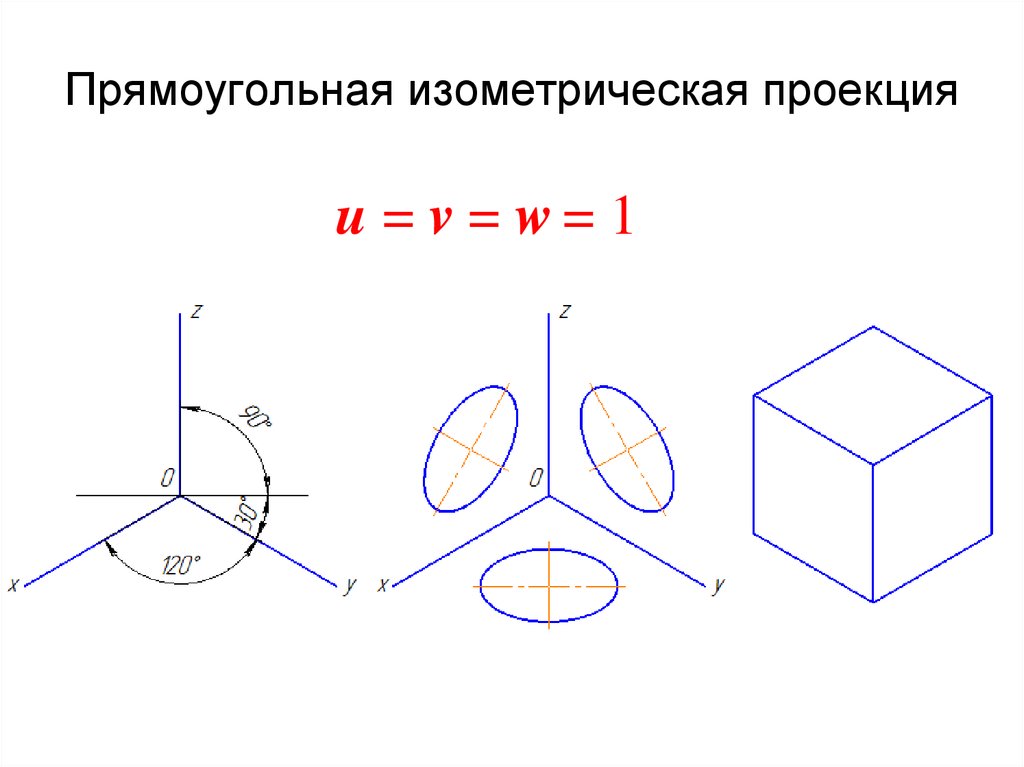 107).
107).
Наиболее употребляемой является так называемая прямоугольная изометрическая проекция (в дальнейшем будем использовать ее сокращенное название — изометрическая проекция). Изометрической проекцией (см. рис. 107, а) называется такая проекция, у которой коэффициенты искажения по всем трем осям равны, а углы между аксонометрическими осями составляют 120°. Изометрическая проекция получается с помощью параллельного проецирования.
Рис. 107. Аксонометрические проекции, установленные ГОСТ 2.317-69:
а — прямоугольная изометрическая проекция; б — прямоугольная диметрическая проекция;
в — косоугольная фронтальная изометрическая проекция;
г — косоугольная фронтальная диметрическая проекция
Рис. 107. Продолжение: д — косоугольная горизонтальная изометрическая проекция
При этом проецирующие лучи перпендикулярны аксонометрической плоскости проекций, а координатные оси одинаково наклонены к аксонометрической плоскости проекций (cм.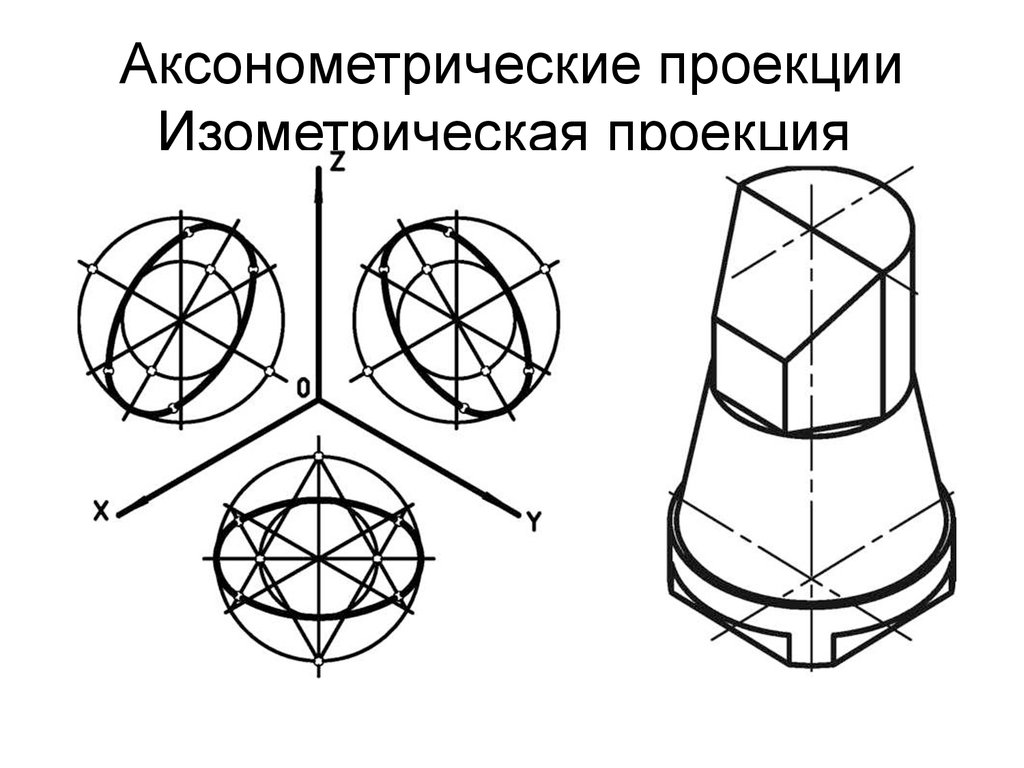 рис. 106). Если сравнить линейные размеры предмета и соответствующие им размеры аксонометрического изображения, то можно увидеть, что на изображении эти размеры меньше, чем действительные. Величины, показывающие отношение размеров проекций отрезков прямых к действительным их размерам, называют коэффициентами искажения. Коэффициенты искажения (К) по осям изометрической проекции одинаковы и равны 0,82, однако для удобства построения используют так называемые практические коэффициенты искажения, которые равны единице (рис. 108).
рис. 106). Если сравнить линейные размеры предмета и соответствующие им размеры аксонометрического изображения, то можно увидеть, что на изображении эти размеры меньше, чем действительные. Величины, показывающие отношение размеров проекций отрезков прямых к действительным их размерам, называют коэффициентами искажения. Коэффициенты искажения (К) по осям изометрической проекции одинаковы и равны 0,82, однако для удобства построения используют так называемые практические коэффициенты искажения, которые равны единице (рис. 108).
Рис. 108. Положение осей и коэффициенты искажения изометрической проекции
Существуют изометрические, диметрические и триметрические проекции. К изометрическим проекциям относятся такие проекции, которые имеют одинаковые коэффициенты искажения по всем трем осям. Диметрическими проекциями называются такие проекции, у которых два коэффициента искажения по осям одинаковые, а величина третьего отличается от них. К триметрическим проекциям относятся проекции, у которых все коэффициенты искажения различны.
Отображать различные геометрические предметы с помощью чертежей и посредством компьютерной графики можно с применением принципов изометрии и аксонометрии. В чем специфика каждого из них?
Что представляет собой аксонометрия?
Под аксонометрией или аксонометрической проекцией понимается способ графического отображения тех или иных геометрических предметов посредством параллельных проекций.
Аксонометрия
Геометрический предмет в данном случае чаще всего рисуется с использованием определенной системы координат — так, чтобы та плоскость, на которую он проецируется, не соответствовала положению плоскости других координат соответствующей системы. Получается, что предмет отображается в пространстве посредством 2 проекций и выглядит объемно.
При этом по той причине, что плоскость отображения предмета не расположена строго параллельно какой-либо из осей системы координат, отдельные элементы соответствующего отображения могут искажаться — по одному из 3 следующих принципов.
Во-первых, искажение элементов отображения предметов может наблюдаться по всем 3 осям, используемым в системе, в равной величине. В этом случае фиксируется изометрическая проекция предмета, или изометрия.
Во-вторых, искажение элементов может наблюдаться только по 2 осям в равной величине. В этом случае наблюдается диметрическая проекция.
В-третьих, искажение элементов может фиксироваться как различающееся по всем 3 осям. В этом случае наблюдается триметрическая проекция.
Рассмотрим, таким образом, специфику первого типа искажений, формируемых в рамках аксонометрии.
Что представляет собой изометрия?
Итак, изометрия — это разновидность аксонометрии, которая наблюдается при прорисовке предмета в случае, если искажение его элементов по всем 3 осям координат одинаковое.
ИзометрияРассматриваемый вид аксонометрической проекции активно применяется в промышленном проектировании. Он позволяет хорошо просматривать те или иные детали в рамках чертежа.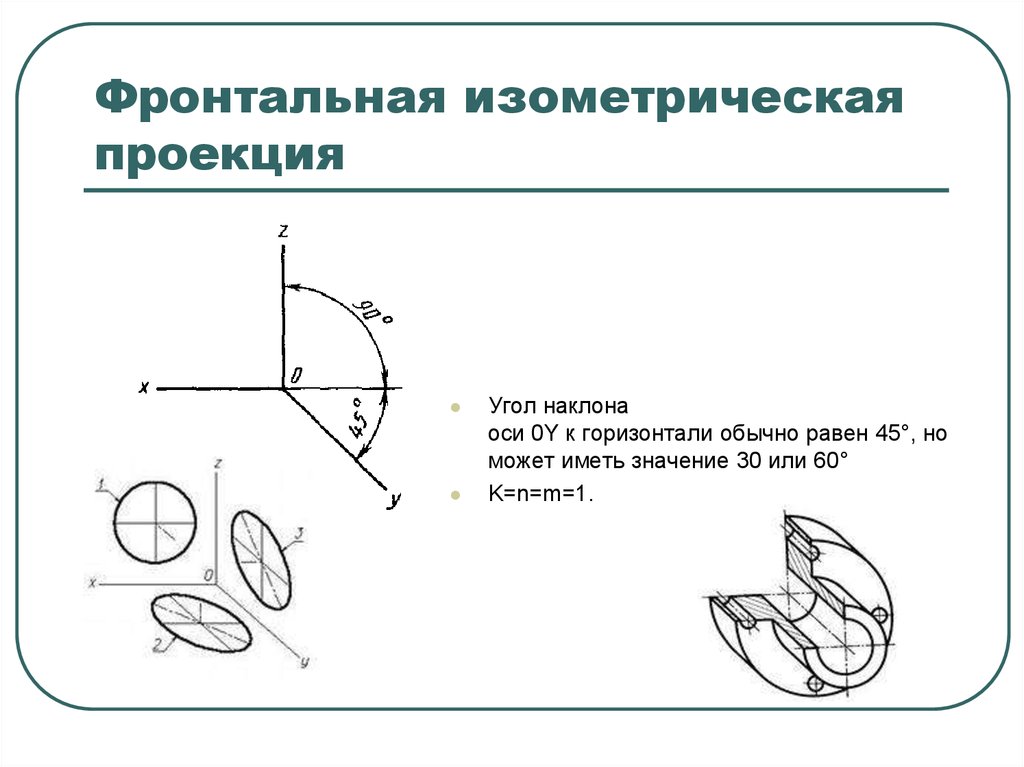 Распространено использование изометрии и при разработке компьютерных игр: с помощью соответствующего типа проекции становится возможным эффективно отображать трехмерные картинки.
Распространено использование изометрии и при разработке компьютерных игр: с помощью соответствующего типа проекции становится возможным эффективно отображать трехмерные картинки.
Можно отметить, что в сфере современных промышленных разработок под изометрией в общем случае понимается прямоугольная проекция. Но иногда она может быть представлена и в косоугольной разновидности.
Сравнение
Главное отличие изометрии от аксонометрии заключается в том, что первый термин соответствует проекции, являющейся только лишь одной из разновидностей той, которая обозначается вторым термином. Изометрическая проекция, таким образом, существенно отличается от других разновидностей аксонометрии — диметрии и триметрии.
Отобразим более наглядно то, в чем разница между изометрией и аксонометрией, в небольшой таблице.
АКСОНОМЕТРИЯ И ИЗОМЕТРИЯ… Аксонометрия в CorelDraw
Те окружности, которые располагаются в плоскостях, лежащих параллельно фронтальной плоскости проекций, на аксонометрическую плоскость проецируются в виде окружностей.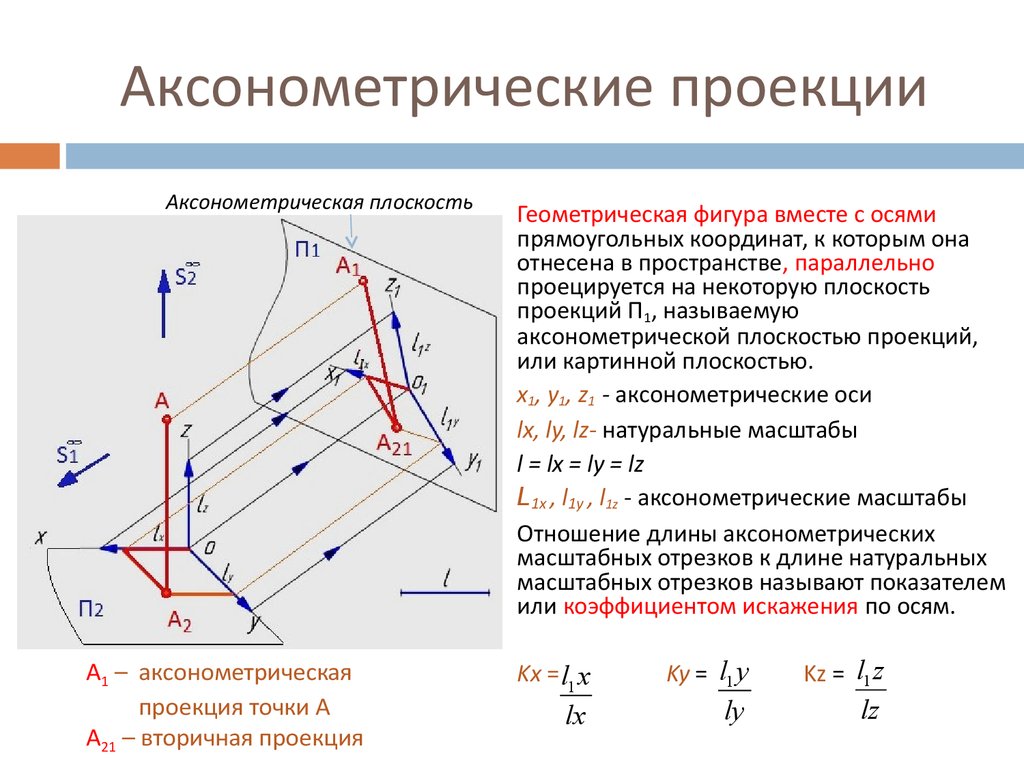 Изображение деталей в косоугольной фронтальной изометрии, используется для того, чтобы наиболее наглядно передать форму изделий и предметов.
Изображение деталей в косоугольной фронтальной изометрии, используется для того, чтобы наиболее наглядно передать форму изделий и предметов.
Изометрическая проекция используется в машиностроительном черчении и САПР для построения наглядного изображения детали на чертеже, а также в компьютерных играх для трёхмерных объектов и панорам.
Что представляет собой изометрия?
В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°, ось Z’ направлена вертикально. Имеется 8 различных вариантов получения изометрической проекции в зависимости от того, в какой октант смотрит наблюдатель. Это происходит из-за приблизительно равных по размеру и площади проекций такого объекта. Большинство современных компьютерных игр избегают этого за счёт отказа от аксонометрической проекции в пользу перспективноготрёхмерного рендеринга.
Вместо этого использовалась пропорция пиксельного узора 2:1 для рисования осевых линий x и y, в результате чего эти оси располагались под углом arctg 0,5 ≈ 26,565° к горизонтали.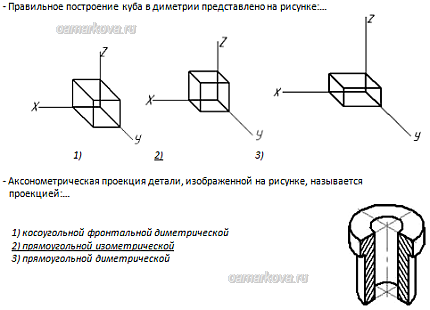
Изометрия фронтальная
Однако большинство представителей сообществ компьютерных игр и растровой графики продолжает называть эту проекцию «изометрической перспективой». Интересный пример использования особенностей изометрической проекции наблюдается в игре echochrome(яп.無限回廊муген кайро:). Очевидно, этот эффект достигается отсутствием перспективы в изометрии. Год спустя, в 1983 году, была выпущена аркадная игра Congo Bongo (англ.), работавшая на тех же игровых автоматах, что и Zaxxon.
То же самое предлагается и в аркадной игре Marble Madness (1984). На протяжении 1990-х некоторые очень успешные игры вроде Civilization II и Diablo использовали фиксированную изометрическую перспективу. С приходом 3D ускорителей на персональные компьютеры и игровые консоли игры с трёхмерной перспективой в основном переключились на полноценную трёхмерность вместо изометрической перспективы.
Отображать различные геометрические предметы с помощью чертежей и посредством компьютерной графики можно с применением принципов изометрии и аксонометрии. Под аксонометрией или аксонометрической проекцией понимается способ графического отображения тех или иных геометрических предметов посредством параллельных проекций.
Под аксонометрией или аксонометрической проекцией понимается способ графического отображения тех или иных геометрических предметов посредством параллельных проекций.
В этом случае наблюдается диметрическая проекция. Рассмотрим, таким образом, специфику первого типа искажений, формируемых в рамках аксонометрии. Итак, изометрия — это разновидность аксонометрии, которая наблюдается при прорисовке предмета в случае, если искажение его элементов по всем 3 осям координат одинаковое. Рассматриваемый вид аксонометрической проекции активно применяется в промышленном проектировании.
Распространено использование изометрии и при разработке компьютерных игр: с помощью соответствующего типа проекции становится возможным эффективно отображать трехмерные картинки.
Что представляет собой аксонометрия?
Но иногда она может быть представлена и в косоугольной разновидности. Главное отличие изометрии от аксонометрии заключается в том, что первый термин соответствует проекции, являющейся только лишь одной из разновидностей той, которая обозначается вторым термином. Изометрическая проекция, таким образом, существенно отличается от других разновидностей аксонометрии — диметрии и триметрии. Наиболее употребляемой является так называемая прямоугольная изометрическая проекция (в дальнейшем будем использовать ее сокращенное название — изометрическая проекция).
Главное отличие изометрии от аксонометрии заключается в том, что первый термин соответствует проекции, являющейся только лишь одной из разновидностей той, которая обозначается вторым термином. Изометрическая проекция, таким образом, существенно отличается от других разновидностей аксонометрии — диметрии и триметрии. Наиболее употребляемой является так называемая прямоугольная изометрическая проекция (в дальнейшем будем использовать ее сокращенное название — изометрическая проекция).
Положение осей изометрической проекции показано на рис. 85, г. Оси х и у располагают под углом 30° к горизонтальной линии (угол 120° между осями). При построении изометрической проекции по осям х, у, z и параллельно им откладывают действительные размеры предмета, отсюда и название «изометрия», что по-гречески означает «равные измерения».
Косоугольные проекции
В этом случае, чтобы получить угол 45°, проводят диагонали в квадратных клетках (рис. 85, в). Наклон оси в 30° (рис. 85, г) получается при соотношении длин отрезков 3 : 5 (3 и 5 клеток). Построение фронтальной диметрической и изометрической проекций.
85, г) получается при соотношении длин отрезков 3 : 5 (3 и 5 клеток). Построение фронтальной диметрической и изометрической проекций.
Из сопоставления этих рисунков и приведенного к ним текста можно сделать вывод о том, что порядок построения фронтальной диметрической и изометрической проекций в общем одинаков. В ряде случаев построение аксонометрических проекций удобнее начинать с построения фигуры основания. Поэтому рассмотрим, как изображают в аксонометрии плоские геометрические фигуры, расположенные горизонтально. Вдоль оси х откладывают сторону квадрата а, вдоль оси у — половину стороны а/2 для фронтальной диметрической проекции и сторону а для изометрической проекции.
Если взять квадрат и окружность, то окружность преобразуется вслед за квадратом в эллипс
1. Понятие об аксонометрических проекциях и их применение. Обычно плоскость (или предмет) располагают так, чтобы на аксонометрической проекции предмета были видны три стороны: верхняя (или нижняя), передняя и левая (или правая). А’, В’ и т.д. Изображение аксонометрических осей и показатели искажения.
А’, В’ и т.д. Изображение аксонометрических осей и показатели искажения.
Для аксонометрии есть основное правило: параллельность прямых линий (как и плоскостей) сохраняется. Пример. Построить квадрат и вписанную в нее окружность на координатных плоскостях прямоугольной диметрии. Если координатные плоскости образованы из перпендикуляных осей, то в ней проекция детали изображается в натуральную (истинную) величину. Далее с помощью операций объема, указания типа (параллельное назад), задания точки направления и высоты дедали, получаем деталь в объеме.
В этом случае фиксируется изометрическая проекция предмета, или изометрия. Во-вторых, искажение элементов может наблюдаться только по 2 осям в равной величине. 4.1 В зависимости от направления проецирования по отношению к плоскости проекций аксонометрические проекции делят на прямоугольные и косоугольные. В большинстве случаев диметрическая проекция выполняется с коэффициентом искажения по оси аксонометрии y, равным 0,5, и по осям аксонометрии z и x, равным единице.
1 Аксонометрические проекции. Изометрия, диметрия, триметрия
1 Аксонометрические проекции. Изометрия, диметрия, триметрия 2
2 Алгоритмы разложения в растр отрезка прямой линии и окружности 5
3 B-сплайновые модели кривых, поверхностей и их разновидности 7
4 Использование методов порталов и иерархических подсцен при создании виртуальной реальности. 9
5 Классификация цветовых моделей и форматов компьютерной графики 10
6 Колориметрия. Цветовые модели, смешение цветов и законы Гроссмана 13
7 Математическая модель и виды перспективного проецирования 15
8 Методы геометрического моделирования 17
9 Моделирование кривых и поверхностей в форме Безье 19
10 Моделирование кривых и поверхностей в форме Эрмита 21
11. Моделирование прозрачности и теней при построении реалистических изображений 23
12. Моделирование трехмерных поверхностей порциями поверхностей Кунса 25
13 Моделирование фотореалистичных изображений при помощи метода излучательности 27
14. Построение реалистических изображений
методом Торренсанса-Сперроу 29
Построение реалистических изображений
методом Торренсанса-Сперроу 29
15. Построение реалистичных изображений. Формула закраски 31
16. Преобразования на плоскости и в пространстве. Система однородных координат 33
17. Развертка сплошных областей. Алгоритмы построчной развертки и заполнения с затравкой. 37
Построение В-сплайновой модели поверхности происходит на базе В-сплайновой модели кривых и полностью аналогично построению модели по форме Эрмита и Безье. Формат поверхности формы В-сплановой поверхности описывается следующим уравнениями: 41
41
19. Формирование изображений трехмерного пространства методом отсечения лучей. 42
20. Формирование изображений трехмерного пространства при помощи алгоритмов, основанных на построении BSP-деревьев 44
21. Формирование окраски методом Гуро 47
22. Формирование окраски методом Фонга 49
23. Формирование реалистических изображений методом трассировки лучей 50
24. ЦВЕТОВЫЕ МОДЕЛИ, ОРИЕНТИРОВАННЫЕ НА
АППАРАТУРУ И ВОСПРИЯТИЕ ЧЕЛОВЕКОМ 52
ЦВЕТОВЫЕ МОДЕЛИ, ОРИЕНТИРОВАННЫЕ НА
АППАРАТУРУ И ВОСПРИЯТИЕ ЧЕЛОВЕКОМ 52
25. Цветовые форматы и стандарты МКО 55
Параллель проекция – аксонометр, если линии проецирования перпендик-ны плоск-ти проецир-я.
У параллель проекции центр проецир-я удален в бесконечность, и линии проециря-я параллельны.
При их построении используется аппарат аффинной геометрии. С формальной точки зрения аффинные преобразования определяются матрицей преобразований Т, в которой четвертый столбец имеет вид:
Среди аксонометрических проекций различают прямоугольную, диметрическую, изометрическую и триметрическую проекции.
Прямоугольные проекции
Ортографические проекции — частный случай ортогональных (прямоугольных) проекций, проецирование здесь — на координатные плоскости. Общий вид матрицы преобразований для получения прямоугольной (ортографической) проекции:
При этом
два из трёх диаг-х элементов (а,
е, i)
равны единице, а третий должен быть
нулевым.
В общем случае для выполнения ортогональных построений необходимо сместить плоскость проецирования параллельно одной из координатных плоскостей.
Ортогональное проецирование определяется матрицей преобразований с нулевой строкой, соответствующей той оси, перпендикулярно которой находится плоскость проецирования.
Ортогональные и ортографические проекции находят широкое применение в техническом черчении. Совокупность двух или трех ортографических проекций называется эпюром Монжа.
Диметрия и изометрия
Для построения более сложных аксонометрических проекций необходимо использовать комбинацию преобразований поворотов и проекций из бесконечности. Рассмотрим пример проецирования на плоскость Z = 0 .
Для получения данн изобр-я необх воспользоваться пространственным преобразованием:
,
где (Ry —
матрица поворота вокруг оси OY по
часовой стрелке, Rx –
матрица поворота вокруг оси OX против
часовой стрелки (α<0, β>0)).
Диметрическая проекция
Для построения необх, чтобы масштаб по осям ОX и ОY были — 1:1, а по оси OZ — 1:2.
Рассмотрим единичные векторы eX, eY и eZ, расположенные в исходном трёхмерном пространстве. В системе однородных координат их величины будут выглядеть следующим образом:
После преобразований по уравнению получим:
При этом по определению диметрии имеем следующие соотношения:
Используя теорему Пифагора, последние равенства можно записать в виде:
Решая эту систему относительно α и β получим углы поворота β =-20.705°; α = 22.208°.
Подставим полученные значения тригонометрических функций в уравнение и получим значения элементов матрицы преобразований для построения диметрической проекции в плоскости XOY (Z = 0):
Угол, образуемый проекцией оси ОХ с горизонталью плоскости проецир-я будет опред-ся через tgφ:
Для оси OY:
Для оси OZ:
Изометрическая проекция
При построении изометрии масштаб по всем трём осям должен быть одинаковым, поэтому соотношение длин единичных векторов:
Аналогично, с использованием теоремы Пифагора, составим систему уравнений:
Решая эту
систему относительно α и β получим углы поворота β
=35. 264°; α
= 45°.
264°; α
= 45°.
После подстановки значений тригонометрических функций вычисленных углов в уравнение получим матрицу преобразований для построения изометрии:
По аналогии с диметрией рассчитываются углы, которые составляют проекции осей координат с горизонталью плоскости проекции:
Последний вид аксонометрической проекции – триметрическая проекция — не ограничена каким-либо соотношением по координатным осям, поэтому для её построения в любом случае нужно производить самостоятельные расчёты углов поворота и матриц преобразований Т, аналогично тому, как это было сделано для диметрии и изометрии.
Понятие об аксонометрических проекциях • Блог архитектора
Наглядные изображения применяют для пояснения чертежей деталей и машин. По ним легче представить форму предмета, чем по чертежу в трёх видах.
Одним из видов наглядных изображений являются аксонометрические изображения.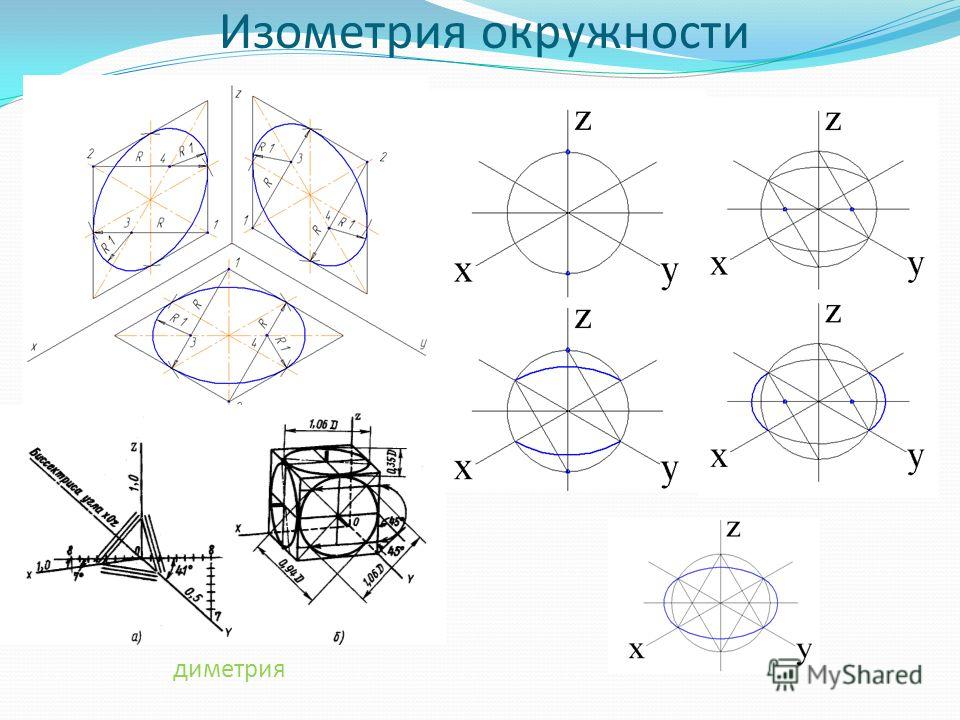
Аксонометрия в переводе с греческого означает «измерение по осям».
Аксонометрические проекции получают путём проецирования параллельными лучами
предмета, который связан с осями прямоугольных координат, на некоторую плоскость Р (рис. 103).
Рис. 103Таким образом, аксонометрическая проекция – это проекция только на одну плоскость.
Чтобы изображение получилось наглядным, проецирующие лучи не должны быть параллельны ни одной оси координат. Тогда на плоскости Р будут, хоть и с искажениями, изображены все три измерения предмета.
Аксонометрические проекции в зависимости от направления проецирования делятся на два вида: прямоугольные, когда направление проецирования перпендикулярно плоскости Р (угол φ=90°), и косоугольные, когда угол φ≠90°.
Если плоскость Р не параллельна ни одной из координатных плоскостей x,y,z, то на аксонометрической проекции у предмета искажаются все три его измерения. Если же плоскость Р параллельна одной или двум осям координат, то у предмета искажаются размеры соответственно по двум его измерениям или по одному.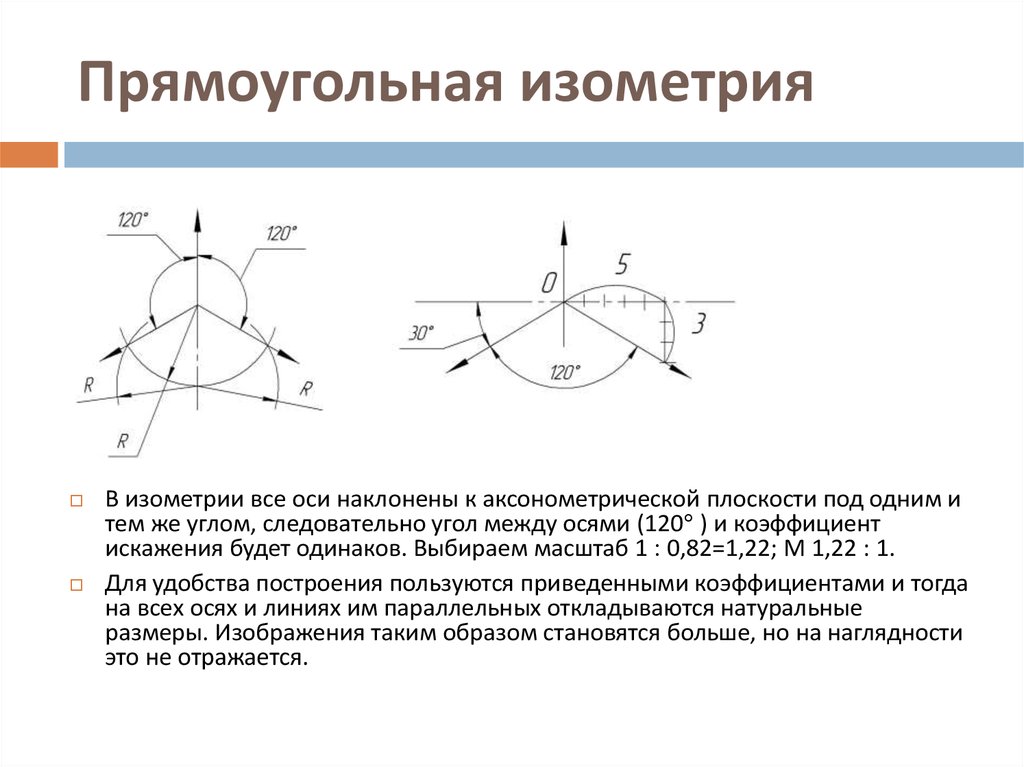
Величина искажения определяется коэффициентом искажения, который равен отношению длины аксонометрической проекции отрезка, параллельного соответствующей оси координат, к его действительной длине. Любая аксонометрическая проекция имеет три коэффициента искажения по числу осей координат.
В зависимости от того, разные они или одинаковые, аксонометрические проекции делят на изометрические (коэффициенты искажения равны по всем трём осям) и триметрические (коэффициенты искажения по всем осям разные).
Стандартные виды аксонометрии. Изометрия. Диметрия
Наиболее распространёнными видами аксонометрических проекций являются прямоугольная изометрическая проекция (изометрия) и прямоугольная диметрическая проекция (диметрия), основные правила построения которых определены стандартом.
Прямоугольная изометрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным к плоскости аксонометрических проекций одинаковыми по всем трём осям коэффициентами искажения, равными 0,82.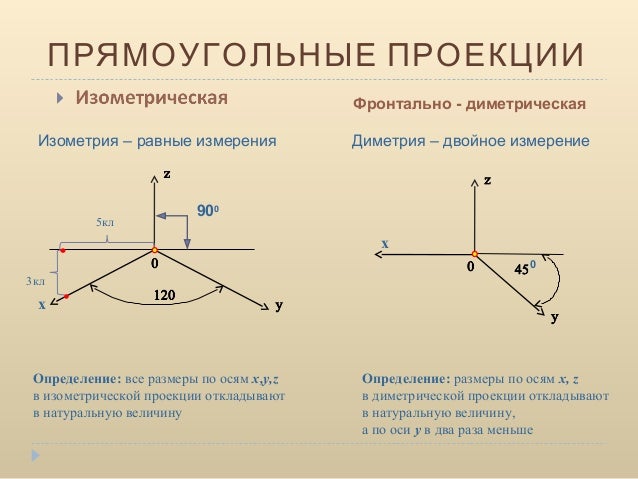
Оси изометрии (рис. 104а) составляют между собой углы 120°. Ось Z расположена вертикально. Для упрощения построения коэффициент искажения принимают равным 1.
Изображение при этом получается увеличенным, но вид его не меняется, т.к. сохраняется пропорциональность всех его размеров.
На рис. 104б и в приведены два способа построения осей в изометрии.
Рис. 104Прямоугольная диметрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным аксонометрической плоскости проекций Р и одинаковыми коэффициентами искажения по осям х и z.
Ось х (рис. 105а) составляет с горизонтальной прямой угол 7°10′, а ось у – угол 41°25′.
Ось z занимает вертикальное положение. На рис. 105б показан графический способ построения осей диметрии.
Рис. 105В диметрии коэффициенты искажения по осям х и z равны 0,94, а по оси у – 0,47. При построениях первый коэффициент округляют до 1, а второй – до 0,5. Таким образом, отрезки, параллельные осям координат х и z, откладывают в натуральную величину, а длину отрезков, параллельных оси у, уменьшают в два раза.
Построение окружности в аксонометрии
Изометрия. Изометрические проекции окружностей, расположенных в плоскостях проекций или в плоскостях, им параллельных, есть эллипсы (рис. 106).
Рис. 106Большие оси этих эллипсов равны l,22Dокр, а малые 0,71Dокр, где Dокр – диаметр изображаемой окружности. Большая ось эллипсов всегда перпендикулярна к той аксонометрической оси, которая отсутствует в плоскости окружности, а малая совпадает с этой осью или параллельна ей.
Практически при построении изометрии окружности эллипс обычно заменяют близким к нему по форме овалом, т.к. построение овала значительно проще.
Наиболее простой способ построения овала показан на рис. 107.
Рис. 107Этот способ заключается в построении изометрии квадрата, описанного вокруг окружности. Точки Np и Lp (вершины квадрата) являются центрами для дуг радиуса R 1 . Соединив точку Np с точками 2р и 3р, получим точки О1 и О2 – центры дуг радиуса R2.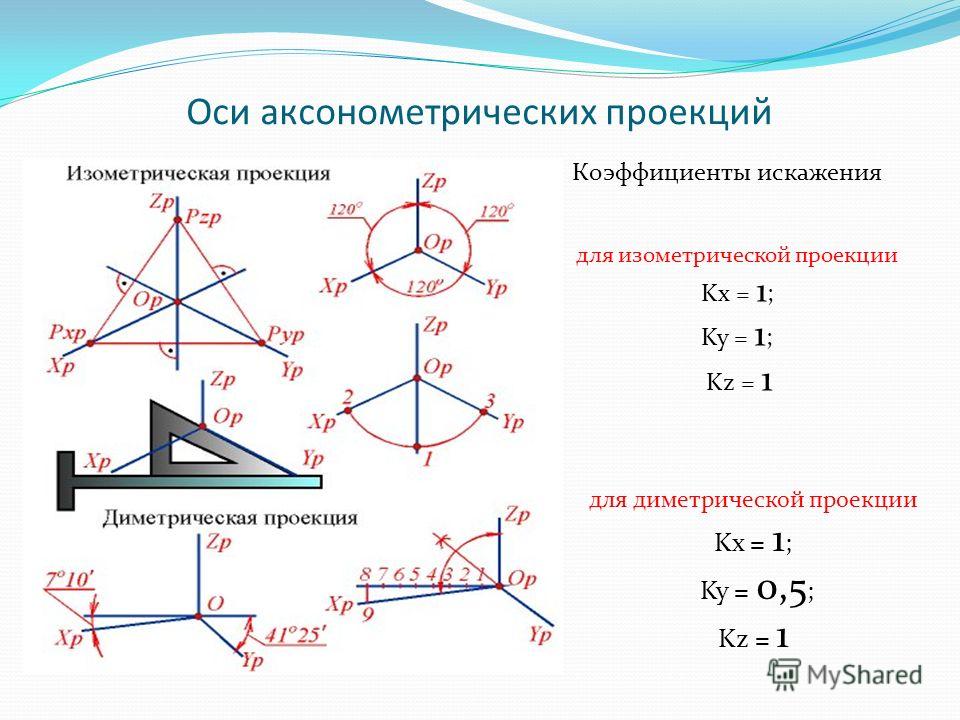
На рис. 108а,б построены изометрии окружностей, расположенных во фронтальной и профильной плоскостях.
Рис. 108Диметрия. Окружности, расположенные в горизонтальной и профильной плоскостях, проецируются в эллипсы с большой осью, равной 1,06Dокp , а малой – 0,35Dокр (рис. 109).
Окружности, расположенные во фронтальной плоскости, проецируются в виде эллипсов с большой осью, равной 1,06Dокр, а малой – 0,94Dокр. Большие оси эллипсов, как и в изометрии, перпендикулярны к той аксонометрической оси, которая отсутствует в данной плоскости, а малые оси совпадают с направлением этой оси.
Рис. 109Диметрии окружностей (эллипсы) обычно заменяют овалами, размеры осей которых равны размерам соответствующих осей эллипсов. Построение этих овалов показано на рис. 110. На рис. 110а построения понятны по чертежу.
На рис. 110б строим оси диметрии хр, ур, zр. Затем строим прямую, перпендикулярную оси ур. Отложив на осях хр и zр радиус заданной окружности, получим точки М, К, N, L, которые являются точками сопряжения дуг овала.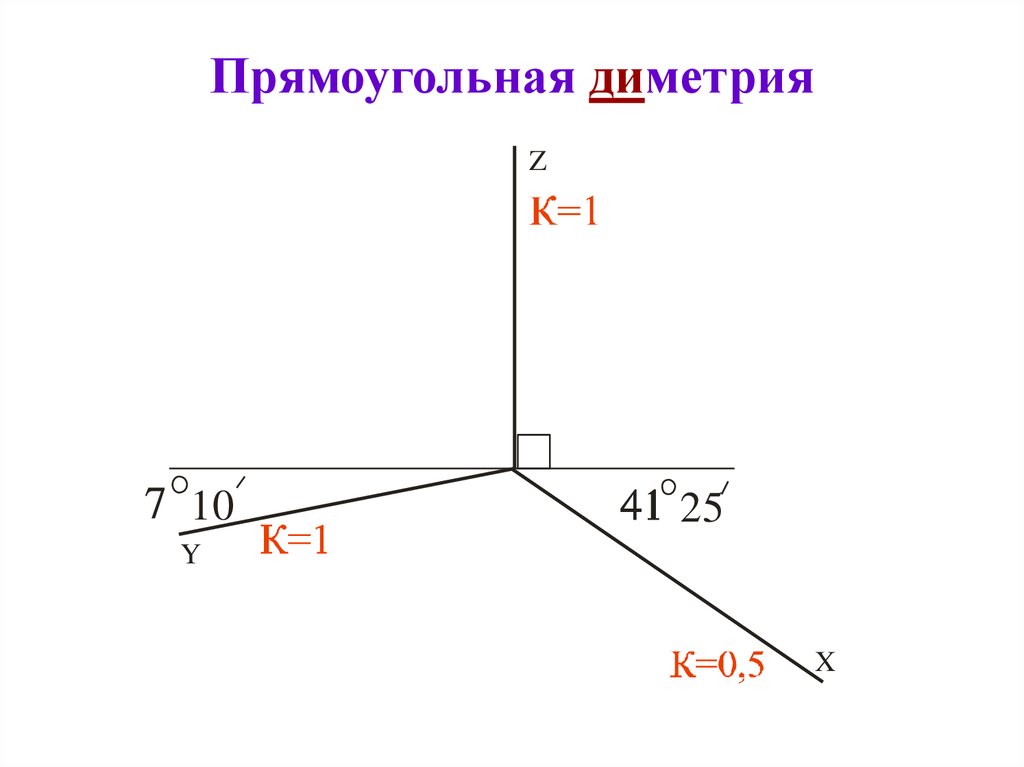 Через точки М и N проводим горизонтальные прямые. В пересечении этих прямых с осью ур и перпендикуляром к ней получим точки О1, О2, О3, О4. Из центров O1 и О3 опишем дуги радиусом R1=О3 K, а из центров О2 и О4 – дуги радиусом R2=О2M.
Через точки М и N проводим горизонтальные прямые. В пересечении этих прямых с осью ур и перпендикуляром к ней получим точки О1, О2, О3, О4. Из центров O1 и О3 опишем дуги радиусом R1=О3 K, а из центров О2 и О4 – дуги радиусом R2=О2M.
Аксонометрические изображения предметов
Приступая к построению аксонометрической проекции предмета, следует выбрать вид аксонометрии, обеспечивающий наибольшую наглядность изображения. Затем предмет связывают с системой прямоугольных координат, оси которой обычно совмещают с осями симметрии предмета. Только после этого можно приступить к построению аксонометрии.
Построение аксонометрии предмета обычно начинают с построения аксонометрии одной из его проекций (вторичной проекции). Затем полученное изображение дополняют построением третьего измерения всех его точек.
На рис. 111 показан пример построения прямоугольной изометрии предмета через построение его горизонтальной проекции.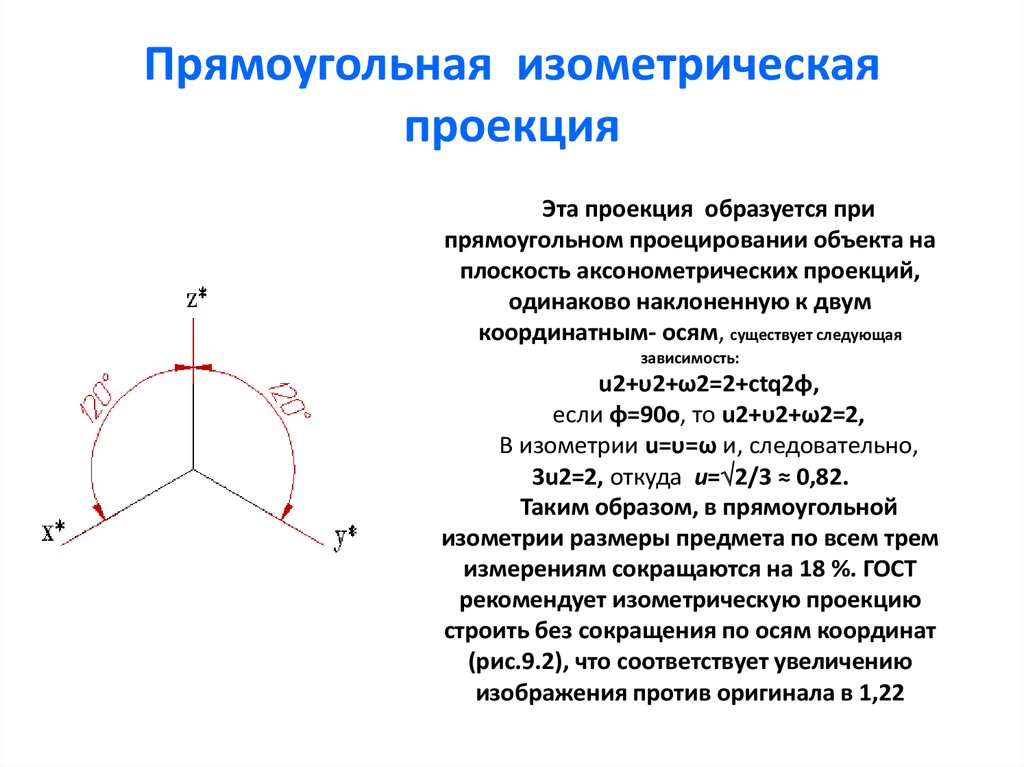
На рис. 112 приведен пример построения прямоугольной изометрии детали путём построения её вторичной фронтальной проекции.
Для выявления внутренней формы предмета, изображённого в аксонометрии, в некоторых случаях применяют разрезы, которые условно называют вырезами. При этом используют две секущие плоскости, обычно совпадающие с плоскостями симметрии предмета (рис. 113).
рис. 111рис. 112рис. 113Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Стороны квадратов параллельны аксонометрическим осям (рис. 114).
Рис. 114Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…ГОСТРАБОЧИЕ ТЕТРАДИУЧЕБНЫЕ ПОСОБИЯТеоретический материал Инженерная графика (инженерная и компьютерная графика).ОбъявленияДОЛГИ (выполненные задания) загружать сюда Теоретический материал БИ-21И1Задания по Инженерной и компьютерной графике БИ-21И1 ЛЕКЦИИТитульный лист для отчета по РГРЗадания АТб-21А1/А2Задания по Инженерной графике (ТЛб-21Z1)Задание по Начертательной геометрии (ТЛб-21Z1)Задание по инженерной графике ЭУб-21Z1ТЕСТ к ЭКЗАМЕНУ — ЭУб-21Z1Задания по Начертательной геометрии (ЭУб-21Z1)Лекция № 1 Образование проекций.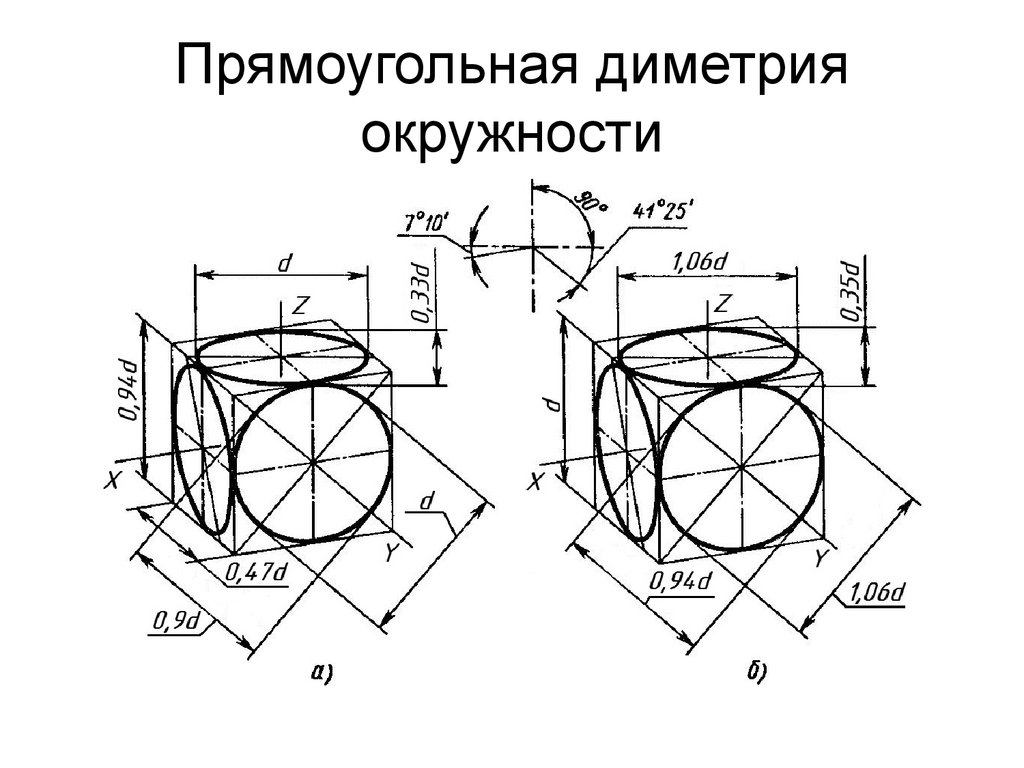 Лекция № 2 «Основные правила выполнения чертежей»Лекция № 3 «Проекции плоскости»Лекция № 4 «Сечения»Лекция 4.1 Сечение поверхности плоскостьюЛекция № 5 «Сложные разрезы»Лекция № 6 «Виды изделий»Лекция № 7 «Выполнение эскизов деталей машин»Лекция 8 «Проекции с числовыми отметками» ГОСТы, которые Вам помогуЗадания по Начертательной геометрии и инженерной графики (ГЕОб-21Z1)Итоговый тест ГЕОб-21Z1Графические работы АПб-21Z2Вопросы к экзаменуТЕСТ к ЭКЗАМЕНУ — АПб-21Z1/АПб-21Z2Теоретический материал Задание на графические работы по дисциплине «Компьютерная графика» Учебное пособиеНачертат геом установка ШИИЛекция 2Указания по выполнению заданийОформление работ заочниковГрафическая работа «Проекции с числовыми отметками»Графическая работа «Арх.- строит. чертеж здания»Отправка заданийГеометрическое компьютерное моделирование (Автокад) Отправка задания «ВАЛ» и «СОПРЯЖЕНИЕ»Отправка задания «План здания» (ГЕОб-20Z1)Задание для зачетаГрафическая работа № 1 Чертеж ВалаГрафическая работа № 2 СопряжениеГрафическая работа № 3 Проекционное черчениеВАЛСопряжениеРазвязкаЛекция 5 Кривые линии и поверхностиЛекция 6 Сечение поверхности плоскостью, построение развертокЛекция 7 Пересечение прямой с поверхностямиФлэш-плеер 1Флэш-плеер 23,4 и 5 темы загружать сюдаЛЕКЦИИ ЭУб-20А1ЗАДАНИЯ НА РАСЧЕТНО-ГРАФИЧЕСКИЕ РАБОТЫРешенные задачи (1 к.
Лекция № 2 «Основные правила выполнения чертежей»Лекция № 3 «Проекции плоскости»Лекция № 4 «Сечения»Лекция 4.1 Сечение поверхности плоскостьюЛекция № 5 «Сложные разрезы»Лекция № 6 «Виды изделий»Лекция № 7 «Выполнение эскизов деталей машин»Лекция 8 «Проекции с числовыми отметками» ГОСТы, которые Вам помогуЗадания по Начертательной геометрии и инженерной графики (ГЕОб-21Z1)Итоговый тест ГЕОб-21Z1Графические работы АПб-21Z2Вопросы к экзаменуТЕСТ к ЭКЗАМЕНУ — АПб-21Z1/АПб-21Z2Теоретический материал Задание на графические работы по дисциплине «Компьютерная графика» Учебное пособиеНачертат геом установка ШИИЛекция 2Указания по выполнению заданийОформление работ заочниковГрафическая работа «Проекции с числовыми отметками»Графическая работа «Арх.- строит. чертеж здания»Отправка заданийГеометрическое компьютерное моделирование (Автокад) Отправка задания «ВАЛ» и «СОПРЯЖЕНИЕ»Отправка задания «План здания» (ГЕОб-20Z1)Задание для зачетаГрафическая работа № 1 Чертеж ВалаГрафическая работа № 2 СопряжениеГрафическая работа № 3 Проекционное черчениеВАЛСопряжениеРазвязкаЛекция 5 Кривые линии и поверхностиЛекция 6 Сечение поверхности плоскостью, построение развертокЛекция 7 Пересечение прямой с поверхностямиФлэш-плеер 1Флэш-плеер 23,4 и 5 темы загружать сюдаЛЕКЦИИ ЭУб-20А1ЗАДАНИЯ НА РАСЧЕТНО-ГРАФИЧЕСКИЕ РАБОТЫРешенные задачи (1 к. н.) загружать сюдаГрафическую работу № 0 загружать сюда Задание Графическая работа № 1Решенные задачи (2 к.н.) загружать сюдаГрафическую работу № 1 загружать сюдаРешенные задачи (3 к.н.) загружать сюдаЗадание Графическая работа № 2Графическую работу № 2 загружать сюдаГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Винтовая параГр. работа 4. Эскиз валаГр. работа 5. Эскиз зубчатого колесаГр. работа 6. Эскиз штуцераГр. работа 7. СоединенияГр. работа 8. ДеталированиеЛекция 2Лекция 4Лекция 5Лекция 6Лекция 7Лекция 8Macromedia Flash PlayerСписок 1й подгруппы группы АТб-20Z1Список 1й подгруппы группы АТб-20Z2Теоретический материалГрафические работыОтправка графических работ АТб-20Z1/АТб-20Z2Теоретический материалЗадание на графические работы по дисциплине «Компьютерная графика» АТб-20Z1/АТб-20Z2Учебное пособие для ЗаочниковЛекция часть 1Лекция часть 2Лекция часть 3Задание для ЗаочниковОтправка выполненных чертежей1. Теоретический материал 2. Проекционное черчение3.
н.) загружать сюдаГрафическую работу № 0 загружать сюда Задание Графическая работа № 1Решенные задачи (2 к.н.) загружать сюдаГрафическую работу № 1 загружать сюдаРешенные задачи (3 к.н.) загружать сюдаЗадание Графическая работа № 2Графическую работу № 2 загружать сюдаГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Винтовая параГр. работа 4. Эскиз валаГр. работа 5. Эскиз зубчатого колесаГр. работа 6. Эскиз штуцераГр. работа 7. СоединенияГр. работа 8. ДеталированиеЛекция 2Лекция 4Лекция 5Лекция 6Лекция 7Лекция 8Macromedia Flash PlayerСписок 1й подгруппы группы АТб-20Z1Список 1й подгруппы группы АТб-20Z2Теоретический материалГрафические работыОтправка графических работ АТб-20Z1/АТб-20Z2Теоретический материалЗадание на графические работы по дисциплине «Компьютерная графика» АТб-20Z1/АТб-20Z2Учебное пособие для ЗаочниковЛекция часть 1Лекция часть 2Лекция часть 3Задание для ЗаочниковОтправка выполненных чертежей1. Теоретический материал 2. Проекционное черчение3. Компьютерное черчениеОтправка заданий на весенний семестрЭкзамен ЭУб-20Z1/ЭУб-20Z21. Теоретический материал Задание по инженерной и компьютерной графике1. Теоретический материал Задание по инженерной графикеГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Наклонное сечениеГр. работа 4. ИзометрияГр. работа 5. Эскиз валаГр. работа 6. Винтовая параГр. работа 7. Эскиз штуцераГр. работа 8. Эскиз зубчатого колесаГр. работа 9. ПриводВопросы к экзамену по Начертательной геометрииИнструкция для прохождения интернет-тестирования 11.01.2021 в 10:00Список студентов записанных на интернет-тестированиеMacromedia Flash PlayerЛекция 7Лекция 8Лекция 9Задание Графическая работа № 0Решенные задачи (1 к.н.) загружать сюдаГрафическую работу № 0 загружать сюда Задание Графическая работа № 1 Решенные задачи (2 к.н.) загружать сюдаГрафическую работу № 1 загружать сюда Задание на графическую работу № 2Решенные задачи (3 к.н.) загружать сюдаГрафическую работу № 2 загружать сюдаФото отчета пройденного теста загружать сюдаТема 8Тема № 9Лекция ПЧОЗадание графическая работа № 1Решенные задачи (1 к.
Компьютерное черчениеОтправка заданий на весенний семестрЭкзамен ЭУб-20Z1/ЭУб-20Z21. Теоретический материал Задание по инженерной и компьютерной графике1. Теоретический материал Задание по инженерной графикеГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Наклонное сечениеГр. работа 4. ИзометрияГр. работа 5. Эскиз валаГр. работа 6. Винтовая параГр. работа 7. Эскиз штуцераГр. работа 8. Эскиз зубчатого колесаГр. работа 9. ПриводВопросы к экзамену по Начертательной геометрииИнструкция для прохождения интернет-тестирования 11.01.2021 в 10:00Список студентов записанных на интернет-тестированиеMacromedia Flash PlayerЛекция 7Лекция 8Лекция 9Задание Графическая работа № 0Решенные задачи (1 к.н.) загружать сюдаГрафическую работу № 0 загружать сюда Задание Графическая работа № 1 Решенные задачи (2 к.н.) загружать сюдаГрафическую работу № 1 загружать сюда Задание на графическую работу № 2Решенные задачи (3 к.н.) загружать сюдаГрафическую работу № 2 загружать сюдаФото отчета пройденного теста загружать сюдаТема 8Тема № 9Лекция ПЧОЗадание графическая работа № 1Решенные задачи (1 к.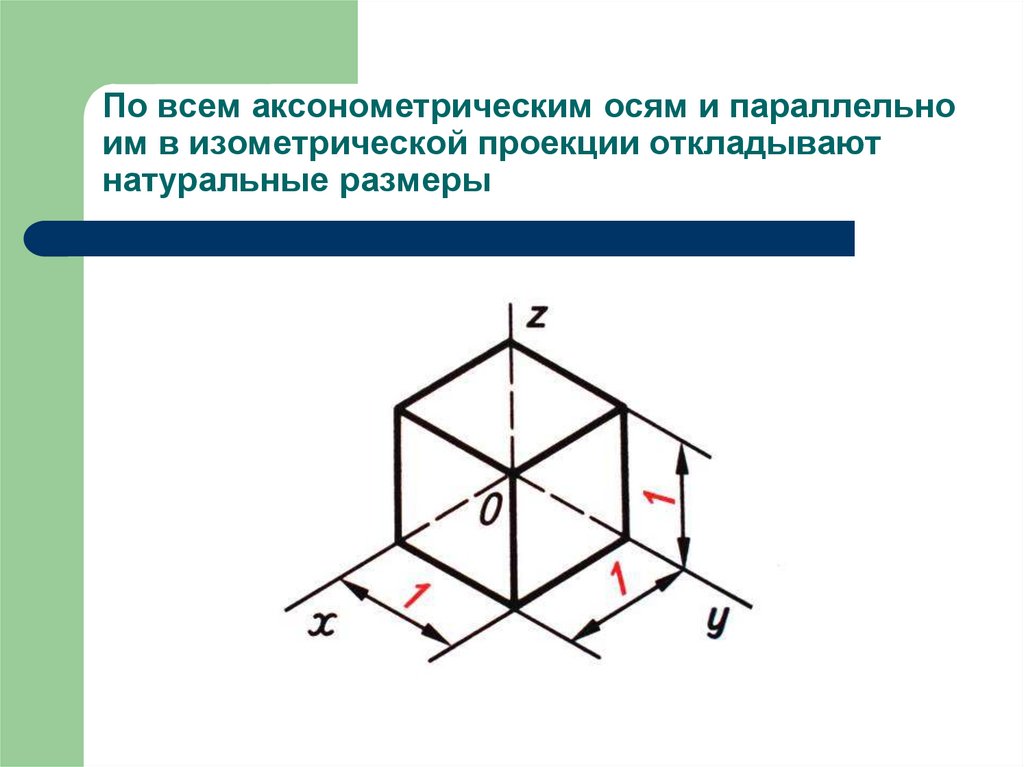 н.) загружать сюда Графическую работу № 1 загружать сюда Задание Графическая работа № 2 Решенные задачи (2 к.н.) загружать сюдаГрафическую работу № 2 загружать сюдаЗадание Графическая работа № 3Решенные задачи (3 к.н.) загружать сюда Графическую работу № 3 загружать сюдаЗадание Графическая работа «Проекции с числовыми отметками»Теоретический материалГОСТыГрафическая работа № 1Графическая работа № 2Графическая работа № 3 (ЭСКИЗ)Гр. работа № 4 План этажа зданияТеоретический материал по теме (компьютерная графика)1. Проекционное черчение (Сложный разрез)2. Сопряжение.3. СлоиВилкаВкладышВыполненные чертежи Вилки и Вкладыша загружать сюда (копия)Методические указания к работеИсходные чертежиВыполненную работу загружать сюдаТема 8Задание графическая работа (Инженерная графика)Решенные задачи (1 к.н.) загружать сюда Графическую работу (Инженерная графика) загружать сюда Задание Графическая работа № 2 Решенные задачи (2 к.н.) загружать сюда Графическую работу № 2 загружать сюдаЗадание ГР № 3Решенные задачи (3 к.
н.) загружать сюда Графическую работу № 1 загружать сюда Задание Графическая работа № 2 Решенные задачи (2 к.н.) загружать сюдаГрафическую работу № 2 загружать сюдаЗадание Графическая работа № 3Решенные задачи (3 к.н.) загружать сюда Графическую работу № 3 загружать сюдаЗадание Графическая работа «Проекции с числовыми отметками»Теоретический материалГОСТыГрафическая работа № 1Графическая работа № 2Графическая работа № 3 (ЭСКИЗ)Гр. работа № 4 План этажа зданияТеоретический материал по теме (компьютерная графика)1. Проекционное черчение (Сложный разрез)2. Сопряжение.3. СлоиВилкаВкладышВыполненные чертежи Вилки и Вкладыша загружать сюда (копия)Методические указания к работеИсходные чертежиВыполненную работу загружать сюдаТема 8Задание графическая работа (Инженерная графика)Решенные задачи (1 к.н.) загружать сюда Графическую работу (Инженерная графика) загружать сюда Задание Графическая работа № 2 Решенные задачи (2 к.н.) загружать сюда Графическую работу № 2 загружать сюдаЗадание ГР № 3Решенные задачи (3 к. н.) загружать сюда Графическую работу № 3 загружать сюдаЗадание Графическая работа № 4 «Проекции с числовыми отметками»Решенные задачи (1 к.н.) загружать сюдаГрафическую работу загружать сюдаЗадание Графическая работа № 1Решенные задачи (2 к.н.) загружать сюдаГрафическую работу № 1 загружать сюдаЗадание Графическая работа № 2Решенные задачи (3 к.н.) загружать сюдаГрафическую работу № 2 загружать сюдаГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Винтовая параГр. работа 4. Эскиз валаГр. работа 5. Эскиз зубчатого колесаГр. работа 6. Эскиз штуцера Гр. работа 7. СоединенияГр. работа 8. ДеталированиеЗадания для должников ГЕОб-20Д1Задание графическая работа № 1Решенные задачи (1 к.н.) загружать сюда Графическую работу № 1 загружать сюдаГрафическая работа № 2 (исходные чертежи)Графическая работа № 3 (задание)Решенные задачи (2 к.н.) загружать сюда Графическую работу № 2 загружать сюдаГрафическую работу № 3 загружать сюда Решенные задачи (3 к.н.) загружать сюда Задание Графическая работа № 3Графическую работу № 3 загружать сюдаЗадание Графическая работа № 4 «Проекции с числовыми отметками»Задание на графическую № 5 работу «Проекционное черчение»Графическую работу № 5 «Проекционное черчение» загружать сюдаГрафическая работа № 1Решенные задачи (1 к.
н.) загружать сюда Графическую работу № 3 загружать сюдаЗадание Графическая работа № 4 «Проекции с числовыми отметками»Решенные задачи (1 к.н.) загружать сюдаГрафическую работу загружать сюдаЗадание Графическая работа № 1Решенные задачи (2 к.н.) загружать сюдаГрафическую работу № 1 загружать сюдаЗадание Графическая работа № 2Решенные задачи (3 к.н.) загружать сюдаГрафическую работу № 2 загружать сюдаГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Винтовая параГр. работа 4. Эскиз валаГр. работа 5. Эскиз зубчатого колесаГр. работа 6. Эскиз штуцера Гр. работа 7. СоединенияГр. работа 8. ДеталированиеЗадания для должников ГЕОб-20Д1Задание графическая работа № 1Решенные задачи (1 к.н.) загружать сюда Графическую работу № 1 загружать сюдаГрафическая работа № 2 (исходные чертежи)Графическая работа № 3 (задание)Решенные задачи (2 к.н.) загружать сюда Графическую работу № 2 загружать сюдаГрафическую работу № 3 загружать сюда Решенные задачи (3 к.н.) загружать сюда Задание Графическая работа № 3Графическую работу № 3 загружать сюдаЗадание Графическая работа № 4 «Проекции с числовыми отметками»Задание на графическую № 5 работу «Проекционное черчение»Графическую работу № 5 «Проекционное черчение» загружать сюдаГрафическая работа № 1Решенные задачи (1 к. н.) загружать сюдаГрафическую работу №1 загружать сюдаРешенные задачи (2 к.н.) загружать сюдаГрафическую работу № 2,3 загружать сюдаЭСКИЗ Решенные задачи (3 к.н.) загружать сюдаГрафическую работу «Эскиз» загружать сюда Задание «Проекционное черчение»Графическую работу «Проекционное черчение» загружать сюдаЗадание Привод* Выполненные чертежи «Привод» загружать сюдаЗадание 3D модель 2* Выполненный чертеж «3D модель 2» загружать сюдаСоединенияГрафическая работа № 1Решенные задачи (1 к.н.) загружать сюдаГрафическую работу №1 загружать сюдаРешенные задачи (2 к.н.) загружать сюдаГрафическую работу № 2, 3 загружать сюдаЭСКИЗРешенные задачи (3 к.н.) загружать сюдаГрафическую работу «Эскиз» загружать сюда Задание «Проекционное черчение» Графическую работу «Проекционное черчение» загружать сюда Занятие НТС-19Т2 15:25 27.05.2020Занятие CМб-19Т1 08:20 21.05.2020Занятие НТС-19Т2 15:25 20.05.2020Лекция 1 Введение. Основные правила выполнения чертежей. Стандарты ЕСКД. Виды конструкторской документации.
н.) загружать сюдаГрафическую работу №1 загружать сюдаРешенные задачи (2 к.н.) загружать сюдаГрафическую работу № 2,3 загружать сюдаЭСКИЗ Решенные задачи (3 к.н.) загружать сюдаГрафическую работу «Эскиз» загружать сюда Задание «Проекционное черчение»Графическую работу «Проекционное черчение» загружать сюдаЗадание Привод* Выполненные чертежи «Привод» загружать сюдаЗадание 3D модель 2* Выполненный чертеж «3D модель 2» загружать сюдаСоединенияГрафическая работа № 1Решенные задачи (1 к.н.) загружать сюдаГрафическую работу №1 загружать сюдаРешенные задачи (2 к.н.) загружать сюдаГрафическую работу № 2, 3 загружать сюдаЭСКИЗРешенные задачи (3 к.н.) загружать сюдаГрафическую работу «Эскиз» загружать сюда Задание «Проекционное черчение» Графическую работу «Проекционное черчение» загружать сюда Занятие НТС-19Т2 15:25 27.05.2020Занятие CМб-19Т1 08:20 21.05.2020Занятие НТС-19Т2 15:25 20.05.2020Лекция 1 Введение. Основные правила выполнения чертежей. Стандарты ЕСКД. Виды конструкторской документации. Лекция 2 Сечения.Лекция 3 Сложные разрезы.Лекция 4 Виды изделий. Разъемные и неразъемные соединения. Выполнение сборочных чертежей.Лекция 5 Выполнение эскизов деталей машин.Лекция 6 Деталирование чертежа общего вида.Курс лекций Инженерная графика презентацияТеоретический материал———ГОСТы, которые Вам помогутВыполненные графические работы и эскизы загружать сюдаСодержание работыРазъемные и неразъемные соединения (теория)Методические указанияВарианты (согласно списку в журнале *у старосты*)Исходный чертежПример выполнения сборочного чертежа «Привод»Пример выполнения спецификации «Привод»Пример выполнения чертежа «Корпус»Пример выполнения спецификации «Корпус»Пустые листы спецификацииВыполненные чертежи по заданию «Разъемные и неразъемн…» загружаем сюдаТеоретический материал——-Методические указания (Эскиз)Выполненные эскизы загружать сюдаВарианты заданияОбразецВыполненный чертеж винтовой пары загружать сюдаПринятые обозначения Лекция 1. Образование проекций. Метод Монжа. Проекции точки и прямой.
Лекция 2 Сечения.Лекция 3 Сложные разрезы.Лекция 4 Виды изделий. Разъемные и неразъемные соединения. Выполнение сборочных чертежей.Лекция 5 Выполнение эскизов деталей машин.Лекция 6 Деталирование чертежа общего вида.Курс лекций Инженерная графика презентацияТеоретический материал———ГОСТы, которые Вам помогутВыполненные графические работы и эскизы загружать сюдаСодержание работыРазъемные и неразъемные соединения (теория)Методические указанияВарианты (согласно списку в журнале *у старосты*)Исходный чертежПример выполнения сборочного чертежа «Привод»Пример выполнения спецификации «Привод»Пример выполнения чертежа «Корпус»Пример выполнения спецификации «Корпус»Пустые листы спецификацииВыполненные чертежи по заданию «Разъемные и неразъемн…» загружаем сюдаТеоретический материал——-Методические указания (Эскиз)Выполненные эскизы загружать сюдаВарианты заданияОбразецВыполненный чертеж винтовой пары загружать сюдаПринятые обозначения Лекция 1. Образование проекций. Метод Монжа. Проекции точки и прямой.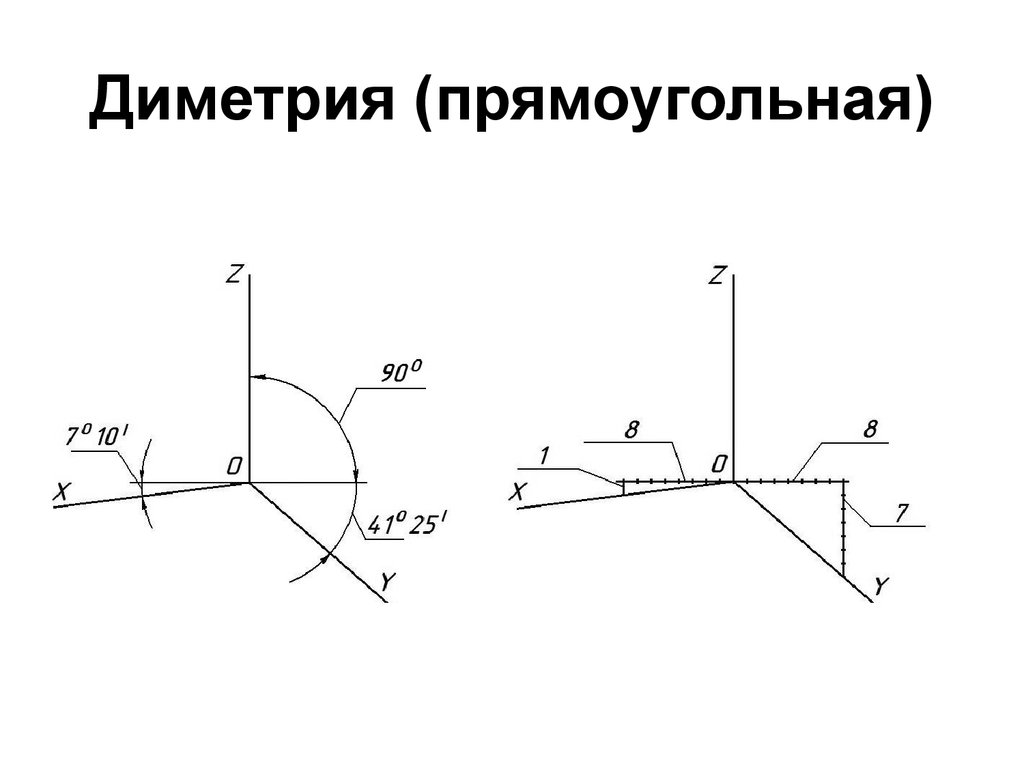 Лекция 2. Проекции плоскоти. Прямая линия и точка в плоскости.Лекция 3. Взаимное положение плоскостей. Взаимное положение прямой и плоскости.Лекция 4. Способы преобразования чертежа. (Метрические задачи)Лекция 5. Кривые линии и поверхности.Лекция 6. Сечение поверхности плоскостью. Построение разверток поверхностей.Лекция 7. Пересечение прямой линии с поверхностями.Лекция 8. Взаимное пересечение поверхностей.Лекция 9 Аксонометрические проекцииВыполненный чертеж загружать сюдаРабочая тетрадь Решенные задачи загружать сюдаКарточки с исходным чертежом на ГР № 1 (по вариантам)Карточки с исходным чертежем на ГР № 2 (по вариантам)Методические указания по выполнению графических работПример выполнения ГР № 1Пример выполнения ГР № 2Загружать на проверку Графическую работа № 1 сюдаЗагружать на проверку Графическую работа № 2 сюдаТЕСТТеоретический материал Инженерная графика (инженерная и компьютерная графика)ГОСТы, которые Вам помогутГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр.
Лекция 2. Проекции плоскоти. Прямая линия и точка в плоскости.Лекция 3. Взаимное положение плоскостей. Взаимное положение прямой и плоскости.Лекция 4. Способы преобразования чертежа. (Метрические задачи)Лекция 5. Кривые линии и поверхности.Лекция 6. Сечение поверхности плоскостью. Построение разверток поверхностей.Лекция 7. Пересечение прямой линии с поверхностями.Лекция 8. Взаимное пересечение поверхностей.Лекция 9 Аксонометрические проекцииВыполненный чертеж загружать сюдаРабочая тетрадь Решенные задачи загружать сюдаКарточки с исходным чертежом на ГР № 1 (по вариантам)Карточки с исходным чертежем на ГР № 2 (по вариантам)Методические указания по выполнению графических работПример выполнения ГР № 1Пример выполнения ГР № 2Загружать на проверку Графическую работа № 1 сюдаЗагружать на проверку Графическую работа № 2 сюдаТЕСТТеоретический материал Инженерная графика (инженерная и компьютерная графика)ГОСТы, которые Вам помогутГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр.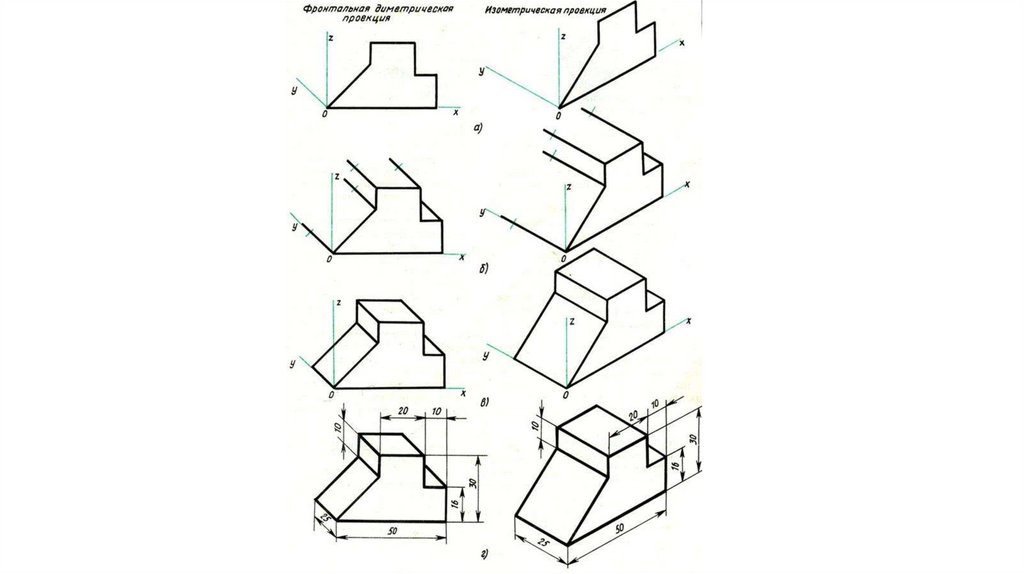 работа 3. Винтовая параГр. работа 4. Эскиз валаТеоретический материал по теме (компьютерная графика)Разъемные и неразъемные соединения (теория)Исходный чертежПример выполнения сборочного чертежа «Привод»Пример выполнения спецификации «Привод»Выполненные чертежи Привода загружать сюдаВыполненный чертеж редуктора загружать сюдаГр. работа 6. Эскиз штуцера (копия)Лекция 1 Введение. Основные правила выполнения чертежей. Стандарты ЕСКД. Виды конструкторской документации.Теоретический материал—ГОСТы, которые Вам помогутГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Винтовая параГр. работа 4. Эскиз валаТеоретический материал по теме (компьютерная графика)ЗАДАНИЕ (исходный чертеж)Выполненный чертеж поршня загружать сюдаВилкаВкладышВыполненный чертеж поршня загружать сюдаЛекция 1 Введение. Основные правила выполнения чертежей. Стандарты ЕСКД. Виды конструкторской документации.Лекция 2 Сечения.Лекция 3 Сложные разрезы.Лекция 4 Виды изделий. Разъемные и неразъемные соединения.
работа 3. Винтовая параГр. работа 4. Эскиз валаТеоретический материал по теме (компьютерная графика)Разъемные и неразъемные соединения (теория)Исходный чертежПример выполнения сборочного чертежа «Привод»Пример выполнения спецификации «Привод»Выполненные чертежи Привода загружать сюдаВыполненный чертеж редуктора загружать сюдаГр. работа 6. Эскиз штуцера (копия)Лекция 1 Введение. Основные правила выполнения чертежей. Стандарты ЕСКД. Виды конструкторской документации.Теоретический материал—ГОСТы, которые Вам помогутГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа 3. Винтовая параГр. работа 4. Эскиз валаТеоретический материал по теме (компьютерная графика)ЗАДАНИЕ (исходный чертеж)Выполненный чертеж поршня загружать сюдаВилкаВкладышВыполненный чертеж поршня загружать сюдаЛекция 1 Введение. Основные правила выполнения чертежей. Стандарты ЕСКД. Виды конструкторской документации.Лекция 2 Сечения.Лекция 3 Сложные разрезы.Лекция 4 Виды изделий. Разъемные и неразъемные соединения.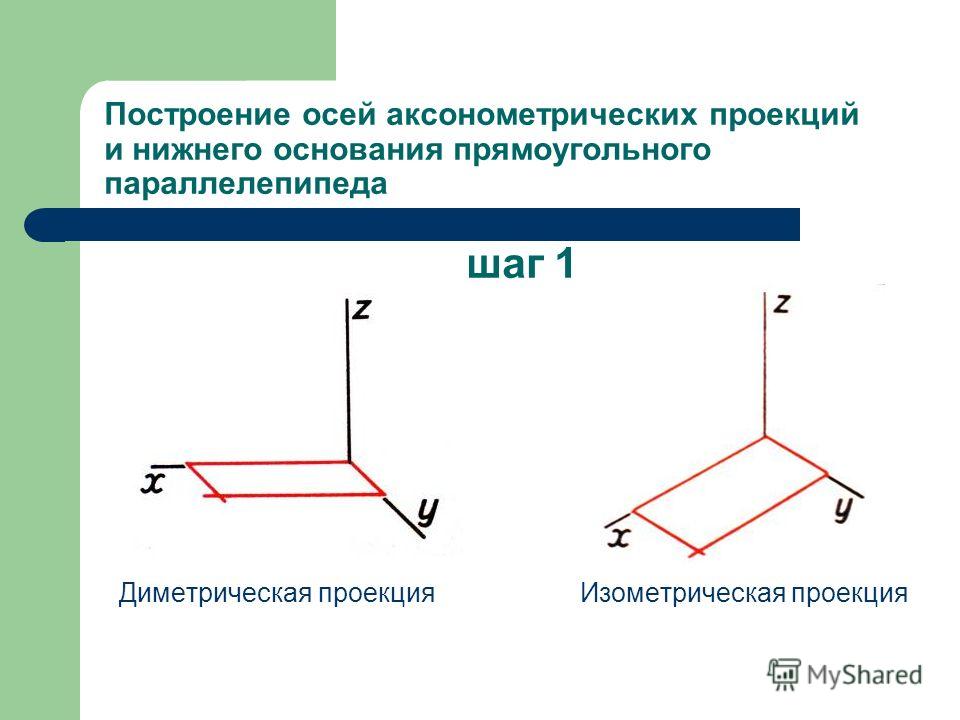 Выполнение сборочных чертежей.Лекция 5 Выполнение эскизов деталей машин.Лекция 6 Деталирование чертежа общего вида.Курс лекций Инженерная графика презентацияТеоретический материал—-ГОСТы, которые Вам помогутГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа № 3 ЭСКИЗЛекция 1 Введение. Основные правила выполнения чертежей. Стандарты ЕСКД. Виды конструкторской документации.Лекция 2 Сечения.Лекция 3 Сложные разрезы.Лекция 4 Виды изделий. Разъемные и неразъемные соединения. Выполнение сборочных чертежей.Лекция 5 Выполнение эскизов деталей машин.Лекция 6 Деталирование чертежа общего вида.Курс лекций Инженерная графика презентацияТеоретический материал——-ГОСТы, которые Вам помогутВыполненные графические работы и эскизы загружать сюдаСодержание работыРазъемные и неразъемные соединения (теория)Методические указанияВарианты (согласно списку в журнале *у старосты*)Исходный чертежПример выполнения сборочного чертежа «Привод»Пример выполнения спецификации «Привод»Пример выполнения чертежа «Корпус»Пример выполнения спецификации «Корпус»Пустые листы спецификацииВыполненные чертежи по заданию «Разъемные и неразъемн.
Выполнение сборочных чертежей.Лекция 5 Выполнение эскизов деталей машин.Лекция 6 Деталирование чертежа общего вида.Курс лекций Инженерная графика презентацияТеоретический материал—-ГОСТы, которые Вам помогутГр. работа 1. Проекционное черчениеГр. работа 2. Проекционное черчениеГр. работа № 3 ЭСКИЗЛекция 1 Введение. Основные правила выполнения чертежей. Стандарты ЕСКД. Виды конструкторской документации.Лекция 2 Сечения.Лекция 3 Сложные разрезы.Лекция 4 Виды изделий. Разъемные и неразъемные соединения. Выполнение сборочных чертежей.Лекция 5 Выполнение эскизов деталей машин.Лекция 6 Деталирование чертежа общего вида.Курс лекций Инженерная графика презентацияТеоретический материал——-ГОСТы, которые Вам помогутВыполненные графические работы и эскизы загружать сюдаСодержание работыРазъемные и неразъемные соединения (теория)Методические указанияВарианты (согласно списку в журнале *у старосты*)Исходный чертежПример выполнения сборочного чертежа «Привод»Пример выполнения спецификации «Привод»Пример выполнения чертежа «Корпус»Пример выполнения спецификации «Корпус»Пустые листы спецификацииВыполненные чертежи по заданию «Разъемные и неразъемн. ..» загружаем сюдаТеоретический материал——Методические указания (Эскиз)Выполненные эскизы загружать сюдаПоследовательность выполнения работыТеоретический материал——Образец (пример)Задания по вариантамВыполненный чертеж железобетонной конструкции загружать сюдаЗанятие 13:45 27.05.2020Занятие 13:45 20.05.2020Занятие 15:25 15.05.2020Теоретический материал по теме (компьютерная графика)ВилкаВкладышВыполненные чертежи Вилки и Вкладыша загружать сюдаМетодические указания к работеИсходные файлыВыполненную работу загружать сюдаТеоретический материал по теме (компьютерная графика)ВилкаВкладышВыполненные чертежи Вилки и Вкладыша загружать сюдаМетодические указания к работеИсходные чертежи -Выполненную работу загружать сюдаЗАДАНИЕ (инженерная графика)Теоретический материал (инженерная графика)Задание № 1 загружать сюдаЗадание № 2 загружать сюдаЗадание № 3 загружать сюдаЗадание № 4 загружать сюдаТеоретический материал (компьютерная графика)Деталь № 1Деталь № 2Деталь № 3Деталь № 1 загружать сюдаДеталь № 2 загружать сюдаДеталь № 3 загружать сюдаЗанятия 1-4 (16.
..» загружаем сюдаТеоретический материал——Методические указания (Эскиз)Выполненные эскизы загружать сюдаПоследовательность выполнения работыТеоретический материал——Образец (пример)Задания по вариантамВыполненный чертеж железобетонной конструкции загружать сюдаЗанятие 13:45 27.05.2020Занятие 13:45 20.05.2020Занятие 15:25 15.05.2020Теоретический материал по теме (компьютерная графика)ВилкаВкладышВыполненные чертежи Вилки и Вкладыша загружать сюдаМетодические указания к работеИсходные файлыВыполненную работу загружать сюдаТеоретический материал по теме (компьютерная графика)ВилкаВкладышВыполненные чертежи Вилки и Вкладыша загружать сюдаМетодические указания к работеИсходные чертежи -Выполненную работу загружать сюдаЗАДАНИЕ (инженерная графика)Теоретический материал (инженерная графика)Задание № 1 загружать сюдаЗадание № 2 загружать сюдаЗадание № 3 загружать сюдаЗадание № 4 загружать сюдаТеоретический материал (компьютерная графика)Деталь № 1Деталь № 2Деталь № 3Деталь № 1 загружать сюдаДеталь № 2 загружать сюдаДеталь № 3 загружать сюдаЗанятия 1-4 (16.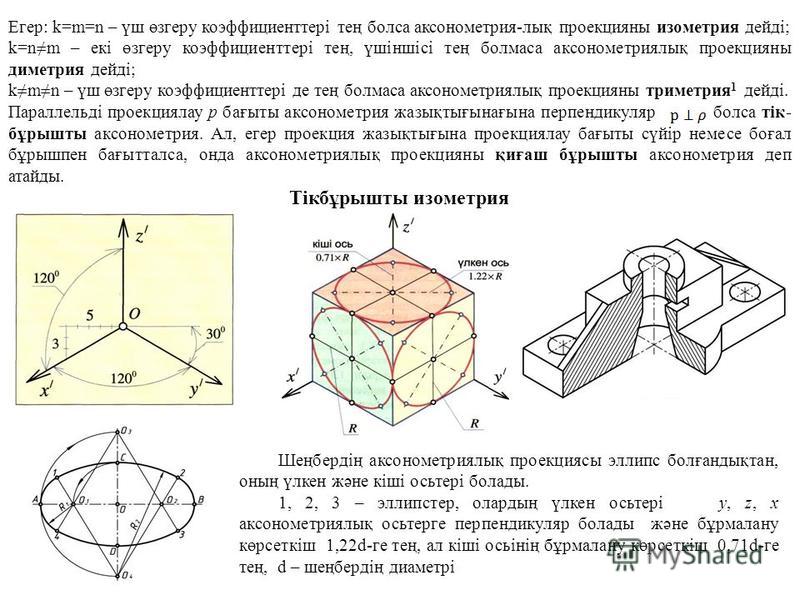 06.2020 15:25 — 21:50)Занятия 5-6 (20.06.2020 13:45 — 16:55) ЭКЗАМЕНТеоретический материал Начертательная геометрияУказания к выполнению графических работРешения задачОтправка выполненных заданийТеоретический материал Начертательная геометрияУказания к выполнению графических работРешения задачОтправка выполненных заданийЧертеж для занятия 13.11.2020ЗАДАНИЯ-Теоретический материал по теме (компьютерная графика)* Выполненные чертежи (1 файлом) загружать сюдаКонтроль выполнения ЗАДАНИЙ
06.2020 15:25 — 21:50)Занятия 5-6 (20.06.2020 13:45 — 16:55) ЭКЗАМЕНТеоретический материал Начертательная геометрияУказания к выполнению графических работРешения задачОтправка выполненных заданийТеоретический материал Начертательная геометрияУказания к выполнению графических работРешения задачОтправка выполненных заданийЧертеж для занятия 13.11.2020ЗАДАНИЯ-Теоретический материал по теме (компьютерная графика)* Выполненные чертежи (1 файлом) загружать сюдаКонтроль выполнения ЗАДАНИЙ
- R
- A
- A
- A
(always?)
Skip StatisticsАксонометрические проекции – технический обзор
Перейти к основному содержанию (пропустить меню навигации)
Пожалуйста, включите JavaScript для отображения математики на этой странице.
Реферат
В этой статье обсуждается, как аксонометрические проекции могут использоваться в компьютерных технологиях.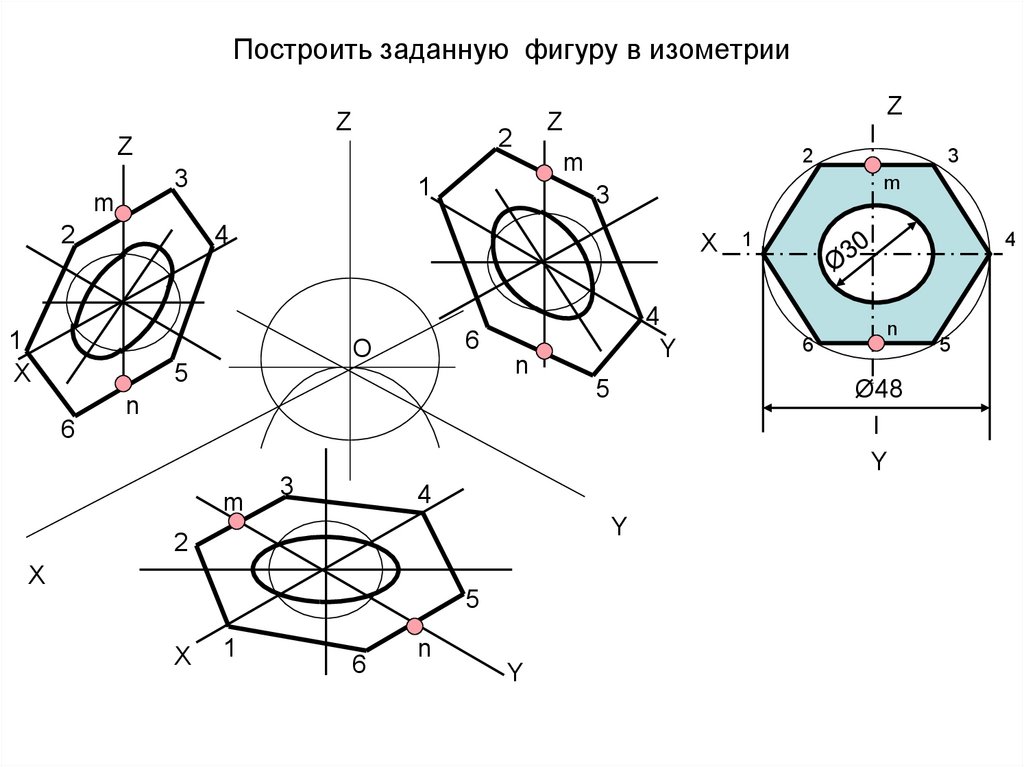 графика, мультимедийные приложения и компьютерные игры. Он сравнивает
аксонометрическая проекция, или параллельная перспектива , на линейную
перспектива, перечисляет основные свойства и решает некоторые вопросы реализации
Детали. Более ранняя версия этой статьи включена в книгу
«Продвинутое программирование игр».
графика, мультимедийные приложения и компьютерные игры. Он сравнивает
аксонометрическая проекция, или параллельная перспектива , на линейную
перспектива, перечисляет основные свойства и решает некоторые вопросы реализации
Детали. Более ранняя версия этой статьи включена в книгу
«Продвинутое программирование игр».
Основное внимание в этой статье уделяется изометрическим и диметрическим проекциям. наиболее широко используемые разновидности аксонометрической проекции. Эта бумага также представляет две диметрические проекции, которые подходят для (плиточного) компьютера графика.
Введение — первая попытка
В западном мире мы привыкли к линейной перспективе, которая
пытается добиться визуального реализма в картинах трехмерных сред.
Линейная перспектива, которая совершенствовалась на протяжении 17 -й век в
Европе, основан на евклидовой оптике: глаз как точечный объект, улавливающий
прямые световые лучи и воспринимает только цвет, интенсивность и
угол лучей, а не их длина.
В восточном искусстве развилась еще одна перспектива: «китайская перспектива». была неотъемлемой частью классической живописи на свитках (на самом деле, «китайской перспектива» немного неправильное название, потому что та же самая перспектива также использовалась в искусстве Японии и других восточных стран). Типичный китайский свиток картина имела размер примерно 40 сантиметров в высоту на несколько метров широкий. Картину рассматривают, развернув ее (справа налево). на столе сегментами шириной около 60 сантиметров. Китайский свиток картины показывают развитие во времени — форма «нарративного искусства», напротив к картинам, которые были сделаны в Европе в то время, которые показывают «ситуацию» а не разработка.
Для этих картин на свитках китайским художникам нужна была перспектива, которая
не имел явных точек схода; каждая сцена картины свитка была бы
видны по отдельности, а точка схода, находящаяся за пределами области просмотра, создает
дезориентированный взгляд на сцену.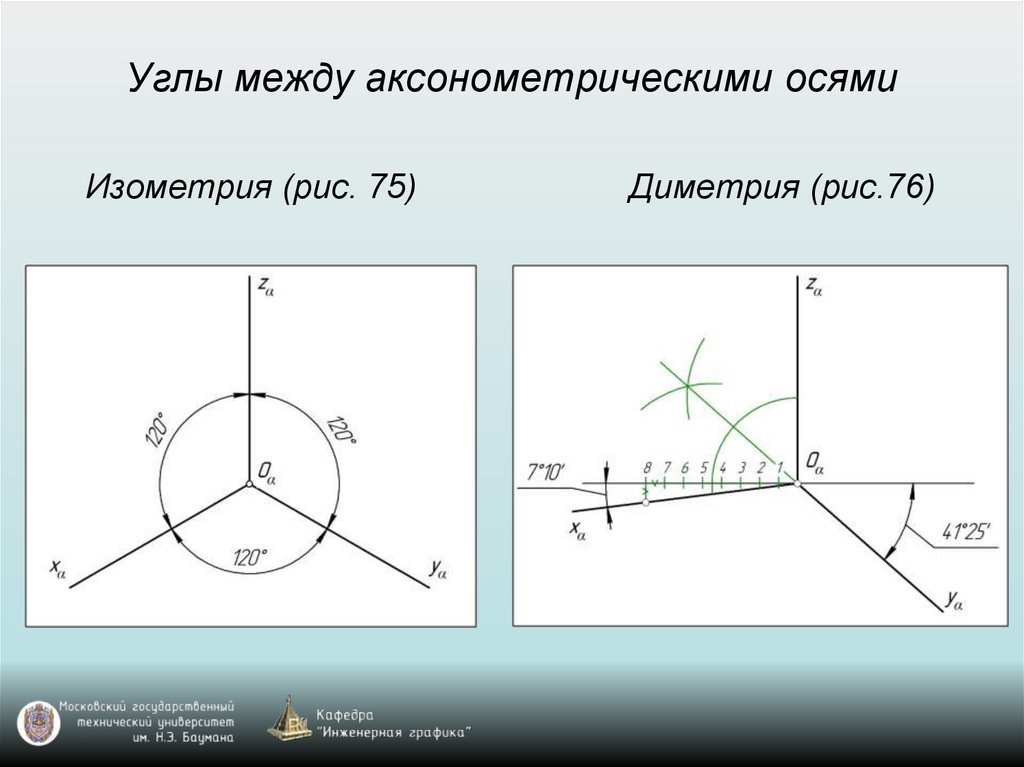 (По той же причине китайский свиток
картины обычно не имеют явного источника света или отбрасывают тени.)
Китайские художники решили эту проблему, нарисовав линии вдоль оси Z в виде
параллельные линии в живописи свитка. Это приводит к размещению
горизонт на воображаемой линии, бесконечно высоко над картиной.
аксонометрическая проекция — это технический термин для класса перспектив,
которому также принадлежит китайская параллельная перспектива. Эти перспективы
не только отсутствие точки схода, но и несколько других, в основном полезных,
характеристики. Они обсуждаются ниже.
(По той же причине китайский свиток
картины обычно не имеют явного источника света или отбрасывают тени.)
Китайские художники решили эту проблему, нарисовав линии вдоль оси Z в виде
параллельные линии в живописи свитка. Это приводит к размещению
горизонт на воображаемой линии, бесконечно высоко над картиной.
аксонометрическая проекция — это технический термин для класса перспектив,
которому также принадлежит китайская параллельная перспектива. Эти перспективы
не только отсутствие точки схода, но и несколько других, в основном полезных,
характеристики. Они обсуждаются ниже.
Свиток
Введение — вторая попытка
Технические чертежи должны быть точными, точными и однозначными. Технические
чертежи предназначены для инженеров и монтажников. Национальные институты официально
стандартизировать технические чертежи, чтобы плотник мог построить конкретный
стул, который придумал дизайнер мебели. Технические чертежи – это средство
общение, для тех, кто может это понять.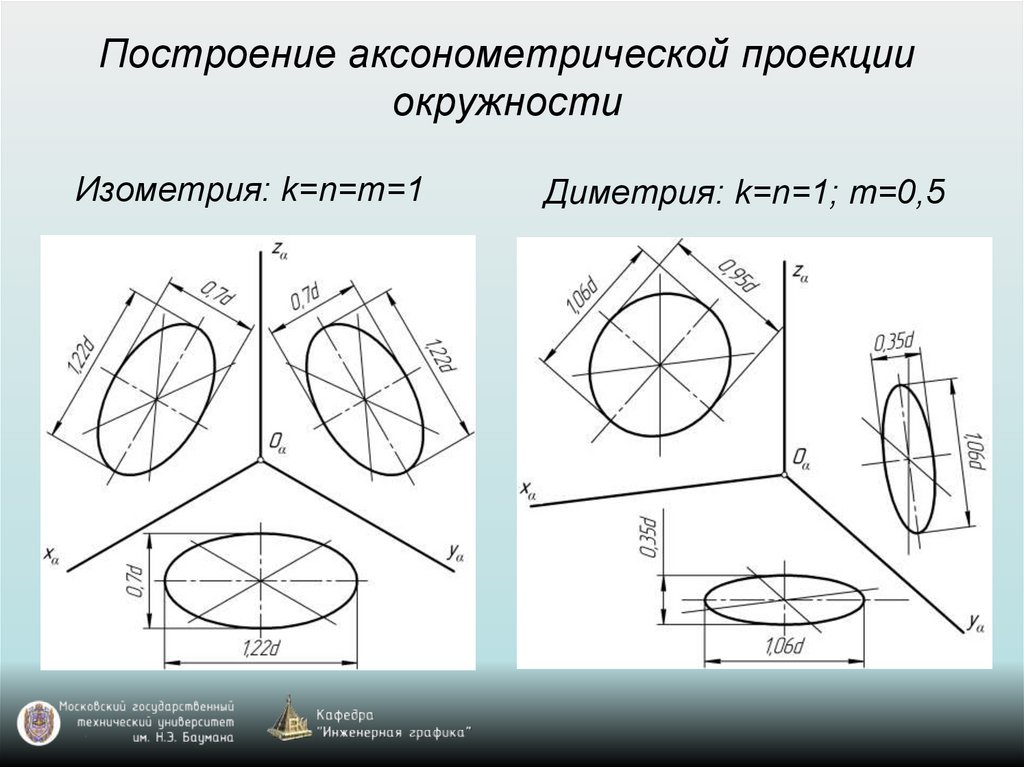
Если бы мир был населен инженерами, все остальное не имело бы значения — но это не так, и инженеры (и монтажники, и плотники) должны общаться с менеджерами и клиентами. Проблема, конечно, в том, что технические рисунки трудно разобрать непосвященному. Хотя они показывают объекта под шестью углами, все эти углы нереалистичны: прямо спереди, прямо сверху и т.д. Что надо передать общая форма объекта представляет собой перспективный рисунок, на котором показаны три сторон куба одновременно.
На данный момент следующий вопрос: как? Инженеры такие, какие они есть, они хотят простой метод, который не теряет большую часть точности оригинала рисунков и не требующих художественных навыков. Также обратите внимание, что в большинстве случаях объект, который вы должны нарисовать, еще не существует, поэтому обычно вы не можете взгляните на объект, чтобы понять его пропорции. Это делает это почти невозможно правильно расположить точки схода и оценить ракурс.
Компромисс, который стал известен как аксонометрия, представляет собой технику рисования
где ортогональные оси x, y и z (трехмерного) мирового пространства равны
проецируется на (неортогональные) оси на бумаге.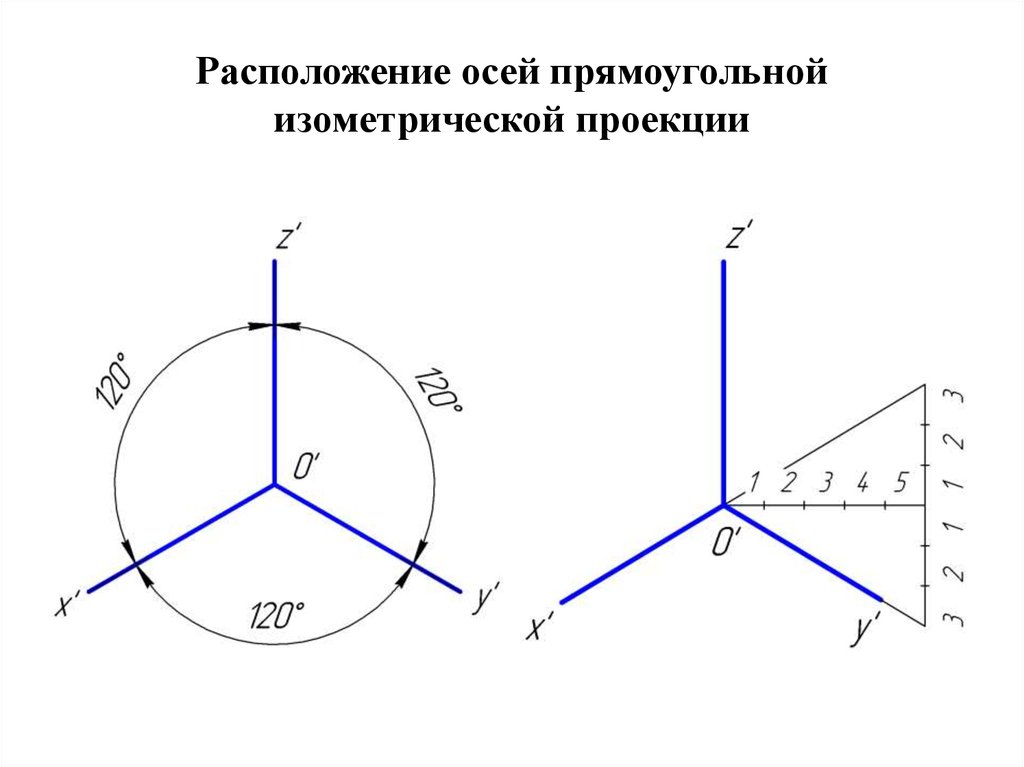 В проекции ось Y
обычно остается вертикальной осью, ось z скошена, а ось x может
либо быть горизонтальным, как на рисунке справа, либо также быть наклонным.
Более важным свойством аксонометрии является ее фиксированное соотношение между размерами
объектов в мировом пространстве и в проекционном пространстве, независимо от
положения объектов в проецируемом пространстве. В линейной перспективе объекты
становятся меньше, когда они удаляются дальше; не так в аксонометрической перспективе.
Это означает, что вы можете измерить размер объекта аксонометрического чертежа.
и знать, насколько велик реальный объект (вам нужно знать масштаб чертежа
и свойства проекции, но не более того), то, что не может
быть выполнено с линейной перспективой. Это приводит к названию проекции:
слово «аксонометрия» означает «измеряемый от осей».
В проекции ось Y
обычно остается вертикальной осью, ось z скошена, а ось x может
либо быть горизонтальным, как на рисунке справа, либо также быть наклонным.
Более важным свойством аксонометрии является ее фиксированное соотношение между размерами
объектов в мировом пространстве и в проекционном пространстве, независимо от
положения объектов в проецируемом пространстве. В линейной перспективе объекты
становятся меньше, когда они удаляются дальше; не так в аксонометрической перспективе.
Это означает, что вы можете измерить размер объекта аксонометрического чертежа.
и знать, насколько велик реальный объект (вам нужно знать масштаб чертежа
и свойства проекции, но не более того), то, что не может
быть выполнено с линейной перспективой. Это приводит к названию проекции:
слово «аксонометрия» означает «измеряемый от осей».
Хотя существует бесчисленное множество возможных аксонометрических проекций, только две из них
стандартизированы для технических чертежей. Они подробно описаны ниже.
Введение — третья попытка
Компьютерные игры традиционно изобилуют графикой и анимация. На самом деле игры классифицируются по типу графики. они использовали. Два популярных типа игр — это «игры-платформеры», в которых вы смотреть со стороны, а «настольные игры» откуда смотришь в основном выше. Эти игры также объединяет то, что они часто используют плитки для построения «мир» из. Учитывая это сходство и учитывая тупость нереалистичные точки зрения как платформеров, так и настольных игр, попытка поиск компромисса между этими крайними точками зрения является логичным следующим шаг.
Итак, что нужно сделать, это взять доску настольной игры, масштабировать ее высоту (она станет
ось z для «глубины») и наклоните ее так, чтобы эта ось z на дисплее компьютера
представляет собой диагональную линию. Для лучшего внешнего вида вы также можете наклонить ось X.
(новый) ось Y остается вертикальной. Это все, что нужно, при условии, что вы получаете
пропорции масштабирования и наклона вправо.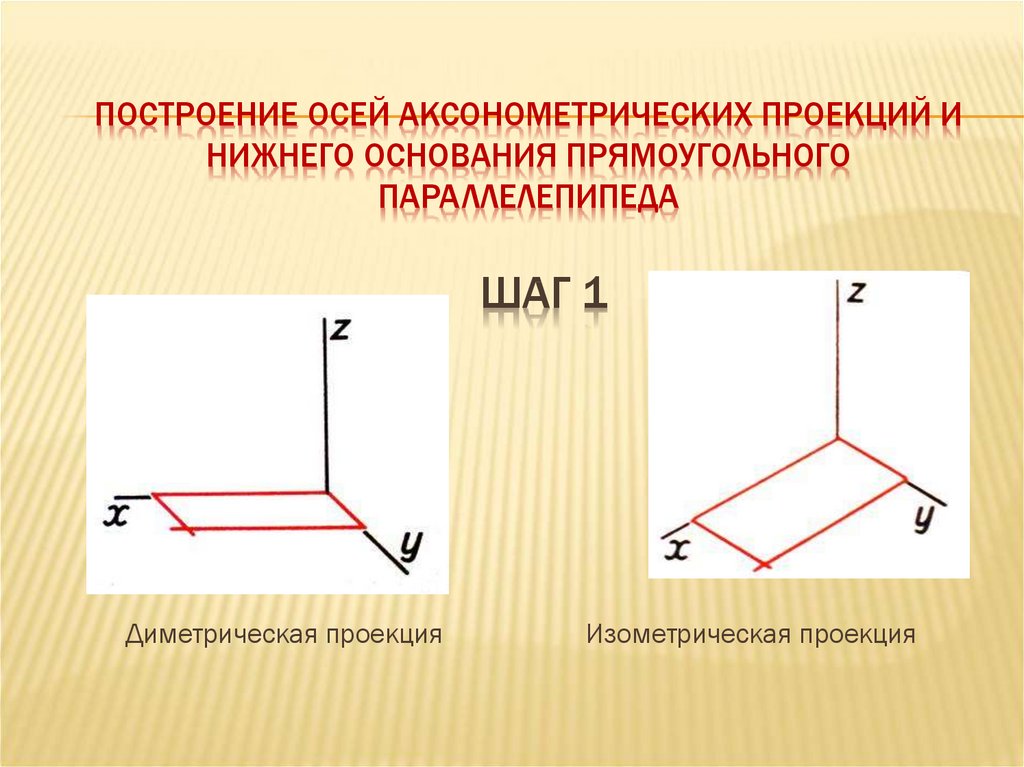
Из-за грубости цифровых координат и требования, края плиток (шахматной доски) должны точно совпадать, без каких-либо пикселей перекрытия или промежутки, углы наклона и коэффициенты масштабирования, которые разработчики игр использование является приближением к визуально оптимальным пропорциям. Один из упрощение, которое сделали разработчики игр, заключается в использовании аксонометрического проекция, в которой единица вдоль оси имеет одинаковую длину для всех трех оси. То есть каждая ось имеет одинаковую метрику; следовательно, проекция называется «изометрический». Аксонометрические проекции и тайловые изображения не обязательно связаны. Но большинство компьютерных игр, использующих изометрическую перспективу также используйте изображения на основе плитки.
А теперь, вперед…
Три вопроса, которые занимали меня при планировании этой статьи:
- Каковы общие (или пропорциональные) аксонометрические проекции и как убедительно каждый выглядит?
- Под какими углами смотреть на доску в аксонометрической проекции? это
заманчиво использовать визуализированные трехмерные объекты на аксонометрической карте в качестве спрайтов.
 К
указать положение и ориентацию «камеры» по отношению к
объекта, вам нужно будет знать внутренние углы аксонометрической карты
что вы используете.
К
указать положение и ориентацию «камеры» по отношению к
объекта, вам нужно будет знать внутренние углы аксонометрической карты
что вы используете. - Что вообще пишут во введении?
Целью этой статьи является представление двух общих аксонометрических проекций, изометрическая проекция (кратко представленная выше) и диметрическая проекции и дать ответ на поставленные выше вопросы.
Я намеренно пренебрежение правильными определениями терминов и категорий; аксонометрический проекции и «косые параллельные» проекции настолько похожи, что я просто объединили их под термином «аксонометрия». В любом случае косая параллель проекцию следует рассматривать как частный случай диметрики (иногда изометрическая) проекция. Косые параллельные проекции, кавалерные проекции, кабинетные проекции, военные проекции, аксонометрические проекции,… плюс ça изменение, плюс c’est la même выбрал.
Подводя итог, основные свойства аксонометрических проекций:
- Нет точек схода.
 Это позволяет прокручивать большое изображение под
видового экрана и иметь одинаковую перспективу в любой точке. В случае
мозаичные изображения, изображение строится на лету и не требует
физические границы или края.
Это позволяет прокручивать большое изображение под
видового экрана и иметь одинаковую перспективу в любой точке. В случае
мозаичные изображения, изображение строится на лету и не требует
физические границы или края. - Прямые, параллельные в трехмерном пространстве, остаются параллельными и в 2-х мерная картинка. Это отличается от linear. перспектива , где параллельные линии вдоль оси z в трехмерном космический коллапс в единую точку схода на горизонте в 2-х мерная картинка.
- Удаленные объекты имеют тот же размер, что и близкие; объекты не становятся меньше по мере удаления от зрителя. Если вы знаете масштаб осей, можно измерить размеры (ширину, высоту, длину, глубины) объекта прямо с картинки, вне зависимости от его положения на ось Z; отсюда и название аксонометрия .
- Аксонометрические проекции стандартизированы для технических чертежей. Эти
стандарты оптимизированы для простоты использования по сравнению с визуальным реализмом. Даже если ты
решите отклониться от стандартов, используйте их как источник вдохновения.
 Два
прогнозы, стандартизированные институтом стандартизации ISO,
представлены в этой статье.
Два
прогнозы, стандартизированные институтом стандартизации ISO,
представлены в этой статье.
Одно слово предостережения относительно любого из приведенных ниже рисунков и проекции углы, которые представляют эти фигуры: углы только приблизительны. Я рассчитал углы, исходя из форм ромбов одного или двух сторон спроецированного куба. Эти расчеты были бы справедливы, если бы перспективные проекции не исказили исходный куб. Теперь пропорции большинство проекций были выбраны так, чтобы свести к минимуму искажения (особенно те, стандартизированы для технических чертежей), но тем не менее не являются точно . Углы, которые я даю, также являются хорошим приближением, но не более того.
Изометрическая проекция
В изометрической проекции оси x, y и z имеют одинаковую метрику: a
единица (скажем, сантиметр) по оси абсцисс одинаково длинна по оси у и
оси Z. Другими словами, если вы визуализируете каркасный куб, все ребра в
2-мерные изображения имеют одинаковую длину.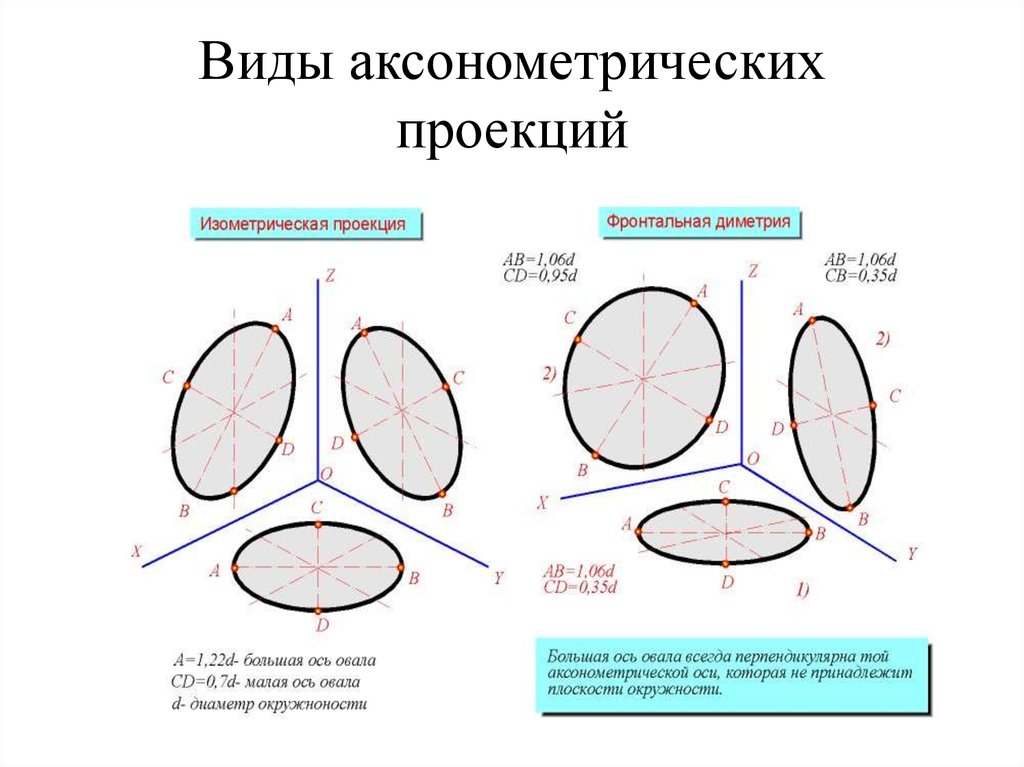 Еще одно свойство изометрии
проекции заключается в том, что спроецированный каркасный куб также симметричен. Все стороны
спроецированного куба являются ромбами.
Еще одно свойство изометрии
проекции заключается в том, что спроецированный каркасный куб также симметричен. Все стороны
спроецированного куба являются ромбами.
NEN 2536 описывает изометрическую проекцию, которая симметричны относительно вертикальной оси; угол между осями x и y, а между осями z и y — 60 градусов. Проекция показывает три стороны куба, а поверхности каждой стороны равны. Угол 30° между оси x и z и «горизонт» удобны для технических чертежей, потому что синус 30° равен ½. Эта проекция объясняется Уильям Фариш, опубликовавший трактат об этом в 1822 году (ссылка: Ян Крикке). NEN 2536 был пересмотрен и переиздан. в качестве международного стандарта ISO 5456-3.
На рисунке ниже показан куб в изометрической проекции, как определено
ISO 5456-3. Первый объект слева на рисунке — куб без украшений; в
второй объект — это тот же куб с аннотациями углов и мер вокруг него.
Третий и четвертый рисунки представляют собой вид сверху и сбоку в перспективе.
сцену, и они дают положение камеры, которое соответствует перспективному виду.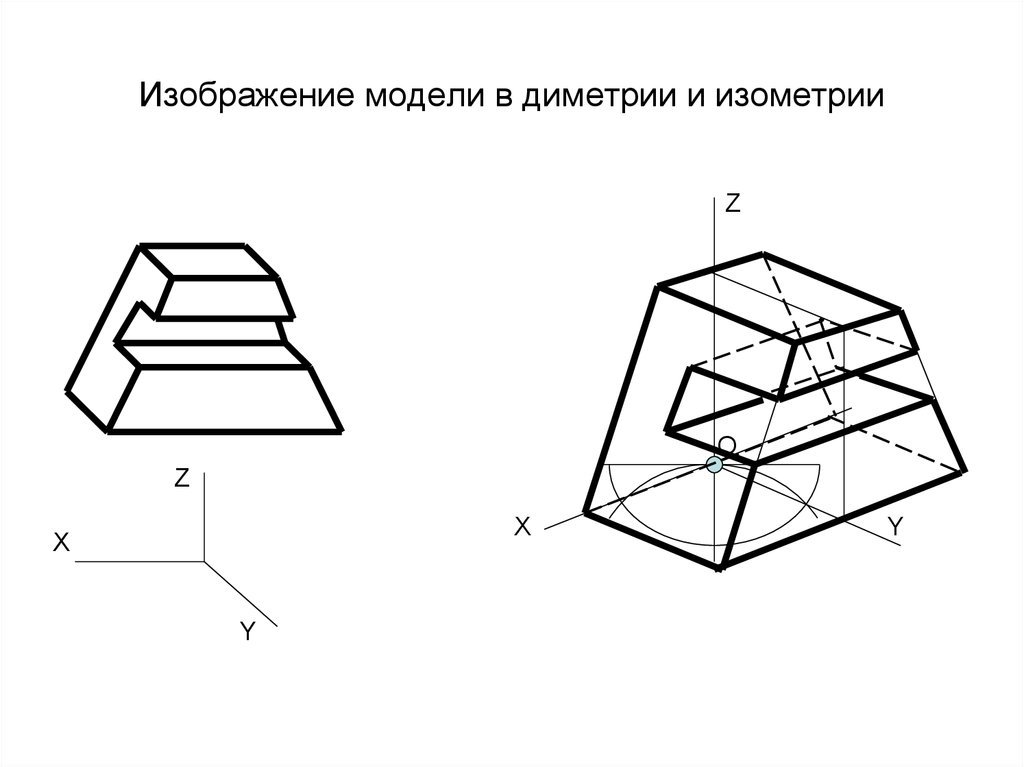 положение камеры — это то, что вы вводите в 3D-рендерер (или трассировщик лучей) для
создайте спрайты или тайлы для изометрической проекции.
положение камеры — это то, что вы вводите в 3D-рендерер (или трассировщик лучей) для
создайте спрайты или тайлы для изометрической проекции.
Изометрическая проекция 30° (NEN/ISO)
Компьютерные игры с изометрическими картами часто основаны на тайлах. Для изготовления плитки
соответствия, геймдизайнер должен учитывать, как прочерчены диагональные линии
дискретными шагами (Bresenham
и все такое). Как оказалось, очередь на 30
градусов (синус равен 0,5) дает слишком неравномерные шаги. Линия в
угол, где тангенс равен 0,5 имеет ли хороший правильный узор: два
шаг вправо, шаг вверх. Таким образом, изометрическая проекция, используемая большинством
игры наклоняют оси x и z примерно на 27 градусов (точный угол
«арктангенс (0,5)»). Кстати, поскольку тангенс угла
ромб равен 0,5, ширина ромба вдвое больше его высоты. Вот почему
во многих источниках упоминается масштаб 1: 2 для изометрической перспективы. (Чтобы сделать
ребра ромбов совпадают, ширина ромба должна быть кратна
четыре пикселя, а высота должна быть на один пиксель меньше ½ ширины. В других
Другими словами, отношение высоты к ширине ромба обычно не равно 9.0011 ровно 1:2,
а скорее около 1:2.1. Это никак не влияет на принципы
изометрическая перспектива.)
В других
Другими словами, отношение высоты к ширине ромба обычно не равно 9.0011 ровно 1:2,
а скорее около 1:2.1. Это никак не влияет на принципы
изометрическая перспектива.)
Опять же, на рисунке ниже показано, как выглядит эта изометрическая проекция как.
Изометрическая проекция 1:2
Две упомянутые выше изометрические проекции «искажают» все грани примера куб. В приложениях, где наиболее важными гранями являются горизонтальные, например, в приложениях, где карты или планы этажей имеют первостепенное значение, другой распространена изометрическая проекция. Называется «военная» проекция, наверное из-за его происхождения или использования.
«Военная» проекция
В военной проекции углы осей x и z составляют 45°,
это означает, что угол между осью x и осью z составляет 90°.
То есть плоскость x-z имеет наклон , а не . это повернутый
45°, однако.
На виде сбоку военного выступа (график справа) у меня есть указано, что угол обзора вниз на объект (куб) примерно 45°. Военная проекция дает довольно неточную перспектива — в числовом выражении, и схема, которую я использовал для расчета углов не работает на этой проекции. Таким образом, этот угол является оценка, основанная на концепции симметрии, а не на визуальной точности.
Диметрическая проекция
В диметрической проекции одна из трех осей имеет другой масштаб чем два других. На практике масштабируемой осью является ось z и, следовательно, куб, нарисованный в диметрической проекции, не является симметричным рисунком (как в изометрическая проекция).
Диметрические проекции более гибкие, чем изометрические, т.к.
вы меняете масштабный коэффициент (и соответственно настраиваете другие параметры).
асимметрия в диметрической проекции также дает вам дополнительную
угол для игры. С художественной точки зрения мне также нравятся диметрические
проекции лучше, чем изометрические проекции, из-за асимметрии.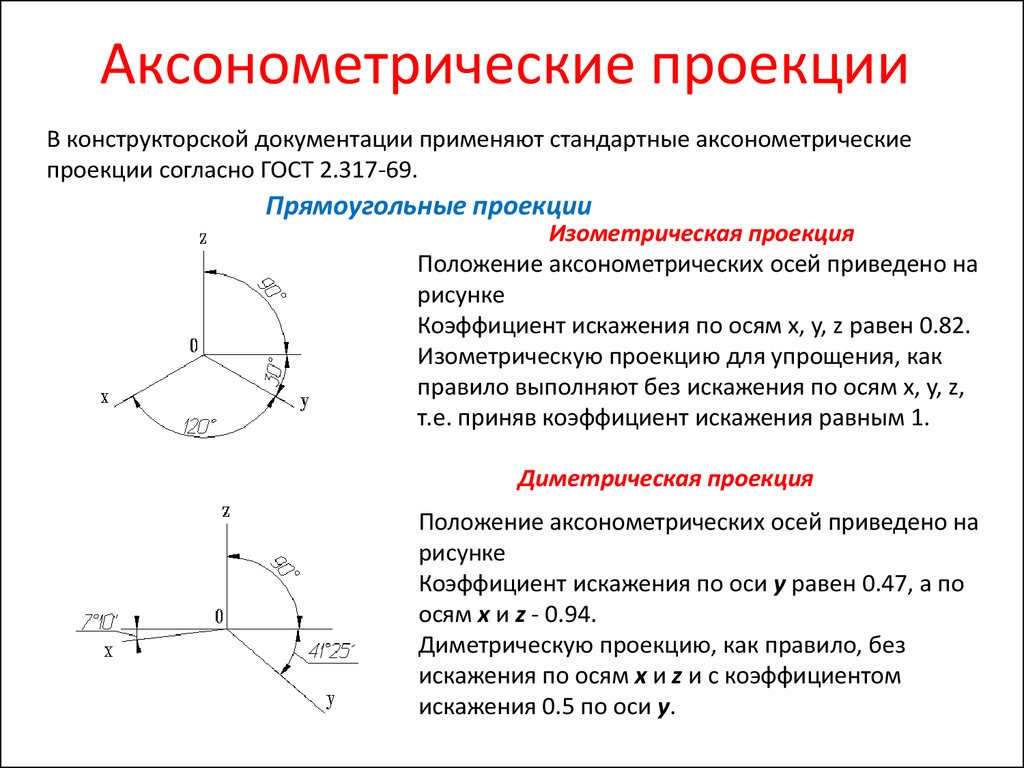 Или же
скорее, симметрия изометрической проекции придает сцене вид
«искусственный» или сюрреалистический. Еще одним преимуществом является то, что в компьютере
игра, что если вы отразите графику диметрической проекции, вы
глядя на сцену в новом, « свежий «, перспектива, в то время как
основные вычисления для системы координат остаются прежними.
Или же
скорее, симметрия изометрической проекции придает сцене вид
«искусственный» или сюрреалистический. Еще одним преимуществом является то, что в компьютере
игра, что если вы отразите графику диметрической проекции, вы
глядя на сцену в новом, « свежий «, перспектива, в то время как
основные вычисления для системы координат остаются прежними.
NEN 2536 также представляет диметрическую проекцию для технические рисунки. Это кратко показано на рисунке ниже. Любое расстояние вдоль ось z (нарисованная под углом 42°) масштабируется с коэффициентом ½.
Проекция 42°/7° (NEN/ISO)
Во введении упоминались китайские свитки, и мне потребовалось некоторое время. взяв метрики (репродукции) двух картин на свитках. Проекция отличается на этих двух картинах, и я предполагаю, что существует больше вариаций. Во всех виденных мною до сих пор картинах на свитках заметно то, что ось x остается горизонтальной.
Первая прокрутка проецирует ось Z под довольно малым углом
(примерно 30 градусов). В результате вид в перспективе,
расчетно далеко не точно. Причины, по которым мы все еще видим
3-мерный куб, а не какой-то плоский многоугольник, заключается в том, что угол
в «виде сбоку» перспективного вида тоже мало и потому что наш визуальный
система вполне снисходительна к ошибкам в коррекции перспективы.
В результате вид в перспективе,
расчетно далеко не точно. Причины, по которым мы все еще видим
3-мерный куб, а не какой-то плоский многоугольник, заключается в том, что угол
в «виде сбоку» перспективного вида тоже мало и потому что наш визуальный
система вполне снисходительна к ошибкам в коррекции перспективы.
Масштаб оси Z не может быть точно определен по прокрутке картина. По моей оценке, ось Z на картине (с углом наклона 30°) спроецированная ось Z) масштабируется вдвое (50%).
«Китайская перспектива»
Также обратите внимание (снова), что перспектива искажена и что углы вид сверху и вид сбоку следует рассматривать как «эмпирическое правило»; Я рассчитал эти углы так же, как и углы в диметрике. прогноз представлен в NEN 2536/ISO 5456-3, но эти расчеты фактически уже не применимы.
Другая картина, воспроизведенная ниже, имеет спроецированную ось z на
чуть менее 40 градусов, но с наклоном в другую сторону. С одной стороны,
Я мог бы сказать, что ось Z наклонена примерно на 130° (90° + 40°),
но с другой стороны направление наклона несущественно для
обсуждение аксонометрической проекции.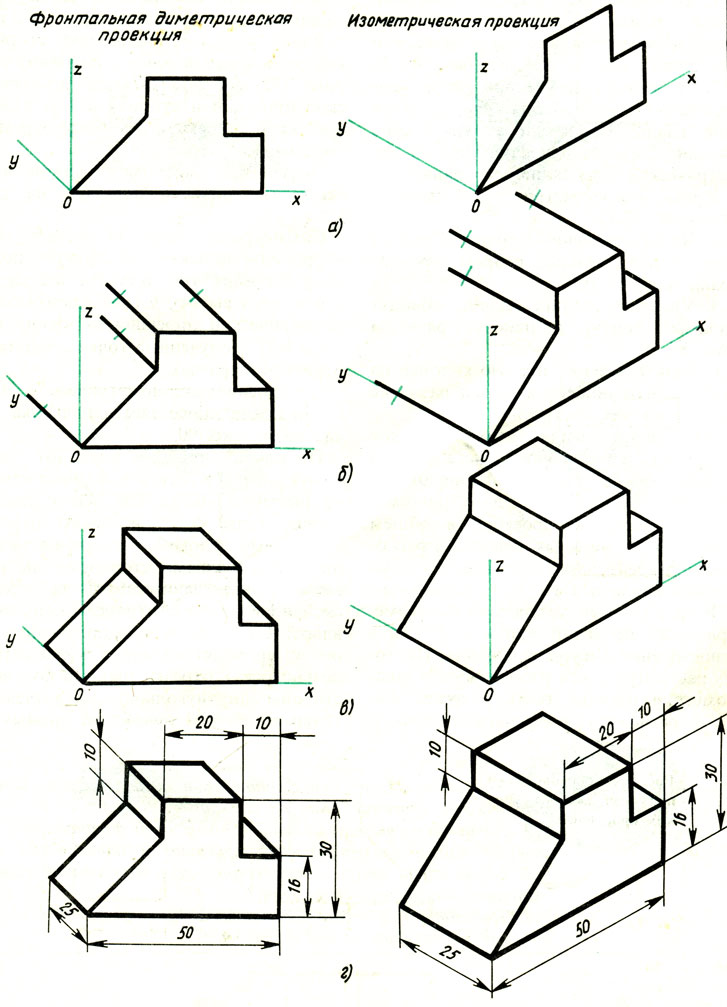
Репродукция 18 го века ремейка 11-метрового свитка, созданного художниками двора Цин, опубликованного в «Город Катай»
Я могу дать только приблизительную оценку масштабирование оси Z в этот свиток («Город Катай»): между 0,6 и 0,7 (но, вероятно, ближе к 0,6).
Диметрические проекции для компьютерной графики и игр
Как и в случае с изометрической проекцией, в компьютерной графике некоторые
углы предпочтительнее других. Первая диметрическая проекция, которую я предлагаю
для (тайловой) компьютерной графики очень похоже на проекцию китайской
прокручивать картины. Разница заключается в масштабе оси Z и угле, который
это делает с осью x. Начнем с угла, ось Z наклонена с
примерно 27 градусов (точный угол равен «арктангенс (0,5)»).
Это тот же угол, что и в изометрической проекции для использования в компьютерной графике.
Масштаб таков, что ширина бокового вида куба при измерении
по оси абсцисс составляет половину ширины лицевой стороны.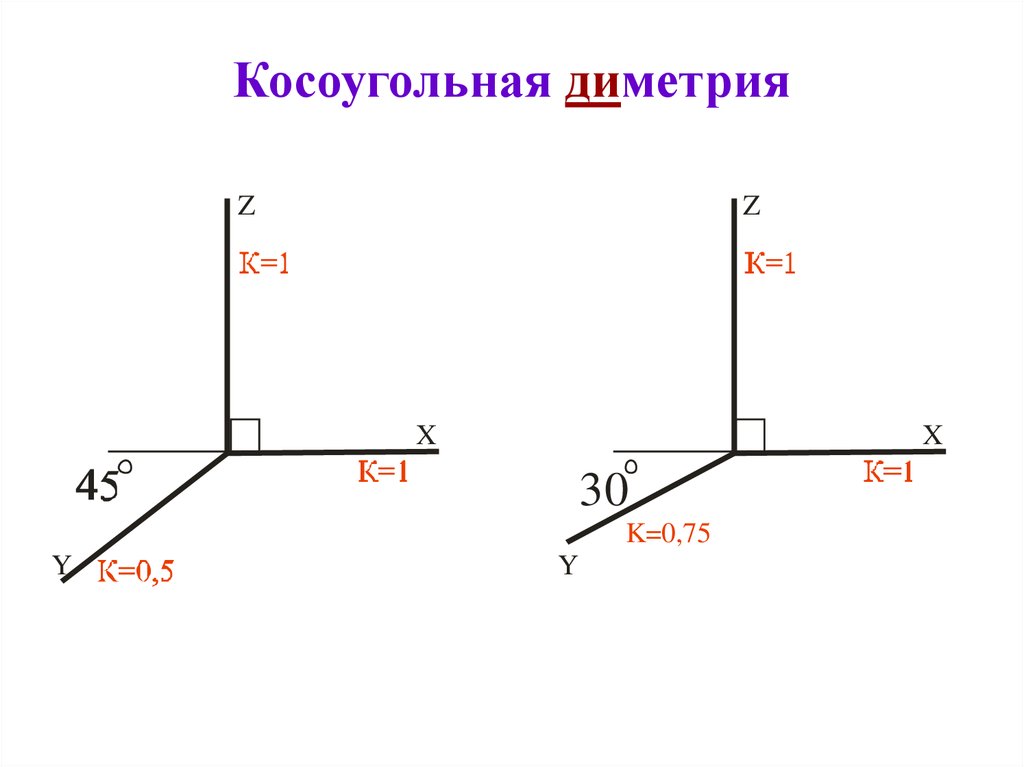 Ключевая фраза в
предыдущее предложение «при измерении по оси X». в
две предыдущие проекции, масштабный коэффициент, примененный к расстояниям, измеренным вдоль
ось Z.
Ключевая фраза в
предыдущее предложение «при измерении по оси X». в
две предыдущие проекции, масштабный коэффициент, примененный к расстояниям, измеренным вдоль
ось Z.
Диметрическая проекция 1:2 «вид сбоку»
Вышеупомянутая проекция дает перспективу, которая видна в основном с сторона. Мне может быть полезно добавить немного глубины боковой прокрутке (или «платформа») игра. Для настольных игр перспектива, которая просматривается с большей высоты более уместно. Второй предлагаемый диметр проекция для игр служит этой цели.
Диметрическая проекция 1:2 «вид сверху»
Опять же, обратите внимание, что перспектива двух предложенных выше проекций
искаженный. Углы на видах сверху и сбоку равны , на самом деле приблизительные.
Например, во второй проекции угол, под которым смотришь сверху
на месте дается как 24 градуса. Однако использование угла в 30 градусов может
на самом деле выглядеть лучше. Кроме того, 30-градусный угол позволяет использовать тот же
объекты как для диметрической, так и для изометрической проекций для игр.
Кроме того, 30-градусный угол позволяет использовать тот же
объекты как для диметрической, так и для изометрической проекций для игр.
Другие диметрические проекции приведены в таблице ниже. Эти прогнозы были взяты из программы CARTESIO. За каждой проекции я даю имя, которое программа дает проекции, наклон для осей x и z и масштаб для оси z. Во всех представленных здесь проекциях, ось y остается вертикальной, а x- и оси Y имеют одинаковый масштаб.
| projection name | x-axis angle | z-axis angle | z-axis scale |
|---|---|---|---|
| 130, 130, 100 | 10 | 40 | 0.59 |
| 1, 1 , 2/3 | 12.8 | 38.6 | 0.667 |
| 1, 1, 3/4 | 16.3 | 36.8 | 0.75 |
Программа CARTESIO перечисляет больше проекций, чем несколько приведенных выше, в том числе те,
стандартов NEN 2536/ISO 5456-3 и нескольких таких
искажено, что я не вижу в них практического применения.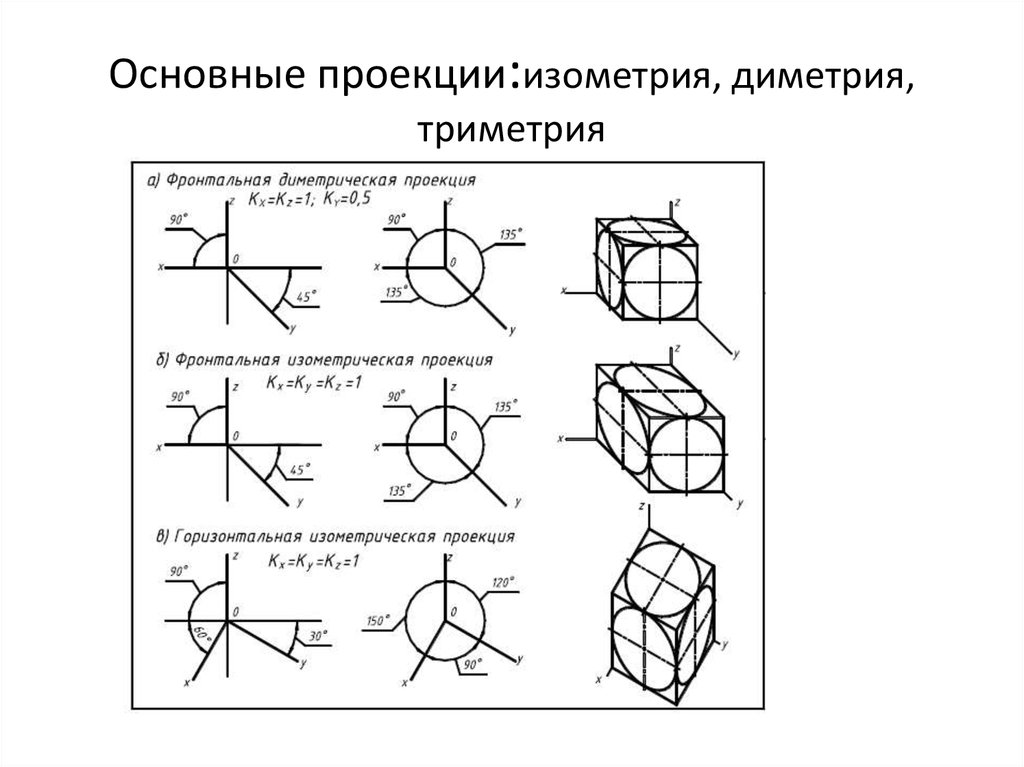
Перемещение по аксонометрической проекции
Преобразование пространственных координат (x, y, z) в пиксельные координаты (x’, y’) в проекция требует только тривиальной геометрии. В таблице ниже представлены формулы полноты. Пожалуйста, обратитесь к системе координат на рисунке справа мое определение осей x, y и z; в трехмерном пространстве ось Y указывает вверх, а плоскость определяется осями x и z.
| Преобразование 3D-координат в 2D-координаты проекции 9\circ}) \cr} \] | ||
|---|---|---|
| Китайские свитки | \[ \выравнивание{ х’ &= х + {\bf n} \cdot z \cdot \cos ({\bf T}) \cr y’ &= y + {\bf n} \cdot z \cdot \sin ({\bf T}) \cr} \] где \( {\bf n} \) от 0,5 до 0,7 и \( {\bf T} \) от 30° до 40° | |
| Компьютерные игры: вид сбоку | \[ \выравнивание{ х’ &= х + {z \более 2} \cr y’ &= y + {z \более 4} \cr} \] | |
| Компьютерные игры: вид сверху | \[ \выравнивание{ х’ &= х + {z \более 4} \cr y’ &= y + {z \over 2} \cr} \] | |
Обратите внимание, что в приведенных выше уравнениях различные синусы и косинусы постоянны.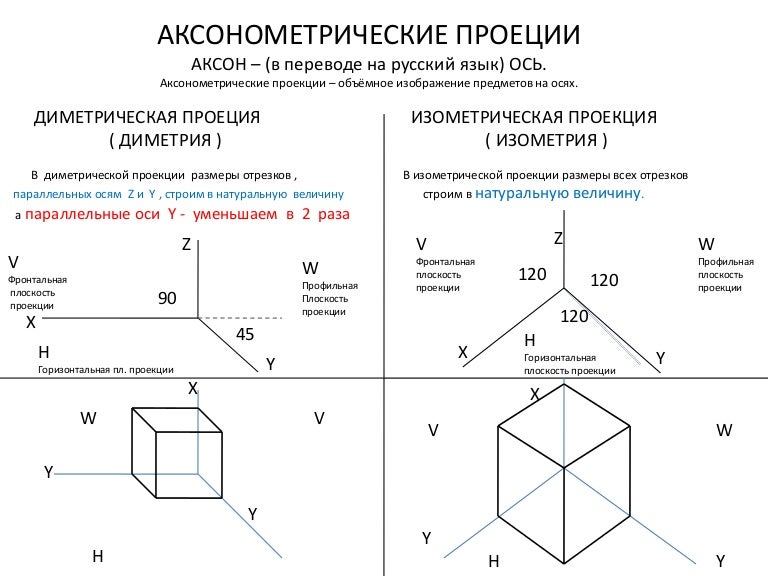 для данной проекции и их нужно вычислить только один раз.
для данной проекции и их нужно вычислить только один раз.
Преобразование координат в проекции в пространственные координаты другое дело. В общем виде это просто невозможно сделать: нельзя вычислить три независимых выходных параметра из двух входных параметров. Если можно «зафиксировать» один из выходных параметров, два других можно рассчитать из входных параметров. Пример: если аксонометрическая проекция представляет собой карту, и вы можете предположить, что область на карте практически не имеет рельеф, то можно зафиксировать положение по оси Y равным нулю (уровень земли), и вам нужно только вычислить x и z из x’ и y’. (Опять же отметим, что в трехмерная система координат, которую я использую, точки оси Y вверх.) 9\circ })}} \cr} \]
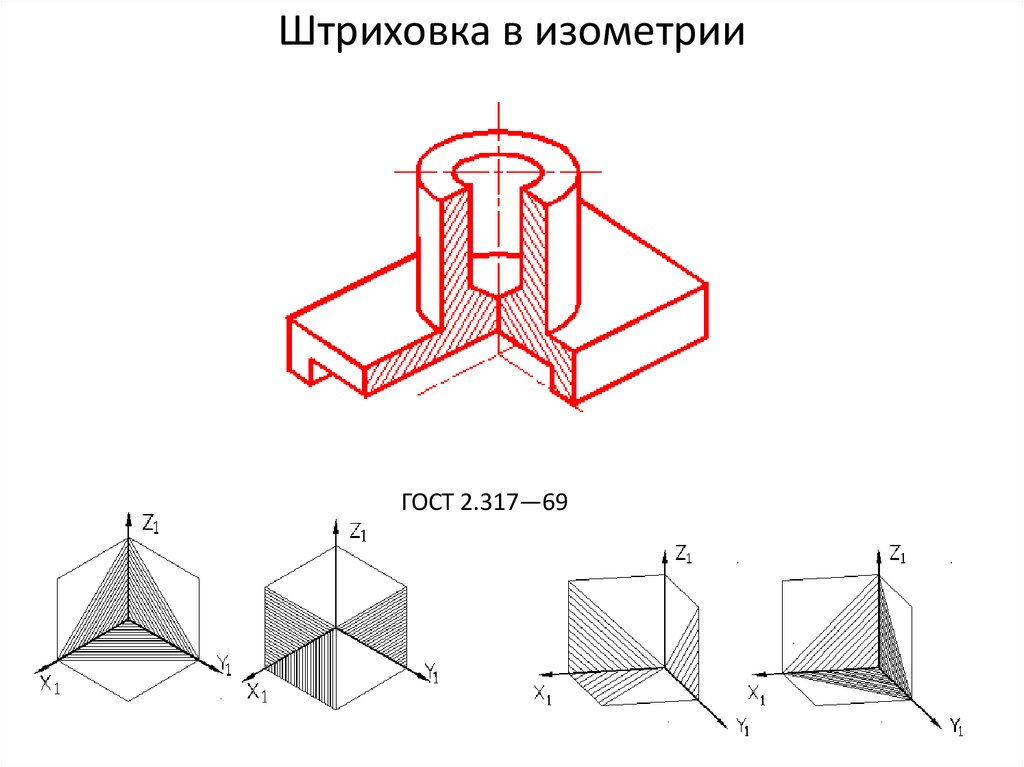
Уточнение вышеизложенного заключается в поддержке некоторого облегчения. расчет выходных координат начинается как и прежде, только теперь y-координата является оценкой, а не «известным» значением. После расчета координаты x и z, вы можете найти соответствующее значение «высоты» в положение (х, z). Как правило, они не будут совпадать с координатой Y, которую вы угадали при вычислении координат x и z. Теперь вы можете настроить вас оценка координаты y и вычисление соответствующих координат x и z опять таки. Эта итерация продолжается до тех пор, пока предполагаемая координата y (до вычисления x и z) достаточно близко подходит к искомому значению (после расчет x и z).
Главный вопрос при следовании этой итеративной процедуре:
сходятся?» Следуя интуиции, процедура считается сходящейся, если нет
пятно на поверхности проекта закрывает другое место в 3D-пространстве. То есть,
если уклоны рельефа поверхности остаются ниже угла обзора (в
«направление взгляда»), у каждого местоположения на карте в 3D-пространстве есть уникальный «близнец».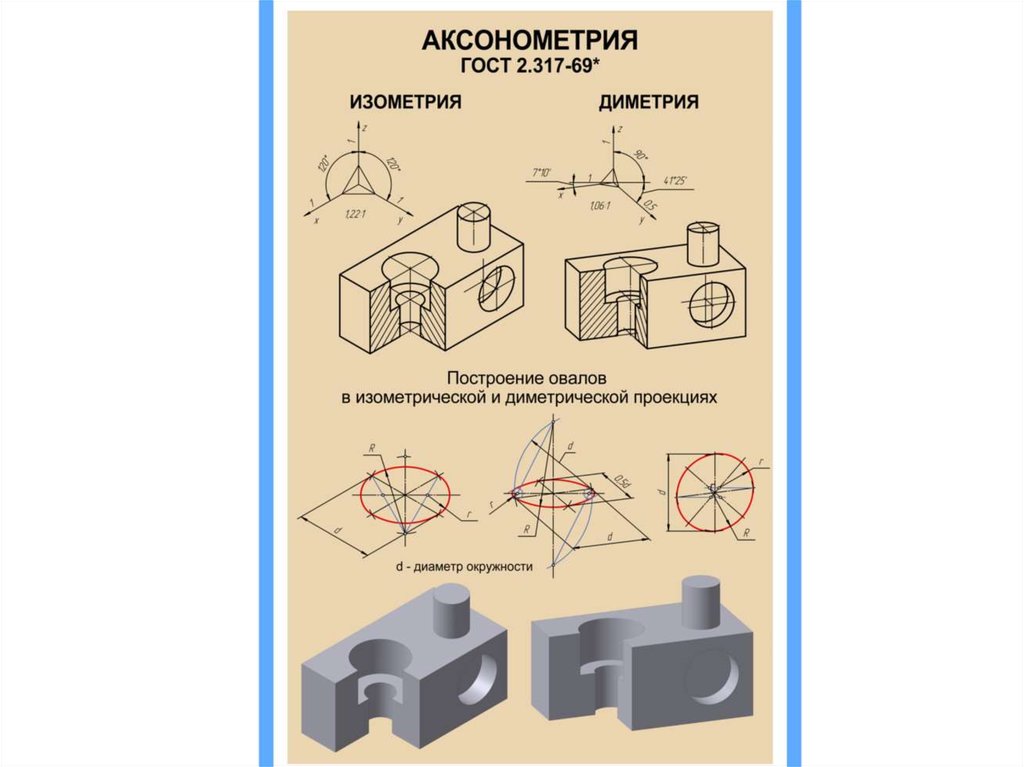 расположение в аксонометрической проекции, которое видно с точки обзора.
расположение в аксонометрической проекции, которое видно с точки обзора.
На приведенном выше изображении угол обзора от горизонтальной плоскости составляет 30 градусов. и самый крутой уклон в направлении взгляда составляет примерно половину этого. Рисунки с проволочными каркасными кубами в этой статье показывают угол, под которым вы смотрите на плоскость (для изометрической проекции NEN 2536 это 35° а для проекции 1:2, используемой в большинстве изометрических игр, это 30°). Если склоны на вашей доске остаются ниже этого предела, итеративная процедура расчета x и z при заданном y, а затем корректировка y до тех пор, пока y больше не изменится, будет сходятся.
Если у вас есть экстремальный рельеф или перекрывающиеся «уровни земли», такие как мосты
или зданий, я предлагаю вам разделить спроецированную карту на части, которые,
себя, придерживайтесь ограничения не более крутых углов, чем угол обзора
угол. Эти части могут быть отдельными «слоями» или «спрайтами», и вы строите
полную карту, объединив их.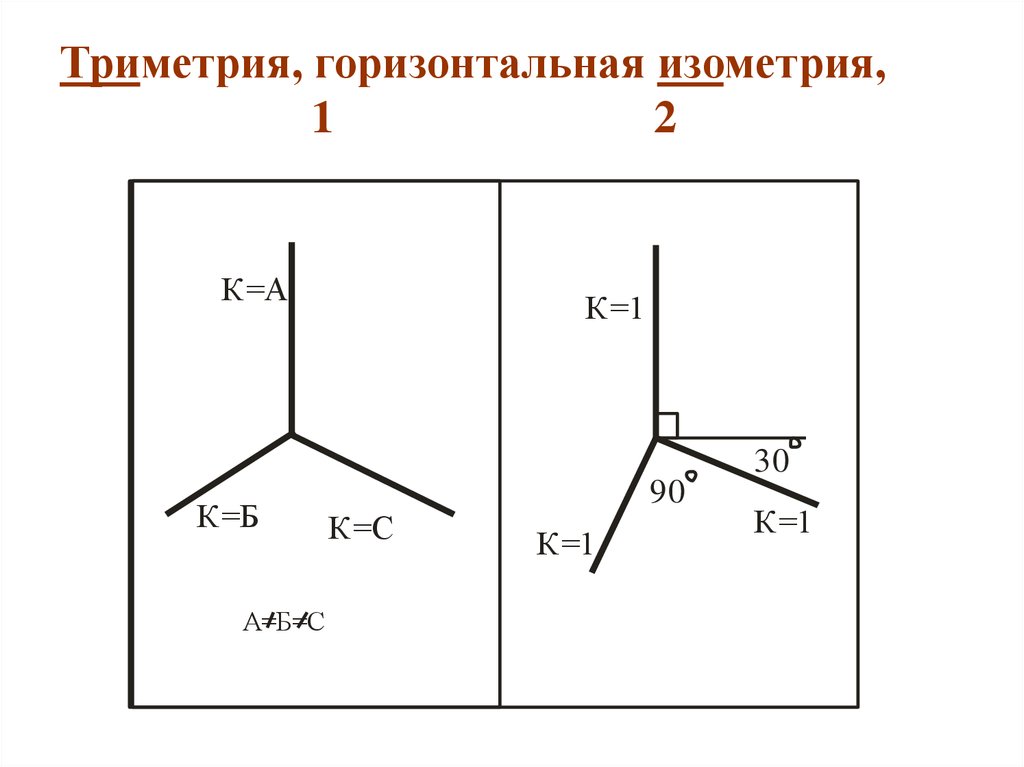 Чтобы вычислить (x, y, z) из (x’, y’), вы сначала решаете
на каком слое/спрайте находится местоположение (x’,y’), а затем используйте итеративный
Процедура нахождения значений x, y и z.
Чтобы вычислить (x, y, z) из (x’, y’), вы сначала решаете
на каком слое/спрайте находится местоположение (x’,y’), а затем используйте итеративный
Процедура нахождения значений x, y и z.
Дополнительная информация
- Культурное кафе; «Город Катай: взгляд на китайскую жизнь через известную картину»; компакт-диск; Том 2; без даты .
- Этот компакт-диск содержит подробную презентацию знаменитой картины на свитке.
- Фоли, Джеймс Д. [ et al. ]; «Компьютерная графика: принципы и практика»; Аддисон-Уэсли; второе издание, 1990 г.; ISBN 0-201-121107.
- Эта энциклопедическая книга посвящена перспективным проекциям в пятой главе.
- Крикке, Дж.; «Аксонометрия: вопрос перспективы»; Компьютерная графика и приложения IEEE; Июль/август 2000 г.
- (исторический) обзор аксонометрических проекций с точек зрения
восточного искусства, технических рисунков и компьютерных игр — в том же духе
как три введения к этой статье, но в более подробном и
связная статья.

В статье утверждается, что слово «аксонометрия» должно относятся только к конкретной проекции, используемой восточными художниками (т. так называемая «китайская перспектива»), тогда как общий термин — «орфографическая прогнозы». Со ссылкой на NEN 2536 и Фоли [и др.] в качестве эталона я рассматриваю аксонометрические проекции и параллельные проекции как синонимы, в то время как орфографический проекция — это та, где направление взгляда перпендикулярно плоскости, вообще без перспективы. - НЕН 2536; «Инженерный чертеж. Аксонометрическая проекция»; Нидерланды Институт нормализации; август 1966 года.
- Голландский стандарт аксонометрических проекций для технических чертежей.
Этот стандарт был заменен NEN 5456-3, опубликовано в 1997 г. (голландский язык) и соответствует стандарту ISO 5456-3 под названием «Технические чертежи». — Методы проекции — Часть 3: Аксонометрические представления», опубликовано в 1999 г. (на английском языке). - Тревизан, Камилло; КАРТЕСИО
программа; версия 3.
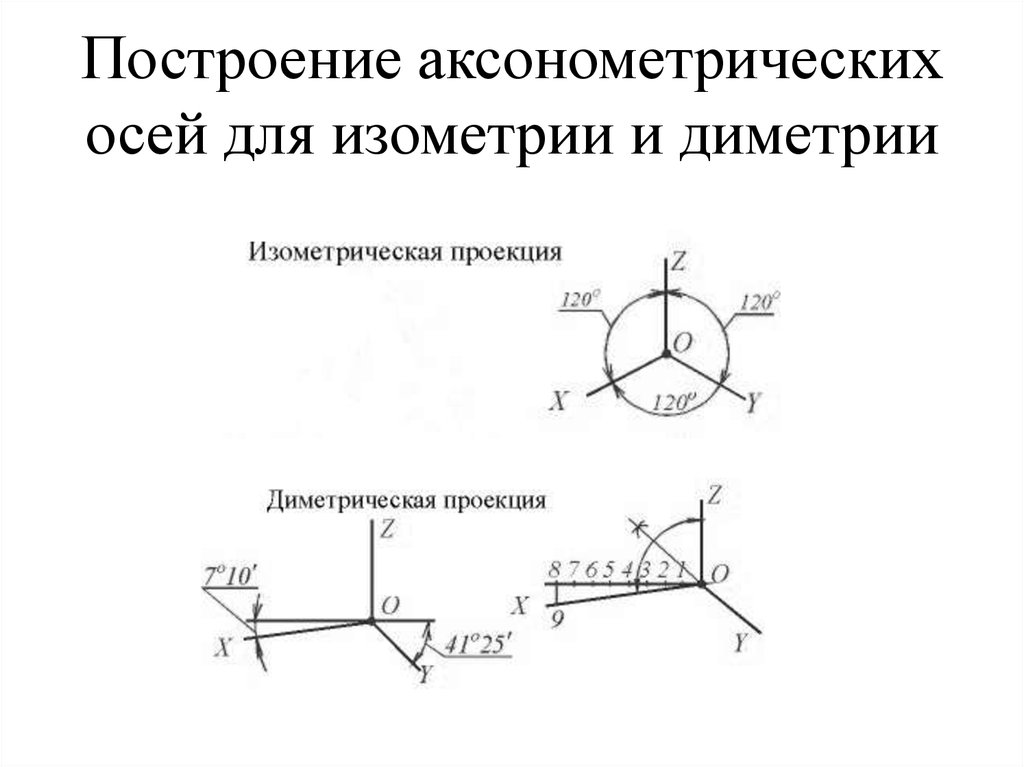 03e.
03e. - Образовательное и интерактивное приложение, содержащее множество геометрических проекции. Это бесплатно для личного использования.
Аксонометрические проекции – использование, типы и значение
В области проектирования и производства нам приходится изготавливать различные виды деталей, и все эти детали имеют трехмерную форму. Как правило, в производстве редко приходится иметь дело с 2D-деталями, за исключением деталей из листового металла. Но если вам нужно показать эти 3D-детали на технических чертежах, мы ожидаем показать эти 3D-детали на листе вашего 2D-чертежа. Но также мы можем добавить аксонометрический вид на лист технического чертежа, чтобы упростить визуализацию 3D-детали. Здесь вы можете узнать о важности аксонометрических видов в инженерных чертежах и других приложениях.
Для этого существует множество правил и методов инженерного черчения, например, вы можете показывать 3D-детали и 2D-виды. Читатель может понять и визуализировать 3D-часть из этих 2D-видов.
Что такое аксонометрия?
В геометрии аксонометрия — это метод рисования, при котором трехмерные детали изображаются в двухмерных плоскостях. Существуют разные методы аксонометрических рисунков.
Три типа аксонометрической проекции
В зависимости от ракурса краев различают три типа аксонометрической проекции.
- Изометрическая проекция: В трехосевом направлении величина ракурса одинакова.
- Диметрическая проекция: В этой проекции две оси тела укорачиваются на одинаковую величину, а третья ось укорачивается на разную величину.
- Триметрическая проекция: Ракурсы в трех направлениях разные.
Изометрический чертеж
Первый метод аксонометрического просмотра и рисования — отображение трехмерной детали в изометрическом виде. В этом методе аксонометрии мы размещаем все основные стороны объектов под равными углами, как показано ниже.
Техника диметрического просмотра
Второй метод аксонометрии заключается в отображении всех сторон трехмерного объекта с двумя равными первичными сторонами объекта. Мы называем этот метод диметрическим, что означает, что позиционирование двух сторон одинаково. Взгляните на базовый пример ниже.
Мы называем этот метод диметрическим, что означает, что позиционирование двух сторон одинаково. Взгляните на базовый пример ниже.
Триметрический просмотр
Третий метод аксонометрического рисования показывает все основные стороны 3D-детали одинаково. Чтобы понять это, проверьте базовый пример ниже.
Три типа аксонометрических проекций.Какие методы аксонометрического рисования мы используем?
Мы используем все виды аксонометрических методов рисования как в инженерии, так и в архитектуре. Особенно в архитектуре аксонометрия является очень важным методом, чтобы показать разные стороны зданий и моделей.
Выбор одного из этих трех методов аксонометрии зависит от потребностей модели.
Например, если вам нужно показать детали всех сторон модели, может быть лучше предпочесть изометрический метод просмотра другим методам аксонометрического рисования.
Изометрический вид архитектуры интерьера (Источник изображения: freepik.com). Как вы видите на фотографии выше, они используют технику изометрического просмотра, чтобы показать все детали внутренней архитектуры плана дома. Вы можете легко и одинаково увидеть все детали интерьера с помощью этой техники аксонометрического рисования. Из-за этого мы используем технику изометрического рисования, как правило, в иллюстрациях внутреннего плана дома, подобных приведенным выше. Вы можете видеть все детали одинаково.
Вы можете легко и одинаково увидеть все детали интерьера с помощью этой техники аксонометрического рисования. Из-за этого мы используем технику изометрического рисования, как правило, в иллюстрациях внутреннего плана дома, подобных приведенным выше. Вы можете видеть все детали одинаково.
Изометрический метод может быть наиболее часто используемым методом по сравнению с другими аксонометрическими видами из-за этих фактов.
Пример диметрического аксонометрического вида
Мы используем метод диметрического просмотра, как правило, для отображения деталей лицевой стороны объектов. В этом методе просмотра аксонометрии передняя сторона объектов находится на переднем плане.
Взгляните на пример ниже. Дизайнер этого макета здания намеревался показать детали фасада здания, проиллюстрировав его в технике диметрического просмотра. Первое, что привлекает внимание зрителя, — это книжный магазин на фасадной стороне здания.
 clip-studio.com).
clip-studio.com).Мы установили, что при диметрическом просмотре лицевая сторона моделей находится на переднем плане, а другие стороны на самом деле нет. Существует еще одна техника аксонометрического просмотра, при которой бока и верх модели выводятся на передний план. Это триметрический вид аксонометрии.
Пример трехмерного представления
В трехмерном представлении правая сторона и верхняя часть моделей находятся в витрине, но передняя сторона не находится на переднем плане. Мы обычно используем этот вид аксонометрического стиля рисования в картографии. Если на карте важна глубина зданий, картография обычно использует этот триметрический метод, чтобы показать как верхнюю часть карты, так и правые стороны зданий и 3D-объектов, чтобы они выглядели одинаково.
Взгляните на приведенный ниже пример аксонометрического вида. Вы можете видеть как вид сверху, не теряя его из виду. Вы можете видеть дороги, внутренние связи и т. д. Но также этот метод аксонометрического просмотра дает очень хорошее преимущество для отображения необходимых деталей о трехмерных объектах в городе.
Заключение по аксонометрическим проекциям
Как вы понимаете, различные виды техники аксонометрического черчения широко используются в различных профессиях, таких как архитектура, механика и гражданское строительство. В соответствии с вашей профессией выбор правильной техники аксонометрии очень важен, чтобы показать все детали вашей модели.
Наконец, не забудьте оставить свои комментарии и вопросы ниже о методах аксонометрического просмотра и областях их применения!
Нам очень важны ваши отзывы!
Часто задаваемые вопросы об аксонометрических видах
В чем разница между изометрическим и аксонометрическим?
Основное различие между этими двумя терминами заключается в типе другого. Если вы посмотрите на статью выше, вы увидите, что изометрический вид — это тип аксонометрического вида. Кроме того, существуют и другие типы, такие как диметрические и триметрические представления.
Аксонометрический под углом 45 градусов?
Нет, существуют разные степени в зависимости от типа. Вы можете взглянуть на общие степени, которые вы рисуете для типов аксонометрических представлений.
Какой угол является аксонометрическим?
Вы можете найти различные ракурсы техники аксонометрического рисования. Проверьте различные типы, такие как изометрические, триметрические и диметрические представления выше. Таким образом, вы можете найти их углы.
Как нарисовать аксонометрическую проекцию?
Это можно сделать разными способами. Если вы используете рисунки от руки, вам необходимо указать точку горизонта. А также вам нужно сделать свой рисунок в соответствии с этой точкой горизонта, чтобы получить успешные рисунки.
Что такое аксонометрический расчет?
Аксонометрия не является фактическим дизайном. Это метод просмотра 3D-объектов в 2D-плоскостях. Таким образом, вы можете представить свои 3D-проекты, используя методы аксонометрического рисования, которые мы объяснили выше.
Это метод просмотра 3D-объектов в 2D-плоскостях. Таким образом, вы можете представить свои 3D-проекты, используя методы аксонометрического рисования, которые мы объяснили выше.
Какова основная функция аксонометрической проекции?
Основная функция этих проекций заключается в том, что мы без проблем показываем 3D-объекты в 2D-плоскостях. Таким образом, зритель этих видов может увидеть все детали в этих методах проекции.
Какое значение имеет аксонометрическая проекция?
Важность этой проекционной техники вытекает из необходимости объяснения трехмерных объектов на двухмерных бумагах и поверхностях. Таким образом, это очень полезные методы, которые мы используем в приложениях для технического рисования.
Как нарисовать изометрическую фигуру. Выполнение прямоугольной изометрии, прямоугольной диметрии для заданных видов
Для выполнения изометрической проекции любой детали необходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.
Правила построения изометрических проекций геометрических фигур. Построение любой плоской фигуры следует начинать с осей изометрических проекций.
При построении изометрической проекции квадрата (рис. 109), от точки О по аксонометрическим осям откладывается половина длины стороны квадрата в обе стороны. Через получившиеся засечки проводят прямые линии, параллельные осям.
При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси Y от точки О откладывается высота треугольника. Соедините получившиеся засечки отрезками прямых линий.
Рис. 109. Прямоугольная и изометрическая проекции квадрата.
Рис. 110. Прямоугольная и изометрическая проекции треугольника.
При построении изометрической проекции шестиугольника (черт. 111) от точки О по одной из осей откладывают (в обе стороны) радиус описанной окружности, а по другой — Н/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соедините получившиеся засечки отрезками прямых линий.
Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соедините получившиеся засечки отрезками прямых линий.
Рис. 111. Прямоугольная и изометрическая проекции шестиугольника.
Рис. 112. Прямоугольная и изометрическая проекции окружности.
При построении изометрической проекции окружности (рис. 112) по осям координат от точки О откладывают отрезки, равные ее радиусу. Через полученные засечки проводят прямые, параллельные осям, получая аксонометрическую проекция квадрата. Из вершин 1, 3 проведены дуги CD и KL радиусом 3C. Соедините точки 2 с 4, 3 с С и 3 с D. На пересечениях прямых получаются центры а и b малых дуг, после проведения которых получают овал, заменяющий аксонометрическую проекцию окружности.
С помощью описанных построений можно выполнять аксонометрические проекции простых геометрических тел (табл. 10).
10. Изометрические прогнозы простых геометрических тел
Изометрические прогнозы простых геометрических тел
Методы для конструкции. формообразующая грань используется для деталей, форма которых имеет плоскую грань, называемую формообразующей гранью; ширина (толщина) детали одинакова на всем протяжении, на боковых поверхностях отсутствуют канавки, отверстия и другие элементы. Последовательность построения изометрической проекции следующая:
1) построение осей изометрической проекции;
2) построение изометрической проекции формообразующей грани;
3) построение проекций остальных граней по изображению ребер модели;
Рис. 113. Построение изометрической проекции детали, начиная с формообразующей грани
4) штрих изометрической проекции (рис. 113).
- Метод построения изометрической проекции на основе последовательного удаления объемов применяется в тех случаях, когда отображаемая форма получается в результате удаления каких-либо объемов из исходной формы (рис.
 114).
114). - Методом построения изометрической проекции на основе последовательного приращения (добавления) объемов выполняют изометрическое изображение детали, форма которой получается из нескольких объемов, соединенных определенным образом друг с другом (рис. 115). ).
- Комбинированный метод построения изометрической проекции. Изометрическую проекцию детали, форма которой получена в результате сочетания различных способов формообразования, выполняют методом комбинированного построения (рис. 116).
Аксонометрическая проекция детали может выполняться с изображением (рис. 117, а) и без изображения (рис. 117, б) невидимых частей формы.
Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов
Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов
Рис. 116. Использование комбинированного метода построения изометрической проекции детали
Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей
Прямоугольной изометрией называют аксонометрическую проекцию, в которой коэффициенты искажения по всем трем осям равны, а углы между аксонометрическими осями равны 120. На рис. 1 показано положение аксонометрических осей прямоугольной изометрии и способы их построения.
Рис. 1. Построение аксонометрических осей прямоугольной изометрии с помощью: а) отрезков; б) компас; в) квадраты или транспортир.
В практических конструкциях коэффициент искривления (К) по аксонометрическим осям по ГОСТ 2.317-2011 рекомендуется принимать равным единице. В этом случае изображение получается больше теоретического или точного изображения при коэффициенте искажения 0,82. Увеличение 1,22. На рис. 2 показан пример изображения детали в прямоугольной изометрической проекции.
Рис. 2. Изометрическая деталь.
Построение в изометрии плоских фигур
Дан правильный шестиугольник ABCDEF, расположенный параллельно горизонтальной плоскости проекции H (P 1).
а) Строим изометрические оси (рис. 3).
б) Коэффициент искажения по осям в изометрии равен 1, поэтому от точки О 0 по осям откладываем натуральные значения отрезков: А 0 О 0 = АО ; О 0 D 0 = ОД; К 0 О 0 = КО; О 0 Р 0 = ИЛИ.
в) Линии, параллельные осям координат, также проводят в изометрии параллельно соответствующим осям изометрии в натуральную величину.
В нашем примере стороны BC и FE параллельно оси X .
В изометрии их также проводят параллельно оси X в натуральную величину B 0 C 0 = BC; F 0 E 0 = КЭ.
г) Соединив полученные точки, получим изометрическое изображение шестиугольника в плоскости H(P 1).
Рис. 3. Изометрическая проекция шестиугольника на чертеже
и в горизонтальной плоскости проекции
На рис. 4 показаны проекции наиболее распространенных плоских фигур на различные плоскости проекций.
Наиболее распространенной формой является круг. Изометрическая проекция круга обычно представляет собой эллипс. Эллипс строится по точкам и обводится по шаблону, что очень неудобно в практике рисования. Поэтому эллипсы заменяются овалами.
Эллипс строится по точкам и обводится по шаблону, что очень неудобно в практике рисования. Поэтому эллипсы заменяются овалами.
На рис. 5 построен изометрический куб с кругами, вписанными в каждую грань куба. При изометрических построениях важно правильно расположить оси овалов в зависимости от плоскости, в которой предполагается провести окружность. Как видно на рис. 5 большие оси овалов расположены по большей диагонали ромбов, в которые проецируются грани куба.
Рис. 4 Изометрическое изображение плоских фигур
а) на чертеже; б) на плоскости Н; в) на плоскости V; г) на плоскости W.
Для прямоугольной аксонометрии любого вида правило определения главных осей овального эллипса, на который проецируется окружность, лежащего в любой плоскости проекций, можно сформулировать следующим образом: большая ось овала перпендикулярна отсутствующей в этой плоскости аксонометрической оси, а малая совпадает с направлением этой оси. Форма и размеры овалов в каждой плоскости изометрических проекций одинаковы.
Для того чтобы получить аксонометрическую проекцию объекта (рис. 106), необходимо мысленно: расположить объект в системе координат; выберите плоскость аксонометрической проекции и поместите объект перед ней; выбрать направление параллельных проецирующих лучей, которое не должно совпадать ни с одной из аксонометрических осей; направить проецирующие лучи через все точки объекта и координатные оси до пересечения с плоскостью аксонометрической проекции, получив тем самым изображение проецируемого объекта и координатных осей.
На плоскость аксонометрической проекции получают изображение — аксонометрическую проекцию объекта, а также проекции осей систем координат, которые называются аксонометрическими осями.
Аксонометрическая проекция – изображение, полученное на аксонометрической плоскости в результате параллельного проецирования объекта вместе с системой координат, четко отображающее его форму.
Система координат состоит из трех взаимно пересекающихся плоскостей, имеющих неподвижную точку — начало координат (точка О) и трех осей (X, Y, Z), исходящих из нее и расположенных под прямым углом друг к другу. Система координат позволяет производить измерения по осям, определяя положение объектов в пространстве.
Система координат позволяет производить измерения по осям, определяя положение объектов в пространстве.
Рис. 106. Получение аксонометрической (прямоугольной изометрической) проекции
Можно получить множество аксонометрических проекций, по-разному располагая объект перед плоскостью и выбирая разное направление проецирующих лучей (рис. 107).
Наиболее часто используется так называемая прямоугольная изометрическая проекция (далее мы будем использовать ее сокращенное название — изометрическая проекция). Изометрической проекцией (см. рис. 107, а) называется такая проекция, в которой коэффициенты дисторсии по всем трем осям равны, а углы между аксонометрическими осями равны 120°. Изометрическая проекция получается с помощью параллельной проекции.
Рис. 107. Аксонометрические проекции, установленные ГОСТ 2.317-69:
а — прямоугольная изометрическая проекция; б — прямоугольная диметрическая проекция;
в — косая фронтальная изометрическая проекция;
d — косая фронтальная диметрическая проекция
Рис. 107. Продолжение: е — косая горизонтальная изометрическая проекция
107. Продолжение: е — косая горизонтальная изометрическая проекция
В этом случае проекционные лучи перпендикулярны плоскости аксонометрической проекции, а оси координат одинаково наклонены к плоскости аксонометрической проекции (см. рис. 106). Если сравнить линейные размеры объекта и соответствующие размеры аксонометрического изображения, то можно увидеть, что на изображении эти размеры меньше реальных. Величины, показывающие отношение размеров проекций отрезков к их действительным размерам, называются коэффициентами искажения. Коэффициенты дисторсии (К) по осям изометрической проекции одинаковы и равны 0,82, однако для удобства построения используются так называемые практические коэффициенты дисторсии, равные единице (рис. 108).
Рис. 108. Положение осей и коэффициенты искажения изометрической проекции
Существуют изометрические, диметрические и триметрические проекции. Изометрические проекции — это те проекции, которые имеют одинаковые коэффициенты искажения по всем трем осям. Диметрическими проекциями называются такие проекции, у которых два коэффициента искажения по осям одинаковы, а значение третьего отличается от них. К триметрическим проекциям относятся проекции, в которых все коэффициенты искажения различны.
Диметрическими проекциями называются такие проекции, у которых два коэффициента искажения по осям одинаковы, а значение третьего отличается от них. К триметрическим проекциям относятся проекции, в которых все коэффициенты искажения различны.
Диметрия — один из видов аксонометрической проекции. Благодаря аксонометрии одним трехмерным изображением можно рассматривать объект сразу в трех измерениях. Поскольку коэффициенты искажения всех размеров по 2 осям одинаковы, эта проекция называется диметрией.
Прямоугольный диметрий
Когда ось Z расположена вертикально, а оси X» и Y» образуют углы 7 градусов 10 минут и 41 градус 25 минут от горизонтального отрезка. В прямоугольной диметрии коэффициент искажения по оси Y будет 0,47, а по осям X и Z в два раза больше, т.е. 0,94.
Для построения приближенно аксонометрических осей обычной диметрии необходимо принять, что tg 7 градусов 10 минут равно 1/8, а tg 41 градус 25 минут равно 7/8.
Как построить диметрию
Сначала нужно провести оси для изображения объекта в диметрии. В любой прямоугольной диметрии углы между осями X и Z составляют 97 градусов 10 минут, а между осями Y и Z — 131 градус 25 минут и между Y и X — 127 градусов 50 минут.
В любой прямоугольной диметрии углы между осями X и Z составляют 97 градусов 10 минут, а между осями Y и Z — 131 градус 25 минут и между Y и X — 127 градусов 50 минут.
Теперь требуется нанести оси на ортогональные проекции изображаемого объекта с учетом выбранного положения объекта для рисования в диметрической проекции. После завершения перевода в объемное представление габаритных размеров объекта можно приступать к рисованию второстепенных элементов на поверхности объекта.
Стоит помнить, что окружности в каждой диметрической плоскости изображаются соответствующими эллипсами. В диметрической проекции без искажений по осям X и Z большая ось нашего эллипса во всех 3-х плоскостях проекции будет равна 1,06 диаметра нарисованного круга. А малая ось эллипса в плоскости XOZ составляет 0,95 диаметра, а в плоскостях ZOY и XOY — 0,35 диаметра. В диметрической проекции с искажением по осям X и Z большая ось эллипса равна диаметру окружности во всех плоскостях. В плоскости XOZ малая ось эллипса равна 0,9диаметра, а у самолетов ZOY и XOY — 0,33 диаметра.
Для получения более детального изображения необходимо прорезать детали по диметру. Заштриховку при удалении выреза следует наносить параллельно диагонали проекции выделенного квадрата на требуемую плоскость.
Что такое изометрия
Изометрия – это один из видов аксонометрической проекции, при котором расстояния отдельных сегментов по всем трем осям одинаковы. Изометрическая проекция активно используется в инженерных чертежах для отображения внешнего вида объектов, а также в различных компьютерных играх.
В математике изометрия известна как преобразование метрического пространства, сохраняющее расстояние.
Прямоугольная изометрия
В прямоугольной (ортогональной) изометрии аксонометрические оси образуют между собой углы, равные 120 градусам. Ось Z находится в вертикальном положении.
Как рисовать изометрию
Построение изометрии предмета позволяет получить наиболее выразительное представление о пространственных свойствах изображаемого предмета.
Прежде чем приступить к построению чертежа в изометрической проекции, необходимо выбрать такое расположение изображаемого объекта, чтобы его пространственные свойства были максимально видны.
Теперь вам нужно определиться с типом изометрии, которую вы будете рисовать. Бывает двух видов: прямоугольная и горизонтальная косая.
Нарисуйте оси светлыми тонкими линиями так, чтобы изображение располагалось по центру листа. Как упоминалось ранее, углы в прямоугольной изометрической проекции должны составлять 120 градусов.
Начните рисовать изометрию точно с верхней поверхности изображения объекта. От углов получившейся горизонтальной поверхности нужно провести две вертикальные прямые и отложить на них соответствующие линейные размеры предмета. В изометрической проекции все линейные размеры по всем трем осям останутся кратными единице. Затем последовательно требуется соединить созданные точки вертикальными линиями. В результате получается внешний контур объекта.
Следует иметь в виду, что при изображении любого предмета в изометрической проекции обязательно будет искажена видимость криволинейных деталей. Круг должен быть нарисован как эллипс. Отрезок между точками окружности (эллипса) по осям изометрической проекции должен быть равен диаметру окружности, а оси эллипса не будут совпадать с осями изометрической проекции.
Если изображаемый объект имеет скрытые полости или сложные элементы, попробуйте заштриховать. Он может быть простым или ступенчатым, все зависит от сложности элементов.
Помните, что все построения должны выполняться строго с помощью чертежных инструментов. Используйте несколько карандашей разной твердости.
Аксонометрия
Аксонометрия (от греч. axcon — ось и metreo — измеряю) дает визуальное изображение предмета на одной плоскости.
Аксонометрическое изображение объекта получают путем проецирования его параллельно на одну плоскость проекции вдоль осей прямоугольных координат, к которым относится этот объект.
Коэффициенты искажения по осям в аксонометрии определяются отношением отрезков аксонометрических координат к их натуральному значению при тех же единицах измерения.
Среднее значение коэффициентов естественной дисторсии:
- по оси x – u ;
- по оси y – v ;
- по оси z – w .
В зависимости от сравнительного значения коэффициентов дисторсии по осям различают три вида аксонометрии:
изометрия — все три коэффициента дисторсии равны между собой: u=v=w .
Диметрия — два коэффициента искажения равны друг другу и отличаются от третьего u=v≠w ; v=w≠u ; и=ш≠в .
Триметрия — все три коэффициента искажения не равны между собой: u≠v≠w .
В зависимости от направления проекции аксонометрические проекции делятся на прямоугольные (направление проекции перпендикулярно плоскости аксонометрических проекций) и косые (направление проекции не перпендикулярно плоскости аксонометрических проекций) ).
Прямоугольные проекции
Изометрия
Положение аксонометрических осей показано на рис.1.
| Рис.1. |
Коэффициент осевого искажения x , y , z равен 0,82.
Изометрию для простоты, как правило, выполняют без искажения по осям х , у , z , т. е. принимая коэффициент искажения равным 1.
Построенное таким образом изображение будет 1,22 раз больше самого объекта, т.е. масштаб изображения будет М 1,22:1 .
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проектируются на плоскость аксонометрической проекции в виде эллипсов (рис. 2). Если произвести изометрическую проекцию без искажения по осям х , у , z , то большая ось эллипсов 1, 2, 3 равна 1,22, а малая ось 0,71 диаметра эллипса. круг. Если изометрическая проекция выполняется с искажением по осям х , y , z , то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось равна 0,58 диаметра окружности.
Пример изометрической проекции детали показан на рис.3.
Диметрия
Положение аксонометрических осей показано на рис.4.
| Рис.4. |
Коэффициент искажения оси у равен 0,47, а по осям х и z – 0,94.
Диметрическая проекция, как правило, выполняется без искажения по осям х и z и с коэффициентом искажения 0,5 по оси у .
Аксонометрическая шкала будет M 1.06:1 .
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проектируются на плоскость аксонометрической проекции в виде эллипсов (рис. 5). Если диметрическую проекцию выполнить без искажений по осям x и z , то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 равна 0,95, эллипсов 2 и 3 равна 0,35 диаметра круга. Если диметрическую проекцию выполнить с искажением по осям х и z , то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 равна 0,9, от эллипсы 2 и 3 составляют 0,33 диаметра окружности.
Пример диметрической проекции детали показан на рис.6.
Косые проекции
Изометрические фронтальные
Положение аксонометрических осей показано на рис.7.
Допускается использование фронтальных изометрических проекций с углом наклона оси у 30 и 60°.
Фронтальная изометрическая проекция выполняется без искажений по осям x , y , z .
Окружности, лежащие в плоскостях, параллельных плоскости фронтальной проекции, проектируются на аксонометрическую плоскость в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекции, проектируются в эллипсы (рис. 8). Большая ось эллипсов 2 и 3 равна 1,3, а малая ось — 0,54 диаметра окружности.
Пример фронтальной изометрической проекции детали показан на рис. 9.
Изометрическая горизонталь
Положение аксонометрических осей показано на рис.10.
Допускается использовать горизонтальные изометрические проекции с углом наклона оси y 45 и 60°, выдерживая угол между осями х и y 90°.
Горизонтальная изометрическая проекция выполняется без искажения по осям x , y и z .
Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекции, проектируются на плоскость аксонометрической проекции в окружности, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскостям проекции, проектируются в эллипсы (рис. 11). Большая ось эллипса 1 составляет 1,37, а малая ось — 0,37 диаметра окружности. Большая ось эллипса 3 составляет 1,22, а малая ось — 0,71 диаметра окружности. Оси фронтальной диметрии
Допускается применение фронтальных диметрических проекций с углом наклона оси у 30 и 60°.
Коэффициент искажения оси у равен 0,5, а по осям х и z – 1. в плоскостях, параллельных горизонтальной и профильной проекциям, плоскости проецируются в эллипсы (рис. 14). Большая ось эллипсов 2 и 3 равна 1,07, а малая ось — 0,33 диаметра окружности.
Пример фронтальной диметрической проекции детали показан на рис. 15.
15.
Что такое диметрическая и триметрическая проекция? – Ru-facts.com
Что такое диметрическая и триметрическая проекция?
Приблизительные размеры обычно используются в диметрических чертежах. В триметрической проекции направление взгляда таково, что все три оси пространства кажутся неодинаково укороченными. Масштаб по каждой из трех осей и углы между ними определяются отдельно в зависимости от угла обзора.
В чем разница между изометрической и триметрической проекциями?
Изометрия – все размеры в одном масштабе. Диметрический – di=2; 2 оси/размеры в ракурсе. Триметрический – три=3; 3 оси/размеры в ракурсе.
Что вы подразумеваете под аксонометрической проекцией?
/ (ˌæksənəˈmɛtrɪk) / существительное. геометрический рисунок объекта, такого как здание, в трех измерениях, показывающий вертикальные и горизонтальные проекции в масштабе, но с искаженными диагоналями и кривыми, так что все кажется наклонным.
В чем разница между изометрией и аксонометрией?
Аксонометрический означает «измерение вдоль осей»; оси объекта нарисованы в постоянном масштабе. И в этом углу: изометрическая проекция — это тип аксонометрической проекции, в котором для каждой оси используется один и тот же масштаб, и поэтому это наиболее часто используемый тип рисования.
И в этом углу: изометрическая проекция — это тип аксонометрической проекции, в котором для каждой оси используется один и тот же масштаб, и поэтому это наиболее часто используемый тип рисования.
В чем разница между изометрическими и триметрическими проекциями?
В изометрии линии проекции составляют равные углы с плоскостью проекции. На диметрических чертежах две главные оси имеют одинаковый ракурс. На трехмерных чертежах все три главные оси показаны в ракурсе. План просто наклоняется под любым нужным углом.
Что такое изометрическая проекция и вид?
Изометрическая проекция — это метод визуального представления трехмерных объектов в двух измерениях на технических и инженерных чертежах. Это аксонометрическая проекция, в которой три оси координат кажутся одинаково укороченными, а угол между любыми двумя из них составляет 120 градусов.
В чем разница между истинным масштабом и изометрическим масштабом?
Ответ: Истинный масштаб или Естественный масштаб используются для рисования ортогональных видов. В этих видах направление зрителя точно перпендикулярно плоскости обзора, поэтому видны истинные размеры. Но в изометрическом виде объект виден под углом, чтобы увидеть все три плоскости.
В этих видах направление зрителя точно перпендикулярно плоскости обзора, поэтому видны истинные размеры. Но в изометрическом виде объект виден под углом, чтобы увидеть все три плоскости.
Что понимается под аксонометрией?
Определение аксонометрии: быть или подготовлено путем проецирования объектов на поверхность чертежа таким образом, что они кажутся наклонными с тремя видимыми сторонами и с горизонтальными и вертикальными расстояниями, выполненными в масштабе, но диагональные и изогнутые линии искажают аксонометрический рисунок.
Какое значение имеет аксонометрическая проекция?
Практика аксонометрического черчения дает дизайнерам возможность исследовать компоненты с помощью чертежей в разрезе и в разобранном виде, а также в широком диапазоне масштабов, начиная от исследований интерьера и мебели и заканчивая городскими проектами, которые трудно воспроизвести другими способами.
Axo и ISO — это одно и то же?
В изометрической проекции все углы между аксонометрическими осями равны. Чтобы создать изометрическую проекцию, вы ориентируете объект так, чтобы его главные края (или оси) образовывали равные углы с плоскостью проекции и, следовательно, были одинаково укорочены.
Чтобы создать изометрическую проекцию, вы ориентируете объект так, чтобы его главные края (или оси) образовывали равные углы с плоскостью проекции и, следовательно, были одинаково укорочены.
Что такое аксонометрическая архитектура?
Аксонометрический, или планометрический, чертеж, как его иногда называют, представляет собой метод рисования вида в плане с третьим измерением. Его используют дизайнеры интерьеров, архитекторы и ландшафтные дизайнеры. Вид в плане рисуется под углом 45 градусов, а глубина добавляется по вертикали.
Что такое диметрическая проекция в искусстве?
Диметрическая проекция определяется как способ рисования объекта, при котором одна ось имеет другой масштаб, чем две другие оси на чертеже. Примером диметрической проекции является технический чертеж, на котором изображен трехмерный куб, одна сторона которого меньше пропорционально двум другим сторонам.
Что такое метрическая проекция Di Di?
диметрическая проекция. существительное. Диметрическая проекция определяется как способ рисования объекта, при котором одна ось имеет другой масштаб, чем две другие оси на чертеже.
существительное. Диметрическая проекция определяется как способ рисования объекта, при котором одна ось имеет другой масштаб, чем две другие оси на чертеже.
Что такое аксонометрическая проекция?
Аксонометрическая проекция — это технический термин для класса перспектив, к которому также относится китайская параллельная перспектива. Этим перспективам не только не хватает точки схода, они также обладают несколькими другими, в основном полезными, характеристиками. Они обсуждаются ниже.
Что такое угол изометрической проекции в видеоиграх?
Таким образом, изометрическая проекция, используемая в большинстве игр, наклоняет оси x и z примерно на 27 градусов (точный угол — «арктангенс (0,5)»). Кстати, поскольку тангенс угла ромба равен 0,5, ромб в два раза больше в ширину, чем в высоту. Вот почему во многих источниках упоминается масштаб 1:2 для изометрической перспективы.
com/embed/2BaEBFxgaIQ?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Прогнозы и представления | Инженерное проектирование
Трехмерный объект может быть представлен в одной плоскости, например, на листе бумаги, с использованием проекционных линий и плоскостей. Вся теория проекций основана на двух переменных: линия взгляда t (проекционные линии) и плоскость проекции .
Линия прямой видимости (LOS) — это воображаемая линия между глазом наблюдателя и объектом. Плоскость проекции (то есть плоскость изображения или изображения) — это воображаемая плоская плоскость, на которую проецируется изображение. Проекция создается путем соединения точек, в которых линии взгляда пересекают плоскость проекции. В результате 3D-объект преобразуется в 2D-вид.
Если расстояние от наблюдателя до объекта бесконечно, то линии проекции предполагаются параллельными, а проекция называется параллельной проекцией. Параллельная проекция орфографическая , если плоскость проекции расположена между наблюдателем и объектом, и эта плоскость перпендикулярна параллельным линиям зрения.
Параллельная проекция орфографическая , если плоскость проекции расположена между наблюдателем и объектом, и эта плоскость перпендикулярна параллельным линиям зрения.
Технику параллельного проецирования можно использовать для создания как многоракурсных, так и графических (изометрических и наклонных) видов.
- В многоракурсной ортогональной проекции (подробности см. ниже) поверхность объекта и плоскость проекции параллельны, и вы видите только два измерения.
- В изометрическом виде (орфографическом) поверхность больше не параллельна плоскости проекции, а последняя перпендикулярна лучам зрения, при этом видны три измерения.
- В косой проекции (неортогональной) поверхность объекта и плоскость проекции также параллельны, но линии визирования не перпендикулярны плоскости проекции, и вы снова можете видеть три измерения.
Если расстояние от наблюдателя до объекта конечно, то линии проекций не параллельны (поскольку все линии взгляда начинаются в одной точке), и рисунок классифицируется как перспективная проекция . В перспективе поверхность объекта и плоскость проекции также могут быть параллельны.
В перспективе поверхность объекта и плоскость проекции также могут быть параллельны.
Многоракурсная проекция
Изменяя положение объекта относительно линии взгляда, вы можете создавать разные виды одного и того же объекта. Рисование более чем одной грани объекта путем поворота объекта относительно линии взгляда помогает понять трехмерную форму. Имея несколько видов на одном чертеже, вы используете концепцию многоракурсная проекция , основанная на методе ортогональной (параллельной) проекции, где
- плоскость проекции расположена между наблюдателем и объектом,
- плоскость проекции перпендикулярна параллельным лучам зрения, а
- объект ориентирован так, что показаны только два его измерения.
Основные принципы создания многоракурсных проекций
Плоскость проекции можно ориентировать для создания бесконечного числа видов объекта. Однако наиболее распространенными видами являются шесть взаимно перпендикулярных видов, которые создаются шестью взаимно перпендикулярными плоскостями проекции:
- Вид спереди — тот, который показывает большинство функций или характеристик.

- Вид слева — показывает, что становится левой стороной объекта после установления положения вида спереди.
- Вид справа — показывает, что становится правой стороной объекта после установления положения вида спереди.
- Вид сверху — показывает, что становится верхней частью объекта после определения положения вида спереди.
- Вид снизу — показывает, что становится нижней частью объекта после установки положения вида спереди.
- Вид сзади — показывает, что становится задней частью объекта после установки положения вида спереди.
В качестве основного вида (вида спереди) обычно выбирают наиболее информативный (наглядный) вид изображаемого объекта. Это вид A , связанный с соответствующим направлением обзора A , и он обычно показывает объект в рабочем, производственном или монтажном положении.
Виды на чертежах и соответствующие направления взгляда
Положение других видов относительно основного вида на чертеже зависит от метода проецирования.
Количество видов и разделов должно быть ограничено до минимума, необходимого для полного представления объекта без двусмысленности.
Следует избегать ненужного повторения деталей.
Обычное размещение видов
Как правило, трех видов объекта достаточно, однако чертеж должен содержать столько видов, сколько необходимо для иллюстрации детали, обычно под прямым углом друг к другу.
Фронтальная плоскость проекции
В многоракурсной проекции объект просматривается перпендикулярно основным граням, так что в каждом виде отображается только одна грань объекта. Фронтальная плоскость проекции — это плоскость, на которую проецируется вид спереди многовидового чертежа.
В виде спереди вы можете видеть высоту и ширину объекта, но вы не можете видеть его глубину .
Горизонтальная плоскость проекции
Вид сверху проецируется на горизонтальную плоскость проекции , которая является плоскостью, подвешенной над верхней частью объекта и параллельной ей.
Вид сверху объекта показывает размеры ширины и глубины .
Профиль плоскости проекции
На многовидовых чертежах вид справа является стандартным видом сбоку. Вид справа проецируется на правая плоскость профиля проекции, которая представляет собой плоскость, параллельную правой стороне объекта. Однако вы также можете использовать вид слева, если он более нагляден и информативен. Более того, при необходимости вы можете включить оба вида сбоку в один чертеж.
Вид сбоку объекта показывает размеры глубины и высоты .
Трехракурсный многоракурсный чертеж является стандартом, используемым в технике и технологии, потому что часто другие три общих вида являются зеркальными отображениями и не добавляют знаний об объекте.
Стандартные виды, используемые в трехвидовом чертеже , это
- верх,
- спереди и
- видов справа,
расположены, как показано на рисунке:
Размер ширины является общим для видов спереди и сверху. Размер высоты является общим для видов спереди и сбоку. Размер глубины является общим для видов сверху и сбоку.
Размер высоты является общим для видов спереди и сбоку. Размер глубины является общим для видов сверху и сбоку.
Для простых деталей часто бывает достаточно одного или двух видовых чертежей. На чертежах с одним видом третий размер может быть выражен примечанием или описательными словами, символами или аббревиатурами, такими как Ø, HEX и т. д.
Квадратные участки могут быть обозначены светлыми пересекающимися диагональными линиями, как показано выше, что применимо независимо от того, параллельна ли поверхность плоскости чертежа или наклонена.
Другой пример чертежа с одним видом:
Дополнительные виды могут быть добавлены, если они улучшают визуализацию.
Виды также следует выбирать таким образом, чтобы по возможности избегать скрытых характерных линий. Это означает, что должен быть показан наиболее описательный вид .
Кроме того, необходимо выбрать минимальное количество просмотров, необходимое для полного описания объекта. Удалите виды, которые являются зеркальным отображением других видов.
Удалите виды, которые являются зеркальным отображением других видов.
Почему техника многоракурсных чертежей так важна?
Для производства нового продукта необходимо знать его истинные размеры, а истинные размеры не представлены должным образом на большинстве графических чертежей. Например, фотография представляет собой живописное перспективное изображение. Однако, как видите, t изображение искажает истинные расстояния, а последние необходимы для производства и строительства , и в данном примере речь идет о ширине дороги, а не о столбе!
В машиностроении перспективные проекции искажают измерения.
Как видите, два измерения ширины на виде спереди блока выглядят разными по длине в перспективной проекции. Другими словами, равные расстояния не кажутся равными на чертеже в перспективе.
Таким образом, поскольку разработка и технология зависят от точных описаний размеров и форм для проектирования, наилучшим подходом является использование метода параллельного проецирования (ортогональное проецирование) для создания чертежей с несколькими видами, где каждый вид показывает только два из трех измерений. (ширина высота Глубина).
(ширина высота Глубина).
Подводя итог :
Преимущество многоракурсных чертежей по сравнению с графическими рисунками заключается в том, что многоракурсные чертежи показывают истинный размер и форму различных особенностей объекта, тогда как изображения искажают истинные размеры, которые имеют решающее значение в производстве и строительстве.
1
st & 3 rd Уголки (стеклянная коробка)Что именно разместить на правой боковой проекции?
Это то, что мы можем видеть с левой стороны или с правой стороны объекта?
Ответить на эти вопросы можно двумя способами, основанными на двух разных принципах
- Проекция под первым углом
- Проекция под третьим углом .
Третий угол используется в Канаде и США. Первый угол используется в Европе.
В ортогональной проекции под третьим углом можно предположить, что объект заключен в стеклянную коробку.
Каждый вид представляет то, что видно, если смотреть перпендикулярно на каждую сторону коробки.
Результирующие представления идентифицируются по именам, как показано.
Виды спереди, сзади и сбоку иногда называют eleva ts , например, вид спереди. Вид сверху можно назвать планом .
При желании вид сзади может быть показан в обоих направлениях – в крайнем левом или крайнем правом углу. Когда нецелесообразно показывать вид сзади в крайнем левом или правом углу из-за длины детали, особенно с панелями и монтажными пластинами, вид сзади не следует проецировать вверх или вниз, так как это приведет к тому, что он будет показан вверх ногами. вниз.
Вместо этого он должен быть нарисован так, как если бы он был проецирован вбок, но расположен в каком-то другом положении, и должен быть четко помечен как ЗАДНИЙ ВИД УДАЛЕН.
В орфографических проекциях первого угла объект считается перевернутым на любую сторону, так что правая сторона объекта отрисована слева от фасада:
Обязательно указывать метод многоракурсной проекции путем включения соответствующего проекционного символа ISO (Международная организация по стандартизации) – усеченный конус :
Этот символ следует поместить в нижний правый угол чертежа в основной надписи или рядом с ней.
Аксонометрическая проекция
Это одна из проекций графических чертежей, которые используются в иллюстративных целях, в качестве учебных пособий, чертежей по установке и техническому обслуживанию, проектных эскизов и т.п.
Греческое слово аксон означает ось и метрика означает измерять. Аксонометрическая проекция — это метод параллельного проецирования, используемый для создания графического рисунка объекта путем вращения объекта на оси относительно плоскости проекции .
Аксонометрические проекции, такие как изометрическая , диметрическая и триметрическая проекции являются ортогональными, поскольку все линии проекций параллельны, но угол обзора выбран таким образом, чтобы три грани прямоугольного объекта были показаны в одном представлении.
Аксонометрические чертежи классифицируются по углам между линиями, составляющими аксонометрических осей . Аксонометрические оси — это оси, которые встречаются и образуют угол объекта, ближайший к наблюдателю.
Когда все три угла не равны, рисунок классифицируется как триметрический . Когда два из трех углов равны, рисунок классифицируется как диметрический . Когда все три угла равны, рисунок классифицируется как 9.0100 изометрический .
Хотя существует бесконечное количество позиций, которые можно использовать для создания такого рисунка, используются лишь немногие из них.
Увеличенный
ДетальДля устранения скученности деталей или размеров можно использовать увеличенный удаленный вид.
- Увеличенный вид должен быть ориентирован так же, как и основной вид,
- должен быть показан масштаб увеличения, а
- оба вида должны быть обозначены одним из способов, показанных на рисунках, – линией выноски или линией окружности. Окружность, охватывающая область на основном виде, должна быть нарисована тонкой линией.
วิธี ทำ Аксонометрия Диметрия และ Изометрия ของ การ ฉาย สาม มิติ หน้า ผาก Аксонометрическая
GOST 2. 317-68* กำหนด โครง แบบ Аксонометрический แบบ สี่ และ แบบ แบบ
317-68* กำหนด โครง แบบ Аксонометрический แบบ สี่ และ แบบ แบบ
การ การ ฉาย ภาพ แบบ แบบ แบบ ประกอบ ด้วย การ ฉาย ภาพ เรขาคณิต ร่วม กับ แกน ของ พิกัด พิกัด เหลี่ยม ที่ รูป นี้ ถึง ใน ฉาย แกน ของ พิกัด พิกัด สี่ ที่ รูป นี้ ถึง ใน ฉาย ใน แนว ขนาน ขนาน สี่ เหลี่ยม เฉียง นี้ อ้าง ใน ใน แนว ขนาน การ ภาพ ภาพ ภาพ ภาพ ภาพ ภาพ ภาพ ภาพ ภาพ ภาพ ภาพ ภาพ ภาพ ภาพ ภาพ ภาพ แบบ ภาพ ฉาย ระนาบ เดียว ใน กรณี นี้ ทิศทาง การ ฉาย ภาพ จะ ถูก เพื่อ ไม่ ให้ ตรง กับ แกนพิกัด ใด ๆ
เมื่อ การ ฉาย ภาพ แบบ แบบ Аксонометрический เหล่า นี้ ชื่อ «Аксонометрия» มา คำ ว่า ว่า ว่า — аксон — ось и метерео — I วัด
ประเภท ของ เส้น โครง Аксонометрический
การ ภาพ แบบ แบบ ขึ้น ขึ้น กับ ทิศทาง ของ การ ฉาย แบ่ง ออก เป็น:
- เฉียง เมื่อ ทิศทาง ของ การ ฉาย ไม่ ตั้ง ฉาก กับ ระนาบ ของ การ ฉาย ภาพ แบบ Аксонометрический
- สี่ เหลี่ยม เมื่อ ทิศทาง ของ การ ฉาย ตั้ง ฉาก กับ ระนาบ ของ การ ฉาย ภาพ แบบ Аксонометрический
ขึ้น กับ ค่า เปรียบเทียบ ของ ค่า สัมประสิทธิ์ การ บิด เบือน ตาม แกน มี สาม ประเภท ของ Аксонометрия:
- มี เท่า เท่า กัน — ค่า การ บิด เบือน ทั้ง สาม มี ค่า เท่า กัน
- ไดเมเทรีย — ค่า สัมประสิทธิ์ การ บิด เบือน ค่า เท่า กัน และ แตกต่าง จาก ค่า ที่ สาม
- ไตรรงค์ — ค่า สัมประสิทธิ์ การ บิด เบือน ทั้ง ไม่ เท่า กัน
Номер телефона
ใน สี่ เหลี่ยม มี มิติ เท่า กัน มุม ระหว่าง แกน คือ คือ 120 ° เมื่อ การ ฉาย ภาพ สาม มิติ ตาม แนว แกน x, y, z และ กับ พวก มิติ ตาม ธรรมชาติ ของ จะ ถูก วาง ลง ดัง ชื่อ มิติ เท่า ธรรมชาติ ของ วัตถุ ถูก วาง ดัง นั้น มิติ » ซึ่งในภาษากรีกหมายถึง «การวัดที่เท่ากัน»
การ การ ฉาย ภาพ สาม มิติ ของ รูป ทรง เรขาคณิต แบน
พิจารณา การ สร้าง สาม เหลี่ยม ระนาบ แนว นอน การ ฉาย แบบ มิติ มิติ เท่า กัน เมื่อ ก่อน ก่อน จำเป็น กำหนด ที่ แหล่ง แหล่ง แหล่ง แหล่ง แหล่ง แหล่ง แหล่ง แหล่ง แหล่ง แหล่ง แหล่ง แหล่ง แหล่ง ทำ เช่น ระยะ ห่าง m จะ ถูก วาง ตาม แกน แกน x เท่า ออฟเซ็ต ของ แกน สาม เหลี่ยม ที่ สัมพันธ์ กับ y เส้น ตรง ที่ กับ แกน y ถูก จาก จุด ที่ พบ และ ที่ เท่า กับ กับ ถูก พัก กระจัด ที่ พบ และ ที่ เท่า กับ ถูก การ กระจัด ของ พบ และ ที่ เท่า ถูก พัก ฐาน ของ สาม เหลี่ยม จาก แกน x ได้ จุด ที่ 1 สมมาตร กับ ที่ 1 ตาม เส้น ขนาน กับ แกน แกน x วาง ส่วน กับ ครึ่ง หนึ่ง ของ ของ รูป สาม ทั้ง ทั้ง ทิศทาง พบ จุด ที่ 3, 4 จาก ที่ ตาม ตรง สอง ทิศทาง ขนาน กับ แกน y ส่วน เท่า กับ ความ สูง ของ สาม เหลี่ยม ถูก เลิก จ้าง กำหนด จุด ที่ 2 จุด ที่ เกิด เชื่อมต่อ กัน ใน ทำนอง เดียว การ ฉาย ด้าน หน้า และ โปรไฟล์ ร่าง ถูก สร้าง ขึ้น กัน การ ภาพ ด้าน และ โปรไฟล์ ร่าง ถูก สร้าง ขึ้น กัน กัน ฉาย ด้าน และ โปรไฟล์ ร่าง สร้าง ขึ้น ขึ้น กัน กัน ฉาย ภาพ และ0003
Аксонометрический аксонометрический
Аксонометрическийตำแหน่ง แกน แกน การ ฉาย ภาพ ภาพ ไดเมทริก ผาก ถูก จัด เรียง ดัง แสดง ใน รูป ที่ 85, a: แกน x เป็น นอน แกน แกน เป็น แนว ตั้ง, แกน y อยู่ ที่ มุม 45 ° กับ นอน นอน
มุม 45 ° สามารถ สร้าง โดย ใช้ ใช้ สี่ เหลี่ยม ร่าง 45 °, 45 ° และ 90 ° ดัง แสดง ใน รูป ที่ 85b.
ตำแหน่งของแกนฉายภาพสามมิติแสดงในรูปที่ 85. แกน x และ y ถูก ที่ มุม มุม 30 ° กับ เส้น แนว นอน (มุม 120 ° ระหว่าง แกน) การ สร้าง แกน ทำ ได้ อย่าง โดย ใช้ สี่ เหลี่ยมจัตุรัส ที่ มุม 30, 60 และ 90° (รูปที่ 85, e)
ใน สร้าง แกน ของ การ ฉาย ภาพ แบบ มี มิติ เท่า โดย ใช้ เข็มทิศ คุณ ต้อง วาด แกน Z อธิบาย จุด จุด ส่วน ของ รัศมี ตาม ใจ โดย ไม่ ต้อง เปลี่ยน แก้ ปัญหา ของ เข็มทิศจาก จุด ของ และ แกน แกน เปลี่ยน วิธี ปัญหา ของ เข็มทิศจาก ตัด โค้ง แกน แกน เปลี่ยน วิธี วิธี ปัญหา สร้าง สร้าง 3
เมื่อ การ ฉาย ภาพ ไดเมทริก ส่วน หน้า ตาม แกน x และ z (และ กัน กัน) มิติ จริง จะ ถูก กัน ไว้ ตาม แกน y (และ ขนาน กัน) มิติ จะ ลด ลง 2 ภาษากรีกหมายถึง «มิติคู่»
เมื่อ การ ฉาย ภาพ สาม มิติ ตาม แกน x, y, z ขนาน กัน มิติ ที่ แท้จริง ของ วัตถุ จะ วาง ลง ดัง นั้น ชื่อ ชื่อ มิติ กัน ซึ่ง ใน ภาษา กรีก ถึง «การ วัด เท่า กัน»
ใน รูป 85 ใน และ e แสดง การ สร้าง แกน แกน บน บน ที่ เรียงราย อยู่ ใน กรง ใน กรณี นี้ เพื่อ ได้ มุม 45 ° เส้นทแยง จะ ถูก วาด ใน เซลล์ สี่ (รูป ที่ 85, c) แกนเอียง 30 ° (รูป ที่ เซลล์ 85, d) ได้ มา จาก ของ ความ ยาว ของ ส่วน 3: 5 (3 และ 5 เซลล์)
การ การ ฉาย ภาพ แบบ ไดเมทริก และ ไอ โซเมตริก ที่ หน้า ผาก . สร้าง การ คะเนไดเมทริก และ ไอ โซเมทริกซ์ ส่วน หน้า ของ ส่วน หน้า ซึ่ง สาม มุม มอง ที่ แสดง ใน รูป ที่ 86.
สร้าง การ คะเนไดเมทริก และ ไอ โซเมทริกซ์ ส่วน หน้า ของ ส่วน หน้า ซึ่ง สาม มุม มอง ที่ แสดง ใน รูป ที่ 86.
ลำดับของการสร้างประมาณการมีดังนี้ (รูปที่ 8):
1. วาด ด้าน หน้า ของ ชิ้นส่วน ถูก สร้าง ขึ้น โดย ตั้ง ค่า ของ ความ สูง — ตาม แกน z, ความ ยาว — ตาม แกน x (รูป ที่ 87, a)
2. จาก ยอด ของ ผลลัพธ์ ที่ ได้ ขนาน กับ แกน v ซี่ จะ ถูก วาด ออก ไป ใน ระยะ ทาง หนา ของ ชิ้นส่วน ถูก ตาม นั้น นั้น การ ฉาย ภาพ ไดเมทริก หน้า ผาก ชิ้นส่วน ถูก วาง ตาม นั้น การ ฉาย ภาพ ไดเมทริก หน้า ผาก ผาก ลด 2 ครั้ง; สำหรับภาพสามมิติ — จริง (ул. 87, б)
3. ผ่าน จุด ได้ รับ เส้น ตรง ขนาน กับ ขอบ ด้าน หน้า (รูป ที่ 87, c)
4. ลบ พิเศษ ลาก เส้น โครง ร่าง ที่ มอง เห็น ได้ และ ใช้ มิติ ข้อมูล (รูป ที่ 87, ง)
เปรียบเทียบ ซ้าย และ ขวา ใน รูป ที่ 87. อะไร คือ ที่ เหมือน กัน อะไร คือ ความ แตกต่าง ระหว่าง สิ่ง ปลูก สร้าง ที่ ไว้ กับ พวก เขา เขา เขา เขา เขา เขา เขา เขา เขา เขา เขา เขา เขา เขา เขา
จาก เปรียบเทียบ ตัว เลขเหล่า นี้ กับ ข้อ ความ ที่ มอบ เรา สามารถ สรุป ได้ ลำดับ ลำดับ การ สร้าง ฉาย ภาพ แบบ ไดเมทริก ไอ โซเมทริกซ์ ส่วน นั้น เหมือน กัน ความ แตกต่าง ที่ ตำแหน่ง ของ และ ความ ของ เหมือน ความ แตกต่าง อยู่ ตำแหน่ง ของ และ ยาว ของ เหมือน ความ แตกต่าง ที่ ของ และ ความ Номер
ใน กรณี การ สร้าง การ ฉาย ภาพ แบบ แบบ จะ จะ กว่า เมื่อ เริ่ม ด้วย การ การ สร้าง รูป ของ ฐาน ดัง นั้น จะ พิจารณา ว่า รูป แบน ที่ วาง นอน นั้น แสดง ใน รูป ของ อย่างไร เรขาคณิต แบน วาง แนว นั้น แสดง ใน รูป ของ อย่างไร
การ การ ฉาย ภาพ Аксонометрический ของ เหลี่ยมจัตุรัส เหลี่ยมจัตุรัส แสดง ใน ที่ ที่ 88, ก และ ข.
ตาม แกน x ให้ วาง ด้าน ข้าง ของ สี่ เหลี่ยม a แนว แกน y — ครึ่ง ของ ด้าน ด้าน a / 2 สำหรับ ฉาย ภาพ แบบ ไดเมทริก ที่ หน้า และ ด้าน สำหรับ การ ฉาย แบบ มี มิติ เท่า ปลาย ส่วน ด้าน สำหรับ การ ภาพ แบบ มี เท่า ปลาย ส่วน เชื่อม สำหรับ ฉาย ภาพ มี มิติ ปลาย ปลาย เชื่อม เชื่อม Номер
การ การ ฉาย ภาพ Аксонометрический ของ สาม สาม เหลี่ยม แสดง รูป ที่ 89, ก และ ข.
สมมาตร จุด จุด O (จุด กำเนิด แกนพิกัด แกนพิกัด) ครึ่ง หนึ่ง ของ ข้าง ของ รูป สาม เหลี่ยม a / 2 ถูก ตาม แนว แกน x และ สูง h อยู่ แนว แกน y (สำหรับ การ ภาพ ไดเมทริก ส่วน ความ สูง แนว แกน y (สำหรับ ฉาย ไดเมทริก ส่วน ความ สูง สูง สูง สูง สูง Разделы / 2).
การ การ ฉาย ภาพ ภาพ Аксонометрический ของ หก เหลี่ยม ปกติ จะ แสดง ใน รูป ที่ 90.
บน แกน x ไป ขวา และ ทาง ซ้าย ของ จุด o วาง ส่วน กับ ด้าน ข้าง ของ รูป หก เหลี่ยม ส่วน s / 2 ถูก ตาม แนว แกน แบบ สมมาตร จน จุด จุด เท่า กับ ครึ่ง หนึ่ง ของ ระยะ ระหว่าง ข้าม ถึง จุด จุด เท่า กับ ครึ่ง หนึ่ง ระยะ ระหว่าง รูป จุด จุด เท่า เท่า เท่า เท่า เท่า เท่า เท่า เหลี่ยม จาก จุด m และ n ที่ ได้ บน แกน y ส่วน ต่าง ๆ จะ ถูก ไป ทาง ขวา และ ซ้าย ขนาน กับ แกน เท่า กับ ครึ่ง หนึ่ง ของ ข้าง ของ หก เหลี่ยม จุด ที่ เชื่อมต่อ กัน ด้วย ตรง ด้าน ข้าง รูป หก เหลี่ยม ที่ เชื่อมต่อ เชื่อมต่อ ด้วย ตรง ตรง ข้าง ของ หก เหลี่ยม ที่ เกิด เชื่อมต่อ ด้วย ตรง ตรง ข้าง ของ หก เหลี่ยม
ตอบคำถาม
1. แกน ของ ฉาย ภาพ แบบ ไดเมทริก และ ไอ โซเมทริกซ์ ด้าน หน้า เป็น อย่างไร? Как это сделать?
แกน ของ ฉาย ภาพ แบบ ไดเมทริก และ ไอ โซเมทริกซ์ ด้าน หน้า เป็น อย่างไร? Как это сделать?
แบบ ๆ เป็น แบบ แบบ axonometric และ ทั้ง ทั้ง ทั้ง ทั้ง ด้วย โดย ก็ ออก เป็น มุม ฉาก กับ ระนาบ การ ฉาย ภาพ แนว เฉียง โดย มี . ตาม มาตรฐาน ของ โซเวียต โซเวียต (ดู) การ คาด คะเน Аксонометрический ตะวัน ตก ฉาย ภาพ แบบ มี มิติ เท่า กัน จึง ถูก กำหนด แคบ ลง และ นอก เหนือ จาก ความ เท่าเทียม กัน ของ ขนาด แกน แล้ว ยัง ถึง เงื่อนไข ความ กัน กัน มุม มุม มุม มุม ระหว่าง ฉาย ภาพ แกน ๆ กัน ของ มุม มุม มุม มุม มุม มุม มุม มุม มุม มุม มุม มุม มุม มุม มุม มุม มุม สับสน เว้น จะ ระบุ ไว้ เป็น อย่าง อื่น การ ฉาย ภาพ สาม มิติ จะ หมาย ถึง. เท่า นั้น มุมมองสามมิติสี่เหลี่ยม .
Номер телефона
การฉายภาพสามมิติแบบสี่เหลี่ยม
ใน ฉาย ภาพ แบบ มี มิติ เท่า กัน รูป สี่ เหลี่ยม ผ้า แกน แกน axonometric จะ ทำ มุม มุม มุม มุม ค่า ค่า สัมประสิทธิ์ บิด เบือน เบือน เบือน มี กฎ กฎ แล้ว แล้ว แล้ว แล้ว แล้ว แล้ว แล้ว แล้ว แบบ มี เท่า กัน จะ ถูก ดำเนิน การ โดย ไม่ มี บิด เบือน ตาม แนว แกน นั่น คือ ค่า สัมประสิทธิ์ การ เบือน จะ เท่า กับ 1 ใน นี้ จะ มิติ เชิง เส้น ขึ้น โดย หนึ่ง หนึ่ง
มุมมองสามมิติหน้าผากเฉียง
แกน z «มี ทิศทาง ใน ตั้ง มุม มุม ระหว่าง แกน x และ z» คือ 90 ° แกน y เอียง 135 ° (อนุญาต 120 ° และ 150 °) จาก แกน z «
การ ภาพ สาม มิติ ที่ หน้า ผาก จะ ดำเนิน การ ตาม แกน x «, y» และ z «โดย ไม่ ผิด เพี้ยน
เส้น ขนาน กับ ระนาบ ด้าน หน้า ถูก ฉาย โดย ไม่ มี บิด เบือน
Код
แกน z «กำหนด ทิศทาง แนว ตั้ง ระหว่าง แกน แกน z» และ แกน y «มุม คือ คือ 120 ° (135 ° และ 150 ° อนุญาต) ใน ที่ ยัง คง มุม ระหว่าง แกน x» และ y «ให้ กับ 90°.
การ ภาพ สาม มิติ ใน แนว นอน ทำ ได้ โดย ไม่ เพี้ยน ตาม แกน x «, y» และ z «
Аксонометрический анализ
การ ภาพ สาม มิติ ใน เกม คอมพิวเตอร์ และ ศิลปะพิกเซล
การ ชุด ทีวี ใน งาน ศิลปะพิก เซล ที่ มี มิติ ใกล้เคียง รูปแบบ พิกเซล มี อัตราส่วน ภาพ 2: 1
หมายเหตุ
- ตาม GOST 2 .317-69 — ระบบ รวม เอกสาร การ ออก แบบ การ ฉาย ภาพ แบบ Аксонометрический
- ใน นี้ ระนาบ แนว นอน คือ ระนาบ ที่ ตั้ง ฉาก กับ แกน z (ซึ่ง เป็น ต้น ของ ของ แกน z «)
- อิงกริด คาร์บอม, โจเซฟ ปาซิโอเรก. การ ฉาย เรขาคณิตระนาบ และ การ ดู การ เปลี่ยนแปลง เปลี่ยนแปลง // การ คอมพิวเตอร์ ACM (CSUR) : นิตยสาร. — ACM, ธันวาคม 1978. — Vol. 10. — № 4 — С. 465-502. — ISSN 0360-0300. — Номер: 10.1145/356744.356750
- เจฟฟ์ กรีน. ตัวอย่าง GameSpot: Arcanum (ภาษาอังกฤษ) . GameSpot (29 กุมภาพันธ์ 2000 г.) 29 กันยายน 2551.
- สตีฟ บัตต์. ดูตัวอย่าง SimCity 4: Rush Hour IGN (92546) เก็บถาวร
- GDC 2004: ประวัติ ของ Zelda (ภาษา อังกฤษ) IGN (25 มีนาคม 2547) เก็บ จาก ต้น ฉบับ เมื่อ เมื่อ วัน ที่ 19 กุมภาพันธ์ 2555 สืบค้น เมื่อ 29 กันยายน 2551
เพื่อ ให้ การ ฉาย ภาพ แบบ Axometric ของ (รูป 106). จำเป็น ต้อง จิตใจ จิตใจ: การ วาง ใน ระบบ พิกัด เลือ กระนาบ การ ฉาย ภาพ ภาพ และ วาง วัตถุ ไว้ ไว้ ข้าง หน้า เลือก ของ รังสี ที่ ขนาน กัน ไม่ ควร ตรง กับ แกน axonometric ใด ฉาย ที่ ทุก วัตถุ กับ กับ และ และ และ และ และ และ และ และ แกน ประสาน กว่า จะ ตัด กับ ระนาบ การ ฉาย ภาพ แบบ Аксонометрический จึง ภาพ ของ วัตถุ ที่ ฉาย และ แกนพิกัด
จำเป็น ต้อง จิตใจ จิตใจ: การ วาง ใน ระบบ พิกัด เลือ กระนาบ การ ฉาย ภาพ ภาพ และ วาง วัตถุ ไว้ ไว้ ข้าง หน้า เลือก ของ รังสี ที่ ขนาน กัน ไม่ ควร ตรง กับ แกน axonometric ใด ฉาย ที่ ทุก วัตถุ กับ กับ และ และ และ และ และ และ และ และ แกน ประสาน กว่า จะ ตัด กับ ระนาบ การ ฉาย ภาพ แบบ Аксонометрический จึง ภาพ ของ วัตถุ ที่ ฉาย และ แกนพิกัด
บน การ ฉาย ภาพ แบบ แบบ Аксонометрический
การ ภาพ แบบ แบบ Аксонометрический
ระบบ ประกอบ ด้วย ระนาบ ที่ ตัด กัน สาม ระนาบ ซึ่ง จุด คง ที่ — จุด กำเนิด ของ พิกัด พิกัด (จุด o) และ แกน แกน แกน แกน แกน แกน แกน ที่ เล็ดลอด มา มา จาก มัน ตั้ง อยู่ ใน มุม ฉาก กัน ระบบ จาก จาก มัน มัน และ ใน ฉาก ช่วย พิกัด จาก ให้ คุณ การ วัด ตาม แนว แกน กำหนด ตำแหน่ง ของ วัตถุ ใน อวกาศ
ข้าว. 106. รับการฉายภาพแบบ аксонометрический
คุณ รับ การ ฉาย ภาพ แบบ แบบ แบบ แบบ แบบ ได้ มาก โดย วาง วัตถุ ไว้ หน้า หน้า ระนาบ ด้วย วิธี ๆ และ เลือก ทิศทาง แตกต่าง กัน ของ ที่ ฉาย ออก มา (รูป ที่ 107)
ที่ กัน มาก ที่ สุด คือ สิ่ง ที่ เรียก ว่า การ ภาพ ที่ มี มิติ เท่า กัน สี่ เหลี่ยม เหลี่ยม เหลี่ยม ไป นี้ เรา ใช้ ชื่อย่อ การ ฉาย ภาพ สาม สาม มิติ) การ ภาพ แบบ สาม มิติ มิติ มิติ ดู ที่ ภาพ มิติ มิติ การ การ แบบ สาม มิติ ฉาย ภาพ สัมประสิทธิ์ การ บิด เบือน ตาม แกน ทั้ง สาม จะ เท่า กัน มุม ระหว่าง แกน แกน แกน จะ เท่า กับ กับ 120 ° ได้ ฉาย ภาพ แบบ มี เท่า กัน โดย ใช้ ฉาย ภาพ แบบ ขนาน
ข้าว. 107. ประมาณ การ Аксонометрический ที่ กำหนด โดย โดย โดย โดย โดย โดย สาม มิติ มิติ เป็น รูป สี่ ผืน ผ้า ผ้า b — การ ภาพ ไดเมทริก เหลี่ยม เหลี่ยม
107. ประมาณ การ Аксонометрический ที่ กำหนด โดย โดย โดย โดย โดย โดย สาม มิติ มิติ เป็น รูป สี่ ผืน ผ้า ผ้า b — การ ภาพ ไดเมทริก เหลี่ยม เหลี่ยม
C — การ ฉาย สาม มิติ ผาก เฉียง สี่ สี่ เหลี่ยม
C — การ ภาพ สาม หน้า เฉียง
d — การฉายภาพสามมิติหน้าผากเฉียง
ข้าว. 107. ความต่อเนื่อง: e — การฉายภาพสามมิติแนวนอนยฉุ
ใน นี้ รังสี ที่ พุ่ง ออก มา จะ ตั้ง ฉาก กับ ระนาบ ฉาย ภาพ แบบ แบบ แบบ แบบ และ แกนพิกัด จะ เอียง กัน กับ การ ฉาย ภาพ แบบ แบบ แบบ วัตถุ กับ ดู ดู รูป 106) หาก เปรียบเทียบ เชิง วัตถุ กับ ที่ ที่ ที่ ที่ ที่ สอดคล้องกัน ของ ภาพ Аксонометрический K) ตาม ฉาย ภาพ สาม มิติ จะ เท่า กัน และ เท่า กับ 0,82 อย่าง ก็ ตาม เพื่อ ความ สะดวก ใน การ ก่อสร้าง ใช้ ค่า สัมประสิทธิ์ การ เบือน เชิง ปฏิบัติ ที่ เรียก ซึ่ง มี ค่า เท่า หนึ่ง หนึ่ง บิด เชิง เชิง ที่ เรียก ซึ่ง มี ค่า กับ หนึ่ง หนึ่ง รูป ที่ เชิง ปฏิบัติ เรียก ซึ่ง มี เท่า กับ หนึ่ง หนึ่ง หนึ่ง ที่ เชิง ปฏิบัติ เรียก ซึ่ง ค่า0003
ข้าว. 108. ตำแหน่ง แกน และ ค่า สัมประสิทธิ์ การ บิด เบือน ของ การ ฉาย สาม มิติ
มี ฉาย ภาพ แบบ สาม มิติ ไดเมทริก และ ไตรเมตริก การ ภาพ แบบ ไอ โซเมตริก การ การ ฉาย ภาพ ที่ ค่า สัมประสิทธิ์ การ เบือน เท่า กัน ทั้ง สาม แกน การ ภาพ แบบ ไดเมตริก เรียก การ ฉาย ดัง สาม การ ฉาย ภาพ ไดเมตริก เรียก การ ฉาย กล่าว สาม การ ฉาย แบบ เรียก การ ฉาย ดัง ซึ่ง ค่า การ บิด เบือน สอง ค่า ตาม แกน จะ เท่า และ ค่า ของ ค่า ที่ สาม แตกต่าง จาก ค่า กล่าว การ ฉาย ภาพ ไตรเมตริก ประกอบ ด้วย ฉาย ภาพ ที่ สัมประสิทธิ์ บิด เบือน ทั้งหมด กัน
เป็น ได้ ที่ จะ แสดง วัตถุ ทาง เรขาคณิต ต่าง ๆ โดย ใช้ วาด และ คอมพิวเตอร์ กราฟิก โดย ใช้ หลัก การ ภาพ สาม มิติ และ และ ความ ของ แต่ละ คน คือ อะไร?
Аксонометрия คืออะไร?
ภาย ใต้ Аксонометрический หรือ ฉาย ภาพ ภาพ ภาพ เป็น ที่ เข้าใจ กัน ว่า เป็น วิธี การ กราฟิก ของ วัตถุ เรขาคณิต บาง โดย โดย ใช้ ฉาย คู่ ขนาน ขนาน ขนาน ของ วัตถุ เรขาคณิต อย่าง โดย ใช้ การ ภาพ คู่ ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน ขนาน นี้ นี้ นี้ นี้ นี้ นี้ นี้ นี้ วาด วาด วาด วาด วาด วาด วาด วาด วาด วาด วาด วาด วาด วาด วาด วาด วาด วาด วาด วาด วาด นี้.