Инженерная графика сопряжение окружностей: Страница не найдена — НИЖНЕКАМСКИЙ ХИМИКО-ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

Содержание

Сопряжения в инженерной графике на чертежах с примерами

Автор Анна Евкова

Преподаватель который помогает студентам и школьникам в учёбе.

Содержание:

В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.

Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный в точку касания К, перпендикулярен к касательной прямой.
Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).

Точка касания К и центры окружностей

Центром сопряжения О называется точка, равноудаленная от сопрягаемых линий (рис. 12).
Точкой сопряжения А (В) называется точка касания двух сопрягаемых линий (рис. 12).
Дуга сопряжения АВ – это дуга окружности, с помощью которой выполняется сопряжение (рис. 12).
Радиус сопряжения R – это радиус дуги сопряжения (рис. 12).

Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.

Сопряжение двух пересекающихся прямых линий

Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.

Выполним следующие построения:

Построим множество точек центров сопряжения, удаленных от прямой n на расстояние радиуса R сопряжения. Таким множеством является прямая параллельная данной прямой n и отстоящая от неё на расстояние R.
Построим множество точек центров сопряжения, удаленных от прямой m на расстояние радиуса сопряжения.
Таким множеством является прямая параллельная m и отстоящая от последней на расстояние R.
В пересечении построенных прямых найдем центр сопряжения О.
Определим точку А сопряжения на прямой n. Для этого опустим из центра О перпендикуляр на прямую n . Для определения точки сопряжения В на прямой m необходимо опустить соответственно перпендикуляр из центра О на прямую m.

Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.

Сопряжения прямой с окружностью

Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.

Пример 1. Пусть задана окружность радиусом R с центром в точке и прямая m. Требуется построить сопряжение окружности с прямой дугой окружности заданного радиуса R (рис. 13).

Для решения задачи выполним следующие построения:

Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает прямая параллельная m и отстоящая от неё на расстояние R.
Множество точек центров сопряжения, удаленных от окружности n на рас- стояние R, есть окружность проведенная радиусом
Центр сопряжения О находим как точку пересечения линий
Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо про- вести линию центров т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
Проведем дугу сопряжения АВ.

Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра , радиусом

Заказать чертежи

Сопряжение двух окружностей

Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.

Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами дугой заданного радиуса R (рис. 15а).

Для нахождения центра сопряжения О проведем окружность удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности равен
Радиусом проведем окружность , удаленную от данной окружности n на расстояние R.
Найдем центр сопряжения О как точку пересечения окружностей .

Найдем точку сопряжения А как пересечение линии центров с дугой m.
Аналогично найдем точку В как пересечение линии центров с дугой n .
Проведем дугу сопряжения АВ.

Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами дугой радиусом R (рис. 15б).

Для нахождения центра сопряжения О проведем окружность на расстоянии от данной окружности m.
Проведем окружность на расстоянии от данной окружности n.
Центр сопряжения О найдем как точку пересечения окружностей
Точку сопряжения А найдем как точку пересечения линии центров с заданной окружностью m.
Точку сопряжения В найдем как точку пересечения линии центров c заданной окружностью n.
Проведем дугу сопряжения AВ с центром в точке O.

Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.

Построение касательных

Пример 1. Дана окружность с центром в точке и точка вне её. Через данную точку провести касательную к данной окружности (рис. 17).

Для решения задачи выполним следующие построения.

Соединим точку с центром окружности
Находим середину С отрезка
Из точки С, как из центра, проведем вспомогательную окружность радиусом
В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку с точкой А.

Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов (рис. 18).

Находим середину С отрезка
Из точки С, как из центра, радиусом проведем вспомогательную окружность.

Из центра большей окружности проведем вторую вспомогательную окружность радиусом
Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус идущий в точку касания В. 5. Для построения второй точки касания А проведем
Соединим точки А и В отрезком прямой линии.

Особенности построения — Всё для чайников

Подробности: Категория: Инженерная графика

Содержание материала

Особенности построения
Деление окружности
Сопряжение линий
Коробовые кривые линии
Построение уклона и конусности
Лекальные кривые
Все страницы

Страница 1 из 6

НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

ДЕЛЕНИЕ ОТРЕЗКОВ ПРЯМЫХ НА РАВНЫЕ ЧАСТИ

Из многочисленных построений здесь рассматриваются только те, которые часто встречаются при выполнении чертежей.

Деление отрезка прямой на две и четыре равные части выполняется в следующей последовательности.

Из концов отрезка А В циркулем проводят две дуги окружности радиусом R, несколько большим половины данного отрезка, до взаимного пересечения в точках n и m (рис. 43, а). Точки тип соединяют прямой, которая пересекает отрезок АВ в точке С. Точка С делит отрезок А В на две равные части. Проделав подобное построение для отрезка АС, находим его середину — точку D. Повторив построение для отрезка

СВ, разделим отрезок на четыре равные части.

При вычерчивании детали, показанной на рис. 43, б, применяется способ деления отрезка на четыре части.

Деление отрезка прямой на любое число равных частей. Пусть отрезок А В требуется разделить на И равных частей. Для этого из любого конца данного отрезка, например из точки В (рис. 44, проводят под произвольным острым углом вспомогательную прямую линию ВС, на которой от точки В измерительным циркулем откладывают 11 равных отрезков произвольной величины. Крайнюю точку 11 последней отложенной части соединяют с точкой А прямой Затем с помощью линейки и угольника проводят ряд прямых, параллельных прямой которые и разделяют отрезок А В на 11 равных частей.

На рис. 44, б показана деталь, при изготовлении которой необходимо разместить 10 центров отверстий; отверстия равномерно расположены на длине L. В этом случае применяется описанный выше способ деления отрезка прямой на равные части.

ПОСТРОЕНИЕ И ИЗМЕРЕНИЕ УГЛОВ ТРАНСПОРТИРОМ

Транспортир — это прибор для измерения и построения углов. Это полукруг с разбивкой на градусы, соединенный с опорной планкой.

Для измерения угла транспортир прикладывают опорной планкой к одной из сторон данного угла (рис. 45, а) так, чтобы вершина угла (точка А) совпадала с точкой О на транспортире. Величину угла САВ

в градусах определяют по шкале транспортира.

Для построения угла заданной величины (в градусах) со стороной А В и вершиной в точке к прикладывают транспортир так, чтобы его центр (точка О) совпал с точкой А прямой АВ, затем у деления шкалы транспортира, соответствующего заданному числу градусов (например, 55°), наносят точку n.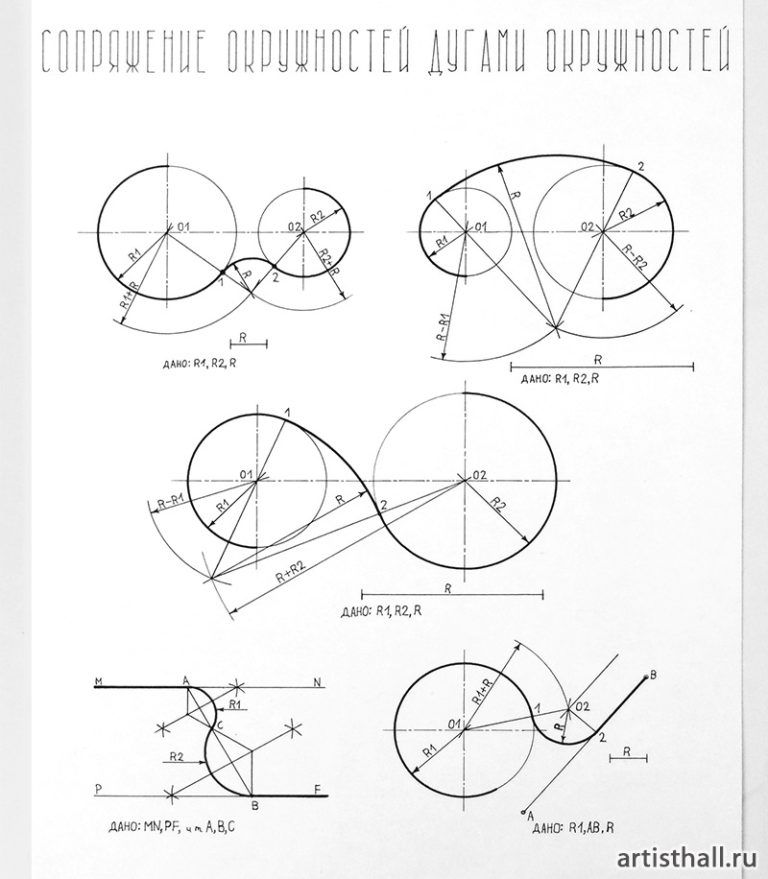 Транспортир убирают и проводят через точку n отрезок АС — получают заданный угол САВ (рис. 45, б).

Углы можно строить при помощи угольников с углами 45, 30 и 60° и линейки или рейсшины. На рис. 46 показано, как при различных положениях угольников на рейсшине можно строить углы 60 (120), 30 (150), 45° (135°) и другие при использовании одновременно двух угольников..

ПОСТРОЕНИЕ И ДЕЛЕНИЕ УГЛОВ

Деление угла на две и четыре равные части. Из вершины угла провести произвольным радиусом дугу до пересечения со сторонами угла в точках (рис. 47, а). Из полученных точек проводят две дуги радиусом R, несколько большим половины длины дуги n и к, до взаимного пересечения в точке m. Вершину угла соединяют с точкой т прямой, которая делит угол ВАС пополам. Эта прямая называется биссектрисой угла ВАС. Повторяя это построение с полученными углами В Ат и nАС угол ВАС можно разделить на четыре равные части и т. д.

Деление прямого угла на три равные части. Из вершины А прямого угла (рис. 47, б) произвольным радиусом R описывают дугу окружности до пересечения ее со сторонами прямого угла в точках a и b из которых проводят дуги окружности того же радиуса R до пересечения с дугой ab в точках m и n. Точки m и n соединяют с вершиной угла А прямыми и получают стороны Аm и Аn углов В Аm и nА С,равных 1/3 прямого угла, т. е. 30°. Если каждый из этих углов разделить пополам, то прямой угол будет разделен на шесть равных частей, каждый из углов будет равняться 15°. Прямой угол АВС можно разделить на три равные части угольником с углами 30 и 60° (рис. 48, а). При выполнении чертежей нередко требуется разделить прямой угол на две равные части. Это можно выполнять угольником с углом 45° (рис. 48, б).

Построение угла, равного данному. Пусть задан угол ВАС. Требуется построить такой же угол. Через произвольную точку А₁ проводим прямую А₁С₁. Из точки А описываем дугу произвольным радиусом R, которая пересечет угол ВАС в точках (рис. 49,а). Из точки A ₁ проводим дугу тем же радиусом и получаем точку m₁. Из точки A₁проводим дугу радиусом R₁равным отрезку mn, до пересечения с ранее проведенной дугой радиуса R в точке n₁ (рис. 49, б). Точку n₁ соединяем с точкой А₁ и получаем угол B₁A₁C₁величина которого равна заданному углу ВАС.

Применение вышеизложенного построения угла по заданному показано на рис. 49, в и г. На рис. 49, в изображена деталь, чертеж которой надо вычертить, а на рис. 49, г показан этот чертеж, при выполнении которого использован способ построения угла по заданному.

СПОСОБЫ ПОСТРОЕНИЯ МНОГОУГОЛЬНИКОВ

Способ триангуляции. Построение многоугольников этим способом основано на последовательном построении ряда треугольников, примыкающих сторонами друг к другу. Этот способ будет применяться в дальнейшем при построении разверток поверхностей геометрических тел.

Рассмотрим пример такого построения. На рис. 50, а показана пластина с пятиугольным отверстием. Измеряя длины сторон пятиугольника, можно построить на чертеже контурное очертание многоугольного отверстия.

Треугольники в рассматриваемом многоугольнике можно получить, проведя диагонали 14 (рис. 50, а). Последовательность построения многоугольника на чертеже в данном примере следующая.

На детали произвольно выбираем базовую линию (например, А В), на которую из точек 7 и 2 опускаем перпендикуляр, и получаем точки E и G. На чертеже наносим базовую линию A₁B₁ на которой откладываем отрезок E₁G₁ равный отрезку EG. Из точек и G, восставляем перпендикуляры, на которых откладываем взятые с детали отрезки и G1 (рис. 50, б). Получим точки 1₁и2₁. Из точек как из центров, циркулем описываем две дуги радиусами, равными отрезками 13 и 23, взятых с детали. Точка пересечения дуг является вершиной 3₁ искомого треугольника 1₁2₁3₁. Таким же способом из точек 7₁ и 3₁описываем две дуги радиусами, равными отрезкам 34 и 14, находим вершину 4₁. Затем из точек 4₁и 1₁, как из центров, описываем две дуги радиусами, равными отрезкам 45 и 15, определяем последнюю вершину пятиугольника 5₁(рис. 50, б).

Построение многоугольника методом прямоугольных координат показано на рис. 50, в. В этом случае из вершин многоугольника 12345 (рис. 50, а) опускаем перпендикуляры на линию АВ, получаем точки GDEFG. Расстояние между этими точками откладываем на прямой A₁B₁(pиc. 50, в). Из полученных точек C₁D₁E₁F₁G₁восставляем перпендикуляры, на которых откладываем отрезки С₅D₄, E₁, F₃, G₂. Искомые точки 7₁, 2₁, 3₁, 4₁, 5₁на чертеже соединяют и получают чертеж многоугольника.

ОПРЕДЕЛЕНИЕ ЦЕНТРА ДУГИ ОКРУЖНОСТИ

Многие детали машин и приборов имеют контур очертания, состоящий из прямых линий, лекальных кривых и дуг окружностей. При вычерчивании деталей часто приходится определять величину радиусов дуг окружностей контурных очертаний детали и находить положение центров этих дуг. На рис. 51, а показана деталь (кронштейн), левая часть ребра которой выполнена по дуге окружности.

Чтобы найти положение центра и величину радиуса данной дуги, предварительно делают отпечаток дуги на бумаге. При помощи циркуля и линейки можно определить центр и размер радиуса дуги окружности, для этого на отпечатке дуги намечают три произвольно расположенные на ней точки А, В и С (рис. 51, б) и проводят хорды АВ и ВС. При помощи циркуля и линейки проводят перпендикуляры через середины хорд А В и ВС. Точка пересечения перпендикуляров

(точка О) является искомым центром дуги детали, а расстояние от точки О до любой точки дуги будет размером радиуса.

Вперёд

3 Сопряжения . Инженерная графика

При выполнении машиностроительных чертежей, а также при разметке заготовок деталей на производстве часто приходится плавно соединять прямые линии с дугами окружностей или дугу окружности с дугами других окружностей, т. е. выполнять сопряжение.

Сопряжением называют плавный переход отрезка прямой в дугу окружности или дуги одного радиуса в дугу другого радиуса.

Для построения сопряжений необходимо знать величину радиуса сопряжения, определить центры, из которых проводят дуги, т. е. центры сопряжений (рисунок 9). Затем нужно найти точки, в которых одна линия переходит в другую, т.е. точки сопряжений. При построении чертежа сопрягающиеся линии нужно доводить точно до этих точек.

Рисунок 9 – Элементы сопряжений

Точка сопряжения дуги окружности и прямой лежит на перпендикуляре, опущенном из центра дуги на сопрягаемую прямую (рисунок 10,а), или на линии, соединяющей центры сопрягаемых дуг (рисунок 10б). Следовательно, для построения любого сопряжения дугой заданного радиуса нужно найти центр сопряжения и точку (точки) сопряжения.

Сопряжение двух пересекающихся прямых дугой заданного радиуса. Даны пересекающиеся под прямым, острым и тупым углами прямые линии (рисунок 11а). Нужно построить сопряжения этих прямых дугой заданного радиуса R.

Рисунок 10 – Определение точки сопряжения

Для всех трех случаев можно применять следующее построение.

Находят точку О – центр сопряжения, который должен лежать на расстоянии R от сторон угла, т.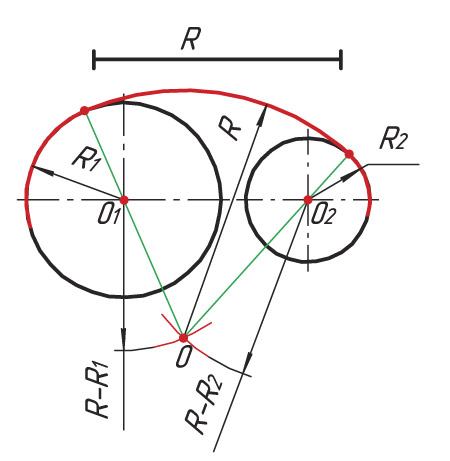 е. в точке пересечения прямых, проходящих параллельно сторонам угла на расстоянии R от них (рисунок 11б).

1. Для проведения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, равным R, делают засечки и к ним проводят касательные (рисунок 11б).

2. Находят точки сопряжений (рисунок 11в). Для этого из точки 0 опускают перпендикуляры на заданные прямые.

3. Из точки 0, как из центра, описывают дугу заданного радиуса R между точками сопряжений (рисунок 11в).

Рисунок 11 – Построение сопряжения двух пересекающихся прямых

Сопряжение трёх пересекающихся прямых. Положение центра сопрягаемой окружности определяется точкой пересечения биссектрис углов. Радиус окружности (дуги сопряжения) равен длине перпендикуляра, опущенного из центра 0 на любую из заданных прямых (рисунок 12).

Рисунок 12 – Сопряжение трёх пресекающихся прямых

Сопряжение двух параллельных прямых. Заданы две параллельные прямые и на одной из них точка сопряжения М (рисунок 13а). Требуется построить сопряжение.

Построение выполняют следующим образом:

1) находят центр сопряжения и радиус дуги (рисунок 13б). Для этого из точки М восставляют перпендикуляр до пересечения с прямой в точке N.

Отрезок прямой MN делят пополам;

2) из точки О – центра сопряжения радиусом OM = ON описывают дугу от точек сопряжения М и N (рисунок 13 в).

Упражнение. Выполните чертеж шаблона (рисунок 14), применив правила построения сопряжений. Линии построений не стирайте. Нанесите размеры и обозначения шероховатости поверхностей, имея в виду, что внутренние поверхности шаблона должны иметь шероховатости Ra 0,80, а остальные Rг 12,5. Масштаб 1:1. Заполните основную надпись (материал – сталь 45 по ГОСТ 1050-88).

Рисунок 13 – Построение сопряжения двух параллельных прямых

Рисунок 14 – Задание для упражнений

Сопряжение дуги окружности и прямой линии дугой заданного радиуса.

Внешнее касание (рисунок 15а).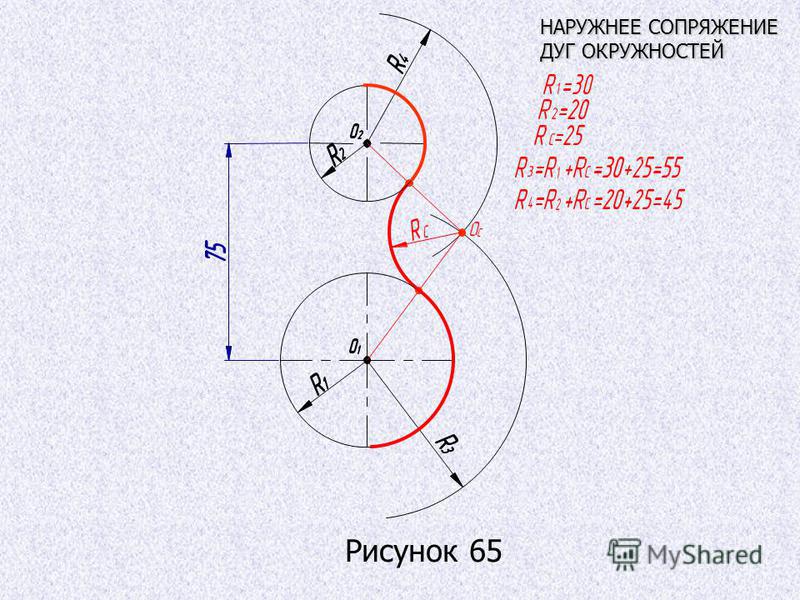 Центр 01 дуги сопряжения находится на пересечении вспомогательной прямой, отстоящей от заданной прямой на величину радиуса R1, и дуги радиуса R + R1 из центра 0. Точки сопряжения K и M находятся соответственно в основании перпендикуляра 01K и на пересечении прямой 001 с основной окружностью.

Внутреннее касание (рисунок 15б). Центр 01 дуги сопряжения находится на пересечении вспомогательной прямой, отстоящей от заданной прямой на величину радиуса R, и дуги радиуса R ? R1 из центра 0. Точки сопряжения – соответственно в основании перпендикуляра 01 K и на пересечении продолжения луча 001 с основной окружностью.

Рисунок 15 – Сопряжение дуги окружности и прямой линии дугой заданного радиуса: а – внешнее касание, б – внутреннее касание.

Сопряжение окружности и прямой при условии, что дуга сопряжения проходит через заданную точку А на окружности (рисунок 16).

Центр дуги сопряжения определяется точкой пересечения луча OA, проведённого через точку сопряжения А и центр O заданной окружности, и биссектрисы угла ABK, образованного касательной AB в точке сопряжения и заданной прямой t. Радиус сопрягающей дуги равен расстоянию O₁A; O₁K? t, где K – точка сопряжения на прямой t.

Рисунок 16 – Сопряжение окружности и прямой при заданной точке сопряжения на окружности: а – внешнее касание, б – внутреннее касание.

Построение окружности, проходящей через данную точку A и касаю щейся данной окружности м центром O в заданной точке B (рисунок 17, 18, 19). Центр O₁ дуги сопряжения определяется точкой пересечения луча, проведённого через центр O заданную точку сопряжения B, с перпендикуляром, восстановленным из середины хорды AB; O₁B – радиус искомой окружности.

Рисунок 17 – Сопряжение окружности в заданной точке B с окружностью, проходящей через заданную точку A: а – внешнее касание, б – внутреннее касание.

Рисунок 18 – Проведение касательной к окружности

Рисунок 19 – Сопряжение дуг окружностей

Проведение касательной к окружности. Даны окружность с центром О и точка А. Провести из точки А касательную к окружности.

1. Точку А соединяют прямой с заданным центром О окружности. Строят вспомогательную окружность диаметром, равным ОА (рисунок 20а). Для определения центра О1, делят отрезок ОА пополам.

2. Точки М и N являются точками пересечения вспомогательной окружности с заданной – искомые точки касания. Точку А соединяют прямыми с точками М или N (рисунок 20б). Прямая AM будет перпендикулярна прямой ОМ, так как угол АМО опирается на диаметр.

Данный текст является ознакомительным фрагментом.

Презентация по инженерной графике Сопряжение доклад, проект

Главная
Разное
Образование
Спорт
Естествознание
Природоведение
Религиоведение
Французский язык
Черчение
Английский язык
Астрономия
Алгебра
Биология
География
Геометрия
Детские презентации
Информатика
История
Литература
Математика
Музыка
МХК
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
Педагогика
Русский язык
Технология
Физика
Философия
Химия
Шаблоны, фоны, картинки для презентаций
Экология
Экономика

Презентация на тему Презентация по инженерной графике Сопряжение, предмет презентации: Черчение.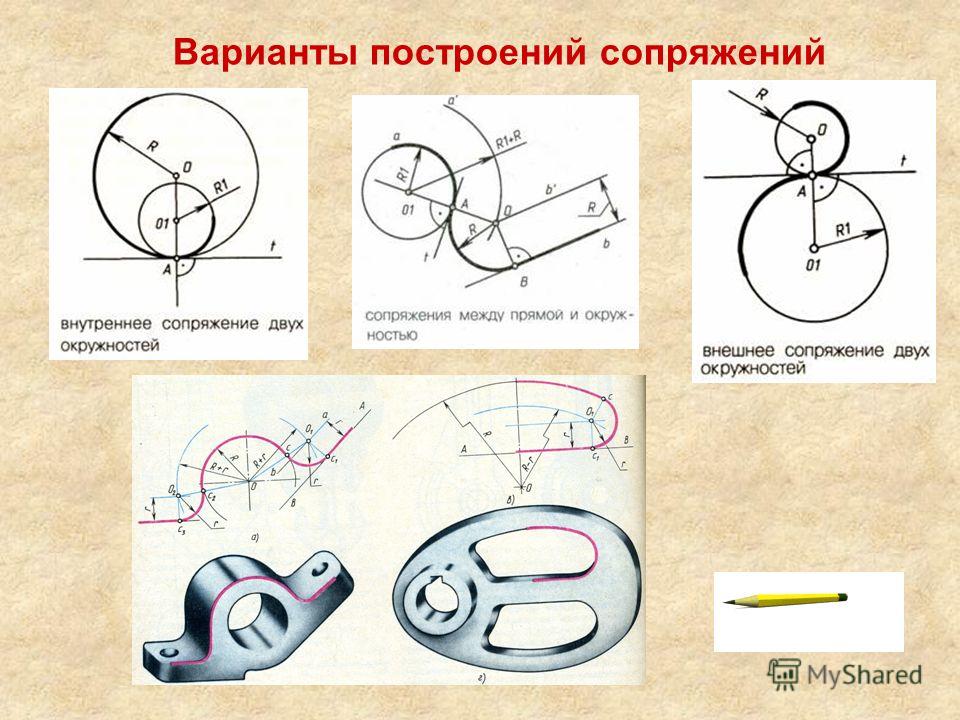 Этот материал в формате pptx (PowerPoint) содержит 14 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.

Слайд 1Текст слайда:

АЛЬБОМ
по дисциплине «Инженерная графика»
тема: «Сопряжение»

Слайд 2Текст слайда:

Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений. Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.

Слайд 3Текст слайда:

построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.

Слайд 4Текст слайда:

Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b.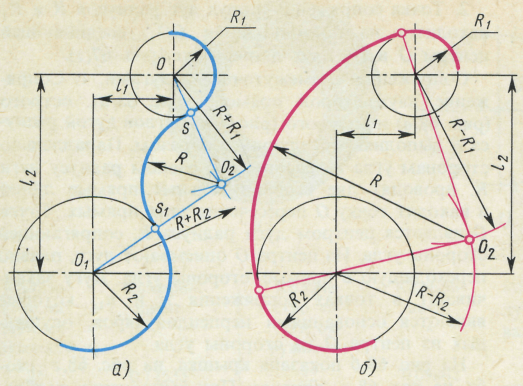 Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a и b. Сопряжение острого угла построено.

Сопряжение острого угла

Слайд 5Текст слайда:

Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.

Сопряжение тупого угла

Слайд 6Текст слайда:

Сопряжение параллельных прямых линий

Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b.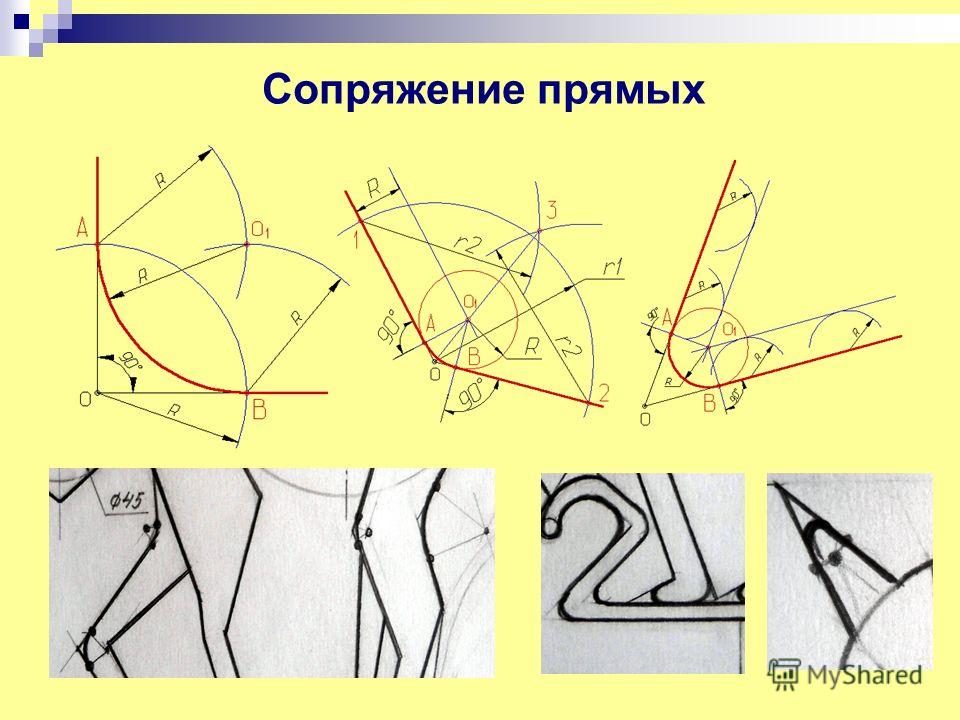 Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.

Слайд 7Текст слайда:

Внешнее сопряжение дуги и прямой линии

В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.
Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.
Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией.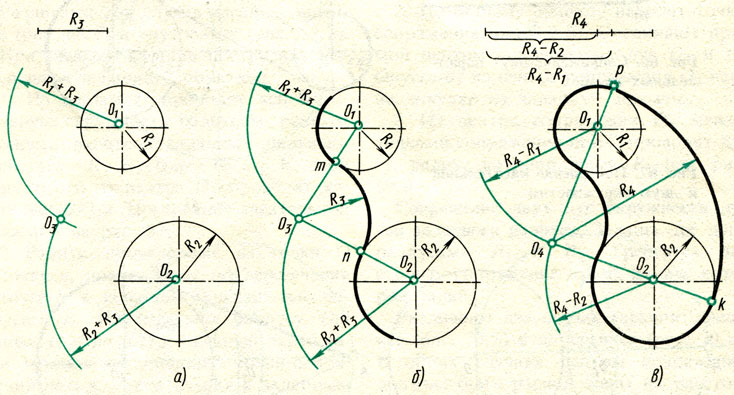 Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.

Слайд 8Текст слайда:

Внутреннее сопряжение прямой линии с дугой

По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r. Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.
Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.
Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.

Слайд 9Текст слайда:

Внешнее сопряжение дуг окружностей

Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

Слайд 10Текст слайда:

Внутреннее сопряжение дуг окружностей

Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

Слайд 11Текст слайда:

Смешанное сопряжение дуг окружностей

Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

Слайд 12Текст слайда:

Применение сопряжений в контурах
технических деталей

Слайд 13Текст слайда:

Творческие работы

Слайд 14Текст слайда:

Графическая работа

Скачать презентацию

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Пр.раб. 3 Инженерная графика — Сопряжение.

ПРАКТИЧЕСКАЯ РАБОТА № 3

по предмету «Инженерная графика»

специальность 220703

Тема: Сопряжение линий

Цель: 1. Закрепить на практике алгоритм выполнения сопряжения

2. Научиться выполнять сопряжение угла, прямой и окружности, двух окружностей

3. Развивать глазомер, аккуратность, самостоятельность

Методы: Индивидуальная работа студентов по заданию

Оснащение: — чертежные инструменты, чертежная бумага формата А4;

— методическое пособие;

— плакаты «Сопряжения»;

— Учебник Боголюбов С.К. Черчение, М., 1989., с.35-39

— Боголюбов С.К. Индивидуальные задания по курсу черчения, М., 1989., с.15-36

Ход работы:

1. Организационный этап:

— Проверка наличия у студентов чертежной бумаги, карандашей, чертежных инструментов, ластика

— Проверка выполнения на бумаге формата А4 рамки и основной надписи

2. Повторение изученного материала:

Ответить на вопросы:

-Как называются плавные линии перехода окружностей в прямые на чертеже?

— Какие элементы необходимо найти для выполнения сопряжения?

3. Самостоятельная работа по выполнению задания:

Для точного и правильного выполнения чертежей необходимо уметь выполнять построения сопряжений, которые основаны на двух положениях:

1. Для сопряжения прямой линии и дуги необходимо, чтобы центр окружности, которой принадлежит дуга, лежал на перпендикуляре к прямой, восстановленном из точки сопряжения ( см.рисунок 1).

Рисунок 1

2. Для сопряжения двух дуг необходимо, чтобы центры окружностей, которым принадлежат дуги, лежали на прямой, проходящей через точку сопряжения ( см.рисунок 2).

Рисунок 2

Сопряжение двух сторон угла (острого и тупого) дугой заданного радиуса R выполняют следующим образом (см. рисунки 3 и 4):

Рисунок 3 и 4

Параллельно сторонам угла на расстоянии, равном радиусу дуги R, проводят две вспомогательные прямые линии. Точка пересечения этих прямых (точка О) будет центром дуги радиуса R, т.е. центром сопряжения. Из центра О описывают дугу, плавно переходящую в прямые – стороны угла. Дугу заканчивают в точках сопряжения n и n₁, которые являются основаниями перпендикуляров, опущенных из центра О на стороны угла.

При построении сопряжения сторон прямого угла центр дуги сопряжения проще находить с помощью циркуля (см.рисунок 5).

Рисунок 5

Из вершины угла А проводят дугу радиусом R, равным радиусу сопряжения. На сторонах угла получают точки сопряжения n и n₁_. Из этих точек, как из центров, проводят дуги радиусом R до взаимного пересечения в точке О, являющейся центром сопряжения. Из центра О описывают дугу сопряжения.

Сопряжение прямой с дугой окружности может быть выполнено при помощи дуги с внешним касанием (см. рисунок 6)

Рисунок 6

и внутренним касанием (см. рисунок 7).

Рисунок 7

На рисунке 6 показано сопряжение дуги окружности радиусом R и прямой линии АВ дугой окружности радиуса r с внешним касанием. Для построения такого сопряжения проводят окружность радиуса R и

прямую АВ. Параллельно заданной прямой на расстоянии, равном радиусу r (радиус сопрягающей дуги), проводят прямую ab. Из центра О проводят дугу окружности радиусом, равным сумме радиусов R и r, до пересечения ее с прямой ab в точке О₁. Точка О₁ является центром дуги сопряжения.

Точку сопряжения с находят на пересечении прямой ОО₁ с дугой окружности радиуса R. Точка сопряжения с₁ является основанием перпендикуляра, опущенного из центра О₁на данную прямую АВ. При помощи аналогичных построений могут быть найдены точки О₂, с₂, с₃.

На рисунке 7 выполнено сопряжение дуги радиуса R с прямой АВ дугой радиуса r с внутренним касанием. Центр дуги сопряжения О₁ находится на пересечении вспомогательной прямой, проведенной параллельно данной прямой на расстоянии r, с дугой вспомогательной окружности, описанной из

центра О радиусом, равным разности R – r. Точка сопряжения с₁ является основанием перпендикуляра, опущенного из точки О₁ на данную прямую. Точку сопряжения с находят на пересечении прямой ОО₁ с сопрягаемой дугой.

Сопряжение дуги с дугой может быть внутренним, внешним и смешанным.

При внутреннем сопряжении центры О и О₁ сопрягаемых дуг находятся внутри сопрягающей дуги радиуса R (см.рисунок 8).

Рисунок 8

При внешнем сопряжении центры О и О₁ сопрягаемых дуг радиусов R₁ и R₂ находятся вне сопрягающей дуги радиуса R (см.рисунок 9).

Рисунок 9

При смешанном сопряжении центр О₁ одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R, а центр О другой сопрягаемой дуги вне ее (см. рисунок 10).

Рисунок 10

Построение внутреннего сопряжения

Задано:

а) радиусы сопрягаемых окружностей R₁ и R₂ ;

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

Требуется:

а) определить положение центра О₂ сопрягающей дуги;

б) найти точки сопряжения s₁ и s;

в) провести дугу сопряжения.

Построение сопряжения показано на рисунке 8. По заданным расстояниям между центрами l₁ и l₂_{на чертеже
намечают центры О и О₁, из которых описывают сопрягаемые дуги
радиусов R₁ и R₂. Из центра О₁ проводят вспомогательную дугу окружности радиусом, равным разности радиусов
сопрягающей дуги R и сопрягаемой R₁. Вспомогательные
дуги пересекутся в точке О₂, которая и будет искомым центром
сопрягающей дуги.}

Для нахождения точек сопряжения точку О₂ соединяют с точками О и О₁ прямыми линиями. Точки пересечения продолжения прямых О₂О и О₂О₁ с сопрягаемыми дугами являются искомыми точками сопряжения (точки s и s₁).

Радиусом R из центра О₂ проводят сопрягающую дугу между точками сопряжения s и s₁.

Построение внешнего сопряжения

Задано:

а) радиусы R₁ и R₂ сопрягаемых дуг окружностей;

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

Требуется:

а) определить положение центра О₂ сопрягающей дуги;

б) найти точки сопряжения s₁ и s;

в) провести дугу сопряжения.

Построение внешнего сопряжения показано на рисунке 9. По заданным расстояниям между центрами l₁ и l₂ на чертеже намечают центры О и О₁, из которых описывают сопрягаемые дуги радиусов R₁ и R₂. Из

центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягающей дуги R и сопрягаемой R₁, а из центра О₁ – радиусом, равным сумме радиусов сопрягаемой дуги R₂ и сопрягающей R. Вспомогательные дуги пересекутся в точке О₂, которая будет искомым центром сопрягающей дуги.

Для нахождения точек сопряжения центры дуг соединяют прямыми линиями ОО₂ и О₁О₂. Эти две прямые пересекают сопрягаемые дуги в точках сопряжения s и s₁.

Радиусом R из центра О₂_{проводят сопрягающую дугу, ограничивая ее точками сопряжения s₁ и s .}

Построение смешанного сопряжения

Задано:

а) радиусы R₁ и R₂ сопрягаемых дуг окружностей;

б) расстояния l₁ и l₂ между центрами этих дуг;

в) радиус R сопрягающей дуги.

Требуется:

а) определить положение центра О₂ сопрягающей дуги;

б) найти точки сопряжения s₁ и s;

в) провести дугу сопряжения.

Построение внешнего сопряжения показано на рисунке 10. По заданным расстояниям между центрами l₁ и l₂_{на чертеже
намечают центры О и О₁, из которых описывают сопрягаемые дуги
радиусов R₁ и R₂. Из}

центра О проводят вспомогательную дугу окружности радиусом, равным сумме радиусов сопрягающей дуги R и сопрягаемой R₁, а из центра О₁ – радиусом, равным разности радиусов R₂ и R. Вспомогательные дуги пересекутся в точке О₂, которая будет искомым центром сопрягающей дуги.

Соединив точки О и О₂ прямой, получают точку сопряжения s₁; соединив точки О₁ и О₂, находят точку сопряжения s. Из центра О₂ проводят дугу сопряжения от s до s₁.

При вычерчивании контура детали н6еобходимо разобраться, где имеются плавные переходы, и представить себе, где надо выполнить те или иные виды сопряжения.

4.Задание:

В тетради выполнить сопряжения острого и тупого углов.

На листе формата А4 по прилагаемому заданию вычертить изображения контуров детали и эллипса ( см.рисунок 11)

Рисунок 11

5. Ответить на вопросы:

1. Что такое сопряжение?

2. Назовите элементы, обязательные в каждом сопряжении.

3. Сопряжения каких типов линий мы рассмотрели.

Литература

1. Боголюбов С.К., Черчение, М., 1989., с.35-39

2. Боголюбов С. К., Индивидуальные задания по курсу черчения, М., 1989., с.15-36

Преподаватель Н.В.Карабанова

Занятие по инженерной графике «Геометрические построения. Сопряжение» – Документ 1 – УчМет

ПЛАН

ОТКРЫТОГО ЗАНЯТИЯ

по дисциплине

Инженерная графика

1 Цикл дисциплин: общепрофессиональный

2 Специальность: 220204 Автоматика и телемеханика на транспорте

(по видам транспорта) (на железнодорожном транспорте)

группа: А-21

3 Вид занятия: комбинированный

4 Дата проведения: 9 февраля 2010 года

5 Место проведения: ауд. 307

6 Преподаватель: Войнова Елена Анатольевна

7 Тема занятия: Геометрические построения. Сопряжение

8 Цель занятия:

1 Научить определять тип сопряжений и практически овладеть приемами

выполнения сопряжений;

2 Развитие умения аналитически рассуждать;

3 Воспитание аккуратности и умения работать чертежными инструментами

9 Задачи занятия:

Образовательная

1 Формирование новых понятий.

2 Познакомить учащихся с применением сопряжений в технических формах,

предметах быта;

3 Углубление знаний.

4 Систематизация обобщения знаний.

Развивающая

1 Развитие творческого мышления.

2 Развивать логическое мышление, познавательный интерес, умение

работать чертежными инструментами;

3 Формирование качеств творческой личности.

4 Научить строить сопряжение между сторонами углов;

5 Познакомиться со способами построения сопряжения между двумя

окружностями, окружностью и прямой

Воспитательная

1 Показ важности изучаемой темы.

2 Воспитывать точность, аккуратность, внимательность.

3 Показ значимости приобретенных знаний.

4 Формирование умений осуществлять контроль.

10 Методы проведения: фронтальный опрос, рассказ с демонстрацией,

выполнение графической работы

11 Средства обучения и наглядные пособия:

1 Мультимедийная презентация;

2 Мультимедийный проектор с экраном;

3 Карточки-задания;

4 Образцы графических работ

12 Структура открытого занятия:

1 Организационная момент;

2 Повторение ранее изученного материала;

3 Получение новых знаний;

4 Закрепление полученных знаний;

5 Выполнение графической работы;

6 Подведение итогов

12 Ход занятия:

1 Организационный момент

2 Повторение ранее изученного материала.

по теме «Геометрические построения.

Деление окружностей на равные части».

Фронтальный опрос.

Задание:

Разделить окружности на 3 и 6 равных частей, 4 и 8 частей, 3 и 12; 8 и 6

Ответить на вопрос: Где в повседневной жизни можно встретить предметы, в которых применили деление окружности на равные части? (по окончании работы сдаются на проверку преподавателю).

В декоративно-прикладном искусстве дизайнеры, ювелиры с успехом применяли деление окружности, создавая прекрасные произведения: ордена, медали, монеты, ювелирные изделия и многое другое (показ слайдов).

Ордена и медали

На 8 частей

Звезда ордена Святого апостола

Андрея Первозванного

На 7 частей: На 4 части На 5 частей

Орден Верности Орден Жукова Знак ордена Орден Красной Звезды

(Афганистан) святого Георгия

Ювелирные украшения

Обратите внимание на технические детали, к примеру, различные гаечные ключи, гайки, колеса, диски, плашки и т. д. (показ слайдов)

3 Получение новых знаний

Что же такое сопряжение?

Сопряжение – это плавный переход из одной линии в другую.

Задумывались ли вы когда — нибудь о роли сопряжений?

Мало кто знает, что эти кривые диаграммы нашей жизни называются сопряжениями. Эти кривые повороты, сглаженные формы окружают человечество с незапамятных времен. Нет такой отрасли, в которой невозможно не встретить сопряжение.

Сопряжение применяется для того, чтобы построить контур технической детали, (показ двух технических деталей), где можно наблюдать плавные переходы одной поверхности в другую. Для того чтобы построить чертежи данных деталей, необходимо знать способы построения сопряжений. Плавные переходы одной поверхности в другую на технических деталях применяются для того, чтобы повысить стойкость и увеличить прочность, удобного и безопасного обращения.

Где же берет начало сопрягающая линия?

Поворот скоростной автотрассы чаще всего имеет форму дуги. Одно направление скоростной трассы должно плавно переходить в другое. Величина радиуса поворота должна быть строго рассчитана с учетом веса и скорости автомашин, едущих по данной дороге. Ведь если автомобилист на скорости не «вписался» в поворот, его отбросит центробежная сила, и тогда произойдет катастрофа. Поэтому каждая категория трасс рассчитана на свою скорость и радиусы вставок-поворотов строго нормированы

Если вы бывали на соревнованиях лыжников по прыжкам с трамплина, то видели плавный переход от стартовой поверхности, на которой спортсмен разгоняется, к другой поверхности, которая дает ему возможность взлететь. Но стоит незначительному дефекту нарушить плавность траектории спуска, и со спортсменом, мчащимся на огромной скорости, случится непоправимое несчастье.

Сопряжение в технике

Что же позволяет сегодня машине, локомотиву двигаться быстрее ветра, самолету быстрее звука? Ответ по наивному прост — обтекаемые формы (показ слайдов).

Сопряжения в архитектуре и интерьере

Первое, что всегда «оказывается» под рукой — природа с ее изяществом и пластикой невероятных форм. Дизайнер взывает к нашей фантазии, апеллируя простыми, а порой и бессмысленными образами, создавая предметы привычного нам обихода.

Сопряжения в декоративно-прикладном искусстве

Используя правила построения сопряжения, выполнены несколько вариантов чертежей подсвечника в стиле модерн.

Применение сопряжений настолько разнообразно и многопланово, что дать все примеры их использования просто невозможно.

А .Изучение нового материала.

Сегодня на уроке мы научимся строить такие линии.

— Сопряжением называется плавный переход от одной линии к другой.

Б.Сопряжение двух сторон угла дугой окружности

— Попробуем научиться сопрягать элементы деталей. Начнем с самого простого построения — скругления углов. Основа всех таких построений — определение точек сопряжения (точек касания линий), центра сопряжения и радиуса сопряжения.

Глоссарий

Центр сопряжения.
Радиус сопряжения.
Точка сопряжения.
Сопрягаемые прямые.
Сопрягающая дуга.

В. Демонстрация выполнения сопряжения.

Для скругления острого, тупого и прямого углов применяют общий способ построения.

В остром углу В тупом углу В прямом углу

— От каждой стороны угла /сопрягаемые прямые/ (возьмем скругление прямого угла) проводим параллельные прямые на расстоянии, равном радиусу сопряжения.

— Радиус сопряжения обычно известен и указан на чертеже.

— В точке пересечения этих прямых находится точка О — центр сопряжения.

— Найдем точки сопряжения. Для этого проведем перпендикуляры из центра сопряжения к заданным прямым. Полученные точки являются точками сопряжений.

— Из найденного центра раствором циркуля, равным радиусу сопряжения, проведем дугу окружности, /сопрягающая дуга/ являющейся плавным переходом от одной стороны угла к его другой стороне.

(Студенты работают в тетрадях. Выполняют сопряжение острого и тупого угла, сопряжение в прямом углу – дома на оценку).

Г. Сопряжение дуги с дугой

Сопряжение двух дуг окружностей может быть внутренним, внешним и смешанным.

При внутреннем сопряжении центры сопрягаемых дуг радиусов R1 и R2 находятся внутри сопрягающей дуги радиуса R.

При внешнем сопряжении центры сопрягаемых дуг радиусов R1 и R2 находятся вне сопрягающей дуги радиуса R.

Деталь «Серьга» —

пример внутреннего

и внешнего сопряжений

При смешанном сопряжении центр одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R, а центр другой сопрягаемой дуги — вне ее.

Рассмотрим на примере построение сопряжений (демонстрация этапов построения на доске и выполнение в рабочих тетрадях).

Построение внутреннего сопряжения

Дано:

А. Радиусы сопрягаемых окружностей R = 15 и R1= 25

Б. Расстояние между центрами окружностей – l=60

В. Радиус сопрягающей дуги- R2=70.
R3 = 70-15=55

R4= 70-25= 45

Требуется:

А. Определить положение центра О2 сопрягающей дуги.

Б. Найти точки сопряжения

В. Провести дугу сопряжения.

Решение:

По заданному расстоянию между центрами l на чертеже намечают центры О и О1 , из которых описывают радиусы сопрягаемых окружностей R и R1. Из центра О проводят вспомогательную дугу окружности радиусом R3, равным разности радиусов сопрягающей дуги R2 и сопрягаемой R, а из центра О1 – радиусом, равным разности радиусов сопрягающей дуги R2 и сопрягаемой R1. Вспомогательные дуги пересекутся в точке О2, которая и будет искомым центром сопрягающей дуги.

Для нахождения точек сопряжения точку О2 соединяют с точками О и О1 прямыми линиями. Точки пересечения продолжения прямых О2О и О2О1 с сопрягаемыми дугами являются искомыми точками сопряжения.

Радиусом R2 из центра О2 проводят сопрягающую дугу между точками сопряжения.

Построение внешнего сопряжения.

Дано:

А. Радиусы сопрягаемых окружностей R = 15 и R1= 25

Б. Расстояние между центрами окружностей – l=60

В. Радиус сопрягающей дуги- R2=70.
R3 = 70+15=85

R4= 70+25= 95

Требуется:

А. Определить положение центра O2 сопрягающей дуги.

Б. Найти точку сопряжения.

В. Провести дугу сопряжения.

Решение:

По заданному расстоянию между центрами l на чертеже намечают центры О и О1 , из которых описывают радиусы сопрягаемых окружностей R и R1. Из центра О проводят вспомогательную дугу окружности радиусом R3, равным сумме радиусов сопрягающей дуги R2 и сопрягаемой R, а из центра О1 – радиусом, равным сумме радиусов сопрягающей дуги R2 и сопрягаемой R1. Вспомогательные дуги пересекутся в точке О2, которая и будет искомым центром сопрягающей дуги.

Для нахождения точек сопряжения центры дуг соединяют прямыми линиями ОО2 и О1О2. Эти две прямые пересекают сопрягаемые дуги в точках сопряжения.

Из центра О2 радиусом R проводят сопрягающую дугу, ограничивая ее точками сопряжения.

(смешанное сопряжение студенты строят дома на оценку)

4 Закрепление полученных знаний

Что называется сопряжением?

(-это плавный переход из одной линии в другую)

2 Где можно встретить сопряжение?

(в технических деталях, в предметах быта)

2 Для чего в деталях делают плавные переходы между поверхностями?

(Плавные переходы одной поверхности в другую на технических деталях применяются для того, чтобы повысить стойкость и увеличить прочность, удобного и безопасного обращения).

Далее преподаватель предлагает студентам попробовать свои силы у доски 2 человека. Студентам на слайде показывают устройства СЦБ и их кинематическое изображение. По заданию надо определить где и какой вид сопряжения применили для из выполнения).

1 студент

Стрелочный электропривод Конструкция Семафор

микропереключателя ПП-1

2 студент

Замыкатель остряков ВЗ-4

Стрелочный электропривод Кабельная муфта

5 Выполнение графических заданий.

Форма работы – индивидуальная.

5. Подведение итога урока.

Рекомендуемая литература

Строительство эллипса — вопросы и ответы по техническим чертежам

Этот набор вопросов и ответов с несколькими вариантами ответов (MCQ) по инженерным чертежам посвящен теме «Построение эллипса — 1».

1. Что из перечисленного неверно в отношении Ellipse?
a) Эксцентриситет меньше 1
b) Математическое уравнение X ² /a ² + Y ² /b ² = 1
c) Если плоскость параллельна оси конуса, то он пересекает конус тогда сечение дает эллипс
d) Сумма расстояний от двух фокусов до любой точки эллипса постоянна
Посмотреть Ответ

Ответ: c
Объяснение: Если плоскость параллельна оси конуса и пересекает конус, то поперечное сечение дает гиперболу . Если плоскость параллельна основанию, она дает окружность. Если плоскость наклонена под углом, большим внешнего угла конуса, она дает параболу. Если плоскость наклонена и пересекает все образующие, то она образует эллипс.

2. В какой из следующих конструкций не используются эллиптические кривые?
a) Градирни
b) Плотины
c) Мосты
d) Люки
Просмотр Ответ

Ответ: a
Пояснение: Градирни, водные каналы используют гиперболические кривые в качестве конструкции. Арки, мосты, звукоотражатели, светоотражатели и т. д. используют параболические кривые. Арки, мосты, дамбы, памятники, люки, сальники и сальники и т. д. используют эллиптические кривые.

3. Линия, проходящая через фокус и перпендикулярно большой оси, ________
а) Малая ось
b) Широкая прямая кишка
c) Директриса
d) Касательная
Просмотреть Ответ

Ответ: b
Пояснение: Линия, делящая большую ось пополам под прямым углом и оканчивающаяся кривой, называется малой осью. Линия, проходящая через очаг и перпендикулярно большой оси, называется широкой прямой кишкой. Касательная – это линия, которая касается кривой только в одной точке.

Примечание: присоединяйтесь к бесплатным занятиям по санфаянсу в Telegram или на Youtube

4. Что из следующего является эксцентриситетом эллипса?
a) 1
b) 3/2
c) 2/3
d) 5/2
Посмотреть ответ

Ответ: c
Объяснение: Эксцентриситет эллипса всегда меньше 1. Эксцентриситет всегда равен 1 для любого парабола. Эксцентриситет всегда равен 0 для окружности. Эксцентриситет гиперболы всегда больше 1.

5. Оси называются сопряженными, если они параллельны касательным, проведенным в их крайних точках.
а) Правда
b) False
View Answer

Ответ: a
Объяснение: В эллипсе существуют две оси (большая и малая), перпендикулярные друг другу, крайние точки которых имеют касательные, параллельные им. Существуют две сопряженные оси для эллипса и по одной для параболы и гиперболы.

6. Приведены шаги по рисованию эллипса петлей методом нити. Расположите ступеньки.
я. Проверьте, достаточно ли длины резьбы, чтобы коснуться конца малой оси.
ii. Проведите две оси AB и CD, пересекающиеся в точке O. Найдите фокусы F1 и F2.
III. Перемещайте карандаш по фокусам, сохраняя равномерное натяжение нити на всем протяжении, и получите эллипс.
ив. Вставьте булавку в каждую точку фокусировки и обвяжите кусок нити в виде петли вокруг булавки.
a) i, ii, iii, iv
b) ii, iv, i, iii
c) iii, iv, i, ii
d) iv, i, ii, iii
Посмотреть ответ

Ответ: b
Объяснение : Это самый простой способ рисования эллипса, если мы знаем расстояние между фокусами и малой осью, большой осью. Это возможно, поскольку эллипс можно очертить точкой, движущейся в той же плоскости и таким образом, что сумма расстояний от нее до двух фокусов всегда одинакова.

7. Даны шаги по рисованию эллипса методом траммель. Расположите ступеньки.
я. Поместите трамблер так, чтобы R находилась на малой оси CD, а Q — на большой оси AB. Тогда P окажется на эллипсе.
ii. Проведите две оси AB и CD, пересекающие друг друга в точке O.
iii. Перемещая трамвай в новые позиции, всегда удерживая R на CD и Q на AB, получайте другие точки и соединяйте их, чтобы получить эллипс.
ив. Вдоль края полоски бумаги, которую можно использовать в качестве трамвая, отметьте PQ, равный половине малой оси, и PR, равный половине большой оси.
a) i, ii, iii, iv
b) ii, iv, i, iii
c) iii, iv, i, ii
d) iv, i, ii, iii
Посмотреть ответ

Ответ: b
Объяснение : В этом методе используются трамплины PQ и PR, концы которых Q и R должны располагаться на большой и малой осях соответственно. Это возможно, поскольку эллипс можно очертить точкой, движущейся в той же плоскости и таким образом, что сумма расстояний от нее до двух фокусов всегда одинакова.

8. Даны шаги по проведению нормали и касательной к эллипсу в точке Q на нем. Расположите ступеньки.
я. Проведите линию ST через Q и перпендикулярно NM.
ii. ST – требуемый тангенс.
III. Соедините Q с фокусами F1 и F2.
ив. Нарисуйте линию NM, разделив пополам угол между линиями, нарисованными перед ней, который является нормальным.
a) i, ii, iii, iv
b) ii, iv, i, iii
c) iii, iv, i, ii
d) iv, i, ii, iii
Посмотреть ответ

Ответ: c
Объяснение : Касательные — это линии, которые касаются кривых только в одной точке. Нормали — это перпендикуляры касательных. Как и в окружностях, сначала мы нашли нормаль с помощью фокусов (центр в окружности), а затем перпендикуляр в данной точке дает касательную.

9. Что из перечисленного не принадлежит эллипсу?
а) Широкая прямая кишка
б) Директриса
в) Большая ось
г) Асимптоты
Просмотреть Ответ

Ответ: г
Пояснение: Широкая прямая кишка — это линия, соединяющая один из фокусов и перпендикулярная большой оси. Асимптоты – это касательные, пересекающие гиперболу на бесконечном расстоянии. Большая ось состоит из фокусов и перпендикулярна малой оси.

Sanfoundry Global Education & Learning Series – Engineering Drawing.

Чтобы попрактиковаться во всех областях инженерного черчения, здесь есть полный набор из более чем 1000 вопросов и ответов с несколькими вариантами ответов .

Следующие шаги:

Получите бесплатную грамоту за заслуги перед инженером-чертежником
Участие в конкурсе на сертификацию технических чертежей
Стать лучшим специалистом по инженерному черчению
Пройдите тесты по инженерным чертежам
Практические тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Пробные тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

Категории Инженерный чертеж MCQ

Подпишитесь на наши информационные бюллетени (тематические). Участвуйте в конкурсе сертификации Sanfoundry, чтобы получить бесплатный Сертификат отличия. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!

Маниш Бходжасиа, ветеран технологий с более чем 20-летним опытом работы в Cisco и Wipro, является основателем и техническим директором компании Sanfoundry . Он живет в Бангалоре и занимается разработкой Linux Kernel, SAN Technologies, Advanced C, Data Structures & Alogrithms. Оставайтесь на связи с ним в LinkedIn.

Подпишитесь на его бесплатные мастер-классы на Youtube и технические обсуждения в Telegram SanfoundryClasses.

Desktop Help

Чтобы получить доступ к этой справочной системе на другом языке:

Войдите в свою учетную запись Onshape.
Доступ к настройкам учетной записи.
В разделе «Настройки» выберите нужный язык отображения.

Язык отображения изменяет текст интерфейса пользовательского интерфейса, а также текст справки на выбранный вами язык. Вам может потребоваться снова войти в Onshape, чтобы изменения вступили в силу.

Чтобы начать работу с Onshape и настроить параметры учетной записи и поведения по умолчанию, мы настоятельно рекомендуем сначала пройти курс «Учебник». Это проведет вас через соответствующие установки и настройки учетной записи, как начать набросок, сделать деталь и другие основы Onshape. Расчетное время прохождения всех разделов составляет 50 минут, но вы можете выбрать модули по вашему выбору.

Праймер Onshape

ScreenOnly»> Выберите категорию информации ниже или выберите из оглавления слева. У нас также есть глоссарий, если вы хотите изучить список терминов Onshape и их определения.

Предприятие

Узнайте об инструментах управления процессами, безопасности и разрешениях для нескольких пользователей, которым требуется контроль доступа, отслеживание и отчетность

Моделирование

Узнайте о САПР корпоративного уровня с развертыванием и доступом в реальном времени, управлением данными, а также аналитикой и управления

Управление релизами

Узнайте о контроле версий в сочетании с процессами управления релизами в разных группах

Onshape предоставляет вам множество возможностей для самостоятельного обучения. Выберите предпочтительный метод обучения по ссылкам ниже. Заходите почаще, так как мы регулярно обновляем наши ресурсы.

Учебный центр

Доступ к инструментам обучения, включая видео, учебные пособия и онлайн-классы

Видеотека

Доступ к нашей видеотеке, включая функции на основе браузера и мобильные функции

Вебинары

Доступ к записанным вебинарам Onshape по широкому кругу тем, как для Onshape, так и для всей отрасли

Если вы новичок в Onshape, знакомство с основами Onshape — это хороший способ познакомиться с концепциями Onshape и некоторыми основными функциями.

Эта основная справочная система содержит справку для всех платформ, на которых работает Onshape. В каждой теме объясняется информация для всех платформ. В некоторых разделах информация зависит от платформы, и для каждой платформы есть раскрывающиеся списки. В других разделах информация не зависит от платформы, поэтому информация относится ко всем платформам.

Кнопки панели инструментов

В правом верхнем углу каждой страницы расположены четыре кнопки, обозначенные ниже слева направо:

Развернуть все / Свернуть все — Кнопка-переключатель, которая разворачивает или сворачивает все выпадающие текстовые области на текущей странице. Перед печатью страницы рекомендуется развернуть все раскрывающиеся списки. Это настраивает страницу для печати со всеми видимыми текстовыми областями.
Печать — открывает диалоговое окно «Печать»; для отправки страницы на подключенный принтер или сохранения страницы в виде файла PDF.
Предыдущая страница — переход на предыдущую страницу на основе оглавления.
Следующая страница — переход к следующей странице на основе оглавления.

Условные обозначения примечаний

В этой справочной системе вы увидите следующие примечания:

Ссылки на наш учебный центр, где вы можете узнать больше о конкретных функциях программного обеспечения.

Полезные советы, идеи или альтернативные рабочие процессы.

Предупреждающие сообщения о возможных подводных камнях, известных проблемах или потенциальных проблемах.

Сообщения об устранении неполадок, которые помогут вам справиться с проблемами.

Обратная связь

Чтобы оставить отзыв о самой справочной системе, нажмите синюю кнопку обратной связи в правой части браузера.

Используйте инструмент в Onshape, чтобы зарегистрировать тикет для поддержки Onshape. Разверните меню «Справка» (щелкните значок) и выберите Связаться со службой поддержки . Корпоративные клиенты также могут обратиться к своему менеджеру по работе с клиентами.

Внизу каждого раздела справки вы найдете Была ли эта статья полезной? Инструмент обратной связи (как показано ниже). Оставьте свой отзыв, нажав кнопку Да или Нет.

Была ли эта статья полезной?

Спасибо! Спасибо. Пожалуйста, используйте кнопку обратной связи, чтобы предоставить дополнительную информацию.

Последнее обновление: 22 сентября 2022 г.

Содержание технического чертежа и дизайна

Содержание книги «Технический чертеж и дизайн» / Сесил Дженсен, Джей Д. Хелсел, Деннис Р. Шорт.

Библиографическая запись и ссылки на соответствующую информацию из каталога Библиотеки Конгресса.

Примечание: Данные о содержимом генерируются машиной на основе предварительной публикации, предоставленной издателем. Содержание может отличаться от печатной книги, быть неполным или содержать другую кодировку.

 Обзор деталей
Глава 1
Инженерная графика как язык
Глава 2
Компьютерное черчение (САПР)
Глава 3
Носители для рисования, архивирование, хранение и воспроизведение
Глава 4
Основные навыки черчения
Глава 5
Прикладная геометрия
Глава 6
Теория описания формы
Глава 7
Вспомогательные взгляды и обороты
Глава 8
Основные размеры
Глава 9
Разделы
Стандарт
Размеры чертежа
34
Формат чертежа
35
3-2
Подача и
Хранилище
38
Файловые системы
38
Предисловие
xii
САПР
40
Подтверждение
нц
xiv
3-3
Рисунок
Воспроизведение
41
О
Авторы
xv
Воспроизведение
Оборудование
41
Рисунок
Стандарты
Обновлять
xv
Компьютеризированный
Рисунок
45
Обзор и
Задания
47
Часть
Базовый
Рисунок
и дизайн
1
Глава 4 Основные
Навыки рисования
48
1
4-1
Прямая линия
работа,
а также
Глава 1
Инжиниринг
Графика как
Стирание
48
язык
2
Ручное составление
48
1-1
Язык
промышленности
2
САПР
54
Рисунок
Стандарты
3
Координация
Вход
54
1-2
Карьера в
Инжиниринг
Графика
3
4-2
Окружности и дуги
56
Студент
3
Осевые линии
56
Места
Трудоустройство
5
САПР
56
Подготовка,
Квалификация,
а также
Продвижение
5
Рисование кругов
и дуги
56
Трудоустройство
Перспектива
6
САПР
56
1-3
Составление
Офис
6
4-3
Рисунок
Неправильные кривые
58
1-4
Составление доски
7
САПР
58
Составление
Мебель
7
4-4
Эскиз
59Составление
Оборудование
7
Бумага для рисования
59
Обзор и
Задания
16
Основные шаги к
Следуйте, когда
Эскиз
62
Компьютеризированный
Рисунок
63
Глава 2
Компьютерное черчение (САПР)
19
Обзор и
Задания
66
2-1
Обзор
19
Глава 5
Применяемый
Геометрия
78
2-2
Составные части
САПР
Система
20
5-1
Начало
Геометрия:
Прямой
Линии
78
Аппаратное обеспечение
20
Программного обеспечения
25
5-2
Дуги и
Круги
81
2-3
Коммуникати
на
Окружающая среда
28
5-3
Полигоны
83
Окрестности
сети
(локальные сети)
28
5-4
Эллипс
84
Широкая область
сети
(глобальные сети) и
5-5
Хеликс и
Парабола
85
мир
Интернет
(ВВВ)
29спираль
85
Кооператив
Работа
Окружающая среда
с
29
Парабола
86
2-4
Компьютер-
Помощь
Производство
г (КАМ)
30
Компьютер-
Помощь
Рисунок
87
Компьютер
Числовой
Контроль
30
Обзор и
Задания
91
Робототехника
30
Глава 6
Теория
Форма
Описание
98
Компьютер-
Интегрированный
Производство
г (ЦИМ)
30
Обзор и
Задания
32
6-1
Орфографический
Представительство
нс
98
Теория
Форма
Описание
98
Глава 3 Носители для рисования, архивирование, хранение и воспроизведение
34
Орфографические представления
98
99
Методы представления
Ввод координат САПР для
Орфографическое представление
102
34
3-1
Носители для рисования и формат
III
Средства для рисования
34
5090a_fma_i-xvi 31. 05.01
16:21
Страница IV
7-5
Революции
156
Ссылка
Самолеты
156
6-2
Договоренность
а также
Строительство
из
Революции
156
Просмотры
104
Правило
Революция
158
Расстояние между
Просмотры
104
Истинная форма
косой
Поверхность
Использование
Митра Лайн
105
Найдено
Последовательный
Революции
158
САПР
106
Вспомогательный
Просмотры и
вращается
Просмотры
159
6-3
Все поверхности
Параллельно и
Все грани
Истинная длина
линии
160
и линии
Видимый
106
7-6
Расположение
Очки и
Линии в
Пространство
161
6-4
Скрытый
Поверхности и
Края
107
Очки в
Пространство
161
Линии в
Пространство
161
Истинная длина косой линии на
САПР
108
6-5
Наклонный
Поверхности
108
Вспомогательный
Вид
Проекция
162
6-6
Циркуляр
Функции
109Укажите на
Линия
162
Осевые линии
109
Точка на-
Вид точки
линии
164
6-7
Косой
Поверхности
110
7-7
Самолеты в
Пространство
164
6-8
Одно- и
Два вида
Чертежи
111
Как найти
Линия в
Самолет
164
Вид
Выбор
111
Как найти
Укажите на
Самолет
165
Расположение
Пирсинг
Точка
Линия
и
Самолет?
Резка-
Самолет
Метод
165
Определение точки прокола линии
Один просмотр
Чертежи
111
Два вида
Чертежи
111
6-9
Специальный
Просмотры
111
и
Самолет?
Вспомогательный
Вид
Метод
166
Частичные просмотры
111
7-8
Создание
Видимость
Линии
Вид сзади
и увеличенный
Просмотры
112
в космосе
168
6-10
Общепринятый
Представительство
п из
Видимость
Косой
Строки по
Тестирование
168
Общий
Функции
113
Видимость
Линии и
Поверхности по
Тестирование
169Видимость линий и поверхностей
Повторяющийся
Подробности
113
Повторяющийся
Части
114
по
Наблюдение
169
Площадь
Разделы
114
7-9
Расстояния
между
Линии и
Точки
170
6-11
Общепринятый
Перерывы
114
Расстояние
из точки
к линии
170
Кратчайшее расстояние между двумя
6-12
Материалы
из
Конструкты
на
114
Прозрачный
т Материалы
115
Косой
Линии
170
6-13
Цилиндрический
Пересечение
нс
115
7-10
Край и
Истинное представление
самолетов
173
6-14
Форшорт
Нед
Проекция
116
Самолеты в
Комбинаты
на
174
Отверстия
вращается
показывать
Истинный
7-11
Углы
между
Линии и
Самолеты
176
Расстояние
из
Центр
116
Угол
линия
Делает
с
Самолет
176
6-15
Пересечение
нс из
Незаконченный
Поверхности
116
Линии края
из двух
Самолеты
177
Компьютер-
Помощь
Рисунок
118
Компьютер-
Помощь
Рисунок
179Обзор
а также
Назначатели
тс
121
Обзор
а также
Назначатели
тс
181
Глава 7
Вспомогательный
Просмотры и
Революция
нс
148
Глава 8
Базовый
Измерение
инг
195
7-1
Начальный
Вспомогательный
Просмотры
148
8-1
Базовый
Измерение
инг
195
Измерение
инг
Вспомогательный
Просмотры
150
Измерение
инг
195
7-2
Циркуляр
Особенности в
Вспомогательный
Единицы
Измерение
энт
199
Проекция
151
Двойной
Измерение
инг
200
7-3
Мульти-
Вспомогательный-
Вид
Чертежи
152
Угловой
Единицы
200
7-4
Среднее
Вспомогательный
Просмотры
153
Чтение
Направление
201
IV
Содержание
5090a_fma_i-xvi 31. 05.01
16:21
Страница v
Основные правила
за
Измерениев
грамм
201
Глава 9
Разделы
256
Симметричный
Контуры
202
9-1
Секционный
Просмотры
256
Ссылка
Габаритные размеры
202
Резка-
Линии плоскости
256
Не в масштабе
Габаритные размеры
202
Полные разделы
257
Оперативный
Имена
202
Раздел
Оболочка
258
Сокращенное название
с
202
9-2
Два или более
Секционный
Просмотры
8-2
Измерениев
г Циркуляр
Функции
203
на одном
Рисунок
259
Диаметры
203
9-3
Половина разделов
260
Радиусы
204
9-4
Темы в
Раздел
261
8-3
Измерениев
г Общий
Функции
207
Резьбовой
Сборки
261
Повторяющийся
Особенности и
Габаритные размеры
207
9-5
Сборки
в разделе
262
Фаски
207
Раздел
Подкладка на
Сборка
Чертежи
262
Склоны и
конусы
208
Накатки
209
9-6
Компенсировать
Разделы
263
Формованные детали
209
9-7
ребра, отверстия,
и Лаги в
Раздел
265
Подрезы
210
Ребра в
Разделы
265
Ограничено
Длины и
Области
210
Отверстия в
Разделы
266
Проволока, лист
Металл и
Буровая штанга
210
Втыкается
Раздел
266
8-4
Измерениев
г Методы
210
9-8
вращается
а также
Удаленный
Разделы
266
Прямоугольный
Координация
Измерениев
грамм
211
Размещение
Секционный
Просмотры
267
Полярный
Координация
Измерениев
грамм
211
9-9
Спицы и
Оружие в
Раздел
268
хордовый
Измерениев
грамм
211
9-10
Частичное или
Разразился
Разделы
268
Истинное положение
Измерениев
грамм
211
9-11
Фантом или
Скрытый
Разделы
269
Цепь
Измерениев
грамм
211
Датум или общая точка
9-12
Секционный
Рисунок
Обзор
269
Измерениев
грамм
213
Компьютер-
Помощь
Рисунок
270
8-5
Ограничения и
Допуски
213
Обзор и
Задания
272
Ключ
Концепции
214
Допуск
215
Крепления деталей, материалы и
2
Формирование
Процессы
292
Дополнительный
Правила для
Измерениев
грамм
218
8-6
Подходит и
Пособия
219Глава 10
Резьбовой
Крепеж
294
Подходит
219
10-1
упрощенный
Нить
Представительство
н
294
Разрешение
219
Винт
Потоки
295
Описание
подходит
220
Нить
Формы
295
Interchangea
способность частей
220
Нить
Представительство
н
295
Стандарт
Дюйм подходит
220
Право- и
Левая рука
Потоки
296
Основное отверстие
Система
222
Одноместный и
Несколько
Потоки
296
Основной вал
Система
223
упрощенный
Нить
Представительство
н
297
Предпочтительный
Метрика
Ограничения и
Подходит
223
Резьбовой
Сборки
297
8-7
Поверхность
Текстура
226
дюймовая резьба
297
Поверхность
Текстура
Характеристики
cs
227
Метрика
Потоки
298
Поверхность
Текстура
Символ
227
Трубная резьба
300
Заявление
231
10-2
Подробные и
Схема
Нить
обработанный
Поверхности
231
Представительство
н
301
Компьютер-
Помощь
Рисунок
234
Подробный
Нить
Представительство
н
301
Обзор и
Задания
237
Схема
Нить
Представительство
н
302
в
Содержание
5090a_fma_i-xvi 31. 05.01
16:21
Страница vi
Маленькие заклепки
342
Глухие заклепки
345
10-3
Общий
Резьбовой
Крепеж
303
11-6
Сварной
Крепеж
347
Застежка
Выбор
303
Сопротивление-
Сварной
Крепеж
347
Застежка
Определения
303
Дуговая сварка
Шпильки
347
Изменение
в метрическую
Крепеж
304
11-7
Клей
Крепления
349Застежка
Конфигурация
н
304
Адгезия
против стресса
349
Имущество
Классы
Крепеж
305
Совместный дизайн
350
Рисование
Болт и гайка
306
11-8
Застежка
Обзор для
Главы 10
Шпильки
307
и 11
351
Шайбы
307
Обзор и
Задания
352
Условия
Относится к
Резьбовой
Крепеж
308
Указание
Крепеж
308
Глава 12
Мануфактуры
материалы
365
10-4
Специальный
Крепеж
309
12-1
Чугуны
и черный
Металлы
365
Установочные винты
309
Железный
Металлы
365
Хранение
Крепеж
Тугой
310
Чугун
365
Контргайки
310
12-2
Углеродистая сталь
367
Пленник или
Себя-
Сохранение
Орехи
312
Углерод и
Низколегированный
Литые стали
367
Вставки
312
Высоколегированный
Литые стали
367
Герметизация
Крепеж
312
Углерод
стали
367
10-5
Крепеж для
Light-Gage
Металл,
Стали
Технические характеристики
367
Пластик и
Древесина
313
SAE и AISI? Системы из стали
Нажатие
Винты
313
Удостоверение личности
369Специальный
Нажатие
Винты
315
Высокая-
Прочность
Низколегированный
стали
372
Компьютер-
Помощь
Рисунок
317
Низко- и
Середина-
Легированные стали
372
Обзор и
Задания
319
Нержавеющая сталь
стали
372
Свободно-
Обработка
стали
372
Разное
нас Типы
Крепеж
329
Глава 11
12-3
Цветной
Металлы
373
11-1
Ключи,
Сплайны и
Зубцы
329
Производство
г с металлами
373
Ключи
329
Алюминий
373
Сплайны и
Зубцы
330
Медь
373
никель
374
11-2
Штифтовые застежки
332
Магний
374
полупостоянный
нт контакты
333
Цинк
374
Быстрый-
Выпускные булавки
335
Титан
374
11-3
Сохранение
Кольца
336
Бериллий
374
Штампованный
Сохранение
Кольца
336
Огнеупорный
Металлы
375
проволочный
Сохранение
Кольца
337
Драгоценный
Металлы
375
Спираль-
Ранить
Сохранение
Кольца
337
12-4
Пластмассы
375
11-4
пружины
337
Термопласты
cs
376
Типы
пружины
337
термореактивный
г Пластмассы
376
Весна
Чертежи
339Обработка
376
Весенние зажимы
339
Материал
Выбор
376
11-5
Заклепки
341
Формирование
Процессы
376
Стандарт
Заклепки
341
12-5
Резина
381
Большие заклепки
341
Материал и
Характеристики
cs
381
Заклепки для
Аэрокосмическая промышленность
Оборудование
341
Виды
Резина
381
ви
Содержание
5090a_fma_i-xvi 31. 05.01
16:21 Страница vii
Сборка
Методы
381
14-5
Рисунок
Редакции
433
Дизайн
Рассмотрение
нс
381
14-6
Сборка
Чертежи
434
Обзор и
Задания
383
Дизайн
Сборка
Чертежи
435
Глава 13
Формирование
Процессы
388
Монтаж
Сборка
Чертежи
435
Сборка
Чертежи для
Каталоги
435
13-1
Металл
Отливки
388
Список предметов
435
Формирование
Процессы
388
14-7
Взорван
Сборка
Чертежи
437
Кастинг
Процессы
388
14-8
Деталь
Сборка
Чертежи
437
Выбор
Процесс
392
Дизайн
Рассмотрение
нс
393
14-9
Подсборка
Чертежи
440
Составление
Практики
395
Компьютер-
Помощь
Рисунок
441
Кастинг
Датумы
397
Обзор и
Задания
442
Обработка
Датумы
398
Глава 15
Живописный
Чертежи
483
13-2
Поковки
399
Закрытая матрица
Ковка
399
15-1
Живописный
Чертежи
483
Общий
Правила дизайна
400
Аксонометрический
Проекция
483
Составление
Практики
402
Изометрический
Чертежи
486
13-3
Пудра
Металлургия
404
Неизометрический
Линии
486
Дизайн
Рассмотрение
нс
404
Измерениев
г Изометрический
Чертежи
486
13-4
Пластик
Формованные детали
404
Изометрический
Эскиз
487
Отдельные части
404
Основные шаги
следить за
Изометрический
Сборки
407
Эскиз
(Рис.  15-1-
12)
488
Чертежи
410
САПР
488
Обзор и
Задания
411
15-2
Изогнутый
Поверхности в
Изометрический
490
Круги и
Дуги в
Изометрический
490
Рабочие чертежи деталей и
490
Рисование неправильных кривых в изометрии
САПР
490
3
Дизайн
420
15-3
Общий
Особенности в
Изометрический
491
Глава 14
Деталь и
Сборка
Чертежи
422
Изометрический
Разделение
491
14-1
Рисунок
Качественный
гарантия
422
Филе и
Раунды
493
Обзор
Рассмотрение
нс
422
Потоки
493
Рисунок
Рассмотрение
нс
423
Линии разрыва
493
Изготовление
Рассмотрение
нс
424
Изометрический
Сборка
Чертежи
493
Монтаж
Рассмотрение
нс
424
15-4
Косой
Проекция
493
14-2
Функциональный
Составление
424
Наклонный
Поверхности
494
процедурный
Ярлыки
424
Косой
Эскиз
494
Сокращение
Количество
Чертежи
Основные шаги
следить за
Косой
Необходимый
426
Эскиз
(Рис. 15-4-7)
496
упрощенный
Представительство
нс в
Чертежи
427
Измерениев
г косая
Чертежи
496
Воспроизведение
Ярлыки
427
САПР
496
фоторисунок
гс
427
15-5
Общий
Особенности в
Косой
497
14-3
Деталь
Чертежи
429
Круги и
Дуги
497
Деталь
Рисунок
Требование
с
429
Косой
Разделение
498
Рисунок
Контрольный список
429Лечение
Общепринятый
Функции
498
Квалификация
с
Детейлер
430
САПР
499
Производство
г Методы
431
15-6
Параллельно или
Один пункт,
Перспектива
501
14-4
Несколько
Деталь
Чертежи
433
Перспектива
Проекция
501
Содержание
VII
5090a_fma_i-xvi 31. 05.01
16:21 Страница viii
16-6
Ориентация
Допуск
квартиры
Поверхности
565
Типы
Перспектива
Чертежи
502
Ссылка на
датум
565
Параллельно или
Один пункт,
Перспектива
502
Угловатость
Толерантность
565
Основные шаги
следить за
Параллельно
Перпендикула
справедливость
Толерантность
565
Перспектива
Эскиз
(Рис. 15-6-9)
503
Параллелизм
Толерантность
565
15-7
Угловой или
двухточечный,
Перспектива
506
Примеры
Ориентация
Допуск
565
Угловой-
Перспектива
Эскиз
507
Контроль в
Два
Направления
566
Основные этапы создания эскиза в угловой перспективе (рис. 15-7-10)
510
510
САПР
16-7
Базовые элементы зависят от размера
Вариация
567
Детали с
Цилиндрический
Датум
Функции
567
15-8
Твердый
Моделирование
511
РФС и
ММС
Приложения
568
Каркас
Моделирование
512
16-8
Ориентация
Допуск
для функций
Поверхность
Моделирование
512
Размер
572
Твердый
Моделирование
512
Угловатость
Толерантность
572
Изображение
Поколение
514
Параллелизм
Толерантность
573
Данные
Добыча
514
Перпендикула
справедливость
Толерантность
573
Компьютер-
Помощь
Рисунок
517
Контроль в
Два
Направления
573
Обзор и
Задания
521
Контроль над
Основа ММС
573
Глава 16 Геометрические размеры и допуски
Внутренние цилиндрические элементы
575
540
Внешний
Цилиндрический
Функции
578
16-9Позиционный
Допуск
579
16-1
Современный
Инжиниринг
Допуск
540
Допуск
Методы
579
Базовый
Концепции
541
Координация
Допуск
580
Размер
Габаритные размеры
541
Интерпретация рисунков и
Позиционный
Толеранцин
грамм
583
Измерение
с
543
16-10
Прогнозируемый
Толерантность
Зона
589
Предполагается
Датумы
543
16-11
Датум
Цели
591
16-2
Геометрический
Толеранцин
грамм
547
Датум
Цель
Символ
592
Особенность
Контроль
Рамка
547
Идентификация
по целям
592
Размещение
характеристик
Контроль
Рамка
547
Цели
Не в
Такой же
Самолет
593
Форма
Допуски
548
Частичный
Поверхности как
Датумы
595
Straightnes
с
549
Измерение
для
Цель
Расположение
595
16-3
Плоскостность
552
16-12
Циркулярность
а также
Цилиндрит
у
595
Плоскостность
поверхность
552
Циркулярность
595
Плоскостность
за единицу
Область
552
Цилиндрит
у
597
Два или
Больше квартиры
Поверхности в
Один самолет
552
16-13
Профиль
Толеранцин
грамм
599
16-4
Straightnes
с
Особенность
Размер
553
Профили
599
Особенности
Размер
553
Профиль
Символы
599
Материал
Условие
Символы
(Модификаторы
)
554
Профиль-
трапеция
Толерантность
599
Применимо
т РФС,
ММС и
БМО
555
Профиль-
поверхность
Толерантность
602
Straightnes
с
Особенность
Размер
557
16-14
коррелят
Допуски
604
16-5
Датумы
и
Три-
Самолет
Концепция
559
Копланарит
у
604
Датумы
559
Концентрический
город
605
Базы для
Геометрический
Толеранцин
грамм
559
Соосность
606
Три-
Самолет
Система
561
Симметрия
607
Идентификация
на из
Датумы
562
Закончиться
609
viii
Содержание
5090a_fma_i-xvi 31. 05.01
16:21
Страница IX
16-15
Позиционный
Допуск
за
Точечная сварка
695
Нецилиндрический
все особенности
610
Сварные швы
699
Некруглый
Особенности в
ММС
610
Наплавка
Сварные швы
700
16-16
Позиционный
Допуск
для нескольких
Фланцевый
Сварные швы
701
Образцы
Функции
614
Сварные шпильки
702
Композитный
Позиционный
Допуск
614
Компьютер-
Помощь
Рисунок
704
16-17
Формулы для
Позиционный
Допуск
621
Обзор и
Задания
705
Плавающий
Крепеж
621
Расчет
Распродажа
622
Глава 19
Дизайн
Концепции
718
Исправлено
Крепеж
622
19-1
Дизайн
Процесс
718
Неравный
Допуски
и отверстие
Размеры
624
Дизайн
Процесс
718
Инженерный подход к
Коаксиальный
Функции
624
Перпендикула
Ошибки
625
Успешный
Дизайн
71916-18
Резюме
Правила для
Геометрический
Часть
Технические характеристики
с
720
Допуск
625
Делать и
Запрещается
Дизайнеры
721
Когда использовать
Геометрический
Допуск
625
19-2
Сборка
Рассмотрение
нс
722
Основные правила
625
Стоимость
Сборка
722
Компьютер-
Помощь
Рисунок
628
Вложения
722
Дизайн
Контрольный список
728
Подход к проектированию готового изделия
Обзор и
Задания
629
Глава 17
Чертежи
за
Числовой
Контроль
660
Структура
730
17-1
Двухосный
Контроль
Системы
660
19-3
Параллельно
Инжиниринг
730
Параллельное проектирование через
Компьютер Числовой
Управление (ЧПУ)
660
Компьютеры
730
Размеры для
Числовое управление
661
Размеры для двух осей
19-4
Проект
Управление
731
Координация
Система
661
Обзор и
Задания
734
17-2
Трехосный
Контроль
Системы
664
Размеры и допуски
666
Часть
738
Силовые передачи
Обзор и задания
667
4
Глава 18 Сварка
Чертежи
672
Глава 20 Ремни,
Цепи и шестерни
740
18-1
Дизайн для
Сварка
672
20-1
Ременные передачи
740
Сварочные процессы
672
Плоские ремни
740
18-2
Сварочные символы
674
Обычная квартира
Ремни
741
клиновые ремни
742
Дизайн
Сварные соединения
679
Как выбрать
Клиновой ремень для легких условий эксплуатации
Водить машину
744
18-3
Угловые сварные швы
681
20-2
Цепные приводы
749Символы углового сварного шва
681
Основные типы
749
Размер угловых швов
684
звездочки
751
18-4
Сварные швы
686
Дизайн ролика
Цепные приводы
751
Использование Break in Arrow of Bevel
761
и J-
Канавка
Сварка
Символы
686
20-3
Механизм
Диски
761
Канавка
сварка
Символы
686
Цилиндрические шестерни
Канавка
Соединение
Дизайн
691
20-4
Сила-
Трансмитти
нг
Вместимость
из
767
18-5
Другой
Базовый
Сварные швы
693
Цилиндрические шестерни
767
Затыкать
Сварные швы
693
Выбор
шпора
Шестеренчатый привод
769
Сварные швы
694
20-5
Стойка и
Шестерня
икс
Содержание
5090a_fma_i-xvi 31. 05.01
16:21
Страница х
Глава 22
Камеры,
Связи и
Приводы
823
22-1
кулачки, связи,
и приводы
823
20-6
Конические шестерни
770
Кэм
Номенклатура
824
Работающий
Чертежи
Конические шестерни
770
Подписчики на камеру
825
20-7
Червь и
Червячные передачи
772
кулачковые движения
825
Упрощенный метод разметки
830
Кулачковое движение
Рабочие чертежи червяка и
Червячные передачи
774
20-8
Сравнение
цепи,
Шестерня и
Кэм
смещение
Диаграммы
830
Ременные передачи
775
22-2
Пластинчатые кулачки
830
Цепи
775
сопряжение
Камеры
830
Шестерни
775
Сроки
Диаграммы
830
Ремни
775
Измерениев
г Камеры
832
Цепные приводы
По сравнению
с шестерней
Диски
775
Размер камеры
833
Цепные приводы
По сравнению
с ремнем
Диски
776
22-3
Положительный-
Камеры движения
835
Вывод
776
22-4
Барабанные кулачки
836
Компьютер-
Помощь
Рисунок
777
Обзор и
Задания
778
22-5
Индексация
838
22-6
Связи
840
Глава 21
Муфты,
подшипники,
и уплотнения
788
Местонахождение
Точка
840
Камеры против
Связи
840
21-1
Муфты
и гибкий
Валы
788
Прямая линия
Механизм
841
Муфты
788
Системы
Имея
Связи и
Камеры
842
Гибкий
Валы
790
22-7
Храповик
Колеса
843
21-2
Подшипники
791
Компьютер-
Помощь
Рисунок
845
Простой
Подшипники
791
Обзор и
Задания
846
21-3
Анти-трение
Подшипники
792
Несущий
Нагрузки
792
Шарикоподшипники
792
Часть
5
Специальные области черчения 854
Роликовые подшипники
794
Несущий
Выбор
794
Глава 23
События
а также
Перекрестки
856
Несущий
Классификации
795
23-1
Поверхность
События
856
Вал и
Корпус подходит
795
Листовой металл
Разработка
856
Несущий
Символы
797
Прямая линия
Разработка
858
21-4
предварительно смонтированный
Подшипники
799
23-2
Упаковка
Промышленность
858
21-5
Смазочные материалы и
Радиальные уплотнения
800
23-3
Радиальная линия
Развитие
Смазочные материалы
800
Плоские поверхности
860
Смазка и масло
Уплотнения
801
23-4
Параллельная линия
Развитие
Радиальные уплотнения
802
Цилиндрический
Поверхности
863
Символы печати
806
21-6
Статические уплотнения и
Герметики
806
23-5
Радиальная линия
Развитие
Конический
Поверхности
866
Уплотнительные кольца
806
Плоский неметаллический
Прокладки
807
23-6
Развитие
Переход
Частей
Металлические прокладки
808
по триангуляции
868
Герметики
808
23-7
Развитие
Сфера
871
Печати исключения
808
23-8
Пересечение плоских поверхностей? Перпендикулярные линии
Обзор и задания
811
872
Икс
Содержание
5090a_fma_i-xvi 31. 05.01
16:21
Страница XI
23-9
Перекресток
из
Цилиндрический
Поверхности
875
Сверлильные приспособления
957
23-10
Пересекающиеся
призмы
876
Сверлить
Втулки
957
23-11
Штамповки
879
26-2
Сверлильный станок
Составные части
959
Дизайн
Рассмотрение
нс
879
Джиг Тело
959
Компьютер-
Помощь
Рисунок
885
Колпачковые винты
и дюбель
Пины
959
Расположение
Устройства
959
Обзор и
Задания
886
зажим
Устройства
962
Глава 24
Трубка
Чертежи
900
Стопорные штифты
963
Разное
с Стандарт
Части
963
24-1
Трубы
900
Дизайн
Примеры
963
Виды
Трубы
900
Соединения труб
и установка
901
26-3
Измерениев
г Джиг
Чертежи
965
Клапаны
903
26-4
Светильники
966
Трубопровод
Чертежи
904
Фрезерование
Светильники
966
24-2
Изометрический
Проекция
Трубопровод
приспособление
Составные части
967
Чертежи
908
приспособление
Дизайн
Рассмотрение
нс
968
24-3
Дополнения
трубопровод
Информация
910
Последовательность в
Выкладка
приспособление
971
Компьютер-
Помощь
Рисунок
913
Обзор и
Задания
972
Обзор и
Задания
915
Глава 27
Электрический
а также
Электроника
Чертежи
976
Глава 25
Структурный
Составление
922
27-1
Электрический
а также
Электроника
Чертежи
976
25-1
Структурный
Составление
922
стандартизировать
на
976
Здание
Процесс
922
Использование САПР
для электрики
Чертежи
977
Структурный
Сталь? Обычная
Материал
923
27-2
Схема
Диаграммы
977
Структурный
Рисунок
Практики
928
Выкладка
Схема
Диаграмма
978
25-2
Балки
929
Графика
Символы
978
Сборка
Зазоры
930
27-3
Электропроводка
(Связь)
Диаграммы
981
Простой
Площадь-
В рамке
Балки
931
Основные правила прокладки проводки
25-3
Стандарт
Соединения
933
Диаграмма
982
на болтах
Соединения
933
27-4
Напечатано
Схема
Доски
983
25-4
Разделение
939
САПР для
Напечатано
Схема
Доски
984
Основные правила оформления печатной
Нижний
Просмотры
939
Ликвидация
Топ и
Нижний
Просмотры
940
Схема
987
Право- и
Левая рука
Подробности
940
27-5
Блокировать и
Логика
Диаграммы
987
25-5
Сидячий луч
Соединения
942
Блокировать
Диаграммы
987
25-6
Измерениев
грамм
944
Логика
Диаграммы
987
Векселя
Материал
944
Графика
Символы
987
Расчеты
весов
(массы)
945
Компьютер-
Помощь
Рисунок
992
Компьютер-
Помощь
Рисунок
946
Обзор и
Задания
993
Глоссарий
Г-1
Приложение?Стандартные детали и
Обзор и
Задания
948
Глава 26 Джиги
и приспособления
955
26-1
Джиг и приспособление
Дизайн
955
Технические данные
А-1
Джиги
955
Индекс
И-1

Библиотека Конгресса Тематические заголовки для этой публикации:

Механический чертеж.
Инженерный проект.

Круг на 10 равных частей. Деление круга на равные части с помощью циркуля и линейки

Иногда для изготовления трафаретов шаблоны, рисунки, выкройки, поделки необходимо разделить на 6 частей .
Например, нам нужно было сделать шаблон для цветка в виде шестиконечной звезды.

Для тех, кто забыл геометрию, напомню, что разделить окружность на 6 частей можно двумя способами:

С помощью транспортира .
С помощью компаса .

1. Как разделить окружность на 6 частей с помощью транспортира

Разделить окружность с помощью транспортира очень просто.

Проводим линию, соединяющую центр и любую точку (например, точку 1) на окружности. От этой линии с помощью транспортера откладываем угол 60, 120, 180 градусов. На окружности ставим точки (например, точки 2, 3, 4) Разворачиваем транспортир и точно так же делим другую часть окружности.

2. Как разделить круг на 6 частей с помощью циркуля

Бывает, что нет под рукой транспорта. Затем круг можно разделить на 6 равных частей с помощью циркуля.

Рисуем круг, например, радиусом 5 см (красный круг). Не меняя радиуса, переносим катет циркуля на окружность (точка 1) и рисуем еще одну окружность. Получаем две точки пересечения черных и красных кругов 6 и 2.

Переносим ножку циркуля в точку 2 и снова рисуем круг. Получаем точку 3.

Переместите ножку циркуля в точку 3. Снова нарисуйте окружность.

Таким образом продолжаем делить круг, пока не разделим его на 6 равных частей.

Категория деталей: Инженерная графика

Страница 2 из 6

Деление окружности на равные части

Некоторые детали машин и устройств имеют элементы, равномерно расположенные по окружности, например детали на рис. 52- 59. При выполнении чертежей таких частей необходимо знать правила деления окружности на равное количество частей.

Деление круга на четыре и восемь равных частей. На рис. 52, и Показана крышка, в которой имеется восемь отверстий, равномерно расположенных по окружности. При построении чертежа контура крышки (рис. 52 Г) Разделите круг на восемь равных частей. Это можно сделать с помощью угольника с углами 45° (рис. 52, в), квадрат угольника должен проходить через центр круга, или построением.

Два взаимно перпендикулярных диаметра окружности делят ее на четыре равные части (точки 7, 3, 5, 7 на рис. 52, б). Для деления окружности на восемь равных частей используется известный прием деления прямого угла с помощью циркуля на две равные части. Получите очки 2, 4, 6, 8.

Деление круга на три, шесть и двенадцать равных частей. Во фланце (рис. 53, а) По кругу равномерно расположены три отверстия. При выполнении чертежа фланцевой схемы (рис. 53, г) необходимо окружность разделить на три равные части.

Чтобы найти точки, делящие окружность радиусом R на три равные части, достаточно из любой точки окружности, например, точки А, нарисовать дугу радиусом R . Пересечения дуги с окружностью дают две искомые точки 2 и 3; третья точка деления будет располагаться на пересечении оси окружности, проведенной из точки L, с окружностью (рис. 53, б).

Можно также окружность разделить на три равные части квадратом с углами 30 и 60° (рис. 53, в), квадрат квадрата должен проходить через центр круга.

На рис. 54, б показано деление окружности на шесть равных частей. При этом выполняется то же построение, что и на рис. 53, б, но дуга описывается не один, а два раза, из точек и радиусом R, равным радиусу окружности.

Можно также разделить круг на шесть равных частей квадратом с углами 30 и 60° (рис. 54, в). На рис. 54, а Показана крышка, при выполнении чертежа которой необходимо разделить окружность на шесть частей.

Чтобы сделать чертеж детали (рис. 55, а), имеющей 12 отверстий, равномерно расположенных по окружностям, нужно осевую окружность разделить на 12 равных частей (рис. 55, г).

При делении окружности на 12 равных частей с помощью окружности можно использовать тот же прием, что и при делении окружности на шесть равных частей (рис. 54, б ), но дуги радиусом R описать четыре раза из пунктов 1, 7, 4 и 10 (рис. 55, б).

С помощью квадрата с углами 30 и 60° с последующим поворотом его на 180° разделите круг на 12 равных частей (рис. 55, в).

Деление круга на пять, десять и семь равных частей. В плашке (рис. 56, а) имеется пять отверстий, равномерно расположенных по окружности. При вычерчивании игральной кости (рис. 56, в) необходимо разделить окружность на пять равных частей. Через намеченный центр О (рис. 56, б)

с помощью Т-угольника и угольника проводят осевые линии и из точки О описывают циркулем окружность заданного диаметра. Из точки А радиусом R, равным радиусу данной окружности, проводится дуга, пересекающая окружность в точке n. Из точки n опускается перпендикуляр к средней линии горизонтали, получается точка С. Из точки С радиусом R 1 , равным расстоянию от точки С до точки 1, проводится дуга, пересекающая горизонтальную центральную линию в точке t. Из точки 1 радиусом R, равным расстоянию от точки 1 до точки М, провести дугу, пересекающую окружность в точке 2. Дуга 12 составляет 1/5 длины окружности. Точки 3,4 и 5 находят, откладывая циркулем отрезки, равные m1.

Деталь «звездочка» (рис. 57, а) Имеет 10 одинаковых элементов, равномерно расположенных по окружности. Чтобы нарисовать звездочку (рис. 57, и), окружность следует разделить на 10 равных частей. При этом следует применять ту же конструкцию, что и при делении окружности на пять частей (см. рис. 56, б). Отрезок p 1 Будет равна хорда, которая делит окружность на 10 равных частей.

На рис. 58, и показан шкив, а на рис. 58, в — чертеж шкива, где окружность разделена на семь равных частей.

Деление окружности на семь равных частей показано на рис. 58, б. Из точки А проводится вспомогательная дуга радиусом R , равно радиусу этой окружности, которая пересекает окружность в точке. Из точки по опустите перпендикуляр к центральной горизонтальной линии. С точки 1 радиус равен сегменту нс , сделайте семь надрезов по кругу и получите семь рисунков.

Деление круга на любое количество равных частей. С достаточной точностью можно разделить окружность на любое количество равных частей, используя таблицу коэффициентов для подсчета длины хорды (таблица 9).

Зная, на сколько (n) надо разделить круг, найдите по таблице коэффициент. При умножении коэффициента k на диаметр окружности D получается длина хорды l, которую откладывают циркулем на окружности и один раз.

При построении чертежа кольца (рис. 59, а) Необходимо разделить окружность диаметром D = 142 мм на 32 равные части. Число частей окружности n = 32 соответствует коэффициенту K = 0,098. Вычислить длину хорды l = ДК = 142х0,098 = 13,9 мм, укладывается по окружности 32 раза (рис. 59, б и в).

Деление круга на три равные части. Установите угольник с углами 30 и 60° большим катетом параллельно одной из осевых линий. По гипотенузе из точки 1 (первое деление) проводим хорду (рис. 2.11, а ), получая второе деление — точка 2. Поворачивая квадрат и проводя вторую хорду, получаем третье деление — точка 3 (рис. 2.11, б ). Путем соединения точек 2 и 3; 3 и 1 прямых образуют равносторонний треугольник.

Рис. 2.11.

а, б — в с использованием угольника; в — с помощью круга

Эту же задачу можно решить с помощью компаса. Разместив опорную ножку компаса на нижнем или верхнем конце диаметра (рис. 2.11, в ) описывают дугу, радиус которой равен радиусу окружности. Получите первый и второй дивизионы. Третье деление находится на противоположном конце диаметра.

Деление окружности на шесть равных частей

Отверстие компаса устанавливается равным радиусу R окружности. От концов одного из диаметров окружности (от точек 1, 4 ) описывают дуги (рис. 2.12, а, б). точки 1, 2, 3, 4, 5, 6 Разделите круг на шесть равных частей. Соединив их прямыми линиями, получают правильный шестиугольник (рис. 2.12, б ).

Рис. 2.12.

Ту же задачу можно выполнить с помощью линейки и угольника с углами 30 и 60° (рис. 2.13). Гипотенуза квадрата при этом должна проходить через центр окружности.

Рис. 2.13.

Разделение круга на восемь равных частей

точки 1, 3, 5, 7 лежат на пересечении осевых линий с окружностью (рис. 2.14). Еще четыре точки находятся с помощью угольника с углами 45°. При получении баллов 2, 4, 6, 8 гипотенуза квадрата проходит через центр окружности.

Рис. 2.14.

Разделение круга на любое количество равных частей

Чтобы разделить круг на любое количество равных частей, используйте коэффициенты, приведенные в табл. 2.1.

Длина л хорды, откладываемые на данной окружности, определяются по формуле л = дк, где л — длина хорды; d — диаметр данной окружности; k — коэффициент, определяемый из табл. 1.2.

Таблица 2.1

Коэффициенты деления кругов

Чтобы разделить круг заданного диаметра 90 мм, например, на 14 частей, поступают следующим образом.

В первом столбце табл. 2.1 находим количество дивизий Р, т.е. 14. Из второго столбца выпишите коэффициент к, соответствующий числу делений р. В данном случае он равен 0,22252. Диаметр данной окружности умножается на коэффициент и получается длина хорды l=dk= 90 0,22252 = 0,22 мм. Полученную длину хорды откладывают циркулем 14 раз на заданную окружность.

Нахождение центра дуги и определение величины радиуса

Дана дуга окружности, центр и радиус которой неизвестны.

Для их определения необходимо провести две непараллельные хорды (рис. 2.15, а ) и поставить перпендикуляры к серединам хорд (рис. 2.15, б ). Центр дуги O находится на пересечении этих перпендикуляров.

Рис. 2.15.

При выполнении машиностроительных чертежей, а также при маркировке заготовок в производстве часто возникает необходимость плавного соединения прямых с дугами окружностей или дуги окружности с дугами других окружностей, т. е. выполнения сопряжения.

Спариванием называется плавный переход прямой линии в дугу окружности или одной дуги в другую.

Для построения сопряжений необходимо знать значение радиуса сопряжений, найти центры, из которых проводятся дуги, т.е. центры сопряжения (рис. 2.16). Затем нужно найти точки, в которых одна линия переходит в другую, т.е. точки соединения. При построении чертежа линии сопряжения необходимо доводить точно до этих точек. Точка сопряжения дуги окружности и прямой лежит на перпендикуляре, опущенном из центра дуги к линии сопряжения (рис. 2.17, а ), либо на линии, соединяющей центры сопряженных дуг (рис. 2.17, б ). Следовательно, для построения любого сопряжения дугой заданного радиуса нужно найти центра сопряжения и точки ( точки ) сопряжения.

Рис. 2.16.

Рис. 2.17.

Сопряжение двух прямолинейных дуг заданного радиуса. Даны прямые, пересекающиеся под прямыми, острыми и тупыми углами (рис. 2.18, и ). Необходимо построить сопряжение этих прямых дуг заданного радиуса Р.

Рис. 2.18.

Для всех трех случаев можно применить следующую конструкцию.

1. Найдите точку О — центр сопряжения, которая должна лежать на расстоянии R от сторон угла, т. е. в точке пересечения прямых, проходящих параллельно сторонам угла при расстояние R из них (рис. 2.18, б ).

Для проведения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, с циркулем, равным R, делают засечки и проводят к ним касательные (рис. 2.18, б ).

2. Найти точки сопряжения (рис. 2.18, в). Для этого из точки O опустить перпендикуляры к заданным прямым.
3. Из точки О, как из центра, описать дугу заданного радиуса R Между точками сопряжения (рис. 2.18, в).

На вопрос, как разделить круг на три равные части с помощью циркуля)? подскажите пожалуйста!! задано автором Посольство лучший ответ
_______
Пусть дан круг радиуса R. Мы должны разделить его на три равные части с помощью циркуля. Расширьте циркуль на радиус окружности. Можно использовать для этого линейку, а можно поставить стрелку циркуля в центр круга, а ножку отвести к звену, описывающему круг. В любом случае линейка пригодится позже.
Установить иглу циркуля в произвольном месте на окружности, описывающей окружность, и провести маленькую дугу, пересекающую контур внешнего контура печатью. Затем установите стрелку компаса на найденную точку отсчета и еще раз начертите дугу того же радиуса (равного радиусу окружности).
Повторяйте эти шаги до тех пор, пока следующая точка пересечения не совпадет с самой первой. Вы получите шесть эталонных кругов, расположенных через равные промежутки. Осталось выделить через одну три точки и соединить их линейкой с центром круга, и у вас получится круг, разделенный на три части.
________
Круг можно разделить на три части, если с помощью циркуля от точки пересечения прямой, проведенной через центр круга О, сделать на линии круга засечки В и С циркулем, равные радиус этой окружности.
Таким образом, будут найдены две искомые точки, а третья — противоположная точка А, где пересекаются окружность и прямая.
Далее при необходимости линейкой и карандашом

можно нарисовать вложенный треугольник.

_________
Для разметки на три части используйте радиус окружности.

Переверните циркуль вверх ногами. Иглу располагают на
пересечении центральной линии с окружностью, а перо в центре. нарисуйте
дугу, пересекающую окружность.

Пересечения будут вершинами треугольника.

Разделение окружности на четыре равные части и построение правильного вписанного четырехугольника (рис. 6).

Две взаимно перпендикулярные осевые линии делят круг на четыре равные части. Соединив точки пересечения этих прямых с окружностью прямыми линиями, получится правильный вписанный четырехугольник.

Разделение окружности на восемь равных частей и построение правильного вписанного восьмиугольника (рис. 7).

Деление окружности на восемь равных частей осуществляется с помощью циркуля следующим образом.

Из точек 1 и 3 (точки пересечения осевых линий с окружностью) произвольного радиуса R проводят дуги до взаимного пересечения, с таким же радиусом из точки 5 делают насечку на дуге, проведенной из пункт 3.

Через точки пересечения засечек и центра окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.

Если полученные восемь точек последовательно соединяются прямыми линиями, тогда получится правильный вписанный восьмиугольник.

Разделение окружности на три равные части и построение правильного вписанного треугольника (рис. 8).

Опция 1.

При делении окружности циркулем на три равные части из любой точки окружности, например, точки А пересечения осевых линий с окружностью, провести дугу радиусом R, равным радиусу окружности, получить точки 2 и 3. Третья точка деления (точка 1) будет располагаться на противоположном конце диаметра, проходящего через точку А. Соединив последовательно точки 1, 2 и 3, получится правильный вписанный треугольник.

Вариант 2.

При построении правильного вписанного треугольника, если одной из его вершин задана, например, точка 1, находится точка А. Для этого через заданную точку проводят диаметр (рис. 8). Точка А будет на противоположном конце этого диаметра. Затем проводится дуга радиусом R, равным радиусу заданной окружности, получаются точки 2 и 3.

Разделение окружности на шесть равных частей и построение правильного вписанного шестиугольника (рис. 9).

При делении окружности на шесть равных частей циркулем из двух концов одного диаметра с радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 Соединив последовательно полученные точки, получится правильный вписанный шестиугольник.

Деление круга на двенадцать равных частей и построение правильного вписанного двенадцатиугольника (рис. 10).

При делении окружности циркулем от четырех концов двух взаимно перпендикулярных диаметров окружности проводится дуга радиусом, равным радиусу данной окружности, до пересечения с окружностью (рис. 10). Соединив последовательно полученные точки пересечения, получится правильный вписанный двенадцатиугольник.

Разделение окружности на пять равных частей и построение правильного вписанного пятиугольника ( Рис.11).

При делении окружности циркулем половина любого диаметра (радиуса) делится пополам, получается точка А. Из точки А, как из центра, проводится дуга радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра в точке В. Отрезок 1В равен хорде а стягивающая дуга, длина которой составляет 1/5 длины окружности. Делая надрезы на окружности радиусом R1, равным отрезку 1В, окружность делится на пять равных частей. Начальная точка А выбирается в зависимости от расположения пятиугольника.

Из точки 1 строятся точки 2 и 5, затем из точки 2 строится точка 3, а из точки 5 строится точка 4. Расстояние от точки 3 до точки 4 проверяется компасом; если расстояние между точками 3 и 4 равно отрезку 1В, то построения выполнены точно.

Нельзя выполнять засечки последовательно, в одном направлении, так как накапливаются ошибки измерения и последняя сторона пятиугольника получается перекошенной. Последовательно соединяя найденные точки, получается правильный вписанный пятиугольник.

Деление круга на десять равных частей и построение правильного вписанного десятиугольника (рис. 12).

Деление окружности на десять равных частей производится аналогично делению окружности на пять равных частей (рис. 11), но сначала окружность делится на пять равных частей, начиная с точки 1, а затем с точки 6, расположенный на противоположном конце диаметра. Соединяя все точки последовательно, получается правильный вписанный десятиугольник.

Разделение окружности на семь равных частей и построение правильного вписанного семиугольника (рис. 13).

Из любой точки окружности, например, точки А радиуса данной окружности провести дугу до пересечения с окружностью в точках В и D прямой.

Половина полученного отрезка (в данном случае отрезка BC) будет равна хорде, стягивающей дугу, которая составляет 1/7 длины окружности. Радиусом, равным отрезку ВС, на окружности делаются засечки в последовательности, показанной при построении правильного пятиугольника.

Сопряжения в инженерной графике на чертежах с примерами

Особенности построения — Всё для чайников

Содержание материала

НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

3 Сопряжения . Инженерная графика

Презентация по инженерной графике Сопряжение доклад, проект

Что такое shareslide.ru?

Обратная связь

Пр.раб. 3 Инженерная графика — Сопряжение.

Занятие по инженерной графике «Геометрические построения. Сопряжение» – Документ 1 – УчМет

Строительство эллипса — вопросы и ответы по техническим чертежам

Desktop Help

Кнопки панели инструментов

Условные обозначения примечаний

Последнее обновление: 22 сентября 2022 г.

Содержание технического чертежа и дизайна

Содержание книги «Технический чертеж и дизайн» / Сесил Дженсен, Джей Д. Хелсел, Деннис Р. Шорт.

Круг на 10 равных частей. Деление круга на равные части с помощью циркуля и линейки

Деление окружности на равные части

Деление окружности на шесть равных частей

Разделение круга на восемь равных частей

Разделение круга на любое количество равных частей

Нахождение центра дуги и определение величины радиуса

Добавить комментарий Отменить ответ