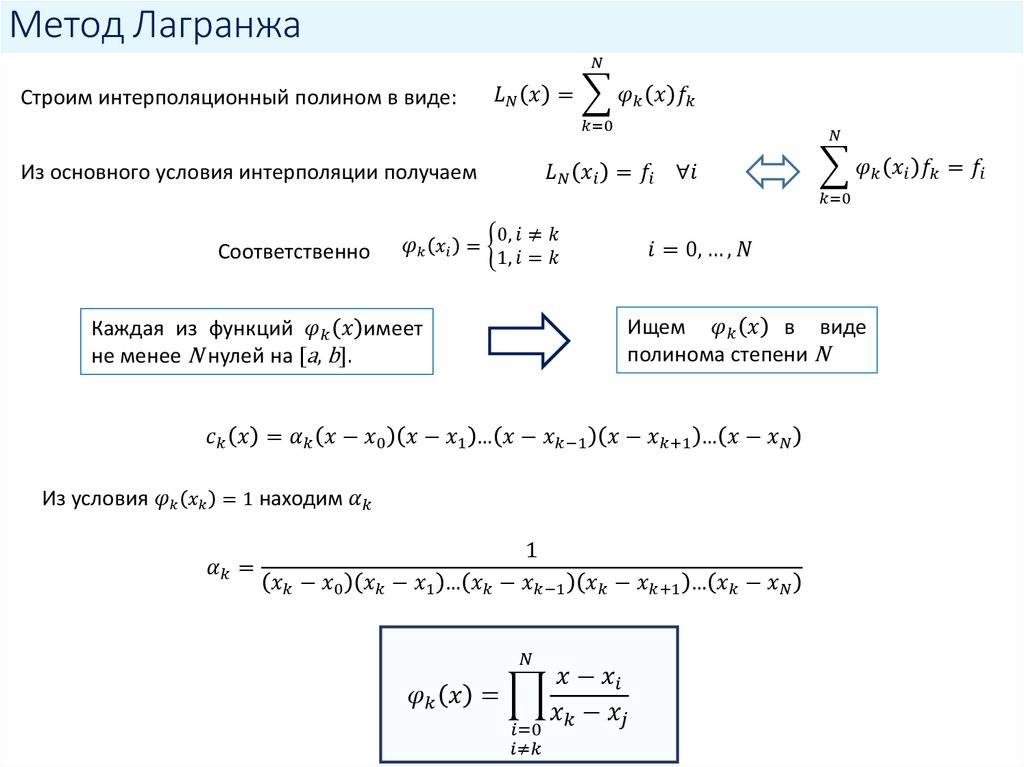
первая формула Ньютона, формула Лагранжа
ЦЕЛЬ
Получение практических навыков интерполяции функции в моделях сложных объектов и систем. Выбор и сравнительный анализ способов решения задачи интерполяции функции.
ПОСТАНОВКА ЗАДАЧИ
Разработать алгоритм построения полинома Ньютона и полинома Лагранжа для заданной функции: \[ \ln{x} + \sqrt{1+x}\] В качестве заданных узлов интерполяции возьмем точки, принадлежащие интервалу [1,16] с шагом h = 2.5. Таким образом, у нас заданы 7 точек:
| 1.0 | 1.41 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3.5 | 3.37 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6.0 | 4.44 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8.5 | 5.22 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11.0 | 5.86 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13.5 | 6.41 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
16. ky_0\) — конечные разности для первого узла ky_0\) — конечные разности для первого узла\(q=\frac{x-x_0}h\), где \(x_0\) — значение функции в первом узле, \(h\) — шаг интерполяции Очевидно, что для того, чтобы его построить, необходимо сначала составить таблицу конечных разностей. Напишем функцию, вычисляющую конечные разности и записывающую результаты в новый вектор: И проверим результаты ее работы. Найдем вектор первых конечных разностей:
Аналогично найдем другие конечные разности и составим таблицу:
Для использования первой интерполяционной формулы Ньютона нам достаточно воспользоваться разностями для первого узла, то есть по сути, нам нужны значения из первого ряда полученной формулы:
Когда мы подставим в формулу Ньютона полученных конечные разности, то получим формулу вида: \[\begin{eqnarray*}
P_n(x) & = & 1.4142136 + (1.9598697)q + (-0.8964423) \frac{q(q-1)}{2!} \\
& + & (0.6177772) \frac{q(q-1)(q-2)}{3!} + (-0.4841508) \frac{q(q-1)(q-2)(q-3)}{4!} \\
& + & (0.
Как видим, в итоге действительно получилась функция, проходящая через заданные точки. Теперь построим графики обеих функций. Моделирование в электроэнергетике — Интерполяционный многочлен в форме ЛагранжаВыборка экспериментальных данных представляет собой массив данных, который характеризует процесс изменения измеряемого сигнала в течение заданного времени (либо относительно другой переменной). Для выполнения теоретического анализа измеряемого сигнала необходимо найти аппроксимирующую функцию, которая свяжет дискретный набор экспериментальных данных с непрерывной функцией — интерполяционным полиномом n-степени. Одним из способов представления данного интерполяционного полинома n-степени может быть использован многочлен в форме Лагранжа. Интерполяционный многочлен в форме Лагранжа – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений. 1. Интерполяционная формула Лагранжа В общем виде интерполяционный многочлен в форме Лагранжа записывается в следующем виде: где ˗ степень полинома ; ˗ значение значения интерполирующей функции в точке ; ˗ базисные полиномы (множитель Лагранжа), которые определяются по формуле: Так, например, интерполяционный многочлен в форме Лагранжа, проходящий через три заданных точки , будет записываться в следующем виде: Многочлен в форме Лагранжа в явном виде содержит значения функций в узлах интерполяции, поэтому он удобен, когда значения функций меняются, а узлы интерполяции неизменны. Число арифметических операции, необходимых для построения многочлена Лагранжа, пропорционально и является наименьшим для всех форм записи. К недостаткам этой формы записи можно отнести то, что при построении полинома степени n+1 полностью теряется информация о предыдущем полиноме степени n, т.е. с изменением числа узлов приходится все вычисление выполнить заново. 2. Погрешность интерполяционного полинома в форме Лагранжа Рассмотрим функцию f(x), которая непрерывна и дифференцируема на рассматриваемом отрезке [a, b]. Интерполяционный полином L(x) в форме Лагранжа принимает в точках заданные значения функции . В остальных точках интерполяционный полином L(x) отличается от значения функции f(x) на величину остаточного члена, который определяет абсолютную погрешность интерполяционной формулы Лагранжа: Абсолютную погрешность интерполяционной формулы Лагранжа определяют следующим образом: где n ˗ степень полинома Переменная представляет собой верхнюю границу значения модуля (n +1)-й производной функции f(x) на заданном интервале [a, b] Погрешность интерполяции методом Лагранжа зависит от свойств функции f(x), а также от расположения узлов интерполяции и точки x. В случае если погрешность не достигает нужной точности, то нужно разбить отрезок на части и интерполировать каждую часть в отдельности – кусочная интерполяция. Выбор узлов интерполяции С помощью корректного выбора узлов можно минимизировать значение в оценке погрешности, тем самым повысить точность интерполяции. Данная задача может быть решена с помощью многочлена Чебышева:
3. Методика вычисления полинома в форме Лагранжа Алгоритм вычисления полинома в форме Лагранжа позволяет разделить задачи определения коэффициентов и вычисления значений полинома при различных значениях аргумента: 1. В качестве исходных данных задается выборка из n-точек, которая включает в себя значения функции и значения аргумента функции. 2. Выполняется вычисление полинома n-степени в форме Лагранжа по следующей формуле: Алгоритм вычисления полинома в форме Лагранжа представлен на рисунке 1.
Методика вычисления полинома в форме Лагранжа Рис. В качестве примера рассмотрим следующую практическую задачу. В рамках задачи известен набор шести значений, которые получены методом случайной выборки для различных моментов времени. Следует отметить, что данная выборка значений описывает функция на интервале [0, 10]. Необходимо построить многочлен в форме Лагранжа для представленного набора значений. С помощью интерполяционной формулы вычислить приближенное значение функции в точке , а также определить оценку погрешности результата вычислений. Многочлен в форме Лагранжа, который строится на основании шести значений, представляет собой полином 5 степени. Результат построения полинома в форме Лагранжа показан в графическом виде. Рис.2. Исходная функция и полином в форме Лагранжа, построенный по шести заданным точкам С помощью найденного полинома можно определить значение функции в любой точке заданного интервала. Определение промежуточных значений величины по имеющемуся дискретному набору известных значений называется «интерполяцией». Интерполяционный полином в форме Лагранжа часто оказывается удобным для проведения различных теоретических исследований в области вычислительной математики. Так, например, полином в форме Лагранжа используются для интерполяции, а также для численного интегрирования таблично-заданной функцией. Линейные интерполяционные полиномы Лагранжа — MathonlineЛинейные интерполяционные полиномы Лагранжа
Теперь мы приступим к обсуждению различных методов интерполяции. Учитывая набор дискретных точек, мы иногда хотим построить функцию из многочленов, которая является приближением другой известной (или, возможно, неизвестной) функции. Первый метод интерполяции, который мы рассмотрим, это линейная полиномиальная интерполяция Лагранжа. Предположим, что у нас есть две точки $(x_0, y_0)$ и $(x_1, y_1)$, где $x_0 \neq x_1$. Мы определим линейный интерполяционный полином Лагранжа как прямую линию, проходящую через обе эти точки. Построим эту прямую. Сначала заметим, что наклон этой линии будет равен $\frac{y_1 — y_0}{x_1 — x_0}$, и поэтому в форме точки-наклона мы имеем: (1) \begin{align} \quad y — y_1 = \frac{y_1 — y_0}{x_1 — x_0} (x — x_1) \\ \quad y = y_1 + \frac{y_1 — y_0}{x_1 — x_0} (x — x_1) \\ \quad y = \frac{y_1(x_1 — x_0) + (y_1 — y_0)(x — x_1)}{x_1 — x_0} \\ \quad y = \frac{y_1x_1 — y_1x_0 + y_1x — y_1x_1 — y_0x + y_0x_1}{x_1 — x_0} \\ \quad y = \frac{- y_1x_0 + y_1x — y_0x + y_0x_1}{x_1 — x_0} \\ \quad y = \frac{y_1(x — x_0) ) + y_0(x_1 — x)}{x_1 — x_0} \\ \quad y = y_0 \frac{(x_1 — x)}{x_1 — x_0} + y_1 \frac{(x — x_0)}{(x_1 — x_0)} \\ \quad y = y_0 \left ( \frac{x — x_1}{x_0 — x_1}\right ) + y_1 \left ( \frac{x — x_0}{x_1 — x_0} \right ) \end {выравнивание} Если мы допустим $L_0(x) = \frac{x — x_1}{x_0 — x_1}$ и $L_1(x) = \frac{x — x_0}{x_1 — x_0}$, то приведенный выше многочлен можно можно переписать как $P_1(x) = y_0 L_0(x) + y_1 L_1(x)$.
Давайте теперь рассмотрим несколько примеров применения линейных интерполяционных многочленов Лагранжа. Пример 1Найдите линейный интерполяционный многочлен Лагранжа $P_1(x)$, проходящий через точки $(1, 2)$ и $(3, 4)$. Функцию $P_1$ можно получить напрямую, подставив точки $(1, 2)$ и $(3, 4)$ в приведенную выше формулу, чтобы получить: (2) \begin{align} \quad P_1(x) = \frac{4(x — 1) + 2(3 — x)}{3 — 1} = \frac{4x — 4 + 6 — 2x}{2 } = \frac{2x + 2}{2} = x + 1 \end{align} Пример 2 Оценить значение $\sqrt{5}$ с помощью линейного интерполяционного многочлена Лагранжа $P_1(x)$, проходящего через точки $(1, 1)$ и $(9, 3)$ и оцените ошибку этого приближения с истинным значением $\sqrt{5} \ приблизительно 2,23606. Обратите внимание, что $(1, 1)$ и $(9, 3)$ — точки на функции $f(x) = \sqrt{x}$. Сначала зададим линейный интерполяционный многочлен Лагранжа $P_1(x)$ следующим образом: (3) \begin{align} \quad P_1(x) = \frac{3(x -1) + 1(9- x)}{9 — 1} = \frac{3x — 3 + 9 — x}{8} = \frac{2x + 6}{8} = \frac{x + 3}{4} \end{align } Теперь наша аппроксимация $f(5) = \sqrt{5}$ определяется как $P_1(5)$: (4) \begin{align} \quad P_1(5) = \frac{5 + 3}{4} = 2 \end{align} Как мы видим, наша аппроксимация занижает истинное значение $\ кв{5}$. Мы получили только одну значащую цифру точности. Если не указано иное, содержимое этой страницы находится под лицензией Creative Commons Attribution-ShareAlike 3.0 License Квадратичные интерполяционные многочлены Лагранжа — Mathonline
Вспомним со страницы «Линейные интерполяционные многочлены Лагранжа», что по двум точкам, $(x_0, y_0)$ и $(x_1, y_1)$, где $x_0$ и $x_1$ различны, мы можем построить линию $P_1$ который проходит через эти точки. (1) \begin{equation} P_1(x) = y_0L_0(x) + y_1L_1(x) \end{equation} На самом деле, использование прямолинейного интерполяционного полинома для аппроксимации функции, как правило, не очень практично, потому что многие функции кривые . Точность аппроксимации значений функции прямой линией зависит от того, насколько прямая/изогнута функция изначально между этими двумя точками и насколько близко мы находимся к точкам $(x_0, y_0)$ и $(x_1, y_1). )$. Теперь мы введем квадратичные интерполяционные полиномы Лагранжа На этот раз нам понадобятся три точки для интерполяции. Пусть $(x_0, y_0)$, $(x_1, y_1)$ и $(x_2, y_2)$ будут точками, которые мы хотим интерполировать, где $x_0 \neq x_1 \neq x_2$, и определим функции $L_0 (x)$, $L_1(x)$ и $L_2(x)$ следующим образом: (2) \begin{align} \quad L_0(x) = \frac{(x — x_1)(x — x_2)}{(x_0 — x_1)(x_0 — x_2)} \end{align} (3) \begin{align} \quad L_1(x) = \frac{(x — x_0)(x — x_2)}{(x_1 — x_0)(x_1- x_2)} \end{align} (4) \begin{align} \quad L_2(x) = \frac{(x-x_0)(x — x_1)}{(x_2 — x_0)(x_2 — x_1)} \end{align} Затем мы определяем квадратичный интерполяционный многочлен Лагранжа, $P_2$ через точки $(x_0, y_0)$, $(x_1, y_1)$ и $(x_2, y_2)$ в виде следующей функции: (5) \begin{align} \quad P_2(x) = y_0L_0(x) + y_1L_1(x) + y_2L_2(x) = y_0 \frac{(x — x_1)(x — x_2)}{(x_0 — x_1) (x_0 — x_2)} + y_1 \frac{(x — x_0)(x — x_2)}{(x_1 — x_0)(x_1- x_2)} + y_2 \frac{(x-x_0)(x — x_1)} {(x_2 — x_0)(x_2 — x_1)} \end{выравнивание} Обратите внимание, что $P_2$ на самом деле проходит через все указанные выше точки, поскольку $P_2(x_0) = y_0$, $P_2(x_1) = y_1$ и $P_2(x_2) = y_2$.
Важно отметить, что, хотя мы определяем $P_2$ как «квадратичный» интерполирующий многочлен Лагранжа, возможно, что степень $P_2$ может быть меньше $2$. Рассмотрим теперь несколько примеров построения квадратичных интерполяционных многочленов Лагранжа. Пример 1Построить квадратичный интерполяционный многочлен Лагранжа $P_2(x)$, интерполирующий точки $(1, 4)$, $(2, 1)$ и $(5, 6)$. Применяя непосредственно приведенную выше формулу, мы получаем, что: (6) \begin{align} \quad P_2(x) = 4 \frac{(x — 2)(x — 5)}{(1 — 2)(1 — 5)} + 1 \frac{(x — 1) )(x — 5)}{(2 — 1)(2- 5)} + 6 \frac{(x-1)(x — 2)}{(5 — 1)(5 — 2)} \\ \ quad P_2(x) = (x — 2)(x-5) — \frac{1}{3} (x — 1)(x — 5) + \frac{1}{2} (x — 1)( x-2) \end{align} График $y = P_2(x)$ приведен ниже: Пример 2 Построить квадратичный интерполяционный многочлен Лагранжа $P_2(x)$, интерполирующий точки $ (1, 2)$, $(3, 4)$ и $(5, 6)$. |
 5
5
 8957
8957 6\] Теперь проверим, что мы действительно нашли то, что нужно и полученный полином в узлах совпадает с исходной функцией, то есть, что: \[P_6(x_i) = y_i\]
6\] Теперь проверим, что мы действительно нашли то, что нужно и полученный полином в узлах совпадает с исходной функцией, то есть, что: \[P_6(x_i) = y_i\] Небольшие расхождения объясняются округлением при вычислении значений исходной функции в узлах и последующим округлением.
Небольшие расхождения объясняются округлением при вычислении значений исходной функции в узлах и последующим округлением.


 1. Методика вычисления полинома в форме Лагранжа
1. Методика вычисления полинома в форме Лагранжа В соответствии с условиями задачи полином в форме Лагранжа в точке x=9,5 принимает следующее значение: L(9,5)= – 4,121. Из графика видно, что полученное значение не совпадает cо значением функции f(x) на величину абсолютной погрешности интерполяционной формулы Лагранжа.
В соответствии с условиями задачи полином в форме Лагранжа в точке x=9,5 принимает следующее значение: L(9,5)= – 4,121. Из графика видно, что полученное значение не совпадает cо значением функции f(x) на величину абсолютной погрешности интерполяционной формулы Лагранжа. Интерполяции могут быть полезны, поскольку исходная функция не может быть легко интегрируемой или хорошо дифференцируемой, в то время как полиномы относительно легко интегрируются и дифференцируются. Иногда мы используем интерполяции, потому что с ними легче работать в целом для вычислений.
Интерполяции могут быть полезны, поскольку исходная функция не может быть легко интегрируемой или хорошо дифференцируемой, в то время как полиномы относительно легко интегрируются и дифференцируются. Иногда мы используем интерполяции, потому что с ними легче работать в целом для вычислений.
 ..$.
..$.  Мы также увидели, что можем аппроксимировать функцию этой линией, которая также проходит через эти две точки.
Мы также увидели, что можем аппроксимировать функцию этой линией, которая также проходит через эти две точки. Формальное определение многочлена выше дано ниже.
Формальное определение многочлена выше дано ниже.