If pascal abc: Справка PascalABC.NET

Содержание

«Мандалорец» приближается к третьему сезону на Disney+, актеры обещают больше экшена, драмы, сюрпризов и Грогу Среда, 1 марта 2023 г. «Мандалорец» воссоединяется с Грогу, поскольку они вместе продолжают свое путешествие в третьем сезоне популярного сериала Disney +. В новом сезоне мы увидим старых союзников, новых врагов и, как сказал нам сам «Мандалорец», актер Педро Паскаль… еще больше мандалорцев!

ГОЛЛИВУД — «Мандалорец» воссоединяется с Грогу, и они вместе продолжают свое путешествие в третьем сезоне популярного сериала Disney+. В Голливуде прошел специальный показ, посвященный его долгожданному возвращению.

Второй сезон закончился в конце 2020 года, и фанаты хотят продолжения. Как мы видим, в новом сезоне мы увидим старых союзников, новых врагов и, как сказал нам сам «Мандалорец», актер Педро Паскаль… даже больше.

«Я могу сказать вам, что мы собираемся встретить больше мандалорцев», сказал Паскаль. «Мы собираемся узнать намного больше о Мандалоре. И я очень, очень, очень взволнован Бо-Катаном».

Нам придется подождать и выяснить, почему, потому что Кэти Сакхофф, актриса, играющая Бо-Катан, не разговаривает. Она даже с подозрением относится к раскрытию секретов отцу!

«Я заставляю отца подписывать фальшивые соглашения о неразглашении!» — засмеялся Сакхофф. «Да. Я занимаюсь этим со времен «Лонгмайра». Я сделал это для второго сезона «Мандалорца». Я сделал это для «Звезды битвы». Я просто продолжаю заставлять его подписывать эти фальшивые соглашения о неразглашении, потому что он любит Facebook».

Остальной актерский состав довольно молчалив о том, что ждет впереди, но некоторые губы приоткрылись.

«Это несравнимо ни с чем, что вы видели раньше, потому что все в этой вселенной становится больше, а мифологическая история, на которой она основана, становится глубже», — сказал Джанкарло Эспозито.

«Поклонники будут очень взволнованы и заинтригованы тем, как в этом сезоне раскрываются некоторые вещи, о которых они давно думали», — сказала Эмили Суоллоу.

«Проработав в этой индустрии уже 50 лет как профессионал, я действительно встречаюсь с самим собой. Для меня это один из лучших опытов, которые я когда-либо имел», — сказал Карл Уэзерс.

Чувствуется волнение от актера-ветерана к многообещающему молодому актеру, который даже не сказал людям, что он в «Мандалорце!»

«Я удивляю всех своих друзей, и все они большие фанаты «Звездных войн». Так что будет интересно посмотреть на их реакцию», — сказал Уэсли Киммел.

«Мандалорец» сейчас транслируется на Disney+.

Disney является материнской компанией этой станции ABC.

Сообщить об исправлении или опечатке

Связанные темы

Arts & Entertainment Голливудский диснеевский Disney+ Streaming Service Star Wars на красной ковровой дорожке

Звездные войны

Этот шеф -повар вдохновляет коллеги, а гости

Сезон 3 -го сезона. говорит

Джон Фавро получает звезду на Аллее славы в Голливуде

Пекарня CA создает статую «Пан Соло» из «Звездных войн» из хлеба

Главные новости

3, including high school student, found dead in NJ home

25 minutes ago

1 killed, several injured in Yonkers apartment fire

15 minutes ago

9 пожарных пострадали в результате пожара в 4 домах в Квинсе

1 час назад

Невеста тележурналиста, убитая во Флориде, планирует родить ребенка с помощью ЭКО

2 часа назад

Подростки причина причина принесена на ущерб в размере 20 тыс.

Долл. час назад

AccuWeather: Ветрено, но солнечно

Нехватка лекарств для лечения проблем с дыханием, которые могут ухудшиться

2 часа назад

Регулярные выражения

Точно так же, как конечные автоматы используются для распознавания шаблонов. строк, регулярные выражения используются для генерации образцы струн. Регулярное выражение — это алгебраическая формула, значение которой это шаблон, состоящий из набора строк, называется языком выражения.

Операнды в регулярном выражении могут быть:

символов из алфавита над которым регулярное выражение определено.
переменные , чьи значения являются любым шаблоном определяется регулярным выражением.
эпсилон , который обозначает пустую строку, не содержащую символов.
null обозначает пустой набор строк.

Операторы, используемые в регулярных выражениях, включают:

Объединение: Если R1 и R2 являются регулярными выражениями, то R1 | R2 (также пишется как R1 U R2 или R1 + R2) также является регулярным выражением.
L(R1|R2) = L(R1) U L(R2).
Конкатенация: Если R1 и R2 являются регулярными выражениями, тогда R1R2 (также пишется как R1.R2) также является регулярным выражением.
L(R1R2) = L(R1), связанный с L(R2).
Закрытие Клини: если R1 является регулярным выражением, тогда R1* (замыкание Клини R1) также является регулярным выражением.
L(R1*) = эпсилон U L(R1) U L(R1R1) U L(R1R1R1) U …

Замыкание имеет наивысший приоритет, за ним следует конкатенация, с последующим союзом.

Примеры

Набор строк более {0,1}, заканчивающихся тремя последовательными единицами.

      (0 | 1)* 111

Набор строк более {0,1}, в которых есть хотя бы одна единица.

      0* 1 (0 | 1)*

Набор строк более {0,1}, в которых есть не более одной единицы.

      0* | 0* 1 0*

Набор строк над {A..Z,a..z}, содержащих слово «main».

      Пусть <буква> = А | Б | ... | Я | а | б | ... | г
  
      <буква>* главная <буква>*

Набор строк над {A..Z,a..z}, содержащих 3 x.

      <буква>* x <буква>* x <буква>* x <буква>*

Набор идентификаторов в Паскале.

      Пусть <буква> = А | Б | ... | Я | а | б | ... | г
      Пусть <цифра> = 0 | 1 | 2 | 3 ... | 9
  
      <буква> (<буква> | <цифра>)*

Множество действительных чисел в Паскале.

      Пусть <цифра> = 0 | 1 | 2 | 3 ... | 9Пусть <выражение> = 'E' <знак> <цифра> <цифра>* | эпсилон
      Пусть <знак> = '+' | '-' | эпсилон
      Пусть <десятичный> = '.' <цифра> <цифра> * | эпсилон
  
      <цифра> <цифра>* <десятичное число> <выражение>

Расширения оператора Unix

Регулярные выражения часто используются в Unix:

В командной строке
В текстовых редакторах
В контексте программ сопоставления с образцом например 9′
конец строки: ‘$’
подстановочный знак, соответствующий любому символу, кроме новой строки: ‘. ‘
необязательный экземпляр: R? = эпсилон | р
один или несколько экземпляров: R+ == RR*

Эквивалентность регулярных выражений и конечных автоматов

Регулярные выражения и конечные автоматы имеют эквивалентную выразительную силу:

Для каждого регулярного выражения R, существует соответствующий FA, который принимает набор строк, сгенерированных R.
Для каждой FA A существует соответствующее регулярное выражение, которое генерирует набор строк, принятых A.

Доказательство состоит из двух частей:

алгоритм, который по заданному регулярному выражению R создает FA A такое, что L(A) == L(R).
алгоритм, который на основе FA A создает регулярное выражение R такое, что L(R) == L(A).

Наша конструкция FA из регулярных выражений позволит «эпсилон-переходы» (переход из одного состояния в другое с эпсилон в качестве метки). Такой переход всегда возможен, поскольку эпсилон (или пустая строка) можно сказать, что она существует между любыми двумя входными символами. Мы можем показать, что такие эпсилон-переходы удобны при записи; для каждой FA с эпсилон-переходами существует соответствующая FA без них.

Построение ТВС из RE

Начнем с того, что покажем, как построить FA для операнды в регулярном выражении.

Если операндом является символ c, то наш FA имеет два состояния, s0 (начальное состояние) и sF (конечное, принимающее состояние), и переход от s0 к sF с меткой c.
Если операнд эпсилон, то наш FA имеет два состояния, s0 (начальное состояние) и sF (конечное, принимающее состояние), и эпсилон-переход от s0 к sF.
Если операнд нулевой, то наш FA имеет два состояния, s0 (начальное состояние) и sF (конечное, принимающее состояние), и никаких переходов.

Учитывая FA для R1 и R2, мы теперь покажем, как построить FA для R1R2, R1|R2 и R1*.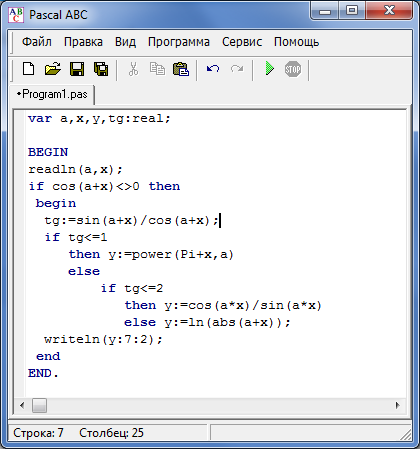 Пусть A (с начальным состоянием a0 и конечным состоянием aF) быть машиной, принимающей L(R1) и B (с начальным состоянием b0 и конечным состоянием bF) — машина, принимающая L(R2).

Машина C, принимающая L(R1R2), включает A и B, с начальным состоянием a0, конечное состояние bF и эпсилон-переход из aF в b0.

Машина C, принимающая L(R1|R2), включает A и B, с новым начальным состоянием c0, новое конечное состояние cF, и эпсилон-переходы из c0 к а0 и b0, и от aF и bF до cF.
Машина C, принимающая L(R1*) включает А, с новым начальным состоянием c0, новое конечное состояние cF и эпсилон-переходы из c0 до a0 и cF, и от aF до a0, и от aF до cF.

Устранение переходов Эпсилон

Если мы сможем исключить эпсилон-переходы из FA, то наша конструкция FA из регулярного выражения (что дает FA с эпсилон-переходами) можно завершить.

Обратите внимание, что эпсилон-переходы подобны недетерминизму. в том, что они предлагают выбор: эпсилон-переход позволяет нам оставаться в состоянии или двигаться в новое состояние, независимо от входного символа.

Если начать в состоянии s1, мы можем достичь состояния s2 через серию эпсилон-переходов за которым следует переход по входному символу x, мы можем заменить все эпсилон-переходы одним переход от s1 к s2 по символу x.

Алгоритм исключения эпсилон-переходов

Мы можем построить конечный автомат F2 без эпсилон-переходов из конечного автомата F1, содержащего эпсилон-переходы, следующим образом:

Состояния F2 — это все состояния F1 которые имеют входящий переход, помеченный некоторым символом кроме эпсилон, плюс начальное состояние F1, которое также является начальным состоянием F2.
Для каждого состояния в F1, определить, какие другие состояния достижимы только через эпсилон-переходы. Если состояние F1 может достичь конечного состояния в F1 через эпсилон-переходы, то соответствующие состояние является конечным состоянием в F2.
Для каждой пары состояний i и j в F2, существует переход из состояния i в состояние j на входе x, если существует состояние k, достижимое из состояния i через эпсилон переходы в F1, и в F1 есть переход из состояния k в состояние j на входе x.

Создание RE из ТВС

Чтобы построить регулярное выражение из DFA (и тем самым завершить доказательство того, что регулярные выражения и конечные автоматы имеют одинаковую выразительную силу), мы заменяем каждое состояние в DFA одно за другим соответствующим регулярное выражение.

Так же, как мы построили небольшую FA для каждого оператора и операнда в регулярном выражении, теперь мы создадим небольшое регулярное выражение для каждого состояния в ДФА.

Основная идея состоит в том, чтобы исключать состояния FA одно за другим, замена каждого состояния регулярным выражением, которое генерирует часть входной строки который обозначает переходы в и из ликвидируемого государства.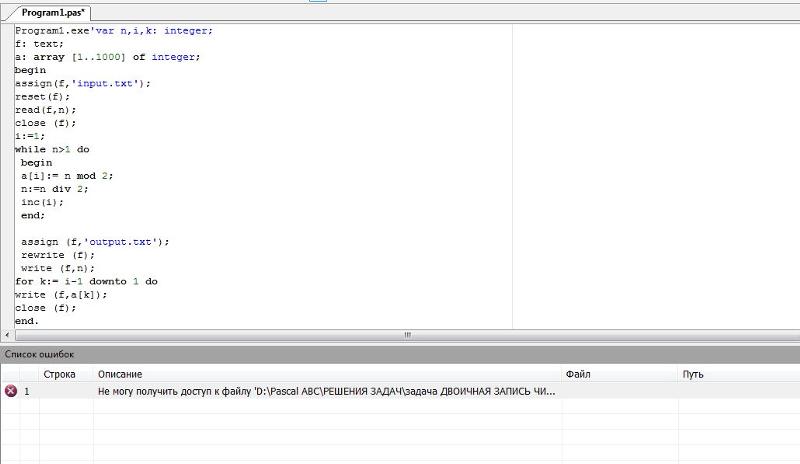

Алгоритм построения RE из ТВС

По заданному DFA F мы строим регулярное выражение R такое, что
L(F) == L(R).

Препроцессируем FA, включаем метки переходит в регулярные выражения. Если есть переход с меткой {a,b}, затем мы заменяем метку регулярным выражением a | б. Если нет перехода из состояния в себя, мы можем добавить один с меткой NULL.

Для каждого принимающего состояния sF в F исключить все состояния в F, кроме начального состояния s0 и sF.

Чтобы исключить состояние sE, рассмотрим все пары состояний sA и sB таких, что существует переход от sA к sE с меткой R1, переход от sE к sE с меткой R2 (возможно, ноль, что означает отсутствие перехода), и переход от sE к sB с меткой R3. Введите переход от sA к sB с меткой R1R2*R3. Если уже есть переход от sA к sB с метка R4, затем замените эту метку на R4|R1R2*R3.

После исключения всех состояний, кроме s0 и sF:

Если s0 == sF, то результирующее регулярное выражение есть R1*, где R — метка на переходе от s0 к s0.