Проверка статистических гипотез — Questionstar
5.2 Индуктивная статистика
5.2.1 Проверка статистических гипотез
Проверка статистических гипотез
Проверка статистических гипотез – это пятиступенчатая процедура, которая на основании данных выборки и при помощи теории вероятностей позволяет сделать вывод об обоснованности гипотезы.
Другими словами, этот способ проверить, действительны ли результаты, полученные на выборке, и для генеральной совокупности.
Люди «ошибочно уверенны» в своих знаниях и недооценивают вероятность того, что их убеждения могут оказаться ложными. Им свойственно искать искать такую дополнительную информацию, которая лишь подтверждает их собственные убеждения.
Макс Базерман
Пошаговый алгоритм:
1.Формулировка основной и альтернативной гипотезы
2.Выбор уровня значимости
3.Определение подходящего статистического критерия
4.Формулировка правила принятия решения
5.
Принятие решения на основании данных выборки
Пол и частота пользования интернетом:
| Пол | |||
| Пользование интернетом | Мужской | Женский | Сумма по строке |
| редко | 5 | 10 | 15 |
| часто | 10 | 5 | 15 |
| Сумма по столбцу | 15 | 15 | n=30 |
Вопрос:
Можем ли мы на основании этой выборки утверждать, что во всем населении среди мужчин больше активных интернет пользователей, чем среди женщин?
Шаг 1: Формулировка основной и альтернативной гипотезы
Нулевая гипотеза (H0) – это утверждение статус-кво, что никакой разницы или никакого эффекта на самом деле нет.
Альтернативная гипотеза (H1) утверждает, что некоторая разница (или эффект) все таки должна быть.
H0: в отношении частоты пользования интернетом разницы между мужчинами и женщинами нет.
H1: мужчины и женщины пользуются интернетом с разной частотой.
Шаг 2: Выбор уровня значимости
Значимость (α) – вероятность того, что верная нулевая гипотеза будет отвергнута.
β – вероятность того, что ложная нулевая гипотеза будет принята.
| Нулевая гипотеза (H0) верна | Нулевая гипотеза (H0) ложна | |
| Нулевая гипотеза отвергнута | ложноположительное (ошибка первого рода) | H0 верно принята |
| Нулевая гипотеза | H0 верно отвергнута | ложноотрицательное (ошибка второго рода) |
Аналогия: суд над маньяком
H0: заключенный не виновен
Аналогия: шорох в кустах – это лев?
H0: льва в кустах нет
Уровни значимости, принятые в маркетинговых исследованиях:
α – уровень значимости
0,01 (1%)
0,05 (5%)
(1-α) – уровень доверия (доверительная вероятность)
0,99 (99%)
0,95 (95%)
Шаг 3: Определение статистического критерия
Критерий χ2 (хи-квадрат) используется для проверки статистической значимости взаимосвязей между переменными, наблюдаемых в перекрестных таблицах.
H0: взаимосвязи между переменными нет
Тест χ2 проверяет равенство частотных распределений.
Какие распределения/частоты мы должны проверить?
fо – ожидаемые частоты (расчётные значения), которые бы стояли в ячейках, в случае когда связи между переменными нет.
fн – реально наблюдаемые частоты, т.е. значения, которые стоят в составленной нами таблице
Расчёт χ2 следует производить только на основе абсолютных значений частот. Если исходные данные представлены в процентах, то их необходимо пересчитать а абсолютные частоты.
В нашем примере:
Шаг 4: Формулировка правила принятия решения
Kн – наблюдаемое (расчётное) значение статистического критерия.
Kкрит– критическое значение статистического критерия для заданного уровня значимости.
Если вероятность Kн меньше уровня значимости (α), то H0 надо отклонить.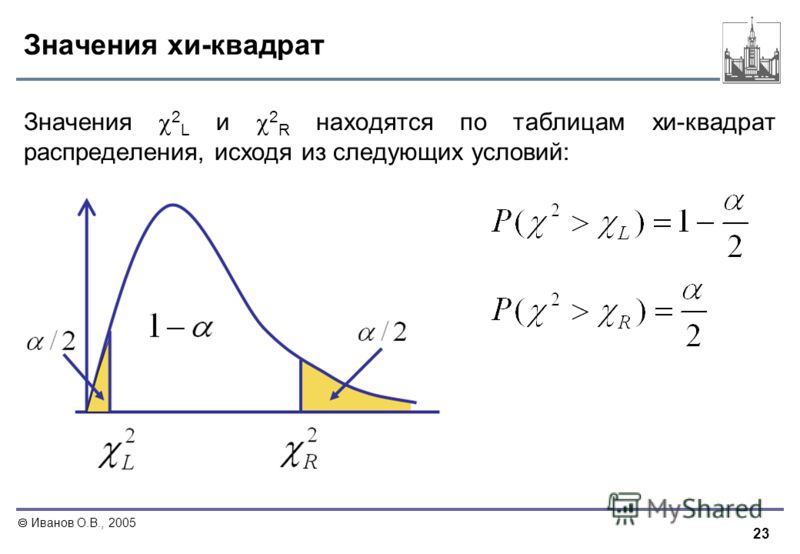
или
Если Kн>Kкрит , то H0 надо отклонить.
Таблица критических значений χ2 для различных α
df=(r-1)(c-1)
df – количество степеней свободы
r – количество строк
c – количество столбцов
df=(2-1)(2-1)=1
H0 не может быть отклонена
Шаг 5: Принятие решения
Нашлись ли доказательства? Что из этого следует?
— H
— Различия не являются статистически значимыми на уровне 0,05
— Полученные на выборке результаты не могут быть обобщены на генеральную совокупность
Пол и частота пользования интернетом
| Пол | |||
| Пользование интернетом | Мужской | Женский | Сумма по строке |
| редко | 5 | 10 | 15 |
| часто | 10 | 5 | 15 |
| Сумма по столбцу | 15 | 15 | n=30 |
Вопрос:
Можем ли мы на основании этой выборки утверждать, что во всем населении среди мужчин больше активных интернет пользователей, чем среди женщин?
Ответ:
Данная выборка не дает оснований для таких утверждений.
Если выборка была произведена должным образом, то мы можем с 95% доверительной вероятностью констатировать, что взаимосвязи между полом и частотой пользования интернетом нет. В противном случае – мы не знаем ответа.
Значение P образца Калькулятор | Вычислить Значение P образца
✖Доля выборки — это отношение успехов, необходимых для исследования выборки, к размеру выборки.ⓘ Образец пропорции [PSample] | +10% -10% | ||
✖Предполагаемая доля населения — это отношение успехов, необходимых в исследовании населения, к размеру населения, которое предполагается в нулевой гипотезе теста.ⓘ Предполагаемая доля населения [P0(Population)] | +10% -10% | ||
✖Размер выборки — это общее количество лиц, присутствующих в данной выборке в исследуемой популяции.ⓘ Размер образца [N] | +10% -10% |
|
✖P Значение выборки — это статистическая мера, используемая для определения того, верна ли гипотеза в статистическом тесте. |
⎘ копия |
ⓘ Значение P образца [P]
👎
Формула
сбросить
👍
Значение P образца Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Образец пропорции: 0.7 —> Конверсия не требуется
Предполагаемая доля населения: 0.6 —> Конверсия не требуется
Размер образца: 20 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.
912870929175277 —> Конверсия не требуется
< 10+ Основные формулы в статистике Калькуляторы
Значение P образца формула
Значение P образца = (Образец пропорции-Предполагаемая доля населения)/sqrt((Предполагаемая доля населения*(1-Предполагаемая доля населения))/Размер образца)
Что такое значение P в статистике?
Значение p — это число, рассчитанное на основе статистического теста, которое описывает, насколько вероятно, что вы найдете определенный набор наблюдений, если нулевая гипотеза верна. Значения P используются при проверке гипотез, чтобы решить, следует ли отклонить нулевую гипотезу. Чем меньше значение p, тем больше вероятность того, что вы отклоните нулевую гипотезу.
Значение p, или значение вероятности, говорит вам, насколько вероятно, что ваши данные могли появиться при нулевой гипотезе. Он делает это, вычисляя вероятность вашей тестовой статистики, которая представляет собой число, рассчитанное статистическим тестом с использованием ваших данных.
Share
Copied!
| Variable | Value | ||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| $_SERVER[‘LSPHP_ENABLE_USER_INI’] | on | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘PATH’] | /usr/local/bin:/usr/bin :/bin | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘TEMP’] | /tmp | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘TMP’] | /tmp | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘TMPDIR’] | /tmp | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘PWD’] | / | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP_ACCEPT’] | text/html,application/xhtml+xml,application/xml;q=0.9,*/*;q=0.8 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP_ACCEPT_CHARSET’] | windows- 1251,utf-8;q=0. 7,*;q=0.7 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP_ACCEPT_ENCODING’] | gzip | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP_ACCEPT_USA1;1 9000en 0.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘CONTENT_TYPE’] | application/x-www-form-urlencoded;charset=UTF-8 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _server [‘content_length’] | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _server [‘http_host’] | www.statskdom.com | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _server [‘http_user_agent’] | 110$ _server [‘http_user_agent’] | 110$ _server [‘http_user_agent’] | 110$ _server x86_64; rv:33.0) Gecko/20100101 Firefox/33.0 | ||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP_CACHE_CONTROL’] | no-cache | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP_X_FORWARDED_FOR’] | 161.97.168.212 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER [‘HTTP_CF_IPCOUNTRY’] | DE | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP_CDN_LOOP’] | cloudflare | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP_CF_RAY’] | 79f2270b2ab0cae5-DUS | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP_X_FORWARDED_PROTO’] | https | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP_CF_VISITOR’] | {«scheme»:»https»} | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP_CF_CONNECTING_IP’] | 161. 97.168.212 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP_X_HTTPS’] | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REDIRECT_UNIQUE_ID’] | Y_pFB04REpqYc014sezL-wAAMBw | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REDIRECT_SCRIPT_URL’] | /310goodnesschi.html | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REDIRECT_SCRIPT_URI’] | https://www .statskingdom.com/310goodnesschi.html | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REDIRECT_GD-USERNAME’] | qtlgsguvxu0r | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REDIRECT_HTTPS’] | on | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REDIRECT_SSL_TLS_SNI’] | www.statskingdom.com | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _server [‘redirect_http2’] | на | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _server [‘redirect_h3push’] | OFF | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ | |||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _server [‘redirect_h3_pushed’] | Нет значения | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _server [‘redirect_h3_pushed_on’] | no value | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ | no value 9008 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ | . 0011 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REDIRECT_h3_STREAM_TAG’] | 1772772-1275-1 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REDIRECT_REQUEST_METHOD’] | GET | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REDIRECT_STATUS’] | 404 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘UNIQUE_ID’] | Y_pFB04REpqYc014sezL-wAAMBw | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘SCRIPT_URL’] | /310goodnesschi.html | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘SCRIPT_URI’] | https://www .statskingdom.com/310goodnesschi.html | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘GD-USERNAME’] | qtlgsguvxu0r | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTPS’] | on | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘SSL_TLS_SNI’] | www.statskingdom.com | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘HTTP2’] | on | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘h3PUSH’] | off | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘h3_PUSH’] | off | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘h3_PUSHED’ ] | нет значения | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘h3_PUSHED_ON’] | no value | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘h3_STREAM_ID’] | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘h3_STREAM_TAG’] | 1772772-1275-1 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _server [‘server_signature’] | Нет значения | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _server [‘Server_Software’] | Apache | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _Server [‘Server_NAME’] | |||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _Server [‘Server_NAME’] | |||||||||||||||||||||||||||||||||||||||||||||||||||
. | $ _server [‘server_addr’] | 166.62.72.160 | |||||||||||||||||||||||||||||||||||||||||||||||||
| $ _server [‘Server_port’] | 443 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _Server [‘remote_addr’] | 198,242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.242.2377 ‘DOCUMENT_ROOT’] | /home/qtlgsguvxu0r/public_html | |||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REQUEST_SCHEME’] | https | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘CONTEXT_PREFIX’] | no value | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[ ‘CONTEXT_DOCUMENT_ROOT’] | /home/qtlgsguvxu0r/public_html | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _server [‘server_admin’] | [email protected] | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _server [‘script_filename’] | |||||||||||||||||||||||||||||||||||||||||||||||||||
| $ _Server [‘script_filenam | |||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REMOTE_PORT’] | 39596 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REDIRECT_URL’] | /310goodnesschi.html | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘SERVER_PROTOCOL’] | HTTP/2. 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REQUEST_METHOD’] | GET | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘QUERY_STRING’] | no value | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REQUEST_URI’] | /310goodnesschi.html | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘SCRIPT_NAME’] | /404.php | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘PHP_SELF’] | /404.php | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REQUEST_TIME_FLOAT’] | 1677346055.4292 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_SERVER[‘REQUEST_TIME’] | 1677346055 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_ENV[‘LSPHP_ENABLE_USER_INI’] | на | ||||||||||||||||||||||||||||||||||||||||||||||||||
| $_ENV[‘PATH’] | /usr/local/bin:/usr/bin:/bin |
| /TMP | |
| $ _ENV [‘TMP’] | /TMP |
| $ _ENV [‘TMPDIR’] | /TMP |
| $ _ENV [‘PWD’] | |
| $ _ENV [‘PWD’] | |
| $ _ENV [‘PWD’] | |
| $ _ENV [‘PWD’] | |
| $ |
Калькулятор хи-квадрата — критерий независимости, однородности или согласия
Используйте этот калькулятор хи-квадрат, чтобы легко проверить таблицы непредвиденных обстоятельств категориальных переменных на независимость или на критерий согласия.
Может использоваться в качестве калькулятора критерия согласия хи-квадрат , в качестве калькулятора критерия независимости хи-квадрат или в качестве критерия однородности. Поддерживает неограниченное количество строк и столбцов (групп и категорий): 2×2, 3×3, 4×4, 5×5, 2×3, 2×4 и произвольные таблицы непредвиденных обстоятельств N x M. Выходы Χ 2 и p-значение.
Быстрая навигация:
- Использование калькулятора хи-квадрат
- В качестве критерия независимости или однородности хи-квадрат
- В качестве критерия согласия хи-квадрат
- Критерий независимости хи-квадрат
- Критерий однородности хи-квадрат
- Критерий согласия хи-квадрат
- Сравнение трех типов критерия Хи-квадрат -Квадратные тесты
- Другие тесты
Упомянутый выше простой в использовании инструмент может работать в двух основных режимах: как тест на согласие и как тест на независимость/однородность.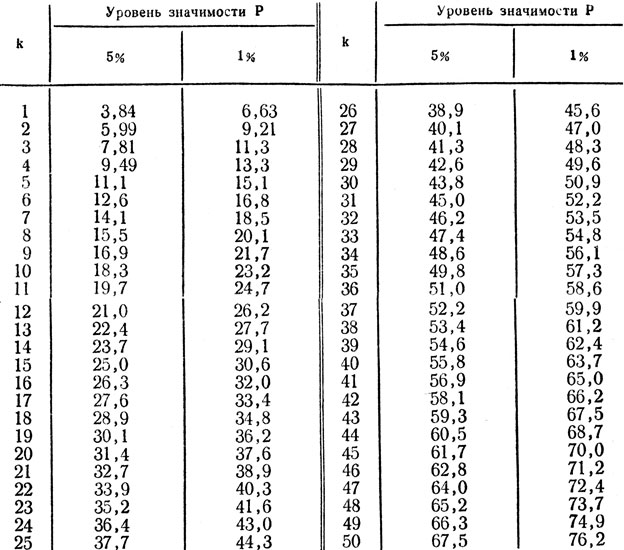
Эти режимы применяются к различным ситуациям, подробно описанным ниже. Режим работы можно выбрать с помощью переключателя под полем ввода данных в интерфейсе калькулятора хи-квадрат.
В качестве теста хи-квадрат независимости или однородности
Скопируйте/вставьте данные из файла электронной таблицы в поле ввода данных калькулятора или введите их вручную, используя пробел ( ) в качестве разделителя столбцов и новую строку в качестве разделителя строк. Данные во всех ячейках следует вводить в виде счетчиков (целые числа, целые числа). Например, если у вас есть эти данные в Excel:
, просто скопируйте и вставьте числовые ячейки в поле ввода калькулятора выше. Щелкните здесь, чтобы увидеть, как работает этот пример. Если известно, что данные выборки независимы, результат можно рассматривать как тест на однородность. Если данные основаны на двух категориальных переменных, измеренных в одной и той же совокупности, результат можно интерпретировать как тест на независимость между переменными.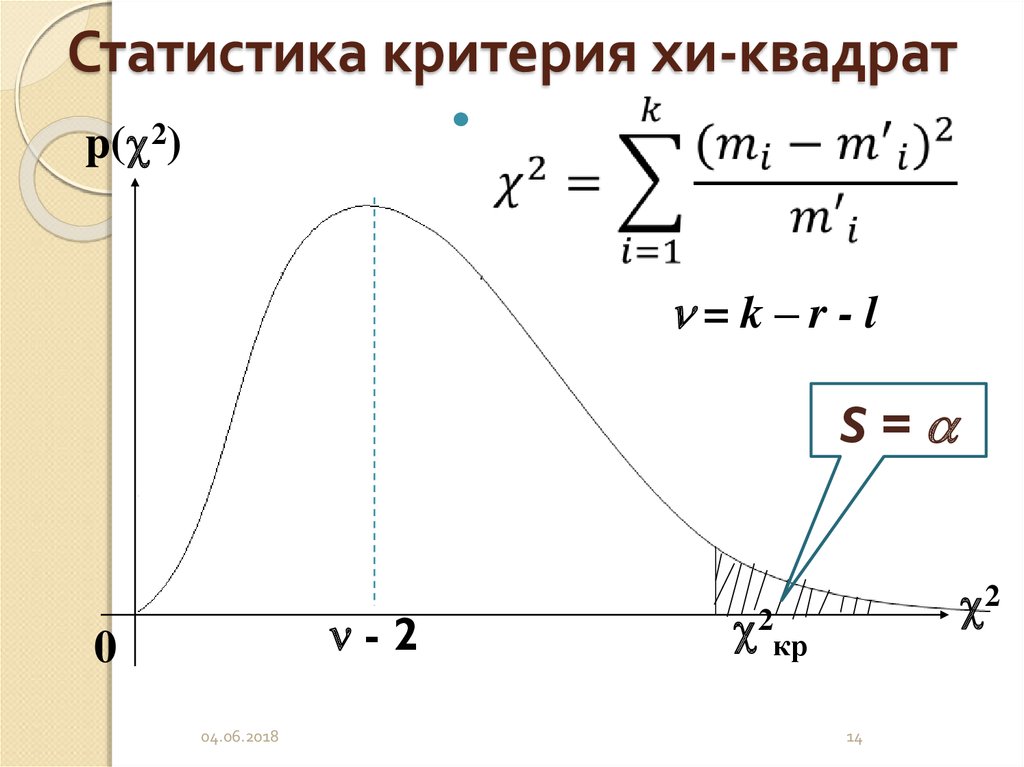
В качестве критерия согласия хи-квадрат
Калькулятор критерия хи-квадрат можно использовать в качестве калькулятора согласия, введя наблюдаемые значения (числа) в первый столбец и ожидаемые частоты для каждый результат во втором столбце. Ожидаемые частоты должны суммироваться до ~1. Например, если мы проверяем, является ли игральная кость честной, у нас будет ожидаемая частота 0,1666 (6) для каждого числа. Примерный набор данных может выглядеть так:
| Номер | Количество показов | Ожидаемая частота |
|---|---|---|
| 1 | 168 | 0,1666 |
| 2 | 170 | 0,1666 |
| 3 | 160 | 0,1666 |
| 4 | 163 | 0,1666 |
| 5 | 173 | 0,1666 |
| 6 | 166 | 0,1666 |
| Итого | 1000 | 1 |
Щелкните здесь, чтобы загрузить примеры данных в калькулятор и выполнить тест на соответствие.
Убедитесь, что выбран соответствующий тип теста «Хи-квадрат критерия согласия».
Что такое «тест хи-квадрат»?Критерий хи-квадрат — это любой статистический тест, в котором выборочное распределение параметра является Χ 2 -распределенным в соответствии с нулевой гипотезой и, таким образом, относится к целому ряду различных видов тестов, основанных на этом распределении. В своей первоначальной версии он был разработан Карлом Пирсоном в 1900 году как тест на соответствие: проверка того, соответствует ли конкретный набор наблюдаемых данных частотному распределению из семейства распределений Пирсона (критерий хи-квадрат Пирсона). Пирсон в 1904 расширил свое приложение до проверки независимости между строками и столбцами таблицы непредвиденных обстоятельств категориальных переменных [1] . В дальнейшем она была расширена Р. Фишером в 1922-24 гг.
Статистическая модель , стоящая за тестами, требует, чтобы переменные были результатом простой случайной выборки и, таким образом, были независимыми и одинаково распределенными (ID) (при нулевой гипотезе).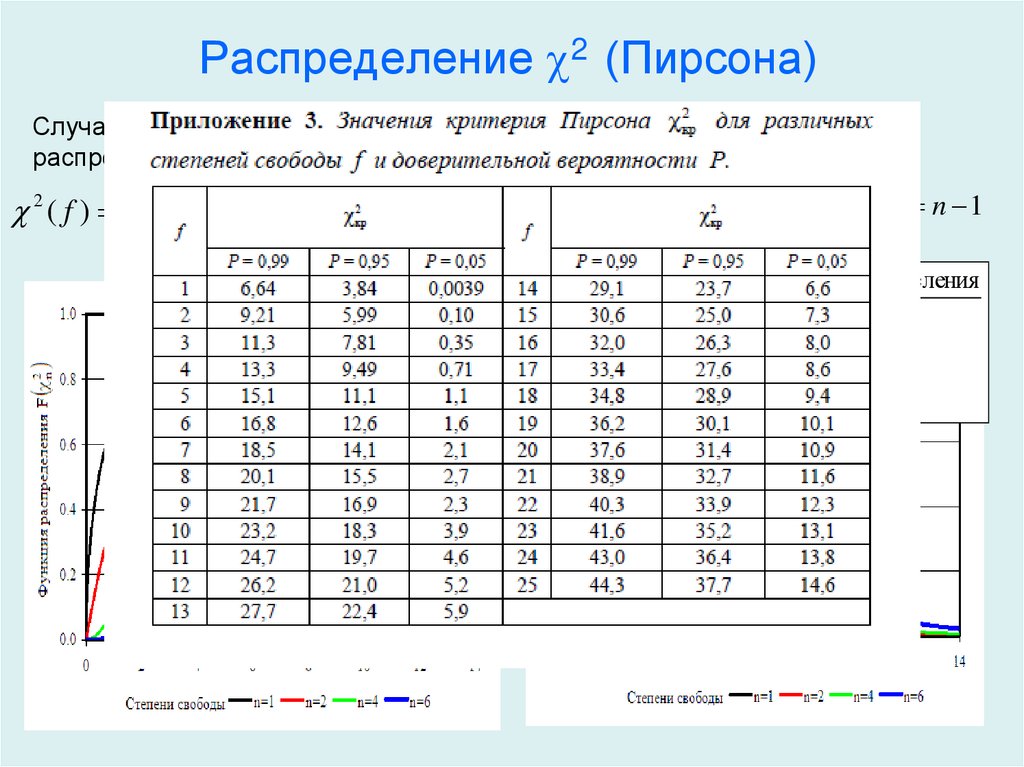
Следовательно, тест можно использовать как тест на независимость или тест на однородность (идентичность распределений). В некоторых ограниченных ситуациях он также может функционировать как тест на разницу в дисперсиях. Это, однако, также означает, что если кто-то хочет протестировать данные, отличные от IID, следует выбрать другой тест.
Как и большинство статистических тестов, он плохо работает при очень малом размере выборки, в частности потому, что допущение Χ 2 может не соответствовать имеющимся данным. Для простой таблицы непредвиденных обстоятельств 2 на 2 требуется, чтобы каждая ячейка имела значение больше 5. Для больших таблиц не более 20% всех ячеек должны иметь значения меньше 5. Наш калькулятор хи-квадрат проверит некоторые из этих условий. и выдавать предупреждения, где это уместно.
Хи-квадрат Формула Формула одинакова независимо от того, проводите ли вы тест на соответствие, тест на независимость или на однородность .
Однако, несмотря на то, что формула всех трех тестов одинакова, все три имеют разные нулевые гипотезы и интерпретации (см. Ниже). Формула хи-квадрат выглядит просто:
, где n — количество ячеек в таблице, а O i и E i — наблюдаемые и ожидаемые значения каждой ячейки. В результате Χ 2 Кумулятивная функция распределения статистики вычисляется из распределения хи-квадрат с (r — 1) · (c — 1) степенями свободы (r — количество строк, c — количество столбцов).
Типы тестов хи-квадратЗдесь мы рассмотрим три применения теста хи-квадрат: в качестве теста на независимость, в качестве теста на однородность (идентичное распределение) и в качестве теста на согласие.
Тест независимости хи-квадрат
Этот тест также иногда называют «тест ассоциации» , и он определяет, являются ли две категориальные переменные для одного образца независимыми или связанными друг с другом.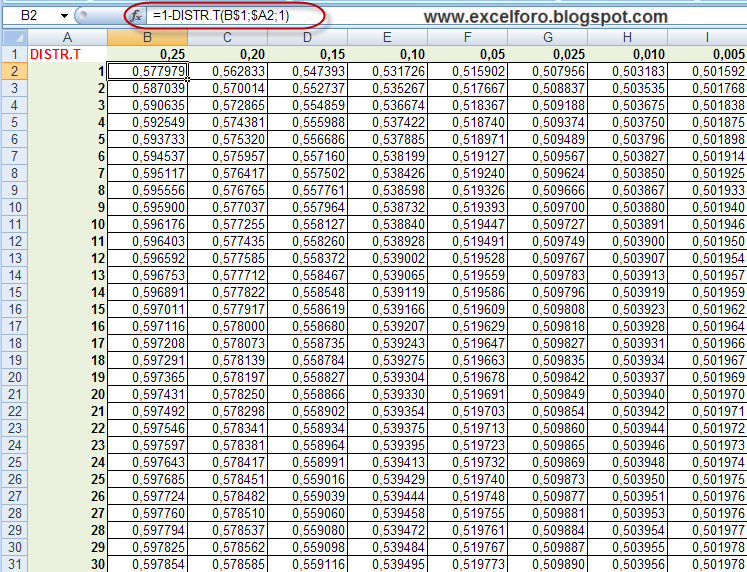
Например, в ходе опроса респондентов могут попросить указать уровень их образования, рост и состояние, чтобы определить, существует ли зависимость одной переменной от других. Таким образом, нулевая гипотеза H 0 будет следующей: переменные образование, рост и богатство независимы . Альтернативная гипотеза H 1 означает: «некоторые переменные образование, рост и чистое состояние зависят друг от друга». Обратите внимание, что в случае наличия более двух переменных значение null будет отклонено, даже если некоторые переменные не зависят друг от друга: достаточно одной зависимости в таблице, чтобы потенциально сделать значение null недействительным.
При использовании калькулятора в качестве теста на независимость получение небольшого значения p следует интерпретировать как свидетельство того, что две (или более) группы не являются независимыми. Обратите внимание, что если имеется более двух переменных, вы не можете сказать, какие из них независимы, а какие нет: это могут быть все они или только некоторые из них.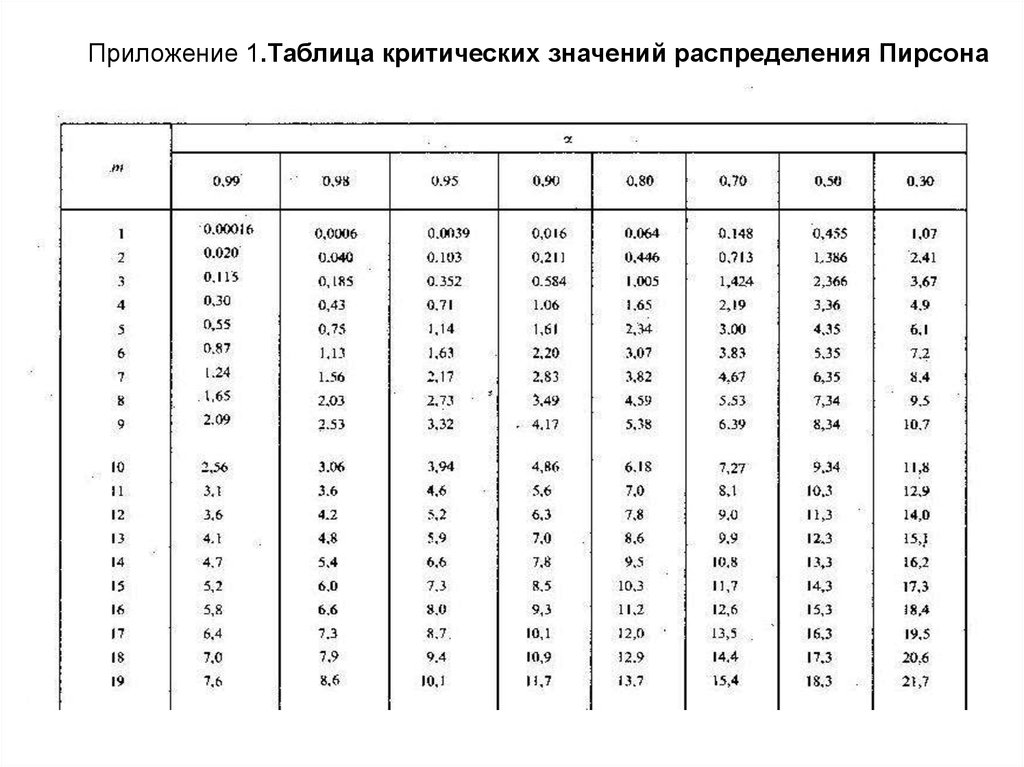
Тест однородности хи-квадрат
Этот тест относится к проверке того, имеют ли две или более переменные одно и то же распределение вероятностей , и также поддерживается этим онлайн-калькулятором хи-квадрат. Тест на однородность используется для определения того, различаются ли две или более 90 501 независимых выборок 90 502 в своих распределениях по одной интересующей переменной: сравнение двух или более групп по категориальному результату. Например, можно сравнить образовательные уровни групп людей из разных городов страны, чтобы определить, одинаковы ли пропорции между группами или есть статистически значимая разница. Нулевая гипотеза H 0 заключается в том, что пропорции между группами одинаковы, а альтернатива H 1 заключается в том, что они разные.
Обратите внимание, что при наблюдении низкого значения p можно только сказать, что по крайней мере одна пропорция отличается по крайней мере от одной другой пропорции, но мы не можем сказать, какая.
Необходимо использовать дополнительные процедуры, такие как Шеффе, Холм или Данн-Бонферрони, чтобы выбрать подходящее критическое значение для дальнейших тестов для выявления попарно значимых различий.
Когда это технически возможно, рандомизация часто используется для получения независимых выборок.
Критерий согласия хи-квадрат
Критерий согласия можно использовать для оценки того, насколько хорошо определенное частотное распределение соответствует ожидаемому (или известному) распределению . Нулевая гипотеза H 0 состоит в том, что данные следуют заданному распределению, в то время как альтернатива H 1 состоит в том, что они не следуют этому распределению. Отказ от нулевого значения означает, что выборка отличается от генеральной совокупности по интересующей нас переменной.
Например, если мы знаем, что игра в кости должна выдавать каждое число с частотой 1/6, то мы можем бросить кости 1000 раз, записать, сколько раз мы наблюдали данное число, а затем сравнить его с идеальным распределением костей.
чтобы убедиться, что это справедливо. Если мы получаем 168 единиц, 170 двоек, 160 троек, 163 четверки, 173 пятерки и 166 шестерок, есть ли у нас доказательства того, что кости подстроены? Загрузите пример данных в калькулятор, чтобы выполнить расчет.
Другим примером являются обследования населения, когда требуется репрезентативное обследование по определенному демографическому параметру или географическому региону. Зная возрастное распределение всего населения из недавней переписи или регистров рождений и смертей, вы можете сравнить частоты в своей выборке с частотами всего населения. При достаточно большой выборке тест будет достаточно чувствительным, чтобы выявить любое существенное несоответствие между вашей выборкой и совокупностью, которую вы пытаетесь представить.
Сравнение трех типов тестов хи-квадрат
Эта таблица дает краткий обзор различий между тремя основными вариантами использования теста Χ 2 и должна быть полезна всем, кто использует наш калькулятор X 2 для любых целей.
.
| Атрибут | Тест на независимость | Тест на однородность | Тест на соответствие |
|---|---|---|---|
| Тип выборки | Отдельный зависимый образец | 2 или более независимых образца | Выборка из популяции |
| Нулевая гипотеза | Переменные независимы | Пропорции между группами одинаковые | Распределение выборки совпадает с распределением генеральной совокупности |
| Нуль отклонен | Сделать вывод, что переменные зависимы | Сделать вывод, что пропорции другие | Сделайте вывод, что распределение выборки отличается от распределения населения |
Другие тесты
При определенных условиях тест X 2 можно использовать в качестве теста на различие дисперсий. Когда оба предельных распределения фиксированы, критерий хи-квадрат также можно использовать в качестве теста несвязанной классификации.