Пример расчета коэффициента корреляции Пирсона
Рассмотрим пример использования коэффициента корреляции Пирсона.
Например, нам необходимо определить взаимосвязь двух переменных агрессивности и IQ у школьников по полученным данным тестирования.
Данные сведем в одну таблицу:
| № | Данные по агрессивности () | Данные по IQ () |
| 1 | 24 | 100 |
| 2 | 27 | 115 |
| 3 | 26 | 117 |
| 4 | 21 | 119 |
| 5 | 20 | 134 |
| 6 | 31 | 94 |
| 7 | 26 | 105 |
| 8 | 22 | 103 |
| 9 | 20 | 111 |
| 10 | 18 | 124 |
| 11 | 30 | 122 |
| 12 | 29 | 109 |
| 13 | 24 | 110 |
| 14 | 26 | 86 |
1.
Вычисляем суму значений и
= 344
= 1549
2. Вычисляем среднее арифметическое для и
= 24,6
= 110,5
3. Вычисляем для каждого испытуемого отклонения от среднего арифметического для и
| № | ||
| 1 | 0,6 | 10,6 |
| 2 | -2,4 | -4,4 |
| 3 | -1,4 | -6,4 |
| 4 | 3,6 | -8,4 |
| 5 | 4,6 | -23,4 |
| 6 | -6,4 | 16,6 |
| 7 | -1,4 | 5,6 |
| 8 | 2,6 | 7,6 |
| 9 | 4,6 | -0,4 |
| 10 | 6,6 | -13,4 |
| 11 | -5,4 | -11,4 |
| 12 | -4,4 | 1,6 |
| 13 | 0,6 | 0,6 |
| 14 | -1,4 | 24,6 |
4.
Затем мы возводим в квадрат каждое отклонение:
| № | ||
| 1 | 0,36 | 112,36 |
| 2 | 5,76 | 19,36 |
| 3 | 1,96 | 40,96 |
| 4 | 12,96 | 70,56 |
| 5 | 21,16 | 547,56 |
| 6 | 40,96 | 275,56 |
| 7 | 1,96 | 31,36 |
| 8 | 6,76 | 57,79 |
| 9 | 21,16 | 0,16 |
| 10 | 43,56 | 179,56 |
| 11 | 29,16 | 129,96 |
| 12 | 19,36 | 2,56 |
| 13 | 0,36 | 0,36 |
| 14 | 1,96 | 605,16 |
5. Потом рассчитываем сумма квадратов отклонений: и
= 207,44
= 2073,24
6. Рассчитываем для каждого наблюдения произведение разности среднего арифметического и значения
| № | |
| 1 | 6,36 |
| 2 | 10,56 |
| 3 | 8,96 |
| 4 | -30,24 |
| 5 | -107,64 |
| 6 | -106,24 |
| 7 | -7,84 |
| 8 | 19,76 |
| 9 | -1,84 |
| 10 | -88,44 |
| 11 | 61,56 |
| 12 | -7,04 |
| 13 | 0,36 |
| 14 | -34,44 |
7.
Рассчитываем сумму
= -276,16
8. Подставляем полученные значения , , в формулу коэффициента корреляции Пирсона:
9. Вывод: В соответствии с таблицей значений величин коэффициента корреляции делаем вывод о том, что это слабая по силе отрицательная корреляция.
| Расчет коэффициента корреляции Пирсона | |
| Расчет коэффициента корреляции Пирсона в SPSS | Пример расчета коэффициента корреляции Пирсона в SPSS |
| Расчет коэффициента корреляции Пирсона в Excell | Пример расчета коэффициента корреляции Пирсона в Excell |
| Коэффициент корреляции Пирсона | |
Маркетинговые исследования с применением SPSS
Таблицы сопряженности служат для описания связи двух и более номинальных переменных.
С помощью анализа таблиц сопряженности можно найти ответы, например, на следующие вопросы:
- Как много женщин среди приверженцев данной марки товара?
- Связана ли интенсивность потребления данного товара с изменением климатических условий?
- Связана ли частота потребления товара с уровнем дохода потребителя?
Для установления степени связи между переменными используется критерий независимости χ2 (Хи—квадрат Пирсона). Чем больше значение χ2, тем больше зависимость между переменными. Значения χ2 близкие к 0 свидетельствуют о независимости переменных.
Вместе с χ2 вычисляется p—уровень значимости. При p>0,05 считается, что переменные независимы. При P
Для определения силы связи между переменными вычисляется коэффициент Крамера V.
Значения этого коэффициента всегда лежат между 0 и 1. Для более точной оценки силы связи между
переменными могут определяться коэффициенты “фи”, Лямбда и Тау Гудмена и Краскала.
Пример. В результате опроса 50 респондентов (1— мужчины, 2 — женщины) выявили их предпочтения в потреблении соков А и B (1 — А, 2 — В) (таблица 4.1). Выясните, есть ли зависимость между полом респондента и тем соком, который он предпочитает.
| № п/п | Пол | Сок | № п/п | Пол | Сок | № п/п | Пол | Сок | № п/п | Пол | Сок |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.0 | 1.0 | 14 | 1.0 | 2.0 | 27 | 1.0 | 1.0 | 40 | 1.0 | 2.0 |
| 2 | 1.0 | 2.0 | 15 | 2.0 | 1.0 | 28 | 2.0 | 1.0 | 41 | 1.0 | 1.0 |
| 3 | 2.0 | 2.0 | 16 | 2. 0 | 1.0 | 29 | 2.0 | 1.0 | 42 | 1.0 | 2.0 |
| 4 | 1.0 | 1.0 | 17 | 1.0 | 2.0 | 30 | 1.0 | 2.0 | 43 | 2.0 | 1.0 |
| 5 | 1.0 | 1.0 | 18 | 2.0 | 1.0 | 31 | 1.0 | 1.0 | 44 | 1.0 | 1.0 |
| 6 | 2.0 | 2.0 | 19 | 2.0 | 2.0 | 32 | 2.0 | 2.0 | 45 | 1.0 | 2.0 |
| 7 | 2.0 | 2.0 | 20 | 1.0 | 2.0 | 33 | 2.0 | 1.0 | 46 | 1.0 | 1.0 |
| 8 | 1.0 | 1.0 | 21 | 1.0 | 1.0 | 34 | 1.0 | 2.0 | 47 | 2.0 | 2.0 |
| 9 | 2.0 | 1.0 | 22 | 2.0 | 1.0 | 35 | 1.0 | 2. 0 | 48 | 2.0 | 1.0 |
| 10 | 1.0 | 1.0 | 23 | 1.0 | 1.0 | 36 | 1.0 | 2.0 | 49 | 2.0 | |
| 11 | 2.0 | 1.0 | 24 | 2.0 | 2.0 | 37 | 2.0 | 1.0 | 50 | 1.0 | |
| 12 | 1.0 | 2.0 | 25 | 1.0 | 2.0 | 38 | 2.0 | 1.0 | |||
| 13 | 1.0 | 1.0 | 26 | 1.0 | 2.0 | 39 | 2.0 | 1.0 |
Таблица 4.1 — Информация для анализа
Вверх
Пошаговая инструкция
Шаг 1. Анализ — Описательные статистики — таблицы сопряженности
Шаг 2. В строке — сок, в столбце — пол
Шаг 3. Установить флажок Вывести кластеризованные столбиковые диаграммы
Шаг 4.
Статистики — отметить ХИ—квадрат, Корреляции, Фи и Лямбда.
Шаг 5. Ячейки — отметить Частоты: наблюденные, ожидаемые; Остатки: нестандартизированные, стандартизированные, скорректированные; Проценты: по строке, по столбцу, по таблице.
Шаг 7. ОК.
Интерпретация результатов
| пол респондента | итого | ||||
|---|---|---|---|---|---|
| мужчины | женщины | ||||
| предпочитаемый сок | А | Частота | 13 | 14 | 27 |
| Ожидаемая частота | 15 | 11,9 | 27 | ||
| % по категории переменной предпочитаемый сок | 48,1% | 51,9% | 100,0% | ||
| % по категории переменной пол респондента | 46,4% | 63,6% | 54,0% | ||
| % по таблице (слою) | 26,0% | 28,0% | 54,0% | ||
| Остаток | -2,1 | -2,1 | |||
| B | Частота | 15 | 8 | 23 | |
| Ожидаемая частота | 12,9 | 10 | 23 | ||
| % по категории переменной предпочитаемый сок | 65,2% | 34,2% | 100,0% | ||
| % по категории переменной пол респондента | 53,6% | 36,4% | 46,0% | ||
| % по таблице (слою) | 30,0% | 16,0% | 46,0% | ||
| Остаток | -2,1 | -2,1 | |||
| Итого | Частота | 28 | 22 | 50 | |
| Ожидаемая частота | 28,0 | 22,0 | 50,0 | ||
| % по категории переменной предпочитаемый сок | 56,0% | 44,0% | 100,0% | ||
Таблица 4.
2 — Таблица сопряженности предпочитаемый сок * пол респондента
| Значение | ст.св. | Асимпт. значимость (2-стор.) | Точная значимость (2-стор.) | Точная значимость (1-стор.) | |
|---|---|---|---|---|---|
| Хи-квадрат Пирсона | 1,469a | 1 | ,226 | ||
| Поправка на непрерывностьb | ,858 | 1 | ,354 | ||
| Отношение правдоподобия | 1,480 | 1 | ,224 | ||
| Точный критерий Фишера | ,264 | ,177 | |||
| Линейно-линейная связь | 1,439 | 1 | ,230 | ||
| Кол-во валидных наблюденийb | 50 |
Таблица 4.3 — Критерии хи—квадрат
a. В 0 (,0%) ячейках ожидаемая частота меньше 5. Минимальная ожидаемая частота равна 10,12.
b. Вычисляется только для таблицы 2×2.
| Значение | Асимпт. стдандартная ошибкаa | Прибл. Tb | Прибл. значимость | |||
|---|---|---|---|---|---|---|
| Номинальная по номинальной | Лямбда | Симметричная | ,06 | ,19 | ,33 | ,73 |
| Зависимая предпочитаемый сок | ,087 | ,220 | ,379 | ,705 | ||
| Зависимая пол респондента | ,045 | ,231 | ,193 | 847 | ||
| Тау Гудмена и Краскала | Зависимая предпочитаемый сок | ,029 | ,048 | ,230c | ||
| Зависимая пол респондента | ,029 | ,048 | ,230c | |||
Таблица 4.4 — Направленные меры
a. Не подразумевая истинность нулевой гипотезы.
Для предварительного анализа влияния пола на потребление сока рассмотрим величины скорректированного остатка, в нашем случае он не выходит за границы стандартизированного остатка, следовательно гипотеза о наличии связи не подтверждается
- также показатель Хи—квадрат Пирсона (таблица 4.
4) имеет малое значение 1,469, а значимость существенно превышает 0,05 (0,226), что также подтверждает отсутствие связи между полом и
выбором сока. - коэффициенты Лямбда и Тау Гудмена и Краскала ( таблица 4.5) очень малы, что также говорит об отсутствии связи.
- величины коэффициентов Фи и V Крамера (таблица 4.3) также говорят о низкой связи между переменными, а значимость 0,226 также подтверждает гипотезу об отсутствии связи.
4) имеет малое значение 1,469, а значимость существенно превышает 0,05 (0,226), что также подтверждает отсутствие связи между полом и
выбором сока.| Значение | Значение Асимптотическая стдандартная ошибкаa | Прибл. Tb | Прибл. значимость | s||
|---|---|---|---|---|---|
| Номинальная по номинальной | Фи | -,17 | ,22 | ||
| V Крамера | ,17 | ,22 | |||
| Интервальная по интервальной | R Пирсона | -,17 | ,139 | -1,20 | ,23 |
| Порядковая по порядковой | Корреляция Спирмена | -,17 | ,139 | -1,20 | ,23 |
| Кол-во валидных наблюдений | 50 | ||||
Таблица 4.
5 — Симметричные меры
a. Не подразумевая истинность нулевой гипотезы.
Рисунок 4.1 — График предпочитаемых напитков
Таким образом, на основе проведенного анализа можно сделать вывод о том, что между полом респондента и соком, который он предпочитает нет зависимости.
lectur11
Лекция 11
Хи-квадрат
Хи-квадрат (или X 2 после
греческая буква c) является широко используемым статистическим тестом, который официально
известный как хи-квадрат Пирсона в честь его изобретателя Карла Пирсона.
Одна из причин, по которой он широко используется, заключается в том, что он может помочь ответить на ряд различных
типы аналитических вопросов. Дэниел обсуждает несколько из этих различных
использует. Несмотря на все эти потенциальные применения, вероятно, 90% всех применений
хи-квадрат включает анализ таблиц непредвиденных обстоятельств, описанных на стр. 59.5-598. А 2 х
2 таблица непредвиденных обстоятельств представляет собой таблицу, в которой представлено количество участников в каждом из
четыре ячейки.
Четыре ячейки образованы двумя дихотомическими переменными.
анализ таблицы непредвиденных обстоятельств — единственный критерий хи-квадрат, который мы вычислим
в этом классе, но вам важно понимать другие варианты использования
хи-квадрат. Итак, я посвящу эту лекцию анализу таблицы непредвиденных обстоятельств, а затем
упомянуть некоторые другие виды использования хи-квадрата.
Хи-квадрат можно представить в несколько путей. Первый способ, которым мы можем думать о тесте хи-квадрат, — это аналогия с t-тестом, в котором нас интересует сравнение двух групп. Только Вместо этого используется хи-квадрат, потому что зависимая переменная является дихотомической. Так, хи-квадрат 2 X 2 («два на два») используется, когда есть два уровня независимой переменной и два уровня зависимой переменной. Этот можно назвать тест на доморощенность потому что мы проверяем, являются ли два группы одинаковые. Homegenous означает «тот же тип».
Другой способ думать о том же
тест аналогичен тесту на соответствие .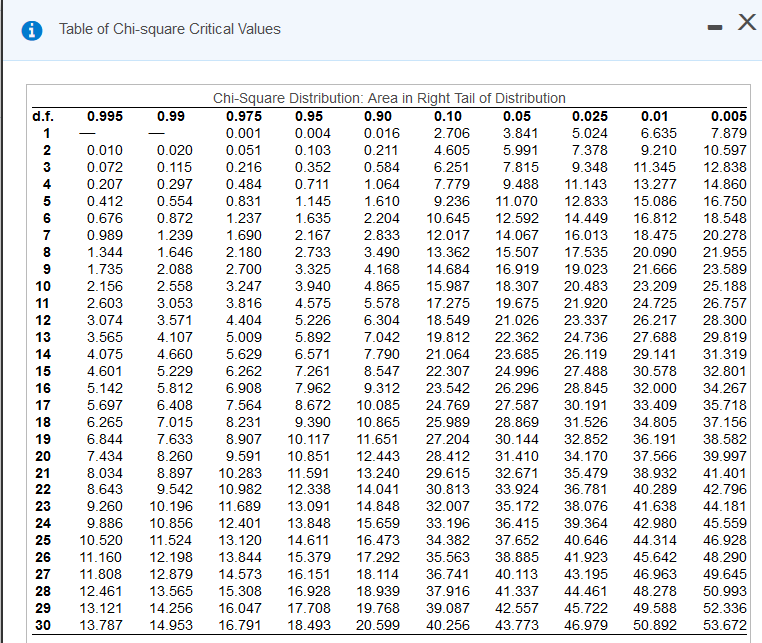
Тест на пригодность касается
частоты участников в выборке, и являются ли эти частоты
являются частотой, которую мы ожидаем из-за случайности. Например, частоты
может включать в себя, сколько участников сказали «нет» и «да» в
ответ на вопрос анкеты. Представьте вопрос опроса на английском языке, который был
для иммигрантов, которые плохо понимали английский язык. Если
респонденты опроса не поняли заданного вопроса, частота
Ответы «нет» и «да» могут быть случайными. Аналитика согласия
Затем вопрос касается того, ответили ли респонденты опроса да или нет
с частотой, которую мы ожидаем из-за случайности или нет. Если респонденты
не поняли вопроса, мы ожидаем, что около 50% ответят да и
50% ответить нет. Тогда качество соответствия касается того, действительно ли
частота ответов да/нет соответствует частоте, которую мы ожидаем из-за
шанс.
Теперь выясняется, что вопрос
однородности (групповых различий) и вопрос о согласии
тот же вопрос. Если мы спросим, являются ли две группы (скажем, мужчины и женщины)
одинаково склонны отвечать «да» на вопросы анкеты, мы также просим
является ли скорость, с которой каждая группа отвечает «да» и «нет», той скоростью, с которой мы хотели бы
ожидать от случая.
Таким образом, вычисление хи-квадрата касается совпадения
между ожидаемыми частотами, исходя из общего количества людей в каждом
группу и полученные частоты.
Хи-квадрат можно рассматривать как проверка того, являются ли две переменные независимыми или нет, и, таким образом, считается тестом на независимость . Вопрос о независимости может озабоченность тем, связан ли пол (мужской или женский) с ответами на вопрос да/нет. вопрос опроса. Если пол связан с утвердительным ответом на вопрос, две переменные не независимы друг от друга — они зависимы или связанные с.
Итак, исследователи используют хи-квадрат для ответить на вопросы об однородности, соответствии или независимости. если ты хорошенько подумайте над этими тремя вопросами, все они окажутся тот же вопрос! Тяжелый, да?!
Таблицы непредвиденных обстоятельств
(2 X 2)
Таблица непредвиденных обстоятельств — это просто сводная таблица данных. Давайте возьмем
пример типичного использования хи-квадрата, который сравнивает две группы на некоторых
дихотомическая мера.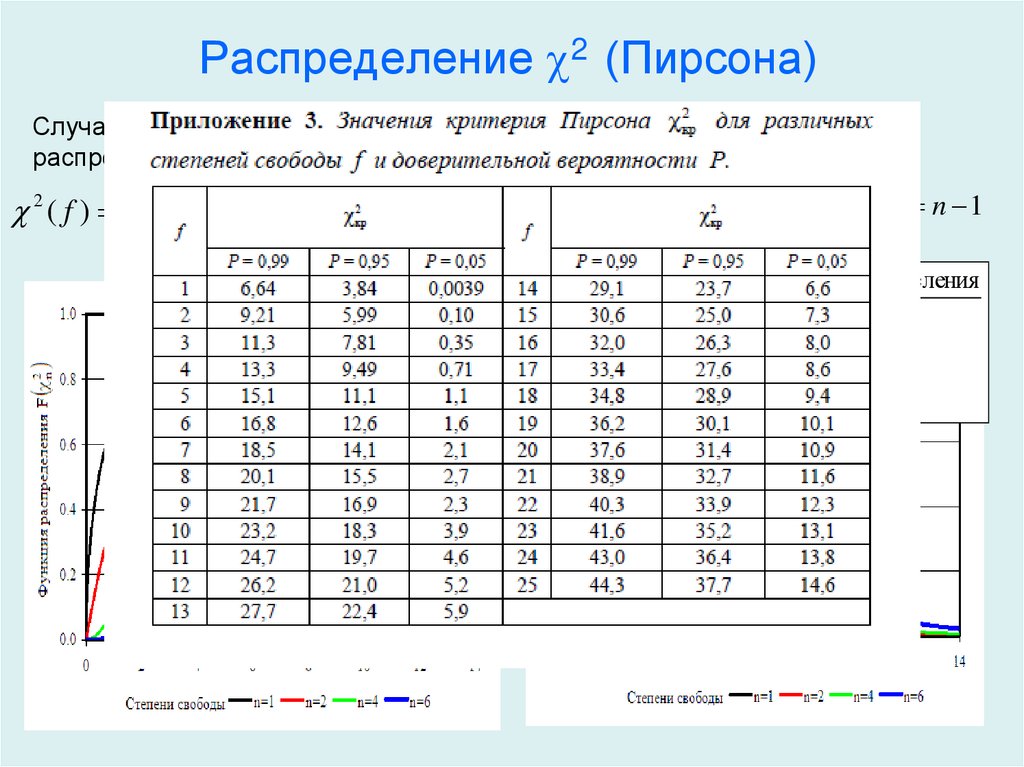
Допустим, мы получили доступ к некоторым локальным данным о регистрации избирателей.
чтобы увидеть, с одинаковой вероятностью мужчины и женщины будут республиканцами или демократами.
Мы получили список из 180 избирателей и внесли их политическую принадлежность в
база данных. Для этого нам просто нужны две переменные (кроме идентификатора
переменная) — пол и политическая принадлежность. Мы вводим эти данные в
обычным способом (используя коды 0 и 1 для обозначения мужчин и женщин и т. д.), но для
для удобства мы (или компьютер) свели бы эту информацию в таблицу
вот так:
| Самки | Кобели | Всего |
Демократы | 50 | 70 | 120 |
Республиканцы | 19 | 41 | 60 |
Всего | 69 | 111 | 180 |
Всего 180 ящиков, из них 120
демократы, 60 республиканцев, 69 женщин и 111 мужчин.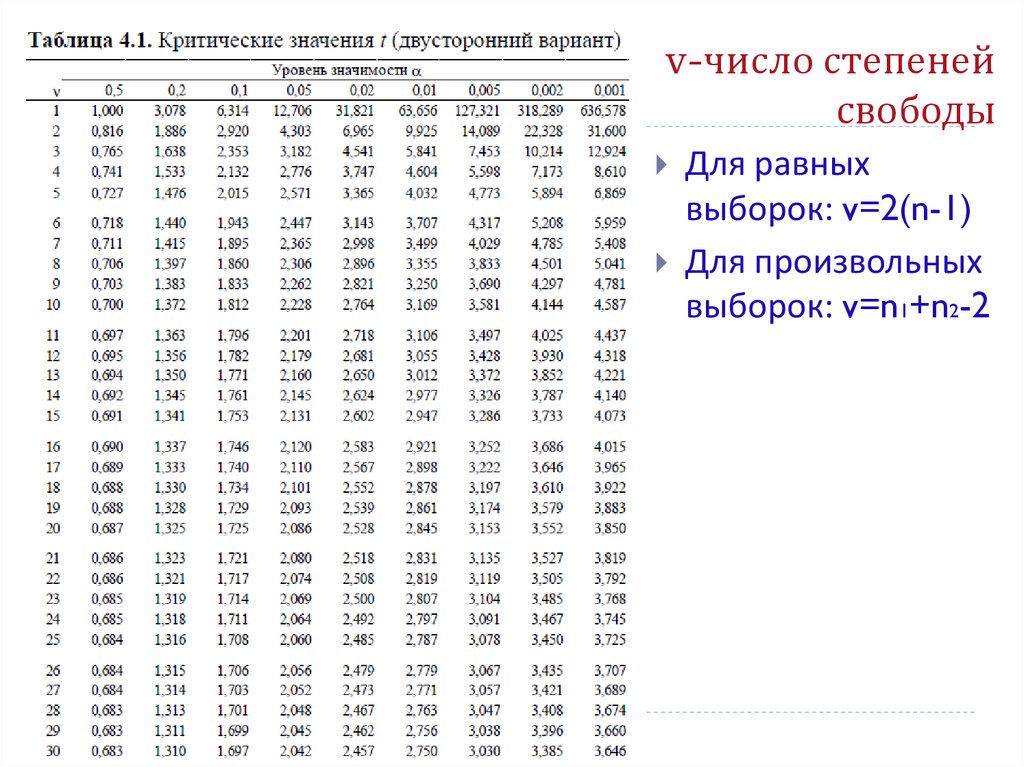
В целом их больше
мужчины, чем женщины, чтобы знать, мужчины или женщины чаще
Демократ или республиканец, нам нужно учитывать общее количество каждого.
Поскольку мужчин больше, мы ожидаем, что мужчин будет больше.
как в республиканской, так и в демократической группах. Итак, нам нужно взять эти базы
ставки во внимание, чтобы выяснить частоты, которые мы ожидаем из-за случайности.
Формула вычисления хи-квадрата заключается в измерении того, насколько близки наблюдаемые нами частоты в каждой ячейке таблицы соответствуют ожидаемым частотам.
В таблице О и стоит для наблюдаемой частоты в одной ячейке, а E i обозначает ожидаемая частота этой ячейки. Как видно из формулы, мы вычисляем хи-квадрат путем суммирования различий между наблюдаемым и ожидаемым частоты для каждой ячейки.
Когда у нас нет никакой информации
об ожидаемой частоте в каждой ячейке, мы можем вычислить ее на основе общего
количество мужчин и женщин или да и нет ответов.
Пока мы тестируем
понятие о том, что ячейки равны или не равны в их ожидаемой скорости, мы можем использовать
следующую удобную формулу вычисления вместо того, чтобы проходить через
включал процесс вычисления ожидаемых частот, вычисления
различия и их суммирование. Вот сокращенный метод:
Это намного проще, чем кажется, потому что a, b, c и d просто относятся к частоте в каждой из ячеек. н, как обычно — количество случаев в выборке. Формула не делает слишком много смысле, потому что это всего лишь кратчайший путь для вычисления хи-квадрата, когда у нас есть 2 X 2 таблица непредвиденных обстоятельств.
| Самки | Кобели |
Демократы | и | б |
Республиканцы | с | д |
Мы просто умножаем, складываем,
вычитание, возведение в квадрат и, вуаля, хи-квадрат.
Вот:
Чтобы увидеть, есть ли это несоответствие между наблюдается и ожидается, вероятно, из-за ошибки выборки, мы проверяем рассчитанный хи-квадрат для значимости. ф.р. равно (r — 1)(c — 1) = (2 — 1)(2 — 1) = 1, где r — количество строк, а c — количество столбцы. Мы смотрим в таблицу F в конце книги под .95 колонка (для альфа = 0,05). Критическое значение в таблице равно , и мы заключаем, что существуют нет существенных различий между мужчинами и женщинами в их политической принадлежности.
Более 2
категории
Хи-квадрат также можно использовать с более чем двумя категориями. Например, мы
может исследовать пол и политическую принадлежность с 3 категориями для политических
принадлежность (демократическая, республиканская и независимая) или 4 категории
(Демократическая, Республиканская, Независимая и Партия зеленых). В таком случае мы не можем
используйте нашу удобную формулу для столов 2 X 2, но мы можем использовать компьютер!
Поскольку хи-квадрат можно рассматривать как критерий согласия, он не
действительно имеет значение, думаем ли мы о гендере или политической принадлежности как
независимая переменная.
Тест будет одинаковым в любом случае. Хи-квадрат тогда
применяется к ситуациям, когда у нас есть столы 2 X 3, 3 X 4 или 5 X 6. Когда там
больше, чем таблица 2 X 2, у нас есть комплексный тест, потому что тест просто
указывает, есть ли какие-либо различия между ячейками. Для поиска конкретных
различий между ячейками исследователи обычно анализируют отдельные подтаблицы 2 X 2 или
другой метод, называемый логлинейным анализом (который мы не будем рассматривать в классе).
Прочие меры
подходят
Вы также увидите некоторые
альтернативы хи-квадрату Пирсона. Два, в частности, вероятность
критерий отношения (G 2 ) и взвешенный метод наименьших квадратов Неймана хи-квадрат
(В). Мы обсудим тест отношения правдоподобия позже, а тест Неймана
используется не очень часто. Все три очень похожи, особенно с большим
размер образца.
Исправление Йейта
и точный тест Фишера
. Вы часто будете видеть две другие статистики, распечатываемые статистическими пакетами.
Коррекция непрерывности Йейта — это коррекция хи-квадрата Пирсона, которая корректирует
хи-квадрат для меньших выборок.
Причина исправления заключается в том, что
выборка основана на дихотомических данных, а критические значения хи-квадрат основаны на
на непрерывном распределении. Между прочим, или , так что хи-квадрат является функцией нормального
распределения (помните конец лекции о биномиальном распределении?).
Поправка Йейтса обычно является консервативной оценкой хи-квадрата, потому что
значение хи-квадрат корректируется в сторону уменьшения. Есть значительные разногласия
о том, является ли поправка Йейта слишком консервативной или нет, и судить
из большинства текстов статистики, которые я видел, я думаю, что большинство статистиков предпочитают не использовать
Это.
Точный критерий Фишера используется, когда
в группах неравное количество, и точность теста
беспокойство, потому что в ячейках очень низкие ожидаемые частоты. Фишера
точный тест корректирует хи-квадрат для этой задачи. Обычно хи-квадрат Пирсона равен
хорошо, если ожидаемая частота 5 или более в 80% ячеек, и
ожидаемая частота 1 или более в оставшихся 20% клеток.
Компьютер
пакеты обычно выводят предупреждение, когда эти ожидаемые частоты низки. Когда
это предупреждение возникает, многие исследователи любят проверять точный критерий Фишера.
Непредвиденный случай
Анализ с Хи-квадрат
Выше я упомянул, что
вычисления хи-квадрата, которые я использовал, были основаны на предположении, что случайно мы
ожидать, что существует равная вероятность появления в каждой группе. За
Например, шанс ответить да или нет составляет 50% для каждого. Обычно ожидаемый
частота неизвестна и должна быть рассчитана на основе данных, а предположение
заключается в том, что будут равные пропорции (например, 50% для 2 групп, 33% для трех
группы и так далее). Однако иногда пропорция, ожидаемая от случайности,
известен исследователю или есть основания ожидать, что распределение
будет как. В этом случае распределение Пуассона или другое распределение
можно использовать для вычисления ожидаемых частот. Эти другие ситуации
более подробно обсуждался Даниэлем. Я думаю, вы должны просмотреть их и
понять, когда они используются, но, поскольку они воспринимаются относительно
нечасто, я не хочу, чтобы вы тратили на них много времени.
Когда вы бежите
в таких ситуациях текст Даниила станет хорошим справочником, если
вам нужно выяснить, как рассчитать их или ваша ситуация
Соответствующий.
Нажмите здесь, чтобы просмотреть пример вывода SPSS.
Пример теста хи-квадрат для ассоциации
Ежедневный отчет показывает, сколько отбракованных ручек было произведено каждым из трех прессов на объекте в течение каждой из трех смен. Инженер по качеству хочет определить, связаны ли между собой пресс и сдвиг.
Инженер выполняет тест хи-квадрат на взаимосвязь, чтобы определить, связаны ли между собой пресс и смена, которая произвела бракованные ручки.
- Откройте образец данных UmbrellaHandles.MTW.
- Выберите Stat > Tables > Chi-square Test for Association.
- В раскрывающемся списке данных выберите Сводные данные в двусторонней таблице.
- В столбцах, содержащих таблицу, введите «1-я смена», «2-я смена», «3-я смена».
- под этикетками для таблицы (необязательно), в ряды, введите идентификатор машины.
- Нажмите Статистику.
- Выберите вклад каждой ячейки в хи-квадрат. Оставьте выборы по умолчанию теста хи-квадрат, подсчет отображения в каждой ячейке, отображение предельного количества и выбранного ожидаемого количества ячеек.
- Нажмите OK в каждом диалоговом окне.
Для этих данных статистика хи-квадрат Пирсона составляет 11,788 (p-значение = 0,019), а коэффициент вероятности числа хи-квадрат составляет 11,816 (p-значение = 0,019). Оба p-значения меньше уровня значимости 0,05. Таким образом, инженер делает вывод, что переменные взаимосвязаны и производительность прессов меняется в зависимости от смены.
Первая смена выпускает больше всего бракованных ручек (160), и большая часть бракованных ручек приходится на пресс 2 (76). Количество плохих ручек, произведенных на прессе 2 во время смены 1, намного больше, чем можно было бы ожидать, если бы переменные были независимыми.