Gwtm вейвлет поиск пиков в спектре – поиск пиков на спектре гамма изл. (вейвлет преобразование) : Чулан (М)

ОСОБЕННОСТИ ФУРЬЕ – И ВЕЙВЛЕТ-СПЕКТРОВ ПРИ НЕСТАЦИОНАРНОМ РЕЖИМЕ РАБОТЫ

 

ОСОБЕННОСТИ ФУРЬЕ – И ВЕЙВЛЕТ-СПЕКТРОВ

ПРИ НЕСТАЦИОНАРНОМ РЕЖИМЕ РАБОТЫ

Коваленко Дмитрий Валерьевич

аспирант,

Омский государственный технический университет,

РФ, г. Омск

E—mail: Dmitrii_Kovalenko92@mail.ru

 

PARTICULARLY THE FOURIER AND WAVELET SPECTRUM

FOR NON-STATIONARY OPERATING MODE

Dmitriy Kovalenko

graduate, Omsk State Technical University,

Russia, Omsk

 

АННОТАЦИЯ

В статье рассмотрены графики тока, напряжения и спектра Фурье при различных режимах работы простейшей электрической системы, а также показан эффект «растекания спектра», который появляется при построении спектра Фурье для нестационарных сигналов. Рассмотрены пространственные вейвлет-спектры нестационарного режима при различных значениях масштаба.

ABSTRACT

The article describes the graphs of current, voltage and Fourier spectrum for different modes of operation of the simplest electrical system, and shows the effect of «spectrum leakage» that appears when you build a Fourier spectrum for non-stationary signals. Considered, the spatial wavelet spectra of non-stationary modes for different values of the scale.

 

Ключевые слова: вейвлет-преобразование; преобразование Фурье; стационарный режим; нестационарный режим; Фурье-спектр; вейвлет-спектр.

Keywords: wavelet transform; Fourier transform; stationary regime; non-stationary regime; Fourier spectrum; wavelet spectrum.

Существует два основных метода, позволяющих проводить спектральный анализ сигналов: преобразование Фурье и метод вейвлет-преобразования. Описанию этих методов посвящено достаточно большое количество работ [1–9]. В работах [2; 7] достаточно подробно рассматривается теория дискретного и непрерывного вейвлет-преобразования. Также, в этих работах выполнен краткий обзор практического применения этих методов. В настоящей статье внимание читателя обращено на Фурье-спектры гармоник простейшей электрической системы при различных режимах работы (стационарном и нестационарном) и на трехмерные вейвлет-спектры при различных значениях параметра масштаба.

На рисунке 1 приведена схема замещения простейшей электрической системы. Параметры элементов: R=22,5 Ом, L=38,2 мГн.

 

Рисунок 1. Схема замещения простейшей электрической системы

 

Вначале смоделируем стационарный режим работы. Это такой режим работы, при котором не происходит внезапных изменений («скачков») сигнала за рассматриваемый промежуток времени.

Зададим источник ЭДС периодическим несинусоидальным сигналом, имеющим постоянную составляющую, основную (первую), третью, пятую, седьмую и девятую гармоники (начальную фазу для упрощения расчета примем равной нулю).

,

где:  f – частота сети (50 Гц).

Индуктивные и полные сопротивления отдельных гармоник определяются по следующим формулам (Ом)[1]:

, .

Фазы токов отдельных гармоник (градус):

.

Амплитудные значения токов отдельных гармоник определяются как (А):

.

Отсюда уравнение сигнала тока будет иметь следующий вид:

Результаты расчетов приведены в таблице 1.

Таблица 1.

Результаты расчетов

№	Амплитудное значение напряжения	Индуктив-ное сопротивле-ние	Полное сопротивление	Амплитудное значение тока	Фаза тока
0		0	22,5	18,86	0
1		12,00	25,50	14,97	28,07
3		36,00	42,46	6,00	58,00
5		60,00	64,08	2,43	69,45
7		84,01	86,97	1,46	75,01
9		108,01	110,33	0,90	78,23

Примечание к таблице: индуктивное сопротивление постоянной составляющей рассчитывается как индуктивное сопротивление постоянному току, т. е. при  и полное сопротивление равно активному

 

Графики напряжения, тока и Фурье-спектр приведены на рисунке 2.

 

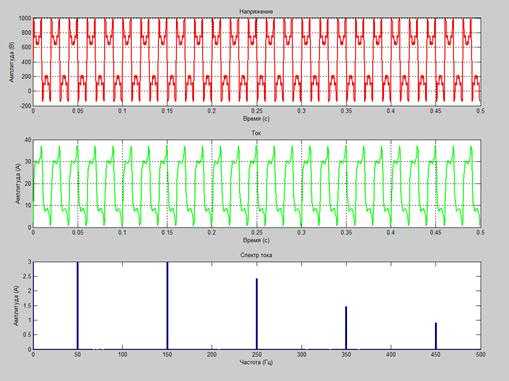
Рисунок 2. Графики напряжения, тока и Фурье-спектра при стационарном режиме работы

 

Далее смоделируем нестационарный режим работы. Нестационарный режим – это такой режим, при котором происходит внезапное изменение («скачок») сигнала за рассматриваемый промежуток времени.

Параметры системы рассчитываются по аналогии со стационарным режимом (поэтому и результаты вычислений будут подобными), однако графики режима будут несколько иные (рисунок 3).

Также на рисунках 4–6 показаны трехмерные графики вейвлет-спектров (графики вейвлет-спектров приведены для нестационарного режима за исключением вейвлет-спектра, приведенного на рисунок 7. – Это стационарный режим).

В работе [2] автор дает следующее определение вейвлет-спектра: «Вейвлет-спектр представляет собой поверхность в трехмерном пространстве. Вид поверхности определяет изменения во времени спектральных компонентов различного масштаба и называется частотно-временным спектром».

При построении трехмерных графиков вейвлет-спектров использовались: вейвлет Морле, непрерывное вейвлет-преобразование (CWT). Значения масштабирующего параметра в различных диапазонах: а=(1; 35) для спектра, изображенного на рисунке 4, а=(1; 25) для рисунка 5, а=(1; 5) для рисунка 6). При внимательном рассмотрении рисунка 6 нетрудно убедиться, что левая и правая части спектра (по оси времени) различны: в правой части заметны «штрихи», которые сообщают нам, что мы имеем дело с нестационарным режимом. Если бы мы строили вейвлет-спектр для стационарного режима, то он был бы ровным и не имел бы никаких «штрихов». Это хорошо иллюстрируется графиком вейвлет-спектра, приведенного на рисунке 7.

 

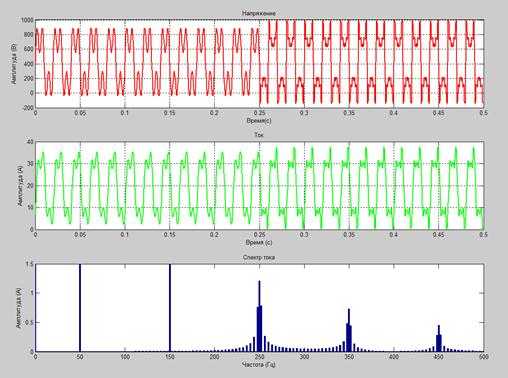
Рисунок 3. Графики напряжения, тока и Фурье-спектра при нестационарном режиме работы

 

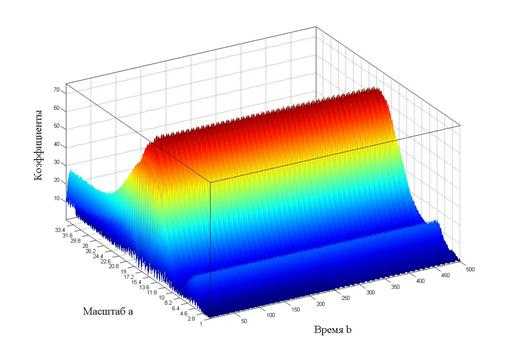
Рисунок 4. Вейвлет-спектр при коэффициенте масштаба а=35 (нестационарный режим)

 

Рисунок 5. Вейвлет-спектр при коэффициенте масштаба а=25 (нестационарный режим)

 

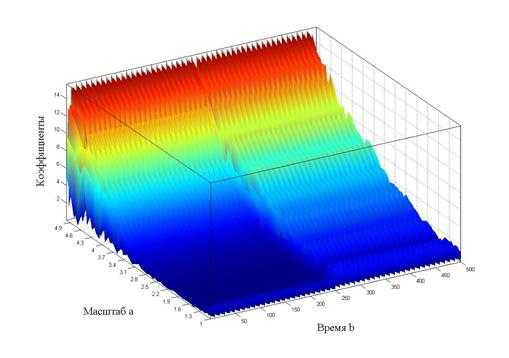
Рисунок 6. Вейвлет-спектр при коэффициенте масштаба а=5 (нестационарный режим)

 

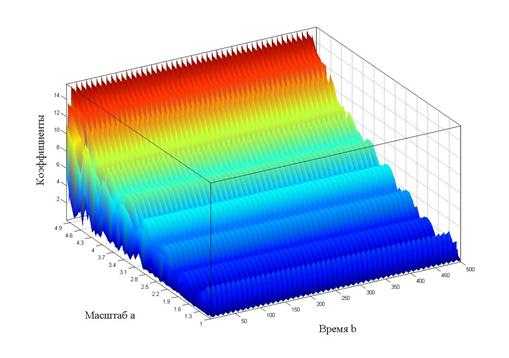
Рисунок 7. Вейвлет-спектр при коэффициенте масштаба а=5 (стационарный режим)

 

Рассматривая графики стационарного и нестационарного режимов (рисунки 2, 3), можно сделать следующие выводы:

1. Графики напряжения и тока в первом случае (рисунок 2) одинаковые на всем рассматриваемом промежутке времени (стационарный режим работы). Во втором случае (рисунок 3) форма графиков напряжения и тока резко изменяется (в момент t=0,25 с). Это связано с тем, что в этот момент времени в системе происходят резкие и серьезные изменения, что нашло отражение в графиках напряжения и тока (нестационарный режим работы).
2. Из графика Фурье-спектра видно, что в стационарном режиме Фурье-спектр четкий (видны только вертикальные линии – постоянная составляющая и гармоники – 50 (основная), 150 (третья), 250 (пятая), 350 (седьмая) и 450 (девятая), Гц – четные гармоники отсутствуют, так как рассматриваемая нами система не имеет выпрямителей или частотных преобразователей). В нестационарном режиме наблюдается эффект «растекания спектра» с появлением огромного количества ложных частот, которых не существует в реальности – появляется множество «штрихов» на графике (особенно сильно это проявляется в спектре пятой, седьмой и девятой гармониках, имеющих частоты 250, 350 и 450 Гц).

Анализируя графики вейвлет-спектров (рисунки 4–7), можно сделать следующие выводы.

1. Трехмерный вейвлет-спектр – это представление сигнала в трехмерном пространстве (именно поэтому он является поверхностью).
2. Изменение параметра масштаба позволяет рассмотреть, как общую картину спектра (при большом диапазоне изменения параметра а), так и локальные области спектра (при малом диапазоне изменения параметра а). Таким образом, мы получаем своеобразный «микроскоп», который позволяет «просматривать» как весь спектр, так и его отдельные области.
3. Вейвлет-спектр (при правильно выбранном масштабе) позволяет нам судить о характере режима (стационарный или нестационарный).

Заключение.

Преобразование Фурье основано на представлении сигнала в базисе функций синусов и косинусов, бесконечно повторяющихся (периодичных) во времени. Фурье-спектр при нестационарном режиме работы имеет множество ложных частот (проявляется эффект «растекания спектра»).

Вейвлет-преобразование основано на разложении сигнала базисными функциями, которые имеют временное ограничение. Поэтому при анализе нестационарных режимов оно имеет преимущество перед преобразованием Фурье.

 

Список литературы:

1.    Бессонов Л.А. Теоретические основы электротехники. Электрические цепи / Л.А. Бессонов. – Москва: «Высшая школа». – 1996. – 638 с.

2.    Вейвлет-анализ в примерах: учебное пособие / О.В. Нагорнов, В.Г. Никитаев, В.М. Простокишин и др. – Москва: НИЯУ МИФИ, 2010. – 120 с.

3.    Воробьев В.П. Теория и практика вейвлет-преобразования / В.П. Воробьев, В.Г. Грибунин. – Санкт-Петербург. – 1999. – 203 с.

4.    Давыдов А.В. Цифровая обработка сигналов: Тематические лекции / Екатеринбург: УГГУ, ИГиГ, кафедра геоинформатики. – 2007 – 2010.

5.    Осипов Д.С. Применение вейвлет-преобразования для расчета мощности в системах электроснабжения при нестационарных режимах работы / Д.С. Осипов, Д.В. Коваленко, Л.А. Файфер // Инновации в науке: Сборник статей по материалам LI Международной научно-практической конференции. – Новосибирск: изд. СибАК. – 2015. – № 11 (48).

6.    Осипов Ю.М. Частотный и временной анализ стационарных и переходных характеристик линейных электрических цепей: учебное пособие по курсам электротехники и ТОЭ, в 2-х ч. / Ю.М. Осипов; Санкт-Петербургский государственный институт точной механики и оптики (Технический университет). – Санкт-Петербург. – 2002. – 129 с. – 2 ч.

7.    Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в MATLAB / Н.К. Смоленцев. – Москва: ДМК Пресс. – 2005. – 304 с.

8.    Яковлев А.Н. Введение в вейвлет-преобразования: учебное пособие / А.Н. Яковлев. – Новосибирск: Изд-во НГТУ, 2003. – 104 с.

9.    Paul S. Addison. The Illustrated Wavelet Transform Handbook: Introductory Theory and Application in Science, Engineering, Medicine and Finance / Paul S. Addison. – Institute of Physics Publishing Bristol and Philadelphia. – 2002. – 362 p.

 

[1] Здесь и далее в скобках приводятся единицы измерения величин

sibac.info

Вейвлет-преобразование (Спектральный метод) — Национальная библиотека им. Н. Э. Баумана

Материал из Национальной библиотеки им. Н. Э. Баумана
Последнее изменение этой страницы: 16:19, 2 июня 2016.

Статья по учебной дисциплине
Название дисциплины:	Обнаружение и распознавание сигналов
Раздел:	8. Распознавание и идентификация сигналов на физическом уровне
Глава:	8.2 Обнаружение и распознавание объектов изображений
Преподаватель:	Чичварин Н. В.

Вейвлет-преобразование — интегральное преобразование, которое представляет собой свертку вейвлет-функции с сигналом. Вейвлет-преобразование переводит сигнал из временного представления в частотно-временное.

Принцип вейвлет-преобразования

Гармонические базисные функции преобразования Фурье предельно локализованы в частотной области и не локализованы во временной (определены во всем временном интервале от −∞{\displaystyle -\infty } до ∞{\displaystyle \infty }). Вейвлеты должны быть локализованными как во временной, так и в частотной области представления. Однако при проектировании таких функций неминуемо сталкиваются с принципом неопределенности, связывающим эффективные значения длительности функций и ширины их спектра. Чем точнее осуществляется локализация временного положения функции, тем шире становится ее спектр, и наоборот, что наглядно видно на рис. 1.

Рис. 1. Функции вейвлетов и спектр.

Отличительной особенностью вейвлет-анализа является то, что в нем можно использовать семейства функций, реализующих различные варианты соотношения неопределенности. Вейвлетный базис пространства L2(R), R(−∞,∞){\displaystyle L_{2}(R),\ R(-\infty ,\infty )}, целесообразно конструировать из финитных функций, принадлежащих этому же пространству, которые должны стремиться к нулю на бесконечности. Чем быстрее эти функции стремятся к нулю, тем удобнее использовать их в качестве базиса преобразования при анализе реальных сигналов. Допустим, что такой функцией является psi-функция ψ(t){\displaystyle \psi (t)}, равная нулю за пределами некоторого конечного интервала и нулевое среднее значение по интервалу задания. Последнее необходимо для задания определенной локализации спектра вейвлета в частотной области.

Функция изменения частотной независимой переменной в спектральном представлении сигналов отображается во временном представлении растяжением/сжатием сигнала. Для вейвлетного базиса это можно выполнить функцией типа ψ(t)⇒ψ(amt), a=const, m=0,1,…,M{\displaystyle \psi (t)\Rightarrow \psi (a_{m}t),\ a=const,\ m=0,1,\dots ,M}, т.е. путем линейной операции растяжения/сжатия, обеспечивающей самоподобие функции на разных масштабах представления. Однако конечность (локальность) функции ψ(t){\displaystyle \psi (t)} на временной оси требует дополнительной независимой переменной последовательных переносов (сдвигов) функции ψ(t){\displaystyle \psi (t)} вдоль оси (параметра локализации), типа ψ(t)⇒ψ(t+k){\displaystyle \psi (t)\Rightarrow \psi (t+k)}, для перекрытия всей числовой оси пространства R(−∞,∞){\displaystyle R(-\infty ,\infty )}. C учетом обоих условий одновременно структура базисной функции может быть принята следующей:

ψ(t)⇒ψ(amt+k)(1){\displaystyle \psi (t) \Rightarrow \psi(a^m t+k)\quad \quad {\color{Maroon}(1)}}

Для упрощения дальнейших выкладок значения переменных m{\displaystyle m} и k{\displaystyle k} примем целочисленными. При приведении функции к единичной норме, получаем:

ψmk(t)=am/2ψ(amt+k)(2){\displaystyle \psi_mk(t)=a^{m/2}\psi(a^m t+k)\!\quad \quad {\color{Maroon}(2)}}

Если для семейства функций ψmk(t){\displaystyle \psi _{m}k(t)} выполняется условие ортогональности:

⟨ψnk(t),ψlm(t)⟩=∫−∞∞ψnk(t)ψlm(t)dt=δnl⋅δkm(3){\displaystyle \left\langle\psi_{nk}(t),\psi_{lm}(t) \right \rangle = \int\limits_{-\infty}^{\infty}\psi_{nk}(t)\psi_{lm} (t) dt=\delta_{nl}\cdot\delta{km}\quad \quad {\color{Maroon}(3)}}

то семейство ψmk(t){\displaystyle \psi _{mk}(t)} может использоваться в качестве ортонормированного базиса пространства L2(R){\displaystyle L_{2}(R)}. Отсюда следует, что произвольная функция этого пространства может быть представлена в виде ряда (разложения по базису ψmk(t){\displaystyle \psi _{mk}(t)\!}):

s(t)=∑m,k=−∞∞Smkψmk(t)dt(4){\displaystyle s(t)=\sum_{m,k=-\infty}^\infty S_{mk}\psi_{mk}(t)\,dt\quad \quad {\color{Maroon}(4)}}

где коэффициенты представления сигнала – проекции сигнала на новый ортогональный базис функций, как и в преобразовании Фурье, определяются скалярным произведением

Smk=⟨s(t),ψmk(t)⟩=∫−∞∞s(t)ψmk(t)dt{\displaystyle S_{mk}=\left\langle s(t),\psi _{mk}(t)\right\rangle =\int \limits _{-\infty }^{\infty }s(t)\psi _{mk}(t)dt} при этом ряд равномерно сходится, то есть

limM,K⇒∞∥s(t)∑m=−MM∑k=−KKSmkψmk(t)∥=0{\displaystyle \lim _{M,K\Rightarrow \infty }\lVert s(t)\sum _{m=-M}^{M}\sum _{k=-K}^{K}S_{mk}\psi _{mk}(t)\rVert =0}

При выполнении этих условий базисная функция преобразования ψ(t){\displaystyle \psi (t)} называется ортогональным вейвлетом. Простейшим примером ортогональной системы функций такого типа являются функции Хаара. Базисная функция Хаара определяется соотношением

h(t)={1,0<t<1/2−1,1/2<t<10,t<0,t>1(5){\displaystyle h(t) = \begin{cases} 1, &\qquad 0<t<1/2 \\ -1, &\qquad 1/2<t<1 \\ 0, &\qquad t<0,t>1 \end{cases}\quad \quad {\color{Maroon}(5)}}

Легко проверить, что при a=2, m=0,1,2,…, k=0,1,2,…{\displaystyle a=2,\ m=0,1,2,\dots ,\ k=0,1,2,\dots } две любые функции, полученные с помощью этого базисного вейвлета путем масштабных преобразований и переносов, имеют единичную норму и ортогональны. На рис. 2 приведены примеры функций для первых трех значений m{\displaystyle m} и b{\displaystyle b} при различных их комбинациях, где ортогональность функций видна наглядно.

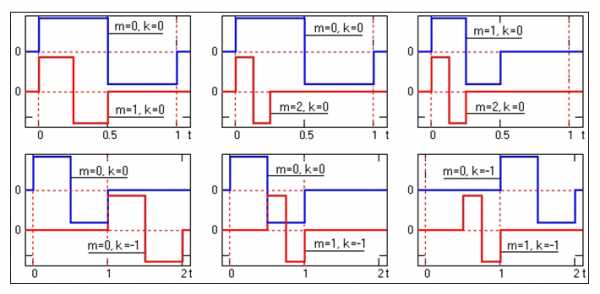Рис. 2. Функции Хаара.

Определение вейвлета

В общем случае к вейвлетам относятся локализованные функции, которые конструируются из одного материнского вейвлета ψ(t){\displaystyle \psi (t)} (или по любой другой независимой переменной) путем операций сдвига по времени b{\displaystyle b} и изменения временного масштаба a{\displaystyle a}:

ψab(t)=(1/|a|)ψt−ba,(a,b)∈R,ψ(t)∈L2(R)(6){\displaystyle \psi_{ab}(t)= (1/\sqrt{|a|})\psi\tfrac{t-b}{a},\quad (a,b)\in R,\quad \psi (t)\in L^2(R)\quad \quad {\color{Maroon}(6)}}

где множитель (1/|a|{\displaystyle 1/{\sqrt {|a|}}}) обеспечивает независимость нормы функций от масштабирующего числа a{\displaystyle a}.

Непрерывное (интегральное) вейвлет-преобразование сигнала s(t)∈L2(R){\displaystyle s(t)\in L^{2}(R)}, которое применяется для качественного частотно-временного анализа, по смыслу соответствует преобразованию Фурье с заменой гармонического базиса exp(−jωt){\displaystyle exp(-j\omega t)} на вейвлетный ψ(t−ba){\displaystyle \psi \left ( \tfrac{t-b}{a} \right )}:

ψab(t)=⟨s(t),ψab(t)⟩=(1/|a|)∫−∞∞s(t)ψ((t−b)/a)dta,b∈R,a≠0(7){\displaystyle \psi_{ab}(t)= \left\langle s(t),\psi_{ab}(t)\right\rangle =(1/\sqrt{|a|})\int\limits_{-\infty}^{\infty} s(t) \psi((t-b)/a)\,dt \qquad\qquad a,b\in R, a\ne 0\quad \quad {\color{Maroon}(7)}}

Вейвлетный масштабно-временной спектр W(a,b){\displaystyle W(a,b)} в отличие от Фурье-спектра является функцией двух аргументов: временного масштаба вейвлета a{\displaystyle a} (в единицах, обратных частоте), и временному смещению вейвлета по сигналу b{\displaystyle b} (в единицах времени), при этом параметры a{\displaystyle a} и b{\displaystyle b} могут принимать любые значения в пределах областей их определения. На рис. 3 приведены примеры простейших неортогональных вейвлетов четного (Mhat) и нечетного (Wave) типов.

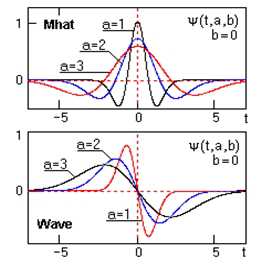Рис. 3. Вейвлеты Mhat и Wave.

Для количественных методов анализа (декомпозиция сигналов с возможностью последующей линейной реконструкции сигналов из обработанных вейвлет-спекторов) строго с математических позиций в качестве вейвлетных базисов можно использовать любые локализованные функции ψ(t)∈L2(R){\displaystyle \psi (t)\in L^{2}(R)}, если для них существуют функции-двойники (парные функции) ψ#(t){\displaystyle \psi ^{\#}(t)}, такие, что семейства ψab(t){\displaystyle \psi ^{ab}(t)} и ψab#(t){\displaystyle \psi _{ab}^{\#}(t)} могут образовывать парные базисы функционального пространства L2(R){\displaystyle L_{2}(R)}. Вейвлеты, определенные таким образом, позволяют представить любую произвольную функцию в пространстве L2(R){\displaystyle L_{2}(R)} в виде ряда:

s(t)=∑a,bC(a,b)ψab#(t),(a,b)∈I(8){\displaystyle s(t)=\sum_{a,b} C(a,b)\psi^{\#}_{ab} (t), (a,b)\in I\quad \quad {\color{Maroon}(8)}}

где коэффициенты C(a,b){\displaystyle C(a,b)} – проекции сигнала на вейвлетный базис пространства, которые определяются скалярным произведением

C(a,b)=⟨s(t),ψab(t)⟩=∫−∞∞s(t)ψab(t)dt{\displaystyle C(a,b)=\left\langle s(t),\psi _{ab}(t)\right\rangle =\int \limits _{-\infty }^{\infty }s(t)\psi _{ab}(t)\,dt}

Если вейвлет ψ(t){\displaystyle \psi (t)} обладает свойством ортогональности, то ψ#(t)≡ψ(t){\displaystyle \psi ^{\#}(t)\equiv \psi (t)} и вейвлетный базис ортогонален. Вейвлет может быть неортогональным, однако если он имеет двойника, и пара (ψ(t),ψ#(t)){\displaystyle (\psi (t),\psi ^{\#}(t))} дает возможность сформировать семейства {ψmk(t)}{\displaystyle \{\psi _{mk}(t)\}} и {ψ#}zp(t)}{\displaystyle \{\psi ^{\#}\}_{zp}(t)\}}, удовлетворяющие условию биортогональности на целых числах I:

⟨ψmk(t),ψzp#(t)⟩=δmz⋅δkp;(9){\displaystyle \left\langle \psi_{mk}(t),\psi_{zp}^{\#} (t) \right \rangle = \delta_{mz}\cdot\delta_{kp};\quad \quad {\color{Maroon}(9)}}

m,k,z,p∈I{\displaystyle m,k,z,p\in I}

то возможно разложение сигналов на вейвлетные ряды с построением обратной формулы реконструкции. С точностью обратного вейвлет-преобразования связано большинство ограничений, накладываемых на вейвлеты.

Свойства вейвлета

• Локализация. Вейвлет должен быть непрерывным, интегрируемым, иметь компактный носитель и быть локализованным как во времени (в пространстве), так и по частоте. Если вейвлет в пространстве сужается, то его «средняя» (доминирующая) частота повышается, спектр вейвлета перемещается в область более высоких частот и расширяется. Этот процесс должен быть линейным – сужение вейвлета вдвое должно повышать его доминирующую частоту и ширину спектра также вдвое.

Вейвлетную функцию можно считать достаточно хорошо локализованной при выполнении условий:

ψ(t)≤C/(1+|t|)1+ϵ{\displaystyle \psi (t)\leq C/(1+|t|)^{1+\epsilon }}

Ψ(f)≤C/(1+|f|)1+ϵ{\displaystyle \Psi (f)\leq C/(1+|f|)^{1+\epsilon }}, при ϵ<0(10){\displaystyle \epsilon < 0\!\quad \quad {\color{Maroon}(10)}}

• Нулевое среднее значение, т.е. выполнение условия для нулевого момента:

∫−∞∞ψ(t)dt=0(11){\displaystyle \int\limits_{-\infty}^{\infty}\psi(t)\,dt=0\quad \quad {\color{Maroon}(11)}},

что обеспечивает выделение локальных особенностей сигналов в пределах вейвлетного носителя на уровне региональных изменений и тренда, нулевое усиление постоянной составляющей сигналов с нулевым значением частотного спектра вейвлета при ω=0{\displaystyle \omega =0}, и локализацию спектра вейвлета в виде полосового фильтра с центром на определенной (доминирующей) частоте ω0{\displaystyle \omega _{0}} вейвлетной функции. Для игнорирования регулярных полиномиальных составляющих сигнала и анализа мелкомасштабных флюктуаций и особенностей высокого порядка, как правило, требуются и нулевые значения определенного количества последующих моментов:

∫−∞∞tmψ(t)dt=0(12){\displaystyle \int\limits_{-\infty}^{\infty} t_m\psi(t)\,dt=0\quad \quad {\color{Maroon}(12)}}

Такие вейвлеты называются вейвлетами m{\displaystyle m}-го порядка.

• Ограниченность. Необходимое и достаточное условие:

∥ψ(t)∥2=∫−∞∞|ψ(t)|2dt<∞(13){\displaystyle \lVert\psi (t)\rVert^2=\int\limits_{-\infty}^{\infty} |\psi(t)|^2\,dt < \infty\quad \quad {\color{Maroon}(13)}}

Оценка хорошей ограниченности и локализации может выполняться с использованием выражений:

|ψ(t)|<1/(1+|t|n){\displaystyle |\psi (t)|<1/(1+|t|^{n})\!}, или |Ψ(ω)|<1/(1+|ωo|n)(14){\displaystyle |\Psi(\omega)|<1/(1+|\omega_o|^n) \!\quad \quad {\color{Maroon}(14)}}

где ωo{\displaystyle \omega _{o}} – средняя частота вейвлета.

Число n{\displaystyle n} должно быть как можно больше.

• Автомодельность базиса или самоподобие. Форма всех базисных вейвлетов ψab(t){\displaystyle \psi _{ab}(t)} должна быть подобна материнскому вейвлету ψ(t){\displaystyle \psi (t)}, т.е. должна оставаться одной и той же при сдвигах и масштабировании (растяжении/сжатии), иметь одно и то же число осцилляций.

Отображение преобразования.

Результатом вейвлет-преобразования одномерного числового ряда (сигнала) является двумерный массив значений коэффициентов C(a,b){\displaystyle C(a,b)}. Распределение этих значений в пространстве (a,b){\displaystyle (a,b)} — временной масштаб, временная локализация, дает информацию об изменении во времени относительного вклада в сигнале вейвлетных компонент разного масштаба и называется спектром коэффициентов вейвлет-преобразования, масштабно-временным (частотно-временным) спектром или просто вейвлет-спектром (wavelet spectrum).

Спектр C(a,b){\displaystyle C(a,b)} одномерного сигнала представляет собой поверхность в трехмерном пространстве.

Вейвлетные функции

Выбор анализирующего вейвлета во многом определяется тем, какую информацию необходимо извлечь из сигнала. С учетом характерных особенностей различных вейвлетов во временном и в частотном пространстве, можно выявлять в анализируемых сигналах те или иные свойства и особенности, которые незаметны на графиках сигналов, особенно в присутствии сильных шумов. При этом задача реконструкции сигнала может и не ставиться, что расширяет семейство используемых регулярных и симметричных вейвлетных функций. Более того, вейвлет может конструироваться непосредственно под ту локальную особенность в сигнале, которая подлежит выделению или обнаружению, если ее форма априорно известна.

При анализе сигналов вейвлетами четного типа (симметричными или близкими к симметричным) гармоническим сигналам обычно соответствуют яркие горизонтальные полосы вейвлетных пиков и впадин на доминирующих частотах вейвлетов, совпадающих с частотой гармоник сигналов. Нарушения гладкости сигналов фиксируются вертикальными полосами, пики в сигналах выделяются максимумами, а впадины – минимумами вейвлетных коэффициентов. Напротив, вейвлеты нечетного типа более резко реагируют на скачки и быстрые изменения в сигналах, отмечая их максимумами или минимумами в зависимости от знака дифференциалов. Чем резче выражены особенности сигналов, тем сильнее они выделяются на спектрограммах.

Вейвлетный спектр

В отличие от преобразования Фурье, является двумерным и определяет двумерную поверхность в пространстве переменных m{\displaystyle m} и k{\displaystyle k}. При графическом представлении параметр растяжения/сжатия спектра m откладывается по оси абсцисс, параметр локализации k по оси ординат – оси независимой переменной сигнала.

Для выбранного начального значения масштабного коэффициента сжатия m определяется функция вейвлета и вычисляется скалярное произведение сигнала с вейвлетом ⟨ψ1(t),s(t+k)⟩{\displaystyle \left\langle \psi _{1}(t),s(t+k)\right\rangle } с аргументом по сдвигу k{\displaystyle k}. Максимальные значения скалярного произведения отмечаются в сигнале там, где локализована эта же вейвлетная функция.

Чем точнее локальная особенность сигнала совпадает с соответствующей функцией вейвлета, тем эффективнее выделение этой особенности на соответствующей масштабной строке вейвлетного спектра. Нетрудно видеть также, что для сильно сжатого вейвлета Хаара характерной хорошо выделяемой локальной особенностью является скачок сигнала, причем выделяется не только скачок функции, но и направление скачка.

Чем точнее локальная особенность сигнала совпадает с соответствующей функцией вейвлета, тем эффективнее выделение этой особенности на соответствующей масштабной строке вейвлетного спектра. Нетрудно видеть также, что для сильно сжатого вейвлета Хаара характерной хорошо выделяемой локальной особенностью является скачок сигнала, причем выделяется не только скачок функции, но и направление скачка.

Основы вейвлет-преобразования

В основе вейвлет-преобразований, в общем случае, лежит использование двух непрерывных, взаимозависимых и интегрируемых по независимой переменной функций:

• вейвлет-функции ψ(t){\displaystyle \psi (t)}, как psi-функции времени с нулевым значением интеграла и частотным фурье-образом Ψ(ω){\displaystyle \Psi (\omega )}. Этой функцией, которую обычно и называют вейвлетом, выделяются детали сигнала и его локальные особенности. В качестве анализирующих вейвлетов обычно выбираются функции, хорошо локализованные и во временной, и в частотной области.
• масштабирующей функции ϕ(t){\displaystyle \phi (t)}, как временной скейлинг-функции phi с единичным значением интеграла, с помощью которой выполняется грубое приближение (аппроксимация) сигнала.

Рис. 4. Вейвлетные функции в двух масштабах.

Phi-функции присущи не всем, а, как правило, только ортогональным вейвлетам. Они необходимы для преобразования нецентрированных и достаточно протяженных сигналов при раздельном анализе низкочастотных и высокочастотных составляющих.

Базисные функции вейвлет – преобразования

Базисными функциями вейвлет-преобразований, которые собственно и называются вейвлетами, могут быть самые различные функции с компактным носителем — модулированные импульсами синусоиды, функции со скачками уровня и т.п. Они обеспечивает хорошее отображение и анализ сигналов с локальными особенностями, в том числе со скачками, разрывами и перепадами значений с большой крутизной, при подборе соответствующего типа вейвлетов.^[1]

Следует, однако, различать вейвлеты по целевым задачам вейвлетных преобразований с позиций декомпозиции – реконструкции сигналов. По аналогии с преобразованием Фурье, было бы желательно иметь такое вейвлет-преобразование сигналов, которое обеспечивало бы полную информационную эквивалентность нового представления сигналов (вейвлетного спектра) временному (динамическому, координатному) представлению, и, соответственно, однозначность как декомпозиции сигналов, так и их реконструкции из вейвлетных спектров. Однако это возможно только при использовании ортогональных базисных функций, к числу которых относится достаточно ограниченное количество ортогональных и биортогональных вейвлетов. Вместе с тем для качественного анализа сигналов и локальных особенностей в сигналах может применяться гораздо более обширная номенклатура вейвлетных функций, которые хотя и не обеспечивают реконструкцию сигналов, но позволяют по новому оценить информационное содержание сигналов и динамику изменения этой информации.

Свойства вейвлет – преобразования

Результаты вейвлет-преобразования, как скалярного произведения вейвлета и сигнальной функции, содержат комбинированную информацию об анализируемом сигнале и самом вейвлете. Получение определенной объективной информации об анализируемом сигнале базируется на свойствах вейвлет-преобразования, общих для вейвлетов всех типов. Рассмотрим основные из этих свойств. Для обозначения операции вейвлет-преобразования произвольных функций s(t){\displaystyle s(t)} будем применять индекс TW[s(t)]{\displaystyle TW[s(t)]}.

TW[α⋅s1(t)+β⋅s2(t)]=α⋅TW[s1(t)]+β⋅TW[s2(t)](15){\displaystyle TW[\alpha\cdot s_1 (t)+\beta\cdot s_2 (t)]=\alpha\cdot TW[s_1 (t)]+\beta\cdot TW[s_2 (t)]\quad \quad {\color{Maroon}(15)}}

Для векторных функций из этого следует, что TW{\displaystyle TW} векторной функции есть вектор с компонентами TW{\displaystyle TW} каждой из компонент анализируемого вектора в отдельности.

• Инвариантность относительно сдвига. Сдвиг сигнала во времени на t0{\displaystyle t_{0}} приводит к сдвигу вейвлет-спектра также на t0{\displaystyle t_{0}}:

TW[s(t−to)]=C(a,b−to)(16){\displaystyle TW[s(t-t_o)]=C(a,b-t_o)\!\quad \quad {\color{Maroon}(16)} }

• Инвариантность относительно масштабирования. Растяжение (сжатие) сигнала приводит к растяжению (сжатию) вейвлет-спектра сигнала:

TW[s(t/ao)]=(1/ao⋅C(a/ao,b/ao)(17){\displaystyle TW[s(t/a_o)]=(1/a_o\cdot C(a/a_o,b/a_o)\!\quad \quad {\color{Maroon}(17)}}

• Дифференцирование

dnTW[s(t)]/dtn=TW[dn(s(t))/dtn]{\displaystyle d^{n}{TW[s(t)]}/dt^{n}=TW[d^{n}(s(t))/dt^{n}]}

TW[dn(s(t))/dtn]=(−1)n∫−∞∞s(t)[dn(ψ(t))/dtn]dt(18){\displaystyle TW[d^n(s(t))/dt^n]=(-1)^n \int\limits_{-\infty}^{\infty} s(t)[d^n(\psi (t))/dt^n]\,dt\quad \quad {\color{Maroon}(18)}}

Отсюда следует, что безразлично, дифференцировать ли функцию или анализирующий вейвлет. Если анализирующий вейвлет задан формулой, то это может быть очень полезным для анализа сигналов. Проанализировать особенности высокого порядка или мелкомасштабные вариации сигнала s(t){\displaystyle s(t)} с игнорированием крупномасштабных полиномиальных составляющих (тренда и регионального фона) можно дифференцированием нужного числа раз либо вейвлета, либо самого сигнала. Это свойство особенно полезно, когда сигнал задан дискретным рядом.

∫Rs1(t)⋅s2dt=CΨ−1∫Ra−2C(a,b)C(a,b)dadb(19){\displaystyle \int\limits_{R} s_1 (t) \cdot s_2 dt = C_{\Psi}^{-1}\int\limits_{R} a^{-2} C(a,b) C (a,b)\,da \,db\quad \quad {\color{Maroon}(19)}}

Определения и свойства одномерного непрерывного вейвлет-преобразования обобщаются на многомерный и на дискретный случаи.

Идея вейвлет-преобразования

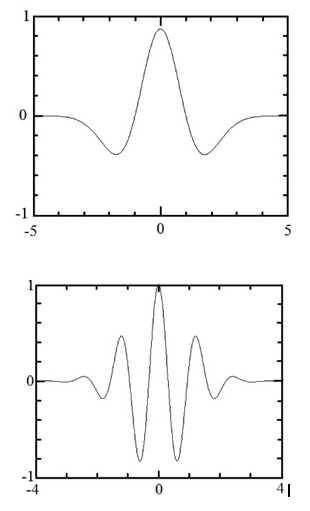Рис. 5. Примеры материнских вейвлетов

Идея вейвлет — преобразования состоит в разложении сигнала (функции-изображения) по системе функций, имеющих локальный всплеск и быстро убывающих на бесконечности. Обычно такие функции вейвлет-преобразования выводятся из так называемого материнского вейвлета. Материнский вейвлет — это функция ψ{\displaystyle \psi }:

∫−∞∞|ψ(t)|dt<∞{\displaystyle \int \limits _{-\infty }^{\infty }|\psi (t)|dt<\infty } ∫−∞∞|ψ(t)|2dt<∞(20){\displaystyle \int\limits_{-\infty}^{\infty} |\psi(t)|^2 dt < \infty\quad \quad {\color{Maroon}(20)}}

т.е. ψ∈L2(R)∩L1(R){\displaystyle \psi \in L_{2}(R)\cap L_{1}(R)}; также предполагается, что

∫−∞∞ψ(t)dt=0{\displaystyle \int \limits _{-\infty }^{\infty }\psi (t)\,dt=0} ∫−∞∞|ψ(t)|2dt=1(21){\displaystyle \int\limits_{-\infty}^{\infty} |\psi(t)|^2 \,dt = 1\quad \quad {\color{Maroon}(21)}}

Материнский вейвлет преобразовывается следующим образом:

ψab(t)=1|a|ψ(t−ba)(22){\displaystyle \psi_{ab} (t) = \frac{1}{\sqrt{|a|}} \psi \big( \frac{t-b}{a} \big)\quad \quad {\color{Maroon}(22)}}

где (a,b)∈R∖{0}×R{\displaystyle (a,b)\in R\backslash \{0\}\times R}

В общем случае вейвлет — преобразование записывается так:

WΨf(a,b)=1|a|∫−∞∞Ψ(t−ba)f(t)dt{\displaystyle W_{\Psi }f(a,b)={\frac {1}{\sqrt {|a|}}}\int \limits _{-\infty }^{\infty }\Psi {\big (}{\frac {t-b}{a}}{\big )}f(t)dt}

При практическом применении вейвлет — преобразования анализ такого мощного (а именно континуум) множества коэффициентов невозможен. Поэтому (a,b){\displaystyle (a,b)} выбираются из счетного подмножества плоскости R∖{0}×R{\displaystyle R\backslash \{0\}\times R}. Обычно материнский вейвлет и множество значений (a,b){\displaystyle (a,b)} выбирают так, чтобы система {ψab}{\displaystyle \{\psi _{ab}\}} образовывала ортонормированный базис в пространстве L2(R){\displaystyle L_{2}(R)} . Тогда любую функцию f(x){\displaystyle f(x)} из этого пространства можно разложить по этому базису f(x)=∑j,kcjkϕjk(x){\displaystyle f(x)=\sum _{j,k}c_{jk}\phi _{jk}(x)}.

Применение вейвлет — преобразования к дискретному сигналу (например, изображению). Для простоты рассмотрим одномерный случай — последовательность конечной длины {sj}j=0N−1{\displaystyle \{s_{j}\}_{j=0}^{N-1}}. Тогда, при условии, что материнский вейвлет ψ∈L2(R){\displaystyle \psi \in L_{2}(R)}, преобразование можно записать так:

Ws(a,b)=1a∑j=0N−1sj∫jj+1ψt−badt(23){\displaystyle W_s (a,b)=\frac{1}{\sqrt{a}} \sum_{j=0}^{N-1} s_j \int\limits_{j}^{j+1} \psi \frac{t-b}{a}\,dt\quad \quad {\color{Maroon}(23)}}

где

a=1…N,b=0…N−1{\displaystyle a=1\dots N,b=0\dots N-1}

В алгоритме JPEG2000 используются вейвлеты Добеши.

В матричном виде для действия на вектор A{\displaystyle A} длины 8 данное преобразование задается так:

D4=(h0h2h3h4000000g0g1g2g300000000h0h2h3h4000000g0g1g2g300000000h0h2h3h4000000g0g1g2g300000000h0h2h3h4000000g0g1g2g3)(24){\displaystyle D_4 =\begin{pmatrix} h_0 & h_1 & h_2 & h_3 & 0 & 0 & 0 & 0 & 0 & 0 \\ g_0 & g_1 & g_2 & g_3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & h_0 & h_1 & h_2 & h_3 & 0 & 0 & 0 & 0 \\ 0 & 0 & g_0 & g_1 & g_2 & g_3 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & h_0 & h_1 & h_2 & h_3 & 0 & 0 \\ 0 & 0 & 0 & 0 & g_0 & g_1 & g_2 & g_3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & h_0 & h_1 & h_2 & h_3 \\ 0 & 0 & 0 & 0 & 0 & 0 & g_0 & g_1 & g_2 & g_3\end{pmatrix}\quad \quad {\color{Maroon}(24)} }

где:

h0=1+342{\displaystyle h_{0}={\frac {1+{\sqrt {3}}}{4{\sqrt {2}}}}}, h2=3+342{\displaystyle h_{1}={\frac {3+{\sqrt {3}}}{4{\sqrt {2}}}}}, h3=3−342{\displaystyle h_{2}={\frac {3-{\sqrt {3}}}{4{\sqrt {2}}}}}, h4=1−342{\displaystyle h_{3}={\frac {1-{\sqrt {3}}}{4{\sqrt {2}}}}}, g0=h4{\displaystyle g_{0}=h_{3}\!}, g1=−h3{\displaystyle g_{1}=-h_{2}}, g2=h2{\displaystyle g_{2}=h_{1}}, g3=−h0{\displaystyle g_{3}=-h_{0}}.

Как видно, матрица имеет размеры 8∗10{\displaystyle 8*10} из-за необходимости участия в суммировании четырех компонент. Т.е. на самом деле, такая матрица умножается на следующий вектор: A=(a1a2a3a4a5a6a7a8a9a10)T

ru.bmstu.wiki

77-30569/355664 Применение вейвлет-преобразования для анализа спектрограмм, полученных на Оже-спектрометре

77-30569/355664 Применение вейвлет-преобразования для анализа спектрограмм, полученных на Оже-спектрометре

авторы: Романова Т. Н., Плаксина М. В.

УДК 537.5; 004.9

МГТУ им. Н.Э. Баумана

[email protected]

В настоящее время в области анализа гетероструктур актуальны методы исследования состава и структуры внешней поверхности твердых тел. Одним из таких методов является метод Оже-электронной спектроскопии. Оже-эффект заключается в извлечении электрона с одной из внутренних электронных оболочек атома под действием первичного электронного пучка. При каждом значении напряжения всегда найдется такое магнитное поле, при котором вылетевший с поверхности образца электрон попадет в щель измерителя. Численные значения напряжения записываются в цифровой форме, поэтому импульс  тока в измерителе будет соответствовать какому-то напряжению. Оно равно энергии связи электрона, вылетевшего из того или иного атома. Величина импульса заносится в память компьютера и выдается  на экран в виде спектра. На нем пики принадлежат разным элементам. В настоящее время спектрограммы, полученные на Оже-спектрометре ЭСО-3, анализируются экспертами вручную с использованием специальных атласов Оже-спектров чистых материалов. Анализ элементного состава производится методом сопоставления Оже-спектров с данными из атласов. Расположение пика в энергетическом спектре Оже-электронов несет информацию о химической природе атомов, его амплитуда — об их концентрации. Взаимодействия атома с его окружением проявляются в форме Оже-пиков и их энергетических сдвигах. Таким образом, определяющими факторами при Оже-анализе являются энергетическое положение и форма Оже-линий. Однако, в реальных спектрах эти характеристики Оже-линий могут несколько изменяться из-за того, что измерение полезного сигнала (тока) при заданном напряжении на аноде Оже-спектрометра всегда сопровождается генерацией шума разного происхождения. Источники помех могут находиться как вне, так и внутри самой системы. Помехи в Оже-спектрометре носят непредсказуемый случайный характер и представляют собой комплекс различных шумов. Борьба с такими помехами представляет наибольшие трудности. Помехи понижают контрастность полезного сигнала и повышают погрешность измерения как энергии связи  электрона с атомом, так и численных значений интенсивности силы тока I.

Для повышения контрастности полезного сигнала и понижения погрешности измерения энергии связи  электрона с атомом и численных значений самого сигнала Iнеобходимо разработать методы фильтрации от шума Оже-электронных спектров. Хорошее разрешение сигнала по интенсивности тока  требуется для проведения количественного анализа исследуемого образца материала, а хорошее  разрешение сигнала по энергии связи электронов  требуется для его качественного химического анализа.

На рис. 1 представлен общий вид электронного спектра, полученного на Оже-спектрометре ЭСО-3. Символами отмечены пики, соответствующие химическим элементам: P – фосфор, С – углерод, In – индий, Sb – сурьма, O – кислород. На вертикальной оси указана относительная интенсивность тока электронов, попадающих в измерительный цилиндр после усиления при 1200 значениях энергии связи электрона с атомом. Наличие электронных шумов, как положительных, так и отрицательных, отчётливо прослеживается. При увеличении спектра характер шумов наблюдается самый различный: некоторые пики имеют чётко выраженный треугольный, т.е. пилообразный характер, другие имеют плато той или иной протяжённости, третьи состоят из ряда следующих друг за другом шумовых импульсов.

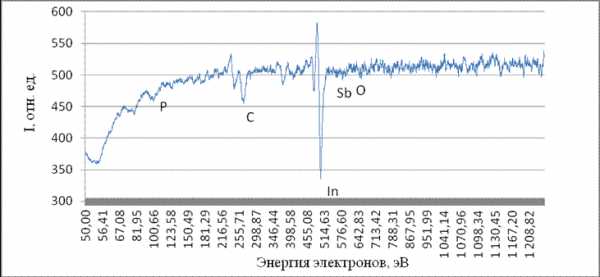
Рис. 1. Электронный спектр, полученный на Оже-спектрометре

 

Был проведен обзор существующих исследований методов очистки сигналов от шума. В результате были найдены:

1)     исследование метода очистки от шума спектров, полученных на масс-спектрометре; метод основан на дискретном вейвлет-преобразовании с применением вейвлета Добеши [1].

2)     исследование метода очистки сигнала электрокардиограмм; метод основан на быстром вейвлет-преобразовании с применением вейвлетов Добеши, Симлета, Хаара и Мейера [2].

Так как спектры масс-спектрометра, электрокардиограммы и спектры Оже-спектрометра имеют свои характерные особенности — форма, величина пиков, периодичность (для электрокардиограмм), случайный характер пиков (для Оже- и масс-спектров), то необходимо проводить исследование  очистки от шума с учетом особенностей каждого из сигналов, которые и надо учитывать при выборе материнского вейвлета.

Целью  данного исследования является оценка эффективности вейвлет-преобразования для очистки от комплексных помех электронного спектра, полученного на Оже-спектрометре.

Для автоматизации анализа химической структуры вещества с применением Оже-спектрометра разработан программно-технический комплекс. На начальном этапе создания комплекса была  разработана экспертная система, которая, используя базу знаний, определяет химический состав образца [2]. В качестве фактов, используемых для формирования правил в базе знаний используются данные об энергии связи электронов (эВ) [3]. Спектр перед подачей на вход экспертной системы необходимо очистить от шума.

Для фильтрации спектра от шума было принято решение использовать вейвлет-преобразование. Вейвлет-преобразование имеет существенное преимущество перед преобразованием Фурье, прежде всего за счет свойства локальности у вейвлетов. В вейвлет-преобразовании операция умножения на окно содержится в самой базисной функции, которая сужает и расширяет окно. Отсюда появляется возможность адаптивного к сигналу выбора параметров окна. Подвижное частотно-временное окно одинаково хорошо выделяет и низкочастотные, и высокочастотные характеристики сигналов. Это свойство вейвлет-преобразования дает ему большое преимущество при анализе локальных свойств сигналов. Вейвлет-преобразование позволяет судить не только о частотном спектре сигнала, но также о том, в какой момент времени появилась та или иная гармоника. С помощью вейвлетов  можно анализировать прерывистые сигналы, либо сигналы с острыми всплесками. Кроме того, вейвлеты позволяют анализировать данные согласно масштабу, на одном из заданных уровней (мелком или крупном) [4].

При решении серьезных задач в области обработки сигналов желательно применение хотя бы нескольких типов вейвлетов с последующим сравнением результатов и выбором наилучших из них. Выбор используемого вейвлета, в общем случае, зависит от свойств конкретного сигнала. Более гладкие вейвлеты создают более гладкую аппроксимацию сигнала, «короткие» вейвлеты лучше отслеживают пики аппроксимируемой функции.

Исследование применения вейвлет-преобразования для очистки спектра от шума проводилось с применением следующих типов вейвлетов: Хаара, Симлета и Коифлетса (рис. 2). Разработаны программы в среде MatLab, реализующие очистку спектра от шума с применением вышеуказанных вейвлетов [4,5].

а)              б)             в)

Рис. 2. Типы вейвлетов: а) вейвлет Хаара; б) вейвлет Симплета 8-го порядка; в) вейвлет Коифлетса 1-го рода

 

Вейвлет Хаара является ортогональным (рис. 2а). Для частотно-временного анализа этот базис плохо подходит, так как частотная локализация у него слабая. Также вейвлет Хаара имеет резкие границы, т.е. недостаточную гладкость, при этом нет ясности относительно того, насколько последнее обстоятельство может повлиять на качество синтеза непрерывных сигналов.

На  рис. 3 видно, что после очистки спектра с применением вейвлета Хаара уменьшилась интенсивность пиков, соответствующих элементам Sb (сурьма) и O (кислород) (рис. 1) на интервале энергии от 570 до 700 эВ, это в дальнейшем ведет к возможным ошибкам экспертной системы при дальнейшем анализе спектра.

 

Рис. 3. Очистка спектра с применением вейвлета Хаара

 

Рассмотрим близкий к симметричным вейвлет Симплета. Различают вейвлеты Симплета разного рода, для нашей задачи в качестве материнского был выбран вейвлет 8-го порядка (рис. 2б). На рис. 4 видно, что пики на спектре, соответствующие химическим элементам, стали уже наиболее выраженными, чем после применения вейвлета Хаара. Спектр стал более сглаженным.

 

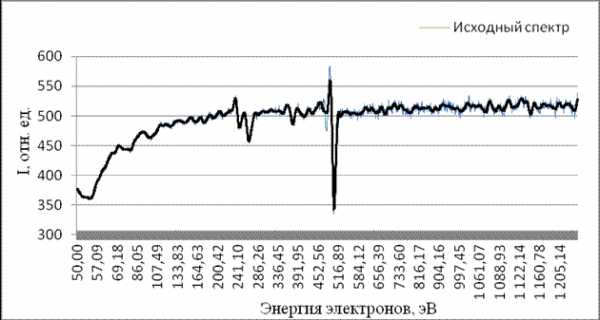
Рис. 4. Очистка спектра с применением вейвлета Симлета 8-го порядка

 

В качестве вейвлета Коифлетса был выбран вейвлет 1-го рода (рис. 2в). На рис. 5 представлен результат очистки спектра с использованием в качестве материнского вейвлета Коифлетса. Очищенный спектр, имеет более острые пики, это обусловлено формой выбранного вейвлета.

 

Рис. 5. Очистка спектра с применением вейвлета Коифлетса 1-го рода

 

Для оценки погрешности каждого из вышеуказанных  методов очистки от шума выбран интервал от 257 до 277 эВ. Результат очистки на данном интервале сравнивался с эталонным пиком (обозначен линией с окружностями), который соответствует углероду (рис. 6).

 

    

а)                                         б)                                         в)

Рис. 6. Результаты очистки спектра на интервале от 257 эВ до 277 эВ с использованием вейвлетов:  а) Хаара; б) Симлета 8-го рода; в) Коифлетса 1-го рода

 

Для каждого метода была вычислена средняя квадратическая погрешность (cреднеквадратическое отклонение) по формуле 1.1.  

                             (1.1)

Результаты вычислений приведены в таблице 1.

Таблица 1.

Результаты вычисления средней квадратической погрешности.

№	Тип материнского вейвлета	Средняя квадратическая погрешность
1	Вейвлет Хаара	0.201398
2	Вейвлет Симлета 8-го порядка	0.238398
3	Вейвлет Коифлетса 1-го рода	0.318164

 

Наименьшая погрешность у метода с применением вейвлета Хаара. Однако, для очистки спектрограммы применение этого вейвлета нецелесообразно, так как для дальнейшего анализа спектра необходимо анализировать непосредственно форму пика, а преобразование на основе вейвлета Хаара значительно изменяют эту форму, что в дальнейшем приведет к ошибке определения химического элемента или соединения. Значительно лучший  результат относительно формы пика дает метод, основанный на вейвлете Симлета 8-го рода. Форма пика почти совпадает с формой пика эталона, нет лишних изгибов и изломов. Погрешность этого метода также небольшая и отличается от погрешности предыдущего метода всего на 0.037. Анализируя результат, полученный методом, основанным на вейвлете Коифлетса 1-го рода (рис. 6в), нетрудно заметить, что форма пика нарушена, присутствуют лишние изгибы и изломы, что для дальнейшего анализа является минусом. Погрешность метода больше погрешностей двух предыдущих методов и равна 0.318164.

Очищенная от шума с применением вейвлет-преобразования спектрограмма далее подается на вход экспертной системе, которая будет производить дальнейший анализ спектра с целью идентификации химических элементов входящих в состав вещества.

Выводы

1. На основании проведенного анализа существующих подходов к фильтрации нестационарных сигналов в качестве математического аппарата выбран кратномасштабный вейвлет-анализ, применение которого позволяет выделить и сохранить локальные особенности сигнала – пики Оже-спектрограммы, по которым проводится качественный химический анализ.

2. Материнский вейвлет для проведения фильтрации должен обладать свойством ортогональности  и возможностью реконструкции сигнала. В результате проведенного исследования в качестве материнских вейвлетов были выбраны: вейвлет Хаара, вейвлет Симплета 8-го порядка, вейвлет Коифлетса 1-го рода.

3. Разработаны программы в среде MatLab, реализующие очистку эталонного спектра от шума с применением вышеуказанных вейвлетов. Проведено сравнение полученных результатов с применением среднеквадратической погрешности.

4. Проведенные исследования показали, что из всех трех вейвлетов наилучший результат дал метод, основанный на вейвлете Симплета 8-го рода.

5.  Разработан программно-технический комплекс, который решает следующие задачи:

·       проводит фильтрацию Оже-спектрограммы  от комплексного шума с использованием выбранных вейвлетов;

·       на основе работы модуля экспертной системы получает качественный химический состав исследуемого образца материала;

·       автоматизированное рабочее место эксперта предоставляет дружественный интерфейс для модификации базы знаний с целью улучшения качества проводимого химического анализа.

 

Литература

1.   Kevin R. Coombes, Spiridon Tsavachidis, Jeffrey S. Morris, Keith A.Baggerly, Mien-Chie Hung, and Henry M. Kuerer. Improved Peak Detection and Quantification of Mass Spectrometry Data Acquired from Surface-Enhanced Laser Desorption and Ionization by Denoising Spectra with the Undecimated Discrete Wavelet Transform // Proteomics 2005, 5:4107-4117.

2.   Марченко Н. А., Литовских Ю. А.. Использование вейвлет-преобразования для очистки сигналов электрокардиограмм// Вестник Национального технического университета «ХПИ», Сборник научных трудов, тематический выпуск «Системный анализ, управление и  информационные технологии», №67. – Харьков. –­ 2010.

3.   Плаксина М.В., Зленко В.Я., Валюхов Д.П. База знаний для создания экспертной системы Оже-спектрометра// Материалы научно-практической конференции «Инфо — 2007»,  c. 176-178

4.   Зигбан К., Нордлинг К., Фальман А. и др. Электронная спектроскопия. – М.: Мир. – 1971. – 493 с.

5.   Дьяконов В.П., Абраменкова И.В. MATLAB. Обработка сигналов и изображений. Специальный справочник. – СПб: Питер. – 2002. – 608 с.

engineering-science.ru

4.8.7. Анализ сигналов по вейвлет-спектрограммам

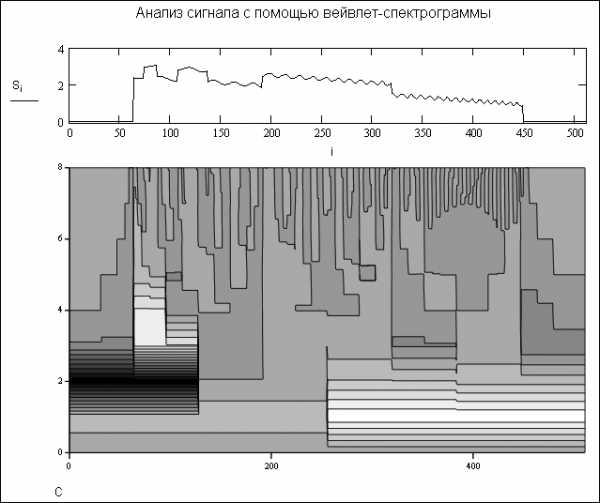Вейвлет-спектрограммами называют диаграммы типа «уровень-время», или, точнее, «уровень-индекс» для вейвлет-коэффициентов. Обычно такие спектрограммы строятся как графики поверхностей или графики линий равного уровня с функциональной закраской. На рис. 4.43 показана вейвлет-спектрограмма для примера, представленного выше.

Рис. 4.43. Вейвлет-спектрограмма сложного нестационарного сигнала

В нижней части вейвлет-спектрограммы представлены грубые разложения сигнала, а в верхней части — более точные, соответствующие большим значением L. И та и другая части спектрограммы могут использоваться для распознавания особенностей сигналов, как глобальных (грубых), так и самых тонких. Для пояснения этого на рис. 4.41 сверху спектрограммы построен график исходного сигнала.

Нетрудно заметить (особенно когда спектрограмма цветная), что на ней отражены малейшие нюансы сигнала с их четкой привязкой ко времени. Например, в верхней части спектрограммы отчетливо выделяются перепады импульса, хорошо видны все пики и точки перегиба синусоиды с возрастающей во времени частотой, можно сразу сделать вывод о характере нестационарности сигнала и оценить количественно изменение длительности периода прямоугольных и синусоидальных колебаний на вершине импульса.

Примененные в описанном примере вейвлеты Добеши 4 довольно грубые. Но даже в этом случае опытный пользователь может по вейвлет-спектрограмме распознать многие особенности сигнала, порою даже скрытые. Например, очень четко на вейвлет-спектрограммах выделяются даже незаметные разрывы во временной зависимости сигналов. Высококачественные вейвлет-спектрограммы позволяет строить система MATLAB с пакетом расширения Wavelets Toolbox.

Область применения вейвлет-спектрограмм весьма широка и охватывает такие сферы обработки сигналов, как:

• распознавание тонких особенностей сигналов и функций, в том числе на фоне шумов;

• обнаружение месторождений полезных ископаемых по данным геологоразведки;

• исследование климатических и иных изменений в жизни Земли и ее отдельных регионов;

• анализ рентгенограмм и томограмм в медицинской практике;

• выявление и предсказание экономических и социальных явлений;

• предсказание возможных катастрофических ситуаций и др.

Большой интерес представляет описание вейвлет-технологии обработки типичного временного ряда, демонстрирующего динамику изменения событий, характеризующих процесс Эль-Ньньо – глобального потепления океанических вод вблизи тихоокеанского побережья Центральной Америки. Эта работа была выполнена Н. М. Астафьевой. С помощью ряда как прямых измерений (примерно за последние 100 лет), так и косвенных событий процесс Эль-Ньньо удалось представить за весьма внушительный срок в 500 лет (это половина тысячелетия). Полученный при этом временной ряд и результаты его вейвлет-анализа в виде спектрограмм представлены на рис. 4.44 (данные за последнее столетие подчеркнуты).

Представленные на рис. 4.44 данные дают хорошую пищу для оценки процесса Эль-Ньньо и связанных с ним других процессов – например, процесса Южное Колебание. Из представленных данных можно сделать выводы о различных долговременных и кратковременных фазах процесса Эль-Ньньо, например, о периодах глубокого потепления, о 40-летних периодических циклах и о многих иных деталях этого сложнейшего процесса. Так вейвлеты способствуют открытию новых закономерностей.

Р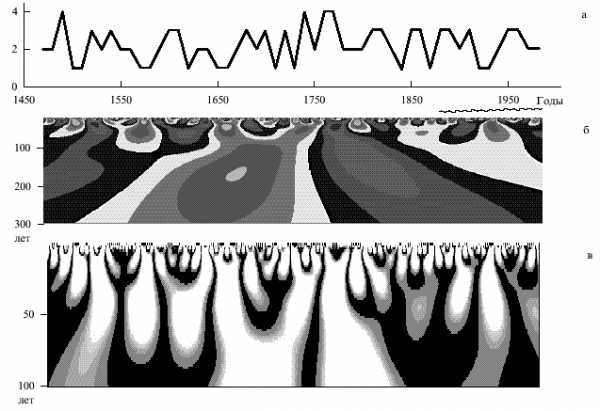ис. 4.44. График зависимости числа событий Эль-Ньньо от времени за 500 лет (a), спектрограмма вейвлет-коэффициентов (b) и распределение плотности энергии (c)

Из приведенных выше примеров видно, что вейвлеты являются весьма эффективным средством обработки сигналов и временных рядов. Зачастую они используются там же, где применяется БПФ, например, для очистки сигналов от шума (в простейшем случае ограничением уровня композиции), выделения нужных составляющих, компрессии сигналов и т. д. При этом расчеты, выходящие за рамки учебного курса, показывают, что вейвлеты делают это более эффективно, чем техника БПФ.

studfiles.net

python — найти местоположение пиков в спектре numpy

Это, я думаю, может послужить отправной точкой. Я не специалист по обработке сигналов, но я пробовал это по сгенерированному сигналу Y, который выглядит как ваш, и один с гораздо большим шумом:

from scipy.signal import convolve
import numpy as np
from matplotlib import pyplot as plt
#Obtaining derivative
kernel = [1, 0, -1]
dY = convolve(Y, kernel, 'valid') 

#Checking for sign-flipping
S = np.sign(dY)
ddS = convolve(S, kernel, 'valid')

#These candidates are basically all negative slope positions
#Add one since using 'valid' shrinks the arrays
candidates = np.where(dY < 0)[0] + (len(kernel) - 1)

#Here they are filtered on actually being the final such position in a run of
#negative slopes
peaks = sorted(set(candidates).intersection(np.where(ddS == 2)[0] + 1))

plt.plot(Y)

#If you need a simple filter on peak size you could use:
alpha = -0.0025
peaks = np.array(peaks)[Y[peaks] < alpha]

plt.scatter(peaks, Y[peaks], marker='x', color='g', s=40)

Примеры результатов: 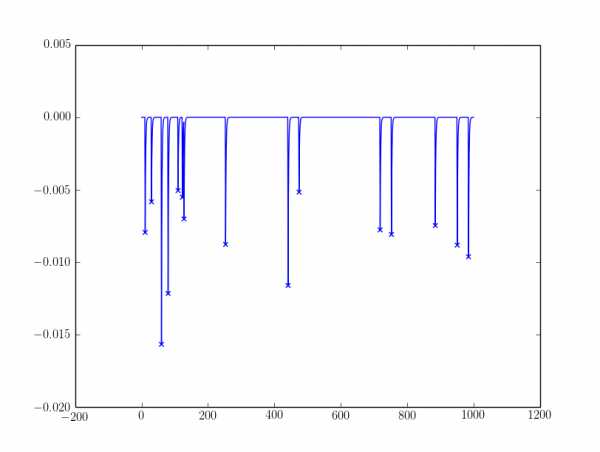Для шумного я фильтровал пики с alpha: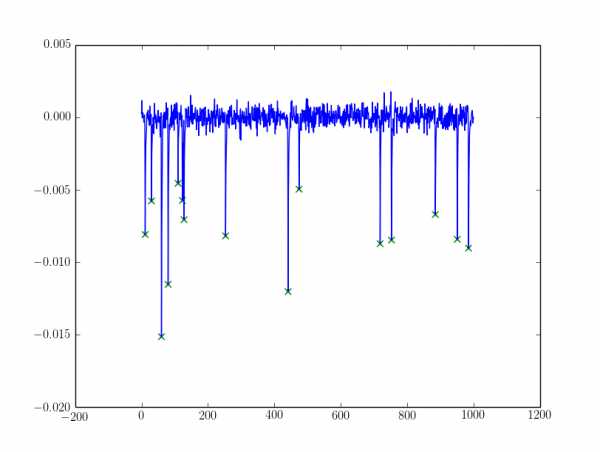

Если alpha нуждается в большей сложности, вы можете попробовать динамически установить альфа из пиков, обнаруженных с помощью, например, предположения о том, что они являются смешанными гауссовыми (мой любимый, являющийся порогом Otsu, существует в cv и skimage) или какой-то кластеризации (k-средства могут работать).

И для справки, это я использовал для генерации сигнала:

Y = np.zeros(1000)

def peaker(Y, alpha=0.01, df=2, loc=-0.005, size=-.0015, threshold=0.001, decay=0.5):  
    peaking = False
    for i, v in enumerate(Y):
        if not peaking:
            peaking = np.random.random() < alpha
            if peaking:
                Y[i] = loc + size * np.random.chisquare(df=2)
                continue
        elif Y[i - 1] < threshold:
            peaking = False

        if i > 0:
            Y[i] = Y[i - 1] * decay

peaker(Y)

EDIT: поддержка ухудшения базовой линии

Я смоделировал наклонную базовую линию, выполнив следующее:

Z = np.log2(np.arange(Y.size) + 100) * 0.001
Y = Y + Z[::-1] - Z[-1]

Затем для обнаружения с фиксированной альфа (обратите внимание, что я изменил знак на альфа):

from scipy.signal import medfilt

alpha = 0.0025
Ybase = medfilt(Y, 51) # 51 should be large in comparison to your peak X-axis lengths and an odd number.
peaks = np.array(peaks)[Ybase[peaks] - Y[peaks] > alpha] 

Результат в следующем результате (базовая линия изображается штриховой черной линией):

РЕДАКТИРОВАТЬ 2: Упрощение и комментарий

Я упростил код для использования одного ядра для обоих convolve, как прокомментировал @skymandr. Это также устранило магическое число при настройке усадки, чтобы сделать любой размер ядра.

Для выбора "valid" в качестве опции convolve. Вероятно, это сработало бы так же, как и с "same", но я выбираю "valid", поэтому мне не нужно было думать о краевых условиях, и если бы алгоритм обнаружил пики spurios.

qaru.site

найти местоположение пиков в спектре numpy Ru Python

Это, я думаю, могло бы послужить отправной точкой. Я не специалист по обработке сигналов, но я попробовал это на сгенерированном сигнале Y который выглядит как ваш, и у вас гораздо больше шума:

 from scipy.signal import convolve import numpy as np from matplotlib import pyplot as plt #Obtaining derivative kernel = [1, 0, -1] dY = convolve(Y, kernel, 'valid') #Checking for sign-flipping S = np.sign(dY) ddS = convolve(S, kernel, 'valid') #These candidates are basically all negative slope positions #Add one since using 'valid' shrinks the arrays candidates = np.where(dY < 0)[0] + (len(kernel) - 1) #Here they are filtered on actually being the final such position in a run of #negative slopes peaks = sorted(set(candidates).intersection(np.where(ddS == 2)[0] + 1)) plt.plot(Y) #If you need a simple filter on peak size you could use: alpha = -0.0025 peaks = np.array(peaks)[Y[peaks] < alpha] plt.scatter(peaks, Y[peaks], marker='x', color='g', s=40) 

Исходные результаты: 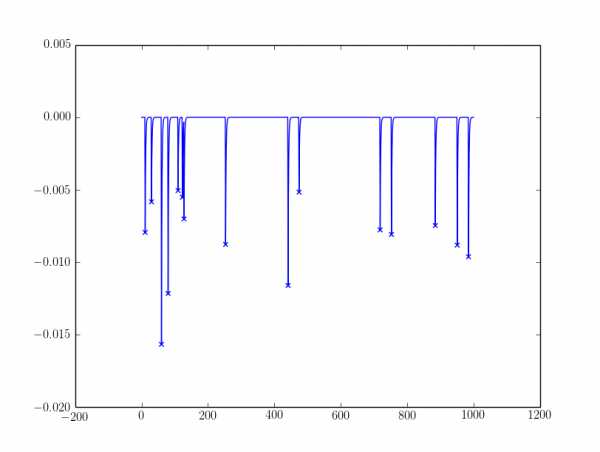Для шумного я фильтровал пики с alpha :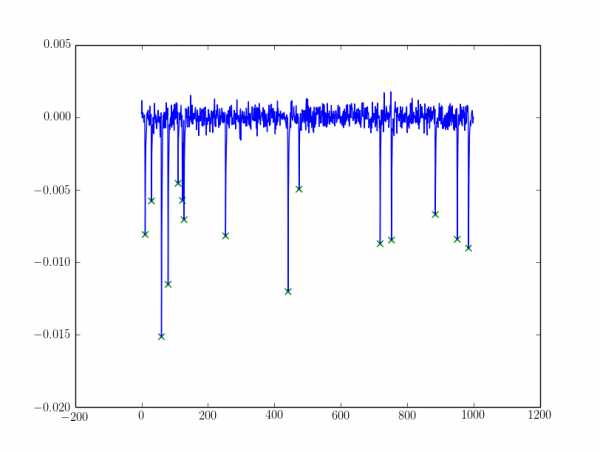

Если alpha нуждается в большей сложности, вы можете попробовать динамически установить альфа из обнаруженных пиков, например, предположения о том, что они являются смешанными гауссовыми (мой любимый, являющийся порогом Otsu, существует в cv и skimage ) или какой-то кластеризации (k-средства могут работать ).

И для справки, это я использовал для генерации сигнала:

 Y = np.zeros(1000) def peaker(Y, alpha=0.01, df=2, loc=-0.005, size=-.0015, threshold=0.001, decay=0.5): peaking = False for i, v in enumerate(Y): if not peaking: peaking = np.random.random() < alpha if peaking: Y[i] = loc + size * np.random.chisquare(df=2) continue elif Y[i - 1] < threshold: peaking = False if i > 0: Y[i] = Y[i - 1] * decay peaker(Y) 

EDIT: поддержка деградации базовой линии

Я смоделировал наклонную базовую линию, выполнив следующее:

 Z = np.log2(np.arange(Y.size) + 100) * 0.001 Y = Y + Z[::-1] - Z[-1] 

Затем для обнаружения с фиксированной альфа ( обратите внимание, что я изменил знак на альфа ):

 from scipy.signal import medfilt alpha = 0.0025 Ybase = medfilt(Y, 51) # 51 should be large in comparison to your peak X-axis lengths and an odd number. peaks = np.array(peaks)[Ybase[peaks] - Y[peaks] > alpha] 

Результат в следующем результате (базовая линия изображается штриховой черной линией):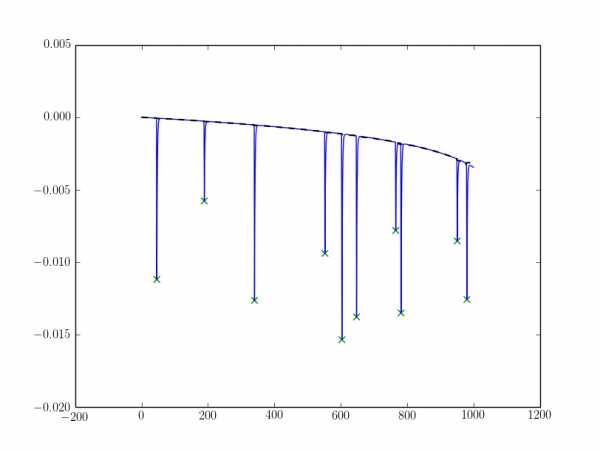

EDIT 2: Упрощение и комментарий

Я упростил код для использования одного ядра для обоих convolve s, как прокомментировал @skymandr. Это также устранило магическое число при настройке усадки, чтобы сделать любой размер ядра.

Для выбора "valid" как вариант convolve . Вероятно, он работал так же хорошо, как и "same" , но я выбираю "valid" поэтому мне не нужно было думать о краевых условиях, и если бы алгоритм обнаружил пики spurios.

Найти минимум или максимум не так просто, потому что нет универсального определения для «локального максимума».

Ваш код, похоже, ищет микшимум, а затем принимает его как максимум, если сигнал падает после максимума ниже максимума минус некоторое значение дельты. После этого он начинает искать минимум с аналогичными критериями. Неважно, если ваши данные падают или медленно растут, так как максимум записывается, когда он достигнут, и добавляется в список максимумов после падения уровня ниже порога гистерезиса.

Это возможный способ найти локальные минимумы и максимумы, но он имеет несколько недостатков. Один из них заключается в том, что метод не симметричен, т. Е. Если одни и те же данные запускаются в обратном направлении, результаты не обязательно одинаковы.

К сожалению, я не могу больше помочь, потому что правильный метод действительно зависит от данных, которые вы смотрите, от его формы и от шума. Если у вас есть образцы, тогда мы сможем предложить некоторые предложения.

www.rupython.com

Вейвлетные преобразования сигналов

11

Тема 20. Свойства вейвлет-преобразования

Изложение вопроса будет неполным, пока в той или иной форме мы не оговорим всех условий.

Джон Стюарт Милль. Английский философ, XIX в.

Оговорить можно, но увлекаться не стоит. Можно такой забор нагородить, что за ним и смысл самого вопроса не рассмотришь.

Игорь Широков. Московский геофизик Уральской школы, XX в.

Содержание

Введение.

1. Базисные функции вейвлет-преобразования. Определение вейвлета. Свойства вейвлета. Отображение преобразования. Вейвлетные функции.

2. Свойства вейвлет-преобразования.

3. Вейвлет-преобразование простых сигналов.

Введение.

Аналитика вейвлетных преобразований сигналов определяются математической базой разложения сигналов, которая аналогична преобразованиям Фурье. Основной отличительной особенностью вейвлет-преобразований является новый базис разложения сигналов — вейвлетные функции. Свойства вейвлетов принципиально важны как для самой возможности разложения сигналов по единичным вейвлетным функциям, так и для целенаправленных действий над вейвлетными спектрами сигналов, в том числе с последующей реконструкцией сигналов по обработанным вейвлетным спектрам.

Вейвлеты могут быть ортогональными, полуортогональными, биортогональными. Вейвлетные функции могут быть симметричными, асимметричными и несимметричными, с компактной областью определения и не имеющие таковой, а также иметь различную степень гладкости. Некоторые функции имеют аналитическое выражение, другие – быстрый алгоритм вычисления вейвлет-преобразования. Для практики желательно было бы иметь ортогональные симметричные и асимметричные вейвлеты, но таких идеальных вейвлетов не существует. Наибольшее применение находят биортогональные вейвлеты.

2.1. Базисные функции вейвлет-преобразования /1, 3/.

Базисными функциями вейвлет-преобразований могут быть самые различные функции с компактным носителем — модулированные импульсами синусоиды, функции со скачками уровня и т.п. Они обеспечивает хорошее отображение и анализ сигналов с локальными особенностями, в том числе со скачками, разрывами и перепадами значений с большой крутизной.

Следует различать вейвлеты по целевым задачам вейвлетных преобразований с позиций декомпозиции – реконструкции сигналов. Было бы желательно иметь такое вейвлет-преобразование сигналов, которое обеспечивало бы полную информационную эквивалентность вейвлетного спектра сигналов временному (динамическому, координатному) представлению, и, соответственно, однозначность как декомпозиции сигналов, так и их реконструкции из вейвлетных спектров. Однако это возможно только при использовании ортогональных и биортогональных вейвлетов. Этим вейвлетам и будет уделено основное внимание. Для качественного анализа сигналов и локальных особенностей в сигналах может применяться более обширная номенклатура вейвлетных функций, которые хотя и не обеспечивают реконструкцию сигналов, но позволяют оценить информационное содержание сигналов и динамику изменения этой информации.

Определение вейвлета. К вейвлетам относятся локализованные функции, которые конструируются из одного материнского вейвлета(t) (или по любой другой независимой переменной) путем операций сдвига по аргументу (b) и масштабного изменения (а):

_ab(t) = (1/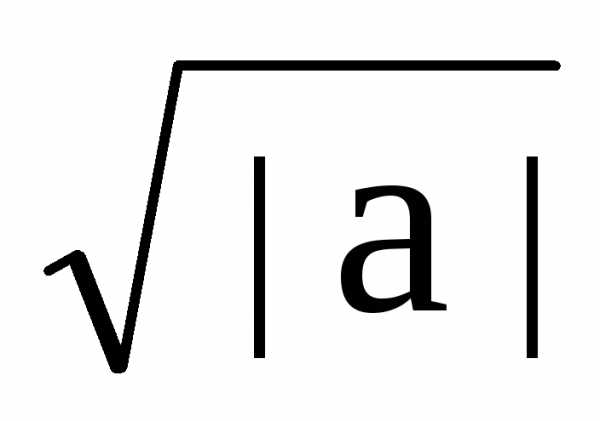) ((t-b)/a), (a, b)R, (t)L²(R).

где множитель (1/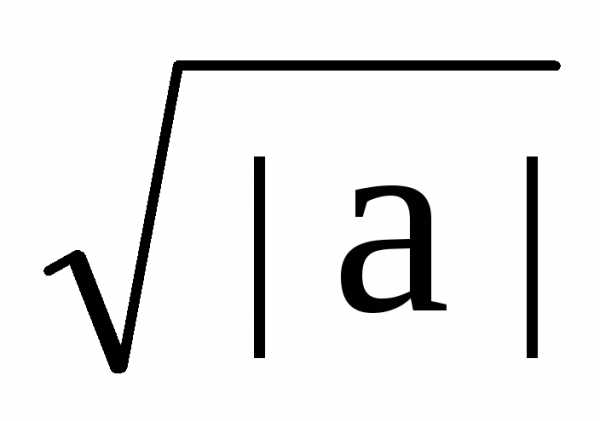) обеспечивает независимость нормы функций от масштабного числа ‘a’.

Непрерывное вейвлет-преобразование сигнала s(t)L²(R), которое применяется для качественного частотно-временного анализа, по смыслу соответствует преобразованию Фурье с заменой гармонического базисаexp(-jt) на вейвлетный((t-b)/a):

С(a, b) = s(t), _ab(t) = (1/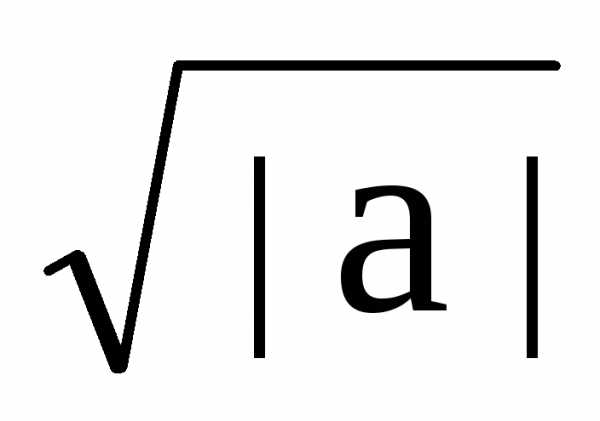)s(t)((t-b)/a) dt, (a, b)R, a0.

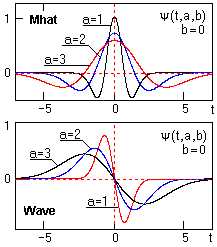
Рис. 2.1.1. Вейвлеты Mhat и Wave.

Вейвлетный масштабно-временной спектр С(a,b) в отличие от фурье-спектра является функцией двух аргументов: масштаба вейвлета ‘а’ (в единицах, обратных частоте), и временного смещения вейвлета по сигналу ‘b’ (в единицах времени), при этом параметры ‘а’ и ‘b’ могут принимать любые значения в пределах областей их определения.

На рис. 2.1.1 приведены примеры простейших неортогональных вейвлетов четного (Mhat) и нечетного (Wave) типов.

Для количественных методов анализа (декомпозиция сигналов с возможностью последующей линейной реконструкции сигналов из обработанных вейвлет-спектров) в качестве вейвлетных базисов можно использовать любые локализованные функции (t), если для них существуют функции-двойники^#(t), такие, что семейства {_ab(t)} и {^_ab(t)} могут образовывать парные базисы функционального пространства L²(R). Вейвлеты, определенные таким образом, позволяют представить любую произвольную функцию в пространстве L²(R) в виде ряда:

s(t) = 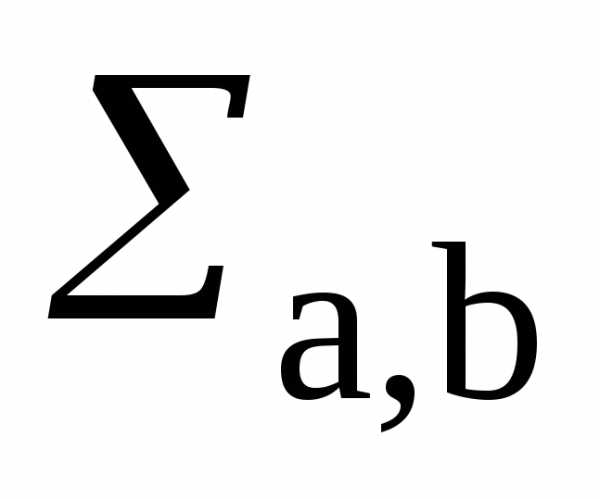С(a,b)^_ab(t), (a, b)I,

где коэффициенты С(a,b) – проекции сигнала на вейвлетный базис пространства, которые определяются скалярным произведением

С(a,b) = s(t), _ab(t) =s(t)_ab(t) dt.

Если вейвлет (t) обладает свойством ортогональности, то^(t) ≡(t) и вейвлетный базис ортогонален. Вейвлет может быть неортогональным, однако если он имеет двойника, и пара ((t),^(t)) дает возможность сформировать семейства {_mk(t)} и {^_zp(t)}, удовлетворяющие условию биортогональности на целых числахI:

_mk(t),^_zp(t)=_mz·_kp, m,k,z,pÎI,

то возможно разложение сигналов на вейвлетные ряды с обратной формулой реконструкции.

Свойства вейвлета,

• Локализация.Вейвлет должен быть непрерывным, интегрируемым, иметь компактный носитель и быть локализованным как во времени (в пространстве), так и по частоте. Если вейвлет в пространстве сужается, то его «средняя» частота повышается, спектр вейвлета перемещается в область более высоких частот и расширяется. Этот процесс должен быть линейным – сужение вейвлета вдвое должно повышать его «среднюю» частоту и ширину спектра также вдвое.

Вейвлетную функцию можно считать хорошо локализованной при выполнении условий:

(t) ≤C/(1+|t|)^1+,(f) ≤C/(1+|f|)^1+, С=const, при> 0.

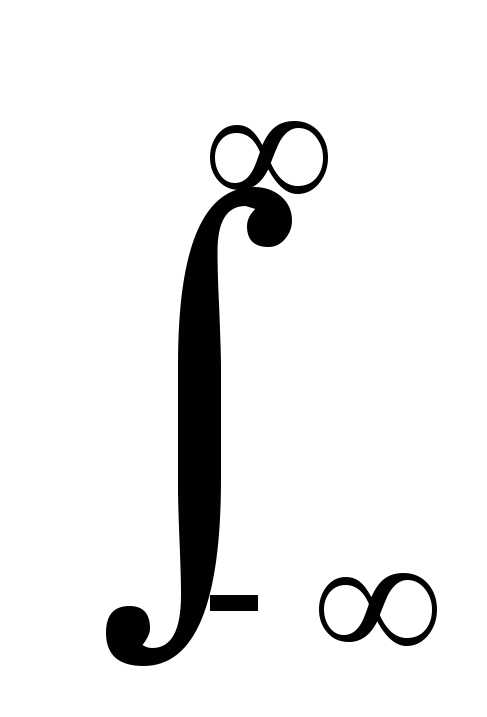(t) dt = 0,

что обеспечивает выделение локальных особенностей сигналов в пределах вейвлетного носителя на уровне региональных изменений и тренда, нулевое усиление постоянной составляющей сигналов, нулевое значение частотного спектра вейвлета при =0, и локализацию спектра вейвлета в виде полосового фильтра с центром на определенной (доминирующей) частоте₀. Для анализа мелкомасштабных флюктуаций и особенностей высокого порядка, как правило, требуются и нулевые значения определенного количества последующих моментов:

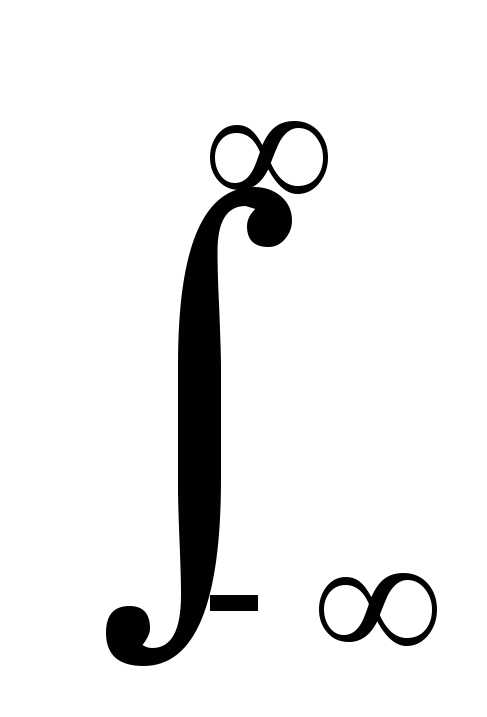t^m(t) dt = 0.

Такие вейвлеты называются вейвлетами m-го порядка.

||(t)||²=|(t)|²dt <

Оценка ограниченности и локализации может выполняться с использованием выражений:

|(t)| < 1/(1+|t|ⁿ), или |(ω)| < 1/(1+|ω_o|ⁿ),

где _o– средняя частота вейвлета. Числоn должно быть как можно больше.

• Автомодельность базисаили самоподобие. Форма всех базисных вейвлетов_ab(t) должна быть подобна материнскому вейвлету(t), т.е. должна оставаться одной и той же при сдвигах и масштабировании (растяжении/сжатии), иметь одно и то же число осцилляций.

Отображение преобразования.Результатом вейвлет-преобразования одномерного числового ряда (сигнала) является двумерный массив значений коэффициентов С(a,b). Распределение этих значений в пространстве (a,b) — временной масштаб, временная локализация, дает информацию об изменении во времени относительного вклада в сигнале вейвлетных компонент разного масштаба и называется спектром коэффициентов вейвлет-преобразования, масштабно-временным (частотно-временным) спектром или просто вейвлет-спектром (wavelet spectrum).

Спектр C(a,b) одномерного сигнала представляет собой поверхность в трехмерном пространстве. Способы визуализации спектра могут быть самыми различными. Наиболее распространенный способ – проекция на плоскость abс изолиниями (изоуровнями), что позволяет проследить изменения коэффициентов на разных масштабах во времени, а также выявить картину локальных экстремумов этих поверхностей («холмов» и «впадин»), так называемый «скелет» (skeleton) структуры анализируемого процесса. При широком диапазоне масштабов применяются логарифмические координаты (loga,b). Пример вейвлетного спектра простейшего сигнала при его разложении вейвлетомMhatприведен на рис. 2.1.2.

Рис. 2.1.2. Сигнал, вейвлетный Mhat — спектр и масштабные сечения спектра.

По вертикальным сечениям (сечениям сдвига b) вейвлет-спектр отражает компонентный состав сигнала (из данного комплекта вейвлетов) в каждый текущий момент. По смыслу преобразования, как скалярного произведения сигнала с вейвлетом, ясно, что значения коэффициентов в каждой текущей временной точке по масштабным сечениям тем больше, чем сильнее корреляция между вейвлетом данного масштаба и поведением сигнала в окрестностях этой точки. Соответственно, сечения по параметру ‘а’ демонстрируют изменения в сигнале компоненты данного масштаба ‘a’ со временем.

Вейвлетные составляющие сигнала в сечениях его спектра не имеют ничего общего с синусоидами, и представлены, как правило, сигналами достаточно сложной и не всегда понятной формы, что может затруднять их наглядное представление и понимание.

Вейвлетные функции. Выбор анализирующего вейвлета определяется тем, какую информацию необходимо извлечь из сигнала. С учетом характерных особенностей различных вейвлетов во временном и в частотном пространстве, можно выявлять в анализируемых сигналах те или иные свойства и особенности, которые незаметны на графиках сигналов, особенно в присутствии шумов. При этом задача реконструкции сигнала может и не ставится, что расширяет семейство используемых регулярных вейвлетных функций, в том числе неортогональных. Более того, вейвлет может конструироваться непосредственно под ту локальную особенность в сигнале, которая подлежит выделению или обнаружению, если ее форма априорно известна.

При анализе сигналов вейвлетами четного типа (симметричными или близкими к симметричным) гармоническим сигналам обычно соответствуют яркие горизонтальные полосы вейвлетных пиков и впадин на доминирующих частотах вейвлетов, совпадающих с частотой гармоник сигналов. Нарушения гладкости сигналов фиксируются вертикальными полосами, пики в сигналах выделяются максимумами, а впадины – минимумами вейвлетных коэффициентов. Напротив, вейвлеты нечетного типа более резко реагируют на скачки и быстрые изменения в сигналах, отмечая их максимумами или минимумами в зависимости от знака дифференциалов. Чем резче выражены особенности сигналов, тем сильнее они выделяются на спектрограммах.

Для конструирования таких вейвлетов часто используются производные функции Гаусса, которые имеют наилучшую локализацию как во временной, так и в частотной областях. В общей форме уравнение базового вейвлета:

_n(x) = (-1)ⁿ⁺¹ dⁿ[exp(-x²/2)]/dxⁿ, n ≥ 1, (2.1.1)

Уравнения базовых вейвлетов для первых четырех производных:

₁(x) = -x exp(-x²/2), ₂(x) = (1-x²) exp(-x²/2),

₃(x) = (3x-x³) exp(-x²/2), ₄(x) = (-4x⁴+6x²-3) exp(-x²/2),

Уравнения нормированных базисов для временных сигналов:

(t, a, b) = (K_n/) _n(x), x=(t-b)/a, K₁=1.062, K₂=0.867, K₃ =0.548, K₄=0.293.

Для сужения базовой формы вейвлетов применяется также упрощенная форма:

_n(x) = (-1)ⁿ⁺¹ dⁿ[exp(-x²)]/dxⁿ, n ≥ 1, (2.1.1′)

WАVE-вейвлет вычисляется по первой производной (n=1) и приведен на рис. 2.1.3 во временной и частотной области для трех значений масштабных коэффициентов ‘а’. Форма вейвлета относится к нечетным функциям и, соответственно, спектр вейвлета является мнимым. Уравнение вейвлета по (2.1.1′) с единичной нормой:

. (2.1.2)

Рис. 2.1.3. Вейвлет Wave.

На рис. 2.1.4 приведен пример применения вейвлета для анализа двух однотипных сигналов, один из которых осложнен шумами с мощностью на уровне мощности самого сигнала. Как следует из рисунка, контурная масштабно-временная картина вейвлетных коэффициентов, а равно и ее сечения на больших значениях масштабных коэффициентов ‘а’ (малых доминирующих частотах вейвлетов) очень точно и уверенно фиксирует положение вершины информационного сигнала сменой знака коэффициентов С(a,b).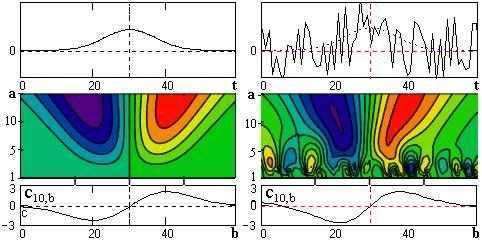

Рис. 2.1.4.

МНАТ-вейвлет(Mexican hat – мексиканская шляпа) вычисляется по второй производной (n=2) и приведен на рис. 2.1.5. Вейвлет симметричен, спектр вейвлета представлен только действительной частью и хорошо локализован по частоте, нулевой и первый моменты вейвлета равны нулю. Применяется для анализа сложных сигналов. Уравнение вейвлета по (2.1.1′):

. (2.1.3)

Рис. 2.1.5. Вейвлет MHAT.

На рис. 2.1.6 приведен пример использования вейвлета для анализа сложного сигнала y(t). Модель сигнала образована суммой сигналов разной структуры. Сигналы у1-у2 представляют собой функции Гаусса разного масштабного уровня, сигнал у3 — прямоугольный импульс, сигнал у4 задан в виде тренда с постоянным значением дифференциала. На контурном графике вейвлет-коэффициентов можно видеть выделение всех трех основных структур сигнала при полном исключении тренда. Особенно четко выделяются границы скачков прямоугольной структуры. Справа на рисунке приведена полная трехмерная картина вейвлет-преобразования.

Рис. 2.1.6.

Вейвлет широко используется в двумерном варианте для анализа изотропных полей. На его основе возможно также построение двумерного неизотропного базиса с хорошей угловой избирательностью при добавлении к сдвигам и масштабированию вейвлета его вращения.

Рис. 2.1.7.

При повышении номера производной функции (2.1.1) временная область определения вейвлета несколько увеличивается при существенном повышении доминирующей частоты вейвлета и степени его локализации в частотной области. Вейвлетыn-го порядка позволяют анализировать более тонкие высокочастотные структуры сигналов, подавляя низкочастотные компоненты. Пример вейвлета по восьмой производной приведен на рис. 2.1.7.

Рис. 2.1.8.

Практическое следствие повышения степени локализации вейвлетов в частотной области наглядно видно на рис. 2.1.8 на примере преобразования той же функции, что и на рис. 2.1.6. Сравнение рисунков показывает существенное повышение чувствительности вейвлета к высокочастотным составляющим сигнала на малых масштабных коэффициентах.

studfiles.net