График онлайн функции заданной неявно: График неявной функции

2*arctgh(x)*arcctgh(x)

Содержание

Исследование графика функции

Для периодических функций идет исследование графика функции только на промежутке периода

Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции

Что умеет находить этот калькулятор:

Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
Умеет определять точки пересечения графика функции с осями координат: Да
Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)

Горизонтальные асимптоты графика функции: Да
Наклонные асимптоты графика функции: Да
Четность и нечетность функции: Да

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x): Абсолютное значение x
(модуль x или |x|)
arccos(x): Функция — арккосинус от x
arccosh(x): Арккосинус гиперболический от x
arcsin(x): Арксинус от x
arcsinh(x): Арксинус гиперболический от x
arctg(x): Функция — арктангенс от x
arctgh(x): Арктангенс гиперболический от x
exp(x): Функция — экспонента от x (что и e^x)
log(x) or ln(x): Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
sin(x): Функция — Синус от x
cos(x): Функция — Косинус от x
sinh(x): Функция — Синус гиперболический от x
cosh(x): Функция — Косинус гиперболический от x
sqrt(x): Функция — квадратный корень из x
sqr(x) или x^2: Функция — Квадрат x
ctg(x): Функция — Котангенс от x
arcctg(x): Функция — Арккотангенс от x
arcctgh(x): Функция — Гиперболический арккотангенс от x
tg(x): Функция — Тангенс от x
tgh(x): Функция — Тангенс гиперболический от x
cbrt(x): Функция — кубический корень из x
gamma(x): Гамма-функция
LambertW(x): Функция Ламберта
x! или factorial(x): Факториал от x

В выражениях можно применять следующие операции:

Действительные числа: вводить в виде 7. 3; — возведение в степень
x + 7: — сложение
x — 6: — вычитание

Другие функции:

asec(x): Функция — арксеканс от x
acsc(x): Функция — арккосеканс от x
sec(x): Функция — секанс от x
csc(x): Функция — косеканс от x
floor(x): Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
ceiling(x): Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
sign(x): Функция — Знак x
erf(x): Функция ошибок (или интеграл вероятности)
laplace(x): Функция Лапласа
asech(x): Функция — гиперболический арксеканс от x
csch(x): Функция — гиперболический косеканс от x
sech(x): Функция — гиперболический секанс от x
acsch(x): Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3.

n или p(x,n)Возведение x в степень nexp(x)Экспоненциальная функция, т.е. возведение e в степень xroot(x,n)Корень n-степени из xsqr(x) или sqrt(x)Квадратный корень из xcbr(x) или cbrt(x)Кубический корень из xlogn(x,a)Логарифм x по основанию aln(x)Натуральный логарифм x, т.е. логарифм x по основанию elb(x)Логарифм x по основанию 2lg(x)Логарифм x по основанию 10sin(x)Синус от xcos(x)Косинус от xtan(x)Тангенс от x

cotan(x)Котангенс от xsec(x)Секанс от xcsc(x)Косеканс от xasin(x)Арксинус от xacos(x)Арккосинус от xatan(x)Арктангенс от xacot(x)Арккотангенс от xasec(x)Арксеканс от xacsc(x)Арккосеканс от xsinh(x)Гиперболический синус от xcosh(x)Гиперболический косинус от xtanh(x)Гиперболический тангенс от x coth(x)Гиперболический котангенс от xsech(x)Гиперболический секанс от xcsch(x)Гиперболический косеканс от xasinh(x)Гиперболический арксинус от xacosh(x)Гиперболический арккосинус от xatanh(x)Гиперболический арктангенс от xacoth(x)Гиперболический арккотангенс от xasech(x)Гиперболический арксеканс от xacsch(x)Гиперболический арккосеканс от xgaussd(x,m,n)Нормальное распределение (распределение Гаусса) со средним значением m и стандартным отклонением n

min(n1,n2)Возвращает наименьшее из двух значенийmax(n1,n2)Возвращает наибольшее из двух значенийround(x)Классическое округление x до целого числаfloor(n1,n2)Округление x вниз до ближайшего целого числаceil(n1,n2)Округление x вверх до ближайшего целого числаabs(x)Модуль xrandСлучайное число от 0 до 1sgn(x)Сигнум x.

Возвращает 1, если x>0
Возвращает 0, если x=0
Возвращает -1, если x<0e

Число Эйлера: 2.7182818284…PhiЗолотое отношение: 1.6180339887…piЧисло Пи: 3.1415926535…

Производная неявной функции онлайн

Неявная функция — это функция, например y(x), заданная в виде уравнения:

F(x,y(x))=0

Как правило, вместо уравнения F(x,y(x))=0 пишут просто F(x,y)=0 подразумевая, что y есть функция от x.

В качестве примера неявного задания функции, можно привести уравнение окружности:

x²+y²=a²,

уравнение декартового листа:

x³+y³=3∙a∙x∙y (a=const≠0),

и т. д. Все эти примеры можно записать в виде уравнения F(x,y)=0: уравнение окружности: F(x,y)=x²+y²−a²=0, уравнение декартового листа: F(x,y)= x³+y³−3∙a∙x∙y =0.

В связи с тем, что для исследования любой функции (в том числе и заданной неявно) необходимо вычислять производную, задача нахождения производной функции заданной неявно возникает довольно часто. Так, как же найти производную неявной функции? Исчерпывающий ответ на этот вопрос вы получите, воспользовавшись нашим онлайн калькулятором.
Для того, чтобы решить вашу задачу, для начала перепишите свою функцию в виде уравнения F(x,y)=0. Как это сделать, подробно описано выше (нужно просто перенести все слагаемые в левую часть уравнения, оставив справа 0).

Далее вам необходимо определиться, как у вас обозначается переменная и как обозначается функция, которая зависит от этой переменной. В приведенных выше примерах, x — переменная, y — функция, зависящая от x.
Затем, вам необходимо ввести свое уравнение F(x,y) в наш онлайн калькулятор и получить решение вашей задачи.

График неявно-заданной функции

uses graph;
const
x1=-7;{начало и конец графика в реальных значениях}
x2=7;
var
mx,my,a,x,dx,y1,y2,y3,y4:real;
x0,y0,grD,px,py,grM,i,k:integer;
s,s1:string;
begin
grD:=detect;
initgraph(grD,grM,'');
X0:=getmaxX div 2;{начало координат в центре экрана}
Y0:=getmaxY div 2;
{коэффициенты по осям для перевода реальных координат в экранные}
mx:=600/(x2-x1);{длина в пикселах по оси Х/реальная длина}
my:=420/(2*1.
  5*sin(1)/cos(1));{длина оси по У/(2*макс}
SetBkColor(7); {цвет фона}
setlinestyle(0,0,1);{сплошная линия}
SetColor(1);{цвет линий осей}
line(0,y0,getmaxX,y0); {ось Х}
line(x0,getmaxy,x0,0); {ось У}
setlinestyle(1,0,0);  {пунктирная линия}
Setcolor(9);  {цвет сетки}
for i:=1 to 7 do   {максимальное количество засечек в одну сторону}
   begin
    line(10,y0-round(i*my),630,y0-round(i*my));{засечки на оси У}
    line(10,y0+round(i*my),630,y0+round(i*my));
    line(x0+round(i*mx),0,x0+round(i*mx),getmaxY); {засечки на оси Х}
    line(x0-round(i*mx),0,x0-round(i*mx),getmaxY);
    str(i,s);
    {подпись оси У}
    outtextXY(x0-10,y0-round(i*my),s);{соответственно засечкам}
    outtextXY(x0-15,y0+round(i*my),'-'+s);
    {подпись оси Х}
    str(i,s);
    outtextXY(x0+round(i*mx),y0+10,s);
    outtextXY(x0-round(i*mx),y0+10,'-'+s);
  end;
{центр}
outtextXY(x0+5,y0+10,'0');
{подписи концов осей}
outtextXY(getmaxX-10,y0-10,'X');
outtextXY(x0-10,10, 'Y');
dx:=0.001;
{график}
x:=x1;
while x<=x2 do
   begin
     px:=x0+round(x*mx); {изменение по оси Х}
     y1:=-sin(cos(x))/cos(cos(x)); {график в реальных координатах}
     py:=y0-round(y1*my);{в экранных}
     putpixel(px,py,4);
     y2:=0.  5*sin(cos(x))/cos(cos(x)); {график в реальных координатах}
     py:=y0-round(y2*my);{в экранных}
     putpixel(px,py,2);
     y3:=sin(cos(x))/cos(cos(x)); {график в реальных координатах}
     py:=y0-round(y3*my);{в экранных}
     putpixel(px,py,9);
     y4:=1.5*sin(cos(x))/cos(cos(x)); {график в реальных координатах}
     py:=y0-round(y4*my);{в экранных}
     putpixel(px,py,14);
     x:=x+dx; {наращиваем х}
   end;
setcolor(10);
setlinestyle(0,0,1);
outtextXY(75,30,'Grafik functii Y=A*tg(cosx)');
setcolor(4);
outtextXY(135,40,'A=-1');
setcolor(2);
outtextXY(135,50,'A=0.5');
setcolor(9);
outtextXY(135,60,'A=1');
setcolor(14);
outtextXY(135,70,'A=1.5');
readln
end.

Найти производную неявной функции онлайн. Производная неявной функции

Очень часто при решении практических задач (например, в высшей геодезии или аналитической фотограмметрии) появляются сложные функции нескольких переменных, т. е. аргументы x, y, z одной функцииf (x,y,z) ) сами являются функциями от новых переменныхU, V, W ).

Так, например, бывает при переходе от неподвижной системы координат Oxyz в подвижную системуO 0 UVW и обратно. При этом важно знать все частные производные по «неподвижным» — «старым» и «подвижным» — «новым» переменным, так как эти частные производные обычно характеризуют положение объекта в этих системах координат, и, в частности, влияют на соответствие аэрофотоснимков реальному объекту. В таких случаях применяются следующие формулы:

То есть задана сложная функцияT трех «новых» переменныхU, V, W посредством трёх «старых» переменныхx, y, z, тогда:

Замечание. Возможны вариации в количестве переменных. Например: если

В частности, еслиz = f(xy), y = y(x) , то получаем так называемую формулу «полной производной»:

Эта же формула «полной производной» в случае:

примет вид:

Возможны и иные вариации формул (1.27) — (1. 32).

Замечание: формула «полной производной» используется в курсе физики, раздел «Гидродинамика» при выводе основополагающей системы уравнений движения жидкости.

Пример 1.10. Дано:

Согласно (1.31):

§7 Частные производные неявно заданной функции нескольких переменных

Как известно, неявно заданная функция одной переменной определяется так: функция у независимой переменной x называется неявной, если она задана уравнением, не разрешенным относительноy :

Пример 1.11.

Уравнение

неявно задаёт две функции:

А уравнение

не задаёт никакой функции.

Теорема 1.2 (существования неявной функции).

Пусть функция z =f(х,у) и ее частные производныеf» x иf» y определены и непрерывны в некоторой окрестностиU M0 точкиM 0 (x 0 y 0 ) . Кроме того,f(x 0 ,y 0 )=0 иf»(x 0 ,y 0 )≠0 , тогда уравнение (1.33) определяет в окрестностиU M0 неявную функциюy= y(x) , непрерывную и дифферен

Онлайн-калькулятор неявной производной

Неявно вызванная функция у (х), задается уравнением:

F (х, у (х)) = 0

Как правило, вместо уравнения F (х, у (х)) = 0 использовать обозначение F (х, у) = 0 предполагая, что y — функция от x.

В качестве примера неявно определенной функции можно указать уравнение круга:

x ² + y ² = a ²,

декартово уравнение фолия:

x ³ + y ³ = 3 ∙ a ∙ x ∙ y (a = const ≠ 0),

и т. д.Все эти примеры имеют уравнение общего вида F (x, y) = 0: уравнение круга: F (x, y) = x ² + y ² −a ² = 0, декартово уравнение фолия: F (х, у) = x ³ + y ³ −3 ∙ a ∙ x ∙ y = 0.

Обычная задача вычисляет производную неявной функции , особенно при функциональном анализе. Возникает вопрос: «Как вычислить производную неявной функции»? Исчерпывающий ответ на этот вопрос дает наш онлайн-калькулятор.
Первое, что вам нужно сделать для решения вашей задачи, — это переписать вашу функцию в виде уравнения F (х, у) = 0. Для этого посмотрите подробное описание выше (вам просто нужно перенести все члены в левую часть уравнения, оставив 0 с правой стороны). Затем вам нужно выбрать переменную дифференцирования и обозначения неявной функции. В приведенных выше примерах Икс — переменная дифференцирования, у — неявная функция, зависящая от Икс.
Затем вам нужно ввести свое уравнение F (х, у) в наш онлайн-калькулятор и нажмите кнопку «Рассчитать».

Графики функций рисования — Плоттер

Математика / Анализ — Плоттер — Калькулятор 4.0

Функции:

Корпус:

Первый график:

f (x) Производный интеграл

+ C: Синий 1Синий 2Синий 3Синий 4Синий 5Синий 6Красный 1Красный 2Красный 3Красный 4Желтый 1Желтый 2Зеленый 1Зеленый 2Зеленый 3Зеленый 3Зеленый 5Зеленый 6ЧерныйСерый 1Серый 2Серый 3Синий 4БелыйОранжевыйБирюзовыйФиолетовый 1Традиционный 2Фиолетовый 3Фиолетовый 3Фиолетовый 4Фиолетовый 2Фиолетовый 1Фиолетовый 1Фиолетовый 7ФиолетовыйЯ 1, я 2, я 3
От до ConnectDottedDashed –Dashed –Заполнить заполнить Показать термин

Второй график:

г (x) Производный интеграл

+ C: Синий 1Синий 2Синий 3Синий 4Синий 5Синий 6Красный 1Красный 2Красный 3Красный 4Желтый 1Желтый 2Зеленый 1Зеленый 2Зеленый 3Зеленый 3GЗеленый 5Зеленый 6ЧерныйСерый 1Серый 2Серый 3Синий 4БелыйОранжевыйБирюзовыйФиолетовый 1Традиционный 2Фиолетовый 3Фиолетовый 3Фиолетовый 4Фиолетовый 1Фиолетовый 2Фиолетовый 3Фиолетовый 4Фиолетовый 1Фиолетовый 5Фиолетовый 1 От до ConnectDottedDashed –Dashed –Заполнить заполнить Показать термин

Третий график:

h (x) Производный интеграл

Свойства отображения:

Тип изображения: pnggifjpeg

Ширина:	Высота:
Диапазон оси x от	до
Диапазон оси y от	до
Интервалы оси x:	Ось Y:
Линии прицельной сетки Ось X:	Ось Y:
Длина штрихов Ось x:	Ось Y:
Десятичные разряды:	Разрыв в начале координат:
Толщина графика:	Круг в начале координат:
Журнал. масштаб x: Нет 2 е 10 100		или
Журнал. масштаб y: Нет 2 е 10 100		или

Квадранты: Размер:

MathGrapher: Графический калькулятор с функцией Grapher — eMathHelp

Бесплатный онлайн-калькулятор для построения 2D-графиков (плоттер) или калькулятор кривых, который может строить кусочно, линейно, квадратично, кубической, четвертой, полиномиальной, тригонометрической, гиперболической, экспоненциальной, логарифмической, обратными функциями, заданными в различных формах: явных, неявных, полярных , и параметрический.Он также может отображать конические сечения, произвольные неравенства или системы неравенств, поля наклона (векторные поля или поля направлений) и визуализировать сумму Римана. Участки можно оформить и настроить в соответствии с потребностями.

Чтобы построить трехмерный график, используйте трехмерный график.

Показать инструкции

В общем случае знак умножения можно пропустить, поэтому «5x» эквивалентно «5 * x». (3x) `.3 (х).
Из приведенной ниже таблицы вы можете заметить, что sech не поддерживается, но вы все равно можете ввести его, используя идентификатор `sech (x) = 1 / cosh (x)`.
Если вы получили сообщение об ошибке, дважды проверьте свое выражение, добавьте круглые скобки и знаки умножения там, где это необходимо, и обратитесь к таблице ниже.
Все предложения и улучшения приветствуются. Пожалуйста, оставьте их в комментариях.

В следующей таблице перечислены поддерживаемые операции и функции:

9 0047 acsc (x)

Тип	Get
Константы
e	e
pi	`pi`
i	i (мнимая единица)
Операции
a + b	a + b
ab	ab
a * b	`a * b`
a ^ b, a ** b	` a ^ b`
sqrt (x), x ^ (1/2)	`sqrt (x)`
cbrt (x), x ^ (1/3)	`root (3 ) (x) `
корень (x, n), x ^ (1 / n)	` root (n) (x) `
x ^ (a / b)	` x ^ (a / b) `
x ^ a ^ b	` x ^ (a ^ b) `
abs (x)	` \| x \| `
Функции
e ^ x	`e ^ x`
ln (x), журнал (x)	ln (x)
ln (x) / ln (a)	`log_a (x)`
Тригонометрические функции
sin (x)	sin (x)
cos (x)	cos (x)
tan (x)	tan (x), tg (x)
кроватка (x)	кроватка (x), ctg ( x)
сек (x)	сек (x)
csc (x)	csc (x), cosec (x)
Обратные тригонометрические функции
asin (x) , arcsin (x), sin ^ -1 (x)	asin (x)
acos (x), arccos (x), cos ^ -1 (x)	acos (x)
atan (x), arctan (x), tan ^ -1 (x)	atan (x)
acot (x), arccot (x), cot ^ -1 (x)	acot (x)
asec (x), arcsec (x), sec ^ -1 (x)	asec (x)
acsc (x), arccsc (x), csc ^ -1 (x)
Гиперболические функции
sinh (x)	sinh (x)
cosh (x)	cosh (x)
tanh (x)	tanh (x)
coth (x)	coth (x)
1 / cosh (x)	sech (x)
1 / sinh (x)	csch (x)
Обратные гиперболические функции
asinh (x), arcsinh (x), sinh ^ -1 (x)	asinh (x)
acosh (x), arccosh (x), cosh ^ — 1 (x)	acosh (x)
atanh (x), arctanh (x), tanh ^ -1 (x)	atanh (x)
acoth (x), arccoth (x) , кроватка ^ -1 (x)	acoth (x)
acosh (1 / x)	asech (x)
asinh (1 / x)	acsch (x)

Чтобы нарисовать параболу, круг, эллипс или гиперболу, выберите вариант «Неявный».

Вы можете передать функцию в качестве параметра: https://www.emathhelp.net/calculators/calculus-1/online-graphing-calculator/?y=sin(x)&y=cos(x) будет рисовать y = sin (x) и y = cos (x).

Варианты участка Касательная / нормальная линия

Явный: y = f (x) Явный: x = f (y) Полярный: r = r (t) ParametricImplicitInequalitiesPointsSlope FieldRiemann SumAdd

Панорамируйте график (перемещайте его), удерживая клавишу Shift и перетаскивая график мышью.

Увеличивайте и уменьшайте масштаб графика, удерживая клавишу Shift и используя колесо мыши.

Указанные выше операции могут быть очень медленными для более чем двух графиков. Чтобы этого избежать, удалите все графики, выполните панорамирование и масштабирование, а затем снова постройте графики.

Прямая ссылка на этот участок:

Как определить функцию из графика

Эффективным инструментом, который определяет функцию на графике, является «Тест вертикальной линии»

Следующие этапы теста вертикальной линии:

Шаг 1:

Нарисуйте вертикальную линию в любом месте данного графика. .

Шаг 2:

Мы должны проверить, пересекает ли вертикальная линия, проведенная на графике, график не более чем в одной точке.

Шаг 3:

Если вертикальная линия пересекает график не более чем в одной точке, то данный график представляет функцию.

Если вертикальная линия пересекает график более чем в одной точке, то данный график не представляет функцию.

Внимание:

Для некоторых графиков вертикальная линия пересекает график в одной точке в одном положении и более чем в одной точке в другом положении.

В приведенной выше ситуации график не будет отображать функцию.

Основная концепция:

График представляет функцию только в том случае, если каждая вертикальная линия пересекает график не более чем в одной точке.

Мы можем лучше понять тест вертикальной линии для функций с помощью следующих примеров.

Пример 1:

Используйте тест вертикальной линии, чтобы определить, представляет ли следующий график функцию.

Решение:

Шаг 1:

Проведите вертикальную линию в любом месте данного графика.

Шаг 2:

Шаг 3:

На приведенном выше графике вертикальная линия пересекает график не более чем в одной точке, затем данный график представляет функцию.

Пример 2:

Используйте тест вертикальной линии, чтобы определить, представляет ли следующий график функцию.

Решение:

Шаг 1:

Проведите вертикальную линию в любом месте данного графика.

Шаг 2:

Шаг 3:

На приведенном выше графике вертикальная линия пересекает график более чем в одной точке (трех точках), тогда данный график не представляет функцию.

Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть отзывы о наших математических материалах, напишите нам:

v4formath @ gmail.com

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Алгебраные задачи со словами

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямой и обратной вариациям

Проблемы со словами по цене за единицу

Word задачи по сравнению ставок

Преобразование обычных единиц в текстовые задачи

Преобразование метрических единиц в текстовые задачи

Word задачи по простому проценту

Word по сложным процентам

Word по типам ngles

Проблемы с дополнительными и дополнительными углами в словах

Проблемы со словами с двойными фактами

Проблемы со словами тригонометрии

Проблемы со словами в процентах

Проблемы со словами о прибылях и убытках

Разметка и разметка Задачи

Задачи с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы со словами о линейных неравенствах

Соотношение и пропорции Задачи со словами

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Проблемы со словами на возрастах

Проблемы со словами по теореме Пифагора

Процент числового слова pr проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами на сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибылей и убытков

Сокращение в процентах

Сокращение в таблице времен

Сокращение времени, скорости и расстояния

Сокращение соотношения и пропорции

Домен и диапазон рациональных функций

Область и диапазон рациональных функций функции с отверстиями

Графики рациональных функций

Графики рациональных функций с отверстиями

Преобразование повторяющихся десятичных дробей в дроби

Десятичное представление рациональных чисел

Поиск квадратного корня с помощью long di видение

L. Метод CM для решения временных и рабочих задач

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 степени 256 на 17

Остаток при делении 17 степени 23 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

Использование преобразований в графические функции

Вертикальный и горизонтальный перевод

Когда график функции изменяется по внешнему виду и / или местоположению, мы называем это преобразованием. 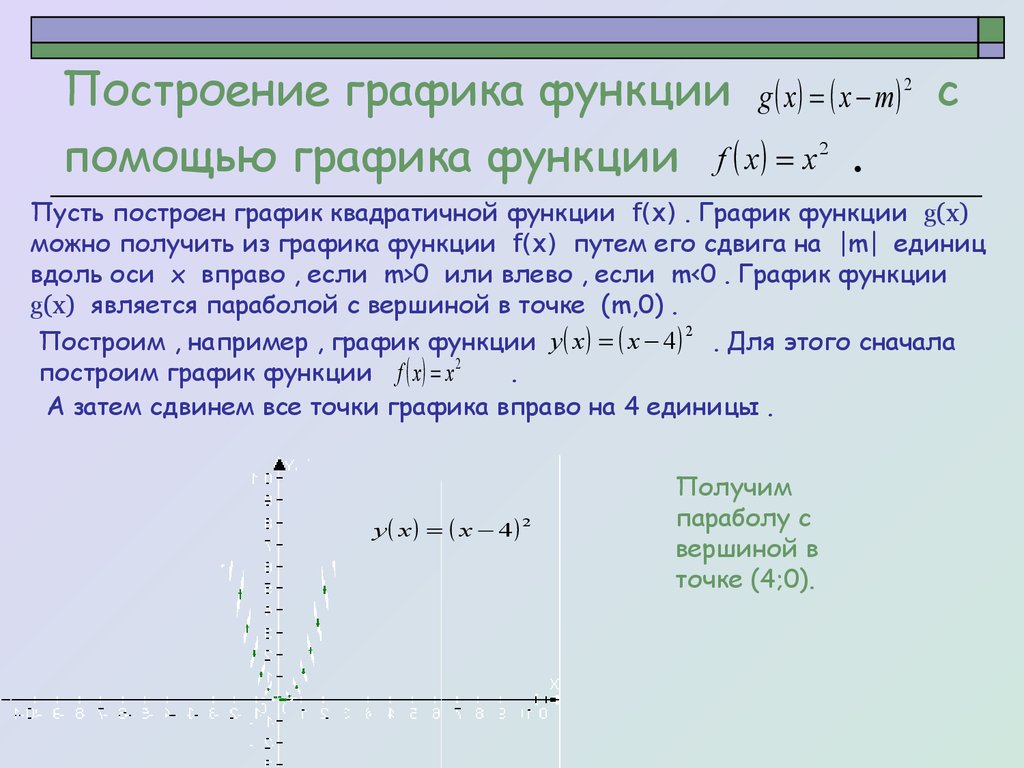Есть два типа преобразований. Жесткое преобразование — набор операций, которые изменяют положение графика в координатной плоскости, но оставляют неизменными размер и форму. изменяет расположение функции в координатной плоскости, но оставляет размер и форму графика неизменными. Нежесткое преобразование — набор операций, которые изменяют размер и / или форму графа в координатной плоскости. изменяет размер и / или форму графика.

Вертикальный сдвиг — жесткое преобразование, которое сдвигает график вверх или вниз.- жесткое преобразование, сдвигающее граф вверх или вниз относительно исходного графа. Это происходит, когда к какой-либо функции добавляется константа. Если мы добавим положительную константу к каждой координате y , график сдвинется вверх. Если мы добавим отрицательную константу, график сместится вниз. Например, рассмотрим функции g (x) = x2−3 и h (x) = x2 + 3. Начните с оценки некоторых значений независимой переменной x .

Теперь постройте точки и сравните графики функций g и h с основным графиком f (x) = x2, который показан ниже с помощью пунктирной серой кривой.

Функция g сдвигает основной график на 3 единицы вниз, а функция h сдвигает основной график на 3 единицы вверх. В общем, это описывает вертикальные переводы; если k — любое положительное вещественное число:

Вертикальный сдвиг вверх k единиц:	F (x) = f (x) + k
Вертикальное смещение вниз k единиц:	F (x) = f (x) −k

Пример 1

Нарисуйте график функции g (x) = x + 4.

Решение:

Начните с базовой функции, определенной как f (x) = x, и сдвиньте график на 4 единицы вверх.

Ответ:

Горизонтальный сдвиг — жесткое преобразование, смещающее график влево или вправо. — жесткое преобразование, которое сдвигает граф влево или вправо относительно исходного графа. Это происходит, когда мы добавляем или вычитаем константы из координаты x перед применением функции.Например, рассмотрим функции, определенные как g (x) = (x + 3) 2 и h (x) = (x − 3) 2, и создадим следующие таблицы:

Здесь мы складываем и вычитаем координаты x , а затем возводим результат в квадрат. Это дает горизонтальный перевод.

Обратите внимание, что это противоположное тому, что вы могли ожидать. В общем, это описывает горизонтальные переводы; если h — любое положительное вещественное число:

Горизонтальный сдвиг влево ч единиц:	F (x) = f (x + h)
Горизонтальный сдвиг вправо ч единиц:	F (x) = f (x − h)

Пример 2

Нарисуйте график функции g (x) = (x − 4) 3.

Решение:

Начните с базовой функции кубирования, определяемой как f (x) = x3, и сдвиньте график на 4 единицы вправо.

Ответ:

Часто встречаются комбинации переводов.

Пример 3

Нарисуйте график функции g (x) = | x + 3 | −5.

Решение:

Начните с функции абсолютного значения и примените следующие преобразования.

y = | x | Базовая функция y = | x + 3 | Горизонтальный сдвиг влево на 3 единицы y = | x + 3 | −5 Вертикальный сдвиг вниз на 5 единиц

Ответ:

Порядок, в котором мы применяем горизонтальный и вертикальный переводы, не влияет на окончательный график.

Пример 4

Нарисуйте график функции g (x) = 1x − 5 + 3.

Решение:

Начните с обратной функции и определите переводы.

y = 1x Основная функция y = 1x − 5 Горизонтальный сдвиг вправо 5 единиц y = 1x − 5 + 3 Вертикальный сдвиг вверх на 3 единицы

Позаботьтесь о том, чтобы сместить вертикальную асимптоту с оси y на 5 единиц вправо и сместить горизонтальную асимптоту с оси x вверх на 3 единицы.

Ответ:

Создайте график онлайн и найдите кратчайший путь или используйте другой алгоритм.

Создайте график и найдите кратчайший путь.На странице справки вы найдете обучающее видео.

Установить матрицу смежности. Используйте запятую «,» в качестве разделителя

Матрица мультиграфа содержит вес минимальных ребер между вершинами.

Матрица неверна. Используйте запятую «,» в качестве разделителя. Матрица должна быть квадратной

Установите матрицу инцидентности. Используйте запятую «,» в качестве разделителя.

Матрица неверна. Используйте запятую «,» в качестве разделителя.

Ваш алгоритм отправлен на проверку и в случае успеха будет добавлен на сайт.

Невозможно создать график. Матрица смежности имеет неправильный формат. Нажмите кнопку «исправить матрицу», чтобы исправить матрицу, или кнопку «справка», чтобы открыть справку о формате матрицы смежности

Невозможно создать график. Матрица заболеваемости имеет неправильный формат. Нажмите кнопку «исправить матрицу», чтобы исправить матрицу, или кнопку «справка», чтобы открыть справку о формате матрицы заболеваемости

Выделяйте и перемещайте объекты мышью или перемещайте рабочее пространство.

Перетащите курсор для перемещения объектов

Выделяйте и перемещайте объекты мышью или перемещайте рабочее пространство.

Перетащите курсор для перемещения объектов

Щелкните в рабочей области, чтобы добавить новую вершину. Перечисление вершин

Выбрать первую вершину ребра

Выбрать вторую вершину ребра

Выбрать начальную вершину кратчайшего пути

Выбрать конечную вершину кратчайшего пути

Наименьшая длина пути% d

Путь не существует

Нажмите на объект, чтобы удалить

Добавить край

Направленный

Неориентированный

Матрица смежности

Сохранить

Отмена

наименьшее расстояние

Матрица заболеваемости

График сохранения

закрыть

Количество подключаемых компонентов

Количество слабосвязных компонент

Что вы думаете о сайте?

Имя (адрес электронной почты для обратной связи)

Обратная связь

Отправить

Чтобы задать нам вопрос или отправить комментарий, напишите нам по телефону

исправить матрицу

справка

Матрица имеет неправильный формат

Сохранить изображение графика

Полный отчет

Краткое сообщение

График не имеет эйлерова цикла

График имеет эйлеров цикл

Обработка. ..

Добавить вершину

Переименовать вершину

Переименовать

Изменить вес

не имеет веса

Переименовать группу

Голосовать

Рекомендовать алгоритмы

График не имеет эйлерова пути

График имеет эйлеров путь

График минимальных расстояний

Отметьте, чтобы сэкономить

Показать матрицу расстояний

Матрица расстояний

Выберите источник максимального расхода

Выбрать мойку максимального расхода

Максимальный расход от% 2 до% 3 равен% 1

Поток из% 1 в% 2 не существует

Источник

Мойка

Граф не имеет гамильтонова цикла

Граф имеет гамильтонов цикл

График не имеет гамильтонова траектория

График имеет гамильтонов путь

Выбрать начальную вершину обхода

Порядок обхода:

Отвод края

Отменить

Сохранить график

По умолчанию

Vertex Style

Edge Style

Цвет фона

Multigraph поддерживает не все алгоритмы

не имеет веса

Используйте Cmd⌘ для выбора нескольких объектов.

Используйте Ctrl для выбора нескольких объектов.

Перетащите группу.

Группа копий

Удалить группу

Поиск в ширину

Раскраска графика

Найти подключенные компоненты

Поиск в глубину

Найдите цикл Эйлера

Найдите эйлеров путь

Алгоритм Флойда – Уоршалла

Упорядочить график

Найти гамильтонов цикл

Найти гамильтонов путь

Найти максимальный расход

Поиск минимального остовного дерева

Визуализация по весу

Радиус и диаметр поисковой диаграммы

Найдите кратчайший путь с помощью алгоритма Дейкстры

Вычислить степень вершин

Масса минимального остовного дерева

Во время расчета мы игнорировали направление ребер.

График отключен

График онлайн функции заданной неявно: График неявной функции · онлайн

Исследование графика функции

Правила ввода выражений и функций

Производная неявной функции онлайн

График неявно-заданной функции

Найти производную неявной функции онлайн. Производная неявной функции

§7 Частные производные неявно заданной функции нескольких переменных

Онлайн-калькулятор неявной производной

Графики функций рисования — Плоттер

Функции:

Свойства отображения:

MathGrapher: Графический калькулятор с функцией Grapher — eMathHelp

Как определить функцию из графика

Использование преобразований в графические функции

Вертикальный и горизонтальный перевод

Пример 1

Пример 2

Пример 3

Пример 4

Создайте график онлайн и найдите кратчайший путь или используйте другой алгоритм.

Добавить комментарий Отменить ответ