| | Брянск 2011
Составители: Баранова И.М., зав. кафедрой математики, Алексеева Г.Д., доцент кафедры математики, Часова Н.А., доцент кафедры математики, Муравьев А.Н., доцент кафедры математики
Рецензент: Евтюхов К.Н. – к., ф.- м.н., профессор кафедры физики
Рассмотрены УМК МТФ Протокол № от
ВВЕДЕНИЕ
Многим явлениям, в том числе экономическим, присуща многофакторная зависимость. Исследование таких зависимостей потребовало совершенствования математического аппарата, в частности, введения понятия функции нескольких переменных. В настоящих методических указаниях рассматриваются вопросы: — основные понятия; — частные производные; — дифференциал функции; — применение дифференциала к приближенным вычислениям; — производная по направлению, градиент; — экстремум функции нескольких переменных; — наибольшее и наименьшее значения функции; — условный экстремум, метод множителей Лагранжа; — понятие об эмпирических формулах, метод наименьших квадратов. Сведения из теории изложены лишь конспективно. Опущены строгие доказательства, однако практические вопросы рассмотрены довольно подробно, что необходимо для выполнения расчетно-графической работы. 1. Функции нескольких переменных, основные понятия
1) Если каждой точке М из некоторого множества точек евклидова пространства ставится в соответствие по известному закону некоторое число , то говорят, что на множестве задана функция или . Если множество принадлежит или евклидовой прямой, или евклидовой плоскости, говорят о функциях одной, двух, трех, …, n переменных. Пример 1.1 Площадь прямоугольника со сторонами, длины которых равны и , выражается формулой . Пример 1.2. Объем прямоугольного параллелепипеда с ребрами, длины которых равны выражается формулой . Пример 1.3. Величина силы притяжения двух материальных точек, имеющих массы и занимающих соответственно положение и , согласно закону Ньютона равна , где . Следовательно, есть функция от шести переменных 2) Всякая функция от нескольких переменных становится функцией от меньшего числа переменных, если часть переменных зафиксировать, т.е. придать постоянные значения. Если положить то мы получим функцию от двух переменных , если зафиксировать переменную то получим функцию одной переменной . Таким образом, в разных вопросах по желанию, функцию можно рассматривать как функцию одной, двух или трех переменных. 3) Геометрическим изображением (графиком) функции двух переменных является, вообще говоря, поверхность в пространстве . Линией уровня функции называется множество всех точек плоскости , для которых данная функция имеет одно и то же значение (изокривая). Ее уравнение где – некоторая постоянная. Поверхностью уровня функции определяется уравнением где . Пример 1.4. Соединив на карте поверхности Земли точки с одинаковой средней суточной температурой или давлением, получим соответственно изотермы и изобары, являющиеся важными исходными данными для прогноза погоды. 4) Пусть задана функция двух переменных . Если зафиксировать переменную и дать переменной приращение , то разность называется частным приращением функции по переменной . Аналогично, зафиксировав переменную и дав приращение переменной , получим частное приращение функции по : . Придавая приращение сразу двум переменным и , можно получить полное приращение функции . Пример 1.5. Найти полное приращение функции , где изменяется от 2 до 2,2 и от 1 до 0,9; ; ; , ; . 5) Частной производной функции от нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при условии, что последнее стремится к нулю. Таким образом, по определению, для функций двух переменных ; . Пример 1.6. Пусть , тогда ; . 6) Функция называется дифференцируемой в данной точке если ее полное приращение в этой точке может быть представлено в виде где А, В – некоторые не зависящие от и числа, а и – бесконечно малые при . Полным дифференциалом функции называется главная линейная часть полного приращения этой функции . Если функция дифференцируема в точке , то и . Тогда , или Пример 1.7. Найти дифференциал функции . , , . 7) Частными производные второго порядка для функции называются: . Продолжая таким путем дальше, можно определить частные производные третьего порядка, четвертого, …. Справедливо следующее утверждение: если все входящие в вычисления частные производные непрерывны, то смешанные частные производные не зависят от последовательности дифференцирования, т.е. в случае непрерывности, например . Пример 1.8. Пусть , тогда: ; ; ; ; . Градиент, дивергенция, ротор Если каждой точке М пространства или некоторой его области V поставлена в соответствие скалярная величина u(М), то говорят, что в этой области задано скалярное поле. Вектор grad u Если каждой точке М некоторой области V поставлен в соответствие определенный вектор , то говорят, что в этой области задано векторное поле. В декартовой системе координат задание векторного поля равносильно заданию трех скалярных функций: P(x,y,z), Q(x,y,z) и R(x,y,z) – проекций этого вектора на оси координат. а функции P(x,y,z), Q(x,y,z) и R(x,y,z) являются непрерывно дифференцируемыми в области V. В качестве примера векторного поля можно рассмотреть поле скоростей стационарного потока жидкости. Дивергенцией векторного поля называется скаляр Ротором (вихрем) векторного поля называется вектор Все рассмотренные величины полей: grad u, div и rot вычисляются с помощью частного дифференцирования скалярного поля u и компонентов P, Q, R векторного поля . Таким образом, мы имеем дело с дифференциальными операциями первого порядка. Наряду с ними можно рассмотреть дифференциальные операции второго порядка: grad div , rot rot и div grad u. Рассмотрим последнюю операцию: Эту операцию можно записать кратко, вводя оператор Лапласа Для векторного поля
| |
градиент, дивергенция и ротор информационного поля
Некоторые вещи очень легко найти. Настолько легко, что нужно прикладывать усилия, чтобы их не найти. Реклама, новости, etc.
Настолько легко, что нужно прикладывать усилия, чтобы их не найти. Реклама, новости, etc.
Есть информация, которая существенно более актуальна (чем политические трения и дебаты) и которая так же очень легко обнаруживаема. События в жизни близких, коллег, новости по работе и т.д.
(важная замечание)
Во всём последующем я буду употреблять слово «находится» не в контексте поиска, а в контексте обнаружения факта существования. Например, довольно легко обнаружить кулинарию и рецепты, но сложно, например, существование W-техники при покраске стен. Так что я говорю именно про процесс autodiscovery, а не про процесс осмысленного поиска.
(продолжаю)
Как только мы выходим за круг вещей, которые о себе объявляют сами, довольно легко оказывается, что некоторые вещи являются мейнстримом и довольно легко найти, а есть огромные куски культуры, которые весьма скрытны, и при том, что информация про них свободно доступна, вероятность (плотность вероятности) узнать про её существование без специальных усилий довольно низкая.
При том, что мы можем говорить про понятие «discoverability», мне кажется, что его скалярность будет упрощением. Правильно будет говорить про подобие векторного поля (в физическом смысле слова — как в электомагнитном или гравитационном поле). Даже не поля, а полей.
Когда мы работаем с информацией, то помимо текущей работы с текущими фактами, мы получаем «указания» на другую информацию. Эти указания могут быть очень прямыми и сильными (подробнее о partial equivalence можно прочитать по ссылке), или крайне ленивыми (например, упоминание «ленивый» в этом контексте было не про бытовую лень, а про lazy в контексте регулярных выражений) или даже крайне завуалированными (удачи найти его в этом предложении).
Фактически, каждый мем (в оригинальном смысле слова «мем» — кусок культурной информации) имеет какое-то своё поле, допустим, векторное (скалярное оно, векторное или даже тензорное — это уже вопрос интерпретации). Эти поля взаимно накладываются. В общем случае для данного мема можно попытаться построить значения векторов для всех других мемов, которые с ним связаны.
При движении по определённой траектории мы получаем усиление значения вектора по мере приближения к источнику мема, и это можно считать примерным описанием процесса поиска информации — мы методом градиентного спуска пытаемся максимизировать модуль этого вектора. (Процесс поиска осложняется дискретно-аналоговой природой поиска — дискретными являются поисковые запросы, аналоговым является чтение большого текста).
В принципе, любой текст можно классифицировать как кусочек пространства, в разных местах которого (разных предложениях?) значения полей мемом различны.
Аналогия с полями мне ещё очень нравится тем, что в общем случае поле определено всюду и там может быть множество точек атракции (что похоже на распределение информации в окружающем мире), более того, нет единой Истины к которой приближаешься, потому что мем — и есть своё поле, где-то выраженный сильно, где-то слабо. Вполне могут быть такие интересные мемы, которые нигде не выражены ярко, но зато определённые почти всюду. Или даже всюду. Например, в любом тексте будет присутствовать мем письменной речи, и будет присутствовать мем своего языка, а так же (с разной степенью выраженности) мемы стиля, жанра и т.д.
Или даже всюду. Например, в любом тексте будет присутствовать мем письменной речи, и будет присутствовать мем своего языка, а так же (с разной степенью выраженности) мемы стиля, жанра и т.д.
Эта модель с лёгкостью позволяет описать что такое сарказм — сарказм это ещё один мем, который может нетривиальным в некоторых частях текста. То же касается любого рода скрытых смыслов и аллюзий, так же как и первичного смысла предложения.
В этой модели можно описать типы мемов:
* равномерно заданные на всём пространстве (письменная речь)
* равномерно заданные на подмножестве (язык)
* имеющие единственный пик («соленоид» довольно однозначное понятие)
* имеющий множество экстремумов («счастье»)
* имеющий несколько выраженных экстремумов (понятие «поле»)
Соотвественно, можно говорить про выраженность окрестности пиков — некоторые явления имеют узкие пики («Carcinoembryonic antigen»), некоторые — крайне обширные («соль»).
Сама величина поля в точке — это вектор (тензор?), который описывает взаимодействие с другими существующими мемами.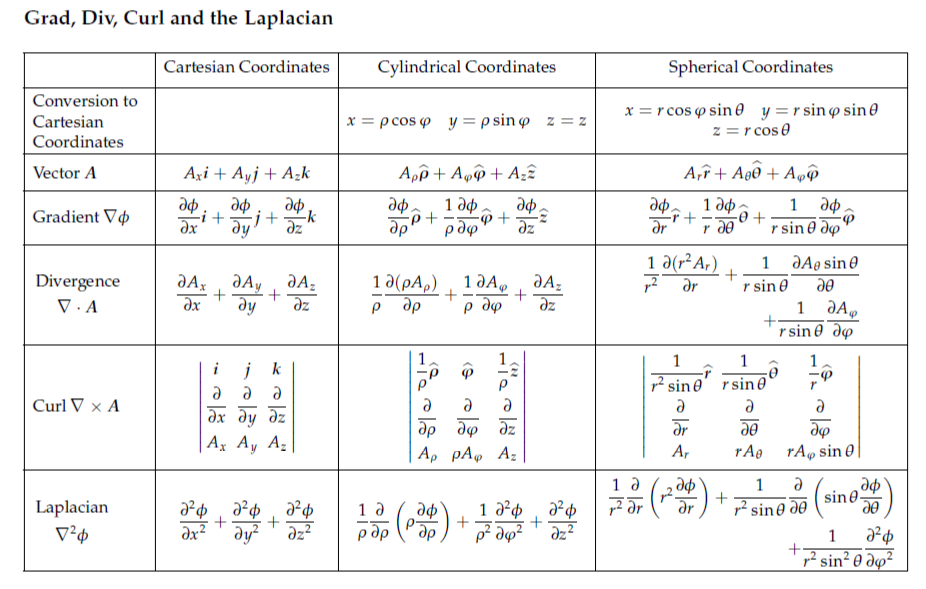
Например, если мы читаем статью по физике, то «градиент» однозначно указывает на «поле».
Если же мы читаем статью про веб-дизайн, то «градиент» так же однозначно указывает на плавный переход от одного цвета к другому.
Очевидно, что предварительные знания и ожидания читателя так же влияют на интерпретацию, поскольку неподготовленный читатель полностью пропустит любые взаимодействия сетоидов с классами эквивалентности, поскольку и то и другое для него будет отфильтровано. Хотя даже неподготовленный читатель сумеет заметить явное ненулевое значение в районе «сетоид» — «можно погуглить».
В контексте субъективности читателя возникает вопрос: а есть ли вот эта, «объективная» составляющая информационной связи?
Я попробую заявить что «да», в том смысле, что после анализа корпуса текстов мы можем установить эту свять механическим путём (забудьте про нейронные сети, просто цепочки Маркова для отдельных слов уже дадут хоть что-то).
Однако, субъективность читателя исключать нельзя, поскольку в момент чтения «объективной» составляющей нет.
На этом может строиться концепция «скрытого смысла» для группы людей — не смотря на то, что объективно связь никак не выделяется, субъективно связь очевидно выступает (и наличие этой выделяющейся связи в каком-то смысле группу и определяет).
В рамках задачи анализа текстов можно говорить, что объективная составляющая — это объединение всего множества субъективных составляющих (этакое интегрирование по популяции, причём как по живым, так и по мёртвым). «Анализ связей по текстам» берёт из этого множества только выраженное в письменном виде, хотя оно может быть расширено и на устную речь без коренных изменений.
Остаётся понять что выражает компонента вектора (которая скаляр). Степень связности? Близость? В силу того, что отношения между мемами могут быть различными по природе, получается, что используя скаляр в этом месте мы теряем эти разнообразия. Получается, что не скаляр. Я бы мог придумать тензор, но мне кажется, что тут возникает куда более соблазнительная идея: отношение двух мемов описывается вектором других мемов. Такой выверт позволяет решить проблему включения онтологических терминов в систему онтологии. Мы описываем два термина с помощью третьего (четвёртого и т.д.) термина.
Такой выверт позволяет решить проблему включения онтологических терминов в систему онтологии. Мы описываем два термина с помощью третьего (четвёртого и т.д.) термина.
Получается, что в заданной точке заданного поля мы имеем список отношений этого поля (мема) с всеми другими мемами, описываемых как (потенциально бесконечные) векторы из других мемов.
Я часто переключаюсь между «мем» и «слово», потому что для слов легче показывать конкретные примеры, но схема так же применима для мемов несловестного характера, например, языка, наличия сарказма и т.д.
Рассмотрим пример:
«фестиваль черешни на Кипре» и «съездить»: {«уныло», «деревеские пенсионеры», «далеко», «того не стоит», «были»}
Можно ли говорить про то, что это вектор значений для всех остальных мемов? Увы, нет, потому что числа являются всего лишь подмножеством мемов. Например, «фестиваль черешни на Кипре», «съездить» имеют нетривиальное (ненулевое) значение в районе «были», но само значение описывается в свою очередь мемом «два года назад».
Получается, что мы не можем свести схему до чисел, и элемент вектора — такой же вектор.
Попробуем задать формальное описание:
Для каждого элемента множества мемов M, существует поле, описывающе отношение R мема в каждой точке поля с всеми другими мемами M посредством вектора из R.
Остаётся понять, что такое «каждая точка» — и что такое пространственные измерения. Если мы будем считать текст набором мемов из того же множества, то определение становится проще:
Для каждого элемента m можества мемов M существует отношение с всеми другими элементами M, такое, что m1Rm2 представляет собой список отношений R с другими элементами. Заметим, что числовые или сравнительные прилагательные (много, мало, «три» и т.д.) являются частью этого списка.
Теперь вопрос: а кто-то исследовал свойства рекурсивно заданных отношений на множестве?
точных последовательностей | расхождение, градиент, завиток
Пару дней назад, ближе к концу поста, я упомянул точные последовательности. Этот термин означает не то, что вы могли бы разумно подумать. Это не значит точно в том смысле, что не является приблизительным.
Этот термин означает не то, что вы могли бы разумно подумать. Это не значит точно в том смысле, что не является приблизительным.
Это означает, что то, что получается на одном шаге, точно такое же, что и на следующем шаге. То есть образ каждой функции является в точности ядром следующей функции в последовательности [1].
Градиент и завиток
Например, пусть f — градиент, а g — завиток. Тогда следующая последовательность является точной
, если A — набор гладких функций от ℝ³ до ℝ, а B и C — набор гладких функций от ℝ³ до ℝ³.
Это говорит о том, что образ f векторных полей, являющихся градиентом чего-то, является ядром g векторных полей с нулевым завихрением. Другими словами, градиентные векторные поля являются безвихревыми, а все безвихревые векторные поля являются градиентом некоторой потенциальной функции.
, чтобы показать, что
Изображение F = ядра G
Мы должны показать две вещи:
Изображение F ⊂ Ядра G
и
Изображение F ⊃ Kernel G. и Изображение F ⊃ Kernel G.1110 и . Как это часто бывает, первое проще второго. Распространенной домашней задачей [2] является показать, что ротор дивергенции равен нулю, т. е. ∇×(∇φ) = 0 0009 F 
Короткие точные последовательности
Короткая точная последовательность — это точная последовательность следующего вида. (Это называется коротким, потому что точные последовательности часто длиннее.)
На стрелке от 0 до нет метки A , потому что есть только одна функция от 0 до любого места. Также нет метки на стрелке от C до 0, потому что есть только одна функция, которая идет из любой точки в 0 [3].
Нуль слева означает, что функция f является однозначной (инъективной). Его изображение — это только один элемент, поэтому ядро f — это только один элемент.
Точно так же ноль справа означает, что функция г на (сюръективное). Ядром последней стрелки является все в C , поэтому образ g должен быть всем в C .
Например, пусть B — группа, а φ — гомоморфизм B в другую группу. Пусть A будет ядром φ и пусть f будет отображением включения из ядра в B . Пусть г будет частным отображением, принимающим C = B / А . Тогда так называемая «теорема о первом групповом гомоморфизме» утверждает, что приведенная выше последовательность точна.
Div, grad, curl и все такое.
Выше мы сказали, что ротор градиента равен нулю и что все векторные поля с нулевым ротором являются градиентами. Верно также и то, что дивергенция завитка равна нулю, и что векторное поле имеет нулевую дивергенцию, если оно представляет собой завиток чего-либо. То есть для векторного поля F ,
То есть для векторного поля F ,
∇ · (∇ × F ) = 0
и если ∇ · G = 0 для векторного поля G , то существует векторное поле × F 3 такое, что Ф = Г .
Это означает, что мы можем расширить наш пример до
, если тщательно определим A .
Обсуждение в этом разделе оправдывает только обозначенные стрелки. Нам нужно выровнять две немаркированные стрелки на концах.
Нуль слева требует, чтобы градиент был один к одному. Но в целом градиент равен , а не один к одному: функции, отличающиеся на константу, имеют одинаковый градиент. Но если мы определим A как набор i интегрируемых функций на ℝ³, тогда градиент будет взаимно однозначным. Требование существования интеграла функции по ℝ³ означает, что функции должны в конечном итоге приближаться к нулю во всех направлениях.
Нуль справа требует, чтобы каждая гладкая функция на ℝ³ была дивергенцией чего-либо. Это легко. Дана функция φ от ℝ³ до ℝ, пусть F — векторное поле, первый компонент которого в точке ( x , y , z) является интегралом от φ от начала координат до ( x , 0, 0), а второй и третий компоненты равны 0. Тогда расхождение F равно φ.
Это легко. Дана функция φ от ℝ³ до ℝ, пусть F — векторное поле, первый компонент которого в точке ( x , y , z) является интегралом от φ от начала координат до ( x , 0, 0), а второй и третий компоненты равны 0. Тогда расхождение F равно φ.
Длинные точные последовательности
Точная последовательность в предыдущем разделе длиннее короткой точной последовательности, и на практике встречаются более длинные точные последовательности. Точная последовательность может быть бесконечной в одном или обоих направлениях. Например, последовательность Майера-Виеториса, основополагающий инструмент гомологии, бесконечна слева и оканчивается 0 на правом конце.
Похожие сообщения
- Поиск диаграмм: четыре, пять и девять лемм
- Следующие области математики, которые необходимо применить
- Как связаны области математики
[1] Термин «ноль» здесь перегружен. Это может быть целое число 0, начало векторного пространства, ядро группы и т.
Здесь все обобщается на объекты и морфизмы в категории, и в этом случае объекты не обязательно являются множествами, а не обязательно являются функциями. Тогда мы говорим не об образах и ядрах, а о морфизмах, являющихся мономорфизмами и эпиморфизмами.
[2] В учебниках много предзнаменований. Обычно автор включает упражнения и примеры, которые важны позже. Часто это делается намеренно, своего рода пасхальное яйцо. Но иногда автор неосознанно тянет из опыта.
[3] Это наблюдение превращается в определение в теории категорий: нулевой объект определяется как начальный и конечный. То есть существует только один морфизм от него к любому другому объекту и только один морфизм от любого объекта к нему.
Примеры Wolfram|Alpha: векторный анализ
Примеры Wolfram|Alpha: векторный анализОго! Wolfram|Alpha не работает без JavaScript.
Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь.

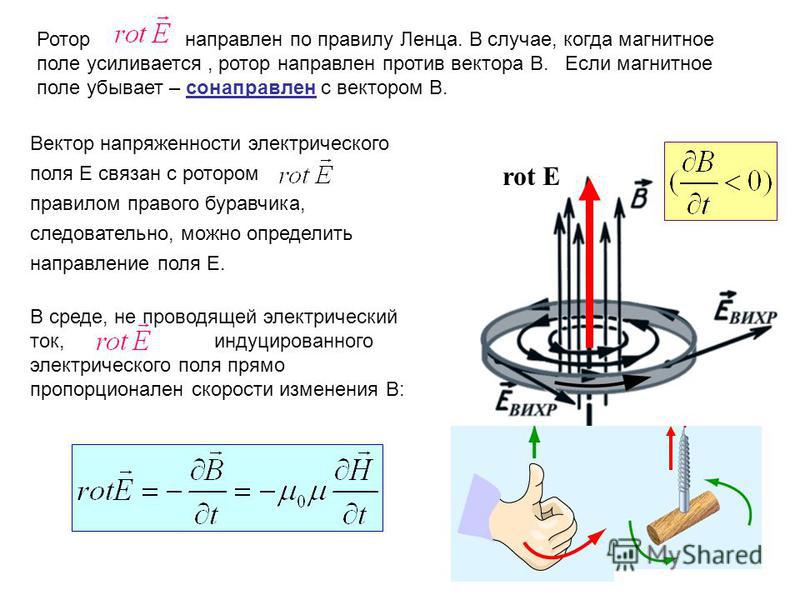

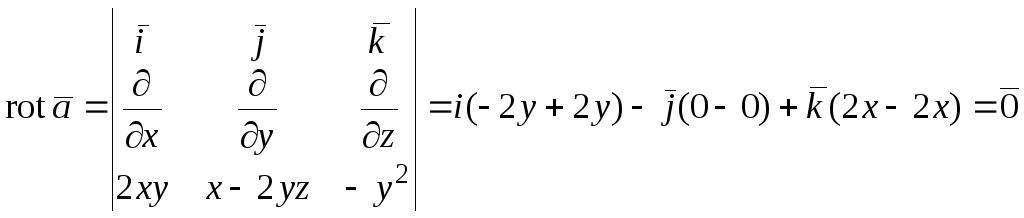
 В декартовой системе координат задание скалярного поля эквивалентно заданию функции трех переменных u(М) = u(x,y,z). Примерами скалярных полей могут служить поле температур данного тела, поле атмосферного давления и т.д. Пусть функция u(x, y, z) является непрерывно дифференцируемой в области V. В каждой точке этой области определен вектор, проекциями которого на оси координат являются значения частных производных функции u(x,y,z):
В декартовой системе координат задание скалярного поля эквивалентно заданию функции трех переменных u(М) = u(x,y,z). Примерами скалярных полей могут служить поле температур данного тела, поле атмосферного давления и т.д. Пусть функция u(x, y, z) является непрерывно дифференцируемой в области V. В каждой точке этой области определен вектор, проекциями которого на оси координат являются значения частных производных функции u(x,y,z): Вектор в этом случае записывается в виде
Вектор в этом случае записывается в виде