8.1.1. Вычислительный блок Given/ Find MathCAD 12 руководство
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная /
- База знаний /
- CAD / CAM /
- Системы линейных уравнений
- 8.1. Хорошо обусловленные системы с квадратной матрицей
- 8.1.1. Вычислительный блок Given / Find
- 8.1.2. Функция lsolve
- 8.2. Произвольные системы линейных уравнений
- 8.2.1. Переопределенные системы
- 8.2.2. Недоопределенные системы
- 8.2.3. Вырожденные и плохо обусловленные системы
- 8.3. Матричные разложения
- 8.3.1. СЛАУ с треугольной матрицей
- 8.3.2. Разложение Холецкого
- 8.3.3. LU-разложение
- 8.3.4. QR-разложение
- 8.3.5. SVD-(сингулярное) разложение
- 8.4. Собственные векторы и собственные значения матриц
Для того чтобы численным методом решить СЛАУ при помощи вычислительного блока (он был подробно описан в главе 5), следует после ключевого слова
Given выписать ее, пользуясь логическими операторами.
ПРИМЕЧАНИЕ
Если матрица СЛАУ является невырожденной (точнее, если ее число обусловленности не слишком велико), то известно, что численное решение системы уравнений единственно. Поэтому начальные значения могут быть произвольными, т. к. результат работы численного метода все равно сойдется к точному решению.
Листинг 8.1. Решение СЛАУ с помощью вычислительного блока
Листинг 8.1 демонстрирует запись каждого уравнения системы (в промежутке между
Given и Find), что очень неудобно, когда система содержит большое число уравнений.
В последнем случае намного лучше применить матричную запись СЛАУ, как это показано в листинге 8.2. Первая строка листинга представляет собой определение матрицы СЛАУ А и вектора правых частей ь, а в остальном работа блока
Given/Find полностью идентична предыдущему листингу.
Листинг 8.2. Решение СЛАУ, записанной в матричной форме
Проверка правильности решения СЛАУ прямой подстановкой, причем в матричной форме, приведена в листинге 8.3. Обратите внимание на матрицу в первой строке листинга, представляющую рассматриваемую систему уравнений. Во второй строке листинга 8.3 производится вычисление нормы невязки, характеризующей точность полученного решения СЛАУ.
ПРИМЕЧАНИЕ
Такая большая невязка может вызвать совершенно обоснованное удивление читателя. На самом
деле точность решения гораздо выше (в данном примере ~10-15, а полученное значение невязки
-10-3 объясняется соответствующим представлением вещественных чисел результата на экране (по умолчанию с точностью до 3-го знака).
Листинг 8.3. Проверка правильности решения СЛАУ
Нравится
Твитнуть
Теги MathCad САПР
Сюжеты MathCad
Глава 1 Основы работы с системой Mathcad 11
9926 0
Глава 10 Работа с информационными ресурсами Mathcad 11
6951 0
Глава 2 Работа с файлами Mathcad 11
12424 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster.ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2330 s
3 Решение систем уравнений: вычислительный блок Given/Find
Рассмотрим решение системы n нелинейных уравнений с m неизвестными:
Здесь
,
…,
–
некоторые скалярные
выражения, зывисящие от скалярных
переменных и возможно еще
каких–то переменных.
Для решения систем в MathCAD применяется специальный вычислительный блок Given/Find (Дано/Найти), состоящий из трех частей, идущих последовательно друг за другом:
Given – ключевое слово;
система, записанная логическими операторами в виде равенств и, возможно, неравенств;
Find() – встроенная функция для решения системы относительно переменных
Вставлять логические
операторы следует, пользуясь панелью
инструментов Boolean (Булевы операторы).
Блок Given/Find использует для поиска решения итерационные
методы, поэтому, как и для функции root,
требуется задать начальные значения
всех
.
Сделать это необходимо до ключевого
слова Given.
Значение функции Find представляет собой матрицу, составленную
из всевозможных решений по каждой
переменной, причем количество ее строк
в точности равно числу аргументов
Задание: Решить систему уравнений .
Решение:
Результат: В первых двух строках вводятся функции, которые определяют систему уравнений. Затем переменным x и y, относительно которых она будет решаться, присваиваются начальные значения. После этого следует ключевое слово Given и два логических оператора, выражающих рассматриваемую систему уравнений. Завершает вычислительный блок функция Find, значение которой присваивается вектору v. В последних двух строках осуществляется проверка правильности решения системы уравнений.
Вычислительным
блоком с функцией Find можно найти корень уравнения с одним
неизвестным.
Задание: Решить алгебраическое уравнение
Решение:
Оптимизация
1 Экстремум функции одной переменной
Задача поиска экстремума функции означает нахождение ее максимума (наибольшего значения) или минимума (наименьшего значения) в некоторой области определения ее аргументов.
Для решения задач
поиска минимума или максимума в MathCAD имеются встроенные функции Minimize и Maximize.
Поиск экстремума функции включает в
себя задачи нахождения локального и
глобального экстремумов.
Для поиска локальных экстремумов имеются две встроенные функции, которые применяются как в пределах вычислительного блока, так и автономно.
Minimize(f, ) – вектор значений аргументов, при которых функция f достигает минимума
Maximize(f, ) – вектор значений аргументов, при которых функция f достигает максимума, где
f() – функция,
–
аргументы, по
которым проводится минимизация
(максимизация).
Всем аргументам функции f следует присвоить предварительно некоторые значения, причем для тех переменных, по которым проводится минимизация, они будут восприниматься как начальные приближения.
Существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются различные локальные экстремумы.
Задание: Найти минимум и максимум функции одной переменной .
Решение:
Результат: Как вы заметили, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются различные локальные экстремумы.
Найти единичный вектор в том же направлении, что и заданный вектор
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы Precalculus
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
Precalculus Help » Матрицы и векторы » Алгебраические векторы и параметрические уравнения » Найдите единичный вектор в том же направлении, что и заданный вектор
Найдите единичный вектор, направленный в том же направлении, что и вектор Пояснение:
Чтобы найти единичный вектор в том же направлении, что и вектор, мы разделим его на его модуль.
Величина равна .
Мы делим вектор на его модуль, чтобы получить единичный вектор:
или
Все единичные векторы имеют модуль, поэтому для проверки правильности:
Сообщить об ошибке
Единичный вектор имеет длину .
По заданному вектору
найдите единичный вектор в том же направлении.
Возможные ответы:
Правильный ответ:
Пояснение:
Во-первых, вы должны найти длину вектора. Это дается уравнением:
Затем, деление вектора на его длину дает единичный вектор в том же направлении.
Сообщить об ошибке
Представить вектор в форме единичного вектора.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы получить единичный вектор, направленный в том же направлении, что и исходный вектор , мы делим вектор на модуль вектора.
Для , величина:
.
Это означает, что единичный вектор в том же направлении равен,
.
Сообщить об ошибке
Найти единичный вектор числа
.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти единичный вектор u заданного вектора v , мы следуем формуле
Пусть
Модуль v следует формуле
9017Для этого вектора в задаче
.
Следуя формуле единичного вектора и заменяя вектор и величину
.
Как таковой,
.
Сообщить об ошибке. Объяснение:
Чтобы найти единичный вектор u заданного вектора v , we follow the formula
Let
The magnitude of v follows the formula
For this vector in the problem
Following the unit vector formula and подстановка вектора и величины
Как таковая,
Сообщить об ошибке
Уведомление об авторских правах
Посмотреть наставников по предварительному исчислению
Натаниэль
Сертифицированный преподаватель
Калифорнийский университет в Лос-Анджелесе, бакалавр наук, прикладная математика.
Посмотреть репетиторов по математике
Sita
Сертифицированный репетитор
Калифорнийский университет в Беркли, бакалавр искусств, математика. Портлендский государственный университет, магистр наук, математика.
Посмотреть репетиторов по математике
Юджин
Сертифицированный репетитор
Общественный колледж Сан-Хасинто, ассоциированный специалист по искусству, математике. Университет Хьюстона, бакалавр наук, инженер-механик…
Все ресурсы Precalculus
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
Нахождение процента заданного числа – Математика для сделок: Том 1
Проценты
Сейчас Рождество, и у учеников есть шанс выиграть банку с конфетами слева. Единственное требование – угадать количество конфет в банке.
Правильный ответ = 117
Победителем стал Брайс, студент-сантехник 4-го уровня.
Он приписывает свой успех в игре со счетом конфет тому факту, что его семья владела магазином сладостей, когда он был ребенком, и это, наконец, окупилось.
Брайс решает раздать конфеты. Фактически, он решает отдать 12% своему другу Патрику, 25% своему другу Мэтту и 17% своему инструктору.
Возникает вопрос, сколько процентов составляет каждый из этих процентов от общего числа? И, может быть, в конце концов мы сможем узнать, сколько конфет Брайс оставит себе.
Начнем с Патрика, который получит 12% конфет. Первое, что нужно сделать, это превратить 12% в дробь.
[латекс]\БОЛЬШОЙ\dfrac{12}{100}[/латекс]
В конце концов это покажет нам, что из каждых 100 конфет в банке Патрик получит 12 из них. Теперь превратите эту дробь в десятичную, разделив 12 на 100.
[латекс]\НАИБОЛЕЕ12÷100=0,12[/латекс]
Вы заметили закономерность, когда речь заходит о десятичных дробях? Вот соотношение, показывающее несколько различных способов, которыми мы можем получить 12%:
[латекс]\БОЛЬШОЙ12\%=\dfrac{12}{100}=0,12[/латекс]
Все три числа представляют одну и ту же сумму.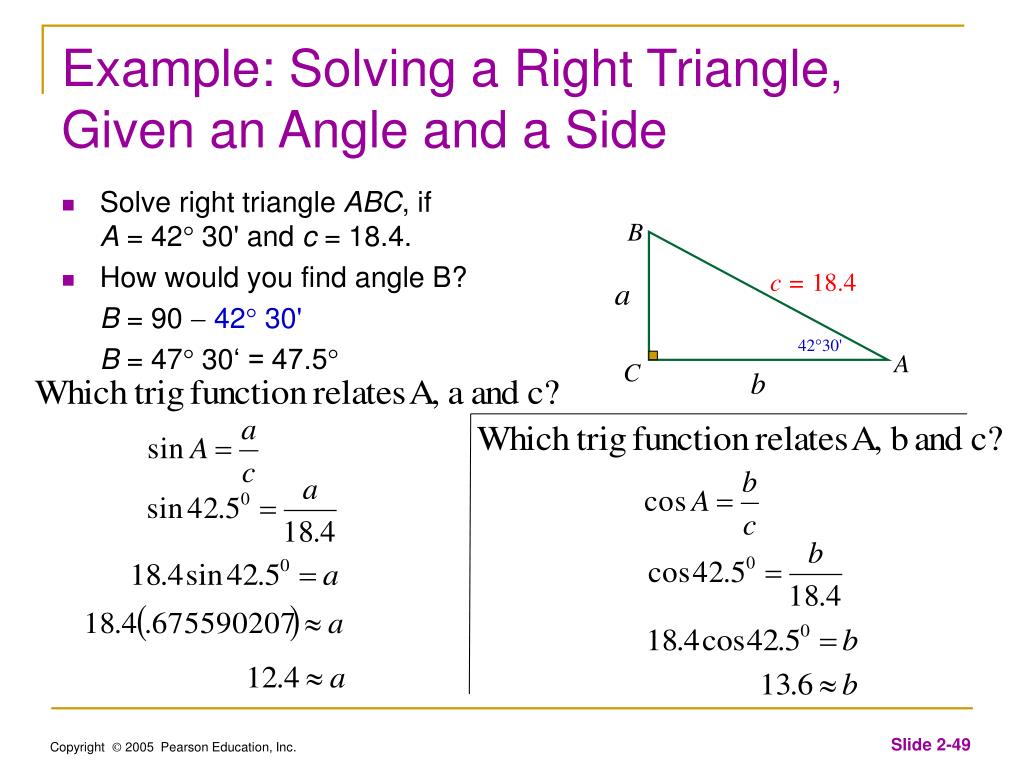
Научиться работать между ними важно в математике, и также важно начать видеть отношения между числами. Ладно, вернемся к Патрику.
Последний шаг в этой ситуации — взять 0,12, что на самом деле составляет 12%, и умножить его на количество конфет в банке.
[латекс]\НАИБОЛЬШИЙ0.12\times117=14.04[/латекс]
Теперь отрезать 0,04 конфеты сложно, поэтому воспользуемся нашими навыками округления и округлим до 14 конфет.
Теперь перейдем к следующему другу Брайса, Мэтту. Мэтт получает 25% конфет.
Шаг 1 : Превратите процент в дробь со знаменателем 100.
[latex]\LARGE\dfrac{25}{100}[/latex]
Шаг 2 : Возьмите 25 и разделите это на 100.
[латекс]\LARGE25÷100=0,25[/латекс]
Шаг 3 : Возьмите 0,25 и умножьте его на количество конфет в банке.
[латекс]\НАИБОЛЬШИЙ0,25\times117=29,25[/латекс]
Мы снова округлим в меньшую сторону, чтобы получить окончательный ответ 29.
Мы не будем беспокоиться о том, сколько конфет получит инструктор, а посчитаем, сколько конфет Брайс оставляет себе. Мы хотим рассчитать процент конфет, которые в итоге получит Брайс, а затем вычислить, сколько это конфет.
Шаг 1 : Сложите процент конфет, которые есть у трех других людей, а затем вычтите сумму из 100.
- Патрик получает 12%
- Мэтт получает 25%
- Инструктор получает 17%
[латекс]\БОЛЬШОЙ12\%+25\%+17\%=54\%[/латекс]
[латекс]\БОЛЬШОЙ\текст{Брайс получает}100\%-54\%=46\ %[/latex]
Шаг 2 : К этому моменту мы сделали пару примеров, в которых мы сначала взяли процент и превратили его в дробь больше 100. Затем мы взяли процент и разделили его на 100. Что, если мы просто пропустим этот шаг? Что мы в конечном итоге делаем для процента, так это просто берем десятичную точку и перемещаем ее на 2 знака влево (это представляет собой деление на 100). Попробуй это.