Разное

Гауссовы числа: Конспект урока по математике на тему «Гауссова кривая. Закон больших чисел»

Конспект урока по математике на тему «Гауссова кривая. Закон больших чисел»

Конспект по алгебре и началам анализа

Учитель: Денисенко Н.В.

Тема: Гауссова кривая. Закон больших чисел.

Класс: 11.

Цели:

  1. Познакомить учащихся с гауссовой кривой, показать ее значение в теории вероятностей и статистике.

  2. Показать на примерах красоту и универсальность некоторых математических моделей реальных явлений жизни.

  3. Познакомить учащихся с законом больших чисел, обозначить его применение в реальной жизни.

  4. Обучить методам приближенного вычисления вероятностей наступления «успехов» в независимых повторениях одного и того же испытания с двумя исходами при большом количестве испытаний.

  5. Расширить культуроведческую компетенцию школьников, затронув биографии великих математиков Гаусса и Лапласа.

  6. Обучить учащихся работе с таблицами приближенных значений для гауссовой функции.

  7. Научить работе с алгоритмами использования функции Гаусса в приближенных вычислениях.

План:

1. Вступительное слово учителя. Разбор и анализ самостоятельной работы по теме «Независимые повторения испытаний с двумя исходами».

2. Примеры использования для разных физических явлений одинаковых математических моделей.

3. Функция Гаусса и ее график. Работа с гистограммами – примеры их разных областей жизни.

4. Формула гауссовой функции: причина ее возникновения, особенности.

5. Таблица приближенных значений для гауссовой функции. Примеры.

6. Алгоритм использования функции Гаусса в приближенных вычислениях. Задача.

7. Вероятность того, что число «успехов» в испытаниях Бернулли находится в пределах от до .

8. Функция Ее геометрический смысл и график.

9. Алгоритм использования функции в приближенных вычислениях. Задача.

10. Анализ и сравнение изученных вероятностей.

11. Закон больших чисел.

12. Заключительное слово учителя, подведение итогов урока.

13. Домашнее задание.

Оборудование: тетрадь, интерактивная доска, карточки.

Организация: вступительное слово учителя, работа с таблицами и гистограммами, объяснение нового материала, решение задач, заключительные выводы по теме.

Ход урока:

  1. Организационный момент.

  2. Разбор и анализ самостоятельной работы по теме «Независимые повторения испытаний с двумя исходами».

  3. Примеры использования для разных физических явлений одинаковых математических моделей.

Уникальность и красота математики состоит в том, что очень многие физические явления реального мира, имеющие совершенно разную природу, могут быть описаны одними и теми же математическими объектами.

На физико-математических факультетах университетов в первом семестре изучают механические колебания. Они могут быть созданы пружинными или математическими маятниками. В следующем семестре рассматриваются темы, связанные со светом. Как известно, свет, с одной стороны, имеет корпускулярную природу, а с другой – волновую. Несмотря на то, что механические колебания и свет имеет принципиально разную природу и совершенно разные причины, оба эти явления задаются одним и тем же уравнением колебаний.

Более того, еще в эпоху древнейших цивилизаций ученые-математики делали поразительной точности вычисления. Древние египтяне и майя не имели полного представления о движении и положении небесных светим, не знали, по каким орбитам движутся планеты и как они расположены относительно Солнца. Им, как наблюдателям с Земли, было видно, что красная планета через определенные промежутки времени останавливается и начинает движение в обратную сторону. Сегодня нам известно, что планеты движутся не «туда-обратно», а по эллиптическим орбитам вокруг Солнца. Древнейшим математикам это было неизвестно. Тем не менее, это не помешало им с поразительной точностью вычислить год и день, когда Марс вновь изменит свою траекторию движения.

Как видите, успехи в математике иногда опережали реальные открытия. То же самое можно сказать и о теории относительности Эйнштейна. Еще никому из людей не приходилось летать со скоростью света, однако четко выверенные математические формулы и модели уже существуют.

  1. Функция Гаусса и ее график. Работа с гистограммами – примеры их разных областей жизни.

Так и в теории вероятностей и математической статистике существуют свои универсальные модели, которые могут быть применимы для изучения самых различных явлений. К таковым относится, например, функция Гаусса. Эта функция введена немецким математиком К.-Ф. Гауссом (1777-1855).

Карл Фридрих Гаусс — немецкий математик, астроном, геодезист и физик. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта проблематики. Труды Гаусса оказали большое влияние на развитие алгебры (доказательство основной теоремы алгебры), теории чисел, дифференциальной геометрии, математической физики, теории электричества и магнетизма, геодезии и многих разделов астрономии.

Гауссова функция задается весьма сложной формулой

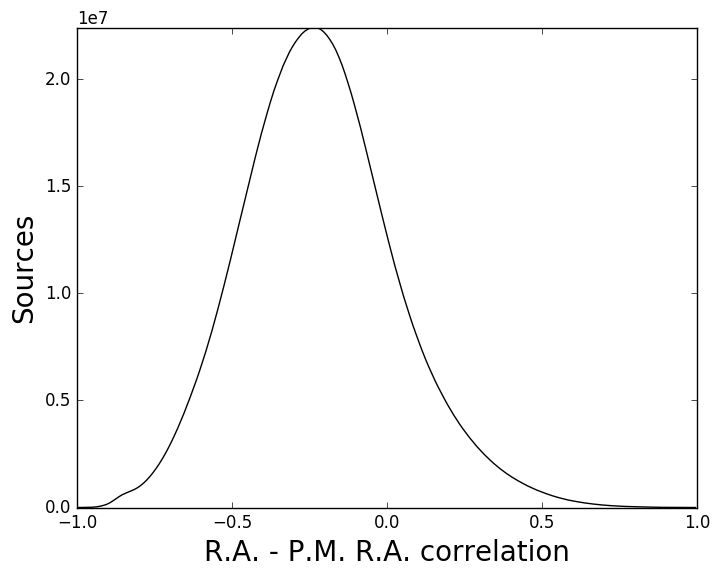
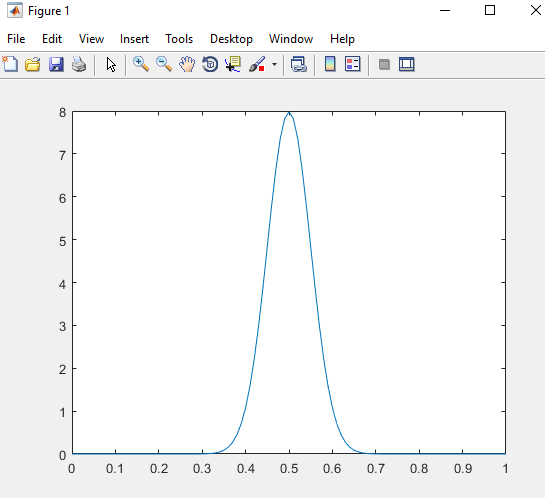
На интерактивную доску выводится изображение гауссовой кривой.

Это «колоколообразная» кривая. Она имеет единственную точку максимума, симметрична относительно оси ординат, площадь под этой кривой равна единице. Она очень быстро асимптотически приближается к оси абсцисс:если оценить площадь под гауссовой кривой на отрезке [-3;3], то получится более 99% всей площади.

Удивительно, что в формуле гауссовой функции одновременно присутствуют два замечательных иррациональных числа: и , в первоначальных определениях которых, казалось бы, нет ничего общего. Число возникло при нахождении длины окружностей и площади кругов, а число появляется в связи с введением показательных и логарифмических функций. Оказывается, что эти столь различные числа вместе используются при описании многих статистических и вероятностных явлений.

Гауссова кривая появляется при статистической обработке данных. Как мы видели на предыдущих уроках, гистограммы (столбчатые диаграммы) распределения большого объема информации незаменимы в случаях, когда ряд данных состоит из очень большого количества чисел. Если ширина вертикальных столбцов гистограммы достаточно мала, а основания столбцов в объединении дают некоторый промежуток, то сама гистограмма похожа на график некоторой непрерывной функции, заданной на этом промежутке. Иногда такую функцию называют

выравнивающей функцией. Например, на рис. 1 представлена гистограмма роста женщин, построенная по выборке, в которой было 1375 женщин.

На интерактивную доску выводится рисунок 1.


Приведем пример из военного дела. Производилось 500 измерений боковой ошибки при стрельбе с самолета. На графике (рис. 2) по оси абсцисс отложены величины ошибок («левее или правее» цели), а по оси ординат — частоты этих ошибок.

На интерактивную доску выводится рисунок 2.

Приведем пример из биологии. Измерялся размер 12 000 бобов, и по оси абсцисс откладывались величины отклонений от среднего размера бобов, а по оси ординат — соответствующие частоты (рис.

3).

На интерактивную доску выводится рисунок 3.


Примеры, как видите, взяты из совершенно различных областей, а графики функций, выравнивающих гистограммы, похожи друг на друга. Оказывается, что такому же закону подчиняется распределение и горошин по весу, и новорожденных младенцев по весу, и частиц газа по скорости движения, и множества других явлений окружающего нас мира. Подобно тому как графики всех парабол получаются с помощью линейных преобразований вдоль координатных осей из одной-единственной параболы у = х2, все эти кривые распределения получаются из одной-единственной кривой, а именно из гауссовой кривой. Ее очень часто называют также кривой нормального распределения.

5. Формула гауссовой функции: причина ее возникновения, особенности.

Как же возникла эта кривая? В теории вероятностей гауссова кривая возникает при попытке практического использования формулы Бернулли.

Теорема Бернулли дает абсолютно точный ответ для вероятности наступления «успехов» в независимых повторениях одного и того же испытания с двумя исходами:

Но если мы будем вычислять по этой формуле, например,

,

то абсолютная точность не упростит, а усложнит нам задачу. Поэтому используются методы приближенного вычисления вероятностей. Оказывается, что в огромном числе различных ситуаций все приближения могут быть произведены с помощью одной-единственной функции – гауссовой функции .

Доказал возможность такого использования функции французский математик Пьер Симон Лаплас (1749-1827) — французский астроном, математик, физик, иностранный почетный член Петербургской АН, автор классических трудов по теории вероятностей и небесной механике, и, наконец, человек, который составил космогоническую гипотезу образования всех тел солнечной системы, называемую его именем и в общих чертах, неизмененную поныне.

  1. Таблица приближенных значений для гауссовой функции. Примеры.

Для использования столь громоздкой формулы гауссовой функции имеются подробные таблицы ее значений. Они составлены для значений аргумента с шагом 0,01.

На интерактивную доску выводится таблица.

Для знакомства и работы с таблицей к доске приглашается ученик, который вместе с классом находит по данному значения аргумента значение функции в таблице, и наоборот (всего 2 примера).

Рассмотрим способ использования гауссовой кривой для приближенных вычислений в теореме Бернулли.

7. Алгоритм использования функции Гаусса в приближенных вычислениях.

Алгоритм использования функции в приближенных вычислениях

Для вычисления вероятности следует:

  1. проверить справедливость неравенства npq 10;

  2. вычислить по формуле

  3. по таблице значений гауссовой функции вычислить

  4. предыдущий результат разделить на

Рассмотрим внимательнее неравенство npq 10. Так как , то и наибольшее значение этого квадратичного выражения (относительно ) достигается при . Наибольшее значение равно 0,25. Значит,

Поэтому из условия 1) алгоритма следует, что . Это значит, что указанный алгоритм дает хорошую точность приближения, когда испытание с двумя исходами независимо повторяется как минимум несколько десятков раз. При меньшем числе повторений точность приближения резко ухудшается.

Задача.

Вероятность рождения мальчика примем равной 50%. Найти вероятность того, что среди 200 новорожденных будет 110 мальчиков.

Решение:

Будем действовать по предложенному алгоритму. В нашем случае п =

гауссово число 🎓 ⚗ перевод с английского на русский

  • — целое комплексное число а+bi, где аи b любые целые рациональные числа. С геометрич. точки зрения Г. ч. образуют на плоскости решетку всех точек с целыми рациональными координатами. Г. ч. впервые были рассмотрены К. Гауссом (С. Gauss) в 1832 в… …   Математическая энциклопедия

  • Гауссово число — …   Википедия

  • Гауссовы целые числа — (гауссовы числа, целые комплексные числа)  это комплексные числа, у которых как вещественная, так и мнимая часть  целые числа. Введены Гауссом в 1825 году. Содержание 1 Определение и операции 2 Теория делимости …   Википедия

  • ДИОФАНТОВЫ ПРОБЛЕМЫ АДДИТИВНОГО ТИПА — диофантовы уравнения, для к рых ставится задача нахождения целочисленных решений и к рые могут одновременно рассматриваться как аддитивные проблемы, т. е. как задачи о разбиении целого числа п(произвольного или подчиненного дополнительным… …   Математическая энциклопедия

  • Список алгоритмов — Эта страница информационный список. Основная статья: Алгоритм Ниже приводится список алгоритмов, группированный по категориям. Более детальные сведения приводятся в списке структур данных и …   Википедия

  • Программируемые алгоритмы —       Служебный список статей, созданный для координации работ по развитию темы.   Данное предупреждение не устанавл …   Википедия

  • Список парадоксов — …   Википедия

  • Парадоксы —       Служебный список статей, созданный для координации работ по развитию темы.   Данное предупреждение не устанавливается на информационные статьи списки и глоссари …   Википедия

  • ОПТИЧЕСКИЙ РЕЗОНАТОР — устройство, в к ром могут возбуждаться стоячие или бегущие эл. магн. волны оптич. диапазона. О. р. представляет собой совокупность неск. зеркал и явл. открытым резонатором, в отличие от большинства объёмных резонаторов, применяемых в диапазоне… …   Физическая энциклопедия

  • Магнетизм — 1) Свойства магнитов. Наиболее характерное магнитное явление притяжение магнитом кусков железа известно со времен глубокой древности. Однако в Европе вплоть до XII столетия наблюдали это явление лишь с естественными магнитами, т. е. с кусками… …   Энциклопедический словарь Ф.А. Брокгауза и И.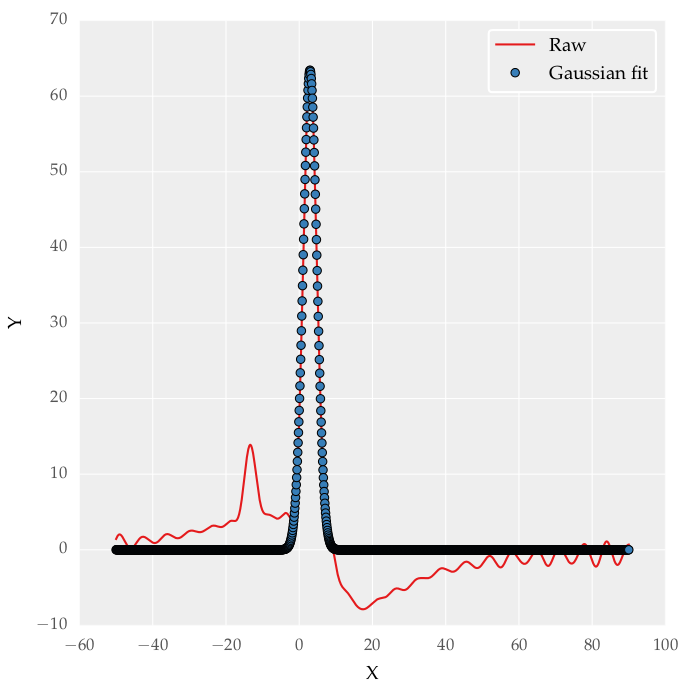 А. Ефрона

  • САМОДЕФОКУСИРОВКА СВЕТА — нелинейное расплывание высокоинтенсивногосветового пучка, распространяющегося в нелинейной среде, показатель преломленияк рой уменьшается с ростом интенсивности поля: Здесь А комплексная амплитуда поля, n0 линейнаячасть показателя преломления… …   Физическая энциклопедия

  • гамодим — * гамадзім * hamodeme группа особей одного вида, часть из которых по типу размножения занимает в пространстве и во времени пограничное положение, но может спариваться со всеми остальными особями данного дима. Гамон * гамон * gamone любой… …   Генетика. Энциклопедический словарь

  • КВАНТОВАЯ ОПТИКА — раздел статистической оптики, изучающий микроструктуру световых полей и оптич. явления, в к рых видна квант. природа света. Представление о квант. структуре излучения введено нем. физиком М. Планком в 1900. Статистич. структуру интерференц. поля… …   Физическая энциклопедия

  • СЛУЧАЙНОЕ ПОЛЕ — случайная ф ция носк. непрерывных переменных (параметров) ,т. е. такая ф ция, реализации к рой подчиняются вероятностным законам …   Физическая энциклопедия

  • Гаусс Карл Фридрих — (Gauß) (1777 1855), немецкий математик, иностранный член корреспондент (1802) и иностранный почетный член (1824) Петербургской АН. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта… …   Энциклопедический словарь

  • Гаусс, Карл Фридрих — У этого термина существуют и другие значения, см. Гаусс. Карл Фридрих Гаусс Carl Friedrich Gauß …   Википедия

    • Великий математик Гаусс: биография, фото, открытия

    Математик Гаусс был замкнутым человеком. Эрик Темпл Белл, который изучал его биографию, считает, что если бы Гаусс опубликовал все свои исследования и открытия в полном объеме и вовремя, то могло бы прославиться еще с полдюжины математиков. А так им пришлось потратить львиную долю времени, чтобы узнать, каким образом ученый получил те или другие данные. Ведь он редко публиковал методы, его всегда интересовал только результат. Выдающийся математик, странный человек и неподражаемая личность – это все Карл Фридрих Гаусс.

    Ранние годы

    Будущий математик Гаусс родился 30.04.1777 г. Это, конечно, странное явление, но выдающиеся люди чаще всего рождаются в бедных семьях. Так случилось и в этот раз. Его дедушка был обычным крестьянином, а отец работал в герцогстве Брауншвейг садовником, каменщиком или водопроводчиком. Родители узнали, что их ребенок вундеркинд, когда малышу исполнилось два года. Спустя год Карл уже умеет считать, писать и читать.

    В школе его способности заметил учитель, когда дал задание подсчитать сумму чисел от 1 до 100. Гауссу быстро удалось понять, что все крайние числа в паре составляют 101, и за считанные секунды он решил это уравнение, умножив 101 на 50.

    Юному математику несказанно повезло с учителем. Тот помогал ему во всем, даже похлопотал за то, чтобы начинающему дарованию выплачивали стипендию. С ее помощью Карл сумел окончить колледж (1795 год).

    Студенческие годы

    После колледжа Гаусс учится в Геттингенском университете. Этот период жизни биографы обозначают как самый плодотворный. В это время ему удалось доказать, что начертить правильный семнадцатиугольник, используя лишь циркуль, представляется возможным. Он уверяет: можно нарисовать не только семнадцатиугольник, но и другие правильные многоугольники, пользуясь только циркулем и линейкой.

    В университете Гаусс начинает вести специальную тетрадь, куда заносит все записи, которые касаются его исследований. Большинство из них были скрыты от глаз общественности. Для друзей он всегда повторял, что не сможет опубликовать исследование или формулу, в которых не уверен на 100%. По этой причине большинство из его идей были открыты другими математиками спустя 30 лет.

    «Арифметические исследования»

    Вместе с окончанием университета математик Гаусс закончил свой выдающийся труд «Арифметические исследования» (1798), но его напечатали лишь спустя два года.

    Это обширное сочинение определило дальнейшее развитие математики (в частности, алгебры и высшей арифметики). Основная часть работы сосредоточена на описании абиогенеза квадратичных форм. Биографы уверяют, что именно с него начинаются открытия Гаусса в математике. Ведь он был первым математиком, у кого получилось вычислять дроби и переводить их в функции.

    Также в книге можно отыскать полную парадигму равенств деления круга. Гаусс умело применяет эту теорию, пытаясь решить проблему начертания многоугольников при помощи линейки и циркуля. Доказывая эту вероятность, Карл Гаусс (математик) вводит ряд чисел, которые называют числами Гаусса (3, 5, 17, 257, 65337). Это значит, что при помощи простых канцелярских предметов можно построить 3-угольник, 5-угольник, 17-угольник и т.д. А вот 7-угольник построить не получится, ведь 7 не является «числом Гаусса». К «своим» числа математик также относит двойки, что умноженные на любую степень его ряда чисел (23, 25 и т. д.)

    Этот результат можно назвать «чистой теоремой существования». Как уже было сказано вначале, Гаусс любил публиковать итоговые результаты, но никогда не указывал методы. Так же и в этом случае: математик утверждает, что построить правильный многоугольник вполне реально, вот только не уточняет, как именно это сделать.

    Астрономия и царица наук

    в 1799 году Карл Гаусс (математик) получает титул приват-доцента Брауншвейнского университета. Спустя два года ему предоставляют место в Петербургской Академии наук, где он выступает в качестве корреспондента. Он все еще продолжает изучать теорию чисел, но круг его интересов расширяется после открытия небольшой планеты. Гаусс пытается вычислить и указать ее точное местонахождение. Многие задаются вопросом, как называлась планета по вычислениям математика Гаусса. Однако немногим известно, что Церера — не единственная планета, с которой работал ученый.

    В 1801 году впервые было обнаружено новое небесное тело. Это случилось неожиданно и внезапно, точно так же неожиданно планета была утеряна. Гаусс попытался обнаружить ее, применяя математические методы, и, как ни странно, она была именно там, куда указал ученный.

    Астрономией ученый занимается более двух десятилетий. Всемирную известность получает метод Гаусса (математика, которому принадлежит множество открытий) для определения орбиты с помощью трех наблюдений. Три наблюдения – это место, в котором располагается планета в разный период времени. С помощью этих показателей была вновь найдена Церера. Точно таким же образом обнаружили еще одну планету. С 1802 года на вопрос, как называется планета, обнаруженная математиком Гаусса, можно было отвечать: «Паллада». Забегая немного вперед, стоит отметить, что в 1923 году именем известного математика назвали крупный астероид, вращающийся вокруг Марса. Гауссия, или астероид 1001, – это официально признанная планета математика Гаусса.

    Это были первые исследования в области астрономии. Возможно, созерцание звездного неба стало причиной того, что человек, увлеченный числами, принимает решение обзавестись семьей. В 1805 году берет в жены Иоганну Остгоф. В этом союзе у пары рождается трое детей, но младший сын умирает в младенчестве.

    В 1806 году скончался герцог, который покровительствовал математику. Страны Европы наперебой начинают приглашать Гаусса к себе. С 1807 года и до последних своих дней Гаусс возглавляет кафедру в Геттингенском университете.

    В 1809 году умирает первая жена математика, в этом же году Гаусс издает свое новое творение — книгу под названием «Парадигма перемещения небесных тел». Методы для вычисления орбит планет, что изложены в этом труде, актуальны и сегодня (правда, с небольшими поправками).

    Главная теорема алгебры

    Начало ХІХ века Германия встретила в состоянии анархии и упадка. Эти годы были тяжелыми для математика, но он продолжает жить дальше. В 1810 году Гаусс второй раз связывает себя узами брака — с Минной Вальдек. В этом союзе у него появляется еще трое детей: Тереза, Вильгельм и Ойген. Также 1810 год был ознаменован получением престижной премии и золотой медали.

    Гаусс продолжает свою работу в областях астрономии и математики, исследуя все больше и больше неизвестных составляющих этих наук. Его первая публикация, посвященная основной теореме алгебры, датируется 1815 годом. Главная идея заключается в следующем: число корней многочлена прямопропорциональна его степени. Позже высказывание приобрело несколько иной вид: любое число в степени, не равной нолю, априори имеет как минимум один корень.

    Впервые он доказал это еще в 1799 году, но не был доволен своей работой, поэтому публикация вышла в свет спустя 16 лет, с некоторыми поправками, дополнениями и вычислениями.

    Неевклидова теория

    Согласно данным, в 1818 году Гауссу первому удалось построить базу для неевклидовой геометрии, теоремы которой были бы возможны в реальности. Неевклидовая геометрия представляет собой область науки, отличимой от евклидовой. Основная особенность евклидовой геометрии — в наличии аксиом и теорем, которые не требуют подтверждений. В своей книге «Начала» Евклид вывел утверждения, которые должны приниматься без доказательств, ведь они не могут быть изменены. Гаусс был первым, кому удалось доказать, что теории Евклида не всегда могут восприниматься без обоснований, так как в определенных случаях они не имеют прочной базы доказательств, которая удовлетворяет всем требованиям эксперимента. Так появилась неевклидова геометрия. Конечно, основные геометрические системы были открыты Лобачевским и Риманом, но метод Гаусса — математика, умеющего смотреть вглубь и находить истину, — положил начало этому разделу геометрии.

    Геодезия

    В 1818 году правительство Ганновера решает, что назрела необходимость измерить королевство, и это задание получил Карл Фридрих Гаусс. Открытия в математике на этом не закончились, а лишь приобрели новый оттенок. Он разрабатывает необходимые для выполнения задания вычислительные комбинации. В их число вошла гауссова методика «малых квадратов», которая подняла геодезию на новый уровень.

    Ему пришлось составлять карты и организовывать съемку местности. Это позволило приобрести новые знания и поставить новые эксперименты, поэтому в 1821 году он начинает писать работу, посвященную геодезии. Этот труд Гаусса опубликовали в 1827, под названием «Общий анализ неровных плоскостей». В основу этой работы были положены засады внутренней геометрии. Математик считал, что необходимо рассматривать предметы, которые находятся на поверхности, как свойства самой поверхности, обращая внимание на длину кривых, игнорируя при этом данные объемлющего пространства. Несколько позже эта теория была дополнена трудами Б. Римана и А. Александрова.

    Благодаря этому труду в научных кругах начало появляться понятие «гауссова кривизна» (определяет меру искривления плоскости в определенной точке). Начинает свое существование дифференциальная геометрия. И чтобы результаты наблюдений были достоверными, Карл Фридрих Гаусс (математик) выводит новые методы получения величин с высоким уровнем вероятности.

    Механика

    В 1824 году Гаусс был заочно включен в состав членов Петербургской Академии наук. На этом его достижения не заканчиваются, он все так же упорно занимается математикой и презентует новое открытие: «целые числа Гаусса». Под ними подразумевают числа, имеющие мнимую и вещественную часть, которые являются целыми числами. По сути, своими свойствами гауссовские числа напоминают обычные целые, но те небольшие отличительные характеристики позволяют доказать биквадратичный закон взаимности.

    В любое время он был неподражаем. Гаусс — математик, открытия которого так тесно переплетены с жизнью, — в 1829 году внес новые коррективы даже в механику. В это время вышел его небольшой труд «О новом универсальном принципе механики». В нем Гаусс доказывает, что принцип малого воздействия, можно по праву считать новой парадигмой механики. Ученный уверяет, что этот принцип можно применять ко всем механическим системам, которые связаны между собой.

    Физика

    С 1831 года Гаусс начинает страдать от тяжелой бессонницы. Болезнь проявилась после смерти второй супруги. Он ищет утешения в новых исследованиях и знакомствах. Так, благодаря его приглашению в Геттинген приехал В. Вебер. С молодой талантливой личностью Гаусс быстро находит общий язык. Они оба увлечены наукой, и жажду знаний приходится унимать, обмениваясь своими наработками, догадками и опытом. Эти энтузиасты быстро принимаются за дело, посвящая свое время исследованию электромагнетизма.

    Гаусс, математик, биография которого имеет большую научную ценность, в 1832 году создал абсолютные единицы, которыми и сегодня пользуются в физике. Он выделял три основные позиции: время, вес и расстояние (длина). Наряду с этим открытием в 1833 году, благодаря совместным исследованиям с физиком Вебером, Гауссу удалось изобрести электромагнитный телеграф.

    1839 год ознаменован выходом еще одного сочинения — «Об общем абиогенезе сил тяготения и отталкивания, что действуют прямопропорционально расстоянию». На страницах подробно описан знаменитый закон Гаусса (еще известный как теорема Гаусса-Остроградского, или просто теорема Гаусса). Этот закон является одним из основных в электродинамике. Он определяет связь между электрическим потоком и суммой заряда поверхности, делимые на электрическую постоянную.

    В этом же году Гаусс освоил русский язык. Он направляет письма в Петербург с просьбой выслать ему русские книги и журналы, особенно желал он ознакомиться с произведением «Капитанская дочка». Этот факт биографии доказывает, что, помимо способностей к вычислению, у Гаусса было множество других интересов и увлечений.

    Просто человек

    Гаусс никогда не спешил публиковаться. Он долго и кропотливо проверял каждую свою работу. Для математика все имело значение: начиная от правильности формулы и заканчивая изяществом и простотой слога. Он любил повторять, что его работы — как только что построенный дом. Владельцу показывают только конечный результат работы, а не остатки леса, которые раньше были на месте жилого помещения. Также и с его работами: Гаусс был уверен, что никому не стоит показывать черновые наброски исследования, только готовые данные, теории, формулы.

    Гаусс всегда проявлял живой интерес к наукам, но особенно его интересовала математика, которую он считал «царицей всех наук». И природа не обделила его умом и талантами. Даже находясь в преклонном возрасте, он, по обычаю, проводил большую часть сложных вычислений в уме. Математик никогда заранее не распространялся о своих работах. Как и каждый человек, он боялся, что его не поймут современники. В одном из своих писем Карл говорит о том, что устал вечно балансировать на грани: с одной стороны, он с удовольствием поддержит науку, но, с другой, ему не хотелось ворошить «осиное гнездо непонятливых».

    Всю свою жизнь Гаусс провел в Геттингене, только один раз ему удалось побывать в Берлине на научной конференции. Он мог длительное время проводить исследования, опыты, вычисления или измерения, но очень не любил читать лекции. Этот процесс он считал лишь досадной необходимостью, но если у него в группе появлялись талантливые ученики, он не жалел для них ни времени, ни сил и долгие годы поддерживал переписку обсуждая важные научные вопросы.

    Карл Фридрих Гаусс, математик, фото, которого размещены в этой статье, был поистине удивительным человеком. Выдающимися знаниями мог похвастаться не только в области математики, но и с иностранными языками «дружил». Свободно разговаривал на латыни, английском и французском, освоил даже русский. Математик читал не только научные мемуары, но и обычную художественную литературу. Особенно ему нравились произведения Диккенса, Свифта и Вальтера Скотта. После того как его младшие сыновья эмигрировали в США, Гаусс начал интересоваться американскими писателями. Со временем пристрастился к датским, шведским, итальянским и испанским книгам. Все произведения математик непременно читал в оригинале.

    Гаусс занимал весьма консервативную позицию в общественной жизни. С ранних лет он ощущал зависимость от людей, наделенных властью. Даже когда в 1837 году в университете начался протест против короля, который урезал профессорам содержание, Карл не стал вмешиваться.

    Последние годы

    В 1849 год Гаусс отмечает 50-летие присвоения докторской степени. К нему приехали известные математики, и это обрадовало его намного больше, чем присвоение очередной награды. В последние годы своей жизни уже много болел Карл Гаусс. Математику было сложно передвигаться, но ясность и острота разума от этого не пострадали.

    Незадолго до смерти здоровье Гаусса ухудшилось. Врачи диагностировали болезнь сердца и нервное перенапряжение. Лекарства практически не помогали.

    Математик Гаусс умер 23 февраля 1855 года, в возрасте семидесяти восьми лет. Известного ученого похоронили в Геттингене и, согласно его последней воле, выгравировали на надгробной плите правильный семнадцатиугольник. Позже его портреты напечатают на почтовых марках и денежных купюрах, страна навсегда запомнит своего лучшего мыслителя.

    Таким был Карл Фридрих Гаусс – странным, умным и увлеченным. И если спросят, как называется планета математика Гаусса, можно не спеша ответить: «Вычисления!», ведь именно им он посвятил всю свою жизнь.

    Гауссова кривая — Энциклопедия по экономике

    При внедрении статистических методов контроля важно установить, какой закономерности подчиняется распределение контролируемых параметров изделий электронной техники (кривой нормального распределения Гаусса распределению, характеризуемому кривой Максвелла, и т. д.). Изменение величины конкретного контролируемого параметра изделия или технологического режима проявляется в изменении функ-  [c.159]
    Уравнение Лапласа — Гаусса предполагает непрерывное изменение / и неограниченное возрастание п. Поэтому площадь нормальной кривой, заключенную между ординатами /, и t2, определяют, интегрируя функцию (7.7).  [c.168]

    Ее фафик — колоколообразная кривая Гаусса, имеющая максимум в точке F= mF, представленная на рис. 10.5.  [c.214]

    В попытке более точно определить размах различных типов распределения знаменитый математик статистической ориентации Карл Гаусс (1777—1855) предложил формулу, описывающую так называемое нормальное распределение. Эта формула характеризует размах событий, которые чаще встречаются в биологических процессах. Обычно ее представляют в виде колокола, когда большая часть событий расположена ближе к центру или средней величине. В немногих случаях они отклоняются от средней и в совсем редких случаях весьма отличны от нее. В математическом представлении края («хвосты») кривой распределения никогда не касаются горизонтальной оси.  [c.406]

    Наиболее распространены статистические методы предупредительного контроля, основывающиеся на законе нормального распределения, характеризующегося известной кривой Гаусса.  [c.155]

    Наиболее распространенной теоретической кривой, описывающей симметричное распределение, является кривая Гаусса, называемая также нормальной кривой (фиг. 27). Ее уравнение  [c.77]

    По существу, кривая Гаусса соответствует только симметричным распределениям. Однако она может быть получена и как предельная кривая, к которой стремятся прочие кривые распределения по мере беспредельного возрастания числа независимых обстоятельств, от которых зависят наблюдаемые явления.  [c.77]

    Вместо исправления кривой Гаусса можно непосредственно применять несимметричные кривые распределения (Пуассона, Пирсона и др. ).  [c.78]

    Поэтому, чтобы подобрать нормальную кривую Гаусса, необходимо  [c.79]

    Распределение имеет вид симметричной колоколообразной кривой, распространяющейся по всей числовой оси. Распределение Гаусса зависит от двух параметров (//, сг).  [c.34]

    Единственная переменная величина в методе фиксированных пропорций называется дельта. Эта переменная просто обеспечивает математическую формулировку метода, а также определяет, насколько агрессивно или консервативно следует вести управление. Чем меньше значение переменной, тем более агрессивным должно быть управление ресурсами. Чем больше величина переменной, тем более консервативно управление. Кривая Гаусса в Фиксированно-Пропорциональном методе не используется.  [c.89]

    В качестве меры крутости графи ков распределения случайных величин используют коэффициент эксцесса Ek, характеризующий крутость графика по сравнению с кривой Гаусса. Для оценки Ek  [c.48]

    По мере удаления от точки fl плотность распределения уменьшается. Максимальная ордината кривой распределения обратно пропорциональна О. Площадь под кривой Гаусса равна 1 или 100% всех значений случайной величины в генеральной совокупности.  [c.160]

    Идея информационного метода определения закона распределения заключается в следующем. Так как оценка энтропии распределена по закону Гаусса, то гипотеза о совпадении эмпирического и предполагаемого теоретического распределения принимается, если вычисленное по результатам экспериментальных данных значение Я (х) будет находиться в пределах доверительного интервала кривой нормального распределения с параметрами М[Н] и >[Я]. Нормированная по среднеквадратическому отклоне-  [c.28]

    Внимательное изучение данных на Рисунке 9.1 показывает профили продолжительности жизни этих двух индексов демонстрируют распределение по правильной кривой Гаусса распределения S P 500 или любого другого главного индекса коррелируют с подобной последовательностью, то есть движения рынка действительно имеют тенденцию ограничиваться статистически предсказуемой продолжительностью жизни.  [c.157]

    Инвесторы всегда хотят владеть самыми выгодными при данной цене акциями. Ожидаемый доход от портфеля таких акций равен математическому ожиданию, или среднему от ожидаемого дохода отдельных пакетов акций, входящих в портфель. Но пакеты, обещающие наибольшие прибыли, часто приносят разочарование, тогда как другие превосходят самые оптимистичные прогнозы. Марковиц предположил, что распределение вероятностей значения доходности портфеля вокруг ее математического ожидания описывается симметричной нормальной кривой Гаусса.  [c.365]

    График функции нормального распределения описывается, так называемой, нормальной кривой (кривой Гаусса — рис. 3.1.)  [c.47]

    График функции f(t) плотности распределения нормального закона называется нормальной кривой или кривой Гаусса.  [c.115]

    Наиболее известным и, наверное, наиболее распространенным в практической деятельности является нормальное распределение, иногда называемое распределением Гаусса. Данный вид распределения часто встречается в природе. Например, закону нормального распределения подчиняется случайная выборка людей по росту, весу и даже интеллектуальному развитию. Выглядит нормальное распределение как симметричная колоколообразная кривая. Среднеарифметическая ряда, подчиняющегося закону нормального распределения, равна моде и медиане этого ряда.  [c.185]

    Это позволяет описывать кривой Гаусса и несколько несимметричные опытные кривые, предполагая, что они по мере увеличения числа наблюдений выравниваются. Если отклонения от симметрии значительны, то возможно исправление кривой Гаусса введением так называемой пертурбационной функции, в виде многочлена не выше четвертой степени. Эту же кривую можно представить в виде ряда по производным нормального закона Гаусса (ряд Грамма — Шарлье типа А).  [c.77]

    Проф. А. Р. Ржаницын рекомендует [47] для несимметричных законов исправлять кривую Гаусса путем преобразования основной шкалы в логарифмическую  [c.77]

    В нормальной кривой асимметрия и эксцесс равны нулю, а куртозис равен трем. Эти данные могут служить дополнительными признаками соответствия эмпирического материала нормальному закону Гаусса.  [c.79]

    Концепция случайных блужданий проста, но богата своими приложениями не только в финансах, но и в физике, и в описании естественных процессов. Бесспорно, это одна из наиболее важных фундаментальных концепций, как в современной физике, так и в современных финансах, как являющаяся основанием теории элементарных частиц, представляющих собой строительные блоки Вселенной, так и описывающая сложные процессы вокруг нас. В простейшей вы бросаете монету, в результате чего двигаетесь вверх, если выпал «орел» или вниз -если выпала «решка». Где вы окажетесь после множественного повторения таких подбрасываний Ответ на поставленный вопрос многозначен в среднем вы остаетесь в той же самой позиции, так как среднее от одного шага вверх и одного шага вниз эквивалентно отсутствию какого-либо движения. Однако, ясно, что существуют флуктуации вокруг этого нулевого среднего значения, которые увеличиваются с увеличением числа подбрасываний.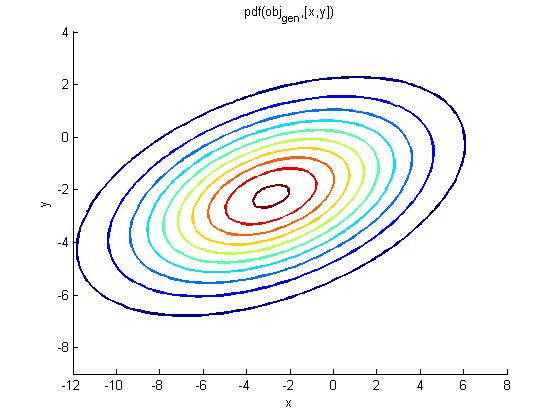 На Рис. 19 представлена траектория синтетически случайной рыночной цены, смоделированная компьютером, для определения конечного ценового сдвига в результате многократного изменения «цен». В данном случае, шаг или приращение имеет случайный «знак», а амплитуды приращений последовательных распределены согласно так называемому закону распределения Гаусса, графически изображаемого в виде хорошо известной колоколообразной кривой.  [c.51]

    Интерес Г. Беккера к религии, возможно, обусловлен тем, что на банкнотах долларов США есть надпись «In God We Trust» («Мы верим в Бога»). Несмотря на этот лозунг, количество финансовых афер в США больше, чем во многих других странах [Известия. 2001. 16 июня. С. 5]. На банкнотах немецкой марки (DM) нет любимого лозунга солдат третьего рейха «Gott mit uns» («С нами Бог»). Такую надпись можно увидеть в» кирхах Германии, а на бумажных деньгах этой страны помещены портреты ГеТе, Лейбница, Гаусса и других деятелей немецкой культуры. Купюру в 10 DM украшает портрет великого математикачКарла Фридриха Гаусса на фоне кривой нормального закона распределения вероятностей. Хочется надеяться, что огда-нибудь на российских десятирублевках появятся портреты Пушкина на фоне лукоморья с зеленым дубом, золотой цепью и ученым котом.  [c.258]

    Генерировалась последовательность псевдослучайных чисел с распределением Гаусса. Использовался универсальный алгоритм, основанный на учете формы кривой плотности распределения [12]. В качестве датчика равномерно распределенных чисел использовался генератор URAND [100].  [c.55]

    Другая математическая проблема заключалась в том, что портфели и сами рынки ценных бумаг описывались только двумя числами — ожидаемой доходностью и дисперсией. Зависимость именно от этих двух чисел оправданна, только если доходность ценных бумаг описывается кривой Гаусса. Отклонения от нормальной кривой недопустимы, и множество значений с каждой стороны от среднего должно быть распределено строго симметрично.  [c.462]

    Поток с ограниченным последействием поток Пальма поток Эрланга k-то порядка закон распределения Эрланга k-то порядка с параметром Я нормированный поток Эрланга k-то порядка центральная предельная теорема для одинаково распределенных слагаемых случайных величин сходимость по вероятности мера последействия нормальное распределение нормальная кривая кривая Гаусса Гаусс К. Ф. Чебышёв П.Л.  [c.121]

    Определение обобщенных внутренних координат | Gaussian.com

    В этом разделе обсуждается задание обобщенных внутренних координат (GIC) во входных файлах Гаусса. У GIC есть много потенциальных применений: определение дополнительных координат, значения которых сообщаются во время оптимизации геометрии, замораживание различных структурных параметров во время оптимизации молекулярной системы, определение параметров, по которым выполняется сканирование, определение ограничений для оптимизации геометрии на основе структурных параметров или сложных отношений. между ними, запрашивая расчет частей Гессе и другие цели.

    Раздел ввода GIC отделяется от более раннего ввода пустой строкой. В нем есть одна или несколько строк, содержащих определения координат, выражения или отдельные параметры. Вот простая секция ввода GIC для воды, иллюстрирующая некоторые из возможных функций:

    R (1,2) Определите координату длины связи для атомов 1 и 2
Bond2 = R [1,3] Определите другую координату длины связи с именем Bond2. 
HOH (стоп-кадр) = A (2,1,3) Определите ограничение оптимизации: координату угла связи с именем HOH (∠2-1-3)

    Для оптимизации эти координаты приведут к тому, что валентный угол останется фиксированным на его начальном значении, а два расстояния связи будут оптимизированы.

    Базовая форма координаты следующая:

     метка (параметры) = выражение

    Все компоненты не являются обязательными. В предыдущих примерах все компоненты присутствовали только в третьей строке. Первая строка содержала только выражение координат, а вторая строка также содержала метку без параметров. Обратите внимание, что параметры также могут быть размещены после выражения:

     HOH = A (2,1,3) Заморозить

    Метки — это присвоенные пользователем идентификаторы для координаты.Они не чувствительны к регистру. Ярлыки многие содержат буквы и цифры, но должны начинаться с буквы. Если метка не указана, программа будет назначать общий (например, R1, R2, A1 и т. Д.). При желании после метки может быть включен список опций, заключенный в скобки и разделенный запятыми. Обратите внимание, что квадратные скобки или фигурные скобки могут быть заменены круглыми скобками в любом месте определения координат.

    Параметры конструкции

    Координаты определяются выражениями. Простейшие выражения просто идентифицируют конкретный структурный параметр в молекуле, используя следующие конструкции.Обратите внимание, что звездочка может использоваться как подстановочный знак для любого номера атома (см. Примеры).

    R (i, j)

    Определите координату связи между атомами i и j. B, Bond и Stretch являются синонимами R

    .

    А (i, j, k)

    Задайте нелинейную угловую координату, включающую атомы i, j и k, где вершина угла находится в атоме j. Угол и Изгиб являются синонимами A.

    Д (и, к, к, л)

    Определите двугранный угол между плоскостью, содержащей атомы i, j и k, и плоскостью, содержащей атомы j, k и l.Двугранный и Крученый — синонимы D.

    .

    L (i, j, k, l, M)

    Определите координату линейного изгиба, включающую атомы i, j и k, где вершина угла находится в атоме j. Linear и LinearBend являются синонимами L.

    .

    Определение линейного изгиба состоит из двух компонентов, обозначенных значениями M -1 и -2 для первого и второго компонентов, соответственно (другие значения не допускаются). Линейный изгиб задается путем определения двух его ортогональных направлений. Их можно указать двумя способами:

    • Для нелинейной молекулы с более чем 3 атомами можно использовать четвертый атом, который не образует линейный угол с i, j и k в любой комбинации.В этом случае l можно установить равным его номеру атома. Например, следующее может использоваться для задания линейного изгиба с участием атомов 1, 2 и 3 с использованием атома 6 для определения двух ортогональных направлений:
      L (1,2,3,6, -1)
L (1,2,3,6, -2)

      Если l установлено на -4, то четвертый атом будет определен автоматически на основе геометрии молекулы.

    • Другой метод — спроецировать линейный изгиб на одну из осевых плоскостей системы координат: значения -1, -2 и -3 для l определяют плоскости YZ, XZ и XY (соответственно).Значение 0 также может использоваться для запроса автоматического определения соответствующей плоскости:
      L (1,2,3,0, -1)
L (1,2,3,0, -2)

    X (i)

    Определите декартову координату x для атома i. Декартово (i, -1) и декартово (i, X) являются синонимами, а декартово может быть сокращено как Cart.

    Y (i)

    Определите декартову координату y для атома i. Декартово (i, -2) и декартово (i, Y) являются синонимами, а декартово может быть сокращено как Cart.

    Z (i)

    Определите декартову координату z для атома i.Декартово (i, -3) и декартово (i, Z) являются синонимами, а декартово может быть сокращено как Cart.

    XCntr (список атомов)
    YCntr (список атомов)
    ZCntr (список атомов)

    Задайте декартовы координаты x, y или z для геометрического центра (центроида) молекулярного фрагмента, содержащего указанные атомы. Список атомов — это список номеров и / или диапазонов атомов, разделенных запятыми. Например, XCntr (1,12-15,27) определяет координату x фрагмента, содержащего атомы 1, 12, 13, 14, 15 и 27. Если список атомов опущен, по умолчанию используется вся молекула.

    DotDiff (i, j, k, l)

    Определите скалярное произведение (a · b) двух векторов декартовой разности координат a и b для атомов i, j, k и l, определенных как a = (X i –X j , Y i –Y j , Z i –Z j ) и b = (X k –X l , Y k –Y l , Z k –Z l ).

    Составные выражения

    Сложные выражения могут быть построены путем объединения нескольких элементов с использованием одной или нескольких математических операций.Аргумент (ы) A и B могут быть метками ранее определенной координаты, допустимого выражения GIC или даже констант (целых или с плавающей запятой). Имена операций не чувствительны к регистру. Доступны следующие операции:

    • Квадратный корень: КОРЕНЬ (A).
    • Мощность e: EXP (A) для e A .
    • Тригонометрические функции: SIN (A), COS (A), TAN (A).
    • Обратный косинус: ARCCOS (A).
    • Дополнение: A + B
    • Вычитание: A – B
    • Умножение: A * B
    • Отдел: A / B
    • Возведение в степень: A ** n для A n (n — целое число).п также принимается.

    Вот несколько простых примеров, которые определяют симметризованные связи ОН в воде:

    R12 (неактивен) = B (1,2)
R13 (неактивный) = B (1,3)
RSym = (R12 + R13) / КОРЕНЬ (2)
RASym = [Связь (1,2) - Связь (1,3)] / SQRT (2)

    Первые две координаты устанавливаются как неактивные, поскольку они являются промежуточными, не предназначенными для использования в оптимизации. Строка 3 иллюстрирует выражение с использованием ранее определенных меток, а строка 4 показывает использование литеральных выражений с операторами.Обратите внимание, что аргументом функции квадратного корня является константа 2.

    Опции

    Список параметров, разделенных запятыми, может следовать за меткой координат, заключенной в круглые скобки. В качестве альтернативы варианты могут следовать за выражением, отделенные от него и друг от друга пробелами. Все параметры нечувствительны к регистру.

    В целях оптимизации геометрии координата может быть обозначена как:

    • Активно: координата является частью списка внутренних координат, используемых при оптимизации геометрии.Напротив, неактивные координаты не включены в набор, используемый для оптимизации геометрии. По умолчанию активные координаты разморожены: разрешено изменять значение (см. Следующий пункт).
    • Заморожено: координата, значение которой остается постоянным в ходе оптимизации геометрии. Значения активных незамороженных координат изменяются во время оптимизации геометрии. Статус замороженных или размороженных неактивных координат не имеет значения во время оптимизации.

    В нижеследующих описаниях координаты, которые «уже существуют», относятся к ранее определенным координатам с той же меткой или тем же выражением значения.Такие координаты могли быть определены ранее во входном потоке или извлечены из файла контрольной точки из предыдущего задания.

    Активный

    Если указанная координата еще не существует, создайте новую координату, определенную данным выражением, и отметьте ее как активную и незамороженную. Если координата была определена ранее, отметьте ее как активную и незамороженную (независимо от ее предыдущего статуса). Это значение по умолчанию. Активировать, Добавить и Построить — синонимы Активного. Может быть сокращено до A, если указано после выражения.

    Замороженные

    Создайте координату, определяемую выражением, если она не существует, и отметьте координату как активную для оптимизации геометрии и зафиксируйте ее на текущем значении.
    Freeze является синонимом Frozen. Может быть сокращено до F, если указано после выражения.

    Неактивный

    Если координата еще не существует, создайте новую координату, определенную выражением, и отметьте ее неактивной. Если координата с данной меткой или для данного выражения уже построена и помечена как активная (замороженная или размороженная), то удалите ее из оптимизации геометрии, отметив ее как неактивную.Удалить является синонимом неактивного. Может быть сокращено до R, если указано после выражения.

    Убить

    Удалите координату из списка внутренних координат, используемых при оптимизации геометрии, вместе с любыми зависимыми координатами, пометив их все как неактивные. Зависимые координаты включают любую координату, которая зависит от тех же атомов, что и данная координата. Например, R (1,5) Kill приведет к удалению координаты R (1,5) — межъядерного расстояния между атомами 1 и 5, а также валентных углов, двугранных углов и любой другой координаты, которая зависит от декартовой системы координат. координаты атомов 1 и 5 в сочетании с другими атомами в молекуле.RemoveAll является синонимом слова «убить». Может быть сокращено до K, если указано после выражения.

    Только для печати

    Включите начальное значение координаты в исходную геометрию в выходной файл Гаусса, а затем отметьте его как неактивное.

    Изменить

    Метка должна быть включена в спецификацию координат для этой опции. Он заменяет старую координату указанной меткой новым выражением и помечает недавно измененную координату как активную и незамороженную.

    Разница

    Вычислить числовые вторые производные для строки и столбца исходного гессиана, соответствующего этой координате. Может быть сокращено до D, если указано после выражения.

    FC = x

    Измените диагональный элемент для данной координаты в начальном гессиане на x, число с плавающей запятой в атомных единицах. ForceConstant — это синоним FC.

    Значение = x

    Установить начальное значение для данной внутренней координаты x, значение с плавающей запятой.Единицы для значения соответствуют гауссовой программе, как определено ключевым словом Units (по умолчанию ангстремы или градусы). Текущие декартовы координаты будут скорректированы для максимального соответствия этому значению. Эту опцию следует использовать осторожно и экономно. Гораздо проще и надежнее установить желаемую исходную молекулярную структуру в графической среде, такой как GaussView.

    StepSize = x, NSteps = n

    Эти параметры используются для задания сканирования поверхности с ослабленной потенциальной энергией, при котором координата увеличивается на x в общей сложности n раз, а ограниченная оптимизация выполняется из каждой результирующей начальной геометрии.x должен быть положительным числом с плавающей запятой в атомарных единицах, N должно быть целым числом> 1. Когда эти параметры следуют за выражением, разделяющую их запятую следует заменить пробелом.

    Мин. = Мин., Макс. = Макс.

    Этот параметр используется в сочетании с активным, фиксированным или неактивным. Он добавляет, замораживает или делает неактивной координату, если ее значение удовлетворяет условию min≤value≤max. min и max — числа с плавающей запятой в единицах, определяемых Единицами (по умолчанию ангстремы или градусы).Если Min или Max опущены, условие становится value≤max или min≥min соответственно. Когда эти параметры следуют за выражением, запятую следует заменить пробелом.

    Только действие Если условие

    действие, если не условие

    Эти параметры обеспечивают операции с условными координатами. Их можно разместить только после выражения, определяющего текущую координату. Действие может быть активным, замороженным или неактивным. Условие — это метка или выражение для другой координаты.Указанное действие будет выполнено для текущей координаты, если координата, указанная в условии, активна для OnlyIf или неактивна для IfNot. Обратите внимание, что условный тест применяется только к действию, указанному перед параметром, а не к другим параметрам, которые могут присутствовать в спецификации координат.

    Автономные опции

    Следующие параметры не зависят от определений координат и применяются глобально. Они должны быть указаны отдельно в строке ввода.

    FreezeВсе

    Зафиксировать все ранее добавленные внутренние координаты как активные.

    Разморозить все

    Разблокировать все внутренние координаты, ранее добавленные как активные замороженные.

    RemoveAll

    Удалить / деактивировать все внутренние координаты, ранее добавленные как активные (замороженные или размороженные).

    Atom i действие

    Применить указанное действие к декартовым координатам атома i. Если i — звездочка, действие применяется ко всем атомам.Действие может быть одним из Активно, Заморозить, Разморозить, Удалить (сделать неактивным), Удалить все и XYZOnly. Эти параметры определены выше; XYZOnly говорит, что нужно удалить все внутренние координаты, которые зависят от атома i, но добавить / сохранить координаты этого атома. Действие по умолчанию — Активно.

    Примеры

    В следующем примере обрабатываются некоторые автоматически сгенерированные координаты, определяются некоторые новые, а затем используются подстановочные знаки для удаления координат, связанных с конкретными атомами:

    R (5,9) заморозить Расстояние замораживания R (5,9).R (8,9) Добавить новую активную координату R (8,9) с меткой по умолчанию.
Ang189 = A (1,8,9) Добавьте новую активную координату A (1,8,9), помеченную как Ang189.
R10 (удалить) Удалите координату, помеченную R10.
Dih6123 (remove) = D (6,1,2,3) Если D (6,1,2,3) существует, удалите координату.
Dis79 (freeze) = R (7,9) Закрепите координату R (7,9): если она новая, то пометьте ее как Dis79; если он уже существует, сохраните старую метку.
G1 = (R16 + R19) * 0.529177 Добавьте новую координату G1.
Ang189a (изменить) = cos (g2) * 57.29577951 Изменить определение координаты Ang189a.
R (11, *) remove Удаляет расстояния между атомом 11 и любым другим атомом.
D (*, 1,17, *) remove Удалите все двугранные, образованные вокруг связи 1-17.

    Обратите внимание, что если указанная координата уже существует, то добавление ее приведет к ошибке (например, строки 1-3 выше).

    В следующем примере сначала определяются центроиды двух фрагментов.Затем он определяет расстояние между фрагментами как координату оптимизации:

    Определите центр фрагмента 1, но не включайте его в оптимизацию.
XC1 (Неактивно) = XCntr (1-10)
YC1 (Неактивный) = YCntr (1-10)
ZC1 (Неактивно) = ZCntr (1-10)
Определите центр фрагмента 2, но не включайте его в оптимизацию.
XC2 (Неактивно) = XCntr (11-21)
YC2 (Неактивный) = YCntr (11-21)
ZC2 (Неактивный) = ZCntr (11-21)
Определите расстояние F1-F2 и включите его в оптимизацию.2] * 0,529177

    В следующем примере запрашивается расслабленное сканирование PES по той же координате:

    F1F2 (NSteps = 10, StepSize = 0,2)

    В следующем примере удаляется угловая координата, созданная по умолчанию, если ≥179,9 °, заменяя линейный изгиб:

    A (1,2,3) Remove Min = 179.9 Удалите угловую координату, если она слишком велика.
L (1,2,3,0, -1) Добавить IfNot A (1,2,3) Добавлять линейный изгиб, только если угловая координата не активна.
L (1,2,3,0, -2) Добавить, если не A (1,2,3)

    В следующем примере удаляется угловая координата, если она меньше указанного значения, для соответствующей силовой константы устанавливается значение 0.2 а.е. Последнее применяется всякий раз, когда это необходимо: поскольку исходная силовая константа и используемая силовая постоянная должны быть переменными, их необходимо повторно активировать. Вторая строка указывает силовую постоянную для координаты связи:

    A (1,2,3) Remove Min = 3,139847 ForceConstant = 0,2
R (1,2) FC = 0,5

    В следующем примере задаются силовые постоянные для различных координат. Он также деактивирует координаты угла связи ≥ 179,8 °:

    R (1, *) FC = 0,8
D (*, 4,5, *) FC = 0.4
А (*, 1, *) FC = 0,5
A (*, *, *) R Мин. = 179,8

    Ограничения GIC в текущей реализации

    В текущей реализации GIC могут успешно использоваться для многих целей, включая ограничения оптимизации и сканирование PES. Однако существуют потенциальные проблемы с активными составными координатами, включая несколько двугранных углов. В общем, координаты, состоящие из комбинаций связующих расстояний и валентных углов, должны вести себя хорошо. Также поддерживаются простые двугранные углы.Сложные выражения, включающие несколько двугранных углов, приемлемы для замороженных координат и для сканирования PES. Однако их следует избегать как активных координат оптимизации.

    При оптимизации без GIC или при использовании GIC только с регулярными двугранными углами программа заботится о периодичности этих координат. Например, при принятии решения о том, является ли шаг в геометрии слишком большим и его необходимо уменьшить, он распознает, что изменение значения с 1 градуса до 359 градусов на самом деле является изменением на -2 градуса, а не на 358 градусов.Точно так же при численном дифференцировании сил для обновления гессиана необходимы смещения между геометрическими формами во внутренних координатах, и учитывается периодичность. Проблема может возникнуть, когда GIC представляет собой комбинацию частей, для которых важна такая периодичность, обычно комбинации нескольких двугранных углов. Например, рассмотрим эти GIC:

    D1 = D (1,2,3,4)
D2 = D (5,6,7,8)
V1 = D1 + 2 * D2

    D1 и D2 — двугранные углы, но они являются промежуточными и не используются в качестве переменных при оптимизации.Их периодичность в настоящее время не распознается в составной координате V1. Предположим, что они имеют значения 1 и 2 градуса в одной геометрии и 1 и 359 градусов в другой. Изменение в переменной оптимизации V1 должно быть 0 + 2 * (- 3) = -6 градусов, но на самом деле это 0 + 2 * (357) = 714 градусов, что выглядит огромным изменением. Это приведет к очень плохой работе алгоритма оптимизации. V1 не является простой периодической функцией; необходимо применять периодичность к ее составным частям по мере ее вычисления, что не выполняется в текущей реализации GIC.

    GIC Units в гауссовском выводе

    Значения GIC, определяемые как чистые расстояния и углы (включая валентные углы, линейные изгибы и двугранные углы / кручения), вычисляются из декартовых координат в атомных единицах (Бора) и сохраняются внутри в Бора и радианах. Однако для удобства пользователя они выражаются как обычно в ангстремах и градусах в гауссовых выходных данных. В случае общего GIC (т. Е. Когда GIC не является чистой декартовой координатой, связующим расстоянием или углом), значение GIC вычисляется как функция декартовых координат и связующих расстояний в Боре и углов в радианах в сочетании с необязательными константы в пользовательских единицах.Такие общие значения GIC (обозначенные как GIC) вычисляются, сохраняются и выводятся в одних и тех же единицах измерения: т. Е. Если GIC представляет собой комбинацию связей или комбинацию валентных углов, тогда произвольные единицы становятся Боровскими для связей и радианами для углы.

    Использование ввода формата ModRedundant

    Модификации GIC могут быть считаны с использованием формата ModRedundant из текущего внутреннего алгоритма координат. Однако старый формат доступен только с GIC, которые включают только чистые расстояния связи, валентные углы или торсионные углы.Кроме того, старый формат и новый формат GIC, описанные выше, нельзя смешивать вместе в одном разделе ввода.

    Последнее обновление: 23 апреля 2020 г. [G16 Rev. C.01]

    Константы | Gaussian.com

    1 Бор (a 0 ) = 0,52917721092 Å [Mohr12, Mohr12a]
    1 Единица атомной массы (а.е.м., м u ) = 1,660538921 × 10 -27 килограмм [Mohr12, Mohr12a]
    1 Заряд электрона (е) = 1.602176565 × 10 -19 Кулоны [Mohr12, Mohr12a]
    = 4,803204 × 10 -10 ESU
    Постоянная Планка (ч) = 6,62606957 × 10 -34 Джоуль-сек [Mohr12, Mohr12a]
    Номер Авогадро (N A ) = 6,02214129 × 10 23 [Mohr12, Mohr12a]
    1 Ккал-моль -1 = 4,184 Джоуль-моль -1 [Constyear79]
    1 Hartree (E h ) = 4.35974434 × 10 -18 Джоулей [Mohr12, Mohr12a]
    Скорость света (c) = 2,99792458 × 10 10 см-с -1 [Mohr12, Mohr12a]
    Постоянная Больцмана (k) = 1,3806488 × 10 -23 Джоуль-градус -1 [Mohr12, Mohr12a]
    Постоянная обратной тонкой структуры (α -1 ) = 137,035999074 [Mohr12, Mohr12a]
    Молярный объем идеального газа при 273.15 К (В м ) = 0,022710953 м 3 [Mohr12, Mohr12a]
    Масса покоя протона (м p ) = 1,672621777 × 10 -27 кг [Mohr12, Mohr12a]
    Магнитный момент электрона (μ e ) = -9,28476430 × 10 -24 Дж T -1 [Mohr12, Mohr12a]
    G-фактор свободных электронов (g e ) = −2,00231930436153 (безразмерный) [Mohr12, Mohr12a]

    Целые числа Гаусса — OeisWiki


    Эта статья требует еще работ .

    Помогите, пожалуйста, расширив его!


    A Целое число по Гауссу — это комплексное число a + bi {\ displaystyle a + bi}, такое, что действительная часть является действительным целым числом, а мнимая часть — действительным целым числом, умноженным на мнимую единицу i = −1 {\ displaystyle я = {\ sqrt {-1}}}. Чисто действительные целые числа можно рассматривать как гауссовские целые числа с мнимой частью 0. Обычным символом для кольца гауссовских целых чисел является Z [i] {\ displaystyle \ mathbb {Z} [i]}, но G {\ displaystyle \ mathbb { G}} и A (−1) {\ displaystyle \ mathbb {A} (-1)} [1] также использовались.В обозначении набора мы можем легко написать Z [i] ⊂C {\ displaystyle \ mathbb {Z} [i] \ subset \ mathbb {C}}, но Z⊂Z [i] {\ displaystyle \ mathbb {Z} \ subset \ mathbb {Z} [i]} не является полностью прямым утверждением, и мы увидим его позже.

    Комплексные единицы 1, −1 {\ displaystyle -1}, i {\ displaystyle i} и −i {\ displaystyle -i}, имеют друг друга как делители. Гауссовские целые числа с большей действительной или мнимой частью (или обеими) имеют не менее 8 делителей. Для целого гауссовского целого числа m + ni {\ displaystyle m + ni} полный список его делителей включает как минимум четыре комплексных единицы, ассоциированные с −m − ni {\ displaystyle -m-ni}, n − mi { \ displaystyle n-mi}, −n + mi {\ displaystyle -n + mi} и, конечно же, m + ni {\ displaystyle m + ni}.Если это единственные делители этого числа, то это гауссовское простое число.

    Гауссовские целые числа образуют уникальную область факторизации. Поскольку умножение коммутативно в Z [i] {\ displaystyle \ mathbb {Z} [i]} (точно так же, как в Z {\ displaystyle \ mathbb {Z}} и C {\ displaystyle \ mathbb {C}} для это имеет значение), порядок факторов не имеет значения. Таким образом, игнорируя влияние единиц, гауссовское целое число может быть разложено на множители только одним способом.

    Теорема . Каждое целое число Гаусса является произведением простых чисел Гаусса, имеющих положительную действительную и мнимую части (и соответствующую комплексную единицу, если необходимо) только одним способом.

    ДОКАЗАТЕЛЬСТВО ИДЕТ ЗДЕСЬ.

    НА ЭТОЙ ТОЧКЕ НЕКОТОРЫЕ ЗАМЕЧАНИЯ ОТНОСИТЕЛЬНО ФОРМАТА канонических разложений на простые множители гауссовых целых чисел БУДУТ Уместными.

    Мы установили, что умножение действительных чисел на другие действительные числа на комплексной плоскости точно такое же, как на прямой [2] действительных чисел и что Z [i] {\ displaystyle \ mathbb {Z} [i] } является уникальной областью факторизации, такой же, как Z {\ displaystyle \ mathbb {Z}} (по фундаментальной теореме арифметики), но было бы ошибкой думать, что факторизации действительных чисел в действительные простые числа всегда одинаковы, когда эти действительные простые числа считаются гауссовскими целыми числами.{2}} имеет решение в виде целых чисел, тогда p = 2 {\ displaystyle p = 2} или p≡1mod4 {\ displaystyle p \ Equiv 1 \ mod 4}. Иными словами, учитывая функцию Gc (d) {\ displaystyle G_ {c} (d)} из задачи Варинга, которая дает наименьшее количество степеней c {\ displaystyle c} th, которые можно сложить до d {\ displaystyle d} у нас есть G2 (p) = 2 {\ displaystyle G_ {2} (p) = 2}, если p = 2 {\ displaystyle p = 2} или p≡1mod4 {\ displaystyle p \ Equiv 1 \ mod 4}. {2}}.{2} \ Equiv 0 \ mod 4}; это последнее сравнение, конечно, также будет выполняться, если m {\ displaystyle m} изначально делится на 4, поэтому мы можем отложить его в сторону. Итак, n {\ displaystyle n} нечетно, и есть две возможности для его соответствия 4:

    numpy.random.normal — NumPy v1.15 Manual

    Нарисуйте случайные выборки из нормального (гауссовского) распределения.

    Функция плотности вероятности нормального распределения, сначала получен Де Муавром и 200 лет спустя Гауссом и Лапласом независимо [2], часто называют кривой колокола из-за его характерная форма (см. пример ниже).

    Нормальные распределения часто встречаются в природе. Например, это описывает часто встречающееся распределение образцов, на которые оказали влияние большим количеством крошечных случайных возмущений, каждое со своими уникальное распределение [2].

    Параметры:
    loc : float или array_like of float

    Среднее («центр») распределения.

    scale : float или array_like of float

    Стандартное отклонение (разброс или «ширина») распределения.

    размер : int или кортеж целых чисел, необязательно

    Форма вывода. Если заданная форма, например, (m, n, k) , то Отобрано м * н * к проб. Если размер Нет (по умолчанию), одно значение возвращается, если loc и scale являются скалярами. В противном случае отрисовывается np.broadcast (loc, scale) .size образцов.

    Возвращает:
    из : ndarray или скаляр

    Выборки из параметризованного нормального распределения.2, называется дисперсией.

    Функция имеет пик в среднем, и ее «разброс» увеличивается с увеличением стандартное отклонение (функция достигает 0,607 раза от своего максимума при x + \ sigma и x — \ sigma [2]). Это означает, что numpy.random.normal с большей вероятностью вернет образцы, лежащие близко к среднее, а не то, что далеко.

    Список литературы

    [2] (1, 2, 3, 4) П. Р. Пиблз мл., «Центральная предельная теорема» в книге «Вероятность, Случайные переменные и принципы случайных сигналов », 4-е изд., 2001 г., стр. 51, 51, 125.

    Примеры

    Рисуем образцы из раздачи:

     >>> mu, sigma = 0, 0.1 # среднее и стандартное отклонение
>>> s = np.random.normal (mu, sigma, 1000)

    Проверить среднее значение и дисперсию:

     >>> абс (mu - np.mean (s)) <0,01
Правда
 
     >>> абс (сигма - np.std (s, ddof = 1)) <0.01
Правда

    Отобразить гистограмму образцов вместе с функция плотности вероятности:

     >>> импортировать matplotlib.pyplot как plt
>>> count, bin, ignored = plt.
    Добавить комментарий 
    Ваш адрес email не будет опубликован. Обязательные поля помечены *