Что такое гармоники или обертона
В этой статье я хочу рассказать о том, что такое гармоники или обертона.
Любой музыкальный звук состоит из основного тона и дополнительных гармоник (обертонов).
Основной тон – это основа звука, отправная точка строения обертонов. Мы воспринимаем именно этот тон с точки зрения его высотности.
Гармоники – это производные основного тона. Причем, кратные производные.
Это значит, что если основной тон ноты «до» малой октавы имеет частоту приблизительно 130 Гц, то его обертона будут иметь частоту 260 Гц, 390 Гц, 520 Гц и т.д. То есть все эти гармоники можно разделить на 130 и получится целое число. Поэтому говорят вторая гармоника, третья гармоника и т.д. За счет этих гармоник и формируется окраска звука. Мы не можем воспринимать каждую гармонику разрозненно. Мы лишь слышим результат сочетания гармоник с основным тоном.
Основной тон всегда лежит ниже гармоник и является более громким, что и определяет его выраженность.
Гармоники – это основа окраски звука. Любой инструмент имеет свой неповторимый тембр, порождённый гармониками. Поэтому мы и слышим различия в звучании фортепиано, гитары и саксофона. Всё дело в гармониках.
Что такое гармоники
Для того чтобы наглядно продемонстрировать вам гармоники, я проведу один простой эксперимент. Для этого мне понадобятся синтезатор Sylenth2 в комплексе с плагином iZotope Ozone 4. C помощью синтезатора я буду генерировать различные звуки и анализировать результаты используя анализатор спектра в iZotope Ozone 4.
Итак, приступим!
1. Выберу пустой пресет, включу один осциллятор, выберу синусоидальную форму волны и сгенерирую звук ноты «Ля» большой октавы.
Как видно из скриншота, я сгенерировал основной тон ноты «Ля» 110 Гц. Кроме него никаких гармоник в сигнале нет.
2. Изменю форму волны на пилообразную.
Из скриншота видно, что у основного тона ноты «Ля» появились гармоники кратные 110.
3. Теперь выберу какой-нибудь пресет. Например, 44. LD Cello.
На скриншоте отчётливо видно, что тембр этого звука сформирован большим количеством дополнительных обертонов.
Из всего вышесказанного следует, что гармоники являются неотъемлемой составляющей любого звука. Без наличия обертонов музыка бы потеряла всю свою колоритность. Все инструменты звучали бы одинаково и примитивно.
Благодаря гармоникам мы имеем огромную палитру разнообразных тембров. Их число бесконечно велико. Это даёт возможность музыкантам и саунд продюсерам постоянно экспериментировать и синтезировать новые более интересные и насыщенные тембры.
В этой статье я рассказал о том, что такое гармоники.
Если есть вопросы, задавайте их в комментариях.
Понравилась статья? Поделись с друзьями.
Читайте также:
Автор: Александр Коваленко
Музыкальные интервалы — первое знакомство
Интервалы в музыке играют очень важную роль. Музыкальные интервалы – первооснова гармонии, «строительный материал» произведения.
Музыкальные интервалы – первооснова гармонии, «строительный материал» произведения.
Вся музыка сложена из нот, но одна нота – это ещё не музыка – равно, как и любая книга написана буквами, но буквы сами по себе ещё не несут смысла произведения. Если взять смысловые единицы крупнее, то в текстах это будут слова, а в музыкальном произведении – созвучия.
Гармонические и мелодические интервалы
Созвучие двух звуков называется интервалом, причём эти два звука можно сыграть, как вместе, так и по очереди, в первом случае интервал будет называться гармоническим, а во втором – мелодическим.
Что значит гармонический интервал и мелодический интервал? Звуки гармонического интервала берутся одновременно и поэтому сливаются в единое созвучие – гармонию, которая может прозвучать очень мягко, а может и остро, колюче. В мелодических интервалах звуки играются (или поются) по очереди – сначала один, потом другой. Эти интервалы можно сравнить с двумя соединенными звеньями цепочки – из таких звеньев состоит любая мелодия.
Эти интервалы можно сравнить с двумя соединенными звеньями цепочки – из таких звеньев состоит любая мелодия.
Роль интервалов в музыке
Какова же сущность интервалов в музыке, например, в мелодии? Представим себе две разные мелодии и проанализируем их самое начало: пусть это будут всем известные детские песенки «Как под горкой, под горой» и «В лесу родилась ёлочка».
Давайте сравним начала этих песенок. Обе мелодии начинаются с ноты «до», но совершенно по-разному развиваются дальше. В первой песенке мы слышим, будто мелодия маленькими шажками поднимается по ступенькам – сперва от нотки до к ноте ре, потом от ре к ми и т.д. А вот на первых же словах второй песенки мелодия сразу скачком уходит вверх, как бы перескакивая сразу через несколько ступенек («в лесу» – ход от до к ля). Действительно, между нотами до и ля поместились бы ещё совершенно спокойно ре ми фа и соль.
Движение вверх и вниз по ступенькам и скачком, а также повторение звуков на одной и той же высоте – это всё музыкальные интервалы, из которых, в конечном счёте, складывается общий мелодический рисунок.
Да, кстати. Если вы взялись изучать музыкальные интервалы, то вы наверняка уже знаете ноты и сейчас хорошо меня поняли. Если пока не знаете нот – ознакомьтесь со статьёй «Нотная грамота для начинающих».
Свойства интервалов
Вы уже поняли, что интервал – это некий промежуток, расстояние от одной ноты до другой. Теперь разберёмся, в чём же это расстояние можно измерить, тем более что пришла пора узнать названия интервалов.
Каждый интервал имеет два свойства (или две величины) – это ступеневая и тоновая величина. Ступеневая величина зависит от того, сколько музыкальных ступеней охватывает интервал – одну, две, три и т.д. (причём сами звуки интервала тоже считаются). Ну, а тоновая величина относится к составу конкретных интервалов – подсчитывается точное число тонов (или полутонов), которые умещаются в интервале. Эти свойства иногда называют по-другому – количественная и качественная величина, суть их при этом не меняется.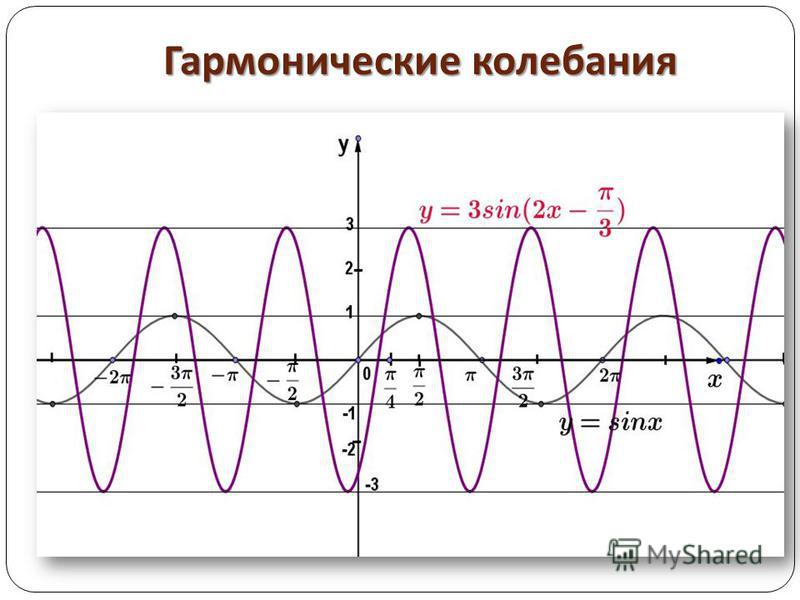
Музыкальные интервалы – названия
Для названия интервалов применяют числительные на латинском языке, название определяется свойствами интервала. В зависимости от того, сколько ступеней охватывает интервал (то есть от ступеневой или количественной величины), даются названия:
1 – прима
2 – секунда
3 – терция
4 – кварта
5 – квинта
6 – секста
7 – септима
8 – октава.
Для названия интервалов используются эти латинские слова, но для записи всё-таки удобнее применять цифровые обозначения. Например, кварту можно обозначить цифрой 4, сексту – цифрой 6 и т.д.
Интервалы бывают чистыми (ч), малыми (м), большими (б), уменьшёнными (ум) и увеличенными (ув). Эти определения исходят из второго свойства интервала, то есть тонового состава (тоновой или качественной величины). Эти характеристики присоединяются к названию, например: чистая квинта (сокращённо ч5) или малая септима (м7) , большая терция (бз) и т. д.
д.
Чистые интервалы – это чистая прима (ч1), чистая октава (ч8), чистая кварта (ч4) и чистая квинта (ч5). Малыми и большими бывают секунды (м2, б2), терции (м3, б3), сексты (м6, б6) и септимы (м7, б7).
Число тонов в каждом интервале нужно запомнить. Например, в чистых интервалах так: в приме 0 тонов, в октаве 6 тонов, в кварте – 2,5 тона, а в квинте – 3,5 тона. Чтобы повторить тему тонов и полутонов – почитайте статьи «Знаки альтерации» и «Как называются клавиши фортепиано», где эти вопросы подробно рассматриваются.
Интервалы в музыке – итоги
В данной статье, которую можно было бы назвать уроком, мы с вами разобрали интервалы в музыке, выяснили, как они называются, какие имеют свойства, и какую роль играют.
В дальнейшем вас ждёт расширение знаний по этой очень важной теме. Почему она так важна? Да потому что музыкальная теория – это универсальный ключ к пониманию любого музыкального произведения.
Что делать, если у вас не получилось разобраться в теме? Первое – отдохнуть и прочитать всю статью ещё раз сегодня или завтра, второе – поискать информацию на других сайтах, третье – связаться с нами в группе вконтакте или задать свои вопросы в комментариях.
Если всё понятно, то я очень рад! Внизу страницы вы найдёте кнопочки различных соцсетей – поделитесь данной статьёй со своими друзьями! Ну, а после вы можете немного расслабиться и посмотреть прикольное видео – пианист Денис Мацуев импровизирует на тему песенки «В лесу родилась ёлочка» в стилях разных композиторов.
Денис Мацуев “В лесу родилась ёлочка”
Паронимы гармонический и гармоничный — в чём разница
существительное — существительное
Паронимы
Все слова парыгармоническийгармоничный
гармонический
Словарь Ефремовой
гармонический

- Соотносящийся по знач. с сущ.: гармония (3), связанный с ним.
- Основанный на принципах гармонии (3).
- То же, что: гармоничный (1).
Примеры:
в музыке — гармонический обертон, ряд, мажор, диссонанс;
гармоническая гамма, обработка;
гармоническое построение, сопровождение;
гармонические ноты, колебания, тоны;
в математике — гармонический ряд, синтезатор, анализатор, баланс;
гармоническое среднее деление;
гармонические колебания.
гармоничный
Словарь Ожегова
гармоничный
ГАРМОНИЧНЫЙ, ая, ое; чен, чна.
1. Благозвучный, стройный. Гармоничные звуки.
2. Исполненный гармонии (во 2 знач.), стройности. Гармоничные движения. Гармоничные краски.
| сущ. гармоничность, и, ж.
Словарь Ефремовой
гармоничный
- Преисполненный гармонии (1).
- Благозвучный, приятный на слух.
Примеры:
гармоничный голос, тембр;
гармоничная мелодия, музыка;
гармоничное пение, движение, расположение, построение;
гармоничный человек;
гармоничная личность, фигура.
Добавить свой пароним
Тембр звука | Digital Music Academy
«Самым сложным субъективно ощущаемым параметром является тембр.
(И. Алдошина)
В природе мы почти не сталкиваемся с чистыми тонами. Звучание любого музыкального инструмента является сложным и состоит из множества частотных составляющих — обертонов.
Даже при очень сложных звуковых колебаниях слух человека способен распознать высоту звучания. Однако, при одинаковой высоте звучание, например, скрипки отличается на слух от звучания рояля. Это связано с тем, что, помимо высоты звучания, слух способен оценивать также “окраску” звучания, т.е. его тембр.
Тембром звука называется такое качество звука, которое, вне зависимости от частоты и амплитуды, позволяет отличить одно звучание от другого. Тембр звука зависит от общего спектрального состава звука (т.е. от того, какие обертоны в нем присутствуют) и соотношения амплитуд спектральных составляющих (т.
Обертоны
Понятие тембра тесно связано с понятием высоты звука. Дело в том, что звуковые колебания, как правило, бывают сложными.
Например, если мы взяли на скрипке ноту «ля» первой октавы (частота 440 Гц), то в колебаниях этой струны будут присутствовать также кратные частоты 880, 1320, 1760, 2200 Гц и т.д.
При этом амплитуды этих частот (обертонов) могут быть различными, т.е. обертоны будут иметь различную громкость.
Немецкий физик Георг Ом впервые высказал мысль, что простое слуховое ощущение вызывается простым синусоидальным колебанием (такое колебание также называется гармоническим, важно не путать гармонические колебания, т.е. те, которые описываются функциями y=sin x и т.п., и гармонические обертоны, которые также являются гармоническими колебаниями, но их частоты еще и кратны частоте основного тона

Пример возникновения сложного колебания путем сложения двух простых (гармонических) колебаний.
Синим цветом обозначено основное гармоническое колебание, розовым — колебание в два раза большей частоты (обертон или первая гармоника), а зеленым — результирующее сложное (негармоническое) колебание.
Ому удалось установить, что ухо воспринимает отдельные гармонические составляющие звука, и эти составляющие вызывают раздельные ощущения. При определенной тренировке можно даже мысленно разделить сложное периодическое колебание и определить, какие гармоники присутствуют в звуке .
Таким образом, человеческий слух способен воспринимать сложную форму звуковых колебаний как окраску или тембр.
Гармонические обертоны или гармоники
Обертоны бывают гармоническими и негармоническими.
Частоты гармонических обертонов кратны частоте основного тона (гармонические обертоны вместе с основным тоном также называются гармониками):
В реальных физических ситуациях (например, при колебаниях массивной и жесткой струны) частоты обертонов могут заметно отклоняться от величин, кратных частоте основного тона — такие обертоны называются негармоническими.
Спектральный состав и тембр
Амплитудно-частотное соотношение всех составных частей сложного колебания называют спектром звука, а звуки, соответствующие каждой частоте, присутствующей в сложном колебании, спектральными составляющими или компонентами.
Набор спектральных составляющих определяет тембр звучания. А поскольку каждая спектральная составляющая — это звук определенной высоты, говорить о тембре как об отдельном свойстве звука не совсем корректно. Однако именно тембр звука (а точнее — спектр) обычно находится в центре внимания, когда речь идет о технологиях обработки звука.
Примеры спектрального состава музыкальных звуков:
Тембр звука, т.е. отношения амплитуд его гармоник, влияет и на воспринимаемую высоту сложного тона.
Фантомные частоты
Иногда человек может слышать звуки в низкочастотной области, хотя в реальности звуков такой частоты не было. Мозг воспринимает высоту тона не только по его основной частоте, но и по периодичности, задаваемой отношением между гармониками.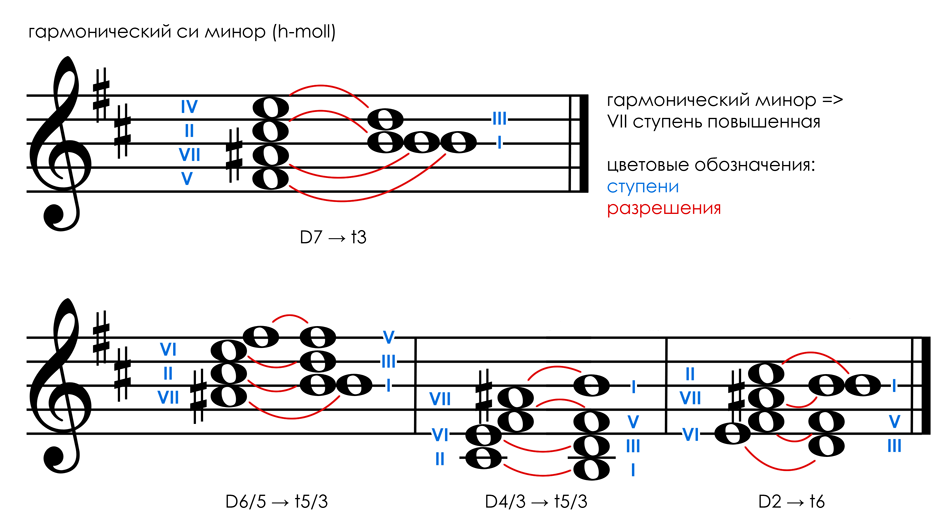 Мы можем воспринять ту же высоту (возможно, с другим тембром) даже если основная частота не слышна (или потеряна) при воспроизведении. ( Частотные сигналы сложного спектра без основной частоты (первой гармоники в спектре) называются резидуальными. )
Мы можем воспринять ту же высоту (возможно, с другим тембром) даже если основная частота не слышна (или потеряна) при воспроизведении. ( Частотные сигналы сложного спектра без основной частоты (первой гармоники в спектре) называются резидуальными. )
Например, если нота (то есть не чистый тон) имеет высоту 100 Гц, она будет состоять из частотных компонентов, которые являются целыми кратными этому значению (например, 100, 200, 300, 400, 500 …. Гц ). Однако, маленькие динамики могут не воспроизводить низкие частоты, поэтому при воспроизведении может отсутствовать компонент 100 Гц. Тем не менее, может быть слышна частота, соответствующая основному тону.
Этот эффект получил название «Феномен пропущенной фундаментальной» — эксперимент 1940 г. продемонстрировал, что ощущение высоты тона спектрально сложного звука не изменится, если удалить его основную частоту, она будет достроена мозгом на основе имеющихся гармоник. Он используется в звуковоспроизводящей аппаратуре, чтобы расширить область воспроизводимых низких частот, если невозможно адекватно воспроизвести такие частоты напрямую, например, в наушниках, мобильных телефонах, малобюджетных динамиках (акустических системах) и т.
Как звуки исцеляют организм
Вы можете настраивать своё тело, как оркестр
Вы когда-нибудь слышали, как настраивают оркестр перед игрой? Какофония из хаотических звуков от духовых и струнных, валторн и литавр воспринимается как довольно сильный шум. Но музыка, которая затем хлынет из инструментов, может принести мало с чем сравнимую умиротворённость, радость или восторг.
«Звук – это не беспорядочный хаос. Это динамический, но упорядоченный паттерн». Доктор Ганс Дженни
По большому счёту, тело работает таким же образом. Если один инструмент (орган или система органов) играет собственную мелодию и не гармонирует с остальным телом, то с большой вероятностью возникнет болезнь.
Звукотерапевт из Северной Дакоты Джон Больё объясняет:
«Основополагающий принцип энергетической медицины заключается в том, что основное энергетическое поле создаёт физическое, эмоциональные и ментальное поведение или симптомы. Если мы изменяем энергетическое поле, то изменения происходят в физическом, эмоциональном и психическом поведении».
Киматика
Киматика – вот один из наиболее эффективных способов изменить энергетическое поле. Швейцарский доктор медицины Ганс Дженни из Базеля, хотя и не был первооткрывателем целительных свойств звука, собрал увлекательные эксперименты, в которых мы можем буквально «видеть» как работает звук.
Дженни стал основоположником «киматики», проведя серию опытов. Он насыпал песок, жидкость или какой-либо порошок на металлическую пластину, которую прикреплял к осциллятору. По сути, осциллятор это вибратор, но в данном случае прибор контролировался генератором, способным производить многие тысячи видов частот. Некоторые из них можно встретить в природе, а другие создаются человеком.
Дженни изменял частоту осциллятора и обнаружил, что песок, вода или другие вещества, которые он использовал для создания видимой среды звука, превращались в очень интересные формы. Они имитировали свойства божественной геометрии. Причём чем выше была частота, тем более сложными представлялись формы.
Он писал:
«Поскольку различные аспекты этих явлений обусловлены вибрацией, мы имеем дело со спектром, который показывает узорчатые, фигуративные образования на одном полюсе и кинетико-динамические процессы на другом, в целом образованные и поддерживаемые необходимой периодичностью».
Эксперименты Дженни представляли собой простой способ наблюдения за тем, как оживает материя. Теперь, благодаря развивающейся области квантовой физики, мы понимаем, что паттерны образуются через волны энергии. Аналогичное явление показывали учёному пластины.
Этот факт был хорошо известен в древнем Шумере. Именно поэтому популярностью пользовались такие практики, как мантры. Например, семенной слог «ОМ» вызывает определённые частоты, отпечатывающиеся на окружающей его «материи» и изменяет энергетическое поле. И тибетцы знали о науке звуков. Они практиковали пение пяти «семенных слогов», чтобы очистить разум. Монахи, поющие в григорианском стиле, также осведомлены об этой целительной силе.
«Этот вид пения успокаивает дух, помогает нам жить в мире с собой и друг с другом», – говорит игумен Филипп Лоуренс, знаток песнопения и настоятель монастыря Христа в пустыне американского ордена монахов-бенедиктинцев из Абикиу, штат Нью-Мексико. «По данным различных исследований, пение удивительно влияет на мозговые волны. Но, конечно, не этот эффект преследуют монахи как и григорианский хор. Мы всегда надеемся, что наше пение принесёт людям мир, внутреннее спокойствие и понимание красоты. Эти ценности способны помочь в создании такого мира, в котором будут преобладать умиротворение и спокойствие», – поясняет игумен Филипп.
Поскольку всякая материя это просто волны разной частоты или квантовое поле, то с помощью звука мы можем создавать другую реальность.
Коллапс волновой функции
Звук и золотое число
В науке о звуке можно найти большой потенциал для исцеления. Йоги в глубокой медитации произносят звук «АУМ» (ОМ) и воображают изображение мандалы Шри-янтры, которая считается визуальным образом этого одного из самых древних звуков в мире. Некоторые называют это проявлением божественного звука. Треугольники в Шри-Янтре прекрасно интегрированы на основе числа Пи, а также построены на базе гармоничных законов Золотого сечения, числа Фи. Греческий философ Пифагор понял связь между звуком и священной геометрией, о чём написал Евклид в своём труде «Начала» примерно в 300 году до нашей эры. Лука Пачоли, современник Леонардо да Винчи, написал об этом в книге «О Божественной пропорции» (De Divina Proportione) в 1509 году, а Иоганн Кеплер – примерно в 1600 году. Многие другие на протяжении веков знали о «космической» математике и её мощной исцеляющей силе.
Некоторые называют это проявлением божественного звука. Треугольники в Шри-Янтре прекрасно интегрированы на основе числа Пи, а также построены на базе гармоничных законов Золотого сечения, числа Фи. Греческий философ Пифагор понял связь между звуком и священной геометрией, о чём написал Евклид в своём труде «Начала» примерно в 300 году до нашей эры. Лука Пачоли, современник Леонардо да Винчи, написал об этом в книге «О Божественной пропорции» (De Divina Proportione) в 1509 году, а Иоганн Кеплер – примерно в 1600 году. Многие другие на протяжении веков знали о «космической» математике и её мощной исцеляющей силе.
Гармонические звуки создают порядок из хаоса. Можно сказать, болезнь – это разновидность хаоса в организме.
Как утверждает доктор Роберт Фридман, связь между золотым сечением и идеальным здоровьем была и ежу понятна.
Наблюдения доктора Фридмана в 1980-е годы позволили ему обнаружить проявление Золотого сечения (или божественных пропорций) по всему телу человека – на анатомическом, физиологическом и молекулярном уровне.
«Чем больше я углублялся, тем глубже открывал этот невероятный и вездесущий код в построении всех систем и функций организма… из этого следует, что чем больше человек гармонизируется в соответствии с этим грандиозным принципом, тем более эффективной и лёгкой может стать его жизнь», – заключил Фридман.
Исцеляющие частоты
Что такое болезнь? «Нерешённые эмоциональные проблемы могут блокировать целительные вибрации или способствовать рецидивам болезни». Ричард Гордон
На протяжении тысячелетий те, кто изучал науку о звуке, стали понимать, что определённые частоты чрезвычайно целебны для человеческого организма.
«Когда две системы колеблются на разных частотах, возникает побуждающая сила под названием резонанс, что вызывает передачу энергии от одной системы к другой. Когда две одинаково настроенные системы вибрируют на разных частотах, возникает другой аспект передачи энергии – вовлечение, которое выравнивает эти две системы и заставляет их вибрировать с одной и той же частотой». Ричард Гордон
Ричард Гордон
Когда мы «вовлекаемся» в целебные частоты, наше тело и разум вибрируют в гармонии. Они включают в себя:
285 Гц – сигналы клеткам и тканям к исцелению. Вызывает в теле ощущение обновления, приятной лёгкости.
396 Гц – освобождает от чувства вины и страха, чтобы расчистить путь для эмоций более высоких вибраций.
417 Гц – способствует «развязыванию» сложных ситуаций.
528 Гц – сигнал к исцелению ДНК, восстановлению клеток и пробуждению сознания.
639 Гц – это вибрация, связанная с сердцем. Она позволяет стереть различие между чувством любви к себе и к «другим». Слушайте эту частоту, чтобы сбалансировать отношения.
741 Гц – сигнал к очищению и исцелению клеток от воздействия электромагнитного излучения. Помогает расширить возможности для создания желаемой реальности.
852 Гц – пробуждает интуицию.
963 Гц – активизирует деятельность шишковидной железы и приводит тело к его совершенному изначальному состоянию.
Безусловно, существуют и другие частоты, многие из которых находятся за пределами диапазона человеческого слуха, но обладают исцеляющими свойствами.
Русский инженер Георгий Лаховский, разработавший устройство, которое назвал «многоволновым» генератором (МВГ), также понимал мощь звука. Он знал, что определённые частоты укрепляют живое существо.
«У истоков всякой силы и движения лежит музыка и ритм, игра повторяющихся частот на фоне матрицы времени. Мы знаем, что каждая частица в физической Вселенной берёт свои характеристики из высоты, узора и обертона определённой частоты, своего пения. До того как мы делаем музыку, музыка делает нас». Йоахим-Эрнст Берендт, «Мир – это звук».
По материалам: themindunleashed.org
Артикул: серия гармоник
Артикул: серия гармоникteoria.com использует файлы cookie. Используя наш сайт, вы соглашаетесь на использование файлов cookie. Прочтите нашу политику конфиденциальности для получения дополнительной информации. Закрыть
Когда мы слышим звук, издаваемый музыкальным инструментом, мы на самом деле слушаем множество звуков, которые образуют гармонический ряд.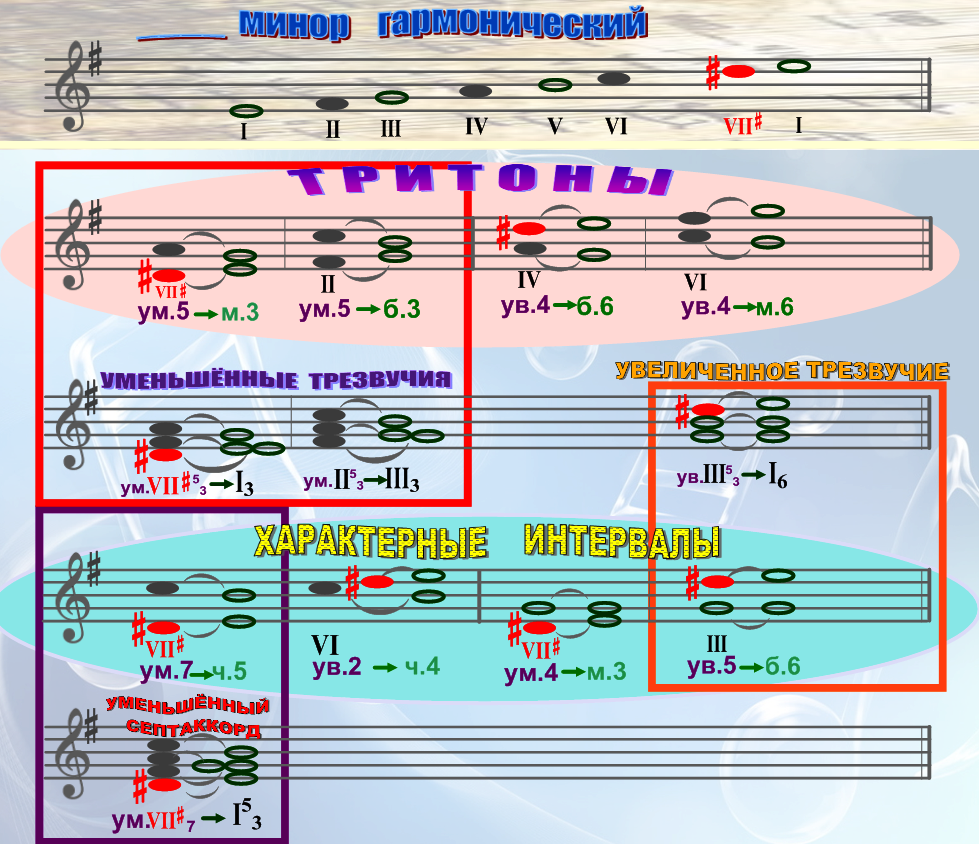 В семнадцатом веке француз Жозеф Совер (1653-1716) и англичанин Томас Пиго (1657-1686) отметили, что струны колеблются по частям — явление, объясняющее, почему одна струна производит такое множество звуков.
В семнадцатом веке француз Жозеф Совер (1653-1716) и англичанин Томас Пиго (1657-1686) отметили, что струны колеблются по частям — явление, объясняющее, почему одна струна производит такое множество звуков.
На видео ниже показан спектральный анализ C на две октавы ниже среднего C (C2):
Примечания:
- Мы написали ноты, соответствующие первым 16 гармоникам серии. Очевидно, что за этими первыми гармониками следует много гармоник.
- Первая гармоника или основная гармоника не обязательно является самой сильной гармоникой.
- Баланс между гармониками постоянно меняется. В сочетании с огромным количеством гармоник это объясняет трудности, с которыми мы сталкиваемся при синтезе звуков.
Важность гармонического ряда
Гармонический ряд определяет многие из наших интервалов. Ниже перечислены октава, пятая, четвертая, мажорная треть и малая седьмая:
. Мы можем вычислить математическое соотношение (или размер), разделив частоты нот. Здесь мы используем частоту некоторых гармоник для вычисления размера интервалов:
Здесь мы используем частоту некоторых гармоник для вычисления размера интервалов:
| Интервал | Передаточное отношение | По гармоникам |
|---|---|---|
| Октава | 130/65 = 2 | 1 и 2 |
| Пятая | 195/130 = 1.5 | 2 и 3 |
| Четвертый | 260/195 = 1,33 | 3 и 4 |
| Большая третья | 325/260 = 1,25 | 4 и 5 |
| Малая седьмая | 455/260 = 1,75 | 4 и 7 |
Интересно, что мы можем вычислить значения, используя номера гармоник:
| Интервал | Передаточное отношение | По гармоникам |
|---|---|---|
| Октава | 2/1 = 2 | 1 и 2 |
| Пятая | 3/2 = 1. 5 5 | 2 и 3 |
| Четвертый | 4/3 = 1,33 | 3 и 4 |
| Большая третья | 5/4 = 1,25 | 4 и 5 |
| Малая седьмая | 7/4 = 1,75 | 4 и 7 |
Расчет частот
Математические соотношения могут использоваться для расчета частоты нот.Из A 440 мы вычисляем частоту C #, E и G:
| А | C # (основная треть) | E (идеальный пятый) | G (второстепенная седьмая) |
| 440 | 440 х 1,25 = 550 | 440 х 1,5 = 660 | 440 x 1,75 = 770 |
Если разделить на математическое соотношение, мы получим убывающие интервалы. Здесь мы вычисляем частоту F, большая треть ниже A:
Tweet Follow @teoriaEng
Гармоники звука | исцеляющие звуки. com
com
До сих пор мы обсуждали различные аспекты звука, включая такие концепции, как «частота», «намерение», «колебательный резонанс», «визуализация», «вокализация» и другие аспекты использования звука для сдвига частоты. В прошлом выпуске мы упоминали идею «гармонического языка». Пришло время перейти к теме гармоник или обертонов, как их еще называют.
Вы слышали термин «гармоники», используемый во многих различных областях — от Гармонической Конвергенции до многих священных научных трудов.Мне особенно нравится упоминание о сдвиге гармонического резонанса щита Энтерпрайзес в «Звездном пути: новое поколение». Но многие ли из вас действительно знают, что такое «гармоники»?
Проще говоря, гармоники — это геометрические кратные, созданные сингулярными колебаниями объекта. Например, если вы приводите струну в движение — скажем, она резонирует с частотой 440 герц, то есть колеблется вверх и вниз 440 раз в секунду — это называется основной частотой.
Итак, эта основная частота — это то, на что люди обращают больше всего внимания. Если бы вы ударили эту ноту 440 герц на пианино (или на любом другом инструменте), вы могли бы назвать эту ноту «А», и вы бы сосредоточили большую часть своего внимания на том, чтобы услышать эту ноту «А», когда она вибрирует. .
Если бы вы ударили эту ноту 440 герц на пианино (или на любом другом инструменте), вы могли бы назвать эту ноту «А», и вы бы сосредоточили большую часть своего внимания на том, чтобы услышать эту ноту «А», когда она вибрирует. .
Но на самом деле эта струна, которая производит фундаментальную вибрацию 440 герц, также производит много других тонов или обертонов. Эти гармоники на самом деле являются результатом других колебаний внутри струны, созданных этой фундаментальной нотой — вибрацией, которая является квантовой по своей природе и является геометрической кратной основной ноте.
Эта нота «А» в 440 герц создает первый обертон, вибрируя на частоте, вдвое превышающей основную — на 880 герц. И это то, что вы называете октавой. Второй обертон вибрирует в 3 раза быстрее, чем основной, на частоте 1320 герц. А следующий обертон вибрирует в 4 раза быстрее. Следующий обертон вибрирует в 5 раз быстрее и так далее. До — по крайней мере концептуально — до бесконечности. Итак, вы видите, что, хотя то, что вы можете воспринимать как простую ноту «ля», вибрирующую с частотой 440 герц, на самом деле представляет собой сложную композицию этой основной ноты и обертонов, вибрирующих вместе.
На самом деле, почти каждый звук, который вы слышите (если он не создается каким-либо электронным лабораторным инструментом), производит эти сложные тона — эти гармоники. Фактически они несут ответственность за создание различных звуков, которые мы слышим. Гармоники определяют так называемый «тембр» или цвет тона инструмента. Когда в лаборатории электроники гармоники были удалены из записей трех разных инструментов, слушатели не могли различить их, но в реальной жизни легко отличить скрипку, трубу и флейту.То же самое и с человеческим голосом — каждый голос индивидуален, потому что каждый голос имеет свой образец гармоники. Хотя гармоники всегда звучат как геометрические кратные основного тона, разные гармоники будут сильнее усиливаться на разных инструментах и у разных людей.
На метафорическом уровне (все еще работая в рамках принципов физики звука), когда кто-то говорит о гармонике чего-то, этот человек говорит о более высокой частоте, которая является геометрическим кратным. Геометрическое кратное — это просто целое число (в отличие от дроби), что означает, что гармоники квантовые. Таким образом, гармоника, скажем, 100 циклов в секунду (или герц) может быть просто 100 Гц, умноженной на любое число (от 1 до бесконечности). Это может быть 200, 500 или 5000.
Геометрическое кратное — это просто целое число (в отличие от дроби), что означает, что гармоники квантовые. Таким образом, гармоника, скажем, 100 циклов в секунду (или герц) может быть просто 100 Гц, умноженной на любое число (от 1 до бесконечности). Это может быть 200, 500 или 5000.
Гармоник звука
мы обсудим частоты колебательных мод струны, которые создают модели стоячих волн, поскольку они оказываются гармониками или целыми числами, умноженными на основную частоту, которая является основой нашей музыкальной гаммы.
У струны есть несколько режимов вибрации. Эти колебательные режимы являются основой нашей западной музыки и музыкальной гаммы, а также основных аккордов.
Каждая форма колебаний струны добавляет узел или неподвижную точку в струне, которая разбивает исходную струну на еще один «кусок», который
резонировать
на его основной частоте. Таким образом, в каждом случае струна могла бы разбиться на одну или несколько более коротких частей, которые, как ни странно, вибрировали с целыми числами, кратными основной гармонике. частота.
частота.
История обнаружения гармоник — Герман фон Гельмгольц (1821-1894)
Герман фон Гельмгольц (1821–1894) разработал резонаторы Гельмгольца — полую стеклянную сферу с двумя короткими горлышками. Одно отверстие было направлено к источнику звука, другое — к уху слушателя. Гельмгольц резонатор затем действовал как резкий частотный фильтр, который позволял слушателю слышать частоты только в определенном диапазоне. Экспериментируя с различными размерами резонаторы настроенный на разные частоты, Гельмгольц смог оценить силу гармоник в различных звуках.
Частотные отношения между модами
Если основная частота струны составляет 100 Гц, первая гармоника или следующая колебательная мода будет на 200 Гц. Это имеет смысл, поскольку струна ровно 1/2 длины и, следовательно, будет вибрировать в два раза быстрее. Эта вторая колебательная мода струны называется второй гармоникой и в два раза превышает частоту основной гармоники.
Третья гармоника
Третья гармоника возникает, когда мы разбиваем струну на три, казалось бы, независимые колебательные
части, которые вибрируют в три раза быстрее основной.