алгоритмы k-means и c-means / Хабр
Добрый день!
Как и обещал, продолжаю серию публикаций о технологии Data Mining. Сегодня хочу рассказать о двух алгоритмах кластеризации (k-means и c-means), описать преимущества и недостатки, дать некоторые рекомендации по их использованию. Итак, поехали…
Кластеризация — это разделение множества входных векторов на группы (кластеры) по степени «схожести» друг на друга.
Кластеризация в Data Mining приобретает ценность тогда, когда она выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику часто легче выделить группы схожих объектов, изучить их особенности и построить для каждой группы отдельную модель, чем создавать одну общую модель для всех данных. Таким приемом постоянно пользуются в маркетинге, выделяя группы клиентов, покупателей, товаров и разрабатывая для каждой из них отдельную стратегию (Википедия).
Меры расстояний
Для того, чтобы сравнивать два объекта, необходимо иметь критерий, на основании которого будет происходить сравнение.
Как правило, таким критерием является расстояние между объектами.
Есть множество мер расстояния, рассмотрим несколько из них:
Евклидово расстояние — наиболее распространенное расстояние. Оно является геометрическим расстоянием в многомерном пространстве.
Квадрат евклидова расстояния. Иногда может возникнуть желание возвести в квадрат стандартное евклидово расстояние, чтобы придать большие веса более отдаленным друг от друга объектам.
Расстояние городских кварталов (манхэттенское расстояние). Это расстояние является просто средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако отметим, что для этой меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат).
Расстояние Чебышева. Это расстояние может оказаться полезным, когда желают определить два объекта как «различные», если они различаются по какой-либо одной координате (каким-либо одним измерением).
Степенное расстояние. Иногда желают прогрессивно увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Это может быть достигнуто с использованием степенного расстояния.
Выбор расстояния (критерия схожести) лежит полностью на исследователе. При выборе различных мер результаты кластеризации могут существенно отличаться.
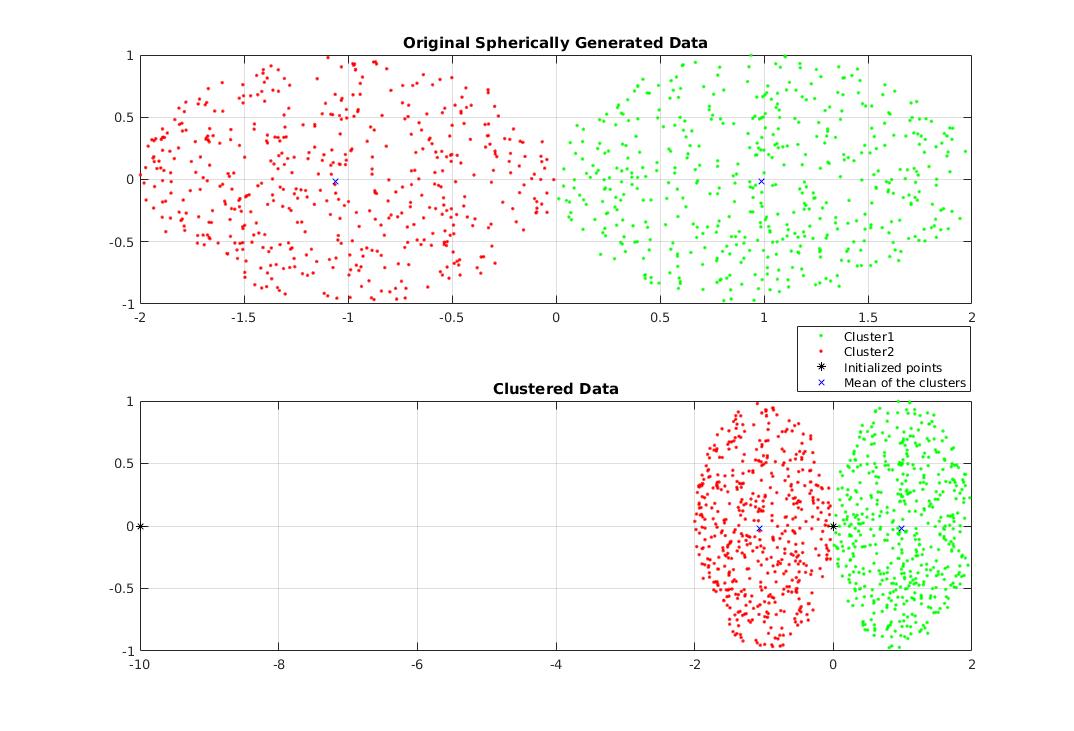
Алгоритм k-means (k-средних)
Наиболее простой, но в то же время достаточно неточный метод кластеризации в классической реализации. Он разбивает множество элементов векторного пространства на заранее известное число кластеров k. Действие алгоритма таково, что он стремится минимизировать среднеквадратичное отклонение на точках каждого кластера. Основная идея заключается в том, что на каждой итерации перевычисляется центр масс для каждого кластера, полученного на предыдущем шаге, затем векторы разбиваются на кластеры вновь в соответствии с тем, какой из новых центров оказался ближе по выбранной метрике.
Проблемы алгоритма k-means:
* необходимо заранее знать количество кластеров. Мной было предложено метод определения количества кластеров, который основывался на нахождении кластеров, распределенных по некоему закону (в моем случае все сводилось к нормальному закону). После этого выполнялся классический алгоритм k-means, который давал более точные результаты.
* алгоритм очень чувствителен к выбору начальных центров кластеров.
* не справляется с задачей, когда объект принадлежит к разным кластерам в равной степени или не принадлежит ни одному.
Материалы по теме:
* Википедия — K-means
* Introduction to K-means
* Описание функции kmeans в Matlab Statistics Toolbox
* K-means — Interactive demo (Java)
Нечеткий алгоритм кластеризации с-means
С последней проблемой k-means успешно справляется алгоритм с-means. Вместо однозначного ответа на вопрос к какому кластеру относится объект, он определяет вероятность того, что объект принадлежит к тому или иному кластеру. Таким образом, утверждение «объект А принадлежит к кластеру 1 с вероятностью 90%, к кластеру 2 — 10% » верно и более удобно.
Классический пример с-means — т.н. «бабочка» (butterfly):
Как видно, точка с координатами (3,2) в равной степени принадлежит как первому так и второму кластеру.
Остальные проблемы у с-means такие же, как у k-means, но они нивелируются благодаря нечеткости разбиения.
Ссылки по теме:
* Формальное описание алгоритма и реализация на C#
* Fuzzy c-means clustering
* Fuzzy C-means cluster analysis
P.
S. Я не описывал математические принципы алгоритмов, с ними легко можно ознакомиться по представленным ссылкам.
Спасибо за внимание!
Моделирование систем — тест 3
Упражнение 1:
Номер 1
Нормальный закон распределения случайных величин характеризуется следующими параметрами:
Ответ:
 (1) математическим ожиданием и стандартным отклонением 
 (2) коэффициентами ковариации и корреляции 
 (3) величиной три-сигма и максимальным значением функции плотности 
 (4) математическим ожиданием и средним квадратическим отклонением 
 (5) средним значением функции распределения и средним значением нормированной корреляционной функции 
Номер 2
Что определяет собой функция распределения нормально распределенных случайных величин?
Ответ:
 (1) значения случайных величин, попадающих в интервал три-сигма 
 (2) вероятность того, что случайная величина будет простым числом 
 (3) вероятность того, что случайная величина не превысит наперед заданную величину 
 (4) вероятность того, что случайная величина попадет в интервал три-сигма 
 (5) определенный интеграл с переменным верхним пределом от функции плотности 
Номер 3
В каких пределах заключена область изменения функции распределе-ния равномерно распределенных случайных величин?
Ответ:
 (1)
 (2) от минус единицы до нуля 
 (3) от минус единицы до плюс единицы 
 (4) всегда равна плюс единице 
Номер 4
В каких пределах заключена область изменения функции распределе-ния экспоненциально распределенной случайной величины?
Ответ:
 (1) от единицы до двух 
 (2) от нуля до единицы 
 (3) от минус единицы до нуля 
 (4) в пределах значений, принимаемой вероятностью появления случайной величины 
Упражнение 2:
Номер 1
Выборка случайных чисел с экспоненциальным распределением может быть определена
Ответ:
 (1) с помощью равномерно распределенных чисел 
 (2) с помощью равномерно распределенных чисел из интервала от нуля до единицы 
 (3) с помощью нормально распределенных случайных чисел 
 (4) с помощью биномиально распределенных случайных чисел 
Номер 2
Что определяет собой функция распределения нормально распределенных случайных величин?
Ответ:
 (1) значения случайных величин, попадающих в интервал три-сигма 
 (2) вероятность того, что случайная величина будет простым числом 
 (3) вероятность того, что случайная величина не превысит наперед заданную величину 
 (4) вероятность того, что случайная величина попадет в интервал три-сигма 
 (5) определенный интеграл с переменным верхним пределом от функции плотности 
Номер 3
В каких пределах заключена область изменения функции распределения нормально распределенных случайных величин?
Ответ:
 (1) от нуля до единицы 
 (2) от минус единицы до нуля 
 (3) от минус единицы до плюс единицы 
 (4) всегда равна плюс единице 
Номер 4
В каких пределах заключена область изменения функции распределения равномерно распределенной случайной величины из интервала от минус десяти до плюс десяти?
Ответ:
 (1) от нуля до десяти 
 (2) от нуля до единицы 
 (3) от минус десяти до нуля 
 (4) в пределах значений, принимаемой вероятностью появления случайной величины 
Упражнение 3:
Номер 1
Функция плотности непрерывно распределенных случайных величин представляет собой
Ответ:
 (1) значение вероятности, приходящейся на единицу длины изменения случайных величин 
 (2) производную от соответствующей функции распределения 
 (3) среднее значение случайных чисел, отнесенных на единицу длины изменения случайных величин 
 (5) определенный интеграл с переменным нижним пределом от функции распределения случайных величин 
Номер 2
Если даны две функции распределения экспоненциально распределенных случайных величин и они различаются значениями своих параметров, то в каких пределах они будут изменяться?
Ответ:
 (1) пределы их изменений будут зависеть от величины параметров 
 (2) они будут изменяться в различных пределах 
 (3) они будут изменяться в пределах изменения вероятностей случайных величин 
 (4) они будут изменяться в пределах от нуля до единицы 
 (5) они будут изменяться от нуля до бесконечности 
Номер 3
Область определения функции распределения экспоненциально распределенных случайных величин заключена в пределах
Ответ:
 (1) от нуля до единицы 
 (2) от минус бесконечности до нуля 
 (3) от нуля до плюс бесконечности 
 (4) от минус бесконечности до плюс бесконечности 
Номер 4
Область определения функции распределения нормально распределенных случайных величин заключена в пределах
Ответ:
 (1) от нуля до единицы 
 (2) от минус бесконечности до нуля 
 (3) от нуля до плюс бесконечности 
 (4) от минус бесконечности до плюс бесконечности 
Упражнение 4:
Номер 1
Чему равно математическое ожидание равномерно распределенных случайных величин из интервала от нуля до единицы?
Ответ:
 (1) 1 
 (2) 0 
 (3) 1/2 
 (4) 1/3 
 (5) 1/4 
Номер 2
Чему равно математическое ожидание экспоненциально распределенных случайных величин, если параметр функции распределения равен одной второй?
Ответ:
 (1) 1/2 
 (2) 1 
 (3) 3/2 
 (4) 4/2 
Номер 3
Чему равен параметр функции распределения экспоненциально распределенных случайных величин, если их математическое ожидание равно двум?
Ответ:
 (1) 1/2 
 (2) 1 
 (3) 3/2 
 (4) 4/2 
Номер 4
От чего зависит функция плотности непрерывной равномерно распределенной случайной величины?
Ответ:
 (1) она переменная и зависит от интервалов изменения случайных величин 
 (2) она постоянная и зависит от интервалов изменения случайных величин 
 (3) она обратно пропорциональна величине интервала, в котором изменяются случайные величины 
 (4) она прямо пропорциональна величине интервала, в котором изменяются случайные величины 
Упражнение 5:
Номер 1
Чему равно математическое ожидание равномерно распределенных случайных величин из интервала от -1 до +1?
Ответ:
 (1) 1 
 (2) 0 
 (3) 1/2 
 (4) 1/3 
 (5) 1/4 
Номер 2
Если случайные величины распределены по закону Эрланга 4-го порядка с параметром равным 1, то чему будет равно математическое ожидание случайных величин?
Ответ:
 (1) 1 
 (2) 2 или 3 
 (3) 3 или 4 
 (4) 4 или 5 
Номер 3
Если случайные величины распределены по закону Эрланга 4-го порядка с параметром равным 1, то чему будет равна дисперсия случайных величин?
Ответ:
 (1) 1 
 (2) 2 или 3 
 (3) 3 или 4 
 (4) 4 или 5 
Номер 4
В каких пределах изменяется функция распределения случайных величин, распределенных по закону Эрланга 4-го порядка с параметром равным 2?
Ответ:
 (1) от 1 до 2 
 (2) от -2 до +2 
 (3) от 0 до +1 
Упражнение 6:
Номер 1
С помощью какой функции системы MATLAB рассчитывается выборочное среднее?
Ответ:
 (1) std 
 (2) mean 
 (3) var 
 (4) cov 
Номер 2
С помощью какой функции системы MATLAB рассчитывается исправленное стандартное отклонение выборки случайных чисел?
Ответ:
 (1) std 
 (2) mean 
 (3) var 
 (4) cov 
Номер 3
С помощью какой функции системы MATLAB рассчитывается исправленная выборочная дисперсия вектора случайных величин?
Ответ:
 (1) std 
 (2) mean 
 (3) var 
 (4) cov 
Номер 4
Для чего применяют исправленную выборочную дисперсию?
Ответ:
 (1) чтобы получить смещенную оценку истинной дисперсии 
 (2) чтобы получить несмещенную оценку истинной дисперсии 
 (3) чтобы упростить расчеты 
 (4) чтобы упростить расчет стандартного отклонения 
Упражнение 7:
Номер 1
С помощью какой функции системы MATLAB можно сформировать выборку равно мерно распределенных случайных чисел из интервала от -3 до +3?
Ответ:
 (1) rand 
 (2) randn 
 (3) sprand 
 (4) unifrnd 
Номер 2
С помощью какой функции системы MATLAB можно сформировать выборку нормально распределенных случайных чисел с математическим ожиданием, равным 0, и стандартным отклонением, равным 1?
Ответ:
 (1) rand 
 (2) randn 
 (3) sprand 
 (4) normrnd 
Номер 3
С помощью какой функции системы MATLAB можно сформировать выборку нормально распределенных случайных чисел с математическим ожиданием, равным 1, и стандартным отклонением, равным 2?
Ответ:
 (1) randn 
 (2) normrnd 
 (3) normfit 
 (4) normspec 
Номер 4
С помощью какой функции системы MATLAB можно сформировать выборку случайных чисел, распределенных по закону Эрланга 4-го порядка с параметром равным 1?
Ответ:
 (1) randn 
 (2) normrnd 
 (3) gamrnd 
 (4) такой функции не существует 
Главная / Алгоритмы и дискретные структуры / Моделирование систем / Тест 3
Получить среднее значение массива с помощью функции mean() в Matlab
В этом руководстве будет обсуждаться нахождение среднего или среднего значения массива с использованием функции mean() в MATLAB.
Чтобы найти среднее значение массива, мы можем использовать встроенную функцию Matlab mean() . Если мы передаем вектор или массив, функция mean() вернет среднее значение всех элементов массива. Например, давайте найдем среднее значение вектора, используя функцию mean() . См. код ниже.
вектор = [1 3 5]; среднее = среднее (вектор)
Выход:
среднее =
3
Если входными данными является матрица, то функция mean() вернет вектор-строку, содержащую среднее значение каждого столбца матрицы. Например, предположим, что у вас есть матрица с тремя столбцами. Затем функция mean() вернет вектор-строку, содержащую три элемента, которые будут средним значением каждого столбца. Например, давайте найдем среднее значение столбцов матрицы, используя mean() функция. См. код ниже.
вектор = [1 3 5; 2 3 6] среднее = среднее (вектор)
Вывод:
вектор =
1 3 5
2 3 6
среднее =
1,5000 3,0000 5,5000
Как видите, входная матрица состоит из трех столбцов, выходная — из трех элементов, и каждый элемент соответствует среднему значению каждого столбца.
Если вы не хотите брать среднее значение столбцов, вам нужно взять среднее значение каждой строки. Вы можете указать это в mean() в качестве второго аргумента, вы должны добавить второй аргумент, который будет целым числом 2. Например, давайте найдем среднее значение строк матрицы, используя функцию mean() . См. код ниже.
вектор = [1 3 5; 2 3 6] среднее = среднее (вектор, 2)
Вывод:
вектор =
1 3 5
2 3 6
среднее =
3.0000
3,6667
Как видите, входная матрица состоит из двух строк, выходная — из двух элементов, и каждый элемент соответствует среднему значению каждой строки. Вы также можете указать тип выходного файла или тип выходных данных в качестве второго аргумента в среднее() функция. Например, вы можете указать, что вывод должен быть двойным или родным. Например, давайте определим тип данных приведенной выше матрицы как double. См. код ниже.
вектор = [1 3 5; 2 3 6] среднее = среднее (вектор, 'двойной')
Вывод:
вектор =
1 3 5
2 3 6
среднее =
1,5000 3,0000 5,5000
Если вы не хотите использовать функцию mean() , вы также можете использовать sum() и length() , чтобы найти среднее значение.
Мы знаем, что среднее равно сумме элементов, деленной на количество элементов. Мы можем получить сумму элементов, используя функцию sum() , и количество элементов, используя функцию length() , и после этого нам нужно разделить сумму на длину, чтобы получить среднее значение.
mean-in-matlab — Googlesuche
AlleVideosBilderNewsMapsShoppingBücher
suchoptionen
M = mean( A ) возвращает среднее значение элементов A по первому измерению массива, размер которого не равен 1.
Если A является вектором, то mean(A) возвращает среднее значение элементов.
Если A является матрицей, то mean(A) возвращает вектор-строку, содержащую среднее значение каждого столбца.
Среднее или среднее значение массива — Среднее значение MATLAB — MathWorks
www.mathworks.com › … › Импорт и анализ данных › Описательная статистика а медиана в MATLAB?
Что означает == в MATLAB?
Как вы берете среднее значение определенной строки в MATLAB?
Как сделать стандартное отклонение в MATLAB?
Среднее или среднее значение массива — Среднее значение MATLAB — MathWorks
de.
mathworks.com › … › Описательная статистика
Если A является вектором, то mean(A) возвращает среднее значение элементов.
Описание · Примеры · Входные аргументы
Среднее или среднее значение элементов матрицы — MATLAB mean2 — MathWorks
www.mathworks.com › help › images › ref › mean2
Эта функция MATLAB вычисляет среднее значение всех значений в массиве A.
Среднее или среднее значение массива с фиксированной точкой — MATLAB mean .mathworks.com › help › fixedpoint › ref › me…
M = mean( A ) вычисляет среднее значение массива A с фиксированной точкой с действительным знаком по его первому неодноэлементному измерению. пример. M = mean( A , dim ) вычисляет …
Описание · Примеры · Входные аргументы
Средняя функция в MATLAB — GeeksforGeeks
www.geeksforgeeks.org › mean-function-in-matlab
29.06.2021 · Среднее или среднее — это среднее значение последовательности чисел. В MATLAB mean (A) возвращает среднее значение компонентов A по первому массиву .
..
mean (функции MATLAB)
matlab.izmiran.ru › help › techdoc › ref › mean
M = mean(A) возвращает средние значения элементов по разным измерениям массива. Если A является вектором, mean(A) возвращает среднее значение A . Если А …
mean (функции MATLAB)
www.ece.northwestern.edu › techdoc › ref › mean
M = mean(A) возвращает средние значения элементов по различным измерениям массива. Если A является вектором, mean(A) возвращает среднее значение A . Если A равно …
Функция Matlab — Среднее значение-среднее () — YouTube
www.youtube.com › смотреть
06.03.2013 · Это учебник Matlab по среднему значению, встроенному в функцию Matlab. средняя функция используется для получения …
Dauer: 2:00
Прислано: 06.03.2013
Вычислить среднее значение массива в MATLAB — Stack Overflow
stackoverflow.com › вопросы › вычислить среднее…
суммы = 0; счетчик = 0; for val = числа, суммы = суммы + val; счетчик = счетчик + 1; end Numbers_mean = суммы/счетчик;.