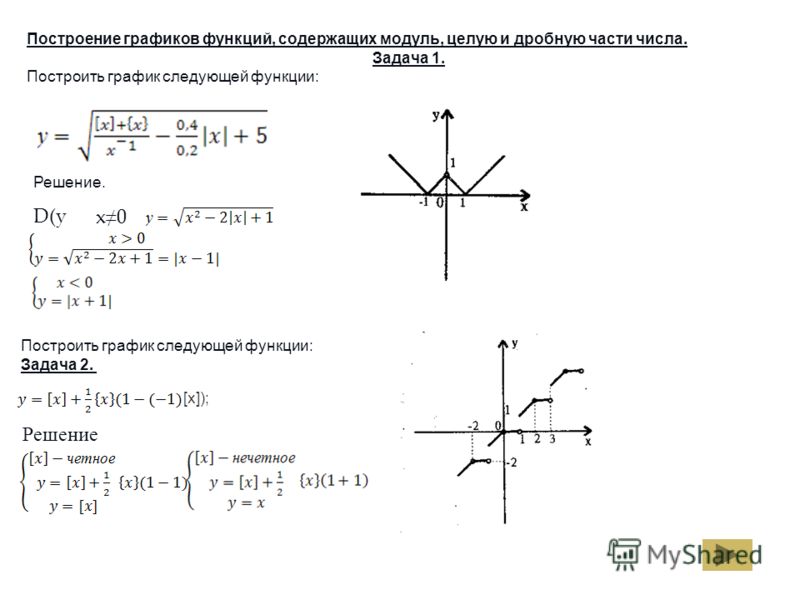
Функция целая часть числа | Алгебра
Определение
Целой частью действительного числа x (x∈R) называется наибольшее целое число, не превосходящее x.
Целую часть числа x обозначают символом [x].
[x] читают «антье от x».
Обозначение [x] в 1808 году ввёл К. Гаусс.
В частности, если n — целое число (n∈Z), то [n]=n.
Примеры.
Вычислить целую часть числа:
7,8; 0,12; -0,7; -4,92; 15 2/3; 5/7; -3/11; 8; -50.
Решение:
Фактически вычисление целой части числа x представляет собой округление до ближайшего к числу x целого числа в меньшую сторону (то есть округление с недостатком).
[7,8]=7;
[0,12]=0;
[ -0,7]= -1;
[-4,92]= -5;
[8]=8;
[-50]= -50.
Определение
Функцию, ставящую в соответствие каждому значению x его целую часть — число [x], называют целой частью числа x и обозначают y=[x] .
Функция целая часть числа определена для любого действительного x (x∈R).
Область значений функции y=[x] — множество целых чисел (y∈Z).
Утверждение.
Для любого k∈Ζ [x+k]=[x]+k.
Доказательство:
Пусть [x]=m.
По определению целой части числа
m≤x<m+1,
m+k≤x+k<(m+k)+1.
Отсюда [x+k]=m+k=[x]+k.
Что и требовалось доказать.
График функции y=[x]
Стрелки на графике показывают, что правые концы отрезков не принадлежат графику.
Другой вариант показать, что левые концы отрезков принадлежат графику, а правые — не принадлежат, выделить их, соответственно, закрашенными и выколотыми точками:
Как решить уравнение с целой частью числа?
Простейшее уравнение [x]=a имеет решения только при целых значениях a. Если a∉Ζ, уравнение не имеет решений.
При a∈Ζ решения уравнения [x]=a удовлетворяют условию a≤x<a+1.
Примеры.
1) [x]=7
7≤x<7+1, то есть 7≤x<8.
Ответ запишем в виде числового промежутка (в данном случае, полуинтервала).
Ответ: x∈[7;8).
2) [x]=3,2.
Это уравнение не имеет решений, так как 3,2∉Ζ.
3) [7,2-0,5x]= -3
-3≤7,2-0,5x<-3+1
-3≤7,2-0,5x<-2.
Прибавим почленно к каждой части неравенства -7,2. Знаки неравенства при этом не изменятся:
-3-7,2≤-0,5x<-2-7,2
-10,2≤-0,5x<-9,2.
Умножим каждую часть неравенства на -2. При умножении на отрицательное число знаки неравенства меняются на противоположные:
20,4≥x>18,4
18,4<x≤20,4.
Ответ: x∈(18,4; 20,4].
4)2x-3[x]=9.
Выразим целую часть числа числа [x]:
Отсюда
Таким образом, x∈[-9;-6) и
На промежутке [-9;-6) [x] принимает три значения.
1. При x∈[-9;-8) [x]= -9.
Подставив в равенство (*) [x]= -9, найдём x:
Так как -9∈[-9;-8), то x= -9 — корень уравнения.
2. При x∈[-8;-7) [x]= -8, откуда
-7,5∈[-8;-7), поэтому x= -7,5 — корень уравнения.
3. При x∈[-7;-6) [x]= -7, и
-6∉[-7;-6), значит x= -6 не является корнем уравнения.
Ответ: -9; -7,5.
Рубрика: Функции | КомментарииЦелая и дробная части числа
- Попугаева Галина Николаевна
Разделы: Математика
Введение
Участвуя в олимпиадах по математике, я столкнулся с трудностями при использовании таких понятий, как »целая» и »дробная» части числа. Эти понятия представляют наибольшую сложность как в логическом, так и в техническом плане. Так как данной темы нет в программе для общеобразовательных школ, то я поставил перед собой следующие цели:
- Познакомиться с понятиями »целая» и »дробная»
части числа.
- Уметь применять эти понятия при решении уравнений и неравенств.
- Рассмотреть функции вида: y=[x] и y={x} их графики и свойства.
Целая часть числа
Целой частью числа x называется наибольшее целое число n, не превышающее x. Целая часть числа x обозначается символом [x] или (реже) E(x) (от фр. entier «антье» — целый).
Примеры: [2,6] = 2; [- 2,6] = -3.
Свойство целой части числа:
Если x принадлежит интервалу [n; n +1), где n — целое число, то [x]=n, т.е. x находится в интервале [ [x]; [x]+1). Значит [x] x < [x] + 1.
Решение уравнений, содержащих целую
часть числа
Решение системы неравенств:
Дробная часть числа
Дробной частью числа называют разность
между самим числом x и его целой частью.
Примеры: {2,81} = 0, 81; {-0,2} = 0,8
Свойство дробной части числа:
Дробная часть числа всегда неотрицательна и не превышает 1, т.е.
Решение уравнений, содержащих дробную часть числа
Решение неравенства, содержащего
дробную и целую части числа
Продолжение (функция у=[x], ее свойства и график; функция у={x}, ее свойства и график; преобразование графиков в системе координат; графики, содержащие целую и дробную части; графическое решение уравнений, содержащих целую и дробную части числа)
Заключение
В ходе своего исследования я пришёл к выводу,
что данный материал можно использовать на
факультативах, элективных уроках, при подготовке
к олимпиадам и вступительным экзаменам в ВУЗ.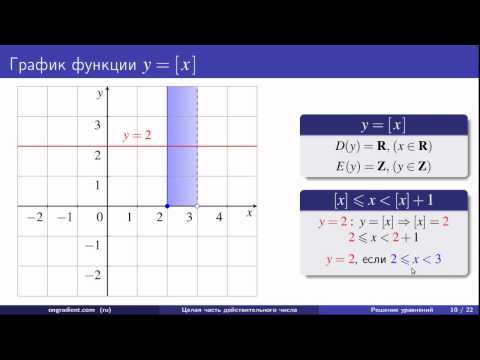
Список литературы
- В.А. Кирзимов, Центр образования “Царицыно” № 548, М. 2000 г.
- Милованова Л.Н. Функции и их исследование.- М.: Академия педагогических наук РСФСР, 1958 г.
- Глаголева Е.Г. Серебринкова Л.Г. Метод координат
- Евсюк С.Л. Математика. Решение задач повышенной сложности. Минск “Мисанта” 2003 г.
- Абрамов А. М. Ивлев Б.М. Задачи повышенной трудности по алгебре и началам анализа “Просвещение” 1990 г.
Функция дробной части | Brilliant Math & Science Wiki
Патрик Корн, Кристофер Уильямс, Хамза А, и
способствовал
Содержимое
- Свойства дробной части
- Решение проблем
- Дробные части и интегральное исчисление
Ниже приведены некоторые свойства дробной части:
- 0≤{x}<1 0 \le \{ x \} < 1 0≤{x}<1, и 0={x} 0 = \{ x \} 0={x} тогда и только тогда, когда x x x является целым числом.
- {x}+{−x}={0если x является целым числом1в противном случае. \{x \} + \{-x\} = \begin{cases} 0 & \text{если } x \text{ является целым числом} \\ 1 & \text{иначе.} \end{cases} {x }+{−x}={01если x является целым числом, иначе.
- Если a a a и b b b целые числа и b>0 b > 0 b>0, то {ab}=rb \big\{ \frac{a}{b} \big\} = \frac{r}{b} { ba}=br, где r r r — остаток от деления a a a на b b b.
{9}+{-9}=0+0=0 \{ 9 \} + \{-9\} = 0+0 = 0 {9}+{-9}=0+0=0, но {9.01 }+{-9,01}=0,01+0,99=1 \{9,01\} + \{-9,01\} = 0,01+0,99 = 1 {9,01}+{-9,01}=0,01+0,99=1. Дробная часть всегда неотрицательна.
Так как 47=13⋅3+8 47 = 13 \cdot 3 + 8 47=13⋅3+8, то {4713}=813 \left\{\frac{47}{13} \right\} = \frac{8}{13}{1347}=138. 92+10r-2 &= 0, \end{выровнено} (5+r)2+r225+10r+2r22r2+10r−2=27=27=0,
, поэтому r=−5+292 r = \frac{-5+\sqrt{29}}2r=2−5+29 по квадратичной формуле.
Следовательно, x=5+r=5+292 x = 5 + r = \frac{5+\sqrt{29}}2x=5+r=25+29.
□_\квадрат□{1x}={x} \left \{\frac 1x \right \} = \{ x \} {x1}={x}
Найдите количество решений xxx в диапазоне [1,6][1,6][1,6] такое, что приведенное выше уравнение выполняется.
Обратите внимание, что {x} \{ x \} {x} обозначает дробную часть xxx.
Найдите наименьшее действительное число m m m такое, что для всех положительных действительных чисел x x x
{x}+{1x}
Если x<1 x < 1 x<1, мы можем записать x=1y,y≥1, x = \frac1y, y \ge 1, x=y1,y≥1 и {x}+{1x }={г}+{1г}. \{ x \} + \big\{ \frac1{x} \big\} = \{ y \} + \big\{ \frac1{y} \big\}. {х}+{х1}={у}+{у1}. Таким образом, мы можем предположить, что x≥1 x \ge 1 x≥1. Тогда {1x}=1x \big\{ \frac1{x} \big\} = \frac1{x}{x1}=x1. Записав x=n+r x = n+r x=n+r, где nn n — положительное целое число, левая часть станет равной 9.- r→1−, сумма получается 1+11+1=32 1+\frac1{1+1} = \frac{3}{2} 1+1+11=23. Таким образом, ответ равен 32 \frac{3}{2} 23.
(((Упражнение: если x x x может быть отрицательным, ответ будет m=2.) m=2.)m=2.)
□_\квадрат□Найдите количество действительных xxx, удовлетворяющих уравнению {x}⌊x⌋−2⌊x⌋={x}−1 \{x\} \lfloor x \rfloor- 2\lfloor x \rfloor = \{x \} -1{х}⌊х⌋−2⌊х⌋={х}−1.
Обозначения :
Есть много интересных интегралов, включающих функцию дробной части. Хороший способ вычислить определенные интегралы этого типа — разбить интервал интегрирования на интервалы, на которых наибольшая целочисленная функция постоянна; тогда исходный интеграл представляет собой сумму интегралов, которые легче вычислить. 9{ 3 } } dx=-\frac { H }{ U } -Mγ+\frac { { M }_{ 1 } }{ U_1 } \ln { (Sπ) } -B\ln { A } ∫01{ x1}3dx=−UH−Mγ+U1M1ln(Sπ)−BlnA
В приведенном выше уравнении AAA — постоянная Глешера–Кинкелина, все остальные переменные — положительные целые числа, а все упомянутые дроби равны взаимное превосходство.
Найти H+U+M+M1+U1+S+B.H+U+M+{ M }_{ 1 }+{ U }_{ 1 }+S+B.
H+U+M+M1 +У1+С+Б.
Примечание : {x}\{x\}{x} обозначает дробную часть x.x.x.
Это часть «Кто готов принять вызов?» 9{ C } }{ D } ∫01{x1/61}dx=BA−DπC
Приведенное выше уравнение верно для натуральных чисел A,B,C,A,B,C,A,B,C и DDD, с взаимно простым числом AAA и BBB.
Найти A+B+C+DA+B+C+DA+B+C+D.
Обозначение : {⋅} \{ \cdot \} {⋅} обозначает функцию дробной части.
Процитировать как: Функция дробной части. Brilliant.org . Извлекаются из https://brilliant.org/wiki/factional-part-function/
Функция дробной части — формула, свойства, диапазон, примеры, предметная область
Функция дробной части — это особый тип функции в алгебре, который определяется как разность действительного числа и его целого значения. Как следует из названия, функция дробной части дает правильную часть числа, которая остается после вычитания из него его целого значения, и, следовательно, диапазон функции равен [0, 1).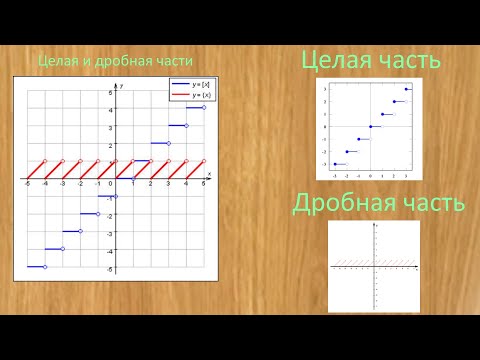
Значение функции дробной части всегда меньше единицы. Математически это обозначается как f(x) = {x}.
В этой статье мы разберемся со свойствами функции дробной части, ее областью определения и диапазоном, ее графиком и формулой. Мы также решим несколько примеров на основе функции дробной части для лучшего понимания концепции.
| 1. | Что такое функция дробной части? |
| 2. | Формула функции дробной части |
| 3. | График функции дробной части |
| 4. | Функциональная область дробной части и диапазон |
| 5. | Свойства функции дробной части |
| 6. | Часто задаваемые вопросы о функции дробной части |
Что такое функция дробной части?
Функция дробной части — это функция, которая дает дробную часть x путем вычитания наибольшего целого числа меньше x из x, где x — действительное число.
Эта функция также известна как функция десятичной части. Другими словами, мы также можем сказать, что функция дробной части определяется как разница между действительным числом и его наибольшим целым значением (которое определяется с помощью функции наибольшего целого числа), то есть, если f является функцией дробной части, то дробная часть x записывается как \(f(x) = \left \{ x \right \} = x — \left \lfloor x \right \rfloor\), где x — действительное число. Если x — целое число, то дробная часть x равна 0,9.0003
Формула функции дробной части
Теперь, когда мы знаем значение функции дробной части, давайте изучим формулу функции и запишем ее математически. Для действительного числа x функция дробной части записывается как \(f(x) = \left \{ x \right \} = x — \left \lfloor x \right \rfloor\). Чтобы понять работу функции, давайте рассмотрим несколько примеров, рассматривающих неотрицательное действительное число и отрицательное действительное число.
- Для неотрицательного действительного числа x = 2,47 функция дробной части работает как:
f(x) = {2,47} = 2,47 — 2 = 0,47, что является дробной частью 2,47· - Для отрицательного действительного числа x = -3,76 функции дробной части работают как:
f(x) = {-3,76} = -3,76 — (-4) = -3,76 + 4 = 0,24, что является дробной частью -3,76 - Для целочисленного значения x = 1 функция дробной части работает следующим образом:
f(x) = {1} = 1 — 1 = 0, что является дробной частью 1
График функции дробной части
Мы знаем, как работает функция дробной части и как определить дробную часть x.
Далее мы построим график функции дробной части, взяв несколько точек на графике. График дробной части x аналогичен графику функции наибольшего целого числа и не содержит никаких целых значений, кроме 0. Ниже приведен график функции дробной части. Как мы видим на графике, всякий раз, когда значение x является целым числом, значение дробной части x равно 0 и показано сплошной синей точкой.
Функциональная область дробной части и диапазон
Как мы видим на графике функции дробной части выше, значение функции лежит между 0 и 1, а для целых значений x значение всегда равно нулю. Из графика видно, что область определения функции дробной части состоит из всех действительных чисел, так как функция определена для всех действительных чисел. Кроме того, мы можем видеть, что, поскольку значение дробной части x лежит между 0 и 1, следовательно, диапазон функции равен [0,1).
Свойства функции дробной части
Итак, мы поняли концепцию функции дробной части.
Давайте теперь обобщим концепцию и разберемся со свойствами дробной части x. Ниже приведен список, отражающий важные свойства функции дробной части:
- Значение дробной части x лежит в диапазоне от 0 до 1, то есть 0 ≤ {x} < 1.
- Для целых значений x функция дробной части всегда равна 0,
- {x} + {-x} = 0, если x является целым числом, и {x} + {-x} = 1 в противном случае.
- Для целых чисел a и b, таких что b > 0, {a/b} = r/b, где r — остаток от деления a на b.
Важные примечания о функции дробной части
- Диапазон функции дробной части — [0, 1), а ее область определения — все действительные числа.
- Дробная часть x равна 0, если x является целым числом.
- Функция дробной части x определяется как разница между x и наибольшим целым числом меньше x.
☛ Похожие темы:
- Графические функции
- Постоянная функция
- Функция модуля
Часто задаваемые вопросы о функции дробной части
Что такое функция дробной части в математике?
Функция дробной части — это особый тип функции в алгебре, который определяется как разность действительного числа и его целочисленного значения (данного наибольшим целым числом, меньшим действительного числа).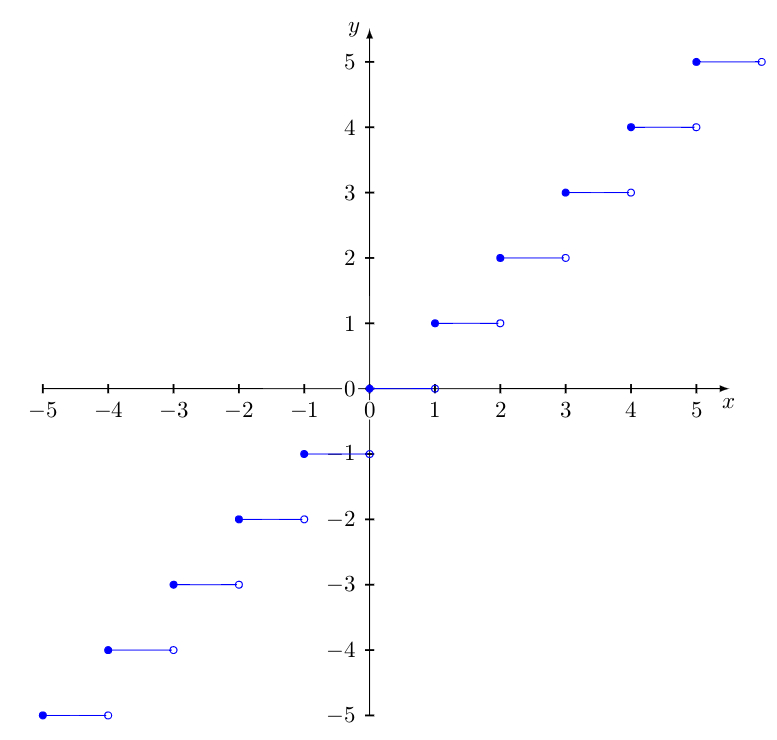
Каков диапазон функции дробной части?
Диапазон функции дробной части равен [0, 1), поскольку значение дробной части x лежит в диапазоне от 0 до 1 и равно 0, если x является целым числом.
Что такое производная функции дробной части?
Производная функции дробной части {x} не существует, если x является целым числом. Однако если x — действительное число, за исключением целых чисел, то производная равна 1.
Является ли функция дробной части непрерывной?
Нет, функция дробной части не является непрерывной, поскольку график прерывается при целых значениях x, поскольку дробная часть x равна 0, когда x является целым числом.
Что такое домен дробной части x?
Дробная часть x определена для всех действительных чисел, поэтому область определения функции дробной части включает все действительные числа.
Является ли функция дробной части периодической?
Да, функция дробной части является периодической и ее период равен 1, поскольку f(x) = f(x + 1), то есть значение дробной части x повторяется через каждую 1 единицу.