Это позиция цифры в числе: Позиционные системы счисления

Таблица разрядов и классов чисел в математике

Числа и цифры

Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.

Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …

• Единица (1) — самое маленькое число, а самого большого числа не существует.
• Ноль (0) означает, что предмета нет. Ноль не является натуральным числом.

От количества цифр в числе зависит его название.

Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.

Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.

Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.

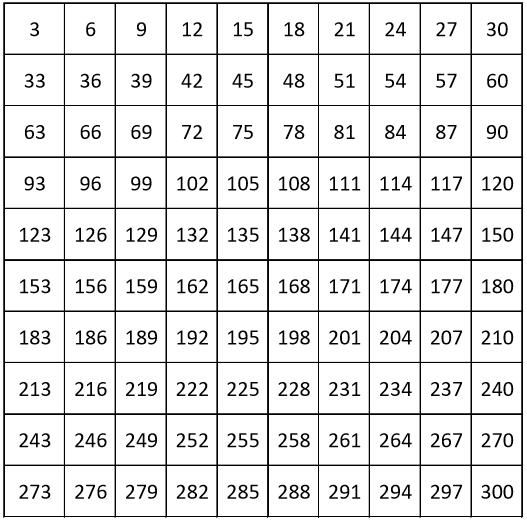
Каждая цифра в записи многозначного числа занимает определенное место — позицию.

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Классы чисел

Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами.

В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.

Таблица классов:

Названия классов многозначных чисел справа налево:

• первый — класс единиц,
• второй — класс тысяч,
• третий — класс миллионов,
• четвертый — класс миллиардов,
• пятый — класс триллионов,
• шестой — класс квадриллионов,
• седьмой — класс квинтиллионов,
• восьмой — класс секстиллионов.

Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:

• 125 911 723 296.

А теперь прочитаем число единиц каждого класса слева направо:

• 125 миллиардов 911 миллионов 723 тысячи 296.

Когда читаем класс единиц, добавлять слово «единиц» в конце не нужно.

Разряды чисел

От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:

• 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу.

Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.

Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.

У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.

Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.

Низший (младший) разряд многозначного натурального числа — разряд единиц.

Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.

Разрядные единицы обозначают так:

• Единицы — единицами первого разряда (или простыми единицами) и пишут на первом месте справа.
• Десятки — единицами второго разряда и записывают в числе на втором месте справа.
• Сотни — единицами третьего разряда и записывают на третьем месте справа.
• Единицы тысяч — единицами четвертого разряда и записывают на четвертом месте справа.
• Десятки тысяч — единицами пятого разряда и записывают на пятом месте справа.
• Сотни тысяч — единицами шестого разряда и записывают в числе на шестом месте справа и так далее.

Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.

Чтобы легче понимать математику — записывайтесь на наши курсы по математике!

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Потренируемся

Пример 1. Записать цифрами число, в котором содержится:

 

1. 55 единиц второго класса и 100 единиц первого класса;


2. 110 единиц второго класса и 5 единиц первого класса;


3. 7 единиц второго класса и 13 единиц первого класса.

Ответ:

 

1. 55 100;


2. 110 005;


3. 7 013.

Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:

• 10 единиц равны 1 десятку;
• 10 десятков равны 1 сотне;
• 10 сотен равны 1 тысяче;
• 10 тысяч равны 1 десятку тысяч;
• 10 десятков тысяч равны 1 сотне тысяч;
• 10 сотен тысяч равны 1 миллиону.

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.

Пример 2.

Сколько сотен содержится в числе 6284?

Как рассуждаем:

В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.

Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.

Значит, в данном числе содержится 62 сотни.

Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.

Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:

• 11 627 — одиннадцать тысяч шестьсот двадцать семь.
• 31 502 — тридцать одна тысяча пятьсот два.

Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.

Тест по информатике на тему «Системы счисления»

Материал опубликовала

8

#10 класс #Информатика и ИКТ #ФГОС #Учебно-дидактические материалы #Тест (специальный формат) #Учитель-предметник #Школьное образование #УМК И. Г. Семакина

Нажмите, чтобы скачать публикацию
в формате MS WORD (*.DOC)

Размер файла: 37.04 Кбайт

ГБПОУ города Москвы «Спортивно-педагогический колледж» Департамента спорта и туризма города Москвы преподаватель информатики и ИКТ, математики: Макеева Е.С.; Тест по информатике «Системы счисления»

Вариант 1

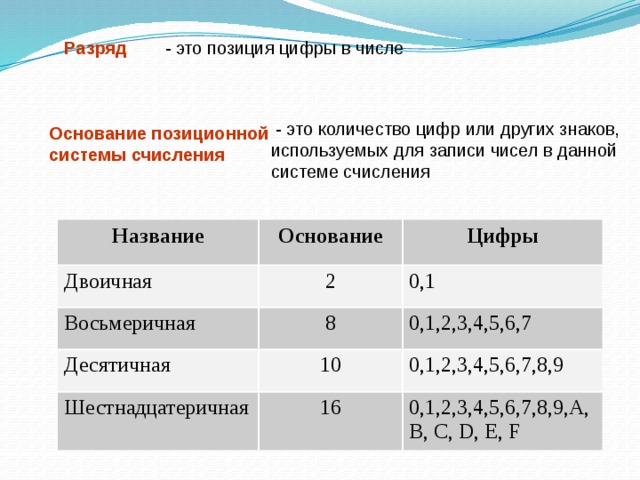
1. Что такое системы счисления?

А) цифры 1,2,3,4,5,6,7,8,9;

В) правила арифметических действий;

С) компьютерная программа для арифметических вычислений;

Д) это знаковая система, в которой числа записываются по определенным правилам, с помощью знаков некоторого алфавита, называемых цифрами.

2. Переведите число 37 из десятичной системы счисления в двоичную:

А) 100101;

В) 10101;

С) 10011;

Д) 101101.

3. Переведите число 11010 2 из двоичной системы счисления в десятичную систему счисления.

А) 18;

В) 24;

С) 26;

Д) 14.

4. Какие системы счисления не используются специалистами для общения с ЭВМ?

А) десятичная;

В) троичная;

С) двоичная;

Д) шестнадцатеричная.

5. На берегу моря лежало 10 камешков. Набежавшая волна выбросила еще несколько. Их стало 1000. Сколько камешков было выброшено волной?

А) 1000;

В) 1010;

С) 1011;

Д) 1110.

Вариант 2

1. Что называется основанием системы счисления?

А) количество цифр, используемых для записи чисел;

В) отношение значений единиц соседних разрядов;

С) арифметическая основа ЭВМ;

Д) сумма всех цифр системы счисления.

2. Переведите число 138 из десятичной системы счисления в двоичную.

А) 1001010;

В) 10001010;

С) 10000110;

Д) 1111110.

3. Переведите число 11011012 из двоичной системы счисления в десятичную систему счисления:

А) 109;

В) 104;

С) 121;

Д) 209.

4. Какая система счисления используется специалистами для общения с ЭВМ:

А) двенадцатеричная;

В) троичная;

С) двоичная;

Д) пятеричная.

5. Греются на солнышке воробьи. На нижней ветке их было 110, а на верхней на 2 меньше. Сколько всего было воробьев?

А) 1000;

В) 1001;

С) 1011;

Д) 1010.

 

Вариант 3

1. Все системы счисления делятся на две группы:

А) римские и арабские;

В) двоичные и десятичные;

С) позиционные и непозиционные;

Д) целые и дробные.

2. Переведите число 243 из десятичной системы счисления в двоичную.

А) 11110011;

В) 11001111;

С) 1110011;

Д) 110111.

3. Переведите число 11012 из двоичной системы счисления в десятичную систему счисления.

А) 11;

В) 13;

С) 15;

Д) 23.

4. Числовой разряд – это:

А) цифра в изображении числа;

В) позиция цифры в числе;

С) показатель степени основания;

D) алфавит системы счисления.

5. Младший брат учится в 101 классе. Старший на 11 старше. В каком классе учится старший брат?

А) 1000;

В) 1111;

С) 1010;

D) 1001.

 

Вариант 4

1. Какое количество цифр используется в десятеричной системе счисления?

А) 9;

В) 10;

С) 2;

Д) бесконечное множество.

2. Переведите число 27 из десятичной системы счисления в двоичную:

А) 11011;

В) 1011;

С) 1101;

Д) 11111.

3. Переведите число 11112 из двоичной системы счисления в десятичную систему счисления.

А) 16;

В) 15;

С) 7;

Д) 14.

4. В позиционной системе счисления:

А) используются только арабские цифры;

В) количественное значение цифры не зависит от ее позиции в числе;

С) цифра умножается на основание системы счисления;

Д) количественное значение цифры зависит от ее позиции в числе.

5. В кабинетах биологии и информатики 1010 кактусов. В биологии их 111. Сколько кактусов в кабинете информатики?

А) 10;

В) 11;

С) 1;

Д) 111.

Вариант 5

1. В позиционных системах счисления основание системы — это:

А) максимальное количество знаков, используемое для записи числа;

В) цифры 1,2,3,4,5,6,7,8,9;

С) правила арифметических действий;

Д) числовой разряд.

2. Переведите число 49 из десятичной системы счисления в двоичную?

А) 100011;

В) 10101;

С) 110001;

Д) 101101.

3. Переведите число 1110112 из двоичной системы счисления в десятичную систему счисления.

А) 58;

В) 63;

С) 59;

Д) 14.

4. Почему в ЭВМ используется двоичная система счисления?

А) потому что составляющие технические устройства могут надежно сохранять и распознавать только два различных состояния;

В) потому что за единицу измерения информации принят 1 байт;

С) потому что ЭВМ умеет считать только до двух;

Д) потому что человеку проще общаться с компьютером на уровне двоичной системы счисления.

5. У первоклассника Миши 1111 палочек для счета. У Коли 101. На сколько палочек у Миши больше, чем у Коли?

А) 1010;

В) 100;

С) 1000;

Д) 1001.

Вариант 6

1. Переведите из двоичной системы счисления в восьмеричную число 11112 .

А) 7;

В) 17;

С) 15;

Д) 33.

2. Переведите число А9 из шестнадцатеричной системы счисления в двоичную.

А) 10101001;

В) 10011010;

С) 10101000;

Д) 101010.

3. Сложите числа в двоичной системе счисления 101112 + 10112

А) 11122;

В) 11010;

С) 10010;

Д) 100010.

4. Переведите число 10101010001110 из двоичной системы в восьмеричную.

А) 25216;

В) 35217;

С) 25027;

Д) 61252.

5. Переведите число А960В из шестнадцатеричной системы в двоичную.

А) 11111111011000001011;

В) 00000001011000001011;

С) 11111111111000001011;

Д) 10101001011000001011.

Вариант 7

1. Переведите из двоичной системы счисления в шестнадцатеричную число 1011112.

А) 27;

В) 2F;

С) 57;

Д) В3.

 

2. Переведите число 71 из восьмеричной системы счисления в двоичную.

А) 111001;

В) 1111;

С) 101010;

Д) 100111.

3. Сложите числа в двоичной системе счисления 1001 2 + 1112.

А) 10000;

В) 10002;

С) 1000;

Д) 11000.

4. Переведите число 111000110101111 из двоичной системы в восьмеричную.

А) 10657;

В) 70657;

С) 75607;

Д) 75600.

5. Переведите число В11D34 из шестнадцатеричной системы в двоичную.

А) 10110001010100110100111;

В) 10110001000100100110100;

С) 101100010001110100110100;

Д) 100000001000111010011010.

 

Вариант 8

1. Переведите из двоичной системы счисления в восьмеричную число 101010112.

А) 253;

В) 523;

С) 185;

Д) 2223.

2. Переведите число F8 из шестнадцатеричной системы счисления в двоичную.

А) 11111000;

В) 1000111;

С) 111000;

Д) 11111111.

3. Сложите числа в двоичной системе счисления 1112 + 1102:

А) 221;

В) 1101;

С) 1001;

Д) 1111.

4. Переведите число 1110001011001011 из двоичной системы в восьмеричную.

А) 161313;

В) 313161;

С) 613113;

Д) 623316.

5. Переведите число BD1103 из шестнадцатеричной системы в двоичную.

А) 101111000000000010000011;

В) 101111111111111111100011;

С) 101111000000010111111111;

Д) 101111010001000100000011

Вариант 9

1. Переведите из двоичной системы счисления в шестнадцатеричную число 10111012.

А) 513;

В) 5D;

С) B5;

Д) 135.

2. Переведите число 478 из восьмеричной системы счисления в двоичную.

А) 100111;

В) 111100;

С) 101000;

Д) 100011111.

3. Найдите разность двоичных чисел 111102 — 10112:

А) 11010;

В) 10111;

С) 10010;

Д) 10011.

4. Переведите число 1010000111010011 из двоичной системы в восьмеричную.

А) 327021;

В) 273021;

С) 120723;

Д) 102327.

5. Переведите число 110D04 из шестнадцатеричной системы в двоичную.

А) 11111111011110000100;

В) 000000000110100000100;

С) 100010000110100000100;

Д) 111111111111111110100.

Вариант 10

1. Переведите из двоичной системы счисления в восьмеричную число 10001102 .

А) 46;

В) 430;

С) 16;

Д) 106.

2. Переведите число С6 из шестнадцатеричной системы счисления в двоичную.

А) 11000110;

В) 10011010;

С) 1110110;

Д) 1100110.

3. Найдите разность двоичных чисел 111102 – 110112 .

А) 11;

В) 11010;

С) 10010;

Д) 100010

4. Переведите число 1011011110001011 из двоичной системы в восьмеричную.

А) 316331;

В) 331613;

С) 613133;

Д) 133613.

5. Переведите число 10С1D0 из шестнадцатеричной системы в двоичную. :

А) 100001100000111111111;

В) 100001100000111010000;

С) 100001100000100000000;

Д) 00000000011101000011

 

Эталон ответов к тестам по теме «Системы счисления»

	1	2	3	4	5
Вариант 1	Д	А	С	В	В
Вариант 2	В	В	А	С	Д
Вариант 3	С	А	В	В	А
Вариант 4	В	А	С	Д	В
Вариант 5	А	С	С	А	А
Вариант 6	В	А	Д	А	Д
Вариант 7	В	А	А	В	С
Вариант 8	А	А	В	А	Д
Вариант 9	В	А	Д	С	С
Вариант 10	Д	А	А	Д	В

Опубликовано 17. 08.17 в 21:33 в группе «УРОКИ, КИМы, ИГРЫ, практикумы, творческие задания по ИНФОРМАТИКЕ, МАТЕМАТИКЕ и другим дисциплинам.»

Чтобы написать комментарий необходимо авторизоваться.

Что такое разрядное значение? Определение, примеры, факты

В математике каждая цифра в числе имеет разрядное значение. Значение места может быть определено как значение, представленное цифрой в числе на основе ее положения в числе.

Например, разряд 7 из 3743 равен 7 сотням или 700. Однако разряд 7 из 7432 равен 7 тысячам или 7000. Здесь мы видим, что, несмотря на то, что цифры в обоих числах одинаковы, его разрядное значение меняется с изменением его положения.

Place Value Chart — это очень полезный формат таблицы, который помогает нам найти разрядное значение каждой цифры на основе ее позиции в числе.

Разрядное значение цифры увеличивается в десять раз по мере того, как мы движемся влево по таблице разрядных значений, и уменьшается в десять раз по мере того, как мы двигаемся вправо.

Вот пример того, как рисование диаграммы разряда может помочь в определении разряда числа.

Понимание разрядности цифр в числах помогает сравнивать числа. Это также помогает в написании чисел в их расширенной форме. Например, расширенная форма приведенного выше числа 13 548 равна 10 000 + 3 000 + 500 + 40 + 8. 

Разрядное значение цифр в числах также может быть представлено с помощью десятичных блоков, что может помочь нам записывать числа в их расширенной форме.

Прежде чем использовать блоки десятичной системы счисления для нахождения разрядного значения каждой цифры в числе, давайте сначала поймем, что представляют собой эти блоки.

Десятичные числа представляют собой дроби или смешанные числа со знаменателем в степени десятки. В десятичном числе цифры слева от запятой представляют собой целое число. Цифры справа от десятичной дроби обозначают части. По мере продвижения сразу после запятой разрядное значение цифр становится в 10 раз меньше.

Первая цифра справа от запятой означает десятые доли, т. е. 110. Следующее место становится в десять раз меньше и называется сотыми, т.е. 1100 и так далее.

В 27.356 27 — это целая часть числа, 2 — это разряд десятков, а его разрядное значение — 20, 7 — разряд единиц, а его разрядное значение — 7. 

Разрядное значение и номинал не совпадают. Номинальное значение цифры — это значение цифры, а разрядное значение цифры — это ее место в числе. Проще говоря, номинальное значение сообщает фактическое значение цифры, тогда как значение разряда сообщает значение цифры на основе ее положения.

Следовательно, номинал цифры никогда не меняется независимо от ее положения в числе. Принимая во внимание, что значение разряда цифры изменяется с изменением позиции.

Например, номинальная стоимость 2 в числах 283 и 823 равна 2. В то время как разряд 2 равен 200 в 283 и 20 в 823. 

1 разряд десяти тысяч в числе 783 425? 7 4 8 5 Правильный ответ: 8 8 стоит в разряде десятков тысяч. 2 Выберите правильный ответ в стандартной форме. $40,000 + 4,000 + 200 + 10 + 1$ 44,221 40,421 44,211 44,201 Correct answer is: 44,211 $40,000 + 4,000 + 200 + 10 + 1 = 44211$ 3 What will быть разрядным значением 8 в числе 13,86? 800 80 0,08 0,8 Правильный ответ: 0,8 8 находится на десятом месте и имеет разрядное значение $\frac{8}{10}$ или 0,8.

Почему важно понимать значение места?

Разрядное значение применяется во многих математических понятиях. Он закладывает основу для перегруппировки, умножения и т. д.

Какие манипуляции используются для обучения разрядному значению?

Манипулятивные средства, такие как блоки с основанием 10, снэп-кубы, unifix-кубы, bean-компоненты и т. д., используются для развития понимания разрядной стоимости.

Увеличивается ли разрядность цифры при ее перемещении слева направо?

Нет. Порядковый номер цифры уменьшается в 10 раз при ее перемещении слева направо.

В чем разница между номиналом и разрядом цифры?

Номинальная стоимость цифры — это величина, которой она обладает естественным образом. Не зависит от положения цифры в числе. Позиция цифры зависит от ее положения в числе. Например, цифра 5 в числе 253 имеет номинальную стоимость 5, а разрядную стоимость — 50.

Что такое десятичный разряд? Определение, схема, примеры, факты

Что такое десятичные числа?

Десятичные числа помогают выражать небольшие денежные единицы и измерять массу, длину и емкость в более высоких единицах.

75 долларов 25 центов можно выразить с помощью десятичных чисел, таких как $\$$75,25.

Десятичное число состоит из целого числа и дробной части, разделенных десятичной точкой. Десятичная точка — это точка, которая стоит между полным числом и дробями.

Например, 25,5 — десятичное число.

Здесь 25 — это целое число, а 5 — его дробь. “.” является десятичной точкой.

Для целых чисел мы знаем, как разместить цифры в таблице разрядности. В этой статье мы изучим место и значение знаков после запятой.

Что такое десятичный разряд?

В зависимости от положения цифры в числе она имеет значение, называемое разрядностью.

Значение цифр в десятичной системе счисления основано на числе десять.

На диаграмме стоимости мест при движении справа налево ценность каждого места увеличивается в 10 раз.

Значение разряда десятков в десять раз больше разряда единиц. Значение разряда сотен в десять раз больше разряда десятков и так далее.

Когда мы перемещаемся с одного места на другое в правой части таблицы стоимости места, место становится одной десятой 110 своего предыдущего места.

Значение разряда сотен равно 110 разряду тысяч. Значение разряда десятков составляет 110 разряда сотен. Значение разряда единиц составляет 110 разряда десятков.

Двигаясь вправо от разряда единиц, мы получаем разряд в десять раз меньше единицы, то есть одну десятую или «десятые», что является дробной частью. Следовательно, мы разделяем его десятичной точкой. Итак, наша диаграмма разрядности с десятичными знаками выглядит так:

Место справа от «десятых» — это «сотые», а место справа от «сотых» — «тысячные».

Теперь у нас есть готовая диаграмма десятичных разрядов. Эта десятичная диаграмма помогает нам найти разрядность цифр в десятичном числе.

Мы разделяем целую часть числа и десятичную часть, ставя точку (точку), называемую десятичной точкой.

В таблице десятичных чисел представлены значения разрядов всех цифр, в том числе до и после запятой.

Запись десятичных чисел в таблице значений десятичных разрядов

Десятичное число может содержать целую часть числа и дробную часть (десятичную часть).

В случае, если десятичные дроби состоят только из одной части, которая является десятичной частью или целой частью, мы будем писать ноль в целом или десятичной части.

Например:

0,23 доллара = 0,23 доллара

42 доллара = 42,0 доллара

Запишем следующие десятичные дроби в таблице разрядов:

452,123; 1000.788; 3,409; 33,005; 710.01

Это помогает нам определить место каждой цифры десятичного числа.

Теперь каждое место связано со значением. Давайте узнаем о разрядном значении десятичных чисел.

Знакомство с таблицей значений десятичных разрядов

Глядя на таблицу значений десятичных разрядов, вы можете увидеть, что разрядные значения до десятичной точки начинаются с единиц, затем десятков, сотен и т. д., но разрядные значения после десятичной точки начинаются с десятыми, потом сотыми, потом тысячными и так далее.

Дробная часть числа представлена ​​цифрами после запятой десятичного числа.

Например, число 0,46 состоит из 4 десятых и 6 сотых.

Это также можно записать как 0,46 доллара США = 0,4 + 0,06 доллара США.

Другими словами, это означает, что 0,46 доллара США = 4/10 + 6/100 долларов США.

Заключение

Номинал цифры в числе есть значение самой цифры, которое не зависит от места цифры, тогда как разрядность есть значение этой цифры на этом месте, которое изменяется по мере место цифры меняется.

Решенные примеры

Пример 1: Определите цифру в тысячных долях заданных десятичных знаков.

1. 14,005 (B) 172,231 (с) 14,3

Решение:

Сначала напишите десятичную диаграмму разрядности. Затем посмотрите на цифру в разряде тысячных.

1. 5
2. 1
3. 0, так как для данного десятичного числа нет разряда тысячных.

14,3 долл. США = 14,300 долл. США   

Пример 2. Определите разрядность подчеркнутых цифр.

1. 893.8 7 1 (B) 3 6 . 657 .

Решение:

Сначала запишите число в таблице разрядов.

Затем посмотрите на место цифры и найдите ее разрядное значение.

1. Цифра 7 стоит в сотых. Следовательно, его разрядное значение равно 7 сотым или 0,07.
2. В данном десятичном разряде две шестерки, но подчеркнутая шестерка стоит на месте единиц. Следовательно, его разрядное значение равно 6 единицам или 6.
3. Цифра 5 стоит на тысячном разряде. Следовательно, его разрядное значение равно 5 тысячным или 0,005.

Пример 3. Какая цифра в числе 1,5327 стоит на сотых?

Сотые доли представляют позицию второй цифры после запятой.

В числе 1,5327 вторая цифра после запятой равна 3. 

Пример 3. Чему равна сумма цифр, стоящих в десятых и сотых долях числа 354,168?

Решение:

Цифра в десятых долях $= 1$

Цифра в сотых долях $= 6$

Сумма цифр $= 1 + 6 = 7$

Пример 3: 7, 1.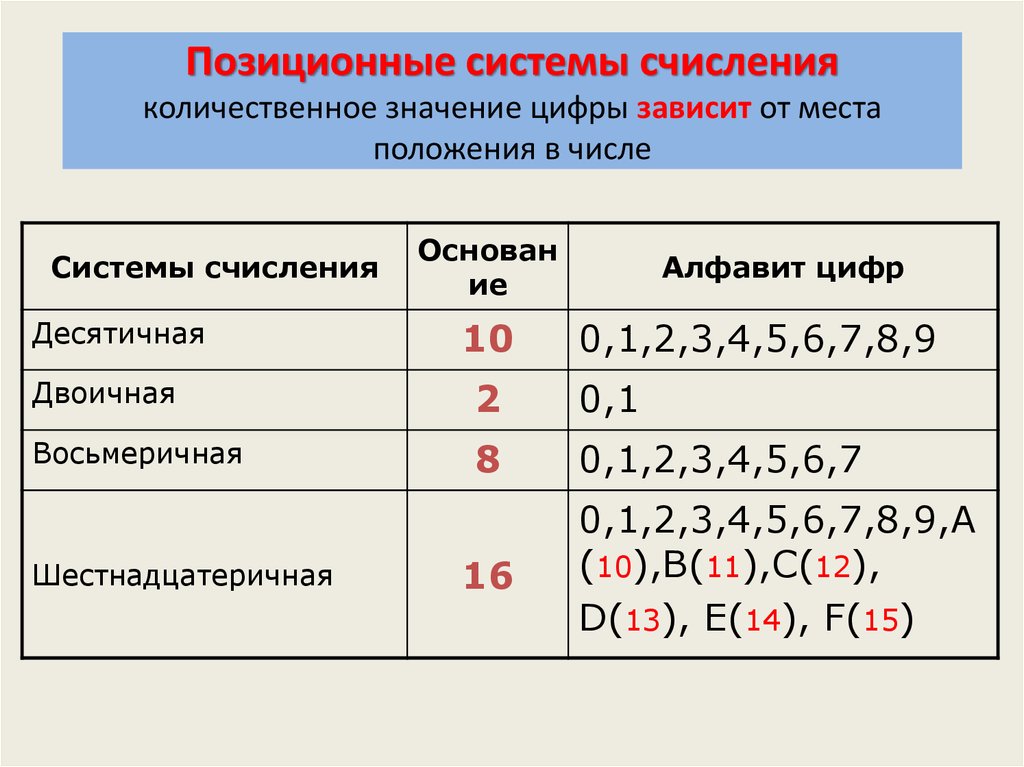 какая цифра стоит в сотых?

Сотые доли представляют позицию второй цифры после запятой.

В 1.5327 вторая цифра после запятой равна 3.

Практические задачи

1

Какие из следующих десятичных знаков можно записать как целое число?

0,455

12,45

45,45

45,00

Правильный ответ: 45,00
В числе 45,00 нет ни десятичной, ни дробной части. Таким образом, это можно записать как 45.

2

4 тысячных можно записать как__________.

4

0,4

0,04

0,004

Правильный ответ: 0,004
4 тысячных $ = 0,004 $

3

В каком из этих чисел 9 соответствует значению 0,09?

25,29

3,956

0,729

9,125

Правильный ответ: 0,729
$0,009 = 9$ тысячных. Таким образом, цифра 9 должна стоять в тысячном разряде. Только в варианте в) стоит 9 в тысячном разряде.

4

Каково место числа 5 в десятичном числе 32,56?

0,5

0,05

5

50

Правильный ответ: 0,5
Число 5 стоит в десятых долях справа от запятой.

5

В числе 124,082 какой десятичный разряд занимает число 8?

0,08

0,8

0,008

8,0

Правильный ответ: 0,08
Число 8 расположено справа от запятой, в сотых долях.

6

Какая цифра в 624.185 стоит на десятом месте?

4

8

1

2

Правильный ответ: 1
Десятые доли — это первое место справа после запятой.

Часто задаваемые вопросы

Чем полезна учащимся таблица десятичных разрядов?

Таблица значений десятичных разрядов полезна при нахождении разрядов десятичных цифр, а также используется для сравнения и упорядочивания десятичных знаков.