Как построить эллипс в изометрии
Эллипс – это изометрическая проекция окружности. Овал строят по точкам и обводят по лекалам или фигурным линейкам. Проще всего построить эллипс в изометрии, вписав фигуру в ромб, иначе изометрическую проекцию квадрата.Вам понадобитсяРассмотрим, как построить эллипс в , лежащий в горизонтальной плоскости. Постройте перпендикулярные оси X и Y. Точку пересечения обозначьте O.
От точки O отложите на осях отрезки, равные радиусу окружности. Обозначенные точки обозначьте цифрами 1, 2, 3, 4. Через эти точки проведите параллельные осям прямые.
От точки O отложите на осях отрезки, равные радиусу окружности. Обозначенные точки обозначьте цифрами 1, 2, 3, 4. Через эти точки проведите параллельные осям прямые.
Проведите дугу из вершины тупого угла, соединив точки 1 и 4. Аналогично соедините точки 2 и 3, проведя дугу из вершины D. Соедините точки 1,2 и 3,4 из центров малых дуг. Таким образом построен эллипс в изометрии, вписанный в ромб.
Второй способ построить эллипс в изометрии заключается в отображении окружности с коэффициентом искажения. Начертите оси X и Y, из точки O проведите две вспомогательные окружности. Диаметр внутренней окружности равен малой оси эллипса, внешней – большой оси.
Начертите оси X и Y, из точки O проведите две вспомогательные окружности. Диаметр внутренней окружности равен малой оси эллипса, внешней – большой оси.
В одной четверти постройте вспомогательные лучи, исходящие из центра эллипса. Количество лучей произвольное, чем больше, тем точнее чертеж. В нашем случае достаточно будет трех вспомогательных лучей.
Получите дополнительные точки эллипса. Из точки пересечения луча с малой окружностью проведите горизонтальную линию параллельную оси X в сторону внешней окружности. Из верхней точки, лежащей на пересечении луча и большой окружности, опустите перпендикуляр.
Полученную точку обозначьте цифрой 2. Повторите операции по нахождению 3 и 4 точек эллипса. Точка 1 находится на пересечении оси Y и малой окружности, точка 5 на оси X в месте прохождения внешней окружности.
Проведите кривую через полученные 5 точек эллипса. В точках 1 и 5 кривая строго пропорциональна осям. Проведите аналогичные построения эллипса в изометрии на оставшихся ¾ чертежа.
11.3. Окружность в аксонометрии
Построение аксонометрических проекций предметов, форма которых имеет поверхность вращения, невозможно без изображения аксонометрической проекции окружности. Аксонометрическая проекция окружности представляет собой замкнутую кривую линию, для удобства построения которой иногда применяют способ сетки. В этом случае окружность делят на определенное количество частей, строят сетку и вписывают эллипс (рис. 147).
Рис. 147. Аксонометрическая проекция окружности
Данный способ используется для всех видов аксонометрических проекций, где окружность проецируется с искажением. Однако там, где это возможно, в аксонометрических проекциях эллипс заменяют овалом. Овалом называется кривая линия, по начертанию похожая на эллипс, но выстроенная с помощью циркуля.
Рассмотрим построение окружности в прямоугольной изометрии. Основное требование к построению аксонометрических проекций окружностей следующее: направление большой оси эллипсов определяется как перпендикуляр к той оси координат, которой нет в плоскости окружности.
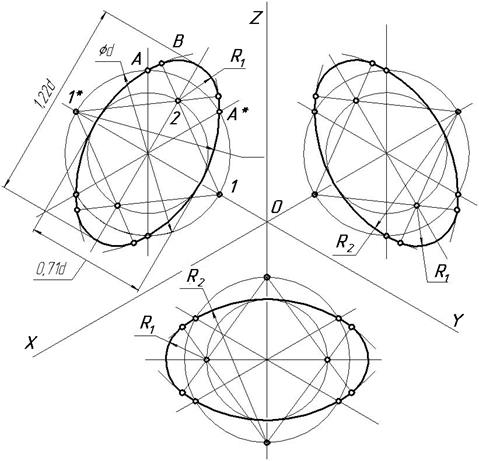
Рис. 148. Аксонометрические проекции окружности
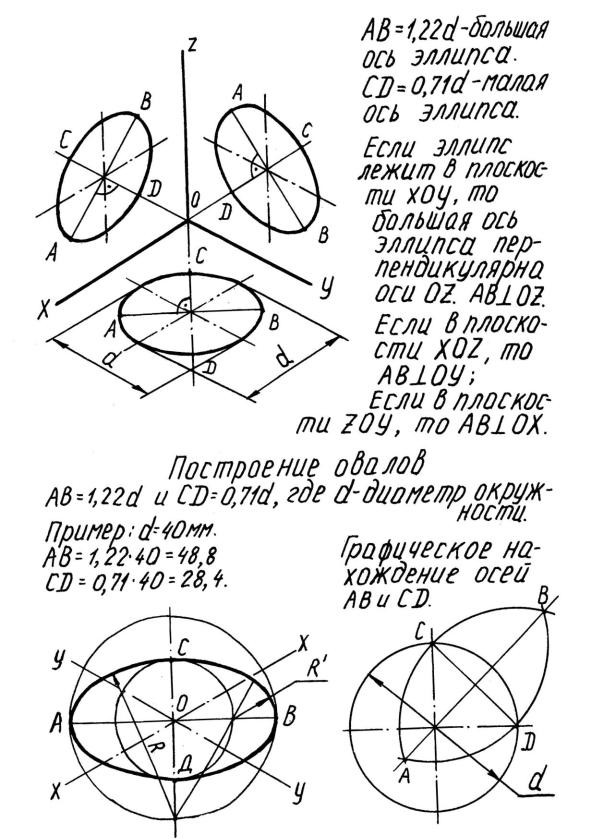
В целях упрощения построений эллипсы могут быть заменены овалами, состоящими из дуг окружностей. В прямоугольной изометрии форма овалов будет одинакова для всех трех координатных плоскостей
проекций. При выполнении прямоугольной изометрии без искажения по осям x, y и z, согласно ГОСТ 2.317—69 большая ось эллипсов равна 1,22, малая ось эллипсов — 0,71 диаметра заданной окружности.
Приведем пример построения овала без вычисления размеров большой и малой осей. Направление большой оси определяется исходя из вышеназванного требования, в нашем примере — перпендикулярно координатной оси z’. Очерчивается окружность заданного радиуса. Через центр окружности проводятся прямые, параллельные координатным осям x’ и y’. Пересечением этих прямых с очерком окружности являются точки сопряжения дуг овала.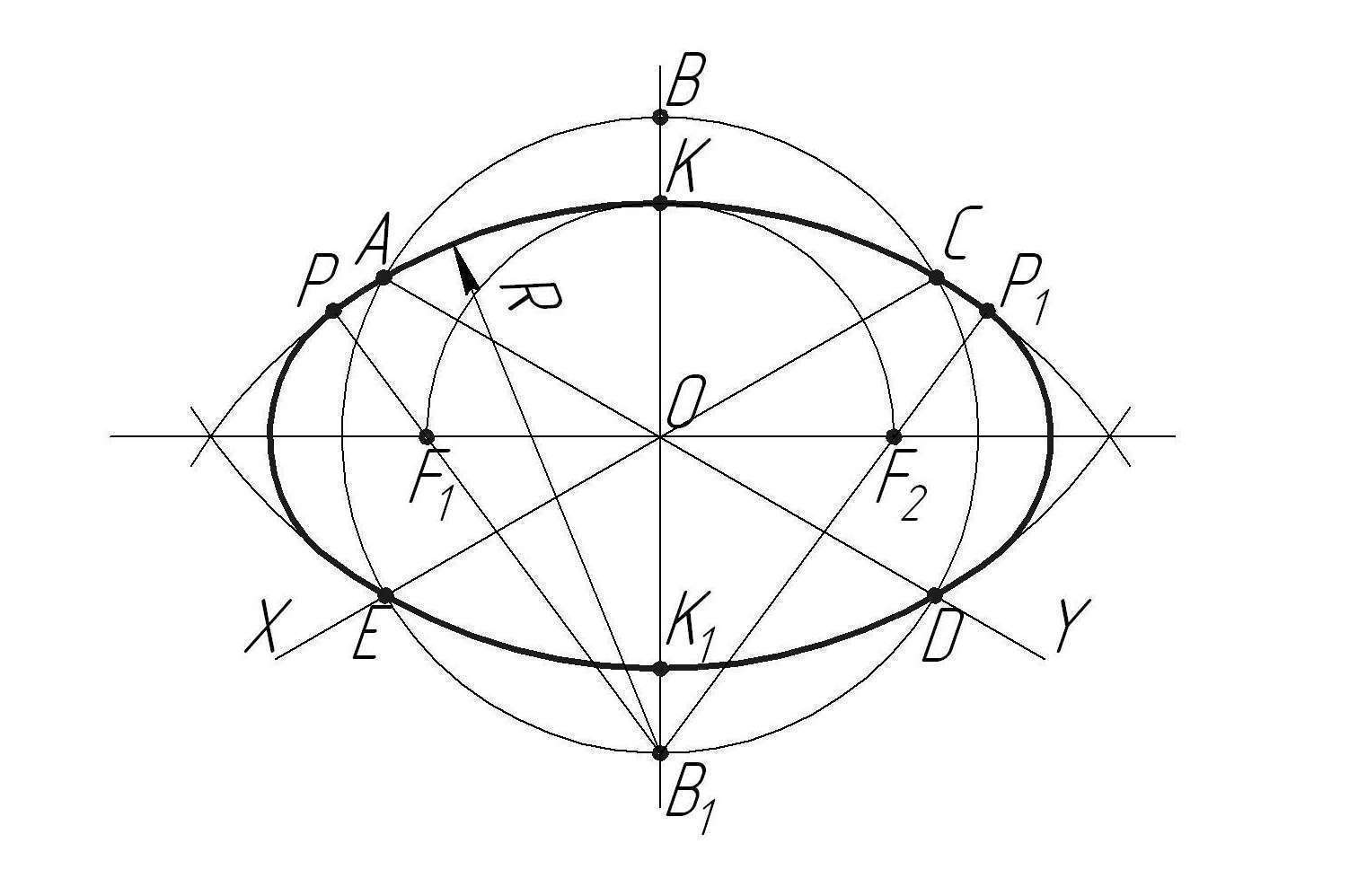
овала (рис. 149).
Рис. 149. Построение овала в прямоугольной изометрии
11.4. Аксонометрические проекции геометрических тел
Построение аксонометрических проекций геометрических тел рекомендуется начинать с построения аксонометрических проекций их оснований, к которым выстраивают изображение других элементов геометрических тел (ребер, граней, оснований, образующих). На рис. 150 показано построение в прямоугольной изометрии аксонометрического изображения правильной прямой шестигранной призмы согласно предложенному чертежу в двух проекциях.
Оси аксонометрии проводят по нижнему основанию призмы. Строят вторичную проекцию основания. Затем на вертикальных прямых от каждой вершины откладывают высоту призмы, получая вершины верхнего основания. Соединяют полученные точки и получают верхнее основание призмы.
На рис. 151 дано построение в прямоугольной изометрии аксонометрического изображения правильной прямой шестигранной пирамиды. Вначале строят вторичную проекцию ее основания. Затем от центра основания, через которое проходят оси аксонометрии, проводят вертикальную прямую и на ней откладывают высоту пирамиды согласно предложенному чертежу в двух проекциях.
Вначале строят вторичную проекцию ее основания. Затем от центра основания, через которое проходят оси аксонометрии, проводят вертикальную прямую и на ней откладывают высоту пирамиды согласно предложенному чертежу в двух проекциях.
Рис. 150. Аксонометрическая проекция призмы
Рис. 151. Аксонометрическая проекция пирамиды
На рис. 152 дано построение в прямоугольной изометрии аксонометрического изображения прямого кругового конуса. Вначале строят вторичную проекцию основания конуса в виде эллипса (овал). Затем от
169центра основания, через которое проходят оси аксонометрии, проводят вертикальную прямую и на ней откладывают высоту конуса согласно предложенному чертежу в двух проекциях.
Рис. 152. Аксонометрическая проекция конуса
На рис. 153 показано построение в прямоугольной изометрии аксонометрического изображения прямого кругового цилиндра с вырезами.
Рис. 153. Аксонометрическая проекция цилиндра с вырезами
ПОСТРОЕНИЕ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ ОКРУЖНОСТЕЙ
Московский государственный технический университет им.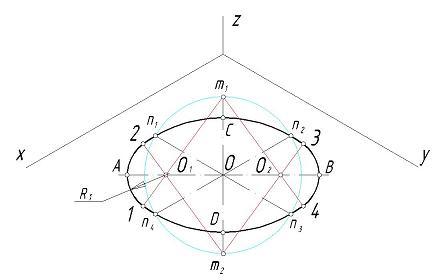 Н.Э. Баумана
Н.Э. Баумана
Номер: 3-3
Год: 2017
Страницы: 41-45
Журнал: Актуальные проблемы гуманитарных и естественных наукКлючевые слова
Аннотация к статье
В статье изложен способ построения аксонометрической проекции окружности, расположенной в плоскости общего положения по отношению к плоскостям, образованным аксонометрическими осями. Приведен пример построения эллипса — проекции окружности для проецирующей плоскости, который без принципиальных изменений может быть распространен и для условий плоскости общего положения. Предлагаемая статья может быть рекомендована для студентов, углубленно изучающих курсы начертательной геометрии и инженерной графики, а также может быть полезна для слушателей факультета повышения квалификации и начинающих молодых преподавателей в качестве вспомогательного материала в работе со студентами.
Предлагаемая статья может быть рекомендована для студентов, углубленно изучающих курсы начертательной геометрии и инженерной графики, а также может быть полезна для слушателей факультета повышения квалификации и начинающих молодых преподавателей в качестве вспомогательного материала в работе со студентами.
Текст научной статьи
Введение В теоретическом аспекте вопрос построения аксонометрической проекции окружности рассмотрен в полном объеме в учебной литературе [1, 234-258; 2, 203-216; 3, 190-200; 4, 300-315; 5, 132-147; 6, 46-48]. В настоящей работе приведены практические приемы построения аксонометрических проекций окружностей, расположенных в плоскостях общего положения. В общем случае окружность проецируется на аксонометрическую плоскость в эллипс, большая ось которого есть проекция диаметра, параллельного аксонометрической плоскости. Аксонометрия любой окружности может быть выполнена как эллипс, проведенный через несколько аксонометрических проекций точек, заданной окружности, каждая из которых найдена по координатной ломанной, соответствующей этой точке.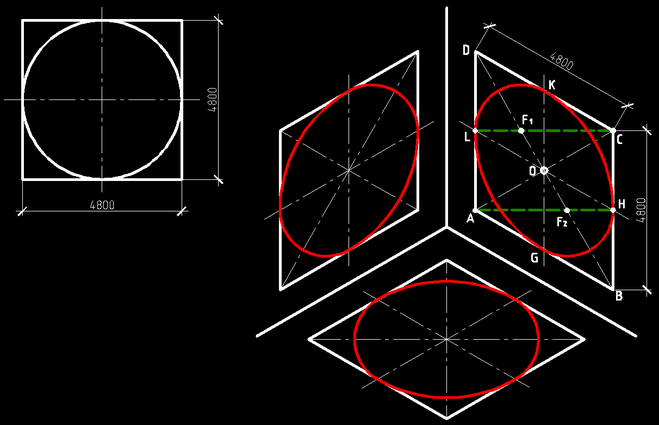
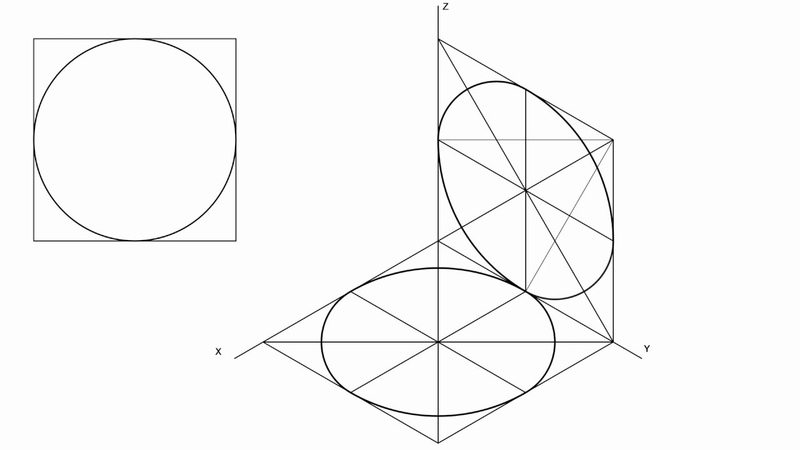
 Длину малой полуоси получают как проекцию радиуса, выходящего из центра окружности по тому же перпендикуляру. Большая ось эллипса перпендикулярна малой оси и равна диаметру окружности. Рассмотрим другой способ построения аксонометрической проекции окружности, когда она расположена в плоскости, непараллельной плоскостям ортогональной системы координат. Аксонометрию окружности будем строить, предварительно вписав ее в квадрат. Пример построения приведен на рис. 1, 2 для условий прямоугольной изометрической проекции (направление проецирования перпендикулярно аксонометрической плоскости и коэффициенты искажения по осям X, Y, Z равны между собой и равны единице). Рис. 1. Построение аксонометрии окружности, лежащей в плоскости, непараллельной плоскостям ортогональной системы координат (исходный комплексный чертеж) Рис. 2. Построение аксонометрии окружности, лежащей в плоскости, непараллельной плоскостям ортогональной системы координат (аксонометрическая проекция) Совместим оси ортогональной системы координат с осями проекций комплексного чертежа, окружность n разместим во фронтально-проецирующей плоскости.
Длину малой полуоси получают как проекцию радиуса, выходящего из центра окружности по тому же перпендикуляру. Большая ось эллипса перпендикулярна малой оси и равна диаметру окружности. Рассмотрим другой способ построения аксонометрической проекции окружности, когда она расположена в плоскости, непараллельной плоскостям ортогональной системы координат. Аксонометрию окружности будем строить, предварительно вписав ее в квадрат. Пример построения приведен на рис. 1, 2 для условий прямоугольной изометрической проекции (направление проецирования перпендикулярно аксонометрической плоскости и коэффициенты искажения по осям X, Y, Z равны между собой и равны единице). Рис. 1. Построение аксонометрии окружности, лежащей в плоскости, непараллельной плоскостям ортогональной системы координат (исходный комплексный чертеж) Рис. 2. Построение аксонометрии окружности, лежащей в плоскости, непараллельной плоскостям ортогональной системы координат (аксонометрическая проекция) Совместим оси ортогональной системы координат с осями проекций комплексного чертежа, окружность n разместим во фронтально-проецирующей плоскости.
 Также равные отрезки Е13»’; 3»’2»’; 2»’1»’; 1»’D1 создаем на половине сопряженного диаметра. Точки эллипса расположены в пересечении лучей, выходящих из B1; D1, и проведенных через точки деления с одинаковыми номерами, как это показано на рис. 3. В аксонометрических проекциях, при «ручном» построении эллипса, лекальную кривую заменяют четырехцентровым овалом, состоящим из четырех последовательно сопряженных дуг окружностей. Для нашего случая по известным аксонометрическим проекциям сопряженных диаметров А1С1 и B1D1 определяют направление и длины большой, и малой осей эллипса [4, 300-315]. Эти данные исходные и достаточные для построения овала. Для окружностей, расположенных в плоскостях общего положения по отношению к плоскостям определяемых аксонометрическими осями, без каких-либо существенных изменений, применим вышеизложенный способ построения аксонометрических проекций окружности, принадлежащей проецирующей плоскости. Далее рассмотрим способ построения эллипса — аксонометрической проекции окружности по восьми точкам.
Также равные отрезки Е13»’; 3»’2»’; 2»’1»’; 1»’D1 создаем на половине сопряженного диаметра. Точки эллипса расположены в пересечении лучей, выходящих из B1; D1, и проведенных через точки деления с одинаковыми номерами, как это показано на рис. 3. В аксонометрических проекциях, при «ручном» построении эллипса, лекальную кривую заменяют четырехцентровым овалом, состоящим из четырех последовательно сопряженных дуг окружностей. Для нашего случая по известным аксонометрическим проекциям сопряженных диаметров А1С1 и B1D1 определяют направление и длины большой, и малой осей эллипса [4, 300-315]. Эти данные исходные и достаточные для построения овала. Для окружностей, расположенных в плоскостях общего положения по отношению к плоскостям определяемых аксонометрическими осями, без каких-либо существенных изменений, применим вышеизложенный способ построения аксонометрических проекций окружности, принадлежащей проецирующей плоскости. Далее рассмотрим способ построения эллипса — аксонометрической проекции окружности по восьми точкам.
 Правомерность таких построений может быть доказана из условий параллельного проецирования [5, 132-147]. Если в заданной детали четыре и более одинаковых окружностей малого диаметра, то оправдано изготовление шаблона, который затем с помощью двух булавок фиксируют в нужных местах чертежа и обводят. В качестве материала шаблона подходит картон. Для прямоугольной изометрической проекции при выполнении малых эллипсов допускается применение готовых промышленных трафаретов с отверстиями в форме эллипсов. Выводы Предложенный способ построения аксонометрической проекции окружности, принадлежащей плоскости общего положения, прост и универсален, не требует знания дополнительных специфических приемов, обеспечивает необходимую точность, кроме того, во всех случаях возможна замена эллипса на четырехцентровой овал.
Правомерность таких построений может быть доказана из условий параллельного проецирования [5, 132-147]. Если в заданной детали четыре и более одинаковых окружностей малого диаметра, то оправдано изготовление шаблона, который затем с помощью двух булавок фиксируют в нужных местах чертежа и обводят. В качестве материала шаблона подходит картон. Для прямоугольной изометрической проекции при выполнении малых эллипсов допускается применение готовых промышленных трафаретов с отверстиями в форме эллипсов. Выводы Предложенный способ построения аксонометрической проекции окружности, принадлежащей плоскости общего положения, прост и универсален, не требует знания дополнительных специфических приемов, обеспечивает необходимую точность, кроме того, во всех случаях возможна замена эллипса на четырехцентровой овал.Начертательная геометрия
13.4.1. Построение эллипсов по восьми точкам
Построение эллипса как аксонометрической проекции окружности начинается с определения положения центра и направления большой и малой осей эллипса. Размеры большой и малой осей рассчитывают или определяют графически и откладывают на чертеже A’B’ большая ось, C’D’ – малая. Затем через центр эллипса проводят вспомогательные прямые в направлении аксонометрических осей. В изометрии в направлении осей откладывается натуральный диаметр окружности 1-2 и 3-4. Полученные восемь точек соединяют плавной лекальной кривой. Построение изометрического эллипса по восьми точкам показано на рис. 171.
Размеры большой и малой осей рассчитывают или определяют графически и откладывают на чертеже A’B’ большая ось, C’D’ – малая. Затем через центр эллипса проводят вспомогательные прямые в направлении аксонометрических осей. В изометрии в направлении осей откладывается натуральный диаметр окружности 1-2 и 3-4. Полученные восемь точек соединяют плавной лекальной кривой. Построение изометрического эллипса по восьми точкам показано на рис. 171.
А’В’=1,22d – большая ось эллипса; С’D’=0,7d – малая ось эллипса; 1′-2′ – размер по оси x, равный диаметру окружности d; 3′-4′ – размер по оси y, равный диаметру окружности d
При построении диметрических эллипсов учитывается коэффициент искажения 0,5 направлении оси y. Построение диметрических эллипсов по восьми точкам показано на рис. 172.
а – для окружностей в плоскостях П1(xOy) и П3(zOy): БОЭ= 1,06d –большая ось эллипса; МОЭ= 0,35d –малая ось эллипса; 1′-2’=d –размер по оси x; 3′-4’=0,5d –размер по оси у; б – для окружностей в плоскости П2(xOz): БОЭ=1,06d –большая ось эллипса; МОЭ=0,94d –малая ось эллипса; 1′-2’=d –размер по оси x; 3′-4’=d –размер по оси z
Если восьми точек недостаточно, эллипс можно построить по двум осям (рис.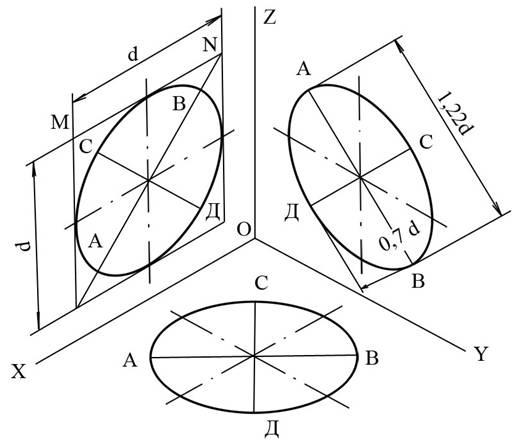 173). Этот способ можно применять и для построения эллипсов с произвольными размерами осей, например, для построения проекций окружности, лежащей в проецирующей плоскости.
173). Этот способ можно применять и для построения эллипсов с произвольными размерами осей, например, для построения проекций окружности, лежащей в проецирующей плоскости.
Рис. 173. Построение эллипса по двум осям: A’B’– большая ось эллипса; С’D’ – малая ось эллипса
Строят две окружности с диаметрами, равными большой и малой оси эллипса, и делят их радиальными отрезками на n частей. Затем из каждой точки пересечения большой окружности проводят вертикальные отрезки в сторону большой оси, а из точек пересечения с малой окружностью – горизонтальные отрезки в сторону от малой оси. Точки пересечения отрезков и являются точками эллипса. Полученные точки соединяют плавной лекальной кривой.
Аксонометрические проекции окружности
Аксонометрические проекции окружностей
Конспект урока
по черчению
8 класс
Окружность в аксонометрии
Фронтальная диметрическая проекция
Z
V
W
НЕТ
X
H
НЕТ
Y
Слайд 1
Построение фронтальной диметрической проекции детали
с цилиндрическим отверстием по чертежу.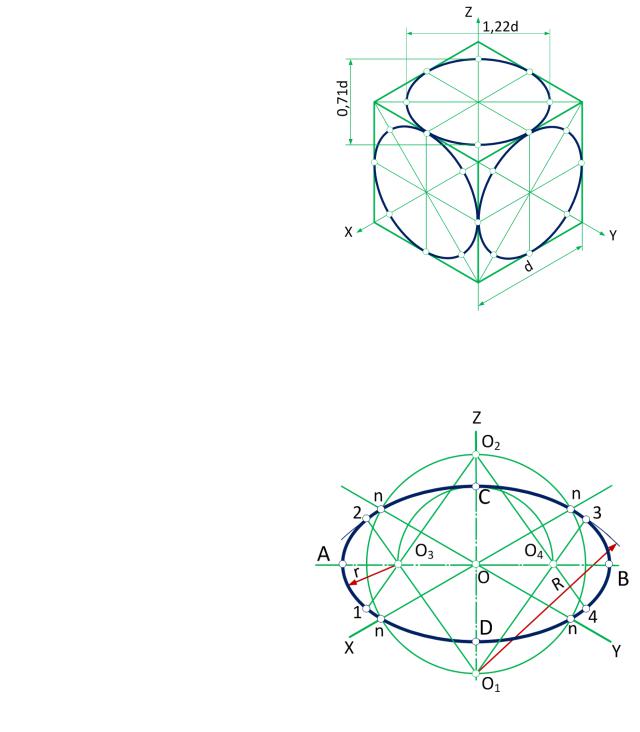
Даны два вида детали:
Слайд 2
Пользуясь осями x, y, z, строят тонкими линиями очертания внешней формы детали.
Находят центр отверстия на передней грани. Через него параллельно оси y проводят ось отверстия и откладывают на ней половину толщины детали.
Получают центр отверстия, расположенный на задней грани.
Слайд 3
Из полученных точек как из центров проводят окружности, диаметр которых равен диаметру отверстия.
Слайд 4
Удаляют лишние линии и обводят видимый контур детали.
Слайд 5
Изометрические проекции окружностей
Изометрической проекцией окружности является эллипс. В практике черчения вместо него строят овал.
Овал – замкнутая кривая, очерченная дугами окружностей.
Овал удобно строить, вписывая в ромб, который является изометрической проекцией квадрата.
Изометрическая проекция
Z
X
y
Окружность:
Окружности в изометрии изображаются в виде эллипсов.
Для упрощения работы эллипсы заменяют овалами, вписанными в ромб со стороной, равной диаметру заданной окружности. Для этого на осях (например x и y) откладывают от точки О в четырех направлениях отрезки, равные радиусу изображаемой окружности.
Через полученные точки a, b, c, d проводят прямые, образующие ромб. Из точек А и В проводят дуги радиусом R между точками a и b, c и d.
Точки C и D являются центрами малых дуг, сопрягающих большие. Малые дуги описывают радиусом R1.
Аналогично строят овалы на осях z и x, z и y.
Содержание
Слайд 6
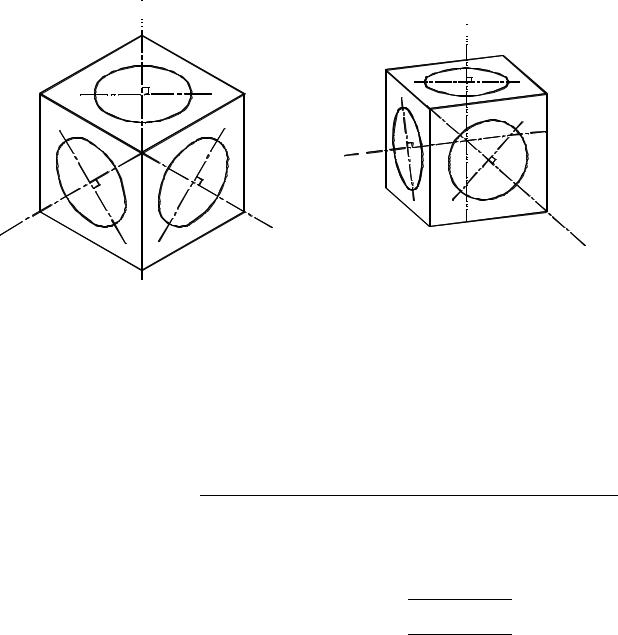
Изображение в изометрической проекции окружностей, вписанных в куб.
Задание: 1. Начертите оси изометрии (оси проходят под углом 30* к линии горизонта)
2.Начертите квадрат в изометрии (сторона квадрата 80 мм) 3. Найдите точки сопряжения дуг (точки пересечения осей и сторон квадрата- а,b,c,d) 4. Найдите центры больших дуг (А,В)
Найдите центры больших дуг (А,В)
5.Из вершин А и В проводят дуги радиусом R=Ас=Аd=Ва=Вb
6 Соедините точки B и b, В и а, 7. Найдите центры D и С малых дуг
8. Радиусом r =Db=Dc=Ca=Cd проведите дуги. 9. У вас получился овал — замкнутая кривая, очерченная дугами окружностей.
10.Начертите куб в изометрической проекции и впишите в каждый ромб овал
11. Начертите геометрическое тело — цилиндр
Проверь себя.
- Как называется окружность выполненная в осях изометрии?
- Как называется геометрическая фигура при вычерчивании квадрата в осях изометрии?
- Сколько центров надо найти при вычерчивании овала?
- Чем на чертеже являются точки a, b, с, d?
Слайд 7
Построение овала, вписанного в ромб
ас = bd = диаметру окружности
Вначале строят ромб со стороной, равной диаметру изображаемой окружности. Для этого через точку О проводят изометрические оси x и y .
Для этого через точку О проводят изометрические оси x и y .
На них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки а, b, с, d проводят прямые параллельные осям; получают ромб.
Большая ось овала располагается на большой диагонали ромба.
Слайд 8
Построение овала, вписанного в ромб
R = Вb = Аd
После этого вписывают в ромб овал. Для этого из вершин тупых углов ( точек А и В ) описывают дуги.
Их радиус R равен расстоянию от вершины тупого угла ( точек А и В ) до точек а, b или с,d соответственно.
Слайд 9
Построение овала, вписанного в ромб
R = Сa = Db
Через точки B и a , B и b проводят прямые. В пересечении прямых Ba и Вb с большей диагональю ромба находятся точки C и D . Эти точки будут центрами малых дуг. Их радиус R , равен Сa (или Db ).
Их радиус R , равен Сa (или Db ).
Дугами этого радиуса плавно соединяют большие дуги овала.
Слайд 10
Задание на дом .
- Повторить последовательность построения овала.
- Построить овалы во фронтальной и профильной плоскостях.
Мы рассмотрели построение овала лежащего в плоскости перпендикулярной оси z (овал 1).
Овалы, находящиеся в плоскостях, перпендикулярных оси y (овал 2) и оси x (овал 3), строят также.
Как начертить круг в изометрии? | Рутвет
- Изображение изометрической проекции
- Как чертить круг в изометрии?
- Круг в изометрии: построение
В первую очередь, необходимо на достаточном для понимания сути уровне разобраться в том, как строить саму изометрию – то есть метрическое плоское пространство. Начинать нужно с самых основ, связанных с работой с изометрическими проекциями и плоскостями. Они включают в себя построение простейших и обычных плоских линий, лишь после освоения которых можно переходить к изучению форм. Вполне естественно, что без знания азов ни у кого не выйдет перескочить сразу к различным цилиндрическим формам, ведь проблема возникнет сразу же на этапе построения таких более сложных по сравнению с линиями фигур, как квадрат, а затем и круг в изометрии. Многие выдвигают такую точку зрения, что именно окружность является одной из наиболее проблематичных для изображения в проекции среди всех плоских фигур.
Они включают в себя построение простейших и обычных плоских линий, лишь после освоения которых можно переходить к изучению форм. Вполне естественно, что без знания азов ни у кого не выйдет перескочить сразу к различным цилиндрическим формам, ведь проблема возникнет сразу же на этапе построения таких более сложных по сравнению с линиями фигур, как квадрат, а затем и круг в изометрии. Многие выдвигают такую точку зрения, что именно окружность является одной из наиболее проблематичных для изображения в проекции среди всех плоских фигур.
Изображение изометрической проекции
Сама суть проекции состоит в том, что какой-либо существующий трехмерный объект или фигура отображается на изометрической плоскости, при этом сохраняется отношение длины спроектированных отрезков к действительной длине. Другими словами, коэффициент искажения остается неизменным по всем трем осям. Этим и отличается изометрическая проекция, так как только при ней все имеющиеся масштабы остаются одинаковыми.
Изометрическая проекция возможна при соблюдении условия, чтобы углы между осями проекции были одинаковыми и равны 120 градусам. У подобной проекции есть достоинство, благодаря чему ее так часто используют в различных чертежах и проектах. Причина кроется в том, что при изменении расстояния сами отражаемые объекты при этом не кажутся меньше или больше, чем они есть на самом деле.
Однако у изометрических проекций существуют и свои недостатки. Так, например, если на рисунке отсутствуют обозначающие тени на разных сторонах, то будет крайне сложно определить, какая из сторон фигуры на данный момент находится к нам ближе и, собственно, наблюдается. Кроме того, будет проблематично понять, где у объекта располагаются верхняя и нижняя грань, из-за наличия двух крайне схожих проекций, равных по площади и размерам.
Смотрите видео об окружности в изометрии.
Как чертить круг в изометрии?
Все, кто на каком-либо из этапов обучения сталкиваются с вопросом, как начертить круг в изометрии, очень часто совершают типичные и распространенные среди новичков ошибки.
Основные факторы при построении изометрической проекции, которые нужно запомнить, заключаются в нескольких деталях:
- Дело в том, что в случаях вычерчивания в изометрии окружность изображается не в своем первоначальном положении. В конечном итоге она должна принять форму эллипса.
- Вдобавок к этому, есть важный элемент, который задает курс всему последующему построению. Нужно ориентироваться на тот момент, что любую окружность можно рассматривать как правильный многоугольник, в котором может быть неограниченное множество сторон.
Как уже было сказано, в изометрическом пространстве окружность отображается в виде эллипса. Но начинающие регулярно сталкиваются с проблемами, так как он достаточно сложен для построения. В связи с данным фактом часто рекомендуется прибегать к использованию овалов как оптимальной замене эллипсам.
В связи с данным фактом часто рекомендуется прибегать к использованию овалов как оптимальной замене эллипсам.
Всего существует несколько инструкций для разных способов, как чертить круг в изометрии через овал. В нашем же случае будет рассмотрен один из наиболее часто используемых и распространенных. Первоочередным этапом является вычисление размеров самих осей фигуры, большой и малой, по формулам через диаметр окружности, изометрическую проекцию которой необходимо вычертить.
Существует также и графический способ определения осей эллипса, который изучается наглядным путем. Для вычисления малой оси требуется соединить между собой ближайшие точки перпендикулярных прямых линий, проведенных через центр окружности, лежащие на этой самой окружности. Дальше через эти точки проводятся дуги радиусов так, чтобы они пересеклись между собой. Данные точки пересечения будут образовывать линию, которая, в свою очередь, является большой осью.
Читайте о том, как найти площать правильного и неправильного шестиугольника.
А также о технике устного счета.
Круг в изометрии: построение
Руководство, как нарисовать круг в изометрии, не заканчивается на вычислении размеров осей. В зависимости от принадлежности к какой-либо из координатных плоскостей, устанавливается направление вычисленных и построенных ранее осей овала. Следом за этим по размерам обеих осей проводятся окружности. При их пересечении выделяются четыре точки, которые впоследствии послужат центрами дуг необходимого нам овала.
Так как приводимая поэтапная инструкция приводится скорее для новичков, которые только учатся, как сделать круг в изометрии, то следует подробнее рассмотреть процесс определения направления осей вычерчиваемого эллипса. Прежде всего, это зависит непосредственно от положения самой окружности, которую требуется спроецировать.
При построении всегда соблюдается одно негласное правило: при любых обстоятельствах большая ось будет расположена перпендикулярно к оси, которая проецируется в точку на данной плоскости.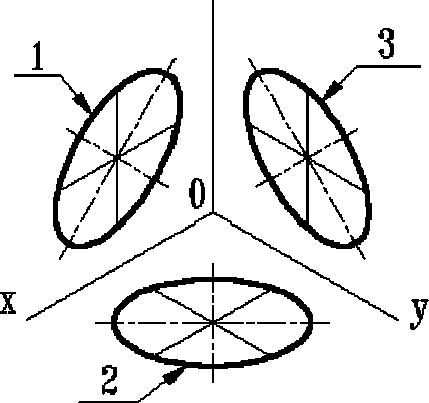 Малая ось при этом обязательно совпадает по направлению с этой осью.
Малая ось при этом обязательно совпадает по направлению с этой осью.
Чтобы впоследствии, после завершения всех расчетов и непосредственного построения проекции, у других людей, не знакомых изначально с вашим чертежом, не возникали трудности с определением сторон, используется нанесение теней и штриховки. При этом очень важным условием является направление имеющихся штрихов. Так, например, принято, что в изометрической проекции линии должны совпадать по своей направленности либо с большими диагоналями квадрата, в который вписана окружность, либо с малыми.
Помимо этого, чтобы в дальнейшем упростить задачу людям, которым предстоит работать по данным чертежам, зачастую на рисунок наносятся еще и тени, отбрасываемые вычерченной проекцией. Это не только сводит к минимуму возникновение недопонимания, но и делает проект в эстетическом плане более приятным для восприятия.
Остались ли у вас вопросы по теме? Задайте их в комментариях! А также смотрите видео о построении изометрии окружности.
Выполнение прямоугольной изометрической проекции — КиберПедия
ТЕОРеТИЧЕСКАЯ ЧАСТЬ
Для наглядного изображения изделий или их составных частей применяются аксонометрические проекции. В настоящей работе рассматриваются правила построения прямоугольной изометрической проекции.
Для прямоугольных проекций, когда угол между проецирующими лучами и плоскостью аксонометрических проекций равен 90°, коэффициенты искажения связаны следующим соотношением:
k2 + т2 + п2 = 2. (1)
Для изометрической проекции коэффициенты искажения равны, следовательно, k = т = п.
Из формулы (1) получается
3k2 =2; ; k = т = п 0,82.
Дробность коэффициентов искажений приводит к усложнению расчетов размеров, необходимых при построении аксонометрического изображения. Для упрощения этих расчетов используются приведенные коэффициенты искажений:
для изометрической проекции коэффициенты искажения составляют:
k = т = n = 1.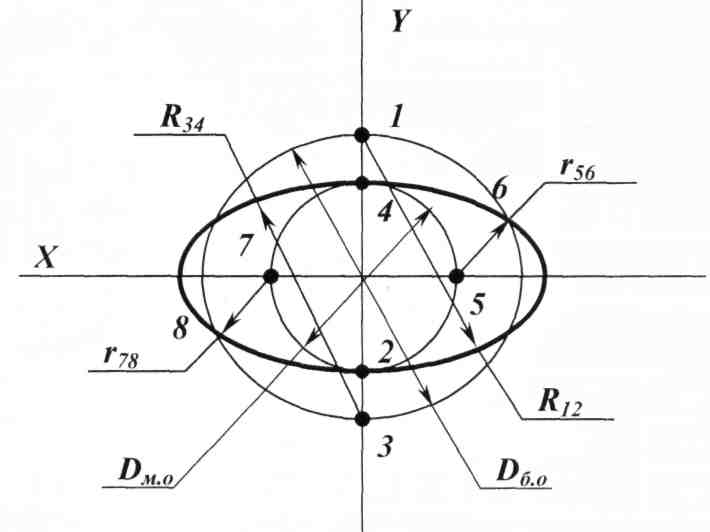
При использовании приведенных коэффициентов искажения аксонометрическое изображение предмета получается увеличенным против его натуральной величины для изометрической проекции в 1,22 раза. масштаб изображения составляет: для изометрии – 1,22 : 1.
Схемы расположения осей и величины приведенных коэффициентов искажений для изометрической проекции изображены на рис. 1. Там же указаны величины уклонов, которыми можно пользоваться для определения направления аксонометрических осей при отсутствии соответствующего инструмента (транспортира или угольника с углом 30°).
Рис. 1
Окружности в аксонометрии, в общем случае, проецируются в виде эллипсов, причем при использовании действительных коэффициентов искажений большая ось эллипса по величине равна диаметру окружности. При использовании приведенных коэффициентов искажений линейные величины получаются увеличенными, и чтобы привести к одному масштабу все элементы изображаемой в аксонометрии детали, большая ось эллипса для изометрической проекции принимается равной 1,22 диаметра окружности.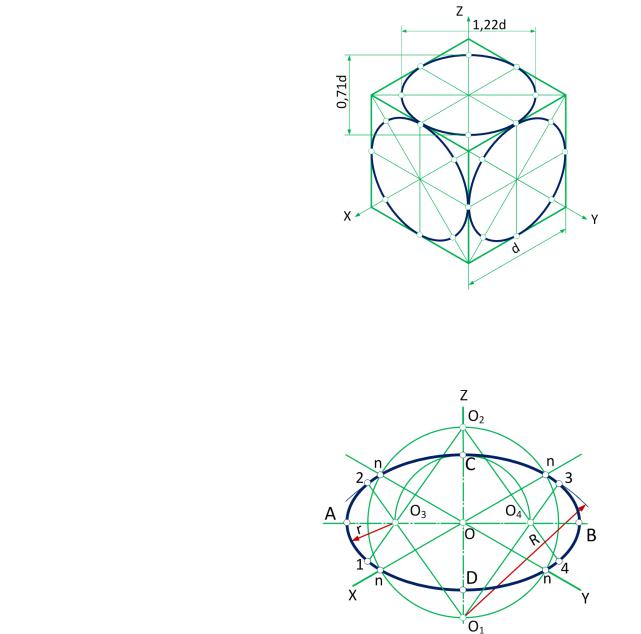
Малая ось эллипса в изометрии для всех трех плоскостей проекций равна 0,71 диаметра окружности (рис. 2).
Рис. 2
Большое значение для правильного изображения аксонометрической проекции предмета имеет расположение осей эллипсов относительно аксонометрических осей. Во всех трех плоскостях прямоугольной изометрической проекции большая ось эллипса должна быть направлена перпендикулярно оси, отсутствующей в данной плоскости. Например, у эллипса, расположенного в плоскости xОz, большая ось направлена перпендикулярно оси у, проецирующейся на плоскость xОz в точку; у эллипса, расположенного в плоскости yОz, — перпендикулярно оси х и т. д. На рис. 2 приведена схема расположения эллипсов в различных плоскостях для изометрической проекции. Здесь же приведены коэффициенты искажений для осей эллипсов, в скобках указаны величины осей эллипсов при использовании действительных коэффициентов.
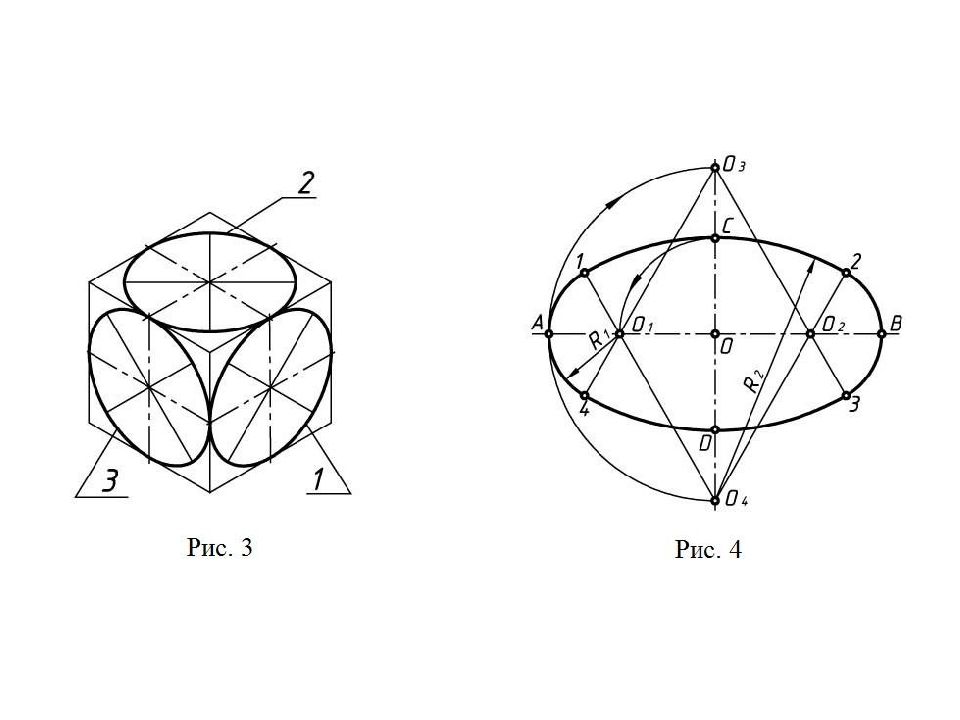
На практике построение эллипсов заменяют построением четырехцентровых овалов.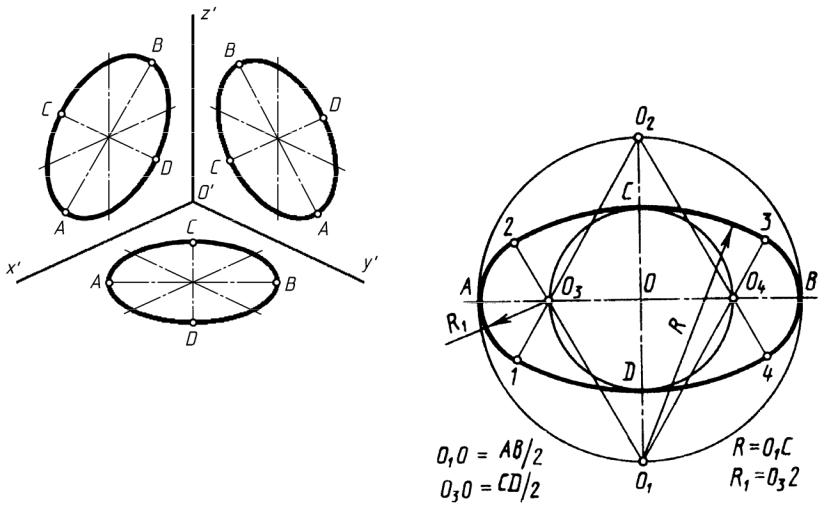 На рис. 3 показано построение овала в плоскости П1. Большая ось эллипса АВ направлена перпендикулярно отсутствующей оси z, а малая ось эллипса CD – совпадает с ней. Из точки пересечения осей эллипса проводят окружность радиусом, равным радиусу окружности. На продолжении малой оси эллипса находят первые два центра дуг сопряжения (О1 и О2), из которых радиусом R1 = О11 = О22 проводят дуги окружностей. На пересечении большой оси эллипса с линиями радиуса R1 определяют центры (О3 и О4), из которых радиусом R2 = О31 = О44 проводят замыкающие дуги сопряжения.
На рис. 3 показано построение овала в плоскости П1. Большая ось эллипса АВ направлена перпендикулярно отсутствующей оси z, а малая ось эллипса CD – совпадает с ней. Из точки пересечения осей эллипса проводят окружность радиусом, равным радиусу окружности. На продолжении малой оси эллипса находят первые два центра дуг сопряжения (О1 и О2), из которых радиусом R1 = О11 = О22 проводят дуги окружностей. На пересечении большой оси эллипса с линиями радиуса R1 определяют центры (О3 и О4), из которых радиусом R2 = О31 = О44 проводят замыкающие дуги сопряжения.
Рис. 3
Обычно аксонометрическую проекцию предмета строят по ортогональному чертежу, причем построение получается более простым, если положение детали относительно осей координат х, у и z остается таким же, как и на ортогональном чертеже. Главный вид предмета следует располагать на плоскости xОz.
Главный вид предмета следует располагать на плоскости xОz.
Построение начинают с проведения аксонометрических осей и изображения плоской фигуры основания, затем строят основные контуры детали, наносят линии уступов, углублений, выполняют отверстия в детали.
При изображении разрезов в аксонометрии на аксонометрических проекциях, как правило, невидимый контур штриховыми линиями не показывают. Для выявления внутреннего контура детали, так же как и на ортогональном чертеже, в аксонометрии выполняют разрезы, но эти разрезы могут не повторять разрезы ортогонального чертежа. Чаще всего на аксонометрических проекциях, когда деталь представляет собой симметричную фигуру, вырезают одну четвертую или одну восьмую часть детали. На аксонометрических проекциях, как правило, не применяют полные разрезы, так как такие разрезы уменьшают наглядность изображения.
При выполнении аксонометрических изображений с разрезами линии штриховки сечений наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (рис. 4).
4).
Рис. 4
При выполнении разрезов секущие плоскости направляют только параллельно координатным плоскостям (xОz, yОz или хОу).
Способы построения изометрической проекции детали:
1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма которых имеет плоскую грань, называемую формообразующей; ширина (толщина) детали на всем протяжении одинакова, на боковых поверхностях отсутствуют пазы, отверстия и другие элементы. Последовательность построения изометрической проекции заключается в следующем:
1) построение осей изометрической проекции;
2) построение изометрической проекции формообразующей грани;
3) построение проекций остальных граней посредством изображения ребер модели;
4) обводка изометрической проекции (рис. 5).
Рис. 5. Построение изометрической проекции детали, начиная от формообразующей грани
2. Способ построения изометрической проекции на основе последовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 6).
3. Способ построения изометрической проекции на основе последовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных определенным образом друг с другом (рис. 7).
4. Комбинированный способ построения изометрической проекции. Изометрическую проекцию детали, форма которой получена в результате сочетания различных способов формообразования, выполняют, используя комбинированный способ построения (рис. 8).
Аксонометрическую проекцию детали можно выполнять с изображением (рис. 9, а) и без изображения (рис. 9, б) невидимых частей формы.
Рис. 6. Построение изометрической проекции детали на основе последовательного удаления объемов
Рис. Способ построения изометрической проекции на основе последовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 6).
3. Способ построения изометрической проекции на основе последовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных определенным образом друг с другом (рис. 7).
4. Комбинированный способ построения изометрической проекции. Изометрическую проекцию детали, форма которой получена в результате сочетания различных способов формообразования, выполняют, используя комбинированный способ построения (рис. 8).
Аксонометрическую проекцию детали можно выполнять с изображением (рис. 9, а) и без изображения (рис. 9, б) невидимых частей формы.
Рис. 6. Построение изометрической проекции детали на основе последовательного удаления объемов
Рис. 7 Построение изометрической проекции детали на основе последовательного приращения объемов
Рис. 8. Использование комбинированного способа построения изометрической проекции детали
Рис. 9. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей; б — без изображения невидимых частей 7 Построение изометрической проекции детали на основе последовательного приращения объемов
Рис. 8. Использование комбинированного способа построения изометрической проекции детали
Рис. 9. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей; б — без изображения невидимых частей
|
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ ПО АКСОНОМЕТРИИ
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.
Построить прямоугольную изометрию детали по выполненному чертежу простого или сложного разреза на выбор студента. Деталь строится без невидимых частей с вырезом ¼ части по осям.
На рисунке показано оформление чертежа аксонометрической проекции детали после удаления лишних линий, обводки контуров детали и штриховки сечений.
ЗАДАНИЕ №5 СБОРОЧНЫЙ ЧЕРТЕЖ ВЕНТИЛЯ
Неуловимый эллипс: рисование эллипсов в перспективе
Любой художник может сказать вам, насколько сложно рисовать эллипсы в перспективе. Вершина цветочного горшка, крышка кувшина, основание силоса сарая — будь то натюрморт или пейзаж, вы обязательно столкнетесь с проблемой изображения укороченного круга или эллипса практически в любом рисунок или живопись. Большинство из нас пытаются «на глаз» надеяться, что все будет достаточно хорошо, но есть более простой и правильный способ сделать это правильно.
Вершина цветочного горшка, крышка кувшина, основание силоса сарая — будь то натюрморт или пейзаж, вы обязательно столкнетесь с проблемой изображения укороченного круга или эллипса практически в любом рисунок или живопись. Большинство из нас пытаются «на глаз» надеяться, что все будет достаточно хорошо, но есть более простой и правильный способ сделать это правильно.
Так что же такое эллипс? В геометрии это замкнутая кривая, похожая на круг, но с длинной осью и короткой осью — овалом. С точки зрения рисования в перспективе, эллипс — это то, что мы видим, когда смотрим на круг с его края, а не с высоты птичьего полета.
При рисовании эллипса в перспективе часто допускаются две распространенные ошибки. Один состоит в том, чтобы нарисовать футбольную фигуру, где внешние края сужаются почти к точкам, а другой — провести две параллельные линии, соединенные кривыми на каждом конце.
Чтобы избежать этих проблем, помогает мыслить «вне эллипса». Если вы можете нарисовать квадрат в перспективе, его легко превратить в эллипс, выполнив следующие действия.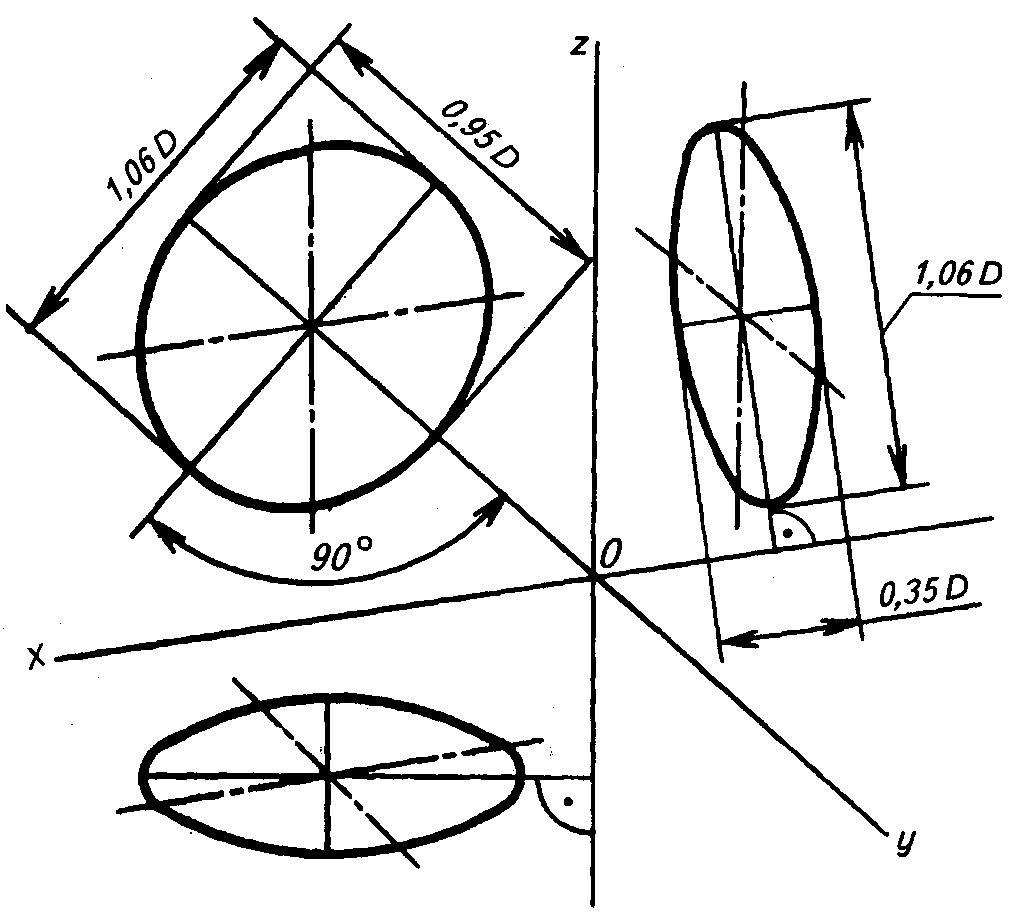
Большинство эллипсов, с которыми мы сталкиваемся, расположены вверху и внизу цилиндрических форм, таких как стаканы, цветочные горшки, бочки, ведра и т. Д. Если вы думаете о цилиндре как о находящемся внутри коробки, рисовать верхний и нижний эллипсы становится намного проще. .
Шаг 1: Нарисуйте прямоугольник в 1- или 2-точечной перспективе, достаточно большой, чтобы вместить ваш цилиндр.Верхняя и нижняя плоскости прямоугольника будут местоположением ваших эллипсов.
Шаг 2. Начнем с нижней квадратной плоскости. Используя линейку, нарисуйте диагональные линии, соединяющие каждый угол, чтобы создать «x».
Шаг 3: Проведите линию от точки схода через центр «x» до внешнего края квадрата.
Шаг 4: Проведите еще одну линию через «x», параллельную переднему и заднему краям квадрата.В 1-точечной перспективе эта линия будет горизонтальной, а в 2-точечной перспективе она будет отступать к вашей второй точке схода. Теперь у вас есть форма креста, которая идеально разделяет ваш квадрат на четыре меньших квадрата в перспективе. Примечание: важно, чтобы вы сначала выполнили шаг 3, иначе вы не найдете истинный центр квадрата в перспективе. Это то, на что вы не можете смотреть.
Примечание: важно, чтобы вы сначала выполнили шаг 3, иначе вы не найдете истинный центр квадрата в перспективе. Это то, на что вы не можете смотреть.
Шаг 5: Сотрите диагональные линии с вашего начального «x».
Шаг 6: Аккуратно нарисуйте свой эллипс на 4 сегмента, соединяя каждую точку, где крест встречается с краями квадрата.Обратите внимание, это требует некоторой практики, но наберитесь терпения. Это определенно будет смотреться лучше, чем если бы вы это делали от руки.
Шаг 7: Повторите шаги 1–6 для верхнего квадрата коробки.
Шаг 8: Сотрите линии перспективы и вертикальные линии в рамке, стараясь не стереть эллипсы!
Шаг 9: Используя линейку, нарисуйте вертикальные линии между правым и левым краями ваших эллипсов. НЕ просто соединяйте точки пересечения креста с краями эллипса, так как это не обязательно самые внешние края.
Шаг 10: Теперь вы можете стереть кресты на обоих эллипсах и задний изогнутый край на нижнем эллипсе.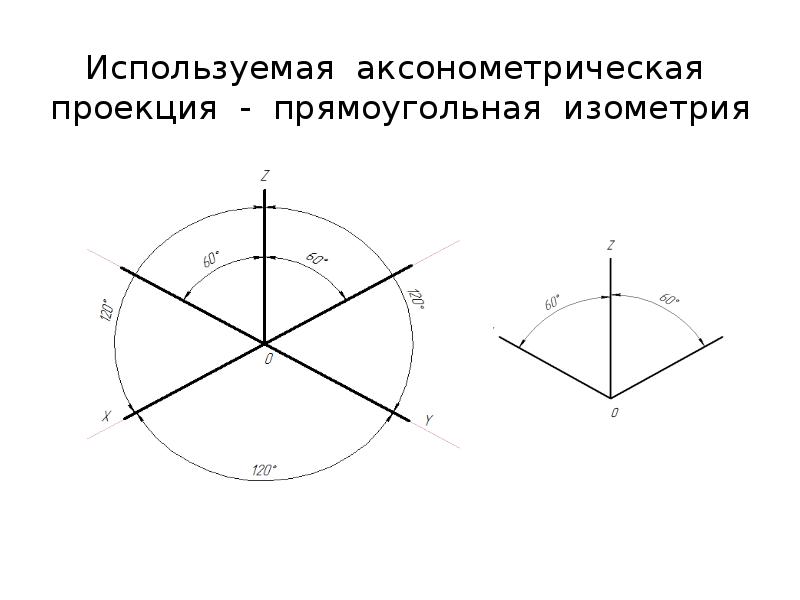
Поздравляем! Вы только что нарисовали два идеальных эллипса в перспективе, чтобы получился цилиндр, который можно использовать в натюрмортах, пейзажах, архитектурных рисунках — что угодно. И эти шаги работают даже в том случае, если эллипс или цилиндр находится на краю или на стене (часы, зеркала, окна и т. Д.)! Что вы нарисуете дальше, включая эллипсы?
Учебники— Рисование эллипсов
Анатомия
ellipse:
Когда мы смотрим на круг под углом, мы видим эллипс.Мы называем этот угол обзора градусом эллипса. Идеально
круг виден под углом 90 градусов, а под меньшими углами мы видим различные
эллипсов на пути вниз к эллипсу нулевого градуса (прямая
линия). Разобраться в механике рисования эллипсов несложно,
освоение рисования эллипсов. У эллипса есть две оси, которые нам нужны
знать о малой оси и большой оси. Малая ось делит
эллипс на две равные половины по его узкому измерению.Основная ось
делит эллипс по длине на две равные половины. В
малая и большая оси пересекают друг друга под углом 90 градусов. См. Рисунок
е-1.
В
малая и большая оси пересекают друг друга под углом 90 градусов. См. Рисунок
е-1.
Как можно использовать эти оси для чертеж:
Если мы посмотрим на
рисуя в e-2, мы видим, что я нарисовал квадрат вокруг нашего эллипса.
После того, как я нарисовал квадрат, я рисую «X» поперек него, чтобы найти его центр в
перспектива.Когда вы наблюдаете малую и большую оси эллипса, мы
посмотрите, что малая ось проходит через центр квадрата, а
большая ось нет. Заметим также, что эллипс касается касательной
ровно посередине каждой стороны квадрата, именно там, где мы бы
ожидайте этого. Это немного изгибает разум. Мы взяли симметричный
фигуру, эллипс, и поместил его в перспективу. Это всегда работает, если
вы делаете свой рисунок в допустимых пределах искажения.Несмотря на
катится ли ваш эллипс по земле или опирается на нее, как мы
см. рисунок e-3, результат конструкции остается прежним.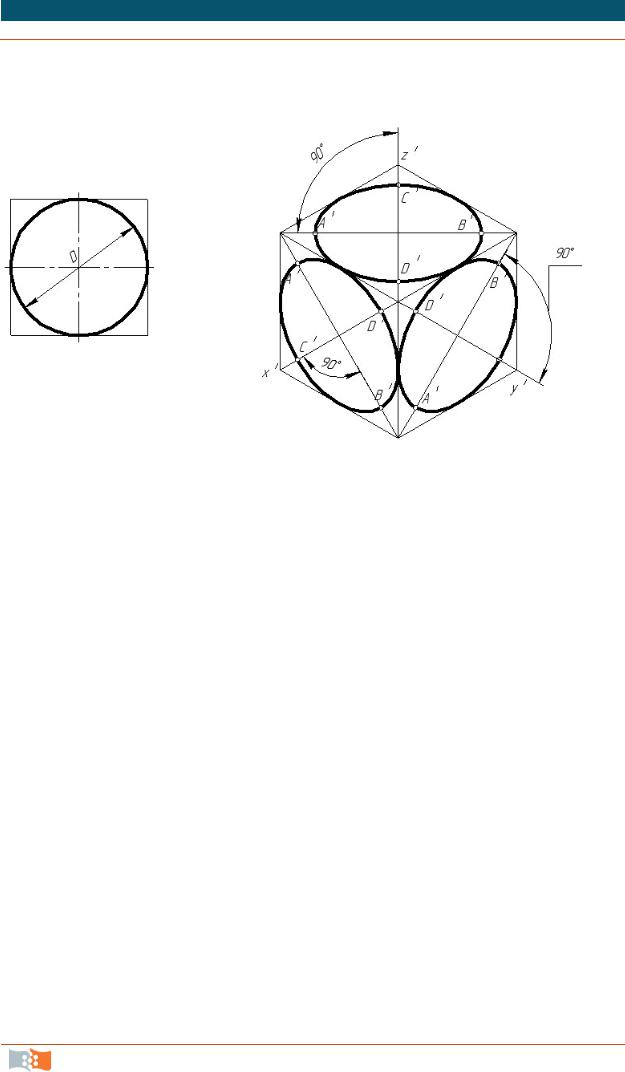 Обучение
из этого наблюдения и теперь зная, где малая и большая оси
наш эллипс должен быть самым большим подспорьем в рисовании эллипсов
должным образом. Поскольку малая ось эллипса всегда проходит через центр
наш квадрат — это то, что мы можем использовать, чтобы помочь нам его нарисовать. И наоборот
главная ось не ссылается ни на что, что могло бы помочь нам найти ее в нашем
перспективный квадрат.Вот почему я не рекомендую использовать большую ось.
при рисовании эллипсов.
Обучение
из этого наблюдения и теперь зная, где малая и большая оси
наш эллипс должен быть самым большим подспорьем в рисовании эллипсов
должным образом. Поскольку малая ось эллипса всегда проходит через центр
наш квадрат — это то, что мы можем использовать, чтобы помочь нам его нарисовать. И наоборот
главная ось не ссылается ни на что, что могло бы помочь нам найти ее в нашем
перспективный квадрат.Вот почему я не рекомендую использовать большую ось.
при рисовании эллипсов.
Практикуйтесь в рисовании эллипсов, не беспокоясь о местонахождении их в перспективе. Вот несколько примеров того, как моя ржавая рука пыталась сегодня утром нарисуйте несколько эллипсов для этого урока. Нарисуйте разные размеры и разной степени. После того, как вы нарисовали эллипс, обозначьте его малую ось с помощью рисование линии через его узкое измерение, которое разделяет каждую сторону в равной степени.
Я нахожу
полезно, если вы представляете, что собираетесь сложить эллипс вдоль
эта строка. Вы хотите, чтобы он сложился по этой линии и приземлился точно на
сам. Если ваша малая ось неверна, мы можем увидеть, что происходит на чертеже
е-4.
Вы хотите, чтобы он сложился по этой линии и приземлился точно на
сам. Если ваша малая ось неверна, мы можем увидеть, что происходит на чертеже
е-4.
После
Вам нравится, как выглядят ваши эллипсы, и вы
Вы уверены, что сможете правильно определить малую ось каждого, к чему готовы
начните пытаться разместить свои эллипсы в перспективных конструкциях.
Начните с чего-нибудь простого, например, с рисования прямой линии, представляющей
малую ось вашего эллипса, а затем попробуйте нарисовать эллипсы различных
размеры и градусы на этой линии.Это немного сложнее, чем рисовать
сначала эллипс, а затем рисование малой оси. После того, как вы прибьете
упражнение попробуйте нарисовать две сходящиеся прямые линии и нарисовать эллипсы
касание касательно каждой линии. Это еще труднее. Один из многих
сложное упражнение — нарисовать страницу из кубиков, а затем нарисовать эллипс на
каждая грань, касающаяся стороны каждого квадрата, как мы наблюдали
на чертежах е-2 и е-3. Рисование концентрических эллипсов тоже хорошо
упражняться.
Рисование концентрических эллипсов тоже хорошо
упражняться.
Вы можете использовать направляющие эллипса, чтобы выпрямить эллипсы, но не пытайтесь эскиз с ними. Я еще не видел, чтобы это было сделано эффективно. Ты много Лучше сделать всю работу над перспективным макетом от руки, а затем выломайте направляющие и эллиптические направляющие, чтобы закрепить детали, если вам нужно к. Как только вы достаточно попрактикуетесь, вы обнаружите, что можете делать очень многое. грамотные чертежи полностью от руки. Есть отличное чувство удовлетворение от достижения хорошего качества линии и надлежащего перспектива в эскизе от руки.
Как проверить
если ваш эллипс нарисован правильно.
Важно
понимать механику эллипсов, чтобы вы могли вносить в них коррективы
после того, как вы их нарисовали. По сути, есть только две вещи, которые делают
эллипс, правильно нарисованный в перспективе или нет.
Малая ось и
ваши точки схода.
Первое, что нужно проверить — есть ли
ваша малая ось верна. В случае установки колес на автомобили
малая ось всегда является общей для оси колеса.Большую часть времени
эта ось также перпендикулярна центральной линии вашего автомобиля. Так что
следует, что второстепенные оси ваших эллипсов (колес) также
перпендикулярно этой средней линии. Бывают случаи, например, когда передняя
колеса повернуты или колеса настроены с экстремальным развалом, который
они больше не перпендикулярны центральной линии вашего автомобиля.
Еще один простой пример для визуализации — это то, что малая ось
винт на самолете параллелен средней линии фюзеляжа и
поэтому они попадают в одну и ту же точку схода.Помните, когда перспектива
рисунок, что «все параллельные линии идут к одной и той же точке схода».
Угол вашего эллипса.
Предполагая
малая ось вашего эллипса правильная, и ваш эллипс все еще выглядит
неправильно это может быть только одно, степень. Прежде чем пытаться отрегулировать
степень эллипса, малая ось должна быть правильной. Нет количества
регулировка степени может компенсировать неправильную малую ось.Проверка
градус — простая перспективная конструкция.
Шаг 1:
Розыгрыш
прямоугольник вокруг и по касательной с каждой стороны к вашему эллипсу. Обязательно следите
ваши перспективные рекомендации при этом.
Шаг 2:
Соблюдайте
где нарисованный эллипс соприкасается с рамкой, которую вы нарисовали вокруг него. Если
ваш эллипс не касается середины каждой стороны поля, тогда
степень неправильная. Отрегулируйте угол эллипса, сделав его шире или
уже до тех пор, пока вы не сможете нарисовать вокруг него рамку, которая касается точно в
середина каждой стороны.Когда вы это сделаете, у вас будет должный
нарисованный эллипс в правильном градусе.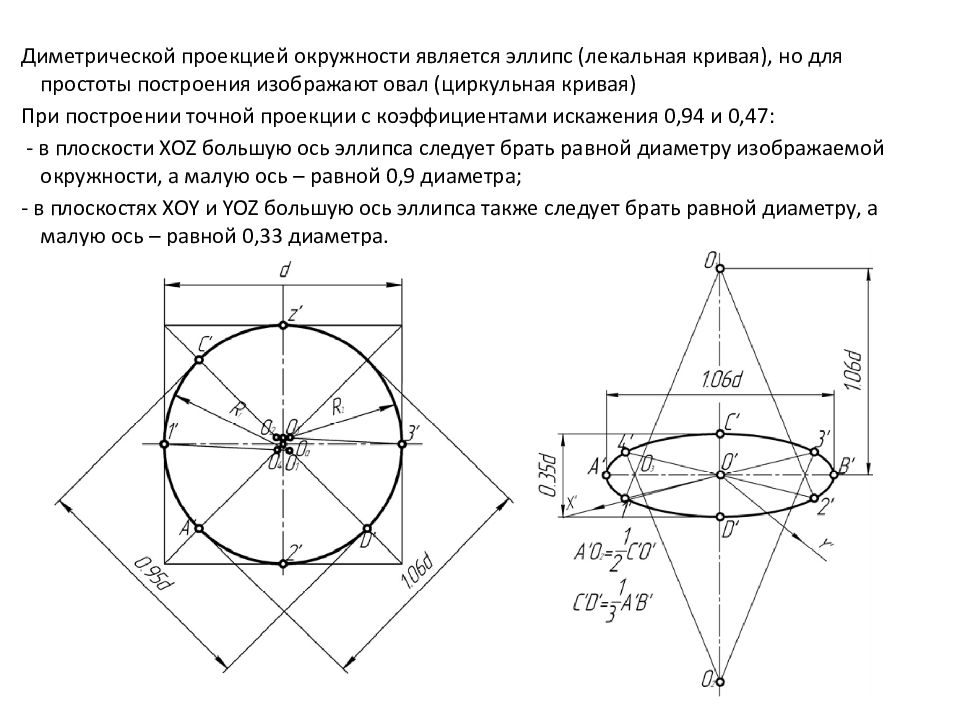
Вот еще несколько эскизы, которые я быстро помещаю поверх рекомендаций, чтобы помочь вам увидеть второстепенные оси эллипсов на чертежах.
Поздравляю, вы теперь мастер
эллипс!
Как использовать малую ось для рисования эллипса в перспективе?
У вас заблуждение.Эллипс — это способ построить перспективное изображение прямоугольной коробки. Эллипс — это тот же вид в перспективе круга на лицевой стороне этого блока. Вы должны построить перспективное изображение прямоугольной грани прямоугольника вокруг эллипса, не пытайтесь превратить эллипс в уже нарисованный 4-угольник. Это потому, что вы можете нарисовать любой эллипс внутри 4-угольника, и это будет идеальное перспективное изображение другого эллипса.
Если ваш эллипс должен быть перспективным изображением круга на квадрате, вопрос актуален.См. ПРИМЕЧАНИЕ 1 и прочтите мою историю, чтобы узнать, как работает «метод аккорда».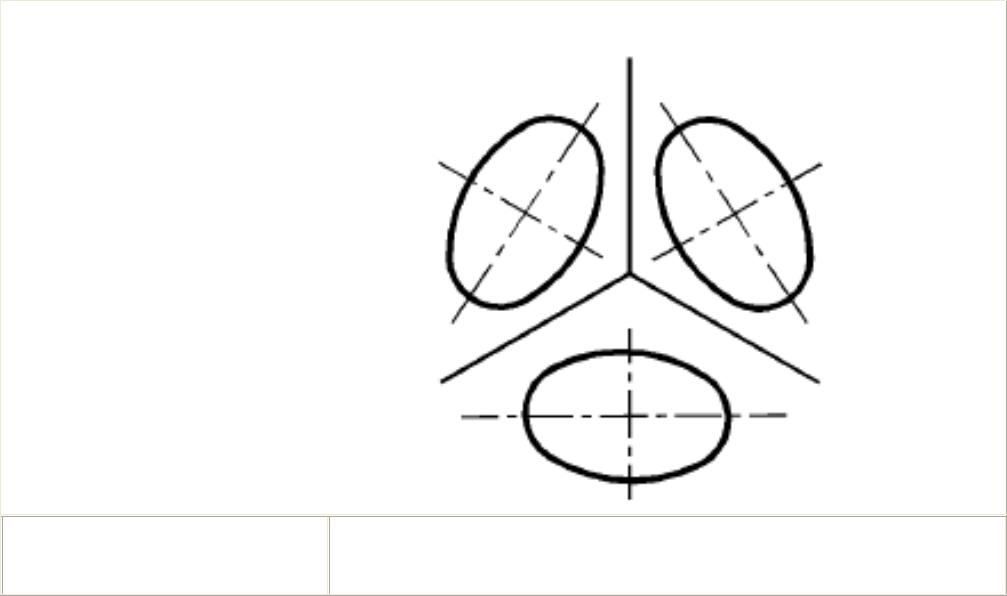
полезная история могла бы рассказать, как можно было бы построить последовательную куб, если линию горизонта и перспективное изображение круга на одной из граней даются. История является своим родом передового Eyeballing для практического рисования на бумаге, это не точная математика. Она не начинается с мер куба и визуализации параметров, она начинается от линии горизонта и один эллипс.
В следующем изображении мы имеем голубую линию горизонта и эллипс, который представляет собой круг на одной грани куба.Для простоты мы предполагаем, что эллипс на самом деле представляет собой круг на вертикальной грани. Кроме того, мы предполагаем, что двухточечная перспектива достаточно хороша, поэтому вертикальные линии отображаются как вертикальные:
Математическая теория утверждает, что малая ось эллипса указывает на точку схода тех горизонтальных ребер куба, которые перпендикулярны его грани. Мы находим точку схода (V), продолжая малую ось эллипса. Это просто в Illustrator, который размещает узлы на концах осей эллипса:
Как уже было сказано, мы предполагаем, что эллипс находится на вертикальной грани куба, и используем 2-точечную перспективу.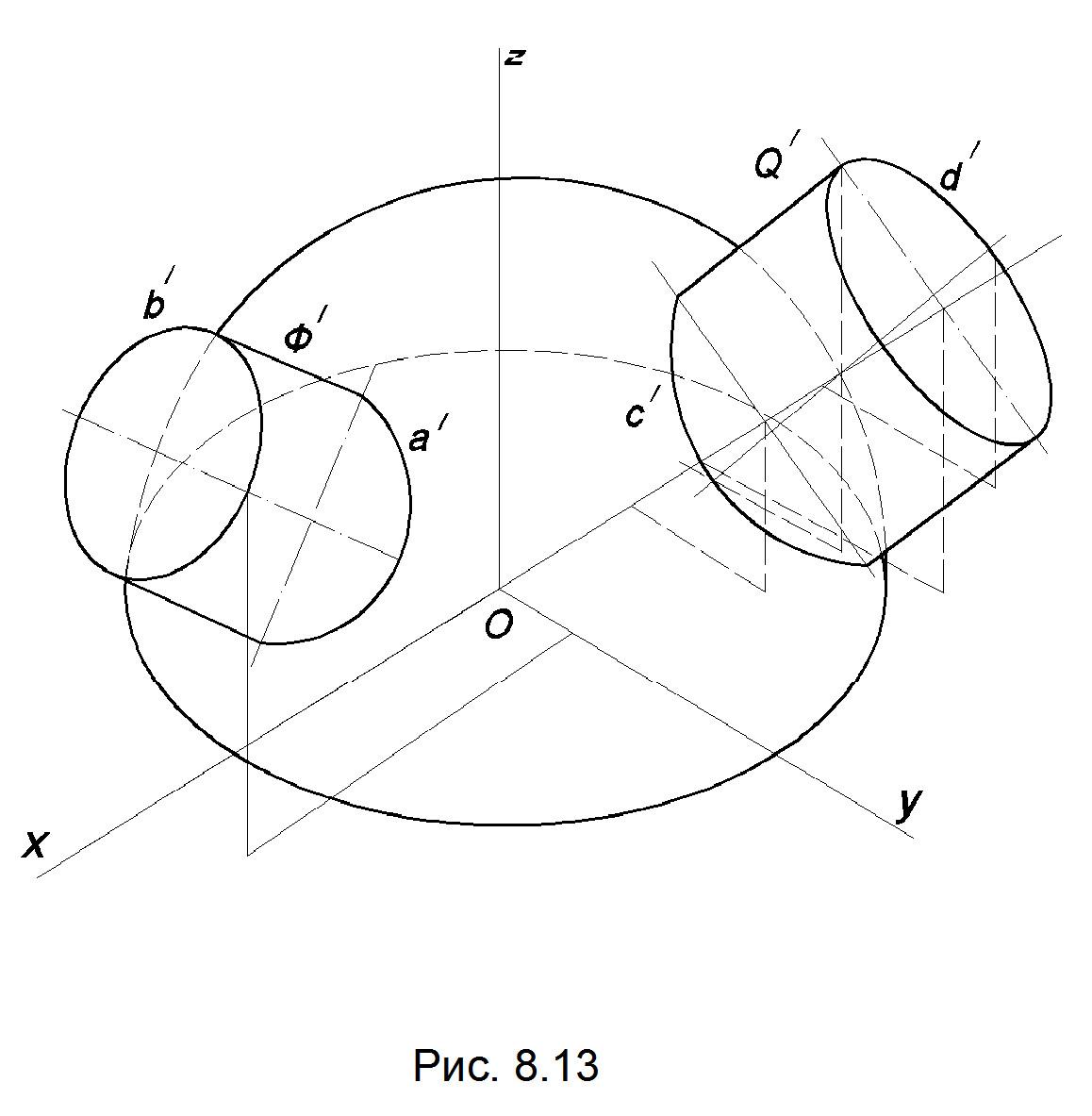 На следующем изображении изображена большая часть, привлекающая внимание :
На следующем изображении изображена большая часть, привлекающая внимание :
В зеленых линиях нет ничего особенного. Все они являются вертикальными линиями (поскольку мы предположили, что вертикальные линии можно нарисовать как вертикальные линии). Одна проходит через середину эллипса, а две другие — касательные. Отличный трюк — найти другую точку схода. Мы проводим из произвольной точки A кривой эллипса прямую линию по направлению к линии горизонта так, чтобы половинные сегменты ABD и CBD визуально выглядели такими же большими.Линия пересекает линию горизонта в желаемой точке схода U.
В инструкциях по рисованию это «Метод аккордов». Хорда — это линия AC.
Теперь мы можем провести часть краев квадратов лица от точек схода и пересечений:
Черные линии — это касательные от U, проведенные на глаз, а оранжевые линии — от V до пересечений.
Нам нужно еще 2 строки, чтобы получить куб. Одна из возможностей — снова использовать эллипс. Мы можем взглянуть на одну с вертикальной малой осью.Это изображение круга внутри горизонтального верхнего квадрата:
Мы можем взглянуть на одну с вертикальной малой осью.Это изображение круга внутри горизонтального верхнего квадрата:
Касательная с глазком от U и вертикальная линия от пересечения завершают куб.
Наверное, смотреть на глаза — плохо. Я использовал Illustrator, который должен иметь точную привязку, и я не использовал его, кроме как в пересечениях. Но: Аккордовый метод предназначен для людей, которые рисуют ручкой и бумагой. Некоторые из них также могут иметь линейку и инструмент для рисования эллипса.
ПРИМЕЧАНИЕ 1: Метод хорды также можно использовать в обратном порядке для определения длин осей правого эллипса (который является изображением круга), если точки схода уже заданы.
Более подробное описание метода аккордов можно найти здесь: https://www.idsa.org/sites/default/files/2002_Randy%20Bartlett.pdf
Остерегайтесь «взятого из математики», но точного соглашения об определении направления плоских поверхностей по направлениям нормалей к поверхности. В обычном доме пол вертикальный, а стены горизонтальные.
В обычном доме пол вертикальный, а стены горизонтальные.
РИСУНОК ЭЛЛИПСОВ в MIKE SIBLEY FINE ART
Эллипс
Насколько точно нужно нарисовать эллипс?
Очень точно! Глаз зрителя может обнаружить любую неровность формы, которую он полностью понимает.«Квадрат», у которого стороны не равной длины, «круг», который не является круглым, и «эллипс», отклоняющийся от совершенства, сразу же отмечаются как не то, что он утверждает, или, точнее, не то, что глаз ожидает увидеть в этой ситуации и определяется как «чужое». Короче говоря, «круговой» круг принимается мимоходом и сохраняется общая реальность сцены. То же самое и с эллипсом.Что такое эллипс?
Эллипс — это просто круг в перспективе.Об этом важно помнить.Следовательно, эллипс должен подчиняться тем же правилам, что и круг.
Он состоит из дуг, не содержит прямых и, если разделен на четверти, каждый сегмент идентичен другим трем.
Устранение проблемы
Итак, как и в случае с кругом, эллипс содержит четыре идентичных сегмента.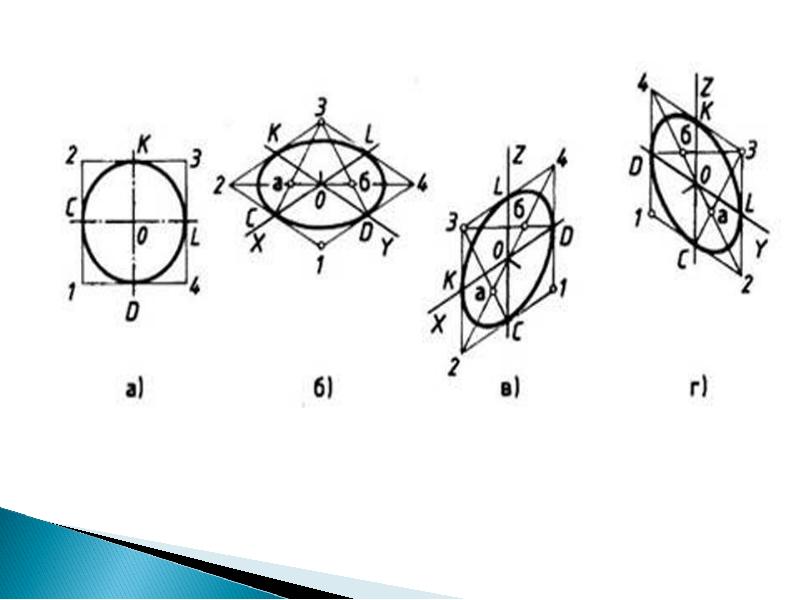 Чтобы изучить это, нарисуйте эллипс, используя шаблон эллипса. Или используйте инструмент круга / эллипса программы компьютерной графики, чтобы нарисовать его (здесь использовалась базовая программа MS Paint), а затем распечатайте его.Теперь проведите вертикальную линию через эллипс, чтобы разделить его пополам, а затем проведите через него еще одну. Сразу становится очевидным, что каждый квартал идентичен другим — только ориентация разная. Верхний левый сегмент — это зеркальное отображение верхнего правого, которое является вертикальным зеркальным отображением нижнего правого сегмента под ним … Вы только что уменьшили проблему на три четверти — с каждой минутой становится все легче!
Чтобы изучить это, нарисуйте эллипс, используя шаблон эллипса. Или используйте инструмент круга / эллипса программы компьютерной графики, чтобы нарисовать его (здесь использовалась базовая программа MS Paint), а затем распечатайте его.Теперь проведите вертикальную линию через эллипс, чтобы разделить его пополам, а затем проведите через него еще одну. Сразу становится очевидным, что каждый квартал идентичен другим — только ориентация разная. Верхний левый сегмент — это зеркальное отображение верхнего правого, которое является вертикальным зеркальным отображением нижнего правого сегмента под ним … Вы только что уменьшили проблему на три четверти — с каждой минутой становится все легче!Изучение геометрии
Теперь давайте нарисуем рамку вокруг нашего эллипса, чтобы мы могли правильно изучить геометрию одного из этих сегментов.Если вы правша, я предлагаю вам сосредоточиться на верхнем левом углу — используя естественное движение запястья, это первая дуга, которую вы захотите нарисовать.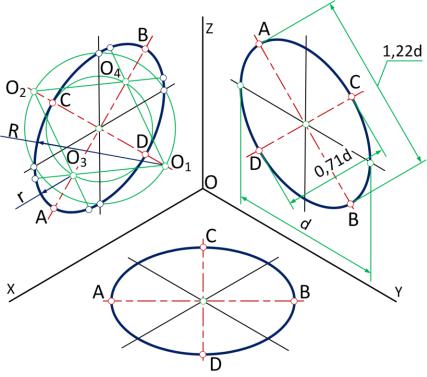 Обратите внимание, что оба конца «плоские» по отношению к сторонам коробки — эллипс никогда не достигает точки вверху или внизу. Обратите также внимание на то, как дуга, перемещаясь сверху вниз, плавно раскручивается от крутого к пологому изгибу. Он делает это плавно, без намека на прямой участок — это, помните, круг в перспективе, поэтому задействованы только кривые.
Обратите внимание, что оба конца «плоские» по отношению к сторонам коробки — эллипс никогда не достигает точки вверху или внизу. Обратите также внимание на то, как дуга, перемещаясь сверху вниз, плавно раскручивается от крутого к пологому изгибу. Он делает это плавно, без намека на прямой участок — это, помните, круг в перспективе, поэтому задействованы только кривые.Первые попытки
Держите под рукой свой шаблон или нарисованные на компьютере примеры — они помогут вам нарисовать правильные кривые в следующих упражнениях. Со временем вы сможете отбросить их и начать рисовать с пониманием, но пока я позволю вам использовать простыню для детской кроватки! Мы начнем с повторения того, к чему вы до сих пор склонялись, но в обратном порядке.(1) Нарисуйте квадрат в перспективе на вертикальной плоскости (поначалу вам, вероятно, будет немного проще рисовать вертикальные эллипсы). Квадрат примерно 8 см высотой на 4 см (3 дюйма × 1 ½ дюйма) будет примерно правильным.Держите его маленьким, чтобы вам не приходилось двигать рукой во время упражнения, и вы могли видеть результат, не двигая глазами.
(2) Разделите его по вертикали пополам (нарисуйте линии, соединяющие противоположные углы — там, где они пересекаются, это истинный центр). Затем разделите его пополам по горизонтали. (3) Теперь приступим. Мы начнем с верхнего левого сегмента, но, если вы левша, вы можете предпочесть начать с верхнего правого. Еще раз изучите кривую, созданную вашим шаблоном, затем попробуйте повторить геометрию в верхнем левом сегменте.Начиная почти ровно до верхней линии квадрата, начинайте изгибаться вниз к средней точке стороны, плавно уменьшая кривую по мере продвижения. Стремитесь встретить сторону так же «ровно», как вы начали. Получение правильной первой кривой — это главный трюк — все последующее будет просто ее копией. Подсказка : Когда вы рисуете свою кривую, часто помогает смотреть на точку, к которой вы стремитесь, а не на линию, которую вы рисуете — смотрите вперед на указатель карандаша к месту назначения.
Теперь поверните бумагу по часовой стрелке на 90 ° и скопируйте кривую, которую вы только что нарисовали, но в обратном порядке .
 ..
.. … Снова поверните бумагу на 90 ° и скопируйте кривую, которую вы только что нарисовали,
в зеркальном отображении.
Наконец, снова переверните бумагу и еще раз скопируйте в зеркальном отображении только что начерченную кривую. Выглядит правильно? Ну нет — в этом случае мне нужно немного поработать — но для первой попытки это вполне презентабельно. Есть ли плоские секции? Плавно ли переходят ваши линии от сегмента к сегменту? Если вы не можете понять, почему он выглядит неправильно, попробуйте рассмотреть свой эллипс в зеркале или перевернуть его вверх дном, чтобы по-новому взглянуть на него.Если ваша бумага достаточно тонкая, чтобы видеть сквозь нее, когда вы пропускаете через нее свет — сложите ее пополам по горизонтальной разделительной линии — две половинки должны точно совпадать, чтобы можно было легко обнаружить любые ошибки. Обнаружив проблему, сотрите линии в этой области, оставив лишь тень, которая будет направлять вас. Теперь перерисуйте, чтобы исправить недостаток, затем снова спросите: «Выглядит правильно?» Помните, глаз всегда может определить неисправность по эллипсу, так что .
 .. Если он выглядит правильно, значит, он правильный!
.. Если он выглядит правильно, значит, он правильный! Чем больше вы тренируетесь, тем легче рисовать эллипсы.Я сомневаюсь, что с первого раза возможно действительно нарисовать идеальный эллипс, но ваши первые попытки будут все ближе и ближе к готовой форме.
Фактор ГОРИЗОНТА
До сих пор мы только что нарисовали наш эллипс в виде круга, искаженного внутри квадрата, соответствующего вертикальной перспективе. Но для правильной работы горизонтальных эллипсов необходимо также учитывать их расстояние выше или ниже горизонта. Если вы держите перед собой банку с фасолью и поднимаете ее выше уровня ваших глаз (до горизонта), вы будете смотреть под банку; ниже уровня ваших глаз, и вы будете видеть это сверху.Держите его прямо перед собой, и вы увидите верхнюю половину банки снизу и нижнюю половину сверху. ХОРОШО?- Исправьте горизонт, проведя горизонтальную линию.
- Определите точку схода (ВП) и проведите через нее вертикальную линию.
- Нарисуйте в перспективе два квадрата одинаковой ширины — один над линией и один под линией.
- Разделите эти квадраты пополам в обе стороны, как вы делали в предыдущем упражнении.
- Постройте эллипсы внутри обоих квадратов — поверните бумагу, если это поможет вам их нарисовать.
- Теперь соедините внешние края и добавьте тона, чтобы сформировать трехмерный цилиндр.
Обратите внимание, как эллипс «перетекает» в сторону. Резкого стыка не бывает.
Повторите упражнение, но сместите горизонт вниз.
На этот раз опустите горизонт так, чтобы оба квадрата оказались над ним.
Если вы перевернете его, эллипсы окажутся ниже горизонта.
И тоже поправьте, если повернули налево…
… или справа от вашей точки просмотра.
А с практикой …
Как только вы поймете основную геометрию задействованных кривых, вы, вероятно, обнаружите, что достаточно лишь слегка нарисовать разделители длины и ширины и добавить точки, отмечающие требуемые размеры.
Если вам нужно нарисовать действительно большие эллипсы, это часто поможет вам сначала нарисовать меньшую версию — достаточно маленькую, чтобы вы могли видеть весь эллипс, не двигая глазами. Затем вы можете увеличить его до конечной поверхности для рисования (используя любые средства, которые вы предпочитаете, от проецирования до механического изменения размера) или использовать его в качестве визуального шаблона, который поможет вам при рисовании в полный размер.
Эллипс внутри эллипса
Наконец, будут моменты, когда вам нужно будет нарисовать один эллипс (или несколько) внутри другого. Например, при рисовании круглого полого объекта со стенками значительной толщины, такого как терракотовый цветочный горшок. В этом конкретном случае вам нужно нарисовать только верхнюю половину внешнего эллипса и сместить внутренний эллипс немного выше, чтобы учесть перспективу (задняя стенка находится дальше, чем передняя, поэтому a уже, чем b). Нижнюю половину внешнего эллипса нужно «видеть» только в вашем уме, поскольку она определяется исключительно освещением и тенью лицевой стороны.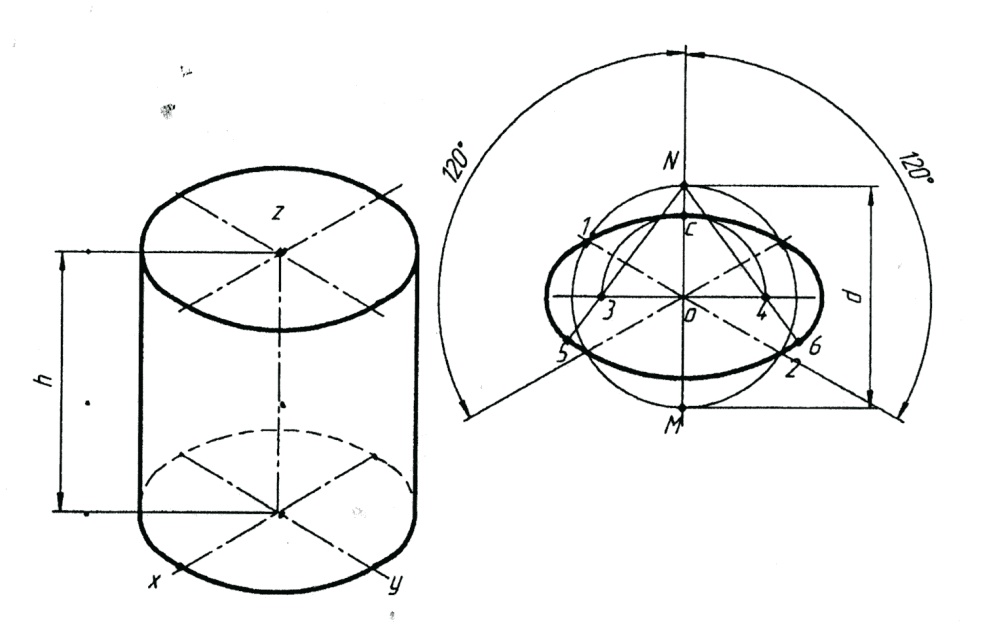 Если вы попытаетесь сначала провести эту линию, хотя и легко, у вас есть хорошие шансы, что она останется преследовать вас — даже после того, как вы ее стерли, ее небольшое углубление, вероятно, привлечет дополнительный графит из вашего затенения и будет присутствовать навсегда!
Если вы попытаетесь сначала провести эту линию, хотя и легко, у вас есть хорошие шансы, что она останется преследовать вас — даже после того, как вы ее стерли, ее небольшое углубление, вероятно, привлечет дополнительный графит из вашего затенения и будет присутствовать навсегда! Этот эллипс идеален? Нет, но в жизни мало что может быть совершенного, и горшки из печей часто имеют изъяны. В данном случае я решил, что небольшой перекос скорее добавлял, чем умалял, реальность …
… но здесь маслобойка и колесо должны были быть настолько совершенными, насколько я мог их нарисовать.
Примеры эллипсов …
Учебник по рисованию эллипса в перспективе с помощью Adobe Illustrator.
Основы перспективы | 2-х точечная перспектива | Трехточечная перспектива | Ракурс | Эллиптическая перспектива | Изометрические Рисунки
Все тексты и изображения учебного пособия — Copyright © 2011 KHI, Inc.
Любая техническая иллюстрация хороша ровно настолько, насколько хорош ее самый слабый элемент.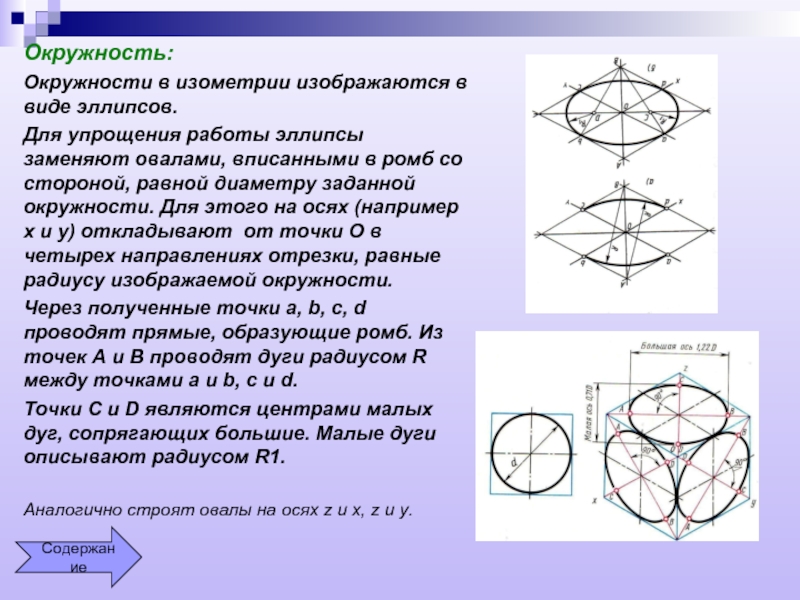 Возможно, наиболее важным (и часто упускаемым из виду) элементом любой иллюстрации является эллипс.Когда эллипс выполнен правильно, он исчезает на общей иллюстрации, но когда эллипс нарисован неправильно, это совершенно очевидно. Даже непосвященный глаз может заметить неправильно нарисованный эллипс, хотя он может быть не в состоянии определить или сформулировать, почему иллюстрация неправильная. Как вы увидите в последней части этого урока, недостаточно просто «сжать», чтобы круг превратился в эллипс, а затем повернуть его на вертикальную или горизонтальную плоскость, поскольку это не учитывает удаляющиеся аспекты этой плоскости. .
Возможно, наиболее важным (и часто упускаемым из виду) элементом любой иллюстрации является эллипс.Когда эллипс выполнен правильно, он исчезает на общей иллюстрации, но когда эллипс нарисован неправильно, это совершенно очевидно. Даже непосвященный глаз может заметить неправильно нарисованный эллипс, хотя он может быть не в состоянии определить или сформулировать, почему иллюстрация неправильная. Как вы увидите в последней части этого урока, недостаточно просто «сжать», чтобы круг превратился в эллипс, а затем повернуть его на вертикальную или горизонтальную плоскость, поскольку это не учитывает удаляющиеся аспекты этой плоскости. .
В этом уроке мы изучим принципы рисования круга как векторного эллипса в 1-точечной перспективе и 2-точечной перспективе с использованием Adobe Illustrator. Для этого урока важно использовать программное обеспечение для векторного рисования, такое как Adobe Illustrator или CorelDRAW. В этом случае мы будем использовать инструмент «Свободное преобразование» Illustrator для искажения формы и «соотношения сторон» или «соотношения эллипса» круга, чтобы он выглядел в перспективе.
Основы рисования эллипса в Illustrator
Начнем с рисования идеально круглого круга с отношением ширины к высоте 90 градусов (1: 1). Рис.1 , используя инструмент «Эллипс» Adobe Illustrator (L). Наш круг расположен внутри квадратного поля (синяя линия) с одинаковой высотой и шириной, созданного с помощью инструмента «Прямоугольник» Illustrator (M). Большая ось круга представлена пурпурной вертикальной линией, и на каждом пересечении большой оси с внешним краем круга есть зеленые точки. Adobe Illustrator Совет: Удерживайте клавишу «Shift» при перетаскивании, чтобы ограничить инструменты «Прямоугольник» и «Эллипс» идеальным кругом и / или квадратом.
В рис. 2 малая ось круга представлена пурпурной горизонтальной линией, и снова есть зеленые точки на каждом пересечении большой оси с внешним краем круга. Большая ось и малая ось круга пересекаются в центральной точке круга и находятся под углом 90 градусов друг к другу, как показано на Рис. 3 .
В рис. 4, 5 и 6 мы повернули большую ось на 20 градусов (по часовой стрелке) и изменили соотношение между большой и малой осями.Левый эллипс (более толстый эллипс) теперь имеет отношение ширины к высоте 40 градусов (1: 1,55), а правый эллипс (более тонкий эллипс) имеет соотношение 20 градусов (1: 2,92). Как и в приведенных выше примерах, мы отметили точки пересечения между внешним диаметром круга и точками большой и малой осей.
Рисование эллипса перспективы в 1 точку
Теперь мы начнем строить эллипс в 1-точечной перспективе. Мы начнем с рисования диагональных линий, которые пересекаются со всеми четырьмя углами синего прямоугольника, окружающего наш круг.На рис. 7 эти точки пересечения отмечены зелеными пунктами. Если бы мы просто уменьшили ширину малой оси по отношению к большой оси, мы бы создали изометрическое изображение нашего круга Рис. 8 . Истинный изометрический эллипс составляет примерно 35 градусов с соотношением 1: 1,75. Изометрическое изображение не имеет перспективы, и все параллельные прямые находятся под одним углом. Для получения дополнительной информации об изометрическом и перспективном рисовании перейдите к: Учебное пособие по рисованию в двухточечной перспективе.
В рис. 9 мы создали искусственную трехмерную среду с «сеткой перспективы с 1 точкой». Это означает, что на линии горизонта есть только одна точка схода. В этом примере линия горизонта также является нашей малой осью. Вы заметите, что главная ось не выровнена по центральной точке эллипса, как это было в нашем изометрическом эллипсе на рис. 8. Новая большая ось теперь выровнена по центральной точке перспективы, отмеченной зеленой точкой маркера, а также левой и Правые части круга очень разные по размеру и форме.Это отличительные характеристики «эллипса перспективы».
Следующим шагом будет разделение удаляющейся плоскости на равные части. Начиная с верхнего левого угла (A) нашего эллипса в прямоугольной рамке (, рис. 10, ), мы нарисуем диагональную линию (сплошного синего цвета), пока она не пересечет среднюю точку (B) прямоугольного эллипса вдоль горизонта и второстепенную. осевая линия. Продолжайте диагональную (сплошную синюю) линию, пока она не пересечется с линией нижней точки схода (C). С этой точки мы проведем вертикальную линию вверх, пока она не пересечет линию верхней точки схода.Теперь это определит квадрат того же «размера», что и наш первый квадрат, содержащий круг (теперь эллипс).
Повторяйте процесс, описанный в предыдущем абзаце, до тех пор, пока не получите пять равноправных квадратов ( Рис. 11 ). Теперь сформируйте второй эллипс в последнем (5-м) месте. Вы заметите, что по мере того, как мы приближаемся к точке схода, уменьшился не только вертикальный размер эллипса, но также изменились ширина и соотношение эллипса. Наш первый эллипс (передний план слева) равен 30 градусам с соотношением 1: 2, а второй эллипс (задний план справа) равен 20 градусам с соотношением 1: 2.92. Это явление связано с тем, что зритель находится под более крутым углом зрения, когда смотрит на объект, который находится в непосредственной близости, в отличие от объекта того же размера, который находится дальше ( Рис. 12 ), и поэтому , если смотреть под меньшим углом. «Картинная плоскость» на рис. 12 представляет восприятие перспективы наблюдателем.
В физическом мире «плоскость изображения» в рис. 12 представляет восприятие перспективы наблюдателем, интерпретируемое линзой глаза.В мире иллюстрации «картинная плоскость» на самом деле является плоской поверхностью бумаги или экрана компьютера, а восприятие трехмерной глубины или перспективы — это иллюзия.
Эллипсы с двухточечной перспективой
Теперь мы создадим сетку перспективы с двумя точками (, рис. 12, ), используя те же принципы, которые использовались на рис. 9–11. Начните с линии горизонта и создайте левую и правую точки схода. Из правой точки схода (RVP) мы будем проецировать центральную линию нашего эллипса, а также линии верхней и нижней точки схода.Создайте равномерно распределенные подразделения, как на рис. 10.
Из левой точки схода (LVP) спроецируйте линию второстепенной оси до пересечения с центральной точкой первого (переднего плана) прямоугольника и далее. Теперь нарисуйте вертикальную линию большой оси так, чтобы она пересекалась с центральной точкой прямоугольника эллипса (зеленая точка). Имейте в виду, что даже несмотря на то, что линия большой оси всегда должна быть под углом 90 градусов к линии второстепенной оси, мы не будем придавать ей меньшее значение при построении двухточечного эллипса перспективы..
Теперь, когда наша сетка перспективы построена, мы начнем заполнять передний план и фоновый эллипс. В нашем прямоугольнике эллипса переднего плана (, рис. 14, ) вы можете увидеть, что если бы мы просто возьмем эллипс 30 градусов (примерно правильное соотношение), созданный с помощью инструмента Ellipse Tool (L) в Adobe Illustrator, и повернем его так, чтобы и второстепенные оси выстраиваются в линию (зеленый эллипс), это выглядит некорректно. Даже если зеленый эллипс касается всех сторон прямоугольника эллипса, он не касается их в правильных местах (см. Рис.15 ). Как упоминалось в предыдущем абзаце, именно поэтому мы не будем полагаться на большую ось при построении нашего двухточечного эллипса перспективы.
В рис. 15 мы видим, что точки, в которых наш зеленый эллипс пересекает синий прямоугольник (красные стрелки), находятся в неправильных местах. Правильный эллипс должен пересекаться с синей рамкой в четырех центральных точках, обозначенных зелеными маркерами. Кроме того, наш зеленый эллипс на рис. 15 не пересекается с диагональными синими линиями в нашем шаблоне коробки.
Решение этой проблемы состоит в том, чтобы использовать наши точки схода для создания меньшего блока с точно такими же пропорциями (равное отношение ширины к высоте) внутри нашего основного блока шаблона. Рис. 16 . Это меньшее поле будет определять правильные точки пересечения, с которыми должен соприкасаться наш эллипс (, рис. 16, ). Имейте в виду, что инструмент Ellipse Tool (L) в Adobe Illustrator не может создать этот тип эллипса. Но не отчаивайтесь, есть простой способ сделать это, используя быстрое решение, которое будет рассмотрено в следующих разделах.
Примечание: Точка внутреннего квадрата, показанная на рис. 16, предназначена для того, чтобы показать, как изометрический эллипс (с использованием инструмента «Эллипс» в Illustrator) не соответствует требованиям истинного перспективного эллипса. Важен не «размер» внутреннего квадрата, а тот факт, что все четыре его угла могут касаться эллипса. Если этого не происходит или не может произойти (как на рис. 15), у вас нет истинного перспективного эллипса.
Наш последний пример в Рис. 17 показывает сравнение эллипса, сгенерированного программой Adobe Illustrator «Ellipse Tool» (пунктирная зеленая линия), и измененного и исправленного эллипса (сплошная черная линия).
Теперь мы удалим блоки нашей сетки ограничений (синие линии) и оценим общий вид исправленного эллипса ( Рис. 18 ). Здесь все становится немного сложнее. Как видите, наш эллипс все еще «не выглядит» правильным. Помните, что наша цель — «обмануть» зрителя, заставив его воспринимать трехмерный объект, глядя на плоское двухмерное изображение. Именно здесь вступает в игру «фактор выдумки». Существуют сложные математические уравнения, которые могут решить некоторые из этих проблем, но в реальном мире коммерческой иллюстрации крайние сроки не позволяют использовать этот метод для завершения иллюстрации.Быстрое и простое решение (, рис. 19, ) — повернуть «исправленный» эллипс настолько, чтобы разделить разницу между нашим исправленным эллипсом (пунктирная красная линия) и изометрическим эллипсом Adobe Illustrator Ellipse Tool (пунктирная зеленая линия).
Наш последний пример в Рис. 20 (выше) показывает компромисс между технической точностью и визуальным обманом. После включения в общую иллюстрацию вы обнаружите, что этот метод создает очень естественные эллипсы, которые хорошо сочетаются с перспективой объекта, которому они принадлежат.
Все принципы, описанные в этом руководстве по эллипсу, были использованы для создания этого линейного рисунка линейного ускорителя, показанного на скриншоте выше. Изучая и следуя этому базовому набору основ рисования, вы можете создавать перспективные иллюстрации любого предмета, независимо от уровня сложности.
Вернуться к: Учебные пособия по иллюстрациям
Домой | Автомобильная иллюстрация | Линия искусства иллюстрации | Автомобиль фондовых изображений | Учебные пособия по иллюстрациям
Авторские права © 1996-2012 KHI, Inc.и AutomotiveIllustrations.com. Все права защищены.
Общие проблемы при рисовании эллипсов • Иллюстрация Роя
Что такое эллипс? Так художники представляют круг в перспективе, и это особая дугообразная форма, лежащая на плоскости. Есть конкретное математическое объяснение, но оно не обязательно для наших целей.
Рисование эллипсов может вызвать множество проблем, которые можно легко преодолеть, однако для этого требуются некоторые исследования и усилия.
В этом посте представлены многие из основных проблем, связанных с рисованием точных эллипсов и эллиптических форм, а также предлагаются некоторые предложения по решению этих проблем.
Малая ось — это решающий элемент для установки ориентации вашего эллипса. Большая ось эллипса основана на малой оси.
Ключевые характеристики эллипса:
- Эллипс всегда идеально симметричен по обеим осям.
- Малая ось эллипса совмещена с большой осью формы.
- Большая ось эллипса перпендикулярна малой оси эллипса.
- Две крышки цилиндра почти всегда различаются:
- В двух- и трехточечной перспективе удаленный эллипс цилиндра должен быть меньше и больше (более «открыт»).
- В перспективе 1 pt с крышкой, обращенной к зрителю, удаленный эллипс станет меньше, но сохранит тот же угол.
- В перспективе 1 точка с боковой стороной к наблюдателю, эллипс, который находится дальше от уровня глаз или точки станции, чем другой эллипс, будет иметь больший градус (более «открытый»)
- Концентрические эллипсы на том же плоскости имеют одинаковый градус и общую малую ось, но внутренний эллипс должен располагаться дальше. Это связано с эффектом перспективы и тем фактом, что центры эллипсов отличаются от центров кругов, которые они представляют.
Типичные ошибки:
- Рисование большой и малой оси как горизонтальной и вертикальной, а не наклоненной к форме (вспомогательная ось эллипса должна быть выровнена с большой осью формы)
- Рисование малой оси правильно, но не сохраняя ось большого эллипса перпендикулярно к ней (это приводит к наклонным или неровным эллипсам)
- Ориентация осей правильно, но переключение их таким образом, чтобы большая ось (более длинная ось) эллипса была выровнена с большой осью формы.В результате получается продолговатая форма, а не круг в перспективе.
- Рисование двух эллипсов формы с одинаковым углом, когда один должен быть более открытым (например, задняя часть цилиндра в 2-точечной перспективе).
- Не делает эллипс симметричным по обеим осям
СОВЕТ: вы можете проверить, правильно ли выровнен ваш эллипс, взяв лист бумаги и удерживая его угол в центре эллипса (на экране или на бумаге, где малая и большая ось пересекаются).Если вы построили его правильно, бумага должна рассечь всю вашу форму пополам по одному краю бумаги и пополам ваш эллипс с другой стороны.
ОСНОВНЫЕ ВЫВОДЫ: Эллипс вращается вместе с формой, его оси перпендикулярны, а несколько эллипсов на форме будут различаться по размеру и форме в зависимости от перспективы.
Вы нашли это полезным? У вас есть собственные советы, которыми вы хотели бы поделиться? Я хотел бы услышать об этом, если вы решите попробовать что-то новое. Если вы используете его по-другому, я тоже хотел бы это услышать!
— Лаура
Большая ось — чертеж в перспективе
Это верно независимо от угла или положения эллипса.
Так что не делайте ошибки, рисуя квадрат в ракурсе и используя его центр для определения главной оси эллипса. В результате фигура будет выглядеть примерно так (справа).
Кроме того, если вы хотите нарисовать полукруг (или цилиндр), вы не можете нарисовать эллипс и рассматривать любую сторону большой оси как половину передней; укороченный круг. Например, цифра слева не половина, а меньше.
Однако две справа являются половинками, потому что диаметр круга используется в качестве разделительной линии.
Этот поразительный факт часто вызывает большие затруднения (даже в книгах по этой теме). Какая связь между центром круга и осями эллипса?
Цилиндры
Независимо от положения или угла эллипса, его большая и малая оси всегда оказываются под прямым углом.
ПРИ ЧЕРТОВАНИИ ЦИЛИНДРА — ЕГО ЦЕНТРАЛЬНАЯ ЛИНИЯ ВСЕГДА ДОЛЖНА БЫТЬ ПРОДОЛЖЕНИЕ МЛАДШЕЙ ОСИ СВЯЗАННОГО ЭЛЛИПСА. Следовательно, это центральная линия (ось колес, перекладина грифов, вал гироскопа и т. Д.)) всегда появляется под прямым углом к главной оси связанного с ним эллипса.
Но обратите внимание, что эта центральная линия соединяется с эллипсом в центральной точке круга, а не с центром эллипса. (В противном случае вал был бы эксцентричным — буквально «не по центру». См. Предыдущую страницу.)
Перерисовывая два объекта выше, мы видим, что квадраты с укороченным ракурсом в любом направлении могут быть построены как направляющие по кругу. Но в любом случае ПРОТИВОПОЛОЖНЫЕ ТОЧКИ ЗАЖИГАНИЯ (точки) ЗАКОНЧИВАЮТ ЛИНИИ ДИАМЕТРА ЧЕРЕЗ ЦЕНТР КРУГА.(На самом деле эти линии расположены под прямым углом.)
Большая ось эллипса (пунктирная) не имеет к этому никакого отношения — это просто направляющая линия для рисования эллипса. (Заметим еще раз, что центр эллипса ближе к наблюдателю, чем центр круга.)
Ниже приведены некоторые примеры применения этих принципов.
У конуса внутри цилиндра (справа), естественно, центральная линия параллельна столешнице. Следовательно, вершина конуса находится в воздухе. Чтобы нарисовать конус, лежащий на столе, его вершина должна опускаться (стрелки) так, чтобы его центральная линия приходилась примерно на пунктирную линию.
Крайний правый конус нарисован этой опущенной центральной линией. (Это движение немного сокращает длину и делает эллипс более округлым.)
ПОЭТОМУ, КОНУСЫ, РАСПОЛОЖЕННЫЕ НА СВОИХ СТОРОНАХ, ИМЕЮТ ЦЕНТРАЛЬНЫЕ ЛИНИИ, НАКЛОНЕННЫЕ К ПЛОЩАДКАМ, НА КОТОРЫХ ОНИ ОСТАВАЮТСЯ.
Сходство эллипсов справа указывает на то, что эти конусы ориентированы одинаково, но разной длины.
В то время как здесь различные эллипсы и укороченная длина предполагают, что конусы направлены в разные стороны и примерно одинаковы.(Обратите внимание, что стороны конуса всегда соединяются с эллипсом по касательной.)
Рисование конусов аналогично рисованию цилиндров. Центральная линия конуса также является продолжением малой оси соответствующего эллипса … она лежит под прямым углом к большой оси эллипса. . . и он соединяется с эллипсом не в центральной точке эллипса, а за ним. Изучите эти различные принципы на рисунках выше.
Рисование конусов аналогично рисованию цилиндров. Центральная линия конуса также является продолжением малой оси соответствующего эллипса… он лежит под прямым углом к большой оси эллипса. . . и он соединяется с эллипсом не в центральной точке эллипса, а за ним. Изучите эти различные принципы на рисунках выше.
- Круги, эллипсы, конусы, цилиндры и сферы, нанесенные на рисунок «космической эры».
Глава 14: ТЕНЬ И ТЕНЬ
Во-первых, давайте проясним наши термины: SHADE существует, когда поверхность отворачивается от источника света. ТЕНЬ существует, когда поверхность обращена к источнику света, но не может получить свет из-за какого-то промежуточного объекта.
Например: этот подвесной куб имеет несколько поверхностей на свету и несколько в тени (те, которые отвернуты от света). Столешница повернута к свету и будет полностью «в свете», за исключением тени, «отбрасываемой» на нее кубом выше. Можно сказать, что затененная поверхность промежуточного объекта «отбрасывает» тень на освещенную поверхность.
ЛИНИЯ ТЕНИ — это линия, которая отделяет те части объекта, которые находятся «в тени», от тех, которые находятся «в свете».«Другими словами, это граница между тенью и светом. Эта линия тени важна, потому что она, по сути, отбрасывает, формирует и определяет тень. (Справа.)
Обратите внимание, что линия тени плоского двухмерного объекта является его непрерывной линией края. (Одна сторона объекта освещена, другая — в тени.)
Тень и тень естественным образом существуют только при свете. Обычно свет бывает двух типов, в зависимости от его источника. Один тип создает узор из параллельных световых лучей, другой — радиальный узор.
Другой тип света исходит от местного точечного источника, такого как лампочка или свеча. Здесь близость источника света означает, что объекты получают световые лучи, которые излучаются наружу из одной точки. Поэтому при рисовании локальными точечными источниками лучи света должны быть радиальными.
Читать здесь: Top Vi
Была ли эта статья полезной?
.