Разное

Экшен частотное разложение: Частотное разложение: записываем правильный action

Содержание

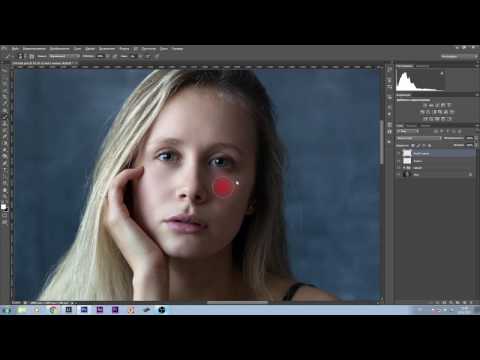
Action Частотное разложение: mommy_irik — LiveJournal

?
Category:
  • Искусство
  • Cancel
Состряпала экшн для фотошопа «Частотное разложение» с разложение изображения на Low и High составляющие.

Работу надо вести в отдельных пустых слоях, помеченных голубым и зеленым цветом.
Чтобы все получалось как надо, если правите High составляющую, отключайте Low и наоборот. Для этого все объединено в группы, достаточно щелкнуть по глазику группы.

Как написано в статье А.Журавлёва, слой Low_Retouch проще зарисовывать штампиком со сниженной прозрачностью и мягкими краями. High_Retouch зарисовывать лечащей кистью, чтобы сохранялась и не замыливалась структура-текстура. Настройка инструмента Sample: Current & Below.

Заметила, что проще работать (например сделать менее выраженными морщины, т.е. фактически убрать из складок тень), если в слое Low_Retouch «сгладить» цвет, а в слое High_Retouch сначала полностью заштамповать морщину, а потом несколько раз пройтись ластиком с прозрачностью 20-40%, чтобы проявить структуру.
Удобно убирать чешуйки-шелушение на лицах детей в слое High_Retouch, при этом не «размазывается» цвет и не появляются круглые пятна на лице от штампика и лечащей кисти.

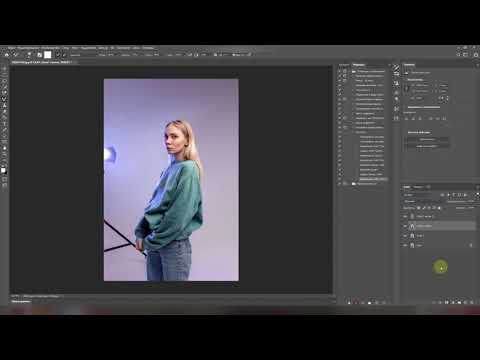
Легко выровнять фон на портретах, если в слое Low_Retouch пройтись кистью с мягкими краями и прозрачность 20-60% и режимом наложения mode: Lighten (можно наверняка и по другому, просто я сейчас именно так сделала. Фон был темный, кстати).

Да, и не забывайте. Радиусы в слоях Gaussian Blur (GB) и High Pass (HP) можно менять, щелкнув по сточке с такими названиями в слоях. Для чего это делать, можно прочитать в статье Ретушь портрета на основе частотного разложения изображения

Скачать action Частотное разложение. atn

Tags: ссылки, фотошоп

Subscribe

  • Kim Cattrall retouch

    Этот месяц учусь на курсах «Издательское дело». Я там ради программ для верстки InDesign, Illustrator, QuarkXPress и Acrobat. Преподавательница -…

  • Fujifilm x-t1 не работает вспышка, радиосинхронизатор, инфракрасный пускатель

    После обновления прошивки у Fujifilm x-t1 появился электронный затвор. Опытным путем, сервисмэны сами этого не знают и помочь не смогли, выяснили,…

  • Фотоштучки

    Оригинал взят у kot_de_azur в Фотоштучки Так я люблю снимать, составил себе несколько шпаргалок. Как отличить объективы? Таблица…

Photo

Hint http://pics.livejournal.com/igrick/pic/000r1edq

  • Kim Cattrall retouch

    Этот месяц учусь на курсах «Издательское дело». Я там ради программ для верстки InDesign, Illustrator, QuarkXPress и Acrobat. Преподавательница -…

  • Fujifilm x-t1 не работает вспышка, радиосинхронизатор, инфракрасный пускатель

    После обновления прошивки у Fujifilm x-t1 появился электронный затвор. Опытным путем, сервисмэны сами этого не знают и помочь не смогли, выяснили,…

  • Фотоштучки

    Оригинал взят у kot_de_azur в Фотоштучки Так я люблю снимать, составил себе несколько шпаргалок. Как отличить объективы? Таблица…

Экшен для ускорения ретуши кожи

Предлагаю вашему вниманию экшен для ускорения процесса ретуши. Он построен на основе методики упрощенного метода частотного разложения с подавлением средних частот. В зарубежных источниках данный метод называется Inverted High Pass.

Скачать экшен

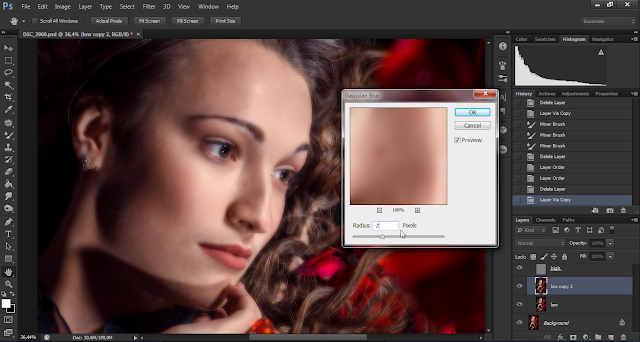
Я несколько усовершенствовал данный метод. Это касается выбора фильтров для размытия. Можно выбирать Размытие по Гауссу (Gaussian Blur), Размытие по поверхности (Surface Blur) и Медиану (Median).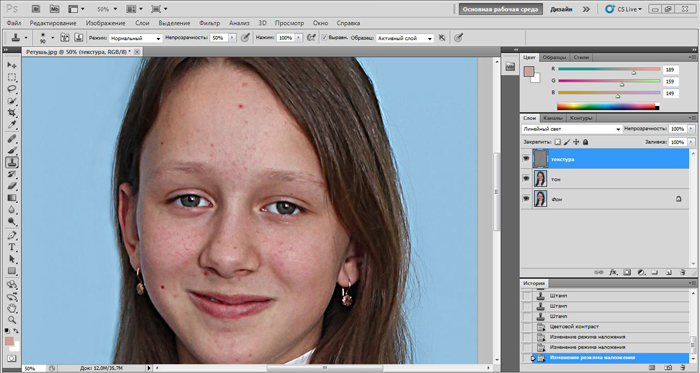 Это позволяет использовать различные методы для фильтрации разных пространственных частот.

Например, метод с Размытием по Гауссу, на мой взгляд, подходит для мелкой и средней текстуры кожи, но не подходит для работы вблизи контрастных границ. Для этого лучше использовать фильтры Размытие по поверхности или Медиана.

Принцип работы с экшеном:

  1. Сначала удаляем явные дефекты с помощью обычной восстанавливающей кисти (Healing Brush). Это нужно сделать на пустом слое. Если вы не знаете, как это делается, лучше сначала изучить основы работы в программе, например, с помощью видеокурса «Photoshop CS5 от А до Я».
  1. Далее запускаем экшен из палитры Операции. Отличительной особенностью работы экшена является то, что он использует информацию со всех предыдущих слоев изображения, то есть, создает слой на основе всех предыдущих и выполняет операцию частотного разложения с заранее выбранным фильтром. 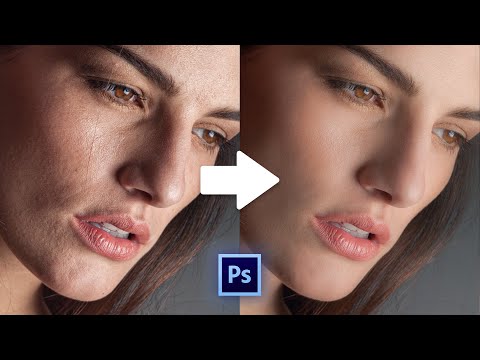Нужный фильтр можно выбирать путем его включения в экшене. Это нужно сделать ДО запуска экшена.

Можно также включать два или все три фильтра. Попробуйте сами, возможно, вам понравится использовать один фильтр или два.

  1. После того, как вы подобрали необходимые параметры фильтров (это потребует некоторой практики), экшен выполняет несколько операций и создает структуру слоев.
  1. Теперь выбираем мягкую белую кисть, непрозрачность кисти регулируем в процессе работы, в зависимости от нужной степени подавления дефектов. Кистью работаем по маске слоя. При фильтрации дефектов больших размеров кистью можно работать «по площадям».
  1. Поработав с крупными дефектами, запускаем экшен еще раз. Перед этим можно переключиться на другой фильтр. При удалении средних и мелких дефектов кистью нужно работать точечно, иначе результатом работы будет «пластиковая» кожа с излишне мелкой текстурой.
  1. Следует также помнить, что данный экшен является всего лишь инструментом для ускорения работы.
    Как и всякий «ускоритель», он имеет свои достоинства, недостатки и область применения. Используя только его, вам не удастся сделать ретушь High-End качества, но никто не запрещает применять его для отдельных этапов работы.

07/01/2015    Просмотров : 202788    Источник: photo-monster.ru    Автор: Евгений Карташов

Версия для печатиСкачать в pdf

Еще уроки из рубрики «Photoshop и Lightroom»

Сортировать: Новые Комментируемые Просматриваемые

Обновленная версия списка горячих клавиш Adobe Camera Raw по состоянию на момент публикации материала. Использование клавиатурных сокращений позволяет значительно увеличить скорость работы п

Читать дальше →

15/09/2020. Обработка фото — Photoshop и Lightroom. Автор: Евгений Карташов

16 535

DxO выделяется на фоне конкурентов благодаря особому способу обработки RAW файлов.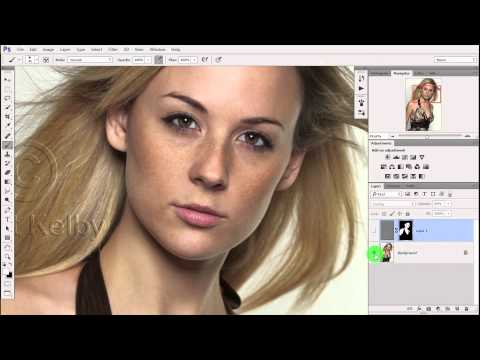 Первая версия DxO PhotoLab была анонсирована в конце 2017 и сразу после…

Читать дальше →

19/07/2019. Обработка фото — Photoshop и Lightroom. Перевод: Алексей Шаповал

18 928

Есть много разных способов исправить геометрию объектива и перспективу с использованием Photoshop. Однако, полезные инструменты также присутствуют в Camera Raw и Lightroom, с которых как раз

Читать дальше →

16/06/2019. Обработка фото — Photoshop и Lightroom. Перевод: Алексей Шаповал

14 206

0

Обработка фотографий с программами на подобие Lightroom обычно требует коррекции экспозиции, контраста, бликов, теней и т.д., что занимает более 90% общего времени. Все…

Читать дальше →

06/06/2019. Обработка фото — Photoshop и Lightroom. Перевод: Алексей Шаповал

12 419

Как стать диджатал ретушером? Эксперт Макс Твейн вам покажет на примерах. Пройдите 2 бонусных урока, скачайте 3 чек листа. Посмотрите трансляцию которая…

Читать дальше →

29/04/2019. Обработка фото — Photoshop и Lightroom. Перевод: Евгений Иванов

18 213

Будь вы новичком или уже опытным пользователем Lightroom, эти 20 советов помогут лучше организовывать коллекцию фотографий и работать эффективнее. 1. Делайте правильно с самого…

Читать дальше →

28/05/2019. Обработка фото — Photoshop и Lightroom. Перевод: Алексей Шаповал

14 897

0


Частотно-временное разложение — SEG Wiki

Содержание

  • 1 Преобразование Фурье
  • 2 Частотно-временное представление
  • 3 Продолжить изучение
  • 4 Автор, ответственный за переписку
  • 5 Благодарностей
  • 6 Внешние ссылки

Рассмотрим форму волны или сигнала s как функцию времени t .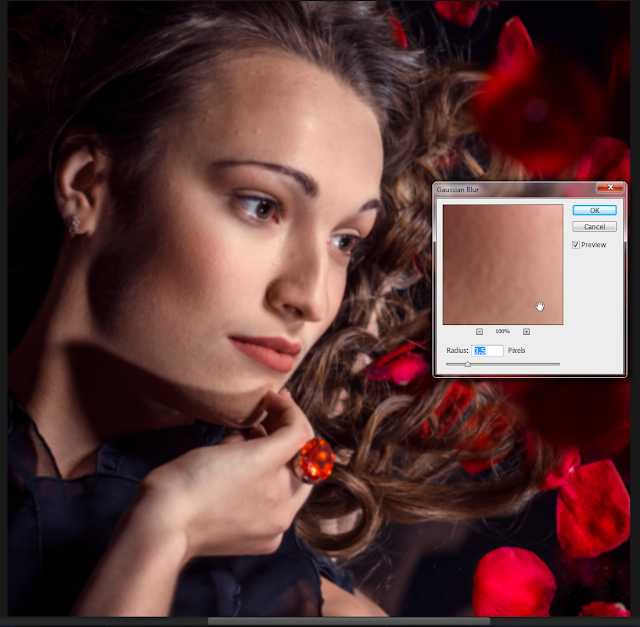 Например, синусоида с некоторой амплитудой a и с некоторой частотой f может быть определен как

s (t) = asin⁡ (2πft) {\ displaystyle s (t) = a \ sin (2 \ pi ft)}.

Мы можем реализовать эту математическую функцию как подпрограмму, обычно также называемую функцией , на языке программирования Python. Поскольку компьютеры живут в дискретном мире, мы необходимо оценить функцию в течение некоторого времени и с некоторой частотой дискретизации:

 по определению sine_wave(f, a, продолжительность, частота дискретизации):
    t = np.arange(0, продолжительность, 1/sample_rate)
    вернуть * np.sin (2 * np.pi * f * t), т

Теперь мы можем вызвать эту функцию, передав ей частоту f = 261,63 Гц. Мы попросим 0,25 с с частотой дискретизации 10 кГц.

 с, t = sine_wave(f=261,63,
                   а=1,
                   продолжительность=0,25,
                   sample_rate=10e3)

Это приводит к следующему сигналу, обычно называемому временным рядом , который мы визуализируем путем построения графика s в зависимости от времени t :

Я изобразил результирующий массив в виде линии, но на самом деле это ряд дискретных точек, представленных в Python в виде массива чисел, начиная с этих четырех:

 array([ 0.  , 0.1636476 , 0.32288289, 0.47341253])

Построим первые 80 точек:

Когда воздух вибрирует на этой частоте, мы слышим среднее До или До4. Вы можете прослушать примечание для себя в Jupyter Notebook, сопровождающем эту статью, по адресу https://github.com/seg/tutorials-2018. (Блокнот также содержит весь код для создания графиков.) Код для вывода массива s в виде звука очень короткий:

 из IPython.display import Audio
фс = 10e3
Аудио(и, скорость=fs)

Этот сигнал длится всего 0,25 с, а покачиваний уже много. Мы бы хотели иметь сейсмические данные на этой частоте! Большинство сейсмических данных воспроизводятся только на нижних 20–30 клавишах 88-клавишного фортепиано — действительно, самая нижняя клавиша — это A0, что на частоте 27,5 Гц превышает пиковую частоту многих старых съемок.

Если бы мы хотели узнать частоту этого сигнала, мы могли бы предположить, что это чистый тон, и просто подсчитать количество циклов в единицу времени. Но естественные сигналы редко бывают монотонными, так что давайте сделаем более интересный сигнал. Мы можем использовать нашу функцию, чтобы создать до-мажорный аккорд с тремя нотами (C4, E4 и G4), передав векторы-столбцы (изменив форму массивов) для частоты 9.0021 f и амплитуда a :

 f = np.массив ([261,6, 329,6, 392,0])
а = np.массив ([1,5, 0,5, 1])
s, t = sine_wave (f = f.reshape (3, 1),
                 а=а.изменить(3, 1),
                 продолжительность=0,25,
                 sample_rate=10e3)

Результатом является набор из трех синусоидальных кривых длиной 0,25 с:

Общий сигнал определяется суммой трех кривых:

 s = np.sum(s, axis=0)

Преобразование Фурье

Хотя это смешанное или политонный сигнал представляет собой просто сумму трех чистых тонов, разобраться в компонентах уже не тривиально. Здесь в дело вступает преобразование Фурье.

Мы не будем вдаваться в подробности того, как работает преобразование Фурье. Лучшее объяснение, которое я видел за последнее время, — это вводное видео Гранта Сандерсона.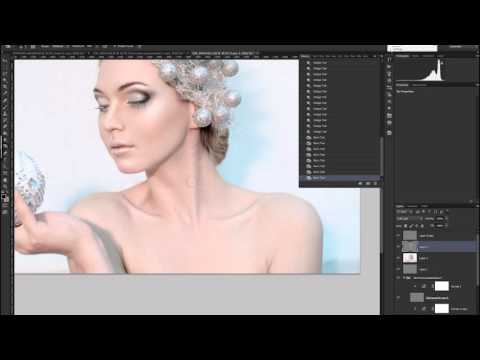 Дело в том, что преобразование описывает сигналы как смеси периодических составляющих. Попробуем на нашем аккорде.

Сначала мы конусность сигнала путем умножения его на функцию окна . Идеальные чистые тона имеют бесконечную продолжительность, а сужение помогает предотвратить влияние краев нашего конечного сигнала на преобразование Фурье.

 s = s * np.blackman(s.size)

Оконная функция (зеленая) оказывает сужающее действие на сигнал:

Поскольку функция s определена для данного момента времени t , мы называем это представление сигнала временем 9(е) {\ Displaystyle {\ шляпа {s}} (е)}). Это новое представление называется частотной областью. Он состоит из массива коэффициентов Фурье :

 S = np.fft.fft(s)

Вспомогательная функция fftfreq() возвращает массив частот, соответствующих коэффициентам.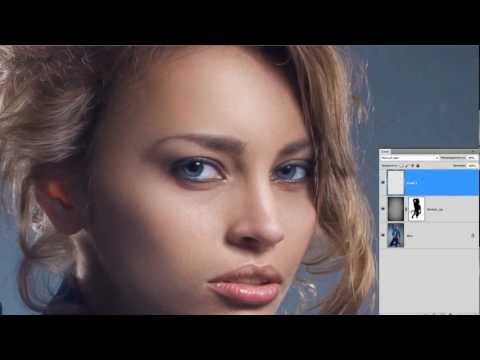 Интервал выборки частоты определяется длительностью сигнала с : чем длиннее сигнал, тем меньше интервал выборки частоты. (Точно так же короткие интервалы выборки по времени соответствуют широкой полосе пропускания по частоте.)

 freq = np.fft.fftfreq(s.size, d=1/10e3)

Результатом является массив из коэффициентов Фурье , большинство из которых равны нулю. Но на частотах аккорда и вблизи них коэффициенты велики. Результат: «рецепт» аккорда с точки зрения синусоидальных монотонов.

Это называется спектром сигнала s . Он показывает величину каждой частотной составляющей.

Частотно-временное представление

Теперь мы знаем, как расплетать политонические сигналы, но давайте введем еще одно усложнение — сигналы, компоненты которых меняются со временем. Такие сигналы называются нестационарный . Например, подумайте о монотонном сигнале, тон которого меняется в какой-то момент (см. Блокнот для кода, который генерирует этот сигнал):

Мы можем вычислить преобразование Фурье этого сигнала, как и раньше:

 с *= np. blackman(s.size)
S = np.fft.fft(s)
freq = np.fft.fftfreq(s.size, d=1/10e3)

И постройте амплитуду S в зависимости от массива частот freq :

Он очень похож на спектр, который мы сделали раньше, но без средней частоты. Пики немного более рассредоточены, потому что продолжительность каждого сигнала вдвое меньше, чем была. (Общий принцип неопределенности распространяет сигналы по частоте по мере того, как они становятся более компактными во времени.)

Дело в том, что нет большой разницы между спектром двух смешанных сигналов и спектром двух последовательных сигналов. Если мы заботимся о локализации сигналов во времени (мы делаем!), это проблема. Одним из решений является обращение к частотно-временным представлениям . Пытаясь разделить сигнал одновременно по времени и частоте, они предлагают способ одновременного использования преимуществ обеих областей.

Библиотека для построения графиков Python matplotlib предлагает удобный способ построения графика время-частота, также известного как спектрограмма . В одной строке кода он создает график 2D-изображения, показывающий зависимость частоты от времени.

 _ = plt.specgram(s, Fs=1/10e3,
                   NFFT=512, noverlap=480)

Немного поработав, мы можем получить очень богатое представление наших данных:

График использует алгоритм, называемый кратковременным преобразованием Фурье, или STFT. Это просто делает преобразование Фурье в скользящем окне длиной NFFT с перекрытием точек, перекрывающихся в предыдущем окне. Мы хотим NFFT должен быть длинным, чтобы получить хорошее разрешение по частоте, и мы хотим, чтобы nooverlap был большим, чтобы получить хорошее разрешение по времени.

Обратите внимание, что мы не можем точно увидеть точную частоту компонентов — они не служат достаточно долго, чтобы их можно было зафиксировать. И есть некоторая неопределенность в отношении сроков перехода, потому что для получения приличного разрешения по частоте нам нужен длинный сегмент сигнала (в данном случае 512 отсчетов) — поэтому мы теряем информацию о времени. Но в целом этот сюжет лучше, чем только спектр: мы видим, что есть по крайней мере два сильных сигнала с частотами около 250 и 400 Гц, и что изменение происходит примерно через 0,125 с.

Фрагмент фортепианной музыки может напоминать такой сюжет. Поскольку клавиши пианино могут воспроизводить только одну ноту, спектрограмма фортепианной музыки выглядит как серия горизонтальных линий:

Существует большое сходство между этим частотно-временным разложением и нотной записью:

Оказывается, самые интересные сигналы — и, возможно, все естественные сигналы — политонны и нестационарны. По этой причине, хотя временные ряды часто полезны, частотно-временная декомпозиция может быть очень показательной. Вот некоторые примеры; в каждом случае частота отложена по вертикальной оси, а время по горизонтальной оси. Цвета указывают мощность от низкой (синий) до высокой (желтый) (пропорционально квадрату амплитуды).

Человеческий голос произносит «SEG». Сонорные гласные имеют гармоники (горизонтальные полосы), а шипящие звуки «С» и первой части «Г» — шумоподобные. спектральные отклики.

На этой спектрограмме показана 5-секундная серия чириканий летучих мышей. Я указал 18 кГц, приблизительный предел человеческого слуха, оранжевой линией, и если вы слушаете звук этого сигнала в Ноутбук, можно убедиться, что чириканье еле слышно при нормальной скорости воспроизведения; только при замедлении клипа они могут быть отчетливо слышны.

Наконец, вот вулканический «крик» — гармонический толчок, предшествующий взрывному извержению на горе Редут, Аляска, в марте 2009 года. На слух это звучит невероятно, но спектрограмма тоже интересно. В отличие от чириканья летучей мыши, этот 15-минутный временной ряд нужно ускорить, чтобы его услышать.

Продолжить изучение

Все рисунки в этой записной книжке можно воспроизвести с помощью кода в записной книжке Jupyter, прилагаемой к этой статье, на https://github.com/seg/tutorials-2018. Вы даже можете запустить код в облаке и поиграть с ним в браузере. Ничего не сломаешь — не волнуйся!

В хранилище вы также найдете больше сигналов, синтетических и естественных, от сердцебиения и загадочного подводного щебетания до гравитационных волн и сейсмических следов. Мало того, есть записная книжка, показывающая, как использовать другой алгоритм — непрерывное вейвлет-преобразование — для проведения частотно-временного анализа другого типа.

Счастливого разложения!

Автор, ответственный за переписку

  • Автор, ответственный за переписку: Matt Hall, Agile Scientific, Mahone Bay, Новая Шотландия, Канада. Электронная почта: mattagilescientific.com

Благодарности

Фортепианная запись из BWV846 Баха лицензирована Кимико Ишизака CC-BY на http://welltemperedclavier.org. Данные чириканья летучих мышей лицензированы CC-BY-NC пользователем http://freesound.org klankschap. Спасибо Алисии Хотовек-Эллис за ее помощь с данными о горе Редут, записанными вулканической обсерваторией Геологической службы США на Аляске.

Внешние ссылки

найти литературу о
Частотно-временное разложение
  • Мадагаскарский рабочий процесс — воспроизводимый с помощью Мадагаскарского программного обеспечения с открытым исходным кодом

Частотный и частотно-временной анализ в Matlab — обмен файлами фид контента

  • Вы можете получать электронные письма, в зависимости от ваших предпочтений в общении

    • Частотный и частотно-временной анализ в Matlab

    Версия 1. 5.2 (1,45 МБ) от Lubos Smolik

    Выполнение частотно-временного анализа без Signal Processing Toolbox™

    https://github.com/CarlistRieekan/autofft

    1,1 тыс. загрузок За все время: 1146 дюймов>

    Обновлено 20 июля 2022 г.

    Из GitHub

    Посмотреть лицензию на GitHub

    • Обзор
    • Функции
    • Примеры
    • История версий
    • Отзывы (3)
    • Обсуждения (4)

    autofft — частотно-временной анализатор для Matlab. Хотя эти функции высокого качества и хорошо документированы, они могут быть громоздкими в некоторых инженерных приложениях.

    Эти приложения включают оценку величины вибрации, шума и других дискретных во времени сигналов в инженерных единицах или сравнение теоретических результатов с измерениями.

    В таких приложениях можно использовать autoofft для оценки дискретного преобразования Фурье (DFT), которое имитирует свойства анализаторов БПФ Brüel & Kjaer. Основываясь на введенных вами данных, автокоррекция сегментирует сигнал, применяет оконные функции и выполняет спектральное усреднение. Результирующий усредненный спектр, также называемый модифицированной периодограммой , может быть возвращен в различных технических единицах измерения спектра, включая децибелы, амплитуду, среднеквадратичное значение (RMS), размах и спектральную плотность мощности (PSD). autofft также может оценить спектральный вывод или спектральный интеграл DFT и выполнить кратковременное преобразование Фурье (STFT).

    Возможности autoofft

    • Не требует Signal Processing Toolbox™.
    • Работает значительно лучше, чем pwelch и pspectrum в задачах с интенсивными вычислениями.
    • Оценивает величины компонентов в ваших данных в инженерных единицах, например дБ, В или Па
    • Обеспечивает контроль над настройкой частотного анализатора, что невозможно с библиотечными функциями.
    • Может применять фильтры верхних частот и частотные взвешивающие фильтры, спектральное дифференцирование или спектральное интегрирование.

    Что нового в v1.5?

    • v1.5.2: Измененная функциональность : Пакет больше не требует Signal Processing Toolbox™.
    • v1.5.2: Изменена функциональность : Цифровой фильтр Баттерворта первого порядка теперь используется для фильтрации верхних частот, а не эллиптический фильтр первого порядка.
    • v1.5.2: Новые функции : Пакет теперь распространяется с функциями, которые могут создавать окна Блэкмана-Харриса, окна с плоской вершиной, окна Хэмминга, Ханна, Кайзера и однородные окна, а также могут проектировать цифровой фильтр Баттерворта n-го порядка. Эти функции можно найти в + утилиты каталог.
    • v1.5.1: Оптимизация кода : STFT теперь вычисляется более эффективно.
    • v1.5.1: Исправление ошибки : В одних и тех же случаях время для STFT оценивалось более одного раза. Это было исправлено.
    • Новая функциональность : выходные спектры могут быть возвращены в децибелах с использованием параметра 'dbReference' .
    • Новая функция : A freqWeight 9Функция 0110, применяющая частотно-взвешивающие фильтры к спектру мощности, теперь включена в пакет.
    • Документация : Добавлен новый пример.
    • Оптимизация кода : Время, в которое оценивается STFT, вычисляется более эффективно.

    Начало работы

    Для получения дополнительной информации прочитайте руководство пользователя или посетите веб-сайт

    . Цитировать как

    Любош Смолик (2023). Частотный и частотно-временной анализ в Matlab (https://github.com/CarlistRieekan/autofft/releases/tag/v1.5.2), GitHub. Получено .

    Совместимость версий MATLAB

    Created with R2022a

    Совместимость с R2016b — R2022a

    Совместимость с платформами
    Windows macOS Linux

    Категории
    • Обработка сигнала > Набор инструментов для обработки сигналов > Спектральный анализ > Спектральные измерения >
    Метки Добавить теги

    fft частотный спектр обработка сигналов спектральный анализ stft вибрация

    Охота за сокровищами сообщества

    Найдите сокровища в MATLAB Central и узнайте, как сообщество может вам помочь!

    На охоту!

    Версии, использующие ветку GitHub по умолчанию, не могут быть загружены

    Версия Опубликовано Примечания к выпуску
    1. 5.2

    См. примечания к этому выпуску на GitHub: https://github.com/CarlistRieekan/autoofft/releases/tag/v1.5.2

    1.5.1

    См. примечания к этому выпуску на GitHub: https://github.com/CarlistRieekan/autoofft/releases/tag/v1.5.1

    1,5

    См. примечания к этому выпуску на GitHub: https://github.com/CarlistRieekan/autoofft/releases/tag/v1.5

    1.4.1

    См. примечания к этому выпуску на GitHub: https://github.com/CarlistRieekan/autoofft/releases/tag/v1.4.1

    1,4

    См. примечания к этому выпуску на GitHub: https://github.com/CarlistRieekan/autoofft/releases/tag/v1.4

    1.3.1

    См. примечания к этому выпуску на GitHub: https://github.com/CarlistRieekan/autoofft/releases/tag/v1.3.1

    1.3.0

    См. https://github.com/CarlistRieekan/autoofft/releases

    1. 2.5.1

    См. примечания к этому выпуску на GitHub: https://github.com/CarlistRieekan/autoofft/releases/tag/1.2.5.1

    1.2.5

    Реализована дополнительная фильтрация верхних частот.

    1.2.4.2

    Длина перекрытия (в выборках), возвращаемая в настройке выходной переменной, теперь корректна. Предыдущие версии неправильно возвращали процент перекрытия.

    1.2.4.1

    Исправлена ​​ошибка при оценке автоспектра.

    1.2.4

    - Улучшенная документация.
    - Новые типы усреднения: медианный фильтр и дисперсия спектральной единицы.
    - Результаты STFT нескольких сигналов теперь возвращаются в виде трехмерного массива.
    — производительность значительно улучшилась.
    - Немного улучшена точность PSD.

    1.2.3

    - Пользователь может определить частотное разрешение анализатора.
    - Оконная функция может быть указана напрямую как вектор.
    - Настройка анализатора может быть возвращена как выходная переменная.
    - Теперь отображаются предупреждающие сообщения.

    1.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *