|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
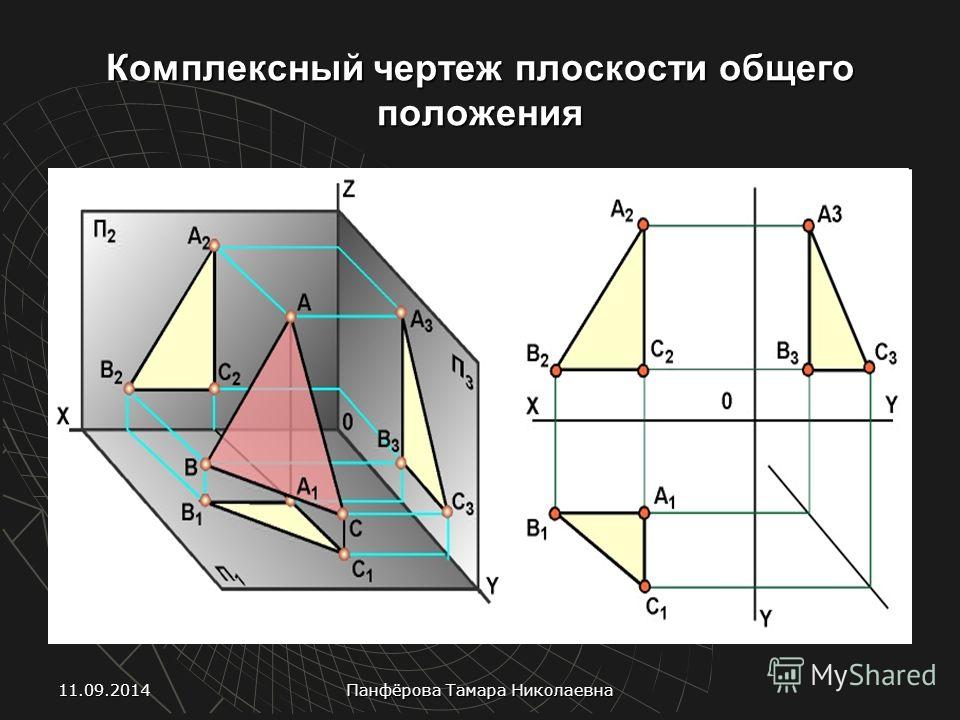
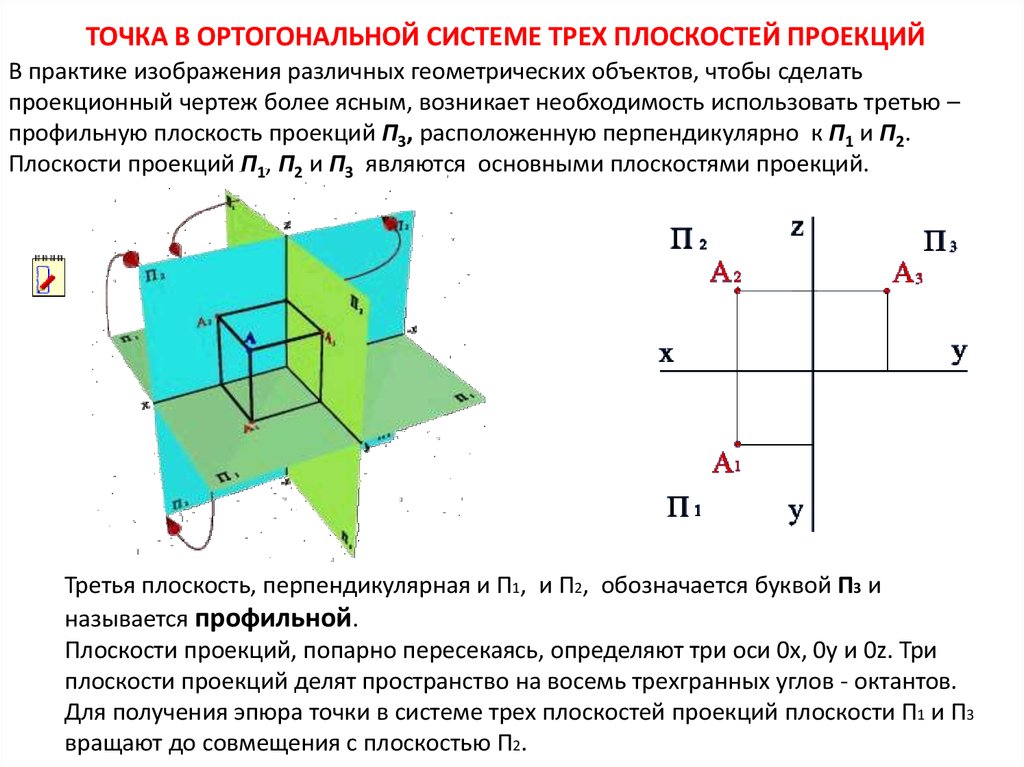
⇐ ПредыдущаяСтр 3 из 3 комплексном чертеже” Краткие теоретические сведения Наибольшее применение на практике получил чертеж, составленный из связанных между собой ортогональных проекций изображаемой фигуры. Такой чертеж называется комплексным чертежом в ортогональных проекциях или комплексным чертежом. Его предложил использовать в конце XVIII века французский инженер Гаспар Монж. Поэтому другое название комплексного чертежа – чертеж Монжа. Принцип образования чертежа состоит в том, что фигура проецируется ортогонально на взаимно перпендикулярные плоскости проекций, которые затем соответствующим образом совмещают с плоскостью чертежа. Одна из плоскостей проекций П1 располагается горизонтально и называется горизонтальной плоскостью проекций. Плоскость П2 располагается вертикально перед наблюдателем и называется фронтальной плоскостью проекций. Третья плоскость П3 называется профильной плоскостью проекций (рисунок 4.12). Прямые пересечения плоскостей проекций называют осями проекций.
Рисунок 4.12 – Плоскости проекций
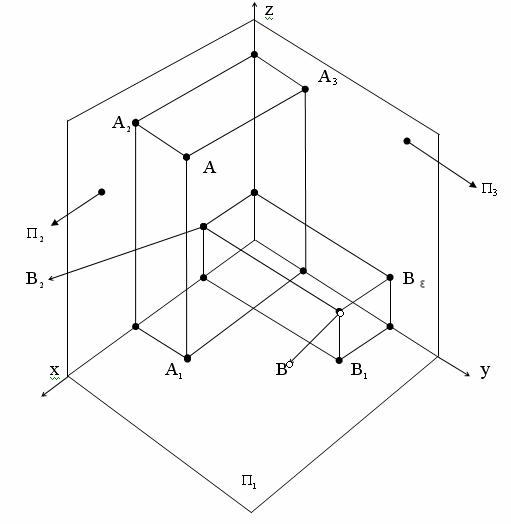
Различают двухкартинный комплексный чертеж, когда рассматриваются только фронтальная и горизонтальная проекции, и трехкартинный – все три плоскости проекции. Двухкартинный комплексный чертеж является обратимым чертежом. Однако реконструкция оригинала часто становится проще, когда помимо двух основных проекций имеется еще одна проекция на третью плоскость. Три плоскости проекций П1, П2 и П3 образуют систему трех взаимно перпендикулярных плоскостей. Линии пересечения плоскостей будем обозначать, используя индексы пересекающихся плоскостей, то есть через x12, y 13, z23. Комплексный чертеж точки. Пусть А – некоторая точка пространства. Опустим из точки А перпендикуляры на плоскости проекций П1, П2, П3 (рисунок 4.13). Основания этих перпендикуляров (точки А1, А2, А3) и являются соответственно горизонтальной, фронтальной и профильной проекциями точки А в системе плоскостей проекций П1, П2, П3. Обозначим на осях проекций точки A12, A13, А23.
Рисунок 4.13 – Проецирование точки на три плоскости проекций
При построении плоского чертежа плоскость П2 считается неподвижной, а остальные плоскости П1 и П3 В результате указанного совмещения плоскостей проекций получим трехкартинный комплексный чертеж точки А, состоящий из трех ортогональных проекций (рисунок 4. Рассмотрим, какой линией связи можно соединять горизонтальную и профильную проекции точки А. Для этого обратим внимание на квадрат А13ОА13А*. Диагональ этого квадрата является биссектрисой угла y13 O y13. Следовательно, линия связи, соединяющая проекции А1 и А3, представляет собой ломаную линию с вершиной на биссектрисе угла y13Oy13, состоящую из двух звеньев (горизонтального и вертикального).
Рисунок 4.14 – Трёхкартинный комплексный чертёж точки В дальнейшем эту линию будем называть горизонтально-вертикальной линией связи. Часть этой ломаной часто заменяют дугой окружности. Множество горизонтальных проекций всех точек пространства назовем полем горизонтальных проекций П1 (соответствующая проекция фигуры в инженерной графике называется видом сверху), а множество фронтальных проекций всех точек пространства – полем фронтальных проекций П2 (соответствующая проекция фигуры называется видом спереди или главным видом).
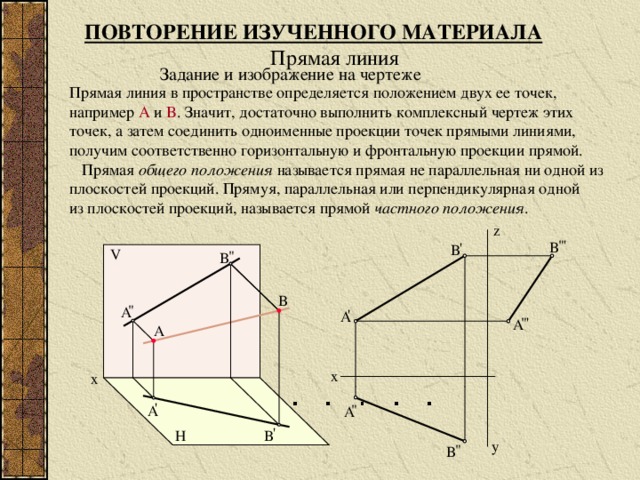
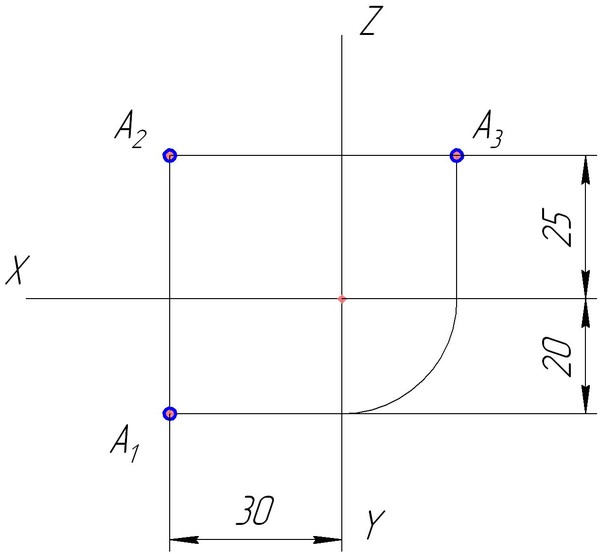
Рассмотрим пример. Требуется построить трёхкартинный комплексный чертёж точки А(25,15,10). По заданным координатам точку А можно построить следующим образом (рисунок 4.15). Сначала на оси x12 от начала координат в положительном направлении откладываем отрезок ОА12, равный 25 единицам (абсцисса точки А или её широта). Через полученную точку А12 проводим вертикальную линию связи, на которой вверх откладываем отрезок А12А2, равный 10 единицам (аппликата точки А или её высота). Получим фронтальную проекцию А2 точки А. Для построения горизонтальной проекции А1 точки А необходимо на вертикальной линии связи отложить вниз отрезок А12А1, равный 15 единицам (ордината точки А или её глубина). Рисунок 4. Через построенные проекции точки А нужно провести горизонтальные линии связи, которые пересекут ось y13 в точке А 13 и ось z23 в точке А23. Точку А13 перенесем на горизонтальную ось y13 с помощью дуги окружности и далее проведём вертикальную линию связи до пересечения с горизонтальной линией связи. Точка их пересечения и будет являться профильной проекцией А3 точки А. Комплексный чертеж прямой. В соответствии со свойством прямолинейности параллельной проекции проекцией прямой линии является прямая линия. Поэтому на комплексном чертеже прямая линия будет задаваться в виде своих проекций – прямых линий. Как известно, прямая линия определяется двумя точками. Отсюда следует, что для построения проекций прямой достаточно взять на ней две произвольные точки (например, точки А и В) и спроецировать их ортогонально на горизонтальную и фронтальную плоскости проекций. Поскольку для определения положения в пространстве точек достаточно двух проекций, то будем рассматривать двухкартинный чертеж, не используя профильную плоскость проекций. Точки пересечения проецирующих лучей с плоскостями П1 и П2 определят проекции точек: горизонтальные – А1, В1 и фронтальные – А2 и В2. Соединив прямыми точки А1 и В1, получим горизонтальную проекцию прямой l1, а точки А2 и В2 – фронтальную проекцию l2 прямой l (рисунок 4.16). Таким образом, построение проекций прямой выполняется однозначно.
Рисунок 4.16 – Комплексный чертеж прямой
Это была рассмотрена прямая общего положения. Прямой общего положения называется прямая, не параллельная и не перпендикулярная ни к одной из плоскостей проекций. Прямые, перпендикулярные или параллельные плоскостям проекций, называются прямыми частного положения. Задание на выполнение
1 По заданным в таблице 4.
Таблица 1
2 По данным таблицы 4.
Таблица 4.6
Указания к выполнению 1 Оба задания выполняются на одном листе чертежной бумаги формата А4: сверху первое задание, а снизу – второе. При этом вычерчивается рамка и заполняется основная надпись в соответствии с требованиями ЕСКД. Все надписи на рисунках выполняются стандартным шрифтом типа Б. Оси координат и границы плоскостей изображаются основной линией, а линии связи – тонкой. 2 При построении наглядного изображения в заданиях 1 и 2 ось OY проводится из точки О под углом 45° к горизонтали; по оси ОY откладывается половина заданного в таблице размера, по осям OX, OZ — натуральная величина. При этом выбирается произвольный масштаб. 2 При построении ортогональных проекций точек и отрезка прямой на комплексном чертеже размеры откладывают по осям координат (X, У и Z) от точки О в натуральную величину. Сверху над чертежами первого задания записываются номер варианта и координаты точек. 3 В графе 1 основной надписи записывается название работы “Точка и отрезок прямой на комплексном чертеже”.
4.3. Графическая работа № 3. “Пересечение прямой и плоскости” ⇐ Предыдущая123 Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
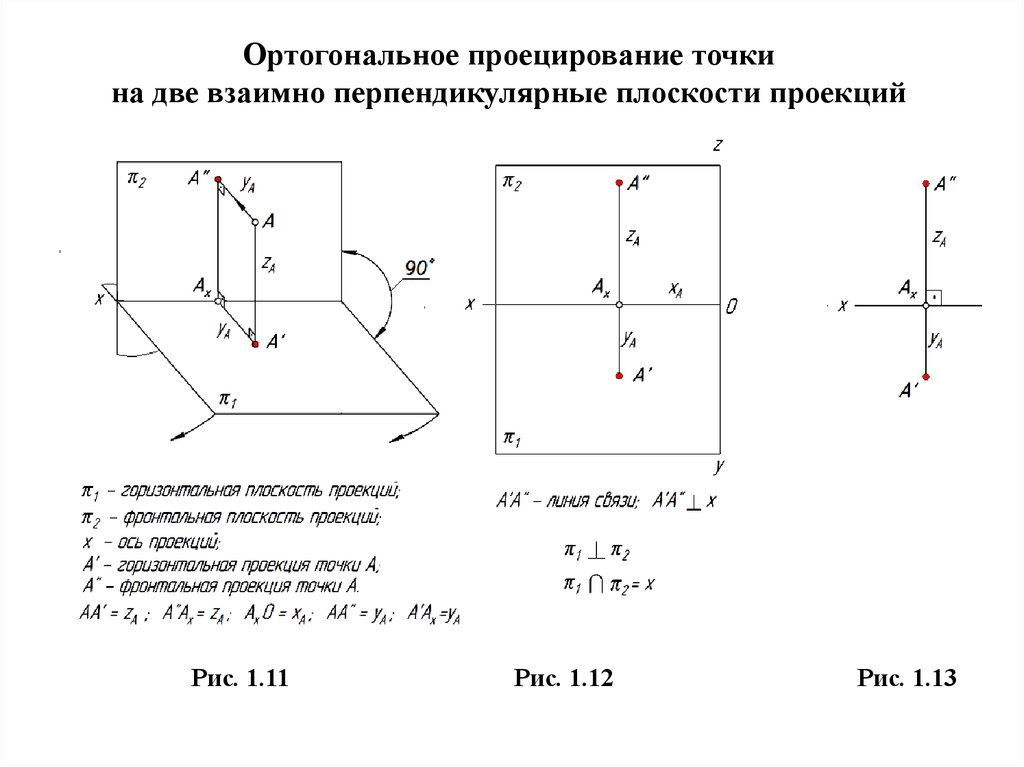
Последнее изменение этой страницы: 2016-07-16; просмотров: 883; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. Одна из плоскостей проекций располагается горизонтально, обозначается П1 и называется горизонтальной плоскостью проекций. 2-я плоскость располагается вертикально перед наблюдателем, обозначается П2 – фронтальная плоскость проекций. Прямая пересечения плоскостей – ось проекций. А1 – горизонтальная проекция А2 – фронтальная проекция hА – высота точки А fА – глубина т.А
Спроецируем ортогонально на плоскости проекций П1 и П2 какую-нибудь точку А, тогда получим две её проекции: горизонтальную проекцию А1 на плоскости П1 и фронтальную проекцию А2 на плоскости П2. Проецирующие прямые AA1 и АА2, при помощи которых точка А проецируется на плоскости проекций, определяют проецирующую плоскость A1AA2, перпендикулярную к обеим плоскостям проекций и к оси проекций X. Обратно, каждая пара точек А1 и А2, соответственно принадлежащих плоскостям П1 и П2 и расположенных на перпендикулярах к оси X, восставленных из одной и той же точки Ах, определяют в пространстве единственную точку А. В самом деле, если провести через точку A1 и А2 перпендикуляры А1А и А2А соответственно к плоскостям П1 и П2, то они, находясь в одной плоскости А1АхА2, пересекутся в некоторой точке А. Расстояние A1А точки А от горизонтальной плоскости проекций называется высотой h точки А, ее расстояние А2А от фронтальной плоскости проекций – глубиной f точки А. Чтобы получить плоский чертеж, совместим плоскость проекций П1 с плоскостью П2, вращая переднюю полуплоскость П1 вокруг оси Х вниз. Полученный комплексный чертеж будет обратимым, т.е. по нему можно восстановить оригинал. В самом деле, рассматривая, например, фронтальную проекцию А2 точки А и имея на чертеже ее глубину f=АхА1, можно построить точку А. Для этого надо восстановить перпендикуляр к плоскости чертежа в его точке А2 и от плоскости чертежа отложить глубину искомой точки, тогда конец перпендикуляра определит положение точки А. На практике часто бывает безразличным положение изображаемой фигуры относительно неподвижной системы плоскостей проекций, поэтому при образовании комплексного чертежа можно отказаться от фиксации плоскостей проекций и оси проекций не изображать. Плоскости проекций П1 и П2 разбивают все пространство на четыре части, называемые квадрантами или четвертями. При этом условимся нумеровать квадранты в порядке, указанном на рис., и называть их I, II, III и IV квадрантами.
Если точка А лежит в I квадранте, то ее горизонтальная проекция A1 будет принадлежать передней полуплоскости П1, а фронтальная проекция А2 — верхней полуплоскости П2. При совмещении плоскостей проекций горизонтальная проекция A1 точки А окажется расположенной ниже оси Х12, а фронтальная проекция А2 — выше оси Х12 (рис. 5). В зависимости от положения точек в различных квадрантах пространства будем иметь соответствующее расположение их проекций на комплексном чертеже (рис. Итак, комплексный чертеж, состоящий из двух ортогональных проекций (называемый еще двухкартинным чертежом), является обратимым чертежом. Однако реконструкция оригинала часто становится проще, когда помимо двух основных проекций имеется еще одна проекция на третью плоскость. В качестве такой плоскости проекций применяется плоскость, перпендикулярная к обеим основным плоскостям П1 и П2, которая называется профильной плоскостью проекций. Ее обозначают П3. Три плоскости проекций П1, П2 и П3 образуют систему трех взаимно перпендикулярных плоскостей (рис. 6). Ребра полученного трехгранника будем обозначать через X, У, Z. Рис. 6
|
 Все правила по сольфеджио
Все правила по сольфеджио

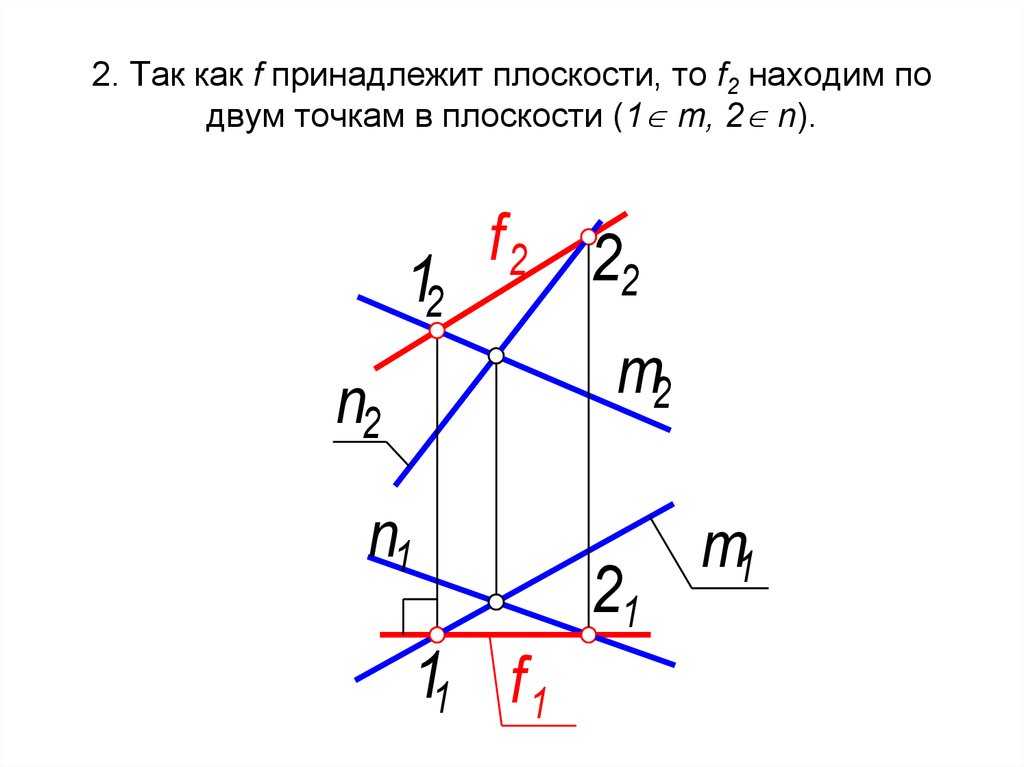
 14).
14). Аналогично множество профильных проекций всех точек пространства назовем полем профильных проекций П3 (соответствующая проекция фигуры называется видом слева).
Аналогично множество профильных проекций всех точек пространства назовем полем профильных проекций П3 (соответствующая проекция фигуры называется видом слева). 15 – Комплексный чертёж точки А
15 – Комплексный чертёж точки А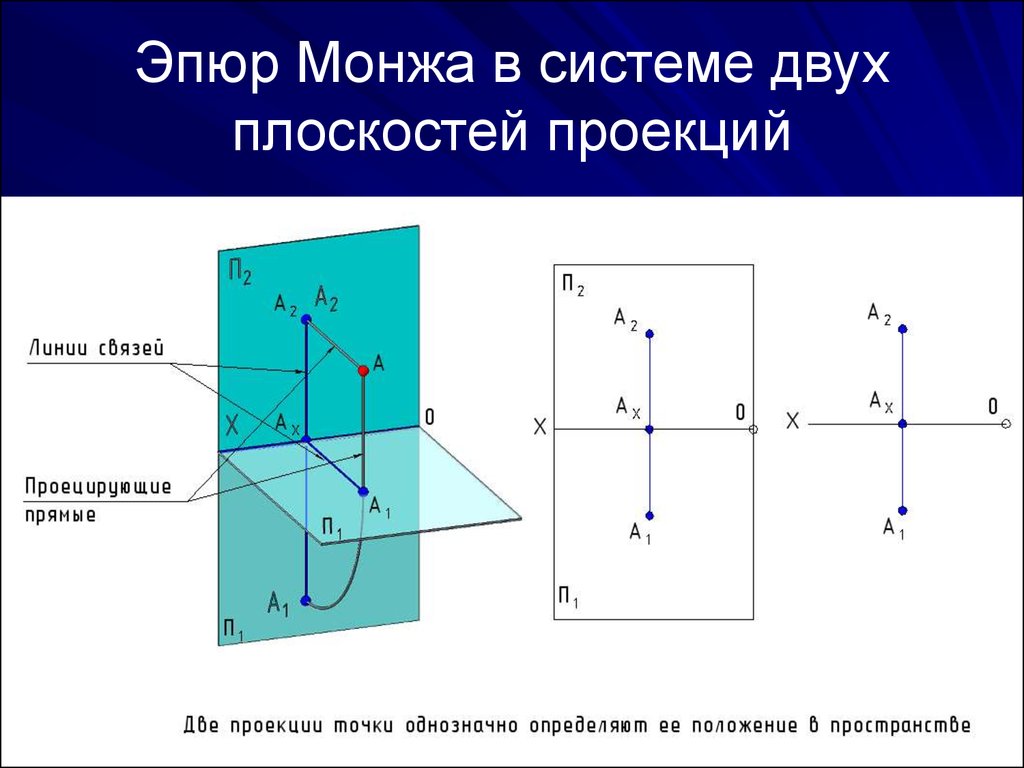
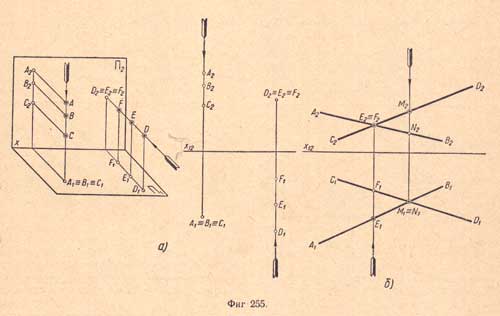 5 координатам постройте наглядное изображение точки А в пространстве и ее комплексный чертеж. На рисунках 4.13, 4.14 изображено, как это должно выглядеть. Номер варианта определяется преподавателем.
5 координатам постройте наглядное изображение точки А в пространстве и ее комплексный чертеж. На рисунках 4.13, 4.14 изображено, как это должно выглядеть. Номер варианта определяется преподавателем.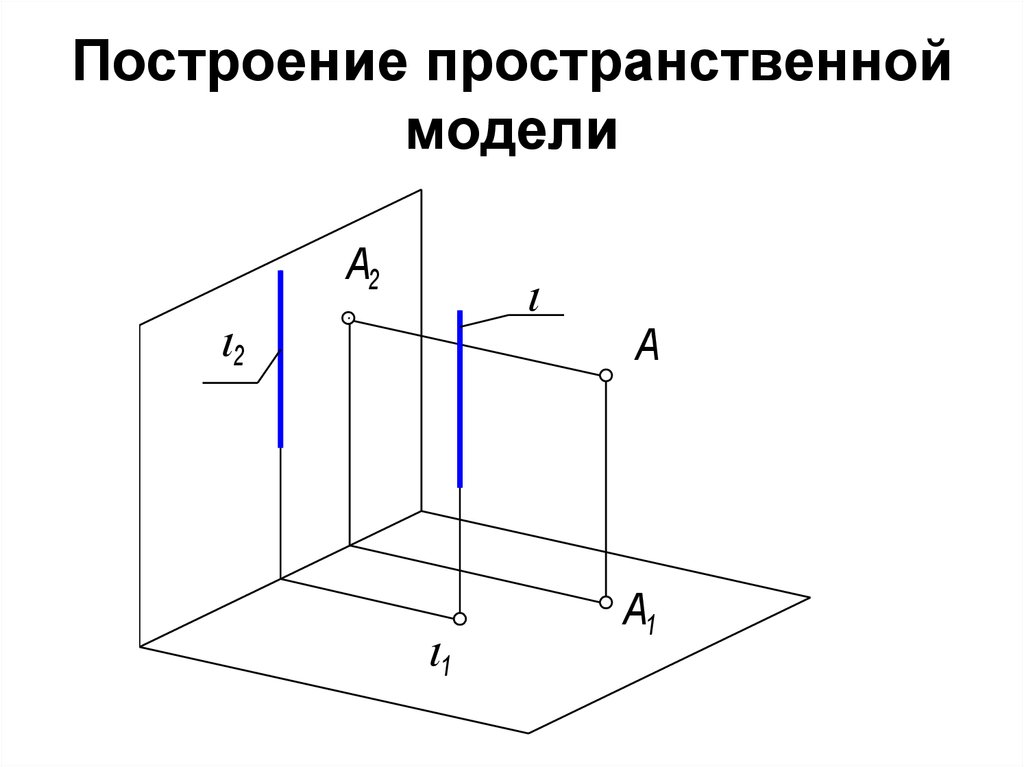 6 постройте наглядное изображение отрезка прямой АB в пространстве и его комплексный чертеж. Обозначьте все точки, оси и плоскости проекций в соответствии с общепринятыми обозначениями. На рисунках 4.17, 4.18 показано, как должно выглядеть выполненное задание (без обозначений).
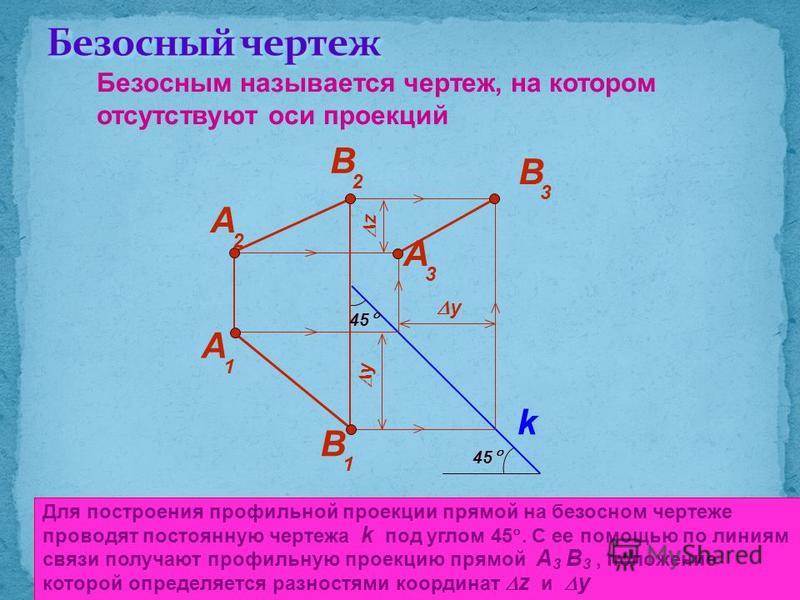
6 постройте наглядное изображение отрезка прямой АB в пространстве и его комплексный чертеж. Обозначьте все точки, оси и плоскости проекций в соответствии с общепринятыми обозначениями. На рисунках 4.17, 4.18 показано, как должно выглядеть выполненное задание (без обозначений). 17 – Отрезок АB прямой
в пространстве (эскиз)
17 – Отрезок АB прямой
в пространстве (эскиз)
 Например, в первом задании: Вариант 8; А(30; 40; 15).
Например, в первом задании: Вариант 8; А(30; 40; 15). -е плоскости проекций, которые затем соответствующим образом совмещают с плоскостью чертежа.
-е плоскости проекций, которые затем соответствующим образом совмещают с плоскостью чертежа.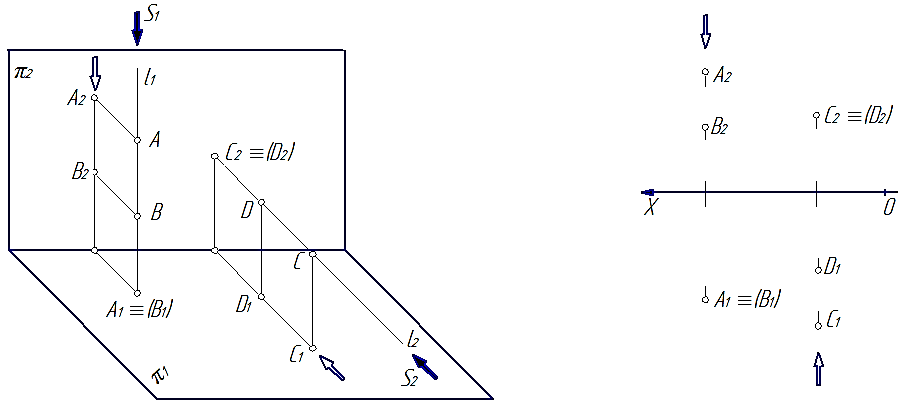 Прямые AхA1 и АхА2, являющиеся проекциями проецирующей плоскости на плоскостях проекций П1 и П2, будут перпендикулярны к оси проекций X.
Прямые AхA1 и АхА2, являющиеся проекциями проецирующей плоскости на плоскостях проекций П1 и П2, будут перпендикулярны к оси проекций X. В результате получим комплексный чертеж точки А (рис. 4), состоящий из двух проекций А1 и А2 точки А, лежащих на одной прямой, перпендикулярной к оси X. Прямая А1А2, соединяющая две проекции точки, называется вертикальной линией связи.
В результате получим комплексный чертеж точки А (рис. 4), состоящий из двух проекций А1 и А2 точки А, лежащих на одной прямой, перпендикулярной к оси X. Прямая А1А2, соединяющая две проекции точки, называется вертикальной линией связи. Основанием этому может служить отмеченное шестое свойство параллельной проекции не изменять проекции фигуры при параллельном переносе плоскости проекций.
Основанием этому может служить отмеченное шестое свойство параллельной проекции не изменять проекции фигуры при параллельном переносе плоскости проекций.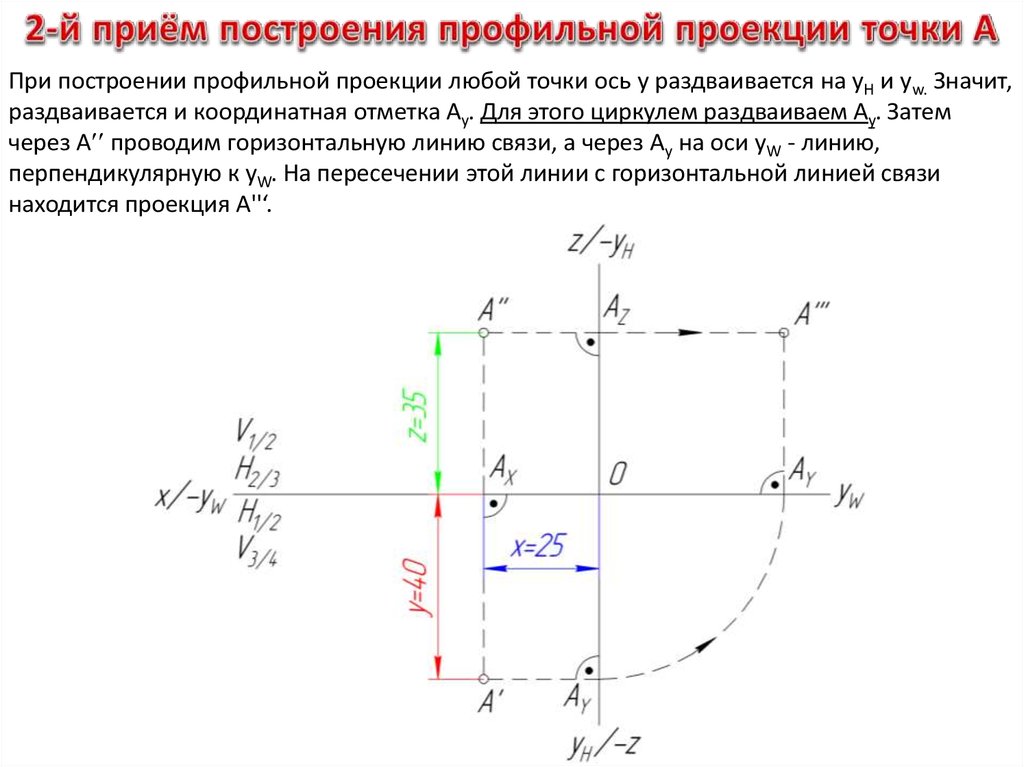 5), так же как и обратно: по расположению проекций можно судить о том, в каком квадранте лежит точка.
5), так же как и обратно: по расположению проекций можно судить о том, в каком квадранте лежит точка.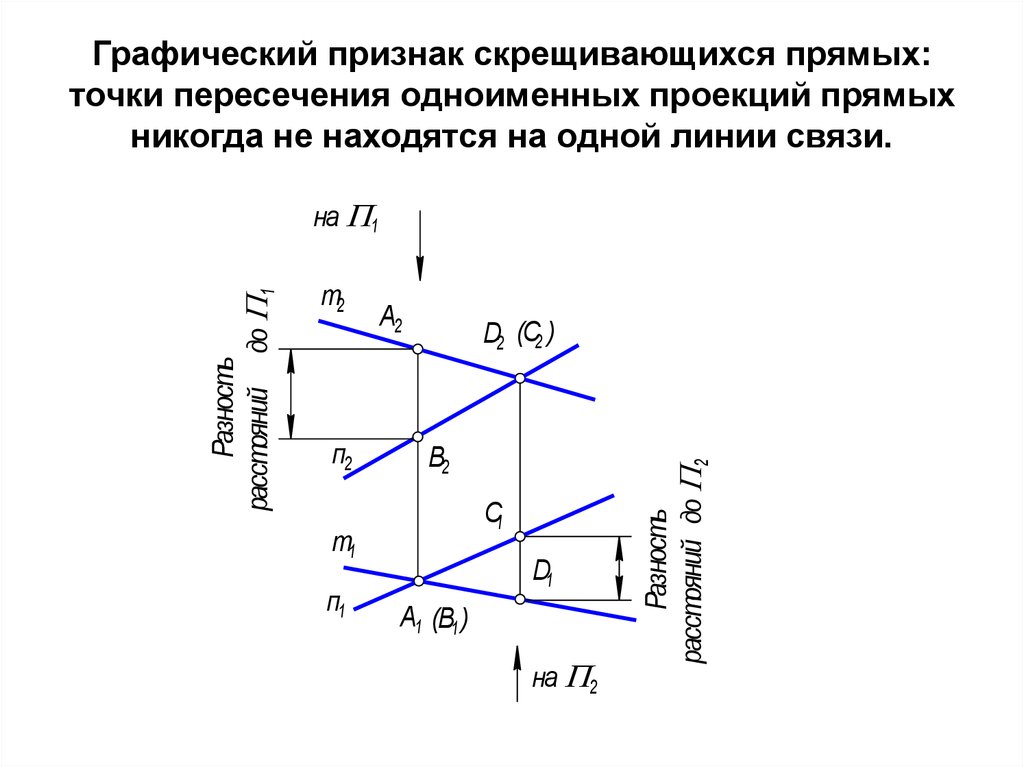 Пi (i = 1, 2, 3). Основания этих перпендикуляров (точки А1, А2, А3) и являются соответственно горизонтальной, фронтальной и профильной проекциями точки А в системе плоскостей проекций П1, П2 и П3. Заметим при этом, что проецирующие плоскости AA1A2, AA1A3 и АА2А3 перпендикулярны соответственно осям X, У, Z. Обозначив точки пересечения этих плоскостей с осями через А12, А13, А23, заметим, что как прямые A1A12 и А12А2 перпендикулярны к оси X, так и две другие пары прямых A1A13, А13А3 и А2А23, А23А3 должны быть перпендикулярны соответственно осям Y и Z. Расстояние точки А от горизонтальной плоскости проекций П1 мы назвали ранее высотой точки А, а расстояние точки А от фронтальной плоскости проекций П2 — ее глубиной; расстояние точки А от профильной плоскости проекций П3 будем называть широтой точки А.
Пi (i = 1, 2, 3). Основания этих перпендикуляров (точки А1, А2, А3) и являются соответственно горизонтальной, фронтальной и профильной проекциями точки А в системе плоскостей проекций П1, П2 и П3. Заметим при этом, что проецирующие плоскости AA1A2, AA1A3 и АА2А3 перпендикулярны соответственно осям X, У, Z. Обозначив точки пересечения этих плоскостей с осями через А12, А13, А23, заметим, что как прямые A1A12 и А12А2 перпендикулярны к оси X, так и две другие пары прямых A1A13, А13А3 и А2А23, А23А3 должны быть перпендикулярны соответственно осям Y и Z. Расстояние точки А от горизонтальной плоскости проекций П1 мы назвали ранее высотой точки А, а расстояние точки А от фронтальной плоскости проекций П2 — ее глубиной; расстояние точки А от профильной плоскости проекций П3 будем называть широтой точки А.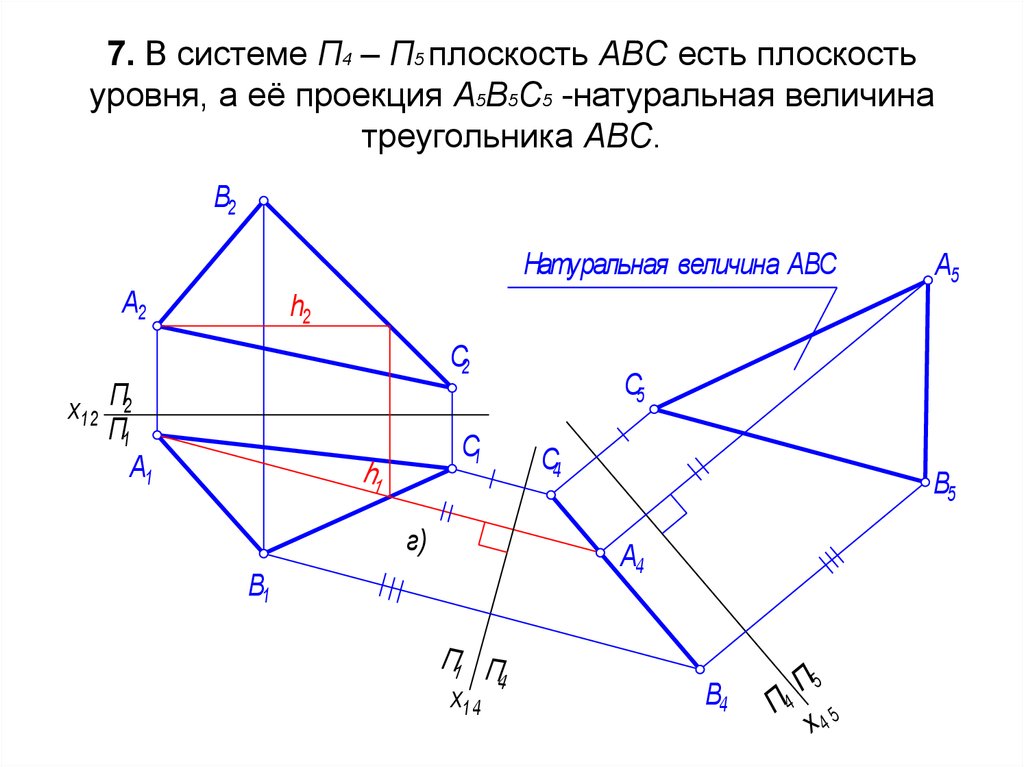 Z23, а отрезки А1А12 и А23А3 равны, ибо А1А12 = А23А3 =А2А есть глубина точки А.
Z23, а отрезки А1А12 и А23А3 равны, ибо А1А12 = А23А3 =А2А есть глубина точки А.
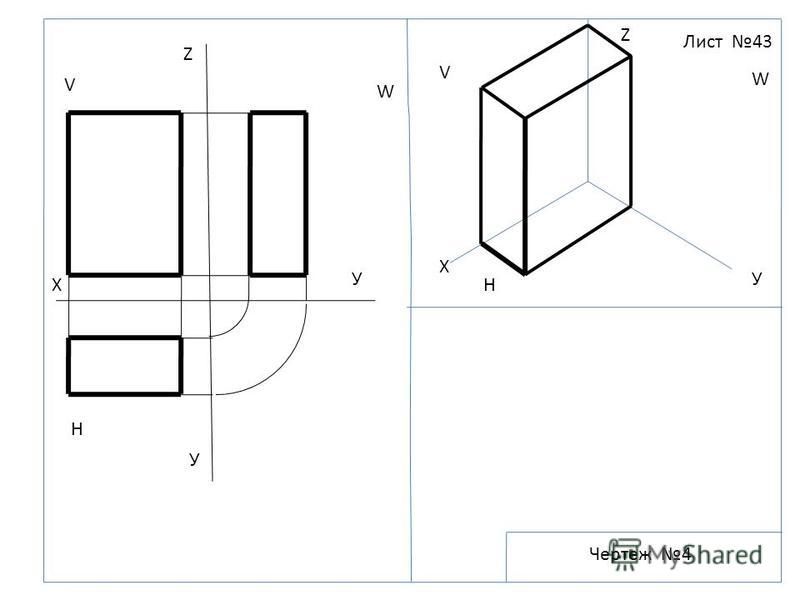 При совмещении плоскостей проекций передняя часть горизонтальной плоскости опускается вниз, а задняя поднимается вверх; передняя часть профильной плоскости удаляется от нас направо, а задняя приближается слева.
При совмещении плоскостей проекций передняя часть горизонтальной плоскости опускается вниз, а задняя поднимается вверх; передняя часть профильной плоскости удаляется от нас направо, а задняя приближается слева.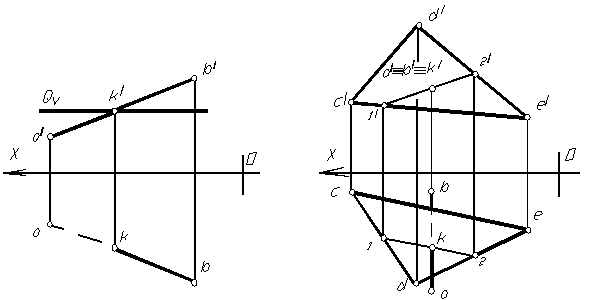 Рассмотрим трехгранник, образованный системой плоскостей проекций П1, П2 и П3. На осях X, У, Z установим единицу измерения е. За начало отсчета примем точку О пересечения трех плоскостей проекций (вершину трехгранника). Положительное направление на каждой оси установим, как показано на рис. Тогда трехгранник OXYZ можем рассматривать как прямоугольную декартову систему координат с координатными осями: Ох — ось абсцисс, Оу — ось ординат, Oz — ось аппликат.
Рассмотрим трехгранник, образованный системой плоскостей проекций П1, П2 и П3. На осях X, У, Z установим единицу измерения е. За начало отсчета примем точку О пересечения трех плоскостей проекций (вершину трехгранника). Положительное направление на каждой оси установим, как показано на рис. Тогда трехгранник OXYZ можем рассматривать как прямоугольную декартову систему координат с координатными осями: Ох — ось абсцисс, Оу — ось ординат, Oz — ось аппликат. Координаты точки называются определителем точки.
Координаты точки называются определителем точки. -я к П3 – профильно проецирующая.
-я к П3 – профильно проецирующая.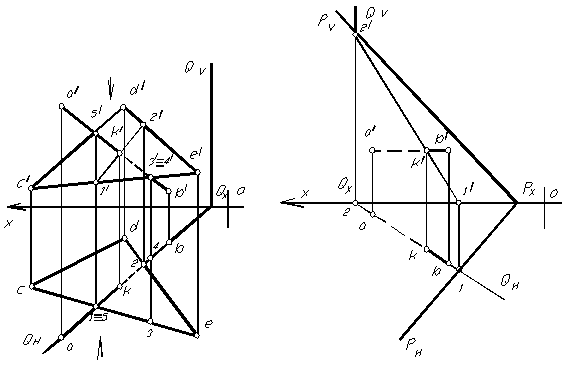 ru — Part 2
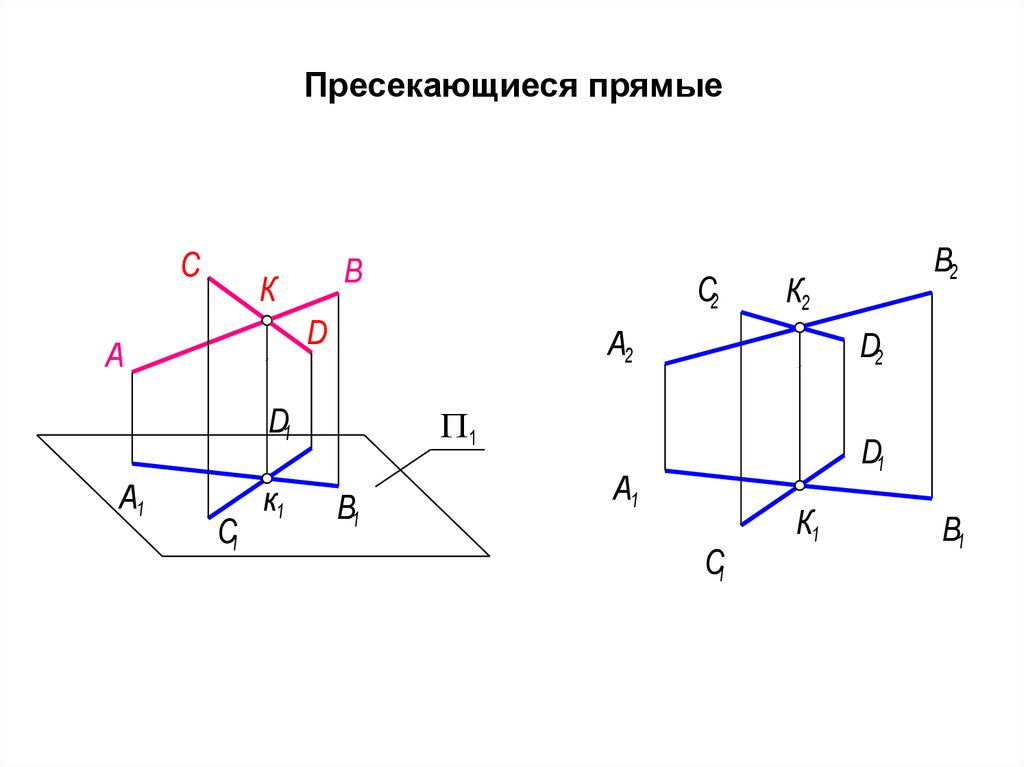
ru — Part 2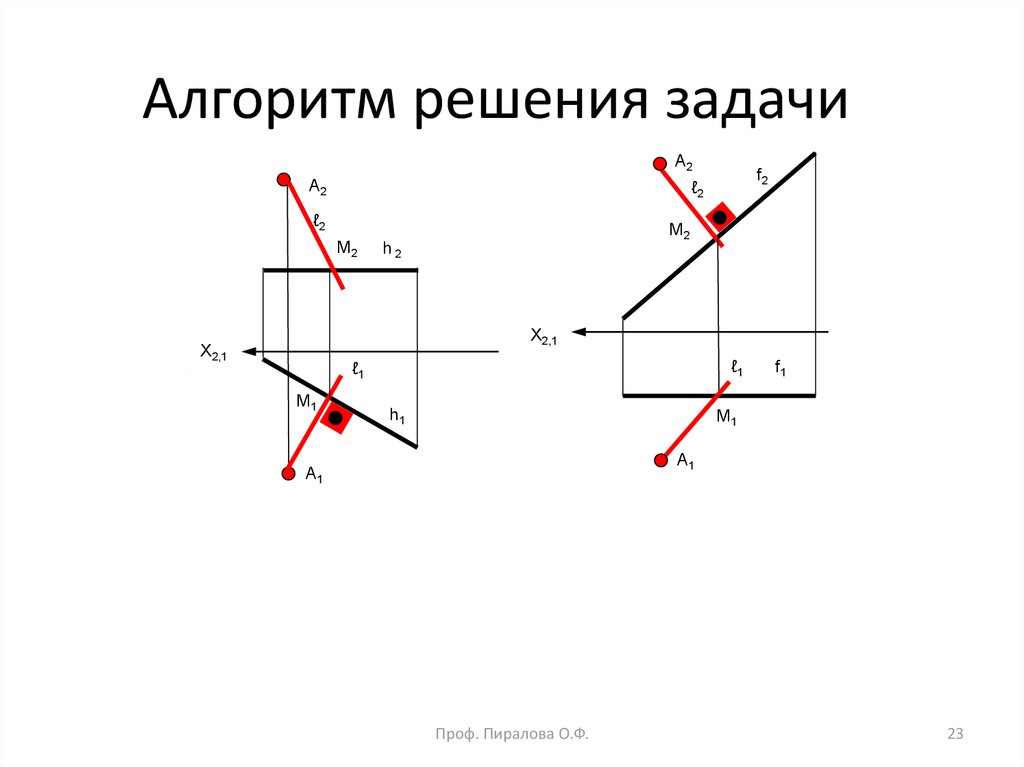 Заданной плоскости принадлежит прямая …
Заданной плоскости принадлежит прямая …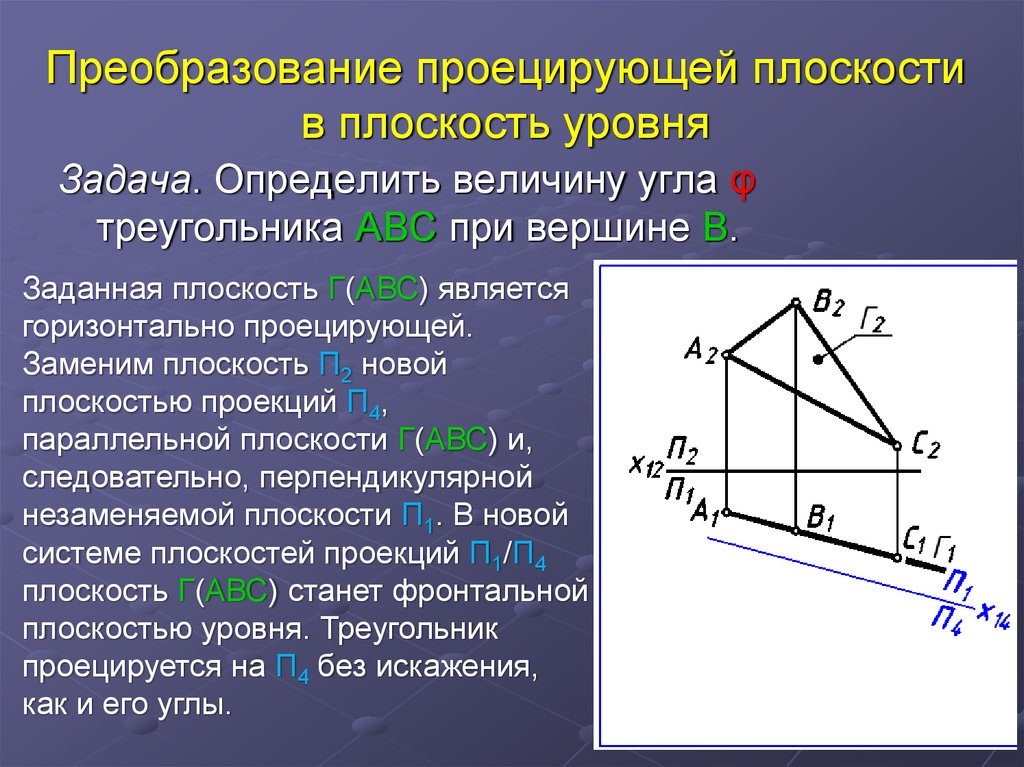

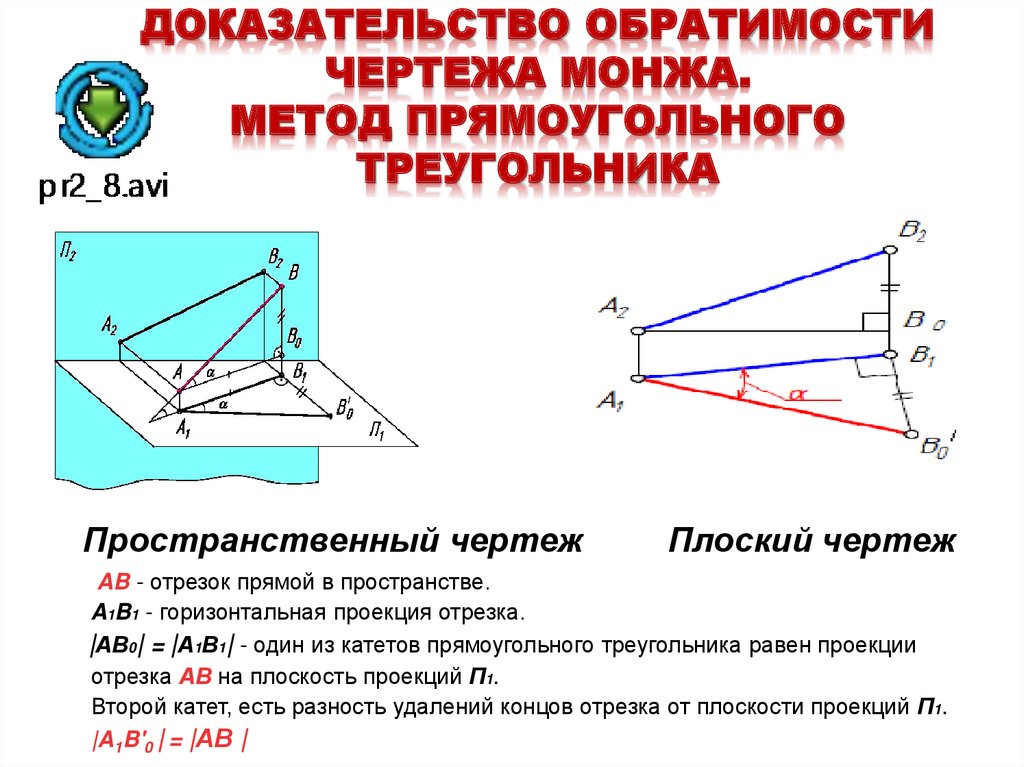
 Если в какой-то момент значение пикселя станет меньше 0, усеките его до 0.
Если в какой-то момент значение пикселя станет меньше 0, усеките его до 0. Тем не менее, случайная и предыдущая конечная точка строки связаны с начальной точкой, и им нужно только вычислить MPI для всех возможных конечных точек. В этом исследовании мы анализируем случай конечной точки предыдущей строки.
Тем не менее, случайная и предыдущая конечная точка строки связаны с начальной точкой, и им нужно только вычислить MPI для всех возможных конечных точек. В этом исследовании мы анализируем случай конечной точки предыдущей строки.
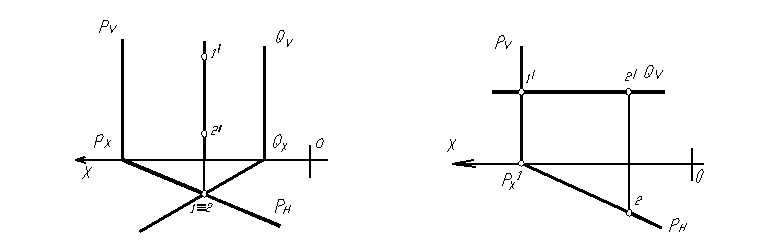 И так далее.
И так далее.
 Если мы выберем параметры высокого качества, такие как 8 уровней серого и 99 колышков (10 пикселей между штырями), мы можем получить изображение высокого качества, такое как показано ниже (7050 строк с LSE = 0,055).
Если мы выберем параметры высокого качества, такие как 8 уровней серого и 99 колышков (10 пикселей между штырями), мы можем получить изображение высокого качества, такое как показано ниже (7050 строк с LSE = 0,055). 2 Определите размер изображения
2 Определите размер изображения

 смещение относительно расположения по умолчанию.
смещение относительно расположения по умолчанию.  :
: д. — см. неофициальное справочное руководство LaTeX2e или The Not So Short Introduction to LaTeX2ε (глава 5) для получения подробной информации о доступных примитивах.
д. — см. неофициальное справочное руководство LaTeX2e или The Not So Short Introduction to LaTeX2ε (глава 5) для получения подробной информации о доступных примитивах.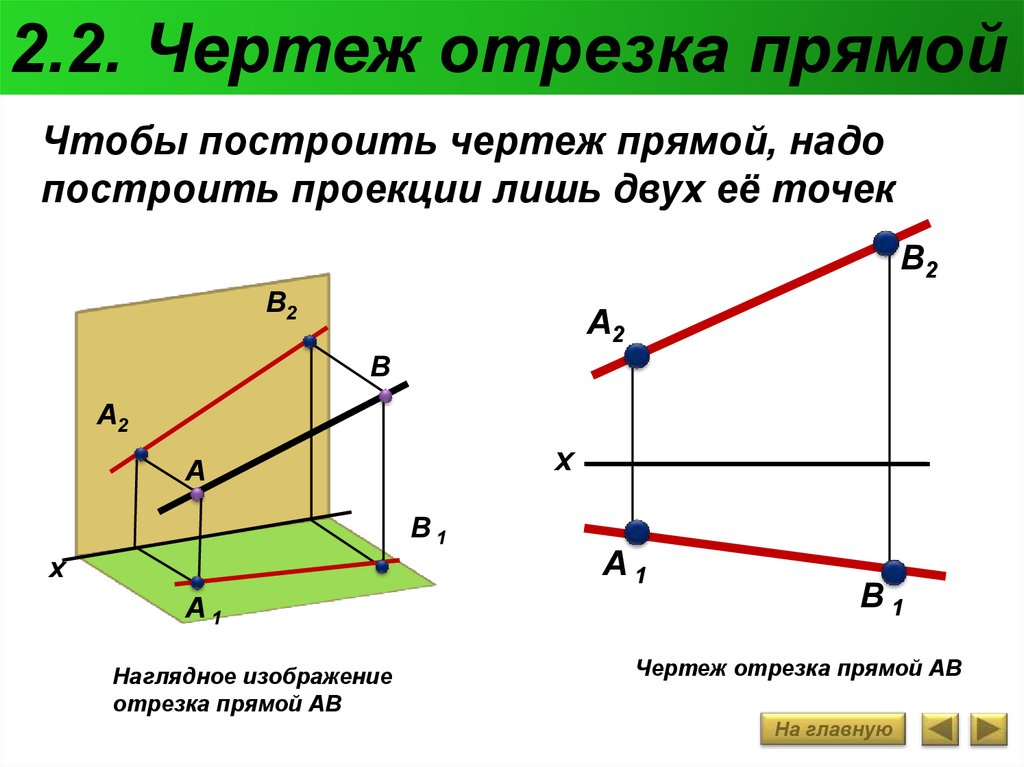
 Например, синяя точка и координата
Например, синяя точка и координата 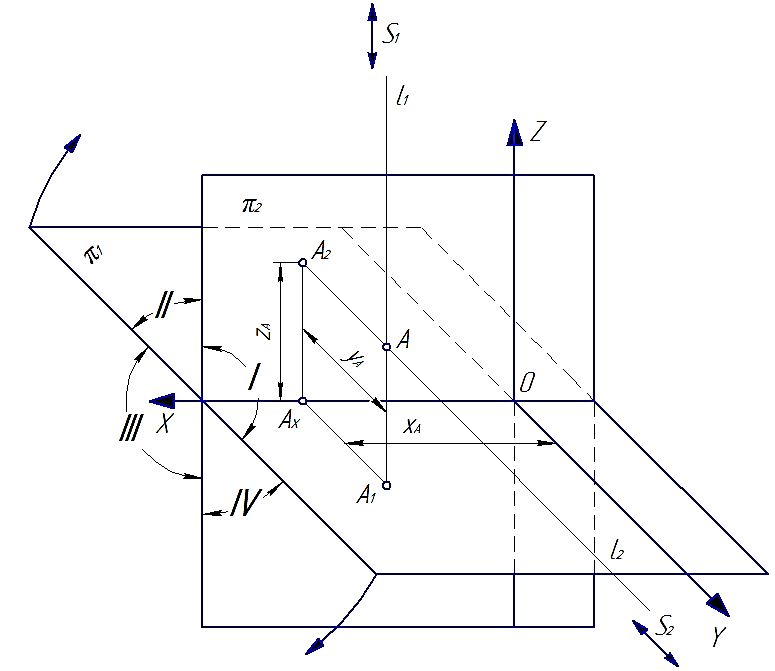 \put(0,0){\vector(2,1){4}} % для каждых 2 над этим вектором увеличивается на 1
\ положить (2,1) {\ makebox (0,0) [l] {\ первая нога}}
\ поставить (4,2) {\ вектор (1,2) {2}}
\ положить (5,4) {\ makebox (0,0) [l] {\ вторая нога}}
\ положить (0,0) {\ вектор (1,1) {6}}
\ поставить (3,3) {\ makebox (0,0) [r] {сумма \}}
\конец{картинка}
\конец{документ}
\put(0,0){\vector(2,1){4}} % для каждых 2 над этим вектором увеличивается на 1
\ положить (2,1) {\ makebox (0,0) [l] {\ первая нога}}
\ поставить (4,2) {\ вектор (1,2) {2}}
\ положить (5,4) {\ makebox (0,0) [l] {\ вторая нога}}
\ положить (0,0) {\ вектор (1,1) {6}}
\ поставить (3,3) {\ makebox (0,0) [r] {сумма \}}
\конец{картинка}
\конец{документ}
 5}} % справа
\thicklines % Использовать более толстые линии для команд \qbezier
\qbezier(2,3)(2.5,2.9)(3,3.25)
\qbezier(3,3.25)(3.5,3.6)(4,3.5)
\thinlines % Вернуться к использованию тонких линий
\ положить (2,3) {\ строка (4,1) {2}}
\put(4.5,2.5){\framebox{Правило трапеций}}
\конец{картинка}
\конец{документ}
5}} % справа
\thicklines % Использовать более толстые линии для команд \qbezier
\qbezier(2,3)(2.5,2.9)(3,3.25)
\qbezier(3,3.25)(3.5,3.6)(4,3.5)
\thinlines % Вернуться к использованию тонких линий
\ положить (2,3) {\ строка (4,1) {2}}
\put(4.5,2.5){\framebox{Правило трапеций}}
\конец{картинка}
\конец{документ}
 5)
\put(2,1){{Кривая Безье}}
\конец{картинка}
\конец{документ}
5)
\put(2,1){{Кривая Безье}}
\конец{картинка}
\конец{документ}
 2){\oval(4,2)[r]}
2){\oval(4,2)[r]}  7,0.5){$a_0$}
\ поставить (10,1) {\ круг * {0,1}}
\положить(9.7,0.5){$a_1$}
\ положить (11,1,66) {\ круг * {0,1}}
\положить(11.1,1.5){$a_3$}
\ положить (9,3) {\ строка (3,-2) {2}}
\ положить (10,1) {\ строка (3,2) {1}}
\ положить (8,1) {\ строка (1,0) {2}}
\ положить (8,1) {\ строка (1,2) {1}}
\ положить (10,1) {\ строка (-1,2) {1}}
\конец{картинка}
\конец{документ}
7,0.5){$a_0$}
\ поставить (10,1) {\ круг * {0,1}}
\положить(9.7,0.5){$a_1$}
\ положить (11,1,66) {\ круг * {0,1}}
\положить(11.1,1.5){$a_3$}
\ положить (9,3) {\ строка (3,-2) {2}}
\ положить (10,1) {\ строка (3,2) {1}}
\ положить (8,1) {\ строка (1,0) {2}}
\ положить (8,1) {\ строка (1,2) {1}}
\ положить (10,1) {\ строка (-1,2) {1}}
\конец{картинка}
\конец{документ}
 Выберите группу, а затем щелкните элемент, чтобы выбрать его.
Выберите группу, а затем щелкните элемент, чтобы выбрать его.